当前位置：文档之家 › 高中物理奥赛辅导课件全套

高中物理奥赛辅导课件全套

  • 格式：ppt
  • 大小：30.10 MB
  • 文档页数：1022

下载文档原格式

  / 254

合集下载

高中物理奥林匹克竞赛专题振动和波(共113张PPT)

高中物理奥林匹克竞赛专题振动和波(共113张PPT)

——简谐振动的 运动学方程
也可用复数表示：x(t)Aeit Aeit
计算结果一般取实部
x，q
x,q
t
t
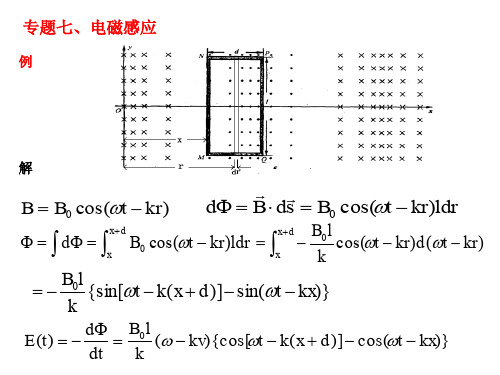
6
9、要学生做的事，教职员躬亲共做；要学生学的知识，教职员躬亲共学；要学生守的规则，教职员躬亲共守。2021/9/62021/9/6Monday, September 06, 2021 10、阅读一切好书如同和过去最杰出的人谈话。2021/9/62021/9/62021/9/69/6/2021 6:53:21 AM 11、只有让学生不把全部时间都用在学习上，而留下许多自由支配的时间，他才能顺利地学习……（这）是教育过程的逻辑。2021/9/62021/9/62021/9/6Sep-216-Sep-21 12、要记住，你不仅是教课的教师，也是学生的教育者，生活的导师和道德的引路人。2021/9/62021/9/62021/9/6Monday, September 06, 2021
You have to believe in yourself. That's the secret of success. 人必须相信自己，这是成功的秘诀。
8
2. 简谐振动的速度、加速度
由xA cots(), 得
x d d x t A s itn ) ( A c( o t s 2 ) a x d d tx 2 A c o t s) ( 2 A c o t s ()
（B）1：2 ；
（C） 3：1 ； 正确答案：（C）
（D） 2：1。
简谐振动的总能量为：E
Ek
Ep
1k 2
A2
当物体的位移为振幅的一半时
其势能为：
Ep
1kx2 1kA2
2
2 2

物理竞赛精品课件(2023版ppt)

物理竞赛精品课件(2023版ppt)

地球绕太阳公转：分 析地球公转轨道、周 期、速度等参数
02
月球绕地球公转：分 析月球公转轨道、周 期、速度等参数
03
太阳系行星运动：分 析各行星公转轨道、 周期、速度等参数
04
双星系统：分析双星 系统的形成、运动规 律等
05
黑洞与恒星运动：分 析黑洞对恒星运动的 影响
06
星系运动：分析星系 的形成、运动规律等
地球环境与天体运动的关系：天体运动的研究将有 助于我们更好地了解地球环境变化和应对气候变化
5
天体运动的总 结与反思
总结天体运动的主要内容
天体运动的基本概念：
01 包括天体、轨道、周
期、速度等
天体运动的基本规律：
02 开普勒三定律、牛顿
万有引力定律等
天体运动的计算方法：
03 轨道方程、能量守恒、
角动量守恒等
引入更多天体运动 的实际案例，提高 学生的兴趣和认知
引入天体运动的前 沿研究，提高学生 的创新意识和能力
增加天体运动实验 环节，提高学生的
动手能力
增加天体运动的互 动环节，提高学生 的参与度和积极性
谢谢
阐述天体运动的基本原理
01
01
万有引力定律：天体运动的基础， 描述物体之间的引力关系
02
02
开普勒三定律：描述天体运动的规 律，包括轨道形状、周期和速度
03
03
牛顿第二定律：描述物体运动的规 律，包括加速度、质量和力
04
04
角动量守恒定律：描述天体运动的 稳定性，包括角动量、质量和速度
2
天体运动的计 算方法
物理竞赛精品课件： 天体运动
演讲人
目录
01. 天体运动的基础知识 02. 天体运动的计算方法 03. 天体运动的典型问题 04. 天体运动的拓展应用 05. 天体运动的总结与反思

高中物理竞赛讲座课件

高中物理竞赛讲座课件


0r 2Q 4R2
dI

0r 2Q
4R2
I
5、 I nqvA
v I nqA
P mvnlA mv nlA mIl
mIl
1
v2 c2
q
1
v2 c2
q 1 ( I )2 nqAc
6、设正方形线框右、左两边载流子 的线密度和速度分别为λ 1、ｖ1、 λ 2、ｖ2，两边的洛伦兹因子分别 为γ 1和γ 2。则有
度相同，带电粒子的数密度为 n ，管内电流强度为 I 。考虑相对论效应，
试给出管内带电粒子的总动量 P ；6、用第5小题中的绝缘空心管做成的
边长为ｌ的正方形电流环取代第3小题中的圆形小电流环，设环很重，不
计其运动。环中同一截面载流子速度相同，不计载流子间相互作用。试
计算正方形环中载流子的总线动量 Phid，这个动量称为“隐藏动量”；
k
E(t) d B0l ( kv){cos[t k(x d )] cos(t kx)}
dt k
i(t) E B0l ( kv){cos[t k(x d )] cos(t kx)}
R kR
f (t) i(t)B(x,t)l i(t)B(x d,t)l
r 处的电阻率与 r 成正比,即 ρ ＝
ρ 0r ,ρ 0为常量。 磁感应强度为 B 的匀强磁场垂直于圆环平面，其方
向向上（见图）。S是电流强度为I 的恒流源，固定电阻R0 跨接在S
圆盘电动机
两端。S一端接金属轴中心 X 处，另一端用环形电刷接圆盘边缘 Y 处。
此装置可看作一圆盘电动机。设电动机空载（不带任何负载）达到稳定

2R1
(2)

高中最新辅导物理竞赛课件

高中最新辅导物理竞赛课件

m
C

rm

MR M m
MO


rM

mR Mm
(1)
2019/12/17
7
整个系统在水平面内不受力(环壁与质点之间的作 用力是一对内力）,因此动量守恒，求出质心的速度
(M
m)vC

mv0
vC

mv0 Mm
(2)
可见系统的质心沿着x轴做匀速直线运动。质心是惯
性坐标系。
qBR m
2

2Rg

3Rg cosq

qBR m

qBR 2m
2

Rg
cosq
2

qBR m
2

Rg cosq


qBR 2m
2

Rg cosq

qBR

2m
Rg(2 cosq )
又因为
0
q

2
，所以上式中

qBR 2m
2
y
m v0
M
x
O
R
2019/12/17
6
【解】质点m与环内壁之间的作用力是一对作用 反作用力，没有摩擦这个力就是与半径方向一致的 支持力，这个力不等于零，则质点就不会离开环的 内壁。
环的质量集中在环心O，初始时系统的质心C位于
y轴上，离环心的距离是OC，长度为
rC

mR Mm
质心C到质点m与环心O的距离分别是
××××v××××0××××m××××R××××Ngqb××××Oqav×××××0 B×××××××××× ×××整化 mmN为gvRv0202mqvgmq0Bvgqm0vR0qBmBvv0RB02RmgvRN02

高中物理奥林匹克竞赛 热学高级班(179张ppt)

高中物理奥林匹克竞赛 热学高级班(179张ppt)
热学
2019/10/2
1
全国中学生物理竞赛内容提要
热学
1． 分子动理论 原子和分子大小的数量级 分子的热运动和碰撞 布朗运动 ※压强的统计解释 ☆麦克斯韦速率分布的定量计算； ※分子热运动自由度 ※能均分定理； 温度的微观意义 分子热运动的动能 ※气体分子的平均平动动能 分子力 分子间的势能 物体的内能
温度的统计意义
t

3 2
kT
“温度”（宏观量）的微观实质 温度只有统计意义:
*是大量分子热运动剧烈程度的标志; *是分子平均平动动能的量度; *是统计平均值;
对个别分子,“温度”没有意义。
2019/10/2
19
道尔顿分压定律
容器中有几种气体 ，分子密度分别为：
n1 、 n2 ...…
单位体积的分子数：
规定气体状态 P0 1.013*105 pa; (1atm) v0 22.4*103 m3; (mol体积） T0＝273.150 C (摄氏零度）
定义气体普适常量
R P0v0 8.31(J /(mol K ))
2019/10/2
T0
13
理想气体状态方程
PV P0v0 T
所以
v2 3kT 3RT
m

在同一温度下，质量大的分子其均方根速率小。
2019/10/2
21
气体分子均方根速率
例： T = 273 K时，
v2 3kT 3RT
m

t
3kT5.651021J 2
H2： v21.84103m/s
O2：v2 4.61102m/s
声 速 =331.6m /s
T0
PV RT

2020年南师附中高中物理竞赛辅导课件16波(共19张PPT)

2020年南师附中高中物理竞赛辅导课件16波(共19张PPT)
23、美好的思想，没有美好的品德来陪伴，它不过是泡影。 79.活在当下，别在怀念过去或者憧憬未来中浪费掉你现在的生活。 3.有希望的地方，痛苦也成快乐。 21、生命永远是尘土中。彼此的疏忽是不必要的。你能理解的是你的身高，你无法理解的是你的真理。您可以感受到他人的辛勤工作，这是 您的道德。您不会感到别人的悲伤，也不会感到自己的责任。
r1 P r2
y 1 A 1 co t s 2r ( 1 1 )S 2 y 2 A 2 co tt ()
其中AA 1 2A 2 22A 1A 2co 2 s(12r2r1)
讨tg论 : A A11csoin s1 1(( 2 2rr1 1)) A A2 2scions2(2 (22rr22))
48.真正的价值并不在人生的舞台上，而在我们扮演的角色中。 12.你不怕困难，困难就怕你。 14.你给我一滴眼泪，我就看见了你心中全部的海洋。 24、当其他人熬夜，睡觉，其他人已经熬夜，您仍在努力再睡几分钟时，您有很多想法，但脑袋已经过去，其他人则坚持一件事。您必须读 很长时间的书。需要工作时，只需轻扫手机即可。您一定不要在早上醒来背诵单词，并且要在晚上加班直到深夜。在许多情况下，这并不是说 您平凡无所事事，而是您所付出的代价并不比其他人高。
入射线、折射线及
A2
i A1
A
B
B'
A' u 2
折射定律
C
分界面法线共面
n21：2介质对1介质的相对折射率
§16-6 波的干涉
一.波的传播规律 独立性：几列波在媒质中相遇时,各 个波将保持本身特性(频率、波长、 振动方向等)沿原方向继续传播，与 未相遇一样 叠加原理：在几列波相遇区域，任 一质点的振动为各个波单独在该点 引起的振动的合成

高中物理奥林匹克竞赛专题 波动(共90张PPT)

高中物理奥林匹克竞赛专题 波动(共90张PPT)

②.不同频率的同一类波在同一介质中波速 相同。
③.波在不同介质中频率不变。
§3 平面简谐波的波函数
用数学表达式表示波动----波函数
一、平面简谐波
·································
简谐振动在弹性介质中的传播，形成平面 简谐波。
波动是集体表现，各质点在同一时刻的振 动位移是不同的，用一个质点的振动方程代替 任意质点的振动方程。

6
10 2
cos 800
t

x 200



/
2
800
T 2 2 1 s 800 400
1 /T 400 Hz uT 200 / 400 0.5m

x u




②
2 , Tu
T
y

A
cos 2 Tt

x





③
y

A
cos
2
ut
x




Acost

2
x

④
•相距一个波长两点相位差是2
u
1 4P 7 10Q13 x
任意两质元间距为 x •相距x的任意两点的相位差
第2章 波 动 §1 机械波的产生与传播 §2波动周期、频率、波长、波速 §3平面简谐波的波函数 §4波的能量 §5惠更斯原理 §6波的干涉 §7 驻波 §8 多普勒效应
§1 机械波的产生与传播
一、机械波 机械振动在弹性介质中传播形成机械波。
二、机械波产生的条件 1.振源 2.弹性介质

高中物理竞赛讲义PPT课件

高中物理竞赛讲义PPT课件

B1 B
三个质点相遇？
解析：根据题意，三质点均做等速率曲线运动，而且任意时刻
三个质点的位置分别在正三角形的三个顶点上，但是这个正三角 形的边长不断缩小，如图所示。现把从开始到追上的时间t分成n
个微小时间间隔△t（△t→0），在每个微小时间间隔内，质点的 运动可以近似为直线运动。于是，第一个末三者的位置A1、B1、 C1如图所示。这样可依次作出以后每经△t，以三个质点为顶点组
例2 如图所示，一个质量均 匀、半径为R、质量密度为σ 的薄板。现沿着一条半径挖去 其中半径为R/2的圆形薄板， 求剩余薄板的质心位置。
R
R/2
●
●
O
质心在原来圆心、挖去薄板圆心所在的直径 上，在圆心O的另一侧，与O点距离为 R/6.
例3 如图所示，一根细长轻质硬棒上等距离地固定着n 个质量不等的质点小球，相邻两个小球之间的距离为a。已 知最左端小球与左端点之间距离也为a，它的质量为m，其 余各球的质量依次为2m、3m、……，一直到nm。求整个 体系的质心位置到左端点的距离。
斜面上放上一块质量为m的滑块B。现将系统由静止释放，求释
放后劈A对物块B的压力、劈A相对地面的加速度各是多少？
（不计一切摩擦）
解析方法1：－牵连加速度
对A, Nsinθ=MaA,
(1)
对B, Nsinθ=maBx,
(2)
mg－Ncosθ=maBy, (3)
A、B加速度关联,
aBy = (aBx+aA)tanθ (4)
（2）若面物体上各质点速度不等，质心将沿曲线运动， 平面物体在空间扫出一个不规则体积。定理可证成立。
例4 一直角三角形板质量分布均匀，两直角边长度分别 为a和b，求质心位置。

高中物理 奥赛(运动学)课件

高中物理 奥赛(运动学)课件

A1 S2
A2
图2
S3
A3 θ
x
碰撞后的速度为v0,与
y轴的夹角为θ，那么
v0 2gh , v0x v0 sin , v0y v0 cos
23
v0 2gh
v0x v0 sin
y v0
θθ
v0 y v0 cos
A
S1
小球空中运动的加速度为
A1 S2
A2 S3
ax g sin , ay g cos 图2
、C，从t＝0开始相互追逐，运动
速率都是v.追逐过程中，A始终向着
当时B所在位置运动，B始终向着当
时C所在位置运动，C始 终向着当时A所在位置运
动. 试问试问这三个小孩
A
●
v
d
d
v
何时相遇在一起？开始时 ● B
他们的加速度大小是多少
vd 图7
●
C
？
8
8.如图8所示，线轴沿水平面做无滑滚动， 并且线端A点的速度为v，方向水平. 以铰链 固定在B点的木板靠在线轴上，线轴的内、 外半径分别为r和R，试求木板的角速度ω 与角α的关系.
S
1 2
gtv0
cos
而小球的水平射程为 L v0 cos t
v0
θ
h
图1 v0
θ β
gt v 图2
28
S
1 2
gtv0
cos
所以有
L 2S g
L v0 cos t
v0 θ β
gt v
这表明只要S最大，则水平射程L就最大.
图2
由于三角形两边v0、v的大小都是恒量，所以当它 们的夹角为90°时，三角形的面积最大.即当

高中物理奥赛入门讲座课件(共33张PPT)

高中物理奥赛入门讲座课件(共33张PPT)
• 参加复赛的学生由地方竞委会根据决赛成绩确 定。参加复赛理论考试的人数不得少于本赛区 一等奖名额的5倍。参加复试实验考试人数不得 少于本赛区一等奖名额的的1.2倍。
考试时间：
初赛：每年九月第一个星期天考试。全国命题，各市、 县组考，市统一阅卷，选前30名（左右）参加（全省） 复赛。
复赛：九月下旬考试。全省命题，各省组织。理论考 试前20名参加试验考试，取理论、试验考试总分前10名 者参加省集训队。集训队成员经短期培训后推荐3~7名 参加（全国）决赛。 决赛：全国统一组织。按成绩挑选15~25名参加国家集 训队，到有关大学强化训练，最后从中选拔5名优秀队 员参加IPhO。
宋雪洋--第14届亚洲杯物理奥林匹克竞赛金牌得主
（全国中学生物理竞赛决赛获第一名）
“选择物理是兴趣使然，我觉得，一路走过来也遇到过困难， 如果没有兴趣和信念所支撑，而是仅仅靠父母或老师的督促，我 肯定走不到今天。”
李佳宸--第16届亚洲物理学奥林匹克竞赛金牌（第三名）
复赛湖南第 2名； 全国决赛第 47名，（湖 南第3名）； 亚赛获评最 佳女选手
林心悦--跟在她后面的72位选手都是男生
（全国中学生物理竞赛决赛获第一名）
首先要适当控制情绪，这是 为理性思维的培养奠定基础。 “统筹规划好每件小事。每 天早上醒来，我会躺在床上 先把今天要做的事情在脑子 里过一遍，具体到要完成哪 些作业，需要花多少时间。 特别是双休日，不要心血来 潮就跑去看电视。”
2、国家（Chinese Physics Olympiad简称CPhO） ①1984年以前，中学物理竞赛经常举行，但被
冠以各种名称，无论是组织，还是考纲、知识体系 都谈不上规范。
② 1984年开始第一届CPhO，此后每学年举办 一届

高中物理奥林匹克竞赛专题课件第11章 机械波(共83张PPT)

高中物理奥林匹克竞赛专题课件第11章 机械波(共83张PPT)

0.4m
T 0.01s
u 0.4 40m/s
T 0.01


1 T
100Hz
0
22
解法2 由物理量的物理意义求各物理量
A不变 A 0.02m
?
同一时刻t 波线上 位相差为 2 的两点之间的距离
5x2 200t 5x1 200t 2
了波的传播问题，称为惠更斯原理。 菲涅耳在光学方面做了重要发展， 称惠－菲原理 经基尔霍夫在数学上描述 发展成“光传播”的重要计算手段
所以说：在研究波的传播问题中 波动方程和惠更斯原理同等重要，相互补充3。7
2、惠更斯原理 基本内容： •子波概念 波面上任一点都是新的振源
发出的波叫子波 •子波面的包络线 -- 新波面
解：由t=2s时的波形图
ym
0.5
t 2s u
2m T / u 2/ 0.5 4s
o
1
2 xm
2 / T / 2 rad/s
（看下一时刻的波形曲线）
t 2, x 0 y 0
0
3 2
y
A
t=2s时在原点x=0处的位相：
3
第十一章
机械波
1
第十一章 机械波
§11.1 §11.2 §11.3
机械波的产生和传播 平面简谐波的波函数 波的能量 波的强度
§11.4 惠更斯原理与波的反射和折射
§11.5 波的叠加 波的干涉 驻 波
§11.6 多普勒效应
2
§11.1 机械波的产生和传播
一、机械波产生的条件
波源（振源） 弹性介质（媒质）
ym
0.5
t 2s u

高中物理奥林匹克竞赛专题绪论(共18张PPT)

高中物理奥林匹克竞赛专题绪论(共18张PPT)
展的基础上，其标志是发电机、电动机、电讯设备的 出现和应用。
发电机
手机
15▲第– 三8次多工普业革勒命效（应20世纪）：建立在第相十对五论章和机量械子波
力学发展的基础上，其标志是以信息技术为代表的一 系列新材料、新能源、新技术的兴起和发展。
激光器
纳米技术
15 – 8 多普勒效应
▲ 物理学的发展
第十五章 机械波
第十五章 机械波
-- 物理学的初级阶段
物理竞赛
力热
学
学
学
电 磁
机械 分子 运动 运动 规律 规律
电磁 运动 规律
光量
相
学
学
子 物
光运 理
动的
规律
微观 领域 的运 动规 律
对 论
高速 领域 的运 动规 律
15 – 8 多普物勒理效学应的研究方法 第十五章 机械波
▲ 物理学是一门理论和实验高度结合的精确 科学，其研究方法可概括为：
提出命题
观测、实验
推测答案
理论预言 实验检验
应用
修改理论
15 – 8 多普勒效应
第十五章 机械波
物理学还有许多有特色的方法，比如：
▲ 对称性分析 ▲ 守恒量的利用 ▲ 简化模型的选取 ▲ 概念和方法的类比
物理的直觉和想象力及 洞察力也常常产生重大 突破和发现
▲ 定性和半定量分析 ▲ 量纲分析 ▲ 能量分析
15 – 8 多普勒效应
第十五章 机械波
1 世界的物质性 物多间普存勒在相效互应作用
第十五章 机械波
引力相互作用
mM f引 G r 2
原子核
引力10-34N
电磁相互作用
qQ f电 k r 2 电力102 N
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

相对运动与伽利略变换
relative motion and Galileo transformation
第一节质点运动的描述 1-1
Description of particle motion
固联在参考系上的正交数轴组成的系统，可定量描 述物体的位置及运动。如直角坐标系、自然坐标系等。
坐标系 θ
印刷
j
0
x
X
= x
+y
i 、j 分别为 X、Y 轴的
单位矢量（大小为1，方向 分别沿 X、Y 轴正向）。
在课本中惯用印刷形式。
在本演示课件中，为了 配合同学做手书作业，采 用手书形式。
矢量加法
服从平行四边形法则 为邻边 若 则 为对角线
反向为
减法相当于将一矢量反向后再相加。
矢量乘法
两矢量的点乘 = 两量大小与它们夹角余弦的乘积
一质点作曲线运动，
（ 1）
aτ 表示切向加速度， （3）
下列四种表达式中， 正确的是
（请点击你要选择的项目）
r 表示位矢， s 表示路程， v 表示速度，
（ 2）
（ 4）
（链接2）
一质点作曲线运动，
（ 1）
aτ 表示切向加速度， （3）
下列四种表达式中， 正确的是
（请点击你要选择的项目）
r 表示位矢， s 表示路程， v 表示速度，
刚体中任 一点 (t+△t) (t) 参考 方向
2. 角位移
描述刚体转过的大小和方向
转动平面（包含p并与转轴垂直） 转轴
3. 角速度
描述刚体转动的快慢和方向，
是转动状态量。
常量 匀角速
静止 常量 变角速
用矢量表 示 或 时，它们 与 刚体的 转动方向 采用右螺 旋定则
续参量
角加速度 14 . . 角位置
运动学
本章内容
质点运动的描述
description of particle motion
Contents
chapter 1
质点运动的两类基本问题
two basic kinds of particle motion problem
圆周运动及刚体转动的描述
descriptions of circular motion and rigid body motion
aτ
R = 0.1 m
关键是设法求 角速率 本题很易求
其运动学方程为
θ = 2 + 4 t 3 (SI)
t = 2 s 时， 质点的
切向加速度 法向加速度
12 t
24 t
t=2
48 (rad· s-1) 12 t 48 (rad· s-2) 4.8 ( m ·s-2 )
（备选例三）
（备选例四）
（续选例四）
（备选例五）
第三节圆周、刚体运动
1-3
一质点A作圆周运动
descriptions of circular motion and rigid body motion
约定：反时针为正
角坐标、角位移
约定：反时针为正
角速度
角加速度
一般方法
求解圆周运动问题的一般方法
卫星
r
φ
运动质点
切线 法线
自然坐标系
由运动曲线上任 一点的法线和切
线组成
n
τ
矢量知识
有大小、有方向，且服从平行四边形运算法则的量。
线段长度（大小）；箭头（方向）。
A
手书 印刷
A
（附有箭头） （用黑体字，不附箭头）
矢量表示式 在 X-Y 平面上的某矢量 A 该矢量
Y
A 的坐标式
手书
y
A i
A = xi +yj
角线量关系
证明题
续证明
角线关系简例
刚体及其平动
刚 体
形状固定的质点系（含无数
质点、不形变、理想体。）
平 动
刚体任意两点的连线保持方 向不变。各点的 相同，可当作质点处理。
刚体定轴转动
刚体的定轴转动
刚体每点绕同一 轴线作圆周运动， 且该转轴空间位置 及方向不变。
定轴转动参量
1. 角位置
描述刚体（上某点）的位置 刚体定轴转动 的运动方程 刚体
两矢量点乘的结果是标量 在直角坐标中 等于对应坐标乘积的代数和 例如
叉乘
两矢量叉乘的结果是矢量 大小 方向 垂直于两矢量决定的平面，指向
的方向
两矢量所在平面
按右螺旋从叉号前的矢量沿小于 角转向叉号后矢量的旋进方向。
若
的空间坐标式为
用一个三阶行列式 表示
位置矢量
动学方程
随时 间变化
其投影式
称为
的曲率半径
ρ
30 º
由法向加速度大小
最高点处
cos30º
得
20× 9.8
30.6(m)
（备选例一）
（备选例二）
随堂小议
一质点作曲线运动，
（ 1）
aτ 表示切向加速度， （3）
下列四种表达式中， 正确的是
（请点击你要选择的项目）
r 表示位矢， s 表示路程， v 表示速度，
（ 2）
（ 4）
（链接1）
描述刚体转动状态改变 描述刚体（上某点）的位置 的快慢和改变的方向 刚体定轴转动 的运动方程 刚体
刚体中任 一点 (t+△t) (t) 参考 方向
2. 角位移
匀角速 常量 匀角加速
转动平面（包含p并与转轴垂直） 转轴
常量 变角加速 描述刚体转过的大小和方向
只有 同描述刚体转动的快慢和方向， 和反 两个方向，故
（ 2）
（ 4）
（链接3）
一质点作曲线运动，
（ 1）
aτ 表示切向加速度， （3）
下列四种表达式中， 正确的是
（请点击你要选择的项目）
r 表示位矢， s 表示路程， v 表示速度，
（ 2）
（ 4）
（链接4）
一质点作曲线运动，
（ 1）
aτ 表示切向加速度， （3）
下列四种表达式中， 正确的是
（请点击你要选择的项目）
r 表示位矢， s 表示路程， v 表示速度，
（ 2）
（ 4）
第二节 两类问题
1-2
由初始条件定积分常量
随堂练习一
跳伞运动员下落加速度大小的变化规律为
随堂练习二
式中 均为大于零的常量 及 时
任一时刻运动员下落速度大小
的表达式
注意到
由
对本题的一维情况有
得
分离变量求积分
（备选例一）
（备选例二）
参 数方程
位移
平均速度
瞬时速度
平均加速度
瞬时加速度
自然坐标系
速度加速度
切向加速度
法向加速度
物理量小结
由运动学方程 投影式 消去 随堂练习一
得轨迹方程 由 运动学方程 坐标式
运动学方程投影式
位矢 质点的轨迹方程 ； 第 2 秒 末的位矢； 第 2 秒 末的速度
和加速度 。
随堂练习二 足球运动轨迹最高点处
3. 角速度 定轴转动的
是转动状态量。 也可用标量
静止
常量 变角速 常量 匀角速 中的正和负表方向代替矢量。
用矢量表 示 或 时，它们 因刚体上任意两点的 与 刚体的 转动方向 距离不变，故刚体上各点 采用右螺 的 相同。旋定则
若由 a τ 随堂练习
an an
关键是设法求 线速率
若由
一质点作圆周运动 半径

相关主题