静态查找表二叉排序树平衡二叉树(AVL树)小结B树哈希表

第九章查找一、选择题1•若查找每个记录的概率均等，则在具有n 个记录的连续顺序文件中采用顺序查找法查找一个记录，其平均查找长度ASL 为()。

A ．(n-1)/2B.n/2C.(n+1)/2D.n 2. 下面关于二分查找的叙述正确的是()A. 表必须有序，表可以顺序方式存储，也可以链表方式存储C.表必须有序，而且只能从小到大排列B. 表必须有序且表中数据必须是整型，实型或字符型D.表必须有序，且表只 能以顺序方式存储3. 用二分(对半)查找表的元素的速度比用顺序法() A. 必然快B.必然慢C.相等D.不能确定4. 具有12个关键字的有序表，折半查找的平均查找长度()A.3.1B.4C.2.5D.55．当采用分块查找时，数据的组织方式为()A. 数据分成若干块，每块内数据有序B. 数据分成若干块，每块内数据不必有序，但块间必须有序，每块内最大(或最小)的数据组成索引块C. 数据分成若干块，每块内数据有序，每块内最大(或最小)的数据组成索引块D. 数据分成若干块，每块(除最后一块外)中数据个数需相同6. 二叉查找树的查找效率与二叉树的((1))有关,在((2))时其查找效率最低(1) ：A.高度B.结点的多少C.树型D.结点的位置(2) :A.结点太多B.完全二叉树C.呈单枝树D.结点太复杂。

7. 对大小均为n 的有序表和无序表分别进行顺序查找，在等概率查找的情况下，对于查找失败,它们的平均查找长度是((1)),对于查找成功,他们的平均查找长度是((2))供选择的答案:A.相同的B.不同的9．分别以下列序列构造二叉排序树，与用其它三个序列所构造的结果不同的是()A ．(100，80，90，60，120，110，130)B.(100，120，110，130，80，60，90) C. (100，60，80，90，120，110，130)D.(100，80，60，90，120，130，110)10. 在平衡二叉树中插入一个结点后造成了不平衡，设最低的不平衡结点为A,并已知A 的左孩子的平衡因子为0右孩子的平衡因子为1，则应作()型调整以使其平衡。

常见的数据结构模型数据结构是计算机科学中重要的基础知识，用于组织和存储数据以便有效地操作和访问。

常见的数据结构模型包括线性结构、树状结构、图状结构和哈希结构。

1.线性结构：线性结构是最简单、最常见的数据结构模型之一，它是一组数据元素按照特定次序排列而成的数据结构。

其中最基本的线性结构是数组和链表。

-数组：数组是一种连续存储的线性结构，所有元素在内存中占用一段连续的地址空间，通过索引值可以快速访问元素。

数组的大小固定，并且插入、删除元素较为复杂。

-链表：链表由节点组成，每个节点包含一个数据元素和一个指向下一个节点的指针。

链表可以分为单向链表、双向链表和循环链表等多种形式。

链表的大小可变，插入、删除元素操作较为简单，但访问元素需要遍历链表。

2.树状结构：树状结构是一种非线性的数据结构，它由节点和边组成，每个节点可以有多个子节点。

树状结构常用来表示层次关系，常见的树状结构包括二叉树、堆、平衡二叉树和B树。

-二叉树：二叉树是一种特殊的树结构，每个节点最多有两个子节点。

二叉树可以分为普通二叉树、满二叉树和完全二叉树等多种形式。

-堆：堆是一种特殊的二叉树，对于任意节点N，N的父节点的值大于等于（或小于等于）N的左右子节点的值。

堆常用于实现优先队列等数据结构。

-平衡二叉树：平衡二叉树是一种特殊的二叉树，它的左右子树的高度差不超过1、平衡二叉树常用于提高查找、插入和删除操作的效率，例如AVL树和红黑树等。

-B树：B树是一种多路树，每个节点可以有多个子节点。

B树常用于存储大量数据的数据库和文件系统等场景，可以有效地减少磁盘I/O次数。

3.图状结构：图状结构是一种由节点和边组成的非线性数据结构，节点之间可以有多个关系。

图状结构常用于表示网络、社交关系等复杂的实际问题。

-有向图：有向图中每条边都有一个方向，表示从一个节点到另一个节点的有向关系。

-无向图：无向图中每条边没有方向，表示节点之间的无向关系。

-加权图：加权图中每条边都有一个权值，表示节点之间的带权关系。

大纲一、考试性质本考试是为在计算机专科生中招收本科生而实施的具有选拔功能的水平考试，其指导思想是既要有利于国家对高层次人材的选拔，又要有利于促进高等学校各类课程教学质量的提高，考试对象为2003年参加专升本考试的考生。

二、考试的基本要求要求学生比较系统地理解数据结构的基本概念和基本知识，掌握表、栈、队列、树和图等数据结构的基本特征和在计算机上实现的方法，要求考生具有抽象思维能力、逻辑推理能力、综合运用所学的知识分析问题和解决问题的能力，以及软件设计和编程能力。

三、考试方法和考试时间考试方法为闭卷笔试，考试时间为120分钟。

四、考试内容和要求1、绪论考试内容:数据结构基本概念和术语，算法、算法的描述和算法分析。

考试要求（1）了解非数值问题的数学模型不是数学方程，而是表、树和图之类的数据结构。

（2）理解数据、数据元素、数据对象、数据结构和数据类型等的定义。

（3）掌握数据的逻辑结构和存储结构及其种类；算法的重要特征等。

（4）会根据语句的最大频度计算算法的时间复杂度的方法。

2、线性表考试内容:线性表的定义、线性表的逻辑结构、线性表的顺序存储结构和链式存储结构，单向链表、循环链表和双向链表，一元多项式的表示及相加。

考试要求（1）了解线性表的定义和线性结构的特点。

（2）理解线性表的顺序存储和链式存储，理解数组与单链表表示表的优缺点。

（3）掌握线性顺序表中数据元素的存储位置的计算，顺序表、单向链表、循环链表和双向链表的插入、删除等有关操作。

（4）会用单链表编写插入、删除等有关算法。

（5）能够从时间和空间复杂度的角度综合比较两存储结构的特点及适用场合。

3、栈和队列考试内容:栈的定义、栈的表示和实现；队列的定义、队列的表示和实现，链队列、循环队列。

考试要求（1）了解栈和队列的定义。

（2）理解线性表、栈和队列特点及区别，栈对实现递归过程的作用。

（3）掌握顺序栈、链栈的入栈和出栈操作，顺序队列、链队列的入队和出队操作，循环队列的队空和队满的判断。

AVL树与B树的比较数据结构中的平衡树对比在数据结构中，平衡树是一种常见的数据结构，用于在插入和删除操作时保持树的平衡，以确保检索效率。

AVL树和B树都是常见的平衡树结构，它们在不同场景下有着各自的优势和特点。

本文将对AVL 树和B树进行比较，探讨它们在数据结构中的应用和区别。

### AVL树AVL树是一种自平衡二叉搜索树，它的特点是任意节点的左右子树高度差不超过1。

当在AVL树中进行插入或删除操作时，系统会通过旋转操作来保持树的平衡。

AVL树的平衡性能较好，适用于对读操作较多的场景。

#### 优点1. **平衡性好**：AVL树能够保持树的平衡，确保检索效率稳定。

2. **适用于静态数据集**：适合对静态数据集进行频繁的搜索操作。

#### 缺点1. **频繁的旋转操作**：在插入和删除操作时，可能需要频繁进行旋转操作，影响性能。

2. **空间需求较大**：由于需要存储额外的平衡因子，占用的空间较大。

### B树B树是一种多路搜索树，常用于文件系统和数据库中。

B树的特点是每个节点可以包含多个子节点，节点中的关键字按顺序排列。

B树的平衡性是通过调整节点的大小和结构来实现的，适用于对写操作较多的场景。

#### 优点1. **适用于磁盘存储**：B树适合在磁盘存储中进行数据检索，减少磁盘I/O次数。

2. **写操作效率高**：B树的平衡性能较好，适合对数据频繁进行插入和删除操作。

#### 缺点1. **平衡性相对较差**：相比AVL树，B树的平衡性能略逊一筹。

2. **节点结构复杂**：B树的节点结构较为复杂，实现和维护相对困难。

### AVL树与B树的比较1. **平衡性能**：AVL树的平衡性能优于B树，适合对静态数据集进行频繁的搜索操作；而B树适合对写操作较多的场景，能够减少磁盘I/O次数。

2. **空间需求**：AVL树由于需要存储额外的平衡因子，空间需求较大；而B树的节点结构较为复杂，实现和维护相对困难。

C#与数据结构--树论--平衡⼆叉树（AVLTree）介绍我们知道在⼆叉查找树中，如果插⼊元素的顺序接近有序，那么⼆叉查找树将退化为链表，从⽽导致⼆叉查找树的查找效率⼤为降低。

如何使得⼆叉查找树⽆论在什么样情况下都能使它的形态最⼤限度地接近满⼆叉树以保证它的查找效率呢？前苏联科学家G.M. Adelson-Velskii 和 E.M. Landis给出了答案。

他们在1962年发表的⼀篇名为《An algorithm for the organization of information》的⽂章中提出了⼀种⾃平衡⼆叉查找树（）。

这种⼆叉查找树在插⼊和删除操作中，可以通过⼀系列的旋转操作来保持平衡，从⽽保证了⼆叉查找树的查找效率。

最终这种⼆叉查找树以他们的名字命名为“AVL-Tree”，它也被称为平衡⼆叉树（Balanced Binary Tree）。

这⾥所说的平衡使我们想到了中庸之道，但有句话说得好，“中不偏，庸不易”。

学会这种平衡术是⼀个相当痛苦的过程。

什么是平衡为了保证平衡，AVL树中的每个结点都有⼀个平衡因⼦（balance factor，以下⽤BF表⽰），它表⽰这个结点的左、右⼦树的⾼度差，也就是左⼦树的⾼度减去右⼦树的⾼度的结果值。

AVL树上所有结点的BF值只能是-1、0、1。

反之，只要⼆叉树上⼀个结点的BF的绝对值⼤于1，则该⼆叉树就不是平衡⼆叉树。

图1演⽰了平衡⼆叉树和⾮平衡⼆叉树。

AVL树的构造如何构造⼀棵平衡⼆叉树呢？动态地调整⼆叉查找树平衡的⽅法为：每插⼊⼀个结点后，⾸先检查是否破坏了树的平衡性，如果因插⼊结点⽽破坏了⼆叉查找树的平衡，则找出离插⼊点最近的不平衡结点，然后将该不平衡结点为根的⼦树进⾏旋转操作，我们称该不平衡结点为旋转根，以该旋转根为根的⼦树称为最⼩不平衡⼦树。

失衡状态可归纳为4种，它们对应着4种旋转类型。

下⾯使⽤了Flash动画演⽰了这四种旋转类型，请确保你的电脑安装了Flash8.0以上版本的播放器，并且浏览器允许使⽤Flash。

以二叉树或树作为表的组织形式，称为树表，它是一类动态查找表，不仅适合于数据查找，也适合于表插入和删除操作。

常见的树表：二叉排序树平衡二叉树B-树B+树9.3.1 二叉排序树二叉排序树（简称BST）又称二叉查找（搜索）树，其定义为：二叉排序树或者是空树，或者是满足如下性质（BST性质）的二叉树：❶若它的左子树非空，则左子树上所有节点值（指关键字值）均小于根节点值；❷若它的右子树非空，则右子树上所有节点值均大于根节点值；❸左、右子树本身又各是一棵二叉排序树。

注意：二叉排序树中没有相同关键字的节点。

二叉树结构满足BST性质：节点值约束二叉排序树503080209010854035252388例如:是二叉排序树。

66不试一试二叉排序树的中序遍历序列有什么特点？二叉排序树的节点类型如下：typedef struct node{KeyType key;//关键字项InfoType data;//其他数据域struct node*lchild,*rchild;//左右孩子指针}BSTNode;二叉排序树可看做是一个有序表，所以在二叉排序树上进行查找，和二分查找类似，也是一个逐步缩小查找范围的过程。

1、二叉排序树上的查找Nk< bt->keybtk> bt->key 每一层只和一个节点进行关键字比较！∧∧p查找到p所指节点若k<p->data，并且p->lchild=NULL，查找失败。

若k>p->data，并且p->rchild=NULL，查找失败。

查找失败的情况加上外部节点一个外部节点对应某内部节点的一个NULL指针递归查找算法SearchBST()如下（在二叉排序树bt上查找关键字为k的记录，成功时返回该节点指针，否则返回NULL）：BSTNode*SearchBST(BSTNode*bt,KeyType k){if(bt==NULL||bt->key==k)//递归出口return bt;if(k<bt->key)return SearchBST(bt->lchild,k);//在左子树中递归查找elsereturn SearchBST(bt->rchild,k);//在右子树中递归查找}在二叉排序树中插入一个关键字为k的新节点，要保证插入后仍满足BST性质。

平衡⼆叉树（AVL树）平衡⼆叉树(AVL树)平衡⼆叉树简介： 平衡树(Balance Tree，BT) 指的是，任意节点的⼦树的⾼度差都⼩于等于1。

常见的符合平衡树的有，B树（多路平衡搜索树）、AVL树（⼆叉平衡搜索树）等。

具有以下特点:它是⼀棵空树或它的左右两个⼦树的⾼度差的绝对值不超过1, 并且左右两个⼦树都是-棵平衡⼆叉树。

平衡⼆叉树的常⽤实现⽅法有红⿊树、AVL、替罪⽺树、Treap、伸展树等。

可以保证查询效率⾼。

举例看下下⾯AVL树的特点吧：左右两个⼦树的⾼度差的绝对值不超过1第三棵树的左⼦树⾼度是3，右⼦树⾼度是1,3-1=2,所以第三个不是AVL树AVL树左旋AVL树左旋图解要求: 给你⼀个数列，创建出对应的平衡⼆叉树.数列 {4,3,6,5,7,8}AVL树左旋步骤：1. 创建⼀个新的节点，值为当前节点的值2. 把新节点的的左⼦树设置为原节点的左⼦树：4-->指向33. 把新节点的右⼦树设置为当前节点的右⼦树的左⼦树4. 把当前节点的值：4 换成当前右⼦节点的值：65. 把当前节点的右⼦树设为右⼦树的右⼦树6. 把当前节点的左⼦树设为新的节点：6-->指向4AVL树的⾼度计算核⼼：⾸先要把⼀棵树的⾼度以及左⼦树和右⼦树的⾼度计算出来Node类中添加这三个⽅法：1/**2 * 返回以当前节点为根节点的树的⾼度3 *4 * @return返回树的⾼度5*/6public int heightTree() {7// ⽐较左⼦树跟右⼦树的⾼度，返回最⼤的。

+1是因为树本⾝还要站⼀层8return Math.max(left == null ? 0 : left.heightTree(), right == null ? 0 : right.heightTree()) + 1;9 }1011/**12 * 返回左⼦树的⾼度13 *14 * @return左⼦树⾼度15*/16public int leftHeight() {17if (left == null) {18return 0;19 }20return left.heightTree();21 }2223/**24 * 返回右⼦树的⾼度25 *26 * @return右⼦树⾼度27*/28public int rightHeight() {29if (right == null) {30return 0;31 }32return right.heightTree();33 }View CodeAVLTree类：直接⽤上个⼆叉排序树的树代码即可！1class AVLTree {2private Node root;34public Node getRoot() {5return root;6 }78/**9 * 查找要删除的节点10 *11 * @param value12 * @return13*/14public Node delSearch(int value) {15if (root == null) {16return null;17 } else {18return root.delSearch(value);19 }20 }2122/**23 * 查找到要删除节点的⽗节点24 *25 * @param value26 * @return27*/28public Node delSearchParent(int value) {29if (root == null) {30return null;31 } else {32return root.delSearchParent(value);33 }34 }3536/**38 *39 * @param node40 * @return返回删除节点的值41*/42public int delRightTreeMin(Node node) {43// 作⼀个辅助节点44 Node target = node;45// 循环往左⼦树进⾏查找，就会找到最⼩值46while (target.left != null) {47 target = target.left;48 }49// 删除最⼩值50 delNode(target.value);51// 返回最⼩值52return target.value;53 }5455/**56 * 删除节点57 *58 * @param value59*/60public void delNode(int value) {61if (root == null) {62return;63 } else {64// 1、找到要删除的节点65 Node targetNode = delSearch(value);66// 没有找到67if (targetNode == null) {68return;69 }70// 表⽰这颗⼆叉排序树只有⼀个节点(⽗节点)71if (root.left == null && root.right == null) {72 root = null;73return;74 }7576// 2、找到要删除节点的⽗节点77 Node parentNode = delSearchParent(value);78// 表⽰要删除的节点是⼀个叶⼦节点79if (targetNode.left == null && targetNode.right == null) {80// 继续判断这个叶⼦节点是⽗节点的左⼦节点还是右⼦节点81if (parentNode.left != null && parentNode.left.value == value) {82// 将这个叶⼦节点置为空83 parentNode.left = null;84 } else if (parentNode.right != null && parentNode.right.value == value) {85 parentNode.right = null;86 }87 } else if (targetNode.left != null && targetNode.right != null) {// 删除有两颗⼦树的节点 88// 找到最⼩值89int minVal = delRightTreeMin(targetNode.right);90// 重置91 targetNode.value = minVal;92 } else {// 删除只有⼀颗⼦树的节点93if (targetNode.left != null) {// 如果要删除的节点有左⼦节点94if (parentNode != null) {95// 待删除节点是⽗节点的左⼦节点96if (parentNode.left.value == value) {97 parentNode.left = targetNode.left;98 } else {// 待删除节点是⽗节点的右⼦节点99 parentNode.right = targetNode.left;100 }101 } else {102 root = targetNode.left;103 }104 } else {// 如果要删除的节点有右⼦节点105if (parentNode != null) {106// 待删除节点是⽗节点的左⼦节点107if (parentNode.left.value == value) {108 parentNode.left = targetNode.right;109 } else {// 待删除节点是⽗节点的右⼦节点110 parentNode.right = targetNode.right;111 }112 } else {113 root = targetNode.right;114 }115 }116 }117 }118 }119120/**121 * 添加节点的⽅法122 *123 * @param node124*/125public void addNode(Node node) {126// root节点为空，就让root成为根节点127if (root == null) {128 root = node;129 } else {// root节点不为空,就继续向树中添加节点130 root.addNode(node);131 }132 }133134/**135 * 进⾏中序遍历136*/137public void infixOrder() {138if (root != null) {139 root.infixOrder();140 } else {141 System.out.println("⼆叉树为空，⽆法进⾏排序！");142 }143 }144 }View Code测试树的⾼度：public static void main(String[] args) {int[] arr = {4, 3, 6, 5, 7, 8};// 创建AVL树对象AVLTree avlTree = new AVLTree();for (int i = 0; i < arr.length; i++) {// 添加节点avlTree.addNode(new Node(arr[i]));}// 中序遍历System.out.println("======================中序遍历======================");System.out.println("======================没有平衡处理前======================");System.out.println("没有平衡处理前树的⾼度：" + avlTree.getRoot().heightTree());System.out.println("没有平衡处理前树的左⼦树⾼度：" + avlTree.getRoot().leftHeight());System.out.println("没有平衡处理前树的右⼦树⾼度：" + avlTree.getRoot().rightHeight());}附上总体代码实现：1package Demo11_平衡⼆叉树_AVL树;23/**4 * @author zhangzhixi5 * @date 2021/3/12 22:586*/7public class AVLTreeDemo {8public static void main(String[] args) {9int[] arr = {4, 3, 6, 5, 7, 8};1011// 创建AVL树对象12 AVLTree avlTree = new AVLTree();1314for (int i = 0; i < arr.length; i++) {15// 添加节点16 avlTree.addNode(new Node(arr[i]));17 }1819// 中序遍历20 System.out.println("======================中序遍历======================");21 avlTree.infixOrder();22 System.out.println("======================没有平衡处理前======================");23 System.out.println("没有平衡处理前树的⾼度：" + avlTree.getRoot().heightTree());24 System.out.println("没有平衡处理前树的左⼦树⾼度：" + avlTree.getRoot().leftHeight());25 System.out.println("没有平衡处理前树的右⼦树⾼度：" + avlTree.getRoot().rightHeight());26 }27 }2829class AVLTree {30private Node root;3132public Node getRoot() {33return root;34 }3536/**37 * 查找要删除的节点38 *39 * @param value40 * @return41*/42public Node delSearch(int value) {43if (root == null) {44return null;45 } else {46return root.delSearch(value);47 }48 }4950/**51 * 查找到要删除节点的⽗节点52 *53 * @param value54 * @return55*/56public Node delSearchParent(int value) {57if (root == null) {58return null;59 } else {60return root.delSearchParent(value);61 }62 }6364/**65 * 找到最⼩值并删除66 *67 * @param node68 * @return返回删除节点的值69*/70public int delRightTreeMin(Node node) {71// 作⼀个辅助节点72 Node target = node;73// 循环往左⼦树进⾏查找，就会找到最⼩值74while (target.left != null) {75 target = target.left;76 }77// 删除最⼩值78 delNode(target.value);79// 返回最⼩值80return target.value;81 }8283/**84 * 删除节点85 *86 * @param value87*/88public void delNode(int value) {89if (root == null) {90return;91 } else {92// 1、找到要删除的节点93 Node targetNode = delSearch(value);94// 没有找到95if (targetNode == null) {96return;97 }98// 表⽰这颗⼆叉排序树只有⼀个节点(⽗节点)99if (root.left == null && root.right == null) {100 root = null;101return;102 }103104// 2、找到要删除节点的⽗节点105 Node parentNode = delSearchParent(value);106// 表⽰要删除的节点是⼀个叶⼦节点107if (targetNode.left == null && targetNode.right == null) {108// 继续判断这个叶⼦节点是⽗节点的左⼦节点还是右⼦节点109if (parentNode.left != null && parentNode.left.value == value) {110// 将这个叶⼦节点置为空111 parentNode.left = null;112 } else if (parentNode.right != null && parentNode.right.value == value) {113 parentNode.right = null;114 }115 } else if (targetNode.left != null && targetNode.right != null) {// 删除有两颗⼦树的节点116// 找到最⼩值117int minVal = delRightTreeMin(targetNode.right);118// 重置119 targetNode.value = minVal;120 } else {// 删除只有⼀颗⼦树的节点121if (targetNode.left != null) {// 如果要删除的节点有左⼦节点122if (parentNode != null) {123// 待删除节点是⽗节点的左⼦节点124if (parentNode.left.value == value) {125 parentNode.left = targetNode.left;126 } else {// 待删除节点是⽗节点的右⼦节点127 parentNode.right = targetNode.left;128 }129 } else {130 root = targetNode.left;131 }132 } else {// 如果要删除的节点有右⼦节点133if (parentNode != null) {134// 待删除节点是⽗节点的左⼦节点135if (parentNode.left.value == value) {136 parentNode.left = targetNode.right;137 } else {// 待删除节点是⽗节点的右⼦节点138 parentNode.right = targetNode.right;139 }140 } else {141 root = targetNode.right;142 }143 }144 }145 }146 }147148/**149 * 添加节点的⽅法150 *151 * @param node152*/153public void addNode(Node node) {154// root节点为空，就让root成为根节点155if (root == null) {156 root = node;157 } else {// root节点不为空,就继续向树中添加节点158 root.addNode(node);159 }160 }161162/**163 * 进⾏中序遍历164*/165public void infixOrder() {166if (root != null) {167 root.infixOrder();168 } else {169 System.out.println("⼆叉树为空，⽆法进⾏排序！");170 }171 }172 }173174class Node {175int value;176 Node left;177 Node right;178179public Node(int value) {180this.value = value;181 }182183 @Override184public String toString() {185return "Node{" +186 "value=" + value +187 '}';188 }189190/**191 * 返回以当前节点为根节点的树的⾼度192 *193 * @return返回树的⾼度194*/195public int heightTree() {196// ⽐较左⼦树跟右⼦树的⾼度，返回最⼤的。

常见基本数据结构——树，⼆叉树，⼆叉查找树，AVL树常见数据结构——树处理⼤量的数据时，链表的线性时间太慢了，不宜使⽤。

在树的数据结构中，其⼤部分的运⾏时间平均为O(logN)。

并且通过对树结构的修改，我们能够保证它的最坏情形下上述的时间界。

树的定义有很多种⽅式。

定义树的⾃然的⽅式是递归的⽅式。

⼀棵树是⼀些节点的集合，这个集合可以是空集，若⾮空集，则⼀棵树是由根节点r以及0个或多个⾮空⼦树T1,T2,T3,......,Tk组成，这些⼦树中每⼀棵的根都有来⾃根r的⼀条有向的边所连接。

从递归的定义中，我们发现⼀棵树是N个节点和N-1条边组成的，每⼀个节点都有⼀条边连接⽗节点，但是根节点除外。

具有相同⽗亲的节点为兄弟，类似的⽅法可以定义祖⽗和孙⼦的关系。

从节点n1到nk的路径定义为节点n1，n2，...，nk的⼀个序列，并且ni是ni+1的⽗亲。

这个路径的长是路径上的边数，即k-1。

每个节点到⾃⼰有⼀条长为0的路径。

⼀棵树从根到叶⼦节点恰好存在⼀条路径。

对于任意的节点ni，ni的深度为从根到ni的唯⼀路径长。

ni的⾼是从ni到⼀⽚叶⼦的最长路径的长。

因此，所有的树叶的⾼度都是0，⼀棵树的⾼等于它的根节点的⾼。

⼀棵树的深度总是等于它最深叶⼦的深度；该深度等于这棵树的⾼度。

树的实现实现树的⼀种⽅法可以是在每⼀个节点除数据外还要有⼀些指针，使得该节点的每⼀个⼉⼦都有⼀个指针指向它。

但是由于每个节点的⼉⼦树可以变化很⼤⽽且事先不知道，故在各个节点建⽴⼦节点的链接是不可⾏的，这样将会浪费⼤量的空间。

实际的做法很简单：将每个节点的所有⼉⼦都放在树节点的链表中。

下⾯是典型的声明：typedef struct TreeNode *PtrToNodestruct TreeNode{ ElementType Element; PtrToNode FirstChild; PtrToNode NextSibling}下⾯是⼉⼦兄弟表⽰法的图⽰：树的遍历及应⽤⼀个常见的使⽤是操作系统中的⽬录结构。

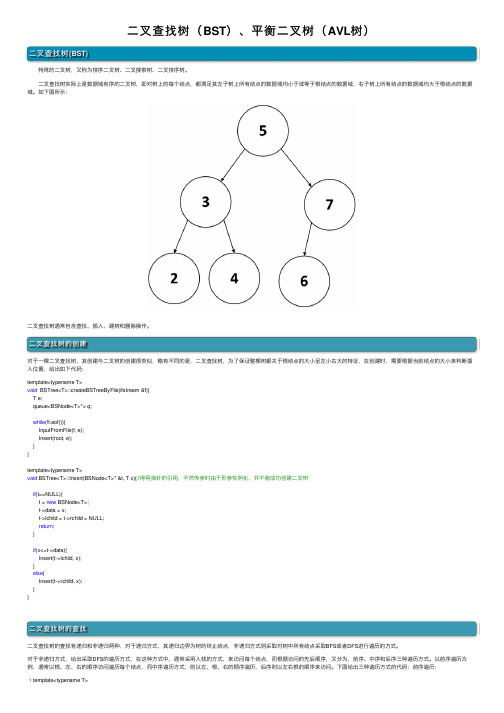
⼆叉查找树（BST）、平衡⼆叉树（AVL树）⼆叉查找树(BST) 特殊的⼆叉树，⼜称为排序⼆叉树、⼆叉搜索树、⼆叉排序树。

⼆叉查找树实际上是数据域有序的⼆叉树，即对树上的每个结点，都满⾜其左⼦树上所有结点的数据域均⼩于或等于根结点的数据域，右⼦树上所有结点的数据域均⼤于根结点的数据域。

如下图所⽰：⼆叉查找树通常包含查找、插⼊、建树和删除操作。

⼆叉查找树的创建对于⼀棵⼆叉查找树，其创建与⼆叉树的创建很类似，略有不同的是，⼆叉查找树，为了保证整棵树都关于根结点的⼤⼩呈左⼩右⼤的特征，在创建时，需要根据当前结点的⼤⼩来判断插⼊位置，给出如下代码：template<typename T>void BSTree<T>::createBSTreeByFile(ifstream &f){T e;queue<BSNode<T>*> q;while(!f.eof()){InputFromFile(f, e);Insert(root, e);}}template<typename T>void BSTree<T>::Insert(BSNode<T>* &t, T x){//得⽤指针的引⽤，不然传参时由于形参实例化，并不能成功创建⼆叉树if(t==NULL){t = new BSNode<T>;t->data = x;t->lchild = t->rchild = NULL;return;}if(x<=t->data){Insert(t->lchild, x);}else{Insert(t->rchild, x);}}⼆叉查找树的查找⼆叉查找树的查找有递归和⾮递归两种，对于递归⽅式，其递归边界为树的终⽌结点，⾮递归⽅式则采取对树中所有结点采取BFS或者DFS进⾏遍历的⽅式。

第九章查找一、选择题1.若查找每个记录的概率均等，则在具有n个记录的连续顺序文件中采用顺序查找法查找一个记录，其平均查找长度ASL为( )。

A． (n-1)/2 B. n/2 C. (n+1)/2 D. n2. 下面关于二分查找的叙述正确的是 ( )A. 表必须有序，表可以顺序方式存储，也可以链表方式存储 C. 表必须有序，而且只能从小到大排列B. 表必须有序且表中数据必须是整型，实型或字符型 D. 表必须有序，且表只能以顺序方式存储3. 用二分（对半）查找表的元素的速度比用顺序法( )A．必然快 B. 必然慢 C. 相等 D. 不能确定4. 具有12个关键字的有序表，折半查找的平均查找长度（）A. 3.1B. 4C. 2.5D. 55．当采用分块查找时，数据的组织方式为 ( )A．数据分成若干块，每块内数据有序B．数据分成若干块，每块内数据不必有序，但块间必须有序，每块内最大（或最小）的数据组成索引块C. 数据分成若干块，每块内数据有序，每块内最大（或最小）的数据组成索引块D. 数据分成若干块，每块（除最后一块外）中数据个数需相同6. 二叉查找树的查找效率与二叉树的( （1）)有关, 在 (（2）)时其查找效率最低(1): A. 高度 B. 结点的多少 C. 树型 D. 结点的位置(2): A. 结点太多 B. 完全二叉树 C. 呈单枝树 D. 结点太复杂。

7. 对大小均为n的有序表和无序表分别进行顺序查找,在等概率查找的情况下,对于查找失败,它们的平均查找长度是((1)) ,对于查找成功,他们的平均查找长度是((2))供选择的答案:A. 相同的B.不同的9．分别以下列序列构造二叉排序树，与用其它三个序列所构造的结果不同的是( ) A．（100，80， 90， 60， 120，110，130） B.（100，120，110，130，80， 60， 90）C.（100，60， 80， 90， 120，110，130）D. (100，80， 60， 90， 120，130，110)10. 在平衡二叉树中插入一个结点后造成了不平衡，设最低的不平衡结点为A,并已知A的左孩子的平衡因子为0右孩子的平衡因子为1,则应作( ) 型调整以使其平衡。

二叉树是一种非线性数据结构，在数据库中通常不直接使用二叉树这种数据结构。

但是，二叉树的一些变种和扩展，如平衡二叉树、AVL树、红黑树等，在数据库中有广泛的应用。

1. 平衡二叉树（Balanced Binary Tree）：这种数据结构在数据库中常用于快速查找和排序。

例如，数据库系统可以使用平衡二叉树来实现索引，从而快速定位到需要的数据。

2. AVL树：AVL树是最早的平衡二叉树之一，它在数据库中也有应用，尽管相对其他数据结构较少。

例如，Windows对进程地址空间的管理就使用到了AVL树。

3. 红黑树：红黑树是另一种平衡二叉树，广泛用于C++的STL （标准模板库）中。

在数据库中，红黑树可用于实现一些高级的数据结构，如B-tree索引。

4. B/B+树：B树和B+树是数据库中常用的索引结构，用于磁盘文件组织、数据索引和数据库索引。

B树通过减少磁盘I/O操作来提高查询效率，而B+树则更适合于范围查询。

5. Trie（字典）树：Trie树也称为字典树，它用于统计和排序大量字符串。

在数据库中，Trie树可用于实现一些特定的索引和查询功能，例如自动机、M数据库索引等。

需要注意的是，尽管二叉树和其变种在数据库中有一定的应用，但它们并不是数据库的主要数据结构。

数据库主要使用的是表格形式的数据结构，如关系型数据库中的表和行。