几种抽样调查方法比较

抽样与抽样分布在统计学中，抽样是一种常用的数据收集方法，通过从总体中选择一部分样本来进行研究和分析。

抽样的目的是通过样本来推断总体的特征和性质。

在进行抽样时，我们需要了解抽样的方法和抽样分布的概念。

一、抽样方法1. 无偏抽样无偏抽样是指所有样本有相同被选中的机会。

这样可以确保样本的代表性，从而减小样本估计值和总体真值之间的误差。

常见的无偏抽样方法包括简单随机抽样、系统抽样和分层抽样等。

2. 有偏抽样有偏抽样是指样本的选择并不具有相等的机会。

这样可能导致样本的代表性不足，从而产生较大的估计误差。

有时，有偏抽样也可以用于特定的研究目的，但需要明确地说明和分析偏差带来的影响。

二、抽样分布1. 抽样分布的概念抽样分布是指统计量在各个可能样本上的取值分布。

统计量可以是样本均值、样本方差等。

抽样分布的性质对于进行统计推断和假设检验非常重要。

2. 样本均值的抽样分布样本均值的抽样分布在中心极限定理的条件下近似服从正态分布。

中心极限定理指出，当样本容量足够大时，无论总体分布如何，样本均值的抽样分布都会接近正态分布。

3. 样本比例的抽样分布样本比例的抽样分布在满足一些条件的情况下也近似服从正态分布。

这些条件包括样本容量足够大、总体比例接近0.5以及样本与总体之间的独立性等。

4. 样本方差的抽样分布样本方差的抽样分布不服从正态分布。

通常情况下，样本方差的抽样分布呈右偏态，即偏度大于0。

为了得到样本方差的抽样分布，可以使用抽样分布的近似分布，如卡方分布。

三、应用案例抽样与抽样分布的方法和理论在实际统计学中有广泛的应用。

以下是一些常见的应用案例：1. 调查研究在进行调查研究时，我们经常需要从总体中选择一部分样本进行问卷调查或面访。

通过利用抽样与抽样分布的方法，我们可以将样本的调查结果推广到总体中，从而得到总体的特征和性质。

2. 假设检验假设检验是统计学中常用的推断方法之一。

通过比较样本统计量与假设的总体参数值，我们可以判断假设的合理性。

工作抽样方法工作抽样方法是指在进行工作调查和研究时，从总体中选择一部分样本来代表总体，以求得关于总体的信息和结论。

正确选择和使用抽样方法能够保证研究结果的可靠性和有效性。

下面将介绍几种常用的工作抽样方法。

一、简单随机抽样法简单随机抽样法是指在总体中每个个体具有相同的选择机会，且每个抽样单位之间相互独立的抽样方法。

简单随机抽样法的步骤如下：1. 确定总体：首先需要明确研究对象的总体是什么，总体可以是某个组织的所有员工，也可以是某个行业的从业人员等。

2. 确定样本容量：根据总体的大小和抽样精度要求，确定抽样的样本容量。

一般情况下，样本容量越大，研究结果的准确性越高。

3. 编制总体名单：根据总体的特点，编制出总体的名单，确保总体中的每个个体都能够被抽中。

4. 使用随机数表或随机数发生器进行随机抽样：根据所确定的样本容量，使用随机数表或随机数发生器，从总体名单中随机选择样本。

5. 进行抽样调查：根据抽样得到的样本名单，进行抽样调查，收集样本的相关数据。

6. 进行数据分析和总体推断：对抽样调查得到的数据进行统计分析，得出关于总体的推断。

简单随机抽样法的优点是抽样结果容易推广到整个总体，适用于总体分布均匀的情况。

缺点是对总体并不知道太多的情况下，有可能遗漏了某些重要的个体。

二、系统抽样法系统抽样法是在总体名单上按照一定的规律选择样本的方法。

系统抽样法的步骤如下：1. 确定总体和样本容量：同样需要明确研究对象的总体和所需的样本容量。

2. 编制总体名单：根据总体的特点，编制出总体的名单。

3. 确定抽样间距：根据总体的大小和所需的样本容量，计算出抽样间距，即每隔多少个个体抽取一个样本。

4. 随机选择一个起始个体：使用随机数表或随机数发生器，选择一个起始个体。

5. 按照抽样间距选择样本：从起始个体开始，按照抽样间距依次选择样本。

6. 进行抽样调查和数据分析：根据抽样得到的样本名单，进行抽样调查和数据分析。

系统抽样法的优点是具有操作简便、可行性强、节省调查时间和费用等特点。

几种抽样调查方法比较抽样调查是一种数据收集的方法，通过选择一部分样本来代表整体群体，以了解群体的特征、态度、行为等。

在进行抽样调查时，有多种方法可供选择。

本文将介绍几种常见的抽样调查方法，并进行比较。

一、简单随机抽样：简单随机抽样是最基本的抽样方法之一、该方法通过随机抽取样本，确保每个个体被抽到的机会相等，使样本更具有代表性。

简单随机抽样方法适用于群体中个体之间差异较小的情况。

二、系统抽样：系统抽样是指按一定的系统、规则从群体中选择样本，例如每隔一定数量选择一个个体。

系统抽样的优点是设计简单、执行方便，适用于群体中个体之间差异较小的情况。

但如果群体中存在周期性的特征，可能会引入偏差。

三、分层抽样：分层抽样是将群体划分为若干层次，然后从每一层中随机抽取样本。

这种方法可以保证每个层次在样本中的代表性，适用于群体内部差异较大或特定层次的群体。

四、整群抽样：整群抽样是指将群体分为若干个较小的群组，然后从每个群组中抽取全部样本进行调查。

整群抽样的优点是简单、高效，适用于以群组为单位进行调查的情况，但可能导致样本与总体差异较大。

五、多阶段抽样：多阶段抽样是结合多种抽样方法进行的一种抽样方式。

该方法一般包括两个或多个阶段，每个阶段选择样本的方法可能不同。

多阶段抽样的优点是适用于群体层次结构复杂、地域分布广泛的情况，但需要更复杂的设计和执行。

六、整备抽样：整备抽样也称为方便抽样或自愿抽样，是指研究者主观选择方便的个体作为样本。

这种方法的优点是简便、省时，但样本可能不具有代表性，结果的可靠性受到质疑。

七、配额抽样：配额抽样是研究者按照一些特定属性（例如性别、年龄）确定配额，然后在每个配额中选择样本。

该方法的优点是方便、快速，适用于快速获取数据但不能保证代表性的情况。

综上所述，每种抽样调查方法都有其适用的情况和特点。

在选择抽样方法时，需要考虑群体的特征、研究目的、资源限制等因素。

根据具体情况，可以选择简单随机抽样、系统抽样、分层抽样、整群抽样、多阶段抽样等方法。

谈谈几种典型的抽样方法（案例）摘要：本文以抽样方法为中心，主要阐述几种常见的抽样方法，如简单随机抽样，分层抽样，整群抽样，系统抽样以及配额抽样，探讨了各种抽样方法在实际生活的应用以及各自的优缺点等。

关键词：抽样调查，应用，缺点。

导语：抽样调查是一种非全面调查，它是从全部调查研究对象中，抽选一部分单位进行调查，并据以对全部调查研究对象作出估计和推断的一种调查方法。

显然，抽样调查虽然是非全面调查，但它的目的却在于取得反映总体情况的信息资料，因而，也可起到全面调查的作用。

抽样调查是建立在随机原则基础上，从总体中抽取部分单位进行调查，并概率估计原理，应用所的资料对总体的数量特征进行推断的一种调查方法。

例如，从某地区全部职工当中随机抽取部分职工，以家庭为单位按月调查取得有关收入、支出等方面的资料，并依据这些资料推断出全区职工的收支情况，这就是一种抽样调查。

从调查方法上来看，它是属于一种非全面调查。

但又与一般调查不同，它不只停留于搜集资料和整理资料，而且还要对资料进行分析，并据以推断总体的数量特征，从而提高统计的认识能力。

因此，抽样调查的理论和方法在统计中占有很重要的地位。

下面介绍一下常用的抽样方法：一. 简单随机抽样一般，设一个总体含有N个个体，从中逐个不放回地抽取n个个体作为样本（n≤N），如果每次抽取时总体内的个体被抽到的机会相等，就把这种抽样方法叫做简单随机抽样。

简单随机抽样的具体作法有：直接抽选法，抽签法，随机数法。

直接抽选法例如某项调查采用抽样调查的方法对某市职工收入状况进行研究，该市有职工56，000名，抽取5，000名职工进行调查，他们的年平均收入为10，000元，据此推断全市职工年收入为8，000--12，000元之间。

抽签法又称“抓阄法”。

它是先将调查总体的每个单位编号，然后采用随机的方法任意抽取号码，直到抽足样本。

在这里选取一个案例说明，如要在10个人中选取3个人作为代表，先把总体中的10个个体编号，把号码写在号签上，将号签放在一个容器中，搅拌均匀后，每次从中抽取一个号签，连续抽取3次，就得到一个容量为3的样本。

抽样调查的五种方法
抽样调查是研究人员在研究中采取的一种常见的数据收
集方法。

通过从总体中选择一部分样本，并在样本上进行测量和分析，研究人员可以推断总体的特征和情况。

以下是五种常见的抽样调查方法：
1. 简单随机抽样：这是抽样调查中最基本的一种方法。

它要求所有个体有等同的机会被选中，并且选取的每个个体都是独立的。

研究人员可以使用随机数表或随机数生成器来进行样本选择。

2. 系统抽样：系统抽样是一种有规律的抽样方法。

研究
人员首先确定样本量，然后按照一个固定的规则选择样本。

例如，研究人员可以选择每10个人中的一个进行调查。

3. 分层抽样：分层抽样将总体分成若干层，然后从每个
层中进行抽样。

这种方法可确保样本在每个层上的代表性。

例如，如果研究人员研究一个城市的居民，他们可以将城市分成不同的区域，然后从每个区域中抽取一定数量的样本。

4. 整群抽样：整群抽样是一种将总体分成若干群体，然
后从选定的群体中进行抽样的方法。

这种方法通常用于人口较少或封闭的群体研究。

例如，如果研究人员研究一个学校的学生，他们可以将学校分成不同班级，然后从每个班级中抽取样本。

5. 方便抽样：方便抽样是一种简便的抽样方法，研究人
员选择方便获得的个体作为样本。

这种方法的优点是操作简单、节省时间和成本，但样本的代表性可能较差。

每种抽样调查方法都有其特点和适用场景。

研究人员在选择抽样方法时需要考虑研究目的、总体特征、时间和资源限制等因素。

正确选择和应用合适的抽样方法可以提高研究的准确性和可靠性。

抽样调查方法抽样调查是一种常用的研究方法，通过从总体中选取部分样本进行调查，以此推断总体的特征和规律。

在实际应用中，抽样调查方法的选择对于研究结果的准确性和可靠性有着重要的影响。

本文将介绍几种常见的抽样调查方法，并对其特点和适用场景进行简要分析。

一、简单随机抽样。

简单随机抽样是最基本的抽样方法之一，其特点是每个样本被选中的概率相等，相互独立。

简单随机抽样通常需要使用随机数表或随机数发生器来进行样本的选择，以确保样本的代表性和客观性。

这种抽样方法适用于总体各个单位相对均匀分布的情况，且适用于小样本和大样本调查。

二、分层抽样。

分层抽样是将总体按照某种特征分成若干层，然后从每一层中分别进行简单随机抽样，最终将各层的样本合并为总体样本。

分层抽样能够保证各层样本的代表性，适用于总体结构复杂、各层差异较大的情况。

例如，在对某个城市的居民进行调查时，可以按照年龄、性别、职业等因素进行分层抽样，以保证样本的多样性和代表性。

三、整群抽样。

整群抽样是将总体按照某种特征分成若干群，然后从中随机选择若干群作为样本进行调查。

整群抽样适用于总体分群明显、各群内相对均匀的情况，能够减少调查成本和提高效率。

例如，在对某个学校的学生进行调查时，可以先按照年级将学生分成若干群，然后随机选择若干群作为样本进行调查。

四、系统抽样。

系统抽样是按照一定的规则从总体中选取样本，例如每隔若干单位选择一个样本。

系统抽样适用于总体有序排列的情况，能够保证样本的随机性和代表性。

例如，在对某个市场的顾客进行调查时，可以按照顾客到达的顺序进行系统抽样，以确保样本的客观性和代表性。

综上所述，抽样调查方法的选择应根据具体的研究对象和调查目的来确定。

在实际应用中，研究者需要结合总体特点和调查条件，合理选择抽样方法，以确保调查结果的准确性和可靠性。

同时，在进行抽样调查时，还需要注意样本容量的确定、抽样误差的控制等问题，以提高调查的科学性和实用性。

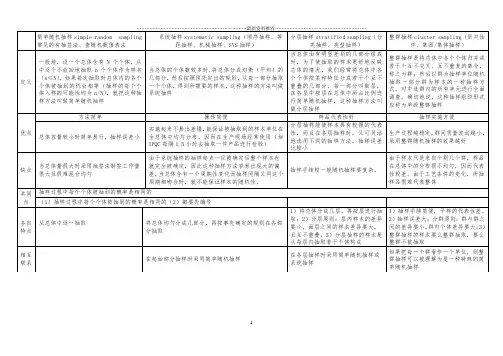
抽样方法几种分析抽样方法的几种分析1.抽样的基本方法抽样方法基本上可分为随机抽样法和预定抽样法。

2.随机抽样法这种抽样方法是以概率理论的原理为基础的，即基本整体中的每一个具体单元都有相同被抽中的机会（例如：掷骰子）。

⑴简单随机抽样法它直接从基本整体中抽出子样，前提条件是该整体至少能以标记形式来表示（例如：卡片），并可以混合至保证使每个单元都能有相同的被抽样的机会。

简单随机抽样法简单易行，至于整体的某些特征及其分布情况不需要知道。

但如果整体情况比较分散，彼此的差距比较大，则误差就可能较大。

所有的随机抽样方法都是以票箱模型为基础的（如抽彩票），即所有的票单（组成样本的单元）都标上号，装入票箱，封闭，然后抽票。

一张票单在认定结果后再放回票箱，即整体数量保持不变。

用这种方法来确定调查对象，就像用掷骰子来确定对象一样（整体数量不大时可以使用）。

如果将抽样的票单放在一边可以避免出现重复。

当整体数量很大时，常采用下列方法代替票箱模式，因为在实际运用中它们的速度更快，也更完善。

①乱数表抽样。

例如用两只骰子掷数，可得下表所列数字：13、45、65、36、22、24、31、43、61、52、55、16、23、14、25。

每隔两位取一个数字，即可得到：65、24、61、16、25。

从整体中抽出的这些数字就是所取得的子样。

②尾数抽样（根据最后一个数字抽样）。

将整体中的每一个单元都按顺序编上号，然后将例如 7、17、27、37等号抽出作为子样。

③字母抽样。

例如将整体中所有以“P”为姓名的第一个字母的人抽出来作为样本，但条件是必须在整体中所有姓的第一个字母均匀分布情况下得到“P”。

⑵分层随机抽样法分层随机抽样法是将混合着多种主要调查特征的综合性整体，分成不同类型的小组（层次），要求小组成员具有尽可能一致的特征，然后再从这些特征比较一致的小组（层次）中用相应的简单随机抽样法抽出所需的样本。

例如：以一个国家为基本整体，各省份为小组。

常见随机方案随机方案是在实验设计或决策过程中常用的一种方法。

通过随机抽取或生成随机数，可以使实验或决策结果具有一定的随机性和代表性。

下面，介绍几种常见的随机方案。

1. 简单随机抽样简单随机抽样是最常用的一种随机抽样方案。

其思想是从总体中随机选择若干个样本，使得每个样本具有相同的被选中的概率。

简单随机抽样常用于民调、调查研究等领域，可以有效保证样本的代表性。

2. 系统抽样系统抽样也是一种常见的随机抽样方案。

它的思想是在总体中选择一个随机开始的位置，然后按照固定的间隔选择样本。

例如在一条街道上进行调查，可以从某个起始点开始，每隔一定数量的房屋选择一个样本。

系统抽样相对于简单随机抽样可以提高调查的效率，并且仍具有一定的随机性。

3. 分层抽样分层抽样是一种将总体划分为若干层次，然后从每个层次中进行随机抽样的方法。

分层抽样可以有效保证样本的多样性和代表性。

例如，在一项教育调查中，可以按照不同年级划分层次，然后从每个年级中进行随机抽样。

这样可以确保每个年级的样本数量均衡，并且能够覆盖到各个层次的特征。

4. 簇抽样簇抽样又称作群体抽样，它是将总体划分为若干个相互独立的群体，然后从每个群体中抽取所有样本的方法。

簇抽样常用于地理学调查、社会学调查等领域。

例如在一项城市调查中，可以将城市划分为多个区域，然后从每个区域中随机选择一个样本点进行调查。

5. 整群抽样整群抽样是将总体划分为若干个群体，然后从每个群体中随机选择一个或多个群体作为样本的方法。

与簇抽样不同的是，整群抽样不需要对每个群体进行全面抽样，而是选择部分群体作为样本。

这种抽样方式在一些大规模调查中常用，例如在国家或地区层面的统计调查中，可以将各个省份或城市作为群体进行抽样。

总结起来，以上介绍了几种常见的随机方案，包括简单随机抽样、系统抽样、分层抽样、簇抽样和整群抽样。

每种随机方案都有其适用的场景和应用领域。

在实际应用中，可以根据具体需求选择合适的随机方案，确保实验或决策结果的可靠性和代表性。

抽样调查技术课程论文---抽样调查方法比较分析专业：林学班级：林学四班指导教师：朱光玉作者：姚帅 20130221 日期： 2016年1月3日抽样调查方法比较分析一．调查目的这学期我们学习了几种抽样调查方法，如简单随机抽样，整群抽样，二阶抽样等。

各个方法在应用时有其特点和优缺点。

本文通过计算对这些调查方法做出简单的总结和计算，以求在实际生活的数理统计中能灵活运用这些方法。

二．抽样方法介绍1.简单随机抽样设一个总体的个体数为N．如果通过逐个抽取的方法从中抽取一个样本，且每次抽取时各个个体被抽到的机会相等，就称这样的抽样为简单随机抽样。

对于简单随机抽样需要注意：①它是不放回抽样；②它是逐个地进行抽取；③它是一种个体机会均等的抽样；④简单随机抽样适用于总体中的个体数不多的情况．生活中有许多用抽签法或类似抽签法的案例，如彩票摇奖、电视节目中电话号码抽奖、纳税凭证抽奖等．抽样时也要防止出现貌似合理的抽样方法，如到某星级宾馆问卷调查客人的收入情况来推断该地区的人均收入，或每隔一周到某一路口调查当地车流量等等。

2.系统抽样当总体中的个体数较多时，可将总体平均分成几个部分，从每个部分抽取一个个体，得到所需的样本，这样的抽样方法称为系统抽样。

对于系统抽样需要注意：①系统抽样适用于总体中的个体数较多的情况，它与简单随机抽样的联系在于：将总体均分后的每一部分进行抽样时，采用的是简单随机抽样；②与简单随机抽样一样，系统抽样是等可能抽样，它是客观的、公平的；③总体中的个体数恰好能被样本容量整除时，可用它们的比值作为系统抽样的间隔；当总体中的个体数不能被样本容量整除时，可用简单随机抽样先从总体中剔除少量个体，使剩下的个体数能被样本容量整除再进行系统抽样。

3.二阶段抽样二阶抽样是一种随机抽样技术。

在规模甚大的总体中(例如在一个省、市中)对居民进行随机抽样观察,为了使样本较好地反映全省(市)居民的情况,又便于调查工作的组织,可以按居民管辖的行政组织分层,对于二阶段抽样是分成二层,例如第一层是乡,第二层是村。

浅析市场调查中几种常用的抽样方法抽样调查几乎是市场调查中最常用的方法。

这是因为，在市场调查中往往面对的是顾客数量非常多，全部调查不可能或者是成本太高，所以此种情况下就会考虑选择抽样调查。

但如何保证抽样调查的准确性和精确性，甚或是如何保证所调查的样本能较为真实地反映总体情况一直是市场调查中的重点和难点。

综合服务一些企业市场调查相关业务的实践经验和目前理论界的一些研究成果，此文拟对常用的几种抽样调查方法进行简析，只当是自我总结和理论进步，当然，如果有可能也可以作为相应的一点参考资料。

抽样调查最基本一种方法就是简单随机抽样。

简单随机抽样所面对的往往某一类客户，在此情况下，从总体中随机抽取一定样本量进行分析计算便可能达到估计总体的调查目的。

但实践表明，市场调查中面对的被调查客户很多情况下都不是一类顾客，一般都会有多类顾客，例如有批发商客户、零售商客户、VIP客户、战略客户、TOP客户等等多种分类，所以，市场调查中采用单随机抽样的方法是不科学的。

这是因为，各类顾客的占比不同，所抽取的被调查客户可能并不是企业想调查的客户，或者企业想调查的客户存在遗漏；或者客户分类之间又存在着一定的交叉关系，批发商客户可能是VIP客户，零售商客户也可能是VIP 客户；再考虑到企业不同的调查目的等等其它因素，所以简单随机抽样在多类客户的情况下是难以保证调查的的精确性的。

为了避免上述情况出现，甲方企业或市场调查公司就选择多类客户的抽样调查方式，主要有分层抽样、多阶段抽样、整群抽样。

1、分层抽样分层抽样是指将被调查客户分为若干个层，然后再在不同的层内进行随机抽样。

例如，如果调查某一政策的实施效果，调查对象是全国范围内的相关客户，则可以按照行政区划、行业或者是经济圈等进行分层，然后再在各个层内进行抽样；再例如，如果调查某一产品的满意度情况，可以将客户分为东部、中部、西部客户，即所谓的分层，然后再进行随机抽样。

分层抽样有将客户横向分类的意味，其好处有：1）不仅可以估计总体情况，还可以对每一层的情况进行估计，从而可以各个层与总体相比较、也方便层与层之间相比较；2）调查实施比较方便，客户可以按照调查者的主观意图进行分类；3）由于事先进行了分类，能较为全面的选择客户样本，从而可以降低抽样误差。

社会调查方法04抽样社会调查的抽样是指从总体中选择一部分个体进行调查的过程，目的是通过样本数据对总体进行估计和推断。

在社会调查中，抽样是一个关键的环节，合理的抽样方法能够保证样本的代表性和可靠性。

本文将介绍社会调查中常用的抽样方法之一，随机抽样和分层抽样。

随机抽样是最常用的抽样方法之一，也是最容易理解和操作的一种方法。

它是在总体中随机选择个体作为样本，每个个体被选中的概率相等。

随机抽样能够避免主观因素，保证样本的公正性和客观性。

随机抽样有以下几种具体方法：一、简单随机抽样：从总体中随机抽取若干个个体作为样本。

这种抽样方法简单直接，适用于总体比较小的情况。

二、系统抽样：按一定规则从总体中选择个体作为样本，例如每隔若干个个体选择一个个体作为样本。

系统抽样相对简单，但样本可能不具有代表性。

三、整群抽样：将总体按照其中一种特征分为若干个群体，再从群体中随机选择个体作为样本。

整群抽样适用于总体结构复杂的情况，可以减小样本数目。

分层抽样是将总体按照其中一种特征分为若干层，再从每层中随机选择一部分个体作为样本。

分层抽样能够更好地反映总体的特征，提高样本的代表性。

分层抽样有以下几种具体方法：一、按比例分层抽样：按照总体中不同层的比例确定每层的个体数目，再从每层中按照比例抽取个体作为样本。

这种抽样方法能够保证每层的权重，适用于不同层之间差异较大的情况。

二、聚类抽样：将总体划分为若干个聚类，再从聚类中随机选择个体作为样本。

聚类抽样适用于总体属性差异较小的情况，可以减小调查成本。

三、多阶段抽样：将总体按照不同的阶段进行抽样，先从大的单位抽取样本，再从小的单位抽取样本。

多阶段抽样适用于总体结构复杂的情况，可以减小样本数目及调查成本。

在社会调查中，抽样是获取样本数据的重要步骤，合理的抽样方法能够保证样本的代表性和可靠性。

随机抽样和分层抽样是常用的抽样方法，具体的选择需要根据调查目的和总体特征进行。

同时，抽样过程中需要注意抽样误差的控制和样本的质量保证，以提高调查结果的准确性。

简述企业市场调查常用的抽样方法篇一：常用的抽样方法总结常用的抽样方法总结1．非概率抽样（Non-probability sampling）又称非随机抽样，指根据一定主观标准抽取样本，令总体中每个个体的被抽取不是依据其本身的机会，而是完全决定于调研者的意愿。

其特点为不具有从样本推断总体的功能，但能反映某类群体的特征，是一种快速、简易且节省的数据收集方法。

当研究者对总体具有较好的了解时可以采用此方法，或是总体过于庞大、复杂，采用概率方法有困难时，可以采用非概率抽样来避免概率抽样中容易抽到实际无法实施或“差”的样本，从而避免影响对总体的代表度。

常用的非概率抽样方法有以下四类：方便抽样（Convenience sampling）指根据调查者的方便选取的样本，以无目标、随意的方式进行。

例如：街头拦截访问（看到谁就访问谁）；个别入户项目谁开门就访问谁。

优点：适用于总体中每个个体都是“同质”的，最方便、最省钱；可以在探索性研究中使用，另外还可用于小组座谈会、预测问卷等方面的样本选取工作。

缺点：抽样偏差较大，不适用于要做总体推断的任何民意项目，对描述性或因果性研究最好不要采用方便抽样。

判断抽样（Judgment sampling）指由专家判断而有目的地抽取他认为“有代表性的样本”。

例如：社会学家研究某国家的一般家庭情况时，常以专家判断方法挑选“中型城镇”进行；也有家庭研究专家选取某类家庭进行研究，如选三口之家（子女正在上学的）；在探索性研究中，如抽取深度访问的样本时，可以使用这种方法。

优点：适用于总体的构成单位极不相同而样本数很小，同时设计调查者对总体的有关特征具有相当的了解（明白研究的具体指向）的情况下，适合特殊类型的研究（如产品口味测试等）；操作成本低，方便快捷，在商业性调研中较多用。

缺点：该类抽样结果受研究人员的倾向性影响大，一旦主观判断偏差，则根易引起抽样偏差；不能直接对研究总体进行推断。

配额抽样（Quota sampling）指先将总体元素按某些控制的指标或特性分类，然后按方便抽样或判断抽样选取样本元素。

教育研究抽样的基本方法在教育研究中，抽样是一种常见且重要的数据收集方法。

正确选择适当的抽样方法可以确保研究结果的可靠性和有效性。

本文将介绍教育研究中常用的几种抽样方法，包括随机抽样、系统抽样、整群抽样和方便抽样。

1. 随机抽样随机抽样是根据概率理论和随机数产生器进行的数据抽取方法。

通过随机抽样，可以保证样本的代表性和可比性。

在教育研究中，随机抽样可以用于选取不同学校、不同年级、不同性别等不同类型的个体。

例如，在调查学生对某一教学方法的反应时，可以使用随机抽样方法从全校学生中选取一定数量的样本。

2. 系统抽样系统抽样是一种按照一定规则进行抽取的方法。

在教育研究中，系统抽样可以用于选取一定比例的样本。

例如，在调查学校教师对新课程改革的看法时，可以使用系统抽样方法从全校教师中按照一定规则（如每隔五个教师选取一个）进行抽取，以获取一定数量的样本。

3. 整群抽样整群抽样是一种按照群体进行抽取的方法。

在教育研究中，整群抽样可以用于选取学校、班级等群体作为样本。

例如，在研究不同学校的教学效果时，可以使用整群抽样方法从不同学校中随机选取一定数量的学校作为样本，然后再从选取的学校中抽取一定数量的学生进行调查。

4. 方便抽样方便抽样是一种便捷而常用的抽样方法，也是最不严谨的一种抽样方法。

在教育研究中，方便抽样常用于小规模调查和预研阶段。

例如，在调查学生的学习方法偏好时，可以选择身边容易接触到的学生作为样本。

然而，方便抽样可能导致样本的偏差和不可靠性，因此在研究的正式阶段应尽量避免使用方便抽样。

总结起来，随机抽样、系统抽样、整群抽样和方便抽样是教育研究中常用的抽样方法。

合理选择适当的抽样方法可以保证研究结果的准确性和代表性。

在实际应用中，研究者需要根据研究问题和资源限制等因素来选择最合适的抽样方法，以达到研究目的并提高研究成果的可靠性。

抽样调查心得要做出正确的选择，我个人对这六种抽样调查方法做出如下比较讨论：一、电话调查电话调查是指调查员通过查找电话号码簿，根据调查方案规定的随机拨号的方法，拨通电话，遵照问卷和培训的要求筛选被访问对象，然后对合格的被调查者对比问卷逐题逐字提问并将答案记录下来，以到达搜集调查资料目的的调查方式。

〔一〕电话调查的优点：1、搜集资料速度快、费用低，可节约大量的调查时间和调查经费。

2、搜集的资料掩盖面广，可以对任何有电话的地区、单位和个人直接进行电话询问调查。

3、可能访问到平常不易接触的被调查者。

例如，有些高收入或高地位的特别阶层，面访调查是很难接触到的，但是利用随机拨号的方法，则有可能访问胜利；又比方有些被调查者拒绝生疏人入户访问，有些人工作太忙拒绝面访，但却有可能接受短暂的电话调查。

4、可以解除被调查者对生疏人的心理压力，在某些特别问题上得到坦诚的回答。

例如，有些关于个人方面的问题，或者是对某些特别商品的看法〔如卫生棉、健胸食品等〕，面访调查时可能回答不自然或不真实，但是在电话调查中可以得到比较坦诚的回答。

5、易于掌握调查的质量。

调查员被集中在某个场所或特地的电话访问间，在固定的时间内工作，督导员可以在现场随时订正调查员不正确的操作。

6、易于订正调查本身的系统性误差。

督导可以随时把握项目的进度，调查员在调查过程中发觉的问题也可以在第一时间反馈给督导，便于准时发觉调查方案本身存在的系统性问题，使错误得到快速地修正。

7、调查的操作流程简洁，对调查员的业务素养要求较低。

〔二〕电话调查的缺点：1、无法访问到没有电话的单位和个人。

2、电话访问的时间不宜过长，问题不宜过于冗杂，因此难于调查比较深化的问题。

3、访问的胜利率可能较低。

随机拨打的电话可能是空号或错号；被访对象可能不在或正忙不能接电话；被访对象不情愿接受调查；等等。

4、无法出示卡片、照片、产品等相关资料。

5、无法了解被调查者当时的看法，难以区分答案的真伪。

城镇住户调查抽样方法引言在进行城镇住户调查时，抽样方法是非常重要的一环。

通过合理的抽样方法，我们可以从全体城镇住户中选取到具有代表性的样本，从而进行更加准确和有效的调查。

本文将介绍几种常用的城镇住户调查抽样方法，以及其优缺点和适用场景。

1. 简单随机抽样简单随机抽样是一种根本的抽样方法，其原理是从总体中随机抽取样本。

具体步骤如下：•确定目标总体：确定城镇住户总体范围和特征。

•确定样本容量：确定需要抽取的样本容量。

•编制抽样框：编制包含全体城镇住户的名单或编号。

•进行随机抽样：使用随机数表或随机数发生器，随机选择样本。

简单随机抽样的优点是简单易行，能够保证每个城镇住户被选中的概率相等。

然而，由于随机性的影响，可能会存在样本不具有代表性的情况。

2. 系统抽样系统抽样是在总体中按照一定的规那么选择样本。

具体步骤如下：•确定抽样框：编制包含全体城镇住户的名单或编号。

•确定抽样间隔：根据样本容量和总体规模确定抽样间隔。

•选取起始样本：使用随机数表或随机数发生器，随机选择一个起始样本。

•进行系统抽样：从起始样本开始，按照抽样间隔逐步选取后续样本。

系统抽样的优点是比简单随机抽样更加有组织，能够保证样本具有一定的分布规律。

缺点是如果系统抽样的规那么与总体特征不匹配，可能导致样本不具有代表性。

3. 分层抽样分层抽样是将总体按照一定的特征进行划分，然后在每个层级内进行抽样。

具体步骤如下：•将总体划分为假设干层级：根据城镇住户的特征，将总体划分为不同的层级，如不同的年龄、教育程度等。

•确定每个层级的样本容量：确定每个层级抽取的样本容量，可以根据层级在总体中所占比例进行分配。

•进行分层抽样：在每个层级内按照简单随机抽样或系统抽样的方法进行抽样。

分层抽样的优点是能够更好地保证样本的代表性，在分析时可以对各个层级进行比拟。

但是，分层抽样需要对总体进行较为准确的划分，否那么可能导致抽样误差。

4. 集群抽样集群抽样是将总体划分为假设干个群体或区域，然后在每个群体或区域内进行抽样。

谈谈几种典型的抽样方法（案例）摘要：本文以抽样方法为中心，主要阐述几种常见的抽样方法，如简单随机抽样，分层抽样，整群抽样，系统抽样以及配额抽样，探讨了各种抽样方法在实际生活的应用以及各自的优缺点等。

关键词：抽样调查，应用，缺点。

导语：抽样调查是一种非全面调查，它是从全部调查研究对象中，抽选一部分单位进行调查，并据以对全部调查研究对象作出估计和推断的一种调查方法。

显然，抽样调查虽然是非全面调查，但它的目的却在于取得反映总体情况的信息资料，因而，也可起到全面调查的作用。

抽样调查是建立在随机原则基础上，从总体中抽取部分单位进行调查，并概率估计原理，应用所的资料对总体的数量特征进行推断的一种调查方法。

例如，从某地区全部职工当中随机抽取部分职工，以家庭为单位按月调查取得有关收入、支出等方面的资料，并依据这些资料推断出全区职工的收支情况，这就是一种抽样调查。

从调查方法上来看，它是属于一种非全面调查。

但又与一般调查不同，它不只停留于搜集资料和整理资料，而且还要对资料进行分析，并据以推断总体的数量特征，从而提高统计的认识能力。

因此，抽样调查的理论和方法在统计中占有很重要的地位。

下面介绍一下常用的抽样方法：一. 简单随机抽样一般，设一个总体含有N个个体，从中逐个不放回地抽取n个个体作为样本（n≤N），如果每次抽取时总体内的个体被抽到的机会相等，就把这种抽样方法叫做简单随机抽样。

简单随机抽样的具体作法有：直接抽选法，抽签法，随机数法。

直接抽选法例如某项调查采用抽样调查的方法对某市职工收入状况进行研究，该市有职工56，000名，抽取5，000名职工进行调查，他们的年平均收入为10，000元，据此推断全市职工年收入为8，000--12，000元之间。

抽签法又称“抓阄法”。

它是先将调查总体的每个单位编号，然后采用随机的方法任意抽取号码，直到抽足样本。

在这里选取一个案例说明，如要在10个人中选取3个人作为代表，先把总体中的10个个体编号，把号码写在号签上，将号签放在一个容器中，搅拌均匀后，每次从中抽取一个号签，连续抽取3次，就得到一个容量为3的样本。

篇一：几种抽样调查方法比较几种抽样调查方法比较数理统计是用概率论的思想，方法去解决实际问题.在实际问题中出现的总的研究对象，我们称为总体，其分布一般是未知的，所以，首先要对总体进行抽样，以获取总体的有关信息——样本，再利用这些信息对总体进行分析.对于如何选取样本这个问题，经过人们不断的尝试、试验，渐渐地就有了“抽样论”，“试验设计”的发展.1895年，kiaer在国际统计学（isi）最早提出了“代表性抽样”的概念，后来经过neyman、hansen和mahalanobis等人的杰出贡献，抽样调查理论与方法在过去的一百年间，已经取得了很大发展.从概率抽样方法的发展和完善到收集信息与控制误差方面日益复杂的方法的应用，抽样调查已经取得了很大的进步.特别是近几十年来，在实践中实施的大型调查所涌现出的关于抽样设计和数据分析的难题，更是推动了理论研究的发展.在现实生活中，有很多实际问题将会用到数理统计的知识，它会有效地帮助我们分析和论证，从而得到我们需要的信息.为了更加有效地应用这些知识，就需要在总体中选取一个最合适的样本来为我们服务.从这个方面来说，样本的选取方法就成了一个至关重要的问题.只有找一个最简洁又具有代表性的样本，才能获得隐藏在数据背后的真相.本文主要介绍抽样调查理论，以及抽样调查的几种方法，并通过举例子介绍对比这几种方法.最后，本文又对抽样调查的这几种方法做了简单的总结和比较，显示了抽样调查理论在我们的生活中无处不在的强大生命力.一、基本概念1.抽样调查.它是一种非全面调查，它是从全部调查研究对象中，抽选一部分单位进行调查，并据以对全部调查研究对象作出估计和推断的一种调查方法.2.总体与样本.总体是我们所研究（调查）的对象的全体.例如在全国儿童情况调查中，全国所有0—14岁的儿童就构成调查的总体.调查的目的是为了得到有关这个总体的某些数据.例如全国儿童总数、每个年龄男女儿童的平均身高和平均体重等.这些有关总体的指标就是调查的目标量.如果进行一次对全国儿童的普查，对每个儿童都进行有关指标的调查，就可以获得这些总体目标量的数据，当然这实际上是很难做到的，为此我们按某种方法只从总体中抽取一部分进行调查，这一部分儿童就构成样本.根据这些样本数据就可以对总体目标量进行估计.3.概率抽样.抽取样本是抽样调查中的一个重要方法.最常用且最科学的方法是进行概率抽样，也称随机抽样.其优点是能保证样本的代表性，避免人为的误差，而且它可以对抽样误差进行估计，从而可以获得估计的精度.为了抽样便利，使概率抽样能够实施，通常将总体划分成互不重叠且又穷尽的若干个部分，每个部分称为一个抽样单元.4.误差与精度.抽样调查中有两类误差，一类是由于调查中获得的原始数据不正确，抽样框有缺陷，或在调查中由于种种原因无法得到按方案的全部样本数据等等，这类误差统称为非抽样误差；另一类误差是由于抽样引起的，即用样本估计总体所产生的误差，称为抽样误差.抽样误差通常用估计量的均方误差、标准差（或方差）等来表示.抽样误差越小，调查的精度就越高，精度的另一种表示方法是给出总体目标量的置信区间，即以一定的置信度（也用概率表示，例如95%）表示总体目标量落在一定的范围内.在相同的置信度下，置信区间长度愈短，精度就愈高.1二、抽样调查的优缺点1.优点：①经济性好，实效性强，适应面广，准确性高；②调查单位少，代表性强，所需调查人员少；③抽选的调查样本数量经过科学的计算确定的，有可靠的保证；④抽样调查的误差，是在调查前就可以根据调查样本数量和总体中各单位之间的差异程度进2.缺点：①所抽取样本是否具有代表性是抽样调查的关键；②具有不稳定性，有所偏差,存在一定的误差率；③抽样调查也存在调查的误差和偏误问题.通常误差有两种：一种是工作误差（也称登记误差或调查误差），一种是代表性误差（也称抽样误差）.三、抽样调查的特点抽样调查的本质特点是以部分来说明或代表总体.它是按照科学的原理和计算，从若干单位组成的事物总体中，抽取部分样本单位来进行调查、观察，用所得到的调查标志的数据以代表总体，推断总体.四、基本的抽样方法1.简单随机抽样设一个总体的个体数为n．如果通过逐个抽取的方法从中抽取一个样本，且每次抽取时各个个体被抽到的机会相等，就称这样的抽样为简单随机抽样．简单随机抽样是系统抽样和分层抽样不可或缺的基础，如何实施简单随机抽样有两种常用方法：抽签法和随机数表法．用抽签法抽取样本过程中，每一个个体被抽到的机会是均等的，这也是一个样本是否具有良好的代表性的关键前提．没有每个个体机会均等，就没有样本的公平性和合理性．同抽签法抽取样本一样，用随机数表法抽取样本的过程中，关键也是要保证每一个剩余个体被抽到的机会是均等的，这就要求：随机数表的确是随机产生的，不含人为因素在内；在选择随机数表中开始位置和方向时，也要保证随机性，如果在看过随机数表后再使用，所抽取的样本就失去了公平性，也就没有实际意义了．对于简单随机抽样需要注意：①它是不放回抽样；②它是逐个地进行抽取；③它是一种个体机会均等的抽样；④简单随机抽样适用于总体中的个体数不多的情况．生活中有许多用抽签法或类似抽签法的案例，如彩票摇奖、电视节目中电话号码抽奖、纳税凭证抽奖等．抽样时也要防止出现貌似合理的抽样方法，如到某星级宾馆问卷调查客人的收入情况来推断该地区的人均收入，或每隔一周到某一路口调查当地车流量等等．2.系统抽样当总体中的个体数较多时，可将总体平均分成几个部分，从每个部分抽取一个个体，得到所需的样本，这样的抽样方法称为系统抽样．从总体中抽取一个样本来估计总体，样本的抽取是否公平合理固然重要，样本抽取的方法是否经济可行也是十分重要的．面对容量很大的总体，抽取的样本容量显然不可太小，此时采用简单随机抽样是不经济也不可行的，这种情况下采用系统抽样也就更为合理可行．系统抽样以简单随机抽样为基础，通过将容量很大的总体分组，只需在某一个组内用简单随机抽样方式来抽取一个个体，然后在一定规则下就能抽取出全部样本，在保证公平客观的前提下简化抽样过程．对于系统抽样需要注意：①系统抽样适用于总体中的个体数较多的情况，它与简单随机抽样的联系在于：将总体均分后的每一部分进行抽样时，采用的是简单随机抽样；②与简单随机抽样一样，系统抽样是等可能抽样，它是客观的、公平的；③总体中的个体数恰好能被样本容量整除时，可用它们的比值行计算，并控制在允许范围以内，调查结果的准确程度较高.2作为系统抽样的间隔；当总体中的个体数不能被样本容量整除时，可用简单随机抽样先从总体中剔除少量个体，使剩下的个体数能被样本容量整除再进行系统抽样．3.分层抽样一般地，当总体由差异明显的几部分组成时，为了使样本更客观地反映总体情况，常将总体中的个体按不同的特点分成层次比较分明的几部分，然后按照各部分所占的比例实施抽样，这种抽样方法叫做分层抽样，其中所分成的各个部分叫做层．分层抽样同样是以简单随机抽样为基础的一种抽样方式，对于容量较大、个体差异不明显的总体通常采用系统抽样方法，但对于许多容量较大、个体差异较大且明显分成几部分的总体，系统抽样虽然保证公平性和客观性，但样本还是不具有良好的代表性，这时就考虑用分层抽样的方法来抽取样本.对于分层抽样需要注意：①分层抽样适用于总体由差异比较明显的几个部分组成的情况，是等可能抽样，它也是客观的、公平的；②分层抽样是建立在简单随机抽样或系统抽样的基础上的，由于它充分利用了已知信息，使样本具有较好的代表性，而且在各层抽样时可以根据情况采用不同的抽样方法，因此在实践中有着非常广泛的应用.五、简单例子eg1. 某校高一年级有20个班，每班有50名学生．为了了解高一学生的视力状况，从这1000人中抽取一个容量为100的样本进行检查，应该怎样抽样?由分析可得，本例抽取方式可能有：1）以班级为单位，在每个班级内采用随机抽样方法来获取5人样本，最后汇总形成100人的所需样本；2）在班级抽样时，可以将50人按学号分成10组，分别由每组随机抽出一个个体来组成10人样本．这两种抽样方式，虽然总体工作量还是大，但每个班级的每个小组的工作量却很小，也基本能保证样本的公平性．主要因为参与抽样的人多了，易受到人为因素影响．如果在某个班级由学号分成的10个小组中任取一个小组来，采用随机抽样的方式抽出一名学生，其他小组直接抽出与这位学生学号个位数一致的学生，最后在其余班级中找出与该班级学号一致的学生共同组成样本.从而，系统抽样方法为：先将容量较大的总体平均分成容量较小的几个小组，在某一个小组内用简单随机抽样的方法来抽取一定个体，再按一定规则从其他小组抽出同样数量的个体，最后组成样本．这样，使得整个抽样过程大大简化．这个简单的例子说明：当样本容量过大时，应该采用系统抽样的方法，既可简化工作量，又能够简单快速的得到人们想要的结果.eg2. 某单位在岗职工共624人，为了调查工人用于上班途中的时间，决定抽取10%的工人进行调查．如何采取抽样方法完成这一抽样?由分析可得，因为此样本容量过多，符合系统抽样的要求，且能简化工作量，因此我们采用系统抽样的方法. 根据系统抽样的步骤，由于624的10%约为62，624不能被62整除，为了保证“等距”分段，应剔除4人，得到如下解法：1）将624名职工用随机方式进行编号；2）从总体中剔除4人（剔除方法可用随机数表法），将剩下的620名职工重新编号（分别为000，001，002，??，619），并分成62段；3）在第一段000，??，009这十个编号中用简单随机抽样确定起始号码i0;4）将编号为i0，i0+10，??，i0+610的个体抽出，组成样本.如果只采用最简单的随机抽样，由于不知道应该抽取多少的个体才会使构成的样本具有代表性，会产生很多不必要的误差，所以在这种情况下，采用系统抽样会更好一点.需要注意的是，系统抽样适合于容量较大而差异不太大的总体，而现实生活中，许多总体的容量非常庞大，甚至不可数，如测量某一棉田中棉株的平均高度，测量某一路口在某一时段的车流量等，这时用简单随机抽样已无法完成抽样，那么可以用系统抽样的方法．测量某一棉田中棉株的平均高度，其样本的抽取可采用如下方式：先确定所要测量的样本容量大小（n），测量这块棉田中所有行的长度之和(s)，然后从第一行第一株开始，每隔s/（n-1）距离就测一株棉花的高度，也就能得到全部样本的高度．测量某一路口在某一时段的车流量，其样本采集可用类似方式：每隔3天（从测量的第一天开始，在第1，4，7，??天测量），测量n次后，就可获得一个容量为n的样本．在确定时间间隔时，要考虑如下因素：车流量变化一般以周为周期，还受季节气候的影响.3上述两个例子表明在使用抽样方法时，为了使结果客观、合理、公平，应该把系统抽样，简单随机抽样以及分层抽样结合起来，而不是单独使用其中一种，他们三者之间是相互辅助，相互渗透的关系. eg3. 某电视台在因特网上就观众对某一节目的喜爱程度进行调查，参加查的总人数为12000人，其中? 对于这个问题可以有以下三种解法：①采用简单随机抽样方法，其总体容量为12000. 可以随机抽取60人进行调查.②采用系统抽样方法，其总体容量为12000.依照系统抽样的步骤，可先把这12000人编号00000到11999；再每200人分为一组编号零零一组到二零零组；从每组中分别随机抽取一个个体；抽取的这60个个体就组成了一个样本；对这组样本进行调查.③采用分层抽样方法，其总体容量为12000．“很喜爱”占2415/12000，应取60×2415/12000≈12人；“喜爱”占4567/12000，应取60×4567/12000≈23人；“一般”占3926/12000，应取60×3926/12000≈20人；“不喜爱”占1072/12000，应取60×1072/12000≈5人．因此，采用分层抽样的方法在“很喜爱”、“喜爱”、“一般”、“不喜爱”的人中分别抽取12人、23人、20人和5人．然后对这组样本进行调查.根据上面的分析解答，由于样本容量过多，采用简单的随机抽样会使问题不具有代表性，所以不适合采用简单随即抽样；而由于持有不同态度的人差异较大，进行系统抽样的话，因喜爱此节目的人较多，使得在这种情况下选取的样本不具有公平和等概率性，所以也不适合采用系统抽样方法；采用分层抽样，得到的样本既具有代表性，又具有公平性和随机性，是最适合的抽样方法.六、小结系统抽样是对于样本容量较大而相互之间差距不是很大的总体比较好，它包括抽样和估计两个环节；而分层抽样是对于样本容量较大且差距较明显的总体比较适合，他包括分层、抽样和估计三个环节.简单随机抽样是系统抽样和分层抽样得以进行的基础.在很多问题中，应该把三者结合起来，才会达到更好的效果.它们之间是相辅相成，相互影响的，只有把这三者结合起来，才能使抽样调查的技术走向前进.样本的抽取是否得当对研究总体来说十分关键，掌握正确的抽样方法是十分重要的.抽样调查是根据数理统计理论建立起来的一种科学的统计调查方法.它虽然是非全面调查，但它的目的却在于取得反映总体情况的信息资料，因而，也可起到全面调查的作用.抽样调查在人类活动的许多领域，特别是在社会经济领域中有着广泛的应用.我国目前还处在抽样调查理论和技术发展相对落后的阶段，仅仅是在国外研究的基础上稍加改进.但是我相信，在我国相关人士的努力下，我国在这方面一定会奋起直追，研究出新的适合我国国情的抽样调查理论新方法.参考文献：[1] 盛骤概率论与数理统计[m] 北京高等教育出版社 2008[2] 夏宁茂新编概率论与数理统计[m] 上海华东理工大学出版社 2005[3] 赵雪慧抽样调查理论与方法的最新进展[j] 北京系统与信息论坛 2003.9[4] 克拉美h 统计学数学方法(魏宗舒等译)[j] 上海上海科学技术出版社 1966[5] 费史m 概率论于数理统计（王福保译）[j] 上海上海科学技术出版社 1962[6] 郝向东浅谈系统抽样与分层抽样[j] 北京统计与信息论坛 1996:04[7] greg dickman business statistics[j] nelson 1998[9] b efron bootstrap methods:another look at the jackknife[j] annals of statistics 1979:25-264[10]r musil,m baur,w pfister testing practices for the ac breakdown voltage “testing ofinsulation liquids”[j] ieee electrical insulation magazine 1995:21-26[11]e.l.lehmann nonparametrics:statistical methods based on ranks[j]美国holden-day 公司 1975[12]fisher r a theory of statistical estimation proceedings of the cambridge philosophicalsociety 1925(22):710-715[13]barr d r darling d a a.kolmogorov-smirnov test for gensored samples[j] technometrics1973(15):739-757[14]kaziol j a byar d p percentage points of the asymptotic distributions of one and two samplesk-s statistics for truncated or censored date[j] technometrics 1975(17):507-510 [15]finklestein j m,schafer r e improved goodness of fit tests[j] biometrika 1971(58):641-6455篇二：抽样调查方法简介抽样调查方法简介（一）抽样调查的类别抽样调查可以分为两种：随机抽样和非随机抽样。

谈谈几种典型的抽样方法（案例）摘要:本文以抽样方法为中心，主要阐述几种常见的抽样方法,如简单随机抽样，分层抽样，整群抽样，系统抽样以及配额抽样，探讨了各种抽样方法在实际生活的应用以及各自的优缺点等。

关键词：抽样调查，应用，缺点。

导语：抽样调查是一种非全面调查，它是从全部调查研究对象中，抽选一部分单位进行调查，并据以对全部调查研究对象作出估计和推断的一种调查方法.显然,抽样调查虽然是非全面调查，但它的目的却在于取得反映总体情况的信息资料,因而,也可起到全面调查的作用。

抽样调查是建立在随机原则基础上，从总体中抽取部分单位进行调查，并概率估计原理，应用所的资料对总体的数量特征进行推断的一种调查方法.例如,从某地区全部职工当中随机抽取部分职工，以家庭为单位按月调查取得有关收入、支出等方面的资料，并依据这些资料推断出全区职工的收支情况,这就是一种抽样调查。

从调查方法上来看，它是属于一种非全面调查.但又与一般调查不同，它不只停留于搜集资料和整理资料，而且还要对资料进行分析，并据以推断总体的数量特征,从而提高统计的认识能力。

因此，抽样调查的理论和方法在统计中占有很重要的地位。

下面介绍一下常用的抽样方法：一。

简单随机抽样一般，设一个总体含有N个个体,从中逐个不放回地抽取n个个体作为样本（n≤N），如果每次抽取时总体内的个体被抽到的机会相等，就把这种抽样方法叫做简单随机抽样.简单随机抽样的具体作法有:直接抽选法，抽签法，随机数法。

直接抽选法例如某项调查采用抽样调查的方法对某市职工收入状况进行研究，该市有职工56，000名，抽取5，000名职工进行调查，他们的年平均收入为10，000元，据此推断全市职工年收入为8，000——12，000元之间。

抽签法又称“抓阄法”。

它是先将调查总体的每个单位编号,然后采用随机的方法任意抽取号码,直到抽足样本。

在这里选取一个案例说明，如要在10个人中选取3个人作为代表，先把总体中的10个个体编号，把号码写在号签上，将号签放在一个容器中，搅拌均匀后，每次从中抽取一个号签，连续抽取3次，就得到一个容量为3的样本。