中考二次函数压轴试题分类汇编及答案(1)

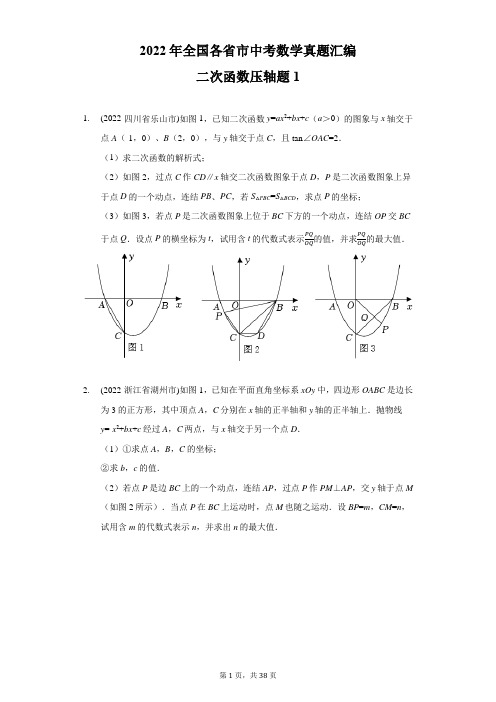
2022年全国各省市中考数学真题汇编二次函数压轴题11.(2022·四川省乐山市)如图1，已知二次函数y=ax2+bx+c（a＞0）的图象与x轴交于点A（-1，0）、B（2，0），与y轴交于点C，且tan∠OAC=2．（1）求二次函数的解析式；（2）如图2，过点C作CD∥x轴交二次函数图象于点D，P是二次函数图象上异于点D的一个动点，连结PB、PC，若S△PBC=S△BCD，求点P的坐标；（3）如图3，若点P是二次函数图象上位于BC下方的一个动点，连结OP交BC于点Q．设点P的横坐标为t，试用含t的代数式表示PQOQ的值，并求PQOQ的最大值．2.(2022·浙江省湖州市)如图1，已知在平面直角坐标系xOy中，四边形OABC是边长为3的正方形，其中顶点A，C分别在x轴的正半轴和y轴的正半轴上．抛物线y=-x2+bx+c经过A，C两点，与x轴交于另一个点D．（1）①求点A，B，C的坐标；②求b，c的值．（2）若点P是边BC上的一个动点，连结AP，过点P作PM⊥AP，交y轴于点M （如图2所示）．当点P在BC上运动时，点M也随之运动．设BP=m，CM=n，试用含m的代数式表示n，并求出n的最大值．3.(2022·湖南省邵阳市)如图，已知直线y=2x+2与抛物线y=ax2+bx+c相交于A，B两点，点A在x轴上，点B在y轴上，点C（3，0）在抛物线上．（1）求该抛物线的表达式．（2）正方形OPDE的顶点O为直角坐标系原点，顶点P在线段OC上，顶点E在y轴正半轴上，若△AOB与△DPC全等，求点P的坐标．（3）在条件（2）下，点Q是线段CD上的动点（点Q不与点D重合），将△PQD 沿PQ所在的直线翻折得到△PQD'，连接CD'，求线段CD'长度的最小值．4.(2022·湖南省衡阳市)如图，已知抛物线y=x2-x-2交x轴于A、B两点，将该抛物线位于x轴下方的部分沿x轴翻折，其余部分不变，得到的新图象记为“图象W”，图象W交y轴于点C．（1）写出图象W位于线段AB上方部分对应的函数关系式；（2）若直线y=-x+b与图象W有三个交点，请结合图象，直接写出b的值；（3）P为x轴正半轴上一动点，过点P作PM∥y轴交直线BC于点M，交图象W 于点N，是否存在这样的点P，使△CMN与△OBC相似？若存在，求出所有符合条件的点P的坐标；若不存在，请说明理由．5.(2022·江苏省苏州市)如图，二次函数y=-x2+2mx+2m+1（m是常数，且m＞0）的图象与x轴交于A，B两点（点A在点B的左侧），与y轴交于点C，顶点为D．其对称轴与线段BC交于点E，与x轴交于点F．连接AC，BD．（1）求A，B，C三点的坐标（用数字或含m的式子表示），并求∠OBC的度数；（2）若∠ACO=∠CBD，求m的值；（3）若在第四象限内二次函数y=-x2+2mx+2m+1（m是常数，且m＞0）的图象上，始终存在一点P，使得∠ACP=75°，请结合函数的图象，直接写出m的取值范围．6.(2022·山东省泰安市)若二次函数y=ax2+bx+c的图象经过点A（-2，0），B（0，-4），其对称轴为直线x=1，与x轴的另一交点为C．（1）求二次函数的表达式；（2）若点M在直线AB上，且在第四象限，过点M作MN⊥x轴于点N．①若点N在线段OC上，且MN=3NC，求点M的坐标；②以MN为对角线作正方形MPNQ（点P在MN右侧），当点P在抛物线上时，求点M的坐标．7.(2022·湖南省株洲市)已知二次函数y=ax2+bx+c（a＞0）．（1）若a=1，b=3，且该二次函数的图象过点（1，1），求c的值；（2）如图所示，在平面直角坐标系xOy中，该二次函数的图象与x轴相交于不同的两点A（x1，0）、B（x2，0），其中x1＜0＜x2、|x1|＞|x2|，且该二次函数的图象的顶点在矩形ABFE的边EF上，其对称轴与x轴、BE分别交于点M、N，BE与y轴相交于点P，且满足tan∠ABE=34．①求关于x的一元二次方程ax2+bx+c=0的根的判别式的值；②若NP=2BP，令T=1a2+165c，求T的最小值．阅读材料：十六世纪的法国数学家弗朗索瓦•韦达发现了一元二次方程的根与系数之间的关系，可表述为“当判别式△≥0时，关于x的一元二次方程ax2+bx+c=0（a≠0）的两个根x1、x2有如下关系：x1+x2=−ba ，x1x2=ca”．此关系通常被称为“韦达定理”．8.(2022·湖南省怀化市)如图一所示，在平面直角坐标中，抛物线y=ax2+2x+c经过点A（-1，0）、B（3，0），与y轴交于点C，顶点为点D．在线段CB上方的抛物线上有一动点P，过点P作PE⊥BC于点E，作PF∥AB交BC于点F．（1）求抛物线和直线BC的函数表达式．（2）当△PEF的周长为最大值时，求点P的坐标和△PEF的周长．（3）若点G是抛物线上的一个动点，点M是抛物线对称轴上的一个动点，是否存在以C、B、G、M为顶点的四边形为平行四边形？若存在，求出点G的坐标，若不存在，请说明理由．9.(2022·甘肃省武威市)如图1，在平面直角坐标系中，抛物线y=1（x+3）（x-a）与x4轴交于A，B（4，0）两点，点C在y轴上，且OC=OB，D，E分别是线段AC，AB上的动点（点D，E不与点A，B，C重合）．（1）求此抛物线的表达式；（2）连接DE并延长交抛物线于点P，当DE⊥x轴，且AE=1时，求DP的长；（3）连接BD．①如图2，将△BCD沿x轴翻折得到△BFG，当点G在抛物线上时，求点G的坐标；②如图3，连接CE，当CD=AE时，求BD+CE的最小值．10.(2022·云南省)已知抛物线y=-x2-√3x+c经过点（0，2），且与x轴交于A、B两点．设k是抛物线y=-x2-√3x+c与x轴交点的横坐标，M是抛物线y=-x2-√3x+c上的点，常数m＞0，S为△ABM的面积．已知使S=m成立的点M恰好有三个，设T为这三个点的纵坐标的和．（1）求c的值；（2）直接写出T的值；的值．（3）求k4k8+k6+2k4+4k2+1611.(2022·四川省达州市)如图1，在平面直角坐标系中，已知二次函数y=ax2+bx+2的图象经过点A（-1，0），B（3，0），与y轴交于点C．（1）求该二次函数的表达式；（2）连接BC，在该二次函数图象上是否存在点P，使∠PCB=∠ABC？若存在，请求出点P的坐标；若不存在，请说明理由；（3）如图2，直线l为该二次函数图象的对称轴，交x轴于点E．若点Q为x轴上方二次函数图象上一动点，过点Q作直线AQ，BQ分别交直线l于点M，N，在点Q的运动过程中，EM+EN的值是否为定值？若是，请求出该定值；若不是，请说明理由．12.(2022·江苏省连云港市)已知二次函数y=x2+（m-2）x+m-4，其中m＞2．（1）当该函数的图象经过原点O（0，0），求此时函数图象的顶点A的坐标；（2）求证：二次函数y=x2+（m-2）x+m-4的顶点在第三象限；（3）如图，在（1）的条件下，若平移该二次函数的图象，使其顶点在直线y=-x-2上运动，平移后所得函数的图象与y轴的负半轴的交点为B，求△AOB面积的最大值．13.(2022·浙江省舟山市)已知抛物线L1：y=a（x+1）2-4（a≠0）经过点A（1，0）．（1）求抛物线L1的函数表达式．（2）将抛物线L1向上平移m（m＞0）个单位得到抛物线L2．若抛物线L2的顶点关于坐标原点O的对称点在抛物线L1上，求m的值．（3）把抛物线L1向右平移n（n＞0）个单位得到抛物线L3．已知点P（8-t，s），Q（t-4，r）都在抛物线L3上，若当t＞6时，都有s＞r，求n的取值范围．14.(2022·安徽省)如图1，隧道截面由抛物线的一部分AED和矩形ABCD构成，矩形的一边BC为12米，另一边AB为2米．以BC所在的直线为x轴，线段BC的垂直平分线为y轴，建立平面直角坐标系xOy，规定一个单位长度代表1米．E（0，8）是抛物线的顶点．（1）求此抛物线对应的函数表达式；（2）在隧道截面内（含边界）修建“”型或“”型栅栏，如图2、图3中粗线段所示，点P1，P4在x轴上，MN与矩形P1P2P3P4的一边平行且相等．栅栏总长l 为图中粗线段P1P2，P2P3，P3P4，MN长度之和，请解决以下问题：（ⅰ）修建一个“”型栅栏，如图2，点P2，P3在抛物线AED上．设点P1的横坐标为m（0＜m≤6），求栅栏总长l与m之间的函数表达式和l的最大值；（ⅱ）现修建一个总长为18的栅栏，有如图3所示的“”型和“”型两种设计方案，请你从中选择一种，求出该方案下矩形P1P2P3P4面积的最大值，及取最大值时点P1的横坐标的取值范围（P1在P4右侧）．15.(2022·四川省德阳市)抛物线的解析式是y=-x2+4x+a．直线y=-x+2与x轴交于点M，与y轴交于点E，点F与直线上的点G（5，-3）关于x轴对称．（1）如图①，求射线MF的解析式；（2）在（1）的条件下，当抛物线与折线EMF有两个交点时，设两个交点的横坐标是x1，x2（x1＜x2），求x1+x2的值；（3）如图②，当抛物线经过点C（0，5）时，分别与x轴交于A，B两点，且点A 在点B的左侧．在x轴上方的抛物线上有一动点P，设射线AP与直线y=-x+2交于点N．求PN的最大值．AN16.(2022·四川省凉山彝族自治州)在平面直角坐标系xOy中，已知抛物线y=-x2+bx+c经过点A（-1，0）和点B（0，3），顶点为C，点D在其对称轴上，且位于点C 下方，将线段DC绕点D按顺时针方向旋转90°，点C落在抛物线上的点P处．（1）求抛物线的解析式；（2）求点P的坐标；（3）将抛物线平移，使其顶点落在原点O，这时点P落在点E的位置，在y轴上是否存在点M，使得MP+ME的值最小，若存在，求出点M的坐标；若不存在，请说明理由．17.(2022·四川省泸州市)如图，在平面直角坐标系xOy中，已知抛物线y=ax2+x+c经过A（-2，0），B（0，4）两点，直线x=3与x轴交于点C．（1）求a，c的值；（2）经过点O的直线分别与线段AB，直线x=3交于点D，E，且△BDO与△OCE 的面积相等，求直线DE的解析式；（3）P是抛物线上位于第一象限的一个动点，在线段OC和直线x=3上是否分别存在点F，G，使B，F，G，P为顶点的四边形是以BF为一边的矩形？若存在，求出点F的坐标；若不存在，请说明理由．18.(2022·四川省遂宁市)如图，在平面直角坐标系中，抛物线y=x2+bx+c与x轴交于A、B两点，与y轴交于点C，其中点A的坐标为（-1，0），点C的坐标为（0，-3）．（1）求抛物线的解析式；（2）如图1，E为△ABC边AB上的一动点，F为BC边上的一动点，D点坐标为（0，-2），求△DEF周长的最小值；（3）如图2，N为射线CB上的一点，M是抛物线上的一点，M、N均在第一象限内，B、N位于直线AM的同侧，若M到x轴的距离为d，△AMN面积为2d，当△AMN 为等腰三角形时，求点N的坐标．参考答案1.解：（1）∵A （-1，0），∴OA =1，∵∠AOC =90°，∴tan ∠OAC =OC OA =2，∴OC =2OA =2，∴点C （0，-3），设二次函数的解析式为：y =a （x +1）•（x -2），∴a •1×（-2）=-2，∴a =1，∴y =（x +1）•（x -2）=x 2-x -2；（2）设点P （a ，a 2-a -2），如图1，当点P 在第三象限时，作PE ∥AB 交BC 于E ，∵B （2，0），C （0，-2），∴直线BC 的解析式为：y =x -2，∴当y =a 2-a -2时，x =y +2=a 2-a ，∴PE =a 2-a -a =a 2-2a ，∴S △PBC =12PE •OC ，∵抛物线的对称轴为直线y =12，CD ∥x 轴，C （0，-2），∴点D （1，-2），∴CD =1，∴S △BCD =12CD ⋅OC ，∴12PE •OC =12CD •OC ，∴a 2-2a =1，∴a1=1+√2（舍去），a2=1-√2，当x=1-√2时，y=a2-a-2=a-1=-√2，∴P（1-√2，-√2），如图2，当点P在第一象限时，作PE⊥x轴于E，交直线BC于F，∴F（a，a-2）∴PF=（a2-a-2）-（a-2）=a2-2a，∴S△PBC=12PF⋅OB=12CD•OC，∴a2-2a=1，∴a1=1+√2，a2=1-√2（舍去），当a=1+√2时，y=a2-a-2=a2-2a+a-2=1+1+√2-2=√2，∴P（1+√2，√2），综上所述：P（1+√2，√2）或（1-√2，-√2）；（3）如图3，作PN⊥AB于N，交BC于M，∵P（t，t2-t-2），M（t，t-2），∴PM=（t-2）-（t2-t-2）=-t2+2t，∵PN∥OC，∴△PQM∽△OQC，∴PQ OQ =PM OC =−t 2+2t 2=-12(t −1)2+12， ∴当t =1时，（PQ OQ ）最大=12．2.解：（1）①四边形OABC 是边长为3的正方形，∴A （3，0），B （3，3），C （0，3）；②把A （3，0），C （0，3）代入抛物线y =-x 2+bx +c 中得：{−9+3b +c =0c =3， 解得：{b =2c =3； （2）∵AP ⊥PM ，∴∠APM =90°，∴∠APB +∠CPM =90°，∵∠B =∠APB +∠BAP =90°，∴∠BAP =∠CPM ，∵∠B =∠PCM =90°，∴△MCP ∽△PBA ，∴PC AB =CM PB ，即3−m 3=n m ， ∴3n =m （3-m ），∴n =-13m 2+m =-13（m -32）2+34，∵-13＜0，∴当m =32时，n 的值最大，最大值是34． 3.解：在直线y =2x +2中，当x =2时，y =2，当y =0时，x =-1，∴点A 的坐标为（-1，0），点B 的坐标为（0，2），把点A （-1，0），点B （0，2），点C （3，0）代入y =ax 2+bx +c ，{a −b +c =0c =29a +3b +c =0，解得{a =−23b =43c =2，∴抛物线的解析式为y =-23x 2+43x +2；（2）①当△AOB≌△DPC时，AO=DP，又∵四边形OPDE为正方形，∴DP=OP=AO=1，此时点P的坐标为（1，0），②当△AOB≌△CPD时，OB=DP，又∵四边形OPDE为正方形，∴DP=OP=OB=2，此时点P的坐标为（2，0），综上，点P的坐标为（1，0）或（2，0）；（3）如图，点D′在以点P为圆心，DP为半径的圆上运动，∴当点D′′，点P，点C三点共线时，CD′′有最小值，由（2）可得点P的坐标为（1，0）或（2，0），且C点坐标为（3，0），∴CD′′的最小值为1．4.解：（1）当x=0时，y=-2，∴C（0，2），当y=0时，x2-x-2=0，（x-2）（x+1）=0，∴x1=2，x2=-1，∴A（-1，0），B（2，0），设图象W的解析式为：y=a（x+1）（x-2），把C（0，2）代入得：-2a=2，∴a=-1，∴y=-（x+1）（x-2）=-x2+x+2，∴图象W位于线段AB上方部分对应的函数关系式为：y=-x2+x+2（-1≤x≤2）；（2）由图象得直线y=-x+b与图象W有三个交点时，存在两种情况：①当直线y=-x+b过点C时，与图象W有三个交点，此时b=2；②当直线y=-x+b与图象W位于线段AB上方部分对应的函数图象相切时，如图1，-x+b=-x2+x+2，x2-2x+b-2=0，Δ=（-2）2-4×1×（b-2）=0，∴b=3，综上，b的值是2或3；（3）∵OB=OC=2，∠BOC=90°，∴△BOC是等腰直角三角形，如图2，CN∥OB，△CNM∽△BOC，∵PN∥y轴，∴P（1，0）；如图3，CN ∥OB ，△CNM ∽△BOC ，当y =2时，x 2-x -2=2，x 2-x -4=0，∴x 1=1+√172，x 2=1−√172， ∴P （1+√172，0）； 如图4，当∠MCN =90°时，△OBC ∽△CMN ，∴CN 的解析式为：y =x +2，∴x +2=x 2-x -2，∴x 1=1+√5，x 2=1-√5（舍），∴P （1+√5，0），综上，点P 的坐标为（1，0）或（1+√172，0）或（1+√5，0）．5.解：（1）当y =0时，-x 2+2mx +2m +1=0，解方程，得x 1=-1，x 2=2m +1，∵点A在点B的左侧，且m＞0，∴A（-1，0），B（2m+1，0），当x=0时，y=2m+1，∴C（0，2m+1），∴OB=OC=2m+1，∵∠BOC=90°，∴∠OBC=45°；（2）如图1中，连接AE．∵y=-x2+2mx+2m+1=-（x-m）2+（m+1）2，∴D（m，（m+1）2），F（m，0），∴DF=（m+1）2，OF=m，BF=m+1，∵A，B关于对称轴对称，∴AE=BE，∴∠EAB=∠OBC=45°，∵∠ACO=∠CBD，∠OCB=∠OBC，∴∠ACO+∠OCB=∠CBD+∠OBC，即∠ACE=∠DBF，∵EF∥OC，∴tan∠ACE=AECE =BECE=BFOF=m+1，∴m+1m=m+1，∴m=1或-1，∵m＞0，∴m=1；（3）如图，设PC交x轴于点Q．当点P 在第四象限时，点Q 总是在点B 的左侧，此时∠CQA ＞∠CBA ，即∠CQA ＞45°， ∵∠ACQ =75°，∴∠CAO ＜60°，∴2m +1＜√3， ∴m ＜√3−12， ∴0＜m ＜√3−12． 6.解：（1）∵二次函数y =ax 2+bx +c 的图象经过点B （0，-4），∴c =-4，∵对称轴为直线x =1，经过A （-2，0），∴{−b2a =14a −2b −4=0， 解得{a =12b =−1， ∴抛物线的解析式为y =12x 2-x -4；（2）①如图1中，设直线AB 的解析式为y =kx +n ，∵A （-2，0），B （0，-4），∴{−2k +n =0n =−4，解得{k =−2n =−4， ∴直线AB 的解析式为y =-2x -4，∵A ，C 关于直线x =1对称，∴C （4，0），设N （m ，0），∵MN ⊥x 轴，∴M （m ，-2m -4），∴NC =4-m ，∵MN =3NC ，∴2m +4=3（4-m ），∴m =85， ∴点M （85，-365）；②如图2中，连接PQ ，MN 交于点E ．设M （t ，-2t -4），则点N （t ，0），∵四边形MPNQ 是正方形，∴PQ ⊥MN ，NE =EP ，NE =12MN ，∴PQ ∥x 轴，∴E （t ，-t -2），∴NE =t +2，∴ON +EP =ON +NE =t +t +2=2t +2，∴P （2t +2，-t -2），∵点P 在抛物线y =12x 2-x -4上，∴12（2t +2）2-（2t +2）-4=-t -2，解得t 1=12，t 2=-2，∵点P在第四象限，∴t=-2舍去，∴t=12，∴点M坐标为（12，-5）．7.解：（1）当a=1，b=3时，y=x2+3x+c，把x=1，y=1代入得，1=1+3+c，∴c=-3；（2）①由ax2+bx+c=0得，x1=−b−√b2−4ac2a ，x2=−b+√b2−4ac2a，∴AB=x2-x1=√b2−4aca，∵抛物线的顶点坐标为：（-b2a ，4ac−b24a），∴AE=b2−4ac4a ，OM=b2a，∵∠BAE=90°，∴tan∠ABE=AEAB =3 4，∴b2−4ac4a ÷√b2−4aca=34，∴b2-4ac=9；②∵b2-4ac=9，∴x2=−b+32a，∵OP∥MN，∴NPBP =OMOB，∴b2a ：−b+32a=2，∴b=2，∴22-4ac=9，∴c=-54a，∴T=1a2+165c=1a2-54a⋅165=1a2-4a=（1a-2）2+4，∴当1a =2时，T 最小=4， 即a =12时，T 最小=4．8.解：（1）∵抛物线y =ax 2+2x +c 经过点A （-1，0）、B （3，0），∴{a −2+c =09a +6+c =0， 解得{a =−1c =3，∴抛物线的解析式为y =-x 2+2x +3， 令x =0，可得y =3， ∴C （0，3），设直线BC 的解析式为y =kx +b ，则{b =33k +b =0，∴{k =−1b =3， ∴直线BC 的解析式为y =-x +3；（2）如图一中，连接PC ，OP ，PB ．设P （m ，-m 2+2m +3），∵B （3，0），C （0，3）， ∴OB =OC =3， ∴∠OBC =45°， ∵PF ∥AB ，∴∠PFE =∠OBC =45°， ∵PE ⊥BC ，∴△PEF 是等腰直角三角形，∴PE 的值最大时，△PEF 的周长最大， ∵S △PBC =S △POB +S △POC -S △OBC=12×3×（-m 2+2m +3）+12×3×m -12×3×3 =-32m 2+92m=-32（m -32）2+94， ∵-32＜0，∴m =32时，△PBC 的面积最大，面积的最大值为94，此时PE 的值最大， ∵12×3√2×PE =94， ∴PE =√32，∴△PEF 的周长的最大值=√32+√32+√62=√3+√62，此时P （32，154）；（3）存在．理由：如图二中，设M （1，t ），G （m ，-m 2+2m +3）．当BC 为平行四边形的边时，则有|1-m |=3， 解得m =-2或4，∴G （-2，-5）或（4，-5），当BC 为平行四边形的对角线时，12（1+m ）=12（0+3）， ∴m =2， ∴G （2，3），综上所述，满足条件的点G 的坐标为（-2，5）或（4，-5）或（2，3）．9.解：（1）∵抛物线y =14（x +3）（x -a ）与x 轴交于A ，B （4，0）两点，∴14（4+3）（4-a ）=0， 解得a =4，∴y =14（x +3）（x -4）=14x 2-14x -3， 即抛物线的表达式为y =14x 2-14x -3；（2）在y =14（x +3）（x -4）中，令y =0，得x =-3或4， ∴A （-3，0），OA =3， ∵OC =OB =4， ∴C （0，4）， ∵AE =1，∴DE =AE •tan ∠CAO =AE ⋅OCOA =1×43=43，OE =OA -AE =3-1=2， ∴E （-2，0）， ∵DE ⊥x 轴， ∴x P =x D =x E =-2，∴y P =14（-2+3）（-2-4）=-32， ∴PE =32，∴DP =DE +PE =43+32=176；（3）①如下图，连接DG 交AB 于点M ，∵△BCD 与BFG 关于x 轴对称， ∴DG ⊥AB ，DM =GM ，设OM =a （a ＞0），则AM =OA -OM =3-a ， MG =MD =AM •tan ∠CAO =43（3-a ）， ∴G （-a ，43（a -3）），∵点G （-a ，43（a -3））在抛物线y =14（x +3）（x -4）上， ∴14（-a +3）（-a -4）=43（a -3）， 解得a =43或3（舍去）， ∴G （-43，-209）；②如下图，在AB 的下方作∠EAQ =∠DCB ，且AQ =BC ，连接EQ ，CQ ，∵AE =CD ，∴△AEQ ≌△CDB （SAS ）， ∴EQ =BD ，∴当C 、E 、Q 三点共线时，BD +CE =EQ +CE 最小，最小为CQ ， 过点C 作CH ⊥AQ ，垂足为H ， ∵OC ⊥OB ，OC =OB =4， ∴∠CBA =45°，BC =4√2，∵∠CAH =180°-∠CAB -∠EAQ =180°-∠CAB -∠DCB =∠CBA =45°， AC =√OA 2+OC 2=√32+42=5，AH =CH =√22AC =5√22，HQ =AH +AQ =AH +BC =5√22+4√2=13√22，∴CQ =√CH 2+HQ 2=√(5√22)2+(13√22)2=√97，即BD +CE 的最小值为√97．10.解：（1）把点（0，2）代入抛物线y =-x 2-√3x +c 中得：c =2；（2）由（1）知：y =-x 2-√3x +2=-（x +√32）2+114，∴顶点的坐标为（-√32，114），∵使S =m 成立的点M 恰好有三个，常数m ＞0，S 为△ABM 的面积， ∴其中一个点M 就是抛物线的顶点， ∴T =-114×2+114=-114；（3）当y =0时，-x 2-√3x +2=0， x 2+√3x -2=0，∵k 是抛物线y =-x 2-√3x +c 与x 轴交点的横坐标，即x =k 是x 2+√3x -2=0的解， ∴k 2+√3k -2=0， ∴k 2=2-√3k ，∴k 4=（2-√3k ）2=4-4√3k +3k 2=4-4√3k +3（2-√3k ）=10-7√3k ， ∵k 8+k 6+2k 4+4k 2+16=（10-7√3k ）2+（2-√3k ）（10-7√3k ）+2（10-7√3k ）+4（2-√3k ）+16 =100-140√3k +147k 2+20-24√3k +21k 2+20-14√3k +8-4√3k +16 =164-182√3k +168（2-√3k ） =500-350√3k ， ∴k 4k 8+k 6+2k 4+4k 2+16=10−7√3k50(10−7√3k) =150．11.解：（1）∵抛物线y =ax 2+bx +2经过点A （-1，0），B （3，0），∴{a −b +2=09a +3b +2=0， 解得：{a =−23b =43，∴该二次函数的表达式为y =−23x 2+43x +2； （2）存在，理由如下： 如图1，当点P 在BC 上方时， ∵∠PCB =∠ABC ， ∴CP ∥AB ，即CP ∥x 轴，∴点P 与点C 关于抛物线对称轴对称， ∵y =−23x 2+43x +2， ∴抛物线对称轴为直线x =-432×(−23)=1，∵C （0，2）， ∴P （2，2）；当点P 在BC 下方时，设CP 交x 轴于点D （m ，0）， 则OD =m ，DB =3-m ，∵∠PCB =∠ABC ， ∴CD =BD =3-m ，在Rt △COD 中，OC 2+OD 2=CD 2， ∴22+m 2=（3-m ）2， 解得：m =56， ∴D （56，0），设直线CD 的解析式为y =kx +d ，则{56k +d =0d =2，解得：{k =−125d =2，∴直线CD 的解析式为y =−125x +2， 联立，得{y =−125x +2y =−23x 2+43x +2， 解得：{x 1=0y 1=2（舍去），{x 2=225y 2=−21425， ∴P （225，-21425），综上所述，点P 的坐标为（2，2）或（225，-21425）；（3）由（2）知：抛物线y =−23x 2+43x +2的对称轴为直线x =1， ∴E （1，0），设Q （t ，−23t 2+43t +2），且-1＜t ＜3， 设直线AQ 的解析式为y =ex +f ，则{−e +f =0te +f =−23t 2+43t +2，解得：{e =−23t +2f =−23t +2， ∴直线AQ 的解析式为y =（−23t +2）x -23t +2， 当x =1时，y =-43t +4， ∴M （1，-43t +4），同理可得直线BQ 的解析式为y =（-23t -23）x +2t +2， 当x =1时，y =43t +43， ∴N （1，43t +43），∴EM =-43t +4，EN =43t +43， ∴EM +EN =-43t +4+43t +43=163， 故EM +EN 的值为定值163．12.（1）解：把O （0，0）代入y =x 2+（m -2）x +m -4得：m -4=0， 解得m =4，∴y =x 2+2x =（x +1）2-1，∴函数图象的顶点A 的坐标为（-1，-1）；（2）证明：由抛物线顶点坐标公式得y =x 2+（m -2）x +m -4的顶点为（2−m 2，−m 2+8m−204），∵m ＞2， ∴2-m ＜0， ∴2−m 2＜0，∵−m 2+8m−204=-14（m -4）2-1≤-1＜0，∴二次函数y =x 2+（m -2）x +m -4的顶点在第三象限；（3）解：设平移后图象对应的二次函数表达式为y =x 2+bx +c ，其顶点为（-b2，4c−b 24），当x =0时，B （0，c ）， 将（-b2，4c−b 24）代入y =-x -2得：4c−b 24=b2-2， ∴c =b 2+2b−84，∵B （0，c ）在y 轴的负半轴， ∴c ＜0， ∴OB =-c =-b 2+2b−84，过点A 作AH ⊥OB 于H ，如图：∵A （-1，-1）， ∴AH =1， 在△AOB 中， S △AOB =12OB •AH =12×（-b 2+2b−84）×1=-18b 2-14b +1=-18（b +1）2+98， ∵-18＜0，∴当b =-1时，此时c ＜0，S △AOB 取最大值，最大值为98， 答：△AOB 面积的最大值是98．13.解：（1）把A （1，0）代入y =a （x +1）2-4得：a （1+1）2-4=0， 解得a =1，∴y =（x +1）2-4=x 2+2x -3；答：抛物线L 1的函数表达式为y =x 2+2x -3；（2）抛物线L 1：y =（x +1）2-4的顶点为（-1，-4），将抛物线L 1向上平移m （m ＞0）个单位得到抛物线L 2，则抛物线L 2的顶点为（-1，-4+m ）， 而（-1，-4+m ）关于原点的对称点为（1，4-m ）， 把（1，4-m ）代入y =x 2+2x -3得： 12+2×1-3=4-m ， 解得m =4， 答：m 的值为4；（3）把抛物线L 1向右平移n （n ＞0）个单位得到抛物线L 3，抛物线L 3解析式为y =（x -n +1）2-4，∵点P （8-t ，s ），Q （t -4，r ）都在抛物线L 3上， ∴s =（8-t -n +1）2-4=（9-t -n ）2-4， r =（t -4-n +1）2-4=（t -n -3）2-4，∵当t ＞6时，s ＞r ， ∴s -r ＞0，∴[（9-t -n ）2-4]-[（t -n -3）2-4]＞0， 整理变形得：（9-t -n ）2-（t -n -3）2＞0， （9-t -n +t -n -3）（9-t -n -t +n +3）＞0， （6-2n ）（12-2t ）＞0， ∵t ＞6， ∴12-2t ＜0， ∴6-2n ＜0， 解得n ＞3，∴n 的取值范围是n ＞3．14.解：（1）由题意可得：A （-6，2），D （6，2），又∵E （0，8）是抛物线的顶点，设抛物线对应的函数表达式为y =ax 2+8，将A （-6，2）代入， （-6）2a +8=2， 解得：a =-16，∴抛物线对应的函数表达式为y =-16x 2+8；（2）（ⅰ）∵点P 1的横坐标为m （0＜m ≤6），且四边形P 1P 2P 3P 4为矩形，点P 2，P 3在抛物线AED 上，∴P 2的坐标为（m ，-16m 2+8）， ∴P 1P 2=P 3P 4=MN =-16m 2+8，P 2P 3=2m ，∴l =3（-16m 2+8）+2m =-12m 2+2m +24=-12（m -2）2+26， ∵-12＜0，∴当m =2时，l 有最大值为26，即栅栏总长l 与m 之间的函数表达式为l =-12m 2+2m +24，l 的最大值为26； （ⅱ）方案一：设P 2P 1=n ，则P 2P 3=18-3n ，∴矩形P 1P 2P 3P 4面积为（18-3n ）n =-3n 2+18n =-3（n -3）2+27， ∵-3＜0，∴当n =3时，矩形面积有最大值为27， 此时P 2P 1=3，P 2P 3=9，令-16x 2+8=3， 解得：x =±√30，∴此时P 1的横坐标的取值范围为-√30+9≤P 1横坐标≤√30， 方案二：设P 2P 1=n ，则P 2P 3=18−2n 2=9-n ，∴矩形P 1P 2P 3P 4面积为（9-n ）n =-n 2+n =-（n -92）2+814， ∵-1＜0，∴当n =92时，矩形面积有最大值为814， 此时P 2P 1=92，P 2P 3=92， 令-16x 2+8=92， 解得：x =±√21，∴此时P 1的横坐标的取值范围为-√21+92≤P 1横坐标≤√21．15.解：（1）∵点F 与直线上的点G （5，-3）关于x 轴对称，∴F （5，3），∵直线y =-x +2与x 轴交于点M ， ∴M （2，0），设直线MF 的解析式为y =kx +b ， 则有{2k +b =05k +b =3，解得{k =1b =−2，∴射线MF 的解析式为y =x -2（x ≥2）；（2）如图①中，设折线EMF 与抛物线的交点为P ，Q ．=2，点M（2，0），∵抛物线的对称轴x=-4−2∴点M值抛物线的对称轴上，∵直线EM的解析式为y=-x+2，直线MF的解析式为y=x-2，∴直线EM，直线MF关于直线x=2对称，∴P，Q关于直线x=2对称，，∴2=x1+x22∴x1+x2=4；（3）如图②中，过点P作PT∥AB交直线ME于点T．∵C（0，5），∴抛物线的解析式为y=-x2+4x+5，∴A（-1，0），B（5，0），设P（t，-t2+4t+5），则T（t2-4t-3，-t2+4t+5），∵PT∥AM，∴PN AN =PT AM =13（t -（t 2-4t -3）=-13（t -52）2+3712，∵-13＜0，∴PN AN 有最大值，最大值为3712． 16.解：（1）把A （-1，0）和点B （0，3）代入y =-x 2+bx +c ，得{−1−b +c =0c =3， 解得：{b =2c =3， ∴抛物线解析式为y =-x 2+2x +3；（2）∵y =-（x -1）2+4，∴C （1，4），抛物线的对称轴为直线x =1，如图，设CD =t ，则D （1，4-t ），∵线段DC 绕点D 按顺时针方向旋转90°，点C 落在抛物线上的点P 处，∴∠PDC =90°，DP =DC =t ，∴P （1+t ，4-t ），把P （1+t ，4-t ）代入y =-x 2+2x +4得：-（1+t ）2+2（1+t ）+3=4-t ，整理得t 2-t =0，解得：t 1=0（舍去），t 2=1，∴P （2，3）；（3）∵P 点坐标为（2，3），顶点C 坐标为（1，4），将抛物线平移，使其顶点落在原点O ，这时点P 落在点E 的位置，∴E 点坐标为（1，-1），∴点E 关于y 轴的对称点F （-1，-1），连接PF 交y 轴于M ，则MP +ME =MP +MF =PF 的值最小，设直线PF 的解析式为y =kx +n ，∴{2k +n =3−k +n =−1， 解得：{k =43n =13， ∴直线PF 的解析式为y =43x +13，∴点M 的坐标为（0，13）．17.解：（1）把A （-2，0），B （0，4）两点代入抛物线y =ax 2+x +c 中得：{4a −2+c =0c =4解得：{a =−12c =4； （2）由（2）知：抛物线解析式为：y =-12x 2+x +4，设直线AB 的解析式为：y =kx +b ，则{−2k +b =0b =4，解得：{k =2b =4， ∴AB 的解析式为：y =2x +4，设直线DE 的解析式为：y =mx ，∴2x +4=mx ，∴x =4m−2，当x =3时，y =3m ，∴E （3，3m ），∵△BDO 与△OCE 的面积相等，CE ⊥OC ，∴12•3•（-3m ）=12•4•42−m ，∴9m 2-18m -16=0，∴（3m +2）（3m -8）=0，∴m 1=-23，m 2=83（舍），∴直线DE 的解析式为：y =-23x ；（3）存在，B ，F ，G ，P 为顶点的四边形是以BF 为一边的矩形有两种情况：设P （t ，-12t 2+t +4），①如图1，过点P 作PH ⊥y 轴于H ，∵四边形BPGF 是矩形，∴BP =FG ，∠PBF =∠BFG =90°，∴∠CFG +∠BFO =∠BFO +∠OBF =∠CFG +∠CGF =∠OBF +∠PBH =90°， ∴∠PBH =∠OFB =∠CGF ，∵∠PHB =∠FCG =90°，∴△PHB ≌△FCG （AAS ），∴PH =CF ，∴CF =PH =t ，OF =3-t ，∵∠PBH =∠OFB ，∴PH BH =OB OF ，即t −12t 2+t+4−4=43−t ，解得：t 1=0（舍），t 2=1，∴F （2，0）；②如图2，过点G 作GN ⊥y 轴于N ，过点P 作PM ⊥x 轴于M ，同①可得：NG =FM =3，OF =t -3，∵∠OFB =∠FPM ，∴tan ∠OFB =tan ∠FPM ， ∴OB OF =FM PM ，即4t−3=3−12t 2+t+4，解得：t 1=1+√2014，t 2=1−√2014（舍）， ∴F （√201−114，0）； 综上，点F 的坐标为（2，0）或（√201−114，0）．18.解：（1）∵抛物线y =x 2+bx +c 经过点A （-1，0），点C （0，-3）． ∴{1−b +c =0c =−3， ∴{b =−2c =−3， ∴抛物线的解析式为y =x 2-2x -3；（2）如图，设D 1为D 关于直线AB 的对称点，D 2为D 关于ZX 直线BC 的对称点，连接D 1E ，D 2F ，D 1D 2．由对称性可知DE =D 1E ，DF =D 2F ，△DEF 的周长=D 1E +EF +D 2F ，∴当D 1，E ．F ．D 2共线时，△DEF 的周长最小，最小值为D 1D 2的长， 令y =0，则x 2-2x -3=0，解得x =-1或3，∴B （3，0），∴OB =OC =3，∴△BOC 是等腰直角三角形，∵BC 垂直平分DD 2，且D （-2，0），∴D 2（1，-3），∵D ，D 1关于x 轴的长，∴D 1（0，2），∴D 1D 2=√D 2C 2+D 1C 2=√52+12=√26，∴△DEF 的周长的最小值为√26．（3）∵M 到x 轴距离为d ，AB =4，连接BM ．∴S △ABM =2d ，又∵S △AMN =2d ，∴S △ABM =S △AMN ，∴B ，N 到AM 的距离相等，∵B ，N 在AM 的同侧，∴AM ∥BN ，设直线BN 的解析式为y =kx +m ，则有{m =−33k +m =0，∴{k =1m =−3， ∴直线BC 的解析式为y =x -3，∴设直线AM 的解析式为y =x +n ，∵A （-1，0），∴直线AM 的解析式为y =x +1，由{y =x +1y =x 2−2x −3，解得{x =1y =0或{x =4y =5， ∴M （4，5），∵点N 在射线BC 上，∴设N （t ，t -3），过点M 作x 轴的平行线l ，过点N 作y 轴的平行线交x 轴于点P ，交直线l 于点Q ．∵A （-1，0），M （4，5），N （t ，t -3），∴AM =5√2，AN =√(t +1)2+(t −3)2，MN =√(t −4)2+(t −8)2，∵△AMN 是等腰三角形，当AM =AN 时，5√2=√(t +1)2+(t −3)2，解得t =1±√21，当AM =MN 时，5√2=√(t −4)2+(t −8)2，解得t =6±√21，当AN =MN 时，√(t +1)2+(t −3)2=√(t −4)2+(t −8)2，解得t =72，∵N 在第一象限，∴t ＞3，∴t 的值为72，1+√21，6+√21， ∴点N 的坐标为（72，12）或（1+√21，-2+√21）或（6+√21，3+√21）．。

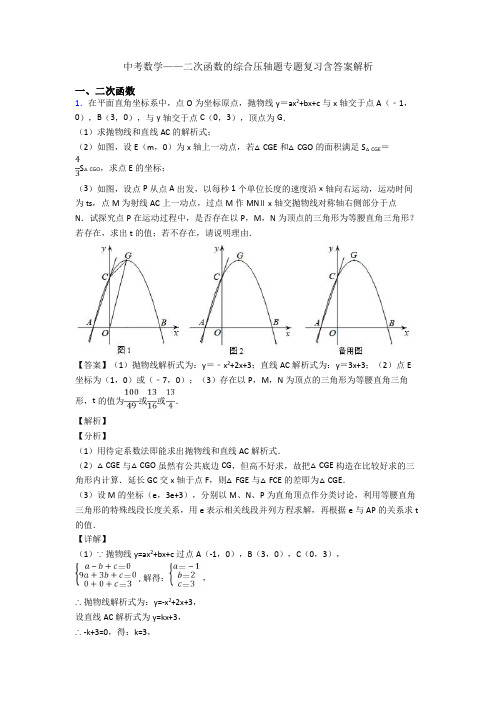
中考数学——二次函数的综合压轴题专题复习含答案解析一、二次函数1．在平面直角坐标系中，点O为坐标原点，抛物线y＝ax2+bx+c与x轴交于点A（﹣1，0），B（3，0），与y轴交于点C（0，3），顶点为G．（1）求抛物线和直线AC的解析式；（2）如图，设E（m，0）为x轴上一动点，若△CGE和△CGO的面积满足S△CGE＝S△CGO，求点E的坐标；（3）如图，设点P从点A出发，以每秒1个单位长度的速度沿x轴向右运动，运动时间为ts，点M为射线AC上一动点，过点M作MN∥x轴交抛物线对称轴右侧部分于点N．试探究点P在运动过程中，是否存在以P，M，N为顶点的三角形为等腰直角三角形？若存在，求出t的值；若不存在，请说明理由．【答案】（1）抛物线解析式为：y＝﹣x2+2x+3；直线AC解析式为：y＝3x+3；（2）点E 坐标为（1，0）或（﹣7，0）；（3）存在以P，M，N为顶点的三角形为等腰直角三角形，t的值为或或．【解析】【分析】（1）用待定系数法即能求出抛物线和直线AC解析式．（2）△CGE与△CGO虽然有公共底边CG，但高不好求，故把△CGE构造在比较好求的三角形内计算．延长GC交x轴于点F，则△FGE与△FCE的差即为△CGE．（3）设M的坐标（e，3e+3），分别以M、N、P为直角顶点作分类讨论，利用等腰直角三角形的特殊线段长度关系，用e表示相关线段并列方程求解，再根据e与AP的关系求t 的值．【详解】（1）∵抛物线y=ax2+bx+c过点A（-1，0），B（3，0），C（0，3），, 解得：，∴抛物线解析式为：y=-x2+2x+3，设直线AC解析式为y=kx+3，∴-k+3=0，得：k=3，∴直线AC解析式为：y=3x+3.（2）延长GC交x轴于点F，过G作GH⊥x轴于点H，∵y=-x2+2x+3=-（x-1）2+4，∴G（1，4），GH=4，∴S△CGO=OC•x G=×3×1=，∴S△CGE=S△CGO=×=2，①若点E在x轴正半轴上，设直线CG：y=k1x+3，∴k1+3=4 得：k1=1，∴直线CG解析式：y=x+3，∴F（-3，0），∵E（m，0），∴EF=m-（-3）=m+3，∴S△CGE=S△FGE-S△FCE=EF•GH-EF•OC=EF•（GH-OC）=（m+3）•（4-3）=，∴=2，解得：m=1，∴E的坐标为（1，0）.②若点E在x轴负半轴上，则点E到直线CG的距离与点（1，0）到直线CG距离相等，即点E到F的距离等于点（1，0）到F的距离，∴EF=-3-m=1-（-3）=4，解得：m=-7 即E（-7，0），综上所述，点E坐标为（1，0）或（-7，0）.（3）存在以P，M，N为顶点的三角形为等腰直角三角形，设M（e，3e+3），则y N=y M=3e+3，①若∠MPN=90°，PM=PN，如图2，过点M作MQ⊥x轴于点Q，过点N作NR⊥x轴于点R，∵MN∥x轴，∴MQ=NR=3e+3，∴Rt△MQP≌Rt△NRP（HL），∴PQ=PR，∠MPQ=∠NPR=45°，∴MQ=PQ=PR=NR=3e+3，∴x N=x M+3e+3+3e+3=7e+6，即N（7e+6，3e+3），∵N在抛物线上，∴-（7e+6）2+2（7e+6）+3=3e+3，解得：e1=-1（舍去），e2=−，∵AP=t，OP=t-1，OP+OQ=PQ，∴t-1-e=3e+3，∴t=4e+4=，②若∠PMN=90°，PM=MN，如图3，∴MN=PM=3e+3，∴x N=x M+3e+3=4e+3，即N（4e+3，3e+3），∴-（4e+3）2+2（4e+3）+3=3e+3，解得：e1=-1（舍去），e2=−，∴t=AP=e-（-1）=−+1＝，③若∠PNM=90°，PN=MN，如图4，∴MN=PN=3e+3，N（4e+3，3e+3），解得：e=−，∴t=AP=OA+OP=1+4e+3=，综上所述，存在以P，M，N为顶点的三角形为等腰直角三角形，t的值为或或．【点睛】本题考查了待定系数法求函数解析式，坐标系中三角形面积计算，等腰直角三角形的性质，解一元二次方程，考查了分类讨论和方程思想．第（3）题根据等腰直角三角形的性质找到相关线段长的关系是解题关键，灵活运用因式分解法解一元二次方程能简便运算．2．如图，抛物线y＝x2﹣mx﹣（m+1）与x轴负半轴交于点A（x1，0），与x轴正半轴交于点B（x2，0）（OA＜OB），与y轴交于点C，且满足x12+x22﹣x1x2＝13．（1）求抛物线的解析式；（2）以点B为直角顶点，BC为直角边作Rt△BCD，CD交抛物线于第四象限的点E，若EC ＝ED，求点E的坐标；（3）在抛物线上是否存在点Q，使得S△ACQ＝2S△AOC？若存在，求出点Q的坐标；若不存在，说明理由．【答案】（1）y＝x2﹣2x﹣3；（2）E 113+113+3）点Q的坐标为（﹣3，12）或（2，﹣3）．理由见解析.【解析】【分析】（1）由根与系数的关系可得x1+x2＝m，x1•x2＝﹣（m+1），代入x12+x22﹣x1x2＝13，求出m1＝2，m2＝﹣5．根据OA＜OB，得出抛物线的对称轴在y轴右侧，那么m＝2，即可确定抛物线的解析式；（2）连接BE、OE．根据直角三角形斜边上的中线等于斜边的一半得出BE＝12CD＝CE．利用SSS证明△OBE≌△OCE，得出∠BOE＝∠COE，即点E在第四象限的角平分线上，设E点坐标为（m，﹣m），代入y＝x2﹣2x﹣3，求出m的值，即可得到E点坐标；（3）过点Q作AC的平行线交x轴于点F，连接CF，根据三角形的面积公式可得S△ACQ＝S△ACF．由S△ACQ＝2S△AOC，得出S△ACF＝2S△AOC，那么AF＝2OA＝2，F（1，0）．利用待定系数法求出直线AC的解析式为y＝﹣3x﹣3．根据AC∥FQ，可设直线FQ的解析式为y＝﹣3x+b，将F（1，0）代入，利用待定系数法求出直线FQ的解析式为y＝﹣3x+3，把它与抛物线的解析式联立，得出方程组22333y x xy x⎧=--⎨=-+⎩，求解即可得出点Q的坐标．【详解】（1）∵抛物线y＝x2﹣mx﹣（m+1）与x轴负半轴交于点A（x1，0），与x轴正半轴交于点B（x2，0），∴x1+x2＝m，x1•x2＝﹣（m+1），∵x12+x22﹣x1x2＝13，∴（x1+x2）2﹣3x1x2＝13，∴m2+3（m+1）＝13，即m2+3m﹣10＝0，解得m1＝2，m2＝﹣5．∵OA＜OB，∴抛物线的对称轴在y轴右侧，∴m＝2，∴抛物线的解析式为y＝x2﹣2x﹣3；（2）连接BE、OE．∵在Rt△BCD中，∠CBD＝90°，EC＝ED，∴BE＝12CD＝CE．令y＝x2﹣2x﹣3＝0，解得x1＝﹣1，x2＝3，∴A（﹣1，0），B（3，0），∵C（0，﹣3），∴OB ＝OC ，又∵BE ＝CE ，OE ＝OE ，∴△OBE ≌△OCE （SSS ），∴∠BOE ＝∠COE ，∴点E 在第四象限的角平分线上，设E 点坐标为（m ，﹣m ），将E （m ，﹣m ）代入y ＝x 2﹣2x ﹣3，得m ＝m 2﹣2m ﹣3，解得m ＝1132±， ∵点E 在第四象限，∴E 点坐标为（113+，﹣113+）； （3）过点Q 作AC 的平行线交x 轴于点F ，连接CF ，则S △ACQ ＝S △ACF ．∵S △ACQ ＝2S △AOC ，∴S △ACF ＝2S △AOC ，∴AF ＝2OA ＝2，∴F （1，0）．∵A （﹣1，0），C （0，﹣3），∴直线AC 的解析式为y ＝﹣3x ﹣3．∵AC ∥FQ ，∴设直线FQ 的解析式为y ＝﹣3x +b ，将F （1，0）代入，得0＝﹣3+b ，解得b ＝3，∴直线FQ 的解析式为y ＝﹣3x +3．联立22333y x x y x ⎧=--⎨=-+⎩， 解得11312x y =-⎧⎨=⎩，2223x y =⎧⎨=-⎩， ∴点Q 的坐标为（﹣3，12）或（2，﹣3）．【点睛】本题是二次函数综合题，其中涉及到一元二次方程根与系数的关系，求二次函数的解析式，直角三角形的性质，全等三角形的判定与性质，二次函数图象上点的坐标特征，三角形的面积，一次函数图象与几何变换，待定系数法求直线的解析式，抛物线与直线交点坐标的求法，综合性较强，难度适中．利用数形结合与方程思想是解题的关键．3．已知如图，抛物线y=x2+bx+c过点A（3，0），B（1，0），交y轴于点C，点P是该抛物线上一动点，点P从C点沿抛物线向A点运动（点P不与点A重合），过点P作PD∥y 轴交直线AC于点D．（1）求抛物线的解析式；（2）求点P在运动的过程中线段PD长度的最大值；（3）△APD能否构成直角三角形？若能请直接写出点P坐标，若不能请说明理由；（4）在抛物线对称轴上是否存在点M使|MA﹣MC|最大？若存在请求出点M的坐标，若不存在请说明理由．【答案】（1）y=x2﹣4x+3；（2）94；（3）点P（1，0）或（2，﹣1）；（4）M（2，﹣3）．【解析】试题分析：（1）把点A、B的坐标代入抛物线解析式，解方程组得到b、c的值，即可得解；（2）求出点C的坐标，再利用待定系数法求出直线AC的解析式，再根据抛物线解析式设出点P的坐标，然后表示出PD的长度，再根据二次函数的最值问题解答；（3）①∠APD是直角时，点P与点B重合，②求出抛物线顶点坐标，然后判断出点P为在抛物线顶点时，∠PAD是直角，分别写出点P的坐标即可；（4）根据抛物线的对称性可知MA=MB，再根据三角形的任意两边之差小于第三边可知点M为直线CB与对称轴交点时，|MA﹣MC|最大，然后利用待定系数法求出直线BC的解析式，再求解即可．试题解析：解：（1）∵抛物线y=x2+bx+c过点A（3，0），B（1，0），∴93010b cb c++=⎧⎨++=⎩，解得43bc=-⎧⎨=⎩，∴抛物线解析式为y=x2﹣4x+3；（2）令x=0，则y=3，∴点C（0，3），则直线AC的解析式为y=﹣x+3，设点P（x，x2﹣4x+3）．∵PD∥y轴，∴点D（x，﹣x+3），∴PD=（﹣x+3）﹣（x2﹣4x+3）=﹣x2+3x=﹣（x﹣32）2+94．∵a=﹣1＜0，∴当x=32时，线段PD的长度有最大值94；（3）①∠APD是直角时，点P与点B重合，此时，点P（1，0），②∵y=x2﹣4x+3=（x ﹣2）2﹣1，∴抛物线的顶点坐标为（2，﹣1）．∵A（3，0），∴点P为在抛物线顶点时，∠PAD=45°+45°=90°，此时，点P（2，﹣1）．综上所述：点P（1，0）或（2，﹣1）时，△APD能构成直角三角形；（4）由抛物线的对称性，对称轴垂直平分AB，∴MA=MB，由三角形的三边关系，|MA﹣MC|＜BC，∴当M、B、C三点共线时，|MA﹣MC|最大，为BC的长度，设直线BC的解析式为y=kx+b（k≠0），则3k bb+=⎧⎨=⎩，解得：33kb=-⎧⎨=⎩，∴直线BC的解析式为y=﹣3x+3．∵抛物线y=x2﹣4x+3的对称轴为直线x=2，∴当x=2时，y=﹣3×2+3=﹣3，∴点M （2，﹣3），即，抛物线对称轴上存在点M（2，﹣3），使|MA﹣MC|最大．点睛：本题是二次函数综合题，主要利用了待定系数法求二次函数解析式，二次函数的最值问题，二次函数的对称性以及顶点坐标的求解，（2）整理出PD的表达式是解题的关键，（3）关键在于利用点的坐标特征作出判断，（4）根据抛物线的对称性和三角形的三边关系判断出点M的位置是解题的关键．4．如图，在平面直角坐标系中，抛物线y=ax2+2x+c与x轴交于A（﹣1，0）B（3，0）两点，与y轴交于点C，点D是该抛物线的顶点．（1）求抛物线的解析式和直线AC的解析式；（2）请在y轴上找一点M，使△BDM的周长最小，求出点M的坐标；（3）试探究：在拋物线上是否存在点P，使以点A，P，C为顶点，AC为直角边的三角形是直角三角形？若存在，请求出符合条件的点P的坐标；若不存在，请说明理由．【答案】（1）抛物线解析式为y=﹣x2+2x+3；直线AC的解析式为y=3x+3；（2）点M的坐标为（0，3）；（3）符合条件的点P的坐标为（73，209）或（103，﹣139），【解析】分析：（1）设交点式y=a（x+1）（x-3），展开得到-2a=2，然后求出a即可得到抛物线解析式；再确定C（0，3），然后利用待定系数法求直线AC的解析式；（2）利用二次函数的性质确定D的坐标为（1，4），作B点关于y轴的对称点B′，连接DB′交y轴于M，如图1，则B′（-3，0），利用两点之间线段最短可判断此时MB+MD的值最小，则此时△BDM的周长最小，然后求出直线DB′的解析式即可得到点M的坐标；（3）过点C作AC的垂线交抛物线于另一点P，如图2，利用两直线垂直一次项系数互为负倒数设直线PC的解析式为y=-13x+b，把C点坐标代入求出b得到直线PC的解析式为y=-13x+3，再解方程组223133y x xy x⎧-++⎪⎨-+⎪⎩＝＝得此时P点坐标；当过点A作AC的垂线交抛物线于另一点P时，利用同样的方法可求出此时P点坐标．详解：（1）设抛物线解析式为y=a（x+1）（x﹣3），即y=ax2﹣2ax﹣3a，∴﹣2a=2，解得a=﹣1，∴抛物线解析式为y=﹣x2+2x+3；当x=0时，y=﹣x2+2x+3=3，则C（0，3），设直线AC的解析式为y=px+q，把A（﹣1，0），C（0，3）代入得3p qq-+=⎧⎨=⎩，解得33pq=⎧⎨=⎩，∴直线AC的解析式为y=3x+3；（2）∵y=﹣x2+2x+3=﹣（x﹣1）2+4，∴顶点D的坐标为（1，4），作B点关于y轴的对称点B′，连接DB′交y轴于M，如图1，则B′（﹣3，0），∵MB=MB′，∴MB+MD=MB′+MD=DB′，此时MB+MD的值最小，而BD的值不变，∴此时△BDM的周长最小，易得直线DB′的解析式为y=x+3，当x=0时，y=x+3=3，∴点M的坐标为（0，3）；（3）存在．过点C作AC的垂线交抛物线于另一点P，如图2，∵直线AC的解析式为y=3x+3，∴直线PC的解析式可设为y=﹣13x+b，把C（0，3）代入得b=3，∴直线PC的解析式为y=﹣13x+3，解方程组223133y x xy x⎧-++⎪⎨-+⎪⎩＝＝，解得3xy=⎧⎨=⎩或73209xy⎧=⎪⎪⎨⎪=⎪⎩，则此时P点坐标为（73，209）；过点A作AC的垂线交抛物线于另一点P，直线PC的解析式可设为y=﹣x+b，把A（﹣1，0）代入得13+b=0，解得b=﹣13，∴直线PC的解析式为y=﹣13x﹣13，解方程组2231133y x xy x⎧-++⎪⎨--⎪⎩＝＝，解得1xy=-⎧⎨=⎩或103139xy⎧=⎪⎪⎨⎪=-⎪⎩，则此时P点坐标为（103，﹣139）.综上所述，符合条件的点P的坐标为（73，209）或（103，﹣139）.点睛：本题考查了二次函数的综合题：熟练掌握二次函数图象上点的坐标特征和二次函数的性质；会利用待定系数法求函数解析式，理解两直线垂直时一次项系数的关系，通过解方程组求把两函数的交点坐标；理解坐标与图形性质，会运用两点之间线段最短解决最短路径问题；会运用分类讨论的思想解决数学问题．5．已知，点M 为二次函数2()41y x b b =--++图象的顶点，直线5y mx =+分别交x 轴正半轴，y 轴于点,A B .（1）如图1，若二次函数图象也经过点,A B ，试求出该二次函数解析式，并求出m 的值. （2）如图2，点A 坐标为(5,0)，点M 在AOB ∆内，若点11(,)4C y ，23(,)4D y 都在二次函数图象上，试比较1y 与2y 的大小.【答案】（1）2(2)9y x =--+,1m =-；（2）①当102b <<时，12y y >；②当12b =时，12y y =；③当1425b <<时，12y y < 【解析】 【分析】 （1）根据一次函数表达式求出B 点坐标，然后根据B 点在抛物线上，求出b 值，从而得到二次函数表达式，再根据二次函数表达式求出A 点的坐标，最后代入一次函数求出m 值.（2）根据解方程组，可得顶点M 的纵坐标的范围，根据二次函数的性质，可得答案． 【详解】（1）如图1，∵直线5y mx =+与y 轴交于点为B ，∴点B 坐标为(0,5)又∵(0,5)B 在抛物线上，∴25(0)41b b =--++，解得2b =∴二次函数的表达式为2(2)9y x =--+ ∴当0y =时，得15=x ，21x =- ∴(5,0)A代入5y mx =+得，550m +=，∴1m =-（2）如图2，根据题意，抛物线的顶点M 为(,41)b b +，即M 点始终在直线41y x =+上，∵直线41y x =+与直线AB 交于点E ，与y 轴交于点F ，而直线AB 表达式为5y x =-+解方程组415y xy x=+⎧⎨=-+⎩，得45215xy⎧=⎪⎪⎨⎪=⎪⎩∴点421(,)55E，(0,1)F∵点M在AOB∆内，∴45b<<当点,C D关于抛物线对称轴（直线x b=）对称时，1344b b-=-，∴12b=且二次函数图象的开口向下，顶点M在直线41y x=+上综上：①当12b<<时，12y y>；②当12b=时，12y y=；③当1425b<<时，12y y<.【点睛】本题考查二次函数与一次函数的综合应用，难度系数大同学们需要认真分析即可.6．如图，在平面直角坐标系中有抛物线y＝a（x﹣2）2﹣2和y＝a（x﹣h）2，抛物线y＝a （x﹣2）2﹣2经过原点，与x轴正半轴交于点A，与其对称轴交于点B；点P是抛物线y＝a（x﹣2）2﹣2上一动点，且点P在x轴下方，过点P作x轴的垂线交抛物线y＝a（x﹣h）2于点D，过点D作PD的垂线交抛物线y＝a（x﹣h）2于点D′（不与点D重合），连接PD′，设点P的横坐标为m：（1）①直接写出a的值；②直接写出抛物线y＝a（x﹣2）2﹣2的函数表达式的一般式；（2）当抛物线y＝a（x﹣h）2经过原点时，设△PDD′与△OAB重叠部分图形周长为L：①求PDDD'的值；②直接写出L与m之间的函数关系式；（3）当h为何值时，存在点P，使以点O、A、D、D′为顶点的四边形是菱形？直接写出h 的值．【答案】（1）①12；②y ＝212x ﹣2x ； （2）①1；②L ＝2(22)(02)21(221)4(24)2m m m m π⎧+<⎪⎨-++<<⎪⎩…； （3）h ＝±3 【解析】 【分析】（1）①将x ＝0，y ＝0代入y ＝a （x ﹣2）2﹣2中计算即可；②y ＝212x ﹣2x ； （2）将（0，0）代入y ＝a （x ﹣h ）2中，可求得a ＝12，y ＝12x 2，待定系数法求OB 、AB 的解析式，由点P 的横坐标为m ，即可表示出相应线段求解；（3）以点O 、A 、D 、D ′为顶点的四边形是菱形，DD ′＝OA ，可知点D 的纵坐标为2，再由AD ＝OA ＝4即可求出h 的值． 【详解】解：（1）①将x ＝0，y ＝0代入y ＝a （x ﹣2）2﹣2中， 得：0＝a （0﹣2）2﹣2， 解得：a ＝12； ②y ＝212x ﹣2x ；． （2）∵抛物线y ＝a （x ﹣h ）2经过原点，a ＝12； ∴y ＝12x 2， ∴A （4，0），B （2，﹣2），易得：直线OB 解析式为：y ＝﹣x ，直线AB 解析式为：y ＝x ﹣4 如图1，222111,2,,,(,0),(,),,222P m m m D m m E m F m m D m m '⎛⎫⎛⎫⎛⎫--- ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭，①221122,222PD m m m m DD m '⎛⎫=--== ⎪⎝⎭PD 2m 1DD 2m'∴== ②如图1，当0＜m ≤2时，L ＝OE +EF +OF ＝2(22)m m m m ++=+，当2＜m ＜4时，如图2，设PD ′交x 轴于G ，交AB 于H ，PD 交x 轴于E ，交AB 于F ，则222111,2,,,(,0),(,4),,222P m m m D m m E m F m m D m m '⎛⎫⎛⎫⎛⎫--- ⎪ ⎪⎪⎝⎭⎝⎭⎝⎭， 2211(4)23422PF m m m m m ⎛⎫=---=-+- ⎪⎝⎭，2222322m 22,PG m 22m 2422FH PH PF ===-+-=-+ ∵DD ′∥EGEG PE DD PD '∴=，即：EG •PD ＝PE •DD ′，得：EG •（2m ）＝（2m ﹣12m 2）•2m ∴EG ＝2m ﹣12m 2，EF ＝4﹣m ∴L ＝EG +EF +FH +GH ＝EG +EF +PG2212242222m m m m ⎛⎫=-+-+-+ ⎪ ⎪⎝⎭221m (221)m 42+=-+++ 2(22)m(0m 2)21m (221)m 4(2m 4)L ⎧+<⎪∴=⎨+-+++<<⎪⎩…；（3）如图3，∵OADD ′为菱形 ∴AD ＝AO ＝DD ′＝4， ∴PD ＝2，23PA =23h ∴=±【点睛】本题是二次函数综合题，考查了待定系数法求函数解析式，菱形的性质，抛物线的平移等，解题时要注意考虑分段函数表示方法．7．如图，抛物线y ＝ax 2+bx ﹣1(a ≠0)交x 轴于A ，B (1，0)两点，交y 轴于点C ，一次函数y ＝x +3的图象交坐标轴于A ，D 两点，E 为直线AD 上一点，作EF ⊥x 轴，交抛物线于点F (1)求抛物线的解析式；(2)若点F 位于直线AD 的下方，请问线段EF 是否有最大值？若有，求出最大值并求出点E 的坐标；若没有，请说明理由；(3)在平面直角坐标系内存在点G ，使得G ，E ，D ，C 为顶点的四边形为菱形，请直接写出点G 的坐标．【答案】(1)抛物线的解析式为y＝13x2+23x﹣1；(2)4912，(12，72)；(3)点G的坐标为(2，1)，(﹣2，﹣2﹣1)，2，2﹣1)，(﹣4，3)．【解析】【分析】（1）利用待定系数法确定函数关系式；（2）由函数图象上点的坐标特征：可设点E的坐标为（m，m+3），点F的坐标为（m，1 3m2+23m﹣1），由此得到EF＝﹣13m2+13m+4，根据二次函数最值的求法解答即可；（3）分三种情形①如图1中，当EG为菱形对角线时．②如图2、3中，当EC为菱形的对角线时，③如图4中，当ED为菱形的对角线时，分别求解即可．【详解】解：(1)将y＝0代入y＝x+3，得x＝﹣3．∴点A的坐标为(﹣3，0)．设抛物线的解析式为y＝a(x﹣x1)(x﹣x2)，点A的坐标为(﹣3，0)，点B的坐标为(1，0)，∴y＝a(x+3)(x﹣1)．∵点C的坐标为(0，﹣1)，∴﹣3a＝﹣1，得a＝13，∴抛物线的解析式为y＝13x2+23x﹣1；(2)设点E的坐标为(m，m+3)，线段EF的长度为y，则点F的坐标为(m，13m2+23m﹣1)∴y＝(m+3)﹣( 13m2+23m﹣1)＝﹣13m2+13m+4即y＝-13(m﹣12) 2+4912，此时点E的坐标为(12，72)；(3)点G的坐标为(2，1)，(﹣2，﹣2﹣1)，2，2﹣1)，(﹣4，3)．理由：①如图1，当四边形CGDE为菱形时．∴EG 垂直平分CD ∴点E 的纵坐标y ＝132-+＝1， 将y ＝1带入y ＝x +3，得x ＝﹣2． ∵EG 关于y 轴对称， ∴点G 的坐标为(2，1)；②如图2，当四边形CDEG 为菱形时，以点D 为圆心，DC 的长为半径作圆，交AD 于点E ，可得DC ＝DE ，构造菱形CDEG 设点E 的坐标为(n ，n +3)， 点D 的坐标为(0，3)∴DE ＝22(33)n n ++-＝22n ∵DE ＝DC ＝4， ∴22n ＝4，解得n 1＝﹣22，n 2＝22．∴点E 的坐标为(﹣22，﹣22+3)或(22，22+3) 将点E 向下平移4个单位长度可得点G ，点G 的坐标为(﹣22，﹣22﹣1)(如图2)或(22，22﹣1)(如图3)③如图4，“四边形CDGE 为菱形时，以点C 为圆心，以CD 的长为半径作圆，交直线AD 于点E ，设点E 的坐标为(k ，k +3)，点C 的坐标为(0，﹣1)． ∴EC ＝22(0)(31)k k -+++＝22816k k ++． ∵EC ＝CD ＝4， ∴2k 2+8k +16＝16， 解得k 1＝0(舍去)，k 2＝﹣4． ∴点E 的坐标为(﹣4，﹣1) 将点E 上移1个单位长度得点G ． ∴点G 的坐标为(﹣4，3)．综上所述，点G 的坐标为(2，1)，(﹣22，﹣22﹣1)，(22，22﹣1)，(﹣4，3)．【点睛】本题考查二次函数综合题、轴对称变换、菱形的判定和性质等知识，解题的关键是学会利用对称解决最值问题，学会用分类讨论的思想思考问题，属于中考压轴题．8．已知抛物线2(5)6y x m x m =-+-+-. （1）求证：该抛物线与x 轴总有交点；（2）若该抛物线与x 轴有一个交点的横坐标大于3且小于5，求m 的取值范围；（3）设抛物线2(5)6y x m x m =-+-+-与y 轴交于点M ，若抛物线与x 轴的一个交点关于直线y x =-的对称点恰好是点M ，求m 的值.【答案】（1）证明见解析；（2）1?<?m?3<；（3）56m m ==或 【解析】 【分析】（1）本题需先根据判别式解出无论m 为任何实数都不小于零，再判断出物线与x 轴总有交点．（2）根据公式法解方程，利用已有的条件，就能确定出m 的取值范围，即可得到结果． （3）根据抛物线y=-x 2+（5-m ）x+6-m ，求出与y 轴的交点M 的坐标，再确定抛物线与x 轴的两个交点关于直线y=-x 的对称点的坐标，列方程可得结论． 【详解】（1）证明：∵()()()222454670b ac m m m ∆=-=-+-=-≥ ∴抛物线与x 轴总有交点.（2）解：由（1）()27m ∆=-，根据求根公式可知，方程的两根为：257m m x （）-±-=即1216x x m =-=-+， 由题意，有 3<-m 6<5+1<?m 3∴<(3)解：令 x = 0， y =6m -+ ∴ M （0，6m -+）由（2）可知抛物线与x 轴的交点为（-1，0）和（6m -+，0）， 它们关于直线y x =-的对称点分别为（0 ， 1）和（0， 6m -）， 由题意，可得：6166m m m 或-+=-+=- 56m m ∴==或 【点睛】本题考查对抛物线与x 轴的交点，解一元一次方程，解一元一次不等式，根的判别式，对称等，解题关键是熟练理解和掌握以上性质，并能综合运用这些性质进行计算．9．如图，菱形ABCD 的边长为20cm ，∠ABC ＝120°，对角线AC ，BD 相交于点O ，动点P 从点A 出发，以4cm /s 的速度，沿A →B 的路线向点B 运动；过点P 作PQ ∥BD ，与AC 相交于点Q ，设运动时间为t 秒，0＜t ＜5．（1）设四边形PQCB 的面积为S ，求S 与t 的关系式；（2）若点Q 关于O 的对称点为M ，过点P 且垂直于AB 的直线l 交菱形ABCD 的边AD （或CD ）于点N ，当t 为何值时，点P 、M 、N 在一直线上？（3）直线PN 与AC 相交于H 点，连接PM ，NM ，是否存在某一时刻t ，使得直线PN 平分四边形APMN 的面积？若存在，求出t 的值；若不存在，请说明理由． 【答案】(1) S=﹣231003t +0＜t ＜5）； (2) 307;(3)见解析. 【解析】 【分析】（1）如图1，根据S=S △ABC -S △APQ ，代入可得S 与t 的关系式；（2）设PM=x ，则AM=2x ，可得3，计算x 的值，根据直角三角形30度角的性质可得3AM=AO+OM ，列方程可得t 的值；（3）存在，通过画图可知：N 在CD 上时，直线PN 平分四边形APMN 的面积，根据面积相等可得MG=AP ，由AM=AO+OM ，列式可得t 的值． 【详解】解：（1）如图1，∵四边形ABCD 是菱形， ∴∠ABD=∠DBC=12∠ABC=60°，AC ⊥BD ， ∴∠OAB=30°， ∵AB=20，∴OB=10，3 由题意得：AP=4t ，∴PQ=2t ，AQ=23t ， ∴S=S △ABC ﹣S △APQ ， =11··22AC OB PQ AQ -， =111020322322t t ⨯⨯-⨯⨯ ， =﹣23t 2+1003（0＜t ＜5）； （2）如图2，在Rt △APM 中，AP=4t ， ∵点Q 关于O 的对称点为M ， ∴OM=OQ ， 设PM=x ，则AM=2x ， ∴AP=3x=4t ， ∴x=3， ∴AM=2PM=3， ∵AM=AO+OM ，∴3=103+103﹣23t ，t=307； 答：当t 为307秒时，点P 、M 、N 在一直线上； （3）存在，如图3，∵直线PN 平分四边形APMN 的面积， ∴S △APN =S △PMN ，过M 作MG ⊥PN 于G ，∴11··22PN AP PN MG = ， ∴MG=AP ，易得△APH ≌△MGH ，∴3，∵AM=AO+OM ，同理可知：3﹣3，3333t ，t=3011． 答：当t 为3011秒时，使得直线PN 平分四边形APMN 的面积．【点睛】考查了全等三角形的判定与性质，对称的性质，三角形和四边形的面积，二次根式的化简等知识点，计算量大，解答本题的关键是熟练掌握动点运动时所构成的三角形各边的关系.10．已知，抛物线y ＝﹣x 2+bx +c 经过点A （﹣1，0）和C （0，3）． （1）求抛物线的解析式；（2）在抛物线的对称轴上，是否存在点P ，使PA +PC 的值最小？如果存在，请求出点P 的坐标，如果不存在，请说明理由；（3）设点M 在抛物线的对称轴上，当△MAC 是直角三角形时，求点M 的坐标．【答案】（1）223y x x =-++；（2）当PA PC +的值最小时，点P 的坐标为()1,2；（3）点M 的坐标为()1,1、()1,2、81,3⎛⎫ ⎪⎝⎭或21,3⎛⎫- ⎪⎝⎭. 【解析】 【分析】()1由点A 、C 的坐标，利用待定系数法即可求出抛物线的解析式；()2连接BC 交抛物线对称轴于点P ，此时PA PC +取最小值，利用二次函数图象上点的坐标特征可求出点B 的坐标，由点B 、C 的坐标利用待定系数法即可求出直线BC 的解析式，利用配方法可求出抛物线的对称轴，再利用一次函数图象上点的坐标特征即可求出点P 的坐标；()3设点M 的坐标为()1,m ，则22CM (10)(m 3)=-+-，()22AC [01](30)10=--+-=，()22AM [11](m 0)=--+-，分AMC 90∠=o 、ACM 90∠=o 和CAM 90∠=o 三种情况，利用勾股定理可得出关于m 的一元二次方程或一元一次方程，解之可得出m 的值，进而即可得出点M 的坐标． 【详解】解：()1将()1,0A -、()0,3C 代入2y x bx c =-++中， 得：{103b c c --+==，解得：{23b c ==，∴抛物线的解析式为223y x x =-++．()2连接BC 交抛物线对称轴于点P ，此时PA PC +取最小值，如图1所示．当0y =时，有2230x x -++=， 解得：11x =-，23x =，∴点B 的坐标为()3,0．Q 抛物线的解析式为2223(1)4y x x x =-++=--+， ∴抛物线的对称轴为直线1x =．设直线BC 的解析式为()0y kx d k =+≠， 将()3,0B 、()0,3C 代入y kx d =+中， 得：{303k d d +==，解得：{13k d =-=，∴直线BC 的解析式为3y x =-+． Q 当1x =时，32y x =-+=，∴当PA PC +的值最小时，点P 的坐标为()1,2．()3设点M 的坐标为()1,m ，则22(10)(3)CM m =-+-，()22[01](30)10AC =--+-=()22[11](0)AM m =--+-分三种情况考虑：①当90AMC ∠=o 时，有222AC AM CM =+，即22101(3)4m m =+-++，解得：11m =，22m =，∴点M 的坐标为()1,1或()1,2；②当90ACM ∠=o 时，有222AM AC CM =+，即224101(3)m m +=++-，解得：83m =， ∴点M 的坐标为81,3⎛⎫⎪⎝⎭；③当90CAM ∠=o 时，有222CM AM AC =+，即221(3)410m m +-=++，解得：23m =-， ∴点M 的坐标为21,.3⎛⎫- ⎪⎝⎭综上所述：当MAC V 是直角三角形时，点M 的坐标为()1,1、()1,2、81,3⎛⎫⎪⎝⎭或21,.3⎛⎫- ⎪⎝⎭【点睛】本题考查待定系数法求二次(一次)函数解析式、二次(一次)函数图象的点的坐标特征、轴对称中的最短路径问题以及勾股定理，解题的关键是：()1由点的坐标，利用待定系数法求出抛物线解析式；()2由两点之间线段最短结合抛物线的对称性找出点P 的位置；()3分AMC 90∠=o 、ACM 90∠=o 和CAM 90∠=o 三种情况，列出关于m 的方程．11．如图，直线y ＝﹣x +4与x 轴交于点B ，与y 轴交于点C ，抛物线y ＝﹣x 2+bx +c 经过B ，C 两点，与x 轴另一交点为A ．点P 以每秒2个单位长度的速度在线段BC 上由点B 向点C 运动（点P 不与点B 和点C 重合），设运动时间为t 秒，过点P 作x 轴垂线交x 轴于点E ，交抛物线于点M ．（1）求抛物线的解析式；（2）如图①，过点P 作y 轴垂线交y 轴于点N ，连接MN 交BC 于点Q ，当12MQ NQ =时，求t 的值；（3）如图②，连接AM 交BC 于点D ，当△PDM 是等腰三角形时，直接写出t 的值． 【答案】（1）y ＝﹣x 2+3x +4；（2）t 的值为12；（3）当△PDM 是等腰三角形时，t ＝1或t ﹣1． 【解析】 【分析】（1）求直线y=-x+4与x 轴交点B ，与y 轴交点C ，用待定系数法即求得抛物线解析式． （2）根据点B 、C 坐标求得∠OBC=45°，又PE ⊥x 轴于点E ，得到△PEB 是等腰直角三角形，由PB =求得BE=PE=t ，即可用t 表示各线段，得到点M 的横坐标，进而用m 表示点M 纵坐标，求得MP 的长．根据MP ∥CN 可证MPQ NCQ V V ∽，故有12MP MQ NC NQ ＝＝，把用t 表示的MP 、NC 代入即得到关于t 的方程，求解即得到t 的值． （3）因为不确定等腰△PDM 的底和腰，故需分3种情况讨论：①若MD=MP ，则∠MDP=∠MPD=45°，故有∠DMP=90°，不合题意；②若DM=DP ，则∠DMP=∠MPD=45°，进而得AE=ME ，把含t 的式子代入并解方程即可；③若MP=DP ，则∠PMD=∠PDM ，由对顶角相等和两直线平行内错角相等可得∠CFD=∠PMD=∠PDM=∠CDF 进而得CF=CD ．用t 表示M 的坐标，求直线AM 解析式，求得AM 与y 轴交点F 的坐标，即能用t 表示CF 的长．把直线AM 与直线BC 解析式联立方程组，解得x 的值即为点D 横坐标．过D 作y 轴垂线段DG ，得等腰直角△CDG ，用DG 即点D 横坐标，进而可用t 表示CD 的长．把含t 的式子代入CF=CD ，解方程即得到t 的值． 【详解】（1）直线y ＝﹣x +4中，当x ＝0时，y ＝4 ∴C （0，4）当y ＝﹣x +4＝0时，解得：x ＝4 ∴B （4，0）∵抛物线y ＝﹣x 2+bx +c 经过B ，C 两点 ∴1640004b c c -++=⎧⎨++=⎩ 解得：34b c =⎧⎨=⎩∴抛物线解析式为y ＝﹣x 2+3x +4（2）∵B （4，0），C （0，4），∠BOC ＝90° ∴OB ＝OC∴∠OBC ＝∠OCB ＝45° ∵ME ⊥x 轴于点E ，PBt ∴∠BEP ＝90°∴Rt △BEP 中，2PE sin PBE PB ∠=＝∴BE PE t ＝＝， ∴4M P P x x OE OBBE t y PE t ＝＝＝﹣＝﹣，＝＝ ∵点M 在抛物线上∴2243445M y t t t t +++＝﹣（﹣）（﹣）＝﹣， ∴24MP MP y y t t +＝﹣＝﹣ ， ∵PN ⊥y 轴于点N∴∠PNO ＝∠NOE ＝∠PEO ＝90° ∴四边形ONPE 是矩形 ∴ON ＝PE ＝t ∴NC ＝OC ﹣ON ＝4﹣t ∵MP ∥CN ∴△MPQ ∽△NCQ ∴12MP MQ NC NQ == ∴24142t t t -+=-解得：12142t t ＝，＝（点P 不与点C 重合，故舍去） ∴t 的值为12（3）∵∠PEB ＝90°，BE ＝PE ∴∠BPE ＝∠PBE ＝45° ∴∠MPD ＝∠BPE ＝45°①若MD ＝MP ，则∠MDP ＝∠MPD ＝45° ∴∠DMP ＝90°，即DM ∥x 轴，与题意矛盾 ②若DM ＝DP ，则∠DMP ＝∠MPD ＝45° ∵∠AEM ＝90° ∴AE ＝ME∵y ＝﹣x 2+3x +4＝0时，解得：x 1＝﹣1，x 2＝4 ∴A （﹣1，0）∵由（2）得，x M ＝4﹣t ，ME ＝y M ＝﹣t 2+5t ∴AE ＝4﹣t ﹣（﹣1）＝5﹣t ∴5﹣t ＝﹣t 2+5t解得：t 1＝1，t 2＝5（0＜t ＜4，舍去）③若MP ＝DP ，则∠PMD ＝∠PDM如图，记AM 与y 轴交点为F ，过点D 作DG ⊥y 轴于点G ∴∠CFD ＝∠PMD ＝∠PDM ＝∠CDF ∴CF ＝CD∵A （﹣1，0），M （4﹣t ，﹣t 2+5t ），设直线AM 解析式为y ＝ax +m ∴()2045a m a t m t t -+=⎧⎨-+=-+⎩ 解得：a tm t =⎧⎨=⎩ ， ∴直线AM ：y tx t +＝ ∴F （0，t ） ∴CF ＝OC ﹣OF ＝4﹣t ∵tx +t ＝﹣x +4，解得：41tx t -=+， ∴41D x tt DG -=+＝＝， ∵∠CGD ＝90°，∠DCG ＝45° ∴)2421t CD DG t -+＝＝，∴)2441t t t -+﹣ 解得：21t ＝﹣综上所述，当△PDM 是等腰三角形时，t ＝1或21t ＝﹣． 【点睛】本题考查了二次函数的图象与性质，解二元一次方程组和一元二次方程，等腰直角三角形的性质，相似三角形的判定和性质，涉及等腰三角形的分类讨论，要充分利用等腰的性质作为列方程的依据．12．已知，如图，抛物线2(0)y ax bx c a =++≠的顶点为(1,9)M ，经过抛物线上的两点(3,7)A --和(3,)B m 的直线交抛物线的对称轴于点C ．（1）求抛物线的解析式和直线AB 的解析式．（2）在抛物线上,A M 两点之间的部分（不包含,A M 两点），是否存在点D ，使得2DAC DCM S S ∆∆=？若存在，求出点D 的坐标；若不存在，请说明理由．（3）若点P 在抛物线上，点Q 在x 轴上，当以点,,,A M P Q 为顶点的四边形是平行四边形时，直接写出满足条件的点P 的坐标．【答案】（1）抛物线的表达式为：228y x x =-++，直线AB 的表达式为：21y x =-；（2）存在，理由见解析；点P (6,16)-或(4,16)--或(17,2)+或(17,2)．【解析】 【分析】（1）二次函数表达式为：y=a （x-1）2+9，即可求解； （2）S △DAC =2S △DCM ，则()()()()()21112821139112222DAC C A S DH x x x x x x =-=-++-++=--⨯V ，，即可求解；（3）分AM 是平行四边形的一条边、AM 是平行四边形的对角线两种情况，分别求解即可． 【详解】解：（1）二次函数表达式为：()219y a x =-+， 将点A 的坐标代入上式并解得：1a =-， 故抛物线的表达式为：228y x x =-++…①， 则点()3,5B ，将点,A B 的坐标代入一次函数表达式并解得： 直线AB 的表达式为：21y x =-； （2）存在，理由：二次函数对称轴为：1x =，则点()1,1C ， 过点D 作y 轴的平行线交AB 于点H ，设点()2,28D x x x -++，点(),21H x x -，∵2DAC DCM S S ∆∆=， 则()()()()()21112821139112222DAC C A S DH x x x x x x =-=-++-++=--⨯V ， 解得：1x =-或5（舍去5）， 故点()1,5D -；（3）设点(),0Q m 、点(),P s t ，228t s s =-++， ①当AM 是平行四边形的一条边时，点M 向左平移4个单位向下平移16个单位得到A ，同理，点(),0Q m 向左平移4个单位向下平移16个单位为()4,16m --，即为点P ， 即：4m s -=，6t -=，而228t s s =-++， 解得：6s =或﹣4， 故点()6,16P -或()4,16--； ②当AM 是平行四边形的对角线时，由中点公式得：2m s +=-，2t =，而228t s s =-++， 解得：17s =±故点()17,2P 或()17,2；综上，点()6,16P -或()4,16--或()17,2或()17,2． 【点睛】本题考查的是二次函数综合运用，涉及到一次函数、平行四边形性质、图形的面积计算等，其中（3），要注意分类求解，避免遗漏．13．已知矩形ABCD 中，AB =5cm ，点P 为对角线AC 上的一点，且AP =25cm .如图①，动点M 从点A 出发，在矩形边上沿着A B C →→的方向匀速运动(不包含点C ).设动点M 的运动时间为t (s )，APM ∆的面积为S (cm ²)，S 与t 的函数关系如图②所示： (1)直接写出动点M 的运动速度为 /cm s ，BC 的长度为 cm ;(2)如图③，动点M 重新从点A 出发，在矩形边上，按原来的速度和方向匀速运动.同时，另一个动点N 从点D 出发，在矩形边上沿着D C B →→的方向匀速运动，设动点N 的运动速度为()/v cm s .已知两动点M 、N 经过时间()x s 在线段BC 上相遇(不包含点C )，动点M 、N 相遇后立即停止运动，记此时APM DPN ∆∆与的面积为()()2212,S cm S cm . ①求动点N 运动速度()/v cm s 的取值范围;②试探究12S S ⋅是否存在最大值.若存在，求出12S S ⋅的最大值并确定运动速度时间x 的值；若不存在，请说明理由.【答案】(1)2，10；(2)①2/6/3cm s v cm s ≤＜；②当154x =时，12S S ⋅取最大值2254. 【解析】 【分析】（1）由题意可知图像中0~2.5s 时，M 在AB 上运动，求出速度，2.5~7.5s 时，M 在BC 上运动，求出BC 长度；（2）①分别求出在C 点相遇和在B 点相遇时的速度，取中间速度，注意C 点相遇时的速度不能取等于；②过M 点做MH ⊥AC ，则125MH CM ==得到S 1，同时利用12()PAD CDM ABM N ABCD S S S S S S ∆∆∆+=---（N ）矩形=15，得到S 2，再得到12S S ⋅关于x 的二次函数，利用二次函数性质求得最大值 【详解】(1)5÷2.5=2/cm s ；（7.5-2.5）×2=10cm (2)①解：在C 点相遇得到方程57.5v= 在B 点相遇得到方程152.5v= ∴5=7.515=2.5vv⎧⎪⎪⎨⎪⎪⎩解得 23=5v v ⎧=⎪⎨⎪⎩。

一、二次函数 真题与模拟题分类汇编（难题易错题）1．如图，已知抛物线2y ax bx c =++经过A （－3，0），B （1，0），C （0，3）三点，其顶点为D ，对称轴是直线l ，l 与x 轴交于点H ．（1）求该抛物线的解析式；（2）若点P 是该抛物线对称轴l 上的一个动点，求△PBC 周长的最小值；（3）如图（2），若E 是线段AD 上的一个动点（ E 与A 、D 不重合），过E 点作平行于y 轴的直线交抛物线于点F ，交x 轴于点G ，设点E 的横坐标为m ，△ADF 的面积为S ． ①求S 与m 的函数关系式；②S 是否存在最大值？若存在，求出最大值及此时点E 的坐标； 若不存在，请说明理由．【答案】（1）2y x 2x 3=--+.（2）3210. （3）①2S m 4m 3=---.②当m=﹣2时，S 最大，最大值为1，此时点E 的坐标为（﹣2，2）. 【解析】 【分析】（1）根据函数图象经过的三点，用待定系数法确定二次函数的解析式即可.（2）根据BC 是定值，得到当PB+PC 最小时，△PBC 的周长最小，根据点的坐标求得相应线段的长即可.（3）设点E 的横坐标为m ，表示出E （m ，2m+6），F （m ，2m 2m 3--+），最后表示出EF 的长，从而表示出S 于m 的函数关系，然后求二次函数的最值即可. 【详解】解：（1）∵抛物线2y ax bx c =++经过A （－3，0），B （1，0）， ∴可设抛物线交点式为()()y a x 3x 1=+-.又∵抛物线2y ax bx c =++经过C （0，3），∴a 1=-. ∴抛物线的解析式为：()()y x 3x 1=-+-，即2y x 2x 3=--+. （2）∵△PBC 的周长为：PB+PC+BC ，且BC 是定值. ∴当PB+PC 最小时，△PBC 的周长最小. ∵点A 、点B 关于对称轴I 对称，∴连接AC 交l 于点P ，即点P 为所求的点.∵AP=BP ，∴△PBC 的周长最小是：PB+PC+BC=AC+BC.∵A （－3，0），B （1，0），C （0，3），∴2，10. ∴△PBC 的周长最小是：3210.（3）①∵抛物线2y x 2x 3=--+顶点D 的坐标为（﹣1，4），A （﹣3，0），∴直线AD 的解析式为y=2x+6∵点E 的横坐标为m ，∴E （m ，2m+6），F （m ，2m 2m 3--+） ∴()22EF m 2m 32m 6m 4m 3=--+-+=---.∴()22DEF AEF 1111S S S EF GH EF AG EF AH m 4m 32m 4m 32222∆∆=+=⋅⋅+⋅⋅=⋅⋅=⋅---⋅=---.∴S 与m 的函数关系式为2S m 4m 3=---. ②()22S m 4m 3m 21=---=-++，∴当m=﹣2时，S 最大，最大值为1，此时点E 的坐标为（﹣2，2）.2．如图，抛物线y ＝﹣x 2﹣2x+3的图象与x 轴交于A 、B 两点(点A 在点B 的左边)，与y 轴交于点C ，点D 为抛物线的顶点． (1)求点A 、B 、C 的坐标；(2)点M(m ，0)为线段AB 上一点(点M 不与点A 、B 重合)，过点M 作x 轴的垂线，与直线AC 交于点E ，与抛物线交于点P ，过点P 作PQ ∥AB 交抛物线于点Q ，过点Q 作QN ⊥x 轴于点N ，可得矩形PQNM ．如图，点P 在点Q 左边，试用含m 的式子表示矩形PQNM 的周长；(3)当矩形PQNM 的周长最大时，m 的值是多少？并求出此时的△AEM 的面积； (4)在(3)的条件下，当矩形PMNQ 的周长最大时，连接DQ ，过抛物线上一点F 作y 轴的平行线，与直线AC 交于点G(点G 在点F 的上方)．若FG ＝2，求点F 的坐标．【答案】(1)A(﹣3，0)，B(1，0)；C(0，3) ；(2)矩形PMNQ的周长＝﹣2m2﹣8m+2；(3) m＝﹣2；S＝12；(4)F(﹣4，﹣5)或(1，0)．【解析】【分析】（1）利用函数图象与坐标轴的交点的求法，求出点A，B，C的坐标；（2）先确定出抛物线对称轴，用m表示出PM，MN即可；（3）由（2）得到的结论判断出矩形周长最大时，确定出m，进而求出直线AC解析式，即可；（4）在（3）的基础上，判断出N应与原点重合，Q点与C点重合，求出DQ＝DC＝2，再建立方程（n+3）﹣（﹣n2﹣2n+3）＝4即可．【详解】(1)由抛物线y＝﹣x2﹣2x+3可知，C(0，3)．令y＝0，则0＝﹣x2﹣2x+3，解得，x＝﹣3或x＝l，∴A(﹣3，0)，B(1，0)．(2)由抛物线y＝﹣x2﹣2x+3可知，对称轴为x＝﹣1．∵M(m，0)，∴PM＝﹣m2﹣2m+3，MN＝(﹣m﹣1)×2＝﹣2m﹣2，∴矩形PMNQ的周长＝2(PM+MN)＝(﹣m2﹣2m+3﹣2m﹣2)×2＝﹣2m2﹣8m+2．(3)∵﹣2m2﹣8m+2＝﹣2(m+2)2+10，∴矩形的周长最大时，m＝﹣2．∵A(﹣3，0)，C(0，3)，设直线AC的解析式y＝kx+b，∴303k bb-+=⎧⎨=⎩解得k＝l，b＝3，∴解析式y＝x+3，令x＝﹣2，则y＝1，∴E(﹣2，1)，∴EM＝1，AM＝1，∴S ＝12AM×EM ＝12． (4)∵M(﹣2，0)，抛物线的对称轴为x ＝﹣l ， ∴N 应与原点重合，Q 点与C 点重合， ∴DQ ＝DC ，把x ＝﹣1代入y ＝﹣x 2﹣2x+3，解得y ＝4， ∴D(﹣1，4)， ∴DQ ＝DC ＝2． ∵FG ＝22DQ ， ∴FG ＝4．设F(n ，﹣n 2﹣2n+3)，则G(n ，n+3)， ∵点G 在点F 的上方且FG ＝4， ∴(n+3)﹣(﹣n 2﹣2n+3)＝4． 解得n ＝﹣4或n ＝1， ∴F(﹣4，﹣5)或(1，0)． 【点睛】此题是二次函数综合题，主要考查了函数图象与坐标轴的交点的求法，待定系数法求函数解析式，函数极值的确定，解本题的关键是用m 表示出矩形PMNQ 的周长．3．如图，已知二次函数的图象过点O （0，0）．A （8，4），与x 轴交于另一点B ，且对称轴是直线x ＝3．（1）求该二次函数的解析式；（2）若M 是OB 上的一点，作MN ∥AB 交OA 于N ，当△ANM 面积最大时，求M 的坐标；（3）P 是x 轴上的点，过P 作PQ ⊥x 轴与抛物线交于Q ．过A 作AC ⊥x 轴于C ，当以O ，P ，Q 为顶点的三角形与以O ，A ，C 为顶点的三角形相似时，求P 点的坐标．【答案】（1）21342y x x =-；（2）当t ＝3时，S △AMN 有最大值3，此时M 点坐标为（3，0）；（3）P 点坐标为（14，0）或（﹣2，0）或（4，0）或（8，0）．【解析】 【分析】（1）先利用抛物线的对称性确定B （6，0），然后设交点式求抛物线解析式； （2）设M （t ，0），先其求出直线OA 的解析式为12y x =直线AB 的解析式为y=2x-12，直线MN 的解析式为y=2x-2t ，再通过解方程组1222y x y x t ⎧=⎪⎨⎪=-⎩得N （42t,t 33），接着利用三角形面积公式，利用S △AMN =S △AOM -S △NOM 得到AMN 112S 4t t t 223∆=⋅⋅-⋅⋅然后根据二次函数的性质解决问题； （3）设Q 213m,m m 42⎛⎫- ⎪⎝⎭，根据相似三角形的判定方法，当PQ PO OC AC=时，△PQO ∽△COA ，则213m m 2|m |42-=；当PQ POAC OC=时，△PQO ∽△CAO ，则2131m m m 422-=，然后分别解关于m 的绝对值方程可得到对应的P 点坐标． 【详解】解：（1）∵抛物线过原点，对称轴是直线x ＝3， ∴B 点坐标为（6，0），设抛物线解析式为y ＝ax （x ﹣6）， 把A （8，4）代入得a•8•2＝4，解得a ＝14， ∴抛物线解析式为y ＝14x （x ﹣6），即y ＝14x 2﹣32x ； （2）设M （t ，0），易得直线OA 的解析式为y ＝12x ， 设直线AB 的解析式为y ＝kx+b ，把B （6，0），A （8，4）代入得6084k b k b +=⎧⎨+=⎩，解得k 2b 12=⎧⎨=-⎩，∴直线AB 的解析式为y ＝2x ﹣12， ∵MN ∥AB ，∴设直线MN 的解析式为y ＝2x+n ， 把M （t ，0）代入得2t+n ＝0，解得n ＝﹣2t ， ∴直线MN 的解析式为y ＝2x ﹣2t ，解方程组1222y x y x t ⎧=⎪⎨⎪=-⎩得4323x t y t ⎧=⎪⎪⎨⎪=⎪⎩，则42N t,t 33⎛⎫ ⎪⎝⎭， ∴S △AMN ＝S △AOM ﹣S △NOM1124t t t 223=⋅⋅-⋅⋅ 21t 2t 3=-+21(t 3)33=--+，当t ＝3时，S △AMN 有最大值3，此时M 点坐标为（3，0）； （3）设213m,m m 42⎛⎫- ⎪⎝⎭， ∵∠OPQ ＝∠ACO ， ∴当PQ PO OC AC =时，△PQO ∽△COA ，即PQ PO 84=， ∴PQ ＝2PO ，即213m m 2|m |42-=， 解方程213m m 2m 42-=得m 1＝0（舍去），m 2＝14，此时P 点坐标为（14，0）； 解方程213m m 2m 42-=-得m 1＝0（舍去），m 2＝﹣2，此时P 点坐标为（﹣2，0）； ∴当PQ PO AC OC =时，△PQO ∽△CAO ，即PQ PO 48=， ∴PQ ＝12PO ，即2131m m m 422-=，解方程2131m m m 422=-=得m 1＝0（舍去），m 2＝8，此时P 点坐标为（8，0）； 解方程2131m m m 422=-=-得m 1＝0（舍去），m 2＝4，此时P 点坐标为（4，0）； 综上所述，P 点坐标为（14，0）或（﹣2，0）或（4，0）或（8，0）． 【点睛】本题考查了二次函数的综合题：熟练掌握二次函数图象上点的坐标特征和二次函数的性质；会利用待定系数法求函数解析式；理解坐标与图形性质；灵活运用相似比表示线段之间的关系；会运用分类讨论的思想解决数学问题．4．已知抛物线2(5)6y x m x m =-+-+-. （1）求证：该抛物线与x 轴总有交点；（2）若该抛物线与x 轴有一个交点的横坐标大于3且小于5，求m 的取值范围；（3）设抛物线2(5)6y x m x m =-+-+-与y 轴交于点M ，若抛物线与x 轴的一个交点关于直线y x =-的对称点恰好是点M ，求m 的值.【答案】（1）证明见解析；（2）1?<?m?3<；（3）56m m ==或 【解析】 【分析】（1）本题需先根据判别式解出无论m 为任何实数都不小于零，再判断出物线与x 轴总有交点．（2）根据公式法解方程，利用已有的条件，就能确定出m 的取值范围，即可得到结果． （3）根据抛物线y=-x 2+（5-m ）x+6-m ，求出与y 轴的交点M 的坐标，再确定抛物线与x 轴的两个交点关于直线y=-x 的对称点的坐标，列方程可得结论． 【详解】（1）证明：∵()()()222454670b ac m m m ∆=-=-+-=-≥ ∴抛物线与x 轴总有交点.（2）解：由（1）()27m ∆=-，根据求根公式可知，方程的两根为：x =即1216x x m =-=-+， 由题意，有 3<-m 6<5+1<?m 3∴<(3)解：令 x = 0， y =6m -+ ∴ M （0，6m -+）由（2）可知抛物线与x 轴的交点为（-1，0）和（6m -+，0）， 它们关于直线y x =-的对称点分别为（0 ， 1）和（0， 6m -）， 由题意，可得：6166m m m 或-+=-+=- 56m m ∴==或 【点睛】本题考查对抛物线与x 轴的交点，解一元一次方程，解一元一次不等式，根的判别式，对称等，解题关键是熟练理解和掌握以上性质，并能综合运用这些性质进行计算．5．已知，抛物线y ＝﹣x 2+bx +c 经过点A （﹣1，0）和C （0，3）． （1）求抛物线的解析式；（2）在抛物线的对称轴上，是否存在点P ，使PA +PC 的值最小？如果存在，请求出点P 的坐标，如果不存在，请说明理由；（3）设点M 在抛物线的对称轴上，当△MAC 是直角三角形时，求点M 的坐标．【答案】（1）223y x x =-++；（2）当PA PC +的值最小时，点P 的坐标为()1,2；（3）点M 的坐标为()1,1、()1,2、81,3⎛⎫ ⎪⎝⎭或21,3⎛⎫- ⎪⎝⎭. 【解析】 【分析】()1由点A 、C 的坐标，利用待定系数法即可求出抛物线的解析式；()2连接BC 交抛物线对称轴于点P ，此时PA PC +取最小值，利用二次函数图象上点的坐标特征可求出点B 的坐标，由点B 、C 的坐标利用待定系数法即可求出直线BC 的解析式，利用配方法可求出抛物线的对称轴，再利用一次函数图象上点的坐标特征即可求出点P 的坐标；()3设点M 的坐标为()1,m ，则22CM (10)(m 3)=-+-，()22AC [01](30)10=--+-=，()22AM [11](m 0)=--+-，分AMC 90∠=、ACM 90∠=和CAM 90∠=三种情况，利用勾股定理可得出关于m 的一元二次方程或一元一次方程，解之可得出m 的值，进而即可得出点M 的坐标． 【详解】解：()1将()1,0A -、()0,3C 代入2y x bx c =-++中，得：{103b c c --+==，解得：{23b c ==，∴抛物线的解析式为223y x x =-++．()2连接BC 交抛物线对称轴于点P ，此时PA PC +取最小值，如图1所示．当0y =时，有2230x x -++=， 解得：11x =-，23x =，∴点B 的坐标为()3,0．抛物线的解析式为2223(1)4y x x x =-++=--+，∴抛物线的对称轴为直线1x =．设直线BC 的解析式为()0y kx d k =+≠， 将()3,0B 、()0,3C 代入y kx d =+中， 得：{303k d d +==，解得：{13k d =-=，∴直线BC 的解析式为3y x =-+．当1x =时，32y x =-+=，∴当PA PC +的值最小时，点P 的坐标为()1,2．()3设点M 的坐标为()1,m ，则22(10)(3)CM m =-+-，()22[01](30)10AC =--+-=，()22[11](0)AM m =--+-．分三种情况考虑：①当90AMC ∠=时，有222AC AM CM =+，即22101(3)4m m =+-++，解得：11m =，22m =，∴点M 的坐标为()1,1或()1,2；②当90ACM ∠=时，有222AM AC CM =+，即224101(3)m m +=++-，解得：83m =， ∴点M 的坐标为81,3⎛⎫⎪⎝⎭；③当90CAM ∠=时，有222CM AM AC =+，即221(3)410m m +-=++，解得：23m =-， ∴点M 的坐标为21,.3⎛⎫- ⎪⎝⎭综上所述：当MAC 是直角三角形时，点M 的坐标为()1,1、()1,2、81,3⎛⎫ ⎪⎝⎭或21,.3⎛⎫- ⎪⎝⎭【点睛】本题考查待定系数法求二次(一次)函数解析式、二次(一次)函数图象的点的坐标特征、轴对称中的最短路径问题以及勾股定理，解题的关键是：()1由点的坐标，利用待定系数法求出抛物线解析式；()2由两点之间线段最短结合抛物线的对称性找出点P 的位置；()3分AMC 90∠=、ACM 90∠=和CAM 90∠=三种情况，列出关于m 的方程．6．如图，抛物线y=ax 2+bx 过点B （1，﹣3），对称轴是直线x=2，且抛物线与x 轴的正半轴交于点A ．（1）求抛物线的解析式，并根据图象直接写出当y≤0时，自变量x 的取值范围； （2）在第二象限内的抛物线上有一点P ，当PA ⊥BA 时，求△PAB 的面积．【答案】（1）抛物线的解析式为y=x 2﹣4x ，自变量x 的取值范图是0≤x≤4；（2）△PAB 的面积=15． 【解析】 【分析】（1）将函数图象经过的点B 坐标代入的函数的解析式中，再和对称轴方程联立求出待定系数a 和b ；（2）如图，过点B 作BE ⊥x 轴，垂足为点E ，过点P 作PE ⊥x 轴，垂足为F ，设P （x ，x 2-4x ），证明△PFA ∽△AEB,求出点P 的坐标，将△PAB 的面积构造成长方形去掉三个三角形的面积． 【详解】（1）由题意得，322a b b a+-⎧⎪⎨-⎪⎩＝＝，解得14a b -⎧⎨⎩＝＝，∴抛物线的解析式为y=x 2-4x ， 令y=0，得x 2-2x=0，解得x=0或4， 结合图象知，A 的坐标为（4，0），根据图象开口向上，则y≤0时，自变量x 的取值范围是0≤x≤4；（2）如图，过点B 作BE ⊥x 轴，垂足为点E ，过点P 作PE ⊥x 轴，垂足为F ，设P （x ，x 2-4x ）, ∵PA ⊥BA ∴∠PAF+∠BAE=90°, ∵∠PAF+∠FPA=90°, ∴∠FPA=∠BAE 又∠PFA=∠AEB=90° ∴△PFA ∽△AEB,∴PF AF AE BE =，即244213x x x--=-， 解得，x= −1，x=4（舍去） ∴x 2-4x=-5∴点P 的坐标为（-1，-5），又∵B 点坐标为（1，-3），易得到BP 直线为y=-4x+1 所以BP 与x 轴交点为（14，0） ∴S △PAB=115531524⨯⨯+= 【点睛】本题是二次函数综合题，求出函数解析式是解题的关键，特别是利用待定系数法将两条直线表达式解出，利用点的坐标求三角形的面积是关键．7．如图，（图1，图2），四边形ABCD 是边长为4的正方形，点E 在线段BC 上，∠AEF=90°,且EF 交正方形外角平分线CP 于点F ，交BC 的延长线于点N, FN ⊥BC ． （1）若点E 是BC 的中点（如图1），AE 与EF 相等吗？（2）点E 在BC 间运动时（如图2），设BE=x ，△ECF 的面积为y ． ①求y 与x 的函数关系式；②当x 取何值时，y 有最大值，并求出这个最大值.【答案】（1）AE=EF ；（2）①y=-12x 2+2x （0＜x ＜4)，②当x=2,y 最大值=2. 【解析】 【分析】（1）在AB 上取一点G ，使AG=EC ，连接GE ，利用ASA ，易证得：△AGE ≌△ECF ，则可证得：AE=EF ；（2）同（1）可证明AE=EF ，利用AAS 证明△ABE ≌△ENF ，根据全等三角形对应边相等可得FN=BE ，再表示出EC ，然后利用三角形的面积公式即可列式表示出△ECF 的面积为y ，然后整理再根据二次函数求解最值问题． 【详解】（1）如图，在AB 上取AG=EC ， ∵四边形ABCD 是正方形， ∴AB=BC ，有∵AG=EC ，∴BG=BE ， 又∵∠B=90°， ∴∠AGE=135°，又∵∠BCD=90°，CP 平分∠DCN ， ∴∠ECF=135°，∵∠BAE ＋∠AEB=90°，∠AEB ＋∠FEC=90°， ∴∠BAE=∠FEC ， 在△AGE 和△ECF 中，AGE ECF AG ECGAE CEF ∠=∠⎧⎪=⎨⎪∠=∠⎩, ∴△AGE ≌△ECF ， ∴AE=EF ；(2)①∵由（1）证明可知当E 不是中点时同理可证AE=EF ， ∵∠BAE=∠NEF ，∠B=∠ENF=90°， ∴△ABE ≌△ENF ， ∴FN=BE=x ， ∴S △ECF =12(BC-BE)·FN ， 即y=12x(4-x ）， ∴y=-12x 2+2x （0＜x ＜4)， ②()()222111y x 2x x 4x x 22222=-+=--=--+， 当x=2，y 最大值=2. 【点睛】本题考查了正方形的性质，全等三角形的判定与性质，二次函数的最值问题，综合性较强，正确添加辅助线、熟练掌握相关知识是解题的关键．8．如图，在平面直角坐标系中，抛物线y=ax 2+2x+c 与x 轴交于A （﹣1，0）B （3，0）两点，与y 轴交于点C ，点D 是该抛物线的顶点． （1）求抛物线的解析式和直线AC 的解析式；（2）请在y 轴上找一点M ，使△BDM 的周长最小，求出点M 的坐标；（3）试探究：在拋物线上是否存在点P ，使以点A ，P ，C 为顶点，AC 为直角边的三角形是直角三角形？若存在，请求出符合条件的点P 的坐标；若不存在，请说明理由．【答案】（1）抛物线解析式为y=﹣x 2+2x+3；直线AC 的解析式为y=3x+3；（2）点M 的坐标为（0，3）；（3）符合条件的点P 的坐标为（73，209）或（103，﹣139）， 【解析】分析：（1）设交点式y=a （x+1）（x-3），展开得到-2a=2，然后求出a 即可得到抛物线解析式；再确定C （0，3），然后利用待定系数法求直线AC 的解析式；（2）利用二次函数的性质确定D 的坐标为（1，4），作B 点关于y 轴的对称点B′，连接DB′交y 轴于M ，如图1，则B′（-3，0），利用两点之间线段最短可判断此时MB+MD 的值最小，则此时△BDM的周长最小，然后求出直线DB′的解析式即可得到点M的坐标；（3）过点C作AC的垂线交抛物线于另一点P，如图2，利用两直线垂直一次项系数互为负倒数设直线PC的解析式为y=-13x+b，把C点坐标代入求出b得到直线PC的解析式为y=-13x+3，再解方程组223133y x xy x⎧-++⎪⎨-+⎪⎩＝＝得此时P点坐标；当过点A作AC的垂线交抛物线于另一点P时，利用同样的方法可求出此时P点坐标．详解：（1）设抛物线解析式为y=a（x+1）（x﹣3），即y=ax2﹣2ax﹣3a，∴﹣2a=2，解得a=﹣1，∴抛物线解析式为y=﹣x2+2x+3；当x=0时，y=﹣x2+2x+3=3，则C（0，3），设直线AC的解析式为y=px+q，把A（﹣1，0），C（0，3）代入得3p qq-+=⎧⎨=⎩，解得33pq=⎧⎨=⎩，∴直线AC的解析式为y=3x+3；（2）∵y=﹣x2+2x+3=﹣（x﹣1）2+4，∴顶点D的坐标为（1，4），作B点关于y轴的对称点B′，连接DB′交y轴于M，如图1，则B′（﹣3，0），∵MB=MB′，∴MB+MD=MB′+MD=DB′，此时MB+MD的值最小，而BD的值不变，∴此时△BDM的周长最小，易得直线DB′的解析式为y=x+3，当x=0时，y=x+3=3，∴点M的坐标为（0，3）；（3）存在．过点C作AC的垂线交抛物线于另一点P，如图2，∵直线AC的解析式为y=3x+3，∴直线PC的解析式可设为y=﹣13x+b，把C（0，3）代入得b=3，∴直线PC的解析式为y=﹣13x+3，解方程组223133y x xy x⎧-++⎪⎨-+⎪⎩＝＝，解得3xy=⎧⎨=⎩或73209xy⎧=⎪⎪⎨⎪=⎪⎩，则此时P点坐标为（73，209）；过点A作AC的垂线交抛物线于另一点P，直线PC的解析式可设为y=﹣x+b，把A（﹣1，0）代入得13+b=0，解得b=﹣13，∴直线PC的解析式为y=﹣13x﹣13，解方程组2231133y x xy x⎧-++⎪⎨--⎪⎩＝＝，解得1xy=-⎧⎨=⎩或103139xy⎧=⎪⎪⎨⎪=-⎪⎩，则此时P点坐标为（103，﹣139）.综上所述，符合条件的点P的坐标为（73，209）或（103，﹣139）.点睛：本题考查了二次函数的综合题：熟练掌握二次函数图象上点的坐标特征和二次函数的性质；会利用待定系数法求函数解析式，理解两直线垂直时一次项系数的关系，通过解方程组求把两函数的交点坐标；理解坐标与图形性质，会运用两点之间线段最短解决最短路径问题；会运用分类讨论的思想解决数学问题．9．已知抛物线C1：y=ax2﹣4ax﹣5（a＞0）．（1）当a=1时，求抛物线与x轴的交点坐标及对称轴；（2）①试说明无论a为何值，抛物线C1一定经过两个定点，并求出这两个定点的坐标；②将抛物线C1沿这两个定点所在直线翻折，得到抛物线C2，直接写出C2的表达式；（3）若（2）中抛物线C2的顶点到x轴的距离为2，求a的值．【答案】（1）（﹣1，0）或（5，0）（2）①（0，﹣5），（4，﹣5）②y=﹣ax2+4ax﹣5（3）a=或【解析】试题分析：（1）将a=1代入解析式，即可求得抛物线与x轴交点；（2）①化简抛物线解析式，即可求得两个点定点的横坐标，即可解题；②根据抛物线翻折理论即可解题；（3）根据（2）中抛物线C2解析式，分类讨论y=2或﹣2，即可解题试题解析：（1）当a=1时，抛物线解析式为y=x2﹣4x﹣5=（x﹣2）2﹣9，∴对称轴为y=2；∴当y=0时，x﹣2=3或﹣3，即x=﹣1或5；∴抛物线与x轴的交点坐标为（﹣1，0）或（5，0）；（2）①抛物线C1解析式为：y=ax2﹣4ax﹣5，整理得：y=ax（x﹣4）﹣5；∵当ax（x﹣4）=0时，y恒定为﹣5；∴抛物线C1一定经过两个定点（0，﹣5），（4，﹣5）；②这两个点连线为y=﹣5；将抛物线C1沿y=﹣5翻折，得到抛物线C2，开口方向变了，但是对称轴没变；∴抛物线C2解析式为：y=﹣ax2+4ax﹣5，（3）抛物线C2的顶点到x轴的距离为2，则x=2时，y=2或者﹣2；当y=2时，2=﹣4a+8a﹣5，解得，a=；当y=﹣2时，﹣2=﹣4a+8a﹣5，解得，a=；∴a=或；考点：1、抛物线与x轴的交点；2、二次函数图象与几何变换10．抛物线，若a，b，c满足b=a+c，则称抛物线为“恒定”抛物线．（1）求证：“恒定”抛物线必过x轴上的一个定点A；（2）已知“恒定”抛物线的顶点为P，与x轴另一个交点为B，是否存在以Q为顶点，与x轴另一个交点为C的“恒定”抛物线，使得以PA，CQ为边的四边形是平行四边形？若存在，求出抛物线解析式；若不存在，请说明理由．【答案】（1）证明见试题解析；（2），或．【解析】试题分析：（1）由“恒定”抛物线的定义，即可得出抛物线恒过定点（﹣1，0）；（2）求出抛物线的顶点坐标和B的坐标，由题意得出PA∥CQ，PA=CQ；存在两种情况：①作QM⊥AC于M，则QM=OP=，证明Rt△QMC≌Rt△POA，MC=OA=1，得出点Q的坐标，设抛物线的解析式为，把点A坐标代入求出a的值即可；②顶点Q在y轴上，此时点C与点B重合；证明△OQC≌△OPA，得出OQ=OP=，得出点Q坐标，设抛物线的解析式为，把点C坐标代入求出a的值即可．试题解析：（1）由“恒定”抛物线，得：b=a+c，即a﹣b+c=0，∵抛物线，当x=﹣1时，y=0，∴“恒定”抛物线必过x轴上的一个定点A（﹣1，0）；（2）存在；理由如下：∵“恒定”抛物线，当y=0时，，解得：x=±1，∵A（﹣1，0），∴B（1，0）；∵x=0时，y=，∴顶点P的坐标为（0，），以PA，CQ为边的平行四边形，PA、CQ是对边，∴PA∥CQ，PA=CQ，∴存在两种情况：①如图1所示：作QM⊥AC于M，则QM=OP=，∠QMC=90°=∠POA，在Rt△QMC和Rt△POA中，∵CQ=PA，QM=OP，∴Rt△QMC≌Rt△POA（HL），∴MC=OA=1，∴OM=2，∵点A和点C是抛物线上的对称点，∴AM=MC=1，∴点Q的坐标为（﹣2，），设以Q为顶点，与x轴另一个交点为C的“恒定”抛物线的解析式为，把点A（﹣1，0）代入得：a=，∴抛物线的解析式为：，即；②如图2所示：顶点Q在y轴上，此时点C与点B重合，∴点C坐标为（1，0），∵CQ∥PA，∴∠OQC=∠OPA，在△OQC和△OPA中，∵∠OQC=∠OPA，∠COQ=∠AOP，CQ=PA，∴△OQC≌△OPA（AAS），∴OQ=OP=，∴点Q坐标为（0，），设以Q为顶点，与x轴另一个交点为C的“恒定”抛物线的解析式为，把点C（1，0）代入得：a=，∴抛物线的解析式为：；综上所述：存在以Q为顶点，与x轴另一个交点为C的“恒定”抛物线，使得以PA，CQ为边的四边形是平行四边形，抛物线的解析式为：，或．考点：1．二次函数综合题；2．压轴题；3．新定义；4．存在型；5．分类讨论．。

一、二次函数真题与模拟题分类汇编〔难题易错题〕1 .童装店销售某款童装,每件售价为60元,每星期可卖100件,为了促销该店决定降价销售, 经市场调查发现：每降价1元,每星期可多卖10件,该款童装每件本钱30元,设降价后该款童装每件售价工元,每星期的销售量为〕'件.⑴降价后,当某一星期的销售量是未降价前一星期销售量的3倍时,求这一星期中每件童装降价多少元？⑵当每件售价定为多少元时,一星期的销售利润最大,最大利润是多少？【答案】〔1〕这一星期中每件童装降价20元；〔2〕每件售价定为50元时,一星期的销售利润最大,最大利润4000元.【解析】【分析】〔1〕根据售量与售价x 〔元/件〕之间的关系列方程即可得到结论.〔2〕设每星期利润为W元,构建二次函数利用二次函数性质解决问题.【详解】解：〔1〕根据题意得,〔60-x〕 xl0+100=3xl00,解得：x=40,60 - 40 = 20 元,答：这一星期中每件童装降价20元：〔2〕设利润为w,根据题意得,w= 〔x- 30〕 [ 〔60-X〕xl0+100]= - 10x2+1000x - 21000=-10 〔x- 50〕 2+4000,答：每件售价定为50元时,一星期的销售利润最大,最大利润4000元.【点睛】此题考查二次函数的应用,一元二次不等式,解题的关键是构建二次函数解决最值问题, 利用图象法解一元二次不等式,属于中考常考题型.2 .阅读：我们约定,在平面直角坐标系中,经过某点且平行于坐标轴或平行于两坐标轴夹角平分线的直线,叫该点的“特征线〞.例如,点M 〔1, 3〕的特征线有：x=l, y=3,备用图问题与探究：如图,在平面直角坐标系中有正方形0A8C,点8在第一象限,A、C分别在x轴和y轴上,抛物线＞ =；*一〃?〕2+〃经过8、C两点,顶点.在正方形内部.〔1〕直接写出点.〔m, n〕所有的特征线：〔2〕假设点.有一条特征线是y=x+l,求此抛物线的解析式：〔3〕点P是48边上除点八外的任意一点,连接0P,将AOAP沿着0P折登,点4落在点々的位置,当点4在平行于坐标轴的.点的特征线上时,满足〔2〕中条件的抛物线向下平移多少距离,其顶点落在0P上？【答案】〔1〕 x=m, y=n, y=x+n - m, y= - x+m+n；〔2〕 y = - 〔x-2〕2 + 3 ；〔3〕抛物4线向下平移上二正或W距离,其顶点落在OP上. 3 12【解析】试题分析：〔1〕根据特征线直接求出点.的特征线：〔2〕由点.的一条特征线和正方形的性质求出点.的坐标,从而求出抛物线解析式；〔2〕分平行于x轴和y轴两种情况,由折卷的性质计算即可.试题解析：解：〔1〕・二点D 〔m,.〕,,••点.〔m, n〕的特征线是x=m, y=n, y=x+n - m,y= - x+m+n；〔2〕点.有一条特征线是y=x+l, .•.〃=m+l. •.•抛物线解析式为了 = !〔工一"?了+〃,.•.y = =〔x—〃?〕2+〃? + 1, ,四边形OA8C是正方形,且.点为正方4 4形的对称轴,.〔m, /?〕,「. 8 〔2m, 2m〕 ,y = —〔2m — m〕2 + n = 2m 9将c=m+l 带4入得到m=2, n=3；・・・.〔2, 3〕,・•・抛物线解析式为y = !〔x-2〕2+3.〔3〕①如图,当点A在平行于y轴的.点的特征线时：根据题意可得,D (2, 3),・ .0A=0A=4, 0M=2,N AOM=60°,「・N AOP=N AOP=30°,:MN笺空,抛物线需要向下平移的距离=3—李亨•②如图,当点4在平行于X轴的.点的特征线时,设A〔P,3 〕,那么OA=OA=4, OE=3,EA 二“2.32 =a,,AF=4-a,设P(4, c) (c>0),,在RS AFP 中,(4-V7)2+ (3-c) 2=c2, .•“」6T立,「.p (4, .16 —4" ) ,直线OP解析式为3 3y=匕Lx, ：.N (2, l") •.抛物线需要向下平移的距离=3-3 38-2>/7 _1 + 2>/7-3-- -3综上所述：抛物线向下平移) - 2琳或1 + 2"距离,其顶点落在0P上. 3 3点睛：此题是二次函数综合题,主要考查了折叠的性质,正方形的性质,解答此题的关键是用正方形的性质求出点.的坐标.3.在直角坐标系中,我们不妨将横坐标,纵坐标均为整数的点称之为〃中国结〃.〔1〕求函数y=/x+2的图像上所有“中国结〞的坐标：〔2〕求函数y=±〔HO, k为常数〕的图像上有且只有两个“中国结〃,试求出常数k的值X与相应“中国结〞的坐标；〔3〕假设二次函数丫=〔公一3攵+2〕/+〔2攵2-4%+ 1〕%+公一% 〔k为常数〕的图像与x轴相交得到两个不同的"中国结",试问该函数的图像与x轴所围成的平而图形中〔含边界〕,一共包含有多少个“中国结〞？【答案】〔1〕〔0,2〕 : 〔2〕当k=l时,对应"中国结〞为〔1,1〕〔一1, -D ;当k=-l 时,对应"中国结"为〔1, 一1〕, 〔一1,1〕 ; 〔3〕 6个.【解析】试题分析：〔1〕由于X是整数,XHO时,JJx是一个无理数,所以XHO时,JJx+2不是整数,所以x=o, y=2,据此求出函数y=J^x+2的图象上所有“中国结〃的坐标即可.k〔2〕首先判断出当k=l时,函数/一〔k/0, k为常数〕的图象上有且只有两个〃中国xk结〃：〔1, 1〕、〔-1、-1〕：然后判断出当代1时,函数度一〔kHO, k为常数〕的图X象上最少有4个〃中国结〃,据此求出常数k的值与相应〃中国结〃的坐标即可.(3)首先令(k2-3k+2) x2+ (2k2-4k+l) x+k2 - k=0,那么[(k- 1) x+k][ (k-2) x+ (k-1)]=0,求出X】、X2的值是多少；然后根据X】、X2的值是整数,求出k的值是多少：最后根据横坐标,纵坐标均为整数的点称之为"中国结",判断出该函数的图象与x轴所用成的平面图形中(含边界),一共包含有多少个“中国结〞即可.试题解析：(l);x是整数,XHO时,、^x是一个无理数,xHO时,JJx+2不是整数,x=0> y=2,即函数y=Cx+2的图象上"中国结〞的坐标是(0, 2).(2)①当k=l时,函数度勺(k#0, k为常数)的图象上有且只有两个“中国结〃：x (1, 1)、(-1、-1)：②当匕-1时,函数丫=&(HO, k为常数)的图象上有且只有两个“中国结〃：X(1, -1)、( -1, 1).③当修±1时,函数尸& (HO, k为常数)的图象上最少有4个〃中国结JX(I, k)、( - 1, - k)、(k, 1)、( - k, - 1),这与函数度土(kxo, k 为常数)的x图象上有且只有两个“中国结"矛盾,k综上可得,k=l时,函数y=— (k/0, k为常数)的图象上有且只有两个“中国结J (1, x 1)、( - 1、- 1)；k=-l时,函数y=七(k/0, k为常数)的图象上有且只有两个“中国结J (1, -1)、x (-1、1).(3)令(k2-3k+2) x2+ (2k2-4k+l) x+k2 - k=0,那么[(k- 1) x+k][ (k-2) x+ (k- 1) ]=0, kx.= ---------.•・{ ik-\f x 2x) +1• k =——=-=——. x1 +1 x2 +1 整理,可得XlX2+2X2+l=0t/. xz (xi+2) = T,•••X】、X2都是整数,X)= 1 x, =—1｛- 或｛-玉+2 = _「^+2 = 1匹=T ②当｛X、= —1k ,,/ ------- = -1 ,l — kk=k-l,无解；练上,可得.3K=—, XF-3, x2=l t2y= (k2- 3k+2) x2+ (2k2-4k+l) x+k2 - k3 3 3 3 3 3=[(-)2-3X-+21X2+[2X ( - ) 2-4x-+l]x+ (- ) 2--2 2 2 2 2 2①当x=-2时,1 13 1 1 3y= - - x2- — x+ — = " - x ( - 2) 2 - -x ( - 2) + —4 2 4 4 2 4_3~4②当X=-1时,=13③当x=0时,y=-,另外,该函数的图象与X轴所闱成的平面图形中x轴上的“中国结〞有3个: 〔-2, 0〕、〔 -1、0〕、〔0, 0〕.综上,可得假设二次函数y= 〔k2-3k+2〕 x2+ 〔2k2-4k+l〕 x+l?-k 〔k为常数〕的图象与x轴相交得到两个不同的"中国结〞,该函数的图象与x轴所围成的平面图形中〔含边界〕,一共包含有6个“中国结〞：〔-3, 0〕、〔-2, 0〕、〔 - 1, 0〕〔-1, 1〕、〔0, 0〕、〔1, 0〕.考点：反比例函数综合题4.如图,抛物线〕,= 公+ C的顶点为A〔4,3〕,与轴相交于点3〔0,—5〕,对称轴为直线/,点"是线段A8的中点.〔1〕求抛物线的表达式：〔2〕写出点M的坐标并求直线A3的表达式；〔3〕设动点尸,.分别在抛物线和对称轴I上,当以A,P,Q,例为顶点的四边形是平行四边形时,求.,.两点的坐标.【答案】〔1〕y = --x2+4x-5t〔2〕 A/〔2,-1〕, y = 2x-5：〔3〕点夕、.的坐 2标分别为〔6,1〕或〔2,1〕、〔4,—3〕或〔4』〕.【解析】【分析】〔1〕函数表达式为：〕,= a〔x = 4『+3,将点3坐标代入上式,即可求解：〔2〕 A〔4,3〕、B〔0-5〕,那么点加〔2,-1〕,设直线A8的表达式为：y = ^-5,将点4坐标代入上式,即可求解；〔3〕分当AM是平行四边形的一条边、AM是平行四边形的对角线两种情况,分别求解即可. 【详解】解：〔1〕函数表达式为：y = a〔x = 4〕2+3,将点4坐标代入上式并解得：.=2故抛物线的表达式为：y = -l x2+4x-5:乙(2) 4(4,3)、B(0,-5),那么点M(2,-1),设直线A8的表达式为：y = /oc-5,将点A坐标代入上式得：3 =必一5,解得：k = 2,故直线A8的表达式为：y = 2x-5：( i \(3)设点.(4,s)、点P m,——nr +4/H —5 ,①当AM是平行四边形的一条边时,点A向左平移2个单位、向下平移4个单位得到M,同样点P；"?,-：〃,+4机一5)向左平移2个单位、向下平移4个单位得到0(4,s),即：团一2 = 4, —nr +4m-5-4 = s , 2解得：m = 6 ♦ s = —3,故点P、.的坐标分别为(6,1)、(4,-3)：②当AM是平行四边形的对角线时,由中点定理得：4+2 = 〃z+4, 3-1 = --//r +4w-5 + 5,2解得：〞1 = 2, 5 = 1 >故点尸、.的坐标分别为(2/)、(4,1)；故点尸、.的坐标分别为(6,1), (4,一3)或(2,1)、(分-3), (2,1)或(4,1).【点睛】此题考查的是二次函数综合运用,涉及到一次函数、平行四边形性质、图象的面积计算等,其中(3),要主要分类求解,防止遗漏.5.如图,某足球运发动站在点0处练习射门,将足球从离地面0.5m的A处正对球门踢出 (点A在y轴上),足球的飞行高度y(单位：m)与飞行时间t(单位：s)之间满足函数关系y= at2 + 5t+c,足球飞行0.8s时,离地面的高度为3.5m.⑴足球飞行的时间是多少时,足球离地而最高？最大高度是多少？⑵假设足球飞行的水平距离x(单位：m)与飞行时间t(单位：s)之间具有函数关系x = 10t,己知球门的高度为2.44m,如果该运发动正对球门射门时,离球门的水平距离为28m,他能否将球直接射入球门？8【答案】(1)足球飞行的时间是一s时,足球离地而最高,最大高度是4.5m： (2)能.5【解析】(2)把 x=28 代入 x=10t 得 t=2.8,251・•・当 t=2.8 时,y=-a2・8?+5乂2・8令2・25 V2/4, •L . 乙^ 他能将球直接射入球门. 考点：二次函数的应用.6.如图,在平面直角坐标系中,抛物线y=ax?+2x+c 与x 轴交于A ( - 1, 0) B (3, 0)两 点,与y 轴交于点C,点D 是该抛物线的顶点.(1)求抛物线的解析式和直线AC 的解析式；(2)请在y 轴上找一点M,使△BDM 的周长最小,求出点M 的坐标；(3)试探究：在抛物线上是否存在点P,使以点A, P, C 为顶点,AC 为直角边的三角形 是直角三角形？假设存在,请求出符合条件的点P 的坐标：假设不存在,请说明理由.试题分析：(1)由题意得：函数y=atz+5t+c 的图象经过(0, 0.5) (0.8, 35),于是得0. 5二.到 n,求得抛物线的解析式为:3. 5=0.8 4+5X0. 8+c 、 y=-衰2+514,当t=|时,y 破大=4.5；1(2)把x=28代入x=10t 得t=2.8,当t=2.8时,y=- 竿2.82+5、2.8哈2・25V2.44,于是得 16 2到他能将球直接射入球门.解：(1)由题意得：函数y=a&5t+c 的图象经过(0, 0.5) (0.8, 3.5),"0. 5二c• «, 、3. 5=0. 8 &2+5 X 0. g+c '3=解得：_ 251612・•・抛物线的解析式为：y=・•,y【答案】(1)抛物线解析式为y=-x2+2x+3；直线AC 的解析式为丫=3x+3； (2)点M 的 坐标为(0, 3)：7 20 1013〔3〕符合条件的点P 的坐标为〔或,2〕或〔“,-"〕, 3 93 9【解析】分析：〔1〕设交点式y=a 〔x+1〕 〔x-3〕,展开得到-2a=2,然后求出a 即可得到抛物线解 析式：再确定C 〔0, 3 〕,然后利用待定系数法求直线AC 的解析式：〔2〕利用二次函数的性质确定D 的坐标为〔1, 4〕,作B 点关于y 轴的对称点W,连接DB 咬y 轴于M,如图1,那么B ,〔-3, 0〕,利用两点之间线段最短可判断此时MB+MD 的值最小,那么此时△ BDM 的周长最小,然后求出直线DB ,的解析式即可得到点M 的坐标：〔3〕过点C 作AC 的垂线交抛物线于另一点P,如图2,利用两直线垂直一次项系数互为负倒数设直线PC 的解析式为y=-lx +b,把C 点坐标代入求出b 得到直线PC 的解析式为再解方程组, 1得此时P 点坐标；当过点A 作AC 的垂线交抛物y=--x + 3 I 3线于另一点P 时,利用同样的方法可求出此时P 点坐标. 详解：〔1〕设抛物线解析式为y=a 〔x+1〕〔x-3〕, KP y=ax 2 - 2ax - 3a,,2a=2,解得 a=- 1,・•・抛物线解析式为y= - X 2+2X +3： 当 x=0 时,y= - x 2+2x+3=3,那么 C (0, 3), 设直线AC 的解析式为y=px+q.q = 0把 A ( - 1, 0) , C (0, 3)代入得〈q = 3直线AC 的解析式为y=3x+3；〔2〕 •/ y= - X 2+2X +3= - 〔x- 1〕 2+4, •1•顶点D 的坐标为〔1, 4〕,作B 点关于y 轴的对称点B",连接DB ,交y 轴于M,如图1,那么夕〔-3, 0〕,MB=MB',/. MB+MD=MB /+MD=DB /,此时 MB+MD 的值最小, 而BD 的值不变,・•,此时△ BDM 的周长最小,y=-x 2 +2x + 31 y=- -x+3, 3易得直线DB ,的解析式为y=x+3, 当 x=0 时,y=x+3=3> ・ ・•点M 的坐标为〔0, 3〕；〔3〕存在.过点C 作AC 的垂线交抛物线于另一点P,如图2,把C 〔0, 3 〕代入得b=3,・ ,・直线PC 的解析式为y=- -x+3,过点A 作AC 的垂线交抛物线于另一点P,直线PC 的解析式可设为y=-点+b, 把A ( -1, 0)代入得1+b=0,解得b=- L 3 3・ •・直线PC 的解析式为y=- ：x- 1点睛：此题考查了二次函数的综合题：熟练掌握二次函数图象上点的坐标特征和二次函数 的性质；会利用待定系数法求函数解析式,理解两直线垂直时一次项系数的关系,通过解 方程组求把两函数的交点坐标；理解坐标与图形性质,会运用两点之间线段最短解决最短 路径问题：会运用分类讨论的思想解决数学问题.直线PC 的解析式可设为y=- —x+b,3解方程组?y=-x 2+2x + 31 ,解得?y=——x + 33x = 0)=3或,7x =一3 7 20 ,那么此时P 点坐标为〔一,—〕：2.39y =解方程组?y=-x 2+2x + 31 1 y=——x ——33x = -ly = 010x =—3 13那么此时P 点坐标为〔—, 3综上所述,符合条件的点p 的坐标为〔N, 310 T-?>•直线AC 的解析式为y=3x+3.7.如图,直线A8与抛物线C ：),=⑪2+21+.相交于人(—1,0)和点8(2,3)两点.⑴求抛物线.的函数表达式；⑵假设点M 是位于直线A3上方抛物线上的一动点,以M4、/W8为相邻两边作平行四边形 M4N8,当平行四边形M4N8的而积最大时,求此时四边形M4N8的而积S 及点M 的 坐标： ⑶在抛物线C 的对称轴上是否存在定点尸,使抛物线.上任意一点夕到点尸的距离等于到 直线y ="的距离,假设存在,求出定点厂的坐标：假设不存在,请说明理由.41 27 【答案】〔1〕 y =—厂 + 2x + 3 ：〔2〕当 〃 =—,S ZMANB = 2S △ ABM =—,此时2 415 \ :⑶存在.当/A — 时,无论％取任何实数,均有= 理由见解析. \ 4 )【解析】【分析】 (1)利用待定系数法,将A, B 的坐标代入y=ax2+2x+c 即可求得二次函数的解析式； (2)过点M 作MH_Lx 轴于H,交直线AB 于K,求出直线AB 的解析式,设点M (a,- a?+2a+3),那么K (a, a+1),利用函数思想求出MK 的最大值,再求出△ AMB 面积的最大 值,可推出此时平行四边形MANB 的面积S 及点M 的坐标：17(3)如图2,分别过点B, C 作直线y=—的垂线,垂足为N. H,设抛物线对称轴上存在 4点F,使抛物线C 上任意一点P 到点F 的距离等于到直线y=—的距离,其中F (1, a), 4 连接BF, CF,那么可根据BF=BN, CF=CN 两组等量关系列出关于a 的方程组,解方程组即 可.【详解】(1)由题意把点(-1, 0)、(2, 3)代入 y=ax2+2x+c, .- 2 + c = 0得, ,4a + 4 + c = 3 解得 a=-l, c=3,,此抛物线c 函数表达式为：y=*2+2x+3：〔2〕如图1,过点M 作MHLx 轴于H,交直线AB 于K,MH4 〕>>将点〔・1, 0〕、〔2, 3〕代入y=kx+b中, 一k+b=0得,2y 解得,k=l, b=l,/.Y AB=X+1,设点M (a, -a2+2a+3),那么K (a, a+1), 贝lj MK=-a2+2a+3- (a+1)=-(a- - ) 2+—, 2 41 9根据二次函数的性质可知,当合二彳时,MK有最大长度丁, 2 4S A AMB以大=S A AMK+S A BMK=—MK*AH+ —MK> (x B-x H)2 2=—MK e (XB-XA)21 9=x — x32 4_27-—,8以MA、MB为相邻的两边作平行四边形MANB,当平行四边形MANB的面积最大时,27 27 1 15s 餐大=2S A AMB 4U=2X —=—,M (-, —).(3)存在点F,•/ y=-x2+2x+3=-(x-1) 2+4,「・对称轴为直线x=l.当y=0 时,xi=-l, X2=3,,抛物线与点x轴正半轴交于点C (3, 0),17如图2,分别过点B, C作直线y:一的垂线,垂足为N, H, 4抛物线对称轴上存在点F,使抛物线C上任意一点P到点F的距离等于到直线y=—的距4离,设 F (1, a ),连接BF, CF,IT1 17 5 17那么BF=BN二一-3二一,CF=CH=—, 4 4 4(5、(2-1)2+3—3)2 =由题意可列:(3 — 1)2+/=阴【点睛】此题考查了待定系数法求解析式,还考查了用函数思想求极值等,解题关键是能够判断出当平行四边形MANB的面积最大时,aABM的面积最大,且此时线段MK的长度也最大.8.如图,己知二次函数%=a' + "过(-2, 4) , ( - 4. 4)两点.〔1〕求二次函数力的解析式：〔2〕将为沿x轴翻折,再向右平移2个单位,得到抛物线及,直线y=m 〔m>0〕交及于M、N 两点,求线段MN的长度〔用含m的代数式表示〕：〔3〕在〔2〕的条件下,力、及交于A、B两点,如果直线y=m与力、刃的图象形成的封闭曲线交于C、D两点〔C在左侧〕,直线y=-m与力、刃的图象形成的封闭曲线交于E、F两点〔E在左侧〕,求证：四边形CEFD是平行四边形.1yi =_/2_3%【答案】〔1〕2【解析】〔2〕 5 +范〔3〕证实见解析.试题分析：〔1〕根据待定系数法即可解决问题.〔2〕先求出抛物线yz的顶点坐标,再求出其解析式,利用方程组以及根与系数关系即可求出MN.〔3〕用类似〔2〕的方法,分别求出CD、EF即可解决问题.试题解析：⑴・•・二次函数月=°/ + "过〔-2, 4〕 , 〔-4, 4〕两点,4a - 2b = 416a -4b = 4解得:1a=~2=_1 2_ -「.二次函数力的解析式为一寸3X2-3% -# + 3)2 +9,二顶点坐标〔-3, >〕 , ,「将力沿x釉翻折,再向右平移2个单位,得到抛物线〞,9.・・抛物线y2的顶点坐标〔-1, -、〕,•,・抛物线均为1 9y=#+i)2_] 消去y整理得到/ + 2x_8_2m = 0,设打,也是它的两个根,那么"21A〔q+ x2〕-似/2=、阳而千J5：〔3〕由y = my =一/2-3欠,消去y整理得到x +6%+2m = 0,设两个根为打,0那么y =-m1 9______ y =—〔x --CD」"I一亚15〔修+ OF - 4町2«36 -所,由2 2,消去丫得到x2 + 2x-8 + 2m = 0,设两个根为勺,％2,那么EF」X1 - "zlK,dl + 工2〕2 - 4XI%2=«36 - 8m, ... EF=CD, EFII CD,四边形CEFD 是平行四考点：二次函数综合题.9 .抛物避= a/ + M + c,假设a, b, c满足b=a+c,那么称抛物线,=.壮+必+ c为“恒定〞抛物线. 〔1〕求证："恒定"抛物线'=°/ +丘+,必过*轴上的一个定点人；〔2〕"恒定〃抛物线y = -于的顶点为P,与X轴另一个交点为B,是否存在以Q为顶点,与X轴另一个交点为C的“恒定〞抛物线,使得以PA, CQ为边的四边形是平行四边形？假设存在,求出抛物线解析式：假设不存在,请说明理由.【答案】〔1〕证实见试题解析：〔2〕 y = \/^2 + 4v-^x + 3-V3 那么=- v取2 + y3.【解析】试题分析：〔1〕由"恒定〞抛物线的定义,即可得出抛物线恒过定点〔-1, 0〕:〔2〕求出抛物线F = W"一小的顶点坐标和B的坐标,由题意得出PAII CQ, PA=CQ：存在两种情况：①作QMXAC于M,那么QM=0P=\3,证实RtA QM〔^ RtA POA. MC=OA=1,得出点Q的坐标,设抛物线的解析式为,=矶" + 2〕2-\/3,把点A坐标代入求出a的值即可：②顶点Q在y轴上,此时点C与点B重合：证实△0QS4 0PA,得出OQ=OP=\B,得出点Q坐标,设抛物线的解析式为' =以2+«3,把点C坐标代入求出a的值即可.试题解析：〔1〕由“恒定〃抛物线,二仙2 +%+ 4得：b=a+c,即a-b+c=0,二•抛物线y = ax2 + bx + c t当x=-l时,y=0, 恒定〞抛物线,=必+八+〔；必过乂轴上的一个定点 A 〔 - 1, 0〕：〔2〕存在：理由如下：：“恒定"抛物线卜"*丫一道,当尸0时,\8/-、6=0,解得：x=±l, V A ( - 1, 0) , /. B (1, 0):.・x=O 时,y=一\'3,顶点P 的坐标为(0, 一\3),以PA, CQ为边的平行四边形,PA、CQ是对边,「.PAII CQ, PA=CQ, .,.存在两种情况：①如图1所示：作QM_LAC 于M,那么QM=0P=y3, Z QMC=90°=Z POA,在RtA QMC 和RtA POA 中,: CQ=PA, QM=OP,J RtA QMC合RtA POA (HL) , /. MC=OA=1, OM=2, 丁点 A 和点C 是抛物线上的对称点,AM=MC=1, .,.点Q的坐标为(-2, 一\3),设以Q为顶点,与x轴另一个交点为C的“恒定〞抛物线的解析式为y = a(% + 2)2-«3,把点A(-l, 0)代入得：aS% .•.抛物线的解析式为：丫 = \乃(% + 2)273,即,=\访2 + 4、%+3日②如图2所示：顶点Q在y轴上,此时点C与点B重合,.•.点C坐标为(1, 0),CQII PA, /. Z OQC=Z OPA,在^ OQC 和4 OPA 中,: Z OQC=Z OPA, Z COQ=Z AOP,CQ=PA,OQC2△ OPA (AAS) ,「・0Q=0P=、3,「•点Q 坐标为(0, \§),设以Q为顶点,与X轴另一个交点为C的“恒定〞抛物线的解析式为y = a%2 + g3,把点C(l, 0)代入得：a=-W, .•.抛物线的解析式为：?=一臼2 + 口；综上所述：存在以Q为顶点,与x轴另一个交点为C的“恒定〞抛物线,使得以PA, CQ为边的四边形是平行四边形,抛物线的解析式为：«3/ + 4\,做+3\3,或y =-%即 + 0考点：1.二次函数综合题：2.压轴题：3.新定义：4.存在型：5.分类讨论.3 910 .二次函数y=—-x2+bx+c的图象经过A (0, 3) , B ( - 4,--)两点.(1)求b, c的值.3(2)二次函数y= -「xZ+bx+c的图象与x轴是否有公共点,求公共点的坐标：假设没有,请16说明情况.【答案】⑴j 8 : 〔2〕公共点的坐标是〔-2, 0〕或〔8, 0〕. c = 3【解析】【分析】〔1〕把点A、B的坐标分别代入函数解析式求得b、c的值；〔2〕利用根的判别式进行判断该函数图象是否与x轴有交点,由题意得到方程-3 o—X2+-X+3=0,通过解该方程求得x的值即为抛物线与x轴交点横坐标.16 89 3【详解】(1)把 A (0, 3) , B ( - 4,--)分别代入y=- - x2+bx+c,2 16c = 3得4 39------ x l6-4〃 + c =——16 26 = ?解得彳8 ；[c = 33 9〔2〕由〔1〕可得,该抛物线解析式为：y=- -x2+-x+3, 1 o 83 225-4x ( - -- ) x3= >0»16 6483所以二次函数y=- - x2+bx+c的图象与x轴有公共点, 163 9.「- -x2+-x+3=0 的解为：x产・2, X2=8,16 8公共点的坐标是〔-2, 0〕或〔8, 0〕.【点睛】此题考查了抛物线与x轴的交点,二次函数图象上点的坐标特征.注意抛物线解析式与一元二次方程间的转化关系.。

2025年中考数学复习：二次函数综合压轴题常考热点试题汇编1.如图，已知抛物线y =-x 2+bx +c 与一直线相交于A -1，0 ，C 2，3 两点，与y 轴交于点N ．其顶点为D ．(1)求抛物线及直线AC 的函数表达式；(2)设点M 3，m ，求使MN +MD 的值最小时m 的值；(3)若点P 是抛物线上位于直线AC 上方的一个动点，过点P 作PQ ⊥x 轴交AC 于点Q ，求PQ 的最大值．【答案】(1)解：由抛物线y =-x 2+bx +c 过点A -1，0 ，C 2，3 得-1-b +c =0-4+2b +c =3，解得b =2c =3 ，∴抛物线为y =-x 2+2x +3；设直线为y =kx +n 过点A -1，0 ，C 2，3 ，得-k +n =02k +n =3，解得k =1n =1 ，∴直线AC 为y =x +1；(2)解：∵y =-x 2+2x +3=-x -1 2+4，∴D 1,4 ，令y =0，则0=-x 2+2x +3，解得x =-1或x =3，即抛物线与x 轴的另一个交点为3，0 ，作直线x =3，作点D 关于直线x =3的对称点D ，得D 坐标为5，4 ，如图，连接ND 交直线x =3于点M ，此时N 、M 、D 三点共线时，NM +MD 最小，即NM +MD 最小，设直线ND 的关系式为：y =ax +b ，把点N 0,3 和D 5,4 代入得b =35a +b =4 ，1∴直线NM 的函数关系式为：y =15x +3，当x =3时，y =185，∴m =185；(3)解：如图，∵PQ ⊥x 轴交AC 于点Q ，∴设Q x ，x +1 ，则P x ，-x 2+2x +3 ，∴PQ =-x 2+2x +3 -x +1 =-x 2+x +2=-x -12 2+94，∵-1<0，∴PQ 有最大值，最大值为94．2.如图，在平面直角坐标系中，已知点B 的坐标为-1,0 ，且OA =OC =5OB ，抛物线y =ax 2+bx +c a ≠0 图象经过A ，B ，C 三点．(1)求A ，C 两点的坐标；(2)求抛物线的解析式；(3)若点P 是直线AC 下方的抛物线上的一个动点，作PD ⊥AC 于点D ，当PD 的值最大时，求此时点P 的坐标及PD 的最大值．【答案】(1)解：∵点B 的坐标为-1,0 ，∴OB =1，∵OA =OC =5OB ，∴OA =OC =5，∴点A 5,0 ,C 0,-5 ；把点C0,-5代入得：-5a=-5，解得：a=1，故抛物线的表达式为：y=x+1x-5=x2-4x-5；(3)解：∵直线CA过点C0,-5，∴可设其函数表达式为：y=kx-5，将点A5,0代入得：5k-5=0解得：k=1，故直线CA的表达式为：y=x-5，过点P作y轴的平行线交CA于点H，∵OA=OC=5，∴∠OAC=∠OCA=45°，∵PH∥y轴，∴∠PHD=∠OCA=45°，∴PD=PH，∵PD⊥AC，∴PD=22PH，设点P x，x2-4x-5，则点H x,x-5，∴PD=22x-5-x2+4x+5=-22x2+522x=-22x-522+2528，∵-22<0，∴PD有最大值，当x=52时，其最大值为252 8，此时点P52,-354 ．3.如图抛物线y=ax2+bx+c经过点A(-1,0)，点C(0,3)，且OB=OC．(1)求抛物线的解析式及其对称轴；(2)点D、E是直线x=1上的两个动点，且DE=1，点D在点E的上方，求四边形ACDE的周长的最小(3)点P 为抛物线上一点，连接CP ，直线CP 把四边形CBP A 的面积分为3:5两部分，求点P 的坐标．【答案】(1)解：∵OB =OC ，点C (0,3)，∴点B (3,0)，则抛物线的表达式为：y =a (x +1)(x -3)=a (x 2-2x -3)=ax 2-2ax -3a ，将点C (0,3)代入得，故-3a =3，解得：a =-1，故抛物线的表达式为：y =-x 2+2x +3，∵y =-x 2+2x +3=-x -1 2+4，函数的对称轴为：x =1；(2)四边形ACDE 的周长=AC +DE +CD +AE ，其中AC =AO 2+CO 2=12+32=10、DE =1是常数，故CD +AE 最小时，周长最小，取点C 关于直线x =1对称点C (2,3)，则CD =C D ，如图所示，取点A -1,1 ，则A D =AE ，点C 与C 关于x =1对称，则C 2,3 ，∴A C =32+22=13，∴CD +AE =A D +DC ，则当A 、D 、C 三点共线时，CD +AE =A D +DC 最小，周长也最小，四边形ACDE 的周长的最小值=AC +DE +CD +AE=10+1+A D +DC=10+1+A C 10+1+13；(3)如图，设直线CP 交x 轴于点E ，直线CP 把四边形CBP A 的面积分为3：5两部分，又∵S △PCB ：S △PCA =12EB ×(y C -y P )：12AE ×(y C -y P )=BE ：AE ，则AE=52或32，即：点E的坐标为32,0或12,0，∵C0,3，设直线CP的表达式：y=kx+3，将点E的坐标代入直线CP的表达式：y=kx+3，解得：k=-6或-2，故直线CP的表达式为：y=-2x+3或y=-6x+3，联立y=-x2+2x+3y=-2x+3，y=-x2+2x+3y=-6x+3，解得：x=4或x=8(x=0舍去)，故点P的坐标为(4,-5)或(8,-45)．4.如图，在平面直角坐标系中，抛物线y=x2+bx+c与x轴交于点A(-1,0),B(3,0)，与y轴交于点C，作直线BC，点P是抛物线在第四象限上一个动点(点P不与点B,C重合)，连结PB，PC，以PB，PC为边作▱CPBD，点P的横坐标为m．(1)求抛物线对应的函数表达式；(2)当▱CPBD有两个顶点在x轴上时，则点P的坐标为；(3)当▱CPBD是菱形时，求m的值．(4)当m为何值时，▱CPBD的面积有最大值？【答案】(1)解：∵抛物线y=x2+bx+c与x轴交于点A(-1,0),B(3,0)，∴抛物线的解析式为y=(x+1)(x-3)，即y=x2-2x-3，(2)解：∵抛物线的解析式为y=x2-2x-3，令x=0，则y=-3，∴C(0,-3)，∵▱CPBD有两个顶点在x轴上时，∴点D在x轴上，∵四边形CPBD是平行四边形，∴CP∥BD，∴点P和点C为抛物线上的对称点，∵抛物线y=x2-2x-3的对称轴为x=--22×1=1，C(0,-3)，∴P(2,-3)，故答案为：(2,-3)；(3)解：设点P的坐标为(m,y)，∵B(3,0)，C(0,-3)，∴BP2=(3-m)2+y2，CP2=m2+(m+3)2，∵▱CPBD 是菱形，∴BP =CP ，∴BP 2=CP 2，∴(3-m )2+y 2=m 2+(y +3)2，9-2m +m 2+y 2=m 2+y 2+6y +9，m +y =0，∵y =m 2-2m -3，∴m +m 2-2m -3=0，m 2-m -3=0，m =-(-1)±(-1)2-4×1×(-3)2×1=1±132，即m 1=1+132，m 2=1-132，∵点P 是抛物线在第四象限上一个动点(点P 不与点B ,C 重合)，∴0<m <3，∴m =1+132；(4)解：如图所示，过点P 作PE ∥y 轴交直线BC 于点E ，设直线BC 的解析式为y =kx +b (k ≠0)，将B (3,0)，C (0,-3)代入得，3k +b =0b =-3 ，解得，k =1b =-3 ，∴直线BC 的解析式为y =x -3，设P (m ,m 2-2m -3)，则E (m ,m -3)，∴PE =-m 2+3m ，∴S △PBC =12×3(-m 2+3m )，∵S ▱CPBD =2S △PBC=2×12×3(-m 2+3m )=-3m 2+9m=-3m -32 2+274，∴当m =32时，平行四边形CPBD 的面积有最大值．5.二次函数y =ax 2+bx +4a ≠0 的图象经过点A -4,0 ,B 1,0 ，与y 轴交于点C ，点P 为第二象限内抛物线上一点，连接BP 、AC ，交于点Q ，过点P 作PD ⊥x 轴于点D ．(1)求二次函数的表达式；(2)在对称轴上是否存在一个点M ，使MB +MC 的和最小，存在的话，请求出点M 的坐标．不存在的话请说明理由．(3)连接BC ，当∠DPB =2∠BCO 时，求直线BP 的表达式．【答案】(1)解：把A -4,0 ,B 1,0 代入y =ax 2+bx +4a ≠0 得：16a -4b +4=0a +b +4=0 ，解得a =-1b =-3 ，∴二次函数的表达式为y =-x 2-3x +4；(2)在对称轴上存在一个点M ，使MB +MC 的和最小，理由如下：连接AC 交对称轴于M ，则MB +MC 的和最小，如图：∵MA =MB ，∴MB +MC =MA +MC ，而C ，M ，A 共线，∴此时MB +MC 最小，在y =-x 2-3x +4中，令x =0得y =4，∴C 0,4 ，设直线AC 的表达式为y =rx +s ，由A -4,0 ，C 0,4 可得-4r +s =0s =4解得r =1s =4 ∴直线AC 解析式为y =x +4，由y =-x 2-3x +4=-x +32 2+254知抛物线对称轴为直线x =-32，在y =x +4中，令x =-32得y =52，∴M -32,52；(3)设BP 交y 轴于K ，如图：∵PD⊥x轴，∴∠DPB=∠OKB，∵∠DPB=2∠BCO，∴∠OKB=2∠BCO，∴∠CBK=∠BCO，∴BK=CK，设OK=m，则CK=BK=4-m，∵OB2+OK2=BK2，∴12+m2=4-m2，解得m=15 8，∴K0,158，设直线BP的表达式为y=px+q，由B1,0，K0,15 8得到p+q=0q=158解得p=-158 q=158∴直线BP的表达式为y=-158x+158．6.如图，抛物线y=14x2-32x交x轴正半轴于点A，M是抛物线对称轴上的一点，过点M作x轴的平行线交抛物线于点B，C(B在C左边)，交y轴于点D，连结OM，已知OM=5．(1)求OD的长．(2)P是第四象限内抛物线上的一点，连结P A，AC，OC，PO．设点P的横坐标为m，四边形OCAP的面积为S．①求S关于m的函数表达式．②当∠POC=∠DOC时，求S的值．【答案】解：(1)抛物线对称轴为x=-b2a=3，∴DM=3，OA=6；∵OM =5，∴OD =OM 2-DM 2=52-32=4．(2)过点P 作PN ⊥OA 于N ,①由y =0得，0=14x 2-32x解得：x =0(舍去)，x =6∴OA =6，∴S 四边形OCAF =S △OAC +S △OAP=12⋅OA ⋅OD +12⋅OA ⋅PN=12×6×4+12×6-14m 2-32m=12+3-14m 2+32m=-34m 2+92m +12所以，S 关于m 的表达式为：S =-34m 2+92m +12②MC =CD -DM =5=OM ，∴∠MOC =∠MCO ．∵BC ∥x 轴，∴∠AOC =∠MCO =∠MOC ．∵∠POC =∠DOC ，∴∠POC -∠AOC =∠DOC -∠MOC ，∴∠POE =∠DOM ，∴tan ∠POA =tan ∠DOM =34，∴-y p x P =34∴y P =-34x p ，代入抛物线解析式得-34x p =14x 2p -32x p解得x P =0(舍去)或x P =3，∴y P =-34x p =-34×3=-94∴S 四边形OCAF =S △OAC +S △OAP=12⋅OA ⋅OD +12⋅OA ⋅PN =18.757.如图，已知抛物线y =-x 2+bx +c 经过B -3,0 ,C 0,3 两点，与x 轴的另一个交点为A ．(1)求抛物线的解析式；(2)在抛物线对称轴上找一点E ，使得AE +CE 的值最小，求点E 的坐标；(3)设点P 为x 轴上的一个动点，写出所有使△BPC 为等腰三角形的点P 的坐标，并把求其中一个点P 的坐标的过程写出来．【答案】(1)解：将点B -3,0 ,C 0,3 代入抛物线解析式得-9-3b +c =0c =3，解得b =-2c =3 ，∴抛物线的解析式为y =-x 2-2x +3；(2)解：∵抛物线解析式为y =-x 2-2x +3=-x +1 2+4，∴抛物线的对称轴为直线x =-1，∵点A 、B 关于对称轴对称，∴BE =AE ，∴AE +CE =BE +CE ，∴当B 、C 、E 三点共线时，BE +CE 最小，即此时AE +CE 最小，∴BC 与对称轴的交点即为点E ，如下图，设直线BC 解析式为y =mx +n ，∴-3m +n =0n =3，解得m =1n =3 ，∴直线BC 的解析式为y =x +3；当x =-1时，y =x +3=2，∴E -1，2 ；(3)解：∵B -3,0 ,C 0,3 ，∴OB =OC =3，∴BC =32+32=32，当B 为顶点时，则PB =BC =32，∴点P 的坐标为32-3,0 或-32-3,0 ；当C为顶点时，则PC=BC，∴点P与点B关于y轴对称，∴点P的坐标为3，0；当BC为底边时，则PC=PB，设点P的坐标为m，0，∴-3-m2=m2+32，解得m=0∴点P的坐标为0，0；综上，点P的坐标为0，0或3，0或32-3,0或-32-3,0．8.如图，在平面直角坐标系xOy中，将抛物线y=12x2平移，使平移后的抛物线仍经过原点O，新抛物线的顶点为M(点M在第四象限)，对称轴与抛物线y=12x2交于点N，且MN=4．(1)求平移后抛物线的表达式；(2)如果点N平移后的对应点是点P，判断以点O、M、N、P为顶点的四边形的形状，并说明理由；(3)抛物线y=12x2上的点A平移后的对应点是点B，BC⊥MN，垂足为点C，如果△ABC是等腰三角形，求点A的坐标．【答案】(1)解：由题意得，平移后的抛物线表达式为：y=12x2+bx，则点M的坐标为：-b,-1 2 b2，当x=-b时，y=12x2=12b2，即点N-b,12b2，则MN=12b2+12b2=4，解得：b=2(舍去)或b=-2，则平移后的抛物线表达式为：y=12x2-2x；(2)解：四边形OMPN是正方形，根据题意可得O0,0，M2,-2，N2,2，P4,0，记MN与OP交于点G，则G2,0，∴OG=GP=2，MG=NP=2，MN=OP=4，NO=NP=22，∴四边形OMPN是平行四边形，∵MN=OP=4，∴四边形OMPN是矩形，∵NO=NP=22，∴四边形OMPN是正方形；(3)解：设A a ,12a 2 ，B a +2,12a 2-2 ，C 2,12a 2-2 ，可得AB =22，AC =a -2 2+22，BC =a 2，①AB =AC ，22=a -2 2+22，即a 2-4a =0，解得a 1=4，a 1=0(舍去0)，∴A 4,8 ；②AB =BC ，22=a 2，解得a 1=22，a 1=-22，∴A 22,4 或A -22,4 ；③AC =BC ，a -2 2+22=a 2，解得a =2，∴A 2,2 ；综上，点A 的坐标是4,8 、22,4 、-22,4、2,2 ．9.综合与探究如图，抛物线y =12x 2-32x -2与x 轴交于A ，B 两点，与y 轴交于点C ．过点A 的直线与抛物线在第一象限交于点D 5,3 ．(1)求A ，B ，C 三点的坐标，并直接写出直线AD 的函数表达式．(2)点P 是线段AB 上的一个动点，过点P 作x 轴的垂线，交抛物线于点E ，交直线AD 于点F ．试探究是否存在一点P ，使线段EF 最大．若存在，请求出EF 的最大值；若不存在，请说明理由．(3)若点M 在抛物线上，点N 是直线AD 上一点，是否存在以点B ，D ，M ，N 为顶点的四边形是以BD 为边的平行四边形？若存在，请直接写出所有符合条件的点M 的坐标；若不存在，请说明理由．【答案】(1)解：令y =0，则12x 2-32x -2=0，解得x =4或x =-1，∴A -1,0 ，B 4,0 ，令x =0，则y =-2，∴C 0,-2 ，设直线AD 的函数表达式为y =kx +b ，将A -1,0 ，D 5,3 的坐标代入得，-k +b =05k +b =3 ，解得：k =12b =12，∴y =12x +12；(2)解：存在，理由如下：设P a ,0 ，则E a ,12a 2-32a -2 ，F a ,12a +12，∵P 线段AB 上的一个动点，∴E 在x 轴下方，∴EF =12a +12-12a 2-32a -2 =-12a 2+2a +52=-12a -2 2+92，∵-12<0，∴当a =2时，EF 有最大值，最大值为92；(3)解：存在，点M 的坐标为0,-2 ，2+14,4+142 或2-14,4-142；设M m ,12m 2-32m -2 ，N n ,12n +12，∵B 4,0 ，D 5,3 ，①当平行四边形对角线为BN 和DM 时，则4+n 2=5+m 20+12n +122=3+12m 2-32m -22 ，解得：m =0n =1 或m =4n =5 (当m =4时，M 4,0 与B 点重合，不符合题意，舍去)∴点M 的坐标为0,-2 ；②当平行四边形对角线为BM 和DN 时，则4+m 2=5+n 20+12m 2-32m -22=3+12n +122 ，解得：m =2+14n =1+14 或m =2-14n =1-14 ，∴点M 的坐标为2+14,4+142 或2-14,4-142，综上所述，点M 的坐标为0,-2 ，2+14,4+142 或2-14,4-142 ．10.如图，已知直线y =34x +3与x 轴交于点D ，与y 轴交于点C ，经过点C 的抛物线y =-14x 2+bx +c 与x 轴交于A -6，0 、B 两点，顶点为E ．(1)求该抛物线的函数解析式；(2)连接DE ，求tan ∠CDE 的值；(3)设P 为抛物线上一动点，Q 为直线CD 上一动点，是否存在点P 与点Q ，使得以D 、E 、P 、Q 为顶点的四边形是平行四边形？如果存在，请求出点Q 的坐标；如果不存在，请说明理由．【答案】(1)解：对于y =34x +3，由x =0，得y =3，∴C 0，3 ，∵抛物线过点A -6，0 、C 0，3 ，-14×-6 2-6b +c =0c =3 ，解得：b =-1c =3 ，∴该抛物线为y =-14x 2-x +3；(2)解：由y =-14x 2-x +3=-14x +2 2+4得顶点E -2，4 ，过点E 分别作EF ⊥x 轴于F ，作EG ⊥y 轴于G ，连接EC ，则EF =4，DF =2，EG =2，CG =1，∴DF EF =12=CG EG，∵∠DFE =∠CGE =90°，∴△DFE ∽△CGE∴∠DEF =∠CEG ，EC DE =CG DF=12．∵∠CEG +∠CEF =90°，∠DEF +∠CEF =90°，∴∠DEC =90°，∴tan ∠CDE =EC DE =12；(3)设Q m ，34m +3 ①若DE 为平行四边形的一边，且点P 在点Q 的上方，∵D -4，0 ，E -2，4 ，Q m ，34m +3 ，∴P m +2，34m +7 ，代入抛物线得：34m +7=-14m +2 2-m +2 +3，解得m 1=-7，m 2=-4(舍去)∴Q -7，-94；②若DE 为平行四边形的一边，且点P 在点Q 的下方，∵D -4，0 ，E -2，4 ，Q m ，34m +3 ，∴P m -2，34m -1 ，同理得Q -3+892,15+3898或Q -3-892,15-3898 ，③若DE 为平行四边形的对角线∵∵D -4，0 ，E -2，4 ，Q m ，34m +3 ，∴P -m -6，-34m +1 代入抛物线得：-34m +1=-14-m -6 2--m -6 +3，解得m 1=-1，m 2=-4(舍去)∴Q -1,94，综上所述，点Q 的坐标为-7，-94 Q -3+892,15+3898 或Q -3-892,15-3898或-1,94 ．11.如图，已知抛物钱经过点A (-1，0)，B (3，0)，C (0，3)三点．(1)求抛物线的解析式；(2)点M 是线段BC 上的点(不与B ，C 重合)，过M 作MN ∥y 轴交抛物线于点N ．若点M 的横坐标为m ，请用含m 的代数式表示MN 的长；(3)在(2)的条件下，连接NB 、NC ，当m 为何值时，△BNC 的面积最大，最大面积是多少？【答案】(1)解：根据题意，抛物钱与x 轴交于点A (-1，0)，B (3，0)设抛物线解析式为y =a x +1 x -3将C (0，3)代入可得：-3a =3，解得a =-1即y =-x +1 x -3 =-x 2+2x +3；(2)设直线BC 的解析式为y =kx +b将B (3，0)、C (0，3)代入可得：3k +b =0b =3 ，解得k =-1b =3即y =-x +3，则M (m ,-m +3)，N (m ,-m 2+2m +3)，MN =-m 2+2m +3--m +3 =-m 2+3m ；(3)由题意可得：S △BNC =S △BNM +S △MNC =12×MN ×OB =32-m 2+3m =-32m 2+92m∵-32<0，开口向下，∴m =-92-2×32=32时，S △BNC 面积最大，∴最大面积为S △BNC =-32×32 2+92×32=278．12.如图，已知抛物线y =-x 2+bx +c 与x 轴交于A ，B 两点，与y 轴交于C 点，顶点为D ，其中A 1,0 ，C 0,3 ．直线y =mx +n 经过B ，C 两点．(1)求直线BC 和抛物线的解析式；(2)在抛物线对称轴上找一点M ，使MA +MC 最小，直接写出点M 的坐标；(3)连接BD ，CD ，求△BCD 的面积．【答案】解:(1)将点A 1,0 ，C 0,3 代入y =-x 2+bx +c ，得-1+b +c =0,c =3,解这个方程组，得b =-2,c =3.∴抛物线的解析式为y =-x 2-2x +3.当y =0时，0=-x 2-2x +3=-x +3 x -1 ，解得x 1=-3，x 2=1，∴点B 的坐标为-3,0 ，∵直线y =mx +n 经过B ，C 两点，∴-3m +n =0n =3，解得m =1n =3 ，∴直线BC 解析式为y =x +3；∴当点M是直线BC和对称轴的交点时，MA+MC取得最小值，∵抛物线y=-x2-2x+3=-x+12+4，∴点D的坐标为-1,4，对称轴为直线x=1，将x=1代入直线y=x+3，得：y=-1+3=2，∴点M的坐标为-1,2；(3)∵点D-1，4，点M-1,2，∴DM=4-2=2，∵点B-3，0，∴BO=3，∴S△BCD=S△DMB+S△DMC=12DM⋅BO=12×2×3=3．13.抛物线y=ax2+bx-4(a≠0)与x轴交于点A-2,0和B4,0，与y轴交于点C，连接BC．点P是线段BC下方抛物线上的一个动点(不与点B,C重合)，过点P作y轴的平行线交BC于M，交x轴于N，设点P的横坐标为t．(1)求该拋物线的解析式；(2)用关于t的代数式表示线段PM，求PM的最大值及此时点M的坐标；(3)过点C作CH⊥PN于点H,S△BMN=9S△CHM，①求点P的坐标；②连接CP，在y轴上是否存在点Q，使得△CPQ为直角三角形，若存在，求出点Q的坐标；若不存在，请说明理由．2∴4a-2b-4=016a+4b-4=0，即2a-b=24a+b=1，∴a=12 b=-1∴抛物线的解析式为：y=12x2-x-4；(2)解：令x=0得y=-4，∴C0,-4设直线BC的解析式为y=kx+b，∴b=-44k+b=0∴k=1b=-4 ，∴直线BC的解析式为：y=x-4 ∵P的横坐标为t，PM∥y轴，∴P t,12t2-t-4，M t,t-4，∴PM=t-4-12t2-t-4=-12t2+2t=-12t-22+2，∵-12<0，∴当t=2时，PM有最大值2，此时M2,-2；(3)解：①∵B4,0、C0,-4，∴OB=OC=4，∵∠BOC=90°，∴∠OBC=∠OCB=45°，∵PN∥y轴∴∠NMB=∠OCB=45°，∠MNB=∠COB=90°，∴∠NBM=∠NMB，∴BN=MN，∴S△BMN=12BN2，又∠CMH=∠NMB=45°，∠CHM=90°，∴△CHM是等腰直角三角形∴S△CHM=12CH2∵S△BMN=9S△CHM∴12BN 2=9×12CH 2∴BN =3CH ，∵BN +CH =OB =4，∴CH =1∴P 1,-92 ；②设Q 0,m ，则CQ 2=4+m 2，CP 2=1+-4+92 2=54，PQ 2=1+m +92 2，(Ⅰ)当∠CQP =90°时，54=4+m 2+1+m +92 2，解得：m =-4(舍去)或m =-92，∴Q 0,-92 ；(Ⅱ)当∠CPQ =90°时，54+1+m +92 2=4+m 2，解得：m =-132， ∴Q 0,-132(Ⅲ)当∠PCQ =90°时54+4+m 2=1+m +92 2解得：m =-4(舍去)综上所述，存在点Q 0,-132 或Q 0,-92使得△CPQ 为直角三角形．14.如图，抛物线y =ax 2+bx +c a >0 交x 轴于A 、B 两点(点A 在点B 左侧)，交y 轴于点C ．(1)若A(-1,0),B(3,0),C(0,-3)，①求抛物线的解析式；②若点P为x轴上一点，点Q为抛物线上一点，△CPQ是以CQ为斜边的等腰直角三角形，求出点P的坐标；(2)若直线y=bx+t t>c与抛物线交于点M、N(点M在对称轴左侧)，直线AM交y轴于点E，直线AN交y轴于点D．试说明点C是线段DE的中点．【答案】解：(1)①把A(-1,0)，B(3,0)，C(0,-3)分别代入y=ax2+bx+c，得a-b+c=09a+3b+c=0c=-3，解得a=1b=-2 c=-3 ，∴抛物线的解析式为y=x2-2x-3．②设P(m，0)，过Q作QH⊥x轴于H，则∠PHQ=90°，∵△CPQ是以CQ为斜边的等腰直角三角形，∴PC=PQ，∠CPQ=90°，∴∠OPC+∠HPQ=90°，∠HQP+∠HPQ=90°，∴∠OPC=∠HQP，在△POC和△QHP中∠OPC=∠HQP∠COP=∠PHQCP=QP，∴△POC≌△QHP AAS，∴QH=OP=m，PH=OC=3．当点H在点P的右侧时，OH=m+3，∴Q(m+3，-m)，把Q(m+3，-m)代入y=x2-2x-3，得-m=m+32-2m+3-3，解得m=0或-5，此时，P(0，0)或P(-5，0)．当点H在点P的左侧时，H(m-3，0)，∴Q (m -3，m )，代入y =x 2-2x -3，得m =m -3 2-2m -3 -3，整理，得m 2-9m +12=0，解得m =9±332，此时P 9+332,0 或9-332,0 综上，点P 的坐标为P (0，0)或P (-5，0)或P 9+332,0或9-332,0 (2)设直线AM 为y =kx +m ，直线AN 为y =k 1x +m 1，联立y =bx +t y =ax 2+bx +c ，得ax 2+c -t =0，∴x M +x N =0．联立y =kx +m y =ax 2+bx +c ，得ax 2+b -k x +c -m =0，∴x A x M =c -m a ．同理，得x A x N =c -m 1a．∴x A x M +x A x N =x A x M +x N =0，∴c -m a +c -m 1a=0，∴c -m =m 1-c ．∵D (0，m 1)，E (0，m )，C (0，c )，∴CD =m 1-c ，CE =c -m ，∴CE =CD ，∴点C 为线段DE 的中点．15.如图，二次函数y =-x 2+c 的图象交x 轴于点A 、点B ，其中点B 的坐标为(2,0)，点C 的坐标为(0,2)，过点A 、C 的直线交二次函数的图象于点D ．(1)求二次函数和直线AC的函数表达式；(2)连接DB，则△DAB的面积为；(3)在y轴上确定点Q，使得∠AQB=135°，点Q的坐标为；(4)点M是抛物线上一点，点N为平面上一点，是否存在这样的点N，使得以点A、点D、点M、点N为顶点的四边形是以AD为边的矩形？若存在，请你直接写出点N的坐标；若不存在，请说明理由．【答案】解：(1)∵二次函数y=-x2+c的图象过点B(2,0)，∴0=-22+c，解得c=4∴二次函数解析式为y=-x2+4∴A点坐标为(-2,0)设直线AC的解析式为y=kx+b∴0=-2k+b2=b，解得：k=1b=2∴直线AC的解析式为y=x+2(2)∵直线AC：y=x+2与二次函数交于点A、D∴联立y=-x2+4y=x+2，解得x=-2y=0或x=1y=3∴D点坐标为：(1,3)∵AB=4∴S△DAB=12AB×y D =12×3×4=6(3)∵C(0,2)，A点坐标为(-2,0)∴∠CAB=45°当Q在正半轴时，∵∠AQB=135°，QA=QB∴∠QAO=22.5°=12∠CAO∴AQ平分∠CAO过Q作PQ⊥AC于P设OQ =x ，则OQ =PQ =x ,CQ =2PQ =2x∴OC =OQ +CQ =2x +x =2解得x =22-2∴Q 点坐标为(0,22-2)当Q 在与轴负半轴时，根据对称性可得Q 点坐标为(0,2-22)∴Q 点坐标为(0,2-22)或(0,22-2)(4)当AD 是矩形边长时过A 作AM ⊥AD 交抛物线于M∵直线AC 的解析式为y =x +2∴设直线AM 的解析式为y =-x +b 1代入A 点(-2,0)得b 1=-2∴直线AM 的解析式为y =-x -2∴联立y =-x 2+4y =-x -2，解得x =-2y =0 或x =3y =-5 ∴M 点坐标为(3,-5)∵此时MN 平行且等于AD∴由A (-2,0)平移到D (1,3)与由M (3,-5)平移到N 的平移方式一致∴N 点坐标为(6,-2)同理：:过D 作DM ⊥AD 交抛物线于M ，此时M (0,4)，N (-3,1)综上所述，存在，N 点坐标为(6,-2)或(-3,1)16.如图，在平面直角坐标系中，抛物线y =-x 2+bx +c 与x 轴交于A ，B 两点，与y 轴交于点C ，顶点为D(2,1)，抛物线的对称轴交直线BC 于点E．(1)求抛物线y =-x 2+bx +c 的表达式；(2)把上述抛物线沿它的对称轴向下平移，平移的距离为h (h >0)，在平移过程中，该抛物线与直线BC 始终有交点，求h 的最大值；(3)M 是(1)中抛物线上一点，N 是直线BC 上一点．是否存在以点D ，E ，M ，N 为顶点的四边形是平行四边形？若存在，求出点N 的坐标；若不存在，请说明理由．【答案】(1)解：由D (2,1)可知，-b 2×-1 =24×-1 c -b 24×-1 =1，解得：b =4c =-3 ，∴y =-x 2+4x -3．(2)分别令y =-x 2+4x -3中，x =0，y =0得，B (3，0)，C (0，-3)；设BC 的表达式为：y =kx +n k ≠0 ，将B (3，0)，C (0，-3)代入y =kx +n 得，0=3k +n -3=0+n 解得：k =1n =-3 ；∴BC 的表达式为：y =x -3；抛物线平移后的表达式为：y =-x 2+4x -3-h ，根据题意得，y =-x 2+4x -3-h y =x -3，即x 2-3x +h =0，∵该抛物线与直线BC 始终有交点，∴-3 2-4×1×h ≥0，∴h ≤94，∴h 的最大值为94．(3)存在，理由如下：将x =2代入y =x -3中得E 2，-1 ，①当DE 为平行四边形的一条边时，∵四边形DEMN 是平行四边形，∴DE ∥MN ，DE =MN ，∵DE ∥y 轴，∴MN ∥y 轴，∴设M m，-m2+4m-3，N m，m-3，当-m2+4m-3-m-3=2时，解得：m1=1，m2=2(舍去)，∴N1，-2，当m-3--m2+4m-3=2时，解得：m1=3+172，m2=3-172，∴N3+172，17-3 2或N3-172，-17+32；②当DE为平行四边形的对角线时，设M p，-p2+4p-3，N q，q-3，∵D、E的中点坐标为：(2，0)，∴M、N的中点坐标为：(2，0)，∴p+q2=2-p2+4p-3+q-32=0 ，解得：p1=1 q1=3，p2=2q2=2(舍去)，∴此时点N的坐标为(3，0)；综上分析可知，点N的坐标为：1，-2或3+172，17-32或3-172，-17+32或(3，0)．。

2023年九年级数学中考专题：二次函数综合压轴题（面积问题）1．如图，二次函数25y ax bx =++的图象经过点(1,8)，且与x 轴交于A 、B 两点，与y 轴交于点C ，其中点(1,0)A -，M 为抛物线的顶点．(1)求二次函数的解析式； (2)求MCB △的面积；(3)在坐标轴上是否存在点N ，使得BCN △为直角三角形？若存在，求出点N 的坐标；若不存在，请说明理由．2．如图，抛物线212y x bx c =-++（b 、c 为常数）经过()4,0A 和()0,4B 两点，其顶点为C ．(1)求该抛物线的表达式及其顶点坐标；(2)若点M 是拋物线上第一象限的一个动点．设ABM 的面积为S ，试求S 的最大值； (3)若抛物线222y mx mx m =-++与线段AB 有两个交点，直接写出m 的取值范围． 3．如图，抛物线22(0)y ax ax c a =-+>与y 轴交于点C ，与x 轴交于A ，B 两点，点A 在点B 左侧．点A 的坐标为(1,0),3OC OA -=．(1)求抛物线的解析式；(2)在直线BC 下方的抛物线上是否存在一点P ，使得PBC 的面积等于ABC 面积的三分之二？若存在，求出此时OP 的长；若不存在，请说明理由．(3)将直线AC 绕着点C 旋转45︒得到直线l ，直线l 与抛物线的交点为M （异于点C ），求M 点坐标．4．如图1，抛物线24y ax bx a =+-经过()10A -，，()04C ，两点，与x 轴交于另一点B ．(1)求抛物线和直线BC 的解析式；(2)如图2，点P 为第一象限抛物线上一点，是否存在使四边形PBOC 面积最大的点P ？若存在，求出点P 的坐标；若不存在，请说明理由；(3)如图3，若抛物线的对称轴EF （E 为抛物线顶点）与直线BC 相交于点F ，M 为直线BC 上的任意一点，过点M 作MN EF ∥交抛物线于点N ，以E ，F ，M ，N 为顶点的四边形能否为平行四边形？若能，请求出点N 的坐标；若不能，请说明理由． 5．如图，抛物线24y ax bx =+-与x 轴交于点()2,0A -，()4,0B ，与y 轴交于点C ，顶点为D ．(1)求抛物线的解析式和顶点D 的坐标；(2)动点P ，Q 以相同的速度从点O 同时出发，分别在线段,OB OC 上向点B ，C 方向运动，过点P 作x 轴的垂线，交抛物线于点E ． ①当四边形OQEP 为矩形时，求点E 的坐标；①过点E 作EM BC ⊥于点M ，连接,PM QM ，设BPM △的面积为1S ，CQM 的面积为2S ，当PE 将BCE 的面积分成1:3两部分时，请直接写出12S S 的值． 6．如图，抛物线2(0)y ax bx c a =++≠与x 轴相交于A ，B 两点，抛物线的对称轴为直线=1x -，其中点A 的坐标为(3,0)-．(1)求点B 的坐标；(2)已知1a =，C 为抛物线与y 轴的交点，求抛物线的解析式； (3)若点P 在抛物线上，且4POCBOCSS=，求点P 的坐标；(4)设点Q 是线段AC 上的动点，过点Q 作QD y 轴交抛物线于点D ，求线段QD 长度的最大值．7．如图，在平面直角坐标系中，二次函数22y ax bx =++的图象与x 轴交于()30A -,，()10B ,两点，与y 轴交于点C ．(1)求二次函数的解析式；(2)点P 是直线AC 上方的抛物线上一动点，当ACP △的面积最大时，求点P 的坐标；(3)Q 是x 轴上一动点，M 是第二象限内抛物线上一点，若以A ，C ，M ，Q 为顶点的四边形是平行四边形，直接写出点Q 的坐标．8．如图，直线132y x =-+交y 轴于点A ，交x 轴于点C ，抛物线214y x bx c =-++经过点A ，点C ，且交x 轴于另一点B ．(1)直接写出点A ，点B ，点C 的坐标及抛物线的解析式；(2)在直线AC 上方的抛物线上有一点M ，求四边形ABCM 面积的最大值及此时点M 的坐标；(3)将线段OA 绕x 轴上的动点(),0P m 顺时针旋转90°得到线段O A ''，若线段O A ''与抛物线只有一个公共点，请结合函数图象，求m 的取值范围．9．如图，已知抛物线与x 轴交于()1,0A - 、()4,0B 两点，与y 轴交于点()0,3C ．(1)求抛物线的解析式； (2)求直线BC 的函数解析式；(3)在抛物线上，是否存在一点P ，使PAB 的面积等于ABC 的面积？若存在，求出点P 的坐标；若不存在，请说明理由．10．如图，抛物线26y ax bx =++与x 轴交于点()6,0B ，()2,0C -，与y 轴交于点A ，点P 是线段AB 上方抛物线上的一个动点．(1)求抛物线的解析式；(2)当点P 运动到什么位置时，PAB 的面积最大？(3)过点P 作x 轴的垂线，交线段AB 于点D ，再过点P 作PE x ∥轴交抛物线于点E ，连接DE ．是否存在点P ，使PDE △为等腰直角三角形？若存在，求点P 的坐标；若不存在，请说明理由．11．如图，直线l ：112y x =-+与x 轴，y 轴分别交于点B ，C ，经过B ，C 两点的抛物线2y x bx c =++与x 轴的另一个交点为A ．(1)求该抛物线的解析式；(2)若点P 在直线l 下方的抛物线上，过点P 作PD ①x 轴交l 于点D ，PE ①y 轴交l 于点E ，求PD PE +的最大值；(3)若点P 在直线l 下方的抛物线上，F 为直线l 上的点，以A ，B ，P ，F 为顶点的四边形能否构成平行四边形？若能，直接写出点F 的坐标；若不能，请说明理由． 12．已知顶点为()1,5A 的抛物线2y ax bx c =++经过点()5,1B ，(1)求抛物线的解析式；(2)设C ，D 分别是x 轴、y 轴上的两个动点．①当四边形ABCD 的周长最小时，在图1中作直线CD ，保留作图痕迹并直接写出直线CD 的解析式；①点()(),>0P m n m 是直线y x =上的一个动点，Q 是OP 的中点，以PQ 为斜边按图2所示构造等腰Rt PQR △．在①的条件下，记PQR 与COD △的公共部分的面积为S ，求S 关于m 的函数关系式，并求S 的最大值．13．抛物线24y x x =-与直线y x =交于原点O 和点B ， 与x 轴交于另一点A ， 顶点为D ．(1)填空： 点B 的坐标为___________， 点D 的坐标为___________．(2)如图1 ， 连结OD P ，为x 轴上的动点， 当以O D P ，，为顶点的三角形是等腰三角形时， 请直接写出点P 的坐标；(3)如图2， M 是点B 关于拋物线对称轴的对称点， Q 是拋物线上的动点， 它的横坐标为 (05)m m <<， 连结MQ BQ MQ ，，与直线OB 交于点E ． 设BEQ 和BEM △的面积分别为1S 和2S ， 设12S t s =， 试求t 关于m 的函数解析式并求出t 的最值． 14．如图，二次函数的图象经过点()10A -，，()30B ，，()03C -，，直线22y x =-与x 轴、y 轴交于点D ，E ．(1)求该二次函数的解析式(2)点M 为该二次函数图象上一动点．①若点M 在图象上的B ，C 两点之间，求DME 的面积的最大值． ①若MED EDB ∠∠=，求点M 的坐标．15．如图，在平面直角坐标系中，抛物线24y ax bx =+-与x 轴交于()2,0A -，B 两点，其对称轴直线2x =与x 轴交于点D ．(1)求该抛物线的函数表达式为______；(2)如图1，点P 为抛物线上第四象限内的一动点，连接CD ，PB ，PC ，求四边形BDCP 面积最大值和点P 此时的坐标；(3)如图2，将该抛物线向左平移得到抛物线y '，当抛物线y '经过原点时，与原抛物线的对称轴相交于点E ，点F 为抛物线y '对称轴上的一点，点M 是平面内一点，若以点A ，E ，F ，M 为顶点的四边形是以AE 为边的菱形，请直接写出满足条件的点M 的坐标______．16．如图，已知抛物线2y x bx c =++与x 轴交于点()21,0A m -和点()2,0B m +，与y 轴交于点C ，对称轴轴为直线=1x -．(1)求抛物线的解析式；(2)点P 是直线AC 上一动点，过点P 作PQ y ∥轴，交抛物线于点Q ，以P 为圆心，PQ 为半径作P ，当P 与坐标轴相切时，求P 的半径；(3)直线()340y kx k k =++≠与抛物线交于M ，N 两点，求AMN 面积的最小值．17．如图，在平面直角坐标系中，抛物线23y ax bx =+-与x 轴交于两点()1,0A -和()3,0B ，与y 轴交于点C ，抛物线上有一动点P ，抛物线的对称轴交x 轴于点E ，连接EC ，作直线BC ．(1)求抛物线的解析式；(2)若点P 为直线BC 上方抛物线上一动点时，连接,PB PC ，当23EBC PBC S S =△△时，求点P 坐标；(3)如果抛物线的对称轴上有一动点Q ，x 轴上有一动点N ，是否存在四边形PQCN 是矩形？若存在，在横线上直接写出点N 的坐标，若不存在，请说明理由． 18．如图，直线122y x =-+交y 轴于点A ，交x 轴于点C ，抛物线214y x bx c=-++经过点A ，点C ，且交x 轴于另一点B ．(1)直接写出点A ，点B ，点C 的坐标及抛物线的解析式；(2)在直线AC 上方的抛物线上有一点M ，求三角形ACM 面积的最大值及此时点M 的坐标；(3)将线段OA 绕x 轴上的动点(),0P m 顺时针旋转90︒得到线段O A ''，若线段O A ''与抛物线只有一个公共点，请结合函数图象，求m 的取值范围（直接写出结果即可）．参考答案：1．(1)245y x x =-++； (2)15(3)存在，点N 的坐标为(5,0)-或(0,5)-或(0,0)．2．(1)2142y x x =-++，91,2⎛⎫⎪⎝⎭(2)S 的最大值为4 (3)2m ≥或1249m -<≤-3．(1)抛物线的解析式为2=23y x x -- (2)不存在这样的点P ， (3)M 点坐标是(45)，或315()24-，4．(1)抛物线的解析式：234y x x =-++；直线BC 的解析式为4y x =-+；(2)当()26P ，时，四边形PBOC 面积最大； (3)能，点N 的坐标为52124⎛⎫ ⎪⎝⎭，或724⎛- ⎝或724⎛- ⎝．5．(1)2142y x x =--，91,2D ⎛⎫- ⎪⎝⎭．(2)①(-；①1215S S =或1279S S =6．(1)(1,0) (2)223y x x =+- (3)(4,21)或()4,5- (4)947．(1)224233y x x =--+(2)3(2P -，5)2(3)(5,0)-或(1,0)-8．(1)03A （，），20B -（，），60C （，），抛物线解析式为：2134y x x =-++； (2)3a =时，四边形ABCM 面积最大，其最大值为754，此时M 的坐标为153,4⎛⎫⎪⎝⎭；(3)当3m -≤≤-33m ≤≤时，线段O A ''与抛物线只有一个公共点．9．(1)239344y x x =-++(2)334y x =-+(3)存在，点P 的坐标为：()13,3P ，23P ⎫-⎪⎪⎝⎭，33P ⎫-⎪⎪⎝⎭10．(1)21262y x x =-++(2)153,2P ⎛⎫ ⎪⎝⎭(3)点P 坐标为()46，或()55．11．(1)2512y x x =-+ (2)3(3)13,2⎛⎫- ⎪⎝⎭或1(1,)212．(1)21119424y x x =-++(2)①4y x =-+；①当02m <≤时，218PQRSm =；当823m <≤时，27448S m m =-+-；当843m ≤≤时，21244S m m =-+；S 的最大值为：47答案第3页，共3页 13．(1)()5,5；()2,4-；(2)点P的坐标为()或()-或()4,0或()5,0； (3)()2150566t m m m =-+<<，当52m =时，t 的最大值为2524．14．(1)该二次函数的解析式是()()21323y x x x x =+-=--；(2)①DME 的面积的最大值为52；①点M的坐标为⎝⎭或()12--．15．(1)214433y x x =-- (2)PBDC S 四边形的最大值为17，此时点P 的坐标为()3,5-(3)⎛ ⎝⎭或⎛ ⎝⎭或⎛- ⎝⎭或8,⎛- ⎝⎭16．(1)223y x x =+-(2)2或4(3)817．(1)2=23y x x --(2)⎝⎭或⎝⎭ (3)存在，⎫⎪⎪⎝⎭或⎫⎪⎪⎝⎭18．(1)()0,2A ，()2,0B -，()4,0C ，211242y x x =-++ (2)2，()2,2(3)34m -≤≤-或32m -+≤。

中考压轴题-二次函数综合 （八大题型+解题方法）1、求证“两线段相等”的问题：借助于函数解析式,先把动点坐标用一个字母表示出来；然后看两线段的长度是什么距离即是“点点”距离,还是“点轴距离”,还是“点线距离”,再运用两点之间的距离公式或点到x 轴y 轴的距离公式或点到直线的距离公式,分别把两条线段的长度表示出来,分别把它们进行化简,即可证得两线段相等;2、“平行于y 轴的动线段长度的最大值”的问题：由于平行于y 轴的线段上各个点的横坐标相等常设为t,借助于两个端点所在的函数图象解析式,把两个端点的纵坐标分别用含有字母t 的代数式表示出来,再由两个端点的高低情况,运用平行于y 轴的线段长度计算公式-y y 下上,把动线段的长度就表示成为一个自变量为t,且开口向下的二次函数解析式,利用二次函数的性质,即可求得动线段长度的最大值及端点坐标;3、求一个已知点关于一条已知直线的对称点的坐标问题：先用点斜式或称K ,且与已知直线垂直的直线解析式,再求出两直线的交点坐标,最后用中点坐标公式即可;4、“抛物线上是否存在一点,使之到定直线的距离最大”的问题：方法1先求出定直线的斜率,由此可设出与定直线平行且与抛物线相切的直线的解析式注意该直线与定直线的斜率相等,因为平行直线斜率k 相等,再由该直线与抛物线的解析式组成方程组,用代入法把字母y 消掉,得到一个关于x 的的一元二次方程,由题有△=2b -4ac=0因为该直线与抛物线相切,只有一个交点,所以2b -4ac=0从而就可求出该切线的解析式,再把该切线解析式与抛物线的解析式组成方程组,求出x 、y 的值,即为切点坐标,然后再利用点到直线的距离公式,计算该切点到定直线的距离,即为最大距离; 方法2该问题等价于相应动三角形的面积最大问题,从而可先求出该三角形取得最大面积时,动点的坐标,再用点到直线的距离公式,求出其最大距离;方法3先把抛物线的方程对自变量求导,运用导数的几何意义,当该导数等于定直线的斜率时,求出的点的坐标即为符合题意的点,其最大距离运用点到直线的距离公式可以轻松求出;5、常数问题：1点到直线的距离中的常数问题：“抛物线上是否存在一点,使之到定直线的距离等于一个 固定常数”的问题：先借助于抛物线的解析式,把动点坐标用一个字母表示出来,再利用点到直线的距离公式建立一个方程,解此方程,即可求出动点的横坐标,进而利用抛物线解析式,求出动点的纵坐标,从而抛物线上的动点坐标就求出来了;2三角形面积中的常数问题：“抛物线上是否存在一点,使之与定线段构成的动三角形的面积等于一个定常数”的问题：先求出定线段的长度,再表示出动点其坐标需用一个字母表示到定直线的距离,再运用三角形的面积公式建立方程,解此方程,即可求出动点的横坐标,再利用抛物线的解析式,可求出动点纵坐标,从而抛物线上的动点坐标就求出来了;3几条线段的齐次幂的商为常数的问题：用K 点法设出直线方程,求出与抛物线或其它直线的交点坐标,再运用两点间的距离公式和根与系数的关系,把问题中的所有线段表示出来,并化解即可;6、“在定直线常为抛物线的对称轴,或x 轴或y 轴或其它的定直线上是否存在一点,使之到两定点的距离之和最小”的问题：先求出两个定点中的任一个定点关于定直线的对称点的坐标,再把该对称点和另一个定点连结得到一条线段,该线段的长度〈应用两点间的距离公式计算〉即为符合题中要求的最小距离,而该线段与定直线的交点就是符合距离之和最小的点,其坐标很易求出利用求交点坐标的方法;7、三角形周长的“最值最大值或最小值”问题：① “在定直线上是否存在一点,使之和两个定点构成的三角形周长最小”的问题简称“一边固定两边动的问题：由于有两个定点,所以该三角形有一定边其长度可利用两点间距离公式计算,只需另两边的和最小即可;② “在抛物线上是否存在一点,使之到定直线的垂线,与y 轴的平行线和定直线,这三线构成的动直角三角形的周长最大”的问题简称“三边均动的问题：在图中寻找一个和动直角三角形相似的定直角三角形,在动点坐标一母示后,运用=C C 动动定定斜边斜边,把动三角形的周长转化为一个开口向下的抛物线来破解;8、三角形面积的最大值问题：① “抛物线上是否存在一点,使之和一条定线段构成的三角形面积最大”的问题简称“一边固定两边动的问题”：方法1：先利用两点间的距离公式求出定线段的长度；然后再利用上面３的方法,求出抛物线上的动点到该定直线的最大距离;最后利用三角形的面积公式= 12底×高;即可求出该三角形面积的最大值,同时在求解过程中,切点即为符合题意要求的点;方法2：过动点向y 轴作平行线找到与定线段或所在直线的交点,从而把动三角形分割成两个基本模型的三角形,动点坐标一母示后,进一步可得到）（）（左（定）右（定）下（动）上（动）动三角形x x y y 21−⋅−=S ,转化为一个开口向下的二次函数问题来求出最大值;②“三边均动的动三角形面积最大”的问题简称“三边均动”的问题：先把动三角形分割成两个基本模型的三角形有一边在x 轴或y 轴上的三角形,或者有一边平行于x 轴或y 轴的三角形,称为基本模型的三角形面积之差,设出动点在x 轴或y 轴上的点的坐标,而此类题型,题中一定含有一组平行线,从而可以得出分割后的一个三角形与图中另一个三角形相似常为图中最大的那一个三角形;利用相似三角形的性质对应边的比等于对应高的比可表示出分割后的一个三角形的高;从而可以表示出动三角形的面积的一个开口向下的二次函数关系式,相应问题也就轻松解决了;9、“一抛物线上是否存在一点,使之和另外三个定点构成的四边形面积最大的问题”：由于该四边形有三个定点,,即可得到一个定三角形的面积之和,所以只需动三角形的面积最大,就会使动四边形的面积最大,而动三角形面积最大值的求法及抛物线上动点坐标求法与7相同;10、“定四边形面积的求解”问题： 有两种常见解决的方案：方案一：连接一条对角线,分成两个三角形面积之和；方案二：过不在x 轴或y 轴上的四边形的一个顶点,向x 轴或y 轴作垂线,或者把该点与原点连结起来,分割成一个梯形常为直角梯形和一些三角形的面积之和或差,或几个基本模型的三角形面积的和差11、“两个三角形相似”的问题： 两个定三角形是否相似：（1）已知有一个角相等的情形：运用两点间的距离公式求出已知角的两条夹边,看看是否成比例 若成比例,则相似;否则不相似;（2）不知道是否有一个角相等的情形：运用两点间的距离公式求出两个三角形各边的长,看看是否成比例若成比例,则相似;否则不相似;一个定三角形和动三角形相似：（1）已知有一个角相等的情形：先借助于相应的函数关系式,把动点坐标表示出来一母示,然后把两个目标三角形题中要相似的那两个三角形中相等的那个已知角作为夹角,分别计算或表示出夹角的两边,让形成相等的夹角的那两边对应成比例要注意是否有两种情况,列出方程,解此方程即可求出动点的横坐标,进而求出纵坐标,注意去掉不合题意的点;2不知道是否有一个角相等的情形：这种情形在相似性中属于高端问题,破解方法是,在定三角形中,由各个顶点坐标求出定三角形三边的长度,用观察法得出某一个角可能是特殊角,再为该角寻找一个直角三角形,用三角函数的方法得出特殊角的度数,在动点坐标“一母示”后,分析在动三角形中哪个角可以和定三角形中的那个特殊角相等,借助于特殊角,为动点寻找一个直角三角形,求出动点坐标,从而转化为已知有一个角相等的两个定三角形是否相似的问题了,只需再验证已知角的两边是否成比例若成比例,则所求动点坐标符合题意,否则这样的点不存在;简称“找特角,求动点标,再验证”;或称为“一找角,二求标,三验证”;12、“某函数图象上是否存在一点,使之与另两个定点构成等腰三角形”的问题：首先弄清题中是否规定了哪个点为等腰三角形的顶点;若某边底,则只有一种情况；若某边为腰,有两种情况；若只说该三点构成等腰三角形则有三种情况;先借助于动点所在图象的解析式,表示出动点的坐标一母示,按分类的情况,分别利用相应类别下两腰相等,使用两点间的距离公式,建立方程;解出此方程,即可求出动点的横坐标,再借助动点所在图象的函数关系式,可求出动点纵坐标,注意去掉不合题意的点就是不能构成三角形这个题意;13、“某图象上是否存在一点,使之与另外三个点构成平行四边形”问题：这类问题,在题中的四个点中,至少有两个定点,用动点坐标“一母示”分别设出余下所有动点的坐标若有两个动点,显然每个动点应各选用一个参数字母来“一母示”出动点坐标,任选一个已知点作为对角线的起点,列出所有可能的对角线显然最多有3条,此时与之对应的另一条对角线也就确定了,然后运用中点坐标公式,求出每一种情况两条对角线的中点坐标,由平行四边形的判定定理可知,两中点重合,其坐标对应相等,列出两个方程,求解即可;进一步有：①若是否存在这样的动点构成矩形呢先让动点构成平行四边形,再验证两条对角线相等否若相等,则所求动点能构成矩形,否则这样的动点不存在;②若是否存在这样的动点构成棱形呢先让动点构成平行四边形,再验证任意一组邻边相等否若相等,则所求动点能构成棱形,否则这样的动点不存在;③若是否存在这样的动点构成正方形呢先让动点构成平行四边形,再验证任意一组邻边是否相等和两条对角线是否相等若都相等,则所求动点能构成正方形,否则这样的动点不存在;14、“抛物线上是否存在一点,使两个图形的面积之间存在和差倍分关系”的问题：此为“单动问题”〈即定解析式和动图形相结合的问题〉,后面的19实为本类型的特殊情形;先用动点坐标“一母示”的方法设出直接动点坐标,分别表示如果图形是动图形就只能表示出其面积或计算如果图形是定图形就计算出它的具体面积,然后由题意建立两个图形面积关系的一个方程,解之即可;注意去掉不合题意的点,如果问题中求的是间接动点坐标,那么在求出直接动点坐标后,再往下继续求解即可;15、“某图形〈直线或抛物线〉上是否存在一点,使之与另两定点构成直角三角形”的问题：若夹直角的两边与y轴都不平行：先设出动点坐标一母示,视题目分类的情况,分别用斜率公式算出夹直角的两边的斜率,再运用两直线没有与y轴平行的直线垂直的斜率结论两直线的斜率相乘等于-1,得到一个方程,解之即可;若夹直角的两边中有一边与y 轴平行,此时不能使用斜率公式;补救措施是：过余下的那一个点没在平行于y轴的那条直线上的点直接向平行于y的直线作垂线或过直角点作平行于y轴的直线的垂线与另一相关图象相交,则相关点的坐标可轻松搞定;16、“某图象上是否存在一点,使之与另两定点构成等腰直角三角形”的问题;①若定点为直角顶点,先用k点法求出另一直角边所在直线的解析式如斜率不存在,根据定直角点,可以直接写出另一直角边所在直线的方程,利用该解析式与所求点所在的图象的解析式组成方程组,求出交点坐标,再用两点间的距离公式计算出两条直角边等否若等,该交点合题,反之不合题,舍去;②若动点为直角顶点：先利用k点法求出定线段的中垂线的解析式,再把该解析式与所求点所在图象的解析式组成方程组,求出交点坐标,再分别计算出该点与两定点所在的两条直线的斜率,把这两个斜率相乘,看其结果是否为-1 若为-1,则就说明所求交点合题；反之,舍去;17、“题中含有两角相等,求相关点的坐标或线段长度”等的问题：题中含有两角相等,则意味着应该运用三角形相似来解决,此时寻找三角形相似中的基本模型“A”或“X”是关键和突破口;18、“在相关函数的解析式已知或易求出的情况下,题中又含有某动图形常为动三角形或动四边形的面积为定常数,求相关点的坐标或线段长”的问题：此为“单动问题”〈即定解析式和动图形相结合的问题〉,本类型实际上是前面14的特殊情形;先把动图形化为一些直角梯形或基本模型的三角形有一边在x 轴或ｙ轴上,或者有一边平行于x 轴或y 轴面积的和或差,设出相关点的坐标一母示,按化分后的图形建立一个面积关系的方程,解之即可;一句话,该问题简称“单动问题”,解题方法是“设点动点标,图形转化分割,列出面积方程”;19、“在相关函数解析式不确定系数中还含有某一个参数字母的情况下,题中又含有动图形常为动三角形或动四边形的面积为定常数,求相关点的坐标或参数的值”的问题：此为“双动问题”即动解析式和动图形相结合的问题;如果动图形不是基本模型,就先把动图形的面积进行转化或分割转化或分割后的图形须为基本模型,设出动点坐标一母示,利用转化或分割后的图形建立面积关系的方程或方程组;解此方程,求出相应点的横坐标,再利用该点所在函数图象的解析式,表示出该点的纵坐标注意,此时,一定不能把该点坐标再代入对应函数图象的解析式,这样会把所有字母消掉;再注意图中另一个点与该点的位置关系或其它关系,方法是常由已知或利用2问的结论,从几何知识的角度进行判断,表示出另一个点的坐标,最后把刚表示出来的这个点的坐标再代入相应解析式,得到仅含一个字母的方程,解之即可;如果动图形是基本模型,就无须分割或转化了,直接先设出动点坐标一母式,然后列出面积方程,往下操作方式就与不是基本模型的情况完全相同;一句话,该问题简称“双动问题”,解题方法是“转化分割,设点标,建方程,再代入,得结论”;常用公式或结论：1横线段的长 = 横标之差的绝对值 =-x x 大小=-x x 右左纵线段的长=纵标之差的绝对值=-y y 大小=-y y 下上 2点轴距离：点P 0x ,0y 到X 轴的距离为0y ,到Y 轴的距离为o x ; 3两点间的距离公式：若A 11,x y ,B 2,2x y , 则AB=目录：题型1：存在性问题 题型2：最值问题 题型3：定值问题 题型4：定点问题题型5：动点问题综合 题型6：对称问题 题型7：新定义题 题型8：二次函数与圆题型1：存在性问题1．（2024·四川广安·二模）如图，抛物线2y x bx c =−++交x 轴于()4,0A −，B 两点，交y 轴于点()0,4C ．(1)求抛物线的函数解析式．(2)点D 在线段OA 上运动，过点D 作x 轴的垂线，与AC 交于点Q ，与抛物线交于点P ，连接AP 、CP ，求四边形AOCP 的面积的最大值．(3)在抛物线的对称轴上是否存在点M ，使得以点A 、C 、M 为顶点的三角形是直角三角形？若存在，请求出点M【答案】(1)234y x x =−−+；(2)四边形AOCP 的面积最大为16；(3)点M 的坐标为35,22⎛⎫−− ⎪⎝⎭或311,22⎛⎫− ⎪⎝⎭．【分析】本题主要考查了二次函数综合，熟练掌握用待定系数法求解函数解析式的方法和步骤，以及二次函数的图象和性质，是解题的关键． （1）把()4,0A −，()0,4C 代入2y x bx c =−++，求出b 和c 的值，即可得出函数解析式； （2）易得182AOCSOA OC =⋅=，设()2,34P t t t −−+，则(),4Q t t +，求出24PQ t t =−−，则()()212282ACP C A S PQ x x t =⋅−=−++，根据四边形AOCP 的面积()22216ACP AOCS St =+=−++，结合二次函数的增减性，即可解答；（3）设3,2M m ⎛⎫− ⎪⎝⎭，根据两点之间距离公式得出232AC =，22254AM m =+，229(4)4CM m =+−，然后分情况根据勾股定理列出方程求解即可．【解析】（1）解：把()4,0A −，()0,4C 代入2y x bx c =−++得：01644b c c =−−+⎧⎨=⎩，解得：34b c =−⎧⎨=⎩，∴该二次函数的解析式234y x x =−−+；（2）解：∵()4,0A −，()0,4C ，∴4,4OA OC ==，∴1144822AOC S OA OC =⋅=⨯⨯=△，设直线AC 的解析式为4y kx =+， 代入()4,0A −得，044k =−+，解得1k =，∴直线AC 的解析式为4y x =+， 设()2,34P t t t −−+，则(),4Q t t +，∴()223444PQ t t t t t=−−+−+=−−∴()()()22114422822ACPC A SPQ x x t t t =⋅−=−−⨯=−++，∴四边形AOCP 的面积()22216ACP AOCSSt =+=−++，∵20−<，∴当2t =−时，四边形AOCP 的面积最大为16； （3）解：设3,2M m ⎛⎫− ⎪⎝⎭，∵()4,0A −，()0,4C ，∴2224432AC =+=，2222325424AM m m ⎛⎫=−++=+ ⎪⎝⎭，()()2222394424CM m m ⎛⎫=−+−=+− ⎪⎝⎭，当斜边为AC 时，AM CM AC 222+=，即()2225943244m m +++−=，整理得：24150m m ++=，无解；当斜边为AM 时，222AC CM AM +=，即2292532(4)44m m ++−=+，解得：112m =；∴311,22M ⎛⎫− ⎪⎝⎭当斜边为CM 时，222AC AM CM +=，即2225932(4)44m m ++=+−， 解得：52m =−；∴35,22M ⎛⎫−− ⎪⎝⎭综上：点M 的坐标为35,22⎛⎫−− ⎪⎝⎭或311,22⎛⎫− ⎪⎝⎭．2．（2024·内蒙古乌海·模拟预测）如图（1），在平面直角坐标系中，抛物线()240y ax bx a =+−≠与x 轴交于A ，B 两点(点A 在点B 的左侧)，与y 轴交于点C ，点A 的坐标为()1,0−，且OC OB =，点D 和点C 关于抛物线的对称轴对称．(1)分别求出a ，b 的值和直线AD 的解析式；(2)直线AD 下方的抛物线上有一点P ，过点P 作PH AD ⊥于点H ，作PM 平行于y 轴交直线AD 于点M ，交x 轴于点E ，求PHM 的周长的最大值；(3)在（2）的条件下，如图2，在直线EP 的右侧、x 轴下方的抛物线上是否存在点N ，过点N 作NG x ⊥轴交x 轴于点G ，使得以点E 、N 、G 为顶点的三角形与AOC 相似？如果存在，请直接写出点G 的坐标；如果不存在，请说明理由．【答案】(1)1a =，3b =−，=1y x −−(2)4+(3)存在，点G的坐标为⎫⎪⎪⎝⎭或⎫⎪⎪⎝⎭【分析】本题主要考查的是二次函数的综合应用，掌握二次函数的交点式、配方法求二次函数的最值、相似三角形的判定、等腰直角三角形的判定、一元二次方程的求根公式，列出PM 的长与a 的函数关系式是解题的关键．（1）先求得C 的坐标，从而得到点B 的坐标，设抛物线的解析式为()()14y a x x =+−，将点C 的坐标代入求解即可；先求得抛物线的对称轴，从而得到点()3,4D −，然后可求得直线AD 的解析式=1y x −−；（2）求得45BAD ∠=︒，接下来证明PMD △为等腰直角三角形，所当PM 有最大值时三角形的周长最大，设()2,34P a a a −−，()1M a −−，则223PM aa =−++，然后利用配方可求得PM 的最大值，最后根据MPH△的周长(1PM=求解即可；（3）当90EGN ∠=︒时，如果OA EG OC GN = 或OA GNOC EN =时，则AOC ∽EGN △，设点G 的坐标为(),0a ，则()2,34N a a a −−，则1EG a =−，234NG aa =−++，然后根据题意列方程求解即可．【解析】（1）点A 的坐标为()1,0−，1OA ∴=．令0x =，则4y =−，()0,4C ∴−，4OC =，OC OB =Q ， 4OB ∴=，()4,0B ∴，设抛物线的解析式为()()14y a x x =+−，将0x =，4y =−代入得：44a −=−，解得1a =，∴抛物线的解析式为234y x x =−−；1a ∴=，3b =−； 抛物线的对称轴为33212x −=−=⨯，()0,4C −，点D 和点C 关于抛物线的对称轴对称，()3,4D ∴−；设直线AD 的解析式为y kx b =+．将()1,0A −、()3,4D −代入得：034k b k b −+=⎧⎨+=−⎩，解得1k =−，1b =-，∴直线AD 的解析式=1y x −−；（2）直线AD 的解析式=1y x −−，∴直线AD 的一次项系数1k =−，45BAD ∴∠=︒． PM 平行于y 轴，90AEP ∴∠=︒，45PMH AME ∴∠=∠=︒．MPH ∴的周长(122PM MH PH PM MP PM PM =++=++=． 设()2,34P a a a −−，则(),1M a a −−， 则()22213423(1)4PM a a a a a a =−−−−−=−++=−−+．∴当1a =时，PM 有最大值，最大值为4．MPH ∴的周长的最大值(414=⨯=+（3）在直线EP 的右侧、x 轴下方的抛物线上存在点N ，过点N 作NG x ⊥轴交x 轴于点G ，使得以点E 、N 、G 为顶点的三角形与AOC 相似；理由如下：设点G 的坐标为(),0a ，则()2,34N a a a −−①如图2.1，若OA EG OC GN = 时，AOC ∽EGN △． 则 211344a a a −=−++，整理得：280a a +−=．得：a =负值舍去)，∴点G为⎫⎪⎪⎝⎭； ②如图2.2，若OA GN OC EN =时，AOC ∽NGE ，则21434a a a −=−++，整理得：2411170a a −−=，得：a =负值舍去)，∴点G为⎫⎪⎪⎝⎭， 综上所述，点G的坐标为⎫⎪⎪⎝⎭或⎫⎪⎪⎝⎭． 3．（2024·重庆·一模）如图，在平面直角坐标系中，抛物线2y ax bx =+x 轴交于点()1,0A −，()5,0B ，与y 轴交于点C ，连接BC ，AC ．(1)求抛物线的表达式；(2)P 为直线BC 上方抛物线上一点，过点P 作PD BC ⊥于点D ，过点P 作PE x 轴交抛物线于点E，求4+PD PE 的最大值及此时点P 的坐标； (3)点C 关于抛物线对称轴对称的点为Q ，将抛物线沿射线CAy '，新抛物线y '与y 轴交于点M ，新抛物线y '的对称轴与x 轴交于点N ，连接AM ，MN ，点R 在直线BC 上，连接QR ．当QR 与AMN 一边平行时，直接写出点R 的坐标，并写出其中一种符合条件的解答过程．【答案】(1)2y x x =++(2)当154t =时，PE的最大值，15,416P ⎛ ⎝⎭， (3)R点的坐标为⎛ ⎝⎭或6,⎛ ⎝⎭或(．【分析】（1）利用待定系数法求抛物线解析式即可；（2）先求得2y x =2x =，过点P 作PG x ⊥轴交BC 于点F ，利用勾股定理求得BC ==DPF OBC ∽，得PF DP BC OB =即PF PD=，从而得PF =，求出设直线BC的解析式后，设2,P t ⎛+ ⎝，则,F t ⎛+ ⎝，从而2PF =+，当点P在E 点右侧时()424PE t t t =−−=−，从而得2154t ⎫=−⎪⎝⎭，利用二次函数的性质即可求解；当点P 在E 点左侧时：442PE t t t =−−=−时，同理可求．然后比较4+PE 的最大值即可得出答案. （3）先求得1OA=，OC AC =设抛物线2y =H ⎛ ⎝⎭平移后为P ，过点P 作PW ⊥直线2x =，则AOC PWH ∽，得1OA OC AC WP HW PH ====，进而得平移后的抛物线2y x +'=，从而求得()1,0N，M ⎛ ⎝⎭，然后分QR AM ∥，QR MN ∥，QR AN ∥三种情况，利用二次函数的性质及一次函数的与二元一次方程的关系求解即可得解．【解析】（1）解：∵抛物线2y ax bx =+x 轴交于点()1,0A −，()5,0B 两点，代入坐标得：02550a b a b ⎧−=⎪⎨+=⎪⎩，解得：a b ⎧=⎪⎪⎨⎪=⎪⎩，∴抛物线的函数表达式为255y x x =−++（2）解：∵)2225555y x x x =−+=−−+，∴2y x =2x=，顶点为⎛ ⎝⎭ 过点P 作PG x ⊥轴交BC 于点F ，当0x =时，200y =∴(C ∵()5,0B ∴BC ==∵PG x ⊥轴，PD BC ⊥，x 轴y ⊥轴，∴909090CBO BFG DPF PFD PDF BOC ∠∠∠∠∠∠+=︒+=︒==︒，，∵PFD BFG ∠∠=∴DPF CBO ∠∠=∴DPF OBC ∽，∴PF DP BC OB =即PF PD =，∴PF PD =∴44+PD PE =PF +PE ，设直线BC ：y kx b =+，把(C ，()5,0B 代入得：05k b b =+⎧⎪=，解得5k b ⎧=−⎪⎨⎪=⎩， ∴直线BC：y =设2,P t ⎛ ⎝，则,F t ⎛+ ⎝，∴22PF ⎛⎛=−+=+ ⎝⎝，∵2y x =2x =，PE x 轴，∴24,E t ⎛−+ ⎝当点P 在E 点右侧时：()424PE t t t =−−=−，当24PE t =−时：∴+PD PE =PF +()221524545416t t ⎛⎫=−+−=−−+ ⎪⎝⎭ ∴当154t =时，的最大值∴2151544⎛⎫= ⎪⎝⎭，∴154P ⎛ ⎝⎭； 当点P 在E 点左侧时：442PE t t t =−−=−时，∴+PD PE =PF +()225424t t ⎫=−=−⎪⎝⎭， ∴当54t =时，的最大值．2,55P t ⎛−+ ⎝∴25544⎛⎫ ⎪⎝⎭∴5,416P ⎛ ⎝⎭，∵> 综上所诉，当点P 在E 点右侧时：即154t =时，的最大值，154P ⎛ ⎝⎭， （3）解：设直线AC ：y mx n =+，把()1,0A −，(C ， ∴1OA =，OC =∴AC ==设抛物线2y x =H ⎛ ⎝⎭平移后为P ， 过点P 作PW ⊥直线2x =，则AOC PWH ∽，∴1OA OC AC WP HW PH ====∴1PW =，HW=∴21,5P ⎛−⎝即1,5P ⎛ ⎝⎭，∴平移后的抛物线)22155555y x x x =−−+=−++'， ∴()1,0N令0x =，y '=，∴M ⎛ ⎝⎭ 如图，当QR AM ∥时，设直线AM 的解析式为：y px q =+，把M ⎛ ⎝⎭，()1,0A −代入得：0p q q =−+⎧=解得p q ⎧=⎪⎪⎨⎪=⎪⎩， ∴直线AM的解析式为：y =， ∴设直线QR的解析式为：y x n =∵(C ，Q 和C 关于2x =对称，∴(Q把(Q代入5y x n =+45n +，解得n =，∴直线QR的解析式为：y = 联立直线QR的解析式y =与直线BC：y x =+55y x y x ⎧=−⎪⎪⎨⎪=⎪⎩，解得3x y =⎧⎪⎨=⎪⎩，∴R ⎛ ⎝⎭ 同理可得：当QR MN ∥时，6,5R ⎛− ⎝⎭ 当QR AN ∥时，(R所有符合条件的R点的坐标为⎛ ⎝⎭或6,⎛ ⎝⎭或(． 【点睛】本题考查待定系数法求抛物线解析式，勾股定理，抛物线的性质，抛物线平移，一次函数的平移，相似三角形的判定及性质，图形与坐标，掌握待定系数法求抛物线解析式，抛物线的性质，抛物线平移，相似三角形的判定及性质，图形与坐标，利用辅助线画出准确图形是解题关键．题型2：最值问题4．（2024·安徽合肥·二模）在平面直角坐标系中，O 为坐标原点，抛物线23y ax bx =+−与x 轴交于()1,0A −，()3,0B 两点，与y 轴交于点C ，连接BC ．(1)求a ，b 的值；(2)点M 为线段BC 上一动点（不与B ，C 重合），过点M 作MP x ⊥轴于点P ，交抛物线于点N ． （ⅰ）如图1，当3PA PB=时，求线段MN 的长； （ⅱ）如图2，在抛物线上找一点Q ，连接AM ，QN ，QP ，使得PQN V 与APM △的面积相等，当线段NQ 的长度最小时，求点M 的横坐标m 的值．【答案】(1)1a =，2b =−(2)（ⅰ）2MN =；（ⅱ）m 的值为32或12【分析】本题考查诶粗函数的图象和性质，掌握待定系数法和利用函数性质求面积是解题的关键．（1）运用待定系数法求函数解析式即可；（2）（ⅰ）先计算BC 的解析式，然后设(),3M m m −，则3PM PB m ==−，1PA m =+，根据题意得到方程133m m +=−求出m 值，即可求出MN 的长；（ⅱ）作QR PN ⊥于点R ，由（ⅰ）可得1PA m =+，3PB PM m =−−，223PN m m =−++，然后分为点Q 在PN 的左侧和点Q 在PN 的右侧两种情况，根据勾股定理解题即可．【解析】（1）由题意得309330a b a b −−=⎧⎨+−=⎩，解得12a b =⎧⎨=−⎩；（2）（ⅰ）当0x =时，3y =−，∴()0,3C −，设直线BC 为3y kx =−，∵点()3,0B ，∴330k −=，解得1k =，∴直线BC 为3y x =−，设(),3M m m −，则3PM PB m ==−，1PA m =+， ∵3PA PB =， ∴133m m +=−，解得2m =，经检验2m =符合题意，当2m =时，222233y =−⨯−=−， ∴3PN =，31PM PB m ==−=，∴2MN =；（ⅱ）作QR PN ⊥于点R ，由（ⅰ）可得1PA m =+，3PB PM m =−−，223PN m m =−++，PQN V 的面积为()21232m m QR −++⋅，APM △的面积为()()1312m m −+，∴()()()211233122m m QR m m −++⋅=−+，解得1QR =；当点Q 在PN 的左侧时，如图1，Q 点的横坐标为1m QR m −=−，纵坐标为()()2212134m m m m −−⨯−−=−，∴R 点的坐标为()2,4m mm−，∵N 点坐标为()2,23m mm −−，∴32RN m =−，∴()22231NQ m =−+，∴当32m =时，NQ 取最小值；当点Q 在PN 的右侧时，如图2，Q 点的横坐标为1m QR m +=+，纵坐标为()()2212134m m m +−⨯+−=−，∴R 点的坐标为()2,4m m−，∵N 点的坐标为()2,23m mm −−，∴21RN m =−， ∴()222211NQ m =−+，∴当12m =时，NQ 取最小值．综上，m 的值为32或12．。

一、二次函数 真题与模拟题分类汇编（难题易错题）1．如图，抛物线y ＝12x 2+bx ﹣2与x 轴交于A ，B 两点，与y 轴交于C 点，且A （﹣1，0）．（1）求抛物线的解析式及顶点D 的坐标；（2）判断△ABC 的形状，证明你的结论；（3）点M 是抛物线对称轴上的一个动点，当MC +MA 的值最小时，求点M 的坐标．【答案】（1）抛物线的解析式为y ＝213x -22x ﹣2，顶点D 的坐标为 （32，﹣258）；（2）△ABC 是直角三角形，证明见解析；（3）点M 的坐标为（32，﹣54）． 【解析】【分析】 （1）因为点A 在抛物线上，所以将点A 代入函数解析式即可求得答案；（2）由函数解析式可以求得其与x 轴、y 轴的交点坐标，即可求得AB 、BC 、AC 的长，由勾股定理的逆定理可得三角形的形状；（3）根据抛物线的性质可得点A 与点B 关于对称轴x 32=对称，求出点B ，C 的坐标，根据轴对称性，可得MA ＝MB ，两点之间线段最短可知，MC +MB 的值最小．则BC 与直线x 32=交点即为M 点，利用得到系数法求出直线BC 的解析式，即可得到点M 的坐标． 【详解】 （1）∵点A （﹣1，0）在抛物线y 212x =+bx ﹣2上，∴2112⨯-+（）b ×（﹣1）﹣2＝0，解得：b 32=-，∴抛物线的解析式为y 21322x =-x ﹣2． y 21322x =-x ﹣212=（x 2﹣3x ﹣4 ）21325228x =--（），∴顶点D 的坐标为 （32528，-）． （2）当x ＝0时y ＝﹣2，∴C （0，﹣2），OC ＝2． 当y ＝0时，21322x -x ﹣2＝0，∴x 1＝﹣1，x 2＝4，∴B （4，0），∴OA ＝1，OB ＝4，AB＝5．∵AB2＝25，AC2＝OA2+OC2＝5，BC2＝OC2+OB2＝20，∴AC2+BC2＝AB2．∴△ABC是直角三角形．（3）∵顶点D的坐标为（32528，-），∴抛物线的对称轴为x32=．∵抛物线y12=x2+bx﹣2与x轴交于A，B两点，∴点A与点B关于对称轴x32=对称．∵A（﹣1，0），∴点B的坐标为（4，0），当x＝0时，y21322x=-x﹣2＝﹣2，则点C 的坐标为（0，﹣2），则BC与直线x32=交点即为M点，如图，根据轴对称性，可得：MA＝MB，两点之间线段最短可知，MC+MB的值最小．设直线BC的解析式为y＝kx+b，把C（0，﹣2），B（4，0）代入，可得：240bk b=-⎧⎨+=⎩，解得：122kb⎧=⎪⎨⎪=-⎩，∴y12=x﹣2．当x32=时，y1352224=⨯-=-，∴点M的坐标为（3524-，）．【点睛】本题考查了待定系数法求二次函数解析式、一次函数的解析式、直角三角形的性质及判定、轴对称性质，解决本题的关键是利用待定系数法求函数的解析式．2．如图，在平面直角坐标系中有一直角三角形AOB，O为坐标原点，OA＝1，tan∠BAO＝3，将此三角形绕原点O逆时针旋转90°，得到△DOC，抛物线y＝ax2+bx+c经过点A、B、C．（1）求抛物线的解析式；（2）若点P 是第二象限内抛物线上的动点，其横坐标为t ，设抛物线对称轴l 与x 轴交于一点E ，连接PE ，交CD 于F ，求以C 、E 、F 为顶点三角形与△COD 相似时点P 的坐标．【答案】（1）抛物线的解析式为y=﹣x 2﹣2x+3；（2）当△CEF 与△COD 相似时，P 点的坐标为（﹣1，4）或（﹣2，3）．【解析】【分析】（1）根据正切函数，可得OB ，根据旋转的性质，可得△DOC ≌△AOB ，根据待定系数法，可得函数解析式；（2）分两种情况讨论：①当∠CEF ＝90°时，△CEF ∽△COD ，此时点P 在对称轴上，即点P 为抛物线的顶点；②当∠CFE ＝90°时，△CFE ∽△COD ，过点P 作PM ⊥x 轴于M 点，得到△EFC ∽△EMP ，根据相似三角形的性质，可得PM 与ME 的关系，解方程，可得t 的值，根据自变量与函数值的对应关系，可得答案．【详解】（1）在Rt △AOB 中，OA ＝1，tan ∠BAO OB OA==3，∴OB ＝3OA ＝3． ∵△DOC 是由△AOB 绕点O 逆时针旋转90°而得到的，∴△DOC ≌△AOB ，∴OC ＝OB ＝3，OD ＝OA ＝1，∴A ，B ，C 的坐标分别为（1，0），（0，3），（﹣3，0），代入解析式为 09303a b c a b c c ++=⎧⎪-+=⎨⎪=⎩，解得：123a b c =-⎧⎪=-⎨⎪=⎩，抛物线的解析式为y ＝﹣x 2﹣2x +3； （2）∵抛物线的解析式为y ＝﹣x 2﹣2x +3，∴对称轴为l 2b a=-=-1，∴E 点坐标为（﹣1，0），如图，分两种情况讨论：①当∠CEF ＝90°时，△CEF ∽△COD ，此时点P 在对称轴上，即点P 为抛物线的顶点，P （﹣1，4）；②当∠CFE ＝90°时，△CFE ∽△COD ，过点P 作PM ⊥x 轴于M 点，∵∠CFE=∠PME=90°，∠CEF=∠PEM ，∴△EFC ∽△EMP ，∴13EM EF OD MP CF CO ===，∴MP ＝3ME ． ∵点P 的横坐标为t ，∴P （t ，﹣t 2﹣2t +3）． ∵P 在第二象限，∴PM ＝﹣t 2﹣2t +3，ME ＝﹣1﹣t ，t ＜0，∴﹣t 2﹣2t +3＝3（﹣1﹣t ），解得：t 1＝﹣2，t 2＝3（与t ＜0矛盾，舍去）．当t ＝﹣2时，y ＝﹣（﹣2）2﹣2×（﹣2）+3＝3，∴P （﹣2，3）．综上所述：当△CEF 与△COD 相似时，P 点的坐标为（﹣1，4）或（﹣2，3）．【点睛】本题是二次函数综合题．解（1）的关键是利用旋转的性质得出OC ，OD 的长，又利用了待定系数法；解（2）的关键是利用相似三角形的性质得出MP ＝3ME ．3．某市实施产业精准扶贫，帮助贫困户承包荒山种植某品种蜜柚．已知该蜜柚的成本价为6元/千克，到了收获季节投入市场销售时，调查市场行情后，发现该蜜柚不会亏本，且每天的销售量y （千克）与销售单价x （元）之间的函数关系如图所示．（1）求y 与x 的函数关系式，并写出x 的取值范围；（2）当该品种蜜柚定价为多少时，每天销售获得的利润最大？最大利润是多少？（3）某村农户今年共采摘蜜柚12000千克，若该品种蜜柚的保质期为50天，按照（2）的销售方式，能否在保质期内全部销售完这批蜜柚？若能，请说明理由；若不能，应定销售价为多少元时，既能销售完又能获得最大利润？【答案】（1）y ＝﹣20x +500，（x ≥6）；（2）当x ＝15.5时，w 的最大值为1805元；（3）当x ＝13时，w ＝1680，此时，既能销售完又能获得最大利润．【解析】【分析】（1）将点（15，200）、（10，300）代入一次函数表达式：y ＝kx +b 即可求解；（2）由题意得：w ＝y （x ﹣6）＝﹣20（x ﹣25）（x ﹣6），∵﹣20＜0，故w 有最大值，即可求解；（3）当x ＝15.5时，y ＝190，50×190＜12000，故：按照（2）的销售方式，不能在保质期内全部销售完；由50（500﹣20x ）≥12000，解得：x ≤13，当x ＝13时，既能销售完又能获得最大利润．【详解】解：（1）将点（15，200）、（10，300）代入一次函数表达式：y ＝kx +b 得：2001530010k b k b =+⎧⎨=+⎩， 解得：20500k b =-⎧⎨=⎩， 即：函数的表达式为：y ＝﹣20x +500，（x ≥6）；（2）设：该品种蜜柚定价为x 元时，每天销售获得的利润w 最大，则：w ＝y （x ﹣6）＝﹣20（x ﹣25）（x ﹣6），∵﹣20＜0，故w 有最大值，当x ＝﹣2b a ＝312＝15.5时，w 的最大值为1805元； （3）当x ＝15.5时，y ＝190，50×190＜12000，故：按照（2）的销售方式，不能在保质期内全部销售完；设：应定销售价为x 元时，既能销售完又能获得最大利润w ，由题意得：50（500﹣20x ）≥12000，解得：x ≤13，w ＝﹣20（x ﹣25）（x ﹣6），当x ＝13时，w ＝1680，此时，既能销售完又能获得最大利润．【点睛】本题考查了二次函数的性质在实际生活中的应用．最大销售利润的问题常利函数的增减性来解答，我们首先要吃透题意，确定变量，建立函数模型，然后结合实际选择最优方案．其中要注意应该在自变量的取值范围内求最大值（或最小值）.4．如图，已知点A （0，2），B （2，2），C （-1，-2），抛物线F ：y=x 2-2mx+m 2-2与直线x=-2交于点P ．（1）当抛物线F 经过点C 时，求它的解析式；（2）设点P 的纵坐标为y P ，求y P 的最小值，此时抛物线F 上有两点（x 1，y 1），（x 2，y 2），且x 1＜x 2≤-2，比较y 1与y 2的大小.【答案】(1) 221y x x =+-；(2)12y y >.【解析】【分析】 （1）根据抛物线F ：y=x 2-2mx+m 2-2过点C （-1，-2），可以求得抛物线F 的表达式； （2）根据题意，可以求得y P 的最小值和此时抛物线的表达式，从而可以比较y 1与y 2的大小.【详解】(1) ∵抛物线F 经过点C （－1，－2），∴22122m m -=++-.∴m 1=m 2=-1.∴抛物线F 的解析式是221y x x =+-.(2)当x=-2时，2442P y m m =++-=()222m +-. ∴当m=-2时，P y 的最小值为－2.此时抛物线F 的表达式是()222y x =+-.∴当2x ≤-时，y 随x 的增大而减小.∵12x x <≤－2，∴1y >2y .【点睛】本题考查二次函数的性质、二次函数图象上点的坐标特征、待定系数法求二次函数解析式，解题的关键是明确题意，找出所求问题需要的条件，利用数形结合的思想解答问题．5．某商场经营某种品牌的玩具，购进时的单价是3元，经市场预测，销售单价为40元时，可售出600个；销售单价每涨1元，销售量将减少10个设每个销售单价为x 元． （1）写出销售量y （件）和获得利润w （元）与销售单价x （元）之间的函数关系； （2）若玩具厂规定该品牌玩具销售单价不低于44元，且商场要完成不少于540件的销售任务，求商场销售该品牌玩具获得的最大利润是多少？【答案】（1）y ＝﹣10x+1000；w=﹣10x 2+1300x ﹣30000（2）商场销售该品牌玩具获得的最大利润是8640元．【解析】【分析】（1）利用销售单价每涨1元，销售量将减少10个即可表示出y＝600﹣10（x﹣40），再利用w= y•（x﹣30）即可表示出w与x之间的关系式；（2）先将w＝﹣10x2+1300x﹣30000变成顶点式，找到对称轴，利用函数图像的增减性确定在44≤x≤46范围内当x＝46时有最大值，代入求值即可解题.【详解】解：（1）依题意，易得销售量y（件）与销售单价x（元）之间的函数关系：y＝600﹣10（x﹣40）＝﹣10x+1000获得利润w（元）与销售单价x（元）之间的函数关系为：w＝y•（x﹣30）＝（1000﹣10x）（x﹣30）＝﹣10x2+1300x﹣30000（2）根据题意得，x≥14时且1000﹣10x≥540，解得：44≤x≤46w＝﹣10x2+1300x﹣30000＝﹣10（x﹣65）2+12250∵a＝﹣10＜0，对称轴x＝65∴当44≤x≤46时，y随x的增大而增大∴当x＝46时，w最大值＝8640元即商场销售该品牌玩具获得的最大利润是8640元．【点睛】本题考查了二次函数的实际应用，难度较大，求解二次函数与利润之间的关系时,需要用代数式表示销售数量和销售单价，熟悉二次函数顶点式的性质是解题关键.6．某商场购进一批单价为4元的日用品．若按每件5元的价格销售，每月能卖出3万件；若按每件6元的价格销售，每月能卖出2万件，假定每月销售件数y（件）与价格x （元/件）之间满足一次函数关系．（1）试求y与x之间的函数关系式；（2）当销售价格定为多少时，才能使每月的利润最大？每月的最大利润是多少？【答案】（1）y10000x80000=-+（2）当销售价格定为6元时，每月的利润最大，每月的最大利润为40000元【解析】解：（1）由题意，可设y=kx+b，把（5，30000），（6，20000）代入得：5k b300006k b20000+=⎧⎨+=⎩，解得：k10000b80000=-⎧⎨=⎩。

一、二次函数 真题与模拟题分类汇编（难题易错题）1．如图，已知二次函数y=ax 2+bx+c 的图象与x 轴相交于A （﹣1，0），B （3，0）两点，与y 轴相交于点C （0，﹣3）． （1）求这个二次函数的表达式；（2）若P 是第四象限内这个二次函数的图象上任意一点，PH ⊥x 轴于点H ，与BC 交于点M ，连接PC ．①求线段PM 的最大值；②当△PCM 是以PM 为一腰的等腰三角形时，求点P 的坐标．【答案】（1）二次函数的表达式y=x 2﹣2x ﹣3；（2）①PM 最大=94；②P （2，﹣3）或（22﹣2）． 【解析】 【分析】（1）根据待定系数法，可得答案；（2）①根据平行于y 轴直线上两点间的距离是较大的纵坐标减较小的纵坐标，可得二次函数，根据二次函数的性质，可得答案；②根据等腰三角形的定义，可得方程，根据解方程，可得答案． 【详解】（1）将A ，B ，C 代入函数解析式，得09303a b c a b c c -+=⎧⎪++=⎨⎪=-⎩，解得123a b c =⎧⎪=-⎨⎪=-⎩，这个二次函数的表达式y=x 2﹣2x ﹣3； （2）设BC 的解析式为y=kx+b ， 将B ，C 的坐标代入函数解析式，得303k b b +=⎧⎨=-⎩，解得13k b =⎧⎨=-⎩， BC 的解析式为y=x ﹣3，设M （n ，n ﹣3），P （n ，n 2﹣2n ﹣3），PM=（n﹣3）﹣（n2﹣2n﹣3）=﹣n2+3n=﹣（n﹣32）2+94，当n=32时，PM最大=94；②当PM=PC时，（﹣n2+3n）2=n2+（n2﹣2n﹣3+3）2，解得n1=0（不符合题意，舍），n2=2，n2﹣2n﹣3=-3，P（2，-3）；当PM=MC时，（﹣n2+3n）2=n2+（n﹣3+3）2，解得n1=0（不符合题意，舍），n2=3+2（不符合题意，舍），n3=3-2，n2﹣2n﹣3=2-42，P（3-2，2-42）；综上所述：P（2，﹣3）或（3-2，2﹣42）．【点睛】本题考查了二次函数的综合题，涉及到待定系数法、二次函数的最值、等腰三角形等知识，综合性较强，解题的关键是认真分析，弄清解题的思路有方法.2．如图，已知抛物线y=x2＋bx＋c与x轴交于A、B两点（A点在B点左侧），与y轴交于点C（0，－3），对称轴是直线x=1，直线BC与抛物线的对称轴交于点D．（1）求抛物线的函数表达式；（2）求直线BC的函数表达式；（3）点E为y轴上一动点，CE的垂直平分线交CE于点F，交抛物线于P、Q两点，且点P 在第三象限．①当线段PQ=34AB时，求tan∠CED的值；②当以点C、D、E为顶点的三角形是直角三角形时，请直接写出点P的坐标．【答案】（1）抛物线的函数表达式为y=x2－2x－3．（2）直线BC的函数表达式为y=x－3．（3）①23．①P1（122），P2（16，74）．【解析】 【分析】已知C 点的坐标，即知道OC 的长，可在直角三角形BOC 中根据∠BCO 的正切值求出OB 的长，即可得出B 点的坐标．已知了△AOC 和△BOC 的面积比，由于两三角形的高相等，因此面积比就是AO 与OB 的比．由此可求出OA 的长，也就求出了A 点的坐标，然后根据A 、B 、C 三点的坐标即可用待定系数法求出抛物线的解析式． 【详解】（1）∵抛物线的对称轴为直线x=1，∴− 221b ba -⨯＝＝1 ∴b=-2∵抛物线与y 轴交于点C （0，-3）， ∴c=-3，∴抛物线的函数表达式为y=x 2-2x-3； （2）∵抛物线与x 轴交于A 、B 两点， 当y=0时，x 2-2x-3=0． ∴x 1=-1，x 2=3． ∵A 点在B 点左侧， ∴A （-1，0），B （3，0）设过点B （3，0）、C （0，-3）的直线的函数表达式为y=kx+m ，则033k m m ＝＝+⎧⎨-⎩，∴13k m ⎧⎨-⎩＝＝∴直线BC 的函数表达式为y=x-3； （3）①∵AB=4，PQ=34AB ， ∴PQ=3 ∵PQ ⊥y 轴 ∴PQ ∥x 轴，则由抛物线的对称性可得PM=32， ∵对称轴是直线x=1， ∴P 到y 轴的距离是12， ∴点P 的横坐标为−12， ∴P （−12，−74）∴F（0，−74），∴FC=3-OF=3-74=54∵PQ垂直平分CE于点F，∴CE=2FC=5 2∵点D在直线BC上，∴当x=1时，y=-2，则D（1，-2），过点D作DG⊥CE于点G，∴DG=1，CG=1，∴GE=CE-CG=52-1=32．在Rt△EGD中，tan∠CED=23 GDEG＝．②P1（2，-2），P2（1-62-52）．设OE=a，则GE=2-a，当CE为斜边时，则DG2=CG•GE，即1=（OC-OG）•（2-a），∴1=1×（2-a），∴a=1，∴CE=2，∴OF=OE+EF=2∴F、P的纵坐标为-2，把y=-2，代入抛物线的函数表达式为y=x2-2x-3得：2或2∵点P在第三象限．∴P1（2-2），当CD为斜边时，DE⊥CE，∴OE=2，CE=1，∴OF=2.5，∴P和F的纵坐标为：-52，把y=-52，代入抛物线的函数表达式为y=x2-2x-3得：x=1-62，或1+62，∵点P在第三象限．∴P2（1-6，-52）．综上所述：满足条件为P1（1-2，-2），P2（1-62，-52）．【点睛】本题是二次函数的综合题型，其中涉及到的知识点有抛物线的顶点公式和三角形的面积求法．在求有关动点问题时要注意分析题意分情况讨论结果．3．抛物线y＝ax2+bx﹣3（a≠0）与直线y＝kx+c（k≠0）相交于A（﹣1，0）、B（2，﹣3）两点，且抛物线与y轴交于点C．（1）求抛物线的解析式；（2）求出C、D两点的坐标（3）在第四象限抛物线上有一点P，若△PCD是以CD为底边的等腰三角形，求出点P的坐标．【答案】（1）y＝x2﹣2x﹣3;（2）C（0，﹣3）,D（0，﹣1）;（3）P（2，﹣2）.【解析】【分析】（1）把A（﹣1，0）、B（2，﹣3）两点坐标代入y＝ax2+bx﹣3可得抛物线解析式．（2）当x＝0时可求C点坐标，求出直线AB解析式，当x＝0可求D点坐标．（3）由题意可知P点纵坐标为﹣2，代入抛物线解析式可求P点横坐标．【详解】解：（1）把A（﹣1，0）、B（2，﹣3）两点坐标代入y＝ax2+bx﹣3可得30 4233 a ba b--=⎧⎨+-=-⎩解得12 ab=⎧⎨=-⎩∴y＝x2﹣2x﹣3（2）把x＝0代入y＝x2﹣2x﹣3中可得y＝﹣3∴C（0，﹣3）设y ＝kx+b ，把A （﹣1，0）、B （2，﹣3）两点坐标代入23k b k b -+=⎧⎨+=-⎩ 解得11k b =-⎧⎨=-⎩∴y ＝﹣x ﹣1 ∴D （0，﹣1）（3）由C （0，﹣3），D （0，﹣1）可知CD 的垂直平分线经过（0，﹣2） ∴P 点纵坐标为﹣2， ∴x 2﹣2x ﹣3＝﹣2解得：x ＝1±2，∵x ＞0∴x ＝1+2． ∴P （1+2，﹣2） 【点睛】本题是二次函数综合题，用待定系数法求二次函数的解析式，把x ＝0代入二次函数解析式和一次函数解析式可求图象与y 轴交点坐标，知道点P 纵坐标带入抛物线解析式可求点P 的横坐标．4．（12分）如图所示是隧道的截面由抛物线和长方形构成，长方形的长是12 m ，宽是4 m ．按照图中所示的直角坐标系，抛物线可以用y=16-x 2+bx+c 表示，且抛物线上的点C 到OB 的水平距离为3 m ，到地面OA 的距离为172m. （1）求抛物线的函数关系式，并计算出拱顶D 到地面OA 的距离；（2）一辆货运汽车载一长方体集装箱后高为6m ，宽为4m ，如果隧道内设双向车道，那么这辆货车能否安全通过？（3）在抛物线型拱壁上需要安装两排灯，使它们离地面的高度相等，如果灯离地面的高度不超过8m ，那么两排灯的水平距离最小是多少米？【答案】（1）抛物线的函数关系式为y=16-x 2+2x+4，拱顶D 到地面OA 的距离为10 m ；(2)两排灯的水平距离最小是3． 【解析】【详解】试题分析：根据点B 和点C 在函数图象上，利用待定系数法求出b 和c 的值，从而得出函数解析式，根据解析式求出顶点坐标，得出最大值；根据题意得出车最外侧与地面OA 的交点为（2,0）（或（10,0）），然后求出当x=2或x=10时y 的值，与6进行比较大小，比6大就可以通过，比6小就不能通过；将y=8代入函数，得出x 的值，然后进行做差得出最小值．试题解析：（1）由题知点17(0,4),3,2B C ⎛⎫⎪⎝⎭在抛物线上 所以41719326c b c =⎧⎪⎨=-⨯++⎪⎩，解得24b c =⎧⎨=⎩，所以21246y x x =-++ 所以，当62bx a=-=时，10t y =≦ 答：21246y x x =-++，拱顶D 到地面OA 的距离为10米 （2）由题知车最外侧与地面OA 的交点为（2,0）（或（10,0）） 当x=2或x=10时，2263y =>，所以可以通过 （3）令8y =，即212486x x -++=，可得212240x x -+=，解得1266x x =+=-12x x -=答：两排灯的水平距离最小是考点：二次函数的实际应用．5．对于二次函数 y=ax 2+（b+1）x+（b ﹣1），若存在实数 x 0，使得当 x=x 0，函数 y=x 0，则称x 0 为该函数的“不变值”.（1）当 a=1，b=﹣2 时，求该函数的“不变值”；（2）对任意实数 b ，函数 y 恒有两个相异的“不变值”，求 a 的取值范围；（3）在（2）的条件下，若该图象上 A 、B 两点的横坐标是该函数的“不变值”，且 A 、B 两点关于直线 y=kx-2a+3 对称，求 b 的最小值. 【答案】（1）－1，3；（2）0<a<1；（3）－98【解析】 【分析】（1）先确定二次函数解析式为y=x 2-x-3，根据x o 是函数y 的一个不动点的定义，把（x o ，x o ）代入得x 02-x 0-3=x o ，然后解此一元二次方程即可；（2）根据x o 是函数y 的一个不动点的定义得到ax o 2+（b+1）x o +（b-1）=x o ，整理得ax 02+bx o +（b-1）=0，则根据判别式的意义得到△=b 2-4a （b-1）>0，即b 2-4ab+4a>0，把b 2-4ab+4a 看作b 的二次函数，由于对任意实数b ，b 2-4ab+4a>0成立，则（4a ）2-4.4a<0，然后解此不等式即可.（3）（利用两点关于直线对称的两个结论，一是中点在已知直线上，二是两点连线和已知直线垂直.找到a ，b 之间的关系式，整理后在利用基本不等式求解可得. 【详解】解：（1）当a=1，b=-2时，二次函数解析式为y=x 2-x-3，把（x o ，x o ）代入得x 02-x 0-3=x o ，解得x o =-1或x o =3，所以函数y 的不动点为-1和3；（2）因为y=x o ，所以ax o 2+（b+1）x o +（b-1）=x o ，即ax 02+bx o +（b-1）=0，因为函数y 恒有两个相异的不动点，所以此方程有两个不相等的实数解，所以△=b 2-4a （b-1）>0，即b 2-4ab+4a>0，而对任意实数b ，b 2-4ab+4a>0成立，所以（4a ）2-4.4a<0，解得0<a<1.（3）设A （x 1，x 1），B （x 2，x 2），则x 1+x 2b a=- A ，B 的中点的坐标为（1212,22x x x x ++ ），即M （,22b ba a-- ） A 、B 两点关于直线y=kx-2a+3对称， 又∵A ，B 在直线y=x 上，∴k=-1，A ，B 的中点M 在直线y=kx-2a+3上.∴b a -=ba-2a+3 得：b=2a 2-3a 所以当且仅当a=34 时，b 有最小值－98【点睛】本题是在新定义下对函数知识的综合考查，是一道好题.关于两点关于直线对称的问题，有两个结论同时存在，一是中点在已知直线上，二是两点连线和已知直线垂直.6．如图，已知抛物线的图象与x 轴的一个交点为B （5，0），另一个交点为A ，且与y 轴交于点C （0，5）。

中考数学二次函数和几何综合汇编经典和答案解析1一、二次函数压轴题1．如图，在平面直角坐标系xOy 中，抛物线()20y ax bx c a =++>与x 轴相交于()()1, 0, 3, 0A B -两点，点C 为抛物线的顶点．点(0,)M m 为y 轴上的动点，将抛物线绕点M 旋转180︒，得到新的抛物线，其中B C 、旋转后的对应点分别记为’'B C 、．（1）若1a =，求原抛物线的函数表达式；（2）在（1）条件下，当四边形''BCB C 的面积为40时，求m 的值；（3）探究a 满足什么条件时，存在点M ，使得四边形' 'BCB C 为菱形?请说明理由．2．综合与探究如图，抛物线26y ax bx =+-与x 轴相交于A ，B 两点，与y 轴相交于点C ，()2,0A -，()4,0B ，直线l 是抛物线的对称轴，在直线l 右侧的抛物线上有一动点D ，连接AD ，BD ，BC ，CD ．（1）求抛物线的函数表达式：（2）若点D 在x 轴的下方，当BCD △的面积是92时，求ABD △的面积；（3）在直线l 上有一点P ，连接AP ，CP ，则AP CP 的最小值为______；（4）在（2）的条件下，点M 是x 轴上一点，点N 是抛物线上一动点，是否存在点N ，使得以点B ，D ，M ，N 为顶点的四边形是平行四边形，若存在，请直接写出点N 的坐标；若不存在，请说明理由．3．如图1，在平面直角坐标系中，抛物线y ＝ax 2+bx +c （a ≠0）与x 轴交于A （﹣12，0），B （2，0）两点，与y 轴交于点C （0，1）．（1）求抛物线的函数表达式；（2）如图1，点D 为第一象限内抛物线上一点，连接AD ，BC 交于点E ，求DEAE的最大值；（3）如图2，连接AC ，BC ，过点O 作直线l ∥BC ，点P ，Q 分别为直线l 和抛物线上的点．试探究：在第四象限内是否存在这样的点P ，使△BPQ ∽△CAB ．若存在，请直接写出所有符合条件的点P 的坐标，若不存在，请说明理由．4．如图，抛物线y ＝x 2﹣2x ﹣8与x 轴交于A ，B 两点（点A 在点B 的左侧），与y 轴交于点C ，连接AC ，BC ．点P 是第四象限内抛物线上的一个动点，点P 的横坐标为m ，过点P 作PM ⊥x 轴，垂足为点M ，PM 交BC 于点Q ． （1）求A ，B ，C 三点的坐标；（2）试探究在点P 运动的过程中，是否存在这样的点Q ，使得以A 、C 、Q 为顶点的三角形是等腰三角形？若存在，请求出此时点Q 的坐标；若不存在，请说明理由．5．小明结合自己的学习经验，对新函数y ＝21b kx +的解析式、图象、性质及应用进行探究：已知当x ＝0时，y ＝2；当x ＝1时，y ＝1．（1）函数解析式探究：根据给定的条件，可以确定由该函数的解析式为： ． （2）函数图象探究：①根据解析式，补全如表，则m ＝ ，n ＝ ．②根据表中数据，在如图所示的平面直角坐标系中描点，并画出函数图象． x …… ﹣4 ﹣3 ﹣2 ﹣1 ﹣12 0121 2 n 4 ……y……21715 25m85285 12515 217…… （3）函数性质探究：请你结合函数的解析式及所画图象，写出该函数的一条性质： ．（4）综合应用：已知函数y ＝|715x ﹣815|的图象如图所示，结合你所画的函数图象，直接写出不等式|715x ﹣815|≤21bkx +．6．如果抛物线C 1：2y ax bx c =++与抛物线C 2：2y ax dx e =-++的开口方向相反，顶点相同，我们称抛物线C 2是C 1的“对顶”抛物线．（1）求抛物线247y x x =-+的“对顶”抛物线的表达式；（2）将抛物线247y x x =-+的“对顶”抛物线沿其对称轴平移，使所得抛物线与原抛物线247y x x =-+形成两个交点M 、N ，记平移前后两抛物线的顶点分别为A 、B ，当四边形AMBN 是正方形时，求正方形AMBN 的面积．（3）某同学在探究“对顶”抛物线时发现：如果抛物线C 1与C 2的顶点位于x 轴上，那么系数b 与d ，c 与e 之间的关系是确定的，请写出它们之间的关系．7．某校九年级数学兴趣社团的同学们学习二次函数后，有兴趣的在一起探究“函数2||y x x =-的有关图象和性质”．探究过程如下：（1）列表：问m =______． x …3- 2- 1- 0 1 2 122…y (6)20 0 2 m…（2）请在平面直角坐标系中画出图象．（3）若方程2||x x p -=（p 为常数）有三个实数根，则p =______．（4）试写出方程2||x x p -=（p 为常数）有两个实数根时，p 的取值范围是______． 8．定义：如果一条直线把一个封闭的平面图形分成面积相等的两部分，我们把这条直线称为这个平面图形的一条中分线．如三角形的中线所在的直线是三角形的一条中分线．（1）按上述定义，分别作出图1，图2的一条中分线．（2）如图3，已知抛物线2132y x x m =-+与x 轴交于点(2,0)A 和点B ，与y 轴交于点C ，顶点为D ．①求m 的值和点D 的坐标；②探究在坐标平面内是否存在点P ，使得以A ，C ，D ，P 为顶点的平行四边形的一条中分线经过点O ．若存在，求出中分线的解析式；若不存在，请说明理由．9．已知抛物线()2n n n y x a b =--+（n 为正整数，且120n a a a ≤<<<）与x 轴的交点为(0,0)A 和()1,0,2n n nn A c c c -=+．当1n =时，第1条抛物线()2111=--+y x a b 与x 轴的交点为(0,0)A 和1(2,0)A ，其他以此类推． （1）求11,a b 的值及抛物 线2y 的解析式．（2）抛物线n y 的顶点n B 的坐标为（_______，_______）；以此类推，第(1)n +条抛物线1n y +的顶点1n B +的坐标为（______，_______）；所有抛物线的顶点坐标(,)x y 满足的函数关系式是_________． （3）探究以下结论：①是否存在抛物线n y ，使得△n n AA B 为等腰直角三角形？若存在，请求出抛物线n y 的解析式；若不存在，请说明理由．②若直线(0)=>x m m 与抛物线n y 分别交于点12,,,n C C C ，则线段12231,,,n n C C C C C C -的长有何规律？请用含有m 的代数式表示．10．如图1，在平面直角坐标系中，已知抛物线y=a x 2+b x+3经过A(1，0) 、B(－3，0)两点，与y 轴交于点C ．直线BC 经过B 、C 两点．（1）求抛物线的解析式及对称轴；（2）将△COB 沿直线 BC 平移，得到△C 1O 1B 1，请探究在平移的过程中是否存在点 O 1落在抛物线上的情形，若存在，求出点O 1的坐标，若不存在，说明理由；（3）如图2，设抛物线的对称轴与x 轴交于点E ，连结AC ，请探究在抛物线上是否存在一点F ，使直线EF ∥AC ，若存在，求出点F 的坐标，若不存在，说明理由．二、中考几何压轴题11．如图（1），已知点G 在正方形ABCD 的对角线AC 上，,GE BC ⊥垂足为点,E GF CD ⊥，垂足为点F ．（1）证明与推断：①求证：四边形CEGF 是正方形；②推断：AGBE的值为_ _； （2）探究与证明：将正方形CEGF 绕点C 顺时针方向旋转a 角)045(a ︒<<︒，如图（2）所示，试探究线段AG 与BE 之间的数量关系，并说明理由；（3）拓展与运用：若24AB EC ==，正方形CEGF 在绕点C 旋转过程中，当A E G 、、三点在一条直线上时，则BE = ．12．我们定义：连结凸四边形一组对边中点的线段叫做四边形的“准中位线”．（1）概念理解：如图1，四边形ABCD 中，F 为CD 的中点，90ADB ∠=︒，E 是AB 边上一点，满足DE AE =，试判断EF 是否为四边形ABCD 的准中位线，并说明理由．（2）问题探究：如图2，ABC ∆中，90ACB ∠=︒，6AC =，8BC =，动点E 以每秒1个单位的速度，从点A 出发向点C 运动，动点F 以每秒6个单位的速度，从点C 出发沿射线CB 运动，当点E 运动至点C 时，两点同时停止运动．D 为线段AB 上任意一点，连接并延长CD ，射线CD与点,,,A B E F 构成的四边形的两边分别相交于点,M N ，设运动时间为t ．问t 为何值时，MN 为点,,,A B E F 构成的四边形的准中位线．（3）应用拓展：如图3，EF 为四边形ABCD 的准中位线，AB CD =，延长FE 分别与BA ，CD 的延长线交于点,M N ，请找出图中与M ∠相等的角并证明． 13．几何探究： （问题发现）（1）如图1所示，△ABC 和△ADE 是有公共顶点的等边三角形，BD 、CE 的关系是_______（选填“相等”或“不相等”）；（请直接写出答案）（类比探究）（2）如图2所示，△ABC 和△ADE 是有公共顶点的含有30角的直角三角形，（1）中的结论还成立吗?请说明理由； （拓展延伸）（3）如图3所示，△ADE 和△ABC 是有公共顶点且相似比为1 : 2的两个等腰直角三角形，将△ADE 绕点A 自由旋转，若22BC =，当B 、D 、E 三点共线时，直接写出BD 的长．14．定义：有一组邻边相等且对角互补的四边形叫做等补四边形．（问题理解）(1)如图1，点A 、B 、C 在⊙O 上，∠ABC 的平分线交⊙O 于点D ，连接AD 、CD ． 求证：四边形ABCD 是等补四边形；（拓展探究）(2)如图2，在等补四边形ABCD 中，AB ＝AD ，连接AC ，AC 是否平分∠BCD ？请说明理由； （升华运用）(3)如图3，在等补四边形ABCD 中，AB ＝AD ，其外角∠EAD 的平分线交CD 的延长线于点F ．若CD ＝6，DF ＝2，求AF 的长． 15．综合与实践 操作探究（1）如图1，将矩形ABCD 折叠，使点A 与点C 重合，折痕为EF ，AC 与EF 交于点G ．请回答下列问题：①与AEG △全等的三角形为______，与AEG △相似的三角形为______．并证明你的结论：（相似比不为1，只填一个即可）：②若连接AF 、CE ，请判断四边形AFCE 的形状：______．并证明你的结论； 拓展延伸（2）如图2，矩形ABCD 中，2AB =，4BC =，点M 、N 分別在AB 、DC 边上，且AM NC =，将矩形折叠，使点M 与点N 重合，折痕为EF ，MN 与EF 交于点G ，连接ME ．①设22m AM AE =+，22n ED DN =+，则m 与n 的数量关系为______； ②设AE a =，AM b =，请用含a 的式子表示b ：______； ③ME 的最小值为______．16．综合与实践．特例感知．两块三角板△ADB 与△EFC 全等，∠ADB ＝∠EFC ＝90°，∠B ＝45°，AB ＝6．将直角边AD 和EF 重合摆放．点P 、Q 分别为BE 、AF 的中点，连接PQ ，如图1．则△APQ 的形状为 ．操作探究（1）若将△EFC 绕点C 顺时针旋转45°，点P 恰好落在AD 上，BE 与AC 交于点G ，连接PF ，如图2． ①FG ：GA ＝ ；②PF 与DC 的位置关系为 ； ③求PQ 的长； 开放拓展（2）若△EFC 绕点C 旋转一周，当AC ⊥CF 时，∠AEC 为 ． 17．综合与实践动手实践：一次数学兴趣活动，张老师将等腰Rt AEF 的直角顶点A 与正方形ABCD 的顶点A 重合（AE AD >），按如图（1）所示重叠在一起，使点E 在CD 边上，连接BF ．则可证：ADE ≌△△______，______三点共线；发现问题：（1）如图（2），已知正方形ABCD ，E 为DC 边上一动点，DC nDE =，AF AE ⊥交CB 的延长线于F ，连结EF 交AB 于点G ．若2n =，则AG BG =______，AGE BGFS S =△△______； 尝试探究：（2）如图（3），在（1）的条件下若3n =，求证：5AG GB =；拓展延伸：（3）如图（4），在（1）的条件下，当n =______时，AG 为GB 的6倍（直接写结果，不要求证明）． 18．综合与实践数学活动课上，老师让同学们结合下述情境，提出一个数学问题：如图1，四边形ABCD 是正方形，四边形BEDF 是矩形．探究展示：“兴趣小组”提出的问题是：“如图2，连接CE ．求证：AE ⊥CE ．”并展示了如下的证明方法：证明：如图3，分别连接AC ，BD ，EF ，AF ．设AC 与BD 相交于点O ． ∵四边形ABCD 是正方形，∴OA =OC =12AC ，OB =OD =12BD ，且AC =BD ． 又∵四边形BEDF 是矩形，∴EF经过点O，∴OE=OF=1EF，且EF=BD．2∴OE=OF，OA=OC．∴四边形AECF是平行四边形．（依据1）∵AC=BD，EF=BD，∴AC=EF．∴四边形AECF是矩形．（依据2）∴∠CEA=90°，即AE⊥CE．反思交流：（1）上述证明过程中“依据1”“依据2”分别是什么？拓展再探：（2）“创新小组”受到“兴趣小组”的启发，提出的问题是：“如图4，分别延长AE，FB交于点P，求证：EB=PB．”请你帮助他们写出该问题的证明过程．（3）“智慧小组”提出的问题是：若∠BAP=30°，AE=31，求正方形ABCD的面积．请你解决“智慧小组”提出的问题．19．（1）问题发现如图1，△ABC与△ADE都是等腰直角三角形，且∠BAC＝∠DAE＝90°，直线BD，CE交于点F，直线BD，AC交于点G．则线段BD和CE的数量关系是，位置关系是；（2）类比探究如图2，在△ABC和△ADE中，∠ABC＝∠ADE＝α，∠ACB＝∠AED＝β，直线BD，CE交于点F，AC与BD相交于点G．若AB＝kAC，试判断线段BD和CE的数量关系以及直线BD和CE相交所成的较小角的度数，并说明理由；（3）拓展延伸如图3，在平面直角坐标系中，点M的坐标为（3.0），点N为y轴上一动点，连接MN．将线段MN绕点M逆时针旋转90得到线段MP，连接NP，OP．请直接写出线段OP 长度的最小值及此时点N的坐标．20．如图，已知ABC和ADE均为等腰三角形，AC＝BC，DE＝AE，将这两个三角形放置在一起．（1）问题发现：如图①，当60ACB AED ∠∠︒＝＝时，点B 、D 、E 在同一直线上，连接CE ，则CEB ∠＝ °，线段BD 、CE 之间的数量关系是 ；（2）拓展探究：如图②，当90ACB AED ∠∠︒＝＝时，点B 、D 、E 在同一直线上，连接CE ，请判断CEB ∠的度数及线段BD 、CE 之间的数量关系，并说明理由； （3）解决问题：如图③，90ACB AED ∠∠︒＝＝，25AC ＝，AE ＝2，连接CE 、BD ，在AED 绕点A 旋转的过程中，当DE BD ⊥时，请直接写出EC 的长．【参考答案】***试卷处理标记，请不要删除一、二次函数压轴题1．B解析：（1）2 23;y x x =--（2）416m m ==-或；（3）3a ≥M ，使得四边形''BCB C 为菱形，理由见解析【分析】（1）因为1a =，所以2y x bx c =++，将()()1, 0, 3, 0A B -代入得关于b 和c 的二元一次方程组，解方程组得到b 和c 即可求得原抛物线的解析式；（2）连接','CC BB ，延长BC 与y 轴交于点E ，根据题（1）可求出点B 、C 的坐标，继而求出直线BC 的解析式及点E 的坐标，根据题意易知四边形''BCB C 是平行四边形，继而可知()1312BCM MBE MCE S S S ME ME ∆∆∆=-=⨯-⨯=，由此可知ME ＝10，继而即可求解点M 的坐标；（3）如图，过点C 作CD y ⊥轴于点D ，当平行四边形''BCB C 为菱形时，应有MB MC ⊥，故点M 在,O D 之间，继而可证MOB CDM ∆∆，根据相似三角形的性质可得MO MD BO CD •=•代入数据即可求解．【详解】解：（1）∵1a =，∴2y x bx c =++将()()1, 0, 3, 0A B -代入得：10930b c b c -+=⎧⎨++=⎩解得：23b c =-⎧⎨=-⎩∴原抛物线的函数表达式为：2 23y x x =--；（2）连接','CC BB ，并延长BC 与y 轴交于点E ，二次函数2 23y x x =--的项点为(1,4,)-()1,4,C ∴-()3, 0,B∴直线BC 的解析式为： 2 6.y x =--()0,6E ∴-抛物线绕点M 旋转180︒','MB MB MC MC ==∴四边形''BCB C 是平行四边形，()1312BCM MBE MCE S S S ME ME ∆∆∆∴=-=⨯-⨯= 10ME416m m ∴==-或（3）如图，过点C 作CD y ⊥轴于点D当平行四边形''BCB C 为菱形时，应有MB MC ⊥，故点M 在,O D 之间，当MB MC ⊥时，MOB CDM ∆∆，MO BO CD MD∴= 即MO MD BO CD •=•二次函数()()13y a x x =+-的顶点为()()()1,4,0,,3,0a M m B - 1,,4,3CD MO m MD m a ON ∴==-=+=，()43m m a ∴-+=，∴2430m am ，216120,0a a ∆-≥>a ∴≥所以a ≥M ，使得四边形''BCB C 为菱形．【点睛】本题考查二次函数的综合应用，涉及到平行四边形的性质、菱形的性质，难度较大，解题的关键是善于将函数问题转化为方程问题，善于利用几何图形的有关性质及二次函数的性质，注意挖掘题目中的隐藏条件．2．A解析：（1）233642y x x =--；（2）454；（3）134）存在，点N 的坐标为：15114,4⎛⎫ ⎪⎝⎭或15114,4⎛⎫ ⎪⎝⎭或151,4⎛⎫-- ⎪⎝⎭ 【分析】（1）把A 、B 两点坐标代入26y ax bx =+-可得关于a 、b 的二元一次方程组，解方程组求出a 、b 的值即可得答案；（2）过D 作DG x ⊥轴于G ，交BC 于H ，根据抛物线解析式可得点C 坐标，利用待定系数法可得直线BC 的解析式，设233,642D x x x ⎛⎫-- ⎪⎝⎭，根据BC 解析式可表示出点H 坐标，即可表示出DH 的长，根据△BCD 的面积列方程可求出x 的值，即可得点D 坐标，利用三角形面积公式即可得答案；（3）根据二次函数的对称性可得点A 与点B 关于直线l 对称，可得BC 为AP +CP 的最小值，根据两点间距离公式计算即可得答案；（4）根据平行四边形的性质得到MB //ND ，MB =ND ，分MB 为边和MB 为对角线两种情况，结合点D 坐标即可得点N 的坐标．【详解】（1）∵抛物线26y ax bx =+-与x 轴相交于A ，B 两点，()2,0A -，()4,0B ，∴426016460a b a b --=⎧⎨+-=⎩， 解得：3432a b ⎧=⎪⎪⎨⎪=-⎪⎩，∴抛物线的解析式为：233642y x x =--． （2）如图，过D 作DG x ⊥轴于G ，交BC 于H ，当0x =时，6y =-，∴()0,6C -，设BC 的解析式为y kx b =+，则640b k b =-⎧⎨+=⎩， 解得326k b ⎧=⎪⎨⎪=-⎩， ∴BC 的解析式为：362y x =-， 设233,642D x x x ⎛⎫-- ⎪⎝⎭，则3,62H x x ⎛⎫- ⎪⎝⎭， ∴2233336632424DH x x x x x ⎛⎫=----=-+ ⎪⎝⎭， ∵BCD △的面积是92， ∴1922DH OB ⨯=， ∴213943242x x ⎛⎫⨯⨯-+= ⎪⎝⎭， 解得：1x =或3，∵点D 在直线l 右侧的抛物线上，∴153,4D ⎛⎫- ⎪⎝⎭， ∴ABD △的面积11154562244AB DG ⨯=⨯⨯=；（3）∵抛物线26y ax bx =+-与x 轴相交于A ，B 两点，∴点A 与点B 关于直线l 对称，∴BC 为AP +CP 的最小值，∵B （4，0），C （0，-6），∴AP +CP 的最小值=BC =2246+=213． 故答案为：213（4）①当MB 为对角线时，MN //BD ，MN =BD ，过点N 作NE ⊥x 轴于E ，过当D 作DF ⊥x 轴于F ，∵点D （3，154-）， ∴DF =154， 在△MNE 和△BDF 中，NEM DFB NMB DBF MN BD ∠=∠⎧⎪∠=∠⎨⎪=⎩， ∴△MNE ≌△BDF ，∴DF =NE =154， ∵点D 在x 轴下方，MB 为对角线，∴点N 在x 轴上方，∴点N 纵坐标为154， 把y =154代入抛物线解析式得：215336442x x =--， 解得：1114x =-，2114x =+， ∴1N （114-，154），2N （114+，154）如图，当BM 为边时，MB //ND ，MB =ND ，∵点D （3，154-）， ∴点N 纵坐标为154-， ∴233156424x x --=-， 解得：11x =-，23x =（与点D 重合，舍去），∴3N （1-，154-），综上所述：存在点N ，使得以点B ，D ，M ，N 为顶点的四边形是平行四边形，点N 的坐标为：15114,4⎛⎫ ⎪⎝⎭或15114,4⎛⎫ ⎪⎝⎭或151,4⎛⎫-- ⎪⎝⎭． 【点睛】本题考查的是二次函数的综合，首先要掌握待定系数法求解析式，其次要添加恰当的辅助线，灵活运用面积公式和平行四边形的判定和性质，应用数形结合的数学思想解题． 3．A解析：（1）2312y x x =-++；（2）DE AE 的最大值为45；（3）914511924145(P -+-+或9177317()P --+ 【分析】（1）用待定系数法求出函数解析式即可；（2）构造出△AGE ∽△DEH ，可得DE DH AE AG=，而DE 和AG 都可以用含自变量的式子表示，最后用二次函数最大值的方法求值．（3）先发现△ABC 是两直角边比为2：1的直角三角形，由△BPQ ∽△CAB ，构造出△BPQ ，表示出Q 点的坐标，代入解析式求解即可．【详解】解：（1）分别将C （0，1）、A （﹣12，0）、B （2，0）代入y ＝ax 2+bx +c 中得110424201a b c a b c c ⎧++=⎪⎪++=⎨⎪=⎪⎩， 解得：1321a b c =-⎧⎪⎪=⎨⎪=⎪⎩，∴抛物线的函数表达式为2312y x x =-++． （2）过A 作AG ∥y 轴交BC 的延长线于点G ，过点D 作DH ∥y 轴交BC 于点H ，∵B （2，0）C （0，1），∴直线BC ：y ＝12x +1，∵A （-12，0），∴G （-12，54）， 设D （23,12m m m -++），则H （1,12m m -+）， ∴DH ＝（2312m m -++）﹣（112m -+）， ＝﹣m 2+2m ，∴AG=54， ∵AG ∥DH ， ∴()2224415554DE DH m m m AE AG -+===--+，∴当m ＝1时，DE AE 的最大值为45． （3）符合条件的点P 914511924145-+-+9177317--+ ∵l ∥BC ， ∴直线l 的解析式为：y ＝-12x ，设P （n ，-12n ），∵A （-12，0），B （2，0），C （0，1），∴AC 2＝54，BC 2＝5，AB 2＝254．∵AC 2+BC 2＝AB 2，∴∠ACB ＝90°．∵△BPQ ∽△CAB ， ∴12BP AC BQ BC ==， 分两种情况说明：①如图3，过点P 作PN ⊥x 轴于N ，过点Q 作QM ⊥x 轴于M ．∵∠PNB ＝∠BMQ ＝90°， ∠NBP +∠MBQ ＝90°，∠MQB +∠MBQ ＝90°，∴∠NBP ＝∠MQB ．∴△NBP ∽△MQB ，∴12PN NB BM MQ ==， ∵1,2P n n ⎛⎫- ⎪⎝⎭， ∴1,2PN n ON n ==， ∴BN ＝2﹣n ，∴BM ＝2PN ＝n ，QM ＝2BN ＝4﹣2n ，∴OM ＝OB +BM ＝2+n ，∴Q （2+n ，2n ﹣4），将Q 的坐标代入抛物线的解析式得：()()23221242n n n -++++=-， 2n 2+9n ﹣8＝0， 解得：)1291459145n n -+--==舍∴P (914511924145,416-+-+)． ②如图4，过点P 作PN ⊥x 轴于N ，过点Q 作QM ⊥x 轴于M ．∵△PNB ∽△BMQ ，又∵△BPQ ∽△CAB ，∴2BC QM AC BN==， ∵1,2P n n ⎛⎫- ⎪⎝⎭， ∴Q （2﹣n ，4﹣2n ），将Q 的坐标代入抛物线的解析式得：()()23221422n n n --+-+=-， 化简得：2n 2﹣9n +8＝0， 解得：)12917917n n -+==舍， ∴P 9177317--+． 【点睛】本题考查待定系数法求抛物线解析式，平行线分线段成比例，利用二次函数求线段比的最大值，勾股定理逆定理，相似三角形判定与性质，抛物线与一元二次方程，掌握待定系数法求抛物线解析式，平行线分线段成比例，利用二次函数求线段比的最大值，勾股定理逆定理，相似三角形判定与性质，抛物线与一元二次方程的关系是解题关键．4．A 解析：（1）A （﹣2，0），B （4，0），C （0，﹣8）；（2）存在，Q 点坐标为124(85,858)55Q ，21722(,)77Q ． 【分析】(1)解方程2280x x --=，可求得A 、B 的坐标，令0x =，可求得点C 的坐标；(2)利用勾股定理计算出AC =BC 的解析式为28y x =-，可设Q （m ，2m ﹣8）（0＜m ＜4），分三种情况讨论：当CQ ＝AC 时，当AQ ＝AC 时，当AQ ＝QC 时，然后分别解方程求出m 即可得到对应的Q 点坐标．【详解】(1)当0y =，2280x x --=，解得x 1＝﹣2，x 2＝4，所以(2,0)A -，(4,0)B ，x ＝0时，y ＝﹣8，∴(0,8)C -；(2)设直线BC 的解析式为y kx b =+，把(4,0)B ，(0,8)C -代入解析式得：408k b b +=⎧⎨=-⎩，解得28k b =⎧⎨=-⎩， ∴直线BC 的解析式为28y x =-，设Q （m ，2m ﹣8）（0＜m ＜4），当CQ ＝CA 时，22(288)68m m +-+=，解得，1m =2m =∴Q 8)， 当AQ ＝AC 时，22(2)(28)68m m ++-=，解得：128m 5=（舍去），m 2＝0（舍去）； 当QA ＝QC 时，2222(2)(28)(2)m m m m ++-=+，解得177m =， ∴Q 1722(,)77-．综上所述，满足条件的Q 点坐标为18)Q ，21722(,)77Q -． 【点睛】 本题考查了二次函数，熟练掌握二次函数图象上点的坐标特征、二次函数的性质和等腰三角形的性质，会利用待定系数法求函数解析式，理解坐标与图形性质，会利用勾股定理表示线段之间的关系，会运用分类讨论的思想解决数学问题．5．(1) y=221x +;(2)m=1,n=3;(3) 函数存在最大值,当x=0是,y 取得最大值2.(4)-1≤x≤2 【分析】(1)待定系数法求解函数解析式(2)分别将m,n 代入函数解析式,求出对应的横纵坐标即可求解(3)观察图像即可,答案不唯一(4)观察图像选择曲线在上方的区域即可.【详解】解(1)将(0,2),(1,1)代入解析式得20111b b k ⎧=⎪⎪+⎨⎪=⎪+⎩ 解得:12k b =⎧⎨=⎩ ∴函数的解析式为y =221x + (2) ①令x =-1, 则y=1, ∴m =1令y =15,则x =±3,∵2＜n ＜4, ∴n =3②(3)函数存在最大值,当x =0是,y 取得最大值2. (4)直接观察图象可知,当|715x ﹣815|≤时,-1≤x ≤2 【点睛】本题考查了用待定系数法求函数的解析式,函数的图象和性质,根据函数图象求解不等式等问题,综合性强,熟悉函数的图象和性质是解题关键.6．C解析：（1）241y x x =-+-；（2）2；（3）b dc e =-⎧⎨=-⎩【分析】（1）先求出抛物线C 1的顶点坐标，进而得出抛物线C 2的顶点坐标，即可得出结论； （2）设正方形AMBN 的对角线长为2k ，得出B （2，3＋2k ），M （2＋k ，3＋k ），N （2−k ，3＋k ），再用点M （2＋k ，3＋k ）在抛物线y ＝（x −2）2＋3上，建立方程求出k 的值，即可得出结论；（3）先根据抛物线C 1，C 2的顶点相同，得出b ，d 的关系式，再由两抛物线的顶点在x 轴，求出c ，e 的关系，即可得出结论． 【详解】解：（1）解：（1）∵y ＝x 2−4x ＋7＝（x −2）2＋3， ∴顶点为（2，3），∴其“对顶”抛物线的解析式为y ＝−（x −2）2＋3， 即y ＝−x 2＋4x −1； （2）如图，由（1）知，A （2，3）， 设正方形AMBN 的对角线长为2k ，则点B （2，3＋2k ），M （2＋k ，3＋k ），N （2−k ，3＋k ）， ∵M （2＋k ，3＋k ）在抛物线y ＝（x −2）2＋3上， ∴3＋k ＝（2＋k −2）2＋3， 解得k ＝1或k ＝0（舍）；∴正方形AMBN 的面积为12×(2k )2＝2；（3）根据抛物线的顶点坐标公式得，抛物线C 1：y ＝ax 2＋bx ＋c 的顶点为（2b a-，244ac b a-），抛物线C 2：y ＝−ax 2＋dx ＋e 的顶点为（2d a ，244ae d a---），∵抛物线C 2是C 1的“对顶”抛物线， ∴22b d a a-=， ∴=-b d ，∵抛物线C 1与C 2的顶点位于x 轴上，∴224444ac b ae d a a ---=-， ∴c e =-，即b d c e =-⎧⎨=-⎩． 【点睛】此题主要考查了抛物线的顶点坐标公式，正方形的性质，理解新定义式解本题的关键． 7．（1）154m =；（2）见解析；（3）0p =；（4）14p =-或0p >．【分析】（1）把x=122代入解析式，计算即可；（2）按照画图像的基本步骤画图即可；（3）一个方程有两个不同实数根，另一个方程有两个相等的实数根和两个方程都有两个不同的实数根，但是有一个公共根；（4）结合函数的图像，分直线经过顶点和在x 轴上方两种情形解答即可． 【详解】（1）当x=122时，2||y x x =-=25)2|(|52- =154， ∴154m =； （2）画图像如下；（3）当x≥0时，函数为2y x x ；当x ＜0时，函数为2y x x =+；∵方程2||x x p -=（p 为常数）有三个实数根， ∴两个方程有一个公共根，设这个根为a ， 则22a a a a -=+， 解得a=0， 当a=0时，p=0， 故答案为：p=0；（4）∵方程2||x x p -=（p 为常数）有两个实数根， ∴p ＞0； 或△=0 即1+4p=0， 解得14p =-．综上所述，p 的取值范围是14p =-或0p >． 【点睛】本题考查了二次函数图像，二次函数与一元二次方程的关系，熟练掌握抛物线与一元二次方程的关系，灵活运用分类思想，数形结合思想是解题的关键． 8．（1）见解析；（2）①4m =，1(3,)2D -；②存在，76y x =或2y x =或110y x =-【分析】（1）对角线所在的直线为平行四边形的中分线，直径所在的直线为圆的中分线； （2）①将(2,0)A 代入抛物线2132y x x m =-+，得143202m ⨯-⨯+=，解得4m =，抛物线解析式2211134(3)222y x x x =-+=--，顶点为1(3,)2D -；②根据抛物线解析式求出(2,0)A ，(4,0)B ，(0,4)C ，当A 、C 、D 、P 为顶点的四边形为平行四边形时，根据平行四边形的性质，过对角线的交点的直线将该平行四边形分成面积相等的两部分，所以平行四边形的中分线必过对角线的交点．Ⅰ．当CD 为对角线时，对角线交点坐标为37(,)24，中分线解析式为76y x =；Ⅱ．当AC 为对角线时，对角线交点坐标(1,2)．中分线解析式为2y x =；Ⅲ．当AD 为对角线时，对角线交点坐标为51(,)24-，中分线解析式为110y x =-． 【详解】解：（1）如图，对角线所在的直线为平行四边形的中分线， 直径所在的直线为圆的中分线，（2）①将(2,0)A 代入抛物线2132y x x m =-+，得 143202m ⨯-⨯+=， 解得4m =，∴抛物线解析式2211134(3)222y x x x =-+=--，∴顶点为1(3,)2D -；②将0y =代入抛物线解析式21342y x x =-+，得 234201x x -+=， 解得2x =或4，(2,0)A ∴，(4,0)B ， 令0x =，则4y =，(0,4)C ∴，当A 、C 、D 、P 为顶点的四边形为平行四边形时，根据平行四边形的性质，过对角线的交点的直线将该平行四边形分成面积相等的两部分， 所以平行四边形的中分线必过对角线的交点． Ⅰ．当CD 为对角线时，对角线交点坐标为14032(,)22-+，即37(,)24，中分线经过点O ，∴中分线解析式为76y x =；Ⅱ．当AC 为对角线时，对角线交点坐标为2004(,)22++，即(1,2)． 中分线经过点O ，∴中分线解析式为2y x =；Ⅲ．当AD 为对角线时，对角线交点坐标为10232(,)22-+，即51(,)24-， 中分线经过点O ，∴中分线解析式为110y x =-， 综上，中分线的解析式为式为76y x =或为2y x =或为110y x =-．【点睛】本题考查了二次函数，熟练运用二次函数的性质与平行四边形的性质是解题的关键．9．C解析：（1）1111a b =⎧⎨=⎩ ；y 2 ＝−（x−2）2＋4；（2）（n ，n 2 ）；[（n ＋1），（n ＋1）2 ]；y ＝x 2；（3）①存在，理由见详解；②C 1n -C n ＝2m ． 【分析】（1）1(2,0)A ），则1c ＝2，则2c ＝2＋2＝4，将点A 、1A 的坐标代入抛物线表达式得：()2112110=-0(-2-)a b a b ⎧-+⎪⎨=-+⎪⎩，解得：1111a b =⎧⎨=⎩ ，则点2A （4，0），将点A 、2A 的坐标代入抛物线表达式，同理可得：2a ＝2，2b ＝4，即可求解；（2）同理可得：3a ＝3，3b ＝9，故点n B 的坐标为（n ，2n ），以此推出：点1n B +[（n ＋1），（n ＋1）2]，故所有抛物线的顶点坐标满足的函数关系式是：y ＝2x ，即可求解； （3）①△AAnBn 为等腰直角三角形，则AAn 2 ＝2ABn 2，即（2n ）2＝2（n 2＋4n ），即可求解；②y 1n c -＝−（m−n ＋1）2＋（n−1）2，y n c ＝−（m−n ）2＋n 2，C 1n -C n = y n c −y 1n c -，即可求解． 【详解】解：（1）1(2,0)A ，则1c ＝2，则2c ＝2＋2＝4，将点A 、1A 的坐标代入抛物线表达式得：2112110=()0(2)a b a b ⎧--+⎨=---+⎩，解得：1111a b =⎧⎨=⎩， 则点2A （4，0），将点A 、2A 的坐标代入抛物线表达式，同理可得：2a ＝2，2b ＝4； 故y 2 ＝−（x−2a ）2＋2b ＝−（x−2）2＋4；（2）同理可得：3a ＝3，3b ＝9，故点n B 的坐标为（n ，2n ），以此推出：点1n B + [（n ＋1），（n ＋1）2]，故所有抛物线的顶点坐标满足的函数关系式是：y ＝2x ； 故答案为：（n ，n 2 ）；[（n ＋1），（n ＋1）2]；y ＝x 2； （3）①存在，理由：点A （0，0），点An （2n ，0）、点n B （n ，n 2 ），△AAnBn 为等腰直角三角形，则AAn 2 ＝2ABn 2，即（2n ）2＝2（n 2 ＋n 4）， 解得：n ＝1（不合题意的值已舍去）， 抛物线的表达式为：y ＝−（x−1）2 ＋1； ②y 1n c -＝−（m−n ＋1）2＋（n−1）2， y n c ＝−（m−n ）2＋n 2，C 1n -C n ＝y n c −y 1n c -＝−（m−n ）2＋n 2 ＋（m−n ＋1）2−（n−1）2＝2m ． 【点睛】本题考查的是二次函数综合运用，这种找规律类型题目，通常按照题设的顺序逐次求解，通常比较容易．10．F解析：（1）223y x x =--+，1x =-；（2）O 1)3）满足条件的点F 的坐标为F 1(-2，3)，F 2(3，-12)． 【分析】（1）把A （1，0），B （-3，0）代入y=ax 2+bx+3即可求解；（2）先求出直线OO 1的解析式为y x =，再根据223x x x --+=，求解即可或是根据23(23)3x x x +---+=得出x 的值，再根据直线OO 1的解析式为y x =求解；（3）先求出直线EF 解析式为 33y x =--，再根据22333x x x --+=--求解即可． 【详解】解：（1）将点A （1, 0），B （-3, 0）代入抛物线解析式y=a x 2+b x+3 得：{309330a b a b ++=-+=解得：{12a b =-=-∴抛物线解析式为 223y x x =--+ ∴2(1)4y x =++ ∴1x =-（2）∵点C 为223y x x =--+与y 轴的交点∴C （0，3） ∵B(－3，0)∴OB ＝OC ∴ ∠CBO=45° ∵将△COB 沿直线 BC 平移，得到△C 1O 1B 1 ∴直线OO 1∥BC ∴ ∠O 1OA=45° ∴直线OO 1的解析式为y x = 根据题意 得 223x x x --+= 整理得 2330x x +-=解得 1x =2x =∴O 1 )或)解法2 ∵点C 为223y x x =--+与y 轴的交点∴C （0，3）∴OC=3 ∵将△COB 沿直线 BC 平移，得到△C 1O 1B 1 01C 1=3 ∴23(23)3x x x +---+= 整理得 2330x x +-= 解得 13212x -+=23212x --= ∵B(－3，0)∴OB ＝OC ∴ ∠CBO=45° ∵将△COB 沿直线 BC 平移，得到△C 1O 1B 1 ∴直线OO 1∥BC ∴ ∠O 1OA=45° ∴直线OO 1的解析式为y=x ∴O 1(3212-+,3212-+ )或（3212--，3212--）(3)∵抛物线对称轴与x 轴交于点E,则点E 的坐标为E(-1,0),过点C 作CF ∥x 轴 根据抛物线的对称性得F 的坐标为F(-2,3) ∴AE=CF=2 ∵CF ∥AE ∴四边形CFEA 为平行四边形 ∴EF ∥CA设直线EF 的解析式为y kx b =+ 得：{320k bk b =-+=-+ 解得：{33k b =-=-∴直线EF 解析式为 33y x =-- 根据题意 得 22333x x x --+=-- 解得12x =- 23x =满足条件的点F 的坐标为F 1(-2，3)，F 2(3，-12)． 【点睛】本题属于二次函数综合题，考查了二次函数的性质，一次函数的性质，平行线的判定和性质，解题的关键是学会利用参数构建方程组解决问题，学会用转化的思想思考问题．二、中考几何压轴题11．（1）证明见解析；；（2）线段与之间的数量关系为；（3）或 【分析】（1）①由、结合可得四边形CEGF 是矩形，再由即可得证；②由正方形性质知、，据此可得、，利用平行线分线段成比例定理可得； （2解析：（1）①证明见解析；2）线段AG 与BE 之间的数量关系为AG =；（3【分析】（1）①由GE BC ⊥、GF CD ⊥结合BCD 90∠=可得四边形CEGF 是矩形，再由ECG 45∠=即可得证；②由正方形性质知CEG B 90∠∠==、ECG 45∠=，据此可得CGCE=GE //AB ，利用平行线分线段成比例定理可得； （2）连接CG ，只需证ACG BCE 即可得；（3）由（2）证出ACGBCE 就可得到BE AG =，再根据A E G 、、三点在同一直线上分在CD 左边和右边两种不同的情况求出AG 的长度，即可求出BE 的长度． 【详解】（1）①证明：四边形ABCD 是正方形，90,45BCD BCA ∴∠=︒∠=︒ ,,GE BC GF CD ⊥⊥90,CEG CFG ECF ∴∠=∠=∠=︒∴四边形CEGF 是矩形，45,CGE ECG ∠=∠=︒,EG EC ∴=∴四边形CEGF 是正方形；②解：由①知四边形CEGF 是正方形，∴∠CEG=∠B=90°，∠ECG=45°，∴CGCE=，GE ∥AB ，∴AG CGBE CE==（2）如下图所示连接,CG 由旋转性质知,BCE ACG a ∠=∠=在Rt CEG △和Rt CBA 中，45CE cos CG =︒=45CB cos CA =︒=CG CACE CB∴== ,ACGBCE ∴AG CABE CB∴==∴线段AG 与BE 之间的数量关系为2AG BE =；（3）解：①当正方形CEGF 在绕点C 旋转到如下图所示时： 当A E G 、、三点在一条直线上时， 由（2）可知ACG BCE ，2AG CABE CB∴==， 22BE AG ∴=∠CEG=∠CEA=∠ABC=90°，24AB EC ==，222224432AC AB BC ∴=+=+=42AC ∴=22222(42)228AE AC CE ∴=-=-=27AE ∴=272AG AE EG ∴=+=+22(272)14222BE AG ∴==⨯+=+②当正方形CEGF 在绕点C 旋转到如下图所示时：当A E G 、、三点在一条直线上时， 由（2）可知ACG BCE ，2AG CA BE CB∴==， 2BE AG ∴=∠CEA=∠ABC=90°，24AB EC ==，222224432AC AB BC ∴=+=+= 42AC ∴=22222(42)228AE AC CE ∴=-=-= 27AE ∴=272AG AE EG ∴=-=-22(272)14222BE AG ∴==⨯-=-142142【点睛】本题考查了正方形的性质与判定，相似三角形的判定与性质等，综合性较强，有一定的难度，正确添加辅助线，熟练掌握正方形的判定与性质、相似三角形的判定与性质是解题的关键．12．（1）是，理由见解析；（2）或或；（3），证明见解析．【分析】（1）证明，可得，又点F 为CD 中点,即可得出结论；（2）当为点构成的四边形的准中位线．则M 、N 一定是中点，再分两种情况讨论：和，根解析：（1）是，理由见解析；（2）1211t =或2t =或4t =；（3）M CNF ∠=∠，证明见解析．【分析】（1）证明EDB ABD ∠=∠，可得DE BE AE ==，又点F 为CD 中点,即可得出结论； （2）当MN 为点,,,A B E F 构成的四边形的准中位线．则M 、N 一定是中点，再分两种情况讨论：BE AF 和EF AB ∥，根据平行线分线段成比例列方程即可求解；（3）连接BD ，取BD 的中点H ，连接EH ，FH 得两条中位线，根据中位线定理，得平行，可找到相等角和线段，从而可得EFH △是等腰三角形，进而可得M HEF HFE CNF ∠=∠=∠=∠．【详解】解：（1）EF 是四边形ABCD 的准中位线，理由如下：∵DE AE =，。

二次函数解答压轴题(62题)一、解答题1(2023·浙江绍兴·统考中考真题)已知二次函数y=-x2+bx+c．(1)当b=4,c=3时，①求该函数图象的顶点坐标．②当-1≤x≤3时，求y的取值范围．(2)当x≤0时，y的最大值为2；当x>0时，y的最大值为3，求二次函数的表达式．2(2023·浙江·统考中考真题)已知点-m,0和3m,0在二次函数y=ax2+bx+3(a,b是常数，a≠0)的图像上．(1)当m=-1时，求a和b的值；(2)若二次函数的图像经过点A n,3且点A不在坐标轴上，当-2<m<-1时，求n的取值范围；(3)求证：b2+4a=0．3(2023·浙江嘉兴·统考中考真题)在二次函数y=x2-2tx+3(t>0)中，(1)若它的图象过点(2,1)，则t的值为多少？(2)当0≤x≤3时，y的最小值为-2，求出t的值：(3)如果A(m-2,a),B(4,b),C(m,a)都在这个二次函数的图象上，且a<b<3，求m的取值范围．4(2023·浙江杭州·统考中考真题)设二次函数y=ax2+bx+1，(a≠0，b是实数)．已知函数值y和自变量x的部分对应取值如下表所示：x⋯-10123⋯y⋯m1n1p⋯(1)若m=4，求二次函数的表达式；(2)写出一个符合条件的x的取值范围，使得y随x的增大而减小．(3)若在m、n、p这三个实数中，只有一个是正数，求a的取值范围．5(2023·湖南常德·统考中考真题)如图，二次函数的图象与x轴交于A-1,0，B5,0两点，与y轴交于点C，顶点为D．O为坐标原点，tan∠ACO=1 5．(1)求二次函数的表达式；(2)求四边形ACDB的面积；(3)P是抛物线上的一点，且在第一象限内，若∠ACO=∠PBC，求P点的坐标．6(2023·山东烟台·统考中考真题)如图，抛物线y=ax2+bx+5与x轴交于A,B两点，与y轴交于点C,AB=4．抛物线的对称轴x=3与经过点A的直线y=kx-1交于点D，与x轴交于点E．(1)求直线AD及抛物线的表达式；(2)在抛物线上是否存在点M，使得△ADM是以AD为直角边的直角三角形?若存在，求出所有点M的坐标；若不存在，请说明理由；(3)以点B为圆心，画半径为2的圆，点P为⊙B上一个动点，请求出PC+1PA的最小值．27(2023·江苏苏州·统考中考真题)如图，二次函数y=x2-6x+8的图像与x轴分别交于点A,B(点A 在点B的左侧)，直线l是对称轴．点P在函数图像上，其横坐标大于4，连接PA,PB，过点P作PM⊥l，垂足为M，以点M为圆心，作半径为r的圆，PT与⊙M相切，切点为T．(1)求点A,B的坐标；(2)若以⊙M的切线长PT为边长的正方形的面积与△PAB的面积相等，且⊙M不经过点3,2，求PM长的取值范围．8(2023·山东东营·统考中考真题)如图，抛物线过点O0,0，矩形ABCD的边AB在线段，E10,0OE上(点B在点A的左侧)，点C，D在抛物线上，设B t,0，当t=2时，BC=4．(1)求抛物线的函数表达式；(2)当t为何值时，矩形ABCD的周长有最大值？最大值是多少？(3)保持t=2时的矩形ABCD不动，向右平移抛物线，当平移后的抛物线与矩形的边有两个交点G，H，且直线GH平分矩形ABCD的面积时，求抛物线平移的距离．9(2023·内蒙古通辽·统考中考真题)在平面直角坐标系中，已知抛物线y=ax2+83x+c a≠0与x轴交于点A1,0和点B，与y轴交于点C0,-4．(1)求这条抛物线的函数解析式；(2)P是抛物线上一动点(不与点A，B，C重合)，作PD⊥x轴，垂足为D，连接PC．①如图，若点P在第三象限，且tan∠CPD=2，求点P的坐标；②直线PD交直线BC于点E，当点E关于直线PC的对称点E 落在y轴上时，请直接写出四边形PECE 的周长．10(2023·四川自贡·统考中考真题)如图，抛物线y=-43x2+bx+4与x轴交于A(-3,0)，B两点，与y轴交于点C．(1)求抛物线解析式及B，C两点坐标；(2)以A，B，C，D为顶点的四边形是平行四边形，求点D坐标；(3)该抛物线对称轴上是否存在点E，使得∠ACE=45°，若存在，求出点E的坐标；若不存在，请说明理由．11(2023·四川达州·统考中考真题)如图，抛物线y =ax 2+bx +c 过点A -1,0 ,B 3,0 ,C 0,3 ．(1)求抛物线的解析式；(2)设点P 是直线BC 上方抛物线上一点，求出△PBC 的最大面积及此时点P 的坐标；(3)若点M 是抛物线对称轴上一动点，点N 为坐标平面内一点，是否存在以BC 为边，点B 、C 、M 、N 为顶点的四边形是菱形，若存在，请直接写出点N 的坐标；若不存在，请说明理由．12(2023·四川泸州·统考中考真题)如图，在平面直角坐标系xOy中，已知抛物线y=ax2+2x+c与坐标轴分别相交于点A，B，C0,6三点，其对称轴为x=2．(1)求该抛物线的解析式；(2)点F是该抛物线上位于第一象限的一个动点，直线AF分别与y轴，直线BC交于点D，E．①当CD=CE时，求CD的长；②若△CAD，△CDE，△CEF的面积分别为S1，S2，S3，且满足S1+S3=2S2，求点F的坐标．13(2023·全国·统考中考真题)如图，在平面直角坐标系中，抛物线y=-x2+2x+c经过点A(0,1)．点P，Q在此抛物线上，其横坐标分别为m,2m(m>0)，连接AP，AQ．(1)求此抛物线的解析式．(2)当点Q与此抛物线的顶点重合时，求m的值．(3)当∠PAQ的边与x轴平行时，求点P与点Q的纵坐标的差．(4)设此抛物线在点A与点P之间部分(包括点A和点P)的最高点与最低点的纵坐标的差为h1，在点A与点Q之间部分(包括点A和点Q)的最高点与最低点的纵坐标的差为h2．当h2-h1=m时，直接写出m的值．14(2023·重庆·统考中考真题)如图，在平面直角坐标系中，抛物线y=14x2+bx+c与x轴交于点A，B，与y轴交于点C，其中B3,0，C0,-3．(1)求该抛物线的表达式；(2)点P是直线AC下方抛物线上一动点，过点P作PD⊥AC于点D，求PD的最大值及此时点P的坐标；(3)在(2)的条件下，将该抛物线向右平移5个单位，点E为点P的对应点，平移后的抛物线与y轴交于点F，Q为平移后的抛物线的对称轴上任意一点．写出所有使得以QF为腰的△QEF是等腰三角形的点Q的坐标，并把求其中一个点Q的坐标的过程写出来．15(2023·四川凉山·统考中考真题)如图，已知抛物线与x轴交于A1,0两点，与y轴交于和B-5,0点C．直线y=-3x+3过抛物线的顶点P．(1)求抛物线的函数解析式；(2)若直线x=m-5<m<0与抛物线交于点E，与直线BC交于点F．①当EF取得最大值时，求m的值和EF的最大值；②当△EFC是等腰三角形时，求点E的坐标．16(2023·四川成都·统考中考真题)如图，在平面直角坐标系xOy中，已知抛物线y=ax2+c经过点P (4,-3)，与y轴交于点A(0,1)，直线y=kx(k≠0)与抛物线交于B，C两点．(1)求抛物线的函数表达式；(2)若△ABP是以AB为腰的等腰三角形，求点B的坐标；(3)过点M(0,m)作y轴的垂线，交直线AB于点D，交直线AC于点E．试探究：是否存在常数m，使得OD⊥OE始终成立？若存在，求出m的值；若不存在，请说明理由．17(2023·安徽·统考中考真题)在平面直角坐标系中，点O是坐标原点，抛物线y=ax2+bx a≠0经过点A3,3，对称轴为直线x=2．(1)求a,b的值；(2)已知点B,C在抛物线上，点B的横坐标为t，点C的横坐标为t+1．过点B作x轴的垂线交直线OA于点D，过点C作x轴的垂线交直线OA于点E．(ⅰ)当0<t<2时，求△OBD与△ACE的面积之和；(ⅱ)在抛物线对称轴右侧，是否存在点B，使得以B,C,D,E为顶点的四边形的面积为32若存在，请求出点B的横坐标t的值；若不存在，请说明理由．18(2023·浙江金华·统考中考真题)如图，直线y =52x +5与x 轴，y 轴分别交于点A ,B ，抛物线的顶点P 在直线AB 上，与x 轴的交点为C ,D ，其中点C 的坐标为2,0 ．直线BC 与直线PD 相交于点E ．(1)如图2，若抛物线经过原点O ．①求该抛物线的函数表达式；②求BEEC的值．(2)连接PC ,∠CPE 与∠BAO 能否相等？若能，求符合条件的点P 的横坐标；若不能，试说明理由．19(2023·湖南·统考中考真题)如图，二次函数y=x2+bx+c的图象与x轴交于A，B两点，与y轴交于C点，其中B1,0．，C0,3(1)求这个二次函数的表达式；(2)在二次函数图象上是否存在点P，使得S△PAC=S△ABC若存在，请求出P点坐标；若不存在，请说明理由；(3)点Q是对称轴l上一点，且点Q的纵坐标为a，当△QAC是锐角三角形时，求a的取值范围．20(2023·四川遂宁·统考中考真题)在平面直角坐标系中，O 为坐标原点，抛物线y =14x 2+bx +c 经过点O (0，0)，对称轴过点B (2，0)，直线l 过点C 2,-2 ，且垂直于y 轴．过点B 的直线l 1交抛物线于点M 、N ，交直线l 于点Q ，其中点M 、Q 在抛物线对称轴的左侧．(1)求抛物线的解析式；(2)如图1，当BM :MQ =3:5时，求点N 的坐标；(3)如图2，当点Q 恰好在y 轴上时，P 为直线l 1下方的抛物线上一动点，连接PQ 、PO ，其中PO 交l 1于点E ，设△OQE 的面积为S 1，△PQE 的面积为S 2．求S2S 1的最大值．21(2023·四川眉山·统考中考真题)在平面直角坐标系中，已知抛物线y =ax 2+bx +c 与x 轴交于点A -3,0 ,B 1,0 两点，与y 轴交于点C 0,3 ，点P 是抛物线上的一个动点．(1)求抛物线的表达式；(2)当点P 在直线AC 上方的抛物线上时，连接BP 交AC 于点D ．如图1．当PDDB的值最大时，求点P 的坐标及PDDB的最大值；(3)过点P 作x 轴的垂线交直线AC 于点M ，连接PC ，将△PCM 沿直线PC 翻折，当点M 的对应点M '恰好落在y 轴上时，请直接写出此时点M 的坐标．22(2023·江西·统考中考真题)综合与实践问题提出：某兴趣小组开展综合实践活动：在Rt△ABC中，∠C=90°，D为AC上一点，CD=2，动点P 以每秒1个单位的速度从C点出发，在三角形边上沿C→B→A匀速运动，到达点A时停止，以DP为边作正方形DPEF设点P的运动时间为ts，正方形DPEF的而积为S，探究S与t的关系(1)初步感知：如图1，当点P由点C运动到点B时，①当t=1时，S=．②S关于t的函数解析式为．(2)当点P由点B运动到点A时，经探究发现S是关于t的二次函数，并绘制成如图2所示的图象请根据图象信息，求S关于t的函数解析式及线段AB的长．(3)延伸探究：若存在3个时刻t1,t2,t3(t1<t2<t3)对应的正方形DPEF的面积均相等．①t1+t2=；②当t3=4t1时，求正方形DPEF的面积．23(2023·新疆·统考中考真题)【建立模型】(1)如图1，点B 是线段CD 上的一点，AC ⊥BC ，AB ⊥BE ，ED ⊥BD ，垂足分别为C ，B ，D ，AB =BE ．求证：△ACB ≌△BDE ；【类比迁移】(2)如图2，一次函数y =3x +3的图象与y 轴交于点A 、与x 轴交于点B ，将线段AB 绕点B 逆时针旋转90°得到BC 、直线AC 交x 轴于点D ．①求点C 的坐标；②求直线AC 的解析式；【拓展延伸】(3)如图3，抛物线y =x 2-3x -4与x 轴交于A ，B 两点(点A 在点B 的左侧)，与y 轴交于C点，已知点Q (0，-1)，连接BQ ．抛物线上是否存在点M ，使得tan ∠MBQ =13，若存在，求出点M 的横坐标．24(2023·甘肃武威·统考中考真题)如图1，抛物线y=-x2+bx与x轴交于点A，与直线y=-x交于点B4,-4在y轴上．点P从点B出发，沿线段BO方向匀速运动，运动到点O时停止．，点C0,-4(1)求抛物线y=-x2+bx的表达式；(2)当BP=22时，请在图1中过点P作PD⊥OA交抛物线于点D，连接PC，OD，判断四边形OCPD 的形状，并说明理由．(3)如图2，点P从点B开始运动时，点Q从点O同时出发，以与点P相同的速度沿x轴正方向匀速运动，点P停止运动时点Q也停止运动．连接BQ，PC，求CP+BQ的最小值．25(2023·四川乐山·统考中考真题)已知x 1,y 1 ,x 2,y 2 是抛物C 1:y =-14x 2+bx (b 为常数)上的两点，当x 1+x 2=0时，总有y 1=y 2(1)求b 的值；(2)将抛物线C 1平移后得到抛物线C 2:y =-14(x -m )2+1(m >0)．探究下列问题：①若抛物线C 1与抛物线C 2有一个交点，求m 的取值范围；②设抛物线C 2与x 轴交于A ，B 两点，与y 轴交于点C ，抛物线C 2的顶点为点E ，△ABC 外接圆的圆心为点F ，如果对抛物线C 1上的任意一点P ，在抛物线C 2上总存在一点Q ，使得点P 、Q 的纵坐标相等．求EF 长的取值范围．26(2023·内蒙古·统考中考真题)如图，在平面直角坐标系中，抛物线y =-x 2+3x +1交y 轴于点A ，直线y =-13x +2交抛物线于B ,C 两点(点B 在点C 的左侧)，交y 轴于点D ，交x 轴于点E ．(1)求点D ,E ,C 的坐标；(2)F 是线段OE 上一点OF <EF ，连接AF ,DF ,CF ，且AF 2+EF 2=21．①求证：△DFC 是直角三角形；②∠DFC 的平分线FK 交线段DC 于点K ,P 是直线BC 上方抛物线上一动点，当3tan ∠PFK =1时，求点P 的坐标．27(2023·上海·统考中考真题)在平面直角坐标系xOy中，已知直线y=34x+6与x轴交于点A，y轴交于点B，点C在线段AB上，以点C为顶点的抛物线M：y=ax2+bx+c经过点B．(1)求点A，B的坐标；(2)求b，c的值；(3)平移抛物线M至N，点C，B分别平移至点P，D，联结CD，且CD∥x轴，如果点P在x轴上，且新抛物线过点B，求抛物线N的函数解析式．28(2023·江苏扬州·统考中考真题)在平面直角坐标系xOy中，已知点A在y轴正半轴上．(1)如果四个点0,0中恰有三个点在二次函数y=ax2(a为常数，且a≠0)的图象、-1,1、1,1、0,2上．①a=；②如图1，已知菱形ABCD的顶点B、C、D在该二次函数的图象上，且AD⊥y轴，求菱形的边长；③如图2，已知正方形ABCD的顶点B、D在该二次函数的图象上，点B、D在y轴的同侧，且点B在点D的左侧，设点B、D的横坐标分别为m、n，试探究n-m是否为定值．如果是，求出这个值；如果不是，请说明理由．(2)已知正方形ABCD的顶点B、D在二次函数y=ax2(a为常数，且a>0)的图象上，点B在点D的左侧，设点B、D的横坐标分别为m、n，直接写出m、n满足的等量关系式．29(2023·湖南岳阳·统考中考真题)已知抛物线Q1:y=-x2+bx+c与x轴交于A-3,0,B两点，交y 轴于点C0,3．(1)请求出抛物线Q1的表达式．(2)如图1，在y轴上有一点D0,-1，点E在抛物线Q1上，点F为坐标平面内一点，是否存在点E,F使得四边形DAEF为正方形？若存在，请求出点E,F的坐标；若不存在，请说明理由．(3)如图2，将抛物线Q1向右平移2个单位，得到抛物线Q2，抛物线Q2的顶点为K，与x轴正半轴交于点H，抛物线Q1上是否存在点P，使得∠CPK=∠CHK？若存在，请求出点P的坐标；若不存在，请说明理由．30(2023·湖南永州·统考中考真题)如图1，抛物线y =ax 2+bx +c (a ，b ，c 为常数)经过点F 0,5 ，顶点坐标为2,9 ，点P x 1,y 1 为抛物线上的动点，PH ⊥x 轴于H ，且x 1≥52．(1)求抛物线的表达式；(2)如图1，直线OP :y =y 1x 1x 交BF 于点G ，求S △BPG S △BOG的最大值；(3)如图2，四边形OBMF 为正方形，PA 交y 轴于点E ，BC 交FM 的延长线于C ，且BC ⊥BE ,PH =FC ，求点P 的横坐标．31(2023·山东枣庄·统考中考真题)如图，抛物线y=-x2+bx+c经过A(-1,0),C(0,3)两点，并交x轴于另一点B，点M是抛物线的顶点，直线AM与轴交于点D．(1)求该抛物线的表达式；(2)若点H是x轴上一动点，分别连接MH，DH，求MH+DH的最小值；(3)若点P是抛物线上一动点，问在对称轴上是否存在点Q，使得以D，M，P，Q为顶点的四边形是平行四边形？若存在，请直接写出所有满足条件的点Q的坐标；若不存在，请说明理由．32(2023·湖北随州·统考中考真题)如图1，平面直角坐标系xOy中，抛物线y=ax2+bx+c过点A(-1,0)，B(2,0)和C(0,2)，连接BC，点P(m,n)(m>0)为抛物线上一动点，过点P作PN⊥x轴交直线BC 于点M，交x轴于点N．(1)直接写出抛物线和直线BC的解析式；(2)如图2，连接OM，当△OCM为等腰三角形时，求m的值；(3)当P点在运动过程中，在y轴上是否存在点Q，使得以O，P，Q为顶点的三角形与以B，C，N为顶点的三角形相似(其中点P与点C相对应)，若存在，直接写出点P和点Q的坐标；若不存在，请说明理由．33(2023·四川内江·统考中考真题)如图，在平面直角坐标系中，抛物线y =ax 2+bx +c 与x 轴交于B 4,0 ，C -2,0 两点．与y 轴交于点A 0,-2 ．(1)求该抛物线的函数表达式；(2)若点P 是直线AB 下方抛物线上的一动点，过点P 作x 轴的平行线交AB 于点K ，过点P 作y 轴的平行线交x 轴于点D ，求与12PK +PD 的最大值及此时点P 的坐标；(3)在抛物线的对称轴上是否存在一点M ，使得△MAB 是以AB 为一条直角边的直角三角形：若存在，请求出点M 的坐标，若不存在，请说明理由．34(2023·湖南·统考中考真题)已知二次函数y =ax 2+bx +c a >0 ．(1)若a =1，c =-1，且该二次函数的图像过点2,0 ，求b 的值；(2)如图所示，在平面直角坐标系Oxy 中，该二次函数的图像与x 轴交于点A x 1,0 ，B x 2,0 ，且x 1<0<x 2，点D 在⊙O 上且在第二象限内，点E 在x 轴正半轴上，连接DE ，且线段DE 交y 轴正半轴于点F ，∠DOF =∠DEO ，OF =32DF ．①求证：DO EO=23．②当点E 在线段OB 上，且BE =1．⊙O 的半径长为线段OA 的长度的2倍，若4ac =-a 2-b 2，求2a +b 的值．35(2023·山西·统考中考真题)如图，二次函数y =-x 2+4x 的图象与x 轴的正半轴交于点A ，经过点A 的直线与该函数图象交于点B 1,3 ，与y 轴交于点C ．(1)求直线AB 的函数表达式及点C 的坐标；(2)点P 是第一象限内二次函数图象上的一个动点，过点P 作直线PE ⊥x 轴于点E ，与直线AB 交于点D ，设点P 的横坐标为m ．①当PD =12OC 时，求m 的值；②当点P 在直线AB 上方时，连接OP ，过点B 作BQ ⊥x 轴于点Q ，BQ 与OP 交于点F ，连接DF ．设四边形FQED 的面积为S ，求S 关于m 的函数表达式，并求出S 的最大值．36(2023·湖北武汉·统考中考真题)抛物线C1:y=x2-2x-8交x轴于A,B两点(A在B的左边)，交y 轴于点C．(1)直接写出A,B,C三点的坐标；(2)如图(1)，作直线x=t0<t<4，分别交x轴，线段BC，抛物线C1于D,E,F三点，连接CF．若△BDE 与△CEF相似，求t的值；(3)如图(2)，将抛物线C1平移得到抛物线C2，其顶点为原点．直线y=2x与抛物线C2交于O,G两点，过OG的中点H作直线MN(异于直线OG)交抛物线C2于M,N两点，直线MO与直线GN交于点P．问点P是否在一条定直线上？若是，求该直线的解析式；若不是，请说明理由．37(2023·湖北宜昌·统考中考真题)如图，已知A(0,2),B(2,0)．点E位于第二象限且在直线y=-2x 上，∠EOD=90°，OD=OE，连接AB，DE，AE，DB．(1)直接判断△AOB的形状：△AOB是三角形；(2)求证：△AOE≌△BOD；(3)直线EA交x轴于点C(t,0),t>2．将经过B，C两点的抛物线y1=ax2+bx-4向左平移2个单位，得到抛物线y2．①若直线EA与抛物线y1有唯一交点，求t的值；②若抛物线y2的顶点P在直线EA上，求t的值；③将抛物线y2再向下平移，2(t-1)2个单位，得到抛物线y3．若点D在抛物线y3上，求点D的坐标．38(2023·湖南郴州·统考中考真题)已知抛物线y=ax2+bx+4与x轴相交于点A1,0，与y，B4,0轴相交于点C．(1)求抛物线的表达式；(2)如图1，点P是抛物线的对称轴l上的一个动点，当△PAC的周长最小时，求PAPC的值；(3)如图2，取线段OC的中点D，在抛物线上是否存在点Q，使tan∠QDB=12若存在，求出点Q的坐标；若不存在，请说明理由．39(2023·湖北黄冈·统考中考真题)已知抛物线y =-12x 2+bx +c 与x 轴交于A ,B (4,0)两点，与y 轴交于点C (0,2)，点P 为第一象限抛物线上的点，连接CA ,CB ,PB ,PC ．(1)直接写出结果；b =，c =，点A 的坐标为，tan ∠ABC =；(2)如图1，当∠PCB =2∠OCA 时，求点P 的坐标；(3)如图2，点D 在y 轴负半轴上，OD =OB ，点Q 为抛物线上一点，∠QBD =90°，点E ，F 分别为△BDQ 的边DQ ,DB 上的动点，QE =DF ，记BE +QF 的最小值为m ．①求m 的值；②设△PCB 的面积为S ，若S =14m 2-k ，请直接写出k 的取值范围．40(2023·湖南·统考中考真题)如图，在平面直角坐标系中，抛物线y=ax2+x+c经过点A-2,0和点B4,0，且与直线l:y=-x-1交于D、E两点(点D在点E的右侧)，点M为直线l上的一动点，设点M 的横坐标为t．(1)求抛物线的解析式．(2)过点M作x轴的垂线，与拋物线交于点N．若0<t<4，求△NED面积的最大值．(3)抛物线与y轴交于点C，点R为平面直角坐标系上一点，若以B、C、M、R为顶点的四边形是菱形，请求出所有满足条件的点R的坐标．41(2023·四川·统考中考真题)如图1，在平面直角坐标系中，已知二次函数y=ax2+bx+4的图象与x 轴交于点A-2,0，B4,0，与y轴交于点C．(1)求抛物线的解析式；(2)已知E为抛物线上一点，F为抛物线对称轴l上一点，以B，E，F为顶点的三角形是等腰直角三角形，且∠BFE=90°，求出点F的坐标；(3)如图2，P为第一象限内抛物线上一点，连接AP交y轴于点M，连接BP并延长交y轴于点N，在点P运动过程中，OM+12ON是否为定值？若是，求出这个定值；若不是，请说明理由．42(2023·山东聊城·统考中考真题)如图①，抛物线y=ax2+bx-9与x轴交于点A-3,0，，B6,0与y轴交于点C，连接AC，BC.点P是x轴上任意一点．(1)求抛物线的表达式；(2)点Q在抛物线上，若以点A，C，P，Q为顶点，AC为一边的四边形为平行四边形时，求点Q的坐标；(3)如图②，当点P m,0从点A出发沿x轴向点B运动时(点P与点A，B不重合)，自点P分别作PE∥BC，交AC于点E，作PD⊥BC，垂足为点D．当m为何值时，△PED面积最大，并求出最大值．43(2023·湖北荆州·统考中考真题)已知：y关于x的函数y=a-2x+b．x2+a+1(1)若函数的图象与坐标轴有两个公共点，且a=4b，则a的值是；(2)如图，若函数的图象为抛物线，与x轴有两个公共点A-2,0，B4,0，并与动直线l:x=m(0<m<4)交于点P，连接PA，PB，PC，BC，其中PA交y轴于点D，交BC于点E．设△PBE的面积为S1，△CDE 的面积为S2．①当点P为抛物线顶点时，求△PBC的面积；②探究直线l在运动过程中，S1-S2是否存在最大值？若存在，求出这个最大值；若不存在，说明理由．44(2023·福建·统考中考真题)已知抛物线y=ax2+bx+3交x轴于A1,0,B3,0两点，M为抛物线的顶点，C,D为抛物线上不与A,B重合的相异两点，记AB中点为E，直线AD,BC的交点为P．(1)求抛物线的函数表达式；(2)若C4,3,D m,-3 4，且m<2，求证：C,D,E三点共线；(3)小明研究发现：无论C,D在抛物线上如何运动，只要C,D,E三点共线，△AMP,△MEP,△ABP中必存在面积为定值的三角形．请直接写出其中面积为定值的三角形及其面积，不必说明理由．45(2023·山东·统考中考真题)如图，直线y=-x+4交x轴于点B，交y轴于点C，对称轴为x=32的抛物线经过B，C两点，交x轴负半轴于点A．P为抛物线上一动点，点P的横坐标为m，过点P作x轴的平行线交抛物线于另一点M，作x轴的垂线PN，垂足为N，直线MN交y轴于点D．(1)求抛物线的解析式；(2)若0<m<32，当m为何值时，四边形CDNP是平行四边形？(3)若m<32，设直线MN交直线BC于点E，是否存在这样的m值，使MN=2ME？若存在，求出此时m 的值；若不存在，请说明理由．46(2023·山东·统考中考真题)已知抛物线y =-x 2+bx +c 与x 轴交于A ，B 两点，与y 轴交于点C 0,4 ，其对称轴为x =-32．(1)求抛物线的表达式；(2)如图1，点D 是线段OC 上的一动点，连接AD ，BD ，将△ABD 沿直线AD 翻折，得到△AB D ，当点B 恰好落在抛物线的对称轴上时，求点D 的坐标；(3)如图2，动点P 在直线AC 上方的抛物线上，过点P 作直线AC 的垂线，分别交直线AC ，线段BC 于点E ，F ，过点F 作FG ⊥x 轴，垂足为G ，求FG +2FP 的最大值．47(2023·辽宁大连·统考中考真题)如图，在平面直角坐标系中，抛物线C 1:y =x 2上有两点A 、B ，其中点A 的横坐标为-2，点B 的横坐标为1，抛物线C 2:y =-x 2+bx +c 过点A 、B ．过A 作AC ∥x 轴交抛物线C 1另一点为点C ．以AC 、12AC 长为边向上构造矩形ACDE ．(1)求抛物线C 2的解析式；(2)将矩形ACDE 向左平移m 个单位，向下平移n 个单位得到矩形A C D E ，点C 的对应点C 落在抛物线C 1上．①求n 关于m 的函数关系式，并直接写出自变量m 的取值范围；②直线A E 交抛物线C 1于点P ，交抛物线C 2于点Q ．当点E 为线段PQ 的中点时，求m 的值；③抛物线C 2与边E D 、A C 分别相交于点M 、N ，点M 、N 在抛物线C 2的对称轴同侧，当MN =2103时，求点C 的坐标．48(2023·湖南张家界·统考中考真题)如图，在平面直角坐标系中，已知二次函数y=ax2+bx+c的图象与x轴交于点A-2,0．点D为线段BC上的一动点． 和点B6,0两点，与y轴交于点C0,6(1)求二次函数的表达式；(2)如图1，求△AOD周长的最小值；(3)如图2，过动点D作DP∥AC交抛物线第一象限部分于点P，连接PA,PB，记△PAD与△PBD的面积和为S，当S取得最大值时，求点P的坐标，并求出此时S的最大值．49(2023·黑龙江绥化·统考中考真题)如图，抛物线y1=ax2+bx+c的图象经过A(-6,0)，B(-2,0)，C (0,6)三点，且一次函数y=kx+6的图象经过点B．(1)求抛物线和一次函数的解析式．(2)点E，F为平面内两点，若以E、F、B、C为顶点的四边形是正方形，且点E在点F的左侧．这样的E，F两点是否存在？如果存在，请直接写出所有满足条件的点E的坐标：如果不存在，请说明理由．(3)将抛物线y1=ax2+bx+c的图象向右平移8个单位长度得到抛物线y2，此抛物线的图象与x轴交于M，N两点(M点在N点左侧)．点P是抛物线y2上的一个动点且在直线NC下方．已知点P的横坐标为PD有最大值，最大值是多少？m．过点P作PD⊥NC于点D．求m为何值时，CD+1250(2023·四川南充·统考中考真题)如图1，抛物线y=ax2+bx+3(a≠0)与x轴交于A-1,0，B3,0两点，与y轴交于点C．(1)求抛物线的解析式；(2)点P在抛物线上，点Q在x轴上，以B，C，P，Q为顶点的四边形为平行四边形，求点P的坐标；(3)如图2，抛物线顶点为D，对称轴与x轴交于点E，过点K1,3的直线(直线KD除外)与抛物线交于G，H两点，直线DG，DH分别交x轴于点M，N．试探究EM⋅EN是否为定值，若是，求出该定值；若不是，说明理由．51(2023·四川宜宾·统考中考真题)如图，抛物线y=ax2+bx+c与x轴交于点A-4,0，且经、B2,0过点C-2,6．(1)求抛物线的表达式；(2)在x轴上方的抛物线上任取一点N，射线AN、BN分别与抛物线的对称轴交于点P、Q，点Q关于x轴的对称点为Q ，求△APQ 的面积；(3)点M是y轴上一动点，当∠AMC最大时，求M的坐标．52(2023·四川广安·统考中考真题)如图，二次函数y=x2+bx+c的图象交x轴于点A，B，交y轴于点C，点B的坐标为1,0，对称轴是直线x=-1，点P是x轴上一动点，PM⊥x轴，交直线AC于点M，交抛物线于点N．(1)求这个二次函数的解析式．(2)若点P在线段AO上运动(点P与点A、点O不重合)，求四边形ABCN面积的最大值，并求出此时点P 的坐标．(3)若点P在x轴上运动，则在y轴上是否存在点Q，使以M、N、C、Q为顶点的四边形是菱形？若存在，请直接写出所有满足条件的点Q的坐标；若不存在，请说明理由．。

中考二次函数压轴题分类汇编一．极值问题1.二次函数 y=ax2+bx+c 的图象经过点（﹣ 1，4），且与直线 y=﹣x+1 订交于 A、B 两点（如图），A 点在 y 轴上，过点 B 作 BC⊥ x 轴，垂足为点 C（﹣ 3，0）．（1）求二次函数的表达式；（2）点 N是二次函数图象上一点（点 N在 AB上方），过 N作 NP⊥x 轴，垂足为点 P，交 AB于点 M，求MN的最大值；（3）在（ 2）的条件下，点N在何地址时， BM与 NC互相垂直均分并求出所有满足条件的N 点的坐标．解析：（1）第一求得 A、 B 的坐标，尔后利用待定系数法即可求得二次函数的解析式；（2）设 M的横坐标是 x，则依照 M和 N 所在函数的解析式，即可利用 x 表示出 M、 N 的坐标，利用 x 表示出 MN的长，利用二次函数的性质求解；（3）BM与 NC互相垂直均分，即四边形 BCMN是菱形，则 BC=MC，据此即可列方程，求得 x 的值，进而获取 N 的坐标．解：（1）由题设可知A（ 0， 1），B（﹣ 3，），依照题意得：，解得：，则二次函数的解析式是：y=﹣﹣ x+1；（2）设 N（x，﹣ x2﹣x+1），则 M、 P 点的坐标分别是（ x，﹣ x+1），（x，0）．∴MN=PN﹣PM=﹣ x2﹣x+1﹣（﹣ x+1）=﹣x2﹣x=﹣（ x+）2+，则当 x=﹣时， MN的最大值为；（3）连接 MN、BN、BM与 NC互相垂直均分，即四边形 BCMN是菱形，由于 BC∥MN，即 MN=BC，且 BC=MC，即﹣ x2﹣ x=，且（﹣ x+1）2+（ x+3）2=，解得： x=1，故当 N（﹣ 1， 4）时， MN和 NC互相垂直均分．谈论：此题是待定系数法求二次函数的解析式，以及二次函数的性质、菱形的判断的综合应用，利用二次函数的性质能够解决实责问题中求最大值或最小值问题．2. 如图，抛物线 y=x2+bx+c 与 y 轴交于点 C（0，﹣ 4），与 x 轴交于点 A，B，且 B 点的坐标为（ 2， 0）（1）求该抛物线的解析式．（2）若点 P 是 AB上的一动点，过点P 作 PE∥AC，交 BC于 E，连接 CP，求△ PCE面积的最大值．（3）若点 D为 OA的中点，点 M是线段 AC上一点，且△ OMD为等腰三角形，求M点的坐标．考点：二次函数综合题．解析：（1）利用待定系数法求出抛物线的解析式；（2）第一求出△ PCE面积的表达式，尔后利用二次函数的性质求出其最大值；（3）△ OMD为等腰三角形，可能有三种状况，需要分类谈论．2 解答：解：（ 1）把点 C（ 0，﹣ 4）， B（ 2， 0）分别代入 y=x +bx+c 中，得，∴该抛物线的解析式为y=x2+x﹣4．（2）令 y=0，即 x2+x﹣4=0，解得 x1=﹣4，x2=2，∴A（﹣ 4，0）， S△ABC=AB?OC=12．设P 点坐标为（ x， 0），则 PB=2﹣x．∵PE∥AC，∴∠ BPE=∠BAC，∠ BEP=∠BCA，∴△ PBE∽△ ABC，∴，即，化简得： S△PBE=（2﹣x）2．S△PCE=S△PCB﹣S△PBE=PB?OC﹣ S△PBE=×（ 2﹣x）× 4﹣（ 2﹣ x）2=x2﹣x+=（ x+1）2+3∴当 x=﹣1 时， S△PCE的最大值为 3．（3）△ OMD为等腰三角形，可能有三种状况：（ I ）当 DM=DO时，如答图①所示．DO=DM=DA=2，∴∠ OAC=∠AMD=45°，∴∠ ADM=90°，∴M点的坐标为（﹣ 2，﹣ 2）；（II ）当 MD=MO时，如答图②所示．过点 M作 MN⊥ OD于点 N，则点 N 为 OD的中点，∴DN=ON=1， AN=AD+DN=3，又△ AMN为等腰直角三角形，∴ MN=AN=3，∴M点的坐标为（﹣ 1，﹣ 3）；（I II ）当 OD=OM时，∵△ OAC为等腰直角三角形，∴点 O到 AC的距离为× 4=，即 AC上的点与点 O之间的最小距离为．∵＞ 2，∴ OD=OM的状况不存在．综上所述，点 M的坐标为（﹣ 2，﹣ 2）或（﹣ 1，﹣ 3）．谈论：此题是二次函数综合题，观察了二次函数的图象与性质、待定系数法、相似三角形、等腰三角形等知识点，以及分类谈论的数学思想．第（ 2）问将面积的最值转变成二次函数的极值问题，注意其中求面积表达式的方法；第（ 3）问重在观察分类谈论的数学思想，注意三种可能的状况需要一一解析，不能够遗漏．二．组成图形的问题1．如图，抛物线y=ax 2+bx+c（a≠ O）与 y 轴交于点C(O，4) ，与 x 轴交于点 A 和点 B，其中点 A 的坐标为（ -2,0 ），抛物线的对称轴x=1 与抛物线交于点D，与直线 BC交于点 E(1)求抛物线的解析式；(2) 若点 F 是直线 BC上方的抛物线上的一个动点，可否存在点 F 使四边形ABFC的面积为17，若存在，求出点 F 的坐标；若不存在，请说明原由；(3)平行于 DE的一条动直线 Z 与直线 BC订交于点 P，与抛物线订交于点 Q，若以 D、 E、P、Q为极点的四边形是平行四边形，求点 P 的坐标。

2022年中考必备-二次函数压轴题考点分类讲解与真题汇编A 类：特殊四边形问题 一、平行四边形典例讲解1．（2019·河南省商丘市柘城中学初三期中）如图，二次函数2y ax bx =+的图象过点13A -（，）、顶点B 的横坐标为.（1）求这个二次函数的解析式；（2）点P 在该一次函数的图象上，点Q 在x 轴上，若以,,,A B P Q 为顶点的四边形是平行四边形，求点P 的坐标。

【答案】（1）22y x x =-；（2）点P 坐标为(13,2),(13,2),(15,4)+-+和(15,4)- 【分析】分两类：①当AB 为对角线时②当AB 为边时 【详解】二次函数22y x x =-;（2）由（1）得，(11),(1,3)B A --,∴直线AB 解析式为21y x =-+，25AB =，设点()2(,0),,2Q m P n n n -，∵以A B P Q ，，，为顶点的四边形是平行四边形，①当AB 为对角线时，根据中点坐标公式得:202212m n n n +⎧=⎪⎪⎨-⎪=⎪⎩，解得1313m n ⎧=--⎪⎨=+⎪⎩或1313m n ⎧=-+⎪⎨=-⎪⎩， (13,2)P ∴+和1(13,2)-；②当AB 为边时，根据中点坐标公式得:2112221322n m n n +-⎧=⎪⎪⎨--⎪=⎪⎩，解得3515m n ⎧=+⎪⎨=+⎪⎩或3515m n ⎧=-⎪⎨=-⎪⎩， (15,4)P ∴+或(15,4)-,综上所述，点P 坐标为(13,2),(13,2),(15,4)+-+和(15,4)-.迁移运用 提示：找菱形先找等腰三角形2．（2020·重庆中考真题）如图，在平面直角坐标系中，已知抛物线2y x bx c =++与直线AB 相交于A ，B 两点，其中()3,4A --，()0,1B -． （1）求该抛物线的函数表达式；（2）将该抛物线向右平移2个单位长度得到抛物线()211110y a x b x c a =++≠，平移后的抛物线与原抛物线相交于点C ，点D 为原抛物线对称轴上的一点，在平面直角坐标系中是否存在点E ，使以点B ，C ，D ，E 为顶点的四边形为菱形，若存在，请直接写出点E 的坐标；若不存在，请说明理由．二、正方形3．（2020·河北省初三其他）如图1．在平面直角坐标系xOy 中，抛物线2:C y ax bx c =++与x 轴相交于,A B 两点，顶点为()0,442D AB =,，设点(),0F m 是x 轴的正半轴上一点，将抛物线C 绕点F 旋转180︒，得到新的抛物线'C ．（1）求抛物线C 的函数表达式:（2）如图2，P 是第一象限内抛物线C 上一点，它到两坐标轴的距离相等，点P 在抛物线'C 上的对应点P'，设M 是C 上的动点，N 是'C 上的动点，试探究四边形'PMP N 能否成为正方形？若能，求出m 的值；若不能，请说明理由． 【答案】()12142y x =-+；()2222m <<；()3四边形'PMP N可以为正方形，6m =【分析】（3）由题意设(),P n n ，代入解出n ，并作HK OF ⊥，PH HK ⊥于H ，利用正方形性质以及全等三角形性质得出M 为()2,2m m --，将M 代入21: 42C y x =-+即可求得答案. 解：（2）四边形'PMP N 可以为正方形 由题意设(),P n n ，P 是抛物线C 第一象限上的点2142n n ∴-+= 解得:122,2n n ==-(舍去)即()2,2P 如图作HK OF ⊥，PH HK ⊥于H ，MK HK ⊥于K四边形PMP N '为正方形 易证PHK FKM ≌2FK HP m ∴==-2MK HF ==M ∴为()2,2m m --∴将M 代入21: 42C y x =-+得()212242m m -=--+ 解得:126,0m m ==(舍去)∴当6m =时四边形PMP N ''为正方形.迁移运用要点：等腰RT 三角形》正方形4．（2020·江苏省初三其他）如图，已知二次函数212y x bx =+的图像经过点()4,0A -，顶点为B 一次函数122y x =+的图像交y 轴于点,M P 是抛物线上-一点，点M 关于直线AP 的对称点N 恰好落在抛物线的对称轴直线BH 上（对称轴直线BH 与x 轴交于点H ）．（1）求二次函数的表达式； （2）求点P 的坐标；（选做）（3）若点G 是第二象限内抛物线上一点，G 关于抛物线的对称轴的对称点是E ，连接OG ，点F 是线段OG 上一点，点D 是坐标平面内一点，若四边形BDEF 是正方形，求点G 的坐标．B类：特殊三角形一、直角三角形5．（2020·辽宁省初三二模）如图，已知抛物线y=ax2+bx+c(a≠0)的顶点坐标为Q(2，-1)，且与y轴交于点C(0，3)，与x轴交于A，B两点(点A在点B的右侧)，点P是该抛物线上的一动点，从点C沿抛物线向点A运动(点P与A不重合)，过点P作PD∥y轴，交AC于点D．(1)求该抛物线的函数关系式；(2)当△ADP是直角三角形时，求点P的坐标；【答案】(1) y=x2﹣4x+3；(2) P1（1，0），P2（2，﹣1）；【分析】（2）由于PD∥y轴，所以∠ADP≠90°，若△ADP是直角三角形，可考虑两种情况：①以点P为直角顶点，此时AP⊥DP，此时P点位于x轴上（即与B点重合），由此可求出P点的坐标；②以点A为直角顶点，易知OA=OC，则∠OAC=45°，所以OA平分∠CAP，那么此时D、P关于x轴对称，可求出直线AC的解析式，然后设D、P的横坐标，根据抛物线和直线AC的解析式表示出D、P的纵坐标，由于两点关于x轴对称，则纵坐标互为相反数，可据此求出P点的坐标；】（2）分两种情况：①当点P 1为直角顶点时，点P 1与点B 重合；令y=0，得x 2﹣4x+3=0，解得x 1=1，x 2=3；∵点A 在点B 的右边， ∴B （1，0），A （3，0）； ∴P 1（1，0）；②当点A 为△AP 2D 2的直角顶点时； ∵OA=OC ，∠AOC=90°， ∴∠OAD 2=45°；当∠D 2AP 2=90°时，∠OAP 2=45°， ∴AO 平分∠D 2AP 2； 又∵P 2D 2∥y 轴， ∴P 2D 2⊥AO ， ∴P 2、D 2关于x 轴对称；设直线AC 的函数关系式为y=kx+b （k ≠0）．将A （3，0），C （0，3）代入上式得：303k b b +=⎧⎨=⎩， 解得13k b =-⎧⎨=⎩；∴y=﹣x+3；设D 2（x ，﹣x+3），P 2（x ，x 2﹣4x+3）， 则有：（﹣x+3）+（x 2﹣4x+3）=0， 即x 2﹣5x+6=0；解得x 1=2，x 2=3（舍去）；∴当x=2时，y=x 2﹣4x+3=22﹣4×2+3=﹣1；∴P 2的坐标为P 2（2，﹣1）（即为抛物线顶点）．∴P 点坐标为P 1（1，0），P 2（2，﹣1）；迁移运用6．（2020·四川省初三其他）如图，已知抛物2(0)y ax bx c a =++≠经过点,A B ，与y 轴负半轴交于点C ，且OC OB =，其中B 点坐标为(3,0)，对称轴l 为直线12x =．(1)求抛物线的解析式；(2) 在x 轴上方有一点P ，连接PA 后满足PAB CAB ∠=∠，记PBC ∆的面积为S ，求当10.5S =时点P 的坐标(3)在(2)的条件下，当点P 恰好落在抛物线上时，将直线BC 上下平移，平移后的10.5S =时点P 的坐标；直线y x t =+与抛物线交于,C B ''两点(C '在B '的左侧)，若以点,,C B P ''为顶点的三角形是直角三角形，求出t 的值．二、等腰三角形7．（2020·河南省初三其他）如图，若抛物线y ＝x 2+bx+c 与x 轴相交于A ，B 两点，与y 轴相交于点C ，直线y ＝x ﹣3经过点B ，C ．（1）求抛物线的解析式；（2）点P 是直线BC 下方抛物线上一动点，过点P 作PH ⊥x轴于点H ，交BC 于点M ，连接PC ．在点P 运动的过程中，是否存在点M ，恰好使△PCM 是以PM 为腰的等腰三角形？如果存在，请直接写出点P 的坐标；如果不存在，请说明理由．【答案】（1）y ＝x 2﹣2x ﹣3；（2）存在，(2，﹣3)或(3﹣2，2﹣42) 【分析】（2）②分PM ＝PC 、PM ＝MC 两种情况，分别求解即可． 【详解】 解：（2）设：点M （x ，x ﹣3），则点P （x ，x 2﹣2x ﹣3）， ②存在，理由：PM 2＝（x ﹣3﹣x 2+2x+3）2＝（﹣x 2+3x ）2；PC 2＝x 2+（x 2﹣2x ﹣3+3）2； MC 2＝（x ﹣3+3）2+x 2；（Ⅰ）当PM ＝PC 时，则（﹣x 2+3x ）2＝x 2+（x 2﹣2x ﹣3+3）2， 解得：x ＝0或2（舍去0）， 故x ＝2，故点P （2，﹣3）；（Ⅱ）当PM ＝MC 时，则（﹣x 2+3x ）2＝（x ﹣3+3）2+x 2，解得：x ＝0或3±2（舍去0和3+2）， 故x ＝3﹣2，则x 2﹣2x ﹣3＝2﹣42， 故点P （3﹣2，2﹣42）．综上，点P 的坐标为：(2，﹣3)或(3﹣2，2﹣42)．迁移运用（综合）8．（2020·四川省中考真题）如图，已知抛物线2y ax bx c =++经过(2,0)A -，(4,0)B ，(0,4)C 三点．（1）求该抛物线的解析式；（2）经过点B 的直线交y 轴于点D ，交线段AC 于点E ，若5BD DE=．①求直线BD 的解析式；②已知点Q 在该抛物线的对称轴l 上，且纵坐标为1，点P 是该抛物线上位于第一象限的动点，且在l 右侧．点R 是直线BD 上的动点，若PQR 是以点Q 为直角顶点的等腰直角三角形，求点P 的坐标．C 类：最值问题一、面积最值（铅垂线）9．（2020·江门市培英初级中学初三其他）在平面直角坐标系中，二次函数y=ax 2+bx+2的图象与x 轴交于A(﹣3，0)，B(1，0)两点，与y 轴交于点C ． （1）求这个二次函数的关系解析式； （2）求直线AC 的函数解析式；（3）点P 是直线AC 上方的抛物线上一动点，是否存在点P ，使△ACP 的面积最大？若存在，求出点P 的坐标；若不存在，说明理由；【答案】（1）y=﹣23x 2﹣43x+2；（2）223y x =+；（3）存在，(35,22-) 【分析】（3）连接PO ，作PM ⊥x 轴于M ，PN ⊥y 轴于N ，然后求出△ACP 面积的表达式，最后利用二次函数的性质求最值即可． 【详解】 解： （3）存在．如图: 连接PO ，作PM ⊥x 轴于M ，PN ⊥y 轴于N设点P 坐标为（m ，n ）,则n=224233m m --+），PN=-m ，AO=3当x=0时，y=22400233-⨯-⨯+=2，∴点C 的坐标为（0,2），OC=2 ∵PAC PAO PCO ACOS S S S=+-212411322()3223322m m m ⎛⎫=⨯⋅--++⨯⋅--⨯⨯ ⎪⎝⎭ =23m m -- ∵a=-1<0∴函数S △PAC =-m 2-3m 有最大值∴b 当m=()33212-=--⨯-∴当m=32-时，S △PAC 有最大值n=222423435223332322m m ⎛⎫--+=-⨯-⨯+= ⎪⎝⎭∴当△ACP的面积最大时，P的坐标为（35,22-）．二、线段/周长最值（将军饮马模型）10．（2020·四川省中考真题）在平面直角坐标系中，抛物线23y ax bx=++与x轴相交于()30A-,、()B1,0，交y轴于点N，点M抛物线的顶点，对称轴与x轴交于点C．⑴.求抛物线的解析式；⑵.如图1，连接AM,点E是线段AM上方抛物线上的一动点，EF AM⊥于点F；过点E作EH x⊥轴于点H,交AM于点D.点P是y轴上一动点，当EF取最大值时．①.求PD PC+的最小值；②.如图2，Q点是y轴上一动点,请直接写出+1DQ OQ4的最小值．【答案】（1）223y x x=--+；（2）13②52【分析】（2）利用配方法求出M点，求出直线AM的解析式，从而可以得出经过点E且与直线AM平行的直线l解析式，再根据当直线l与抛物线只有一个交点时，EF取最大值，利用根的判别式可求出E点和D 点的坐标，再根据当P,B,D三点共线时，PD+PC有最小值，利用勾股定理即可求出．（3）利用添加辅助线，对线段OQ进行转化，再根据三点共线求出最小值．【详解】1）将A（-3,0）、B（1,0）代入二次函数23y ax bx=++得，9330{30a ba b-+=++=解之得1{2ab=-=-，∴二次函数的解析式为223y x x=--+；（2）①将二次函数223y x x=--+配方得2(1)4y x=-++，∴M（-1,4）设直线AM的解析式为y px q=+，将(3,0),(1,4)A M--代入直线可得，30{4p qp q-+=-+=解得2{6pq==，∴直线AM 的解析式为26y x =+， 过E 作直线l ，平行于直线AM ，且解析式为2y x m =+，∵E 在直线AM 上方的抛物线上， ∴31E x -<<-；当直线l 与AM 距离最大时，EF 取得最大值，∴当l 与抛物线只有一个交点时，EF 取得最大值，将直线l 的解析式代入抛物线得2430x x m ++-=，由题意可得，△=1641(3)0m -⨯-=，经计算得7m =，将7m =代入二次方程可得，2440x x ++=，∴2x =-，即E 点的横坐标为-2，将2x =-代入抛物线得3y =， ∴(2,3)E -， 又∵ED ⊥x 轴，∴2D E x x ==-，将2D x =-代入直线AM ， ∴(2,2)D -， ∵(1,0),(1,0)C B -，∴B 、C 两点关于y 轴对称， ∴PB PC =，∴PC PD PB PD +=+，当P 、B 、D 三点不共线时PB PD BD +>，当P 、B 、D 三点共线时，PB PD BD +=， ∴当P 、B 、D 三点共线时PC+PD 取得最小值，在Rt △BHD 中。

专题16二次函数解答题压轴题（35题）一、解答题1．（2024·内蒙古赤峰·中考真题）如图，是某公园的一种水上娱乐项目．数学兴趣小组对该项目中的数学问题进行了深入研究．下面是该小组绘制的水滑道截面图，如图1，人从点A处沿水滑道下滑至点B处腾空飞出后落入水池．以地面所在的水平线为x轴，过腾空点B与x轴垂直的直线为y轴，O为坐标原点，建立平面直角坐标系．他们把水滑道和人腾空飞出后经过的路径都近似看作是抛物线的一部分．根据测量和调查得到的数据和信息，设计了以下三个问题，请你解决．(1)如图1，点B与地面的距离为2米，水滑道最低点C与地面的距离为78米，点C到点B的水平距离为3米，则水滑道ACB所在抛物线的解析式为______；(2)如图1，腾空点B与对面水池边缘的水平距离12OE 米，人腾空后的落点D与水池边缘的安全距离DE 不少于3米．若某人腾空后的路径形成的抛物线BD恰好与抛物线ACB关于点B成中心对称．①请直接写出此人腾空后的最大高度和抛物线BD的解析式；②此人腾空飞出后的落点D是否在安全范围内？请说明理由（水面与地面之间的高度差忽略不计）；(3)为消除安全隐患，公园计划对水滑道进行加固．如图2，水滑道已经有两条加固钢架，一条是水滑道距地面4米的点M处竖直支撑的钢架MN，另一条是点M与点B之间连接支撑的钢架BM．现在需要在水滑道下方加固一条支撑钢架，为了美观，要求这条钢架与BM平行，且与水滑道有唯一公共点，一端固定在钢架MN上，另一端固定在地面上．请你计算出这条钢架的长度（结果保留根号）．2．（2024·广东深圳·中考真题）为了测量抛物线的开口大小，某数学兴趣小组将两把含有刻度的直尺垂直放置，并分别以水平放置的直尺和竖直放置的直尺为x，y轴建立如图所示平面直角坐标系，该数学小组选择不同位置测量数据如下表所示，设BD 的读数为x ，CD 读数为y ，抛物线的顶点为C ．(1)（Ⅰ）列表：①②③④⑤⑥x023456y 01 2.254 6.259（Ⅱ）描点：请将表格中的(),x y 描在图2中；（Ⅲ）连线：请用平滑的曲线在图2将上述点连接，并求出y 与x 的关系式；(2)如图3所示，在平面直角坐标系中，抛物线()2y a x h k =-+的顶点为C ，该数学兴趣小组用水平和竖直直尺测量其水平跨度为AB ，竖直跨度为CD ，且AB m =，CD n =，为了求出该抛物线的开口大小，该数学兴趣小组有如下两种方案，请选择其中一种方案，并完善过程：方案一：将二次函数()2y a x h k =-+平移，使得顶点C 与原点O 重合，此时抛物线解析式为2y ax =．①此时点B '的坐标为________；②将点B '坐标代入2y ax =中，解得=a ________；（用含m ，n 的式子表示）方案二：设C 点坐标为(),h k ①此时点B 的坐标为________；②将点B 坐标代入()2y a x h k =-+中解得=a ________；（用含m ，n 的式子表示）(3)【应用】如图4，已知平面直角坐标系xOy 中有A ，B 两点，4AB =，且AB x ∥轴，二次函数()211:2C y x h k =++和()222:C y a x h b =++都经过A ，B 两点，且1C 和2C 的顶点P ，Q 距线段AB 的距离之和为10，求a 的值．3．（2024·四川广元·中考真题）在平面直角坐标系xOy 中，已知抛物线F ：2y x bx c =-++经过点()3,1A --，与y 轴交于点()0,2B ．(1)求抛物线的函数表达式；(2)在直线AB 上方抛物线上有一动点C ，连接OC 交AB 于点D ，求CD OD的最大值及此时点C 的坐标；(3)作抛物线F 关于直线1y =-上一点的对称图象F '，抛物线F 与F '只有一个公共点E （点E 在y 轴右侧），G 为直线AB 上一点，H 为抛物线F '对称轴上一点，若以B ，E ，G ，H 为顶点的四边形是平行四边形，求G 点坐标．4．（2024·天津·中考真题）已知抛物线()20y ax bx c a b c a =++>，，为常数，的顶点为P ，且20a b +=，对称轴与x 轴相交于点D ，点(),1M m 在抛物线上，1m O >，为坐标原点．(1)当11a c ==-，时，求该抛物线顶点P 的坐标；(2)当132OM OP ==时，求a 的值；(3)若N 是抛物线上的点，且点N 在第四象限，90MDN DM DN ∠=︒=，，点E 在线段MN 上，点F 在线段DN 上，2NE NF +，当DE MF +15a 的值．5．（2024·内蒙古包头·中考真题）如图，在平面直角坐标系中，抛物线22y x bx c =-++与x 轴相交于()1,0A ，B 两点（点A 在点B 左侧），顶点为()2,M d ，连接AM ．(1)求该抛物线的函数表达式；(2)如图1，若C 是y 轴正半轴上一点，连接,AC CM ．当点C 的坐标为10,2⎛⎫ ⎪⎝⎭时，求证：ACM BAM ∠=∠；(3)如图2，连接BM ，将ABM 沿x 轴折叠，折叠后点M 落在第四象限的点M '处，过点B 的直线与线段AM '相交于点D ，与y 轴负半轴相交于点E ．当87BD DE =时，3ABD S △与2M BD S '△是否相等？请说明理由．6．（2024·吉林·中考真题）小明利用一次函数和二次函数知识，设计了一个计算程序，其程序框图如图（1）所示，输入x 的值为2-时，输出y 的值为1；输入x 的值为2时，输出y 的值为3；输入x 的值为3时，输出y 的值为6．(1)直接写出k ，a ，b 的值．(2)小明在平面直角坐标系中画出了关于x 的函数图像，如图（2）．Ⅰ．当y 随x 的增大而增大时，求x 的取值范围．Ⅱ．若关于x 的方程230ax bx t ++-=（t 为实数），在04x <<时无解，求t 的取值范围．Ⅲ．若在函数图像上有点P ，Q （P 与Q 不重合）．P 的横坐标为m ，Q 的横坐标为1m -+．小明对P ，Q 之间（含P ，Q 两点）的图像进行研究，当图像对应函数的最大值与最小值均不随m 的变化而变化，直接写出m 的取值范围．7．（2024·四川达州·中考真题）如图1，抛物线23y ax kx =+-与x 轴交于点()3,0A -和点()1,0B ，与y 轴交于点C ．点D 是抛物线的顶点．(1)求抛物线的解析式；(2)如图2，连接AC ，DC ，直线AC 交抛物线的对称轴于点M ，若点P 是直线AC 上方抛物线上一点，且2PMC DMC S S =△△，求点P 的坐标；(3)若点N 是抛物线对称轴上位于点D 上方的一动点，是否存在以点N ，A ，C 为顶点的三角形是等腰三角形，若存在，请直接写出满足条件的点N 的坐标；若不存在，请说明理由．8．（2024·四川泸州·中考真题）如图，在平面直角坐标系xOy 中，已知抛物线23y ax bx =++经过点()3,0A ，与y 轴交于点B ，且关于直线1x =对称．(1)求该抛物线的解析式；(2)当1x t -≤≤时，y 的取值范围是021y t ≤≤-，求t 的值；(3)点C 是抛物线上位于第一象限的一个动点，过点C 作x 轴的垂线交直线AB 于点D ，在y 轴上是否存在点E ，使得以B ，C ，D ，E 为顶点的四边形是菱形？若存在，求出该菱形的边长；若不存在，说明理由．9．（2024·四川南充·中考真题）已知抛物线2y x bx c =-++与x 轴交于点()1,0A -，()3,0B ．(1)求抛物线的解析式；(2)如图1，抛物线与y 轴交于点C ，点P 为线段OC 上一点（不与端点重合），直线PA ，PB 分别交抛物线于点E ，D ，设PAD 面积为1S ，PBE △面积为2S ，求12S S 的值；(3)如图2，点K 是抛物线对称轴与x 轴的交点，过点K 的直线（不与对称轴重合）与抛物线交于点M ，N ，过抛物线顶点G 作直线l x ∥轴，点Q 是直线l 上一动点．求QM QN +的最小值．10．（2024·四川成都·中考真题）如图，在平面直角坐标系xOy 中，抛物线L ：()2230y ax ax a a =-->与x轴交于A ，B 两点（点A 在点B 的左侧），其顶点为C ，D是抛物线第四象限上一点．(1)求线段AB 的长；(2)当1a =时，若ACD 的面积与ABD △的面积相等，求tan ABD ∠的值；(3)延长CD 交x 轴于点E ，当AD DE =时，将ADB 沿DE 方向平移得到A EB '' ．将抛物线L 平移得到抛物线L '，使得点A '，B '都落在抛物线L '上．试判断抛物线L '与L 是否交于某个定点．若是，求出该定点坐标；若不是，请说明理由．11．（2024·四川德阳·中考真题）如图，抛物线2y x x c =-+与x 轴交于点()1,0A -和点B ，与y 轴交于点C ．(1)求抛物线的解析式；(2)当02x <≤时，求2y x x c =-+的函数值的取值范围；(3)将拋物线的顶点向下平移34个单位长度得到点M ，点P 为抛物线的对称轴上一动点，求5PA +的最小值．12．（2024·山东·中考真题）在平面直角坐标系xOy 中，点()2,3P -在二次函数()230y ax bx a =+->的图像上，记该二次函数图像的对称轴为直线x m =．(1)求m 的值；(2)若点(),4Q m -在23y ax bx =+-的图像上，将该二次函数的图像向上平移5个单位长度，得到新的二次函数的图像．当04x ≤≤时，求新的二次函数的最大值与最小值的和；(3)设23y ax bx =+-的图像与x 轴交点为()1,0x ，()()212,0x x x <．若2146x x <-<，求a 的取值范围．13．（2024·上海·中考真题）在平面直角坐标系中，已知平移抛物线213y x =后得到的新抛物线经过50,3A ⎛⎫- ⎪⎝⎭和(5,0)B ．(1)求平移后新抛物线的表达式；(2)直线x m =（0m >）与新抛物线交于点P ，与原抛物线交于点Q ．①如果PQ 小于3，求m 的取值范围；②记点P 在原抛物线上的对应点为P '，如果四边形P BPQ '有一组对边平行，求点P 的坐标．14．（2024·四川遂宁·中考真题）二次函数()20y ax bx c a =++≠的图象与x 轴分别交于点()()1,03,0A B -，，与y 轴交于点()0,3C -，P Q ，为抛物线上的两点．(1)求二次函数的表达式；(2)当P C ，两点关于抛物线对称轴对称，OPQ △是以点P 为直角顶点的直角三角形时，求点Q 的坐标；(3)设P 的横坐标为m ，Q 的横坐标为1m +，试探究：OPQ △的面积S 是否存在最小值，若存在，请求出最小值，若不存在，请说明理由．15．（2024·四川凉山·中考真题）如图，抛物线2y x bx c =-++与直线2y x =+相交于()()20,3,A B m -，两点，与x 轴相交于另一点C ．(1)求抛物线的解析式；(2)点P 是直线AB 上方抛物线上的一个动点（不与,A B 重合），过点P 作直线PD x ⊥轴于点D ，交直线AB 于点E ，当2PE ED =时，求P 点坐标；(3)抛物线上是否存在点M 使ABM 的面积等于ABC 面积的一半？若存在，请直接写出点M 的坐标；若不存在，请说明理由．16．（2024·江苏连云港·中考真题）在平面直角坐标系xOy 中，已知抛物线21y ax bx =+-（a 、b 为常数，0a >）．(1)若抛物线与x 轴交于(1,0)A -、(4,0)B 两点，求抛物线对应的函数表达式；(2)如图，当1b =时，过点(1,)C a -、(1,D a +分别作y 轴的平行线，交抛物线于点M 、N ，连接MN MD 、．求证：MD 平分CMN ∠；(3)当1a =，2b ≤-时，过直线1(13)y x x =-≤≤上一点G 作y 轴的平行线，交抛物线于点H ．若GH 的最大值为4，求b 的值．17．（2024·江苏苏州·中考真题）如图①，二次函数2y x bx c =++的图象1C 与开口向下．．．．的二次函数图象2C 均过点()1,0A -，()3,0B ．(1)求图象1C 对应的函数表达式；(2)若图象2C 过点()0,6C ，点P 位于第一象限，且在图象2C 上，直线l 过点P 且与x 轴平行，与图象2C 的另一个交点为Q （Q 在P 左侧），直线l 与图象1C 的交点为M ，N （N 在M 左侧）．当PQ MP QN =+时，求点P 的坐标；(3)如图②，D ，E 分别为二次函数图象1C ，2C 的顶点，连接AD ，过点A 作AF AD ⊥．交图象2C 于点F ，连接EF ，当EF AD ∥时，求图象2C 对应的函数表达式．18．（2024·内蒙古呼伦贝尔·中考真题）如图，在平面直角坐标系中，二次函数()20y ax bx c a =++≠的图像经过原点和点()4,0A ．经过点A 的直线与该二次函数图象交于点()1,3B ，与y 轴交于点C ．(1)求二次函数的解析式及点C 的坐标；(2)点P 是二次函数图象上的一个动点，当点P 在直线AB 上方时，过点P 作PE x ⊥轴于点E ，与直线AB 交于点D ，设点P 的横坐标为m ．①m 为何值时线段PD 的长度最大，并求出最大值；②是否存在点P ，使得BPD △与AOC 相似．若存在，请求出点P 坐标；若不存在，请说明理由．19．（2024·山东威海·中考真题）已知抛物线()20y x bx c b =++<与x 轴交点的坐标分别为()1,0x ，()2,0x ，且12x x <．(1)若抛物线()2110y x bx c b =+++<与x 轴交点的坐标分别为()3,0x ，()4,0x ，且34x x <．试判断下列每组数据的大小（填写<、=或>）：①12x x +________34x x +；②13x x -________24x x -；③23x x +________14x x +．(2)若11x =，223x <<，求b 的取值范围；(3)当01x ≤≤时，()20y x bx c b =++<最大值与最小值的差为916，求b 的值．20．（2024·河北·中考真题）如图，抛物线21:2C y ax x =-过点(4,0)，顶点为Q ．抛物线22211:()222C y x t t =--+-（其中t 为常数，且2t >），顶点为P ．(1)直接写出a 的值和点Q 的坐标．(2)嘉嘉说：无论t 为何值，将1C 的顶点Q 向左平移2个单位长度后一定落在2C 上．淇淇说：无论t 为何值，2C 总经过一个定点．请选择其中一人的说法进行说理．(3)当4t =时，①求直线PQ 的解析式；②作直线l PQ ∥，当l 与2C 的交点到x 轴的距离恰为6时，求l 与x 轴交点的横坐标．(4)设1C 与2C 的交点A ，B 的横坐标分别为,A B x x ，且A B x x <．点M 在1C 上，横坐标为()2B m m x ≤≤．点N 在2C 上，横坐标为()A n x n t ≤≤．若点M 是到直线PQ 的距离最大的点，最大距离为d ，点N 到直线PQ 的距离恰好也为d ，直接用含t 和m 的式子表示n ．21．（2024·四川宜宾·中考真题）如图，抛物线2y x bx c =++与x 轴交于点()1,0A -和点B ，与y 轴交于点()0,4C -，其顶点为D ．(1)求抛物线的表达式及顶点D 的坐标；(2)在y 轴上是否存在一点M ，使得BDM 的周长最小．若存在，求出点M 的坐标；若不存在，请说明理由；(3)若点E 在以点()3,0P 为圆心，1为半径的P 上，连接AE ，以AE 为边在AE 的下方作等边三角形AEF ，连接BF ．求BF 的取值范围．22．（2024·湖南·中考真题）已知二次函数2y x c =-+的图像经过点()2,5A -，点()11,P x y ，()22,Q x y 是此二次函数的图像上的两个动点．(1)求此二次函数的表达式；(2)如图1，此二次函数的图像与x 轴的正半轴交于点B ，点P 在直线AB 的上方，过点P 作PC x ⊥轴于点C ，交AB 于点D ，连接AC DQ PQ ,,．若213x x =+，求证DCPDQ A S S △△的值为定值；(3)如图2，点P 在第二象限，212x x =-，若点M 在直线PQ 上，且横坐标为11x -，过点M 作MN x ⊥轴于点N ，求线段MN 长度的最大值．23．（2024·四川乐山·中考真题）在平面直角坐标系xOy 中，我们称横坐标、纵坐标都为整数的点为“完美点”．抛物线222y ax ax a =-+（a 为常数且0a >）与y 轴交于点A．(1)若1a =，求抛物线的顶点坐标；(2)若线段OA （含端点）上的“完美点”个数大于3个且小于6个，求a 的取值范围；(3)若抛物线与直线y x =交于M 、N 两点，线段MN 与抛物线围成的区域（含边界）内恰有4个“完美点”，求a 的取值范围．24．（2024·四川眉山·中考真题）如图，抛物线2y x bx c =-++与x 轴交于点()3,0A -和点B ，与y 轴交于点()0,3C ，点D 在抛物线上．(1)求该抛物线的解析式；(2)当点D 在第二象限内，且ACD 的面积为3时，求点D 的坐标；(3)在直线BC 上是否存在点P ，使OPD △是以PD 为斜边的等腰直角三角形？若存在，请直接写出点P 的坐标；若不存在，请说明理由．25．（2024·黑龙江绥化·中考真题）综合与探究如图，在平面直角坐标系中，已知抛物线2y x bx c =-++与直线相交于A ，B 两点，其中点()3,4A ，()0,1B ．(1)求该抛物线的函数解析式．(2)过点B 作BC x ∥轴交抛物线于点C ，连接AC ，在抛物线上是否存在点P 使1tan tan 6BCP ACB ∠=∠．若存在，请求出满足条件的所有点P 的坐标；若不存在，请说明理由．（提示：依题意补全图形，并解答）(3)将该抛物线向左平移2个单位长度得到()2111110y a x b x c a =++≠，平移后的抛物线与原抛物线相交于点D ，点E 为原抛物线对称轴上的一点，F 是平面直角坐标系内的一点，当以点B 、D 、E 、F 为顶点的四边形是菱形时，请直接写出点F 的坐标．26．（2024·黑龙江齐齐哈尔·中考真题）综合与探究：如图，在平面直角坐标系中，已知直线122y x =-与x 轴交于点A ，与y 轴交于点C ，过A ，C 两点的抛物线()20y ax bx c a =++≠与x 轴的另一个交点为点(10)B -，，点P 是抛物线位于第四象限图象上的动点，过点P 分别作x 轴和y 轴的平行线，分别交直线AC 于点E ，点F ．(1)求抛物线的解析式；(2)点D 是x 轴上的任意一点，若ACD 是以AC 为腰的等腰三角形，请直接写出点D 的坐标；(3)当EF AC =时，求点P 的坐标；(4)在（3）的条件下，若点N 是y 轴上的一个动点，过点N 作抛物线对称轴的垂线，垂足为M ，连接NA MP ，，则NA MP +的最小值为______．27．（2024·重庆·中考真题）如图，在平面直角坐标系中，抛物线23y ax bx =+-与x 轴交于()1,0A -，B 两点，交y 轴于点C ，抛物线的对称轴是直线52x =．(1)求抛物线的表达式；(2)点P 是直线BC 下方对称轴右侧抛物线上一动点，过点P 作PD x ∥轴交抛物线于点D ，作PE BC ⊥于点E ，求52PD PE +的最大值及此时点P 的坐标；(3)将抛物线沿射线BC 552PD PE +取得最大值的条件下，点F 为点P 平移后的对应点，连接AF 交y 轴于点M ，点N 为平移后的抛物线上一点，若45NMF ABC ∠-∠=︒，请直接写出所有符合条件的点N 的坐标．28．（2024·重庆·中考真题）如图，在平面直角坐标系中，抛物线()240y ax bx a =++≠经过点()1,6-，与y轴交于点C ，与x 轴交于A B ，两点（A 在B 的左侧），连接tan 4AC BC CBA ∠=，，．(1)求抛物线的表达式；(2)点P 是射线CA 上方抛物线上的一动点，过点P 作PE x ⊥轴，垂足为E ，交AC 于点D ．点M 是线段DE 上一动点，MN y ⊥轴，垂足为N ，点F 为线段BC 的中点，连接AM NF ，．当线段PD 长度取得最大值时，求AM MN NF ++的最小值；(3)将该抛物线沿射线CA 方向平移，使得新抛物线经过（2）中线段PD 长度取得最大值时的点D ，且与直线AC 相交于另一点K ．点Q 为新抛物线上的一个动点，当QDK ACB ∠∠=时，直接写出所有符合条件的点Q 的坐标．29．（2024·广东广州·中考真题）已知抛物线232:621(0)G y ax ax a a a =--++>过点()1,2A x 和点()2,2B x ，直线2:l y m x n =+过点(3,1)C ，交线段AB 于点D ，记CDA 的周长为1C ，CDB △的周长为2C ，且122C C =+．(1)求抛物线G 的对称轴；(2)求m 的值；(3)直线l 绕点C 以每秒3︒的速度顺时针旋转t 秒后(045)t ≤<得到直线l '，当l AB '∥时，直线l '交抛物线G 于E ，F 两点．①求t 的值；②设AEF △的面积为S ，若对于任意的0a >，均有S k ≥成立，求k 的最大值及此时抛物线G 的解析式．30．（2024·四川广安·中考真题）如图，抛物线223y x bx c =-++与x 轴交于A ，B 两点，与y 轴交于点C ，点A 坐标为(1,0)-，点B 坐标为(3,0)．(1)求此抛物线的函数解析式．(2)点P 是直线BC 上方抛物线上一个动点，过点P 作x 轴的垂线交直线BC 于点D ，过点P 作y 轴的垂线，垂足为点E ，请探究2PD PE +是否有最大值？若有最大值，求出最大值及此时P 点的坐标；若没有最大值，请说明理由．(3)点M 为该抛物线上的点，当45∠=︒MCB 时，请直接写出所有满足条件的点M 的坐标．31．（2024·山东烟台·中考真题）如图，抛物线21y ax bx c =++与x 轴交于A ，B 两点，与y 轴交于点C ，OC OA =，4AB =，对称轴为直线1:1l x =-，将抛物线1y 绕点O 旋转180︒后得到新抛物线2y ，抛物线2y 与y 轴交于点D ，顶点为E ，对称轴为直线2l ．(1)分别求抛物线1y 和2y 的表达式；(2)如图1，点F 的坐标为()6,0-，动点M 在直线1l 上，过点M 作MN x ∥轴与直线2l 交于点N ，连接FM ，DN ．求FM MN DN ++的最小值；(3)如图2，点H 的坐标为()0,2-，动点P 在抛物线2y 上，试探究是否存在点P ，使2PEH DHE ∠=∠？若存在，请直接写出所有符合条件的点P 的坐标；若不存在，请说明理由．32．（2024·甘肃·中考真题）如图1，抛物线()2y a x h k =-+交x 轴于O ，()4,0A 两点，顶点为(2,B ．点C 为OB 的中点．(1)求抛物线2()y a x h k =-+的表达式；(2)过点C 作CH OA ⊥，垂足为H ，交抛物线于点E ．求线段CE 的长．(3)点D 为线段OA 上一动点（O 点除外），在OC 右侧作平行四边形OCFD ．①如图2，当点F 落在抛物线上时，求点F 的坐标；②如图3，连接BD ，BF ，求BD BF +的最小值．33．（2024·湖北·中考真题）如图1，二次函数23y x bx =-++交x 轴于()1,0A -和B ，交y 轴于C ．(1)求b 的值．(2)M 为函数图象上一点，满足MAB ACO ∠=∠，求M 点的横坐标．(3)如图2，将二次函数沿水平方向平移，新的图象记为,L L 与y 轴交于点D ，记DC d =，记L 顶点横坐标为n ．①求d 与n 的函数解析式．②记L 与x 轴围成的图象为,U U 与ABC 重合部分（不计边界）记为W ，若d 随n 增加而增加，且W 内恰有2个横坐标与纵坐标均为整数的点，直接写出n 的取值范围．34．（2024·湖北武汉·中考真题）抛物线215222y x x =+-交x 轴于A ，B 两点（A 在B 的右边），交y 轴于点C ．(1)直接写出点A ，B ，C 的坐标；(2)如图（1），连接AC ，BC ，过第三象限的抛物线上的点P 作直线PQ AC ∥，交y 轴于点Q ．若BC 平分线段PQ ，求点P 的坐标；(3)如图（2），点D 与原点O 关于点C 对称，过原点的直线EF 交抛物线于E ，F 两点（点E 在x 轴下方），线段DE 交抛物线于另一点G ，连接FG ．若90EGF ∠=︒，求直线DE 的解析式．35．（2024·吉林长春·中考真题）在平面直角坐标系中，点O 是坐标原点，抛物线22y x x c =++（c 是常数）经过点()2,2--．点A 、B 是该抛物线上不重合的两点，横坐标分别为m 、m -，点C 的横坐标为5m -，点C 的纵坐标与点A 的纵坐标相同，连结AB 、AC ．(1)求该抛物线对应的函数表达式；(2)求证：当m 取不为零的任意实数时，tan CAB ∠的值始终为2；(3)作AC 的垂直平分线交直线AB 于点D ，以AD 为边、AC 为对角线作菱形ADCE ，连结DE ．①当DE 与此抛物线的对称轴重合时，求菱形ADCE 的面积；②当此抛物线在菱形ADCE 内部的点的纵坐标y 随x 的增大而增大时，直接写出m 的取值范围．。

2024年中考数学高频压轴题训练——二次函数压轴题（角度问题）（1）求抛物线的解析式；（2）抛物线上是否存在点，使P存在，请说明理由．(1)求该抛物线的函数表达式；(2)在直线上是否存在点，使说明理由．(3)为第一象限内抛物线上的一个动点，且在直线，垂足为，以点为圆心，，且不经过点l C P PM l ⊥M M 2PAB PT S =V M e (4．如图，已知顶点为的抛物线与x 轴交于A ，B 两点，且．(1)求点B 的坐标；(2)求二次函数的解析式；(3)作直线，问抛物线上是否存在点M ，使得，若存在，求出点M 的坐标；若不存在，请说明理由．5．如图，抛物线与x 轴交于A 、B 两点，，，与y 轴交于点C ，连接．()0,6C -()20y ax b a =+≠OC OB =()20y ax b a =+≠CB ()20y ax b a =+≠15MCB ∠=︒24y ax bx =+-()2,0A -()8,0B AC BC 、(1)求抛物线的解析式；(2)求证：；(3)点P 在抛物线上，且，求点P的坐标．6．如图，在平面直角坐标系中，已知抛物线与x 轴交于、两点，与y 轴交于点C ，连接．(1)求抛物线的解析式；(2)在对称轴上是否存在一点M ，使，若存在，请求出点M 的坐标；若不存在，请说明理由；(3)若点P 是直线下方的抛物线上的一个动点，作于点D ，当的值最大时，求此时点P 的坐标及的最大值．∠=∠ACO ABC PCB ACO ∠=∠()230y ax bx a =+-≠()3,0A ()1,0B -AC MCA MAC ∠=∠AC PD AC ⊥PD PD(1)试求抛物线的解析式；(2)点P 是直线下方抛物线上一动点，当的面积最大时，求点P 的坐标；(3)若M 是抛物线上一点，且，请直接写出点M 的坐标．BC BCP V MCB ABC ∠=∠(1)求此抛物线的解析式；(2)点E 是AC 延长线上一点，的平分线CD 交⊙于点D ，连接BD ，求点D 的坐标；(3)在（2）的条件下，抛物线上是否存在点P ，使得？如果存在，请求出点P 的坐标；如果不存在，请说明理由．9．综合与实践：如图，抛物线与x 轴交于点和点，与y 轴交于点C ，连接，点D 在抛物线上．(1)求抛物线的解析式；(2)小明探究点D 位置时发现：如图1，点D 在第一象限内的抛物线上，连接，，面积存在最大值，请帮助小明求出面积的最大值；(3)小明进一步探究点D 位置时发现：点D 在抛物线上移动，连接，存在BCE ∠O 'PDB CBD ∠=∠22y ax bx =++()1,0A -()4,0B BC BD CD BCD △BCD △CD(1)求抛物线的解析式．(2)如图1，过点D 作轴，垂足为M ，点P 在直线P 作，，求的最大值，以及此时点(3)将原抛物线沿射线方向平移个单位长度，在平移后的抛物线上存在点得，请写出所有符合条件的点G 的横坐标，并写出其中一个的求解过DM x ⊥PE AD ⊥PF DM ⊥2PE PF +CA 5245CAG ∠=︒(1)填空：___________，___________；(2)点为直线上方抛物线上一动点．①连接、，设直线交线段于点，求的最大值；②过点作于点，连接，是否存在点，使得中的，若存在，求出点的坐标；若不存在，请说明理由．(1)求抛物线的解析式；b =c =D AC BC CD BD AC E DE EBD DF AC ⊥F CD D CDF V 2DCF BAC ∠=∠D(1)求抛物线的解析式；(2)抛物线上是否存在点D ，使得？若存在，求出所有点不存在，请说明理由；(3)如图2，点E 是点B 关于抛物线对称轴的对称点，点F 是直线OB 动点，EF 与直线OB 交于点G ．设和的面积分别为值．DOB OBC ∠=∠BFG V BEG V S14．如图，在平面直角坐标系中，点为坐标原点，抛物线与轴交于、两点且点，，与轴的负半轴交于点，．(1)求此抛物线的解析式；(2)在(1)的条件下，连接，点为直线下方的抛物线上的一点，过点作交于点，交直线于点，若，求点的坐标．(3)在(1)的条件下，点为该抛物线的顶点，过点作轴的平行线交抛物线于另一点，过点作于点，该抛物线对称轴右侧的抛物线上有一点，连接交于点，当时，求的度数．15．已知抛物线与轴相交于点，，与轴相交于点．O 2y x bx c =++x A B (3B 0)y C OB OC =AC P BC P PQ AC ∥AB Q BC D PD DQ =P D C x R R RH AB ⊥H M DM RH Q 2MQ RQ =MQH ∠24y ax bx =++x ()1,0A ()4,0B y C参考答案：的值最大时，此时，。

1、抛物线y=ax2+bx+c与x轴交于A、B两点，与y轴交于点C，若OB=OC=2OA，则下列结论一定成立的是：A. b < 0B. a+b+c = 0C. 2b2 - 9ac = 0D. a-b+c = 0（答案：C）2、已知二次函数y=ax2+bx+c的图像经过点A(-1,0)，B(3,0)，C(0,-3)，则当y随x的增大而减小时，x的取值范围是：A. x < -1B. x > 3C. -1 < x < 3D. x < -1 或x > 3（答案：D）3、二次函数y=ax2+bx+c的图像开口向上，顶点在x轴上，且图像不经过第三象限，则a，b，c满足：A. a > 0，b2 - 4ac = 0，c < 0B. a < 0，b2 - 4ac = 0，c > 0C. a > 0，b2 - 4ac = 0，c > 0D. a < 0，b2 - 4ac > 0，c < 0（答案：A）4、抛物线y=ax2+bx+c与直线y=x+1交于A、B两点，且A点的横坐标为-2，若抛物线的对称轴是直线x=2，则线段AB的长为：A. 3B. 4C. 5D. 6（答案：D）5、已知二次函数y=ax2+bx+c的图像与x轴交于点A、B，与y轴交于点C，若AC=BC，则下列结论一定成立的是：A. b=2aB. b=-2aC. c=2aD. c=-2a（答案：B）6、二次函数y=ax2+bx+c的图像经过点A(1,0)，B(0,3)，且对称轴是直线x=2，则当y=0时，x的另一个值是：A. 3B. 4C. 5D. 6（答案：A）7、已知二次函数y=ax2+bx+c的图像与x轴交于A、B两点，且AB=4，若点A的坐标为(-1,0)，则点B的坐标为：A. (3,0)B. (-5,0)C. (3,0)或(-5,0)D. 无法确定（答案：C）8、抛物线y=ax2+bx+c与x轴交于A、B两点，与y轴交于点C，若△ABC是等腰直角三角形，且OB=OC，则b的值为：A. 1B. 2C. -1D. ±2（答案：D）。