工科数学分析18-2

张宇高数18讲数学二知识点总结笔记●1.函数极限与连续1)函数极限的定义及使用●定义●使用●是常数、唯一性、局部有界性、局部保号性●等式脱帽法2)函数极限的计算●化简先行●等价无穷小替换●恒等变形●及时提出极限存在且不为0的因式●洛必达法则●泰勒公式●熟记常用公式●展开原则●无穷小比阶●函数极限的存在性●具体性●若洛必达失效，用夹逼准则●抽象性●单调有界准则●连续与间断●研究位置●无定义点、分段函数的分段点●连续●内点处、端点处●间断●2.数列极限1)数列极限的定义及使用●定义●使用●是常数、唯一性、有界性、保号性●收敛的充要条件2)数列极限的存在性与计算●海涅定理的使用●直接计算法●定义法（先斩后奏法）●单调有界准则●用已知不等式●题设给出条件来推证●夹逼准则●用基本放缩法●题设给出条件来推证●综合题总结●用导数、积分、中值定理综合●用方程列、区间列综合●用极限综合●3.一元微分的概念1)导数定义（导数在一点的问题）●分段函数（或含绝对值函数）在分段点●抽象函数在一点●特指点x_0●泛指点x●四则运算中的特殊点●太复杂的函数●f=f_1+f_2●f=f_1* f_2* f_3* ...*●求导公式无定义的点2)微分定义●4.一元微分的计算1)复合函数求导2)隐函数求导3)反函数求导4)分段函数求导（含绝对值）●在分段点用导数定义●在非分段点用导数公式●对数求导法●幂指函数求导法●参数方程确定的函数求导●高阶导数●归纳法（记公式）●莱布尼茨公式●展开式（记公式）5)难点●计算量大●含参数的讨论●高阶导数●5.一元微分的几何应用1)研究对象●“祖孙三代”●f(x)●具体●抽象●f_n(x) 函数族●f_1·f_2·...·f_n● f'(x) ； \frac{\mathrm{d}[f(x)]}{\mathrm{d}{(x^2)}} ; {f}^{(n)}(x)●\int_{a}^{x}f(x)dx●分段函数（含绝对值）●参数方程●x=x(t), y=y(t)●x=r(\theta)cos\theta,y=r(\theta)sin\theta●隐函数F(x,y)=02)研究内容●切线、法线、截距●极值、单调性●单调性的判别●一阶可导点是极值点的必要条件●判别极值的第1,2,3充分条件●拐点、凹凸性●凹凸性的定义●拐点定义●凹凸性与拐点的判别●判别凹凸性的充分必要条件●二阶可导点是拐点的必要条件●判别拐点的第1,2,3充分条件●6.中值定理、微分等式与微分不等式1)中值定理●确定区间●确定辅助函数●确定使用的定理●零点定理●介值定理●费马定理●罗尔定理●拉格朗日中值定理●泰勒公式●柯西中值定理2)微分等式问题●理论依据●考法3)微分不等式问题●用单调性●用最值●用凹凸性●用拉格朗日中值定理●用柯西中值定理●用带有拉格朗日余项的泰勒公式●7.一元微分物理应用1)物理应用●以“A对B的变化率”为核心写\frac{\mathrm{d}A}{\mathrm{d}B}●8.一元积分的概念与性质1)祖孙三代●\int_{a}^{x}f(x)dx ，f(x)，{ f^{'}(x) } 的奇偶性，周期性2)积分比大小●用几何意义●看面积大小●用保号性●做差●看正负3)定积分定义●基本形（能凑成\frac{i}{n}）●\lim_{n \to \infty}\sum_{i=1}^n f(0+\frac{1-0}{n}i)\frac{1-0}{n} =\int_{0}^{1}f(x)dx●\lim_{n \to \infty}\sum_{i=0}^{n-1} f(0+\frac{1-0}{n}i)\frac{1-0}{n} =\int_{0}^{1}f(x)dx●放缩形（凑不成\frac{i}{n}）●夹逼准则●放缩后再凑\frac{i}{n}●变量形●\lim_{n \to \infty}\sum_{i=1}^n f(0+\frac{x-0}{n}i)\frac{x-0}{n} =\int_{0}^{x}f(x)dx4)反常积分的判敛●概念●判别●9.一元积分的计算1)基本积分公式2)不定积分的计算●凑微分法●思想●方法●常用的凑微分公式●程序●换元法●思想●方法●三角函数代换●恒等变形后作三角代换●跟式代换●倒代换●复杂函数的直接带换●思想●方法●u,v的选取原则●推广公式（表格法）●有理函数的积分●定义●思想●方法3)定积分的计算●区间再现公式●华里士公式●其他常用含三角函数的积分等式●区间简化公式●对称性下的积分问题●定积分分部积分法中的“升阶”降阶“”公式●分段函数的定积分●10.一元积分几何应用1)研究对象●f(x)●f_n(x)●参数方程●x=x(t)●y=y(t)●\frac{\partial f}{\partial x}●\int_{a}^{x}f(x)dx●微分方程的解函数f(x)2)研究内容●面积、旋转体体积、平均值●平面曲线的弧长、旋转曲面的面积（侧面积）●“平面上的曲边梯形”的形心坐标公式●平行截面面积为已知的立体体积●11.积分等式与积分不等式1)积分等式●通过证明某特殊积分等式求某特殊积分●积分形式的中值定理2)积分不等式●用函数的单调性●处理被积函数●已知f(x) \leq g(x)，用积分保号性证得\int_{a}^{b}f(x)dx \leq\int_{a}^{b}g(x)dx，a<b●用拉格朗日中值定理●用泰勒公式●用放缩法●用分部积分法●用换元法●用夹逼准则求解一类积分的极限问题●曲边梯形面积的连续化与离散化问题●12.一元积分的物理应用1)位移大小与总路程●位移大小●\int_{t_1}^{t_2}v(t)dt●总路程●\int_{t_1}^{t_2}|v(t)|dt2)变力沿直线做功●W=\int_{a}^{b}F(x)dx3)提取物体做功●W=\rho g\int_{a}^{b}xA(x)dx4)静水压力●P=\rho g\int_{a}^{b}x[f(x)-h(x)]dx5)细杆质心●\bar x=\frac{\int_{a}^{b}x\rho (x)dx}{\int_{a}^{b}\rho (x)dx}6)其他重要应用（微元法总结）●13.多元函数微分学1)概念●极限、连续、偏导数、可微2)复合函数求导法●链式求导规则●全导数●全微分形式不变3)隐函数求导●隐函数存在定理●一个方程的情形●方程组的情形4)多元函数的极值、最值●无条件极值●取极值的必要条件●取极值的充分条件●条件极值与拉氏乘数法5)偏微分方程●已知偏导数（或偏增量）的表达式，求z=f(x,y)●给出变换，化已知偏微分方程为常微分方程，求f(u)●给出变换，化已知偏微分方程为指定偏微分方程及其反问题●14.二重积分1)概念●和式极限●普通对称性●轮换对称性●二重积分比大小●用对称性●用保号性●二重积分中值定理●周期性2)计算●直角坐标系与换序●极坐标系与换序●直极互化3)应用●面积●\iint_{D}dxdy●15.微分方程1)一阶微分方程的求解●能写成 y'=f(x)·g(x)●能写成 y'=f(ax+by+c)●能写成 y'=f(\frac{y}{x})●能写成 \frac{1}{y'}=f(\frac{x}{y})●能写成 y'+p(x)y=q(x)2)二阶可降阶微分方程的求解●能写成 y''=f(x,y')●能写成 y''=f(y,y')3)高阶常系数线性微分方程的求解●能写成 y''+py'+qy=f(x)●能写成 y''+py'+qy=f_1(x)+f_2(x)4)用换元法求解微分方程●用求导公式逆用来换元●用自变量来换元●用因变量来换元●用x,y地位互换来换元5)应用题●用极限、导数定义或积分等式建方程●用几何应用建方程●用曲线切线斜率●用两曲线f(x)与g(x)的公切线斜率●用截距●用面积●用体积●用平均值●用弧长●用侧面积●用曲率●用形心。

2018全国Ⅱ卷理数21题解法分析发表时间：2018-10-30T16:21:45.277Z 来源：《教育学》2018年10月总第155期作者：宁宇[导读] 解答该问题的核心思想是使用一定的方法与技巧将问题转化为函数的单调性、最值问题。

黑龙江省大庆市大庆中学163000函数是高中数学的核心内容，在历年的高考试题中都设置了大量的分值，而其中的导数解答题又处于压轴的地位，难度较大。

解答该问题的核心思想是使用一定的方法与技巧将问题转化为函数的单调性、最值问题。

（18理数Ⅱ卷21题）已知函数f（x）=ex-ax2。

（1）若a=1，证明：当x≥0时，f（x）≥1。

（2）若f（x）在（0，+∞）上只有一个零点，求a。

证明：（1）当a=1，x≥0时，f（x）=ex-x2≥1 =g（x），g`（x）=- ≤0，所以，g（x）在[0，+∞）单调递减，所以，g（x）≤g（0）=1，即f（x）≥1成立。

证明：（2）方法一：变形+带参讨论延续第一问变形的思路，考虑方程f（x）=ex-ax2=0h（x）=1- =0，显然当a≤0时方程无解。

所以当a>0时，令h`（x）= =0，解得x=2，当h`（x）>0，x>2，h（x）在（2，+∞）单调递增；当h`（x）<0，0<x<2，h（x）在（0，2）单调递减。

所以h（x）min=h（2）=1- ，①当h（2）>0，即a< ，h（x）>0，方程无解。

②当h（2）=0，即a= ，方程h（x）=0有唯一解。

③当h（2）<0，即a> 时，要论证此时不满足题意，需要利用零点存在性定理找到两个零点存在的区间，注意到h（0）=1，那么h （x）在（0，2）内存在唯一零点。

现在我们需要在（2,＋∞）上找到一个正值。

当x→+∞时指数函数比二次函数增长速度快，所以1-→1，所以当x足够大时一定存在正值，由于这个函数是多项式比指数型，这时我们考虑第一问得出的结论对h（x）进行放缩,把函数中超越的部分换掉。

18文数试题分析今年的试题整体来看，难度偏低，更加注重基础知识的理解，题目思维的创新度上一般，与平时的备考题目类型没有太大出入;同时客观题的知识考查的侧重有所变化，而主观题目的考查内容没有变化，各个题型的位置与之前无异，整套试卷较为平淡。

难度梯度平缓，过渡较为自然从第1-8和13-15题均为平时练习的基础题，选择到了第9题开始难度稍有上升，立体几何部分稍有创新，至于选填题中的压轴的函数和解三角形题属于常规的套路题，但是只要认真审题和思考，不难得出答案;大题只有在第21题导数综合才出现思维较大的恒成立问题，前面大部分问题的思路是较为顺畅的。

知识板块方面变动较大，侧重函数与立体选择中的第5、9、10、18为立体几何题，比平时多了一道题，同时加入了夹角问题，也就是说文科不考夹角已经成为过去式;第6、8、12、13为函数题，考察了奇偶、切线、周期性、最值、解不等式、求函数值等知识点，比平时多了1道题，但是难度较低，说明更加侧重考生对于函数基础知识和基础方法的理解与应用;考查难度降低较为明显的是解析几何，虽然出现在常规的压轴位置15题和20题，但是试题难度是较低的;减少了框图和命题逻辑语的考查这是符合新课改删掉程序与算法的新变化的。

附知识板块考查统计表预计今后的趋势还是一如既往的重视基础知识的理解深度和全面性，所以考生在全面细致复习的同时，要更加注意代数问题借助图像，图形问题转为解析的考查方向;要更加注意会做的问题的得分率，培养良好的做题习惯，提升自己的数学能力，达到自己期望的目标水准。

18理数试题分析2018年度课标1理科数学延续了一贯的考核形式，在试题分布和考核内容上没有太大的变动，学生应该可以保持心态平稳度过。

纵观试卷，题目整体难度不大，重点考察分析问题和解决问题的能力，在数据处理能力以及应用意识和创新意识上的考察有所提升，也符合当前社会的大数据处理热潮和青少年创新性的趋势。

与历年试卷对比，圆锥曲线和概率的考核顺序变动，这也体现了对于套路性解题的变革，单纯的通过模仿老师的解题步骤不用心理解归纳，是拿到分数的，题目的灵活性要求学生对于基础知识的理解和题目条件的分析和转化能力着重锻炼。

工科数学分析题集一、选择题1. 下列关于函数极限的定义，正确的是（）A. 对于任意给定的正数ε，存在正数δ，当 0 < |x - x₀| < δ时，|f(x) - L| < ε成立，则称函数 f(x) 在 x → x₀时的极限为 LB. 对于任意给定的正数ε，存在正数δ，当 |x - x₀| < δ时，|f(x) - L| < ε成立，则称函数 f(x) 在 x → x₀时的极限为 LC. 对于任意给定的正数ε，存在正数δ，当 0 < |x - x₀| < δ时，|f(x) - L| ≤ε成立，则称函数 f(x) 在 x → x₀时的极限为 LD. 对于任意给定的正数ε，存在正数δ，当 |x - x₀| < δ时，|f(x) - L| ≤ε成立，则称函数 f(x) 在 x → x₀时的极限为 L 答案：A解析：函数极限的精确定义为：对于任意给定的正数ε，存在正数δ，当 0 < |x - x₀| < δ时，|f(x) - L| < ε成立，则称函数 f(x) 在 x → x₀时的极限为 L。

2. 关于无穷小量的描述，正确的是（）A. 以零为极限的变量称为无穷小量B. 绝对值无限趋近于零的变量称为无穷小量C. 函数值无限趋近于零的变量称为无穷小量D. 当自变量趋于某个值时，函数值无限趋近于零的变量称为无穷小量答案：A解析：以零为极限的变量称为无穷小量。

3. 下列关于无穷大量的说法，错误的是（）A. 绝对值无限增大的变量称为无穷大量B. 当自变量趋于某个值时，函数值的绝对值无限增大的变量称为无穷大量C. 无穷大量一定是无界变量D. 无界变量一定是无穷大量答案：D解析：无界变量不一定是无穷大量，但无穷大量一定是无界变量。

4. 对于函数极限的性质，下列说法不正确的是（）A. 函数极限具有唯一性B. 函数极限具有局部有界性C. 函数极限具有局部保号性D. 函数极限具有可加性，即若 lim(x→x₀) f(x) 和 lim(x→x₀) g(x) 存在，则 lim(x→x₀) (f(x) + g(x)) = lim(x→x₀) f(x) + lim(x →x₀) g(x) 一定成立答案：D解析：函数极限具有唯一性、局部有界性、局部保号性。

2023年数学新高考二卷解答第18题摘要：1.题目分析2.解题思路3.解题步骤4.易错点解析5.相似题目推荐正文：随着2023年数学新高考二卷的结束，相信许多同学对于第18题的解答还存在一些疑惑。

下面，我将为大家详细解析这道题目，帮助大家更好地理解和掌握此类题目的解题方法。

一、题目分析2023年数学新高考二卷第18题是一道典型的函数与导数相结合的题目，主要考察了学生的函数分析、导数应用以及方程求解能力。

题目要求解函数的极值点和拐点，从而求出函数的图像与某一直线的关系。

二、解题思路1.首先，对给出的函数进行求导，得到导函数。

2.令导函数等于0，解出方程，得到极值点。

3.通过导数的正负性判断极值点的性质。

4.求出函数的拐点。

5.根据题目要求，分析函数图像与给定直线的关系。

三、解题步骤1.对函数f(x)求导，得到导函数f"(x)。

2.令f"(x)=0，解得极值点x1，x2。

3.判断极值点的性质：通过f(x1)、f(x2)与f(-x1)、f(-x2)的大小关系。

4.求解拐点：计算f""(x)，判断f""(x)的正负性。

5.分析函数图像与给定直线的关系：根据极值点和拐点的坐标，判断函数图像与直线的交点个数。

四、易错点解析1.在求导过程中，注意不要漏掉任何一项，尤其要注意常数项的求导。

2.在求解方程时，要准确计算，防止因粗心导致错误。

3.判断极值点性质时，要仔细分析f(x1)、f(x2)与f(-x1)、f(-x2)的大小关系。

4.求解拐点时，要注意f""(x)的计算，防止遗漏。

五、相似题目推荐1.函数f(x)的图像在区间[0,+∞)上有几个拐点？并求出它们的坐标。

2.已知函数f(x)的图像与直线y=2x+1相交于四个不同的点，求f(x)的解析式。

通过以上解析，希望大家能够更好地掌握这类题目的解题方法。

在练习过程中，要注意细节，提高计算准确度，逐步提高自己的解题能力。

2018考研数学二真题及答案解析今年的考研数学二科目中，涉及了多个不同的数学领域，包括代数、概率论、数理统计等等。

以下是对2018考研数学二真题及答案进行详细解析。

【第一题】已知函数f(x)=ax^2+bx+c(x∈R)的图像经过点P(2, 3)，且在点x=1处的切线方程为y=3x+c1，求a, b, c。

解析：首先，由题意可知，点 (2, 3) 在函数曲线上，则有 f(2) =a(2)^2 + b(2) + c = 3。

解方程得到：4a + 2b + c = 3。

(1)接着，题目还给出了在点 x = 1 处的切线方程为 y = 3x + c1，这说明函数在点 (1, 3+c1) 处的斜率等于切线的斜率，即 f'(1) = 3。

对函数 f(x) 进行求导得到：f'(x) = 2ax + b。

带入 x = 1，得到 2a + b = 3。

(2)综合方程 (1) 和方程 (2)，我们可以解得 a = 1, b = 1, c = -1。

因此，函数 f(x) 的表达式为 f(x) = x^2 + x - 1。

【第二题】假设某学校的学生人数为 N，每个学生中会有80%的人使用微信，而在使用微信的学生中，会有70%的人添加了学校微信公众号。

现在已知学校微信公众号的关注人数为10000人，求学生总数N。

解析：设学生总数为 N，使用微信的学生人数为 0.8N，而添加了学校微信公众号的学生人数为 0.7(0.8N) = 0.56N。

根据题意，已知学校微信公众号的关注人数为10000人，代入上述得到的表达式可得：0.56N = 10000。

解方程得到：N = 10000/0.56 ≈ 17857。

因此，学生总数 N 约为 17857人。

【第三题】设事件A和事件B为两个相互独立的事件，且已知P(A) = 0.6，P(B') = 0.3，求 P(A ∪ B)。

解析：首先，已知 P(B') = 0.3，即事件B的补事件发生的概率为0.3，则事件B发生的概率为1-0.3 = 0.7。

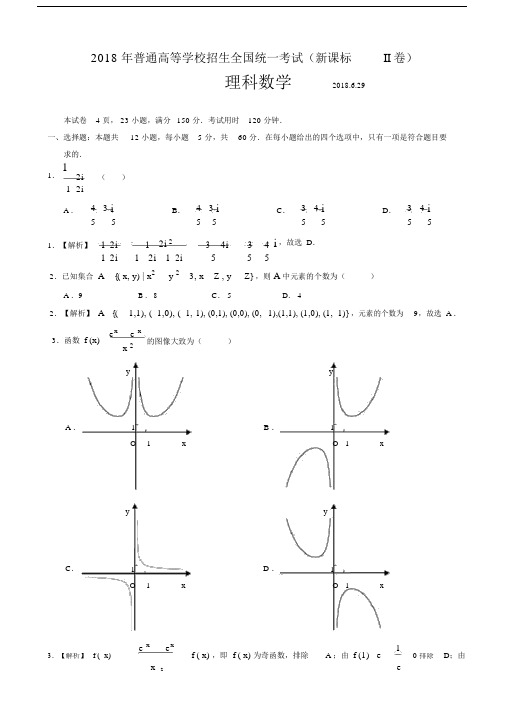
2018 年普通高等学校招生全国统一考试（新课标II 卷）理科数学2018.6.29本试卷 4 页， 23 小题，满分150 分．考试用时120 分钟．一、选择题：本题共12 小题，每小题 5 分，共60 分．在每小题给出的四个选项中，只有一项是符合题目要求的．1．12i（）12iA ． 4 3 i B． 4 3 i C． 3 4 i D． 3 4 i555555551．【解析】12i112i 234i34i，故选 D．12i2i12i5552．已知集合A{( x, y) | x2y 23, x Z , y Z} ，则A中元素的个数为（）A ．9B ． 8C． 5D． 42．【解析】A{(1,1), ( 1,0), (1,1), (0,1), (0,0), (0,1),(1,1), (1,0), (1, 1)} ，元素的个数为9，故选 A ．3．函数f (x)e x e x的图像大致为（）x 2y yA ．1B ．1O1x O 1xy yC．1 D ．1O1x O 1xe x e xf ( x) ，即 f ( x) 为奇函数，排除 A ；由f (1) e 1D；由3．【解析】 f ( x)20 排除x ef (4)e4 e 41211)(e11f (1)排除 C，故选 B ．16(ee2 )(ee)e16e e4．已知向量a, b满足a 1 ， a b1，则a(2a b)（）A ．4B ． 3C． 2D． 04．【解析】a(2a b)2a b 2 1 3 ，故选B．2ax2y 21( a0, b0) 的离心率为 3 ，则其渐近线方程为（）5．双曲线b2a2A ．y2x B．y3x C．y2x D．y3 2x25．【解析】离心率e c3c2 a 2b2b，渐近线方程为y 2 x ，故选A．a a 2a23 ，所以2a6．在ABC 中，cos C5， BC1， AC 5 ，则 AB（）25A ．4 2B ．30C．29D．2 56．【解析】cosC 2 cos2C13，开始25由余弦定理得AB BC 2AC22BC ACcos4 2 ，N0, T0C故选 A ．i17．为计算S11111，设计了右侧的是i100否1349921001程序框图，则在空白框中应填入（）N Ni S N TA ．i i11B ．i i2T T输出 Si 1C．i i3结束D ．i i47．【解析】依题意可知空白框中应填入i i 2 ．第1次循环： N1,T 1,i 3 ；第2次循环：2N 11,T11,i5；；第50 次循环：N111,T111, i101 ，结32439924100束循环得 S11111，所以选 B．1349910028．我国数学家陈景润在哥德巴赫猜想的研究中取得了世界领先的成果．哥德巴赫猜想是“每个大于 2 的偶数可以表示为两个素数的和”，如30723，在不超过30 的素数中，随机选取两个不同的数，其和等于30的概率是（）1B ．1C ．11A ．1415D ．12188．【解析】 不超过 30 的素数有： 2,3,5,7,11,13,17,19,23,29 ，共 10 个．从中选取两个不同的数， 其和等于 30的有： 7 与 23、 11与 19、 13 与 17 ，共 3 对．则所求概率为31，故选 C ．C 102159．在长方体 ABCD A 1B 1C 1 D 1 中， AB BC1， AA 13 ，则异面直线 AD 1 与 DB 1 所成角的余弦值为（）1B ． 5C ． 52A ．65D ．529．【解析】建立如图所示的空间直角坐标系，z则 A(1,1,0) ， D 1 (1,0, 3) ， D (1,0,0) ， B 1 (0,1, 3)C 1，1DA 1 B所以 AD 1(0, 1, 3) ， DB 1 ( 1,1, 3) ，1AD 1 DB 12 5DCBy则cosAD 1, DB 1，故选 C ．AAD 1 DB 12 55x10．若 f ( x)cos x sin x 在 [a,a] 上是减函数，则 a 的最大值是（）A ．B ．3D ．2C ．4410．【解析】 因为 f ( x)cos x sin x2 cos( x) 在区间 [ , 3 ，] 上是减函数， 所以 a 的最大值是44 44故选 A ．11 ． 已 知 f (x) 是 定 义 域 为 ( ,) 的 奇 函 数 ， 满 足 f (1 x)f (1 x) ． 若 f (1)2 ， 则f (1) f ( 2) f (3)f (50)（）A ．50 B ． 0C ． 2D ． 5011．【解析】因为 f ( x)f ( x) ，所以 f (1 x) f (x 1) ，则 f ( x1) f (x 1) ， f ( x) 的最小正周期 为 T4 ． 又 f (1) 2 ， f (2)f ( 0) 0 ， f (3)f (1)2 ， f (4) f (0)0 ， 所 以f (1)f ( 2)f (3)f (50) 12[ f (1) f (2) f (3)f ( 4)] f (49)f (50)f (1)f (2) 2 ，选 C ．x 2y 2 1( a b312．已知 F 1, F 2 是椭圆 C :2b 20) 的左、右焦点， A 是 C 的左顶点， 点 P 在过 A 且斜率为a6的直线上，PF 1F 2 为等腰三角形，F 1F 2 P 120 ，则 C 的离心率为（）2B ．11 1A ．2C ．D ．33412．【解析】如图，因为PF 1F 2 为等腰三角形， F 1 F 2 P 120 且 F 1F 2 2c ，所以 PF 1 F 2 30 ，则 P的坐标为 (2c,3c) ，故 k PA3c 3，化简得 4c a ，所以离心率e c1，故选 D ．2c a6a4yPA F1 O F 2x二、填空题：本题共 4 小题，每小题 5 分，共 20 分．13．曲线y2ln( x1)在点 (0,0)处的切线方程为．13．【解析】y2y|x 0 2 ，则曲线 y2ln( x1)在点 (0,0)处的切线方程为 y2x．x1x 2 y5014．若x, y满足约束条件x 2 y30 ，则z x y 的最大值为．x5014．【解析】可行域为ABC 及其内部，当直线y x z 经过点B(5,4)时，z max9 ．yBAC－3O5x15．已知sin cos1， cos sin0 ，则 sin()．15．【解析】sin cos2sin 2 2 sin cos cos21，cos sin2cos2 2 cos sin sin 20 ，则 sin 22sin cos cos2cos22cos sin sin 20 1 1 ，即2 2 sin cos2cos sin1sin()1．216．已知圆锥的顶点为S ，母线SA, SB所成角的余弦值为7， SA与圆锥底面所成角为45，若SAB的面8积为 515 ，则该圆锥的侧面积为．16．【解析】如图所示，因为cos ASB 7ASB15S ，所以 sin，88SSAB1SA SB sin ASB15SA2 5 15 ，所以 SA4 5 ．216又 SA与圆锥底面所成角为45，即SAO45 ，AO则底面圆的半径 OA210 ，圆锥的侧面积S OA SA40 2 ．B三、解答题：共 70 分．解答应写出文字说明、证明过程或演算步骤．第17~21 题为必考题，每个试题考生都必须作答．第 22、 23 题为选考题，考生根据要求作答．（一）必考题：共 60 分．17．（ 12 分）记 S n 为等差数列 a n 的前 n 项和，已知 a 17 ， S 315 ．（ 1）求 a n 的通项公式；（ 2）求 S n ，并求 S n 的最小值．17．【解析】（ 1）设等差数列a n 的公差为 d ，则 由 1 7 ， S 3 3a 1 3d 15 得 d 2 ，a所以 a n7 (n 1) 22n 9，即 a n 的通项公式为 a n 2n 9 ；（ 2）由（ 1）知 S nn( 72n9) n 2 8n ，2因为 S n (n 4)2 16 ，所以 n4 时， S n 的最小值为 16 ．18．（ 12 分）下图是某地区2000 年至 2016 年环境基础设施投资额y （单位：亿元）的折线图．投资额240220220209200184180 171160148140 122 129120 1006053 568035374242 4740192514202000 2001 2002 2003 2004 2005 2006 2007 2008 2009 2010 2011 2012 2013 2014 2015 2016 年份为了预测该地区2018 年的环境基础设施投资额，建立了y 与时间变量 t 的两个线性回归模型，根据2000 年至 2016年的数据（时间变量 t 的值依次为 1,2, ,17y 30.4 13.5t ；根据 2010年至 2016）建立模型①： ?年的数据（时间变量 t 的值依次为 1,2, ,7 ）建立模型②： y 99 17.5t ．?（ 1）分别利用这两个模型，求该地区2018 年的环境基础设施投资额的预测值；（ 2）你认为哪个模型得到的预测值更可靠？并说明理由．18．【解析】（ 1）将t19代入模型①：?30.4 13.5 19 226.1（亿元），y所以根据模型①得该地区2018 年的环境基础设施投资额的预测值为226.1亿元；将 t 9 代入模型②：?99 17.59256.5 （亿元），y所以根据模型②得该地区2018 年的环境基础设施投资额的预测值为256.5亿元．（ 2）模型②得到的预测值更可靠．理由如下：答案一：从折现图可以看出，2010 年至 2016 年的数据对应的点并没有紧密地均分分布在回归直线y30.413.5t的上下，2009年至2010年的环境基础设施投资额出现了明显的大幅度增加，这说明模型?①不能很好的反应环境基础设施投资额呈线性增长．而2010 年至 2016年的数据对应的点紧密的分布在回归?17.5t 的附近，这说明模型②能更好地反应环境基础设施投资额呈线性增长，所以模型②得到的直线 y 99预测值更可靠．答案二：从计算结果来看，相对于2016 年的环境基础设施投资额为220 亿元，利用模型①得到的该地区2018 年的环境基础设施投资额的预测值为226.1 亿元的增幅明显偏低，而利用模型②得到的该地区2018 年的环境基础设施投资额的预测值为256.5亿元的增幅明显更合理，所以模型②得到的预测值更可靠．19．（ 12 分）设抛物线 C : y24x的焦点为F，过F且斜率为k (k0) 的直线l 与 C 交于A, B两点，AB8 ．（1）求l的方程；（2）求过点A, B且与C的准线相切的圆的方程．19．【解析】（ 1）焦点F为 (1,0)，则直线 l :y k( x1) ，联立方程组y k( x1)，得22( 224)x 20，yy24x k x k k A令 A( x1 , y1 ), B( x2 , y2 ) ，则 x1x22k 24x1 x21．k2，－ 1O F x根据抛物线的定义得AB x1x2 2 8 ，B 即 2k 24 6 ，解得k 1 （舍去 k1），k 2所以 l 的方程为y x1；（ 2）设弦AB的中点为M，由（ 1）知x1x2 3 ，所以M的坐标为(3,2)，2则弦 AB 的垂直平分线为y x5，令所求圆的圆心为(m,5m) ，半径为 r ，2m5m12根据垂径定理得r AB221234 ，22m m由圆与准线相切得m 1221234，解得 m3或 m11 ．m m则所求圆的方程为：( x 3) 2( y 2) 216 或 ( x 11) 2( y 6) 214420．（ 12 分）如图，在三棱锥P ABC 中，AB BC22 ，PA PB PC AC4， O 为 AC 的中点．（ 1）证明：PO平面 ABC ；（ 2）若点M在棱BC上，且二面角M PA C 为30，求 PC 与平面 PAM 所成角的正弦值．P20．【解析】（ 1）证明：连接OB，PA PC ， O 为 AC 的中点，PO AC ，AB BC22, AC 4，AB 2BC 2AC 2，即AB BC ，OB 1AC 2 ，AOC 2又 PO23, PB 4 ，则 OB2PO 2PB 2，即 OP OB ，B MAC OB O ，PO平面 ABC ；（ 2）由（ 1）知OB,OC , OP两两互相垂直，z以 O 为坐标原点建立如图所示的空间直角坐标系，P则 B(2,0,0) ， C (0,2,0) ， A(0,2,0) ， P(0,0,2 3) ，BC ( 2,2,0)， AP(0,2,23)， CP(0,2,23)令 BM BC ，[ 0,1] ．A OC y 则 OM OB BC(22,2,0) ， AM(22,22,0) ，M令平面 PAM 的法向量为 n(x, y, z) ，Bxn AP 2 y 2 3z0，取 x3 1 ，得n ( 3 1 , 3 1 ,1)由n AM(2 2 )x ( 22) y 0易知平面 PAC 的一个法向量为m(1,0,0) ，所以 cos n, mn m3(1)3(1)3，1) 21) 2) 27 2cos302n m3(3((127解得1（舍去3），即n( 43,23,2) ，3333n CP 83因为 cos n, CP333．8，所以PC 与平面 PAM 所成角的正弦值为n CP444 321．（ 12 分）已知函数 f ( x)e x ax2．（ 1）若a1，证明：当 x0 时，f ( x)1；（ 2）若f ( x)在(0,) 只有一个零点，求 a ．21．【解析】（ 1）方法 1：欲证明当x0 时， f ( x)1，即证明e x1 ．x21令 g ( x)e x，则g ( x)e x (x 21)2xe x(x 1) 2 e x0，x 2x 2 1 2x2 1 2 1则 g ( x) 为增函数， g (x)g (0) 1 ，得证．方法 2：a1时， f ( x) e x x2，则 f ( x) e x2x ，令 f (x)g( x) ，则 g ( x)e x 2 ，x[0, ln 2) 时， g (x)0 ， g( x) 为减函数， x(ln 2,) 时， g ( x)0 ， g( x) 为增函数，所以 g( x) min g(ln 2)22ln 20，即当x0 时， f (x)0， f (x) 为增函数，所以 f ( x) f (0) 1 ，因此 a 1 ， x0 时， f (x) 1．（ 2）方法 1：若f ( x)在(0,) 只有一个零点，则方程e xa 只有一个实数根．x2令 h(x)e xh( x) 的图像与直线y a 只有一个公共点．x2，等价于函数y又 h ( x)x2e x2xe x x 2 e xx4x3，x(0,2) 时， h ( x)0 ， h( x) 为减函数， x (2,) 时， h ( x)0 ， h( x) 为增函数，所以 h( x) min h(2)e2， x0 时h(x)， x时 h( x)．4则 a e2) 只有一个零点．时， f ( x) 在 (0,4方法 2：若f ( x)在(0,) 只有一个零点，则方程e xax 只有一个实数根．x令 h(x)e xh(x) 的图像与直线y ax 只有一个公共点．，等价于函数 yx当直线 y ax 与曲线y h(x) 相切时，设切点为(x0, e x0) ，x0又 h ( x)xe x e x x 1 e x x0 1 e x0e x0x0 2 ，此时a h ( x0)e2 x2x 2，则 h ( x0 )x02x02．4又当 x(0,1) 时， h ( x)0 ， h( x) 为减函数，yx (1, ) 时， h ( x) 0 ， h(x) 为增函数，所以 h( x) min h(1) e ，且 x 0 时 h(x)， x 时 h( x)．根据 yh( x) 与 yax 的图像可知，O 1 2xe 2 时，函数 yh(x) 的图像与直线 yax 只有一个公共点，即f ( x) 在 (0,) 只有一个零点．a4（二）选考题：共 10 分．请考生在第 22、 23 题中任选一题作答．如果多做，则按所做的第一题计分．22． [选修 4—4：坐标系与参数方程]（ 10 分）在 直 角 坐 标 系 xOy 中 ， 曲 线 C 的 参 数 方 程 为x 2 cosy( 为 参 数 ) ， 直 线 l 的 参 数 方 程 为4sinx 1 t cos y2 (t 为参数 )t sin（ 1）求 C 和 l 的直角坐标方程；（ 2）若曲线 C 截直线 l 所得线段的中点坐标为(1,2) ，求 l 的斜率．22．【解析】（ 1）消去参数，得 C 的直角坐标方程为x 2 y 2 41；16消去参数 t ，得 l 的直角坐标方程为 sin x cos y sin2 cos0 ；（ l 的直角坐标方程也可写成：y tan (x 1)2() 或 x 1 ．）2（ 2）方法 1：将 l 的参数方程：x 1 t cos x 2 y 2y 2t sin(t 为参数 ) 代入 C :164 4 1 t cos22 t sin216 ，即 1 3 cos2t24 2 cossint由韦达定理得 t 14 2cossint 23 cos 2，1依题意，曲线 C 截直线 l 所得线段的中点对应t 1t 2 0，即 2 cossin2因此 l 的斜率为 2 ．方法 2：令曲线 C 与直线 l 的交点为 A( x 1 , y 1 ), B(x 2 , y 2 ) ，x 1 2 y 1 2 1416x 2 x 1x 2y 1y 2 y 1y 2则由x 10 ，其中 x 1x 2 2 y 2 2 得4 1614161得：8 0 ，0 ，得 tan 2 ．x 2 2, y 1 y 2 4 ．所以x 1x2y 1 y 2y 1 y 2 2 ，即 l 的斜率为 2 ．24x 1 x 223． [选修 4—5：不等式选讲 ]（ 10 分）设函数f (x)5x ax 2 ．（ 1）当 a1时，求不等式f (x)0 的解集；（ 2）若 f ( x)1 ，求 a 的取值范围．23．【解析】（ 1） a1时， f ( x) 5 x 1x 2 ，x 1时， f( x) 5 x1 x2 2x 4 0 ，解得2 x 1 ； 1 x 2 时， f ( x) 5x1 x2 2 0，解得 1 x 2 ； x 2 时， f ( x)5 x 1 x22x6 0 ，解得 2 x3，综上所述，当 a 1 时，不等式 f (x) 0 的解集为 [ 2,3] ．（ 2） f (x)5 x ax2 1，即 xa x2 4 ，又 x a x 2 x a x 2 a 2 ，所以 a 24 ，等价于 a 2 4 或 a 24 ，解得 a 的取值范围为 { a | a2 或 a6} ．。

2018年全国高考新课标2卷理科数学试题(解析版)(2)(word版可编辑修改) 编辑整理：尊敬的读者朋友们：这里是精品文档编辑中心，本文档内容是由我和我的同事精心编辑整理后发布的，发布之前我们对文中内容进行仔细校对，但是难免会有疏漏的地方，但是任然希望（2018年全国高考新课标2卷理科数学试题(解析版)(2)(word版可编辑修改)）的内容能够给您的工作和学习带来便利。

同时也真诚的希望收到您的建议和反馈，这将是我们进步的源泉，前进的动力。

本文可编辑可修改，如果觉得对您有帮助请收藏以便随时查阅，最后祝您生活愉快业绩进步，以下为2018年全国高考新课标2卷理科数学试题(解析版)(2)(word版可编辑修改)的全部内容。

2018年普通高等学校招生全国统一考试新课标2卷理科数学注意事项：1．答卷前,考生务必将自己的姓名、准考证号填写在答题卡上。

2．作答时，将答案写在答题卡上。

写在本试卷及草稿纸上无效。

3．考试结束后，将本试卷和答题卡一并交回。

一、选择题：本题共12小题，每小题5分，共60分，在每小题给出的四个选项中，只有一项是符合题目要求的.1．错误!=（）A．—错误! - 错误!i B．- 错误! + 错误!i C．—错误!—错误!i D．- 错误! + 错误!i解析：选D2．已知集合A=｛（x，y）｜x2+y2≤3,x∈Z,y∈Z ｝，则A中元素的个数为 ( )A．9 B．8 C．5 D．4解析：选A 问题为确定圆面内整点个数3．函数f(x)= e x—e-xx2的图像大致为（ )解析:选B f（x）为奇函数，排除A，x〉0，f(x）>0,排除D，取x=2，f（2)=错误!>1,故选B4．已知向量a，b满足｜a｜=1，a·b=-1，则a·(2a—b）= （）A．4 B．3 C．2 D．0解析：选B a·(2a—b）=2a2—a·b=2+1=35．双曲线错误!－错误!＝1(a＞0，b＞0)的离心率为错误!,则其渐近线方程为（ )A．y=±错误!x B．y=±错误!x C．y=±错误!x D．y=±错误!x解析:选A e=错误! c2=3a2 b=错误!a6．在ΔABC中,cos错误!=错误!，BC=1,AC=5，则AB= （）A．4错误!B．错误!C．错误!D．2错误!解析：选A cosC=2cos2错误! -1= —错误! AB2=AC2+BC2-2AB·BC·cosC=32 AB=4错误!7．为计算S=1- 错误! + 错误!—错误! +……+ 错误! - 错误!,设计了右侧的程序框图，则在空白框中应填入( ）A．i=i+1 B．i=i+2 C．i=i+3 D．i=i+4解析:选B8．我国数学家陈景润在哥德巴赫猜想的研究中取得了世界领先的成果．哥德巴赫猜想是“每个大于2的偶数可以表示为两个素数的和”，如30=7+23．在不超过30的素数中,随机选取两个不同的数,其和等于30的概率是( ）A．错误!B．错误!C．错误!D．错误!解析：选C 不超过30的素数有2，3，5，7,11，13，17,19，23,29共10个，从中选2个其和为30的为7+23，11+19，13+17，共3种情形，所求概率为P=错误!=错误!9．在长方体ABCD-A1B1C1D1中,AB=BC=1，AA1=错误!，则异面直线AD1与DB1所成角的余弦值为（ ) A．错误!B．错误!C．错误!D．错误!解析:选C 建立空间坐标系，利用向量夹角公式可得。

2023年高考全国卷2数学18题总结
2023年高考全国卷2的数学18题，是一道涉及不等式证明的题目，具体考查了数学归纳法和放缩法。

该题要求考生证明一个给定的不等式，通过数学归纳法和放缩法两种策略，逐步推导和证明不等式的正确性。

在解题过程中，考生需要仔细分析题目给出的条件和不等式的结构，选择合适的方法进行推导和证明。

数学归纳法和放缩法是两种常用的策略，但具体使用哪种方法需要根据不等式的特点和题目要求进行判断。

总体而言，该题目难度较大，要求考生具备较强的数学思维和推理能力。

同时，也提醒考生在备考过程中，要注重数学归纳法和放缩法等策略的训练和掌握，以提高解题能力和数学思维能力。

2023 数学高考乙卷理科18题评析全文共四篇示例，供读者参考第一篇示例：2023年数学高考乙卷理科18题主要对于高中数学知识的深度运用和综合能力的考验。

以下将对这些题目进行逐一评析，希望能帮助同学们更好地掌握和理解这些题目。

第一题：已知直线L1：2x+3y＋1＝0，L2：3x-2y＋k＝0，，若直线L1和L2垂直求k的值。

解析：两条直线垂直时，它们的斜率之积为-1。

我们可以分别求出L1和L2的斜率，然后根据斜率之积为-1的条件来求解k的值。

第二题：若f(x)＝x³-3x²+3x-1。

试讨论f(x)的零点个数。

解析：通过对f(x)进行分解，可以得到f(x)=(x-1)³。

由此可知，f(x)只有一个零点x=1。

第三题：若x²+px+q=0的两个根分别为x1和x3那么x1，x2和x3之间的关系是什么。

解析：根据二次方程的基本性质，两个根的乘积等于常数项q，两个根的和等于系数p的相反数。

因此我们可以根据这两个性质来分析x1，x2和x3之间的关系。

第四题：若a，b，c是方程x³-x²+ax+b=0的三个根，求abc的值。

解析：这是一个典型的Vieta定理题目。

根据Vieta定理，三个根的乘积等于常数项b，即abc=b。

第五题：设a∈(0,π/2)，证明：\[|\sin a-\cos a|<1\]。

解析：可以利用三角函数的性质来证明这个不等式。

通过分别计算\[\sin a\]和\[\cos a\]的值，我们可以得出不等式的正确性。

第六题：已知函数f(x)=x³-5x²+10x-2，求f(x)在区间[0,3]上的最大值和最小值。

解析：通过求解f'(x)=0来找出f(x)的驻点，然后通过二次导数判别法来确定这些驻点对应的极值。

最终我们可以得出函数在指定区间上的最大值和最小值。

第七题：若A，B是两个互为逆矩阵的二阶矩阵，证明：\[AB-BA=I\]。

2018考研数学二真题及答案解析2018考研数学二真题及答案解析2018年考研数学二真题是考研数学科目中的重要一环。

对于考生来说，熟悉并掌握真题及答案解析是备考的关键。

本文将对2018年考研数学二真题进行解析，帮助考生更好地备考。

第一部分：选择题选择题是考研数学二真题中的重要组成部分。

2018年考研数学二选择题主要涉及到概率、统计、线性代数、高等数学等知识点。

下面我们就对其中一道选择题进行解析。

题目：设随机变量X的概率密度为f(x)={cx^2, 0<x<10, 其他}其中c为常数，则P(X<1/2)的值为（）A. 1/6B. 1/8C. 1/10D. 1/12解析：根据题目中给出的概率密度函数，我们可以求出c的值。

由于概率密度函数的积分等于1，我们可以得到∫[0,1]cx^2dx=1。

解这个积分方程，得到c=6。

接下来，我们需要求解P(X<1/2)。

由于X的概率密度函数在0<x<1之间为cx^2，我们可以通过求解积分∫[0,1/2]cx^2dx来得到P(X<1/2)的值。

计算∫[0,1/2]cx^2dx，得到P(X<1/2)=∫[0,1/2]6x^2dx=6/8=3/4。

所以，P(X<1/2)的值为3/4，答案选项为D。

第二部分：填空题填空题是考研数学二真题中的另一个重要组成部分。

2018年考研数学二填空题主要涉及到微积分、概率、统计等知识点。

下面我们就对其中一道填空题进行解析。

题目：设X1，X2，...，Xn为来自总体X的一个样本，其概率密度为f(x)={c(1-x^2), -1<x<10, 其他}其中c为常数，若X1，X2，...，Xn相互独立，则c的值为________。

解析：根据题目中给出的概率密度函数，我们可以求出c的值。

由于概率密度函数的积分等于1，我们可以得到∫[-1,1]c(1-x^2)dx=1。

解这个积分方程，得到c=3/4。

20XX年复习资料大学复习资料专业：班级：科目老师：日期：一、单项选择题（每题3分）1. D2. D3. C4. C5. C6. B二、填空题（每题3分） 1. 222a b e -； 2．-1； 3．π-； 421；5．-3/8； 6．342y π=; 7. 20XXXX0XX ； 8. 2-.三、 计算题1解：原式=232200ln(1)ln(1)222(1)2lim lim 3(1)3t t t t t t t t t →+→++-----==-………………… (8分)2 解：()1cos x y y x e --=两边求导()1'sin (1')x y y x e y xy --=--，可得'(0)1y =-……… (4分) 于是022(()(0))lim 2lim 2'(0)2n x f x f n f f n x→∞→⎡⎤--⎛⎫-==-= ⎪⎢⎥⎝⎭⎣⎦……………………… (8分)3解：0lim x y →=∞，垂直渐近线：0x =；……… (3分) lim 1,lim 1x x y y →-∞→+∞=-=，水平渐近线：1y =±；……… (8分)4解：()222210000(1)sin (1)sin 2sin (1)cos lim lim lim lim (1)k k k k x x x x f x bx x ax bx x ax bx x bx x a x bx x x kx -→→→→+-+-++-===+ 当分子为无穷小时，1a =……………………………………… (4分)此时，()22120002sin (1)cos 12sin 4cos (1)sin lim lim lim (1)k k k x x x f x bx x bx x b x bx x bx x x kx k k x --→→→++-+-+==- 2206cos 6sin (1)cos lim (1)k x b x bx x bx x k k x -→--+=- 当分子为无穷小时，1/6b =，故1,1/6a b ==…… (8分)5解：（1）若()f x 在0x =处可导，则在0x =处连续，由罗比达法则000()cos '()sin lim ()lim lim '(0)1x x x x x x x a f x x ϕϕϕ→→→-+====…………………(3分) 此时2000()(0)()cos '(0)'()sin '(0)"(0)1'(0)lim lim lim 22x x x f x f x x x x x f x x x ϕϕϕϕϕ→→→---+-+==== 故2('()sin )()cos 0'()"(0)102x x x x x x x f x x ϕϕϕ+-+⎧≠⎪⎪=⎨+⎪=⎪⎩.…………………………… (5分)（2）2000('()sin )()cos (''()cos )"(0)1lim '()lim lim '(0)22x x x x x x x x x x x f x f x x ϕϕϕϕ→→→+-+++==== 故'()f x 在0x =处连续……………………………………………… (8分)四、证明题1.（1）条件一：()f x 在区间[,]a b 上连续；条件二：()f x 在区间(,)a b 内可导条件三：()()0f a f b ==；结论：(,)a b ξ∃∈使得'()0f ξ=.…………… (4分)（2）令2()()F x x f x =，在[0,]a 上使用罗尔定理………………… (9分)2．（1）条件一：()f x 在区间[,]a b 上连续；条件二：()f x 在区间(,)a b 内可导结论：(,)a b ξ∃∈使得()()'()f b f a f b a ξ-=-.………………… (3分) 证明：令()()()()f b f a F x f x x b a-=--，在[,]a b 上使用罗尔定理…… (5分)（2）对()ln f x x =在[,]a b 上使用拉格朗日定理，(,)a b ξ∃∈使得22ln ln 112b a a b a b a b ξ-=>>-+得证 ………………… (9分)。