人教版七年级下册数学配套练习册及答案

人教版七年级下册数学配套练习册答案：篇一：人教版七年级数学练习册下册答案篇二：七年级下册数学练习册答案人教版篇三：人教版七年级数学下册各单元测试题及答案七年级数学第五章《相交线与平行线》测试卷班级 _______ 姓名 ________ 坐号 _______ 成绩 _______一、选择题（每小题3分，共 30 分）1、如图所示，∠1和∠2是对顶角的是（）A1B1C1D12A2、如图AB∥CD可以得到（）A、∠1＝∠2B、∠2＝∠3C、∠1＝∠4D、∠3＝∠4 3、直线AB、CD、EF相交于O，则∠1＋∠2＋∠3＝（） A、90° B、120°C、180° D、140° 4、如图所示，直线a 、b被直线c所截，现给出下列四种条件：①∠2＝∠6 ②∠2＝∠8 ③∠1＋∠4＝180°④∠3＝∠8，其中能判断是a∥b的条件的序号是（）A、①②B、①③C、①④D、③④5、某人在广场上练习驾驶汽车，两次拐弯后，行驶方向与原来相同，这两次拐弯的角度可能是（） A、第一次左拐30°，第二次右拐30° B、第一次右拐50°，第二次左拐130° C、第一次右拐50°，第二次右拐130° D、第一次向左拐50°，第二次向左拐130°6、下列哪个图形是由左图平移得到的（）3DB1322367ba（第4题）DBDC7、如图，在一个有4×4个小正方形组成的正方形网格中，阴影部分面积与正方形ABCD面积的比是（）ABA、3：4B、5：8 C、9：16 D、1：2（第7题）8、下列现象属于平移的是（）①打气筒活塞的轮复运动，②电梯的上下运动，③钟摆的摆动，。

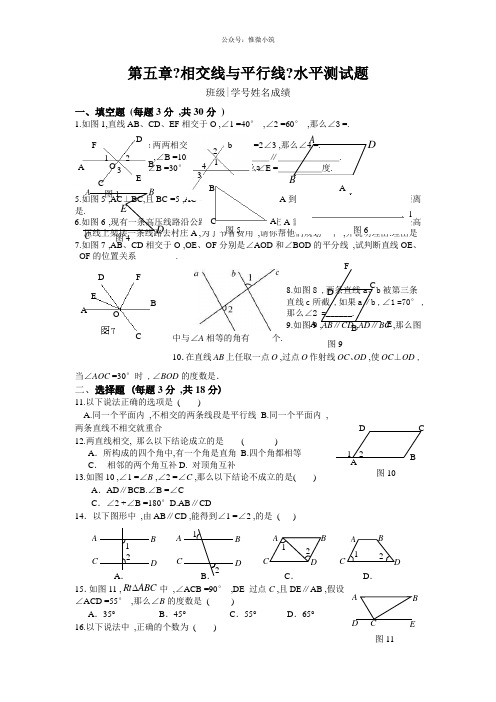
第五章?相交线与平行线?水平测试题班级|学号姓名成绩一、填空题 (每题3分 ,共30分 )1.如图1,直线AB 、CD 、EF 相交于O ,∠1 =40° ,∠2 =60° ,那么∠3 =.2.如图2 ,直线a ,b ,c 两两相交 ,∠1 =80° ,∠2 =2∠3 ,那么∠4 =.3.如图3 ,∠A =75° ,∠B =105° 那么＿＿＿＿＿∥＿＿＿＿＿＿＿.4.如图4 ,AB ∥CD ,∠B =30° ,∠D =40° ,那么∠E =＿＿＿＿＿度. 5.如图5 ,AC ⊥BC,且BC =5 ,AC =12 ,AB =13 ,那么点A 到BC 的距离是点B 到点A 的距离是. 6.如图6 ,现有一条高压线路沿公路l 旁边建立 ,某村庄A 需进行农网改造 ,必须要从这条高压线上架接一条线路去村庄A ,为了节省费用 ,请你帮他们规划一下 ,并说明理由.理由是 7.如图7 ,AB 、CD 相交于O ,OE 、OF 分别是∠AOD 和∠BOD 的平分线 ,试判断直线OE 、OF 的位置关系_________.8.如图8 ,两条直线a 、b 被第三条直线c 所截 ,如果a ∥b ,∠1 =70° ,那么∠2 =______. 9.如图9 ,AB ∥CD ,AD ∥BC ,那么图中与∠A 相等的角有_____个.10．在直线AB 上任取一点O ,过点O 作射线OC 、OD ,使OC ⊥OD ,当∠AOC =30°时 ,∠BOD 的度数是．二、选择题 (每题3分 ,共18分)11.以下说法正确的选项是 ( )A.同一个平面内 ,不相交的两条线段是平行线B.同一个平面内 ,两条直线不相交就重合12.两直线相交, 那么以下结论成立的是 ( )A ．所构成的四个角中,有一个角是直角 B.四个角都相等 C ． 相邻的两个角互补D. 对顶角互补13.如图10 ,∠1 =∠B ,∠2 =∠C ,那么以下结论不成立的是( )A ．AD ∥BCB.∠B =∠CC ．∠2 +∠B =180°D.AB ∥CD14．以下图形中 ,由AB ∥CD ,能得到∠1 =∠2 ,的是 ( )15．如图11 ,ABC Rt 中 ,∠ACB =90° ,DE 过点C ,且DE ∥AB ,假设∠ACD =55° ,那么∠B 的度数是 ( )A ．35°B ．45°C ．55°D ．65°16.以下说法中 ,正确的个数为 ( )B F E D OC A 1 2 3 图1 b a 2c 1 4 3 图2AB C D 图3 A B C D E 图4A ED F BC OA l图6 C A B 图5 图8 E BCF D A 图9A CB D1 2A CBD1 2A ．B ． 12 A C B DC ． BD CA D ．12BCD A1 2 图10A B C D E图11(1)过一点有无数条直线与直线平行 (2 )如果a ∥b ,a ∥c ,那么b ∥c(3如果两线段不相交 ,那么它们就平行 (4 )如果两直线不相交 ,那么它们就平行三、根据以下证明过程填空 (每空1分 ,共18分 )17.如图12 ,(1)因为∠A =_____() ,所以AC ∥ED ( )(2)因为∠2 =_____() ,所以AC ∥ED ( )(3)因为∠A +_____ =180°() ,所以AB ∥FD ( ) (4)因为AB ∥_____() ,所以∠2 +∠AED =180°( ) (5)因为AC ∥_____() ,所以∠C =∠3( )18．如图13 ,∠1 =∠2 ,CF ⊥AB ,DE ⊥AB ,求证：FG ∥BC 证明：因为 CF ⊥AB ,DE ⊥AB ( )所以∠BED =90° ,∠BFC =90° ( )所以∠BED =∠BFC ( ) 所以 ED ∥FC ( ) 所以∠1 =∠BCF ( ) 因为∠2 =∠1 ( ) 所以∠2 =∠BCF ( ) 所以 FG ∥BC ( ) 四、解答题19．画图题：把小船ABCD 通过平移后到''''D C B A 的位置 ,请你根据题中信息 ,画出平移后的小船位置．(5分)20．如图：∠1 +∠2 =180° , ∠3 =110° ,求∠4的度数.(7分)21．如图：AB ,CD ,EF 相交于O 点 ,AB ⊥CD ,OG 平分∠AOE ,∠FOD =30° ,求∠BOE 及∠AOG 的度数.(8分)22．如图：AB ∥DC ,AD ∥BC ,求证：∠B =∠D (8分)23．如图 ,AD ⊥BC 于D,EG ⊥BC 于G ,∠E =∠1 ,那么AD 平分∠BAC 吗? 试说明理由(8分)参考答案： 一、填空题 1．80°提示：从图上可以知道∠1 +∠2 +∠3 =180° ,所以∠3 =80° 2．140°提示：∠1与∠2是对顶角 ,所以∠2 =80° ,又因为∠2 =2∠3 ,所以∠3 =40° ,又因为∠4 =180° -∠3 ,所以∠4 =140°3．AD ∥BC 提示：因为∠A +∠B =1800 ,所以AD ∥BC4．70°提示：过点E 作EF 根据平行线的性质可知∠BED =∠BEF +∠FED =∠B +∠D =70°. 5．AC ,AB ∥AB ,6．作图：过点A 作l 的垂线段最|短.ACB ED G 1 2 3 1DB G FC A E 2CF A E B D 1 2 3 图12图137．垂直8．110°9．3个提示：分别是∠FDC ,∠C ,∠CBE.10．60°或120°提示：点C与D在AB的同侧或异侧两种情况.二、选择题11．C12．C 提示：只有当两直线垂直时A、B、D才成立.13．B提示：∠1 =∠B可得AD∥BC ,∠2 +∠B =180°根据∠C =∠2可得AD∥BC应选B 14．B15．A提示：DE∥AB所以∠B =∠BCE ,所以∠B =180°-90°-55°=35°16．A 提示：只有 (2 )对三、根据以下证明过程填空17． (1 )∠BED同位角相等 ,两直线平行 (2 )∠DFC内错角相等 ,两直线平行 (3 )∠AFD 同旁内角互补 ,两直线平行 (4 )DF 两直线平行 ,同旁内角互补 (5 )ED两直线平行 ,同位角相等18． ,等式的性质 ,等量代换 ,同位角相等 ,两直线平行 ,两直线平行 ,同位角相等 , ,等量代换 ,内错角相等 ,两直线平行四、解答题19．将小船向左移9个格子,再向上移1个格子(画图略)20．解：因为∠1 +∠2 =180°所以l1∥l2所以∠3 =∠6又因为∠4 +∠6 =180°所以∠4 =180°-∠3又因为∠3 =110°所以∠4 =70°21．解：因为∠FOD =30° ,∠COE与∠FOD是对顶角,所以∠EOC =30°因为AB⊥CD所以∠BOC =90° ,∠BOE =∠BOC -∠EOC =60°因为∠AOE =90°+∠EOC =120°且OG平分∠AOE所以∠AOG =60°22．解：因为AB∥DC ( )所以∠B +∠C =180°(两直线平行,同旁内角互补)因为AD∥BC ( )所以∠D +∠C =180°(两直线平行,同旁内角互补)所以∠B =∠D (等角的补角相等)23．解：AD平分∠BAC理由：因为AD⊥BC于D,EG⊥BC于G所以EG∥AD (垂直于同一条直线的两直线平行)所以∠1 =∠2 (两直线平行,内错角相等)∠E =∠3 (两直线平行,同位角相等)又因为∠E =∠1所以∠3 =∠2 (等量代换)所以AD平分∠BAC (角平分的定义)第六章?实数?水平测试题班级|学号姓名成绩一、选择题 (每题3分 ,共30分. 每题只有一个正确答案 ,请将正确答案的代号填在下面的表格中 )1、在实数70107.08221.03、、、、－中 ,其中无理数的个数为 ( ) A 、1 B 、2 C 、3 D 、4 2、16的算术平方根为 ( )A 、4B 、4±C 、2D 、2±3、以下语句中 ,正确的选项是 ( )A 、无理数都是无限小数B 、无限小数都是无理数C 、带根号的数都是无理数D 、不带根号的数都是无理数 4、假设a 为实数 ,那么以下式子中一定是负数的是 ( )A 、2a - B 、2)1(+-a C 、2a - D 、)1(+--a5、以下说法中 ,正确的个数是 ( )(1 )－64的立方根是－4； (2 )49的算术平方根是7±； (3 )271的立方根为31； (4 )41是161的平方根.A 、1B 、2C 、3D 、4 6.估算728-的值在A. 7和8之间B. 6和7之间C. 3和4之间D. 2和3之间 7、以下说法中正确的选项是 ( )A 、假设a 为实数 ,那么0≥aB 、假设a 为实数 ,那么a 的倒数为a1C 、假设y x 、为实数 ,且y x = ,那么y x =D 、假设a 为实数 ,那么02≥a8、假设10<<x ,那么x xx x 、、、12中 ,最|小的数是 ( )A 、xB 、x1 C 、x D 、2x 9、以下各组数中 ,不能作为一个三角形的三边长的是 ( )A 、1、1000、1000B 、2、3、5C 、222543、、 D 、33364278、、10.观察图８寻找规律 ,在 " ?〞处填上的数字是 ( )(A)128 (B)136 (C)162 (D)188 二、填空题 (每题3分 ,共30 ) 11.和数轴上的点一一对应.2 2４8 142648 88?图812.假设实数a b ，满足0a b a b += ,那么________ab ab=． 2a = ,3b = ,那么2a b 的值等于．14.有假设干个数 ,依次记为123n a a a a ，，， ,假设112a =- ,从第２个数起 ,每个数都等于1与它前面的那个数的差的倒数 ,那么2005a =． 15.比拟大小：23-0.02-；16.如图 ,数轴上的两个点A B ，所表示的数分别是a b ， ,在a b + ,a b - ,ab ,a b -中 ,是正数的有个．3+x 是4的平方根 ,那么=x ,假设－8的立方根为1-y ,那么y =________.18.计算：2)4(3-+-ππ的结果是.19.用 "★〞定义新运算：对于任意实数a ,b ,都有a ★21b b +=．例如 , 7★211744+== ,那么5 ★3 =；20..右图是小李创造的填图游戏 ,游戏规那么是：把5 ,6 ,7 ,8四个数分别填入图中的空格内 ,使得网格中每行、每列的数字从左至|右和从上到下都按从小到大的顺序排列．那么一共有种不同的填法． 三、解答题 (共60分 )21.计算: (5分 )2322011)3(8)2()1(--⋅-+-22. (6分 )实数b a 、在数轴上的位置如下图 ,化简：2a b a --.23. (7分 )如图 ,数轴上点A,点A 关于原点的对称点为B ,设点B 所表示的数为x ,求(x 的值．24. (8分 )某数的平方根为1523-+a a 和 ,求这个数的是多少 ?25. (8分 )a 、b0b = ,解关于x 的方程()122-=++a b x a26. (10分 )黄冈某商场在世|界杯足球比赛期间举行促销活动 ,并设计了两种方案：一种是以商品价格的九五折优惠的方式进行销售；一种是采用有奖销售的方式 ,具体措施是：①有奖销售自2006年6月9日起 ,发行奖券10000张 ,发完为止；②顾客累计购物满400元 ,赠送奖券一张 (假设每位顾客购物每次都恰好凑足400元 )；③世|界杯后 ,顾客持奖券参加抽奖；④奖项是：特等奖2名 ,各奖3000元奖品；一等奖10名 ,各奖1000元奖品；二等奖20名 ,各奖300元奖品；三等奖100名 ,各奖100元奖品；四等奖200名 ,各奖50元奖品；纪念奖1 2 439B0 Ax5000名,各奖10元奖品,试就商场的收益而言,对两种促销方法进行评价,选用哪一种更为合算?27 (10分).某单位需以"挂号信〞或"特快专递〞方式向五所学校各寄一封信．这五封信的重量分别是72g ,90g ,215g ,340g ,400g．根据这五所学校的地址及信件的重量范围,在邮局查得相关邮费标准如下：递〞方式寄出呢?(2 )这五封信分别以怎样的方式寄出最|合算?请说明理由．(3 )通过解答上述问题,你有何启示? (请你用一、两句话说明)28.阅读题(6分)先阅读理解,再答复以下问题：因为2112=+,且221<<,因为6222=+,且362<<,因为12332=+,且4123<<,以此类推,我们会发现nnn(2+一、1、B2、C3、A4、D 5二、11.实数12.－1 13.12或12-14.12-15.<；>16. 117. 1 18.1 19. 10三、22. -b 23. x=24. 4925. x =426.解：设在定价销售额为40010000⨯元的情况下 ,采用打折销售的实际销售金额为1W元 ,采用有奖销售的实际销售金额为2W元 ,由题意有140010000953800000W=⨯⨯=% (元 ) ,3908000= (元 ) ,比拟知：21W W>．在定价销售额相同的情况下 ,实际销售额大 ,收益就大 ,就商场的收益而言 ,选用有奖销售方式 ,更为合算．27.解： (1 )重量为90g的信以 "挂号信〞方式寄出 ,那么邮寄费为50.830.57.5⨯++=(元 )；以 "特快专递〞方式寄出 ,邮寄费为 5319++= (元 )．(2 )这五封信的重量均小于1 000g ,∴假设以 "特快专递〞方式寄出 ,邮寄费为5319++= (元 )．由 (1 )得知 ,重量为90g 的信以 "挂号信〞方式寄出 ,费用为元小于9元； 72g<90g ,∴重量为72g 的信以 "挂号信〞方式寄出小于9元； 假设重量为215g 的信以 "挂号信〞方式寄出 ,那么邮寄费为50.82230.511.5⨯+⨯++= (元 )>9 (元 )． 400g>340g>215g ,∴重量为400g ,340g 的信以 "挂号信〞方式寄出 ,费用均超过9元． 因此 ,将这五封信的前两封以 "挂号信〞方式寄出 , 后三封以 "特快专递〞方式寄出最|合算． (3 )学生言之有理即可．28.n 理由∵n 2<n 2+1 ∴2n <12+n ∴n<12+n∵ (n +1 )2>n 2+1∴2)1(+n >12+n ∴n +1>12+n∴n<12+n <n +1∴整数局部为n.第七章平面直角坐标系水平测试题 (一 )一、 (本大题共10小题 ,每题3分 ,共30分. 在每题所给出的四个选项中 ,只有一项为哪一项符合题意的.把所选项前的字母代号填在题后的括号内. 相信你一定会选对 ! ) 1.某同学的座位号为 (4,2 ) ,那么该同学的位置是 ( )(A )第2排第4列 (B )第4排第2列 (C )第2列第4排 (D )不好确定 2.以下各点中 ,在第二象限的点是 ( )(A ) (2 ,3 ) (B ) (2 ,－3 ) (C ) (－2 ,－3 ) (D ) (－2 ,3 )3.假设x 轴上的点P 到y 轴的距离为3,那么点P 的坐标为 ( )(A ) (3,0 ) (B ) (0,3 ) (C ) (3,0 )或 (－3,0 ) (D ) (0,3 )或 (0,－3 ) 4.点M (1m + ,3m + )在x 轴上 ,那么点M 坐标为 ( )． (A ) (0 ,－4 ) (B ) (4 ,0 ) (C ) (－2 ,0 ) (D ) (0 ,－2 )x 轴上方 ,y 轴左侧 ,距离x 轴2个单位长度 ,距离y 轴3个单位长度 ,那么点C 的坐标为( )(A ) (3,2 ) (B ) (3,2-- ) (C ) (2,3- ) (D ) (2,3- ) 6.如果点P (5,y )在第四象限,那么y 的取值范围是 ( )(A )0y < (B )0y > (C )0y ≤ (D )0y ≥7.如图：正方形ABCD 中点A 和点C 的坐标分别为)3,2(-和)2,3(- ,那么点B 和点D 的坐标分别为 ( ).(A ))2,2(和)3,3( (B ))2,2(--和)3,3( (C ))2,2(--和)3,3(-- (D ))2,2(和)3,3(--8.一个长方形在平面直角坐标系中三个顶点的坐标为 (－1,－1 ), (－1,2 ), (3,－1 )•,那么第四个顶点的坐标为 ( )(A ) (2,2 ) (B ) (3,2 ) (C ) (3,3 ) (D ) (2,3 )9.线段AB 两端点坐标分别为A (4,1- ) ,B (1,4- ) ,现将它向左平移4个单位长度 ,得到线段A 1B 1 ,那么A 1、B 1的坐标分别为 ( )(A )A 1 (0,5- ) ,B 1 (3,8-- ) (B )A 1 (7,3 ) , B 1 (0 ,5 ) (C )A 1 (4,5- ) B 1 (－8 ,1 ) (D )A 1 (4,3 ) B 1 (1,0 )10.在方格纸上有A 、B 两点 ,假设以B 点为原点建立直角坐标系 ,那么A 点坐标为 (2 ,5 ) ,假设以A 点为原点建立直角坐标系 ,那么B 点坐标为 ( ).(A ) (－2 ,－5 ) (B ) (－2 ,5 ) (C ) (2 ,－5 ) (D ) (2 ,5 ) 二、细心填一填: (本大题共有8小题 ,每题3分 ,共24分．请把结果直接填在题中的横线上．只要你理解概念 ,仔细运算 ,积极思考 ,相信你一定会填对的 ! )11.七年级| (2 )班教室里的座位共有7排8列 ,其中小明的座位在第3排第7列 ,简记为 (3 ,7 ) ,小华坐在第5排第2列 ,那么小华的座位可记作__________.12. 假设点P (a ,b - )在第二象限,那么点Q (ab -,a b + )在第_______象限.13. 假设点P 到x 轴的距离是12,到y 轴的距离是15,那么P 点坐标可以是________ (写出一个即可 ).14.小华将直角坐标系中的猫的图案向右平移了3个单位长度,平移前猫眼的坐标为 (－4,3 ), (－2,3 ),那么移动后猫眼的坐标为_________.15. 点P (x ,y )在第四象限 ,且|x | =3 ,|y | =5 ,那么点P 的坐标是______. 16. 如图 ,中国象棋中的 "象〞 ,在图中的坐标为 (1 ,0 ) ,•假设 "象〞再走一步 ,试写出下一步它可能走到的位置的坐标________．17.如以下图,小强告诉小华图中A 、B 两点的坐标分别为 (－3,5 ), (3,5 ),•小华一下就说出了C 在同一坐标系下的坐标________.18.点P 的坐标 (2a - ,36a + ) ,且点P 到两坐标轴的距离相等 ,那么点P 的坐标是. 三、认真答一答: (本大题共4小题 ,每题10分 ,共40分. 只要你认真思考, 仔细运算, 一定会解答正确的! )19. 如图,这是某市局部简图,请建立适当的平面直角坐标系,分别写出各地的坐标.20. 适当建立直角坐标系 ,描出点 (0 ,0 ) , (5 ,4 ) , (3 ,0 ) , (5 ,1 ) , (5 , -1 ) , (3 ,0 ) , (4 , -2 ) , (0 ,0 ) ,并用线段顺次连接各点. ⑴看图案像什么 ?⑵作如下变化：纵坐标不变 ,横坐标减2 ,并顺次连接各点 ,所得的图案与原来相比有什么变化 ?21.某学校校门在北侧,进校门向南走30米是旗杆,再向南走30米是教学楼, 从教学楼向东走60米,再向北走20米是图书馆,从教学楼向南走60米,再向北走10 米是实验楼,请你选择适当的比例尺,画出该校的校园平面图.22.坐标平面内的三个点A (1 ,3 ) ,B (3 ,1 ) ,O (0 ,0 ) ,求△ABO的面积．四、动脑想一想:(本大题共有2小题 ,每题13分 ,共26分. 只要你认真探索 ,仔细思考 ,你一定会获得成功的 ! )23. 请自己动手,建立平面直角坐标系,在坐标系中描出以下各点的位置：E(F2,2),D--,3(B-C-),3(-)4,43,3A,)0,0(),,5(5),(你发现这些点有什么位置关系?你能再找出类似的点吗? (再写出三点即可)24.这是一个动物园游览示意图,试设计描述这个动物园图中每个景点位置的一个方法,并画图说明.参考答案：1.D；2.D；3.C；4.C；5.C；6.A；7.B；8.B；9.C；10.A；11. (5 ,2 )；12.三；13. (15,12 )或 (15, -12 )或 ( -15,12 )或 ( -15, -12 )；14. (－1,3 ), (1,3 )；15. (3 ,－5 )；16. (3 ,2 ) , (3 , -2 ) , ( -1 ,2 ) , ( -1 , -2 )；17. (－1,7 )；18. (3 ,3 )或 (6 , -6 )；19.答案不唯一.如图：火车站 (0,0 ),宾馆 (2,2 ) ,市场 (4,3 ) ,超市 (2,－3 ) ,医院 (－2,－2 ) ,文化宫 (－3,1 ) ,体育场 (－4,3 ).20. (1 ) "鱼〞； (2 )向左平移2个单位. 21.略；22.解：如答图所示 ,过A ,B 分别作y 轴 ,x 轴的垂线 ,垂足为C ,E ,两线交于点D , 那么C (0 ,3 ) ,D (3 ,3 ) ,E (3 ,0 )． 又因为O (0 ,0 ) ,A (1 ,3 ) ,B (3 ,1 ) , 所以OC =3 ,AC =1 ,OE =3 ,BE =1． AD =DC -AC =3 -1 =2 , BD =DE -BE =3 -1 =2．那么四边形OCDE 的面积为3×3 =9 , △ACO 和△BEO 的面积都为12×3×1 =32, △ABD 的面积为12×2×2 =2 , 所以△ABO 的面积为9 -2×32-2 =4． 23.这些点在同一直线上 ,在二四象限的角平分线上 ,举例略. 24.答案不唯一 ,略.第八章二元一次方程组水平测试题 (A )一、选择题1、假设23815m n x y -+-=是关于x y 、的二元一次方程 ,那么m n += ( ) A.1- B.2 C.1 D.2-2、以11x y =⎧⎨=-⎩为解的二元一次方程组是 ( )A ．01x y x y +=⎧⎨-=⎩ B ．01x y x y +=⎧⎨-=-⎩ C ．02x y x y +=⎧⎨-=⎩ D ．02x y x y +=⎧⎨-=-⎩3、为紧急安置100名地震灾民 ,需要同时搭建可容纳6人和4人的两种帐篷 ,那么搭建方案共有 ( ) A ．8种B ．9种C ．16种D ．17种4、同时满足方程21132x y +=与325x y +=的解是 ( ) A ．23x y ==， B ．34x y =-=， C ．32x y ==-，D ．32x y =-=-，5、代数式1312a x y -与23b a b x y -+-是同类项 ,那么a 、b 的值分别是 ( ) A.21a b =⎧⎨=-⎩ B.21a b =⎧⎨=⎩ C.21a b =-⎧⎨=-⎩ D.21a b =-⎧⎨=⎩ 6、2(5)23100x y x y +-+--=若 ,那么代数式xy 的值是 ( )A. 6B. -6C.0D. 57、假设方程组⎩⎨⎧=+=-81my nx ny mx 的解是⎩⎨⎧==12y x ,那么m 、n 的值分别是 ( ) A. m =2 ,n =1 B. m =2 ,n =3 C. m =1 ,n =8 D. 无法确定8、如图 ,点O 在直线AB 上 ,OC 为射线 ,1∠比2∠的3倍少︒10 ,设1∠ ,2∠的度数分别为x ,y ,那么以下求出这两个角的度数的方程是 ( )A.⎩⎨⎧-==+10180y x y xB.⎩⎨⎧-==+103180y x y x C.⎩⎨⎧+==+10180y x y x D.⎩⎨⎧-==1031803y x y 9、某校七年级| (2 ),共捐款100元. 捐款情况如表：表格中捐款2元和3.假设设捐款2元的有x 名同学 ,捐款3元的有y 名同学 ,根据题意 ,可得方程组 ( ) A.⎩⎨⎧=+=+663227y x y x B.⎩⎨⎧=+=+1003227y x y x C.⎩⎨⎧=+=+662327y x y x D.⎩⎨⎧=+=+1002327y x y x 10、 "十一黄金周〞期间 ,几位同学一起去郊外游玩. 男同学都背着红色的旅行包 ,女同学都背着黄色的旅行包. 其中一位男同学说 ,我看到红色旅行包个数是黄色旅行包个数的倍. 另一位女同学说 ,我看到红色旅行包个数是黄色旅行包个数的2倍. 如果这两位同学说的都对 ,那么女同学的人数是 ( )A.2B.4 C二、填空题1、二元一次方程132=-y x 中 ,假设3=x 时 ,=y ；假设1=y 时 ,那么=x .2、我们知道解二元一次方程组的根本思想方法是 "消元〞 ,那么解方程组⎩⎨⎧=+=-523224y x ,y x 宜用______法；解方程组⎩⎨⎧=-=322y x ,y x 宜用______法．C A B 1 2 O3、⎩⎨⎧=-=42y x 和⎩⎨⎧-==14y x 都是方程y =ax +b 的解 ,那么a =_______, b =_______.4、方程组⎩⎨⎧=-=+632y x y x 的解满足方程==+k k y x 则,2 .5、a 的相反数是2b －1 ,b 的相反数是3a +1 ,那么a 2 +b 2 =_________.6、假设二元一次方程组⎩⎨⎧=+=-11532by ax y x 和⎩⎨⎧=+=-15y x ay cx 同解 ,那么可通过解方程组 _________ 求得这个解.7、在代数式mx +n 中 ,当x =3时 ,它的值是4 ,当x =4时 ,它的值是7 ,那么m =_________,n =_________.8、陕北的放羊娃隔着沟峁唱着信天游,比他们养的羊数.一个唱到: "你羊没有我羊多,你假设给我一只羊,我的是你的两倍〞,另一个随声唱到: "没那事,你要给我给一只,咱俩的羊儿一样多〞.听了他们的对唱,你能知道他们各有多少只羊吗?答：________________.9、有甲、乙、丙三种商品 ,如果购甲3件、乙2件 ,丙1件共需315元钱 ,购甲1件、乙2件、丙3件共需285元钱 ,那么购甲、乙、丙三种商品各一件共需元钱．10、某商场正在热销2021年北京奥运会桔祥物 "福娃〞玩具和徽章两种奥运商品 ,根据以下图提供的信息 ,那么一盒 "福娃〞玩具的价格是.三、解答题1、解方程组(1 )⎩⎨⎧=+=-)2(523)1(82y x y x (2 )⎪⎩⎪⎨⎧=-+=+.11)1(2,231y x y x 2、假设二元一次方程组233221x y k x y k +=-⎧⎨-=+⎩的解互为相反数 ,求k 的值.3、七年级|三班在召开期末总结表彰会前 ,班主任安排班长李小波去商店买奖品 ,下面是李小波与售货员的对话：李小波：阿姨 ,您好 !售货员：同学 ,你好 ,想买点什么 ?李小波：我只有100元 ,请帮我安排买10支钢笔和15本笔记本．售货员：好 ,每支钢笔比每本笔记本贵2元 ,退你5元 ,请清点好 ,再见．根据这段对话 ,你能算出钢笔和笔记本的单价各是多少吗 ?4、如图 ,在33⨯的方格内 ,填写了一些代数式和数． (1 )在图1中各行、各列及对角线上三个数之和都相等 ,请你求出x ,y 的值；(2 )把满足 (1 )的其它6个数填入图2中的方格内．5、某高校共有5个餐厅和2个小餐厅 ,经过测试：同时开放1个大餐厅、2个小餐厅 ,可供1680名学生就餐；同时开放2个大餐厅、1个小餐厅 ,可供2280名学生就餐． 23-4y 23- (图1 ) (图2 )32x y 3共计145元 共计280元(1 )求1个大餐厅、1个小餐厅分别可供多少名学生就餐；(2 )假设7个大餐厅同时开放 ,能否供全校的5300名学生就餐 ?请说明理由．6、为了保证春节的蔬菜供给 ,某公司准备提前收购蔬菜140吨加工后上市销售．该公司的加工能力是：每天精加工6吨或者粗加工16吨．假设方案用15天完成加工任务 ,该公司应怎样安排加工时间 ,才能按期完成加工任务 ?如果按现在市场价格 ,预计每吨蔬菜粗加工后可获利润800元 ,精加工后可获利润1500元 ,那么该公司出售这些加工后的蔬菜共可获利多少元 ?四、拓广探索1、5·12汶川大地震引起山体滑坡堵塞河谷后 ,形成了许多堰塞湖. 据(中|央）电视台报道：唐家山堰塞湖危险性最|大. 为了尽快排除险情 ,决定在堵塞体外表开挖一条泄流槽, 经计算需挖出土石方万立方米 ,开挖2天后 ,为了加快施工进度 ,又增调了大量的人员和设备 ,每天挖的土石方比原来的2倍还多1万立方米 ,结果共用5天完成任务 ,比方案时间大大提前.根据以上信息 ,求原方案每天挖土石方多少万立方米 ?增调人员和设备后每天挖土石方多少万立方米 ?2、小明在拼图时 ,发现8个一样大小的长方形 ,如图 (1 )所示 ,恰好可以拼成一个大的矩形. 小红看见了 ,说： "我来试一试 ,〞结果小红七拼八凑 ,拼成如图 (2 )那样的正方形 ,咳 !怎么中间还留下了一个洞 ,恰好是边长为2mm 的小正方形 !你能帮他们解开其中的奥秘吗 ? (提示：能求出小长方形的长和宽吗 ? )参考答案一、【解析】根据同类项定义构造方程组⎩⎨⎧=+=+321b a b a 求解. 【解析】根据非负性构造方程组⎩⎨⎧=--=-+0103205y x y x 求解. 二、1. 35 ,2 2. 加减 ,代入 3. 37,65-4. －35. 1【解析】根据相反数定义构造方程组⎩⎨⎧=++=-+013012a b b a 求解. 6. ⎩⎨⎧=+=-11532y x y x 7. 3 ,－58. 7只 ,5只9. 150【解析】由题可得甲、乙、丙商品各4件共需600元 ,那么各一件需150元.10. 125元三、1. 解： (1 )⎩⎨⎧-==23y x ； (2 )⎩⎨⎧==15y x2．解：解方程组得⎪⎪⎩⎪⎪⎨⎧--=-=753738k y k x ,因为x 、y 互为相反数 ,那么有0753738=--+-k k , 解得85k =. 3．解：设钢笔每支为x 元 ,笔记本每本y 元 ,据题意 ,得210151005x y x y =+⎧⎨+=-⎩，．解方程组 ,得53.x y =⎧⎨=⎩， 答：钢笔每支5元 ,笔记本每本3元．4．解： (1 )由条件可得： 234345x y y y +=-⎧⎨+=⎩，．解得11x y =-⎧⎨=⎩，． (2 )求出x 、y 的值后 ,可以发现每行与每列及对角线上三个数之和都为3 ,从而依次可得第二行第|一列的数是5 ,第三行第|一列的数是0 ,第三行第二列的数是－1.5．解： (1 )设1个大餐厅可供x 名学生就餐 ,1个小餐厅可供y 名学生就餐 ,依题意 , 得2168022280.x y x y +=⎧⎨+=⎩， ,解得960360.x y =⎧⎨=⎩， 答：1个大餐厅可供960名学生就餐 ,1个小餐厅可供360名学生就餐．(2 )因为9605360255205300⨯+⨯=> ,所以如果同时开放7个餐厅 ,能够供全校的5300名学生就餐．6．解：设应安排x 天精加工 ,y 天粗加工 ,根据题意 ,得⎩⎨⎧=+=+14016615y x y x ,解得⎩⎨⎧==510y x 所以应安排10天精加工 ,5天粗加工．出售这些加工后的蔬菜一共可获利：1500×6×10＋800×16×5＝154000 (元 )四、1．解：设原方案每天挖土石方x 万立方米 ,增调人员和设备后每天挖y 万立方米 ,那么⎩⎨⎧=-++=4.13)25(212y x x y ,解得：⎩⎨⎧==6.33.1y x 答：原方案每天挖土石方万立方米 ,增调人员和设备后每天挖万立方米.2．解：设长方形长为x ,宽为y ,那么⎩⎨⎧=-=2253x y y x ,解得⎩⎨⎧==1018y x . 故长方形长为18㎝ ,宽为10㎝.2 3-3 2- 5 1 0 1-4 图3第9章不等式与不等式组综合测试题1一、选择题:(每题3分,共30分)1.以下根据语句列出的不等式错误的选项是( )A. "x 的3倍与1的和是正数〞 ,表示为3x +1>0.B. "m 的15与n 的13的差是非负数〞,表示为15m -13n ≥0. C. "x 与y 的和不大于a 的12〞,表示为x +y ≤12a. D. "a 、b 两数的和的3倍不小于这两数的积〞,表示为3a +b ≥ab.2.给出以下命题:①假设a>b,那么ac 2>bc 2;②假设ab>c,那么b>c a;③假设-3a>2a,那么a<0;•④假设a<b,那么a -c<b -c,其中正确命题的序号是( )A.③④B.①③C.①②D.②④ 32<2x -2中,出现错误的一步是( ) A.6x -3<4x -4 B.6x -4x< -4 +3 C.2x< -1 D.x> -1212,39x x -<⎧⎨-≤⎩ 的解集在数轴上表示出来是( ) 5. .以下结论:①4a>3a;②4 +a>3 +a;③4 -a>3 -a 中,正确的选项是( )A.①②B.①③C.②③D.①②③6.某足协举办了一次足球比赛,记分规那么是:胜一场积3分,平一场积1分,负一场积0分.假设甲队比赛了5场共积7分,那么甲队可能平了( )7.某班学生在颁奖大会上得知该班获得奖励的情况如下表:该班共有28人获得奖励,其中获得两项奖励的有13人,那么该班获得奖励最|多的一位同学可获得的奖励为( )│a │> -a,那么a 的取值范围是( )≥9.不等式23>7 +5x 的正整数解的个数是( )(x +3)2 +│3x +y +m │ = 0中,y 为负数,那么m 的取值范围是( )A.m>9B.m<9C.m> -9D.m< -9二、填空题:(每题3分,共24分)11.假设y =2x -3,当x______时,y ≥0;当x______时,y<5.12.假设x =3是方程2x a - -2 =x -1的解,那么不等式(5 -a)x<12的解集是_______. 2123x a x b -<⎧⎨->⎩的解集为 -1<x<1,那么a =_______,b =_______. 14. (2021苏州 )6月1日起 ,某超市开始有偿．．提供可重复使用的三种环保购物袋 ,每只售价分别为1元、2元和3元 ,这三种环保购物袋每只最|多分别能装大米3公斤、5公斤和8公斤．6月7日 ,小星和爸爸在该超市选购了3只环保购物袋用来装刚买的20公斤散装大米 ,他们选购的3只环保购物袋至．|．少．应付给超市元． 204060x x x +>⎧⎪->⎨⎪-<⎩的解集为________.16.小明用100元钱去购置笔记本和钢笔共30分,每本笔记本2元,•每枝钢笔5元,那么小明最|多能买________枝钢笔.212x m x m >+⎧⎨>+⎩的解集是x> -1,那么m 的值是_______. 18.关于x 、y 的方程组321431x y a x y a +=+⎧⎨+=-⎩的解满足x>y,那么a 的取值范围是_________.三、解答题:(共46分)19.解不等式(组)并把解集在数轴上表示出来(每题4分,共16分) (1)5(x +2)≥1 -2(x -1) (2) 2731205y y y +>-⎧⎪-⎨≥⎪⎩ (3) 42x - -3<522x +; (4) 32242539x x x x x +>⎧⎪->-⎨⎪->-⎩20. (5分)k取何值时,方程23x -3k =5(x -k) +1的解是负数.21. (5分)某种客货车车费起点是2km455m车费增加0.5元.现从A处到B处,共支出车费9.8元;如果从A到B,先步行了300m然后乘车也是9.8元,求AB的中点C到B处需要共付多少车费?22.(5分)(1)A、B、C三人去公园玩跷跷板 ,从下面的示意图(1)•中你能判断三人的轻重吗?(2)P、Q、R、S四人去公园玩跷跷板,从示意图(2)•中你能判断这四个人的轻重吗?23. (7分)某市 "全国文明村〞白村果农|王保收获枇杷20吨 ,桃子12吨．现方案租用甲、乙两种货车共8辆将这批水果全部运往外地销售 ,一辆甲种货车可装枇杷4吨和桃子1吨 ,一辆乙种货车可装枇杷和桃子各2吨．(1 )|王保如何安排甲、乙两种货车可一次性地运到销售地 ?有几种方案 ?(2 )假设甲种货车每辆要付运输费300元 ,乙种货车每辆要付运输费240元 ,那么果农|王灿应选择哪种方案 ,使运输费最|少 ?最|少运费是多少 ?24.(8分)2021年我市筹备30周年庆典 ,园林部门决定利用现有的3490盆甲种花卉和2950盆乙种花卉搭配A B，两种园艺造型共50个摆放在迎宾大道两侧 ,搭配一个A种造型需甲种花卉80盆 ,乙种花卉40盆 ,搭配一个B种造型需甲种花卉50盆 ,乙种花卉90盆． (1 )某校九年级| (1 )班课外活动小组承接了这个园艺造型搭配方案的设计 ,问符合题意的搭配方案有几种 ?请你帮助设计出来．(2 )假设搭配一个A种造型的本钱是800元 ,搭配一个B种造型的本钱是960元 ,试说明(1 )中哪种方案本钱最|低 ?最|低本钱是多少元 ?参考答案一、1.D 2.A 3.D 4.A 5. C 6.C 7.B 8.B 9.C 10.A≥32,x<4 ； 12.x<120； 13.a =1,b = -2； 14.8 ；15.4<x<6 ； 16.13； 17. -3； 18.a> -6.三、19. (1 )x≥ -1 (2 )2≤y<8;(3)x> -3; (4) -2<x<320.k<1 221.设走xm需付车费y元,n为增加455m的次数.∴y =2.8 +0.5n,可得n =70.5=14∴2000 +455×13<x ≤2000 +455×14即7915<x ≤8370,又7915<x -300≤8370∴8215<x ≤8670,故8215<x ≤8370,CB 为2x ,且4107.5<2x ≤4185, 4107.52000455- =4.63<5,41852000455- =4.8<5, ∴×5 =5.3(元)∴从C 到B 需支付车费5.3元.22.(1)C 的重量>A 的重量>B 的重量(2)从图中可得S>P,P +R>Q +S ,R>Q +(S -R),∴R>Q;由P +R>Q +S ,S -P<R -Q ∴ (Q +R -P) -P<R -Q ∴P>Q,同理R>S,∴R>S>P>Q23. 解： (1 )设安排甲种货车x 辆 ,那么安排乙种货车 (8－x )辆 ,依题意 ,得4x + 2 (8－x )≥20 ,且x + 2 (8－x )≥12 ,解此不等式组 ,得 x ≥2 ,且 x ≤4 , 即 2≤x ≤4．∵x 是正整数 ,∴x 可取的值为2 ,3 ,4．因此安排甲、乙两种货车有三种方案：甲种货车 乙种货车 方案一2辆 6辆 方案二3辆 5辆 方案三 4辆 4辆(2 )方案一所需运费 300×2 + 240×6 = 2040元；方案二所需运费 300×3 + 240×5 = 2100元；方案三所需运费 300×4 + 240×4 = 2160元．所以|王保应选择方案一运费最|少 ,最|少运费是2040元．24. 解：设搭配A 种造型x 个 ,那么B 种造型为(50)x -个 ,依题意 ,得：8050(50)34904090(50)2950x x x x +-⎧⎨+-⎩≤≤ ,解这个不等式组 ,得：3331x x ⎧⎨⎩≤≥ ,3133x ∴≤≤x是整数 ,x∴可取313233，， ,∴可设计三种搭配方案：①A种园艺造型31个B种园艺造型19个②A种园艺造型32个B种园艺造型18个③A种园艺造型33个B种园艺造型17个．(2 )方法一：由于B种造型的造价本钱高于A种造型本钱．所以B种造型越少 ,本钱越低 ,⨯+⨯= (元 )故应选择方案③ ,本钱最|低 ,最|低本钱为：338001796042720⨯+⨯= (元 )方法二：方案①需本钱：318001996043040⨯+⨯= (元 )方案②需本钱：328001896042880⨯+⨯=元方案③需本钱：338001796042720∴应选择方案③ ,本钱最|低 ,最|低本钱为42720元第十章?数据的收集、整理与描述?单元检测试题一、选择题1.调查下面问题,应该进行抽样调查的是( )A.调查某校七(2 )班同学的体重情况B.调查我省中小学生的视力近视情况C.调查某校七(5 )班同学期（中|考）试数学成绩情况D.调查某中学全体教师家庭的收入情况2.实验中学七年级|进行了一次数学测验,参考人数共540人,为了了解这次数学测验成绩,以下所抽取的样本中较为合理的是( )A.抽取前100名同学的数学成绩B.抽取后100名同学的数学成绩C.抽取(1 )、(2 )两班同学的数学成绩D.抽取各班学号为3号的倍数的同学的数学成绩3.在以下调查中,比拟容易用普查方式的是( )A.了解贵阳市居民年人均收入B.了解贵阳市初中生体育（中|考）的成绩C.了解贵阳市中小学生的近视率D.了解某一天离开贵阳市的人口流量4.统计得到的一组数据有80个,其中最|大值为141 ,最|小值为50 ,取组距为10 ,可以分成( )A.10组B.9组C.8组D.7组5.在频数分布直方图中,各小长方形的高等于相应组的( )A.组距B.组数C.频数D.频率6.某单位有职工100名,按他们的年龄分成8组,在40～42 (岁)组内有职工32名,那么这个小组的频率是( )A. B.0.38 C.0.32 D.327.根据呼和浩特市第|一季度用电量的扇形统计图,那么2月份用电量占第|一季度用电量的百分比为( )A.60%B.64%C.54%D.74%8.一个扇形统计图中,扇形A、B、C、D的面积之比为2∶3∶3∶4 ,那么最|大扇形的圆。

第五章 相交线与平行线1相交线学习要求1．能从两条直线相交所形成的四个角的关系入手，理解对顶角、互为邻补角的概念，掌握对顶角的性质．2．能依据对顶角的性质、邻补角的概念等知识，进行简单的计算．课堂学习检测一、填空题1．如果两个角有一条______边，并且它们的另一边互为____________，那么具有这种关系的两个角叫做互为邻补角．2．如果两个角有______顶点，并且其中一个角的两边分别是另一个角两边的___________ ________，那么具有这种位置关系的两个角叫做对顶角． 3．对顶角的重要性质是_________________．4．如图，直线AB 、CD 相交于O 点，∠AOE ＝90°．(1)∠1和∠2叫做______角；∠1和∠4互为______角； ∠2和∠3互为_______角；∠1和∠3互为______角； ∠2和∠4互为______角．(2)若∠1＝20°，那么∠2＝______；∠3＝∠BOE －∠______＝______°－______°＝______°； ∠4＝∠______－∠1＝______°－______°＝______°． 5．如图，直线AB 与CD 相交于O 点，且∠COE ＝90°，则(1)与∠BOD 互补的角有________________________； (2)与∠BOD 互余的角有________________________； (3)与∠EOA 互余的角有________________________； (4)若∠BOD ＝42°17′，则∠AOD ＝__________； ∠EOD ＝______；∠AOE ＝______． 二、选择题6．图中是对顶角的是( )．7．如图，∠1的邻补角是( )．(A)∠BOC (B)∠BOC 和∠AOF (C)∠AOF (D)∠BOE 和∠AOF 8．如图，直线AB 与CD 相交于点O ，若AOD AOC ∠=∠31，则∠BOD 的度数为( )． (A)30° (B)45° (C)60°(D)135°9．如图所示，直线l1，l2，l3相交于一点，则下列答案中，全对的一组是( )．(A)∠1＝90°，∠2＝30°，∠3＝∠4＝60°(B)∠1＝∠3＝90°，∠2＝∠4＝30°(C)∠1＝∠3＝90°，∠2＝∠4＝60°(D)∠1＝∠3＝90°，∠2＝60°，∠4＝30°三、判断正误10．如果两个角相等，那么这两个角是对顶角．( ) 11．如果两个角有公共顶点且没有公共边，那么这两个角是对顶角．( ) 12．有一条公共边的两个角是邻补角．( ) 13．如果两个角是邻补角，那么它们一定互为补角．( ) 14．对顶角的角平分线在同一直线上．( ) 15．有一条公共边和公共顶点，且互为补角的两个角是邻补角．( )综合、运用、诊断一、解答题16．如图所示，AB，CD，EF交于点O，∠1＝20°，∠BOC＝80°，求∠2的度数．17．已知：如图，直线a，b，c两两相交，∠1＝2∠3，∠2＝86°．求∠4的度数．18．已知：如图，直线AB，CD相交于点O，OE平分∠BOD，OF平分∠COB，∠AOD∶∠DOE＝4∶1．求∠AOF的度数．19．如图，有两堵围墙，有人想测量地面上两堵围墙内所形成的∠AOB的度数，但人又不能进入围墙，只能站在墙外，请问该如何测量?拓展、探究、思考20．如图，O是直线CD上一点，射线OA，OB在直线CD的两侧，且使∠AOC＝∠BOD，试确定∠AOC与∠BOD是否为对顶角，并说明你的理由．21．回答下列问题：(1)三条直线AB，CD，EF两两相交，图形中共有几对对顶角(平角除外)?几对邻补角?(2)四条直线AB，CD，EF，GH两两相交，图形中共有几对对顶角(平角除外)?几对邻补角?(3)m条直线a1，a2，a3，…，a m－1，a m相交于点O，则图中一共有几对对顶角(平角除外)?几对邻补角?2 垂线学习要求1．理解两条直线垂直的概念，掌握垂线的性质，能过一点作已知直线的垂线．2．理解点到直线的距离的概念，并会度量点到直线的距离．课堂学习检测一、填空题1．当两条直线相交所成的四个角中，有一个角是直角时，就说这两条直线______，其中一条直线叫做另一条直线的______线，它们的交点叫做______．2．垂线的性质性质1：平面内，过一点____________与已知直线垂直．性质2：连接直线外一点与直线上各点的_________中，_________最短．3．直线外一点到这条直线的__________________叫做点到直线的距离．4．如图，直线AB，CD互相垂直，记作______；直线AB，CD互相垂直，垂足为O点，记作____________；线段PO的长度是点_________到直线_________的距离；点M到直线AB的距离是_______________．二、按要求画图5．如图，过A点作CD⊥MN，过A点作PQ⊥EF于B．图a 图b 图c6．如图，过A点作BC边所在直线的垂线EF，垂足是D，并量出A点到BC边的距离．图a 图b 图c7．如图，已知∠AOB及点P，分别画出点P到射线OA、OB的垂线段PM及PN．图a 图b 图c8．如图，小明从A村到B村去取鱼虫，将鱼虫放到河里，请作出小明经过的最短路线．综合、运用、诊断一、判断下列语句是否正确(正确的画“√”，错误的画“×”)9．两条直线相交，若有一组邻补角相等，则这两条直线互相垂直．( ) 10．若两条直线相交所构成的四个角相等，则这两条直线互相垂直． ( ) 11．一条直线的垂线只能画一条． ( ) 12．平面内，过线段AB 外一点有且只有一条直线与AB 垂直． ( ) 13．连接直线l 外一点到直线l 上各点的6个有线段中，垂线段最短． ( ) 14．点到直线的距离，是过这点画这条直线的垂线，这点与垂足的距离． ( ) 15．直线外一点到这条直线的垂线段，叫做点到直线的距离． ( ) 16．在三角形ABC 中，若∠B ＝90°，则AC ＞AB ． ( )二、选择题17．如图，若AO ⊥CO ，BO ⊥DO ，且∠BOC ＝α，则∠AOD 等于( )．(A)180°－2α (B)180°－α(C)α2190+︒ (D)2α－90°18．如图，点P 为直线m 外一点，点P 到直线m 上的三点A 、B 、C 的距离分别为P A ＝4cm ，PB ＝6cm ，PC ＝3cm ，则点P 到直线m 的距离为( )． (A)3cm (B)小于3cm (C)不大于3cm (D)以上结论都不对19．如图，BC ⊥AC ，CD ⊥AB ，AB ＝m ，CD ＝n ，则AC 的长的取值范围是( )．(A)AC ＜m (B)AC ＞n (C)n ≤AC ≤m (D)n ＜AC ＜m 20．若直线a 与直线b 相交于点A ，则直线b 上到直线a 距离等于2cm的点的个数是( )． (A)0 (B)1 (C)2 (D)3 21．如图，AC ⊥BC 于点C ，CD ⊥AB 于点D ，DE ⊥BC于点E ，能表示点到直线(或线段)的距离的线段有( )． (A)3条 (B)4条 (C)7条 (D)8条 三、解答题22．已知：OA ⊥OC ，∠AOB ∶∠AOC ＝2∶3．求∠BOC 的度数．23．已知：如图，三条直线AB ，CD ，EF 相交于O ，且CD ⊥EF ，∠AOE ＝70°，若OG 平分∠BOF ．求∠DOG ．拓展、探究、思考24．已知平面内有一条直线m 及直线外三点A ，B ，C ，分别过这三个点作直线m 的垂线，想一想有几个不同的垂足?画图说明．25．已知点M ，试在平面内作出四条直线l 1，l 2，l 3，l 4，使它们分别到点M 的距离是1.5cm ．·M26．从点O 引出四条射线OA ，OB ，OC ，OD ，且AO ⊥BO ，CO ⊥DO ，试探索∠AOC与∠BOD 的数量关系．27．一个锐角与一个钝角互为邻角，过顶点作公共边的垂线，若此垂线与锐角的另一边构成75直角，与钝角的另一边构成直73角，则此锐角与钝角的和等于直角的多少倍?3 同位角、内错角、同旁内角学习要求当两条直线被第三条直线所截时，能从所构成的八个角中识别出哪两个角是同位角、内错角及同旁内角．课堂学习检测一、填空题1．如图，若直线a，b被直线c所截，在所构成的八个角中指出，下列各对角之间是属于哪种特殊位置关系的角?(1)∠1与∠2是_______；(2)∠5与∠7是______；(3)∠1与∠5是_______；(4)∠5与∠3是______；(5)∠5与∠4是_______；(6)∠8与∠4是______；(7)∠4与∠6是_______；(8)∠6与∠3是______；(9)∠3与∠7是______；(10)∠6与∠2是______．2．如图2所示，图中用数字标出的角中，同位角有______；内错角有______；同旁内角有______．3．如图3所示，(1)∠B和∠ECD可看成是直线AB、CE被直线______所截得的_______角；(2)∠A和∠ACE可看成是直线_______、______被直线_______所截得的______角．4．如图4所示，(1)∠AED和∠ABC可看成是直线______、______被直线______所截得的_______角；(2)∠EDB和∠DBC可看成是直线______、______被直线_______所截得的______角；(3)∠EDC和∠C可看成是直线_______、______被直线______所截得的______角．综合、运用、诊断一、选择题5．已知图①～④，图①图②图③图④在上述四个图中，∠1与∠2是同位角的有( )．图2 图3 图4(A)①②③④(B)①②③(C)①③(D)①6．如图，下列结论正确的是( )．(A)∠5与∠2是对顶角(B)∠1与∠3是同位角(C)∠2与∠3是同旁内角(D)∠1与∠2是同旁内角7．如图，∠1和∠2是内错角，可看成是由直线( )．(A)AD，BC被AC所截构成(B)AB，CD被AC所截构成(C)AB，CD被AD所截构成(D)AB，CD被BC所截构成8．如图，直线AB，CD与直线EF，GH分别相交，图中的同旁内角共有( )．(A)4对(B)8对(C)12对(D)16对拓展、探究、思考一、解答题9．如图，三条直线两两相交，共有几对对顶角?几对邻补角?几对同位角?几对内错角?几对同旁内角?4 平行线及平行线的判定学习要求1．理解平行线的概念，知道在同一平面内两条直线的位置关系，掌握平行公理及其推论．2．掌握平行线的判定方法，能运用所学的“平行线的判定方法”，判定两条直线是否平行．用作图工具画平行线，从而学习如何进行简单的推理论证．课堂学习检测一、填空题1．在同一平面内，______的两条直线叫做平行线．若直线a与直线b平行，则记作______．2．在同一平面内，两条直线的位置关系只有______、______．3．平行公理是：_______________________________________________________________．4．平行公理的推论是如果两条直线都与______，那么这两条直线也______．即三条直线a，b，c，若a∥b，b∥c，则______．5．两条直线平行的条件(除平行线定义和平行公理推论外)：(1)两条直线被第三条直线所截，如果____________，那么这两条直线平行．这个判定方法1可简述为：____________，两直线平行．(2)两条直线被第三条直线所截，如果____________，那么____________．这个判定方法2可简述为：____________，____________．(3)两条直线被第三条直线所截，如果____________，那么____________．这个判定方法3可简述为：____________，____________．二、根据已知条件推理6．已知：如图，请分别依据所给出的条件，判定相应的哪两条直线平行?并写出推理的根据．(1)如果∠2＝∠3，那么____________．(____________，____________)(2)如果∠2＝∠5，那么____________．(____________，____________)(3)如果∠2＋∠1＝180°，那么____________．(____________，____________)(4)如果∠5＝∠3，那么____________．(____________，____________)(5)如果∠4＋∠6＝180°，那么____________．(____________，____________)(6)如果∠6＝∠3，那么____________．(____________，____________)7．已知：如图，请分别根据已知条件进行推理，得出结论，并在括号内注明理由．(1)∵∠B＝∠3(已知)，∴______∥______．(____________，____________)(2)∵∠1＝∠D(已知)，∴______∥______．(____________，____________)(3)∵∠2＝∠A(已知)，∴______∥______．(____________，____________)(4)∵∠B＋∠BCE＝180°(已知)，∴______∥______．(____________，____________)综合、运用、诊断一、依据下列语句画出图形8．已知：点P是∠AOB内一点．过点P分别作直线CD∥OA，直线EF∥OB．9．已知：三角形ABC及BC边的中点D．过D点作DF∥CA交AB于M，再过D点作DE∥AB交AC于N点．二、解答题10．已知：如图，∠1＝∠2．求证：AB∥CD．(1)分析：如图，欲证AB∥CD，只要证∠1＝______．证法1：∵∠1＝∠2，(已知)又∠3＝∠2，( )∴∠1＝_______．( )∴AB∥CD．(___________，___________)(2)分析：如图，欲证AB∥CD，只要证∠3＝∠4．证法2：∵∠4＝∠1，∠3＝∠2，( )又∠1＝∠2，(已知)从而∠3＝_______．( )∴AB∥CD．(___________，___________)11．绘图员画图时经常使用丁字尺，丁字尺分尺头、尺身两部分，尺头的里边和尺身的上边应平直，并且一般互相垂直，也有把尺头和尺身用螺栓连接起来，可以转动尺头，使它和尺身成一定的角度．用丁字尺画平行线的方法如下面的三个图所示．画直线时要按住尺身，推移丁字尺时必须使尺头靠紧图画板的边框．请你说明：利用丁字尺画平行线的理论依据是什么?拓展、探究、思考12．已知：如图，CD ⊥DA ，DA ⊥AB ，∠1＝∠2．试确定射线DF 与AE 的位置关系，并说明你的理由．(1)问题的结论：DF ______AE ．(2)证明思路分析：欲证DF ______AE ，只要证∠3＝______． (3)证明过程：证明：∵CD ⊥DA ，DA ⊥AB ，( )∴∠CDA ＝∠DAB ＝______°．(垂直定义) 又∠1＝∠2，( )从而∠CDA －∠1＝______－______，(等式的性质) 即∠3＝＿＿＿．∴DF ＿＿＿AE ．(＿＿＿＿，＿＿＿＿)13．已知：如图，∠ABC ＝∠ADC ，BF 、DE 分别平分∠ABC 与∠ADC ．且∠1＝∠3．求证：AB ∥DC ．证明：∵∠ABC ＝∠ADC ，.2121ADC ABC ∠=∠∴( ) 又∵BF 、DE 分别平分∠ABC 与∠ADC ，.212,211ADC ABC ∠=∠∠=∠∴ ( ) ∴∠______＝∠______．( )∵∠1＝∠3，( ) ∴∠2＝∠______．(等量代换) ∴______∥______．( )14．已知：如图，∠1＝∠2，∠3＋∠4＝180°．试确定直线a 与直线c 的位置关系，并说明你的理由．(1)问题的结论：a ______c ．(2)证明思路分析：欲证a ______c ，只要证______∥______且______∥______． (3)证明过程：证明：∵∠1＝∠2，( )∴a ∥______．(________，________)① ∵∠3＋∠4＝180°，( )∴c ∥______．(________，________)② 由①、②，因为a ∥______，c ∥______， ∴a ______c ．(________，________)5 平行线的性质学习要求1．掌握平行线的性质，并能依据平行线的性质进行简单的推理．2．了解平行线的判定与平行线的性质的区别．3．理解两条平行线的距离的概念．课堂学习检测一、填空题1．平行线具有如下性质：(1)性质1：______被第三条直线所截，同位角______．这个性质可简述为两直线______，同位角______．(2)性质2：两条平行线__________________，_______相等．这个性质可简述为_____________，_____________．(3)性质3：__________________，同旁内角______．这个性质可简述为_____________，__________________．2．同时______两条平行线，并且夹在这两条平行线间的______________叫做这两条平行线的距离．二、根据已知条件推理3．如图，请分别根据已知条件进行推理，得出结论，并在括号内注明理由．(1)如果AB∥EF，那么∠2＝______．理由是____________________________________．(2)如果AB∥DC，那么∠3＝______．理由是____________________________________．(3)如果AF∥BE，那么∠1＋∠2＝______．理由是______________________________．(4)如果AF∥BE，∠4＝120°，那么∠5＝______．理由是________________________．4．已知：如图，DE∥AB．请根据已知条件进行推理，分别得出结论，并在括号内注明理由．(1)∵DE∥AB，( )∴∠2＝______．(__________，__________)(2)∵DE∥AB，( )∴∠3＝______．(__________，__________)(3)∵DE∥AB( )，∴∠1＋______＝180°．(______，______)综合、运用、诊断一、解答题5．如图，∠1＝∠2，∠3＝110°，求∠4．解题思路分析：欲求∠4，需先证明______∥______．解：∵∠1＝∠2，( )∴______∥______．(__________，__________)∴∠4＝______＝______°．(__________，__________)6．已知：如图，∠1＋∠2＝180°．求证：∠3＝∠4．证明思路分析：欲证∠3＝∠4，只要证______∥______．证明：∵∠1＋∠2＝180°，( )∴______∥______．(__________，__________)∴∠3＝∠4．(______，______)7．已知：如图，AB∥CD，∠1＝∠B．求证：CD是∠BCE的平分线．证明思路分析：欲证CD是∠BCE的平分线，只要证______＝______．证明：∵AB∥CD，( )∴∠2＝______．(____________，____________)但∠1＝∠B，( )∴______＝______．(等量代换)即CD是________________________．8．已知：如图，AB∥CD，∠1＝∠2．求证：BE∥CF．证明思路分析：欲证BE∥CF，只要证______＝______．证明：∵AB∥CD，( )∴∠ABC＝______．(____________，____________)∵∠1＝∠2，( )∴∠ABC－∠1＝______－______，( )即______＝______．∴BE∥CF．(__________，__________)9．已知：如图，AB∥CD，∠B＝35°，∠1＝75°．求∠A的度数．解题思路分析：欲求∠A，只要求∠ACD的大小．解：∵CD∥AB，∠B＝35°，( )∴∠2＝∠______＝_______°．(____________，____________)而∠1＝75°，∴∠ACD＝∠1＋∠2＝______°．∵CD∥AB，( )∴∠A＋______＝180°．(____________，____________)∴∠A＝_______＝______．10．已知：如图，四边形ABCD 中，AB ∥CD ，AD ∥BC ，∠B ＝50°．求∠D 的度数．分析：可利用∠DCE 作为中间量过渡． 解法1：∵AB ∥CD ，∠B ＝50°，( )∴∠DCE ＝∠_______＝_______°． (____________，______) 又∵AD ∥BC ，( )∴∠D ＝∠______＝_______°．(____________，____________)想一想：如果以∠A 作为中间量，如何求解? 解法2：∵AD ∥BC ，∠B ＝50°，( )∴∠A ＋∠B ＝______．(____________，____________)即∠A ＝______－______＝______°－______°＝______°． ∵DC ∥AB ，( )∴∠D ＋∠A ＝______．(_____________，_____________) 即∠D ＝______－______＝______°－______°＝______°．11．已知：如图，AB ∥CD ，AP 平分∠BAC ，CP 平分∠ACD ，求∠APC 的度数．解：过P 点作PM ∥AB 交AC 于点M ．∵AB ∥CD ，( )∴∠BAC ＋∠______＝180°．( ) ∵PM ∥AB ，∴∠1＝∠_______，( )且PM ∥_______．(平行于同一直线的两直线也互相平行) ∴∠3＝∠______．(两直线平行，内错角相等) ∵AP 平分∠BAC ，CP 平分∠ACD ，( )∠=∠∴211______，∠=∠214______．( ) 90212141=∠+∠=∠+∠∴ACD BAC ．( )∴∠APC ＝∠2＋∠3＝∠1＋∠4＝90°．( ) 总结：两直线平行时，同旁内角的角平分线______．拓展、探究、思考12．已知：如图，AB ∥CD ，EF ⊥AB 于M 点且EF 交CD 于N 点．求证：EF ⊥CD ．13．如图，DE∥BC，∠D∶∠DBC＝2∶1，∠1＝∠2，求∠E的度数．14．问题探究：(1)如果一个角的两条边与另一个角的两条边分别平行，那么这两个角的大小有何关系?举例说明．(2)如果一个角的两边与另一个角的两边分别垂直，那么这两个角的大小有何关系?举例说明．15．如图，AB∥DE，∠1＝25°，∠2＝110°，求∠BCD的度数．16．如图，AB，CD是两根钉在木板上的平行木条，将一根橡皮筋固定在A，C两点，点E 是橡皮筋上的一点，拽动E点将橡皮筋拉紧后，请你探索∠A，∠AEC，∠C之间具有怎样的关系并说明理由．(提示：先画出示意图，再说明理由)．6 命题学习要求1．知道什么是命题，知道一个命题是由“题设”和“结论”两部分构成的．2．对于给定的命题，能找出它的题设和结论，并会把该命题写成“如果……，那么……”的形式．能判定该命题的真假．课堂学习检测一、填空题1．______一件事件的______叫做命题．2．许多命题都是由______和______两部分组成．其中题设是____________，结论是______ _____．3．命题通常写成“如果……，那么……．”的形式．这时，“如果”后接的部分是______，“那么”后接的部分是______．4．所谓真命题就是：如果题设成立，那么结论就______的命题．相反，所谓假命题就是：如果题设成立，不能保证结论______的命题．二、指出下列命题的题设和结论5．垂直于同一条直线的两条直线平行．题设是___________________________________________________________；结论是___________________________________________________________．6．同位角相等，两直线平行．题设是___________________________________________________________；结论是___________________________________________________________．7．两直线平行，同位角相等．题设是___________________________________________________________；结论是___________________________________________________________．8．对顶角相等．题设是___________________________________________________________；结论是___________________________________________________________．三、将下列命题改写成“如果……，那么……”的形式9．90°的角是直角．__________________________________________________________________．10．末位数字是零的整数能被5整除．__________________________________________________________________．11．等角的余角相等．__________________________________________________________________．12．同旁内角互补，两直线平行．__________________________________________________________________．综合、运用、诊断一、下列语句哪些是命题，哪些不是命题?13．两条直线相交，只有一个交点．( ) 14． 不是有理数．( )15．直线a与b能相交吗?( ) 16．连接AB．( )17．作AB⊥CD于E点．( ) 18．三条直线相交，有三个交点．( )二、判断下列各命题中，哪些命题是真命题?哪些是假命题?(对于真命题画“√”，对于假命题画“×”)19．0是自然数．( )20．如果两个角不相等，那么这两个角不是对顶角．( )21．相等的角是对顶角．( )22．如果AC＝BC，那么C点是AB的中点．( )23．若a∥b，b∥c，则a∥c．( )24．如果C是线段AB的中点，那么AB＝2BC．( )25．若x2＝4，则x＝2．( )26．若xy＝0，则x＝0．( )27．同一平面内既不重合也不平行的两条直线一定相交．( )28．邻补角的平分线互相垂直．( )29．同位角相等．( )30．大于直角的角是钝角．( )拓展、探究、思考31．已知：如图，在四边形ABCD中，给出下列论断：①AB∥DC；②AD∥BC；③AB＝AD；④∠A＝∠C；⑤AD＝BC．以上面论断中的两个作为题设，再从余下的论断中选一个作为结论，并用“如果……，那么……”的形式写出一个真命题．答：_____________________________________________________________________．32．求证：两条平行线被第三条直线所截，内错角的平分线互相平行．7 平移学习要求了解图形的平移变换，知道一个图形进行平移后所得的图形与原图形之间所具有的联系和性质，能用平移变换有关知识说明一些简单问题及进行图形设计．课堂学习检测一、填空题1．如图所示，线段ON是由线段______平移得到的；线段DE是由线段______平移得到的；线段FG是由线段______平移得到的．2．如图所示，线段AB在下面的三个平移中(AB→A1B1→A2B2→A3B3)，具有哪些性质．图a图b 图c(1)线段AB上所有的点都是沿______移动，并且移动的距离都________．因此，线段AB，A1B1，A2B2，A3B3的位置关系是____________________；线段AB，A1B1，A2B2，A3B3的数量关系是________________．(2)在平移变换中，连接各组对应点的线段之间的位置关系是______；数量关系是______．3．如图所示，将三角形ABC平移到△A′B′C′．图a 图b在这两个平移中：(1)三角形ABC的整体沿_______移动，得到三角形A′B′C′．三角形A′B′C′与三角形ABC的______和______完全相同．(2)连接各组对应点的线段即AA′，BB′，CC′之间的数量关系是__________________；位置关系是__________________．综合、运用、诊断一、按要求画出相应图形4．如图，AB∥DC，AD∥BC，DE⊥AB于E点．将三角形DAE平移，得到三角形CBF．5．如图，AB∥DC．将线段DB向右平移，得到线段CE．6．已知：平行四边形ABCD及A′点．将平行四边形ABCD平移，使A点移到A′点，得平行四边形A′B′C′D′．7．已知：五边形ABCDE及A′点．将五边形ABCDE平移，使A点移到A′点，得到五边形A′B′C′D′E′．拓展、探究、思考一、选择题8．如图，把边长为2的正方形的局部进行如图①～图④的变换，拼成图⑤，则图⑤的面积是( )．(A)18 (B)16 (C)12 (D)8二、解答题9．河的两岸成平行线，A，B是位于河两岸的两个车间(如图)．要在河上造一座桥，使桥垂直于河岸，并且使A，B间的路程最短．确定桥的位置的方法如下：作从A到河岸的垂线，分别交河岸PQ，MN于F，G．在AG上取AE＝FG，连接EB．EB交MN于D．在D处作到对岸的垂线DC，那么DC就是造桥的位置．试说出桥造在CD位置时路程最短的理由，也就是(AC＋CD＋DB)最短的理由．10．以直角三角形的三条边BC，AC，AB分别作正方形①、②、③，如何用①中各部分面积与②的面积，通过平移填满正方形③?你从中得到什么结论?第六章 实数6.1平方根学习要求1. 理解算术平方根和平方根的含义。

最新⼈教部编版初中七年数学下册全册同步练习答案同步练习参考答案第五章相交线与平⾏线11．公共，反向延长线．2．公共，反向延长线．3．对顶⾓相等．4．略．5．(1)∠BOC，∠AOD；(2)∠AOE；(3)∠AOC，∠BOD；(4)137°43′，90°，47°43′．6．A．7．D．8．B．9．D．10．×，11．×，12．×，13．√，14．√，15．×．16．∠2＝60°．17．∠4＝43°．18．120°．提⽰：设∠DOE＝x°，由∠AOB＝∠AOD＋∠DOB＝6x＝180°，可得x＝30°，∠AOF＝4x＝120°．19．只要延长BO(或AO)⾄C，测出∠AOB的邻补⾓∠AOC(或∠BOC)的⼤⼩后，就可知道∠AOB的度数．20．∠AOC与∠BOD是对顶⾓，说理提⽰：只要说明A，O，B三点共线．证明：∵射线OA的端点在直线CD上，∴∠AOC与∠AOD互为邻补⾓，即∠AOC＋∠AOD＝180°，⼜∵∠BOD＝∠AOC，从⽽∠BOD＋∠AOD＝180°，∴∠AOB是平⾓，从⽽A，O，B三点共线．∴∠AOC与∠BOD是对顶⾓．21．(1)有6对对顶⾓，12对邻补⾓．(2)有12对对顶⾓，24对邻补⾓．(3)有m(m－1)对对顶⾓，2m(m－1)对邻补⾓．21．互相垂直，垂，垂⾜．2．有且只有⼀条直线，所有线段，垂线段．3．垂线段的长度．4．AB⊥CD；AB⊥CD，垂⾜是O(或简写成AB⊥CD于O)；P；CD；线段MO的长度．5～8．略．9．√，10．√，11．×，12．√，13．√，14．√，15．×，16．√．17．B．18．B．19．D．20．C．21．D．22．30°或150°．23．55°．24．如图所⽰，不同的垂⾜为三个或两个或⼀个．这是因为：(1)当A ，B ，C 三点中任何两点的连线都不与直线m 垂直时，则分别过A ，B ，C 三点作直线m 的垂线时，有三个不同的垂⾜．(2)当A ，B ，C 三点中有且只有两点的连线与直线m 垂直时，则分别过A ，B ，C 三点作直线m 的垂线时，有两个不同的垂⾜．(3)当A ，B ，C 三点共线，且该线与直线m 垂直时，则只有⼀个垂⾜．25．以点M 为圆⼼，以R ＝1.5cm 长为半径画圆M ，在圆M 上任取四点A ，B ，C ，D ，依次连接AM ，BM ，CM ，DM ，再分别过A ，B ，C ，D 点作半径AM ，BM ，CM ，DM 的垂线l 1，l 2，l 3，l 4，则这四条直线为所求．26．相等或互补．27．提⽰：如图，,9073,9075FOC AOE.90710,9072BOC AOB .90712BOC AOB ∴是712倍． 31．(1)邻补⾓，(2)对顶⾓，(3)同位⾓，(4)内错⾓， (5)同旁内⾓，(6)同位⾓，(7)内错⾓，(8)同旁内⾓， (9)同位⾓，(10)同位⾓．2．同位⾓有：∠3与∠7、∠4与∠6、∠2与∠8；内错⾓有：∠1与∠4、∠3与∠5、∠2与∠6、∠4与∠8；同旁内⾓有：∠2与∠4、∠2与∠5、∠4与∠5、∠3与∠6．3．(1)BD，同位．(2)AB，CE，AC，内错．4．(1)ED，BC，AB，同位；(2)ED，BC，BD，内错；(3)ED，BC，AC，同旁内．5．C．6．D．7．B．8．D．9．6对对顶⾓，12对邻补⾓，12对同位⾓，6对内错⾓，6对同旁内⾓．41．不相交，a∥b．2．相交、平⾏．3．经过直线外⼀点有且只有⼀条直线与这条直线平⾏．4．第三条直线平⾏，互相平⾏，a∥c.5．略．6．(1)EF∥DC，内错⾓相等，两直线平⾏．(2)AB∥EF，同位⾓相等，两直线平⾏．(3)AD∥BC，同旁内⾓互补，两直线平⾏．(4)AB∥DC，内错⾓相等，两直线平⾏．(5)AB∥DC，同旁内⾓互补，两直线平⾏．(6)AD∥BC，同位⾓相等，两直线平⾏．7．(1)AB，EC，同位⾓相等，两直线平⾏．(2)AC，ED，同位⾓相等，两直线平⾏．(3)AB，EC，内错⾓相等，两直线平⾏．(4)AB，EC，同旁内⾓互补，两直线平⾏．8．略．9．略．10．略．11．同位⾓相等，两直线平⾏．12．略．13．略．14．略．51．(1)两条平⾏线，相等，平⾏，相等．(2)被第三条直线所截，内错⾓，两直线平⾏，内错⾓相等．(3)两条平⾏线被第三条直线所截，互补．两直线平⾏，同旁内⾓互补．2．垂直于，线段的长度．3．(1)∠5，两直线平⾏，内错⾓相等．(2)∠1，两直线平⾏，同位⾓相等．(3)180°，两直线平⾏，同旁内⾓互补．(4)120°，两直线平⾏，同位⾓相等．4．(1)已知，∠5，两直线平⾏，内错⾓相等．(2)已知，∠B，两直线平⾏，同位⾓相等．(3)已知，∠2，两直线平⾏，同旁内⾓互补．5～12．略．13．30°．14．(1)(2)均是相等或互补．15．95°．16．提⽰：这是⼀道结论开放的探究性问题，由于E点位置的不确定性，可引起对E点不同位置的分类讨论．本题可分为AB，CD之间或之外．如：结论：①∠AEC＝∠A＋∠C②∠AEC＋∠A＋∠C＝360°③∠AEC＝∠C－∠A④∠AEC＝∠A－∠C⑤∠AEC＝∠A－∠C⑥∠AEC＝∠C－∠A．61．判断、语句．2．题设，结论，已知事项，由已知事项推出的事项．3．题设，结论．4．⼀定成⽴，总是成⽴．5．题设是两条直线垂直于同⼀条直线；结论是这两条直线平⾏．6．题设是同位⾓相等；结论是两条直线平⾏．7．题设是两条直线平⾏；结论是同位⾓相等．8．题设是两个⾓是对顶⾓；结论是这两个⾓相等．9．如果⼀个⾓是90°，那么这个⾓是直⾓．10．如果⼀个整数的末位数字是零，那么这个整数能被5整除．11．如果有⼏个⾓相等，那么它们的余⾓相等．12．两直线被第三条直线截得的同旁内⾓互补，那么这两条直线平⾏．13．是，14．是，15．不是，16．不是，17．不是，18．是．19．√，20．√，21．×，22．×，23．√，24．√，25．×，26．×，27．√，28．√，29．×，30．×．31．正确的命题例如：(1)在四边形ABCD中，如果AB∥CD，BC∥AD，那么∠A＝∠C．(2)在四边形ABCD中，如果AB∥CD，BC∥AD，那么AD＝BC(3)在四边形ABCD中，如果AD∥BC，∠A＝∠C，那么AB∥DC．32．已知：如图，AB∥CD，EF与AB、CD分别交于M，N，MQ平分∠AMN，NH平分∠END．求证：MQ∥NH．证明：略．71．LM，KJ，HI．2．(1)某⼀⽅向，相等，AB∥A1B1∥A2B2∥A3B3或在⼀条直线上，AB＝A1B1＝A2B2＝A3B3．(2)平⾏或共线，相等．3．(1)某⼀⽅向，形状、⼤⼩．(2)相等，平⾏或共线．4～7．略．8．B9．利⽤图形平移的性质及连接两点的线中，线段最短，可知：AC＋CD＋DB＝(ED＋DB)＋CD＝EB＋CD．⽽CD 的长度⼜是平⾏线PQ与MN之间的距离，所以AC＋CD＋DB最短．10．提⽰：正⽅形③的⾯积＝正⽅形①的⾯积＋正⽅形②的⾯积．AB2＝AC2＋BC2．第六章实数6.11、算术平⽅根 a 根号a 被开⽅数2、2.23613、0.54、0或15、B6、两个，互为相反数，0，没有平⽅根7、±0.6，平⽅根8、算术，负的9、±2 10、C 11、3 12、0.25 4 13、x=2．14、∵4=16，∴15 < 4 ∵25>22>1,∴215 =2125 >1-0.5>0.5 , ∴215 >0.5 15、22.361500071.750 2361.25 7071.05.0（2）被开⽅数扩⼤或缩⼩100倍，算术平⽅根扩⼤或缩⼩10倍 16、90.424 60.19490.4 周长⼤约是19.60厘⽶ 17、（1）12（2）410 （3）6 （4）151118、B 19、计算；① 91697134② 81404122-9 ③0.4220、解⽅程：① x=±43 ② x=217 ③ 25142 x ④ 223324 x125251425)1(2x x x 3232233249)32(2x x x X=-3.5或1.5 2x=-1.5或-4.5 X=-0.75或-2.2521、解：x=±11，因为被开⽅数⼤于等于零，算术平⽅根⼤于等于零，所以y-2=0，y=2 故xy=±2222、解；因为⼀个数的两个平⽅根互为相反数，所以（2a-3）+（4-a ）=0，得a=-1，即2a-3=-5故这个数的负的平⽅根是-523、解：由题意得1613912b a a ，解得25b a ，所以392252 b a24、①25x 052即x ②3-2x ≥0且2x-3≥0，解得x=1.5 ③5+x ≥0且x+2≠0，解得x ≥-5且x ≠-2 6.21．D 2．D 3．C 4．C1． B 6． B 7． B 8．D 9．Ｃ 10. A11．8 4 12．27 9 13.3m 14.-6 -0.008 15．-3 133 16. ±517.-1. 518. ⑴ -2 ⑵ 0.4 ⑶ 25⑷ 9⑴0.01 0.1 1 10 100⑵被开⽅数⼩数点向左（或右）移动三位，它的⽴⽅根的⼩数点向左（或右）移动⼀位. ⑶① 14.42 0.144221、解析：正⽅体 113 ，球体1 4313433R R R,所以甲不符合要求，⼄符合要求。

新人教版七年级数学下册全册教案附同步练习及单元测试卷（含答案）第五章相交线与平行线5.1.1相交线教学目标：1．理解对顶角和邻补角的概念，能在图形中辨认．2．掌握对顶角相等的性质和它的推证过程．3.通过在图形中辨认对顶角和邻补角，培养学生的识图能力．重点：在较复杂的图形中准确辨认对顶角和邻补角．难点：在较复杂的图形中准确辨认对顶角和邻补角．教学过程一、创设情境，引入课题先请同学观察本章的章前图，然后引导学生观察，并回答问题．学生活动：口答哪些道路是交错的，哪些道路是平行的．教师导入：图中的道路是有宽度的，是有限长的，而且也不是完全直的，当我们把它们看成直线时，这些直线有些是相交线，有些是平行线．相交线、平行线都有许多重要性质，并且在生产和生活中有广泛应用．所以研究这些问题对今后的工作和学习都是有用的，也将为后面的学习做些准备．我们先研究直线相交的问题，引入本节课题．二、探究新知，讲授新课1．对顶角和邻补角的概念学生活动：观察上图，同桌讨论，教师统一学生观点并板书．【板书】∠1与∠3是直线AB、CD相交得到的，它们有一个公共顶点O，没有公共边，像这样的两个角叫做对顶角．学生活动：让学生找一找上图中还有没有对顶角，如果有，是哪两个角？学生口答：∠2和∠4再也是对顶角．紧扣对顶角定义强调以下两点：（1）辨认对顶角的要领：一看是不是两条直线相交所成的角，对顶角与相交线是唇齿相依，哪里有相交直线，哪里就有对顶角，反过来，哪里有对顶角，哪里就有相交线；二看是不是有公共顶点；三看是不是没有公共边．符合这三个条件时，才能确定这两个角是对顶角，只具备一个或两个条件都不行．（2）对顶角是成对存在的，它们互为对顶角，如∠1是∠3的对顶角，同时，∠3是∠1的对顶角，也常说∠1和∠3是对顶角．2．对顶角的性质提出问题：我们在图形中能准确地辨认对顶角，那么对顶角有什么性质呢？学生活动：学生以小组为单位展开讨论，选代表发言，井口答为什么．【板书】∵∠1与∠2互补，∠3与∠2互补（邻补角定义），∴∠l＝∠3（同角的补角相等）．注意：∠l与∠2互补不是给出的已知条件，而是分析图形得到的；所以括号内不填已知，而填邻补角定义．或写成：∵∠1＝180°－∠2，∠3＝180°－∠2（邻补角定义），∴∠1＝∠3（等量代换）．学生活动：例题比较简单，教师不做任何提示，让学生在练习本上独立完成解题过程，请一个学生板演。

ED CBAEDCBA21FED CBA第五章经典例题例1 如图，直线AB,CD,EF 相交于点O ，∠AOE=54°，∠EOD=90°，求∠EOB ，∠COB 的度数。

例2 如图AD 平分∠CAE ，∠B = 350，∠DAE=600，那么∠ACB 等于多少？例3 三角形的一个外角等于与它相邻的内角的4倍，等于与它不 相邻的一个内角的2倍，则这个三角形各角的度数为( )。

A ．450、450、900B ．300、600、900C ．250、250、1300D ．360、720、720例4 已知如图，求∠A ＋∠B ＋∠C ＋∠D ＋∠E ＋∠F 的度数。

例5 如图，AB ∥CD ，EF 分别与AB 、CD 交于G 、H ，MN ⊥AB 于G ，∠CHG=1240，则∠EGM 等于多少度？第六章经典例题例1 一个机器人从O 点出发，向正东方向走3米到达A1点，再向正北方向走NM HGFE DC BA1 ●●● ●●●ABC DEFO x y-1例3再向正东方向走15米到达A5•点，如果A1求坐标为（3，0），求点 A5•的坐标。

例2 如图是在方格纸上画出的小旗图案，若用(0，0)表示A 点，(0，4)表示B 点，那么C 点的位置可表示为( )A 、(0，3)B 、(2，3)C 、(3，2)D 、(3，0)例3 如图2，根据坐标平面内点的位置，写出以下各点的坐标：A( )，B( )，C( )。

例4 如图，面积为12cm2的△ABC 向x轴正方向平移至△DEF 的位置，相应的坐标如图所示（a ，b 为常数）， （1）、求点D 、E 的坐标 （2）、求四边形ACED 的面积。

例5 过两点A （3，4）,B （-2，4）作直线AB ，则直线AB( ) A 、经过原点 B 、平行于y 轴 C 、平行于x 轴 D 、以上说法都不对ABC例2第七章经典例题例1 如图，已知△ABC中，AQ=PQ、PR=PS、PR⊥AB于R，PS⊥AC于S，有以下三个结论：①AS=AR；②QP∥AR；③△BRP≌△CSP，其中( )．(A)全部正确 (B)仅①正确 (C)仅①、②正确 (D)仅①、③正确例2 如图，结合图形作出了如下判断或推理：①如图甲，CD⊥AB，D为垂足，那么点C到AB的距离等于C、D两点间的距离；②如图乙，如果AB∥CD，那么∠B=∠D；③如图丙，如果∠ACD=∠CAB，那么AD∥BC；④如图丁，如果∠1=∠2，∠D=120°，那么∠BCD=60°．其中正确的个数是( )个．(A)1 (B)2 (C)3 (D)4例3在如图所示的方格纸中，画出，△DEF和△DEG(F、G不能重合)，使得△ABC≌△DEF≌DEG．你能说明它们为什么全等吗?例4 测量小玻璃管口径的量具CDE上，CD=l0mm，DE=80mm．如果小管口径AB 正对着量具上的50mm刻度，那么小管口径AB的长是多少?例5 在直角坐标系中，已知A(-4，0)、B(1，0)、C(0，-2)三点．请按以下要求设计两种方案：作一条与轴不重合，与△ABC的两边相交的直线，使截得的三角形与△ABC相似，并且面积是△AOC面积的．分别在下面的两个坐标中系画出设计图形，并写出截得的三角形三个顶点的坐标。

人教版七年级下册数学配套练习册及答案一、选择题（每小题4分，共40分）1、下列实数0，4,71,32,2,3.0π，327-，0.1010010001……中，无理数有（ ）A ．2个 B ．3个 C ． 4个 D ．5个2、81 的算术平方根是（ ）A ：9B ：±9C ：±3D ：33、－8的立方根与4的平方根之和是（ ）A ：0B ：4C ：0或4D ：0或－44、下列各组数中互为相反数的是（ ）A ：－2 与2(2)-B ：－2 与38-C ：－2 与12- D ：2与2- 5、已知：a =5，2b =7，，且a b a b +=+，则a b -的值为（ ）A ：2或12B ：2或－12C ：－2或12D ：－2或－126、不等式组2030x x -<⎧⎨-≥⎩的正整数解的个数是（ ） A ．1个 B ．2个 C ．3个 D ．4个7、不等式组⎩⎨⎧+>+<+1,159m x x x 的解集是2>x ，则m 的取值范围是（ ）A ． m ≤2B ． m ≥2C ．m ≤1D ． m >18、如果关于x 、y 的方程组322x y x y a +=⎧⎨-=-⎩的解是负数，则a 的取值范围是( )A.-4<a<5B.a>5C.a<-4D.无解9、xx y 21-=中自变量x 的取值范围是（ ） A 、x ≤21且x ≠0 B 、x 21->且x ≠0 C 、x ≠0 D 、x 21<且x ≠0 10、实数a ，b 在数轴上的位置，如图所示，那么化简2||a a b -+的结果是（ ）．A ．2a b +B ．bC ．b -D ．2a b -+二、填空题（每小题4分，共20分）11、16= ，38的平方根是 ； b a12、=-2)3(π ;32-= .；13、若11y x x =-+-+1，则20082008y x+= ； 14、比较大小3- 2π-，32 2515、若2)21(x -= 2x －1，则x 的取值范围是_______________三、解答题（共90分）16、计算或化简（每题5分，计20分） ⑴2310.584-- ⑵323(81)28---- 解：原式= 解：原式=⑶2+32—52 ⑷6(61-6) 解：原式= 解：原式=17、（8分） 解不等式：2110155364x x x -+-≥-, 并把它的解集在数轴上表示出来. 18、（8分）解不等式组2(1)4143x x x x +-≤⎧⎪+⎨>⎪⎩ ,并把解集在数轴上表示出来.19、（8分）已知a 是27的整数部分，b 是27的小数部分，计算2a b -的值20、（8分）已知22b a ++|b 2－9|=0,求a+b 的值.21、（8分）已知21a +的平方根是±3，522a b +-的算术平方根是4，求34a b -的平方根。

三一文库（）/初中一年级〔数学练习册答案七年级下册人教版【三篇】〕5.2.1平行线答案基础知识1、D2、A3、A4、∥平行于同一条直线的两条直线平行5、平行和相交6、107、相交8、a∥db∥ec∥f9、略10、做图略∵AD∥BCMN∥AD∴MN∥BC能力提升11、C12、在同一条直线上面，ABC共线13、做图略14、（1）（2）做图略（3）∵AB∥PTAB∥MN∴PN∥MN15、题目略（1）做图略（2）平行∵EF∥BCAD∥BC∴EF∥AD探索研究16、过E点作EF∥AB∵AB∥CDEF∥AB∴EF∥CD5.2.2平行线的判定第1课时答案基础知识1、C2、ADBCADBC180°-∠1-∠2∠3+∠43、ADBEADBCAECD同位角相等，两直线平行4、题目略MNAB内错角相等，两直线平行MNAB同位角相等，两直线平行两直线平行于同一条直线，两直线平行5、B6、∠BED∠DFC∠AFD∠DAF7、证明：∵AC⊥AEBD⊥BF∴∠CAE=∠DBF=90°∵∠1=35°∠2=35°∴∠1=∠2∵∠BAE=∠1+∠CAE=35°+90°=125°∠CBF=∠2+∠DBF=35°+90°=125°∴∠CBF=∠BAE∴AE∥BF（同位角相等，两直线平行）8、题目略（1）DEBC（2）∠F同位角相等，两直线平行（3）∠BCFDEBC同位角相等，两直线平行能力提升9、∠1=∠5或∠2=∠6或∠3=∠7或∠4=∠810、有，AB∥CD∵OH⊥AB∴∠BOH=90°∵∠2=37°∴∠BOE=90°-37°=53°∵∠1=53°∴∠BOE=∠1∴AB∥CD（同位角相等，两直线平行）11、已知互补等量代换同位角相等，两直线平行12、平行，证明如下：∵CD⊥DA，AB⊥DA∴∠CDA=∠2+∠3=∠BAD=∠1+∠4=90°（互余）∵∠1=∠2（已知）∴∠3=∠4∴DF∥AE（内错角相等，两直线平行）探索研究13、对，证明如下：∵∠1+∠2+∠3=180°∠2=80°∴∠1+∠3=100°∵∠1=∠3∴∠1=∠3=50°∵∠D=50°∴∠1=∠D=50°∴AB∥CD（内错角相等，两直线平行）14、证明：∵∠1+∠2+∠GEF=180°（三角形内角和为180°）且∠1=50°，∠2=65°∴∠GEF=180°-65°-50°=65°∵∠GEF=∠BEG=1/2∠BEF=65°∴∠BEG=∠2=65°∴AB∥CD（内错角相等，两直线平行）5.2.2平行线的判定第2课时答案基础知识1、C2、C3、题目略（1）ABCD同位角相等，两直线平行（2）∠C内错角相等，两直线平行（3）∠EFB内错角相等，两直线平行4、108°5、同位角相等，两直线平行6、已知∠ABF∠EFC垂直的性质AB同位角相等，两直线平行已知DC内错角相等，两直线平行ABCD平行的传递性能力提升7、B8、B9、平行已知∠CDB垂直的性质同位角相等，两直线平行三角形内角和为180°三角形内角和为180°∠DCB等量代换已知∠DCB等量代换DEBC内错角相等，两直线平行10、证明：（1）∵CD是∠ACB的平分线（已知）∴∠ECD=∠BCD∵∠EDC=∠DCE=25°（已知）∴∠EDC=∠BCD=25°∴DE∥BC（内错角相等，两直线平行）（2）∵DE∥BC∴∠BDE+∠B=180°即∠EBC+∠BDC+∠B=180°∵∠B=70°∠EDC=25°∴∠BDC=180°-70°-25°=85°11、平行∵BD⊥BE∴∠DBE=90°∵∠1+∠2+∠DBE=180°∴∠1+∠2=90°∵∠1+∠C=90°∴∠2=∠C∴BE∥FC（同位角相等，两直线平行）探索研究12、证明：∵MN⊥ABEF⊥AB∴∠ANM=90°∠EFB=90°∵∠ANM+∠MNF=180°∠NFE+∠EFB=180°∴∠MNF=∠EFB=90°∴MN∥FE。

七年级数学下册练习册答案人教版答案平行线的判定第1课时基础知识1、C2、AD BC AD BC 180°-∠1-∠2 ∠3+∠43、AD BE AD BC AE CD 同位角相等，两直线平行4、题目略MN AB 内错角相等，两直线平行MN AB 同位角相等，两直线平行两直线平行于同一条直线，两直线平行5、B6、∠BED ∠DFC ∠AFD ∠DAF7、证明：∵AC⊥AE BD⊥BF∴∠CAE=∠DBF=90°∵∠1=35° ∠2=35°∴∠1=∠2∵∠BAE=∠1+∠CAE=35°+90°=125° ∠CBF=∠2+∠DBF=35°+90°=125°∴∠CBF=∠BAE∴AE∥BF同位角相等，两直线平行8、题目略1DE BC2∠F 同位角相等，两直线平行3∠BCF DE BC 同位角相等，两直线平行能力提升9、∠1=∠5或∠2=∠6或∠3=∠7或∠4=∠810、有，AB∥CD∵OH⊥AB∴∠BOH=90°∵∠2=37°∴∠BOE=90°-37°=53°∵∠1=53°∴∠BOE=∠1∴AB∥CD同位角相等，两直线平行11、已知互补等量代换同位角相等，两直线平行12、平行，证明如下：∵CD⊥DA，AB⊥DA∴∠CDA=∠2+∠3=∠BAD=∠1+∠4=90°互余∵∠1=∠2已知∴∠3=∠4∴DF∥AE内错角相等，两直线平行探索研究13、对，证明如下：∵∠1+∠2+∠3=180° ∠2=80°∴∠1+∠3=100°∵∠1=∠3∴∠1=∠3=50°∵∠D=50°∴∠1=∠D=50°∴AB∥CD内错角相等，两直线平行14、证明：∵∠1+∠2+∠GEF=180°三角形内角和为180°且∠1=50°，∠2=65°∴∠GEF=180°-65°-50°=65°∵∠GEF=∠BEG=1/2∠BEF=65°∴∠BEG=∠2=65°∴AB∥CD内错角相等，两直线平行平方根第3课时基础知识1、 2、 3、 4、 5、A B A C A6、97、±68、±9/119、12 ±1310、011、913、1x=±5 2x=±9 3x=±3/2 4x=±5/214、1-0.1 2±0.01 311 40.42平方根第2课时基础知识1、2、3、4、BCBB5、47、±58、±11 13/8 ±13/10 -0.5能力提升解得x=2 2x+5=2×2+5=9 所以2x+5的算数平方根为311、解：6.75÷1.2=5.625 5.625的算数平方根约等于2.37cm12、解：设宽是xx>0，长为4x 则4x²=25解得x=2.5 所以4x=10猜你感兴趣：感谢您的阅读，祝您生活愉快。

2023人教版七年级下册数学配套练习册答案【导语】下面是为您整理的2023人教版七班级下册数学配套练习册答案，仅供大家参考。

1、D2、25°3、题目略(1)两直线平行，同位角相等(2)两直线平行，内错角相等(3)两直线平行，同旁内角互补(4)同旁内角互补，两直线平行4、∠1=∠5∠8=∠4∠BAD∠7=∠3∠6=∠2∠BCD5、35°6、52°128°7、北偏东56°甲乙方向是相对的，它们的角相等(互为内错角)8、已知∠BCD两直线平行，内错角相等已知∠2∠BCD等量代换角平分线定义力量提升9、南偏西50°∠AC∠BD∠∠DBA=∠CAB=50°由方位角的方位角的概念可知，小船在南偏西50°10、证明：∠BE∠CF(已知)∠∠2=∠3(两直线平行，内错角相等)∠AB∠CD∠∠ABC=∠1+∠2=∠BCD=∠3+∠4∠∠1=∠411、证明：过C点作CF∠AB∠AB∠DE∠CF∠DE∠AB∠CF∠∠B+∠BCF=180°∠CF∠DE∠∠DCF+∠D=180°∠∠B+∠BCF+∠DCF+∠D=360°∠∠B=150°∠D=140°∠∠BCD+∠DCF=70°∠∠C=∠BCF+∠DCF∠∠C=70°探究讨论12、题目略甲：过P点作EF∠AB∠AB∠CDEF∠AB∠EF∠CD∠AB∠EF∠∠A=∠APE∠EF∠CD∠∠EPC=∠C∠P=∠APE+∠EPC∠∠P=∠A+∠C乙：过P点作PF∠ABAB∠CDPF∠AB∠PF∠CD∠∠FPC+∠C=180°∠AB∠PF∠∠A+∠APF=180°∠P=∠APF+∠FPC∠FPC+∠C+A+∠APF=360° ∠∠A+C+∠P=360°丙：设CD与PB交于点E∠AB∠CD∠∠B=∠PED又∠在∠PDE中，∠BED=∠P+∠D∠∠B=∠D+∠P。

七年级数学下同步练习册答案人教版七年级学生要仔细做人教版数学同步练习册的习题，出错要少，检查要多。

小编整理了关于人教版七年级数学下册同步练习册的答案，希望对大家有帮助!七年级数学下同步练习册答案人教版(一)平方根第2课时基础知识1、 2、 3、 4、B C B B5、47、±58、±11 13/8 ±13/10 -0.59、比较大小能力提升解得x=2 2x+5=2×2+5=9 所以2x+5的算数平方根为311、解：6.75÷1.2=5.625 5.625的算数平方根约等于2.37cm12、解：设宽是x(x>0)，长为4x 则4x²=25解得x=2.5 所以4x=10七年级数学下同步练习册答案人教版(二)同位角、内错角、同旁内角基础知识1、B2、C3、∠1 ∠3 ∠2 ∠6 AB CD EF4、∠C 内错∠BAE5、AB 内错6、题目略(1)∠ADC ∠EBG ∠HEB ∠DCG(2)∠ADC ∠ABE ∠AEB ∠ACD能力提升7、题目略(1)AB CD BE(2)AD BC AB(3)AB CD BC(4)AB CD BE8、∠A和∠B ∠A和∠D ∠D和∠C ∠B和∠C 共4对9、题目略(1)∠DEA同位角是∠C，内错角是∠BDE，同旁内角是∠A、∠ADE(2)∠ADE同位角是∠B，内错角是∠CED，同旁内角是∠A、∠AED探索研究10、证明：∵∠2=∠4(互为对顶角)∴∠1=∠2∴∠1=∠4∵∠2+∠3=180° ∠1=∠2∴∠1+∠3=180°∴∠1和∠3互补七年级数学下同步练习册答案人教版(三)平行线的判定第2课时基础知识1、C2、C3、题目略(1)AB CD 同位角相等，两直线平行(2)∠C 内错角相等，两直线平行(3) ∠EFB 内错角相等，两直线平行4、108°5、同位角相等，两直线平行6、已知∠ABF ∠EFC 垂直的性质 AB 同位角相等，两直线平行已知 DC 内错角相等，两直线平行 AB CD 平行的传递性能力提升7、B 8、B9、平行已知∠CDB 垂直的性质同位角相等，两直线平行三角形内角和为180° 三角形内角和为180° ∠DCB 等量代换已知∠DCB 等量代换 DE BC 内错角相等，两直线平行10、证明：(1)∵CD是∠ACB的平分线(已知)∴∠ECD=∠BCD∵∠EDC=∠DCE=25°(已知)∴∠EDC=∠BCD=25°∴DE∥BC(内错角相等，两直线平行)(2)∵DE∥BC∴∠BDE+∠B=180° 即∠EBC+∠BDC+∠B=180°∵∠B=70° ∠EDC=25°∴∠BDC=180°-70°-25°=85°11、平行∵BD⊥BE∴∠DBE=90°∵∠1+∠2+∠DBE=180°∴∠1+∠2=90°∵∠1+∠C=90°∴∠2=∠C∴BE∥FC(同位角相等，两直线平行)探索研究12、证明：∵MN⊥AB EF⊥AB∴∠ANM=90° ∠EFB=90°∵∠ANM+∠MNF=180° ∠NFE+∠EFB=180°∴∠MNF=∠EFB=90°∴MN∥FE。

8.11.(1)∠A,∠C;(2)∠ABC,∠ABD,∠DBC,∠ADB,∠BDC;(3)3个，∠ABD，∠ABC，∠DBC.2.B.3.（1）∠AEB，∠DAE，∠BEC，∠ADB；(2)∠C,∠D.4.3个⾓;6个⾓;10个⾓.5.9时12分或21时12分.8.21.(1)42°;(2)不变.2.C.3.D.5.46°.提⽰:设∠COE=x°,则x-8=130-2x,x=46.6.(1)45°；（2）不变；提⽰:90+2x2-x=45;(3)不变.提⽰:90-2y2+y=45.8.3第1课时1.（1）42°20′24″；（2）56.35.2.（1）61°38′10″；（2）32.6.3.C.4.C.5.（1）93°12′;（2）47°31′48″;(3)12°9′36″;(4)33°7′12″.6.（1）112°27′；（2）51°55′；（3）125°37′30″.7.0.5°,6°.8.(1)15°;(2)172.5°.9.40分钟.第2课时1.153°.2.53°17′45″.3.C.4.C.5.63°.6.（1）相等；（2）180°.7.60°.8.41.∠3，∠AOD.2.121°.3.C.4.B.5.∠3=25°30′,∠2=45°.6.∠2=63°30′,∠3=53°.7.(1)2对；（2）6对；（3）12对.8.51.70°.2.45°.3.D.4.C.5.132°.6.135°.7.60°,30°.第⼋章综合练习1.130°.2.36°16′30″.3.50°.4.（1）54°34′,125°26′;(2)α-90°.5.47.6.D.7.A.8.C.9.D.10.138°.11.125°.12.∠AOC+∠BOC=2(∠DOC+∠COE)=2×90°=180°，A，O，B共线.13.设∠BOE=x°,∠EOC=2x°,∠AOB=180-3x,∠DOB=72-x.得⽅程（72-x）×2=180-3x,解得x=36.即∠EOC=72°.14.∠BOC+∠COD+∠AOD=270°,∠EOF=170°,∠AOE+∠BOF=190°-90°=100°.∠COF+∠DOE=100°.⼜∠EOF=170°,∠COD=170°-100°=70°.检测站1.45°.2.98.505°.3.∠AOB，∠BOC.∠AOB，∠BOD.4.C.5.D.6.∠BOD，∠FOE，∠BOC；∠BOF.7.45°.8.97.5°.9.11.∠END.2.DE，AB，BC；AB，BC，DE.3.B.4.C.5.∠CAD，∠BAC,∠B.6.同位⾓：∠EAD与∠B；∠EAC与∠B；内错⾓：∠DAC与∠C；∠EAC与∠C.同旁内⾓：∠DAB 与∠B；∠BAC与∠B.7.略.9.21.相交，平⾏.2.不相交.3.⼀.4.C.5.略.6.略.7.正⽅形.8.略.9.31.65°,两直线平⾏，同位⾓相等，65°，对顶⾓相等.2.65°.3.B.4.C.5.130°.6.∠B，∠EFC，∠ADE.7.40°.9.4第1课时1.AC，BD，内错⾓相等，两直线平⾏.2.（1）EN，BD；（2）AB，CD.3.B.4.∠5=∠2=105°，∠5+∠1=180°.5.DE∥MN.由AB∥MN，DE∥AB.6.提⽰：由AD∥BC，得∠A+∠B=180°，∠C+∠B=180°，AB∥CD.7.（1）由∠3=∠B,知FD∥AB，知∠4=∠A；（2）由ED∥AC，知∠1=∠C，∠BED=∠A.第2课时1.4厘⽶.2.BD，BE.3.D.4.由∠B=∠C，知AB∥CD，故∠A=∠D.5.∠1=∠GMC=90°-∠2.6.(1)∠MDF=∠MBE，BE∥DF；（2）不是；它是AB和CD之间的距离.7.在∠B内画射线BF∥AE，则BF∥CD.∠ABF=120°，∠FBC=30°，∠C=180°-30°=150°.第九章综合练习1.110°.2.AD∥BE，BD∥CE，AD∥BE.3.35°.提⽰：过点M画MN⊥AB,MN∥EG,∠HMN=∠E,∠HMN=90°-∠AMH.4.C.5.C.6.D.7.126°.8.∠1=115°.9.25°.10.∠3=80°，∠4=100°.11.因为AB∥CD，所以∠AEF=∠2,∠AEG=∠3,因为∠AEG=∠1+∠2,所以∠3=∠1+∠2.12.22°.提⽰：过点A画直线c∥a.检测站1.内错，同旁内，同位.2.180°.3.A.4.B.5.AB∥CD，AD∥BC.6.AD∥BC.DB平分∠ADC代替第⼆个条件.10.12.5.3.C4.D.6.a=7,b=-9.7.设需要汽车x辆，共有y⼈外出参观，35x+15=y,45(x-1)=y.解得x=6,y=225..8.不是.10.2第1课时1.-35x+85，-53y+83.2.x-1=0.3.B.4.(1)x=-12，y=52;(2)s=-3,t=-3;(3)m=2,n=1.5.x=1,y=-1.6.提⽰：按丙的⽅法，35x=3,25y=4,得x=5,y=10.第2课时1.2.2.-11.3.C.4.B.5.(1)x=-1,y=-8;(2)x=5,y=272.6.令x+y=a,x-y=b,解得a=2,b=-1,⼜解得x=12,y=32.7.k=4.10.3第1课时1.4x+y=6,-5x+4y=-7.2.C.3.(1)x=1,y=1,z=1;(2)x=1,y=2,z=3.4.解三元⼀次⽅程组，⽤a表⽰解，得x=a,y=a+1,z=a-1,代⼊⽅程-x+2y+3z=6,得a=74.5.将z看做已知数，将x,y解出来.得x=1911-z，y=211-z.x+y+2z=1911-z+211-z+2z=2111.第2课时1.加减，①,②.2.B.3.（1）x=2,y=1,z=-1;(2)x=1,y=2,z=2.4.a=1,b=-1,c=1.10.4第1课时1.7x+3=y,8x-5=y.2.320,180.3.C.4.216,1095.90元，100元.6.5元，3元.7.提⽰：设⼩长⽅形宽x，长y，则5x=3y,y+2x=2y+2，得x=6,y=10.第2课时1.112x=0.5+112y,0.5x=(0.5+1)y.2.30，18.3.D.4.C.5.21张铁⽪做盒⾝，28张铁⽪做盒盖.6.长⽊6.5尺，绳长11尺.7.(1)x+y=90,46%x+70%y=90×64%，x=22.5,y=67.5.(2)46%x+70%y=64%（x+y),x∶y=1∶3.*第3课时1.x+y+z=21,x+y-z=5,x-(z-y)=5.2.4,8,10.3.C.4.2,3,5.5.12,8,7.第⼗章综合练习1.43.2.-1.3.-112，5，（113，0）.4.-14.5.x=1，y=2.6.y=23x-53.7.B.8.A.*9.D.10.（1）x=1，z=2；（2）x=6，y=24；（3）x=3，y=2；*（4）x=2，y=-3,z=-1.11.300棵，200棵.12.50⼈，220件.13.23.14.中型15辆，⼩型35辆.15.m=-275.16.30千⽶，70千⽶，42千⽶.17.平均每天1只⼤⽜需⽤饲料20千克，⼩⽜需⽤5千克.所以王⼤伯对⼤⽜⾷量的估计是正确的，对⼩⽜⾷量的估计偏⾼.18.⽕车速度22⽶/秒，列车长276⽶.19.（1）x=2，y=2，也是剩下⼀个⽅程的解.（2）不.如x-y=0. 检测站1.-10.2.a=2，b=1.3.5千克，2千克.4.C.5.C.6.a=5.*7.x=1，y=2,z=3.8.⽜值⾦2两，⽺值⾦1两.9.男⽣270名，⼥⽣260名. 11.11.108.2.x12.3.x4.4.D.5.A.6.1.5×108.7.(1)m9;(2)3×1011.8.(1)(a-b)5;(2)-(2x-3y)3n+1.9.0.10.0.11.2第1课时1.-8t3.2.116a4b4.3.-6x2.4.A.5.C.6.(1)28x3y3;(2)anbn；（3）-9a3x3.7.a2b.8.1.9.1102n.10.14位数.第2课时1.（1）x10;(2)-8x12.2.C.3.D.5.(1)19x2y4;(2)215;(3)x12;(4)64m12n6.6.(1)x6n+2;(2)-(a+b)7;(3)35n-2.7.提⽰：24＜33，（24）25＜（33）25.11.3第1课时1.12xy3.2.-6x2y3.3.B.4.D.5.(1)m5n2;(2)1.2×1020.6.(1)-14x5y4z2;(2)64x6.7.-730(a-b)8n-4.8.C.第2课时1.3x2-5x3.2.x2-y2.3.D.4.C.5.(1)-3x2y+2xy2-52xy;(2)x4+4x2+2x-4;(3)12b3-b2+6b.6.2m3n3-8m2n3.7.x=-12.8.10.11.4第1课时1.x2-7x+10.2.-6x2-xy+2y2.3.B.4.B.5.(1)-6m2+19m-15;(2)-12x3+14x2-4x;(3)-3y2-23y+108.6.4x2-100x+600.7.-x2-29x+32，1854.8.提⽰：该代数式的值恒为22.9.x=-110.b=12.第2课时1.x3+2x2-5x-6.2.2a3+5a2+a-3.3.B.4.C.5.(1)m3+2m2-1;(2)2a3-5a2b+8ab2-3b3;(3)-2x3-x2-7x+10.6.x3+x-5,值为-7.7.x=-12.8.0.11.51.4.2.m8.3.xn.4.D.5.B.6.16.7.(1)-a;(2)a3.8.(1)y-x;(2)(x+2y)6.9.2xy.11.6第1课时1.1.2.1.3.0.4.C.5.D.6.(1)64;(2)a.7.(1)3 129;(2)200.8.7.9.a≠0,m=n.第2课时1.181.2.-164.3.100.4.B.5.C.6.(1)200;(2)10 099;(3)100.7.10-1,10-2,10-3,10-4.8.a＜b＜d＜c.9.x≠-13.10.1.第3课时1.1.2.1a4.3.a8.4.C.5.125.6.(1)10;(2)x5;(3)11 000 000；（4）1a7.7.13a.8.2-101.第4课时1.1.2×10-4.2.0.000 002 76.3.2.5×10-9.4.D.5.D.6.(1)1.5×10-2;(2)2.1×103;(3)1.5×10-3.7.x=-7.8.1.572×104.9.花粉直径较⼤，是兔⽑直径的7.2倍.第⼗⼀章综合练习1.106.2.x9.3.a.4.tn.5.（a+b）2.6.x5.7.a7.8.15x3y3z.9.2a3+2a2b+2ab.10.-2x2+3x-1.11.B.12.B.13.B.14.A.15.（1）x9；（2）-（a+b）4；（3）-a2b2+6ab+23a；（4）-6n+2；（5）2a3+8ab2-14a2b；（6）-3x2-23x+108；（7）6x2-13xy；（8）-x13y12.16.（1）-x，1；（2）5x-1，101.17.x=-1.18.（1）x=4；（2）n=2，m=4；（3）M=x2-6x+9.19.2ab+2b2.20.n（n+5）-（n-3）（n+2）=6（n+1）.检测站1.（x+y）5.2.-6a3b3c.3.-2x3-4x2+2x.4.a6b6.5.C.6.B.7.B.8.1.24×10-6.9.299.10.（1）36x2-114x+90；（2）91x2-277x+210.11.长8、宽5.12.11.b2-9a2.2.x4-4.3.1681m2n2-49.4.5x+3y.5.C.6.B.7.(1)c2-9a2b2;(2)9y2-4x4;(3)a4-b4;(4)-5x2-9.8.(1)(300+3)(300-3)=90 000-9=89 991;(2)1.9.(2n-1)(2n+1)=(2n)2-1. 10.原式×3-23-2=332-232.12.2第1课时1.-2ab.2.a2+4ab+4b2.3.k=8.4.B.5.C.6.A.7.(1)9m2-32n+116;(2)x4-2x2+1;(3)a2+2ab+b2;(4)916s2+st+49t2.8.(a+b)2=4ab+(a-b)2.9.a2+2ab+b2=9,a2-2ab+b2=49.ab=14(9-49)=-10.a2+b2=9-2ab=29.第2课时1.4ab.2.a2+b2+c2+2ab-2ac-2bc.3.x2-y2+z2+2xz.4.B.5.B.6.A.7.(1)2a2b2-b4;(2)2y2+2x+5;(3)(100-3)(100-1)(100+1)(100+3)= (104-9)(104-1)=108-105+9=99 900 009.8.12.9.48π(a+1).10.8.12.31.2x2y.2.2a4-ab+6.3.a-b-2.4.D.5.C.6.(1)xy(x-y);(2)4ab(bc+4);(3)-2xy(1+2x-4x2);(4)-(3a+b)(a+3b);(5)2x(x-y)2(1-2x).7.1999.8.14ax(2a-x)2.9.能.256-510=512-510=510(25-1)=24×510.12.4第1课时1.(x+2y)(x-2y).2.k=-140.3.D.4.C.5.(1)(6+x)(6-x);(2)(12y+1)2;(3)-(m-n)2;(4)(3+14a)(3-14a).6.(1)8 056;(2)90 000.7.(1)(1+a+b)(1-a-b);(2)(a-b+2)2.8.左端=［(a-b)2+(a+b)2+(a-b)2-(a+b)2］•［(a-b)2+(a+b)2-(a-b)2+(a+b)2］=4(a-b)2(a+b)2. 第2课时1.提出公因式，⽤公式法进⾏因式分解.2.x(x+1)(x-1).3.(a-1)(x+y)(x-y).4.D.5.C.6.(1)m(m2+1)(m+1)(m-1).（2）2x3(3y+1)(3y-1).（3）(x+2)2(x-2)2.(4)(x+1)4.7.原式=12•32•23•43•34•54…910•1110=1120.8.2 0122(2 0112-1)+(2 0132-1)=2 0122(2 011+1)(2 011-1)+(2 013+1)(2 013-1)=2 01224 024=1 006.第⼗⼆章综合练习1.9x2-y2.2.25-4b2.3.25a2-20ab+4b2.4.14m4+2m2n+4n2.5.-2m.6.x-y+2.7.(xy+2z)(xy-2z).8.23m-0.1n.9.C.10.C.11.C.12.(1)4x2+4xy+y2-25z2;(2)-280y2+1295;(3)116x4-181y4.13.(1)2a3x2(2+a)(2-a);(2)(x-y)(a+2y)(a-2y);(3)-(a-b)2(a+b)2;(4)(x2+2x+7)(x-1)2.14.(1)31×(573+427)×(573-427)=4 526 000;(2)76 900;(3)10099.15.πR2-4πr2=π(R+2r)(R-2r)=3.14×10×5.6=175.8厘⽶.16.(n+7)2-(n-5)2=(n+7+n-5)(n+7-n+5)=24(n+1).17.x=141.18.x=2,y=-3,16.19.(2n+1)2-(2n-1)2= (2n+1+2n-1)(2n+1-2n+1)=8n.检测站1.2b-3a.2.20或-20.3.5-a2.4.B.5.B.6.(1)x8-y8;(2)-16x2.7.(1)x2y4(xy2+z)(xy2-z);(2)(m-n+4mn)(m-n-4mn);(3)12x(2a-1)2.8.原式= (x+1)(2x-3)x.当x=12时，原式=-32.9.324-1=(312+1)(36+1)(33+1)(33-1)=28×(312+1)(36+1)(33-1).10.原式=12(a-b)2=2.13.1第1课时1.(1)√;(2);(3)√;(4)√;(5).2.△ABC，△BDC，△BEC;△ABE，△DBE.3.14或16.5.(1)∠A,∠ACD,∠ADC;∠A,∠ACB,∠B;(2)△DAE,△DAC,△BAC;△ADC,△BDC;(3)△BDC;△ACD,△EDC.不是.6.当四点中任意三点不共线时，组成4个三⾓形；当四点中有三点共线时，组成3个三⾓形；若该四点共线时，不能组成三⾓形.第2课时1.3.2.105厘⽶或200厘⽶.3.B.4.B.5.9种：4，5，6，7，8，9，10，11，12（单位：厘⽶）.6.4厘⽶,6厘⽶.7.8或10.8.8种：1，4，4；2，3，4；2，4，4；2，4，5；3，4，3；3，4，4；3，4，5；3，4，6.第3课时1.ACE，BCD.2.（1）AE，4厘⽶；（2）DAC，12；（3）AF.3.C.4.C.5.△ABC，△ABD，△ADC，△ABE，△AEC，△ADE.6.相等.∠1=∠DAC=∠DAE=∠2.∠EAF=∠EDF.7.（1）△BCD，△OCD；（2）△ABC，△ABO和△BOC有⼀条⾼重合；△BCD，△OCD和△BOC有⼀条⾼重合.第4课时1.70°.2.45°.提⽰：∠APD=∠A2+∠C2.3.C.4.C.5.(1)125°;(2)35°.6.70°.7.50°.8.（1）105°；（2）115°；（3）90°+12n°.提⽰：延长BO交AC于D，∠BOC=∠BDC+12∠C=∠A+12∠B+12∠C=90°+12∠A.13.2第1课时1.n-3，n-2.2.5.3.B.4.D.5.五⾓星.6.8个;△ABC，△ABD，△BCD，△ACD，△OAB，△OAC，△OBD，△OCD.7.6.8.60厘⽶. 第2课时1.1 440°，360°，144°.2.8.3.12，150°.4.C.5.D.7.36°.8.18，130°.13.3第1课时 1..2.O，2厘⽶.3.圆外，圆内，6.4.弦：AB，BC，CD，AD，BD，AC；半圆：ABC，ADC；优弧：BAD，CAD，BAC，ABD，ACB；劣弧：AB，BC，CD，AD，BCD.6.列⽅程：2π(80+10)8=2π(80+10+x)10,x=22.5（厘⽶）.第2课时 1..2.a2（1-π4）.3.3.4.⼀样远.5.6π.第⼗三章综合练习1.30°，60°.2.95°.3.钝⾓.4.∠A=40°，∠C=140°.5.20°.6.M在圆内部.7.B.8.D.9.B.10.D.11.36°，72°，72°.12.（1）y=90-x2；（2）y=45；（3）60.13.8，8，11或10，10，7.14.（1）将平⾯分为5部分：⼩圆内、⼩圆上、圆环内、⼤圆上、⼤圆外.（2）条件分别是：OP＜5,OP=5,5＜OP＜8,OP=8,OP＞8.15.延长AP到BC上点D，利⽤三⾓形外⾓性质，可推出∠APB＞∠C.16.3圈.检测站1.5，4.2.10个.3.2，1.4.六.5.B.6.C.7.3个.8.∠ADB=80°，∠DAE=10°.9.（1）∠AEF＞∠D＞∠A（由外⾓定理）；（2）∠AFD=∠ACD+∠D=∠A+∠B+∠D.综合与实践第1课时1.条件是：多边形每条边都是该多边形与相邻多边形的公共边，每个顶点处各内⾓之和是360°.2.正六边形.3.B.4.D.6.6,3,3.第2课时1.正三⾓形2.正⽅形.3.C.4.D.5.（1）3,2.6.3n，2n+1.14.11.2,5.2.C.3.储蓄所，诊所(6,9),商店（7,3）,学校（1,1）.4.5排3列.5.23.6.(1)(C,4),(A,4),(0,3),(0,1),(A,0),(C,0),(D,1),(D,3);(2) (E,3)→(G,4)→(H,2)→(F,3)→(G,1)(答案不).14.21.四，5，2.2.x轴或y轴上.3.C.4.D.5.在第⼆、四象限的⾓平分线上，如（1，-1）.6.（2，0），（7，0）；（0，2）,（0，4）.7.第⼆象限，（2，0），（-2，1）；第⼀象限,（2,2）,(0,3).14.3第1课时1.B（3，3），D（-2，-2）.2.C.3.⼩房⼦.4.42.5.(32,3),(64,0).第2课时1.(-2,-3),(3,-4),x′=x-2,y′=y-3.2.A.3.A(0,0),B(5,1),C(0,-3),D(-2,-2).4.(1)(0,0),(0,1.5),(3.8,0),(3.8,1.5),(1.7,0.5);(2)(-3.8,-1.5),(-3.8,0),(0,-1.5),(0,0),(-2.1,-1).5.以（1,1）为原点O′,x′轴∥x轴，y′轴∥y轴，分别以向右、向上为正向，单位长度不变，建⽴直⾓坐标系.A，B，C坐标分别是A(-2,1),B(2,-2),C(-1,2).14.41.北偏西45°,1.5.2.A.3.略.4.略.第⼗四章综合练习1.（9，8）.2.⼀.3.2.4.6.5.D.6.B.7.略.8.⼆，四，三，⼀，x轴，y轴.9.(2,6)或(2,-6).10.x轴上，（0,5）,(5,0).检测站1.(-2,-2).2.(1)3;(2)-2;(3)四.3.B.5.“国”字.6.P,Q,R分别在长⽅形内部、边界上、外部.总复习题1.45°.2.∠DCE=∠A.3.12.4.-2 012.5.125°.6.D.7.D.8.A.9.C.10.75°.11.第⼆象限.12.24.5吨.13.（1）22x-23，21；（2）-2y2+19y,9.14.12.15.y=-12x.16.购⼀等门票3张、三等门票33张，或购⼆等门票7张、三等门票29张.提⽰：分三种情况分别列⼆元⼀次⽅程组，其中购⼀等门票、⼆等门票不可⾏.17.玩具⾛的是正12边形，共⾛了12⽶.总检测站1.44°.2.（1）AB∥DF；（2）ED∥AC；（3）ED∥AC.3.x=2，y=-5.4.a=-73，b=53.5.-y2-7x.6.-7.7.18°.8.C.9.C.10.A.11.B.12.（1）∠DOC=∠B=∠E；（2）不⼀定；还可能互补.13.4.14.3516x3-418x2-32x-12.15.(a+1)2(a-1)2.*16.7，5，6.17.12边形.18.分两种情况讨论：D点在B，C之间和D点在B，C之外.分别由⾯积求出⾼，建⽴直⾓坐标系，以垂⾜为原点，以直线BC 为x轴，以⾼所在直线为y轴.。

七年级下数学配套练习册答案人教版（2019）第8章一元一次不等式§8.1 理解不等式一、1.B 2.B 3.A二、1. ＜；＞；＞ ; ＞ 2. 2x+3＜5 3. 4. ω≤50三、1．（1）2 -1＞3；（2）a+7＜0；（3）2+ 2≥0；（4）≤-2;（5）∣ -4∣≥ ；（6）-2＜2 +3＜4. 2．80+20n＞100+16n; n=6,7,8,…§8.2 解一元一次不等式（一）一、1．C 2．A 3.C二、1.3，0，1，，- ；，，0，1 2. x≥-1 3. -2＜x＜2 4. x＜三、1.不能，因为x＜0不是不等式3-x＞0的所有解的集合，例如x=1也是不等式3-x＞0的一个解. 2.略§8.2 解一元一次不等式（二）一、1. B 2. C 3.A二、1.＞；＜；≤ 2. x≥-3 3. ＞三、1. x＞3；2. x≥-2 3.x＜ 4. x＞5四、x≥-1 图略五、(1) (2) (3)§8.2 解一元一次不等式（三）一、1. C 2.A二、1. x≤-3 2. x≤- 3. k＞2三、1. （1）x＞-2 （2）x≤-3 （3）x≥-1 （4）x＜-2 （5）x≤5(6) x≤-1 (图略)2. x≥3.八个月§8.2 解一元一次不等式（四）一、1. B 2. B 3.A二、1. -3，-2，-1 2. 5 3. x≤1 4. 24三、1. 解不等式6（x-1）≤2（4x+3）得x≥-6，所以，能使6（x-1）的值不大于2（4x+3）的值的所有负整数x的值为-6，-5，-4，-3，-2，-1.2. 设该公司最多可印制x张广告单，依题意得80+0.3x≤1200，解得x≤3733.答：该公司最多可印制3733张广告单.3. 设购买x把餐椅时到甲商场更优惠，当x＞12时，得200×12+50（x-12）＜0.85（200×12+50x）,解得x＜32 所以12＜x＜32; 当0＜x≤12时，得200×12＜0.85（200×12+50x）解得x＞ ,所以＜x≤12 其整数解为9，10，11，12.所以购买大于或等于9张且小于32张餐椅时到甲商场更优惠.§8.3 一元一次不等式组（一）一、1. A 2. B二、1. x＞-1 2. -1＜x≤2 3. x≤-1三、1. (1) x≥6 (2) 1＜x＜3 （3）4≤x＜10 (4) x＞2 (图略)2. 设幼儿园有x位小朋友，则这批玩具共有3x+59件，依题意得1≤3x+59-5（x-1）≤3，解得30.5≤x≤31.5，因x为整数，所以x=31，3x+59=3×31+59=152（件）§8.3 一元一次不等式组（二）一、1. C 2. B. 3.A二、1. m≥2 2. ＜x＜三、1. （1）3＜x＜5 （2）-2≤x＜3 （3）-2≤x＜5 (4) x≥13(图略)2×3+2.5x＜204×3+2x＞202. 设苹果的单价为x元，依题意得解得4＜x＜5，因x恰为整数，所以x=5（元）（答略）3. -2＜x≤3 正整数解是1,2,34. 设剩余经费还能为x名山区小学的学生每人购买一个书包和一件文化衫，依题意得350≤1800-（18+30）x≤400，解得29≤x≤30，因人数应为整数，所以x=30.5.(1)这批货物有66吨 (2)用2辆载重为5吨的车,7辆载重为8吨的车.。

人教版七年级下册数学同步练习全套第五章相交线与平行线5.1.1《相交线》同步练习一、填空题（共15小题）1、下列各图中的∠1和∠2是对顶角的是（）A、B、C、D、2、如图所示，直线a，b相交于点O，若∠1等于50°，则∠2等于（）A、50°B、40°C、140°D、130°3、如图，∠1＝15°，∠AOC＝90°，点B，O，D在同一直线上，则∠2的度数为（）A、75°B、15°C、105°D、165°4、如图，点O在直线AB上，射线OC平分∠AOD，若∠AOC＝35°，则∠BOD等于（）A、145°B、110°C、70°D、35°5、如图，直线AB、CD相交于点O，OE平分∠AOD，若∠BOC＝80°，则∠AOE的度数是（）A、40°B、50°C、80°D、100°6、下列图形中∠1与∠2是对顶角的是（）A、 B、C、 D、7、如图，三条直线a,b,c相交于点O，则∠1+∠2+∠3等于（）A、90°B、120°C、180°D、360°8、如图所示，直线AB和CD相交于点O，OE、OF是过点O的射线，其中构成对顶角的是（）A、∠AOF和∠DOEB、∠EOF和∠BOEC、∠COF和∠BODD、∠BOC和∠AOD9、如图，∠PON＝90°，RS是过点O的直线，∠1=50°，则∠2的度数是（）A、50°B、40°C、60°D、70°10、下列语句正确的是（）A、相等的角是对顶角B、不是对顶角的角都不相等.C、不相等的角一定不是对顶角D、有公共点且和为180°的两个角是对顶角.11、如图所示，∠1和∠2是对顶角的图形有( )A、1个B、2个C、3个D、4个12、如图所示，三条直线AB，CD，EF相交于一点O，则∠AOE+∠DOB+∠COF等于( )A、150°B、180°C、210°D、120°13、下列说法正确的有( ) ①对顶角相等；②相等的角是对顶角；③若两个角不相等，则这两个角一定不是对顶角；④若两个角不是对顶角，则这两个角不相等.A、1个B、2个C、3个D、4个14、如图所示，直线AB和CD相交于点O，若∠AOD与∠BOC的和为236°，则∠AOC 的度数为( )A、62°B、118°C、72°D、59°15、如图所示，直线L1， L2， L3相交于一点，则下列答案中，全对的一组是( )A、∠1＝90°，∠2＝30°，∠3＝∠4＝60°；B、∠1＝∠3＝90°，∠2＝∠4＝30°C、∠1＝∠3＝90°，∠2＝∠4＝60°；D、∠1＝∠3＝90°，∠2＝60°，∠4＝30°二、填空题（共5小题）16、如图，直线a、b相交于点O，∠1＝50°，则∠2＝________度．17、如图，直线AB、CD、EF相交于点O，若∠DOF＝30°，∠AOE＝20°，则∠BOC ＝________°.18、已知∠1与∠2是对顶角，∠1与∠3是邻补角，则∠2+∠3＝________°.19、如图，直线AO与CD交于点O，射线OM平分∠AOC，若∠AOC=76°，则∠COM=________°.20、下列说法中：①因为∠1与∠2是对顶角，所以∠1＝∠2；②因为∠1与∠2是邻补角，所以∠1＝∠2；③因为∠1与∠2不是对顶角，所以∠1≠∠2；④因为∠1与∠2不是邻补角，所以∠1+∠2≠180°.其中正确的有________（填序号）三、解答题（共5小题）21、如图所示，直线AB、CD、EF相交于点O，∠AOE＝40°，∠BOC＝2∠AOC，求∠DOF.22、∠1＝∠2，∠1+∠2＝162°，求∠3与∠4的度数．23、如图，直线AB、CD、EF相交于点O，OG平分∠COF，∠1＝30°，∠2＝45°．求∠3的度数．24、如图，已知直线AB与CD相交于点O ， OE平分∠AOC ，射线OF⊥CD 于点O ，且∠BOF=32°，求∠COE的度数．25、如图所示，直线a，b，c两两相交，∠1＝2∠3，∠2＝65°，求∠4的度数.答案解析部分一、填空题（共15小题）1、【答案】D【考点】对顶角、邻补角【解析】【解答】有公共端点且两条边互为反向延长线的两个角为对顶角．选项A和选项C中∠1和∠2均没有公共端点，所以不是对顶角．选项B中∠1和∠2有公共端点，但是两条边不是互为反向延长线，所以选项B错误．选项D满足对顶角的所有条件，所以选D．【分析】掌握对顶角的概念是解答本题的关键．本题考查对顶角．2、【答案】A【考点】对顶角、邻补角【解析】【解答】两直线相交，对顶角相等．图中∠1和∠2是对顶角，∠1＝50°，所以∠2＝50°．选A．【分析】掌握对顶角的性质是解答本题的关键．本题考查对顶角．3、【答案】C【考点】对顶角、邻补角【解析】【解答】∵∠1＝15°，∠AOC＝90°，∴∠BOC＝75°，∵∠2+∠BOC＝180°，∴∠2＝105°．故选C．【分析】掌握邻补角的性质是解答本题的关键．本题考查邻补角．4、【答案】B【考点】对顶角、邻补角【解析】【解答】∵射线OC平分∠DOA．∴∠AOD＝2∠AOC，∵∠COA＝35°，∴∠DOA ＝70°，∴∠BOD＝180°－70°＝110°，故选：B．【分析】掌握邻补角的性质是解答本题的关键．本题考查邻补角．5、【答案】A【考点】对顶角、邻补角【解析】【解答】根据角平分线的定义计算．∵∠BOC＝80°，∴∠AOD＝∠BOC ＝80度．∵OE平分∠AOD，∴∠AOE＝∠AOD＝80°÷2＝40度．故选A．【分析】掌握对顶角的性质是解答本题的关键．本题考查对顶角．6、【答案】D【考点】对顶角、邻补角【解析】【解答】有公共端点且两条边互为反向延长线的两个角为对顶角．由此可以推导出：只有选项D中的∠1和∠2是对顶角．所以选D．【分析】掌握对顶角的定义是解答本题的关键．本题考查对顶角．7、【答案】C【考点】对顶角、邻补角【解析】【解答】两条直线相交，对顶角相等．由图可知，∠1+∠2+∠3的对顶角＝180°，所以∠1+∠2+∠3＝180°，所以选C．【分析】掌握对顶角和性质解答本题的关键．本题考查对顶角的性质．8、【答案】D【考点】对顶角、邻补角【解析】【解答】有公共端点且两条边互为反向延长线的两个角为对顶角．根据对顶角的含义及图形，即可选出正确选项D．【分析】掌握对顶角和性质解答本题的关键．本题考查对顶角的性质．9、【答案】B【考点】对顶角、邻补角【解析】【解答】根据对顶角的性质，结合图形，我们可以得知：∠MOQ＝∠PON ＝90°．又因为∠MOQ＝∠MOS＋∠2，所以∠2＝∠MOQ－∠MOS；因为∠MOS与∠1是对顶角，所以∠MOS＝50°，所以∠2＝90°－50°＝40°，所以选B．【分析】掌握对顶角和性质解答本题的关键．本题考查对顶角的性质．10、【答案】C【考点】对顶角、邻补角【解析】【解答】有公共端点且两条边互为反向延长线的两个角为对顶角．由此可以推导出：对顶角一定相等，不相等的角一定不是对顶角．但是，有些相等的角，并不是对顶角，所以选项A和B错误；对顶角相等，但并不一定互补，所以选项D错误；所以选C．【分析】掌握对顶角和性质解答本题的关键．本题考查对顶角的性质．11、【答案】A【考点】对顶角、邻补角【解析】【解答】有公共端点且两条边互为反向延长线的两个角为对顶角．根据对顶角的概念，从图中去判断，只有一组为对顶角，所以选A．【分析】掌握对顶角的概念是解答本题的关键．本题考查对顶角．12、【答案】B【考点】对顶角、邻补角【解析】【解答】因为∠COF与∠EOD是对顶角，所以∠AOE+∠DOB+∠COF等于∠AOE+∠DOB+∠EOD＝∠AOB，因为A、O、B三点共线，所以其和为180°．所以选B．【分析】掌握对顶角的性质是解答本题的关键．本题考查对顶角．13、【答案】B【考点】对顶角、邻补角【解析】【解答】有公共端点且两条边互为反向延长线的两个角为对顶角，互为对顶角的两个角相等．所以，可以判断①③正确，②错误．若两个角不是对顶角，但是两个角也有可能相等，所以④错误．所以选B．【分析】掌握对顶角的性质是解答本题的关键．本题考查对顶角．14、【答案】A【考点】对顶角、邻补角【解析】【解答】若∠AOD与∠BOC的和为236°，则∠AOC与∠BOD的和为360°－236°＝124°．因为∠AOC与∠BOD是对顶角，所以∠AOC＝∠BOD＝124°÷2＝62°．所以选B．【分析】掌握对顶角的性质是解答本题的关键．本题考查对顶角．15、【答案】D【考点】对顶角、邻补角【解析】【解答】∠1与∠3是对顶角，∠1＝∠3＝180°－30°－60°＝90°．根据对顶角的概念，从图中还可以直接看出∠2＝60°，∠4＝30°．所以选D．【分析】掌握对顶角的性质是解答本题的关键．本题考查对顶角．二、填空题（共5小题）16、【答案】50【考点】对顶角、邻补角【解析】【解答】直接根据对顶角相等即可求解∵直线a、b相交于点O，∴∠2与∠1是对顶角.∵∠1＝50°，∴∠2＝∠1＝50°．【分析】掌握对顶角的性质是解答本题的关键．本题考查对顶角．17、【答案】130【考点】对顶角、邻补角【解析】【解答】根据平角定义和∠DOF＝30°，∠AOE＝20°先求出∠AOD的度数，再根据对顶角相等即可求出∠BOC的度数．∵∠DOF＝30°，∠AOE＝20°，∴∠AOD＝180°-∠DOF-∠AOE＝180°-30°-20°＝130°，∴∠BOC＝∠AOD＝130°．【分析】掌握对顶角和邻补角的性质是解答本题的关键．本题考查对顶角和邻补角．18、【答案】180【考点】对顶角、邻补角【解析】【解答】根据邻补角定义可知，∠1+∠3＝180°，由对顶角的性质：对顶角相等可得∠1＝∠2，所以∠2+∠3＝180°（等量代换）．【分析】掌握对顶角和邻补角的性质是解答本题的关键．本题考查对顶角和邻补角．19、【答案】38【考点】对顶角、邻补角【解析】【解答】直接根据对顶角相等，得到∠AOC＝∠BOD＝76°．又因为OM平分∠AOC，所以∠COM＝76°÷2＝38°．【分析】掌握对顶角的性质是解答本题的关键．本题考查对顶角．20、【答案】①【考点】对顶角、邻补角【解析】【解答】①满足对顶角的性质，所以正确，②邻补角是特殊位置的补角，由互补的性质可知其和应180°，而不是∠1＝∠2，所以不正确；③中的∠1与∠2不是对顶角是从位置上看的，但它们在数量上是可以相等，所以也不正确；④的原因同③. 所以本题填①.【分析】掌握对顶角和邻补角的性质是解答本题的关键．本题考查对顶角和邻补角．三、解答题（共5小题）21、【答案】解：设∠AOC＝x°，则∠BOC＝(2x)°.因为∠AOC与∠BOC是邻补角，所以∠AOC+∠BOC＝180°所以x+2x＝180解得x＝60所以∠AOC＝60°.因为∠DOF与∠EOC是对顶角，所以∠DOF＝∠EOC＝∠AOC－∠AOE＝60°－40°＝20°【考点】对顶角、邻补角【解析】【解答】图形中∠BOC与∠AOC互为邻补角，结合已知条件：∠BOC＝2∠AOC，则可求出∠AOC，要求∠DOF只需求它的对顶角∠EOC即可，本题可用方程求解．【分析】掌握对顶角和邻补角的性质是解答本题的关键．本题考查对顶角和邻补角．22、【答案】解：由已知∠1＝∠2，∠1+∠2＝162°，解得：∠1＝54°，∠2＝108°．∵∠1与∠3是对顶角，∴∠3＝∠1＝54°．∵∠2与∠4是邻补角，∴∠4＝180°－∠2＝72°．【考点】对顶角、邻补角【解析】【解答】本题首先根据方程思想，求出. ∠1、∠2的度数，再根据对顶角、邻补角的关系求出∠3与∠4的度数．【分析】掌握对顶角和邻补角的性质是解答本题的关键．本题考查对顶角和邻补角．23、【答案】解：∵∠1＝30°，∠2＝45°∴∠EOD＝180°－∠1－∠2＝105°∴∠COF＝∠EOD＝105°又∵OG平分∠COF，∴∠3＝∠COF＝52.5°．【考点】对顶角、邻补角【解析】【解答】根据对顶角的性质，∠1＝∠BOF，∠2＝∠AOC，从而得出∠COF ＝105°，再根据OG平分∠COF，可得∠3的度数．【分析】掌握对顶角和邻补角的性质是解答本题的关键．本题考查对顶角和邻补角．24、【答案】解：∵∠COF是直角，∠BOF=32°，∴∠COB=90°﹣32°=58°，∴∠AOC=180°﹣58°=122°又∵OE平分∠AOC ，∴∠AOE=∠COE=61°【考点】垂线【解析】【解答】利用图中角与角的关系即可求得．【分析】此题主要考查了角平分线的定义，根据角平分线定义得出所求角与已知角的关系转化求解．25、【答案】解：∵∠1＝∠2，∠1＝2∠3∴∠2＝2∠3又∵∠3＝∠4，∴∠2＝2∠4∵∠2＝65°∴∠4＝32.5°.【考点】对顶角、邻补角【解析】【解答】根据对顶角的性质，∠1＝∠2，∠3＝∠4，再根据∠1＝2∠3，∠2＝65°，可得∠4的度数．【分析】掌握对顶角的性质是解答本题的关键．本题考查对顶角．第五章相交线与平行线5.1.2《垂线》一、1、下面说法中错误的是（）A、两条直线相交，有一个角是直角，则这两条直线互相垂直B、若两对顶角之和为1800，则两条直线互相垂直C、两条直线相交，所构成的四个角中，若有两个角相等，则两条直线互相垂直D、两条直线相交，所构成的四个角中，若有三个角相等，则两条直线互相垂直2、如图所示，AB⊥CD，垂足为D，AC⊥BC，垂足为C，那么图中的直角一共有（）A、2个B、3个C、4个D、1个3、如图所示，直线EO⊥CD，垂足为点O，AB平分∠EOD，则∠BOD的度数为（）A、120°B、130°C、135°D、1404、点P为直线外一点，点A、B、C为直线上三点，PA＝4cm，PB＝5cm，PC ＝2cm，则点P到直线的距离为（）A、4cmB、5cmC、小于2cmD、不大于2cm5、如图所示，OA⊥OC，OB⊥OD，下面结论中，其中说法正确的是（）①∠AOB＝∠COD；②∠AOB＋∠COD＝90°；③∠BOC＋∠AOD＝180°；④∠AOC －∠COD＝∠BOC.A、①②③B、①②④C、①③④D、②③④6、如图所示，直线AB⊥CD于点O，直线EF经过点O，若∠1＝26°，则∠2的度数是（ •）．A、26°B、64°C、54°D、以上答案都不对7、在下列语句中，正确的是（）．A、在平面上，一条直线只有一条垂线;B、过直线上一点的直线只有一条;C、过直线上一点且垂直于这条直线的直线有且只有一条;D、垂线段就是点到直线的距离8、如图所示，∠BAC＝90°，AD⊥BC于D，则下列结论中，正确的个数为（）．①AB⊥AC;②AD与AC互相垂直; ③点C到AB的垂线段是线段AB; ④点D到BC的距离是线段AD的长度; ⑤线段AB的长度是点B到AC 的距离; ⑥线段AB是点B到AC的距离; ⑦AD>BD.A、2个B、4个C、7个D、0个9、如图，直线AB，CD相交于点O，射线OM平分∠AOC，ON⊥OM，若∠AOM=35°，则∠CON的度数为（）A、35°B、45°C、55°D、65°10、已知在正方形网格中，每个小方格都是边长为1的正方形，A和B两点在小方格的顶点上，位置如图所示，点C也在小方格的顶点上，且以A，B，C•为顶点的三角形的面积为1个平方单位，则C点的个数为（）．A、3个B、4个C、5个D、6个11、已知直线AB ， CB ， l在同一平面内，若AB⊥l ，垂足为B ， C B⊥l ，垂足也为B ，则符合题意的图形可以是（）A、 B、 C、 D、12、下列语句正确的是（）A、两条直线相交成四个角，如果有两个角相等，那么这两条直线互相垂直B、两条直线相交成四个角，如果有两对角相等，那么这两条直线互相垂直C、两条直线相交成四个角，如果有三个角相等，那么这两条直线互相垂直D、两条直线相交成四个角，如果有两个角互补，那么这两条直线互相垂直13、过线段外一点画这条线段的垂线，垂足一定在（）A、线段上B、线段的端点上C、线段的延长线上D、以上情况都有可能14、如图，直线AD⊥BD，垂足为D，则点B到线段AC的距离是（）A、线段AC的长B、线段AD的长C、线段BC的长D、线段BD的长15、如图，OM⊥NP，ON⊥NP，所以OM和ON重合，理由是（）A、两点确定一条直线B、经过一点有且只有一条直线和已知直线垂直C、过一点只能作一条垂线D、垂线段最短16、当两条直线相交所成的四个角中________，叫做这两条直线互相垂直，其中的一条直线叫________，它们的交点叫________．17、过直线上或直线外一点，________与已知直线垂直．18、如图所示，若AB⊥CD于O，则∠AOD＝________；若∠BOD＝90°，则AB________CD．19、如图所示，已知AO⊥BC于O，那么∠1与∠2________．20、如果CD⊥AB于D，自CD上任一点向AB作垂线，那么所画垂线均与CD重合，这是因为________．21、如图，已知A，O，E三点在一条直线上，OB平分∠AOC，∠AOB＋∠DOE＝90°，试问：∠COD与∠DOE之间有怎样的关系?说明理由.22、如图，∠1＝30°，AB⊥CD ，垂足为O ， EF经过点O ．求∠2、∠3的度数．23、如图，直线AB与CD相交于点O，OP是∠BOC的平分线，OE⊥AB，OF⊥CD，(1)图中除直角外，还有相等的角吗？请写出两对：①________；②________ ．(2)如果∠AOD＝40°，则①∠BOC＝________；②OP是∠BOC的平分线，所以∠COP ＝________度；③求∠BOF的度数________ ．24、如图，已知∠AOB， OE平分∠AOC， OF平分∠BOC.(1)若∠AOB是直角，∠BOC＝60°，求∠EOF的度数；(2)猜想∠EOF与∠AOB的数量关系；(3)若∠AOB＋∠EOF＝156°，则∠EOF是多少度？25、直线AB、CD相交于点O.(1)OE、OF分别是∠AOC、∠BOD的平分线.画出这个图形.(2)射线OE、OF在同一条直线上吗?(直接写出结论)(3)画∠AOD的平分线OG.OE与OG有什么位置关系?并说明理由.答案解析部分一、1、【答案】C【考点】垂线【解析】【解答】垂线的概念是：当两条直线相交，有一个角是直角时，即两条直线互相平行．依据此概念，我们可以判断，选项A正确．选项B中，两对顶角之和为180°，则说明两对顶角均为90°，选项B也正确．在选项D中，两条直线相交，所构成的四个角中，若有三个角相等，根据对顶角的性质，说明四个角都相等，又因为四个角的度数和为360°，则说明四个角都是90°，选项D也正确．因为两条直线相交，形成两对对顶角，对顶角是相等的，但是不能说明该角一定是90°，所以选项C错误．【分析】掌握相交线形成的对顶角知识，以及垂线的概念，就能轻松解答本题．本题考查垂线．2、【答案】B【考点】垂线【解析】【解答】两条直线互相垂直，其所形成的夹角都是直角．根据题意，AB⊥CD，则∠ADC和∠BDC都是直角；同时，AC⊥BC，所以∠ACB也是直角．为此，图形中一共有3个直角．【分析】掌握垂线的概念，就能轻松解答本题．本题考查垂线．3、【答案】C【考点】垂线【解析】【解答】两条直线互相垂直，其所形成的夹角都是直角．根据题意，EO⊥CD，则∠EOD和∠EOC都是直角；又因为AB平分∠EOD，所以∠AOD为45°．∠AOD 与∠COB是对顶角，所以∠COB也是45°．因为∠COB与∠BOD互补，所以∠BOD ＝180°－45°＝135°.【分析】掌握垂线的概念，以及角平分线和对顶角的性质，就能轻松解答本题．本题考查垂线．4、【答案】D【考点】垂线段最短，点到直线的距离【解析】解答：点到直线的最短距离为过点作出的与已知直线的垂线段．在题干中，已知的最短距离为2cm，则选项A和选项B都是不正确的．又因为题干中没有明确告诉PC是否垂直于直线，当两线垂直时，则点P到直线的距离为2cm；若两直线不垂直，则点P到直线的距离为小于2cm．所以，只能选D．分析：点到直线的最短距离为过点作出的与已知直线的垂线段，是解答本题的关键．本题考查点垂线段最短．5、【答案】C【考点】垂线【解析】【解答】由题意可知，OA⊥OC，所以∠AOC＝90°，即∠AOB＋∠BOC＝90°．同时，OB⊥OD，所以∠BOD＝90°，即∠COD＋∠BOC＝90°．依次，可以判定∠AOB＝∠COD，所以①正确．又因为不能推断出∠AOB与∠COD的具体角度，所以②不正确．∠AOD＝∠AOB＋∠BOC＋∠COD，所以∠BOC＋∠AOD＝∠BOC＋∠AOB＋∠BOC＋∠COD＝90°＋90°＝180°．因为∠AOB＝∠COD，所以∠AOC－∠COD＝∠AOC－∠AOB＝∠BOC，所以④正确．为此，选C．【分析】在掌握两直线相互垂直，夹角为直角的基础上，学会角度转换，就能轻松找到正确答案．本题考查垂线．6、【答案】B【考点】垂线【解析】【解答】由题意可知，AB⊥CD于点O，所以∠BOC＝∠AOD＝90°，同时，∠1与∠DOF是对顶角，∠1＝26°，所以∠DOF＝26°．∠AOD＝∠AOF＋∠DOF，所以∠AOF＝∠AOD－∠DOF＝90°－26°＝64°．所以选B．【分析】在掌握两直线相互垂直，夹角为直角的基础上，学会角度转换，就能轻松找到正确答案．本题考查垂线．7、【答案】D【考点】垂线【解析】【解答】概念理解型题．垂直于一条直线的垂线有无数条，所以选项A 错误．两点之间才只有一条直线，过一点的直线有无数条，所以选项B错误．选项C是最容易出现混淆的地方．在概念中，同一平面内，过直线上一点且垂直于这条直线的直线有且只有一条；但是，在该选项中，没有注明同一平面，所以选项C错．点到直线的距离就是垂线段，所以选项D正确．【分析】概念理解型题，在解答时要注意对概念的正确理解，尤其是像选项C这种属于特别容易混淆的题目．本题考查垂线．8、【答案】B【考点】垂线，点到直线的距离【解析】【解答】根据题意，∠BAC＝90，所以AB⊥AC，①正确．AD⊥BC于D，所以AD与AC不垂直，②不正确．点到直线的距离为垂线段，所以点C到AB的垂线段是线段AB，③正确．点D到BC的距离应为过D点垂直于AC的垂线段，AD与AC不垂直，所以④错误．因为AB⊥AC，点B到AC的距离为AB，所以⑤⑥正确．AD与BD的具体长度无法推断，所以不能确定二者的大小关系，⑦错误．【分析】概念理解型题，掌握垂直和点到直线的具体的概念，是解答本题的关键．本题考查垂线．9、【答案】C【考点】垂线【解析】【解答】由射线OM平分∠AOC ，∠AOM=35°，得出∠MOC=35°，由【解答】∵射线OM平分∠AOC ，ON⊥OM ，得出∠CON=∠MON﹣∠MOC得出答案．∠AOM=35°，∴∠MOC=35°，∵ON⊥OM ，∴∠MON=90°，∴∠CON=∠MON﹣∠MOC=90°﹣35°=55°．故选：C．【分析】本题主要考查了垂线和角平分线，解决本题的关键是找准角的关系．10、【答案】B【考点】垂线【解析】【解答】已知每个小方格的边长为1，所以每个小方格的面积为1个平方单位．要使点C也在小方格的顶点上，且以A，B，C为顶点的三角形的面积为1个平方单位，需要从两个方面来思考：一是以A为三角形的顶点，则A到BC 是距离为1，BC的距离为2时才能使面积为1个平方单位，于是，这样的点有2个．同理，若以B为三角形的顶点，这样的点也同样有2个．所以，选B．【分析】从点到直线的距离，以及三角形的面积计算方法入手，就能轻松解答．本题考查垂线．11、【答案】A【考点】垂线【解析】解答：根据题意画出图形即可．故选：C分析：此题主要考查了垂线，关键是掌握垂线的定义：当两条直线相交所成的四个角中，有一个角是直角时，就说这两条直线互相垂直，其中一条直线叫做另一条直线的垂线，它们的交点叫做垂足．12、【答案】C【考点】垂线【解析】【解答】概念理解型题．两条直线相交，其中有一个夹角是直角，说明这两条直线互相垂直．同时，两条直线相交，形成四个角，分为两对对顶角，对顶角是相等的．但是，两条直线垂直必须相交，两条直线相交未必垂直，所以，可以推断出选项A、选项B都错误．在选项D中，两条直线任意相交，都能满足有两个角互补，所以D错误．在选项C中，有三个角相等，可以推导出这四个角都相等，并且都是直角，所以选项C正确．【分析】概念理解型题，掌握垂直的概念，是解答本题的关键．本题考查垂线．13、【答案】D【考点】垂线【解析】【解答】由于线段有两个端点，所线段的长度是固定的．由于点的位置不确定，所以过线段外一点画这条线段的垂线，垂足有可能在线段上、线段的端点上和线段的延长线上．这个知识点可以从三角形的高的画法上得到验证．所以，选D．【分析】概念理解型题，掌握垂直的作法，是解答本题的关键．本题考查垂线．14、【答案】D【考点】点到直线的距离【解析】【解答】点到直线的距离为垂线段，因为直线AD⊥BD，垂足为D，所以点B到线段AC的距离是线段BD的长，所以选D．【分析】概念理解型题，掌握到直线的距离为垂线段，是解答本题的关键．本题考查点到直线的距离．15、【答案】B【考点】垂线【解析】【解答】概念理解型题．经过一点有且只有一条直线与已知直线垂直．因为OM⊥NP，ON⊥NP，两条经过O点的直线都垂直于NP，所以选B．【分析】概念理解型题，掌握经过一点有且只有一条直线与已知直线垂直，是解答本题的关键．本题考查垂线．16、【答案】有一个直角；另一条直线的垂线；垂足【考点】垂线【解析】【解答】概念理解型题．两条直线相交，所形成的夹角中，有一个角为直角，说明这两条直线互相垂直．相互垂直的两条直线，其中一条直线叫另一条直线的垂线．两条直线互相垂直，它们的交点叫垂足．【分析】概念理解型题，掌握垂线的概念，是解答本题的关键．本题考查垂线．17、【答案】有且只有一条直线【考点】垂线【解析】【解答】概念理解型题．过直线外一点，有且只有一条直线与已知直线垂直．【分析】概念理解型题，掌握垂线的概念，是解答本题的关键．本题考查垂线．18、【答案】90°；⊥【考点】垂线【解析】【解答】概念理解型题．两条直线互相垂直，所形成的夹角为直角，也就是90°．如果两条直线相交，所形成的夹角中，有一个角为90°，则这两条直线互相垂直．【分析】概念理解型题，掌握垂线的概念，是解答本题的关键．本题考查垂线．19、【答案】互余【考点】垂线【解析】【解答】概念理解型题．两条直线互相垂直，所形成的夹角为直角，也就是90°．因为AO⊥BC于O，所以∠AOC＝90°．因为∠1＋∠2＝∠AOC．所以，∠1与∠2互余．【分析】概念理解型题，掌握垂线的概念，是解答本题的关键．本题考查垂线．20、【答案】在同一平面内，过一点有且只有一条直线与已知直线垂直【考点】垂线【解析】【解答】概念理解型题．过直线外一点有且只有一条直线与已知直线垂直．因为CD⊥AB于D，所以自CD上任一点向AB作垂线，那么所画垂线均与CD 重合．【分析】概念理解型题，掌握垂线的概念，是解答本题的关键．本题考查垂线．21、【答案】相等，理由：∠AOB＋∠DOE＝90°，且A、O、E三点共线，所以∠BOC ＋∠COD＝90°．因为OB平分∠AOC，所以∠AOB＝∠BOC，通过等量代换，可以得知∠COD与∠DOE相等．【考点】垂线【解析】【解答】由题意可知，∠AOB＋∠DOE＝90°，且A、O、E三点共线，所以∠BOC＋∠COD＝90°．因为OB平分∠AOC，所以∠AOB＝∠BOC，通过等量代换，可以得知∠COD与∠DOE相等．【分析】掌握相交线相关知识，是解答本题的关键．本题考查垂线．22、【答案】∵∠1与∠3是对顶角∴∠1＝∠3，因为∠1＝30°∴∠3＝30°．∵AB⊥CD∴∠BOD＝90°∵∠2＋∠3＝∠BOD∴∠2＝90°－∠3＝60°．【考点】垂线【解析】【解答】因为∠1与∠3是对顶角，所以∠1＝∠3，因为∠1＝30°，所以∠3＝30°．因为AB⊥CD ，所以∠BOD＝90°，因为∠2＋∠3＝∠BOD，所以∠2＝90°－∠3＝60°．【分析】掌握相交线相关知识，是解答本题的关键．本题考查垂线．23、【答案】（1）∠AOD＝∠BOC；∠BOP＝∠COP（2）40°；20°；50°【考点】垂线【解析】【解答】由题意可知，∠AOD与∠BOC是对顶角，所以二者相等．因为OP是∠BOC的角平分线，所以∠BOP＝∠COP．由第一问得到的答案，)如果∠AOD ＝40°，所以∠BOC＝40°．OP是∠BOC的平分线，所以∠COP＝20°．因为OF⊥CD，所以∠COF＝90°，所以∠BOF＝90°－40°＝50°.【分析】掌握相交线相关知识，是解答本题的关键．本题考查垂线．24、【答案】（1）∵∠AOC＝∠AOB＋∠BOC，∴∠AOC＝90°＋60°＝150°.∵OE平分∠AOC，∴∠EOC＝150°÷2＝75°.∵OF平分∠BOC，∴∠COF＝60°÷2＝30°.∵∠EOC ＝∠EOF＋∠COF,∴∠EOF＝75°－30°＝45°.（2）∵OE平分∠AOC，OF平分∠BOC．∴∠COE＝∠AOC，∠COF＝∠BOC∵∠AOB ＝∠AOC－∠BOC∴∠EOF＝∠COE－∠COF＝∠AOC－∠BOC＝（∠AOC－∠BOC）＝∠AOB（3）∵OE平分∠AOC，OF平分∠BOC，∴∠COE＝∠AOC，∠COF＝∠BOC，∴∠EOF＝∠AOC－∠BOC＝（∠AOC－∠BOC）＝∠AOB．又∵∠AOB＋∠EOF ＝156°，∴∠EOF＝52°．【考点】垂线【解析】【分析】此题难度较大，要通过角度转换．本题考查相交线所形成的角度．25、【答案】（1）如图中红线所示（2）射线OE、OF在同一条直线上（3）OE⊥OG理由：∵EF平分∠AOC和∠BOD，并且∠AOC＝∠BOD，∴∠AOE ＝∠DOF．∵OG平分∠AOD，∴∠AOG＝∠DOG．∵∠AOE＋∠DOF＋∠AOG＋∠DOG ＝180°，∴∠DOF＋∠DOG＝180°÷2＝90°，∴OE⊥OG．【考点】垂线【解析】【分析】此题掌握了角平分的性质是解题的关键．本题考查垂线和角平分线．5.1.3《同位角、内错角、同旁内角》一、选择题（共15题）1、如图，三条直线两两相交，则图中∠1和∠2是（）A、同位角B、内错角C、同旁内角D、互为补角2、如图所示，下列说法错误的是（）A、∠1和∠4是同位角B、∠1和∠3是同位角C、∠1和∠2是同旁内角D、∠5和∠6是内错角3、下列图形中，∠1和∠2不是同位角的是（）A、 B、C、 D、4、如图，下列判断正确的是（）A、∠2与∠5是对顶角B、∠2与∠4是同位角C、∠3与∠6是同位角D、∠5与∠3是内错角5、下列四幅图中，∠1和∠2是同位角的是（）A、⑴⑵B、⑶⑷C、⑴⑵⑶D、⑵、⑶⑷6、如图，∠1与∠2是（）A、对顶角B、同位角C、内错角D、同旁内角7、如图，已知AB∥CD，与∠1是同位角的角是（）A、∠2B、∠3C、∠4D、∠58、如图，与∠1是同位角的是（）A、∠2B、∠3C、∠4D、∠59、如图，下列各语句中，错误的语句是（）A、∠ADE与∠B是同位角B、∠BDE与∠C是同旁内角C、∠BDE与∠AED是内错角D、∠BDE与∠DEC是同旁内角10、如图，在所标识的角中，同位角是（）A、∠1和∠2B、∠1和∠3C、∠1和∠4D、∠2和∠311、已知：如图，直线AB、CD被直线EF所截，则∠EMB的同位角是（）A、∠AMFB、∠BMFC、∠ENCD、∠END12、如图，若直线MN与△ABC的边AB、AC分别交于E、F，则图中的内错角有（）A、2对B、4对C、6对D、8对13、如图，下列说法中错误的是（）A、∠3和∠5是同位角B、∠4和∠5是同旁内角C、∠2和∠4是对顶角D、∠1和∠4是内错角14、如图所示，与∠α构成同位角的角的个数为( )A、1B、2C、3D、415、如图，下列6种说法：①∠1与∠4是内错角；②∠1与∠2是同位角；③∠2与∠4是内错角；④∠4与∠5是同旁内角；⑤∠2与∠4是同位角；⑥∠2与∠5是内错角．其中正确的有 ( )A、1个B、2个C、3个D、4个二、填空题（共5题）16、如图，根据图形填空．(1)∠A________,________是同位角；(2)∠B和________,________是内错角；(3)∠A和________,__ ________,________是同旁内角．17、如图所示，与∠C构成同旁内角的有________个．18、如图，与图中的∠1成内错角的角是________ ．。

人教版七年级下册数学配套练习册及答案_下载名师优秀教案（完整版）资料(可以直接使用，可编辑优秀版资料，欢迎下载）人教版七年级下册数学配套练习册及答案_免费下载人教版七年级下册英语配套练习册答案单词:(七下册u1)country, Canada, Japan, Australia, French, language, pal, live, United, Singapore 选择:ABDBBCAACD句型:is from, Where from, What language(s), Where does, Does speak翻译:Where is from is from, does live lives, language speak speaks, Chinese speaks Japanese对话:EFBDASection B单词:write,favorite,difficult,world, wants,介词: for, in ,to, from in, in, with, at, from in, to on 选择:CCAAC BCABCCBBDB翻译:speak speaks French, think interesting, a little,writes to his parents about, playing sports onu2A答案1.library,restaurant,supermarket,bridge,post office, Avenue, neighborhood2:CBCBCCDCCC3Where are ,is a long bridge, Yes, there is, Are there any, There are two smallrestaurants in theneighborhood.SectionB答案1:small, quiet,beginning,through,dirty,hungry,way,garden,visit,tour,supermarket, airport,district,place,tour 2:BABBABCBAC3:Go down/turn left,have a goodtrip,know/arriving,with/next to,tell/the way4:is,postoffice,between,across from,down/along,on,school U3答案:giraffe,cute/clever,tigers,kind,Lions,elephant,Dolphins,pandas,animals,map 句型: Why/do,Why/does/like,Where /are /from,kindof,Does likeSectionB:Animals,leaves,other,quiet,lazy,years,play,relaxes,gras s,Africa翻译句子:Watches TV/at night, other/animals,are/lazy,play with/during,eats leaves 句型: What do to see,Does sleep,Why doyou,doesn’t relax,don’tbeU4答案:单词:doctor,hospital,waiter,policewoman,uniforms,money,t hieves,dangerous,reporter,policewomen三:What do youdo?,What doesdo.Wheredoes,Whatdo,What does四:What,do,Where,station,like,late,to be五:four,policeman,station,dangerous,clerk,money,be,h ospital,wears.doctors,night,restaurant,busy,late,to SectionB:单词:Summer,as,magazines,young,teach,news,stories, children,international,exciting,翻译句子:writing stories,/to work late,/kind of,/police station,/newspapers,magazines/,work for,as,/an international,children of/to teach阅读理解:BDDAC6.two,music7.No,can’t 8.shop 9.eight10.No,can’tU6答案:SectionB:一单词:6.group 7hot cold 8cool 9.having a good time 10.humid翻译句子:1.do do when rains2.weather, are wearing scarfs3.look at playing beach volleyball4.arelying. 5.am surprised/ inthis heat选词填空:Like, warm,looks, right,not,or,in,visit, about, because U7答案:一:acrosshospital,magazines,camera,snows二:us,friendly,beginning,Children’s,surprised四:1.aren’t any, 2.Doeshave,3.Where does,4.Why did, 5.What does,6.What’sdoing,7.is doing,8.does do,9.What’s like,10.having a good time五:What are you doing?Do you have a penpal?,Where does she come from/Where is she from?Are there any famous animals?,How is the weather inAustralia?/What’sthe weather like inAustralia? 书面表达:… I amCarl Smith. I am 21.I want…I like to workwith... I can speak (I)like...I want to be a (I)think I can do well. Please give me a chance. I will do my best. Thank you .This is a pencil.Does heplay And are ,parents,What does have,翻译1 e,from,2.does,want,wants clerk,3.straight,turn right,4.is wearing scarfs, 5.are singing人教版七年级数学上册同步练习题及答案全套人教版七年级数学上册同步练习题及答案全套(课课练)下载人教版七年级数学上册同步练习题及答案全套名称(课课练)学科数学类型试题|试卷0.57 MB 大小年级初一|七年级教材新课标人教版admin 添加审核2021-08-26 11:53 时间点击 20393评价 ?????第三章一元一次方程3.11一元一次方程(1)知识检测,m11(若4x,2=0是一元一次方程，则m=______(2(某正方形的边长为8cm，某长方形的宽为4cm，且正方形与长方形面积相等，•则长方形长为______cm(23(已知(2m,3)x,(2,3m)x=1是关于x的一元一次方程，则m=______( 4(下列方程中是一元一次方程的是( )2 A(3x+2y=5 B(y,6y+5=0 C(x,3= D(4x,3=05(已知长方形的长与宽之比为2:1•周长为20cm，•设宽为xcm，得方程:________( 6()利润问题:利润率=(如某产品进价是400元，•标价为600元，销售利润为5%，设该商品x折销售，得方程( ),400=5%×400(7(某班外出军训，若每间房住6人，还有两间没人住，若每间住4人，恰好少了两间宿舍，设房间为x，两个式子分别为(x,2)6人，(x+2)4，得方程_______(8(某农户2006年种植稻谷x亩，2007•年比2006增加10%，2021年比2006年减少5%，三年共种植稻谷120亩，得方程_______(9(一个两位数，十位上数字为a，个位数字比a大2，且十位上数与个位上数和为6，列方程为______( 10(某幼儿园买中、小型椅子共50把，中型椅子每把8元，小型椅子每把4•元，•买50把中型、小型椅子共花288元，问中、小型椅子各买了多少把,•若设中型椅子买了x把，则可列方程为______( 11(中国人民银行宣布，从2007年6月5日起，上调人民币存款利率，一年定期存款利率上调到3.06%，某人于2007年6月5日存入定期为1年的人民币5000元(到期后银行将扣除5%的利息税)(设到期后银行向储户支付现金x 元，则所列方程正确的是( )A(x,5000=5000×3.06%B(x+5000×5%=5000×(1+3.06%)C(x+5000×3.06%×5%=5000×(1+3.06%)D(x+5000×3.06%×5%=5000×3.06%12(足球比赛的计分方法为:胜一场得3分，平一场得1分，负一场得0分，一个队共打了14场比赛，负了5场，得19分，设该队共平x场，则得方程( )A(3x+9,x=19 B(2(9,x)+x=19C(x(9,x)=19 D(3(9,x)+x=19,|m|113(已知方程(m,2)x+3=m,5是关于x的一元一次方程，求m的值，•并写出其方程(拓展提高14(小明爸爸把家里的空啤酒瓶让小明去换饮料，现有40个空啤酒瓶，1个空啤酒瓶回收是0.5元，一瓶饮料是2元，4个饮料瓶可换一瓶饮料，问小明可换回多少瓶饮料,。