北师大版小学六年级数学总复习资料

小学六年级数学知识点归纳一、常用的数量关系式1、每份数×份数＝总数总数÷每份数＝份数总数÷份数＝每份数2、速度×时间＝路程路程÷速度＝时间路程÷时间＝速度3、单价×数量＝总价总价÷单价＝数量总价÷数量＝单价4、工作效率×工作时间＝工作总量工作总量÷工作效率＝工作时间工作总量÷工作时间＝工作效率5、加数＋加数＝和和－一个加数＝另一个加数6、被减数－减数＝差被减数－差＝减数差＋减数＝被减数7、因数×因数＝积积÷一个因数＝另一个因数8、被除数÷除数＝商被除数÷商＝除数商×除数＝被除数二、小学数学图形计算公式1、正方形（C：周长 S：面积 a：边长）周长＝边长×4 C=4a面积=边长×边长S=a×a正方体（V:体积a:棱长）表面积=棱长×棱长×6 S表=a×a×6体积=棱长×棱长×棱长V=a×a×a2、长方形（C：周长 S：面积 a：边长）周长=(长+宽)×2 C=2(a+b)面积=长×宽S=ab长方体（V:体积 s:面积 a:长 b: 宽 h:高）(1)表面积(长×宽+长×高+宽×高)×2 S=2(ab+ah+bh)(2)体积=长×宽×高V=abh3、三角形（s：面积 a：底 h：高）面积=底×高÷2 s=ah÷2三角形高=面积×2÷底三角形底=面积×2÷高4、平行四边形（s：面积 a：底 h：高）面积=底×高s=ah5、梯形（s：面积 a：上底 b：下底 h：高）面积=(上底+下底)×高÷2 s=(a+b)× h÷26、圆形（S：面积 C：周长л d=直径 r=半径）(1)周长=直径×л=2×л×半径C=лd=2л r(2)面积=半径×半径×л7、圆柱体8、圆锥体9、总数÷总份数＝平均数10、相遇问题相遇路程＝速度和×相遇时间相遇时间＝相遇路程÷速度和速度和＝相遇路程÷相遇时间11、利润与折扣问题三、常用单位换算1、长度单位换算1千米=1000米1米=10分米 1分米=10厘米1厘米=10毫米1米=100厘米2、面积单位换算1平方千米=100公顷1公顷=10000平方米1平方米=100平方分米1平方分米=100平方厘米 1平方厘米=100平方毫米3、体(容)积单位换算1立方米=1000立方分米 1立方分米=1000立方厘米 1立方分米=1升1立方厘米=1毫升 1立方米=1000升4、重量单位换算1吨=1000 千克 1千克=1000克1千克=1公斤5、人民币单位换算1元=10角1角=10分1元=100分3、时间单位换算1世纪=100年 1年=12月大月(31天)有:1\3\5\7\8\10\12月小月(30天)的有:4\6\9\11月平年2月28天, 闰年2月29天平年全年365天, 闰年全年366天 1日=24小时1时=60分 1分=60秒 1时=3600秒第一章数的认识一概念（一）整数1 整数的意义：自然数和0都是整数。

北师大版小学六年级数学上册总复习整理及试题(1)第一单元圆1、圆心决定圆的位置,半径（直径）决定圆的大小。

在同圆或等圆中,所有的直径都相等,所有的半径都相等,直径是半径的2倍。

一个圆有无数条半径,有无数条直径。

2、连接圆心和圆上任意一点的线段叫半径,经过圆心并且两端都在圆上的线段叫直径。

3、圆是轴对称图形,有无数条对称轴,任意一条直径所在的直线都是圆的对称轴。

圆环也有无数条对称轴。

4、一个圆的周长总是它直径的兀倍,也就是3倍多一点,这就是圆周率。

圆周率是一个固定不变的数,不会随着圆的大小而改变,是一个无限不循环小数,一般取其近似值 3.14。

圆的周长与直径的比是兀：1,比值是兀。

我国古代数学家祖冲之首先算出圆周率的值在 3.1415926和 3.1415927之间。

5、周长相等的长方形、正方形和圆,圆的面积最大,正方形面积次之,长方形面积最小。

6、圆的周长=圆周率×直径 C=兀D D= C÷兀圆的面积=圆周率×半径2 S=兀r27、圆环的面积=圆周率×（大圆半径2－小圆半径2） S环=兀（R2－r2）8、圆的半径扩大a倍,则直径扩大a倍,周长也扩大a倍,则面积扩大a2倍。

周长相等的圆,则其半径、直径、面积一定相等,反之则不等。

圆典型题例1、一只挂钟的时针长4厘米,分针长5厘米,从上午8点到11点,分针针尖走过的路线长是多少厘米？时针扫过的面积是多少？2、在一张长10厘米宽8厘米的长方形内剪一个最大的圆,这个圆的面积是多少？3、在一个长30厘米,宽20厘米的长方形内画一个最大的半圆,这个半圆的周长和面积各是多少？4、在一个直径为8米的圆形花坛外修一条宽2米的环形小路,小路的面积是多少平方米？5、用37.68米的铁丝围成一个圆,这个圆的面积是多少平方米？6、一条线长15.7米,正好在一个圆形线圈上绕100圈,这个线圈的直径是多少？7、在一个周长80厘米的正方形内画一个最大的圆,这个圆的面积是多少？8、一张可折叠的圆桌,直径是1.2米,折叠后就成了正方形,折叠后的桌面面积是多少平方米？9、在一个直径4分米的半圆形钢板上取一个最大的三角形,这个三角形的面积是多少平方分米？10、甜甜骑自行车上学,自行车的外胎直径是60厘米,自行车每分钟转80圈,她从家骑车12分钟到学校,求学校和她家的距离。

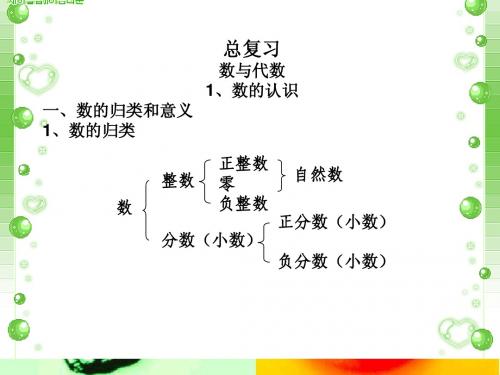
第一部分：数的意义1、自然数：用来表示物体个数的0、1、2、3、4、5……叫做自然数。

自然数的单位是“1”，任何一个自然数都是由若干个“1”组成的，自然数的个数是无限的。

最小的自然数是0。

自然数是整数的一部分。

2、分数：把单位“1”平均分成若干份，表示这样的一份或几份的数叫做分数。

两个整数相除的商也可以用分数来表示，即：a ÷b ＝b a(b ≠0)。

真分数：分子小于分母的分数叫做真分数。

（如：51 109） 分数可以分为假分数：分子大于或等于分母的分数叫做假分数。

（如：8955，）3、小数：把整数“1”平均分成10份、100份、1000份……表示其中的一份或几份的分数改成不带分母形式的数。

叫做小数。

有限小数：小数部分的位数是有限的。

（如：3.125，0.45687）小数按小数部分分为：无限小数：小数部分的位数是无限的。

（如：1415626.3＝ ……循环小数：一个小数，从某一位起一个数字或几个数字 依次不断重复出现，这样的小数叫做循环小数。

（如：2.231231231…… ，0.2787878……）➢ 判断分数能否化成有限小数的方法：把最简分数的分母分解质因数，在质因数中只有2和5两个因数组成的就能化成有限小数。

（如：85的分母8分解质因数是2×2×2中，只有2，所以能化成有限小数。

有如：209中的分母20分解质因数是2×2×5中，只用2和5，也能化成有限小数。

有如：158中的分母15分解质因数是3×5中，不是2和5而是3和5，所以不能化成有限小数。

）纯小数：整数部分是0的小数叫做纯小数。

纯小数都小于1。

（0.3，0.154，0.27878……）小数按整数部分分为：带小数：整数部分不是0的小数叫做带小数。

带小数都大于1。

（1.256，2.4765，3.212121……）4、百分数：表示一个数是另一个数的百分之几的数叫做百分数，也叫百分率或百分比。

北师大版六年级数学下册总复习——常见的量、探
索规律
常见的量：
1. 长度：用米（m）、厘米（cm）、毫米（mm）等作单位来表示，可以用尺量，可
以集中利用尺量一组相同长度的东西，称为长度单位；
2. 面积：用平方米（m²）、平方厘米（cm²）等作单位来表示，可以用方块量，可以
利用尺将一组正方形完全铺满；
3. 容量：用升（L）、毫升（mL）等作单位来表示，可以用容器直接量或间接量；
4. 质量：用千克（kg）、克（g）等作单位来表示，可以用天平直接量或间接量；
5. 体积：用立方米（m³）、立方厘米（cm³）等作单位来表示，可以用尺量或者可以
间接量。

探索规律：
在数学中，探索规律是指通过观察一系列的数、形或者其他事物的变化，去发现其中
的规律和关系，从而推导出一般性的结论。

通过探索规律，可以培养学生的观察能力、发散思维能力和创造力，同时也可以提高学生对数学的兴趣。

探索规律常见的方法有：
1. 观察法：通过观察一系列数或形状的变化，找出其中的规律；
2. 推理法：通过已知的规律和条件进行推理，得出新的结论；
3. 画图法：通过画图来观察数或形状的变化，找出其中的规律；
4. 建立数学模型：通过建立数学模型来描述实际问题，利用模型分析规律。

一、数的认识与应用
1.复习整数的概念，能够在数轴上表示和比较整数。

2.复习小数与整数的比较，能够读写和比较小数。

3.掌握小数和分数之间的转化关系，并能够进行分数和小数的互化。

二、小数的认识与应用
1.复习小数的概念，能够利用小数进行加、减、乘、除运算。

2.掌握小数与小数之间的比较，能够判断大小。

3.学会利用小数进行单位换算，如米和厘米、千克和克的换算。

三、长度、质量和容量单位换算
1.复习长度、质量和容量的基本单位及其符号，如米、千克和升，并能够进行换算。

2.学会利用图形和实物进行长度、质量和容量单位的换算。

四、多边形
1.掌握三角形、四边形、五边形、六边形等不规则多边形的命名和性质。

2.能够根据图形的特点进行分类，并能够分别计算各个多边形的边长和面积。

五、图形的对称
1.复习图形的对称性的概念，能够判断图形是否对称。

2.学会利用折纸对称的方法完成图形的折叠和对称。

六、数学语言的表达
1.学习利用数学语言和符号进行数学问题的描述和解答。

2.掌握常用数学语言和符号的意义和运用，如“是…的几倍”、“小
数点后几位”、“取整数部分”等。

以上是北师大版小学六年级数学知识点的大致内容。

通过学习这些知
识点，学生能够进一步加深对数学概念和运算的理解，提高数学应用能力，为进入中学阶段的学习打下坚实的基础。

总复习半径决定圆的大小。

在食指绕拇指旋转一周的过程中,拇指所按的点不变,食指与拇指间的距离不变。

用图钉、线和笔画圆时,图钉要固定好,线要拉直。

用圆规画圆,针尖所在的位置是圆心,两脚间的距离是半径。

1.同一个圆里有无数条半径,长度都相等。

二、圆的认识(二)1. 圆的对称性:圆是轴对称图形,直径所在的直线是圆的对称轴。

圆有无数条对称轴。

2 . 常见的轴对称图形的对称轴的数量。

正方形有4条、长方形有2条、等边三角形有3条、等腰三角形有1条、等腰梯形有1条和圆有无数条。

3. 利用圆的对称性确定圆心的方法。

方法一把圆形纸片按下面的方法对折,两条折痕的交点就是圆心。

方法二把圆形纸片沿不同的方向任意折出两条直径(直径所在的直线即对称轴),两条直径(折痕)的交点就是圆心。

4.圆与内接或外接正多边形组成的组合图形的对称轴是经过圆心的正多边形的对称轴。

三、欣赏与设计综合运用旋转、轴对称和平移的知识设计图案。

四、圆的周长1.圆的周长的意义。

圆的周长就是圆一周的长度,也可以理解为将圆滚动一圈的长度。

直径的长短决定圆周长的大小。

2.圆周长的测量方法。

方法一用滚动法测量圆的周长。

在圆形硬纸板的边缘上点一点A,使点A对准直尺的0刻度,然后使圆形硬纸板在直尺上向右滚动一周,点A所指的新刻度就是这个圆形硬纸板的周长。

方法二用绕线法测量圆的周长。

在圆形硬纸板的边缘上点一点A,使点A对准线的一个点,然后用线从点A开始绕圆形硬纸板一周,做好标记,再拉直并测量绕圆形硬纸板一周的线的长度,该长度就是圆形硬纸板的周长。

3.圆周率的意义。

圆的周长除以直径的商是一个固定的数,我们把它叫作圆周率,用字母π表示,计算时通常取3.14。

4.圆的周长的计算公式。

如果用字母C表示圆的周长,那么C=πd或C=2πr。

5.圆的周长计算公式的应用。

已知圆的半径、直径和周长三种量中的一种量,就可以求出另外两种量。

(1)已知圆的半径,求圆的周长:C=2πr。

(2)已知圆的直径,求圆的周长:C=πd。

北师大版小学六年级下册数学总复习知识点归纳小学六年级数学总复知识点归纳第一章数和数的运算一、概念1.整数的意义：自然数和它们的相反数组成的数集，都是整数。

2.自然数：用来表示物体个数的数，包括1、2、3……，也包括0.3.计数单位：一、十、百、千、万、十万、百万、千万、亿……都是计数单位，相邻两个计数单位之间的进率都是10.这种计数法叫做十进制计数法。

4.数位：数位按照一定的顺序排列起来，它们所占的位置叫做数位。

5.数的整除：倍数和因数是相互依存的。

一个数的因数的个数是有限的，其中最小的因数是1，最大的因数是它本身。

一个数的倍数的个数是无限的，其中最小的倍数是它本身，没有最大的倍数。

6.偶数和奇数：是2的倍数的数叫做偶数，不是2的倍数的数叫做奇数。

自然数按是不是2的倍数的特征可分为奇数和偶数。

7.质数和合数：一个数，如果只有1和它本身两个因数，这样的数叫做质数（或素数）。

一个数，如果除了1和它本身还有别的因数，这样的数叫做合数。

自然数除了1外，不是质数就是合数。

8.最大公约数：如果较小数是较大数的因数，那么较小数就是这两个数的最大公因数。

9.最小公倍数：如果较大数是较小数的倍数，那么较大数就是这两个数的最小公倍数。

二、分数分数的定义是将单位“1”平均分成若干份，表示其中的一份的数，叫做分数单位。

分数可以分为真分数、假分数和带分数。

真分数小于1，假分数大于或等于1.百分数表示一个数是另一个数的百分之几的数，通常用“%”来表示。

在除法中，被除数和除数同时扩大或缩小相同的倍数（除0外），商不变。

小数的大小不变，即在小数的末尾添上零或去掉零，小数的大小不变。

分数的分子和分母都乘以或除以相同的数（除0外），分数的大小不变。

加法交换律是a+b=b+a，加法结合律是（a+b)+c=a+(b+c)，乘法交换律是a×b=b×a，乘法结合律是(a×b)×c=a×(b×c)，乘法分配律是(a+b)×c=a×c+b×c，减法的性质是a-b-c=a-(b+c)。

北师大版小学六年级数学上册总复习概念整理知识点整理北师大版小学六年级数学上册复知识点精编第一单元：圆1.圆心是圆形纸片对折两次后折痕相交于圆中心的一点，用字母O表示。

圆心到圆上任意一点的距离都相等。

2.半径是连接圆心到圆上任意一点的线段，用字母r表示。

把圆规两脚分开，两脚之间的距离就是圆的半径。

3.圆心和半径分别确定圆的位置和大小。

4.直径是通过圆心并且两端都在圆上的线段，用字母d表示。

在圆内最长的线段是直径。

5.在同一个圆内，所有的半径都相等，所有的直径都相等。

直径的长度是半径的2倍，半径的长度是直径的一半。

用字母表示为：d=2r，r=d/2.用文字表示为：半径=直径÷2，直径=半径×2.6.在同一个圆内，有无数条半径和直径。

7.圆的周长总是直径的3倍多一些，这个比值是一个固定的数，叫做圆周率，用字母π表示。

圆周率是一个无限不循环小数，通常取它的近似值3.14.8.圆的周长公式：C=πd或C=2πr。

圆周长=π×直径，圆周长=π×半径×2.9.把一个圆分割成相等的若干份，可以拼成一个近似的长方形，拼成的长方形的长相当于圆周长的一半，用字母（πr）表示，宽相当于圆的半径，用字母（r）表示。

因为长方形的面积=长×宽，所以圆的面积=圆周长的一半×半径，用字母表示为：S=πr²。

10.在一个正方形里画一个最大的圆，圆的直径等于正方形的边长。

在一个长方形里画一个最大的圆，圆的直径等于长方形的宽。

画圆的方法都是连接对角线找圆心。

11.一个环形，外圆的半径是R，内圆的半径是r，它的面积是S=πR²-πr²或S=π(R²-r²)（其中R=r+环的宽度）。

12.半圆的周长等于圆的周长的一半加直径。

半圆的周长与圆周长的一半的区别在于，半圆有直径，而圆周长的一半没有直径。

半圆的周长公式：C=πd÷2+d或C=πr+2r。

小学六年级数学知识点归纳一、常用的数量关系式1、每份数×份数＝总数总数÷每份数＝份数总数÷份数＝每份数2、速度×时间＝路程路程÷速度＝时间路程÷时间＝速度3、单价×数量＝总价总价÷单价＝数量总价÷数量＝单价4、工作效率×工作时间＝工作总量工作总量÷工作效率＝工作时间工作总量÷工作时间＝工作效率5、加数＋加数＝和和－一个加数＝另一个加数6、被减数－减数＝差被减数－差＝减数差＋减数＝被减数7、因数×因数＝积积÷一个因数＝另一个因数8、被除数÷除数＝商被除数÷商＝除数商×除数＝被除数二、小学数学图形计算公式1、正方形（C：周长 S：面积 a：边长）周长＝边长×4 C=4a面积=边长×边长S=a×a正方体（V:体积a:棱长）表面积=棱长×棱长×6 S表=a×a×6体积=棱长×棱长×棱长V=a×a×a2、长方形（C：周长 S：面积 a：边长）周长=(长+宽)×2 C=2(a+b)面积=长×宽S=ab长方体（V:体积 s:面积 a:长 b: 宽 h:高）(1)表面积(长×宽+长×高+宽×高)×2 S=2(ab+ah+bh)(2)体积=长×宽×高V=abh3、三角形（s：面积 a：底 h：高）面积=底×高÷2 s=ah÷2三角形高=面积×2÷底三角形底=面积×2÷高4、平行四边形（s：面积 a：底 h：高）面积=底×高s=ah5、梯形（s：面积 a：上底 b：下底 h：高）面积=(上底+下底)×高÷2 s=(a+b)× h÷26、圆形（S：面积 C：周长л d=直径 r=半径）(1)周长=直径×л=2×л×半径C=лd=2л r(2)面积=半径×半径×л7、圆柱体8、圆锥体9、总数÷总份数＝平均数10、相遇问题相遇路程＝速度和×相遇时间相遇时间＝相遇路程÷速度和速度和＝相遇路程÷相遇时间11、利润与折扣问题三、常用单位换算1、长度单位换算1千米=1000米1米=10分米 1分米=10厘米1厘米=10毫米1米=100厘米2、面积单位换算1平方千米=100公顷1公顷=10000平方米1平方米=100平方分米1平方分米=100平方厘米 1平方厘米=100平方毫米3、体(容)积单位换算1立方米=1000立方分米 1立方分米=1000立方厘米 1立方分米=1升1立方厘米=1毫升 1立方米=1000升4、重量单位换算1吨=1000 千克 1千克=1000克1千克=1公斤5、人民币单位换算1元=10角1角=10分1元=100分3、时间单位换算1世纪=100年 1年=12月大月(31天)有:1\3\5\7\8\10\12月小月(30天)的有:4\6\9\11月平年2月28天, 闰年2月29天平年全年365天, 闰年全年366天 1日=24小时1时=60分 1分=60秒 1时=3600秒第一章数的认识一概念（一）整数1 整数的意义：自然数和0都是整数。

总产量=单产量X数量3、典型应用题具有独特的结构特征的和特定的解题规律的复合应用题，通常叫做典型应用题。

（1）平均数问题：平均数是等分除法的发展。

解题关键：在丁确定总数量和与之相对应的总份数。

算术平均数：已知几个不相等的同类量和与之相对应的份数，求平■均每份是多少。

数量关系式：数量之和：数量的个数=算术平■均数。

（2）归一问题：已知相互关联的两个量，其中一种量改变，另一种量也随之而改变，其变化的规律是相同的，这种问题称之为归一问题。

数量关系式：单一量x份数=总数量（正归一）总数量士单一量=份数（反归一）（7）行程问题：关丁走路、行车等问题，一般都是计算路程、时间、速度，叫做行程问题。

解答这类问题首先要搞活楚速度、时间、路程、方向、速度和、速度差等概念，了解他们之间的关系，再根据这类问题的规律解答。

（13）鸡兔问题：已知鸡兔”的总头数和总腿数。

求鸡”和兔”各多少只的一类应用题。

通常称为鸡兔问题”乂称鸡兔同笼问题解题关键：解答鸡兔问题一般采用假设法，假设全是一种动物（如全是鸡”或全是兔”，然后根据出现的腿数差，可推算出某一种的头数。

解题规律：（总腿数-鸡腿数x总头数）+一只鸡兔腿数的差=兔子只数兔子只数=（总腿数-2 X总头数）-2如果假设全是兔子，可以有下面的式子：鸡的只数=（4X总头数-总腿数）-2兔的头数=总头数-鸡的只数例鸡兔同笼共50个头，170条腿。

问鸡兔各有多少只？兔子只数（170-2 X50 ）- 2 =35 （只）鸡的只数50-35=15 （只）（二）分数和白分数的应用1分数加减法应用题：分数加减法的应用题与整数加减法的应用题的结构、数量关系和解题方法基本相同，所不同的只是在已知数或未知数中含有分数。

2分数乘法应用题：是指已知一个数，求它的几分之几是多少的应用题。

特征：已知单位“1的量和分率，求与分率所对应的实际数量。

解题关键：准确判断单位“1的量。

找准要求问题所对应的分率，然后根据一个数乘分数的意义正确列式。

北师大版小学(xiǎoxué)六年级数学上册总复习第一(dìyī)单元圆1、圆心决定圆的位置(wèi zhi)，半径（直径）决定圆的大小。

在同圆或等圆中，所有的直径都相等，所有的半径都相等，直径是半径的2倍。

一个圆有无数条半径，有无数条直径。

2、连接圆心和圆上任意一点的线段叫半径(bànjìng)，经过圆心并且两端都在圆上的线段叫直径。

3、圆是轴对称图形，有无数条对称轴，任意一条(yī tiáo)直径所在的直线都是圆的对称轴。

圆环也有无数条对称轴。

4、一个圆的周长总是它直径的兀倍，也就是3倍多一点，这就是圆周率。

圆周率是一个固定不变的数，不会随着圆的大小而改变，是一个无限不循环小数，一般取其近似值3.14。

圆的周长与直径的比是兀：1，比值是兀。

我国古代数学家祖冲之首先算出圆周率的值在3.1415926和3.1415927之间。

5、周长相等的长方形、正方形和圆，圆的面积最大，正方形面积次之，长方形面积最小。

6、圆的周长=圆周率×直径 C=兀D D= C÷兀圆的面积=圆周率×半径2 S=兀r27、圆环的面积=圆周率×（大圆半径2－小圆半径2） S环=兀（R2－r2）8、圆的半径扩大a倍，则直径扩大a倍，周长也扩大a倍，则面积扩大a2倍。

周长相等的圆，则其半径、直径、面积一定相等，反之则不等。

9、在圆形跑道上，相邻两个跑道一圈相差：道差=2兀×跑道宽。

圆典型题例1、一只挂钟的时针长4厘米，分针长5厘米，从上午8点到11点，分针针尖走过的路线长是多少厘米？时针扫过的面积是多少？2、在一张长10厘米宽8厘米的长方形内剪一个最大的圆，这个圆的面积是多少？3、在一个长30厘米，宽20厘米的长方形内画一个最大的半圆，这个半圆的周长和面积各是多少？4、在一个直径为8米的圆形花坛外修一条宽2米的环形小路，小路的面积是多少平方米？5、用37.68米的铁丝围成一个圆，这个圆的面积是多少平方米？6、一条线长15.7米，正好在一个圆形线圈上绕100圈，这个线圈的直径是多少？7、在一个周长80厘米的正方形内画一个最大的圆，这个圆的面积是多少？8、一张可折叠的圆桌，直径是1.2米，折叠后就成了正方形，折叠后的桌面面积是多少平方米？9、在一个直径4分米的半圆形钢板上取一个最大的三角形，这个三角形的面积是多少平方分米？10、甜甜骑自行车上学，自行车的外胎直径是60厘米，自行车每分钟转80圈，她从家骑车12分钟到学校，求学校和她家的距离。