材料科学基础家庭作业-第七章

1.可用金相法求再结晶形核率N和长大线速度G。

具体操作：(1)测定N：把一批经大变形量变形后的试样加热到一定温度(丁)后保温，每隔一定时间t，取出一个试样淬火，把做成的金相样品在显微镜下观察，数得再结晶核心的个数N，得到一组数据(数个)后作N—t图，在N—t曲线上每点的斜率便为此材料在温度丁下保温不同时间时的再结晶形核率N。

(2)测定G：将(1)中淬火后的一组试样进行金相观察，量每个试样(代表不同保温时间)中最大晶核的线尺寸D，作D—t图，在D—t曲线上每点的斜率便为了温度下保温不同时间时的长大线速度G。

2.再结晶退火必须用于经冷塑性变形加工的材料，其目的是改善冷变形后材料的组织和性能。

再结晶退火的温度较低，一般都在临界点以下。

若对铸件采用再结晶退火，其组织不会发生相变，也没有形成新晶核的驱动力(如冷变形储存能等)，所以不会形成新晶粒，也就不能细化晶粒。

3.能。

可经过冷变形而后进行再结晶退火的方法。

4.答案如附表2.5所示。

附表2.5 冷变形金属加热时晶体缺陷的行为5.(1)铜片经完全再结晶后晶粒大小沿片长方向变化示意图如附图2.22所示。

由于铜片宽度不同，退火后晶粒大小也不同。

最窄的一端基本无变形，退火后仍保持原始晶粒尺寸；在较宽处，处于临界变形范围，再结晶后晶粒粗大；随宽度增大，变形度增大，退火后晶粒变细，最后达到稳定值。

在最宽处，变形量很大，在局部地区形成变形织构，退火后形成异常大晶粒。

(2)变形越大，冷变形储存能越高，越容易再结晶。

因此，在较低温度退火，在较宽处先发生再结晶。

6.再结晶终了的晶粒尺寸是指再结晶刚完成但未发生长大时的晶粒尺寸。

若以再结晶晶粒中心点之间的平均距离d表征再结晶的晶粒大小，则d与再结晶形核率N及长大线速度之间有如下近似关系：41][NGkd=且)exp()exp(0RTQGGRTQNN nn-=-=，由于Qn与Qg几乎相等，故退火温度对G／N比值的影响微弱，即晶粒大小是退火温度的弱函数。

第一章 原子排列与晶体结构1. fcc 结构的密排方向是 ，密排面是 ，密排面的堆垛顺序是 ，致密度为 ，配位数是 ,晶胞中原子数为 ，把原子视为刚性球时，原子的半径r 与点阵常数a 的关系是 ；bcc 结构的密排方向是 ，密排面是 ,致密度为 ,配位数是 ,晶胞中原子数为 ，原子的半径r 与点阵常数a 的关系是 ；hcp 结构的密排方向是 ，密排面是 ，密排面的堆垛顺序是 ，致密度为 ，配位数是 ,晶胞中原子数为 ，原子的半径r 与点阵常数a 的关系是 。

2. Al 的点阵常数为0.4049nm ，其结构原子体积是 ，每个晶胞中八面体间隙数为 ，四面体间隙数为 。

3. 纯铁冷却时在912ε 发生同素异晶转变是从 结构转变为 结构，配位数 ，致密度降低 ，晶体体积 ，原子半径发生 。

4. 在面心立方晶胞中画出）（211晶面和]211[晶向，指出﹤110﹥中位于（111）平面上的方向。

在hcp 晶胞的（0001）面上标出）（0121晶面和]0121[晶向。

5. 求]111[和]120[两晶向所决定的晶面。

6 在铅的（100）平面上，1mm 2有多少原子？已知铅为fcc 面心立方结构，其原子半径R=0.175×10-6mm 。

第二章 合金相结构一、 填空1） 随着溶质浓度的增大，单相固溶体合金的强度 ，塑性 ，导电性 ，形成间隙固溶体时，固溶体的点阵常数 。

2） 影响置换固溶体溶解度大小的主要因素是（1） ；（2） ；（3） ；（4） 和环境因素。

3） 置换式固溶体的不均匀性主要表现为 和 。

4） 按照溶质原子进入溶剂点阵的位置区分，固溶体可分为 和 。

5） 无序固溶体转变为有序固溶体时，合金性能变化的一般规律是强度和硬度 ，塑性 ，导电性 。

6）间隙固溶体是 ，间隙化合物是 。

二、 问答1、 分析氢，氮，碳，硼在α-Fe 和γ-Fe 中形成固溶体的类型，进入点阵中的位置和固溶度大小。

已知元素的原子半径如下：氢：0.046nm ，氮：0.071nm ，碳：0.077nm ，硼：0.091nm ，α-Fe ：0.124nm ，γ-Fe ：0.126nm 。

第一章8．计算下列晶体的离于键与共价键的相对比例(1)NaF （2）CaO （3）ZnS解：1、查表得：X Na =0.93,X F =3.98根据鲍林公式可得NaF 中离子键比例为：21(0.93 3.98)4[1]100%90.2%e ---⨯=共价键比例为：1—90.2％=9.8% 2、同理，CaO 中离子键比例为：21(1.00 3.44)4[1]100%77.4%e---⨯=共价键比例为:1—77。

4％=22。

6％3、ZnS 中离子键比例为：21/4(2.581.65)[1]100%19.44%ZnS e --=-⨯=中离子键含量共价键比例为：1-19.44％=80.56％10说明结构转变的热力学条件与动力学条件的意义．说明稳态结构与亚稳态结构之间的关系.答：结构转变的热力学条件决定转变是否可行，是结构转变的推动力，是转变的必要条件;动力学条件决定转变速度的大小，反映转变过程中阻力的大小。

稳态结构与亚稳态结构之间的关系：两种状态都是物质存在的状态，材料得到的结构是稳态或亚稳态，取决于转交过程的推动力和阻力（即热力学条件和动力学条件)，阻力小时得到稳态结构，阻力很大时则得到亚稳态结构.稳态结构能量最低，热力学上最稳定，亚稳态结构能量高，热力学上不稳定，但向稳定结构转变速度慢，能保持相对稳定甚至长期存在。

但在一定条件下，亚稳态结构向稳态结构转变。

第二章1．回答下列问题：（1）在立方晶系的晶胞内画出具有下列密勒指数的晶面和晶向：(001）与[210]，（111）与[112]，(110)与 [111］,(132)与［123],(322)与[236］（2)在立方晶系的一个晶胞中画出（111）和 （112）晶面,并写出两晶面交线的晶向指数。

（3)在立方晶系的一个晶胞中画出同时位于（101)。

（011)和（112）晶面上的[111]晶向。

解：1、2．有一正交点阵的 a=b, c=a/2。

某晶面在三个晶轴上的截距分别为 6个、2个和4个原子间距，求该晶面的密勒指数。

《材料科学基础》课后习题答案第一章材料结构的基本知识4. 简述一次键和二次键区别答：根据结合力的强弱可把结合键分成一次键和二次键两大类。

其中一次键的结合力较强，包括离子键、共价键和金属键。

一次键的三种结合方式都是依靠外壳层电子转移或共享以形成稳定的电子壳层，从而使原子间相互结合起来。

二次键的结合力较弱，包括范德瓦耳斯键和氢键。

二次键是一种在原子和分子之间，由诱导或永久电偶相互作用而产生的一种副键。

6. 为什么金属键结合的固体材料的密度比离子键或共价键固体为高？答：材料的密度与结合键类型有关。

一般金属键结合的固体材料的高密度有两个原因：（1）金属元素有较高的相对原子质量；（2）金属键的结合方式没有方向性，因此金属原子总是趋于密集排列。

相反，对于离子键或共价键结合的材料，原子排列不可能很致密。

共价键结合时，相邻原子的个数要受到共价键数目的限制；离子键结合时，则要满足正、负离子间电荷平衡的要求，它们的相邻原子数都不如金属多，因此离子键或共价键结合的材料密度较低。

9. 什么是单相组织？什么是两相组织？以它们为例说明显微组织的含义以及显微组织对性能的影响。

答：单相组织，顾名思义是具有单一相的组织。

即所有晶粒的化学组成相同，晶体结构也相同。

两相组织是指具有两相的组织。

单相组织特征的主要有晶粒尺寸及形状。

晶粒尺寸对材料性能有重要的影响，细化晶粒可以明显地提高材料的强度，改善材料的塑性和韧性。

单相组织中，根据各方向生长条件的不同，会生成等轴晶和柱状晶。

等轴晶的材料各方向上性能接近，而柱状晶则在各个方向上表现出性能的差异。

对于两相组织，如果两个相的晶粒尺度相当，两者均匀地交替分布，此时合金的力学性能取决于两个相或者两种相或两种组织组成物的相对量及各自的性能。

如果两个相的晶粒尺度相差甚远，其中尺寸较细的相以球状、点状、片状或针状等形态弥散地分布于另一相晶粒的基体内。

如果弥散相的硬度明显高于基体相，则将显著提高材料的强度，同时降低材料的塑韧性。

SOLUTION FOR CHAPTER 71. FIND: Label the phase fields in Figure HP7-1.SOLUTION: There are two regions of single phase equilibrium separated by a region of two-phase equilibrium. The line separating the single phase liquid from the two phaseliquid and solid region is called the liquidus, and the line separating the two phase liquid and solid from the single phase solid is called the solidus.SKETCH:2. FIND: The name given to the type of equilibrium diagram shown in Fig. HP7-1.SOLUTION: The diagram is termed isomorphous. Above the liquidus there is only one phase, namely the liquid, and it has the same structure regardless of composition. Below the solidus is the solid phase, and as well it has the same structure regardless ofcomposition.3. FIND: What is the crystal structure of component B, why?SOLUTION: There are no phase boundaries below the solidus consequently the phase and therefore the structure must be the same. If A is FCC, then B and all compositionsbetween A and B must be the same phase and hence same structure. If A is FCC, then B must also be FCC.4. FIND: Sketch equilibrium cooling curves for alloy X o and pure component B. Explainwhy they have different shapes.SOLUTION: The slope of the temperature versus time behavior for the alloy in thesingle phase region is controlled by the cooling rate and the heat transferred from theliquid. At the liquidus temperature a small amount of solid is formed, releasing anamount of latent heat of fusion related to the volume of solid transformed. Hence, at the liquidus temperature there will be a change in slope. Since heat is being generated theslope will be less than that above the liquidus. As the temperature is reduced through the two-phase region a small amount of solid is formed and a corresponding heat released;once the solidus temperature is reached no additional transformation takes place and there is again a change in slope. The slope is greater as the solid cools than as the liquid andsolid cooled. For the pure component, solid and liquid are in equilibrium at T B, and hence,a horizontal line when liquid transforms to solid at T B.SKETCH:5. FIND: The liquidus temperature and the solidus temperature of alloy X oSOLUTION: From figure HP7-1 the liquidus temperature is approximately 1110o C and the solidus temperature is approximately 1070o C.6. FIND: Determine compositions and phase fractions of each phase in equilibrium at1100o C for alloy X o.SOLUTION: At equilibrium, the temperature of two phases must be the same, and thecomposition of the solid is found where the tie line intersects the solidus and the liquid is at the intersection of the tie line with the liquidus. From the phase diagram thecomposition of solid is 0.35B and that of the liquid is 0.55B. Using the lever rule thefraction of liquid, f L, and fraction of solid, f s is determined.7. FIND: Sketch f L and f S for alloy X o as the alloy is cooled under equilibrium conditionsfrom 1200o C to room temperature.SOLUTION: At the liquidus temperature the amount of liquid is almost 100% with onlya very small amount of solid. Conversely at the solidus temperature, the amount of solidis almost 100% with only a very small amount of liquid. In a two-phase field:f L + f s = 1.8. FIND: Changes in the compositions of the liquid and solid phases during quilibriumcooling of alloy X o through the two-phase field.SOLUTION: At the liquidus temperature, the composition of the solid is approximately0.30B. As equilibrium solidification progresses, the composition of the solid increases to0.5 B, the maximum value it can reach. The liquid on the other hand is initially thecomposition of the alloy X o, and as equilibrium solidification progresses the composition increases in B to the maximum composition in the liquid of approximately 0.7 B.9. FIND:From the following data construct a plausible equilibrium phase diagram.Component A melts at 800︒C and B melts at 1000︒C; A and B are completely soluble in one another at room temperature; and if solid α containing 0.3 B is heated underequilibrium conditions, the solid transforms to liquid having the same composition at500︒C.GIVEN: Melting temperatures for the two components, congruent melting temperature and composition.SOLUTION: The sketch shown below satisfies all of the requirements stated in theproblem. The melting temperature of pure A is 800︒C and that for pure B is 1000︒C. The congruent melting temperature is at 500︒C at a composition containing 0.3 B. Below the congruent melting temperature there is a continuous α solid solution.10. FIND: For alloys containing 10, 22, 25, 27, and 40 wt% Ni, determine the number ofphases present and the composition of the phases in equilibrium at 1200o C.11. FIND: Beginning with a statement of mass balance, derive the lever rule in a two-phasesystem.SOLUTION: In a two phase field for an alloy of some over all composition X o, thesolute is distributed in the two phases: x o = fα xα + fβ xβ where the compositions areexpressed in terms of one of the components, fα + fβ = 1. Then, fα= 1 - fβ. Substituting:x o = (1 - fβ) xα + fβ xβx o = xα - xα fβ + xβfβx o - xα = (xβ - xα) fβ12. FIND: Discuss each of the factors that permit the Cu-Ni system to be isomorphous overthe temperature range 350-1000o C.SOLUTION: The empirical rules of Hume-Rothery identify the characteristics that two elements must have in common for extensive solubility. This should require thata. the two components must have the same crystal structureb. the atomic radii of the two atoms must be similarc. the two components have the comparable electro negativities, andd. the two components have the similar valence.13. FIND: What does the temperature 322O C represent in Figure HP7-2?SOLUTION: 322o C is called the critical temperature. At the critical temperature there is a corresponding critical composition. For an alloy of this composition, cooling under equilibrium conditions from above the critical temperature to below this temperatureresults in the formation of two phases from one phase of the critical composition. Ascooling continues the two phases that form have different compositions.14. FIND: In Figure HP7-2, are α1 and α2 different crystal structures?SOLUTION: α1 and α2 are two phases having the same structure but differentcompositions. The composition of the two phases are determined as in any two phasesystem by using the tie-line. Where the tie-line at the equilibrium temperature intersects the phase boundaries determines the composition of the two phase in equilibrium.15. FIND: Location of the equilibrium phase boundary at temperature T.GIVEN: Alloy 1 containing 30%B and alloy 2 containing 50% B, when equilibrated at temperature T are in the same two-phase (L + S) region. The fraction of liquid in alloy 1 is 0.8 and the fraction of liquid in alloy 2 is 0.4.SKETCH:SOLUTION: Since the fraction of liquid in alloy 1 is greater than that of solid, theliquidus is to the left of 0.3, and since the fraction of solid in alloy 2 is greater than that of liquid, the solidus must lie to the right of alloy 2. Using the lever rule:for alloy 1for alloy 20.8X L - 0.8X s = X s - 0.30.4X L - 0.4X s = X s - 0.5Solve for X s and X L,0.8X s - 0.8X L = X s - 0.30.8X s - 0.8X L = 2X s - 1.0____________________0 = -X s + 0.7, orX s = 0.7BTo find X L, substitute X s into one of the equations:0.4 - 0.56 = -0.8X L-0.16 = -0.8X L, orX L = 0.2BAs a check, use the other equation to calculate the fraction of liquid from thecompositions.16. FIND: Label all regions of the phase diagram and the boundaries of monovariantequilibrium for the diagram shown in Figure HP7-3.SKETCH/SOLUTION:17. FIND: Sketch an equilibrium cooling curve from above the eutectic to roomtemperature for an alloy of eutectic composition.SKETCH/SOLUTION:18. FIND: Explain why the equilibrium cooling curves for alloys on either side of theeutectic composition will be different than the equilibrium cooling curve for a eutecticalloy.SOLUTION: At the eutectic temperature, liquid of composition X E is in equilibriumwith two solids, Xα and Xβ . For a hypoeutectic alloy (composition to the left of theeutectic), the first phase to form at the liquidus temperature of the alloy is α. When the eutectic temperature is reached the liquid of the eutectic composition is in equilibriumwith the two solids, one of composition Xα and the other Xβ. Consequently, depending upon composition, the closer the overall composition of the alloy is to X E, the lessproeutectic α and the more eutectic. Similarly, for alloys to the right, proeutectic β will form. In terms of the phase rule at constant pressure, for the eutectic reactionF = C - P + 1 = 2 - 3 + 1 = 0. The eutectic is invariant, and solidifies under equilibriumconditions at one temperature, T E. For alloys on either side of the eutectic composition but between Xα and Xβ, the proeutectic phase forms and cooling occurs as it does in any two-phase s-l region. Once the eutectic isotherm is reached, the remaining liquid ofeutectic composition solidifies isothermally.19. FIND: The maximum solid solubility of B in A and of A in B in Figure HP7-3.SOLUTION: The maximum solubility of B in A occurs at 0.15 B and the maximumsolubility of A in B is 0.1 A.20. FIND: For an alloy of eutectic composition in Figure HP7-3, determine the compositionof the solid phases in equilibrium with the liquid.SOLUTION: The composition of the two solid phase α and β in equilibrium with liquid at T_ occurs at 0.15 B and 0.9 B.21. FIND: Plot f L, fα, and fβ as a function of temperature for the equilibrium cooling of analloy of eutectic composition.SOLUTION: At just above the eutectic temperature, the microstructure consists of allliquid of composition X E. (Determined from the phase diagram to be approximately0.63B.) Just below the eutectic temperature, the microstructure is a mixture of twophases, α and β. From the phase diagram, Xα ~ 0.15B and Xβ ~ 0.9B. To determine the fractions of α and β at temperatures below T E, use the lever-rule. Tabulated below arecompositions of the phases in equilibrium at several temperatures estimated from thephase diagram. These compositions are then used to calculate the amount of each phase present.Fraction of phases:At 600: f L = 1.0, fα = fβ = 0At 500: f L = 0Instal l Equa tion E ditor a nd do uble-click h ere to view equat ion.Instal l Equa tion E ditor a nd do uble-click h ere to view equat ion.At 400: f L = 0Instal l Equa tion E ditor a nd do uble-click h ere to view equat ion.Instal l Equa tion E ditor a nd do uble-click h ere to view equat ion.At 300: f L = 0Instal l Equa tion E ditor a nd do uble-click h ere to view equat ion.Instal l Equa tion E ditor a nd do uble-click h ere to view equat ion.22. FIND: For alloy X o (in Figure HP7-3), calculate the fraction of α that forms as primary αand the fraction of α that forms by eutectic decomposition when the alloy is cooled from 850o C to room temperature under equilibrium conditions.SOLUTIONS: The fraction of proeutectic α that forms under equilibrium conditionspresent in alloy X o cooled from 850o C to just above the eutectic is:Then the fraction of liquid which is of eutectic composition is:f L = 1 - fα = 1. - 0.69 = 0.31.The fraction of α that forms from liquid of eutectic composition, fα,E is :fα,E = (fraction of α formed from eutectic) (0.31)To check these results, the sum of proeutectic α plus that which forms from the eutectic =0.69 + 0.11 = 0.8. That amount should be the same as if we calculated directly fα that would be present just below the eutectic for alloy of composition X o.23. FIND: The total fraction of α at room temperature for alloy X o in Figure HP7-3.SOLUTION: Solubility of B in α at room temperature is approximately 0.02 A and the solubility of A in β is approximately 0.04 A (in terms of B 0.96 B).24. FIND: Equilibrium phase diagram given the information below.GIVEN: Component A melts at 900o C; component B melts at 1000o C; and there is aninvariant reaction at 600o C. The solubility of B in α is known to increase from almost nil at room temperature to a maximum of 10%. When an alloy containing 30% B is cooled under equilibrium conditions just above 600o C, a two-phase mixture is present, 50% αand 50% liquid. When the alloy is cooled just below 600o C, the alloy contains two solid phases, α and β. The fraction of α is 0.75. After cooling under equilibrium conditions to room temperature, the amount of α in the α + β mixture decreases to 68%.SOLUTION: At just above the invariant temperature there is a region of two phaseequilibrium, a mixture of 50% α and 50% L. Consequently if the overall composition is 50%β, and α is located at 10%β, then the liquid must be at ˜50% B. Just below theinvariant reaction, two solid phases are present, αat ˜10%B and β at some composition, Xβ. If fα = 0.75, then:At room temperature, if fα = 0.68, and the solubility of B in α is nil, thenThe invariant reaction is L _ α + β, a eutectic, hence the diagram shown below fits allconditions.25. FIND: A binary phase diagram consistent with the information given below.GIVEN: The binary system A-B with T B > T A is known to contain two invariantreactions of the type: L _ α + β at T1, and L _ β + γ at T2 where T1 < T A and T2 > T A ,and β (0.5 B) is a congruently melting phase at a temperature higher than T B.SKETCH/SOLUTION: Given T B > T A, and T1 < T2 and T2 > T A, then at the congruent temperature, solid transforms to liquid at the same composition, hence for the threephases, α, β and γ with some solubility, is shown below along with a similar phasediagram in which there is limited solubility of B in A and A in B and the congruent phase appears as a line compound.26. FIND: Which phase diagram in Figure HP7-4 is MgO-NiO and which is NiO-CaO?Label the regions on the diagram and identify the invariant reaction.SOLUTION: To determine whether the isomorphous system is NiO-MgO or NiO-CaO, one needs to know the ionic radii of the three cations. r(Ni2+) = 0.078 nm, r(Mg2+) =0.078 nm, and r(Ca2+) = 0.106 nm. Therefore, based upon size of the ions occupying thecation sublattice we would expect the NiO-MgO system to be the isomorphous system.27. FIND: What is the maximum solid solubility of Ag in Pt?GIVEN: Phase diagram in Figure HP7-5.SOLUTION: Maximum solid solubility of Ag in Pt is 10.5 wt% Ag.28. FIND: For an alloy of peritectic composition, what is the composition of the last liquidto solidify at 1186o C?SOLUTION: The composition of the last liquid to solidify is 66.3% Ag (the peritiectic composition is 42.4% Ag).29. FIND: What is the range of alloy compositions that will peritectically transform duringequilibrium cooling?SOLUTION: Compositions between 10.5 and 66.3 wt % Ag.30. FIND: Plot the fraction of liquid, f L, the fraction of α, fα, and the fraction of β, fβ, as afunction of temperature during equilibrium cooling from 1800 to 400o C. For an alloy of peritectic composition.SOLUTION: First, you must determine the compositions of the phase(s) that is (are) in equilibrium. If, at a particular temperature the alloy is in a single phase then thecomposition of the phase is the composition of the alloy and the microstructure contains 100% of that phase. When the alloy is in a two phase field, the compositions aredetermined in using the tie-lines, and the phase fractions are determined using the lever.If, however, the microstructure is equilibrated at an invariant temperature and thecomposition lies along the invariant line, then only the composition of the phases can be determined, not their relative amounts. For an alloy of 42.4% Ag cooled underequilibrium conditions the approximate compositions of the phases in equilibrium atseveral temperatures are summarized in the following table.Fractions of phases at 1400:At 1300:At 1200At 1100At 1000At 900At 800At 700 At 600At 500At 400Fraction of phases as a function of temperature are plotted below.31. FIND: Sketch a possible diagram given the information below.GIVEN: The two component system A-B with T A > T B contains two invariant reactions of the type L + α _ β at T1, and L _ β + γ at T2 (<T1).SKETCH/SOLUTION: Reaction at T1 is a peritectic, reaction at T2 a eutectic, T A > T B and T1 > T2.In the above figure some B is soluble in A and likewise some A is soluble in B. Thephase that melts incongruently at T1 has a change in solubility with temperature.Alternatively, we can construct a diagram where the solubility of the end members are nil and the incongruently melting phase, X, is a line compound. That diagram wouldresemble the diagram shown below.32. FIND: Label all phase fields and identify the invariant reactions in the Ag-Al Phasediagram shown in figure HP7-6.SKETCH/SOLUTION:33. FIND: Label the phase fields and identify the invariant reactions in the V2O5 - NiOphase diagram.SKETCH/SOLUTION:34. FIND: Apply the 1-2-1...rule to the V2O5 - NiO diagram at 600o C.SOLUTION: At 600o C the single-phase regions are V2O5, N-V, 2N-V, 3N-V and NiO.These narrow single-phase fields define the regions of two-phase equilibrium. Also, itshould be recalled that at a fixed temperature the composition of each phase in a two-phase field is constant. All that varies is the relative amount of each phase (i.e. the lever-rule).35. FIND: Label all phase fields and identify the invariant reactions in the V2O5 - Cr2O3system.SKETCH/SOLUTION:36. FIND: For compositions X and Y, plot the fraction of phases present as a function oftemperature.SOLUTION: From the phase diagram in Figure HP7-8 the relevant we find:Composition of alloy X ~ 0.47BComposition of alloy Y ~ 0.55BComposition of the liquid at the peritectic isotherm ~ 0.44BComposition of the eutectic ~ 0.21BLiquidus temperature of X ~ 1100o CLiquidus temperature of Y ~ 1400o CPeritectic temperature ~ 900o CEutectic temperature ~ 700o CFor alloy X, in the temperature range from the liquidus (1100o C) to just above theperitectic isotherm, f L , decreases from 1.0 to:while the fraction of the oxide increases from 0 to (1 - 0.95) = 0.05. In the temperature range just below the peritectic isotherm to just above the eutectic isotherm, the phase fractions change from:andtoandjust above the eutectic temperature.In the temperature range below the eutectic isotherm, the Instal l Equa tion E ditor a nd do uble -click h ere to view equat ion.areconstant and from the lever rule are:Similarly for alloy Y:In the temperature range from the liquidus temperature (1400o C) to just above theperitectic isotherm the fraction of liquid decreases from f L = 1 towhile the fraction of Cr 2O 3 increasing from 0 toBelow the eutectic isotherm the amount of Cr 2O 3⋅V 2O 5 and Cr 2O 3 are constant.37.FIND: Identify the invariant reactions occurring in the Cu-Pb system.SOLUTION: There are two invariant reactions in the Cu - Pb system, a monotectic at 955o C and a eutectic at 326o C. For a complete illustration examine how the reduction in solubility of the components in each other effect the monotectic systems shown in Figure 7.6-1.38.FIND: Phase diagram HP7-9 indicates no mutual solid solubility of Cu in Pb or Pb in Cu. Explain why this is not strictly true.SOLUTION: Although the phase diagram appears to indicate no solubility of Cu in Pb or Pb in Cu, as pointed out on page 274 of the text, the free energy of a pure component can always be reduced by small additions of a second component since the presence of the second component increases the randomness of the system. It then is a competition between the enthalpy and the entropy terms as to how much is added, since:∆G = ∆H - T ∆S39.FIND: If an alloy containing 63 wt% Pb is cooled under equilibrium conditions from 1100o C to room temperature, plot the fraction of phases present as a function of temperature.SKETCH/SOLUTION: When an alloy containing 63% Pb, is cooled from 1100o C to room temperature under equilibrium conditions the following phases form. Below 991o C and just above the monotectic isotherm, liquid phase separation occurs. The composition of the two liquids follow the liquidus boundary, and the amount is calculated by the lever-rule. Below the monotectic isotherm to just above the eutectic isotherm two phases are present, Cu with essentially no soluble Pb and liquid rich in Pb, the composition of which follows the liquidus. Below the eutectic isotherm there is a two-phase mixture of essentially pure Cu and pure Pb. At 991o C the microstructure is essentially all liquid containing 63% Pb. At 975o C the microstructure has separated into two liquids, one (L I ) containing approximately 80% Pb and the second (L II ) containing approximately 43% Pb.Just above the monotectic isotherm.Below the monotectic isotherm, the fraction of liquid decreases, while the fraction ofsolid Cu increases. Just below 955o CAt 900o CAt 800o CThere is so little solubility of Cu in the liquid that once the temperature drops below 600o C, the system is essentially solid Cu with liquid essentially composed of Pb. Below 326o C the microstructure is a mixture of solid copper and lead. The phase diagramsuggests that there is no measurable change in solubility of the components. Then,40. FIND: Most alloying elements used in commercial titanium alloys can be classified aseither alpha stabilizers or beta stabilizers. Figure HP7.10 contains the Ti-Al and Ti-Vequilibrium phase diagrams. Which alloying element would most likely be consideredthe alpha stabilizer? Explain.GIVEN: The Ti-Al and Ti-V phase diagrams.SOLUTION: Solid titanium exists in two crystal forms. β, the high temperatureallotrope which is bcc, and α, the low temperature form which is hcp. At 882 ︒C thesetwo phases are in equilibrium at 1 atm pressure for pure titanium. When alloyingelements are added the relative stability of the phases may change. For the Ti-Al system, adding aluminum to pure titanium increases the temperature at which α begins to form.Thus, aluminum is said toIn the Ti-V system, thetemperature at which the αphases formsdecrease with increasing V,said to be a βthus V is41. FIND: In the Ti-Al system, identify a phase and its composition that melts congruently.Estimate the congruent melting temperature from the phase diagram.GIVEN: The Ti-Al phase diagram and the definition of a congruently melting phase. A phase melts congruently, when the composition of the solid and the composition of theliquid for an alloy are the same.SOLUTION: Examination of the Ti-Al phase diagram shows that the composition near5 weight % ( ~ 10 atomic %) melts congruently at approximately 1730 ︒C.42.FIND: Label all the two-phase fields on the Ti-Al phase diagram.GIVEN: The Ti-Al phase diagram with all the single phase fields labeled.SOLUTION: To complete this problem, we need only recognize that in a binary system, phases appear across the diagram alternating 1-2-1-2-...-1. Included below is the Al-Ti phase diagram with all phase fields labeled.α + Ti Al 33Ti Al + TiAl TiAl + TiAl 2α + Ti Al 3β + TiAlβ + Lα + TiAlTiAl + LTiAl + δTiAl + δ2α700900110013001500T e m p e r a t u r e , °C23TiAl + βTiAl 23TiAl + αTiAl 3αTiAl + Al 3βTiAl + Al Allotropic phaseL + δα + β3δ + βTiAl 3βTiAl + L 170043. FIND: Label all the invariant reactions occurring in the Ti-Al system.GIVEN: The Ti-Al phase diagram.SOLUTION:See the sketch of the Ti-Al diagram below.44. FIND: From the phase diagram, estimate the temperature at which Ti3Al congruentlytransforms to α Ti.GIVEN: The Ti-Al phase diagram.SOLUTION: The phase Ti3Al transforms the α Ti of the same composition atapproximately 1200︒C and a composition of approximately 21 wt % Al (33 atomic % Al).45. FIND: When the line compound β TiAl3 is heated, what is the composition of the firstliquid that forms in equilibrium with β TiAl3? Does this compound melt congruently?Explain.GIVEN: The Ti-Al phase diagram.SOLUTION: TiAl3 appears as a line compound on the phase diagram. Atapproximately 1375︒C TiAl3 undergoes a peritectic reaction on heating underequilibrium conditions. The composition of the liquid in equilibrium with TiAl3 is notthe composition of TiAl3 and hence the phase does not melt congruently, but meltsincongruently. The composition of the liquid is approximately 63 wt % Al. Theperitectic reaction written on heating is:TiAl3→ liquid (63 wt % Al) + δ Ti.46. FIND: The presence of Ti3Al in Ti-Al alloys has a detrimental effect on the ductility. Tocontrol this problem, the amount of aluminum needs to be less than 6 wt. %.Consequently, all of the products that you are producing contain a maximum of 6 wt. %of aluminum. You have been told that additions of tin, zirconium, and oxygen (oftenpresent as an impurity) are all known to be alpha stabilizers. If there is a possibility thatsmall additions of oxygen may enter the system as your alloy is melted, should youreduce the amount of aluminum in your alloy or not worry about it if ductility is animportant property for your product? Explain your reasoning.GIVEN: The Ti-Al phase diagram.SOLUTION: Since both aluminum and oxygen are α stabilizers, a judicious choicewould be to reduce the amount of aluminum in your alloy. This would be a particularlywise choice since the critical amount is just at 6 % Al, the addition of any alloyingelement that might affect the amount of Ti3Al should be avoided. Therefore reducing the amount of Al should be reduced.47. FIND: Label all the two-phase fields in the Ti-V system.GIVEN: The Ti-V phase diagram with all the single phase fields labeled.SOLUTION: To complete this problem, we need only recognize that in a binary system, phase fields appear across the diagram alternating 1-2-1-2-...-1. Included below is asketch of the Al-V phase diagram with all phase fields labeled.48. FIND: Identify the invariant reaction that is occurring at 675︒C in the Ti-V system.GIVEN: The Ti-V phase diagram.SOLUTION: The invariant reaction that is occurring at 675︒C is a monotectoid reaction and can be written symbolically as:β1→α + β2.from 900︒C down to 500︒C, plot the fraction of phases present as a function of temperature.GIVEN: The Ti-V phase diagram.SOLUTION: The compositions and the fraction of each phase from the phase diagram are shown in the table below. From the table the sketch given below illustrates the relative fraction of phases present as a function of temperature.50.FIND: Consider an alloy containing 52 wt. % V. Describe the phases present and their compositions as the alloy is cooled under equilibrium conditions from 900︒C to 500︒C. GIVEN: The Al-V phase diagram.SOLUTION: An alloy containing 52 wt. % V at 900︒C is in the β Ti,V single phase field. When the alloy is cooled it passes through the critical temperature of a monotectoid at 850︒C. Cooling below this temperature results in the formation of a two phase mixture of V-poor and V-rich solids that have the β Ti,V structure. Decreasing the temperature results in two solid phases whose compositions continuously change. The composition of the two solids follow the solid-solid miscibility boundary as shown in the sketch below. Cooling to 675︒C results in the invariant monotectoid reaction at that temperature. Symbolically that reaction can be written as β1 → α + β2. Cooling below themonotectoid temperature results in the disappearance of the β1 phase. Since the relative solubilities of V in Ti and Ti in V decrease with temperature, cooling to 500︒C changes the compositions of the α and β2 phases following the solvus boundaries as shown in the sketch.51.FIND: If a titanium alloy containing 5 wt. % V is cooled under equilibrium conditions from 900︒C down to 500︒C, plot the fraction of phases present as a function of temperature. Which phase is richer in vanadium, α or β? GIVEN: The Ti-V phase diagram.SOLUTION: The β phase is richer in vanadium than the α phase.L + β ( Ti, V )β ( Ti, V ) + α ( Ti )β1β2+Comp. of β decreases in V along phase boundary12Comp. of β increases in V along phase boundaryMonotectoid isotherm。

绪论一、填空题1、材料科学主要研究的核心问题是结构和性能的关系。

材料的结构是理解和控制性能的中心环节，结构的最微细水平是原子结构，第二个水平是原子排列方式，第三个水平是显微组织。

2. 根据材料的性能特点和用途，材料分为结构材料和功能材料两大类。

根据原子之间的键合特点，材料分为金属、陶瓷、高分子和复合材料四大类。

第一章材料的原子结构一、填空题1. 金属材料中原子结合以金属键为主，陶瓷材料（无机非金属材料）以共价键和离子键结合键为主，聚合物材料以共价键和氢键以及范德华键为主。

第二章材料的结构一、填空题1、晶体是基元（原子团）以周期性重复方式在三维空间作有规则的排列的固体。

2、晶体与非晶体的最根本区别是晶体原子排布长程有序，而非晶体是长程无序短程有序。

3、晶胞是晶体结构中的最小单位。

4、根据晶体的对称性，晶系有三大晶族，七大晶系，十四种布拉菲Bravais点阵，三十二种点群，230种空间群。

5、金属常见的晶格类型有体心立方、面心立方、密排六方。

6、fcc晶体的最密排方向为<110>，最密排面为{111}，最密排面的堆垛顺序为ABCABCABCABC……。

7、fcc晶体的致密度为0.74，配位数为12，原子在（111）面上的原子配位数为6。

8、bcc晶体的最密排方向为<111>，最密排面为{110}，致密度为0.68，配位数为8。

9、晶体的宏观对称要素有对称点、对称轴、对称面。

10、CsCl型结构属于简单立方格子，NaCl型结构属于面心立方格子，CaF2型结构属于面心立方格子。

11、MgO晶体具有NaCl型结构，其对称型是3 L44L36L29PC，晶族是高级晶族，晶系是立方晶系，晶体的键型是离子键。

12、硅酸盐晶体结构中的基本结构单元是硅氧四面体[SiO4]。

？13、几种硅酸盐晶体的络阴离子分别为[Si2O7]6-、[Si2O6]4-、[Si4O10]4-、[AlSi3O8]1-，它们的晶体结构类型分别为组群状，链状，层状，和架状。

第七章答案7-1略7-2浓度差会引起扩散，扩散是否总是从高浓度处向低浓度处进行?为什么?解：扩散是由于梯度差所引起的，而浓度差只是梯度差的一种。

当另外一种梯度差，比如应力差的影响大于浓度差，扩散则会从低浓度向高浓度进行。

7-3欲使Ca2＋在CaO中的扩散直至CaO的熔点（2600℃）时都是非本质扩散，要求三价离子有什么样的浓度？试对你在计算中所做的各种特性值的估计作充分说明。

已知CaO肖特基缺陷形成能为6eV。

解：掺杂M3+引起V’’Ca的缺陷反应如下：当CaO在熔点时，肖特基缺陷的浓度为：所以欲使Ca2＋在CaO中的扩散直至CaO的熔点（2600℃）时都是非本质扩散，M3+的浓度为，即7-4试根据图 7-32查取：（1）CaO在1145℃和1650℃的扩散系数值；（2）Al2O3在1393℃和1716℃的扩散系数值；并计算CaO和Al2O3中Ca2＋和Al3＋的扩散活化能和D0值。

解：由图可知CaO在1145℃和1650℃的扩散系数值分别为，Al2O3在1393℃和1716℃的扩散系数值分别为根据可得到CaO在1145℃和1650℃的扩散系数的比值为：，将值代入后可得，Al2O3的计算类推。

7-5已知氢和镍在面心立方铁中的扩散数据为cm2/s和cm2/s，试计算1000℃的扩散系数，并对其差别进行解释。

解：将T=1000℃代入上述方程中可得，同理可知。

原因：与镍原子相比氢原子小得多，更容易在面心立方的铁中通过空隙扩散。

7-6在制造硅半导体器体中，常使硼扩散到硅单晶中，若在1600K温度下，保持硼在硅单晶表面的浓度恒定（恒定源半无限扩散），要求距表面10－3cm深度处硼的浓度是表面浓度的一半，问需要多长时间（已知D1600℃＝8×10－12cm2/s；当时，）？解：此模型可以看作是半无限棒的一维扩散问题，可用高斯误差函数求解。

其中=0，，所以有0.5=，即=0.5，把=10－3cm，D1600℃＝8×10－12cm2/s代入得t=s。

第二章思考题与例题1. 离子键、共价键、分子键和金属键的特点，并解释金属键结合的固体材料的密度比离子键或共价键固体高的原因？2. 从结构、性能等方面描述晶体与非晶体的区别。

3. 何谓理想晶体？何谓单晶、多晶、晶粒及亚晶？为什么单晶体成各向异性而多晶体一般情况下不显示各向异性？何谓空间点阵、晶体结构及晶胞？晶胞有哪些重要的特征参数？4. 比较三种典型晶体结构的特征。

（Al、α-Fe、Mg三种材料属何种晶体结构？描述它们的晶体结构特征并比较它们塑性的好坏并解释。

）何谓配位数？何谓致密度？金属中常见的三种晶体结构从原子排列紧密程度等方面比较有何异同？5. 固溶体和中间相的类型、特点和性能。

何谓间隙固溶体？它与间隙相、间隙化合物之间有何区别？（以金属为基的）固溶体与中间相的主要差异（如结构、键性、性能）是什么？6. 已知Cu的原子直径为 2.56A，求Cu的晶格常数，并计算1mm3Cu的原子数。

7. 已知Al相对原子质量Ar（Al）=26.97，原子半径γ=0.143nm，求Al晶体的密度。

8 bcc铁的单位晶胞体积，在912℃时是0.02464nm3；fcc铁在相同温度时其单位晶胞体积是0.0486nm3。

当铁由bcc转变为fcc时，其密度改变的百分比为多少？9. 何谓金属化合物？常见金属化合物有几类？影响它们形成和结构的主要因素是什么？其性能如何？10. 在面心立方晶胞中画出[012]和[123]晶向。

在面心立方晶胞中画出（012）和（123）晶面。

11. 设晶面（152）和（034）属六方晶系的正交坐标表述，试给出其四轴坐标的表示。

反之，求（31）及（2112）的正交坐标的表示。

（练习），上题中均改为相应晶向指数，求12相互转换后结果。

12.在一个立方晶胞中确定6个表面面心位置的坐标，6个面心构成一个正八面体，指出这个八面体各个表面的晶面指数，各个棱边和对角线的晶向指数。

13. 写出立方晶系的{110}、{100}、{111}、{112}晶面族包括的等价晶面，请分别画出。

第一章材料的结构一、解释以下基本概念空间点阵、晶格、晶胞、配位数、致密度、共价键、离子键、金属键、组元、合金、相、固溶体、中间相、间隙固溶体、置换固溶体、固溶强化、第二相强化。

二、填空题1、材料的键合方式有四类，分别是（），（），（），（）。

2、金属原子的特点是最外层电子数（），且与原子核引力（），因此这些电子极容易脱离原子核的束缚而变成（）。

3、我们把原子在物质内部呈（）排列的固体物质称为晶体，晶体物质具有以下三个特点，分别是（），（），（）。

4、三种常见的金属晶格分别为（），（）和（）。

5、体心立方晶格中，晶胞原子数为（），原子半径与晶格常数的关系为（），配位数是（），致密度是（），密排晶向为（），密排晶面为（），晶胞中八面体间隙个数为（），四面体间隙个数为（），具有体心立方晶格的常见金属有（）。

6、面心立方晶格中，晶胞原子数为（），原子半径与晶格常数的关系为（），配位数是（），致密度是（），密排晶向为（），密排晶面为（），晶胞中八面体间隙个数为（），四面体间隙个数为（），具有面心立方晶格的常见金属有（）。

7、密排六方晶格中，晶胞原子数为（），原子半径与晶格常数的关系为（），配位数是（），致密度是（），密排晶向为（），密排晶面为（），具有密排六方晶格的常见金属有（）。

8、合金的相结构分为两大类，分别是（）和（）。

9、固溶体按照溶质原子在晶格中所占的位置分为（）和（），按照固溶度分为（）和（），按照溶质原子与溶剂原子相对分布分为（）和（）。

10、影响固溶体结构形式和溶解度的因素主要有（）、（）、（）、（）。

11、金属化合物（中间相）分为以下四类，分别是（），（），（），（）。

12、金属化合物（中间相）的性能特点是：熔点（）、硬度（）、脆性（），因此在合金中不作为（）相，而是少量存在起到第二相（）作用。

13、CuZn、Cu5Zn8、Cu3Sn的电子浓度分别为（），（），（）。

14、如果用M表示金属，用X表示非金属，间隙相的分子式可以写成如下四种形式，分别是（），（），（），（）。

材料科学与基础习题集和答案第七章回复再结晶，还有相图的内容。

第一章1.作图表示立方晶体的()()()421,210,123晶面及[][][]346,112,021晶向。

2.在六方晶体中，绘出以下常见晶向[][][][][]0121,0211,0110,0112,0001等。

3.写出立方晶体中晶面族{100}，{110}，{111}，{112}等所包括的等价晶面。

4.镁的原子堆积密度和所有hcp 金属一样，为0.74。

试求镁单位晶胞的体积。

已知Mg 的密度3Mg/m 74.1=mg ρ，相对原子质量为24.31，原子半径r=0.161nm 。

5.当CN=6时+Na 离子半径为0.097nm ，试问：1) 当CN=4时，其半径为多少？2) 当CN=8时，其半径为多少？6. 试问：在铜（fcc,a=0.361nm ）的<100>方向及铁(bcc,a=0.286nm)的<100>方向,原子的线密度为多少？7.镍为面心立方结构，其原子半径为nm 1246.0=Ni r 。

试确定在镍的（100），（110）及（111）平面上12mm 中各有多少个原子。

8. 石英()2SiO 的密度为2.653Mg/m 。

试问： 1) 13m 中有多少个硅原子（与氧原子）？2) 当硅与氧的半径分别为0.038nm 与0.114nm 时，其堆积密度为多少（假设原子是球形的）？9.在800℃时1010个原子中有一个原子具有足够能量可在固体内移动，而在900℃时910个原子中则只有一个原子，试求其激活能（J/原子）。

10.若将一块铁加热至850℃，然后快速冷却到20℃。

试计算处理前后空位数应增加多少倍（设铁中形成一摩尔空位所需要的能量为104600J ）。

11.设图1-18所示的立方晶体的滑移面ABCD 平行于晶体的上、下底面。

若该滑移面上有一正方形位错环，如果位错环的各段分别与滑移面各边平行，其柏氏矢量b ∥AB 。

《材料科学基础》经典习题及答案材料科学与基础习题集和答案第七章回复再结晶，还有相图的内容。

第一章102??,211?,?346?晶向。

1.作图表示立方晶体的?123?,?012?,?421?晶面及? ?,?2110??,1010??,1120??,1210?等。

2.在六方晶体中，绘出以下常见晶向?0001 3.写出立方晶体中晶面族{100}，{110}，{111}，{112}等所包括的等价晶面。

4.镁的原子堆积密度和所有hcp金属一样，为。

试求镁单位晶胞的体积。

已知Mg的密度，相对原子质量为，原子半径r=。

?5.当CN=6时Na离子半径为，试问：1) 当CN=4时，其半径为多少？2) 当CN=8时，其半径为多少？ 6. 试问：在铜的方向及铁(bcc,a=)的方向,原子的线密度为多少？7.镍为面心立方结构，其原子半径为rNi?。

试确定在镍的2，及平面上1mm中各有多少个原子。

3??SiOMg/m28. 石英的密度为。

试问：?mg?/m31) 1m中有多少个硅原子？2) 当硅与氧的半径分别为与时，其堆积密度为多少？10109.在800℃时个原子中有一个原子具有足够能量可在固体内移9动，而在900℃时10个原子中则只有一个原子，试求其激活能。

10.若将一块铁加热至850℃，然后快速冷却到20℃。

试计算处理前后空位数应增加多少倍。

3 11.设图1-18所示的立方晶体的滑移面ABCD平行于晶体的上、下底面。

若该滑移面上有一正方形位错环，如果位错环的各段分别与滑移面各边平行，其柏氏矢量b∥AB。

1) 有人认为“此位错环运动移出晶体后，滑移面上产生的滑移台阶应为4个b,试问这种看法是否正确？为什么？2)指出位错环上各段位错线的类型，并画出位错运动出晶体后，滑移方向及滑移量。

12.设图1-19所示立方晶体中的滑移面ABCD平行于晶体的上、下底面。

晶体中有一条位错线fed,de段在滑移面上并平行AB，ef段与滑移面垂直。

第2章 例 题（A ）1. 在面心立方晶胞中画出[012]和[123]晶向。

2. 在面心立方晶胞中画出（012）和（123）晶面。

3. 右图中所画晶面的晶面指数是多少？4. 设晶面（152）和（034）属六方晶系的正交坐标表述，试给出其四轴坐标的表示。

反之，求（3121）及（2112）的正交坐标的表示。

5. （练习），上题中均改为相应晶向指数，求相互转换后结果。

答案：2. (2110) 4. （1562）， （0334） 5. [1322] [1214] （123） （212）[033] [302]第2章 例题答案(A)4. （152）)2615(6)51()(⇒-=+-=+-=v u t （034）)4303(3)30()(⇒-=+-=+-=v u t （1213）⇒ （123） （2112） ⇒ （212）5. [152]]2231[22)51(31)(313)152(31)2(311)512(31)2(31⇒⎪⎪⎪⎭⎪⎪⎪⎬⎫==-=+-=+-==-⨯=-=-=-⨯=-=W w V U t U V v V U u [034]]4121[41)30(31)(312)032(31)2(311)302(31)2(31⇒⎪⎪⎪⎭⎪⎪⎪⎬⎫==-=+-=+-==-⨯=-=-=-⨯=-=W w V U t U V v V U u]3121[]033[33)1(20)1(1⇒⎪⎭⎪⎬⎫===--=-==---=-=w W t v V t u U[2112]]302[20)1(13)1(2⇒⎪⎭⎪⎬⎫===---=-==--=-=w W t v V t u U第2章 例 题（B ）1. 已知Cu 的原子直径为2.56A ，求Cu 的晶格常数，并计算1mm 3Cu 的原子数。

2. 已知Al 相对原子质量Ar （Al ）=26.97，原子半径γ=0.143nm ，求Al 晶体的密度。

3. bcc 铁的单位晶胞体积，在912℃时是0.02464nm 3；fcc 铁在相同温度时其单位晶胞体积是0.0486nm 3。

又 C x =2.5 X017/10-6=2.5 X023 个/m 3C 2=C x - 3.05 X019~ 2.5 X023 个/m 37.5 已知氢和镍在面心立方铁中的扩散数据为第七章习题基本动力学过程一扩散7.1解释下列概念： 稳定扩散：在垂直扩散方向的任一平面上，单位时间内通过该平面单位面积的粒子数一定，即任一点的浓度不随时间而变化。

本征扩散： 由热起伏产生的点缺陷作为迁移载体的扩散。

不稳定扩散：扩散物质在扩散介质中浓度随时间发生变化。

非本征扩散：由杂质的不等价置换产生的点缺陷作为迁移载体的扩散。

自扩散：在同一晶体内无化学位梯度时质点的扩散。

扩散通量： 单位时间内通过单位横截面的粒子数。

扩散系数： 单位浓度梯度下的扩散通量。

互扩散：存在化学位梯度的扩散。

7.3当锌向铜内扩散时，已知在 x 点处锌的含量为2.5X1017个锌原子/cm 3, 300 °C 时每分钟每mm 2要扩散60个锌原子，求与x 点相距2mm 处锌原子的 浓度。

（已知锌在铜内的扩散体系中 D o =0.34X 10 -14 2 I m / s ; Q=18.81KJ / mol )?解:将锌向铜内扩散 看成一维稳定扩散，根据菲克第一定律: J —D 匹 J x D x C 2 - C x 3 J x =- D ，其中 C x =2.5 X0 个/cm , X-X 2=2mm , X — X 22 2 J x =60 个/60s mm =1 个/s mm 扩散系数宏观表达式 D=D o exp(- Q/RT)，其中 D o =O.34 M0"14m 2/s , Q=1.881 X04J/mol R=8.314J/mol K , T=300+273=573KD =0.34 10,4exp( _ 1.881 10 )= 6.557 10”m 2/s 8.314 汉573J x (X-X 2) D 阮705 1019 个/m 3从计算结果可知，D H >>D M ，这是由于氢原子与铁原子半径相差较大，形成的是间隙型固溶体，氢原子的扩散属于间隙扩散机制； 而镍原子与铁原子尺寸相差不大， 形成的是置换型 固溶体，镍通过空位机制扩散。

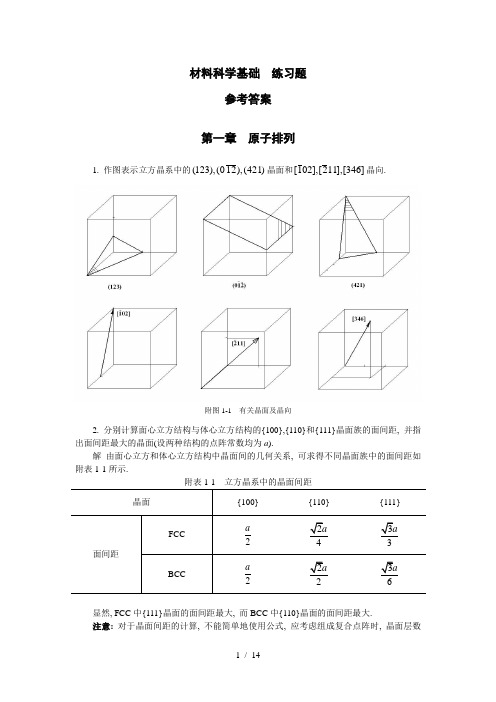
材料科学基础练习题参考答案第一章原子排列1. 作图表示立方晶系中的(123),(012),(421)晶面和[102],[211],[346]晶向.附图1-1 有关晶面及晶向2. 分别计算面心立方结构与体心立方结构的{100},{110}和{111}晶面族的面间距, 并指出面间距最大的晶面(设两种结构的点阵常数均为a).解由面心立方和体心立方结构中晶面间的几何关系, 可求得不同晶面族中的面间距如附表1-1所示.附表1-1 立方晶系中的晶面间距晶面{100} {110} {111}面间距FCC2a24a33aBCC2a22a36a显然, FCC中{111}晶面的面间距最大, 而BCC中{110}晶面的面间距最大.注意:对于晶面间距的计算, 不能简单地使用公式, 应考虑组成复合点阵时, 晶面层数会增加.3. 分别计算fcc和bcc中的{100},{110}和{111}晶面族的原子面密度和<100>,<110>和<111>晶向族的原子线密度, 并指出两种结构的差别. (设两种结构的点阵常数均为a) 解原子的面密度是指单位晶面内的原子数; 原子的线密度是指晶面上单位长度所包含的原子数. 据此可求得原子的面密度和线密度如附表1-2所示.附表1-2 立方晶系中原子的面密度和线密度晶面/晶向{100} {110} {111} <100> <110> <111>面/线密度BCC21a22a233a1a22a233aFCC22a22a2433a1a2a33a可见, 在BCC中, 原子密度最大的晶面为{110}, 原子密度最大的晶向为<111>; 在FCC 中, 原子密度最大的晶面为{111}, 原子密度最大的晶向为<110>.4. 在(0110)晶面上绘出[2113]晶向.解详见附图1-2.附图1-2 六方晶系中的晶向5. 在一个简单立方二维晶体中, 画出一个正刃型位错和一个负刃型位错. 试求:(1) 用柏氏回路求出正、负刃型位错的柏氏矢量.(2) 若将正、负刃型位错反向时, 说明其柏氏矢量是否也随之反向.(3) 具体写出该柏氏矢量的方向和大小.(4) 求出此两位错的柏氏矢量和.解正负刃型位错示意图见附图1-3(a)和附图1-4(a).(1) 正负刃型位错的柏氏矢量见附图1-3(b)和附图1-4(b).(2) 显然, 若正、负刃型位错线反向, 则其柏氏矢量也随之反向.(3) 假设二维平面位于YOZ坐标面, 水平方向为Y轴, 则图示正、负刃型位错方向分别为[010]和[010], 大小均为一个原子间距(即点阵常数a).(4) 上述两位错的柏氏矢量大小相等, 方向相反, 故其矢量和等于0.6. 设图1-72所示立方晶体的滑移面ABCD平行于晶体的上下底面, 该滑移面上有一正方形位错环. 如果位错环的各段分别与滑移面各边平行, 其柏氏矢量b // AB, 试解答:(1) 有人认为“此位错环运动离开晶体后, 滑移面上产生的滑移台阶应为4个b”, 这种说法是否正确? 为什么?(2) 指出位错环上各段位错线的类型, 并画出位错移出晶体后, 晶体的外形、滑移方向和滑移量. (设位错环线的方向为顺时针方向)图1-72 滑移面上的正方形位错环 附图1-5 位错环移出晶体引起的滑移 解 (1) 这种看法不正确. 在位错环运动移出晶体后, 滑移面上下两部分晶体相对移动的距离是由其柏氏矢量决定的. 位错环的柏氏矢量为b , 故其相对滑移了一个b 的距离.(2) A ′B ′为右螺型位错, C ′D ′为左螺型位错, B ′C ′为正刃型位错, D ′A ′为负刃型位错. 位错运动移出晶体后滑移方向及滑移量见附图1-5.7. 设面心立方晶体中的(111)晶面为滑移面, 位错滑移后的滑移矢量为[110]2a .(1) 在晶胞中画出此柏氏矢量b 的方向并计算出其大小.(2) 在晶胞中画出引起该滑移的刃型位错和螺型位错的位错线方向, 并写出此二位错线的晶向指数.解 (1) 柏氏矢量等于滑移矢量, 因此柏氏矢量的方向为[110], 大小为2/2a .(2) 刃型位错与柏氏矢量垂直, 螺型位错与柏氏矢量平行, 晶向指数分别为[112]和[110], 详见附图1-6.附图1-6 位错线与其柏氏矢量、滑移矢量8. 若面心立方晶体中有[101]2a b =的单位位错及[121]6a b =的不全位错, 此二位错相遇后产生位错反应.(1) 此反应能否进行? 为什么?(2) 写出合成位错的柏氏矢量, 并说明合成位错的性质.解 (1) 能够进行.因为既满足几何条件:[111]3a b b ==∑∑后前,又满足能量条件: . 22222133b a b a =>=∑∑后前. (2) [111]3a b =合, 该位错为弗兰克不全位错. 9. 已知柏氏矢量的大小为b = 0.25nm, 如果对称倾侧晶界的取向差θ = 1° 和10°, 求晶界上位错之间的距离. 从计算结果可得到什么结论?解 根据bD θ≈, 得到θ = 1°,10° 时, D ≈14.3nm, 1.43nm. 由此可知, θ = 10° 时位错之间仅隔5~6个原子间距, 位错密度太大, 表明位错模型已经不适用了.第二章 固体中的相结构1. 已知Cd, In, Sn, Sb 等元素在Ag 中的固熔度极限(摩尔分数)分别为0.435, 0.210, 0.130, 0.078; 它们的原子直径分别为0.3042 nm, 0.314 nm, 0.316 nm, 0.3228 nm; Ag 的原子直径为0.2883 nm. 试分析其固熔度极限差异的原因, 并计算它们在固熔度极限时的电子浓度.答: 在原子尺寸因素相近的情况下, 熔质元素在一价贵金属中的固熔度(摩尔分数)受原子价因素的影响较大, 即电子浓度e /a 是决定固熔度(摩尔分数)的一个重要因素, 而且电子浓度存在一个极限值(约为1.4). 电子浓度可用公式A B B B (1)c Z x Z x =-+计算. 式中, Z A , Z B 分别为A, B 组元的价电子数; x B 为B 组元的摩尔分数. 因此, 随着熔质元素价电子数的增加, 极限固熔度会越来越小.Cd, In, Sn, Sb 等元素与Ag 的原子直径相差不超过15%(最小的Cd 为5.5%, 最大的Sb 为11.96%), 满足尺寸相近原则, 这些元素的原子价分别为2, 3, 4, 5价, Ag 为1价, 据此推断它们的固熔度极限越来越小, 实际情况正好反映了这一规律; 根据上面的公式可以计算出它们在固熔度(摩尔分数)极限时的电子浓度分别为1.435, 1.420, 1.390, 1.312.2. 碳可以熔入铁中而形成间隙固熔体, 试分析是α-Fe 还是γ-Fe 能熔入较多的碳.答: α-Fe 为体心立方结构, 致密度为0.68; γ-Fe 为面心立方结构, 致密度为0.74. 显然, α-Fe 中的间隙总体积高于γ-Fe, 但由于α-Fe 的间隙数量多, 单个间隙半径却较小, 熔入碳原子将会产生较大的畸变, 因此, 碳在γ-Fe 中的固熔度较α-Fe 的大.3. 为什么只有置换固熔体的两个组元之间才能无限互熔, 而间隙固熔体则不能?答: 这是因为形成固熔体时, 熔质原子的熔入会使熔剂结构产生点阵畸变, 从而使体系能量升高. 熔质原子与熔剂原子尺寸相差越大, 点阵畸变的程度也越大, 则畸变能越高, 结构的稳定性越低, 熔解度越小. 一般来说, 间隙固熔体中熔质原子引起的点阵畸变较大, 故不能无限互熔, 只能有限熔解.第三章 凝固1. 分析纯金属生长形态与温度梯度的关系.答: 纯金属生长形态是指晶体宏观长大时固-液界面的形貌. 界面形貌取决于界面前沿液相中的温度梯度.(1) 平面状长大: 当液相具有正温度梯度时, 晶体以平直界面方式推移长大. 此时, 界面上任何偶然的、小的凸起深入液相时, 都会使其过冷度减小, 长大速率降低或停止长大, 而被周围部分赶上, 因而能保持平直界面的推移. 长大过程中晶体沿平行温度梯度的方向生长, 或沿散热的反方向生长, 而其它方向的生长则受到限制.(2) 树枝状长大: 当液相具有负温度梯度时, 晶体将以树枝状方式生长. 此时, 界面上偶然的凸起深入液相时, 由于过冷度的增大, 长大速率越来越大; 而它本身生长时又要释放结晶潜热, 不利于近旁的晶体生长, 只能在较远处形成另一凸起. 这就形成了枝晶的一次轴, 在一次轴成长变粗的同时, 由于释放潜热使晶枝侧旁液体中也呈现负温度梯度, 于是在一次轴上又会长出小枝来, 称为二次轴, 在二次轴上又长出三次轴……由此而形成树枝状骨架, 故称为树枝晶(简称枝晶).2. 简述纯金属晶体长大机制及其与固-液界面微观结构的关系.答: 晶体长大机制是指晶体微观长大方式, 即液相原子添加到固相的方式, 它与固-液界面的微观结构有关.(1) 垂直长大方式: 具有粗糙界面的物质, 因界面上约有50% 的原子位置空着, 这些空位都可以接受原子, 故液相原子可以进入空位, 与晶体连接, 界面沿其法线方向垂直推移, 呈连续式长大.(2) 横向(台阶)长大方式: 包括二维晶核台阶长大机制和晶体缺陷台阶长大机制, 具有光滑界面的晶体长大往往采取该方式. 二维晶核模式, 认为其生长主要是利用系统的能量起伏, 使液相原子在界面上通过均匀形核形成一个原子厚度的二维薄层状稳定的原子集团, 然后依靠其周围台阶填充原子, 使二维晶核横向长大, 在该层填满后, 则在新的界面上形成新的二维晶核, 继续填满, 如此反复进行.晶体缺陷方式, 认为晶体生长是利用晶体缺陷存在的永不消失的台阶(如螺型位错的台阶或挛晶的沟槽)长大的.第四章 相图1. 在Al-Mg 合金中, x Mg 为0.15, 计算该合金中镁的w Mg 为多少.解 设Al 的相对原子量为M Al , 镁的相对原子量为M Mg , 按1mol Al-Mg 合金计算, 则镁的质量分数可表示为Mg MgMg Al Al Mg Mg 100%x M w x M x M =⨯+.将x Mg = 0.15, x Al = 0.85, M Mg = 24, M Al = 27代入上式中, 得到w Mg = 13.56%.2. 根据图4-117所示二元共晶相图, 试完成:(1) 分析合金I, II 的结晶过程, 并画出冷却曲线.(2) 说明室温下合金I, II 的相和组织是什么, 并计算出相和组织组成物的相对量.(3) 如果希望得到共晶组织加上相对量为5%的β初的合金, 求该合金的成分.图4-117 二元共晶相图附图4-1 合金I的冷却曲线附图4-2 合金II的冷却曲线解(1) 合金I的冷却曲线参见附图4-1, 其结晶过程如下:1以上, 合金处于液相;1~2时, 发生匀晶转变L→α, 即从液相L中析出固熔体α, L和α的成分沿液相线和固相线变化, 达到2时, 凝固过程结束;2时, 为α相;2~3时, 发生脱熔转变, α→βII.合金II的冷却曲线参见附图4-2, 其结晶过程如下:1以上, 处于均匀液相;1~2时, 进行匀晶转变L→β;2时, 两相平衡共存, 0.50.9L β;2~2′ 时, 剩余液相发生共晶转变0.50.20.9L βα+;2~3时, 发生脱熔转变α→βII .(2) 室温下, 合金I 的相组成物为α + β, 组织组成物为α + βII .相组成物相对量计算如下:αβ0.900.20100%82%0.900.050.200.05100%18%0.900.05w w -=⨯=--=⨯=- 组织组成物的相对量与相的一致.室温下, 合金II 的相组成物为α + β, 组织组成物为β初 + (α+β).相组成物相对量计算如下:αβ0.900.80100%12%0.900.050.800.05100%88%0.900.05w w -=⨯=--=⨯=- 组织组成物相对量计算如下:β(α+β)0.800.50100%75%0.900.500.900.80100%25%0.900.50w w -=⨯=--=⨯=-初 (3) 设合金的成分为w B = x , 由题意知该合金为过共晶成分, 于是有β0.50100%5%0.900.50x w -=⨯=-初 所以, x = 0.52, 即该合金的成分为w B = 0.52.3. 计算w C 为0.04的铁碳合金按亚稳态冷却到室温后组织中的珠光体、二次渗碳体和莱氏体的相对量, 并计算组成物珠光体中渗碳体和铁素体及莱氏体中二次渗碳体、共晶渗碳体与共析渗碳体的相对量.解 根据Fe-Fe 3C 相图, w C = 4%的铁碳合金为亚共晶铸铁, 室温下平衡组织为 P + Fe 3C II + L d ′, 其中P 和Fe 3C II 系由初生奥氏体转变而来, 莱氏体则由共晶成分的液相转变而成, 因此莱氏体可由杠杆定律直接计算, 而珠光体和二次渗碳体则可通过两次使用杠杆定律间接计算出来.L d ′ 相对量: d L 4 2.11100%86.3%4.3 2.11w '-=⨯=-. Fe 3C II 相对量: 3II Fe C 4.34 2.110.77100% 3.1%4.3 2.11 6.690.77w --=⨯⨯=--. P 相对量: P 4.34 6.69 2.11100%10.6%4.3 2.11 6.690.77w --=⨯⨯=--. 珠光体中渗碳体和铁素体的相对量的计算则以共析成分点作为支点, 以w C = 0.001%和w C = 6.69%为端点使用杠杆定律计算并与上面计算得到的珠光体相对量级联得到.P 中F 相对量: F P 6.690.77100%9.38%6.690.001w w -=⨯⨯=-. P 中Fe 3C 相对量: 3Fe C 10.6%9.38% 1.22%w =-=.至于莱氏体中共晶渗碳体、二次渗碳体及共析渗碳体的相对量的计算, 也需采取杠杆定律的级联方式, 但必须注意一点, 共晶渗碳体在共晶转变线处计算, 而二次渗碳体及共析渗碳体则在共析转变线处计算.L d ′ 中共晶渗碳体相对量: d Cm L4.3 2.11100%41.27%6.69 2.11w w '-=⨯⨯=-共晶 L d ′ 中二次渗碳体相对量: d Cm L 6.69 4.3 2.110.77100%10.2%6.69 2.11 6.690.77w w '--=⨯⨯⨯=--IIL d ′ 中共析渗碳体相对量: d Cm L 6.69 4.3 6.69 2.110.770.0218100% 3.9%6.69 2.11 6.690.77 6.690.0218w w '---=⨯⨯⨯⨯=---共析 4. 根据下列数据绘制Au-V 二元相图. 已知金和钒的熔点分别为1064℃和1920℃. 金与钒可形成中间相β(AuV 3); 钒在金中的固熔体为α, 其室温下的熔解度为w V = 0.19; 金在钒中的固熔体为γ, 其室温下的熔解度为w Au = 0.25. 合金系中有两个包晶转变, 即1400V V V 1522V V V (1) β(0.4)L(0.25)α(0.27)(2) γ(0.52)L(0.345)β(0.45)w w w w w w =+===+==℃℃解 根据已知数据绘制的Au-V 二元相图参见附图4-3.附图4-3 Au-V 二元相图第五章 材料中的扩散1. 设有一条直径为3cm 的厚壁管道, 被厚度为0.001cm 的铁膜隔开, 通过输入氮气以保持在膜片一边氮气浓度为1000 mol/m 3; 膜片另一边氮气浓度为100 mol/m 3. 若氮在铁中700℃时的扩散系数为4×10-7 cm 2 /s, 试计算通过铁膜片的氮原子总数.解 设铁膜片左右两边的氮气浓度分别为c 1, c 2, 则铁膜片处浓度梯度为7421510010009.010 mol /m 110c c c c x x x --∂∆-≈===-⨯∂∆∆⨯ 根据扩散第一定律计算出氮气扩散通量为722732410(10)(9.010) 3.610 mol/(m s)c J D x---∂=-=-⨯⨯⨯-⨯=⨯∂ 于是, 单位时间通过铁膜片的氮气量为 3-22-63.610(310) 2.5410 mol/s 4J A π-=⨯⨯⨯⨯=⨯最终得到单位时间通过铁膜片的氮原子总数为-62318-1A () 2.5410 6.02102 3.0610 s N J A N =⨯=⨯⨯⨯⨯=⨯第六章 塑性变形1. 铜单晶体拉伸时, 若力轴为 [001] 方向, 临界分切应力为0.64 MPa, 问需要多大的拉伸应力才能使晶体开始塑性变形?解 铜为面心立方金属, 其滑移系为 {111}<110>, 4个 {111} 面构成一个八面体, 详见教材P219中的图6-12.当拉力轴为 [001] 方向时, 所有滑移面与力轴间的夹角相同, 且每个滑移面上的三个滑移方向中有两个与力轴的夹角相同, 另一个为硬取向(λ = 90°). 于是, 取滑移系(111)[101]进行计算.222222222222k s 0101111cos ,30011110(1)00111cos ,2001(1)011cos cos ,60.646 1.57 MPa.m mϕλϕλτσ⨯+⨯+⨯==++⨯++⨯-+⨯+⨯==++⨯-++====⨯=即至少需要1.57 MPa 的拉伸应力才能使晶体产生塑性变形.2. 什么是滑移、滑移线、滑移带和滑移系? 作图表示α-Fe, Al, Mg 中的最重要滑移系. 那种晶体的塑性最好, 为什么?答: 滑移是晶体在切应力作用下一部分相对于另一部分沿一定的晶面和晶向所作的平行移动; 晶体的滑移是不均匀的, 滑移部分与未滑移部分晶体结构相同. 滑移后在晶体表面留下台阶, 这就是滑移线的本质. 相互平行的一系列滑移线构成所谓滑移带. 晶体发生滑移时, 某一滑移面及其上的一个滑移方向就构成了一个滑移系.附图6-1 三种晶体点阵的主要滑移系α-Fe具有体心立方结构, 主要滑移系可表示为{110}<111>, 共有6×2 = 12个; Al具有面心立方结构, 其滑移系可表示为{111}<110>, 共有4×3 = 12个; Mg具有密排六方结构, 主要滑移系可表示为{0001}1120<>, 共有1×3 = 3个. 晶体的塑性与其滑移系的数量有直接关系, 滑移系越多, 塑性越好; 滑移系数量相同时, 又受滑移方向影响, 滑移方向多者塑性较好, 因此, 对于α-Fe, Al, Mg三种金属, Al的塑性最好, Mg的最差, α-Fe居中. 三种典型结构晶体的重要滑移系如附图6-1所示.3. 什么是临界分切应力? 影响临界分切应力的主要因素是什么? 单晶体的屈服强度与外力轴方向有关吗? 为什么?答:滑移系开动所需的作用于滑移面上、沿滑移方向的最小分切应力称为临界分切应力.临界分切应力τk的大小主要取决于金属的本性, 与外力无关. 当条件一定时, 各种晶体的临界分切应力各有其定值. 但它是一个组织敏感参数, 金属的纯度、变形速度和温度、金属的加工和热处理状态都对它有很大影响.如前所述, 在一定条件下, 单晶体的临界分切应力保持为定值, 则根据分切应力与外加轴向应力的关系: σs= τk/ m, m为取向因子, 反映了外力轴与滑移系之间的位向关系, 因此, 单晶体的屈服强度与外力轴方向关系密切. m越大, 则屈服强度越小, 越有利于滑移.4. 孪生与滑移主要异同点是什么? 为什么在一般条件下进行塑性变形时锌中容易出现挛晶, 而纯铁中容易出现滑移带?答:孪生与滑移的异同点如附表6-1所示.锌为密排六方结构金属, 主要滑移系仅3个, 因此塑性较差, 滑移困难, 往往发生孪生变形, 容易出现挛晶; 纯铁为体心立方结构金属, 滑移系较多, 共有48个, 其中主要滑移系有12个, 因此塑性较好, 往往发生滑移变形, 容易出现滑移带.第七章 回复与再结晶1. 已知锌单晶体的回复激活能为8.37×104 J/mol, 将冷变形的锌单晶体在-50 ℃进行回复处理, 如去除加工硬化效应的25% 需要17 d, 问若在5 min 内达到同样效果, 需将温度提高多少摄氏度?解 根据回复动力学, 采用两个不同温度将同一冷变形金属的加工硬化效应回复到同样程度, 回复时间、温度满足下述关系:122111exp t Q t R T T ⎛⎫⎛⎫=-- ⎪ ⎪ ⎪⎝⎭⎝⎭ 整理后得到221111ln T t R T Q t =+.将41211223 K,/5/(172460),8.3710 J/mol, 8.314 J/(mol K)4896T t t Q R ==⨯⨯==⨯=⋅代入上式得到2274.7 K T =.因此, 需将温度提高21274.722351.7 T T T ∆=-=-=℃.2. 纯铝在553 ℃ 和627 ℃ 等温退火至完成再结晶分别需要40 h 和1 h, 试求此材料的再结晶激活能.解 再结晶速率v 再与温度T 的关系符合阿累尼乌斯(Arrhenius)公式, 即exp()Q v A RT=-再 其中, Q 为再结晶激活能, R 为气体常数.如果在两个不同温度T 1, T 2进行等温退火, 欲产生同样程度的再结晶所需时间分别为t 1, t 2, 则122112122111exp[()]ln(/)t Q t R T T RTT t t Q T T =--⇒=-依题意, 有T 1 = 553 + 273 = 826 K, T 2 = 627 + 273 = 900 K, t 1 = 40 h, t 2 = 1 h, 则58.314826900ln(40/1)3.0810J/mol 900826Q ⨯⨯⨯=⨯-3. 说明金属在冷变形、回复、再结晶及晶粒长大各阶段的显微组织、机械性能特点与主要区别.答: 金属在冷变形、回复、再结晶及晶粒长大各阶段的显微组织、机械性能特点与主要区别详见附表7-1.附表7-1 金属在冷变形、回复、再结晶及晶粒长大各阶段的显微组织、机械性能第八章固态相变。

第二章 思考题与例题1. 离子键、共价键、分子键和金属键的特点，并解释金属键结合的固体材料的密度比离子键或共价键固体高的原因？2. 从结构、性能等方面描述晶体与非晶体的区别。

3. 何谓理想晶体？何谓单晶、多晶、晶粒及亚晶？为什么单晶体成各向异性而多晶体一般情况下不显示各向异性？何谓空间点阵、晶体结构及晶胞？晶胞有哪些重要的特征参数？4. 比较三种典型晶体结构的特征。

（Al 、α-Fe 、Mg 三种材料属何种晶体结构？描述它们的晶体结构特征并比较它们塑性的好坏并解释。

）何谓配位数？何谓致密度？金属中常见的三种晶体结构从原子排列紧密程度等方面比较有何异同？5. 固溶体和中间相的类型、特点和性能。

何谓间隙固溶体？它与间隙相、间隙化合物之间有何区别？（以金属为基的）固溶体与中间相的主要差异（如结构、键性、性能）是什么？6. 已知Cu 的原子直径为2.56A ，求Cu 的晶格常数，并计算1mm 3Cu 的原子数。

7. 已知Al 相对原子质量Ar （Al ）=26.97，原子半径γ=0.143nm ，求Al 晶体的密度。

8 bcc 铁的单位晶胞体积，在912℃时是0.02464nm 3；fcc 铁在相同温度时其单位晶胞体积是0.0486nm 3。

当铁由bcc 转变为fcc 时，其密度改变的百分比为多少？9. 何谓金属化合物？常见金属化合物有几类？影响它们形成和结构的主要因素是什么？其性能如何？10. 在面心立方晶胞中画出[012]和[123]晶向。

在面心立方晶胞中画出（012）和（123）晶面。

11. 设晶面（152）和（034）属六方晶系的正交坐标表述，试给出其四轴坐标的表示。

反之，求（3121）及（2112）的正交坐标的表示。

（练习），上题中均改为相应晶向指数，求相互转换后结果。

12.在一个立方晶胞中确定6个表面面心位置的坐标，6个面心构成一个正八面体，指出这个八面体各个表面的晶面指数，各个棱边和对角线的晶向指数。

材料科学基础练习题参考答案第一章原子排列1作图表示立方晶系中的(123),(011),(421)晶面«[ 102],[211],[346]晶向.2. 分别计算面心立方结构与体心立方结构的｛100｝,｛110｝和｛111｝晶面族的面间距.并指 出面间距最大的晶而(设两种结构的点阵常数均为a)解由而心立方和体心立方结构中晶面间的几何关系，可求得不同晶面族中的面何距如 附表所示.晶面{100}{110} {111} FCC aVTa 面间距 2 4 3BCC a血 >/3a2 23显然,FCC 中｛ill ｝晶向的向间典最大，rfnBCC 中｛110｝晶面的面间跑最大.注意：对于晶面间更的计算，不能简单地使用公式■应考虑组成复合点阵时.晶面层数 （421）附图1・1有关晶面及晶向会增加3.分别计算fee和bee中的｛100｝,｛110｝和｛111｝晶而族的原子面密度和＜100＞,＜110＞和 Vlll＞晶向族的原子线密度，并指出两种结构的差别(设两种结构的点阵常数均为a) 解原子的面密度是指单位晶面内的原子数，原子的线密度是指品面匕单位长度所包含的原子数.据此可求得原子的面密度和线密度如附表所示.附表1・2立方晶系中原子的面密度和线密度可见.在BCC中.原子密度最大的晶面为｛110｝,原子密度最大的晶向为＜111＞,在FCC 中，原子密度最人的晶面为｛111｝,原子密度最犬的晶向为＜110＞.4在(0110)晶面上绘*[2113]晶向附图1-2六方晶系中的晶向5.在一个简单立方二维晶体中，画出一个正刃型位错和一个负刃型位错试求:(1)用柏氏回路求出正、负刃型位错的柏氏矢量.(2)若将正、负刃型位错反向时，说明其柏氏欠量是否也随之反向(3)具体写出该柏氏矢量的方向和大小.(4)求出此两位错的柏氏矢量和.解正负刃型位错示意图见附图l・3(a)和附图l-4(a).(1)止负刃型位错的柏氏矢量见附图1-迪)和附图l-4(b)(b)附图1-3正刃型位错柏氏矢量的确定(a)实际晶体的柏氏回路;(b)完整晶体的相应回路(b)附图1 -4负刃型位错柏氏矢量的确定(a)实际晶体的柏氏回路；(b)完整晶体的相应回路(2)显然，若正、负刃型位错线反向，则其柏氏矢量也随之反向(3)假设二维平而位于YOZ坐标面，水平方向为Y轴，则图示正、负刃型位错方向分别为［010］和［010］,犬小均为一个原子间距(即点阵常数a〉(4)上述两位错的柏氏矢量人小相等，方向相反，故其欠量和等于0.6设图1-72所示立方晶体的滑移面ABCD平行于晶体的上下底面，诊滑移面上有一正方形位错环如果位错环的各段分别与滑移面各边平疔，其柏氏矢量&//AB,试解答：(1)有人认为“此位错环运动离开晶体后，滑移面上产生的滑移台阶应为4个b”，这种说法是否正确。

第一章1. 作图表示立方晶体的()()()421,210,123晶面及[][][]346,112,021晶向。

2. 在六方晶体中，绘出以下常见晶向[][][][][]0121,0211,0110,0112,0001等。

3. 写出立方晶体中晶面族{100}，{110}，{111}，{112}等所包括的等价晶面。

4. 镁的原子堆积密度和所有hcp 金属一样，为0.74。

试求镁单位晶胞的体积。

已知Mg 的密度3Mg/m 74.1=mg ρ，相对原子质量为24.31，原子半径r=0.161nm 。

5. 当CN=6时+Na 离子半径为0.097nm ，试问：1) 当CN=4时，其半径为多少？2) 当CN=8时，其半径为多少？6. 试问：在铜（fcc,a=0.361nm ）的<100>方向及铁(bcc,a=0.286nm)的<100>方向,原子的线密度为多少？7. 镍为面心立方结构，其原子半径为nm 1246.0=Ni r 。

试确定在镍的（100），（110）及（111）平面上12mm 中各有多少个原子。

8. 石英()2SiO 的密度为2.653Mg/m 。

试问：1) 13m 中有多少个硅原子（与氧原子）？2) 当硅与氧的半径分别为0.038nm 与0.114nm 时，其堆积密度为多少（假设原子是球形的）？9. 在800℃时1010个原子中有一个原子具有足够能量可在固体内移动，而在900℃时910个原子中则只有一个原子，试求其激活能（J/原子）。

10. 若将一块铁加热至850℃，然后快速冷却到20℃。

试计算处理前后空位数应增加多少倍（设铁中形成一摩尔空位所需要的能量为104600J ）。

11. 设图1-18所示的立方晶体的滑移面ABCD 平行于晶体的上、下底面。

若该滑移面上有一正方形位错环，如果位错环的各段分别与滑移面各边平行，其柏氏矢量b ∥AB 。

1) 有人认为“此位错环运动移出晶体后，滑移面上产生的滑移台阶应为4个b ,试问这种看法是否正确？为什么？2) 指出位错环上各段位错线的类型，并画出位错运动出晶体后，滑移方向及滑移量。

(家庭作业参考答案) 2006．12．21第四章 固体中原子及分子的运动1 假设内部原子从A 处迁移到B 处，在A 处500℃时的跳跃频率(ΓA )为5×108jumps/s ，在B 处800℃时的跳跃频率(ΓB )为8×108jumps/s ，计算这个过程的激活能Q 。

Solution:由 D=Γd 2P得 Γ=(d 2P)-1D= C 0D= C 0exp(-RTQ) (d ，P 与温度无关，为常数) 代入数据，得 5×108= C 0exp ()⎥⎦⎤⎢⎣⎡⨯-273500987.1＋Q= C 0exp ()Q 000651.0- 8×108= C 0exp ()⎥⎦⎤⎢⎣⎡⨯-273800987.1＋Q= C 0exp ()Q 000469.0-联立以上两方程求解，得 Q=27880cal/mol2 考虑一个纯钨和含1%钍的钨合金之间的扩散偶。

在2000℃下暴露几分钟后，产生了一个0.01cm 的扩散区。

如果扩散机制是①体扩散②晶界扩散③表面扩散，这时钍原子的通量是多少？(D 0和Q 见表1，钨为BCC 结构，晶格常数为0.3165nm)Tab 1钍在钨中不同类型的扩散效应扩散类型钍在钨中的扩散系数(D)D 0 cm 2/s Q cal/mol 表面扩散 0.47 66400 晶界扩散 0.74 90000 体扩散1.00120000Solution ：钨为BCC 结构，每个晶胞含有2个原子，晶格常数为0.3165nm 。

因此每cm 3中含钨原子：W atom/cm 3=()3810165.32-⨯=6.3×1022在含钍1 at.%的钨合金中，钍的原子数为： C Th =0.01×(6.3×1022)=6.3×1020 atom/cm 3在纯钨中，钍的原子数为0。

因此钍浓度梯度为：xc ΔΔ=01.0103.6020⨯-=-6.3×1022 atom/cm 3cm①体扩散 D=1.0exp(2273987.1120000⨯-)=2.89×10-12 cm 2/sJ= -DxcΔΔ=-(2.89×10-12)×(-6.3×1022)=18.2×1010 atom /cm 2s ②晶界扩散 D=0.74exp(2273987.190000⨯-)=1.64×10-9 cm 2/sJ= -D xcΔΔ=-(1.64×10-9)×(-6.3×1022)=10.3×1013 atom /cm 2s③表面扩散 D=0.47exp(2273987.166400⨯-)=1.94×10-7 cm 2/sJ= -D xcΔΔ=-(1.94×10-7)×(-6.3×1022)=12.2×1015 atom /cm 2s3.5. 66.9 为使丁二烯C 4H 6橡胶每一结构单元有一硫原子而完全交联，问在100g 最后的橡胶制品中需 要多少克硫？ Solution ：对于1个硫原子(32)，需要1个丁二烯链节。