PASS样本量估计操作手册

PASS样本量估计操作手册在统计学中，样本量估计是一项重要的工作，它用于确定研究中所需的样本大小。

样本量的确定直接关系到研究结果的可靠性和推广的有效性。

PASS软件作为一种专业的统计工具，为样本量估计提供了简便而准确的方法。

本操作手册将向您介绍如何使用PASS软件进行样本量估计，以及一些注意事项和常见的应用场景。

一、PASS软件简介PASS（Power Analysis and Sample Size）是一款由NCSS（Number Cruncher Statistical System）公司开发的统计分析软件。

它通过输入研究的相关参数，如效应量、显著性水平、统计功效等，能够计算出所需的样本大小。

二、首次使用PASS软件的准备工作1. 下载与安装：请前往NCSS公司的官方网站，下载最新版本的PASS软件，并按照安装向导完成安装。

2. 打开软件：双击桌面上的PASS图标，启动软件。

三、样本量估计的基本步骤1. 选择研究设计：在PASS软件的主界面上，选择合适的研究设计。

常见的设计包括单样本均值检验、两样本均值检验、相关样本设计等。

2. 输入参数：根据具体的研究设计，输入相关的参数，如效应量、显著性水平、统计功效等。

3. 运行计算：点击软件界面上的计算按钮，PASS软件将根据输入的参数进行计算，并给出所需的样本大小。

4. 结果解读：根据PASS软件给出的结果，确定研究中所需的样本大小。

四、注意事项和常见应用场景1. 注意事项：- 参数的选择：在进行样本量估计时，需要合理选择效应量、显著性水平和统计功效等参数。

这些参数的选择应基于研究目的、相关文献和实际情况。

- 结果解读：样本量估计只是一个估计值，并不能完全保证实际研究中获得的数据符合预期。

在进行研究时，还需要根据实际情况进行灵活调整。

2. 常见应用场景：- 医学研究：在进行药物实验或临床试验时，样本量估计能够帮助研究者确定所需的病例数量，为研究结果的准确性提供支持。

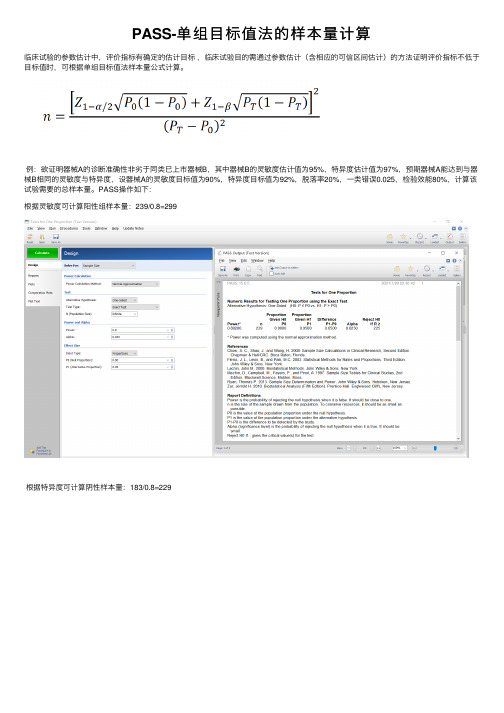
PASS-单组⽬标值法的样本量计算
临床试验的参数估计中，评价指标有确定的估计⽬标，临床试验⽬的需通过参数估计（含相应的可信区间估计）的⽅法证明评价指标不低于⽬标值时，可根据单组⽬标值法样本量公式计算。

例：欲证明器械A的诊断准确性⾮劣于同类已上市器械B，其中器械B的灵敏度估计值为95%，特异度估计值为97%，预期器械A能达到与器械B相同的灵敏度与特异度，设器械A的灵敏度⽬标值为90%，特异度⽬标值为92%，脱落率20%，⼀类错误0.025，检验效能80%，计算该试验需要的总样本量。

PASS操作如下：
根据灵敏度可计算阳性组样本量：239/0.8=299
根据特异度可计算阴性样本量：183/0.8=229
总样本量：299+229=528。

基于PASS及SAS软件的常用样本含量估计方法实现及部分方法比较研究一、本文概述本文旨在深入探讨和分析基于PASS（Power Analysis and Sample Size）及SAS（Statistical Analysis System）软件的常用样本含量估计方法的实现，并对部分方法进行比较研究。

样本含量估计是统计学研究中的重要环节，对于保证研究结果的准确性和可靠性具有至关重要的作用。

本文将首先概述样本含量估计的基本概念和研究背景，然后详细介绍PASS和SAS两款软件在样本含量估计方面的应用，并通过案例分析和实证研究，对两种软件中的常用方法进行比较研究，以期为研究者在实际应用中提供参考和借鉴。

具体来说，本文将分为以下几个部分：阐述样本含量估计的基本原理和重要性，以及在不同研究领域中的应用情况；详细介绍PASS和SAS两款软件的基本功能和特点，以及它们在样本含量估计方面的具体实现方法；接着，通过案例分析和实证研究，对两种软件中的常用方法进行比较研究，分析各方法的优缺点和适用范围；总结本文的研究结果，提出在实际应用中应注意的问题和建议。

本文的研究不仅有助于提高样本含量估计的准确性和可靠性，还为研究者在不同软件和方法之间进行选择提供了有益的参考。

本文的研究也有助于推动统计学和相关领域的研究发展，为实际应用提供更加科学、有效的支持。

二、样本含量估计的基本理论样本含量估计，也称为样本量计算，是统计学中一个至关重要的环节。

它涉及到如何根据研究目的、设计类型、预期效应大小、统计显著性水平以及其它相关因素，确定进行一项研究所需的最少样本数量。

样本含量的大小直接影响到研究结果的精确性、可靠性和推广性。

因此，在进行科学研究时，合理估计样本含量至关重要。

样本含量估计的基本理论主要基于概率论和数理统计的原理。

其中，概率论提供了事件发生的可能性度量，而数理统计则通过收集和分析数据来推断总体的特征。

在样本含量估计中，常用的统计量包括均值、比例、差异等，这些统计量可以帮助我们了解总体特征并构建相应的假设检验。

样本量计算软件PASS集锦2018年8月3-5日（昆明）分享本文，您可以拿到最新的PASS15哦！一样本量估计影响因素分析一、引言：某药与安慰剂对照临床试验，试验药有效率为53.13%（N1=64），安慰剂对照组有效率为50%（N2=60），组间差别无统计学意义。

（P=0.7279）；当两组样本量各扩充为原来的100倍时，其对应的有效率不变，但经过卡方检验，组间差别具有统计学意义（P=0.0005）；两次检验P值的差别事由样本量导致的，因此，临床试验，不能仅仅关注P值，还要关注样本量，结果解释要结合统计和专业两方面，样本量并非越大越好。

二、影响样本量的因素（1）总体平均数(μ)、标准差(σ)或总体率(π)等。

μ、σ、π一般未知,通常以样本的ˉx、S、P作为估计值,可以从预试验、查阅文献、经验估计而获得。

（2）处理组间的差别δ:所比较的两个总体参数间的差别，δ,如δ=μ1-μ2或δ=μ2-μ1。

由于研究者无法得到总体参数的信息,可以通过预试验来估计或用临床上认为有意义的差值(假设)来代替;（3）统计检验的水准α(即第一类错误的概率)；α规定越小,则所需样本量越多。

一般取值为0.05。

U1-0.05/2= 1. 96(双侧),U1-0. 05=1. 64(单侧);为了计算简便,以下所用公式α均取0. 05。

（4）统计检验的效能(1-β,其中β为第二类错误的概率)即在特定的α水准下,若总体间确实存在差异,该次试验能发现此差异的概率。

统计检验效能越大,所需样本例数越多,通常取β= 0. 1或β= 0. 2,此时的检验效能分别为90%或80%。

一般临床试验的检验效能不能低于75%,否则可能出现非真实的阴性结果。

为了计算简便,以下所用公式β均取0. 10,U1-0.10/2=1. 64(双侧),U1-0.10= 1. 28(单侧)。

(1-β,其中β为第二类错误的概率),即在特定的α水准下,若总体间确实存在差异,该次试验能发现此差异的概率。

【视频教程】PASS软件计算样本量的操作技巧
各位医咖会小伙伴：
医咖会最新上线了专栏视频课程《样本量计算理论实操》，讲解了样本量估算的注意事项以及PASS软件操作。

欢迎大家使用电脑，复制以下链接到浏览器，打开医咖会网站查看系列课程：
/zhuanlan/courses/39
上节课我们学习了PASS软件估计样本量的一些操作方法，详情请查看：【视频教程】使用PASS软件计算样本量，限于篇幅，还有一些内容需要补充，这节课我们继续学习剩下的内容，希望本节课程能对你有所帮助。

本专栏视频课程，除了以上内容，还介绍了为何要估算样本量、估算样本量的参数以及在研究实践中的一些考虑。

医咖会既往也推送过样本量计算的图文教程，更喜欢图文形式的伙伴，可查看：
【图文合集】样本量计算全教程，不要错过！。

手把手教学：生存分析的样本量计算一、临床研究问题生存分析研究在临床上非常常见，例如肿瘤科大夫想要评价两种治疗措施对于患者生存期的影响，或者肿瘤复发的影响，一般要用到生存分析。

一般肿瘤治疗药物的临床研究，都会采用Logrank检验比较主要结局。

本文将介绍如何利用PASS软件计算生存分析Logrank检验的样本量。

本文适用于无期中分析的试验设计类型。

对于有期中分析的试验，样本量计算涉及到α消耗函数等调整假阳性率的方法，需要其他模块完成。

二、样本量计算所需参数在介绍样本量计算之前，首先介绍几个参数的概念。

1. 中位生存时间mOS：即50%的患者死亡时所对应的时间。

如果将所有患者生存时间按从小到大排序，中位生存时间即顺序处于中间的患者的生存时间。

2. 入组时间：入组患者很难瞬间完成，尤其对于发病率比较低的肿瘤，因此患者入组往往要经过相对较长的时间。

入组时间为第1例患者入组到最后一例患者入组所经历的时间。

3. 随访时间：在最后一例患者入组完成后，还需对所有患者随访一段时间。

从最后一例患者入组，到试验截止日期的间隔称为随访时间。

注意，这里的随访时间，跟患者的观察时间意义不同。

如果一个临床试验入组时间为6个月，随访时间为12个月，那么对于第一例入组的患者，其观察时间为6+12=18个月（尽管该患者可能在试验截止前就已死亡），而对于最后一例入组的患者，其观察时间为12个月，即各个患者观察时间不同。

观察时间越长，观察到结局发生的可能性越大。

4. 效果参数：HR，风险比，是两组患者瞬时死亡概率之比，是衡量干预效果最常用的参数。

HR可近似计算为：HR=对照组 mOS / 试验组 mOS除此之外该类参数还有死亡风险（Hazard Rate），死亡率（Mortality，如5年死亡率），生存率（Proportion Surviving）。

这些参数都可以进行相互换算，例如在生存数据满足指数分布假设下，试验组与对照组的5. I型错误α和II型错误β，与其他样本量计算意义相同，不再赘述。

PASS样本量估计操作手册1. 背景PASS（Power Analysis and Sample Size）是进行样本量估计的软件，它能够帮助研究者确定实验所需的最小样本量，以获得统计学显著性。

在研究者进行实验之前，样本量估计是非常重要的，因为合理的样本量可以保证研究的可靠性和准确性，同时也能够节约研究者的时间和资源。

2. 操作步骤PASS软件提供了多种方法进行样本量估计，其中最为常用的是参数估计法和置信区间法。

这里我们以参数估计法为例，简要介绍PASS软件进行样本量估计的操作步骤。

2.1 研究设计在进行样本量估计之前，我们需要先确定实验的研究设计，例如实验类型、干预措施、样本分组、主要指标等。

只有明确实验的设计才能进行后续的样本量估计。

2.2 设置假设根据实验设计，我们需要设置假设，包括零假设和备择假设。

零假设通常为无效假设，例如两组在某一指标上没有差异。

备择假设则通常为我们所期望的研究结果，例如两组在某一指标上存在显著差异。

同时，我们还需要设置效应大小和显著性水平等参数。

2.3 选择统计方法根据实验设计和设置的假设，我们需要选择适合的统计方法进行样本量估计。

例如两组均数比较可以采用t检验，两组比例比较可以采用卡方检验等。

2.4 输入参数PASS软件提供了多种统计方法对应的输入参数表格，我们需要根据具体的实验设计和假设设置，输入相应的参数进行计算。

通常包括样本均数、标准差、群体大小、方差比等。

2.5 进行样本量估计输入完参数之后，我们即可点击“Calculate Sample Size” 按钮进行样本量估计。

PASS软件会自动计算出所需的最小样本量，并给出显著性检验的结果。

同时，我们还可以根据不同的置信水平进行多组样本量比较。

3. 注意事项在进行样本量估计时，需要注意以下几个方面：3.1 样本量估计要根据具体的实验设计和假设设置来进行，不同的实验可能需要不同的估计方法；3.2 参数的估计要尽量准确，如果先前没有可靠的基础数据，可以采用规模较小的预试验来获得数据；3.3 样本量过小会导致实验结果的不可靠和显著性统计失效，但过大也会浪费研究资源，因此需要进行合理的估计；3.4 样本量估计是一个动态的过程，实验进行中可能需要不断地对样本量进行更新和调整，以获得更为准确的结果。

参数设置如图：Logrank Test Power AnalysisNumeric Results in Terms of Sample Size when the Test is Two-Sided and T0 is 6Acc-Ctrl Trt rualHaz Prop Prop Acc- Time/ Ctrl TrtRatio Surv Surv rual Total Ctrl Trt to toPower N1 N2 N (HR) (S1) (S2) Pat'n Time Loss Loss Trt Ctrl Alpha Beta 0.8002 220 221 4410.6256 0.7000 0.8000Equal 12 / 18 0.0500 0.0500 0.0000 0.0000 0.0500 0.1998 0.8005 179 179 3580.5908 0.7000 0.8100Equal 12 / 18 0.0500 0.0500 0.0000 0.0000 0.0500 0.1995 0.8007 147 148 2950.5564 0.70000.8200Equal 12 / 18 0.0500 0.0500 0.0000 0.0000 0.0500 0.1993 0.8005 123 123 2460.5224 0.7000 0.8300Equal 12 / 18 0.0500 0.0500 0.0000 0.0000 0.0500 0.1995 0.8016 104 104 2080.4888 0.7000 0.8400Equal 12 / 18 0.0500 0.0500 0.0000 0.0000 0.0500 0.1984 0.8018 88 89 1770.4556 0.7000 0.8500Equal 12 / 18 0.0500 0.0500 0.0000 0.0000 0.0500 0.1982 ReferencesLakatos, Edward. 1988. 'Sample Sizes Based on the Log-Rank Statistic in Complex Clinical Trials', Biometrics, Volume 44, March, pages 229-241.21, pages 1969-1989.Report DefinitionsPower is the probability of rejecting a false null hypothesis. Power should be close to one.N1|N2|N are the sample sizes of the control group, treatment group, and both groups, respectively.E1|E2|E are the number of events in the control group, treatment group, and both groups, respectively.Hazard Ratio (HR) is the treatment group's hazard rate divided by the control group's hazard rate.Proportion Surviving is the proportion surviving past time T0.Accrual Time is the number of time periods (years or months) during which accrual takes place.Total Time is the total number of time periods in the study. Follow-up time = (Total Time) - (Accrual Time).Ctrl Loss is the proportion of the control group that is lost (drop out) during a single time period (year or month).Trt Loss is the proportion of the treatment group that is lost (drop out) during a single time period (year or month).Ctrl to Trt (drop in) is the proportion of the control group that switch to a group with a hazard rate equal to the treatment group.Trt to Ctrl (noncompliance) is the proportion of the treatment group that switch to a group with a hazard rate equal to the control group.Alpha is the probability of rejecting a true null hypothesis. It should be small.Beta is the probability of accepting a false null hypothesis. It should be small.2013/12/28 12:05:31 2Logrank Test Power AnalysisNumeric Results in Terms of Events when the Test is Two-Sided and T0 is 6Acc-Ctrl Trt rualCtrl Trt Total Haz Prop Prop Acc- Time/ Ctrl TrtEvts Evts Evts Ratio Surv Surv rual Total Ctrl Trt to toPower E1 E2 E (HR) (S1) (S2) Pat'n Time Loss Loss Trt Ctrl Alpha Beta 0.8002 84.7 59.1 143.8 0.6256 0.7000 0.8000 Equal 12 / 18 0.0500 0.0500 0.0000 0.0000 0.0500 0.1998 0.8005 68.7 45.8 114.5 0.5908 0.7000 0.8100 Equal 12 / 18 0.0500 0.0500 0.0000 0.0000 0.0500 0.1995 0.8007 56.6 35.9 92.5 0.5564 0.7000 0.8200 Equal 12 / 18 0.0500 0.0500 0.0000 0.0000 0.0500 0.1993 0.8005 47.2 28.4 75.6 0.5224 0.7000 0.8300 Equal 12 / 18 0.0500 0.0500 0.0000 0.0000 0.0500 0.1995 0.8016 39.9 22.7 62.6 0.4888 0.7000 0.8400 Equal 12 / 18 0.0500 0.0500 0.0000 0.0000 0.0500 0.1984 0.8018 34.0 18.2 52.2 0.4556 0.7000 0.8500 Equal 12 / 18 0.0500 0.0500 0.0000 0.0000 0.0500 0.1982 Summary StatementsA two-sided logrank test with an overall sample size of 441 subjects (220 in the control groupand 221 in the treatment group) achieves 80.0% power at a 0.050 significance level to detect ahazard ratio of 00.6256 when the proportion surviving in the control group is 00.7000. Thestudy lasts for 18 time periods of which subject accrual (entry) occurs in the first 12 timeperiods. The accrual pattern across time periods is uniform (all periods equal). The proportiondropping out of the control group is 0.0500. The proportion dropping out of the treatment groupis 0.0500. The proportion switching from the control group to another group with a hazard ratioequal to that of the treatment group is 0.0000. The proportion switching from the treatmentgroup to another group with a hazard equal to that of the control group is is 0.0000.2013/12/28 12:05:32 3Logrank Test Power AnalysisChart Section参数设置：Logrank Test Power AnalysisNumeric Results in Terms of Sample Size when the Test is Two-Sided and T0 is 6Acc-Ctrl Trt rualHaz Prop Prop Acc- Time/Ctrl TrtRatio Surv Surv rual Total Ctrl Trt to toPower N1 N2 N (HR) (S1) (S2) Pat'n Time Loss Loss Trt Ctrl Alpha Beta 0.8004 189 190 3790.6256 0.7000 0.8000Equal 24 / 300.0500 0.0500 0.0000 0.0000 0.0500 0.1996 0.8005 153 154 3070.5908 0.70000.8100Equal 24 / 300.0500 0.0500 0.0000 0.0000 0.0500 0.1995 0.8013 126 127 2530.5564 0.70000.8200Equal 24 / 300.0500 0.0500 0.0000 0.0000 0.0500 0.1987 0.8018 105 106 2110.5224 0.7000 0.8300Equal 24 / 300.0500 0.0500 0.0000 0.0000 0.0500 0.1982 0.8003 88 89 1770.4888 0.7000 0.8400Equal 24 / 300.0500 0.0500 0.0000 0.0000 0.0500 0.1997 0.8021 75 76 1510.4556 0.7000 0.8500Equal 24 / 300.0500 0.0500 0.0000 0.0000 0.0500 0.1979 ReferencesLakatos, Edward. 1988. 'Sample Sizes Based on the Log-Rank Statistic in Complex Clinical Trials', Biometrics,21, pages 1969-1989.Report DefinitionsPower is the probability of rejecting a false null hypothesis. Power should be close to one.N1|N2|N are the sample sizes of the control group, treatment group, and both groups, respectively.E1|E2|E are the number of events in the control group, treatment group, and both groups, respectively.Hazard Ratio (HR) is the treatment group's hazard rate divided by the control group's hazard rate.Proportion Surviving is the proportion surviving past time T0.Accrual Time is the number of time periods (years or months) during which accrual takes place.Total Time is the total number of time periods in the study. Follow-up time = (Total Time) - (Accrual Time).Ctrl Loss is the proportion of the control group that is lost (drop out) during a single time period (year or month).Trt Loss is the proportion of the treatment group that is lost (drop out) during a single time period (year or month).Ctrl to Trt (drop in) is the proportion of the control group that switch to a group with a hazard rate equal to the treatment group.Trt to Ctrl (noncompliance) is the proportion of the treatment group that switch to a group with a hazard rate equal to the control group.Alpha is the probability of rejecting a true null hypothesis. It should be small.Beta is the probability of accepting a false null hypothesis. It should be small.2013/12/28 12:07:40 2Logrank Test Power AnalysisNumeric Results in Terms of Events when the Test is Two-Sided and T0 is 6Acc-Ctrl Trt rualCtrl Trt Total Haz Prop Prop Acc- Time/ Ctrl TrtEvts Evts Evts Ratio Surv Surv rual Total Ctrl Trt to toPower E1 E2 E(HR) (S1) (S2) Pat'n Time Loss Loss Trt Ctrl Alpha Beta 0.8004 83.4 60.2 143.6 0.6256 0.7000 0.8000 Equal 24 / 30 0.0500 0.0500 0.0000 0.0000 0.0500 0.1996 0.8005 67.6 46.7 114.3 0.5908 0.7000 0.8100 Equal 24 / 30 0.0500 0.0500 0.0000 0.0000 0.0500 0.1995 0.8013 55.7 36.8 92.5 0.5564 0.7000 0.8200 Equal 24 / 30 0.0500 0.0500 0.0000 0.0000 0.0500 0.1987 0.8018 46.4 29.2 75.6 0.5224 0.7000 0.8300 Equal 24 / 30 0.0500 0.0500 0.0000 0.0000 0.0500 0.1982 0.8003 39.0 23.2 62.2 0.4888 0.7000 0.8400 Equal 24 / 30 0.0500 0.0500 0.0000 0.0000 0.0500 0.1997 0.8021 33.2 18.7 52.0 0.4556 0.7000 0.8500 Equal 24 / 30 0.0500 0.0500 0.0000 0.0000 0.0500 0.1979 Summary StatementsA two-sided logrank test with an overall sample size of 379 subjects (189 in the control groupand 190 in the treatment group) achieves 80.0% power at a 0.050 significance level to detect ahazard ratio of 00.6256 when the proportion surviving in the control group is 00.7000. Thestudy lasts for 30 time periods of which subject accrual (entry) occurs in the first 24 timeperiods. The accrual pattern across time periods is uniform (all periods equal). The proportiondropping out of the control group is 0.0500. The proportion dropping out of the treatment groupis 0.0500. The proportion switching from the control group to another group with a hazard ratioequal to that of the treatment group is 0.0000. The proportion switching from the treatmentgroup to another group with a hazard equal to that of the control group is is 0.0000.2013/12/28 12:07:41 3Logrank Test Power AnalysisChart Section。

医疗机构应用PASS系统统计分析工作站操作手册年月目录1. 安装 (3)1.1安装服务端 (3)1.1.1拷贝文件 (3)1.1.2附加统计分析库 (3)1.1.3配置服统计分析服务 (4)1.1.4安装与启动统计分析服务 (5)1.2安装客户端 (6)2.使用 (7)2.1服务端 (7)2.1.1启动统计分析服务程序 (7)2.2统计分析工作站使用 (7)2.2.1登录界面 (7)2.2.2统计范围设置界面 (8)2.2.3统计分析主界面 (8)2.2.4 PASS监测结果问题明细清单表 (9)2.2.5 PASS监测结果问题-审查类型统计表 (10)2.2.6PASS监测结果科室问题-审查类型统计表 (11)2.2.7PASS监测结果医生问题-审查类型统计表 (12)2.2.8 PASS监测结果问题-警示级别统计表 (12)2.2.9PASS监测结果科室问题-警示级别统计表 (13)2.2.10 PASS监测结果医生问题-警示级别统计表 (14)2.2.11 PASS监测结果药品-审查类型统计表 (15)2.2.12 PASS监测结果药品-警示级别统计表 (15)2.2.13 筛选界面 (16)2.2.14 用户管理 (17)加粗标识的部分，是需要特别注意的地方。

统计分析数据来源于PASS服务对医生工作站问题医嘱的采集，其中采集的数据随医嘱提交行为执行，数据保存在medicomsave数据库中，发生医嘱行为的次日就会对问题医嘱导入到ClinicStat数据库中，以便临床药师使用统计分析工作站对该院问题医嘱进行查询，以此为平台加强与医生的交流，减少或杜绝不合理用药现象的发生。

统计分析程序建议使用SQLServer数据库，如需要使用ORACLE数据库，则首先要运行产品光盘所在路径下的StaticServer\database目录里面的CreateClinicDB_oracle.sql文件，进行统计分析库及相关表的创建;下面的操作指南以SQLServer数据库类型为例进行介绍，除1.1.2附加统计分析库相关操作与ORACLE类型不同需运行上述脚本外，其它方法一致。

pass 纵向研究广义估计方程样本量估计全文共四篇示例，供读者参考第一篇示例：Pass纵向研究在流行病学的研究中起着重要作用，它是一种用来研究相关数据在不同时间点收集的方法。

广义估计方程（GEE）在Pass 纵向研究中被广泛应用，能够克服传统统计分析中的一些局限性，具有较高的鲁棒性和效率。

在进行Pass纵向研究时，样本量的合理估计是非常重要的，它直接影响到研究结果的可靠性和可信度。

本文将重点介绍Pass纵向研究中的广义估计方程以及样本量的估计方法。

Pass纵向研究是指在研究中跟踪同一组体的变化，并观察这些变化在不同时间点的关系。

通过对同一组体在不同时间点的数据进行收集和比较，可以更深入地了解疾病的发展过程和影响因素。

在进行Pass纵向研究时常常会面临很多挑战，比如数据的相关性、缺失值处理、样本的不平衡等问题。

为了解决这些问题，广义估计方程成为了Pass纵向研究中的重要方法之一。

广义估计方程是一种在纵向研究中用于估计参数并提供回答研究问题的方法。

传统的线性回归模型在样本不独立的情况下会产生偏误的参数估计值，而GEE可以通过考虑数据之间的相关性来减小这种偏误。

GEE的优势在于它不需要对数据的相关性结构做出明确的假设，而是通过对数据的平均模型和协方差矩阵进行估计，从而得到更加鲁棒和准确的结果。

在进行Pass纵向研究时，研究者需要根据研究的目的和问题来确定适当的广义估计方程模型。

通常，研究者首先需要选择一个适当的联结函数和一个合适的协变量模型。

然后，通过拟合广义估计方程模型来估计参数，进行假设检验和置信区间的计算。

除了选择合适的模型和参数估计方法，样本量的估计也是Pass纵向研究中的关键问题之一。

在进行样本量估计时，研究者需要考虑到效应大小、预期的失误率、研究的设计和统计分析方法等因素。

通常，样本量的估计是通过模拟方法或基于已有研究结果的经验估计来进行的。

在进行Pass纵向研究时，除了广义估计方程和样本量的估计外，研究者还需要考虑到数据的搜集和处理、统计分析方法的选择、结果的解释和推断等问题。

PASS样本量估计操作手册在实施医学研究或临床试验时，样本量估计是一项至关重要的工作。

合理确定样本量不仅可以确保结果的准确性和可靠性，还可以避免资源的浪费。

本文将介绍PASS样本量估计软件的操作手册，帮助研究者和临床试验设计者正确使用该软件进行样本量估计。

一、软件简介PASS是一个用于统计功效分析和样本量估计的专业软件。

它提供了各种统计方法和模型，能够帮助用户计算合适的样本量，并综合考虑研究设计的各种因素。

二、安装和启动1. 下载软件安装包，请确保从官方网站下载以避免安全问题。

2. 解压安装包并运行安装程序。

3. 按照安装向导的指示完成安装过程。

4. 安装成功后，双击桌面上的PASS图标启动软件。

三、输入数据1. 打开PASS软件后，点击“New”新建一个项目。

2. 在左侧的菜单栏中选择相应的分析方法，如均值比较、方差比较、生存分析等。

3. 根据研究或试验的具体设计，输入相应的参数和效应量。

4. 点击“Calculate”计算样本量。

四、结果解读1. PASS软件会根据输入的参数和效应量计算得出相应的样本量结果。

2. 结果包括总样本量、每组样本量、效应量、置信水平、统计检验的类型等。

3. 用户可以根据需要对结果进行调整和修改，以满足具体的研究目的。

五、其他功能除了样本量估计，PASS软件还提供其他一些实用的功能，如：1. 统计功效分析：可以帮助用户评估研究设计的合理性和可行性，预估研究结果是否具有统计学意义。

2. 效应量计算：可以根据已知的样本量和观察结果，反推出效应量的大小。

3. 图形展示：可以绘制功效曲线、样本量曲线等图形，直观地展示研究设计和样本量之间的关系。

六、注意事项使用PASS软件进行样本量估计时，需要注意以下几点：1. 确保输入数据的准确性和合理性，包括均值、标准差、效应量、置信水平等。

2. 根据研究或试验的具体需求，选择合适的分析方法和模型，以及对应的参数设置。

3. 如果不确定参数的取值范围，可以参考相关文献或专家意见进行合理估计。

SAS、PASS、Stata三种常用软件样本量计算方法及结果差异的比较作者：林洁孙志明来源：《中国医药导报》2015年第18期[摘要] 目的分析和探讨运用SAS、PASS、Stata 3种软件在两均数（率）比较中进行样本量估计的结果差异，推荐合适的样本量估计软件。

方法通过设定不同的参数情况，分别运用3种软件计算各自样本量，并且与公式计算结果进行比较。

结果在两均数比较时，Stata和PASS的样本量估计结果最准确，不同的参数会影响SAS的结果；在两个率比较时，SAS最准确，PASS的准确性与样本量大小有关系，Stata结果偏大且受不同参数的影响。

结论不同软件计算结果并不一致，综合考虑推荐用SAS软件进行两样本均数（率）比较的样本量估计。

[关键词] 样本量估计；SAS；PASS；Stata[中图分类号] R181 [文献标识码] A [文章编号] 1673-7210（2015）06（c）-0133-05样本量（sample size）是指承受研究实施的样本所包含之观察单位数，或样本例数。

除个别设计方法外，在研究设计中必须确定需要多少实验对象或观察对象。

样本量对研究效果有重要影响，在小样本研究中尤其如此[1]。

一系列规范的的医学研究报告，如加强观察性流行病学研究报告质量的声明和临床试验报告统一标准等均要求在研究报告中描述“如何计算样本含量”[2-6]。

开展一项研究，往往因为各种因素（人力、物力、经费等）限制，只能对总体中的一部分进行研究，即研究样本，然后由样本统计量推断总体参数。

样本过小，结果不稳定，不能真实地反映总体规律；而样本量过大，会增大研究的难度，并造成人力、物力的浪费[7]。

所以合理的样本量，一方面，可以在既定的经费下保证精确度和可靠性；另一方面，可以在既定的精确度和可靠性合理利用资源，保证抽样推断的最大效果。

目前可以用于估计样本含量的软件很多，其中较常用的有SAS、Stata、PASS等。

PASS软件在观察性研究设计样本含量估算中的应用魏凤江;胡良平【摘要】样本含量估算是科研人员进行科研设计所关注的重要问题之一,合理估算样本含量是试验设计中的一个重要内容.本文应用PASS 11.0软件对临床研究中观察性研究(即队列研究、病例-对照研究和横断面研究)的样本含量进行计算.探讨PASS软件在科研过程中计算样本含量的实用性和准确性,为科研工作者在进行观察性研究设计阶段进行科学的样本含量估算提供参考.【期刊名称】《四川精神卫生》【年(卷),期】2017(030)005【总页数】4页(P401-404)【关键词】样本含量;队列研究;病例-对照研究;横断面研究【作者】魏凤江;胡良平【作者单位】天津医科大学公共卫生学院卫生统计学教研室,天津 300070;天津医科大学基础医学院遗传学系,天津 300070;军事医学科学院生物医学统计学咨询中心,北京 100850;世界中医药学会联合会临床科研统计学专业委员会,北京 100029【正文语种】中文【中图分类】R195.1样本含量(sample size)是指承受研究者实施的样本所包含之观察单位数或样本例数。

除个别设计方法外，在研究设计中必须确定需要多少试验对象或观察对象。

因为人力、物力、经费等各种因素的限制，开展一项研究往往只能对总体中的一部分进行研究，即研究样本，然后由样本统计量推断总体参数或总体分布。

样本含量过小，结果不稳定，不能真实地反映总体规律；而样本含量过大，会增大研究的难度，并造成人力、物力的浪费。

所以合理的样本含量一方面可以在既定的科研经费下保证精确度和可靠性，另一方面可以合理利用资源，保证统计推断的最大效果。

目前，能够估算样本含量的方法较多，应用较广泛的方法是以公式为基础的SAS编程；也可以利用SAS/STAT模块中的GLMPOWER和POWER两个过程，对样本含量和检验效能进行更加深入的探讨，但是对于编程软件不太精通的人士，SAS软件使用难度很大。

PASS15样本量估计操作手册概述在实验设计和研究中，样本量估计是一个非常重要的步骤。

它用于确定实验或研究中所需的参与者或样本数量，以确保研究结果的统计显著性和可靠性。

PASS15是一种广泛使用的计算机软件，可以帮助研究人员进行样本量估计。

本操作手册将介绍如何使用PASS15进行样本量估计。

我们将从软件安装开始，然后逐步指导您完成样本量估计的过程。

步骤1：软件安装PASS15是一个商业软件，您可以通过其官方网站购买和下载。

安装过程与其他常规软件相似，您只需按照安装向导的指示进行操作即可。

步骤2：软件启动完成安装后，您可以在桌面或开始菜单中找到PASS15的快捷方式，双击它来启动软件。

步骤3：选择实验设计一旦软件启动，您将看到一个主界面，展示了各种实验设计选项。

根据您的研究需求，选择合适的实验设计。

PASS15提供了广泛的实验设计选项，包括均数差异、比例差异、相关系数、生存分析等等。

选择与您的研究最相关的设计选项，并点击相应的图标以进入下一步。

步骤4：输入参数在进入具体的实验设计界面后，您需要输入相关的参数，以进行样本量估计。

这些参数可能包括效应大小、显著性水平、功效、预期的标准差等等。

根据实验设计的不同，参数的种类和要求也会有所不同。

根据软件提示，逐一输入所需的参数，并确保输入的数据准确无误。

步骤5：运行样本量估计在输入参数后，您可以点击运行按钮以执行样本量估计。

PASS15将根据您提供的数据和参数进行计算，并显示估计的样本量结果。

根据计算的复杂程度和所选的设计，计算结果可能需要一些时间。

请耐心等待，直到结果显示出来。

步骤6：结果解读一旦计算完成，PASS15将显示样本量估计的结果。

这些结果可能包括所需的总样本量、每组的样本量、置信区间等等。

根据您的研究需求和统计分析方法，您可以使用这些结果来决定实际的样本大小。

步骤7：导出结果PASS15还允许您将样本量估计的结果导出到其他文件格式，如Excel或PDF。

SAS、PASS、Stata三种常用软件样本量计算方法及结果差异的比较目的分析和探讨运用SAS、PASS、Stata 3种软件在两均数（率）比较中进行样本量估计的结果差异，推荐合适的样本量估计软件。

方法通过设定不同的参数情况，分别运用3种软件计算各自样本量，并且与公式计算结果进行比较。

结果在两均数比较时，Stata和PASS的样本量估计结果最准确，不同的参数会影响SAS的结果；在两个率比较时，SAS最准确，PASS的准确性与样本量大小有关系，Stata结果偏大且受不同参数的影响。

结论不同软件计算结果并不一致，综合考虑推荐用SAS软件进行两样本均数（率）比较的样本量估计。

标签：样本量估计；SAS；PASS；Stata样本量（sample size）是指承受研究实施的样本所包含之观察单位数，或样本例数。

除个别设计方法外，在研究设计中必须确定需要多少实验对象或观察对象。

样本量对研究效果有重要影响，在小样本研究中尤其如此[1]。

一系列规范的的医学研究报告，如加强观察性流行病学研究报告质量的声明和临床试验报告统一标准等均要求在研究报告中描述“如何计算样本含量”[2-6]。

开展一项研究，往往因为各种因素（人力、物力、经费等）限制，只能对总体中的一部分进行研究，即研究样本，然后由样本统计量推断总体参数。

样本过小，结果不稳定，不能真实地反映总体规律；而样本量过大，会增大研究的难度，并造成人力、物力的浪费[7]。

所以合理的样本量，一方面，可以在既定的经费下保证精确度和可靠性；另一方面，可以在既定的精确度和可靠性合理利用资源，保证抽样推断的最大效果。

目前可以用于估计样本含量的软件很多，其中较常用的有SAS、Stata、PASS 等。

SAS是由美国北卡罗来纳州立大学1966年开发的统计分析软件，在国际上被誉为统计分析的标准软件，在各个领域得到了广泛应用[8]；Stata是Statacorp 于1985年开发的统计程序，在全球范围内被广泛应用于经济学、社会学及流行病学等领域；PASS是由Hintze等人研发，专门用于计算样本量的统计软件，操作简便快捷。