下载文档原格式
曲线拟合法的Matlab实现曲线拟合在许多科学和工程领域中都有广泛应用，包括机器学习，数据科学，信号处理，控制工程等。
在Matlab中实现曲线拟合的方法有多种，其中最常用的是使用fit()函数。
以下是一个基本的示例，演示如何在Matlab中使用fit()函数进行曲线拟合。
我们需要一些数据。
假设我们有一组x和y数据点，我们想要在这些点上拟合一条曲线。
y = 3*x.^2 + 2*x + 1 + randn(size(x));fitresult = fit(x, y, 'poly1');在这里，'poly1'表示我们想要拟合一个一次多项式。
你可以使用'poly2'，'poly3'等来拟合更高次的多项式。
同样，你也可以使用其他类型的模型，如指数、对数、自定义函数等。
然后，我们可以使用plot()函数将原始数据和拟合曲线一起绘制出来。
在这里，'hold on'命令用于保持当前图像，这样我们就可以在同一个图形上绘制多条线了。
我们可以使用fitresult来获取拟合曲线的参数和其他信息。
例如：以上就是在Matlab中进行曲线拟合的基本步骤。
需要注意的是，对于复杂的实际问题，可能需要进行更复杂的模型选择和参数优化。
也可以使用其他工具如curve fitting toolbox进行更详细的分析和拟合。
最小二乘曲线拟合是一种数学统计方法，用于根据给定数据点拟合出一条曲线或曲面，使得该曲线或曲面最小化每个数据点到拟合曲线或曲面的平方误差之和。
这种方法广泛应用于数据分析和科学计算等领域。
本文将介绍最小二乘曲线拟合的基本原理和在Matlab中的实现方法。
假设有一组数据点 (x_i, y_i)，i=1,2,...,n，需要拟合出一条曲线y=f(x)。
最小二乘法要求曲线 f(x)最小化每个数据点到曲线的平方误差之和，即E = sum (f(x_i)-y_i)^2对曲线 f(x)进行求导，得到一元一次方程：f'(x)=sum(f(x)-y)*x-sum(f(x)-y)E = sum [(f'(x))^2] * x^2 - 2 * sum [f(x) * f'(x) * x] + 2 * sum [f(x)^2]令 E对 f'(x)的导数为零，可得到最小二乘曲线拟合的方程：sum [f'(x)^2] * x^2 - 2 * sum [f(x) * f'(x) * x] + 2 * n * f(x)^2 = 0在Matlab中，可以使用polyfit函数实现最小二乘曲线拟合。
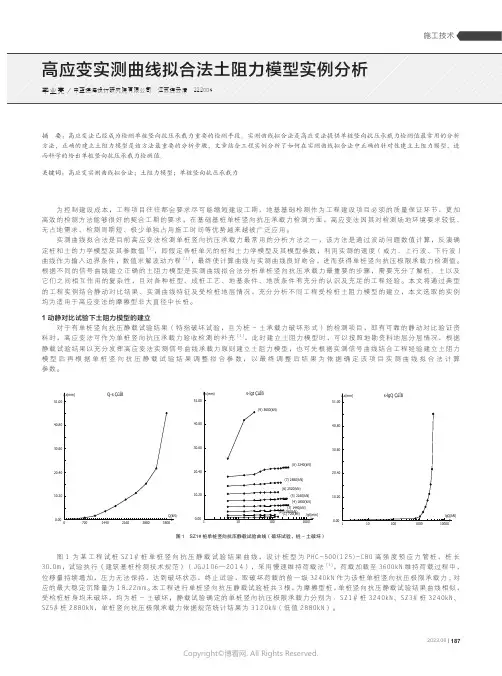
图1为某工程试桩S Z1#桩单桩竖向抗压静载试验结果曲线，设计桩型为P H C-500(125)-C80高强度预应力管桩，桩长30.0m，试验执行《建筑基桩检测技术规范》（J G J106—2014），采用慢速维持荷载法[1]，荷载加载至3600k N维持荷载过程中，位移量持续增加，压力无法保持，达到破坏状态，终止试验，取破坏荷载的前一级3240k N作为该桩单桩竖向抗压极限承载力,对应的最大稳定沉降量为18.22m m。
本工程进行单桩竖向抗压静载试验桩共3根，为摩擦型桩，单桩竖向抗压静载试验结果曲线相似，受检桩桩身均未破坏，均为桩-土破坏，静载试验确定的单桩竖向抗压极限承载力分别为：S Z1#桩3240k N、S Z3#桩3240k N、S Z5#桩2880k N，单桩竖向抗压极限承载力依据规范统计结果为3120k N（低值2880k N）。
图2为尚未进行单桩竖向抗压静载试验前，参考图3地质勘察资料地层分层情况，采用实测曲线拟合法给出的单桩竖向抗压极限承载力检测值为2909k N ，现场采集数据选用5.0T 重锤，落距0.7m ，根据桩-锤反应经验及本地区工程经验判断受检桩已被充分打动；根据地质勘察资料计算的单桩竖向抗压极限承载力约为2031k N （桩顶基本为地面平）；因已知本受检单体工程的工程桩将同时进行单桩竖向抗压静载试验，在拟合时便以充分发挥测试曲线承载力的原则拟合，因考虑到高应变实测曲线拟合法给的单桩竖向抗压极限承载力检测值往往偏于保守，本次拟合主动放弃部分拟合质量，分析人员也有足够的相似地区场地的高应变实测曲线拟合法检测分析经验，所以本次高应变实测曲线拟合法给出的单桩竖向抗压极限承载力检测值高于比平时正常进行工程验收试验拟合给出的单桩竖向抗压极限承载力检测值约20%，高于地勘资料计算单桩竖向抗压极限承载力40%左右，低于单桩竖向抗压静载试验统计结果承载力约10%，高于静载试验结果的低值，但考虑到高应变法检测承载力发挥机理需要受检桩有一定动位移，其承载力检测值必定会低于静阻力，本次高应变实测曲线拟合法承载力检测值结果是非常接近充分休止的受检桩桩-土承载力极限值的，但是，这种充分发挥实测曲线承载力的分析方法在有充分静载资料的情况下才建议使用，这种分析方法是极不保守的，一旦工程桩施工质量有瑕疵或者地质条件有不利的变化时，对于工程是存在风险的。
matplot 拟合曲线在使用 Matplotlib 进行曲线拟合时，可以使用 numpy.polyfit() 函数来进行多项式拟合。
以下是一个简单的示例：import numpy as npimport matplotlib.pyplot as plt# 原始数据x = np.array([1, 2, 3, 4, 5])y = np.array([2, 4, 6, 8, 10])# 多项式拟合degree = 2 # 多项式的阶数coefficients = np.polyfit(x, y, degree)poly = np.poly1d(coefficients)y_fit = poly(x)# 绘制原始数据和拟合曲线plt.scatter(x, y, label='Original Data')plt.plot(x, y_fit, label='Fitted Curve')plt.xlabel('X')plt.ylabel('Y')plt.legend()plt.show()在上述示例中，我们使用 numpy.polyfit() 函数进行二次多项式拟合。
通过指定输入数据 x 和 y，以及多项式的阶数 degree，函数将返回多项式的系数。
我们然后使用 np.poly1d() 函数创建一个多项式对象，并使用该对象计算拟合曲线上的各个点的值 y_fit。
最后，我们使用 Matplotlib 绘制原始数据和拟合曲线，通过 scatter()函数绘制原始数据的散点图，通过 plot() 函数绘制拟合曲线。
添加合适的标签、轴标签和图例，最后使用 show() 函数显示图形。
可以根据需要调整拟合的多项式阶数、数据集等参数。
请注意，多项式拟合可能不适用于所有类型的数据，因此在应用时需要谨慎选择和评估拟合结果。
玻尔兹曼曲线拟合全文共四篇示例，供读者参考第一篇示例：玻尔兹曼曲线拟合是一种常用的数据拟合方法，广泛应用于物理、化学、生物等各个领域。
玻尔兹曼曲线拟合可以帮助研究人员找到数据中隐藏的规律性，从而更好地理解数据背后的物理、化学或生物机制。
本文将介绍玻尔兹曼曲线拟合的基本原理、方法和应用，并分享一些实际案例，希望读者能对这一拟合方法有更深入的了解。
一、玻尔兹曼曲线的基本原理玻尔兹曼曲线是一种S形曲线，通常用来描述某种变量随着另一种变量的变化而变化的关系。
在物理学和化学领域，玻尔兹曼曲线最常用来描述变量之间的非线性关系，例如温度对电导率、溶液浓度对吸光度等的影响。
y = A + \frac{B}{1 + e^{(x-x_0)/C}}y为因变量，x为自变量，A、B、x0、C为拟合参数。
A为曲线的上限，B为曲线的幅度，x0为曲线的中点，C为曲线的斜率。
通过调整这些参数，可以使拟合曲线更好地拟合实际数据。
玻尔兹曼曲线的拟合方法通常是通过最小二乘法来实现的。
最小二乘法是一种常用的数据拟合方法，通过最小化残差的平方和来确定拟合曲线的参数。
在拟合玻尔兹曼曲线时，研究人员需要首先选定拟合的自变量和因变量，然后根据实验数据进行拟合，得到最优的拟合参数。
玻尔兹曼曲线的拟合过程通常分为以下几个步骤：1. 选择适当的自变量和因变量。
在拟合玻尔兹曼曲线时，需要首先确定哪种变量作为自变量，哪种变量作为因变量。
通常情况下，自变量为影响因变量变化的因素，因变量为受影响的结果。
2. 收集实验数据。
在确定了自变量和因变量后，研究人员需要进行实验或者采集数据，得到一组数据点用于拟合。
3. 利用最小二乘法进行拟合。
在得到实验数据后，研究人员可以利用最小二乘法对数据进行拟合，得到最优的拟合参数。
4. 分析拟合结果。
拟合完成后，研究人员需要对拟合结果进行分析，判断拟合曲线与实际数据的拟合程度，以及拟合参数的合理性。
玻尔兹曼曲线拟合在不同领域有着广泛的应用。
数学建模曲线拟合例题一、概述形象的说，拟合就是把平面上一系列的点，用一条光滑的曲线连接起来。
因为这条曲线有无数种可能，从而有各种拟合方法。
拟合的曲线一般可以用函数表示，根据这个函数的不同有不同的拟合名字。
1.名称：如果待定函数是线性，就叫线性拟合，否则叫作非线性拟合。
表达式也可以是分段函数，这种情况下叫作样条插值。
2.区分：拟合以及插值还有逼近是数值分析的三大基础方法，通俗意义上它们的区别在于：拟合是已知点列，从整体上靠近它们；插值是已知点列并且完全经过点列；逼近是已知曲线，或者点列，通过逼近使得构造的函数无限靠近它们。
二、方法及应用我们手工求解时比较简便实用的方法是最小二乘法。
即下图所示：具体推导步骤如下：设拟合直线y=a+bx，有任意观察点（xi，yi）且误差为di=yi-(a+bxi)。
当D等于di平方的累加和取最小值时，直线拟合度最高。
而在matlab中数据拟合的原理是最小拟合也是运用了最小二乘原理，其中polyfit与polyval是最基本的拟合方法。
在实际运用中我们最常使用polyfit与polyval函数用来进行拟合求解。
polyfit函数用以拟合横、纵轴数据得到拟合多项式储存在p中，而polyval用于计算出每个横轴坐标x在拟合多项式p中对应的函数值。
三、例题【例题一】x从1到9，y为9，7，6，3，-1，2，5，7，20，运用polyfit 和polyval命令计算其多项式系数。
得结果多项式系数：P=0.1481-1.40301.85378.2698 y=0.1481x^3-1.4030x^2+1.8537x+8.2698图像如下所示：以下为预测出的部分数据。
结果说明：（1）p-最小二乘拟合多项式系数（向量）最优函数的多项式的各项系数应使得误差平方和S取得极小值。
（2）S-误差估计结构体（结构体）此可选输出结构体主要用作polyval函数的输入，以获取误差估计值。
（3）mu-中心化值和缩放值(二元素向量)中心化值和缩放值，以一个二元素向量形式返回，以单位标准差将x中的查询点的中心置于零值处。
例如：已知数据队列buf=【5410。
】x取值1：n n是队列长度函数f（x）=a+b*sin(c*x+d) .avg 是队列平均值a b c d 为参数a范围（2/3,1）*avgb范围（0,1/3）*avgc的范围（0,24*pi）d （0,2*pi）1、首先定义目标函数function y=ga_curfit(x)global ydata nt=1:n;y=0;for i=1:ny=y+(ydata(i)-(x(:,1)+x(:,2).*sin(x(:,3).*t(i)+x(:,4)))).^2/n; endy=sqrt(y);end2、把数据b.txt放在工作空间目录中然后再命令窗口中输入clearglobal ydata nformat long gload b.txtydata=b';n=length(ydata);avg=sum(ydata)/n;LB=[2/3*avg 0 0 0];UB=[1*avg 1/3*avg 24*pi 2*pi];nvars=4;options=gaoptimset;options=gaoptimset(options,'PopulationSize',300); options=gaoptimset(options,'CrossoverFraction',0.8); options=gaoptimset(options,'MigrationFraction',0.1);options=gaoptimset(options,'Generations',500);options = gaoptimset(options,'TolFun', 1e-50);%options = gaoptimset(options,'InitialPopulation',final_pop);options = gaoptimset(options,'Display', 'final');options = gaoptimset(options,'PopInitRange', [LB;UB]);options = gaoptimset(options,'PlotFcns', @gaplotbestf);options=gaoptimset(options,'Vectorize','on');%目标函数向量化[x,fval,exitflag,output,final_pop,scores]=ga(@ga_curfit,nvars,[],[],[],[],LB,UB,[],options);t=1:n;plot(t,ydata,'r*');hold onplot(t,x(1)+x(2)*sin(x(3)*t+x(4)))legend('数据','拟合')引言之前曾发帖讨论过常微分方程参数拟合问题，就实际应用而言，还是以非线性代数方程参数拟合问题居多。
实现非线性代数方程参数拟合的软件有很多，比如MATLAB、Origin、SPSS和1stOpt等，特别是1stOpt，其代码简单易学，几乎不需调试，即可获得高质量的拟合结果，不过需要指出的是，该软件的拟合过程对操作者而言是一个黑箱。
拟合问题，实际上是一类最优化问题。
既然说到最优化问题，自然要涉及最优化算法、初值、程序代码。
初值的选取一直是困扰局部最优算法的问题，比如在调用MATLAB著名的lsqnonlin函数时，拟合结果对选用的初值具有很大的依赖性。
以具有全局搜索能力算法的计算结果，作为初值供局部最优化算法调用，是一种解决初值选取问题的方法。
本帖的主要目的正是讨论一种基于遗传算法拟合非线性代数方程参数的方法。
1. 本帖讨论的例子出处本帖讨论的问题与数据，取自2013年全国研究生数学建模竞赛E题，直观起见，现将问题表述如下：已知自变量p，因变量L，L和p满足以下函数式：L=(1-(1-p)^k3)^k1*(1-(1-p)^k4)^k2；且k1，k2≥0，k1+k2≥1 )；（需要指出的是，该公式中参数可进一步合并以防止过拟合，拟合结果不唯一，不过，在本帖中并未作合并处理）拟合出k1，k2，k3和k4。
2.结果与讨论运行MATLAB软件，调用lsqnonlin函数，参数初值按k1=1，k2=0，k3=1，k4=0作试探（先不管k1，k2的约束条件，实际上，k1，k2的约束常可自然满足），程序代码如下：clear all;clcformat longdata=;p=data(:,1); %pi Lexp=data(:,2); %Li k0=;lb=;ub=*1e6;%-------------------------------------------------------------------------% 使用函数lsqnonlin()进行参数估计OPTIONS=optimset('MaxFunEvals',1000,'TolFun',1e-12,'Algorithm','trust-region-reflective' );= ...lsqnonlin(@ObjFunc,k0,lb,ub,OPTIONS,p,Lexp); ci = nlparci(k,residual,jacobian); %residual;y=Objfit(p,k);fprintf('\n\n拟合结果:\n') fprintf(' \t残差平方和= %.6e\n\n',resnorm); fprintf('\n\t参数 a = %.9f',k(1)) fprintf('\n\t参数 b = %.9f',k(2)) fprintf('\n\t参数 c = %.9f',k(3)) fprintf('\n\t参数 d = %.9f',k(4)) n=length(p);R2=1-sum((Lexp-y).^2)./sum((Lexp-mean(Lexp)).^2);MSE=1/n*sum((Lexp-y).^2);MAE=1/n*sum(abs(Lexp-y));MAS=max(abs(Lexp-y));fprintf('\n\t决定系数R-Square = %.9f',R2); fprintf('\n\t均方误差MSE = %.9f',MSE); fprintf('\n\t平均绝对误差MAE = %.6f',MAE); fprintf('\n\t最大绝对误差MAS = %.6f',MAS); figure(2)plot(p,y,'b',p,Lexp,'or'),axis(),...text(0.05,0.95,),...text(0.05,0.85,),...text(0.05,0.75,),...text(0.05,0.65,),...xlabel('p'),ylabel('L'), legend('拟合结果','原始数据','Location','Best') %-------------------------------------------------------------------------function f = ObjFunc(k,p,Lexp) f=Objfit(p,k)-Lexp;%------------------------------------------------------------------------fun ction f = Objfit(p,k)f=(1-(1-p).^k(3)).^k(1).*(1-(1-p).^k(4)).^k(2);计算结果：残差平方和= 7.150814e-001参数 a = 1.000000003参数 b = 0.000000188参数 c = 1.000000000参数 d = 0.000000000决定系数R-Square = 0.622496369均方误差MSE = 0.042063615平均绝对误差MAE = 0.186062最大绝对误差MAS = 0.288096 图形结果见附图1。
由结果可见，决定系数R-Square = 0.622，拟合结果相当不理想，于是以其他初值作试探，结果如下：（k1 k2 k3 k4）决定系数R-Square （0 0 0 0） -3.722589381 （ 1 0 0 0） 0.999998738 （0 1 0 0） 0.999836583 （0 0 1 0） -3.723048781 （0 0 0 1） -3.723048781 （ 1 1 0 0） -1.136614242 （ 1 0 1 0） 0.622496369 …… ……可见拟合结果对初值的依赖性明显。
对于调用MATLAB自带的遗传算法GA函数，以其计算结果作为初值，代码如下：clear all;close all;clc data=;p=data(:,1); %pi Lexp=data(:,2); %Li %-------------遗传算法----------------------------------------------------- options = gaoptimset('Generations',1000,'StallGenLimit',300,...'StallTimeLimit',50,'TolFun',1e-12,'TolCon',1e-12); =ga(@objfun,4,options);options = gaoptimset('InitialPopulation',final_pop,'Generations',1000,'StallGenLimit',300,...'StallTimeLimit',50,'TolFun',1e-12,'TolCon',1e-12); =ga(@obj fun,4,options);fprintf('\n\n遗传算法的初始估计数值:\n'); fprintf('\n\t参数a0 = %.9f',k2(1)); fprintf('\n\t参数b0 = %.9f',k2(2)); fprintf('\n\t参数c0 = %.9f',k2(3)); fprintf('\n\t参数d0 = %.9f',k2(4)); %------------------------------最小二乘法---------------------------------- k0=k2;lb=;ub=*1e6;OPTIONS=optimset('MaxFunEvals',1000,'TolFun',1e-12,'Algorithm','trust-region-reflective', 'Display','Off');= ...lsqnonlin(@ObjFunc,k0,lb,ub,OPTIONS,p,Lexp); %-----------------------------------------------------------------%------------------结果输出与图形化---------------------------------------------- k=k3;y=Lorentz(p,k);fprintf('\n\n最终拟合结果:\n') fprintf(' \t残差平方和= %.6e\n\n',resnorm); fprintf('\n\t参数 a = %.9f',k(1)) fprintf('\n\t参数 b = %.9f',k(2)) fprintf('\n\t参数 c = %.9f',k(3)) fprintf('\n\t参数 d = %.9f',k(4)) n=length(p);R2=1-sum((Lexp-y).^2)./sum((Lexp-mean(Lexp)).^2);MSE=1/n*sum((Lexp-y).^2);MAE=1/n*sum(abs(Lexp-y));MAS=max(abs(Lexp-y));fprintf('\n\t决定系数R-Square = %.9f',R2); fprintf('\n\t均方误差MSE = %.6f',MSE); fprintf('\n\t平均绝对误差MAE = %.6f',MAE); fprintf('\n\t最大绝对误差MAS = %.6f',MAS); figureplot(p,y,'b',p,Lexp,'or'),axis(),...text(0.05,0.95,),...text(0.05,0.85,),...text(0.05,0.75,),...text(0.05,0.65,),...xlabel('p'),ylabel('L'), legend('拟合结果','原始数据','Location','Best') %-------------------------------------------------------------------------function f = ObjFunc(k,p,Lexp) f=Lorentz(p,k)-Lexp;%----------------构造拟合目标函数------------------------------------------- function fun=objfun(k) data=;p=data(:,1); %pi Lexp=data(:,2); %Li n=length(p);g1=k(1)+k(2);if (k(1)<0||k(2)<0||g1<1)fun=inf;elsefor i=1:nFF(i)=(Lexp(i)-Lorentz(p(i),k))^2; endfun=sum(FF);end%------------------------------构造待拟合函数------------------------------ fun ction f = Lorentz(p,k) f=(1-(1-p).^k(3)).^k(1).*(1-(1-p).^k(4)).^k(2);计算结果：遗传算法的初始估计数值:参数a0 = 0.942351724参数b0 = 0.889975854参数c0 = 0.655520744参数d0 = 1.049009027 最终拟合结果:残差平方和= 2.390252e-006参数 a = 1.494321551参数 b = 0.522975583参数 c = 0.714822496参数 d = 2.216764819决定系数R-Square = 0.999998738均方误差MSE = 0.000000 平均绝对误差MAE = 0.000315最大绝对误差MAS = 0.000798>> 图形结果见附图2。
