二次函数图像与性质完整归纳

二次函数图象和性质总结表格二次函数知识点总结一、二次函数的图像和性质二次函数的图像开口方向、对称轴、顶点坐标、增减性和最值与函数的参数有关。

当参数a大于0时，图像开口向上，对称轴是y轴，顶点坐标为(0,0)，在对称轴左侧y随x增大而减小，在对称轴右侧y随x增大而增大。

参数a越大，开口越小。

当参数a小于0时，图像开口向下，对称轴是y轴，顶点坐标为(0,0)，在对称轴左侧y随x增大而增大，在对称轴右侧y随x增大而减小。

参数a越小，开口越小。

当二次函数带有平移时，对称轴的位置会发生变化，顶点坐标变为(h,k)。

当参数a大于0时，图像开口向上，对称轴是直线x=h，顶点坐标为(h,k)，在对称轴左侧y随x增大而减小，在对称轴右侧y随x增大而增大。

当参数a小于0时，图像开口向下，对称轴是直线x=h，顶点坐标为(h,k)，在对称轴左侧y随x增大而增大，在对称轴右侧y随x增大而减小。

二、二次函数的解析式二次函数的解析式为y=ax²+bx+c，其中a、b、c均为实数且a≠0.当二次函数带有平移时，解析式为y=a(x-h)²+k，其中a、h、k均为实数且a≠0.三、二次函数的应用二次函数在数学和现实生活中都有广泛的应用。

例如，二次函数可以用来描述物体的运动轨迹、建筑物的结构、金融市场的波动等等。

在应用中，我们需要根据实际情况确定二次函数的参数，并利用二次函数的性质进行分析和计算。

总之，二次函数是数学中非常重要的一个概念，掌握二次函数的图像、解析式和应用是我们研究数学的基础。

当x＞h时，随着x的增大，y会减小。

函数a的符号决定了开口的方向，当a＞0时，开口向上，当a＜0时，开口向下。

对称轴为直线x=-b/2a，顶点坐标为(-b/2a。

c-b^2/4a)。

当a的绝对值越大时，开口越小；b的符号决定了对称轴在y轴的位置，当b＞0时，对称轴在y轴左侧，当b＜0时，对称轴在y轴右侧；c的符号决定了抛物线与y轴的交点在哪个象限，当c＞0时，抛物线与y轴正半轴相交，当c＜0时，抛物线与y轴负半轴相交。

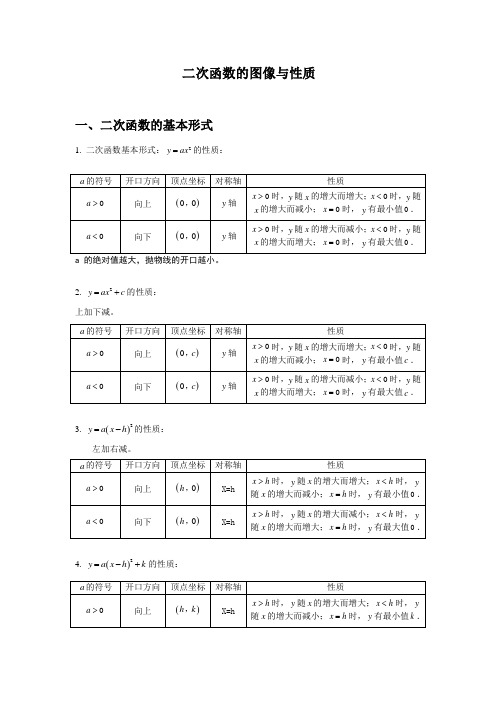
二次函数的图像与性质一、二次函数的基本形式1. 二次函数基本形式：2y ax =的性质：a 的绝对值越大，抛物线的开口越小。

2. 2y ax c =+的性质： 上加下减。

3. ()2y a x h =-的性质：左加右减。

4. ()2y a x h k =-+的性质：二、二次函数图象的平移1. 平移步骤：方法一：⑴ 将抛物线解析式转化成顶点式()2y a x h k =-+，确定其顶点坐标()h k ，； ⑵ 保持抛物线2y ax =的形状不变，将其顶点平移到()h k ，处，具体平移方法如下：【或左(h <0)】向右(h >0)【或左(h 平移|k|个单位2. 平移规律在原有函数的基础上“h 值正右移，负左移；k 值正上移，负下移”． 概括成八个字“左加右减，上加下减”． 方法二：⑴c bx ax y ++=2沿y 轴平移:向上（下）平移m 个单位，c bx ax y ++=2变成m c bx ax y +++=2（或m c bx ax y -++=2）⑵c bx ax y ++=2沿轴平移：向左（右）平移m 个单位，c bx ax y ++=2变成c m x b m x a y ++++=)()(2（或c m x b m x a y +-+-=)()(2）三、二次函数()2y a x h k =-+与2y ax bx c =++的比较从解析式上看，()2y a x h k =-+与2y ax bx c =++是两种不同的表达形式，后者通过配方可以得到前者，即22424b ac b y a x a a -⎛⎫=++ ⎪⎝⎭，其中2424b ac b h k a a -=-=，． 四、二次函数2y ax bx c =++图象的画法五点绘图法：利用配方法将二次函数2y ax bx c =++化为顶点式2()y a x h k =-+，确定其开口方向、对称轴及顶点坐标，然后在对称轴两侧，左右对称地描点画图.一般我们选取的五点为：顶点、与y 轴的交点()0c ，、以及()0c ，关于对称轴对称的点()2h c ，、与x 轴的交点()10x ，，()20x ，（若与x 轴没有交点，则取两组关于对称轴对称的点）. 画草图时应抓住以下几点：开口方向，对称轴，顶点，与x 轴的交点，与y 轴的交点.五、二次函数2y ax bx c =++的性质1. 当0a >时，抛物线开口向上，对称轴为2bx a =-，顶点坐标为2424b ac b a a ⎛⎫-- ⎪⎝⎭，．当2b x a <-时，y 随x 的增大而减小；当2b x a >-时，y 随x 的增大而增大；当2bx a=-时，y 有最小值244ac b a-．2. 当0a <时，抛物线开口向下，对称轴为2bx a =-，顶点坐标为2424b ac b aa ⎛⎫-- ⎪⎝⎭，．当2b x a <-时，y 随x 的增大而增大；当2b x a >-时，y 随x 的增大而减小；当2bx a=-时，y 有最大值244ac b a-．六、二次函数解析式的表示方法1. 一般式：2y ax bx c =++（a ，b ，c 为常数，0a ≠）；2. 顶点式：2()y a x h k =-+（a ，h ，k 为常数，0a ≠）；3. 两根式：12()()y a x x x x =--（0a ≠，1x ，2x 是抛物线与x 轴两交点的横坐标）. 注意：任何二次函数的解析式都可以化成一般式或顶点式，但并非所有的二次函数都可以写成交点式，只有抛物线与x 轴有交点，即240b ac -≥时，抛物线的解析式才可以用交点式表示．二次函数解析式的这三种形式可以互化.七、二次函数的图象与各项系数之间的关系1. 二次项系数a二次函数2y ax bx c =++中，a 作为二次项系数，显然0a ≠．⑴ 当0a >时，抛物线开口向上，a 的值越大，开口越小，反之a 的值越小，开口越大； ⑵ 当0a <时，抛物线开口向下，a 的值越小，开口越小，反之a 的值越大，开口越大．总结起来，a 决定了抛物线开口的大小和方向，a 的正负决定开口方向，a 的大小决定开口的大小． 2. 一次项系数b在二次项系数a 确定的前提下，b 决定了抛物线的对称轴． ⑴ 在0a >的前提下，当0b >时，02ba-<，即抛物线的对称轴在y 轴左侧； 当0b =时，02ba-=，即抛物线的对称轴就是y 轴；当0b <时，02ba->，即抛物线对称轴在y 轴的右侧．⑵ 在0a <的前提下，结论刚好与上述相反，即 当0b >时，02ba->，即抛物线的对称轴在y 轴右侧； 当0b =时，02ba-=，即抛物线的对称轴就是y 轴； 当0b <时，02ba-<，即抛物线对称轴在y 轴的左侧． 总结起来，在a 确定的前提下，b 决定了抛物线对称轴的位置．ab 的符号的判定：对称轴abx 2-=在y 轴左边则0>ab ，在y 轴的右侧则0<ab ，概括的说就是“左同右异” 总结：3. 常数项c⑴ 当0c >时，抛物线与y 轴的交点在x 轴上方，即抛物线与y 轴交点的纵坐标为正； ⑵ 当0c =时，抛物线与y 轴的交点为坐标原点，即抛物线与y 轴交点的纵坐标为0； ⑶ 当0c <时，抛物线与y 轴的交点在x 轴下方，即抛物线与y 轴交点的纵坐标为负． 总结起来，c 决定了抛物线与y 轴交点的位置．总之，只要a b c ，，都确定，那么这条抛物线就是唯一确定的．二次函数解析式的确定：根据已知条件确定二次函数解析式，通常利用待定系数法．用待定系数法求二次函数的解析式必须根据题目的特点，选择适当的形式，才能使解题简便．一般来说，有如下几种情况：1. 已知抛物线上三点的坐标，一般选用一般式；2. 已知抛物线顶点或对称轴或最大（小）值，一般选用顶点式；3. 已知抛物线与x 轴的两个交点的横坐标，一般选用两根式；4. 已知抛物线上纵坐标相同的两点，常选用顶点式．八、二次函数图象的对称二次函数图象的对称一般有五种情况，可以用一般式或顶点式表达 1. 关于x 轴对称2y ax bx c =++关于x 轴对称后，得到的解析式是2y ax bx c =---；()2y a x h k =-+关于x 轴对称后，得到的解析式是()2y a x h k =---；2. 关于y 轴对称2y ax bx c =++关于y 轴对称后，得到的解析式是2y ax bx c =-+；()2y a x h k =-+关于y 轴对称后，得到的解析式是()2y a x h k =++；3. 关于原点对称2y ax bx c =++关于原点对称后，得到的解析式是2y ax bx c =-+-； ()2y a x h k =-+关于原点对称后，得到的解析式是()2y a x h k =-+-； 4. 关于顶点对称（即：抛物线绕顶点旋转180°）2y ax bx c =++关于顶点对称后，得到的解析式是222b y ax bx c a=--+-；()2y a x h k =-+关于顶点对称后，得到的解析式是()2y a x h k =--+．5. 关于点()m n ，对称()2y a x h k =-+关于点()m n ，对称后，得到的解析式是()222y a x h m n k =-+-+- 根据对称的性质，显然无论作何种对称变换，抛物线的形状一定不会发生变化，因此a 永远不变．求抛物线的对称抛物线的表达式时，可以依据题意或方便运算的原则，选择合适的形式，习惯上是先确定原抛物线（或表达式已知的抛物线）的顶点坐标及开口方向，再确定其对称抛物线的顶点坐标及开口方向，然后再写出其对称抛物线的表达式．二次函数图像参考：十一、2-32y=-2x 2y=3(x+4)22y=3x2y=-2(x-3)2【例题精讲】一、一元二次函数的图象的画法【例1】求作函数64212++=x x y 的图象 【解】)128(21642122++=++=x x x x y 2-4)(214]-4)[(21 2222+=+=x x4-=x 【例2】求作函数342+--=x x y 的图象。

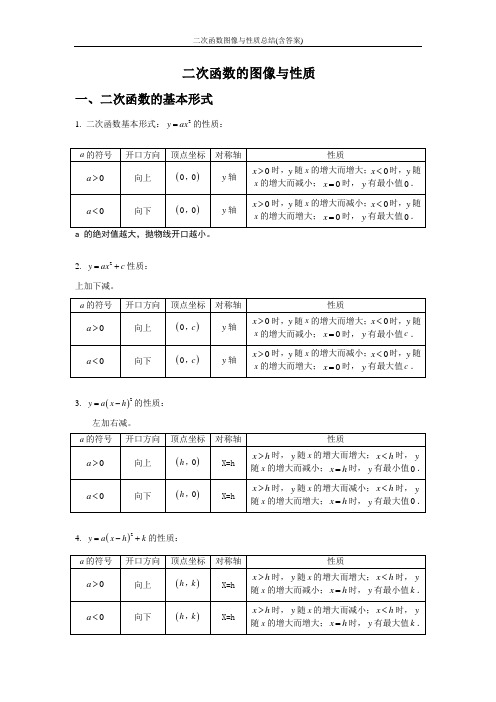
二次函数的图像与性质 一、二次函数的基本形式1. 二次函数基本形式：2y ax =的性质：2. 2y ax c =+性质： 上加下减。

3. ()2y a x h =-的性质：左加右减。

4. ()2y a x h k =-+的性质：二、二次函数图象的平移1. 平移步骤：方法一：⑴ 将抛物线解析式转化成顶点式()2y a x h k =-+，确定其顶点坐标()h k ，； ⑵ 保持抛物线2y ax =的形状不变，将其顶点平移到()h k ，处，具体平移方法如下：【或左(h <0)】向右(h >0)【或左(h 平移|k|个单位2. 平移规律在原有函数的基础上“h 值正右移，负左移；k 值正上移，负下移”． 概括成八个字“左加右减，上加下减”． 方法二：⑴c bx ax y ++=2沿y 轴平移:向上（下）平移m 个单位，c bx ax y ++=2变成m c bx ax y +++=2（或m c bx ax y -++=2）⑵c bx ax y ++=2沿轴平移：向左（右）平移m 个单位，c bx ax y ++=2变成c m x b m x a y ++++=)()(2（或c m x b m x a y +-+-=)()(2）三、二次函数()2y a x h k =-+与2y ax bx c =++的比较从解析式上看，()2y a x h k =-+与2y ax bx c =++是两种不同的表达形式，后者通过配方可以得到前者，即22424b ac b y a x a a -⎛⎫=++ ⎪⎝⎭，其中2424b ac b h k a a -=-=，． 四、二次函数2y ax bx c =++图象的画法五点绘图法：利用配方法将二次函数2y ax bx c =++化为顶点式2()y a x h k =-+，确定其开口方向、对称轴及顶点坐标，然后在对称轴两侧，左右对称地描点画图.一般我们选取的五点为：顶点、与y 轴的交点()0c ，、以及()0c ，关于对称轴对称的点()2h c ，、与x 轴的交点()10x ，，()20x ，（若与x 轴没有交点，则取两组关于对称轴对称的点）. 画草图时应抓住以下几点：开口方向，对称轴，顶点，与x 轴的交点，与y 轴的交点.五、二次函数2y ax bx c =++的性质1. 当0a >时，抛物线开口向上，对称轴为2bx a =-，顶点坐标为2424b ac b a a ⎛⎫-- ⎪⎝⎭，．当2b x a <-时，y 随x 增大而减小；当2b x a >-时，y 随x 的增大而增大；当2bx a=-时，y 有最小值244ac b a-． 2. 当0a <时，抛物线开口向下，对称轴为2bx a =-，顶点坐标为2424b ac b a a ⎛⎫-- ⎪⎝⎭，．当2b x a <-时，y 随x 的增大而增大；当2b x a >-时，y 随x 增大而减小；当2bx a=-时，y 有最大值244ac b a-．六、二次函数解析式的表示方法1. 一般式：2y ax bx c =++（a ，b ，c 为常数，0a ≠）；2. 顶点式：2()y a x h k =-+（a ，h ，k 为常数，0a ≠）；3. 两根式：12()()y a x x x x =--（0a ≠，1x ，2x 是抛物线与x 轴两交点的横坐标）. 注意：任何二次函数的解析式都可以化成一般式或顶点式，但并非所有的二次函数都可以写成交点式，只有抛物线与x 轴有交点，即240b ac -≥时，抛物线的解析式才可以用交点式表示．二次函数解析式的这三种形式可以互化.七、二次函数的图象与各项系数之间的关系1. 二次项系数a二次函数2y ax bx c =++中，a 作为二次项系数，显然0a ≠．⑴ 当0a >时，抛物线开口向上，a 的值越大，开口越小，反之a 的值越小，开口越大； ⑵ 当0a <时，抛物线开口向下，a 的值越小，开口越小，反之a 的值越大，开口越大．总结起来，a 决定了抛物线开口的大小和方向，a 的正负决定开口方向，a 的大小决定开口的大小． 2. 一次项系数b在二次项系数a 确定的前提下，b 决定了抛物线的对称轴． ⑴ 在0a >的前提下，当0b >时，02ba-<，即抛物线的对称轴在y 轴左侧； 当0b =时，02ba-=，即抛物线的对称轴就是y 轴； 当0b <时，02ba->，即抛物线对称轴在y 轴的右侧．⑵ 在0a <的前提下，结论刚好与上述相反，即 当0b >时，02ba->，即抛物线的对称轴在y 轴右侧； 当0b =时，02ba-=，即抛物线的对称轴就是y 轴； 当0b <时，02ba-<，即抛物线对称轴在y 轴的左侧． 总结起来，在a 确定的前提下，b 决定了抛物线对称轴的位置．ab 的符号的判定：对称轴abx 2-=在y 轴左边则0>ab ，在y 轴的右侧则0<ab ，概括的说就是“左同右异” 总结：3. 常数项c⑴ 当0c >时，抛物线与y 轴的交点在x 轴上方，即抛物线与y 轴交点的纵坐标为正； ⑵ 当0c =时，抛物线与y 轴的交点为坐标原点，即抛物线与y 轴交点的纵坐标为0； ⑶ 当0c <时，抛物线与y 轴的交点在x 轴下方，即抛物线与y 轴交点的纵坐标为负． 总结起来，c 决定了抛物线与y 轴交点的位置． 总之，只要a b c ，，都确定，那么这条抛物线就是唯一确定的．二次函数解析式的确定：根据已知条件确定二次函数解析式，通常利用待定系数法．用待定系数法求二次函数的解析式必须根据题目的特点，选择适当的形式，才能使解题简便．一般来说，有如下几种情况：1. 已知抛物线上三点的坐标，一般选用一般式；2. 已知抛物线顶点或对称轴或最大（小）值，一般选用顶点式；3. 已知抛物线与x 轴的两个交点的横坐标，一般选用两根式；4. 已知抛物线上纵坐标相同的两点，常选用顶点式．八、二次函数图象的对称二次函数图象的对称一般有五种情况，可以用一般式或顶点式表达 1. 关于x 轴对称2y ax bx c =++关于x 轴对称后，得到的解析式是2y ax bx c =---；()2y a x h k =-+关于x 轴对称后，得到的解析式是()2y a x h k =---；2. 关于y 轴对称2y ax bx c =++关于y 轴对称后，得到的解析式是2y ax bx c =-+；()2y a x h k =-+关于y 轴对称后，得到的解析式是()2y a x h k =++；3. 关于原点对称2y ax bx c =++关于原点对称后，得到的解析式是2y ax bx c =-+-； ()2y a x h k =-+关于原点对称后，得到的解析式是()2y a x h k =-+-； 4. 关于顶点对称（即：抛物线绕顶点旋转180°）2y ax bx c =++关于顶点对称后，得到的解析式是222b y ax bx c a=--+-；()2y a x h k =-+关于顶点对称后，得到解析式是()2y a x h k =--+．5. 关于点()m n ，对称 ()2y a x h k =-+关于点()m n ，对称后，得到解析式是()222y a x h m n k =-+-+-根据对称的性质，显然无论作何种对称变换，抛物线的形状一定不会发生变化，因此a 永远不变．求抛物线的对称抛物线的表达式时，可以依据题意或方便运算的原则，选择合适的形式，习惯上是先确定原抛物线（或表达式已知的抛物线）的顶点坐标及开口方向，再确定其对称抛物线的顶点坐标及开口方向，然后再写出其对称抛物线的表达式．二次函数图像参考：十一、2-32y=-2x 2y=3(x+4)22y=3x2y=-2(x-3)2【例题精讲】一、一元二次函数的图象的画法【例1】求作函数64212++=x x y 的图象 【解】 )128(21642122++=++=x x x x y2-4)(214]-4)[(21 2222+=+=x x【例2】求作函数342+--=x x y 的图象。

二次函数的图象和性质知识点总结一、知识点回顾1. 二次函数解析式的几种形式：①一般式：（a 、b 、c 为常数，a ≠0） ②顶点式：（a 、h 、k 为常数，a ≠0），其中（h ，k ）为顶点坐标。

③交点式：，其中是抛物线与x 轴交点的横坐标，即一元二次方程的两个根，且a ≠0，（也叫两根式）。

2. 二次函数的图象 ①二次函数的图象是对称轴平行于（包括重合）y 轴的抛物线，几个不同的二次函数，如果a 相同，那么抛物线的开口方向，开口大小（即形状）完全相同，只是位置不同。

②任意抛物线可以由抛物线经过适当的平移得到，移动规律可简记为：[左加右减，上加下减]，具体平移方法如下表所示。

③在画的图象时，可以先配方成的形式，然后y ax bx c =++2y a x h k =-+()2y a x x x x =--()()12x x 12，ax bx c 20++=y ax bx c =++2y ax bx c =++2y a x h k =-+()2y ax =2y ax bx c =++2y a x h k =-+()2将的图象上（下）左（右）平移得到所求图象，即平移法；也可用描点法：也是将配成的形式，这样可以确定开口方向，对称轴及顶点坐标。

然后取图象与y 轴的交点（0，c ），及此点关于对称轴对称的点（2h ，c ）；如果图象与x 轴有两个交点，就直接取这两个点（x 1，0），（x 2，0）就行了；如果图象与x 轴只有一个交点或无交点，那应该在对称轴两侧取对称点，（这两点不是与y 轴交点及其对称点），一般画图象找5个点。

3. 二次函数的性质y ax =2y ax bx c =++2y a x h k =-+()24. 求抛物线的顶点、对称轴和最值的方法①配方法：将解析式化为的形式，顶点坐标为（h ，k ），对称轴为直线，若a ＞0，y 有最小值，当x ＝h 时，；若a ＜0，y 有最大值，当x ＝h 时，。

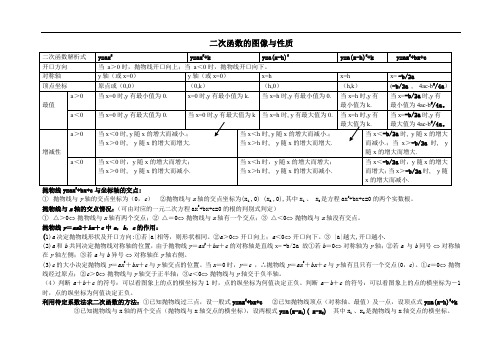
二次函数的图像和性质1.二次函数的图像与性质：解析式a 的取值开口方向函数值的增减顶点坐标对称轴图像与y轴的交点y = ax2当a0时；开口向上；在对称轴的左侧y随x的增大而减小，在对称轴的右侧 y 随 x 的增大而增大。

当a0时；开口向下；在对称轴的左侧y随 x 的增大而增大，在对称轴的右侧 y 随 x 的增大而减小。

（0，0）x=0（0，0）y = ax2+ k（0，c）x =0 (0，k）y = a( x + h)2（- h，0）x = - h(0，ah2）y=a(x+h)2+k（- h，k）x = - h(0，ah2+ k)y = ax2+bx+c b 4ac - b2 (- , )2a4a b x=-2a（0，c）2.抛物线的平移法则：（1）抛物线y = ax2+ k的图像是由抛物线y = ax2的图像平移k个单位而得到的。

当k 0时向上平移；当k0时向下平移。

（2）抛物线y = a（x + h）2的图像是由抛物线y = ax2的图像平移h个单位而得到的。

当h0时向左平移；当h0时向右平移。

（3）抛物线的y = a（x + h）2+ k图像是由抛物线y = ax2的图像上下平移k个单位，左右平移h个单位而得到的。

当k0时向上平移；当k0时向下平移；当h0时向左平移；当h0 时向右平移。

3.二次函数的最值公式：形如y =ax + bx + c的二次函数。

当a0时，图像有最低点，函数有最小值4ac-b24ac-b2y最小值=4a；当a0时，图像有最高点，函数有最大值，y最大值=4a；4.抛物线y =ax + bx + c与y轴的交点坐标是（0，c）5.抛物线的开口大小是由a决定的，a越大开口越小。

6.二次函数y =ax + bx + c的最值问题：（1）自变量的取值范围是一切实数时求最值的方法有配方法、公式法、判别式法。

（2）自变量的取值范围不是一切实数：b 自变量的取值范围不是一切实数时，应当抓住对称轴x = -2a ,把他与取值范围相比较，再进行求最值。

二次函数图像与性质总结-标准化文件发布号：（9556-EUATWK-MWUB-WUNN-INNUL-DDQTY-KII二次函数的图像与性质 一、二次函数的基本形式1. 二次函数基本形式：2y ax =的性质：2. 2y ax c =+的性质： 上加下减。

3. ()2y a x h =-的性质：左加右减。

4. ()2y a x h k =-+的性质：二、二次函数图象的平移 1. 平移步骤：方法一：⑴ 将抛物线解析式转化成顶点式()2y a x h k =-+，确定其顶点坐标()h k ，；⑵ 保持抛物线2y ax =的形状不变，将其顶点平移到()h k ，处，具体平移方法如下：【或左(h <0)】向右(h >0)【或左(h 平移|k|个单位2. 平移规律在原有函数的基础上“h 值正右移，负左移；k 值正上移，负下移”． 概括成八个字“左加右减，上加下减”． 方法二：⑴c bx ax y ++=2沿y 轴平移:向上（下）平移m 个单位，c bx ax y ++=2变成m c bx ax y +++=2（或m c bx ax y -++=2）⑵c bx ax y ++=2沿轴平移：向左（右）平移m 个单位，c bx ax y ++=2变成c m x b m x a y ++++=)()(2（或c m x b m x a y +-+-=)()(2）三、二次函数()2y a x h k =-+与2y ax bx c =++的比较从解析式上看，()2y a x h k =-+与2y ax bx c =++是两种不同的表达形式，后者通过配方可以得到前者，即22424b ac b y a x a a -⎛⎫=++ ⎪⎝⎭，其中2424b ac b h k a a-=-=，． 四、二次函数2y ax bx c =++图象的画法五点绘图法：利用配方法将二次函数2y ax bx c =++化为顶点式2()y a x h k =-+，确定其开口方向、对称轴及顶点坐标，然后在对称轴两侧，左右对称地描点画图.一般我们选取的五点为：顶点、与y 轴的交点()0c ，、以及()0c ，关于对称轴对称的点()2h c ，、与x 轴的交点()10x ，，()20x ，（若与x 轴没有交点，则取两组关于对称轴对称的点）.画草图时应抓住以下几点：开口方向，对称轴，顶点，与x 轴的交点，与y 轴的交点.五、二次函数2y ax bx c =++的性质1. 当0a >时，抛物线开口向上，对称轴为2bx a=-，顶点坐标为2424b ac b a a ⎛⎫-- ⎪⎝⎭，． 当2b x a <-时，y 随x 的增大而减小；当2bx a>-时，y 随x 的增大而增大；当2bx a=-时，y 有最小值244ac b a -．2. 当0a <时，抛物线开口向下，对称轴为2bx a=-，顶点坐标为2424b ac b aa ⎛⎫-- ⎪⎝⎭，．当2b x a <-时，y 随x 的增大而增大；当2bx a >-时，y 随x 的增大而减小；当2bx a=-时，y 有最大值244ac b a -．六、二次函数解析式的表示方法1. 一般式：2y ax bx c =++（a ，b ，c 为常数，0a ≠）；2. 顶点式：2()y a x h k =-+（a ，h ，k 为常数，0a ≠）；3. 两根式：12()()y a x x x x =--（0a ≠，1x ，2x 是抛物线与x 轴两交点的横坐标）.注意：任何二次函数的解析式都可以化成一般式或顶点式，但并非所有的二次函数都可以写成交点式，只有抛物线与x 轴有交点，即240b ac -≥时，抛物线的解析式才可以用交点式表示．二次函数解析式的这三种形式可以互化.七、二次函数的图象与各项系数之间的关系1. 二次项系数a二次函数2y ax bx c =++中，a 作为二次项系数，显然0a ≠．⑴ 当0a >时，抛物线开口向上，a 的值越大，开口越小，反之a 的值越小，开口越大；⑵ 当0a <时，抛物线开口向下，a 的值越小，开口越小，反之a 的值越大，开口越大．总结起来，a 决定了抛物线开口的大小和方向，a 的正负决定开口方向，a 的大小决定开口的大小．2. 一次项系数b在二次项系数a 确定的前提下，b 决定了抛物线的对称轴． ⑴ 在0a >的前提下，当0b >时，02ba-<，即抛物线的对称轴在y 轴左侧； 当0b =时，02ba-=，即抛物线的对称轴就是y 轴； 当0b <时，02ba->，即抛物线对称轴在y 轴的右侧． ⑵ 在0a <的前提下，结论刚好与上述相反，即 当0b >时，02ba->，即抛物线的对称轴在y 轴右侧； 当0b =时，02ba-=，即抛物线的对称轴就是y 轴； 当0b <时，02ba-<，即抛物线对称轴在y 轴的左侧． 总结起来，在a 确定的前提下，b 决定了抛物线对称轴的位置．ab 的符号的判定：对称轴abx 2-=在y 轴左边则0>ab ，在y 轴的右侧则0<ab ，概括的说就是“左同右异” 总结： 3. 常数项c⑴ 当0c >时，抛物线与y 轴的交点在x 轴上方，即抛物线与y 轴交点的纵坐标为正；⑵ 当0c =时，抛物线与y 轴的交点为坐标原点，即抛物线与y 轴交点的纵坐标为0；⑶ 当0c <时，抛物线与y 轴的交点在x 轴下方，即抛物线与y 轴交点的纵坐标为负．总结起来，c 决定了抛物线与y 轴交点的位置．总之，只要a b c ，，都确定，那么这条抛物线就是唯一确定的． 二次函数解析式的确定：根据已知条件确定二次函数解析式，通常利用待定系数法．用待定系数法求二次函数的解析式必须根据题目的特点，选择适当的形式，才能使解题简便．一般来说，有如下几种情况：1. 已知抛物线上三点的坐标，一般选用一般式；2. 已知抛物线顶点或对称轴或最大（小）值，一般选用顶点式；3. 已知抛物线与x 轴的两个交点的横坐标，一般选用两根式；4. 已知抛物线上纵坐标相同的两点，常选用顶点式．八、二次函数图象的对称二次函数图象的对称一般有四种情况，可以用一般式或顶点式表达 1. 关于x 轴对称2y ax bx c=++关于x轴对称后，得到的解析式是2y ax bx c=---；()2y a x h k=-+关于x轴对称后，得到的解析式是()2y a x h k=---；2. 关于y轴对称2y ax bx c=++关于y轴对称后，得到的解析式是2y ax bx c=-+；()2y a x h k=-+关于y轴对称后，得到的解析式是()2y a x h k=++；3. 关于原点对称2y ax bx c=++关于原点对称后，得到的解析式是2y ax bx c=-+-；()2y a x h k=-+关于原点对称后，得到的解析式是()2y a x h k=-+-；4. 关于顶点对称（即：抛物线绕顶点旋转180°）2y ax bx c=++关于顶点对称后，得到的解析式是222by ax bx ca=--+-；()2y a x h k=-+关于顶点对称后，得到的解析式是()2y a x h k=--+．。

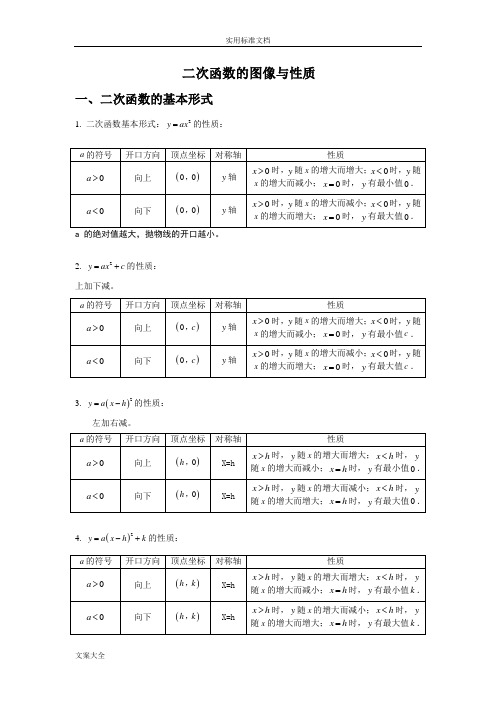
二次函数的图像与性质 一、二次函数的基本形式1. 二次函数基本形式：2y ax =的性质：2. 2y ax c =+的性质： 上加下减。

3. ()2y a x h =-的性质：左加右减。

4. ()2y a x h k =-+的性质：二、二次函数图象的平移1. 平移步骤：方法一：⑴ 将抛物线解析式转化成顶点式()2y a x h k =-+，确定其顶点坐标()h k ，； ⑵ 保持抛物线2y ax =的形状不变，将其顶点平移到()h k ，处，具体平移方法如下：【或左(h <0)】向右(h >0)【或左(h 平移|k|个单位2. 平移规律在原有函数的基础上“h 值正右移，负左移；k 值正上移，负下移”． 概括成八个字“左加右减，上加下减”． 方法二：⑴c bx ax y ++=2沿y 轴平移:向上（下）平移m 个单位，c bx ax y ++=2变成m c bx ax y +++=2（或m c bx ax y -++=2）⑵c bx ax y ++=2沿轴平移：向左（右）平移m 个单位，c bx ax y ++=2变成c m x b m x a y ++++=)()(2（或c m x b m x a y +-+-=)()(2）三、二次函数()2y a x h k =-+与2y ax bx c =++的比较从解析式上看，()2y a x h k =-+与2y ax bx c =++是两种不同的表达形式，后者通过配方可以得到前者，即22424b ac b y a x a a -⎛⎫=++ ⎪⎝⎭，其中2424b ac b h k a a -=-=，． 四、二次函数2y ax bx c =++图象的画法五点绘图法：利用配方法将二次函数2y ax bx c =++化为顶点式2()y a x h k =-+，确定其开口方向、对称轴及顶点坐标，然后在对称轴两侧，左右对称地描点画图.一般我们选取的五点为：顶点、与y 轴的交点()0c ，、以及()0c ，关于对称轴对称的点()2h c ，、与x 轴的交点()10x ，，()20x ，（若与x 轴没有交点，则取两组关于对称轴对称的点）. 画草图时应抓住以下几点：开口方向，对称轴，顶点，与x 轴的交点，与y 轴的交点.五、二次函数2y ax bx c =++的性质1. 当0a >时，抛物线开口向上，对称轴为2bx a =-，顶点坐标为2424b ac b a a ⎛⎫-- ⎪⎝⎭，．当2b x a <-时，y 随x 的增大而减小；当2b x a >-时，y 随x 的增大而增大；当2bx a=-时，y 有最小值244ac b a-．2. 当0a <时，抛物线开口向下，对称轴为2bx a =-，顶点坐标为2424b ac b a a ⎛⎫-- ⎪⎝⎭，．当2b x a <-时，y 随x 的增大而增大；当2b x a >-时，y 随x 的增大而减小；当2bx a=-时，y 有最大值244ac b a-．六、二次函数解析式的表示方法1. 一般式：2y ax bx c =++（a ，b ，c 为常数，0a ≠）；2. 顶点式：2()y a x h k =-+（a ，h ，k 为常数，0a ≠）；3. 两根式：12()()y a x x x x =--（0a ≠，1x ，2x 是抛物线与x 轴两交点的横坐标）. 注意：任何二次函数的解析式都可以化成一般式或顶点式，但并非所有的二次函数都可以写成交点式，只有抛物线与x 轴有交点，即240b ac -≥时，抛物线的解析式才可以用交点式表示．二次函数解析式的这三种形式可以互化.七、二次函数的图象与各项系数之间的关系1. 二次项系数a二次函数2y ax bx c =++中，a 作为二次项系数，显然0a ≠．⑴ 当0a >时，抛物线开口向上，a 的值越大，开口越小，反之a 的值越小，开口越大； ⑵ 当0a <时，抛物线开口向下，a 的值越小，开口越小，反之a 的值越大，开口越大．总结起来，a 决定了抛物线开口的大小和方向，a 的正负决定开口方向，a 的大小决定开口的大小． 2. 一次项系数b在二次项系数a 确定的前提下，b 决定了抛物线的对称轴． ⑴ 在0a >的前提下，当0b >时，02ba-<，即抛物线的对称轴在y 轴左侧； 当0b =时，02ba-=，即抛物线的对称轴就是y 轴； 当0b <时，02ba->，即抛物线对称轴在y 轴的右侧．⑵ 在0a <的前提下，结论刚好与上述相反，即 当0b >时，02ba->，即抛物线的对称轴在y 轴右侧； 当0b =时，02ba-=，即抛物线的对称轴就是y 轴； 当0b <时，02ba-<，即抛物线对称轴在y 轴的左侧． 总结起来，在a 确定的前提下，b 决定了抛物线对称轴的位置．ab 的符号的判定：对称轴abx 2-=在y 轴左边则0>ab ，在y 轴的右侧则0<ab ，概括的说就是“左同右异” 总结：3. 常数项c⑴ 当0c >时，抛物线与y 轴的交点在x 轴上方，即抛物线与y 轴交点的纵坐标为正； ⑵ 当0c =时，抛物线与y 轴的交点为坐标原点，即抛物线与y 轴交点的纵坐标为0； ⑶ 当0c <时，抛物线与y 轴的交点在x 轴下方，即抛物线与y 轴交点的纵坐标为负． 总结起来，c 决定了抛物线与y 轴交点的位置． 总之，只要a b c ，，都确定，那么这条抛物线就是唯一确定的．二次函数解析式的确定：根据已知条件确定二次函数解析式，通常利用待定系数法．用待定系数法求二次函数的解析式必须根据题目的特点，选择适当的形式，才能使解题简便．一般来说，有如下几种情况：1. 已知抛物线上三点的坐标，一般选用一般式；2. 已知抛物线顶点或对称轴或最大（小）值，一般选用顶点式；3. 已知抛物线与x 轴的两个交点的横坐标，一般选用两根式；4. 已知抛物线上纵坐标相同的两点，常选用顶点式．八、二次函数图象的对称二次函数图象的对称一般有五种情况，可以用一般式或顶点式表达 1. 关于x 轴对称2y ax bx c =++关于x 轴对称后，得到的解析式是2y ax bx c =---；()2y a x h k =-+关于x 轴对称后，得到的解析式是()2y a x h k =---；2. 关于y 轴对称2y ax bx c =++关于y 轴对称后，得到的解析式是2y ax bx c =-+；()2y a x h k =-+关于y 轴对称后，得到的解析式是()2y a x h k =++；3. 关于原点对称2y ax bx c =++关于原点对称后，得到的解析式是2y ax bx c =-+-； ()2y a x h k =-+关于原点对称后，得到的解析式是()2y a x h k =-+-； 4. 关于顶点对称（即：抛物线绕顶点旋转180°）2y ax bx c =++关于顶点对称后，得到的解析式是222b y ax bx c a=--+-；()2y a x h k =-+关于顶点对称后，得到的解析式是()2y a x h k =--+．5. 关于点()m n ，对称 ()2y a x h k =-+关于点()m n ，对称后，得到的解析式是()222y a x h m n k =-+-+-根据对称的性质，显然无论作何种对称变换，抛物线的形状一定不会发生变化，因此a 永远不变．求抛物线的对称抛物线的表达式时，可以依据题意或方便运算的原则，选择合适的形式，习惯上是先确定原抛物线（或表达式已知的抛物线）的顶点坐标及开口方向，再确定其对称抛物线的顶点坐标及开口方向，然后再写出其对称抛物线的表达式．二次函数图像参考：十一、2-32y=-2x 2y=3(x+4)22y=3x2y=-2(x-3)2【例题精讲】一、一元二次函数的图象的画法【例1】求作函数64212++=x x y 的图象 【解】 )128(21642122++=++=x x x x y2-4)(214]-4)[(21 2222+=+=x x【例2】求作函数342+--=x x y 的图象。

二次函数的图像与性质抛物线y=ax+bx+c与坐标轴的交点:①抛物线与y轴的交点坐标为（0，c）②抛物线与x轴的交点坐标为(x1,,0) (x2,,0),其中x1,、 x2是方程ax2+bx+c=0的两个实数根。

抛物线与x轴的交点情况：（可由对应的一元二次方程ax2+bx+c=0的根的判别式判定）①△＞0⇔抛物线与x轴有两个交点；②△＝0⇔抛物线与x轴有一个交点；③△＜0⇔抛物线与x轴没有交点。

抛物线y＝ax2＋bx＋c中a，b，c的作用：(1)a决定抛物线形状及开口方向:①若|a|相等，则形状相同。

②a＞0⇔开口向上；a＜0⇔开口向下。

③ |a|越大,开口越小.(2)a和b共同决定抛物线对称轴的位置，由于抛物线y＝ax2＋bx＋c的对称轴是直线x= -b/2a 故①若b＝0⇔对称轴为y轴；②若a与b同号⇔对称轴在y轴左侧；③若a与b异号⇔对称轴在y轴右侧。

(3)c的大小决定抛物线y＝ax2＋bx＋c与y轴交点的位置。

当x＝0时，y＝c ，∴抛物线y＝ax2＋bx＋c与y轴有且只有一个交点(0，c)。

①c＝0⇔抛物线经过原点；②c＞0⇔抛物线与y轴交于正半轴；③c＜0⇔抛物线与y轴交于负半轴。

（4）判断a＋b＋c的符号：可以看图象上的点的横坐标为1时，点的纵坐标为何值决定正负。

判断a－b＋c的符号：可以看图象上的点的横坐标为－1时，点的纵坐标为何值决定正负。

利用待定系数法求二次函数的方法：①已知抛物线过三点，设一般式y=ax2+bx+c ②已知抛物线顶点（对称轴、最值）及一点，设顶点式y=a(x-h)2+k③已知抛物线与x轴的两个交点（抛物线与x轴交点的横坐标），设两根式y=a(x-x1)( x-x2) 其中x1 、x2是抛物线与x轴交点的横坐标。

赠送以下资料《二次函数的应用》中考题集锦10题已知抛物线222(0)y x mx m m =+-≠．（1）求证：该抛物线与x 轴有两个不同的交点；（2）过点(0)P n ，作y 轴的垂线交该抛物线于点A 和点B （点A 在点P 的左边），是否存在实数m n ，，使得2AP PB =？若存在，则求出m n ，满足的条件；若不存在，请说明理由．答案：解：（1）证法1：22229224m y x mx m x m ⎛⎫=+-=+- ⎪⎝⎭，当0m ≠时，抛物线顶点的纵坐标为2904m -<， ∴顶点总在x 轴的下方．而该抛物线的开口向上，∴该抛物线与x 轴有两个不同的交点．（或者，当0m ≠时，抛物线与y 轴的交点2(02)m -，在x 轴下方，而该抛物线的开口向上，∴该抛物线与x 轴有两个不同的交点．）证法2 ：22241(2)9m m m ∆=-⨯⨯-=，当0m ≠时，290m >，∴该抛物线与x 轴有两个不同的交点．（2）存在实数m n ，，使得2AP PB =．设点B 的坐标为()t n ，，由2AP PB =知，①当点B 在点P 的右边时，0t >，点A 的坐标为(2)t n -，， 且2t t -，是关于x 的方程222x mx m n +-=的两个实数根．2224(2)940m m n m n ∴∆=---=+>，即294n m >-．且(2)t t m +-=-（I ），2(2)t t m n -=--（II ）由（I ）得，t m =，即0m >．将t m =代入（II ）得，0n =．∴当0m >且0n =时，有2AP PB =．②当点B 在点P 的左边时，0t <，点A 的坐标为(2)t n ，， 且2t t ，是关于x 的方程222x mx m n +-=的两个实数根．2224(2)940m m n m n ∴∆=---=+>，即 294n m >-．且2t t m +=-（I ），222t t m n =--（II ）由（I ）得，3mt =-，即0m >． 将3m t =-代入（II ）得，2209n m =-且满足294n m >-．∴当0m >且2209n m =-时，有2AP PB =t （秒）间的关系式为210S t t =+，若滑到坡底第11题一人乘雪橇沿如图所示的斜坡笔直滑下，滑下的距离S （米）与时间的时间为2秒，则此人下滑的高度为（ ） Ａ．24米 Ｂ．12米Ｃ．Ｄ．6米答案：Ｂ第12题我市英山县某茶厂种植“春蕊牌”绿茶，由历年来市场销售行情知道，从每年的3月25日起的180天内，绿茶市场销售单价y （元）与上市时间t （天）的关系可以近似地用如图（1）中的一条折线表示．绿茶的种植除了与气候、种植技术有关外，其种植的成本单价z （元）与上市时间t （天）的关系可以近似地用如图（2）的抛物线表示．（2）求出图（2）中表示的种植成本单价z （元）与上市时间t （天）（0t >）的函数关系式； （3）认定市场销售单价减去种植成本单价为纯收益单价，问何时上市的绿茶纯收益单价最大？ （说明：市场销售单价和种植成本单价的单位：元／500克．）答案：解：（1）依题意，可建立的函数关系式为：2160(0120)380(120150)220(150180)5t t y t t t ⎧-+<<⎪⎪=<⎨⎪⎪+⎩，，． ≤ ≤≤ （2）由题目已知条件可设2(110)20z a t =-+．)图(1)图(2)天)图象过点85(60)3，，2851(60110)203300a a ∴=-+∴=．． 21(110)20300z t ∴=-+ (0)t >． （3）设纯收益单价为W 元，则W =销售单价-成本单价．故22221160(110)20(0120)3300180(110)20(120150)3002120(110)20(150180)5300t t t W t t t t t ⎧-+---<<⎪⎪⎪=---<⎨⎪⎪+---⎪⎩，，． ≤ ≤≤ 化简得2221(10)100(0120)3001(110)60(120150)3001(170)56(150180)300t t W t t t t ⎧--+<<⎪⎪⎪=-+<⎨⎪⎪--+⎪⎩，，． ≤ ≤≤①当21(10)100(0120)300W t t =--+<<时，有10t =时，W 最大，最大值为100； ②当21(110)60(120150)300W t t =--+<≤时，由图象知，有120t =时，W 最大，最大值为2593； ③当21(170)56(150180)300W t t =--+≤≤时，有170t =时，W 最大，最大值为56． 综上所述，在10t =时，纯收益单价有最大值，最大值为100元．第13题如图，足球场上守门员在O 处开出一高球，球从离地面1米的A 处飞出（A 在y 轴上），运动员乙在距O 点6米的B 处发现球在自己头的正上方达到最高点M ，距地面约4米高，球落地后又一次弹起．据实验，足球在草坪上弹起后的抛物线与原来的抛物线形状相同，最大高度减少到原来最大高度的一半．（1）求足球开始飞出到第一次落地时，该抛物线的表达式． （2）足球第一次落地点C距守门员多少米？（取7=）（3）运动员乙要抢到第二个落点D，他应再向前跑多少米？（取5=）答案：解：（1）（3分）如图，设第一次落地时， 抛物线的表达式为2(6)4y a x =-+． 由已知：当0x =时1y =． 即1136412a a =+∴=-，． ∴表达式为21(6)412y x =--+．（或21112y x x =-++） （2）（3分）令210(6)4012y x =--+=，．212(6)4861360x x x ∴-===-<．≈，（舍去）． ∴足球第一次落地距守门员约13米．（3）（4分）解法一：如图，第二次足球弹出后的距离为CD根据题意：CD EF =（即相当于将抛物线AEMFC 向下平移了2个单位）212(6)412x ∴=--+解得1266x x =-=+1210CD x x ∴=-=． 1361017BD ∴=-+=（米）． 解法二：令21(6)4012x --+=．解得16x =-，2613x =+．∴点C 坐标为（13，0）．设抛物线CND 为21()212y x k =--+．将C 点坐标代入得：21(13)2012k --+=．解得：11313k =-<（舍去），2667518k =+++=．21(18)212y x =--+ 令210(18)212y x ==--+，0．118x =-，21823x =+． 23617BD ∴=-=（米）．解法三：由解法二知，18k =， 所以2(1813)10CD =-=， 所以(136)1017BD =-+=． 答：他应再向前跑17米．第14题荆州市“建设社会主义新农村”工作组到某县大棚蔬菜生产基地指导菜农修建大棚种植蔬菜．通过调查得知：平均修建每公顷大棚要用支架、农膜等材料费2.7万元；购置滴灌设备，这项费用（万元）与大棚面积（公顷）的平方成正比，比例系数为0.9；另外每公顷种植蔬菜需种子、化肥、农药等开支0.3万元．每公顷蔬菜年均可卖7.5万元． （1）基地的菜农共修建大棚x （公顷），当年收益（扣除修建和种植成本后）为y （万元），写出y 关于x 的函数关系式． （2）若某菜农期望通过种植大棚蔬菜当年获得5万元收益，工作组应建议他修建多少公项大棚．（用分数表示即可）（3）除种子、化肥、农药投资只能当年受益外，其它设施3年内不需增加投资仍可继续使用．如果按3年计算，是否修建大棚面积越大收益越大？修建面积为多少时可以得到最大收益？请帮工作组为基地修建大棚提一项合理化建议．答案：（1）()227.5 2.70.90.30.9 4.5y x x x x x x =-++=-+． （2）当20.9 4.55x x -+=时，即2945500x x -+=，153x =，2103x =从投入、占地与当年收益三方面权衡，应建议修建53公顷大棚． （3）设3年内每年的平均收益为Z （万元）()()2227.50.90.30.30.3 6.30.310.533.075Z x x x x x x x =-++=-+=--+（10分）不是面积越大收益越大．当大棚面积为10.5公顷时可以得到最大收益．建议：①在大棚面积不超过10.5公顷时，可以扩大修建面积，这样会增加收益． ②大棚面积超过10.5公顷时，扩大面积会使收益下降．修建面积不宜盲目扩大．③当20.3 6.30x x -+=时，10x =，221x =．大棚面积超过21公顷时，不但不能收益，反而会亏本．（说其中一条即可）第15题一家用电器开发公司研制出一种新型电子产品，每件的生产成本为18元，按定价40元出售，每月可销售20万件．为了增加销量，公司决定采取降价的办法，经市场调研，每降价1元，月销售量可增加2万件．（1）求出月销售量y （万件）与销售单价x （元）之间的函数关系式（不必写x 的取值范围）； （2）求出月销售利润z （万元）（利润＝售价－成本价）与销售单价x （元）之间的函数关系式（不必写x 的取值范围）； （3）请你通过（2）中的函数关系式及其大致图象帮助公司确定产品的销售单价范围，使月销售利润不低于480万元．答案：略．第16题一座隧道的截面由抛物线和长方形构成，长方形的长为8m ，宽为2m ，隧道最高点P 位于AB 的中央且距地面6m ，建立如图所示的坐标系（1）求抛物线的解析式；（2）一辆货车高4m ，宽2m ，能否从该隧道内通过，为什么？（3）如果隧道内设双行道，那么这辆货车是否可以顺利通过，为什么？答案：（1）由题意可知抛物线经过点()()()024682A P B ，，，，，设抛物线的方程为2y ax bx c =++ 将A P D ，，三点的坐标代入抛物线方程． 解得抛物线方程为21224y x x =-++ （2）令4y =，则有212244x x -++=解得1244x x =+=-212x x -=>∴货车可以通过．（3）由（2）可知21122x x -=>∴货车可以通过．第17题如图，在矩形ABCD 中，2AB AD =，线段10EF =．在EF 上取一点M ，分别以EM MF ，为一边作矩形EMNH 、矩形MFGN ，使矩形MFGN ∽矩形ABCD ．令M N x =，当x 为何值时，矩形EMNH 的面积S 有最大值？最大值是多少？答案：解：矩形MFGN ∽矩形ABCD ，MN MFAD AB∴=． 2AB AD MN x ==，，2MF x ∴=．102EM EF MF x ∴=-=-． (102)S x x ∴=-2210x x =-+ 2525222x ⎛⎫=--+ ⎪⎝⎭．∴当52x =时，S 有最大值为252．B A D MF第18题某企业信息部进行市场调研发现：信息一：如果单独投资A 种产品，则所获利润A y （万元）与投资金额x （万元）之间存在正比例函数关系：A y kx =，并且当投资5万元时，可获利润2万元．信息二：如果单独投资B 种产品，则所获利润B y （万元）与投资金额x （万元）之间存在二次函数关系：2B y ax bx =+，并且当投资2万元时，可获利润2.4万元；当投资4万元时，可获利润3.2万元．（1）请分别求出上述的正比例函数表达式与二次函数表达式； （2）如果企业同时对A B ，两种产品共投资10万元，请你设计一个能获得最大利润的投资方案，并求出按此方案能获得的最大利润是多少？答案：解：（1）当5x =时，12250.4y k k ===，，， 0.4A y x ∴=，当2x =时， 2.4B y =；当4x =时， 3.2B y =．2.4423.2164a ba b=+⎧∴⎨=+⎩ 解得0.21.6a b =-⎧⎨=⎩∴20.2 1.6B y x x =-+．（2）设投资B 种商品x 万元，则投资A 种商品(10)x -万元，获得利润W 万元，根据题意可得220.2 1.60.4(10)0.2 1.24W x x x x x =-++-=-++ 20.2(3) 5.8W x ∴=--+当投资B 种商品3万元时，可以获得最大利润5.8万元，所以投资A 种商品7万元，B 种商品3万元，这样投资可以获得最大利润5.8万元．第19题如图所示，图（1）是一座抛物线型拱桥在建造过程中装模时的设计示意图，拱高为30m ，支柱3350m A B =，5根支柱1122334455A B A B A B A B A B ，，，，之间的距离均为15m ，1515B B A A ∥，将抛物线放在图（2）所示的直角坐标系中． （1）直接写出图（2）中点135B B B ，，的坐标； （2）求图（2）中抛物线的函数表达式； （3）求图（1）中支柱2244A B A B ，的长度．答案：（1）1(30)B -，0，3(030)B ，，5(300)B ，； （2）设抛物线的表达式为(30)(30)y a x x =-+，把3(030)B ，代入得(030)(030)30y a =-+=． 130a =-∴． ∵所求抛物线的表达式为：1(30)(30)30y x x =--+． （3）4B ∵点的横坐标为15， 4B ∴的纵坐标4145(1530)(1530)302y =--+=．B 图(1)图(2)l3350A B =∵，拱高为30，∴立柱44458520(m)22A B =+=． 由对称性知：224485(m)2A B A B ==。

二次函数的图象和性质知识点总结一、知识点回顾1. 二次函数解析式的几种形式：①一般式：（a 、b 、c 为常数，a ≠0） ②顶点式：（a 、h 、k 为常数，a ≠0），其中（h ，k ）为顶点坐标。

③交点式：，其中是抛物线与x 轴交点的横坐标，即一元二次方程的两个根，且a ≠0，（也叫两根式）。

2. 二次函数的图象 ①二次函数的图象是对称轴平行于（包括重合）y 轴的抛物线，几个不同的二次函数，如果a 相同，那么抛物线的开口方向，开口大小（即形状）完全相同，只是位置不同。

②任意抛物线可以由抛物线经过适当的平移得到，移动规律可简记为：[左加右减，上加下减]，具体平移方法如下表所示。

③在画的图象时，可以先配方成的形式，然后将的图象上（下）左（右）平移得到所求图象，即平移法；也可用描点法：也是将配成的形式，这样可以确定开口方向，对称轴及顶点坐标。

然后取图象与y 轴的交点（0，c ），及此点关于对称轴对称的点（2h ，c ）；如果图象与x 轴有两个交点，就直接取这两个点（x 1，0），y ax bx c =++2y a x h k =-+()2y a x x x x =--()()12x x 12，ax bx c 20++=y ax bx c =++2y ax bx c =++2y a x h k =-+()2y ax =2y ax bx c =++2y a x h k =-+()2y ax =2y ax bx c =++2y a x h k =-+()2（x 2，0）就行了；如果图象与x 轴只有一个交点或无交点，那应该在对称轴两侧取对称点，（这两点不是与y 轴交点及其对称点），一般画图象找5个点。

a ＞0 a ＜0 a ＞0 a ＜0(1)抛物线开口向上，(1)抛物线开口向下，(1)抛物线开口(1)抛物线开4. 求抛物线的顶点、对称轴和最值的方法①配方法：将解析式化为的形式，顶点坐标为y ax bx c =++2y a x h k =-+()2（h ，k ），对称轴为直线，若a ＞0，y 有最小值，当x ＝h 时，；若a ＜0，y 有最大值，当x ＝h 时，。

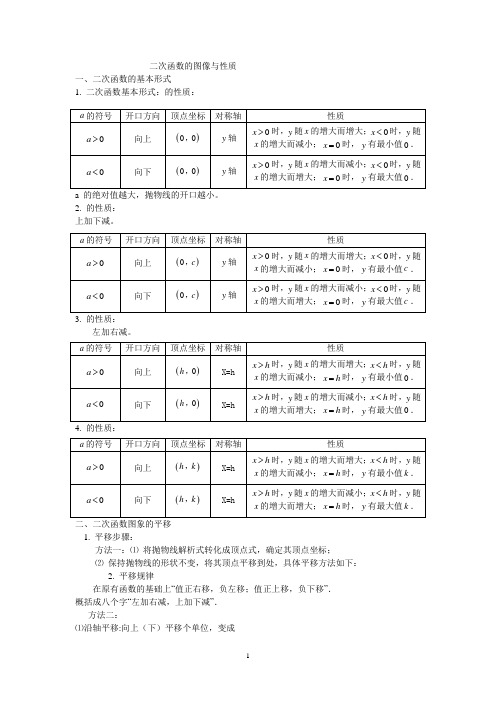
二次函数的图像与性质一、二次函数的基本形式1. 二次函数基本形式：的性质：a 的绝对值越大，抛物线的开口越小。

2. 的性质：上加下减。

3. 的性质：左加右减。

二、二次函数图象的平移1. 平移步骤：方法一：⑴将抛物线解析式转化成顶点式，确定其顶点坐标；⑵保持抛物线的形状不变，将其顶点平移到处，具体平移方法如下：2. 平移规律在原有函数的基础上“值正右移，负左移；值正上移，负下移”．概括成八个字“左加右减，上加下减”．方法二：⑴沿轴平移:向上（下）平移个单位，变成（或）⑵沿轴平移：向左（右）平移个单位，变成（或）三、二次函数与的比较从解析式上看，与是两种不同的表达形式，后者通过配方可以得到前者，即，其中．四、二次函数图象的画法五点绘图法：利用配方法将二次函数化为顶点式，确定其开口方向、对称轴及顶点坐标，然后在对称轴两侧，左右对称地描点画图.一般我们选取的五点为：顶点、与轴的交点、以及关于对称轴对称的点、与轴的交点，（若与轴没有交点，则取两组关于对称轴对称的点）.画草图时应抓住以下几点：开口方向，对称轴，顶点，与轴的交点，与轴的交点.五、二次函数的性质1. 当时，抛物线开口向上，对称轴为，顶点坐标为．当时，随的增大而减小；当时，随的增大而增大；当时，有最小值．2. 当时，抛物线开口向下，对称轴为，顶点坐标为．当时，随的增大而增大；当时，随的增大而减小；当时，有最大值．六、二次函数解析式的表示方法1. 一般式：（，，为常数，）；2. 顶点式：（，，为常数，）；3. 两根式：（，，是抛物线与轴两交点的横坐标）.注意：任何二次函数的解析式都可以化成一般式或顶点式，但并非所有的二次函数都可以写成交点式，只有抛物线与轴有交点，即时，抛物线的解析式才可以用交点式表示．二次函数解析式的这三种形式可以互化.七、二次函数的图象与各项系数之间的关系1. 二次项系数二次函数中，作为二次项系数，显然．⑴当时，抛物线开口向上，的值越大，开口越小，反之的值越小，开口越大；⑵当时，抛物线开口向下，的值越小，开口越小，反之的值越大，开口越大．总结起来，决定了抛物线开口的大小和方向，的正负决定开口方向，的大小决定开口的大小．2. 一次项系数在二次项系数确定的前提下，决定了抛物线的对称轴．⑴在的前提下，当时，，即抛物线的对称轴在轴左侧；当时，，即抛物线的对称轴就是轴；当时，，即抛物线对称轴在轴的右侧．⑵在的前提下，结论刚好与上述相反，即当时，，即抛物线的对称轴在轴右侧；当时，，即抛物线的对称轴就是轴；当时，，即抛物线对称轴在轴的左侧．总结起来，在确定的前提下，决定了抛物线对称轴的位置．的符号的判定：对称轴在轴左边则，在轴的右侧则，概括的说就是“左同右异”总结： 3. 常数项⑴当时，抛物线与轴的交点在轴上方，即抛物线与轴交点的纵坐标为正；⑵当时，抛物线与轴的交点为坐标原点，即抛物线与轴交点的纵坐标为；⑶当时，抛物线与轴的交点在轴下方，即抛物线与轴交点的纵坐标为负．总结起来，决定了抛物线与轴交点的位置．总之，只要都确定，那么这条抛物线就是唯一确定的．二次函数解析式的确定：根据已知条件确定二次函数解析式，通常利用待定系数法．用待定系数法求二次函数的解析式必须根据题目的特点，选择适当的形式，才能使解题简便．一般来说，有如下几种情况：1. 已知抛物线上三点的坐标，一般选用一般式；2. 已知抛物线顶点或对称轴或最大（小）值，一般选用顶点式；3. 已知抛物线与轴的两个交点的横坐标，一般选用两根式；4. 已知抛物线上纵坐标相同的两点，常选用顶点式．八、二次函数图象的对称二次函数图象的对称一般有四种情况，可以用一般式或顶点式表达1. 关于轴对称关于轴对称后，得到的解析式是；关于轴对称后，得到的解析式是；2. 关于轴对称关于轴对称后，得到的解析式是；关于轴对称后，得到的解析式是；3. 关于原点对称关于原点对称后，得到的解析式是；关于原点对称后，得到的解析式是；4. 关于顶点对称（即：抛物线绕顶点旋转180°）关于顶点对称后，得到的解析式是；关于顶点对称后，得到的解析式是．。

二次函数的图像和性质总结二次函数（Quadratic Function）是高中数学中重要的一个部分，是指一种形式为y=ax²+bx+c（a≠0）的函数。

二次函数的图像是一条抛物线，其性质包括：开口方向、顶点、对称轴、最值、零点、增减性等。

下面将对二次函数的图像和性质进行详细总结。

一、图像特征：1.开口方向：-当a>0时，抛物线开口向上；-当a<0时，抛物线开口向下。

2.顶点：-对于抛物线开口向上的情况，顶点是抛物线的最低点；-对于抛物线开口向下的情况，顶点是抛物线的最高点。

3.对称轴（y轴）：- 对于一般的二次函数y=ax²+bx+c，其对称轴的方程为x=-b/2a；-对于抛物线开口向上的情况，对称轴是抛物线的最低点；-对于抛物线开口向下的情况，对称轴是抛物线的最高点。

4.最值：-对于抛物线开口向上的情况，最小值为顶点的纵坐标；-对于抛物线开口向下的情况，最大值为顶点的纵坐标。

5.零点：- 零点是指二次函数y=ax²+bx+c与x轴的交点；-二次函数可能有0个、1个或2个零点；- 当判别式D=b²-4ac>0时，有两个不相等的实数根；- 当判别式D=b²-4ac=0时，有两个相等的实数根；- 当判别式D=b²-4ac<0时，无实数根。

6.增减性：-当a>0时，抛物线开口向上，函数在对称轴两侧递增；-当a<0时，抛物线开口向下，函数在对称轴两侧递减。

二、性质总结：1.函数的解析式：- 二次函数的解析式一般形式为y=ax²+bx+c，其中a、b、c为常数，a≠0；-通过解析式可以得到函数的图像特征。

2.零点：-零点是指函数与x轴的交点；- 零点可以通过解二次方程ax²+bx+c=0来求解；- 当判别式D=b²-4ac>0时，有两个不相等的实数根；- 当判别式D=b²-4ac=0时，有两个相等的实数根；- 当判别式D=b²-4ac<0时，无实数根。

二次函数的图像和性质一、二次函数的一般形式二次函数是一种形式为f(x)=ax2+bx+c的函数，其中a、b、c是实数且a eq0。

二、二次函数的图像1.抛物线二次函数的图像是一条抛物线。

当a>0时，抛物线开口朝上；当a<0时，抛物线开口朝下。

2.判别法利用二次函数的判别式 $\\Delta = b^2 - 4ac$ 的正负性可以确定二次函数的图像开口方向和与x轴的交点情况。

3.最值点二次函数的顶点为抛物线的最值点，当a>0时，最小值在顶点处取得；当a<0时，最大值在顶点处取得。

顶点的横坐标为 $-\\frac{b}{2a}$，纵坐标为 $f\\left(-\\frac{b}{2a}\\right)$。

三、二次函数的性质1.对称轴二次函数的对称轴为直线 $x = -\\frac{b}{2a}$，即抛物线关于对称轴对称。

2.单调性当a>0时，二次函数在对称轴左侧递增，在对称轴右侧递减；当a<0时，二次函数在对称轴左侧递减，在对称轴右侧递增。

3.零点二次函数的零点为方程f(x)=0的解，可以利用求根公式 $x = \\frac{-b \\pm \\sqrt{b^2 - 4ac}}{2a}$ 求得。

4.图像的平移如f(x)=a(x−ℎ)2+k，其中(ℎ,k)为平移后的顶点坐标，抛物线上下平移，方向与a的正负有关。

四、应用二次函数在几何、物理、经济等领域有着广泛的应用。

例如几何问题中的抛物线轨迹、物体自由落体运动方程、经济学中的成本、收益关系等均可用二次函数描述。

结语二次函数作为高中数学中重要的函数类型，在图像和性质上有着独特的表现，通过对其图像和性质的深入理解，可以更好地应用于解决实际问题。

希望本文的介绍能帮助读者更好地掌握二次函数的知识。

二次函数的图象和性质知识点总结一、知识点回顾1. 二次函数解析式的几种形式：①一般式：（a 、b 、c 为常数，a ≠0） ②顶点式：（a 、h 、k 为常数，a ≠0），其中（h ，k ）为顶点坐标。

③交点式：，其中是抛物线与x 轴交点的横坐标，即一元二次方程的两个根，且a ≠0，（也叫两根式）。

2. 二次函数的图象 ①二次函数的图象是对称轴平行于（包括重合）y 轴的抛物线，几个不同的二次函数，如果a 相同，那么抛物线的开口方向，开口大小（即形状）完全相同，只是位置不同。

②任意抛物线可以由抛物线经过适当的平移得到，移动规律可简记为：[左加右减，上加下减]，具体平移方法如下表所示。

③在画的图象时，可以先配方成的形式，然后将的图象上（下）左（右）平移得到所求图象，即平移法；也可用描点法：也是将配成的形式，这样可以确定开口方向，对称轴及顶点坐标。

然后取图象与y 轴的交点（0，c ），及此点关于对称轴对称的点（2h ，c ）；如果图象与x 轴有两个交点，就直接取这两个点（x 1，0），y ax bx c =++2y a x h k =-+()2y a x x x x =--()()12x x 12，ax bx c 20++=y ax bx c =++2y ax bx c =++2y a x h k =-+()2y ax =2y ax bx c =++2y a x h k =-+()2y ax =2y ax bx c =++2y a x h k =-+()2（x 2，0）就行了；如果图象与x 轴只有一个交点或无交点，那应该在对称轴两侧取对称点，（这两点不是与y 轴交点及其对称点），一般画图象找5个点。

a ＞0 a ＜0 a ＞0 a ＜0(1)抛物线开口向上，(1)抛物线开口向下，(1)抛物线开口(1)抛物线开4. 求抛物线的顶点、对称轴和最值的方法①配方法：将解析式化为的形式，顶点坐标为y ax bx c =++2y a x h k =-+()2（h ，k ），对称轴为直线，若a ＞0，y 有最小值，当x ＝h 时，；若a ＜0，y 有最大值，当x ＝h 时，。

适用标准文档二次函数的图像与性质一、二次函数的基本形式1.二次函数基本形式： y ax 2的性质：a 的符号张口方向极点坐标 对称轴性质0，0 x 0时，y 随x 的增大而增大；x0时，y 随向上y 轴x0时，y 有最小值0．x 的增大而减小；a0，0 x 0时，y 随x 的增大而减小；x 0时，y 随向下 y 轴x0时，y 有最大值0．x 的增大而增大；的绝对值越大，抛物线的张口越小。

yax 2c 的性质：上加下减。

a 的符号 张口方向 极点坐标 对称轴 性质a0，c x 0时，y 随x 的增大而增大；x0时，y 随向上y 轴x0时，y 有最小值c ．x 的增大而减小；a 00，c x 0时，y 随x 的增大而减小；x 0时，y 随向下y 轴x0时，y 有最大值c ．x 的增大而增大；3.yax 2h 的性质：左加右减。

a 的符号 张口方向 极点坐标 对称轴 性质a 0 向上 h ，0 X=h x h 时，y 随x 的增大而增大； xh 时，y随x 的增大而减小； x h 时，y 有最小值0．a 0 向下 h ，0 X=h x h 时，y 随x 的增大而减小； xh 时，y随x 的增大而增大； x h 时，y 有最大值0．4.yax 2hk 的性质：a 的符号 张口方向 极点坐标 对称轴性质a0h，k xh时，y随x的增大而增大；xh时，y向上X=hx h时，y有最小值k．随x的增大而减小；a0h，k xh时，y随x的增大而减小；xh时，y向下X=hx h时，y有最大值k．随x的增大而增大；文案大全适用标准文档二、二次函数图象的平移1.平移步骤：方法一：⑴将抛物线分析式转变为极点式yaxh 2h ，k ；k ，确立其极点坐标 ⑵保持抛物线yax 2的形状不变，将其极点平移到h ，k 处，详细平移方法以下：向上(k>0)【或向下(k<0)】平移|k|个单位y=ax2y=ax 2+k向右(h>0)【或左(h<0)】向右(h>0)【或左(h<0)】 向右(h>0) 【或左(h<0) 】平移|k|个单位平移|k|个单位平移|k|个单位向上(k>0)【或下(k<0)】平移|k|个单位y=a(x-h)2向上(k>0)【或下(k<0)】平移|k|个单位y=a(x-h)2+k平移规律在原有函数的基础上 “h 值正右移，负左移； k 值正上移，负下移 ”．归纳成八个字“左加右减，上加下减” ．方法二：⑴y ax 2 bx c 沿y 轴平移:向上（下）平移 m 个单位，y ax 2 bx c 变为yax 2 bx c m （或y ax 2 bx cm ）⑵y ax 2 bx c 沿轴平移：向左（右）平移m 个单位，yax 2 bx c 变为ya(x m)2 b(x m) c （或y a(x m)2 b(x m) c ）三、二次函数yax h 2k 与y2bx c 的比较ax从分析式上看， y a x 2k 与y ax 2 bxc 是两种不一样的表达形式，后者经过配hb 24ac b 2b，k4ac b 2方能够获得前者，即y a x，此中h ．2a4a2a4a四、二次函数yax 2 bx c 图象的画法五点绘图法：利用配方法将二次函数 y ax 2 bx c 化为极点式y a(x h)2k ，确立其张口方向、对称轴及极点坐标，而后在对称轴双侧，左右对称地描点绘图.一般我们选用的五点为：极点、与 y 轴的交点0，c 、以及 0，c 对于对称轴对称的点 2h ，c 、与x 轴的交点x 1，0 ，x 2，0（若与x 轴没有交点，则取两组对于对称轴对称的点）.画草图时应抓住以下几点：张口方向，对称轴，极点，与 x 轴的交点，与y 轴的交点.文案大全五、二次函数yax2bxc的性质1.当a0时，抛物线张口向上，对称轴为x b，极点坐标为b，4ac b2．2a2a4a当x b时，y随x的增大而减小；当x b时，y随x的增大而增大；当x b 2a2a2a 2时，y有最小值4acb．4a2.当a0时，抛物线张口向下，对称轴为x b，极点坐标为b，4ac b2．当2a2a4ax b时，y随x的增大而增大；当xb时，y随x的增大而减小；当x b时，y 2a2a2a 2有最大值4ac b．4a六、二次函数分析式的表示方法1.一般式：y ax2bxc（a，b，c为常数，a0）；2.极点式：y a(x h)2k（a，h，k为常数，a0）；3.两根式：y a(x x1)(x x2)（a0，x1，x2是抛物线与x轴两交点的横坐标）.注意：任何二次函数的分析式都能够化成一般式或极点式，但并不是全部的二次函数都能够写成交点式，只有抛物线与x轴有交点，即b24ac0时，抛物线的分析式才能够用交点式表示．二次函数分析式的这三种形式能够互化.七、二次函数的图象与各项系数之间的关系二次项系数a二次函数2yaxbxc中，a作为二次项系数，明显a0．⑴当a0时，抛物线张口向上，a的值越大，张口越小，反之a的值越小，张口越大；⑵当a0时，抛物线张口向下，a的值越小，张口越小，反之a的值越大，张口越大．总结起来，a决定了抛物线张口的大小和方向，a的正负决定张口方向，a的大小决定张口的大小．一次项系数b在二次项系数a确立的前提下，b决定了抛物线的对称轴．⑴在a0的前提下，当b0时，b0，即抛物线的对称轴在y轴左边；2a当b0时，b0，即抛物线的对称轴就是y轴；2a当b0时，b0，即抛物线对称轴在y轴的右边．2a文案大全⑵在a0的前提下，结论恰好与上述相反，即当b0时，b0，即抛物线的对称轴在y轴右边；2a当b0时，b0，即抛物线的对称轴就是y轴；2a当b0时，b0，即抛物线对称轴在y轴的左边．2a总结起来，在a确立的前提下，b决定了抛物线对称轴的地点．ab的符号的判断：对称轴xb0，在y轴左边则ab0，在y轴的右边则ab2a归纳的说就是“左同右异”总结：常数项c⑴当c0时，抛物线与y轴的交点在x轴上方，即抛物线与y轴交点的纵坐标为正；⑵当c0时，抛物线与y轴的交点为坐标原点，即抛物线与y轴交点的纵坐标为0；⑶当c0时，抛物线与y轴的交点在x轴下方，即抛物线与y轴交点的纵坐标为负．总结起来，c决定了抛物线与y轴交点的地点．总之，只需a，b，c都确立，那么这条抛物线就是独一确立的．二次函数分析式确实定：依据已知条件确立二次函数分析式，往常利用待定系数法．用待定系数法求二次函数的分析式一定依据题目的特色，选择适合的形式，才能使解题简易．一般来说，有以下几种状况：已知抛物线上三点的坐标，一般采用一般式；已知抛物线极点或对称轴或最大（小）值，一般采用极点式；已知抛物线与x轴的两个交点的横坐标，一般采用两根式；已知抛物线上纵坐标同样的两点，常采用极点式．八、二次函数图象的对称二次函数图象的对称一般有五种状况，能够用一般式或极点式表达对于x轴对称y ax2bx c对于x轴对称后，获得的分析式是y ax2bx c；y a x h 2yax h2 k对于x轴对称后，获得的分析式是k；对于y轴对称y ax2bx c对于y轴对称后，获得的分析式是y ax2bx c；y a x h 2y ax h2 k对于y轴对称后，获得的分析式是k；文案大全适用标准文档对于原点对称y ax2bx c对于原点对称后，获得的分析式是y ax2bx c；y ax h 2y a x h2k；k对于原点对称后，获得的分析式是4.对于极点对称（即：抛物线绕极点旋转180°）y ax2bx c对于极点对称后，获得的分析式是y ax2bx c b2；2ay ax h 2y a x h2k．k对于极点对称后，获得的分析式是5.对于点m，n对称y ax h 2y a x h22nk k对于点m，n对称后，获得的分析式是2m依据对称的性质，明显不论作何种对称变换，抛物线的形状必定不会发生变化，所以a永久不变．求抛物线的对称抛物线的表达式时，能够依照题意或方便运算的原则，选择适合的形式，习惯上是先确立原抛物线（或表达式已知的抛物线）的极点坐标及张口方向，再确定其对称抛物线的极点坐标及张口方向，而后再写出其对称抛物线的表达式．二次函数图像参照：y=2x 2y=3(x+4)2y=3x2y=3(x-2)2y=x2y=2x2y=2(x-4)2x2十y=2y=2(x-4)2-3一、y=2x2+2y=2x2y=2x2-4x2y=-2y=-x2y=-2(x+3)2y=-2x2y=-2(x-3)2y=-2x2文案大全适用标准文档【例题精讲】一、一元二次函数的图象的画法【例1】求作函数y1x24x6的图象1x221(x2【解】y4x68x12)22 1[(x24)2-4]1(x24)2-222以x4为中间值，取x的一些值，列表以下：x-7-6-5-4-3-2-1y 53-2352222【例2】求作函数y x24x3的图象。

二次函数的图象和性质知识点总结一、知识点回顾1. 二次函数解析式的几种形式：①一般式：（a 、b 、c 为常数，a ≠0） ②顶点式：（a 、h 、k 为常数，a ≠0），其中（h ，k ）为顶点坐标。

③交点式：，其中是抛物线与x 轴交点的横坐标，即一元二次方程的两个根，且a ≠0，（也叫两根式）。

2. 二次函数的图象 ①二次函数的图象是对称轴平行于（包括重合）y 轴的抛物线，几个不同的二次函数，如果a 相同，那么抛物线的开口方向，开口大小（即形状）完全相同，只是位置不同。

②任意抛物线可以由抛物线经过适当的平移得到，移动规律可简记为：[左加右减，上加下减]，具体平移方法如下表所示。

③在画的图象时，可以先配方成的形式，然后将的图象上（下）左（右）平移得到所求图象，即平移法；也可用描点法：也是将配成的形式，这样可以确定开口方向，对称轴及顶点坐标。

然后取图象与y 轴的交点（0，c ），及此点关于对称轴对称的点（2h ，c ）；如果图象与x 轴有两个交点，就直接取这两个点（x 1，0），y ax bx c =++2y a x h k =-+()2y a x x x x =--()()12x x 12，ax bx c 20++=y ax bx c =++2y ax bx c =++2y a x h k =-+()2y ax =2y ax bx c =++2y a x h k =-+()2y ax =2y ax bx c =++2y a x h k =-+()2（x 2，0）就行了；如果图象与x 轴只有一个交点或无交点，那应该在对称轴两侧取对称点，（这两点不是与y 轴交点及其对称点），一般画图象找5个点。

a ＞0 a ＜0 a ＞0 a ＜0(1)抛物线开口向上，(1)抛物线开口向下，(1)抛物线开口(1)抛物线开4. 求抛物线的顶点、对称轴和最值的方法①配方法：将解析式化为的形式，顶点坐标为y ax bx c =++2y a x h k =-+()2（h ，k ），对称轴为直线，若a ＞0，y 有最小值，当x ＝h 时，；若a ＜0，y 有最大值，当x ＝h 时，。