2014年高考数学理科分类汇编专题06 数列

1. 【2014高考北京版理第5题】设{}n a 是公比为q 的等比数列，则“1>q ”是“{}n a 为递增数列”的（ ）A ．充分而不必要条件B ．必要而不充分条件C ．充分必要条件D ．既不充分也不必要条件2. 【2014高考福建卷第3题】等差数列{}n a 的前n 项和n S ，若132,12a S ==，则6a =( ).8A .10B .12C .14D3. 【2014高考江苏卷第7题】在各项均为正数的等比数列{}n a 中，若21a =，8642a a a =+，则6a 的值是 .4. 【2014辽宁高考理第8题】设等差数列{}n a 的公差为d ，若数列1{2}n a a 为递减数列，则（ ） A ．0d < B ．0d > C ．10a d < D ．10a d >5. 【2014重庆高考理第2题】对任意等比数列{}n a ,下列说法一定正确的是( )139.,,A a a a 成等比数列 236.,,B a a a 成等比数列248.,,C a a a 成等比数列 369.,,D a a a 成等比数列6. 【2014天津高考理第11题】设{}n a 是首项为1a ，公差为1-的等差数列，n S 为其前n 项和．若124,,S S S 成等比数列，则1a 的值为__________．7. 【2014大纲高考理第10题】等比数列{}n a 中，452,5a a ==，则数列{lg }n a 的前8项和等于 （ ）A ．6B ．5C ．4D ．3【答案】C ．8. 【2014高考广东卷理第13题】若等比数列{}n a 的各项均为正数，且512911102e a a a a =+，则1220ln ln ln a a a +++= .9. 【2014高考安徽卷理第12题】数列{}n a 是等差数列，若1351,3,5a a a +++构成公比为q 的等比数列，则q =________.10. 【2014高考北京版理第12题】若等差数列{}n a 满足7897100,0a a a a a ++>+<，则当n = 时，{}n a 的前n 项和最大.【答案】8。

第六章 数列第1讲 数列的概念与简单表示法对应学生用书P84考点梳理1．数列的通项公式(1)定义：如果数列{a n }的第n 项a n 与项数n 之间的函数关系可以用一个公式来表示，那么这个公式就叫做数列的通项公式，记为a n ＝f (n )(n ∈N *)．数列可以用通项公式来描述，也可以通过列表或图象来表示．(2)数列的递推公式：如果已知数列的第一项(或前几项)，且从第二项(或某一项)开始的任一项a n 与它的前一项a n －1(或前几项)间的关系可以用一个公式来表示，那么这个公式就叫做这个数列的递推公式．递推公式也是给出数列的一种方法． 2．数列的分类n n已知S n ，则a n ＝⎩⎨⎧ S 1，n ＝1，S n －S n －1，n ≥2.在数列{a n }中，若a n 最大，则⎩⎨⎧a n ≥a n －1，a n ≥a n ＋1.若a n 最小，则⎩⎨⎧a n ≤a n －1，a n ≤a n ＋1.【助学·微博】 一个考情分析数列的通项公式及前n 项和是高考考查的重点及热点，常以填空的形式考查数列的通项公式．而前n 项和S n 与通项a n 相结合的题目，往往以解答题形式出现．题型比较全面，难度以中档题为主，重点考查学生的运算能力及抽象概括能力．由递推式求通项a n 的三种方法 (1)a n ＋1－a n ＝f (n )型，采用叠加法； (2)a n ＋1a n＝f (n )型，采用叠乘法；(3)a n ＋1＝pa n ＋q (p ≠0,1，q ≠0)型，采用待定系数法转化为等比数列解决．考点自测1．(教材改编题)已知数列{a n }的前4项为1,3,7,15，写出数列{a n }的一个通项公式为________．解析 1,3,7,15分别都加上一个1，则为2,4,8,16， ∴通项公式不难发现为a n ＝2n －1. 答案 a n ＝2n －12．下列对数列的理解有四种：①数列可以看成一个定义在N *(或它的有限子集{1,2,3，…，n })上的函数； ②数列的项数是有限的；③数列若用图象表示，从图象上看都是一群孤立的点； ④数列的通项公式是唯一的． 其中说法正确的所有序号是________．解析 由数列与函数的关系知①对，③对，由数列的分类知②不对，数列的通项公式不是唯一的，④不对． 答案 ①③3．在数列{a n }中，a 1＝1，a 2＝5，a n ＋2＝a n ＋1－a n (n ∈N *)，则a 100＝________. 解析 法一 由a 1＝1，a 2＝5，a n ＋2＝a n ＋1－a n (n ∈N *)可得该数列为1,5,4，－1，－5，－4,1,5,4，…. 由此可得a 100＝－1.法二 a n ＋2＝a n ＋1－a n ，a n ＋3＝a n ＋2－a n ＋1，两式相加可得a n ＋3＝－a n ，a n ＋6＝a n ，∴a 100＝a 16×6＋4＝a 4＝－1. 答案 －14．(2012·无锡二模)设a >0，若a n ＝⎩⎨⎧(3－a )n －3(n ≤7)，a n －6 (n >7)，且数列{a n }是递增数列，则实数a 的范围是________．解析由{a n }是递增数列，得⎩⎨⎧3－a >0，a >1，a 8>a 7，即⎩⎨⎧1<a <3，a 2>(3－a )×7－3，解得2<a <3. 答案 (2,3)5．(2012·苏锡常镇四市调研(一))设u (n )表示正整数n 的个位数，a n ＝u (n 2)－u (n )，则数列{a n }的前2 012项和等于________．解析 因为n 与n ＋10的个位数字相同且周期为10，又a 1＝0，a 2＝4－2＝2，a 3＝9－3＝6，a 4＝6－4＝2，a 5＝5－5＝0，a 6＝6－6＝0，a 7＝9－7＝2，a 8＝4－8＝－4，a 9＝1－9＝－8，a 10＝0，所以a 1＋a 2＋…＋a 10＝0，即a 1＋a 2＋…＋a 2 012＝a 1＋a 2＝2. 答案 2对应学生用书P85考向一 由数列的前几项求数列的通项【例1】 写出下面各数列的一个通项公式： (1)3,5,7,9，…；(2)12，34，78，1516，3132，…； (3)－1，32，－13，34，－15，36，…； (4)3,33,333,3 333，….解 (1)各项减去1后为正偶数，所以a n ＝2n ＋1.(2)每一项的分子比分母少1，而分母组成数列21,22,23，24，…，所以a n ＝2n －12n .(3)奇数项为负，偶数项为正，故通项公式中含因子(－1)n ；各项绝对值的分母组成数列1,2,3,4，…；而各项绝对值的分子组成的数列中，奇数项为1，偶数项为3，即奇数项为2－1，偶数项为2＋1，所以a n ＝(－1)n ·2＋(－1)nn .也可写为a n ＝⎩⎪⎨⎪⎧－1n ，n 为正奇数，3n ，n 为正偶数.(4)将数列各项改写为：93，993，9993，9 9993，…，分母都是3，而分子分别是10－1,102－1,103－1，104－1，…，所以a n ＝13(10n－1)．[方法总结] 根据数列的前几项求通项公式时，需仔细观察分析，抓住以下几方面的特征：(1)分式中分子、分母的特征；(2)相邻项的变化特征；(3)拆项后的特征，把数列的项分成变化的部分和不变的部分；(4)各项符号特征，若关系不明显时，应将部分项作适当的变形，统一成相同的形式，让规律凸现出来． 【训练1】 已知数列{a n }的前四项分别为1,0,1,0，给出下列各式：①a n ＝1－(－1)n 2；②a n ＝1＋(－1)n 2；③a n ＝sin 2n π2；④a n ＝1－cos n π2；⑤a n ＝⎩⎨⎧1(n 为正偶数)0(n 为正奇数)；⑥a n ＝1＋(－1)n ＋12＋(n －1)(n －2)．其中可以作为数列{a n }的通项公式的有________(填序号)． 答案 ①③④考向二 数列的单调性【例2】 (2012·四川卷)已知数列{a n }的前n 项和为S n ，且a 2a n ＝S 2＋S n 对一切正整数n 都成立． (1)求a 1，a 2的值； (2)设a 1>0，数列⎩⎨⎧⎭⎬⎫lg 10a 1a n 的前n 项和为T n .当n 为何值时，T n 最大？并求出T n的最大值．解 (1)取n ＝1，得a 2a 1＝S 2＋S 1＝2a 1＋a 2，①取n ＝2，得a 22＝2a 1＋2a 2，②由②－①，得a 2(a 2－a 1)＝a 2.③ 若a 2＝0，由①知a 1＝0. 若a 2≠0，由③知a 2－a 1＝1.④ 由①④解得，a 1＝2＋1，a 2＝2＋2； 或a 1＝1－2，a 2＝2－ 2.综上可得，a 1＝0，a 2＝0；或a 1＝2＋1，a 2＝2＋2；或a 1＝1－2，a 2＝2－ 2.(2)当a 1>0时，由(1)知a 1＝2＋1，a 2＝2＋2.当n ≥2时，有(2＋2)a n ＝S 2＋S n ，(2＋2)a n －1＝S 2＋S n －1， ∴(1＋2)a n ＝(2＋2)a n －1，即a n ＝2a n －1(n ≥2)， ∴a n ＝a 1(2)n －1＝(2＋1)·(2)n －1.令b n ＝lg 10a 1a n，则b n ＝1－lg(2)n －1＝1－12(n －1)lg 2＝12lg 1002n －1.∴数列{b n }是单调递减的等差数列(公差为－12lg 2)，从而b 1>b 2>…>b 7＝lg 108>lg 1＝0，当n ≥8时，b n ≤b 8＝12lg 100128<12lg 1＝0， 故n ＝7时，T n 取得最大值，且T n 的最大值为 T 7＝7(b 1＋b 7)2＝7(1＋1－3lg 2)2＝7－212lg 2.[方法总结] (1)本题主要考查等比数列、等差数列、对数等基础知识，考查思维能力、运算能力、分析问题与解决问题的能力，并考查方程、分类与整合、化归与转化等数学思想．(2)计算时一定要细心．若a n 计算错误，则b n 就不能判定为等差数列，从而无法求和．【训练2】 已知数列{a n }的前n 项和S n ＝2n 2＋2n ，数列{b n }的前n 项和T n ＝2－b n .(1)求数列{a n }与{b n }的通项公式；(2)设c n ＝a 2n ·b n ，证明：当且仅当n ≥3时，c n ＋1<c n . 解 (1)由于a 1＝S 1＝4，当n ≥2时，a n ＝S n －S n －1＝(2n 2＋2n )－[2(n －1)2＋2(n －1)]＝4n ，显然a 1符合上式，所以a n ＝4n (n ∈N *)．由b 1＝2－b 1，得b 1＝1，当n ≥2时，b n ＝T n －T n －1＝b n －1－b n ，所以2b n ＝b n －1，所以数列{b n }为等比数列，其首项为1，公比为12.所以b n ＝⎝ ⎛⎭⎪⎫12n －1.(2)由(1)，知c n ＝a 2n ·b n ＝16n 2·⎝ ⎛⎭⎪⎫12n －1， 法一 由c n ＋1－c n ＝16(n ＋1)2·⎝ ⎛⎭⎪⎫12n －16n 2·⎝ ⎛⎭⎪⎫12n －1 ＝16·⎝ ⎛⎭⎪⎫12n [(n ＋1)2－2n 2]＝16·⎝ ⎛⎭⎪⎫12n[－(n －1)2＋2]， 当n ≥3时，c n ＋1－c n <0，从而c n ＋1<c n .法二 因c n ＋1c n ＝16(n ＋1)2·⎝ ⎛⎭⎪⎫12(n ＋1)－116n 2·⎝ ⎛⎭⎪⎫12n －1＝(n ＋1)22n 2，若c n ＋1c n <1，即(n ＋1)22n 2<1，所以n >1＋2，即n ≥3时，c n ＋1c n <1恒成立．又c n >0，因此当且仅当n ≥3时，c n ＋1<c n .考向三 由a n 与S n 的关系求通项a n【例3】 已知下面数列{a n }的前n 项和S n ，求{a n }的通项公式： (1)S n ＝2n 2－3n ；(2)S n ＝3n ＋b .审题视点 当n ＝1时，由a 1＝S 1，求a 1；当n ≥2时，由a n ＝S n －S n －1消去S n ，得a n ＋1与a n 的关系．转化成由递推关系求通项．解 (1)a 1＝S 1＝2－3＝－1， 当n ≥2时，a n ＝S n －S n －1＝(2n 2－3n )－[2(n －1)2－3(n －1)]＝4n －5，由于a 1也适合此等式，∴a n ＝4n －5.(2)a 1＝S 1＝3＋b ，当n ≥2时，a n ＝S n －S n －1 ＝(3n ＋b )－(3n －1＋b )＝2·3n －1.当b ＝－1时，a 1适合此等式． 当b ≠－1时，a 1不适合此等式． ∴当b ＝－1时，a n ＝2·3n －1； 当b ≠－1时，a n ＝⎩⎨⎧3＋b ，n ＝1，2·3n －1，n ≥2.[方法总结] 数列的通项a n 与前n 项和S n 的关系是a n ＝⎩⎨⎧S 1，n ＝1，S n －S n －1，n ≥2.当n＝1时，a 1若适合S n －S n －1，则n ＝1的情况可并入n ≥2时的通项a n ；当n ＝1时，a 1若不适合S n －S n －1，则用分段函数的形式表示．【训练3】 (1)(2012·南通一模)已知数列{a n }的前n 项和为S n ，且S n ＝2n －a n ，则数列{a n }的通项公式为________．(2)已知数列{a n }的前n 项和S n ＋a n ＝2－⎝ ⎛⎭⎪⎫12n －1(n 为正整数)．则数列{a n }的通项公式为________．解析 (1)当n ＝1时，由a 1＝S 1＝2－a 1，得a 1＝1；当n ≥2时，由a n ＝S n －S n－1＝(2n －a n )－[2(n －1)－a n －1]＝2－a n ＋a n －1，即a n ＝12a n －1＋1，设a n ＋m ＝12(a n －1＋m )，∴a n ＝12a n －1－12m ，∴m ＝－2，∴数列{a n －2}构成首项为－1，公比为12的等比数列，∴a n －2＝－1·⎝ ⎛⎭⎪⎫12n －1，∴a n ＝2－⎝ ⎛⎭⎪⎫12n －1.(2)由S n ＋a n ＝2－⎝ ⎛⎭⎪⎫12n －1，得S n ＋1＋a n ＋1＝2－⎝ ⎛⎭⎪⎫12n，两式相减，得a n ＋1－a n ＋a n ＋1＝⎝ ⎛⎭⎪⎫12n ，即a n ＋1＝12a n ＋⎝ ⎛⎭⎪⎫12n ＋1，因为S n ＋a n ＝2－⎝ ⎛⎭⎪⎫12n －1，令n ＝1，得a 1＝12.在a n ＋1＝12a n ＋⎝ ⎛⎭⎪⎫12n ＋1中，两端同除以⎝ ⎛⎭⎪⎫12n ＋1，得2n ＋1a n ＋1＝2n a n ＋1，即数列{2n a n }是首项为1，公差为1的等差数列，故2n a n ＝n ，所以a n ＝n2n . 答案 (1)2－⎝ ⎛⎭⎪⎫12n －1 (2)n 2n考向四 已知数列的递推公式求通项【例4】 根据下列条件，确定数列{a n }的通项公式： (1)a 1＝1，a n ＋1＝3a n ＋2； (2)a 1＝1，a n ＝n －1n a n －1(n ≥2)；(3)已知数列{a n }满足a n ＋1＝a n ＋3n ＋2，且a 1＝2，求a n . 解 (1)∵a n ＋1＝3a n ＋2，∴a n ＋1＋1＝3(a n ＋1)， ∴a n ＋1＋1a n ＋1＝3，∴数列{a n ＋1}为等比数列，公比q ＝3， 又a 1＋1＝2，∴a n ＋1＝2·3n －1，∴a n ＝2·3n －1－1.(2)∵a n ＝n －1n a n －1(n ≥2)，∴a n －1＝n －2n －1a n －2，…，a 2＝12a 1.以上(n －1)个式子相乘得a n ＝a 1·12·23·…·n －1n ＝a 1n ＝1n .(3)∵a n ＋1－a n ＝3n ＋2，∴a n －a n －1＝3n －1(n ≥2)，∴a n ＝(a n －a n －1)＋(a n －1－a n －2)＋…＋(a 2－a 1)＋a 1＝n (3n ＋1)2(n ≥2)．当n ＝1时，a 1＝12×(3×1＋1)＝2，符合公式，∴a n ＝32n 2＋n2.[方法总结] 已知数列的递推关系，求数列的通项时，通常用累加、累乘、构造法求解．当出现a n ＝a n －1＋m 时，构造等差数列；当出现a n ＝xa n －1＋y 时，构造等比数列；当出现a n ＝a n －1＋f (n )时，用累加法求解；当出现a na n －1＝f (n )时，用累乘法求解．【训练4】 根据下列各个数列{a n }的首项和基本关系式，求其通项公式． (1)a 1＝1，a n ＝a n －1＋3n －1(n ≥2)； (2)a 1＝2，a n ＋1＝a n ＋ln ⎝ ⎛⎭⎪⎫1＋1n .解 (1)∵a n ＝a n －1＋3n －1(n ≥2)，∴a n －1＝a n －2＋3n －2， a n －2＝a n －3＋3n －3， …a 2＝a 1＋31，以上(n －1)个式子相加得 a n ＝a 1＋31＋32＋…＋3n －1＝1＋3＋32＋…＋3n －1＝3n －12.(2)∵a n ＋1＝a n ＋ln ⎝ ⎛⎭⎪⎫1＋1n ，∴a n ＋1－a n ＝ln ⎝ ⎛⎭⎪⎫1＋1n ＝ln n ＋1n ， ∴a n －a n －1＝ln nn －1，a n －1－a n －2＝ln n －1n －2，…a 2－a 1＝ln 21，∴a n －a 1＝ln n n －1＋ln n －1n －2＋…＋ln 21＝ln n ．又a 1＝2，∴a n ＝ln n ＋2.对应学生用书P86热点突破16 数列中最值问题的求解策略从近几年高考可以看出，对求数列中的最大项是高考的重点．解决这类问题时，要利用函数的单调性研究数列的最值，但要注意数列的单调性与函数的单调性有所不同，其自变量的取值是不连续的，只能取正整数，所以在求数列中的最大(小)项时，应注意数列中的项可以是相同的，故不应漏掉项．【示例1】 (2011·浙江卷)若数列⎩⎨⎧⎭⎬⎫n (n ＋4)⎝ ⎛⎭⎪⎫23n 中的最大项是第k 项，则k ＝________.[审题与转化] 第一步：原问题可利用⎩⎨⎧a k ≥a k ＋1，a k ≥a k －1求最大项．[规范解答] 第二步：由题意知⎩⎪⎨⎪⎧k (k ＋4)⎝ ⎛⎭⎪⎫23k ≥(k －1)(k －1＋4)⎝ ⎛⎭⎪⎫23k－1，k (k ＋4)⎝ ⎛⎭⎪⎫23k ≥(k ＋1)(k ＋1＋4)⎝ ⎛⎭⎪⎫23k ＋1，∴⎩⎨⎧(k －1)2≤10，k 2≥10.∵k ∈N *，∴k ＝4，故填4. [反思与回顾] 第三步：若求数列{a n }的最大项，则可解不等式组⎩⎨⎧a n ≥a n ＋1a n ≥a n －1；若求数列{a n }的最小项，则可解不等式组⎩⎨⎧a n ≤a n ＋1a n ≤a n －1，求出n 的取值范围之后，再确定取得最值的项．【示例2】 (2010·辽宁卷)已知数列{a n }满足a 1＝33，a n ＋1－a n ＝2n ，则a nn 的最小值为________．[审题与转化] 第一步：先利用累加法求a n 的表达式． 第二步：利用基本不等式求a nn 的最小值．[规范解答] 第三步：用累加法求得a n ＝n 2－n ＋33，所以a n n ＝n ＋33n －1≥233－1，当且仅当n ＝33n ，即n ＝33时取等号，但n ∈N *，所以n 取6，∴a nn ＝n ＋33n －1的最小值为10.5.[反思与回顾] 第四步：数列中用基本不等式时，一定注意n ∈N *，本题还可以用“对号函数”性质或示例1的方法求解．高考经典题组训练1．(2010·陕西卷改编)对于数列{a n }，“a n ＋1>|a n |(n ＝1，2，…)”是“{a n }为递增数列”的________条件．解析 由a n ＋1>|a n |(n ＝1,2，…)得数列{a n }为递增数列，反之不成立． 答案 充分不必要2．(2011·江西卷改编)已知数列{a n }的前n 项和S n 满足S n ＋S m ＝S n ＋m ，且a 1＝1，那么a 10＝________.解析 由S n ＋S m ＝S n ＋m ，得S 1＋S 9＝S 10；所以a 10＝S 10－S 9＝S 1＝a 1＝1. 答案 13．(2012·福建卷改编)若数列{a n }的通项公式a n ＝n cos n π2，前n 项和为S n ，则S 2 012＝________.解析 因为a n ＝n cos n π2，当n ＝2k －1(k ∈N *)时，a n ＝0；当n ＝4k －2(k ∈N *)时，a n ＝－n ；当n ＝4k (k ∈N *)时，a n ＝n ，所以a 1＋a 2＋a 3＋a 4＝2，a 5＋a 6＋a 7＋a 8＝2，…，即数列{a n }连续4项之和均为2，所以S 2 012＝S 4×503＝503×2＝1 006. 答案 1 0064．(2009·湖北卷)已知数列{a n }满足a 1＝m (m 为正整数)，a n ＋1＝⎩⎪⎨⎪⎧a n 2，当a n 为偶数时，3a n ＋1，当a n 为奇数时，若a 6＝1，则m 所有可能的取值为________．解析 若a n 为偶数，则a n ＝2a n ＋1；若a n 为奇数，则a n ＝a n ＋1－13.因为a 6＝1，反推得a 5＝2(a 5＝0舍去)，a 4＝4⎝ ⎛⎭⎪⎫a 4＝13舍去.若a 3为偶数，则a 3＝2a 4＝8，a 2＝16⎝ ⎛⎭⎪⎫a 2＝73舍去.所以a 1＝2a 2＝32或a 1＝a 2－13＝5.若a 3为奇数，则a 3＝a 4－13＝1，a 2＝2，a 1＝4. 综上，得m ＝4,5,32. 答案 4,5,32对应学生用书P299分层训练A 级 基础达标演练(时间：30分钟 满分：60分)一、填空题(每小题5分，共30分)1．已知数列，1，3，5，7，…，2n －1，…，则35是它的第________项． 解析 35＝45＝2×23－1. 答案 232．(2013·福州一模)把1,3,6,10,15,21这些数叫做三角形数，这是因为这些数目的点子可以排成一个正三角形(如图所示)．则第七个三角形数是________．解析 观察三角形数的增长规律，可以发现每一项比它的前一项多的点数正好是本身的序号，所以根据这个规律计算即可．根据三角形数的增长规律可知第七个三角形数是1＋2＋3＋4＋5＋6＋7＝28. 答案 283．(2011·四川卷改编)数列{a n }的前n 项和为S n ，若a 1＝1，a n ＋1＝3S n (n ≥1)，则a 6＝________.解析 a 1＝1，a 2＝3S 1＝3，a 3＝3S 2＝12＝3×41，a 4＝3S 3＝48＝3×42，a 5＝3S 4＝3×43，a 6＝3S 5＝3×44. 答案 3×444．(2012·南京调研)已知正数数列{a n }对任意p ，q ∈N *，都有a p ＋q ＝a p ·a q ，若a 2＝4，则a 9＝________.解析 由条件，可有a 1＝2，a 2＝4，a 4＝16，a 8＝256，a 9＝512. 答案 5125．在数列{a n }中，a 1＝2，a n ＋1＝a n ＋n ＋1，则通项a n ＝________. 解析 由a n ＋1－a n ＝n ＋1，可得a n －a n －1＝n ， a n －1－a n －2＝n －1，a n －2－a n －3＝n －2， …a 3－a 2＝3，a 2－a 1＝2，以上n －1个式子左右两边分别相加得， a n －a 1＝2＋3＋…＋n ，∴a n ＝1＋(1＋2＋3＋…＋n )＝n (n ＋1)2＋1. 答案n (n ＋1)2＋16．已知数列{a n }的前n 项和S n ＝n 2－9n ，第k 项满足5＜a k ＜8，则k 的值为________．解析 ∵S n ＝n 2－9n ，∴n ≥2时，a n ＝S n －S n －1＝2n －10， a 1＝S 1＝－8适合上式，∴a n ＝2n －10(n ∈N *)， ∴5＜2k －10＜8，得7.5＜k ＜9.∴k ＝8. 答案 8二、解答题(每小题15分，共30分)7．已知各项均为正数的数列{a n }的前n 项和满足S n ＞1，且6S n ＝(a n ＋1)(a n ＋2)，n ∈N *.求{a n }的通项公式． 解 由a 1＝S 1＝16(a 1＋1)(a 1＋2)，解得a 1＝1或a 1＝2，由已知a 1＝S 1＞1，因此a 1＝2. 又由a n ＋1＝S n ＋1－S n＝16(a n ＋1＋1)(a n ＋1＋2)－16(a n ＋1)(a n ＋2)， 得a n ＋1－a n －3＝0或a n ＋1＝－a n .因a n ＞0，故a n ＋1＝－a n 不成立，舍去． 因此a n ＋1－a n －3＝0.即a n ＋1－a n ＝3，从而{a n }是公差为3，首项为2的等差数列， 故{a n }的通项为a n ＝3n －1.8．在数列{a n }中，已知a 1＝1，a n ＋1＝a n ＋2n －1，求a n . 解 由a n ＋1＝a n ＋2n －1，得a n ＋1－a n ＝2n －1. 所以a 2－a 1＝1， a 3－a 2＝2， a 4－a 3＝22， a 5－a 4＝23， …a n －a n －1＝2n －2(n ≥2)，将以上各式左右两端分别相加，得a n －a 1＝1＋2＋22＋…＋2n －2＝2n －1－1，所以a n ＝2n －1(n ≥2)，又因为a 1＝1适合上式，故a n ＝2n －1(n ∈N *)．分层训练B 级 创新能力提升1．数列{a n }的通项公式是a n ＝n 2＋kn ＋2，若对所有的n ∈N *，都有a n ＋1＞a n 成立，则实数k 的取值范围是________．解析 a n ＋1＞a n ，即(n ＋1)2＋k (n ＋1)＋2＞n 2＋kn ＋2，则k ＞－(2n ＋1)对所有的n ∈N *都成立，而当n ＝1时，－(2n ＋1)取得最大值－3，所以k ＞－3. 答案 (－3，＋∞)2．(2012·合肥三检)在数列{a n }中，a 1＝12，a n ＋1＝1－1a n(n ≥2)，则a 16＝________.解析 由题可知a 2＝1－1a 1＝－1，a 3＝1－1a 2＝2，a 4＝1－1a 3＝12，∴此数列是以3为周期的周期数列，a 16＝a 3×5＋1＝a 1＝12. 答案 123．已知{a n }的前n 项和为S n ，且满足log 2(S n ＋1)＝n ＋1，则a n ＝________. 解析 由已知条件可得S n ＋1＝2n ＋1.∴S n ＝2n ＋1－1， 当n ＝1时，a 1＝S 1＝3，当n ≥2时，a n ＝S n －S n －1＝2n ＋1－1－2n ＋1＝2n ， n ＝1时不适合a n ，∴a n ＝⎩⎨⎧3 (n ＝1)，2n (n ≥2).答案 ⎩⎨⎧3 (n ＝1)2n (n ≥2)4．(2012·南通调研三)已知5×5数字方阵⎣⎢⎢⎡⎦⎥⎥⎤a 11 a 12 a 13 a 14 a 15a 21 a 22 a 23 a 24 a 25a 31a 32 a 33 a 34 a 35a 41a 42 a 43 a 44 a 45a51 a 52 a 53 a 54 a 55中，a ij＝⎩⎨⎧ 1，j 是i 的整数倍，－1，j 不是i 的整数倍， 则∑j ＝25a 3j ＋∑i ＝24a i 4＝________.解析 由条件可知a 32＝－1，a 33＝1，a 34＝－1，a 35＝－1，a 24＝1，a 34＝－1，a 44＝1，从而原式＝－1. 答案 －15．(2012·无锡一中期中)设数列{b n }满足：b 1＝12，b n ＋1＝b 2n ＋b n ， (1)求证：1b n ＋1＝1b n －1b n ＋1；(2)若T n ＝1b 1＋1＋1b 2＋1＋…＋1b n ＋1，对任意的正整数n,3T n －log 2m －5>0恒成立．求m 的取值范围．解 (1)∵b 1＝12，b n ＋1＝b 2n ＋b n ＝b n (b n ＋1)， ∴对任意的n ∈N *，b n >0. ∴1b n ＋1＝1b n (b n ＋1)＝1b n －1b n ＋1，即1b n ＋1＝1b n －1b n ＋1.(2)T n ＝⎝ ⎛⎭⎪⎫1b 1－1b 2＋⎝ ⎛⎭⎪⎫1b 2－1b 3＋…＋⎝ ⎛⎭⎪⎫1b n －1b n ＋1＝1b 1－1b n ＋1＝2－1b n ＋1.∵b n ＋1－b n ＝b 2n >0，∴b n ＋1>b n ，∴数列{b n }是单调递增数列．∴数列{T n }关于n 递增．∴T n ≥T 1.∵b 1＝12，∴b 2＝b 1(b 1＋1)＝34.∴T 1＝2－1b 2＝23.∴T n ≥23.∵3T n －log 2m －5>0恒成立． ∴log 2m <－3，∴0<m <18.6．已知数列{a n }的前n 项和S n ＝(n ＋1)a n2，且a 1＝1. (1)求数列{a n }的通项公式a n ；(2)令b n ＝ln a n ，是否存在k (k ≥2，且k ∈N *)，使得b k ，b k ＋1，b k ＋2成等比数列．若存在，求出所有符合条件的k 值；若不存在，请说明理由．解 (1)法一 当n ≥2时，a n ＝S n －S n －1＝(n ＋1)a n 2－na n －12，即a n n ＝a n －1n －1(n ≥2)．所以⎩⎨⎧⎭⎬⎫a n n 是首项为a 11＝1的常数数列，所以a nn ＝1，即a n ＝n (n ∈N *)．法二 同上，得(n －1)a n ＝na n －1.同理得 na n ＋1＝(n ＋1)a n ，所以2na n ＝n (a n －1＋a n ＋1)，即2a n ＝a n －1＋a n ＋1，所以{a n }成等差数列．又由a 1＝1，得a 2＝S 2－a 1，得a 2＝2，得a n ＝1＋(n －1)＝n (n ∈N *)． 法三 同上，得a n a n －1＝nn －1(n ≥2)，所以a n ＝a n a n －1·a n －1a n －2·a n －2a n －3·…·a 3a 2·a 2a 1·a 1＝n n －1·n －1n －2·…·32·21·1＝n ，当n ＝1时a 1＝1，也满足a n ＝n ，所以a n ＝n (n ∈N *)．(2)假设存在k (k ≥2，k ∈N *)，使得b k ，b k ＋1，b k ＋2成等比数列，则b k b k ＋2＝b 2k ＋1.因为b n ＝ln a n ＝ln n ，所以b k b k ＋2＝ln k ·ln(k ＋2)＜⎣⎢⎡⎦⎥⎤ln k ＋ln (k ＋2)22＝⎣⎢⎡⎦⎥⎤ln (k 2＋2k )22＜⎣⎢⎡⎦⎥⎤ln (k ＋1)222＝[ln(k ＋1)]2＝b 2k ＋1，这与b k b k ＋2＝b 2k ＋1矛盾．故不存在k (k ≥2，k ∈N *)，使得b k ，b k ＋1，b k ＋2成等比数列.第2讲 等差数列及其前n 项和对应学生用书P87考点梳理1．等差数列的定义及通项公式(1)等差数列：一般地，如果一个数列从第二项起，每一项与前一项的差等于同一个常数，那么这个数列就叫做等差数列，这个常数就叫做等差数列的公差(公差常用字母“d ”表示)．即a n －a n －1＝d (n ≥2，n ∈N )．(2)等差中项：如果三个数a ，A ，b 成等差数列，则A 叫做a 与b 的等差中项，其中A ＝a ＋b 2.(3)等差数列的通项公式：若等差数列的首项为a 1，公差为d ，则通项公式为a n ＝a 1＋(n －1)d ；若已知第m 项a m 和公差d ，通项a n 还可写成a n ＝a m ＋(n －m )d .(4)等差数列的公差公式：d ＝a n －a 1n －1或d ＝a n －a mn －m. 2．等差数列的性质(1)若数列{a n }是等差数列，则a n －a m ＝(n －m )d (n 、m ∈N *)．(2)数列{a n }是等差数列，若m ＋n ＝p ＋q (m ，n ，p ，q ∈N *)，则a m ＋a n ＝a p ＋a q .特别地，若m ＋n ＝2p ，则a m ＋a n ＝2a p .(3)在有穷等差数列{a n }中，与首、末两项距离相等的任意两项之和与首、末两项之和相等，如a 1＋a n ＝a 2＋a n －1.(4)若{a n }，{b n }均是等差数列，S n 是{a n }的前n 项和，则{ma n ＋kb n }、⎩⎨⎧⎭⎬⎫S n n 仍为等差数列，其中m ，k 为常数．(5)等差数列中依次k 项的和成等差数列，即S k ，S 2k －S k ， S 3k －S 2k ，…成等差数列，公差为k 2d . (6)项数为偶数2n 的等差数列{a n }，有S 2n ＝n (a 1＋a 2n )＝n (a 2＋a 2n －1)＝…＝n (a n ＋a n ＋1)(a n 与a n ＋1为中间的两项)，S 偶－S 奇＝nd ，S 奇S 偶＝a na n ＋1. (7)项数为奇数2n －1的等差数列{a n }，有 S 2n －1＝(2n －1)a n (a n 为中间项)，S 奇－S 偶＝a n ，S 奇S 偶＝nn －1.3．等差数列的前n 项和(1)公式：若已知首项a 1和末项a n ，则S n ＝n (a 1＋a n )2，或等差数列{a n }的首项是a 1，公差是d ，则其前n 项和公式为S n ＝na 1＋n (n －1)2d .(2)等差数列的前n 项和公式与函数的关系：S n ＝d 2n 2＋⎝ ⎛⎭⎪⎫a 1－d 2n ，数列{a n }是等差数列的充要条件是S n ＝An 2＋Bn (A ，B 为常数)．(3)最值问题：在等差数列{a n }中，a 1＞0，d ＜0，则S n 存在最大值，若a 1＜0，d ＞0，则S n 存在最小值． 【助学·微博】 一个命题解读等差数列是高考考查的重点内容，主要考查等差数列的通项公式，前n 项和公式，等差数列的性质等相关内容．对等差数列的定义，性质及等差中项的考查，以填空为主，难度较小．通项公式与前n 项和相结合的题目，多出现在解答题中，难度中等．对这部分内容的考查仍会坚持小题考性质、大题考灵活运用知识分析问题、解决问题的能力． 等差数列的判断方法(1)定义法：对于n ≥2的任意自然数，验证a n －a n －1为同一常数； (2)等差中项法：验证2a n －1＝a n ＋a n －2(n ≥3，n ∈N *)都成立； (3)通项公式法：验证a n ＝pn ＋q ； (4)前n 项和公式法：验证S n ＝An 2＋Bn .注 后两种方法只能用来判断是否为等差数列，而不能用来证明等差数列．考点自测1．设S n 是等差数列{a n }的前n 项和，已知a 2＝3，a 6＝11，则S 7＝________. 解析 ∵a 1＋a 7＝a 2＋a 6＝3＋11＝14， ∴S 7＝7(a 1＋a 7)2＝49. 答案 492．在等差数列{a n }中，a 3＝7，a 5＝a 2＋6，则a 6＝________. 解析 设公差为d .则a 5－a 2＝3d ＝6， ∴a 6＝a 3＋3d ＝7＋6＝13. 答案 133．已知等差数列的公差d ＜0，前n 项和记为S n ，满足S 20＞0，S 21＜0，则当n ＝________时，S n 达到最大值．解析 ∵S 20＝10(a 1＋a 20)＝10(a 10＋a 11)＞0， S 21＝21a 11＜0，∴a 10＞0，a 11＜0， ∴n ＝10时，S n 最大． 答案 104．(2012·南通第一学期期末考试)已知数列{a n }的前n 项和为S n ＝－2n 2＋3n ，则数列{a n }的通项公式为________．解析 当n ＝1时，a 1＝S 1＝1；当n ≥2时，a n ＝S n －S n －1＝－2n 2＋3n －[－2(n －1)2＋3(n －1)]＝5－4n .显然a 1符合a n ，所以a n ＝5－4n (n ∈N *)． 答案 5－4n5．(2012·南京二模)设S n 是等差数列{a n }的前n 项和．若S 3S 7＝13，则S 6S 7＝________.解析 由S 3＝3a 2，S 7＝7a 4，S 3S 7＝13，得9a 2＝7a 4＝7(a 2＋2d )，即a 2＝7d ，所以a 3＝8d ，a 4＝9d ，从而S 6＝3(a 3＋a 4)＝51d ，S 7＝7a 4＝63d ，所以S 6S 7＝1721.答案 1721对应学生用书P88考向一 等差数列基本量的计算【例1】 (2012·苏锡常镇四市调研)在数列{a n }中，a 1＝1，a 2＝2.数列{b n }满足b n ＝a n ＋1＋(－1)n a n ，n ∈N *.(1)若数列{a n }是等差数列，求数列{b n }的前6项和S 6； (2)若数列{b n }是公差为2的等差数列，求数列{a n }的通项公式． 解 (1)因为a 1＝1，a 2＝2，数列{a n }是等差数列，所以a n ＝n .所以b 1＝b 3＝b 5＝1，b 2＝5，b 4＝9，b 6＝13. 所以S 6＝b 1＋b 2＋…＋b 6＝30.(2)因为b 1＝a 2－a 1＝2－1＝1，数列{b n }是公差为2的等差数列，所以b n ＝2n －1.因为b 2n －1＝a 2n －a 2n －1＝4n －3，b 2n ＝a 2n ＋1＋a 2n ＝4n －1， 所以a 2n ＋1＋a 2n －1＝2.故a 2n ＋3＋a 2n ＋1＝2. 所以a 2n ＋3＝a 2n －1.又a 1＝1，所以a 3＝1.故a 4n －3＝a 1＝1，a 4n －1＝a 3＝1. 所以a 2n －1＝1.则a 2n ＝4n －2. 所以a n ＝⎩⎨⎧1，n 为奇数，2n －2，n 为偶数.[方法总结] 等差数列的通项公式及前n 项和公式中，共涉及五个量，知三可求二，如果已知两个条件，就可以列出方程组解之．如果利用等差数列的性质去考虑也可以．体现了用方程解决问题的思想．【训练1】 (2011·福建)在等差数列{a n }中，a 1＝1，a 3＝－3. (1)求数列{a n }的通项公式；(2)若数列{a n }的前k 项和S k ＝－35，求k 的值． 解 (1)设等差数列{a n }的公差为d ，则a n ＝a 1＋(n －1)d . 由a 1＝1，a 3＝－3可得1＋2d ＝－3.解得d ＝－2. 从而，a n ＝1＋(n －1)×(－2)＝3－2n . (2)由(1)可知a n ＝3－2n . 所以S n ＝n [1＋(3－2n )]2＝2n －n 2.进而由S k ＝－35可得2k －k 2＝－35. 即k 2－2k －35＝0，解得k ＝7或k ＝－5. 又k ∈N *，故k ＝7为所求．考向二 等差数列的判定或证明【例2】 (2012·苏州第一学期期末考试)已知各项均为正数的数列{a n }的前n 项和为S n，满足8S n＝a2n＋4a n＋3(n∈N*)，且a1，a2，a7依次是等比数列{b n}的前三项．(1)求数列{a n}及{b n}的通项公式；(2)是否存在常数a>0且a≠1，使得数列{a n－log a b n}(n∈N*)是常数列？若存在，求出a的值；若不存在，请说明理由．解(1)当n＝1时，8a1＝a21＋4a1＋3，a1＝1或a1＝3.当n≥2时，8S n－1＝a2n－1＋4a n－1＋3，则a n＝S n－S n－1＝18(a2n＋4a n－a2n－1－4a n－1)，从而(a n＋a n－1)(a n－a n－1－4)＝0.因为数列{a n}的各项均为正数，所以a n－a n－1＝4.所以当a1＝1时，a n＝4n－3；当a1＝3时，a n＝4n－1.又因为当a1＝1时，a1，a2，a7分别为1,5,25，能构成等比数列，所以a n＝4n －3，b n＝5n－1；当a1＝3时，a1，a2，a7分别为3,7,27，不能构成等比数列，故舍去．所以a n＝4n－3，b n＝5n－1.(2)假设存在符合条件的a.由(1)知，a n＝4n－3，b n＝5n－1，从而a n－log a b n＝4n－3－log a5n－1＝4n－3－(n－1)log a5＝(4－log a5)n－3＋log a5.由题意，得4－log a5＝0，所以a＝4 5.所以满足条件的a存在，即a＝4 5.[方法总结] 等差数列主要的判定方法是定义法和等差中项法，而对于通项公式法和前n项和公式法主要适合在填空题中简单判断．另外，求数列通项，一般要作出是否是等差数列或等比数列的判断．【训练2】已知数列{a n}中，a1＝1，a2＝2，且a n＋1＝(1＋q)a n－qa n－1(n≥2，q≠0)．(1)设b n＝a n＋1－a n(n∈N*)，证明：{b n}是等比数列；(2)求数列{a n}的通项公式；(3)若a 3是a 6与a 9的等差中项，求q 的值，并证明：对任意的n ∈N *，a n 是 a n ＋3与a n ＋6的等差中项．(1)证明 由题设a n ＋1＝(1＋q )a n －qa n －1(n ≥2)， 得a n ＋1－a n ＝q (a n －a n －1)，即b n ＝qb n －1，n ≥2.由b 1＝a 2－a 1＝1，q ≠0， 所以{b n }是首项为1，公比为q 的等比数列． (2)解 由(1)知，a 2－a 1＝1，a 3－a 2＝q ，…， a n －a n －1＝q n －2(n ≥2)．将以上各式相加，得a n －a 1＝1＋q ＋…＋q n －2(n ≥2)，即a n ＝a 1＋1＋q ＋…＋q n －2(n ≥2)． 所以当n ≥2时，a n ＝⎩⎨⎧1＋1－q n －11－q ，q ≠1，n ， q ＝1.上式对n ＝1显然成立．(3)解 由(2)，当q ＝1时，显然a 3不是a 6与a 9的等差中项，故q ≠1. 由a 3－a 6＝a 9－a 3可得q 5－q 2＝q 2－q 8， 由q ≠0得q 3－1＝1－q 6，①整理得(q 3)2＋q 3－2＝0，解得q 3＝－2或q 3＝1(舍去)． 于是q ＝－32. 另一方面，a n －a n ＋3＝q n ＋2－q n －11－q ＝q n －11－q (q 3－1)，a n ＋6－a n ＝q n －1－q n ＋51－q ＝q n －11－q (1－q 6)．由①可得a n －a n ＋3＝a n ＋6－a n ， 即2a n ＝a n ＋3＋a n ＋6，n ∈N *.所以对任意的n ∈N *，a n 是a n ＋3与a n ＋6的等差中项．考向三 等差数列前n 项和及综合应用【例3】 (1)在等差数列{a n }中，已知a 1＝20，前n 项和为S n ，且S 10＝S 15，求当n 取何值时，S n 取得最大值，并求出它的最大值．(2)已知数列{a n }的通项公式是a n ＝4n －25，求数列{|a n |}的前n 项和． 解 (1)法一 ∵a 1＝20，S 10＝S 15，∴10×20＋10×92d ＝15×20＋15×142d ，∴d ＝－53. ∴a n ＝20＋(n －1)×⎝ ⎛⎭⎪⎫－53＝－53n ＋653.∴a 13＝0. 即当n ≤12时，a n ＞0，n ≥14时，a n ＜0.∴当n ＝12或13时，S n 取得最大值，且最大值为S 12＝S 13＝12×20＋12×112×⎝ ⎛⎭⎪⎫－53＝130. 法二 同法一求得d ＝－53.∴S n ＝20n ＋n (n －1)2·⎝ ⎛⎭⎪⎫－53＝－56n 2＋1256n ＝－56⎝ ⎛⎭⎪⎫n －2522＋3 12524.∵n ∈N *，∴当n ＝12或13时，S n 有最大值， 且最大值为S 12＝S 13＝130. 法三 同法一得d ＝－53.又由S 10＝S 15，得a 11＋a 12＋a 13＋a 14＋a 15＝0. ∴5a 13＝0，即a 13＝0.∴当n ＝12或13时，S n 有最大值， 且最大值为S 12＝S 13＝130.(2)∵a n ＝4n －25，a n ＋1＝4(n ＋1)－25， ∴a n ＋1－a n ＝4＝d ，又a 1＝4×1－25＝－21.所以数列{a n }是以－21为首项，以4为公差的递增的等差数列． 令⎩⎨⎧a n ＝4n －25<0， ①a n ＋1＝4(n ＋1)－25≥0， ② 由①得n <614；由②得n ≥514，所以n ＝6.即数列{|a n |}的前6项是以21为首项，公差为－4的等差数列，从第7项起以后各项构成公差为4的等差数列， 而|a 7|＝a 7＝4×7－25＝3. 设{|a n |}的前n 项和为T n ，则T n ＝⎩⎪⎨⎪⎧21n ＋n (n －1)2×(－4) (n ≤6)66＋3(n －6)＋(n －6)(n －7)2×4 (n ≥7)＝⎩⎨⎧－2n 2＋23n (n ≤6)，2n 2－23n ＋132(n ≥7).[方法总结] 求等差数列前n 项和的最值，常用的方法：(1)利用等差数列的单调性或性质，求出正负转折项，便可求得和的最值． (2)利用等差数列的前n 项和S n ＝An 2＋Bn (A 、B 为常数)为二次函数，根据二次函数的性质求最值．【训练3】 已知数列{a n }的前n 项和为S n ，a 1＝14且S n ＝S n －1＋a n －1＋12，数列{b n }满足b 1＝－1194且3b n －b n －1＝n (n ≥2且n ∈N *)． (1)求{a n }的通项公式；(2)求证：数列{b n －a n }为等比数列； (3)求{b n }前n 项和的最小值． (1)解 由2S n ＝2S n －1＋2a n －1＋1 得2a n ＝2a n －1＋1，a n －a n －1＝12， ∴a n ＝a 1＋(n －1)d ＝12n －14.(2)证明 由3b n －b n －1＝n ，得b n ＝13b n －1＋13n ，所以b n －a n ＝13b n －1＋13n －12n ＋14 ＝13b n －1－16n ＋14＝13⎝ ⎛⎭⎪⎫b n －1－12n ＋34；b n －1－a n －1＝b n －1－12(n －1)＋14＝b n －1－12n ＋34.由上面两式得b n －a n b n －1－a n －1＝13，又b 1－a 1＝－1194－14＝－30，故数列{b n －a n }是以－30为首项，13为公比的等比数列． (3)解 由(2)得b n －a n ＝－30×⎝ ⎛⎭⎪⎫13n －1，∴b n ＝a n －30×⎝ ⎛⎭⎪⎫13n －1＝12n －14－30×⎝ ⎛⎭⎪⎫13n －1(n ≥2)．b n －b n －1＝12n －14－30×⎝ ⎛⎭⎪⎫13n －1－12(n －1)＋14＋30×⎝ ⎛⎭⎪⎫13n －2＝12＋30×⎝ ⎛⎭⎪⎫13n －2⎝ ⎛⎭⎪⎫1－13＝12＋20×⎝ ⎛⎭⎪⎫13n －2>0，∴{b n }是递增数列．当n ＝1时，b 1＝－1194<0； 当n ＝2时，b 2＝34－10<0； 当n ＝3时，b 3＝54－103<0； 当n ＝4时，b 4＝74－109>0，所以，从第4项起的各项均大于0，故前3项之和最小． 且S 3＝14(1＋3＋5)－30－10－103＝－49312.考向四 等差数列的性质及应用【例4】 (1)在等差数列{a n }中，a 1＋a 2＋a 3＝－24，a 18＋a 19＋a 20＝78，则此数列前20项和等于________．(2)(2012·苏北四市二模)已知等差数列{a n }，{b n }的前n 项和分别为S n 和T n ，若S n T n ＝7n ＋45n ＋3，且a n b 2n 是整数，则n 的值为________． 解析 (1)由已知可得(a 1＋a 2＋a 3)＋(a 18＋a 19＋a 20)＝－24＋78⇒(a 1＋a 20)＋(a 2＋a 19)＋(a 3＋a 18)＝54⇒a 1＋a 20＝18⇒S 20＝a 1＋a 202×20＝182×20＝180. (2)令S n ＝7n 2＋45n ，则a n ＝14n ＋38，T n ＝n 2＋3n ， 则b n ＝2n ＋2，则a n b 2n ＝14n ＋384n ＋2＝7n ＋192n ＋1＝72＋12×312n ＋1，由2n ＋1∈N *，则2n ＋1＝31，n ＝15.答案 (1)180 (2)15[方法总结] 高考对等差数列通项公式的考查，常常涉及项与项之间的内在联系，因此突破这些问题的关键是归纳和总结一些基本的性质，并能利用这些性质对问题进行合理的转化，从而求解．【训练4】 设等差数列的前n 项和为S n ，已知前6项和为36，S n ＝324，最后6项的和为180(n ＞6)，求数列的项数n . 解 由题意可知a 1＋a 2＋…＋a 6＝36① a n ＋a n －1＋a n －2＋…＋a n －5＝180② ①＋②得(a 1＋a n )＋(a 2＋a n －1)＋…＋(a 6＋a n －5)＝6(a 1＋a n )＝216. ∴a 1＋a n ＝36.又S n ＝n (a 1＋a n )2＝324，∴18n ＝324.∴n ＝18.对应学生用书P89热点突破17 等差数列的综合问题近几年高考中，对等差数列的概念．通项公式、性质、前n 项和公式的考查始终没有放松．一方面考查知识的掌握情况，另一方面考查数学推理能力． 【示例】 (2011·浙江卷)已知公差不为0的等差数列{a n }的首项a 1为a (a ∈R )，设数列的前n 项和为S n 且1a 1，1a 2，1a 4成等比数列．(1)求数列{a n }的通项公式及S n ；(2)记A n ＝1S 1＋1S 2＋1S 3＋…＋1S n ，B n ＝1a 1＋1a 2＋1a 4＋…＋1a 2n －1，当n ≥2时，试比较A n 与B n 的大小．[审题与转化] 第一步：(1)利用方程求公差，再求a n 、S n .(2)利用裂项法求A n ，利用等比数列求和公式求B n ，再比较大小即可．[规范解答] 第二步：(1)设等差数列{a n }的公差为d ，由⎝ ⎛⎭⎪⎫1a 22＝1a 1·1a 4，得(a 1＋d )2＝a 1(a 1＋3d )，∵d ≠0，∴d ＝a 1＝a ，∴a n ＝na ，S n ＝an (n ＋1)2.(2)∵1S n＝2a ⎝ ⎛⎭⎪⎫1n －1n ＋1，∴A n ＝1S 1＋1S 2＋1S 3＋…＋1S n ＝2a ⎝ ⎛⎭⎪⎫1－1n ＋1. ∵a 2n －1＝2n －1a ，∴B n ＝1a 1＋1a 2＋…＋1a 2n －1＝1a ·1－⎝ ⎛⎭⎪⎫12n1－12＝2a ⎝ ⎛⎭⎪⎫1－12n . 当n ≥2时，2n ＝C 0n ＋C 1n ＋C 2n ＋…＋C nn >n ＋1，即1－1n ＋1<1－12n ， ∴当a >0时，A n <B n ，当a <0时，A n >B n .[反思与回顾] 第三步：高考考查等差数列时，常考查等差数列的通项、性质、求和、裂项法求和和公式法求和等知识．高考经典题组训练1．(2012·重庆卷改编)在等差数列{a n }中，a 2＝1，a 4＝5，则{a n }的前5项和S 5＝________.解析 因为{a n }成等差数列，所以⎩⎨⎧a 2＝a 1＋d ＝1，a 4＝a 1＋3d ＝5，解得⎩⎨⎧a 1＝－1，d ＝2.所以S 5＝5a 1＋5×42d ＝5×(－1)＋10×2＝15.答案 152．(2012·福建卷改编)等差数列{a n }中，a 1＋a 5＝10，a 4＝7，则数列{a n }的公差为________．解析 因为a 1＋a 5＝2a 3＝10，所以a 3＝5，又a 4＝7，所以d ＝a 4－a 3＝2. 答案 23．(2012·江西卷)设数列{a n }，{b n }都是等差数列．若a 1＋b 1＝7，a 3＋b 3＝21，则a 5＋b 5＝________.解析因为(a1＋a5)＋(b1＋b5)＝2(a3＋b3)＝42，所以a5＋b5＝42－7＝35.答案354．(2012·山东卷)在等差数列{a n}中，a3＋a4＋a5＝84，a9＝73.(1)求数列{a n}的通项公式；(2)对任意m∈N*，将数列{a n}中落入区间(9m,92m)内的项的个数记为b m，求数列{b m}的前m项和S m.解(1)因为{a n}是一个等差数列，所以a3＋a4＋a5＝3a4＝84，a4＝28.设数列{a n}的公差为d，则5d＝a9－a4＝73－28＝45，故d＝9.由a4＝a1＋3d得28＝a1＋3×9，即a1＝1.所以a n＝a1＋(n－1)d＝1＋9(n－1)＝9n－8(n∈N*)．(2)对m∈N*，若9m<a n<92m，则9m＋8<9n<92m＋8.因此9m－1＋1≤n≤92m－1，故得b m＝92m－1－9m－1.于是S m＝b1＋b2＋b3＋…＋b m＝(9＋93＋…＋92m－1)－(1＋9＋…＋9m－1)＝9×(1－81m)1－81－1－9m1－9＝92m＋1－10×9m＋180.5．(2010·天津卷)在数列{a n}中，a1＝0，且对任意k∈N*，a2k－1，a2k，a2k＋1成等差数列，其公差为2k.(1)证明：a4，a5，a6成等比数列；(2)求数列{a n}的通项公式；(3)记T n＝22a2＋32a3＋…＋n2a n，证明：32<2n－T n≤2(n≥2)．(1)证明由题设可知，a2＝a1＋2＝2，a3＝a2＋2＝4，a4＝a3＋4＝8，a5＝a4＋4＝12，a6＝a5＋6＝18.从而a6a5＝a5a4＝32.所以a4，a5，a6成等比数列．(2)解由题设，可得a2k＋1－a2k－1＝4k，k∈N*.所以a 2k ＋1－a 1＝(a 2k ＋1－a 2k －1)＋(a 2k －1－a 2k －3)＋…＋(a 3－a 1)＝4k ＋4(k －1)＋…＋4×1＝2k (k ＋1)，k ∈N *.由a 1＝0，得a 2k ＋1＝2k (k ＋1)，从而a 2k ＝a 2k ＋1－2k ＝2k 2.所以数列{a n }的通项公式为a n ＝⎩⎪⎨⎪⎧n 2－12，n 为奇数，n 22，n 为偶数，或写成a n ＝n 22＋(－1)n －14，n ∈N *. (3)证明 由(2)可知a 2k ＋1＝2k (k ＋1)，a 2k ＝2k 2. 以下分两种情况进行讨论：①当n 为偶数时，设n ＝2m (m ∈N *)． 若m ＝1，则2n －∑k ＝2nk 2a k＝2.若m ≥2，则∑k ＝2nk 2a k ＝∑k ＝1m (2k )2a 2k ＋∑k ＝1m －1 (2k ＋1)2a 2k ＋1＝∑k ＝1m 4k 22k 2＋∑k ＝1m －1 4k 2＋4k ＋12k (k ＋1)＝2m ＋∑k ＝1m －1⎣⎢⎡⎦⎥⎤4k 2＋4k 2k (k ＋1)＋12k (k ＋1) ＝2m ＋∑k ＝1m －1⎣⎢⎡⎦⎥⎤2＋12⎝ ⎛⎭⎪⎫1k －1k ＋1 ＝2m ＋2(m －1)＋12⎝ ⎛⎭⎪⎫1－1m ＝2n －32－1n .所以2n －∑k ＝2nk 2a k＝32＋1n ，从而32<2n －∑k ＝2n k 2a k<2，n ＝4,6,8，….②当n 为奇数时，设n ＝2m ＋1(m ∈N *)．∑k ＝2nk 2a k ＝∑k ＝22m k2a k ＋(2m ＋1)2a 2m ＋1＝4m －32－12m ＋(2m ＋1)22m (m ＋1)＝4m ＋12－12(m ＋1)＝2n －32－1n ＋1，所以2n －∑k ＝2nk 2a k ＝32＋1n ＋1，从而32<2n －∑k ＝2n k 2a k<2，n ＝3,5,7，….综合①和②可知，对任意n ≥2，n ∈N *，都有32<2n －T n ≤2.对应学生用书P301分层训练A 级 基础达标演练(时间：30分钟 满分：60分)一、填空题(每小题5分，共30分)1．(2011·重庆卷改编)在等差数列{a n }中，a 2＝2，a 3＝4，则a 10＝________. 解析 设公差为d ，则d ＝a 3－a 2＝2. ∴a 1＝0，a n ＝2n －2∴a 10＝2×10－2＝18. 答案 182．(2012·辽宁卷改编)在等差数列{a n }中，已知a 4＋a 8＝16，则该数列前11项和S 11＝________.解析 由等差数列性质及已知，得S 11＝11(a 1＋a 11)2＝112(a 4＋a 8)＝112×16＝88. 答案 883．(2012·泰州学情调查)在等差数列{a n }中，a 1＞0，S 4＝S 9，则S n 取最大值时，n ＝________.解析 因为a 1＞0，S 4＝S 9，所以a 5＋a 6＋a 7＋a 8＋a 9＝0，所以a 7＝0，所以⎩⎨⎧a 6＞0，a 8＜0，从而当n ＝6或7时S n 取最大值．答案 6或74．在等差数列{a n }中，若a 1＋a 4＋a 7＝39，a 3＋a 6＋a 9＝27，则S 9＝________. 解析 ∵a 1＋a 4＋a 7＝39，a 3＋a 6＋a 9＝27，∴3a 4＝39,3a 6＝27，∴a 4＝13，a 6＝9.∴a 6－a 4＝2d ＝9－13＝－4，∴d ＝－2， ∴a 5＝a 4＋d ＝13－2＝11，∴S 9＝9(a 1＋a 9)2＝9a 5＝99.答案 995．(2012·南通调研)设等差数列{a n }的公差为正数，若a 1＋a 2＋a 3＝15，a 1a 2a 3＝80，则a 11＋a 12＋a 13＝________.解析 由15＝a 1＋a 2＋a 3＝3a 2，得a 2＝5.所以⎩⎨⎧a 1＋a 3＝10，a 1a 3＝16.又公差d ＞0，所以⎩⎨⎧a 1＝2，a 3＝8.所以d ＝3.所以a 11＋a 12＋a 13＝3a 12＝3(a 1＋11d )＝3(2＋33)＝3×35＝105. 答案 1056．(2012·南京模拟)已知数列{a n }的前n 项和为S n ＝2n 2＋pn ，a 7＝11.若a k ＋a k ＋1＞12，则正整数k 的最小值为________．解析 因为a 7＝S 7－S 6＝2×72＋7p －2×62－6p ＝26＋p ＝11，所以p ＝－15，S n ＝2n 2－15n ，a n ＝S n －S n －1＝4n －17(n ≥2)，当n ＝1时也满足．于是由a k ＋a k ＋1＝8k －30＞12，得k ＞214＞5.又k ∈N *，所以k ≥6，即k min ＝6. 答案 6二、解答题(每小题15分，共30分)7．设a 1，d 为实数，首项为a 1，公差为d 的等差数列{a n }的前n 项和为S n ，满足S 5S 6＋15＝0.(1)若S 5＝5，求S 6及a 1； (2)求d 的取值范围．解 (1)由题意知S 6＝－15S 5＝－3，a 6＝S 6－S 5＝－8，所以⎩⎨⎧5a 1＋10d ＝5，a 1＋5d ＝－8.解得a 1＝7，所以S 6＝－3，a 1＝7.(2)因为S 5S 6＋15＝0，所以(5a 1＋10d )(6a 1＋15d )＋15＝0，即2a 21＋9da 1＋10d 2＋1＝0，故(4a 1＋9d )2＝d 2－8，所以d 2≥8. 故d 的取值范围为d ≤－22或d ≥2 2.8．已知数列{a n }满足a n ＝2a n －1＋2n ＋1(n ∈N *，n ≥2)，且a 3＝27. (1)求a 1，a 2的值；(2)记b n ＝12n (a n ＋t )(n ∈N *)，问是否存在一个实数t ，使数列{b n }是等差数列？若存在，求出实数t ；若不存在，请说明理由． 解 (1)由a 3＝27，得2a 2＋23＋1＝27，所以a 2＝9. 又由2a 1＋22＋1＝9，得a 1＝2.(2)假设存在实数t ，使得数列{b n }是等差数列，则2b n ＝b n －1＋b n ＋1，即2×12n (a n ＋t )＝12n －1(a n －1＋t )＋12n ＋1(a n ＋1＋t )，即4a n ＝4a n－1＋a n ＋1＋t ，所以4a n ＝4×a n －2n －12＋2a n ＋2n ＋1＋t ＋1，所以t ＝1. 故存在t ＝1，使得数列{b n }是等差数列．分层训练B 级 创新能力提升1．(2012·南京学期学情)已知数列{a n }，{b n }都是等差数列，S n ，T n 分别是它们的前n 项和，且S n T n ＝7n ＋1n ＋3，则a 2＋a 5＋a 17＋a 22b 8＋b 10＋b 12＋b 16＝________.解析a 2＋a 5＋a 17＋a 22b 8＋b 10＋b 12＋b 16＝2(a 11＋a 12)2(b 11＋b 12)＝a 1＋a 22b 1＋b 22＝S 22T 22＝7×22＋122＋3＝315.答案 3152．已知数列{a n }满足递推关系式a n ＋1＝2a n ＋2n－1(n ∈N *)，且⎩⎪⎨⎪⎧⎭⎪⎬⎪⎫a n ＋λ2n 为等差数列，则λ的值是________．解析 由a n ＋1＝2a n ＋2n－1，可得a n ＋12n ＋1＝a n 2n ＋12－12n ＋1，则a n ＋1＋λ2n ＋1－a n ＋λ2n ＝a n ＋12n ＋1－a n 2n －λ2n ＋1＝12－12n ＋1－λ2n ＋1＝12－λ＋12n ＋1，当λ的值是－1时，数列⎩⎪⎨⎪⎧⎭⎪⎬⎪⎫a n －12n 是公差为12的等差数列．。

2014年高考题专题整理 --不等式和线性规划第I 部分1.【2014年四川卷（理04）】若0a b >>，0c d <<，则一定有A ．a b c d >B ．a b c d <C ．a b d c >D ．a bd c<【答案】D【解析】由1100c d d c <<⇒->->，又0a b >>， 由不等式性质知：0a b d c ->->，所以a bd c<2.【2014年江西卷（理11）】(1).（不等式选做题）对任意,x y R ∈,111x x y y -++-++的最小值为A.1B.2C.3D.4【答案】B【解析】()|1||||1||1|1||11|123x x y y x x y y -++-++≥--+--+=+=3.【2014年安徽卷（理05）】y x ,满足约束条件⎪⎩⎪⎨⎧≥+-≤--≤-+02202202y x y x y x ，若ax y z -=取得最大值的最优解不唯一，则实数 a 的值为（A ）21或1- （B ）2或21（C ）2或1（D ）2或1-【答案】D【解析】可行域如右图所示，ax y z -=可化为z ax y +=，由题意知2=a 或1-2=-+y x 022=--y x 022=+-y x xyO1-=k 2=k 21=k4.【2014年天津卷（理02）】设变量x 、y 满足约束条件20201x y x y y +-≥⎧⎪--≤⎨⎪≥⎩，则目标函数2z x y =+的最小值为A.2B.3C.4D.5【答案】B【解析】画出可行域，如图所示．解方程组⎩⎪⎨⎪⎧x ＋y －2＝0，y ＝1，得⎩⎪⎨⎪⎧x ＝1，y ＝1，即点A (1，1)．当目标函数线过可行域内A 点时，目标函数有最小值，即z min ＝1×1＋2×1＝3.5.【2014年山东卷（理09）】已知y x,满足的约束条件⎩⎨⎧≥≤0,3-y -2x 0,1-y -x 当目标函数0)b 0,by(a ax z >>+=在该约束条件下取得最小值52时，22a b +的最小值为（A ）5（B ）4（C ）5（D ）2【答案】B【解析】10230x y x y --≤⎧⎨--≥⎩求得交点为()2,1，则225a b +=，即圆心()0,0到直线2250a b +-=的距离的平方2225245⎛⎫== ⎪ ⎪⎝⎭。

2014年高考数学真题汇编——数列一．选择题1. （2014大纲）等比数列{}n a 中，452,5a a ==，则数列{lg }n a 的前8项和等于 （ ）A ．6B ．5C ．4D ．3【答案】C ．2. (2014重庆)对任意等比数列{}n a ,下列说法一定正确的是（ ）139.,,A a a a 成等比数列 236.,,B a a a 成等比数列248.,,C a a a 成等比数列 239.,,D a a a 成等比数列【答案】D【解析】.∴D 选要求角码成等差3. (2014北京)设{}n a 是公比为q 的等比数列，则"1"q >是"{}"n a 为递增数列的（ ）.A 充分且不必要条件 .B 必要且不充分条件.C 充分必要条件 .D 既不充分也不必要条件D试题分析：对等比数列}{n a ，若1>q ，则当0,1a 时数列}{n a 是递减数列；若数列}{n a 是递增数列，则4. （2014福建）等差数列{}n a 的前n 项和n S ，若132,12a S ==，则6a =( ).8A .10B .12C .14DC5. （2014辽宁）设等差数列{}n a 的公差为d ，若数列1{2}n a a为递减数列，则（ ）A ．0d <B ．0d >C ．10a d <D ．10a d >【答案】C【解析】 ..0.00;00:.,1111111C d a d a d a a a a a a a n n n 选且或且分情况解得即递减由同增异减知，<∴><<><+二．填空题1. (2014江苏) 在各项均为正数的等比数列}{n a 中,,12=a 4682a a a +=,则6a 的值是 ▲ .2(2014安徽)数列{}n a 是等差数列，若a 1+1，a 3+3，a 5+5构成公比为q 的等比数列，则q= . 12．13(2014北京)若等差数列{}n a 满足7890a a a ++>，7100a a +<，则当n =________时{}n a 的前n 项和最大.4(2014广东)若等比数列{}n a 的各项均为正数,且512911102e a a a a =+,则1220ln ln ln a a a +++= .51011912101112202019151201011:50,,ln ln ln ,ln ln ln ,220ln 20ln 20ln 100,50.a a a a a a e S a a a S a a a S a a a a e S =∴==+++=+++∴====∴=答案提示:设则5 (2014天津)设{}n a 是首项为1a ，公差为-1的等差数列，n S 为其前n 项和.若124,,S S S 成等比数列，则1a 的值为__________. 【答案】21-【解析】 解：12-依题意得2214S S S =，所以()()21112146a a a -=-，解得112a =-.6. (2014上海)设无穷等比数列{n a }的公比为q ，若)(lim 431 ++=∞→a a a n ，则q= 。

2014年全国高考试卷数列部分汇编1. （2014安徽理12）数列{}n a 是等差数列，若135135a a a +++，，构成公比为q 的等比数列，则q =________． 【解析】1 设{}n a 的公差为d ，则315131225144a a d a a d +=++++=+++，，由题意可得23(3)a+=15(1)(5)a a ++．∴2111[(1)2(1)](1)[(1)4(1)]a d a a d +++=++++，∴2221111(1)4(1)(1)[2(1)](1)4(1)(1)a d a d a a d ++++++=++++， ∴1d =-，∴3131a a +=+，∴公比31311a qa +==+． 2. （2014安徽文12）如图，在等腰直角三角形ABC 中，斜边22BC =，过点A 作BC 的垂线，垂足为1A ；过点1A 作AC 的垂线，垂足为2A ；过点2A 作1A C 的垂线，垂足为3A ；…，依此类推，设1BA a =，12123567AA a A A a A A a ===，，…，，则7a =______________．【解析】 14由22BC =得112123222212AB a AA a A A a ==Þ==Þ==´=，由此可归纳出{}n a 是以12a =为首项，22为公比的等比数列，因此667121224a a q æö=´=´=ç÷ç÷èø．3. （2014安徽文18）数列{}n a 满足111(1)(1)n n a na n a n n n *+=,=+++,ÎN ．⑴证明：数列n a n ìüíýîþ是等差数列；是等差数列；⑵设3nnnb a =×，求数列{}nb 的前n 项和nS ．【解析】 ⑴ 由已知可得111n n a a n n +=++，即111n n a a n n+-=-． 所以n a n ìüíýîþ是以111a =为首项，1为公差的等差数列． ⑵ 由⑴得()111na n n n=+-×=，所以2n a n =． 从而3nn b n =×． 1231323333nn S n =×+×+×++×，①()23131323133n nn S n n +=×+×++-×+×．② A 1A 4A 3A 2第（12）题图ABC①－②得12123333n n n S n +-=+++-×()()1131312333132nn nn n n ++×--×-=-×=-．．所以()121334nn n S +-×+=．评析 本题考查等差数列定义的应用，错位相减法求数列的前n 项和，解题时利用题⑴提示对递推关系进行变形是关键．4. （2014北京理5）设{}n a 是公比为q 的等比数列，则“1q >”是“{}n a ”为递增数列的（”为递增数列的（ ） A ．充分而不必要条件 B ．必要而不充分条件．必要而不充分条件 C ．充分必要条件 D ．既不充分也不必要条件．既不充分也不必要条件 【解析】D 对于等比数列{}na ，若1q >，则当10a <时有{}na 为递减数列．故“1q >”不能推出“{}n a 为递增数列”．若{}n a 为递增数列，则{}n a 有可能满足10a <且01q <<，推不出1q >． 综上，“1q >”为“{}n a 为递增数列”的既不充分也不必要条件，即选D ．5. （2014北京理12）若等差数列{}n a 满足7890a a a ++> ，7100a a +<，则当n =____时，{}n a 的前n 项和最大．最大．【解析】8 由等差数列的性质，78983a a a a ++=，71089a a a a +=+，于是有80a >，890a a +<，故90a <．故87S S >，98S S <，8S 为{}n a 的前n 项和n S 中的最大值6. （2014北京文15）已知{}n a 是等差数列，满足13a =，412a =，数列{}n b 满足14b =，420b =，且{}n n b a -为等比数列．为等比数列．⑴求数列{}n a 和{}n b 的通项公式；的通项公式； ⑵求数列{}n b 的前n 项和．项和．【解析】 ⑴ 设等差数列{}n a 的公差为d ，由题意得41123333a a d --===所以()()11312n a a n d n n =+-==，，．设等比数列{}n n b a -的公比为q ，由题意得344112012843b a qb a --===--，解得2q =． 所以()11112n n n n b a b a q ---=-=． 从而()13212n n b n n -=+=，， ⑵ 由⑴知()13212n nn b n n -=+=，，．数列{}3n 的前n 项和为()312n n +，数列{}12n -的前n 项和为1212112nn -=--×．所以，数列{}n b 的前n项和为()31212n n n ++-．7. （2014大纲理10）等比数列{}n a 中，4525a a ==，，则数列{}lg n a 的前8项和等于（项和等于（） A ．6 B ．5 C ．4 D ．3【解析】C8. （2014大纲理18）等差数列{}n a 的前n 项和为n S ，已知110a =，2a 为整数，且4n S S ≤⑴求{}n a 的通项公式；的通项公式； ⑵设11n n n b a a +=，求数列{}n b 的前n 项和n T ． 【解析】 ⑴ 由110a =，2a 为整数知，等差数列{}n a 的公差d 为整数．又4n S S … 故4500a a ，厔于是10301040d d ++≥，≤ 解得10532d --≤≤． 因此3d =-．数列{}n a 的通项公式为133n a n =-．⑵ ()()1111331033103133n b n n n n æö==-ç÷----èø1．于是12n T b b =++…nb 1111111371047103103n n éùæöæöæö=-+-+-ç÷ç÷ç÷êú--èøèøèøëû…+ 111310310n æö=-ç÷-èø()10103n n =-．9. （2014大纲文8）设等比数列{}n a 的前n 项和为n S ，若23S =，415S =，则6S =（ ） A ．31 B ．32 C ．63 D ．64 【解析】C 10. （2014大纲文17）数列{}n a 满足12211222n n na a a a a ++===-+，， ⑴设1nn nb a a +=-，证明{}nb 是等差数列；是等差数列；⑵求{}n a 的通项公式．的通项公式．【解析】 ⑴ 由2122n n n a a a ++=-+得2112n n n n a a a a +++-=-+ 即12n n b b +=+又1211b a a =-=所以{}n b 是首项为1，公差为2的等差数列． ⑵ 由⑴得12(-1)n b n =+ 即+121n n a a n -=- 于是111()(21)nnk k k k aa k +==-=-åå所以211n a a n +-=，即211n a n a +=+．又11a =，所以{}n a 的通项公式为222n a n n =-+．11. （2014福建理3）等差数列{}n a 的前n 项和n S ，若13212a S ==，，则6a =（ ） A ．8B ．10C ．12D ．14【解析】C12. （2014福建文17）在等比数列{}n a 中，25381a a ==，．⑴求n a ；⑵设3log n n b a =，求数列{}n b 的前n 项和n S ．【解析】 本小题主要考查等差数列、等比数列等基础知识，考查运算求解能力，考查化归与转化思想．⑴ 设{}n a 公比为q ，依题意得141381a q a q =ìïí=ïî，， 解得113a q =ìí=î，．因此，13nn a -=．⑵ 因为3log 1n n b a n ==-，所以数列{}n b 的前n 项和21()=22n nn b b n n S +-=．13. （2014广东理13）若等比数列{}n a 的各项均为正数，且510119122e a a a a +=，则1220l n l n l n a a a +++=__________．【解析】50． 由等比数列性质可知，51202193189121011e a a a a a a a a a a =====，可求得1220120219912l n l n l n l n l n l n l n 10550a a a a a a a a a a a +++=++++=´=． 14. （2014广东理19） 设数列{}n a 的前n 项和为n S ，满足21234n n S na n n +=--，*n ÎN ，且315S =．⑴求1a ，2a ，3a 的值；的值；⑵求数列{}n a 的通项公式．的通项公式．【解析】 ⑴ 取2n =得到23420S a =-，又233315S S a a =-=-，于是3342015a a -=-，得37a =取1n =得到11227a S a ==-，又1322158a a a a =--=-， 于是22212785,3a a a a -=-Þ==；⑵ 猜测21na n =+，用归纳法证明：1°1n =时，显然成立；2°假设n k =时，成立，即21k a k =+；3°由22111(1)23432234232k k k k k k S ka k k k ka k k a k +++-=--Þ+×=--Þ=+； 故结论成立，即21n a n =+．15. （2014广东文13）等比数列{}n a 的各项均为正数，且154a a =，则2122232425l og l o g l o g l o g l o g a a a a a ++++=_____．【解析】5． 16. （2014广东文19）设各项均为正数的数列{}n a 的前n 项和为n S ，且n S 满足满足222(3)3()0n n S n n S n n n *-+--+=ÎN ，．⑴求1a 的值；的值；⑵求数列{}n a 的通项公式；的通项公式；⑶证明：对一切正整数n ，有()()()112211111113nna a a a a a+++<+++． 【解析】 ⑴ ∵()()222330n n S n n S n n -+--+=，∴令1n =，得21160a a +-=，解得12a =得13a =-． 又0na >，∴12a =．⑵ 由()()222330n n S n n S n n -+--+=，得()()230n n S n n S éù-++=ëû， 又0n a >，所以30n S +≠，所以2n S n n =+，所以当2n ≥时，()221112n n n a S S n n n n n -éù=-=+--+-=ëû，又由⑴知，12a =，符合上式．所以2n a n =．⑶ 由⑵知，()()111221n n a a n n =++， 所以()()()1122111111n n a a a a a a ++++++… ()1112345221n n =+++´´+…()()11112335572121n n <++++´´´-+…111111116235572121n n éùæöæöæö<+-+-++-ç÷ç÷ç÷êú-+èøèøèøëû… 111162321n æö=+-ç÷+èø11116233<+´=17. （2014湖北理18文19）已知等差数列{}n a 满足：12a =，且125a a a ，，成等比数列．成等比数列．⑴求数列{}n a 的通项公式．的通项公式．⑵记n S 为数列{}n a 的前n 项和，是否存在正整数n ，使得60800n S n >+？若存在，求n 的最小值；若不存在，说明理由．小值；若不存在，说明理由．【解析】 ⑴ 设数列{}n a 的公差为d ，依题意，2224d d ++，，成等比数列，故有 2(2)2(24)d d +=+，化简得240d d -=，解得0d =或4d =．当0d =时，2na =；当4d =时，2(1)442n a n n =+-×=-，从而得数列{}n a 的通项公式为2n a =或42n a n =-． ⑵ 当2na =时，2nS n =．显然260800n n +＜，此时不存在正整数n ，使得60800n S n >+成立．当42na n =-时，[]22(42)22n n n S n +-==．令2260800n n >+，即2304000n n -->，解得40n >或10n <-（舍去），此时存在正整数n ，使得60nS n >+800成立，n 的最小值为41．综上，当2na =时，不存在满足题意的n ；当42na n =-时，存在满足题意的n ，其最小值为41．18. （2014湖南理20）已知数列{}n a 满足111||n n n a a a p +=-=，，*n ÎN ．⑴若{}n a 是递增数列，且1a ，22a ，33a 成等差数列，求p 的值；的值；⑵若12p =，且{}21n a -是递增数列，{}2n a 是递减数列，求数列{}n a 的通项公式．的通项公式． 【解析】 ⑴ 因为数列{}n a 为递增数列，所以10n n a a +-≥，则11n nn n n n a a p a a p ++-=Þ-=，分别令12n =，可得22132a a p a a p -=-=，22311a p a p p Þ=+=++，， 因为12323a a a ，，成等差数列， 所以21343a a a =+()()224113130p p p p p Þ+=+++Þ-=13p Þ=或0， 当0p =时，数列n a 为常数数列不符合数列{}n a 是递增数列，所以13p =．⑵ 由题可得122122212121111222n n n n n n n n n a a a a a a +-++-+-=Þ-=-=，， 因为{}21n a -是递增数列且{}2n a 是递减数列，所以2121n n a a +->且222n n a a +<，则有22222122212121n nn n n n n n a a a a a a a a +-++-+-<-ìÞ->-í<î， 又因为2212112n n n a a ---=22212112n n n a a +++>-=，所以2210n n a a -->，即2212112n n n a a ---=， 同理可得2322212n n n n a a a a +++->-且2322212n n n n a a a a +++-<-，所以212212n nn a a +-=-，则当2n m =()*m ÎN 时，21324322123211111,2222m m m a a a a a a a a ---=-=--=-=，，，，这21m -个等式相加可得2113212422111111222222m m m a a --æöæö-=+++-+++ç÷ç÷èøèø212222111111111224224113321144m m m ----×-×=-=+×--22141332m m a -Þ=+×． 当21n m =+时，2132432122321111,2222m m m a a a a a a a a +-=-=--=-=-，，，，这2m 个等式相加可得2111321242111111222222m m m a a +-æöæö-=+++-+++ç÷ç÷èøèø2122211111111224224113321144m m m--×-×=-=-×-- 21241332m m a +=-×，当0m =时，11a =符合，故212241332m m a --=-×综上()1141332nn n a --=+×． 19. （2014湖南文16）已知数列{}n a 的前n 项和22n n n S n *+=ÎN ，．⑴求数列{}n a 的通项公式；的通项公式；⑵设()21nna n nb a =+-，求数列{}n b 的前2n 项和．项和．【解析】 ⑴ 当1n =时，111a S ==；当2n ≥时，()()2211122n n n n n n n aS Sn--+-+=-=-=． 故数列{}n a 的通项公式为n a n =． ⑵ 由⑴知，()21nn nb n =+-，记数列{}n b 的前2n 项和为2nT ，则()()122222212342nn T n =++++-+-+-+．记122222nA =+++，12342B n =-+-+-+，则()2212122212nn A +-==--，()()()1234212B n n n=-++-+++--+=éùëû． 故数列{}n b 的前2n 项和21222n n T A B n +=+=+-．20. （2014江苏理7）在各项均为正数的等比数列{}n a 中，若21a =，8642a a a =+，则6a 的值为_____．【解析】 4设公比为q (0)q >，则由8642a a a =+得266622a a q a q =+，解得22q =，故4624a a q ==21. （2014江苏理20）设数列{}n a 的前n 项和为nS ．若对任意的正整数n ，总存在正整数m ，使得n m S a =，则称{}n a 是“H 数列”． ⑴若数列{}n a 的前n 项和*2()n nS n =ÎN ，证明：{}n a 是“H 数列”； ⑵设{}n a 是等差数列，其首项11a =，公差0d <，若{}n a 是“H 数列”，求d 的值；的值；⑶证明：对任意的等差数列{}n a ，总存在两个“H 数列”{}n b 和{}nc ，使得n n n a b c =+成立．成立．【解析】 ⑴ 当2n ≥时，111222n n n nnn a S S ---=-=-=当1n =时，112a S ==∴1n =时，11S a =，当2n ³时，1n n S a += ∴{}n a 是“H 数列”⑵1(1)(1)22n n n n n S na d n d --=+=+ 对*n "ÎN ，*m $ÎN 使n m S a =，即(1)1(1)2n n dn m d -+=+-取2n =得1(1)d m d +=-，12md =+∵0d <，∴2m <，又*m ÎN ，∴1m =，∴1d =- ⑶ 设{}na 的公差为d令111(1)(2)n b a n a n a =--=-，对*n "ÎN ，11n n b b a +-=-1(1)()n c n a d =-+，对*n "ÎN ，11n n c c a d +-=+则1(1)n n n b c a n d a +=+-=，且{}n b 、{}n c 为等差数列{}n b 的前n 项和11(1)()2n n n T na a -=+-，令1(2)n T m a =-，则(3)22n n m -=+ 当1n =时1m =；当2n =时1m = 当3n ≥时，由于n 与3n -奇偶性不同，即(3)n n -非负偶数，*m ÎN 因此对n "，都可找到*m ÎN ，使n m T b =成立，即{}n b 为H 数列 {}n c 的前n 项和1(1)()2n n n R a d -=+，令1(1)()m n c m a d R =-+=，则(1)12n n m -=+ ∵对*n "ÎN ，(1)n n -是非负偶数，∴*m ÎN即对*n "ÎN ，都可找到*m ÎN ，使得n m R c =成立，即{}n c 为H 数列因此命题得证22. （2014江西理17）已知首项都是1的两个数列{}n a ,{}n b *0n b n ¹ÎN ，，满足11120n n n n n n a b a b b b +++-+=．⑴令n n na cb =，求数列{}nc 的通项公式；的通项公式；⑵若13n n b -=，求数列{}n a 的前n 项和n S ．【解析】 ⑴ 因为()*111200n n n n n n n a ba b b b b n +++-+=¹ÎN ，， 所以112n n n na ab b ++-=，即12n nc c +-= 所以数列{}n c 是以1为首项，2为公差的等差数列． 故21nc n =-．⑵ 由13n nb -=知()1213n n n n a c b n -==-，于是数列{}n a 的前n 项和()0121133353213n n S n -=×+×+×++-×…． ()()12131333233213n n n S n n -=×+×+-×+-×…+． 相减得()()()1212123332132223n n nn S n n --=+×++--×=---…+， 所以()131nn S n =-+．23. （2014江西文13）在等差数列{}n a 中，17a =，公差为d ，前n 项和为n S ，当且仅当8n =时n S 取最大值，取最大值，则则d 的取值范围_________． 【解析】 718æö--ç÷èø， 24. （2014江西文17） 已知数列{}n a 的前n 项和232n n nS n *-=ÎN ，． ⑴求数列{}n a 的通项公式；的通项公式；⑵证明：对任意1n >，都有m *ÎN ，使得1n m a a a ，，成等比数列．成等比数列．【解析】 ⑴ 由232n n nS -=得111a S ==，当2n ≥时，132n n n a S S n -=-=-．所以数列{}na 的通项公式为32na n =-．⑵ 要使1n m a a a ，，成等比数列，只需要21n m a a a =×，即()()232132n m-=×-，即2342m n n =-+，而因此时m *ÎN ，且m n >，所以对任意的1n >，都存在m *ÎN ，使得1n m a a a ，，成等比数列．25. （2014辽宁理8文9） 设等差数列{}n a 的公差为d .若数列{}12n a a 为递减数列，则（）为递减数列，则（）A ．0d <B ．0d >C ．10a d <D ．10a d >【解析】C 26. （2014山东理19）已知等差数列{}n a 的公差为2，前n 项和为n S ，且124S S S ，，成等比数列．⑴求数列{}n a 的通项公式；的通项公式；⑵令114(1)n n n n n b a a -+=-，求数列{}n b 的前n 项和n T ． 【解析】 ⑴ 1121412S S 246d a a d S a d ===+=+，，，124S S S ，，成等比数列，2214S S S \=解得1121n a a n =\=-，⑵111411(1)(1)()2121n n n n n n b a a n n --+=-=-+-+ 当n 为偶数时，111111111(1)()()()()3355723212121nT n n n n =+-+++-++-+---+1212121n nT n n \=-=++ 当n 为奇数时，111111111(1)()()()()3355723212121n T n n n n =+-+++--+++---+12212121n n T n n +\=+=++2212221n n n n T n n n ìïï+\=í+ï+î，为偶数，为奇数27. （2014山东文19）在等差数列{}n a 中，已知公差2d =，2a 是1a 与4a 的等比中项．的等比中项．⑴求数列{}na 的通项公式；的通项公式；⑵设(1)2n n n b a +=，记1234(1)n n n T b b b b b =-+-+-+-…，求n T ．【解析】 ⑴ 由题意知{}n a 为等差数列，设1(1)n a a n d =+-，2a 为1a 与4a 的等比中项2214a a a \=´且()()2111103a a d a a d ¹Þ+=+，2d =解得：12a =()2122n a n n \=+-´=．⑵ 由⑴知：2n a n =，∴()()121n n n b a n n +==+①当n 为偶数时：()()()()()()()()()()2122334+1213435+11224262+22246+222222n T n n n n n n n nn n n=-´+´-´++=´-++-++--++éùëû=´+´+´+´=´++++×+=´=②当n 为奇数时：()()()()()()()()()()()()()21223341213435+(1)21224262+(1)212246+111212122122n T n n n n n n n n n n n n n n n n n n n =-´+´-´+-+=´-++-++---+-+éùëû=´+´+´+-´-+=´+++--+-+-×++=´-+=-综上：2221222n n n n T n n n ì++-ïï=í+ïïî为为数，奇数，偶．28. （2014陕西文8） 原命题为“若12n n n a aa ++<，+n N ∈”,则{}n a 为递减数列，关于其逆命题，否命题，逆否命题真假性的判断依次如下，正确的是( ) A ．真，真，真．真，真，真 B ．假，假，真．假，假，真 C ．真，真，假．真，真，假 D ．假，假，假．假，假，假【解析】A 29. （2014上海理23）已知数列{}n a 满足1133n n n a a a +≤≤，*n ÎN ，11a =。

1. 【2014高考北京版理第5题】设{}n a 是公比为q 的等比数列，则“1>q ”是“{}n a 为递增数列”的（ ）A ．充分而不必要条件B ．必要而不充分条件C ．充分必要条件D ．既不充分也不必要条件2. 【2014高考福建卷第3题】等差数列{}n a 的前n 项和n S ，若132,12a S ==，则6a =( ).8A .10B .12C .14D3. 【2014高考江苏卷第7题】在各项均为正数的等比数列{}n a 中，若21a =，8642a a a =+，则6a 的值是 .4. 【2014辽宁高考理第8题】设等差数列{}n a 的公差为d ，若数列1{2}n a a 为递减数列，则（ ） A ．0d < B ．0d > C ．10a d < D ．10a d >5. 【2014重庆高考理第2题】对任意等比数列{}n a ,下列说法一定正确的是( )139.,,A a a a 成等比数列 236.,,B a a a 成等比数列248.,,C a a a 成等比数列 369.,,D a a a 成等比数列6. 【2014天津高考理第11题】设{}n a 是首项为1a ，公差为1-的等差数列，n S 为其前n 项和．若124,,S S S 成等比数列，则1a 的值为__________．7. 【2014大纲高考理第10题】等比数列{}n a 中，452,5a a ==，则数列{lg }n a 的前8项和等于 （ ）A ．6B ．5C ．4D ．3【答案】C ．8. 【2014高考广东卷理第13题】若等比数列{}n a 的各项均为正数，且512911102e a a a a =+，则1220ln ln ln a a a +++= .9. 【2014高考安徽卷理第12题】数列{}n a 是等差数列，若1351,3,5a a a +++构成公比为q 的等比数列，则q =________.10. 【2014高考北京版理第12题】若等差数列{}n a 满足7897100,0a a a a a ++>+<，则当n = 时，{}n a 的前n 项和最大.【答案】8。

2014年全国高考数学分类汇编-数列全国2014年高考数学（理科）分类汇编1（2014福建理）3.等差数列｛a n｝的前n项和S.，若a i 2,S3 12，贝V a6 （）A.8B.10C.12D.142（2014广西理）10.等比数列3”｝中，a4 2,35 5，则数列｛lg a…｝的前8项和等于（）A. 6 B . 5 C . 4 D . 33（2014广西文）8.设等比数列｛a”｝的前”项和为S n，若S2 3,S4 15,贝V S6 （）A. 31 B . 32 C . 63 D ・644（2014重庆文）2.在等差数列｛a…｝中,印2,a3 a5 10，则a7 （）A.5B.8C.10D.145（2014辽宁文理）8.设等差数列啣的公差为d, 若数列｛2宀为递减数列，则（A. d 0B. d 0C. a-|d 0D. a1d 06（2014天津文）5.设a…是首项为a,,公差为1的等差数列，S n为其前n项和，若s, S2, S4,成等比数列，则a1=（A.2B.-2C. 1 D . 12 27（2014课标2文）（5）等差数列a n的公差为2,若a 2, 34, a 8成等比数列，则a 的前n 项和S.= () (A ) n n 1 ( B ) n n 18（2014重庆理）2.对任意等比数列{a n},下列说法 一定正确的是 （ ） A. 31,33,39成等比数列 B. a 2,a 3,a 6成等比数列成等比数列 D -a 3,a 6,a 9成等比数列9（2014安徽理）12.数列a n是等差数列，若311， 333， 355构成公比为q 的等比数列，贝y q _____________________ .10（2014安徽文）12.如图，学科网在等腰直角三 角形ABC 中，斜边BC 2迈，过点A 作BC 的垂线，垂足为 几；过点片作AC 的垂线，垂足为 A 2；过点A 作AC的垂线，垂足为A 3；…， 以此类推，设BA 31 , AA 1 32, A 1A 2 33，•…, A 5A 6 37，贝U 37.11（2014北京理）9.若等差数列a n满足a-i a 8 a90 , a 7 a io0 , 则当n _____________________(C )呼(D) n n 12~时a”的前n项和最大.12（2014广东理）13 .若等比数列a n的各项均为正数，且a0a” a g a>2 2e5，则ln a1 In a2In a2n_________ . ______13（2014广东文）13.等比数列a n的各项均为正数，且时 5 4 ,贝U Iog2 a1 Iog2a2 Iog2a3Iog2 a4 Iog2 a5 ___________________________________14（2014江苏文理）7.在各项均为正数的等比数列｛a n｝中,a2 1, a8 a6 2a4,则a6 的值是____15（2014江西文）14.在等差数列｛a…｝中，& i，公差为d，前n项和为｛an｝，当且仅当n 8时S取最大值，则d 的取值范围___________ .16（2014天津理）（11）设a n是首项为&，公差为-1的等差数列，S n为其前n项和.若S0S4成等比数列，则a 的值为_______________ .17（2014课标2文）（16）数列a n满足a n 1,a2=2,贝H a i = __________【答案】CCCBC DAD 9. 1 10. 111. 816.仃.1全国2014年咼考数学（文史）分类汇编 1（2014重庆文）16.已知a n 是首项为1, 公差为2的等差数列，S n表示a n的前n 项和.（I ）求 a n 及 S ；（H ）设b n是首项为2的等比数列，公比q 满足 q 2色1 q S 0，求b n的通项公式 及其前n 项和T n.【点拨】⑴a 2n 1,S n 2；(n )由 q 2a 41 q S 0得 q 4 ,所以 b n22n1,T n 2(4n 1)2（2014重庆理）22.设a 1 1,0.1 .a ： 2a n 2b （n N*）（1）若b 1,求a 2,a 3及数列｛%｝的通项公式；⑵ 若b 〔，冋：是否存在实数C 使得a 2nc a 2n 1对所有 n N*成立？证明你的结论.5n2【点拨】(1) a 1,a2 2,a3 5.2 1,& 1,猜想a n 1 1(可数归完成)；(2)设函数f(x) x2 2x 2 1,令f(x) x 得不动点x 4.仿(1)得a1 1,a2 0,a3 2 1,用数学归纳法可证明:a2n 1 a2m. 事实上,1O当n 1 时,32 0 4 v2 1 a3显然成立.2o.假定当n k时,a2k ： 32k 1成立,那么「"当n k 1 时，Qa2k 2 f (a2k 1) (a2k 1 1)21 1(a2k 2 1)2 (32k 1 1)21 (32k 2 1)2([ 1)2 1这就是说当n k 1时,a2k2 1 a2k 3也成立.3（2014浙江文）19、已知等差数列｛a n｝的公差d 0, 设｛a n｝的前n 项和为S n，a1 1，S2 S3 36.(1)求d及S n ；⑵求m,k （m,k N*）的值，使得i 3m 1 3m 2 L 3m k 65【点拨】（1） d 2,S n n2；⑵Q3m 2m 1, (k 1)(2m 1)冬严 2 654（2014浙江理）19.已知数列｛3n｝和｛b n｝满足a&L 3n（ 2）s（n N ）.若｛a n｝为等比数列，且 3 2,& 6 b又32k 3 f (32k 2) (32k 3 1)2(32k 2 1)2 11 43k2a(k 1)(2m k 1) 5 13 k 1 5 k 4 ... 2m k 1 13 m 5⑴求a n与b n；(2)设c a _L(n N).记数列｛c n｝的前n 项和为S n. ( i ) 求 S ； (ii )求正整数k ，使得对任意nN ，均有& 【点拨】(1)aa 2a 3 \2 ,a i a 2得 a 3268 .从而 q 2, a n a sqn 32n.由 a i a 2L a n( 2户 2 2)2【b n(n 1)(2) G 丄1吉(丄斗).所以a n t n 2n n n 1(i) S cia a L a 古》(分组裂项)(ii)Q^ ML 1 i)鳥 1)2"，易见",C 2,C 3,C 4 0,当n 5寸,c n0. 可见S 4最大,即S 4 S n . k 4■5(2014 a n 13a n1 .(I)证明(U)证明： 【点拨】(I)在a n 1 3(『2),可见数列a 1是以3为公比,以a 1 3为首项 的等比数列.故a n 2贰1叮.(H)法1(放缩法)Q^尹课标2理)17.已知数列a n满足a=1, 1是等比数列，并求a n的通项公式; 丄1…+丄3a 1 a 2 a n2 -a n1 3a n 1中两边加2：a2 3n 1 1 2 1 2 1 L 2 1 1 1 32 1 1 33 1 1 3n 1 1 12 （本题用的是"加点糖定理"）法2（数学归纳法）先证一个条件更強的结论20■假疋对于n 新命题成立,即1 3 1 3a 2 2 3n1 2天津文理）19.已知q 和n 均为给定的大于 1的自然数■设集合M 0,1,2丄,q 1,集合A xx X 1 X 2q L x!q n 1,x M ,i 1,2,L ,n（1） 当q 2 , n 3时，用列举法表示集合A ； （2） ^设 s,t ? A , s ai a 2q L a nq n 1,t b bq L bq n1,其中 a,b M , i 1,2,L ,n .证明：若 3nb ,则 s< t . 【点拨】（I ）解：当q 2 , n 3时，M 0,1 ,2x 2 4x s ,x 酣弓卑,2,3为 x ^x 中^ x,x 2,X 30 0 0 0勺 10 0 1 1 0 1 0 1 0 1 1 0 10 0 1 1 11 a2 31 2 1 1 L 132 93a n L 1a3 1氏1al13n0 ^1 2 3 2 2 1 1 a新命题成立.T,那么对于n一23 21al L 1a1al1al a1-a 1a3 1al3n3n3n6（2014 _ 2 3 2 4 3 5 4 1a2可得， A 0,12,3,4,5,6,7 .(H)证明：由 s,t?A , s a a 2q L a nq n 1, t bi bq L b nq n 1, Q,b Ms ta ib a 2 b ? q L an i b n i q n 2a nq n 1.q 1 q 1 q L q 1 q n 2 q n 17(2014四川文)19.设等差数列｛a n｝的公差为d ，点 (命)在函数f(x) 2x的图象上(nN ). (I)证明：数列⑹为等比数列；(H) 若& 1 ,函数f(x)的图象在点(a 2,b 2)处的切线在x 轴 上的截距为2侖，求数列｛a nb 2｝的前n 项和S n.【点拨】(I) 丫亍2d…(H) f (x) 2xln2 , k 刀2勺n2.切线方程y 2a2 2判n2(x a 2),依题设有a 2爲2爲a 2 2, b 24 . ^从a nb n 2 n 4n(等比差数列,乘公比、错位相减)得(3n 1)4n1 4$ 98(2014四川理)19.设等差数列｛a n｝的公差为d , 点®,b n)在函数f(x) 2x的图象上(nN *).(I) 若4 2，点(a 8,4b 7)在函数f(x)的图象上，求数列｛a n｝i 1,2丄，n 及an bn，可得q 1 1 q n 1q n 1 1 o.所以， s< t .的前n 项和S n；(2) 若 a 1，函数f(x)的图象在点(a 2,b 2)处的切线在X 轴 上的截距为2需，求数列©的前n 项和T n.【点拨】(1) Q4b 72a82a8 2b r2a7d 2. S n 23n ；(2) f (x) 2Xln2， k 切2Tn2 . 切线方程 y 2a2魯n2(x a 2),依题设有a 2爲2爲 比 2 , b24 .从而 b n 21(等比差数列,乘公比、错位相减)得T n2n2n29(2014上海文)23.已知数列满足3a n a n 1 3a n ,n N 1(1) 若322,83x,a 49，求x的取值范围；(2) 若｛a n｝是等比数列，且a m血，求正整数m 的最小值,以及m取最小值时相应｛aj 的公比；(3) 若a 1,a 2,L ,a 100成等差数列，求数列 a 1,B 2,L ,9!00的公差的取值范围.⑵易见 an0,3a n a n 1 3a n3 q 3又am10k 1 qm1 (3)m1 m 8,m 8.q 宦10 -(3) ^①当 n 1 时,a 1, [a a 1d 3a13【点拨】(1)由a 2 a 3 3a 2 a 3 a 4 3a 3x [3,6]；②当 2 n 100时,印 iga.! a n3am d 2器取 n1gd i99.综上島d 2・10（2014上海理）23.已知数列｛a n ｝满足1 3a n an 1 3环门 N 1 -(1)若 a 22,a 3x,a 49 ,⑵没a n是公比为q 等比数列，S n a 1 a> a j L a n，ig,S, 1 3S,n N求q 的取值范围;3（3）若a 1,a 2,L ,ak成等差数列，且a 32L a k1000，求正整数k 的最大值，以及k 取最大值 时相应数列a 1，a 2,L 耳的公差.【点拨】（1）由3：（2）由加 a n q 3a n,ai 1 [3S S a 1q 3S i ,1 q 2.下面证明任意的n 2,上式都成立. ①当q 1时,显然成立. ②当q 1时,显然成立.对于右不等式等价于 亡严 0.令f （x ）—q 二X1）,1 q 1 q f (x) q； l J q(q 3) 0,要使 f(x) 0,只需 f(1) 0即書0 q 2 .结合q /a 3 3a2 ”x [3,6]； a 4 3a3，结合 11 (1 q n) 1(1 q n 1)3 1 q 1 q3罟,其中左不等式11（2014山东文）（19）在等差数列｛a n｝中，已知公 差 d 2, a 2是a 1与a 4的等比中项. （I ）求数列｛a n｝的通项公式;（1）nb ，求 T n.【点拨】（I ） 212 , an 2n（D ） h n （n 1）（分奇偶讨论求和）（n 为奇数）1 n （n 2）（为偶数）12（2014山东理）19.已知等差数列｛a n｝的公差为 2,前n 项和为S n，且S 1,S 2,S 4成等比数列.（I ）求数列｛a n｝的通项公式；（H ）令b （ 1厂盘，求数列｛b n｝的前n 项和T n.得到【点拨】（I ） a 1,a n2n 1；n取2n1 1000 k a i(2 1) dk(k 1) 2 2 2k 1)k 1999,从而当 k 1999时,q2 1999 -(II )设 b，记T nqa3kS n3n 2 n(n ) b n ( 1叱1 2n 1 1](分奇偶讨论,最后合并)Tn2n；m ( 1)n.13（2014课标1文）17.已知a n是递增的等差数 列，a 2，a 4是方程X 25x 6 0的根。

专题6 数列1. 【2014高考安徽卷文第12题】如图，在等腰直角三角形ABC 中，斜边22BC =，过点A 作BC 的垂线，垂足为1A ；过点1A 作AC 的垂线，垂足为2A ；过点2A 作1AC 的垂线，垂足为3A ；…，以此类推，设1BA a =，12AA a =，123A A a =，…，567A A a =，则7a =________.3. 【2014高考广东卷文第13题】等比数列{}n a 的各项均为正数，且154a a =，则212223242l o g l o g l o g l o g l o g a a a a a ++++= .【答案】5.5. 【2014高考江西卷文第13题】在等差数列{}n a 中，71=a ，公差为d ，前n 项和为n S ，当且仅当8=n 时n S 取最大值，则d 的取值范围_________.6. 【2014高考辽宁卷文第9题】设等差数列{}n a 的公差为d ，若数列1{2}n a a为递减数列，则（ ） A ．0d < B ．0d > C ．10a d < D ．10a d > 【答案】C 【解析】试题分析：由已知得，11122nn a a a a -<，即111212n n a a a a -<，1n 1(a )21n a a --<，又n 1a n a d --=，故121a d<，从而10a d <，选C ．【考点定位】1、等差数列的定义；2、数列的单调性．7. 【2014高考全国2卷文第5题】等差数列{}n a 的公差是2，若248,,a a a 成等比数列，则{}n a 的前n 项和n S =（ ）A. (1)n n +B. (1)n n -C.(1)2n n + D. (1)2n n -8.. 【2014高考陕西卷文第8题】原命题为“若12n n n a a a ++<，n N +∈，则{}n a 为递减数列”，关于逆命题，否命题，逆否命题真假性的判断依次如下，正确的是（A ）真，真，真 （B ）假，假，真 （C ）真，真，假 （D ）假，假，假 【答案】A 【解析】试题分析：由12n n n a a a ++<1{}n n n a a a +⇒<⇒为递减数列，所以原命题为真命题； 逆命题：若{}n a 为递减数列，则12n n n a a a ++<，n N +∈；若{}n a 为递减数列，则1n n a a +<，即12nn n a a a ++<，所以逆命题为真； 否命题：若12n n n a a a ++≥，n N +∈，则{}n a 不为递减数列；由11{}2n n n n n n a a a a a a +++≥⇒≤+⇒不为递减数列，所以否命题为真；因为逆否命题的真假为原命题的真假相同，所以逆否命题也为真命题. 故选A考点：命题及命题的真假.10. 【2014高考陕西卷文第14题】已知0,1)(≥+=x xxx f ，若++∈==N n x f f x f x f x f n n )),(()(),()(11，则)(2014x f 的表达式为________.11. 【2014高考天津卷卷文第5题】设{}n a 是首项为1a ，公差为1-的等差数列，n S 为其前n 项和，若，，，421S S S 成等比数列，则1a =（ ）A.2B.-2C.21 D .12-13. 【2014高考安徽卷文第18题】 数列{}n a 满足111,(1)(1),n n a na n a n n n N ++==+++∈（1） 证明：数列{}na n是等差数列； （2） 设3nn n b a =⋅，求数列{}n b 的前n 项和n S14. 【2014高考北京卷文第15题】已知{}n a 是等差数列，满足13a =，412a =，数列{}n b 满足14b =，420b =，且{}n n b a -是等比数列.（1）求数列{}n a 和{}n b 的通项公式； （2）求数列{}n b 的前n 项和.15. 【2014高考大纲卷文第17题】数列{a n }满足a 1=1，a 2=2，a n+2=2a n+1-a n +2.（1）设b n =a n+1-a n ，证明{b n }是等差数列； （2）求数列{a n }的通项公式.16. 【2014高考福建卷文第17题】在等比数列{}n a 中，253,81a a ==.（1）求n a ； （2）设3log nn b a =，求数列{}n b 的前n 项和n S .【答案】(1) 13n n a -=.（2）22n n nS -=.17. 【2014高考广东卷文第19题】设各项均为正数的数列{}n a 的前n 项和为n S ，且n S 满足()223n n S n n S -+--()230n n +=，n N *∈.（1）求1a 的值；（2）求数列{}n a 的通项公式；（3）证明：对一切正整数n ，有()()()112211111113n n a a a a a a +++<+++.【答案】（1）12a =；（2）2n a n =；（3）详见解析.【解析】（1）令1n =得：()2111320S S ---⨯=，即21160S S +-=，()()11320S S ∴+-=，10S >，12S ∴=，即12a =；（2）由()()22233n n S n n S n n -+--+，得()()230n n S S n n ⎡⎤+-+=⎣⎦，()0n a n N *>∈，0n S ∴>，从而30n S +>，2n S n n ∴=+，所以当2n ≥时，()()()221112n n n a S S n n n n n -⎡⎤=-=+--+-=⎣⎦，又1221a ==⨯，()2n a n n N *∴=∈；1111111623213633n n ⎛⎫=+-=-< ⎪++⎝⎭. 【考点定位】本题以二次方程的形式以及n S 与n a 的关系考查数列通项的求解，以及利用放缩法证明数列不等式的综合问题，考查学生的计算能力与逻辑推理能力，属于中等偏难题.18. 【2014高考湖北卷文第19题】已知等差数列}{n a 满足：21=a ，且1a 、2a 、5a 成等比数列. （1）求数列}{n a 的通项公式.（2）记n S 为数列}{n a 的前n 项和，是否存在正整数n ，使得?80060+>n S n 若存在，求n 的最小值；若不存在，说明理由.19. 【2014高考湖南卷文第16题】已知数列{}n a 的前n 项和*∈+=N n n n S n ，22. (1)求数列{}n a 的通项公式；(2)设()n na n ab n 12-+=，求数列{}n b 的前n 2项和. 【答案】(1) n a n = (2) 21222n n T n +=+-20. 【2014高考江苏第20题】设数列{}n a 的前n 项和为n S .若对任意的正整数n ，总存在正整数m ，使得n m S a =，则称{}n a 是“H 数列”.（1）若数列{}n a 的前n 项和为*2()n n S n N =∈，证明：{}n a 是“H 数列”.（2）设{}n a 是等差数列，其首项11a =，公差0d <，若{}n a 是“H 数列”，求d 的值；（3）证明：对任意的等差数列{}n a ，总存在两个“H 数列” {}n b 和{}n c ，使得n n n a b c =+*()n N ∈成立.21. 【2014高考江西文第17题】已知数列{}n a 的前n 项和*∈-=N n n n S n ，232. （1）求数列{}n a 的通项公式；（2）证明：对任意1>n ，都有*∈N m ，使得m n a a a ，，1成等比数列.而此时*∈N m ，且,m n >所以对任意1>n ，都有*∈N m ，使得m n a a a ，，1成等比数列. 考点：由和项求通项，等比数列22. 【2014高考全国1文第17题】已知{}n a 是递增的等差数列，2a ，4a 是方程2560x x -+=的根。

2014年全国高考数学分类汇编-数列全国2014年高考数学（理科）分类汇编1（2014福建理）3.等差数列｛a n｝的前n项和S.，若a i 2,S3 12，贝V a6 （）A.8B.10C.12D.142（2014广西理）10.等比数列3”｝中，a4 2,35 5，则数列｛lg a…｝的前8项和等于（）A. 6 B . 5 C . 4 D . 33（2014广西文）8.设等比数列｛a”｝的前”项和为S n，若S2 3,S4 15,贝V S6 （）A. 31 B . 32 C . 63 D ・644（2014重庆文）2.在等差数列｛a…｝中,印2,a3 a5 10，则a7 （）A.5B.8C.10D.145（2014辽宁文理）8.设等差数列啣的公差为d, 若数列｛2宀为递减数列，则（A. d 0B. d 0C. a-|d 0D. a1d 06（2014天津文）5.设a…是首项为a,,公差为1的等差数列，S n为其前n项和，若s, S2, S4,成等比数列，则a1=（A.2B.-2C. 1 D . 12 27（2014课标2文）（5）等差数列a n的公差为2,若a 2, 34, a 8成等比数列，则a 的前n 项和S.= () (A ) n n 1 ( B ) n n 18（2014重庆理）2.对任意等比数列{a n},下列说法 一定正确的是 （ ） A. 31,33,39成等比数列 B. a 2,a 3,a 6成等比数列成等比数列 D -a 3,a 6,a 9成等比数列9（2014安徽理）12.数列a n是等差数列，若311， 333， 355构成公比为q 的等比数列，贝y q _____________________ .10（2014安徽文）12.如图，学科网在等腰直角三 角形ABC 中，斜边BC 2迈，过点A 作BC 的垂线，垂足为 几；过点片作AC 的垂线，垂足为 A 2；过点A 作AC的垂线，垂足为A 3；…， 以此类推，设BA 31 , AA 1 32, A 1A 2 33，•…, A 5A 6 37，贝U 37.11（2014北京理）9.若等差数列a n满足a-i a 8 a90 , a 7 a io0 , 则当n _____________________(C )呼(D) n n 12~时a”的前n项和最大.12（2014广东理）13 .若等比数列a n的各项均为正数，且a0a” a g a>2 2e5，则ln a1 In a2In a2n_________ . ______13（2014广东文）13.等比数列a n的各项均为正数，且时 5 4 ,贝U Iog2 a1 Iog2a2 Iog2a3Iog2 a4 Iog2 a5 ___________________________________14（2014江苏文理）7.在各项均为正数的等比数列｛a n｝中,a2 1, a8 a6 2a4,则a6 的值是____15（2014江西文）14.在等差数列｛a…｝中，& i，公差为d，前n项和为｛an｝，当且仅当n 8时S取最大值，则d 的取值范围___________ .16（2014天津理）（11）设a n是首项为&，公差为-1的等差数列，S n为其前n项和.若S0S4成等比数列，则a 的值为_______________ .17（2014课标2文）（16）数列a n满足a n 1,a2=2,贝H a i = __________【答案】CCCBC DAD 9. 1 10. 111. 816.仃.1全国2014年咼考数学（文史）分类汇编 1（2014重庆文）16.已知a n 是首项为1, 公差为2的等差数列，S n表示a n的前n 项和.（I ）求 a n 及 S ；（H ）设b n是首项为2的等比数列，公比q 满足 q 2色1 q S 0，求b n的通项公式 及其前n 项和T n.【点拨】⑴a 2n 1,S n 2；(n )由 q 2a 41 q S 0得 q 4 ,所以 b n22n1,T n 2(4n 1)2（2014重庆理）22.设a 1 1,0.1 .a ： 2a n 2b （n N*）（1）若b 1,求a 2,a 3及数列｛%｝的通项公式；⑵ 若b 〔，冋：是否存在实数C 使得a 2nc a 2n 1对所有 n N*成立？证明你的结论.5n2【点拨】(1) a 1,a2 2,a3 5.2 1,& 1,猜想a n 1 1(可数归完成)；(2)设函数f(x) x2 2x 2 1,令f(x) x 得不动点x 4.仿(1)得a1 1,a2 0,a3 2 1,用数学归纳法可证明:a2n 1 a2m. 事实上,1O当n 1 时,32 0 4 v2 1 a3显然成立.2o.假定当n k时,a2k ： 32k 1成立,那么「"当n k 1 时，Qa2k 2 f (a2k 1) (a2k 1 1)21 1(a2k 2 1)2 (32k 1 1)21 (32k 2 1)2([ 1)2 1这就是说当n k 1时,a2k2 1 a2k 3也成立.3（2014浙江文）19、已知等差数列｛a n｝的公差d 0, 设｛a n｝的前n 项和为S n，a1 1，S2 S3 36.(1)求d及S n ；⑵求m,k （m,k N*）的值，使得i 3m 1 3m 2 L 3m k 65【点拨】（1） d 2,S n n2；⑵Q3m 2m 1, (k 1)(2m 1)冬严 2 654（2014浙江理）19.已知数列｛3n｝和｛b n｝满足a&L 3n（ 2）s（n N ）.若｛a n｝为等比数列，且 3 2,& 6 b又32k 3 f (32k 2) (32k 3 1)2(32k 2 1)2 11 43k2a(k 1)(2m k 1) 5 13 k 1 5 k 4 ... 2m k 1 13 m 5⑴求a n与b n；(2)设c a _L(n N).记数列｛c n｝的前n 项和为S n. ( i ) 求 S ； (ii )求正整数k ，使得对任意nN ，均有& 【点拨】(1)aa 2a 3 \2 ,a i a 2得 a 3268 .从而 q 2, a n a sqn 32n.由 a i a 2L a n( 2户 2 2)2【b n(n 1)(2) G 丄1吉(丄斗).所以a n t n 2n n n 1(i) S cia a L a 古》(分组裂项)(ii)Q^ ML 1 i)鳥 1)2"，易见",C 2,C 3,C 4 0,当n 5寸,c n0. 可见S 4最大,即S 4 S n . k 4■5(2014 a n 13a n1 .(I)证明(U)证明： 【点拨】(I)在a n 1 3(『2),可见数列a 1是以3为公比,以a 1 3为首项 的等比数列.故a n 2贰1叮.(H)法1(放缩法)Q^尹课标2理)17.已知数列a n满足a=1, 1是等比数列，并求a n的通项公式; 丄1…+丄3a 1 a 2 a n2 -a n1 3a n 1中两边加2：a2 3n 1 1 2 1 2 1 L 2 1 1 1 32 1 1 33 1 13n 1 112 （本题用的是"加点糖定理"）法2（数学归纳法）先证一个条件更強的结论20■假疋对于n 新命题成立,即1 3 1 3a 2 2 3n1 2天津文理）19.已知q 和n 均为给定的大于 1的自然数■设集合M 0,1,2丄,q 1,集合A xx X 1 X 2q L x!q n 1,x M ,i 1,2,L ,n（1） 当q 2 , n 3时，用列举法表示集合A ； （2） ^设 s,t ? A , s ai a 2q L a nq n 1,t b bq L bq n1,其中 a,b M , i 1,2,L ,n .证明：若 3nb ,则 s< t . 【点拨】（I ）解：当q 2 , n 3时，M 0,1 ,2x 2 4x s ,x 酣弓卑,2,3为 x ^x 中^ x,x 2,X 30 0 0 0勺 10 0 1 1 0 1 0 1 0 1 1 0 10 01 1 11 a2 31 2 1 1 L 132 93a n L1a3 1氏1al13n0 ^1 2 3 2 2 1 1 a新命题成立.T,那么对于n一23 21al L 1a1al1al a1-a 1a3 1al3n3n3n6（2014 _ 2 3 2 4 3 5 4 1a2可得， A 0,12,3,4,5,6,7 .(H)证明：由 s,t?A , s a a 2q L a nq n 1, t bi bq L b nq n 1, Q,b Ms ta ib a 2 b ? q L an i b n i q n 2a nq n 1.q 1 q 1 q L q 1 q n 2 q n 17(2014四川文)19.设等差数列｛a n｝的公差为d ，点 (命)在函数f(x) 2x的图象上(nN ). (I)证明：数列⑹为等比数列；(H) 若& 1 ,函数f(x)的图象在点(a 2,b 2)处的切线在x 轴 上的截距为2侖，求数列｛a nb 2｝的前n 项和S n.【点拨】(I) 丫亍2d…(H) f (x) 2xln2 , k 刀2勺n2 .切线方程y 2a2 2判n2(x a 2),依题设有a 2爲2爲a 2 2, b 24 . ^从a n bn2n 4n(等比差数列,乘公比、错位相减)得(3n 1)4n1 4$ 98(2014四川理)19.设等差数列｛a n｝的公差为d , 点®,b n)在函数f(x) 2x的图象上(nN *).(I) 若4 2，点(a 8,4b 7)在函数f(x)的图象上，求数列｛a n｝i 1,2丄，n 及an bn，可得q 1 1 q n 1q n 1 1 o.所以， s< t .的前n 项和S n；(2) 若 a 1，函数f(x)的图象在点(a 2,b 2)处的切线在X 轴 上的截距为2需，求数列©的前n 项和T n.【点拨】(1) Q4b 72a82a8 2b r2a7d 2. S n 23n ；(2) f (x) 2Xln2， k 切2Tn2 . 切线方程 y 2a2魯n2(x a 2),依题设有a 2爲2爲 比 2 , b24 .从而 b n 21(等比差数列,乘公比、错位相减)得T n2n2n29(2014上海文)23.已知数列满足3a n a n 1 3a n ,n N 1(1) 若322,83x,a 49，求x的取值范围；(2) 若｛a n｝是等比数列，且a m血，求正整数m 的最小值,以及m取最小值时相应｛aj 的公比；(3) 若a 1,a 2,L ,a 100成等差数列，求数列 a 1,B 2,L ,9!00的公差的取值范围.⑵易见 an0,3a n a n 1 3a n3 q 3又am10k 1 qm1 (3)m1 m 8,m 8.q 宦10 -(3) ^①当 n 1 时,a 1, [a a 1d 3a13【点拨】(1)由a 2 a 3 3a 2 a 3 a 4 3a 3x [3,6]；②当 2 n 100时,印 iga.! a n3am d 2器取 n1gd i99.综上島 d 2・10（2014上海理）23.已知数列｛a n ｝满足1 3a n an 1 3环门 N 1 -(1)若 a 22,a 3x,a 49 ,⑵没a n是公比为q 等比数列，S n a 1 a> a j L a n，ig,S, 1 3S,n N求q 的取值范围;3（3）若a 1,a 2,L ,ak成等差数列，且a 32L a k1000，求正整数k 的最大值，以及k 取最大值 时相应数列a 1，a 2,L 耳的公差.【点拨】（1）由3：（2）由加 a n q 3a n,ai 1 [3S S a 1q 3S i ,1 q 2.下面证明任意的n 2,上式都成立. ①当q 1时,显然成立. ②当q 1时,显然成立.对于右不等式等价于 亡严 0.令f （x ）—q 二X1）,1 q 1 q f (x) q； l J q(q 3) 0,要使 f(x) 0,只需 f(1) 0即書0 q 2 .结合q /a 3 3a2 ”x [3,6]； a 4 3a3，结合 11 (1 q n) 1(1 q n 1)3 1 q 1 q3罟,其中左不等式11（2014山东文）（19）在等差数列｛a n｝中，已知公 差 d 2, a 2是a 1与a 4的等比中项. （I ）求数列｛a n｝的通项公式;（1）nb ，求 T n.【点拨】（I ） 212 , an 2n（D ） h n （n 1）（分奇偶讨论求和）（n 为奇数）1 n （n 2）（为偶数）12（2014山东理）19.已知等差数列｛a n｝的公差为 2,前n 项和为S n，且S 1,S 2,S 4成等比数列.（I ）求数列｛a n｝的通项公式；（H ）令b （ 1厂盘，求数列｛b n｝的前n 项和T n.得到【点拨】（I ） a 1,a n2n 1；n取2n1 1000 k a i(2 1) dk(k 1) 2 2 2k 1)k 1999,从而当 k 1999时,q2 1999 -(II )设 b，记T nqa3k2S n3n 2 n(n ) b n ( 1叱1 2n 1 1](分奇偶讨论,最后合并)Tn2n；m ( 1)n.13（2014课标1文）17.已知a n是递增的等差数 列，a 2，a 4是方程X 25x 6 0的根。

一．基础题组1. 【江苏省诚贤中学2014届高三数学月考试题】在等比数列｛n a ｝中,若7944,1a a a ⋅==,则12a 的值是 ．2. 【江苏省诚贤中学2014届高三数学月考试题】已知等比数列}{n a 的前n 项和为n S ，若62,256382-==S a a a a ，则1a 的值是 ．3. 【江苏省灌云高级中学2013-2014学年度高三第一学期期中考试】 若n S 是等差数列}{n a 的前n 项和,且8320S S -=，则11S 的值为 ．4. 【江苏省灌云高级中学2013-2014学年度高三第一学期期中考试】等差数列{}n a 中，公差0d ≠，且2371220a a a -+=，数列{}n b 是等比数列，且77b a =则68b b ＝ ．5. 【江苏省灌云高级中学2013-2014学年度高三第一学期期中考试】已知数列{}n a 满足：121,(0).a a a a ==>数列{}n b 满足1(*)n n n b a a n N +=∈。

(1)若{}n a 是等差数列，且312,b =求a 的值及{}n a 的通项公式；(2)当{}n b 是公比为1a -的等比数列时，{}n a 能否为等比数列？若能，求出a 的值；若不能，请说明理由.试题解析：解：（1）{}n a 是等差数列，121,(0),1(1)(1)n a a a a a n a ==>∴=+--.--- 2分又33412,12,(21)(32)12b a a a a =∴=--=即,解得526a a ==-或，0, 2.n a a a n >∴== 从而. …………………………6分（2）数列{}n a 不能为等比数列. …………………8分11222131,,1,1n n n n n n n n n n n n nb a a a ab a a a a a b a a a a +++++++=∴===-∴=- 则， ………10分假设数列{}n a 能为等比数列，由21231,,a a a a a ===得， ………………12分221,10a a a a ∴=--+=即， 此方程无解，∴数列{}n a 一定不能为等比数列.………14分考点：1.等差数列的通项公式;2.等比数列的定义6. 【江苏省灌云高级中学2013-2014学年度高三第一学期期中考试】设等比数列{}n a 的首项为12a =，公比为q （q 为正整数），且满足33a 是18a 与5a 的等差中项；数列{}n b 满足232()02n n n t b n b -++=（*,t R n N ∈∈）. （1）求数列{}n a 的通项公式；（2）试确定t 的值，使得数列{}n b 为等差数列；（3）当{}n b 为等差数列时，对每个正整数k ，在k a 与1k a +之间插入k b 个2，得到一个新数列{}n c . 设n T 是数列{}n c 的前n 项和，试求满足12m m T c +=的所有正整数m .试题解析：解：（Ⅰ）因为31568a a a =+,所以2468q q =+， 解得2242q q ==或（舍），则2q =………………3分又12a =，所以2nn a =……………………………5分7. 【南京市、盐城市2014届高三第一次模拟考试】已知等比数列{}n a 的首项为43，公比为13-，其前n 项和为n S ，若1n n A S B S ≤-≤对*n N ∈恒成立，则B A -的最小值为8. 【南京市、盐城市2014届高三第一次模拟考试】等差数列{}n a 的前n 项和为n S ，已知12a =，622S =.（1）求n S ；（2）若从{}n a 中抽取一个公比为q 的等比数列{}n k a ，其中11k =，且12n k k k <<< ，*n k N ∈.①当q 取最小值时，求{}n k 的通项公式；②若关于*()n n N ∈的不等式16n n S k +>有解，试求q 的值.试题解析：（1）设等差数列的公差为d ，则611665222S a d =+⋅⋅=，解得23d =， (2)分 所以(5)3n n n S +=. ………4分 （2）因为数列}{n a 是正项递增等差数列，所以数列}{n k a 的公比1>q ， 若22=k ，则由382=a ，得3412==a a q ，此时932)34(223=⋅=k a ，由)2(32932+=n ，9. 【江苏省通州高级中学2013-2014学年度秋学期期中考试】 各项均为正数的等比数列{}n a 中，811=a 12...8(2,)m m a a a m m N +⋅⋅⋅=>∈，若从中抽掉一项后，余下的m-1项之积为1m -，则被抽掉的是第 ▲_ 项.10. 【江苏省通州高级中学2013-2014学年度秋学期期中考试】 设各项均为正实数的数列}{n a 的前n 项和为n S ，且满足2)1(4+=n n a S （*N n ∈）．（Ⅰ）求数列}{n a 的通项公式； （Ⅱ）设数列}{n b 的通项公式为n b nn a a t=+（*N t ∈），若1b ，2b ，m b （*,3N m m ∈≥）成等差数列，求t 和m 的值；（Ⅲ）证明：存在无穷多个三边成等比数列且互不相似的三角形，其三边长为}{n a 中的三项1n a ，2n a ，3n a ．角形的三边2)32(1+=k a n ，)52)(32(2++=k k a n ，2)52(3+=k a n ，再利用三角形两边之和大于第三边来判断能构成一个三角形;又欲证明它们互不相似，这是一个否定性命题，故不难想到运用反证法证明，假设某两个三角形相似，用上述所设某两边代入并整理，可得21k k =，与21k k ≠相矛盾，从而命题得证．11. 【江苏省扬州中学2013—2014学年第一学期月考】在等差数列{}n a 中，若7893a a a ++=，则该数列的前15项的和为 ．【答案】15 【解析】试题分析：对数列问题，能用性质的尽量应用性质解题可以更简捷，由等差数列的性质789833a a a a ++=＝，81a =，1581515S a ==．考点：等差数列的性质，等差数列{}n a 中，2(,,*)m n p m n p N +=∈2m n p a a a ⇒+=12. 【江苏省扬州中学2013—2014学年第一学期月考】 设12()1f x x=+，11()[()]n n f x f f x +=，且(0)1(0)2n n n f a f -=+，则2014a = ．13.【江苏省扬州中学2013—2014学年第一学期月考】设13521A ,,,,2482n n n -⎧⎫=⎨⎬⎩⎭ (),2n N n *∈≥，A n 的所有非空子集中的最小元素的和为S ，则S = ．【答案】⎪⎩⎪⎨⎧∈≥-=*2,3,212,47N n n n n【解析】试题分析：这个问题主要是研究集合n A 中的每个元素在和S 中分别出现多少次，事实上，以12为例，集合14. 【江苏省扬州中学2013—2014学年第一学期月考】已知函数()21f x x =-，设曲线()y f x =在点(),n n x y 处的切线与x 轴的交点为()1,0n x +，其中1x 为正实数．（1）用n x 表示1n x +； （2）12x =,若1lg1n n n x a x +=-，试证明数列{}n a 为等比数列，并求数列{}n a 的通项公式； （3）若数列{}n b 的前n 项和()12n n n S +=，记数列}{n n b a ⋅的前n 项和n T ，求n T ．21321n n a b a b a b +=+++ ，两式相减，即n n T qT -，这个和是容易求得的．15. 【苏北四市2014届高三第一次质量检测】 设等比数列{}n a 的前n 项和为n S ，若435a a a ，，成等差数列，且33k S =，163k S +=-，其中k N *∈，则2k S +的值为 ．16. 【苏北四市2014届高三第一次质量检测】 已知数列{}n a 满足1a x =，23a x =，2*1132(2,)n n n S S S n n n +-++=+∈N ≥，n S 是数列{}n a 的前n 项和．(1)若数列{}n a 为等差数列． （ⅰ）求数列的通项n a ；（ⅱ）若数列{}n b 满足2n a n b =，数列{}n c 满足221n n n n c t b tb b ++=--，试比较数列{}n b 前n 项和n B 与{}n c 前n 项和n C 的大小；(2)若对任意*n ∈N ，1n n a a +<恒成立，求实数x 的取值范围．试题解析：(1)（ⅰ）因为21132(2,*)n n n S S S n n n +-++=+∈N ≥，所以32114S S S ++=，即3212314a a a ++=，又12,3a x a x ==，所以3149a x =-， ……………………2分 又因为数列{}n a 成等差数列，所以2132a a a =+，即()6149x x x =+-，解得1x =，所以()()()1111221*n a a n d n n n =+-=+-⨯=-∈N ； ……………………4分17. 【苏州市2014届高三调研测试】 设S n 为等差数列{a n }的前n 项和，已知S 5 = 5，S 9 =27，则S 7 = ▲ ．18. 【苏州市2014届高三调研测试】 设数列{a n }满足a n +1 = 2a n + n 2 - 4n + 1．（1）若a 1 = 3，求证：存在2()f n an bn c =++（a ，b ，c 为常数），使数列{ a n + f (n ) }是等比数列，并求出数列{a n }的通项公式；（2）若a n 是一个等差数列{b n }的前n 项和，求首项a 1的值与数列{b n }的通项公式．试题解析：解（1）,14221+-+=+n n a a n n设),(2)1()1(221c bn an a c n b n a a n n +++=++++++…………………… 2分 也即,)2(221b a c n a b an a a n n --+-++=+…… 4分19．【江苏省兴化市安丰高级中学2014届高三12月月考】设等比数列{}n a 的公比为q ，前n 项和为n S ．则“||q =是“627S S =” 的条件．20. 【江苏省兴化市安丰高级中学2014届高三12月月考】 数列{}n a 是公差不为0的等差数列，且862a a a =+，则=55a S ．二．能力题组1. 【江苏省兴化市安丰高级中学2014届高三12月月考】已知数列{}n a 中，，31=a 前n 和1(1)(1)12n n S n a =++-（1）求证：数列{}n a 是等差数列 （2）求数列{}n a 的通项公式（3）设数列⎭⎬⎫⎩⎨⎧+11n n a a 的前n 项和为n T ，是否存在实数M ，使得M T n ≤对一切正整数n 都成立？若存在，求M 的最小值，若不存在，试说明理由。

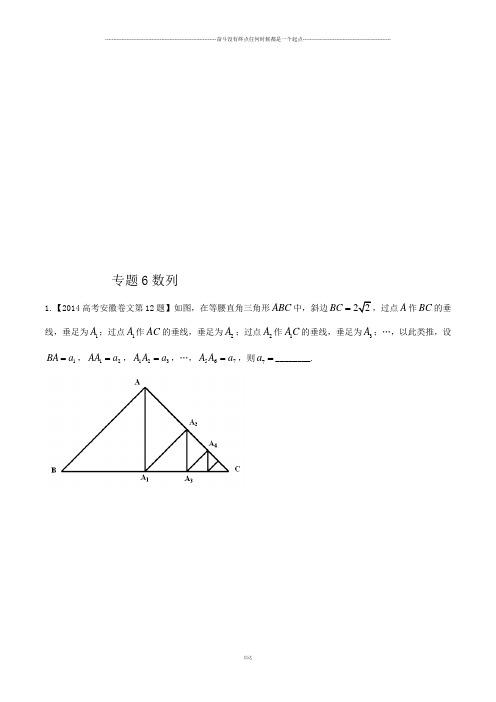
专题6数列1.【2014高考安徽卷文第12题】如图，在等腰直角三角形ABC 中，斜边22BC =，过点A 作BC 的垂线，垂足为1A ；过点1A 作AC 的垂线，垂足为2A ；过点2A 作1AC 的垂线，垂足为3A ；…，以此类推，设1BA a =，12AA a =，123A A a =，…，567A A a =，则7a =________.3.【2014高考广东卷文第13题】等比数列{}n a 的各项均为正数，且154a a =，则2122232425log log log log log a a a a a ++++= .【答案】5.5.【2014高考江西卷文第13题】在等差数列{}n a 中，71=a ，公差为d ，前n 项和为n S ，当且仅当8=n 时n S 取最大值，则d 的取值范围_________.6.【2014高考辽宁卷文第9题】设等差数列{}n a 的公差为d ，若数列1{2}n a a为递减数列，则（） A ．0d <B ．0d >C ．10a d <D ．10a d > 【答案】C 【解析】试题分析：由已知得，11122nn a a a a -<，即111212n n a a a a -<，1n 1(a )21n a a --<，又n 1a n a d --=，故121a d<，从而10a d <，选C ．【考点定位】1、等差数列的定义；2、数列的单调性．7.【2014高考全国2卷文第5题】等差数列{}n a 的公差是2，若248,,a a a 成等比数列，则{}n a 的前n 项和n S =（）A.(1)n n +B.(1)n n -C.(1)2n n + D.(1)2n n -8..【2014高考陕西卷文第8题】原命题为“若12n n n a a a ++<，n N +∈，则{}n a 为递减数列”，关于逆命题，否命题，逆否命题真假性的判断依次如下，正确的是（A ）真，真，真（B ）假，假，真（C ）真，真，假（D ）假，假，假 【答案】A 【解析】试题分析：由12n n n a a a ++<1{}n n n a a a +⇒<⇒为递减数列，所以原命题为真命题； 逆命题：若{}n a 为递减数列，则12n n n a a a ++<，n N +∈；若{}n a 为递减数列，则1n n a a +<，即12n n n a a a ++<，所以逆命题为真；否命题：若12n n n a a a ++≥，n N +∈，则{}n a 不为递减数列；由11{}2n n n n n n a a a a a a +++≥⇒≤+⇒不为递减数列，所以否命题为真；因为逆否命题的真假为原命题的真假相同，所以逆否命题也为真命题. 故选A考点：命题及命题的真假.10.【2014高考陕西卷文第14题】已知0,1)(≥+=x xxx f ，若++∈==N n x f f x f x f x f n n )),(()(),()(11，则)(2014x f 的表达式为________.11.【2014高考天津卷卷文第5题】设{}n a 是首项为1a ，公差为1-的等差数列，n S 为其前n 项和，若，，，421S S S 成等比数列，则1a =（）A.2B.-2C.21D.12-13.【2014高考安徽卷文第18题】数列{}n a 满足111,(1)(1),n n a na n a n n n N ++==+++∈（1） 证明：数列{}na n是等差数列； （2） 设3nn n b a =⋅，求数列{}n b 的前n 项和n S14.【2014高考北京卷文第15题】已知{}n a 是等差数列，满足13a =，412a =，数列{}n b 满足14b =，420b =，且{}n n b a -是等比数列.（1）求数列{}n a 和{}n b 的通项公式； （2）求数列{}n b 的前n 项和.15.【2014高考大纲卷文第17题】数列{a n }满足a 1=1，a 2=2，a n+2=2a n+1-a n +2.（1）设b n =a n+1-a n ，证明{b n }是等差数列； （2）求数列{a n }的通项公式.16.【2014高考福建卷文第17题】在等比数列{}n a 中，253,81a a ==.（1）求n a ； （2）设3log nn b a =，求数列{}n b 的前n 项和n S .【答案】(1)13n n a -=.（2）22n n nS -=.17.【2014高考广东卷文第19题】设各项均为正数的数列{}n a 的前n 项和为n S ，且n S 满足()223n n S n n S -+--()230n n +=，n N *∈.（1）求1a 的值；（2）求数列{}n a 的通项公式；（3）证明：对一切正整数n ，有()()()112211111113n n a a a a a a +++<+++. 【答案】（1）12a =；（2）2n a n =；（3）详见解析.【解析】（1）令1n =得：()2111320S S ---⨯=，即21160S S +-=，()()11320S S ∴+-=，10S >，12S ∴=，即12a =；（2）由()()22233n n S n n S n n -+--+，得()()230n n S S n n ⎡⎤+-+=⎣⎦， ()0n a n N *>∈，0n S ∴>，从而30n S +>，2n S n n ∴=+，所以当2n ≥时，()()()221112n n n a S S n n n n n -⎡⎤=-=+--+-=⎣⎦， 又1221a ==⨯，()2n a n n N *∴=∈；1111111623213633n n ⎛⎫=+-=-< ⎪++⎝⎭. 【考点定位】本题以二次方程的形式以及n S 与n a 的关系考查数列通项的求解，以及利用放缩法证明数列不等式的综合问题，考查学生的计算能力与逻辑推理能力，属于中等偏难题.18.【2014高考湖北卷文第19题】已知等差数列}{n a 满足：21=a ，且1a 、2a 、5a 成等比数列.（1）求数列}{n a 的通项公式.（2）记n S 为数列}{n a 的前n 项和，是否存在正整数n ，使得?80060+>n S n 若存在，求n 的最小值；若不存在，说明理由.19.【2014高考湖南卷文第16题】已知数列{}n a 的前n 项和*∈+=N n n n S n ，22. (1)求数列{}n a 的通项公式；(2)设()n na n ab n 12-+=，求数列{}n b 的前n 2项和.【答案】(1)n a n =(2)21222n n T n +=+-20.【2014高考江苏第20题】设数列{}n a 的前n 项和为n S .若对任意的正整数n ，总存在正整数m ，使得n m S a =，则称{}n a 是“H 数列”.（1）若数列{}n a 的前n 项和为*2()n n S n N =∈，证明：{}n a 是“H 数列”.（2）设{}n a 是等差数列，其首项11a =，公差0d <，若{}n a 是“H 数列”，求d 的值；（3）证明：对任意的等差数列{}n a ，总存在两个“H 数列”{}n b 和{}n c ，使得n n n a b c =+*()n N ∈成立.21.【2014高考江西文第17题】已知数列{}n a 的前n 项和*∈-=N n n n S n ，232. （1）求数列{}n a 的通项公式；（2）证明：对任意1>n ，都有*∈N m ，使得m n a a a ，，1成等比数列.而此时*∈N m ，且,m n >所以对任意1>n ，都有*∈N m ，使得m n a a a ，，1成等比数列. 考点：由和项求通项，等比数列22.【2014高考全国1文第17题】已知{}n a 是递增的等差数列，2a ，4a 是方程2560x x -+=的根。

2014年高考数学理科数列大题专项训练1．（本小题满分12分）已知数列{a n}满足a1=1,a2=3,a n+2=3a n+1-2a n（n∈N+）（1）证明：数列{a n+1-a n }是等比数列；（2）求数列{a n}的通项公式2.（12分）已知数列{a n}的前n项和S n=kc n-k(其中c,k为常数),且a2=4,a6=8a3.(1)求a n;(2)求数列{na n}的前n项和T n.已知数列{}n a 的前n 项和为n S ，且满足：1a a =(0)a ≠，1n n a rS += (n ∈N *，,1)r R r ∈≠-．（Ⅰ）求数列{}n a 的通项公式；（Ⅱ）若存在k ∈ N *，使得1k S +，k S ，2k S +成等差数列，是判断：对于任意的m ∈N *，且2m ≥，1m a +，m a ，2m a +是否成等差数列，并证明你的结论． 4．（本小题满分16分）已知数列{}n a 满足1a x =，23a x =，2*1132(2,)n n n S S S n n n +-++=+∈N ≥，n S 是数列{}n a 的前n 项和．(1)若数列{}n a 为等差数列．（ⅰ）求数列的通项n a ；（ⅱ）若数列{}n b 满足2n a n b =，数列{}n c 满足221n n n n c t b tb b ++=--，试比较数列{}n b前n 项和n B 与{}n c 前n 项和n C 的大小； (2)若对任意*n ∈N ，1n n a a +<恒成立，求实数x 的取值范围．已知函数xnx x f n +=)(，（x ＞0，),1Z n n ∈≥，以点))(,(n f n n 为切点作函数)(x f y n =图像的切线n l ，记函数)(x f y n =图像与三条直线n l n x n x ,1,+==所围成的区域面积为n a 。

（Ⅰ）求n a ； （Ⅱ）求证：n a ＜231n ； （Ⅲ）设n S 为数列{}n a 的前n 项和，求证：n S ＜95.6．（本题满分13分）已知,,a b c 是正数， 1lg a a =，2lg a b =，3lg a c =． （Ⅰ）若,,a b c 成等差数列，比较12a a -与23a a -的大小；（Ⅱ）若122331a a a a a a ->->-，则,,a b c 三个数中，哪个数最大，请说明理由；（Ⅲ）若a t =，2b t =，3c t =（t *∈N ），且1a ，2a ，3a 的整数部分分别是,m 21,m +221,m +求所有t 的值．7（8分）．已知数列{}n a 满足11=a ，且nn n a a 221+=-（n ≥2且n ∈N ）（Ⅰ）求数列{}n a 的通项公式；（Ⅱ）设数列{}n a 的前n 项之和n S ，求n S ,并证明：322-n S n n＞．8．（本小题满分12分）在公差不为零的等差数列{n a }中，已知a 1=l ，．且a 1，a 2，a 5依次成等比数列．数列{n b }满足b n+1=2b n -1且b 1=3.（I ）求{b n }的通项公式； （Ⅱ）设数列{12n n a a +⋅}的前n 项和为S n ，试比较S n 与1一1n b 的大小．9.设等差数列{}n a 的前n 项和为n S ，已知12a =，622S =. （1）求n S ；（2）若从{}n a 中抽取一个公比为q 的等比数列{}n k a ，其中11k =，且12n k k k <<< ，*n k N ∈.①当q 取最小值时，求{}n k 的通项公式；②若关于*()n n N ∈的不等式16n n S k +>有解，试求q 的值.10. (本小题满分16分)设数列{}n a 的各项均为正实数，2log n n b a =，若数列{}n b 满足20b =，12log n n b b p +=+，其中p 为正常数，且1p ≠.（1）求数列{}n a 的通项公式；（2）是否存在正整数M ，使得当n M >时，1473216n a a a a a -⋅⋅⋅⋅⋅⋅⋅>恒成立？若存在，求出使结论成立的p 的取值范围和相应的M 的最小值；若不存在，请说明理由；（3）若2p =，设数列{}n c 对任意的*n N ∈，都有12132n n n c b c b c b --+++⋅⋅⋅1n c b +2n =-成立，问数列{}n c 是不是等比数列？若是，请求出其通项公式；若不是，请说明理由.11．（本小题满分14分）设等差数列{}n a 的公差为d ，前n 项和为n S ，已知35S a =，525S =． （1）求数列{}n a 的通项公式；（2）若p ，q 为互不相等的正整数，且等差数列{}n b 满足p a b p =，q a b q =，求数列{}n b 的前n 项和n T ．12．已知等差数列{}n a 满足{}3577,26,n a a a a =+=的前n 项和为n S 。

数 学D 单元 数列D1 数列的概念与简单表示法 17．、、[2014·江西卷] 已知首项都是1的两个数列{a n }，{b n }(b n ≠0，n ∈N *)满足a n b n ＋1－a n ＋1b n ＋2b n ＋1b n ＝0.(1)令c n ＝a nb n ，求数列{c n }的通项公式；(2)若b n ＝3n －1，求数列{a n }的前n 项和S n .17．解：(1)因为a n b n ＋1－a n ＋1b n ＋2b n ＋1b n ＝0，b n ≠0(n ∈N *)，所以a n ＋1b n ＋1－a nb n＝2，即c n ＋1－c n ＝2，所以数列{c n }是以c 1＝1为首项，d ＝2为公差的等差数列，故c n ＝2n －1.(2)由b n ＝3n －1，知a n ＝(2n －1)3n －1，于是数列{a n }的前n 项和S n ＝1×30＋3×31＋5×32＋…＋(2n －1)×3n －1，3S n ＝1×31＋3×32＋…＋(2n －3)×3n －1＋(2n －1)×3n ，将两式相减得－2S n ＝1＋2×(31＋32＋…＋3n －1)－(2n －1)×3n ＝－2－(2n －2)×3n ，所以S n ＝(n －1)3n ＋1. 17．、[2014·新课标全国卷Ⅰ] 已知数列{a n }的前n 项和为S n ，a 1＝1，a n ≠0，a n a n ＋1＝λS n－1，其中λ为常数．(1)证明：a n ＋2－a n ＝λ.(2)是否存在λ，使得{a n }为等差数列？并说明理由．17．解：(1)证明：由题设，a n a n ＋1＝λS n －1，a n ＋1a n ＋2＝λS n ＋1－1， 两式相减得a n ＋1(a n ＋2－a n )＝λa n ＋1. 因为a n ＋1≠0，所以a n ＋2－a n ＝λ.(2)由题设，a 1＝1，a 1a 2＝λS 1－1，可得 a 2＝λ－1， 由(1)知，a 3＝λ＋1.若{a n }为等差数列，则2a 2＝a 1＋a 3，解得λ＝4，故a n ＋2－a n ＝4. 由此可得{a 2n －1}是首项为1，公差为4的等差数列， a 2n －1＝4n －3；{a 2n }是首项为3，公差为4的等差数列，a 2n ＝4n －1. 所以a n ＝2n －1，a n ＋1－a n ＝2.因此存在λ＝4，使得数列{a n }为等差数列． 17．、、[2014·新课标全国卷Ⅱ] 已知数列{a n }满足a 1＝1，a n ＋1＝3a n ＋1.(1)证明⎩⎨⎧⎭⎬⎫a n ＋12是等比数列，并求{a n }的通项公式；(2)证明1a 1＋1a 2＋…＋1a n ＜32.17．解：(1)由a n ＋1＝3a n ＋1得a n ＋1＋12＝3⎝⎛⎭⎫a n ＋12. 又a 1＋12＝32，所以⎩⎨⎧⎭⎬⎫a n ＋12是首项为32，公比为3的等比数列，所以a n ＋12＝3n2，因此数列{a n }的通项公式为a n ＝3n －12.(2)证明：由(1)知1a n ＝23n －1.因为当n ≥1时，3n －1≥2×3n －1，所以13n －1≤12×3n 1，即1a n ＝23n－1≤13n 1. 于是1a 1＋1a 2＋…＋1a n ≤1＋13＋…＋13n －1＝32⎝⎛⎫1－13n <32. 所以1a 1＋1a 2＋…＋1a n <32.22．，，[2014·重庆卷] 设a 1＝1，a n ＋1＝a 2n －2a n ＋2＋b (n ∈N *)． (1)若b ＝1，求a 2，a 3及数列{a n }的通项公式．(2)若b ＝－1，问：是否存在实数c 使得a 2n <c <a 2n ＋1对所有n ∈N *成立？证明你的结论． 22．解：(1)方法一：a 2＝2，a 3＝2＋1. 再由题设条件知(a n ＋1－1)2＝(a n －1)2＋1.从而{(a n －1)2}是首项为0，公差为1的等差数列， 故(a n －1)2＝n －1，即a n ＝n －1＋1(n ∈N *)． 方法二：a 2＝2，a 3＝2＋1.可写为a 1＝1－1＋1，a 2＝2－1＋1，a 3＝3－1＋1.因此猜想a n ＝n －1＋1. 下面用数学归纳法证明上式． 当n ＝1时，结论显然成立．假设n ＝k 时结论成立，即a k ＝k －1＋1，则a k ＋1＝（a k －1）2＋1＋1＝（k －1）＋1＋1＝（k ＋1）－1＋1， 这就是说，当n ＝k ＋1时结论成立． 所以a n ＝n －1＋1(n ∈N *)．(2)方法一：设f (x )＝（x －1）2＋1－1，则a n ＋1＝f (a n )．令c ＝f (c )，即c ＝（c －1）2＋1－1，解得c ＝14.下面用数学归纳法证明命题 a 2n <c <a 2n ＋1<1.当n ＝1时，a 2＝f (1)＝0，a 3＝f (0)＝2－1，所以a 2<14<a 3<1，结论成立．假设n ＝k 时结论成立，即a 2k <c <a 2k ＋1<1. 易知f (x )在(－∞，1]上为减函数，从而 c ＝f (c )>f (a 2k ＋1)>f (1)＝a 2，即 1>c >a 2k ＋2>a 2.再由f (x )在(－∞，1]上为减函数，得c ＝f (c )<f (a 2k ＋2)<f (a 2)＝a 3<1，故c <a 2k ＋3<1，因此a 2(k ＋1)<c <a 2(k ＋1)＋1<1，这就是说，当n ＝k ＋1时结论成立．综上，存在 c ＝14使a 2n <C <a 2a ＋1对所有n ∈N *成立．方法二：设f (x )＝（x －1）2＋1－1，则a n ＋1＝f (a n )． 先证：0≤a n ≤1(n ∈N *)． ① 当n ＝1时，结论明显成立．假设n ＝k 时结论成立，即0≤a k ≤1. 易知f (x )在(－∞，1]上为减函数，从而 0＝f (1)≤f (a k )≤f (0)＝2－1<1.即0≤a k ＋1≤1.这就是说，当n ＝k ＋1时结论成立．故①成立． 再证：a 2n <a 2n ＋1(n ∈N *)． ②当n ＝1时，a 2＝f (1)＝0，a 3＝f (a 2)＝f (0)＝2－1，所以a 2<a 3，即n ＝1时②成立． 假设n ＝k 时，结论成立，即a 2k <a 2k ＋1. 由①及f (x )在(－∞，1]上为减函数，得 a 2k ＋1＝f (a 2k )>f (a 2k ＋1)＝a 2k ＋2， a 2(k ＋1)＝f (a 2k ＋1)<f (a 2k ＋2)＝a 2(k ＋1)＋1.这就是说，当n ＝k ＋1时②成立．所以②对一切n ∈N *成立． 由②得a 2n <a 22n －2a 2n ＋2－1，即(a 2n ＋1)2<a 22n －2a 2n ＋2，因此a 2n <14. ③又由①②及f (x )在(－∞，1]上为减函数，得f (a 2n )>f (a 2n ＋1)，即a 2n ＋1>a 2n ＋2.所以a 2n ＋1>a 22n ＋1－2a 2n ＋1＋2－1，解得a 2n ＋1>14. ④ 综上，由②③④知存在c ＝14使a 2n <c <a 2n ＋1对一切n ∈N *成立．D2 等差数列及等差数列前n 项和 12．、[2014·安徽卷] 数列{a n }是等差数列，若a 1＋1，a 3＋3，a 5＋5构成公比为q 的等比数列，则q ＝________.12．112．[2014·北京卷] 若等差数列{a n }满足a 7＋a 8＋a 9>0，a 7＋a 10<0，则当n ＝________时，{a n }的前n 项和最大．12．8 3．[2014·福建卷] 等差数列{a n }的前n 项和为S n ，若a 1＝2，S 3＝12，则a 6等于( ) A ．8 B ．10 C ．12 D ．14 3．C 18．、、[2014·湖北卷] 已知等差数列{a n }满足：a 1＝2，且a 1，a 2，a 5成等比数列． (1)求数列{a n }的通项公式．(2)记S n 为数列{a n }的前n 项和，是否存在正整数n ，使得S n >60n ＋800？若存在，求nn ＝4n －2. 800， 成立．2n 2.此时存在正整数n ，使得S n >60n ＋800成立，n 的最小值为41. 综上，当a n ＝2时，不存在满足题意的正整数n ；当a n ＝4n －2时，存在满足题意的正整数n ，其最小值为41. 20．、[2014·湖南卷] 已知数列{a n }满足a 1＝1，|a n ＋1－a n |＝p n ，n ∈N *. (1)若{a n }是递增数列，且a 1，2a 2，3a 3成等差数列，求p 的值；(2)若p ＝12，且{a 2n －1}是递增数列，{a 2n }是递减数列，求数列{a n }的通项公式．20．解：(1)因为{a n }是递增数列，所以a n ＋1－a n ＝|a n ＋1－a n |＝p n .而a 1＝1，因此 a 2＝p ＋1，a 3＝p 2＋p ＋1.又a 1，2a 2，3a 3成等差数列，所以4a 2＝a 1＋3a 3，因而3p 2－p ＝0，解得p ＝13或p ＝0.当p ＝0时，a n ＋1＝a n ，这与{a n }是递增数列矛盾，故p ＝13.(2)由于{a 2n －1}是递增数列，因而a 2n ＋1－a 2n －1>0，于是(a 2n ＋1－a 2n )＋(a 2n －a 2n －1)>0.①因为122n <122n －1，所以|a 2n ＋1－a 2n |<|a 2n －a 2n －1|.②由①②知，a 2n －a 2n －1>0，因此a 2n －a 2n －1＝⎝⎛⎭⎫122n －1＝（－1）2n 22n －1.③ 因为{a 2n }是递减数列，同理可得，a 2n ＋1－a 2n <0，故a 2n ＋1－a 2n ＝－⎝⎛⎭⎫122n＝（－1）2n ＋122n.④由③④可知，a n ＋1－a n ＝（－1）n ＋12n.于是a n ＝a 1＋(a 2－a 1)＋(a 3－a 2)＋…＋(a n －a n －1)＝1＋12－122＋…＋（－1）n2n －1＝1＋12·1－⎝⎛⎭⎫－12n －11＋12＝43＋13·（－1）n2n －1. 故数列{a n }的通项公式为a n ＝43＋13·（－1）n2n －1. 8．[2014·辽宁卷] 设等差数列{a n }的公差为d .若数列{2a 1a n }为递减数列，则( ) A ．d <0 B ．d >0 C ．a 1d <0 D ．a 1d >0 8．C 18．、[2014·全国卷] 等差数列{a n }的前n 项和为S n .已知a 1＝10，a 2为整数，且S n ≤S 4. (1)求{a n }的通项公式；(2)设b n ＝1a n a n ＋1，求数列{b n }的前n 项和T n .18．解：(1)由a 1＝10，a 2为整数知，等差数列{a n }的公差d 为整数． 又S n ≤S 4，故a 4≥0，a 5≤0， 于是10＋3d ≥0，10＋4d ≤0， 解得－103≤d ≤－52，因此d ＝－3.故数列{a n }的通项公式为a n ＝13－3n . (2)b n ＝1（13－3n ）（10－3n ）＝13⎝⎛⎭⎫110－3n －113－3n .于是T n ＝b 1＋b 2＋…＋b n ＝13⎝⎛⎭⎫17－110＋⎝⎛⎭⎫14－17＋…＋⎝⎛⎭⎫110－3n －113－3n ＝13⎝⎛⎭⎫110－3n －110＝n 10（10－3n ）.17．、[2014·新课标全国卷Ⅰ] 已知数列{a n }的前n 项和为S n ，a 1＝1，a n ≠0，a n a n ＋1＝λS n －1，其中λ为常数．(1)证明：a n ＋2－a n ＝λ.(2)是否存在λ，使得{a n }为等差数列？并说明理由．17．解：(1)证明：由题设，a n a n ＋1＝λS n －1，a n ＋1a n ＋2＝λS n ＋1－1， 两式相减得a n ＋1(a n ＋2－a n )＝λa n ＋1. 因为a n ＋1≠0，所以a n ＋2－a n ＝λ.(2)由题设，a 1＝1，a 1a 2＝λS 1－1，可得 a 2＝λ－1， 由(1)知，a 3＝λ＋1.若{a n }为等差数列，则2a 2＝a 1＋a 3，解得λ＝4，故a n ＋2－a n ＝4. 由此可得{a 2n －1}是首项为1，公差为4的等差数列， a 2n －1＝4n －3；{a 2n }是首项为3，公差为4的等差数列，a 2n ＝4n －1. 所以a n ＝2n －1，a n ＋1－a n ＝2.因此存在λ＝4，使得数列{a n }为等差数列． 19．，，[2014·山东卷] 已知等差数列{a n }的公差为2，前n 项和为S n ，且S 1，S 2，S 4成等比数列．(1)求数列{a n }的通项公式；(2)令b n ＝(－1)n－14na n a n ＋1，求数列{b n }的前n 项和T n .19．解： (1)因为S 1＝a 1，S 2＝2a 1S 4＝4a 1＋4×32×2＝4a 1＋12，由题意得(2a 1＋2)2＝a 1(4a 1＋12)所以a n ＝2n －1. (2)由题意可知， b n ＝(－1)n －14na n a n ＋1＝(－1)n－14n（2n －1）（2n ＋1）n －1⎛⎫1＋1－⎝⎛⎭⎫12n －1＋12n ＋1 ⎝⎛⎭⎫12n －1＋12n ＋1 ＝1＋12n ＋1＝2n ＋22n ＋1. 所以T n＝⎩⎪⎨⎪⎧2n ＋22n ＋1，n 为奇数，2n2n ＋1，n 为偶数.⎝ ⎛⎭⎪⎫或T n ＝2n ＋1＋（－1）n －12n ＋116．，，[2014·陕西卷] △ABC 的内角A ，B ，C 所对的边分别为a ，b ，c .(1)若a ，b ，c 成等差数列，证明：sin A ＋sin C ＝2sin(A ＋C )；(2)若a ，b ，c 成等比数列，求cos B 的最小值． 16．解：(1)∵a ，b ，c 成等差数列，∴a ＋c ＝2b . 由正弦定理得sin A ＋sin C ＝2sin B . ∵sin B ＝sin[π－(A ＋C )]＝sin(A ＋C )， ∴sin A ＋sin C ＝2sin(A ＋C )．(2)∵a ，b ，c 成等比数列，∴b 2＝ac . 由余弦定理得cos B ＝a 2＋c 2－b 22ac ＝a 2＋c 2－ac 2ac ≥2ac －ac 2ac ＝12，当且仅当a ＝c 时等号成立， ∴cos B 的最小值为12.11．、[2014·天津卷] 设{a n }是首项为a 1，公差为－1的等差数列，S n 为其前n 项和．若S 1，S 2，S 4成等比数列，则a 1的值为________．11．－1222．，，[2014·重庆卷] 设a 1＝1，a n ＋1＝a 2n －2a n ＋2＋b (n ∈N *)． (1)若b ＝1，求a 2，a 3及数列{a n }的通项公式．(2)若b ＝－1，问：是否存在实数c 使得a 2n <c <a 2n ＋1对所有n ∈N *成立？证明你的结论． 22．解：(1)方法一：a 2＝2，a 3＝2＋1. 再由题设条件知(a n ＋1－1)2＝(a n －1)2＋1.从而{(a n －1)2}是首项为0，公差为1的等差数列， 故(a n －1)2＝n －1，即a n ＝n －1＋1(n ∈N *)． 方法二：a 2＝2，a 3＝2＋1.可写为a 1＝1－1＋1，a 2＝2－1＋1，a 3＝3－1＋1.因此猜想a n ＝n －1＋1. 下面用数学归纳法证明上式． 当n ＝1时，结论显然成立．假设n ＝k 时结论成立，即a k ＝k －1＋1，则a k ＋1＝（a k －1）2＋1＋1＝（k －1）＋1＋1＝（k ＋1）－1＋1， 这就是说，当n ＝k ＋1时结论成立． 所以a n ＝n －1＋1(n ∈N *)．(2)方法一：设f (x )＝（x －1）2＋1－1，则a n ＋1＝f (a n )．令c ＝f (c )，即c ＝（c －1）2＋1－1，解得c ＝14.下面用数学归纳法证明命题 a 2n <c <a 2n ＋1<1.当n ＝1时，a 2＝f (1)＝0，a 3＝f (0)＝2－1，所以a 2<14<a 3<1，结论成立．假设n ＝k 时结论成立，即a 2k <c <a 2k ＋1<1. 易知f (x )在(－∞，1]上为减函数，从而 c ＝f (c )>f (a 2k ＋1)>f (1)＝a 2，即 1>c >a 2k ＋2>a 2.再由f (x )在(－∞，1]上为减函数，得c ＝f (c )<f (a 2k ＋2)<f (a 2)＝a 3<1，故c <a 2k ＋3<1，因此a 2(k ＋1)<c <a 2(k ＋1)＋1<1，这就是说，当n ＝k ＋1时结论成立．综上，存在 c ＝14使a 2n <C <a 2a ＋1对所有n ∈N *成立．方法二：设f (x )＝（x －1）2＋1－1，则a n ＋1＝f (a n )．先证：0≤a n ≤1(n ∈N *)． ① 当n ＝1时，结论明显成立．假设n ＝k 时结论成立，即0≤a k ≤1. 易知f (x )在(－∞，1]上为减函数，从而 0＝f (1)≤f (a k )≤f (0)＝2－1<1.即0≤a k ＋1≤1.这就是说，当n ＝k ＋1时结论成立．故①成立． 再证：a 2n <a 2n ＋1(n ∈N *)． ②当n ＝1时，a 2＝f (1)＝0，a 3＝f (a 2)＝f (0)＝2－1，所以a 2<a 3，即n ＝1时②成立． 假设n ＝k 时，结论成立，即a 2k <a 2k ＋1. 由①及f (x )在(－∞，1]上为减函数，得 a 2k ＋1＝f (a 2k )>f (a 2k ＋1)＝a 2k ＋2， a 2(k ＋1)＝f (a 2k ＋1)<f (a 2k ＋2)＝a 2(k ＋1)＋1.这就是说，当n ＝k ＋1由②得a 2n <a 22n －2a 2n ＋2－1，即(a 2n ＋1)2<a 22n －2a 2n ＋2，因此a 2n <14. ③又由①②及f (x )在(－∞，1]所以a 2n ＋1>a 22n ＋1－2a 2n ＋1＋2－1综上，由②③④知存在c ＝14使a 2n <c <aD3 等比数列及等比数列前n 项和 2．[2014·重庆卷] 对任意等比数列{a n A ．a 1，a 3，a 9成等比数列 B ．a 2，a 3，a 6成等比数列 C ．a 2，a 4，a 8成等比数列 D ．a 3，a 6，a 9，成等比数列 2．D 12．、[2014·安徽卷] 数列{a n }是等差数列，若a 1＋1，a 3＋3，a 5＋5构成公比为q 的等比数列，则q ＝________.12．1 13．、[2014·广东卷] 若等比数列{a n }的各项均为正数，且a 10a 11＋a 9a 12＝2e 5，则ln a 1＋ln a 2＋…＋ln a 20＝________．13．50 10．[2014·全国卷] 等比数列{a n }中，a 4＝2，a 5＝5，则数列{lg a n }的前8项和等于( ) A ．6 B ．5 C ．4 D ．3 10．C 18．、、[2014·湖北卷] 已知等差数列{a n }满足：a 1＝2，且a 1，a 2，a 5成等比数列． (1)求数列{a n }的通项公式．(2)记S n 为数列{a n }的前n 项和，是否存在正整数n ，使得S n >60n ＋800？若存在，求n 的最小值；若不存在，说明理由．18．解：(1)设数列{a n }的公差为d ，依题意得，2，2＋d ，2＋4d 成等比数列， 故有(2＋d )2＝2(2＋4d )，化简得d 2－4d ＝0，解得d ＝0或d ＝4. 当d ＝0时，a n ＝2；当d ＝4时，a n ＝2＋(n －1)·4＝4n －2.从而得数列{a n }的通项公式为a n ＝2或a n ＝4n －2. (2)当a n ＝2时，S n ＝2n ，显然2n <60n ＋800， 此时不存在正整数n ，使得S n >60n ＋800成立．当a n ＝4n －2时，S n ＝n [2＋（4n －2）]2＝2n 2.令2n 2>60n ＋800，即n 2－30n －400>0， 解得n >40或n <－10(舍去)，此时存在正整数n ，使得S n >60n ＋800成立，n 的最小值为41. 综上，当a n ＝2时，不存在满足题意的正整数n ；当a n ＝4n －2时，存在满足题意的正整数n ，其最小值为41. 17．、、[2014·新课标全国卷Ⅱ] 已知数列{a n }满足a 1＝1，a n ＋1＝3a n ＋1.(1)证明⎩⎨⎧⎭⎬⎫a n ＋12是等比数列，并求{a n }的通项公式；(2)证明1a 1＋1a 2＋…＋1a n ＜32.17．解：(1)由a n ＋1＝3a n ＋1得a n ＋1＋12＝3⎝⎛⎭⎫a n ＋12. 又a 1＋12＝32，所以⎩⎨⎧⎭⎬⎫a n ＋12是首项为32，公比为3的等比数列，所以a n ＋12＝3n2，因此数列{a n }的通项公式为a n ＝3n－12.(2)证明：由(1)知1a n ＝23n －1.因为当n ≥1时，3n －1≥2×3n －1，所以13n －1≤12×3n －1，即1a n ＝23n－1≤13n －1. 于是1a 1＋1a 2＋…＋1a n ≤1＋13＋…＋13n －1＝32⎝⎛⎭⎫1－13n <32. 所以1a 1＋1a 2＋…＋1a n <32.19．，，[2014·山东卷] 已知等差数列{a n }的公差为2，前n 项和为S n ，且S 1，S 2，S 4成等比数列．(1)求数列{a n }的通项公式；(2)令b n ＝(－1)n－14na n a n ＋1，求数列{b n }的前n 项和T n . 19．解： (1)因为S 1＝a 1，S 2＝2a 1＋2×12×2＝2a 1＋2，S 4＝4a 1＋4×32×2＝4a 1＋12，由题意得(2a 1＋2)2＝a 1(4a 1＋12)，解得a 1＝1， 所以a n ＝2n －1. (2)由题意可知， b n ＝(－1)n －14na n a n ＋1＝(－1)n－14n（2n －1）（2n ＋1）＝(－1)n －1⎝⎛⎭⎫12n －1＋12n ＋1.当n 为偶数时，T n ＝⎝⎛⎭⎫1＋13－⎝⎛⎭⎫13＋15＋…＋⎝⎛12n －3＋⎭⎫12n －1－⎝⎛⎭⎫12n －1＋12n ＋1 ＝1－12n ＋1＝2n2n ＋1. 当n 为奇数时，T n ＝⎝⎛⎭⎫1＋13－⎝⎛⎭⎫13＋15＋…－⎝⎛12n －3＋＝1＋12n ＋1＝2n ＋22n ＋1. 所以T n＝⎩⎪⎨⎪⎧2n ＋22n ＋1，n 为奇数，2n2n ＋1，n 为偶数.⎝ ⎛或T n16．，，[2014·陕西卷] △ABC (1)若a ，b ，c 成等差数列，证明：(2)若a ，b ，c 成等比数列，求cos c ＝2b . ＝12，n 11的等差数列，S n 为其前n 项和．若S 1，S 2，S 4成等比数列，则a 1的值为________．11．－1219．、、[2014·天津卷] 已知q 和n 均为给定的大于1的自然数．设集合M ＝{0，1，2，…，q －1}，集合A ＝{x |x ＝x 1＋x 2q ＋…＋x n q n －1，x i ∈M ，i ＝1，2，…，n }． (1)当q ＝2，n ＝3时，用列举法表示集合A .(2)设s ，t ∈A ，s ＝a 1＋a 2q ＋…＋a n q n －1，t ＝b 1＋b 2q ＋…＋b n q n －1，其中a i ，b i ∈M ，i ＝1，2，…，n .证明：若a n <b n ，则s <t .19．解：(1)当q ＝2，n ＝3时，M ＝{0，1}，A ＝{x |x ＝x 1＋x 2·2＋x 3·22，x i ∈M ，i ＝1，2，3}，可得A ＝{0，1，2，3，4，5，6，7}．(2)证明：由s ，t ∈A ，s ＝a 1＋a 2q ＋…＋a n q n －1，t ＝b 1＋b 2q ＋…＋b n q n －1，a i ，b i ∈M ，i ＝1，2，…，n 及a n <b n ，可得s －t ＝(a 1－b 1)＋(a 2－b 2)q ＋…＋(a n －1－b n －1)q n －2＋(a n －b n )q n －1≤(q －1)＋(q －1)q ＋…＋(q －1)q n －2－q n －1＝（q －1）（1－q n －1）1－q－q n －1＝－1<0， 所以s <t .D4 数列求和 17．、、[2014·江西卷] 已知首项都是1的两个数列{a n }，{b n }(b n ≠0，n ∈N *)满足a n b n ＋1－a n ＋1b n ＋2b n ＋1b n ＝0.(1)令c n ＝a nb n ，求数列{c n }的通项公式；(2)若b n ＝3n －1，求数列{a n }的前n 项和S n .17．解：(1)因为a n b n ＋1－a n ＋1b n ＋2b n ＋1b n ＝0，b n ≠0(n ∈N *)，所以a n ＋1b n ＋1－a nb n＝2，即c n ＋1－c n ＝2，所以数列{c n }是以c 1＝1为首项，d ＝2为公差的等差数列，故c n ＝2n －1.(2)由b n ＝3n －1，知a n ＝(2n －1)3n －1，于是数列{a n }的前n 项和S n ＝1×30＋3×31＋5×32＋…＋(2n －1)×3n －1，3S n ＝1×31＋3×32＋…＋(2n －3)×3n －1＋(2n －1)×3n ，将两式相减得－2S n ＝1＋2×(31＋32＋…＋3n －1)－(2n －1)×3n ＝－2－(2n －2)×3n ，所以S n ＝(n －1)3n ＋1. 18．、[2014·全国卷] 等差数列{a n }的前n 项和为S n .已知a 1＝10，a 2为整数，且S n ≤S 4. (1)求{a n }的通项公式；(2)设b n ＝1a n a n ＋1，求数列{b n }的前n 项和T n .18．解：(1)由a 1＝10，a 2为整数知，等差数列{a n }的公差d 为整数． 又S n ≤S 4，故a 4≥0，a 5≤0， 于是10＋3d ≥0，10＋4d ≤0， 解得－103≤d ≤－52，因此d ＝－3.故数列{a n }的通项公式为a n ＝13－3n .(2)b n ＝1（13－3n ）（10－3n ）＝13⎝⎛⎭⎫110－3n －113－3n .于是T n ＝b 1＋b 2＋…＋b n ＝13⎝⎛⎭⎫17－110＋⎝⎛⎭⎫14－17＋…＋⎝⎛⎭⎫110－3n －113－3n ＝13⎝⎛⎭⎫110－3n －110＝n 10（10－3n ）.19．，，[2014·山东卷] 已知等差数列{a n }的公差为2，前n 项和为S n ，且S 1，S 2，S 4成等比数列．(1)求数列{a n }的通项公式；(2)令b n ＝(－1)n－14na n a n ＋1，求数列{b n }的前n 项和T n . 19．解： (1)因为S 1＝a 1，S 2＝2a 1＋2×12×2＝2a 1＋2，S 4＝4a 1＋4×32×2＝4a 1＋12，由题意得(2a 1＋2)2＝a 1(4a 1＋12)，解得a 1＝1， 所以a n ＝2n －1. (2)由题意可知， b n ＝(－1)n －14na n a n ＋1＝(－1)n－14n（2n －1）（2n ＋1）＝(－1)n －1⎝⎛⎭⎫12n －1＋12n ＋1.当n 为偶数时，T n ＝⎝⎛⎭⎫1＋13－⎝⎛⎭⎫13＋15＋…＋⎝⎛12n －3＋＝1－12n ＋1＝2n2n ＋1. 当n 为奇数时，20．、[2014·湖南卷] 已知数列{a n }满足a 1＝1，|a n ＋1－a n |＝p n ，n ∈N *. (1)若{a n }是递增数列，且a 1，2a 2，3a 3成等差数列，求p 的值；(2)若p ＝12，且{a 2n －1}是递增数列，{a 2n }是递减数列，求数列{a n }的通项公式．20．解：(1)因为{a n }是递增数列，所以a n ＋1－a n ＝|a n ＋1－a n |＝p n .而a 1＝1，因此 a 2＝p ＋1，a 3＝p 2＋p ＋1.又a 1，2a 2，3a 3成等差数列，所以4a 2＝a 1＋3a 3，因而3p 2－p ＝0，解得p ＝13或p ＝0.当p ＝0时，a n ＋1＝a n ，这与{a n }是递增数列矛盾，故p ＝13.(2)由于{a 2n －1}是递增数列，因而a 2n ＋1－a 2n －1>0，于是(a 2n ＋1－a 2n )＋(a 2n －a 2n －1)>0.①因为122n <122n 1，所以|a 2n ＋1－a 2n |<|a 2n －a 2n －1|.②由①②知，a 2n －a 2n －1>0，因此a 2n －a 2n －1＝⎝⎛⎭⎫122n －1＝（－1）2n 22n －1.③ 因为{a 2n }是递减数列，同理可得，a 2n ＋1－a 2n <0，故a 2n ＋1－a 2n ＝－⎝⎛⎭⎫122n＝（－1）2n ＋122n.④由③④可知，a n ＋1－a n ＝（－1）n ＋12n.于是a n ＝a 1＋(a 2－a 1)＋(a 3－a 2)＋…＋(a n －a n －1)＝1＋12－122＋…＋（－1）n2n －1＝1＋12·1－⎝⎛⎭⎫－12n －11＋12＝43＋13·（－1）n2n －1. 故数列{a n }的通项公式为a n ＝43＋13·（－1）n2n 1.21．、、[2014·安徽卷] 设实数c ＞0，整数p ＞1，n ∈N *. (1)证明：当x ＞－1且x ≠0时，(1＋x )p ＞1＋px ；(2)数列{a n }满足a 1＞c 1p ，a n ＋1＝p －1p a n ＋c p a 1－p n ，证明：a n ＞a n ＋1＞c 1p. 21．证明：(1)用数学归纳法证明如下．①当p ＝2时，(1＋x )2＝1＋2x ＋x 2>1＋2x ，原不等式成立． ②假设p ＝k (k ≥2，k ∈N *)时，不等式(1＋x )k >1＋kx 成立．当p ＝k ＋1时，(1＋x )k ＋1＝(1＋x )(1＋x )k >(1＋x )(1＋kx )＝1＋(k ＋1)x ＋kx 2>1＋(k ＋1)x . 所以当p ＝k ＋1时，原不等式也成立．综合①②可得，当x >－1，x ≠0时，对一切整数p >1，不等式(1＋x )p >1＋px 均成立． (2)方法一：先用数学归纳法证明a n >c 1p .①当n ＝1时，由题设知a 1>c 1p成立．②假设n ＝k (k ≥1，k ∈N *)时，不等式a k >c 1p成立． 由a n ＋1＝p －1p a n ＋c p a 1－p n 易知a n >0，n ∈N *. 当n ＝k ＋1时，a k ＋1a k ＝p －1p ＋c p a －p k ＝1＋1p ⎝⎛⎭⎫c a p k－1. 由a k >c 1p >0得－1<－1p <1p ⎝⎛⎭⎫c a p k－1<0. 由(1)中的结论得⎝⎛⎭⎫a k ＋1a k p＝⎣⎡⎦⎤1＋1p ⎝⎛⎭⎫c a p k －1p>1＋p · 1p ⎝⎛⎭⎫c a p k －1＝c a p k . 因此a p k ＋1>c ，即a k ＋1>c 1p，所以当n ＝k ＋1时，不等式a n >c 1p也成立．综合①②可得，对一切正整数n ，不等式a n >c 1p 均成立．再由a n ＋1a n ＝1＋1p ⎝⎛⎭⎫c a p n －1可得a n ＋1a n <1， 即a n ＋1<a n .综上所述，a n >a n ＋1>c 1p，n ∈N *.方法二：设f (x )＝p －1p x ＋c p x 1－p ，x ≥c 1p ，则x p ≥c ，所以f ′(x )＝p －1p ＋c p (1－p )x －p ＝p －1p ⎝⎛1由此可得，f (x )在[c 1p ，＋∞)①当n ＝1时，由a 1>c 1p>0，即a p 1>c a 2＝p －1p a 1＋c p a 1－p 1＝a 1⎣⎡⎦⎤1＋1p ⎝⎛⎭⎫c a p 1－1<故当n ＝1时，不等式a n >a n ＋1>c 1p成立．②假设n ＝k (k ≥1，k ∈N *)时，不等式a k >c 1p )，a n >a n ＋1>c 1p均成立．n }满足：a 1＝2，且a 1，a 2，a 5成等比数列． n ，使得S n >60n ＋800？若存在，求n 当d ＝0时，a n ＝2；当d ＝4时，a n ＝2＋(n －1)·4＝4n －2.从而得数列{a n }的通项公式为a n ＝2或a n ＝4n －2. (2)当a n ＝2时，S n ＝2n ，显然2n <60n ＋800， 此时不存在正整数n ，使得S n >60n ＋800成立．当a n ＝4n －2时，S n ＝n [2＋（4n －2）]2＝2n 2.令2n 2>60n ＋800，即n 2－30n －400>0， 解得n >40或n <－10(舍去)，此时存在正整数n ，使得S n >60n ＋800成立，n 的最小值为41. 综上，当a n ＝2时，不存在满足题意的正整数n ；当a n ＝4n －2时，存在满足题意的正整数n ，其最小值为41. 17．、、[2014·江西卷] 已知首项都是1的两个数列{a n }，{b n }(b n ≠0，n ∈N *)满足a n b n ＋1－a n ＋1b n ＋2b n ＋1b n ＝0.(1)令c n ＝a nb n ，求数列{c n }的通项公式；(2)若b n ＝3n －1，求数列{a n }的前n 项和S n .17．解：(1)因为a n b n ＋1－a n ＋1b n ＋2b n ＋1b n ＝0，b n ≠0(n ∈N *)，所以a n ＋1b n ＋1－a nb n＝2，即c n ＋1－c n ＝2，所以数列{c n }是以c 1＝1为首项，d ＝2为公差的等差数列，故c n ＝2n －1.(2)由b n ＝3n －1，知a n ＝(2n －1)3n －1，于是数列{a n }的前n 项和S n ＝1×30＋3×31＋5×32＋…＋(2n －1)×3n －1，3S n ＝1×31＋3×32＋…＋(2n －3)×3n －1＋(2n －1)×3n ，将两式相减得－2S n ＝1＋2×(31＋32＋…＋3n －1)－(2n －1)×3n ＝－2－(2n －2)×3n ，所以S n ＝(n －1)3n ＋1. 17．、、[2014·新课标全国卷Ⅱ] 已知数列{a n }满足a 1＝1，a n ＋1＝3a n ＋1.(1)证明⎩⎨⎧⎭⎬⎫a n ＋12是等比数列，并求{a n }的通项公式；(2)证明1a 1＋1a 2＋…＋1a n ＜32.17．解：(1)由a n ＋1＝3a n ＋1得a n ＋1＋12＝3⎝⎛⎭⎫a n ＋12. 又a 1＋12＝32，所以⎩⎨⎧⎭⎬⎫a n ＋12是首项为32，公比为3的等比数列，所以a n ＋12＝3n2，因此数列{a n }的通项公式为a n ＝3n－12.(2)证明：由(1)知1a n ＝23n －1.因为当n ≥1时，3n －1≥2×3n －1，所以13n －1≤12×3n －1，即1a n ＝23n－1≤13n －1. 于是1a 1＋1a 2＋…＋1a n ≤1＋13＋…＋13n －1＝32⎝⎛⎭⎫1－13n <32. 所以1a 1＋1a 2＋…＋1a n <32.19．，[2014·四川卷] 设等差数列{a n }的公差为d ，点(a n ，b n )在函数f (x )＝2x 的图像上(n ∈N *)．(1)若a 1＝－2，点(a 8，4b 7)在函数f (x )的图像上，求数列{a n }的前n 项和S n ；(2)若a 1＝1，函数f (x )的图像在点(a 2，b 2)处的切线在x 轴上的截距为2－1ln 2，求数列⎩⎨⎧⎭⎬⎫a n b n 的前n 项和T n .19．解：(1)由已知得，b 7＝2a 7，b 8＝2a 8＝4b 7，所以 2a 8＝4×2a 7＝2a 7＋2，解得d ＝a 8－a 7＝2，所以S n ＝na 1＋n （n －1）2d ＝－2n ＋n (n －1)＝n 2－3n .(2)函数f (x )＝2x 在点(a 2，b 2)处的切线方程为y －2a 2＝(2a 2ln 2)(x －a 2)， 其在x 轴上的截距为a 2－1ln 2.由题意有a 2－1ln 2＝2－1ln 2，解得a 2＝2.所以d ＝a 2－a 1＝1.从而a n ＝n ，b n ＝2n ，所以数列{a n b n }的通项公式为a n b n ＝n2n ，所以T n ＝12＋222＋323＋…＋n －12n －1＋n 2n ，2T n ＝11＋22＋322＋…＋n2n －1，因此，2T n －T n ＝1＋12＋122＋…＋12n －1－所以，T n ＝2n ＋1－n －22n.19．[2014·浙江卷] 已知数列{a n }和{b 数列，且a 1＝2，b 3＝6＋b 2.(1)求a n 与b n .(2)设c n ＝1a n －1b n(n ∈N *)．记数列{c n }(i)求S n ；(ii)求正整数k ，使得对任意n ∈均有S 19．解：(1)由题意a 1a 2a 3…a n ＝(2)b n 知a 3＝(2)b 3－b 2＝8.又由a 1＝2，得公比q ＝2(q ＝－2舍去， 所以，当n ≥5时，c n <0.综上，若对任意n ∈N *恒有S k ≥S n ，则k ＝4.。

2014年全国高考数学试题分类汇编（数列）1.【2014·全国卷Ⅱ（文5）】等差数列{}n a 的公差为2，若2a ，4a ，8a 成等比数列，则{}n a 的前n 项和n S =（A ） ()1n n + （B ）()1n n - （C ）()12n n + (D)()12n n -【答案】A2.【2014·全国大纲卷（理10）】等比数列{}n a 中，452,5a a ==，则数列{lg }n a 的前8项和等于 （ ）A ．6B ．5C ．4D ．3 【答案】C ．3.【2014·全国大纲卷（文8）】设等比数列{a n }的前n 项和为S n ，若S 2=3，S 4=15，则S 6=( ) A. 31 B. 32 C. 63 D. 64 【答案】C4.【2014·北京卷（理5）】设{}n a 是公比为q 的等比数列，则"1"q >是"{}"n a 为递增数列的（ ）.A 充分且不必要条件 .B 必要且不充分条件 .C 充分必要条件 .D 既不充分也不必要条件【答案】D5.【2014·天津卷（文5）】设{}n a 是首项为1a ，公差为-1的等差数列，n S 为其前n 项和.若124,,S S S 成等比数列，则1a =（ ）（A ）2 （B ）-2 （C ）12 （D ）12- 【答案】D .6.【2014·福建卷（理3）】等差数列{}n a 的前n 项和n S ，若132,12a S ==，则6a =( ) .8A .10B .12C .14D 【答案】C7.【2014·辽宁卷（文9）】设等差数列{}n a 的公差为d ，若数列1{2}n a a为递减数列，则（ ）A ．0d >B ．0d <C ．10a d >D ．10a d <【答案】D8.【2014·陕西卷（理文4）】根据右边框图，对大于2的整数N ，得出数列的通项公式是（ ）.2n A a n = .2(1)n B a n =- .2n n C a = 1.2n n D a -=【答案】C9.【2014·重庆卷（理2）】对任意等比数列{}n a ,下列说法一定正确的是（ ）139.,,A a a a 成等比数列 236.,,B a a a 成等比数列 248.,,C a a a 成等比数列 369.,,D a a a 成等比数列【答案】D10.【2014·重庆卷（文2）】在等差数列{}n a 中,1352,10a a a =+=，则7a =（ ）.5A .8B .10C .14D【答案】B11.【2014·全国卷Ⅱ（文16）】数列{}n a 满足1+n a =n a -11，2a =2，则1a =_________.【答案】2112.【2014·安徽卷（理12）】数列{}a n 是等差数列，若1a 1+，3a 3+，5a 5+构成公比为q 的等比数列，则q =________. 【答案】1q =。

2014年高考数列真题（理科） 1(大纲）18.（本小题满分12分）等差数列{}n a 的前n 项和为n S ，已知110a =，2a 为整数，且4n S S ≤.（1）求{}n a 的通项公式；（2）设11n n n b a a +=，求数列{}n b 的前n 项和n T . 2(新课标2）17.（本小题满分12分）已知数列{}n a 满足1a =1，131n n a a +=+. （Ⅰ）证明{}12n a +是等比数列，并求{}n a 的通项公式； （Ⅱ）证明：1231112n a a a ++<…+. 3(江西）17、（本小题满分12分）已知首项都是1的两个数列（），满足. (1)令，求数列的通项公式； (2)若，求数列的前n 项和.4(广东）19. （14分）设数列{}n a 的前n 和为n S ,满足22*1234,n n S na n n n N +=--∈，且315S =。

(1)求123,,a a a 的值; (2)求数列{}n a 的通项公式;5(湖北）18.（本小题满分12分） 已知等差数列满足：=2，且，成等比数列. （Ⅰ）求数列的通项公式. （Ⅱ）记为数列的前n 项和，是否存在正整数n ，使得若存在，求n 的最小值；若不存在，说明理由.6（湖南）20. （本小题满分13分） 已知数列{}n a 满足111,,.n n n a a a p n N *+=-=∈ （Ⅰ）若{}n a 是递增数列，且123a ,2a ,3a 成等差数列，求p 的值； （Ⅱ）若12p =，且{}12n a -是递增数列，{}2n a 是递减数列，求数列{}n a 的通项公式。

7(四川）19．设等差数列{}n a 的公差为d ，点(,)n n a b 在函数()2x f x =的图象上（*n N ∈）。

（1）若12a =-，点87(,4)a b 在函数()f x 的图象上，求数列{}n a 的前n 项和n S ；（2）若11a =，函数()f x 的图象在点22(,)a b 处的切线在x 轴上的截距为12ln 2-，求数列{}n na b 的前n 项和n T 。