数值积分课件 (《计算方法》)

2016/4/12
(7―7)
19
数值计算方法 这里yi=f(xi),对式(7―6)两边积分得

b
a
f ( x)dx pn ( x )dx Rn ( x )dx
a a n b n
b
b
b x xk 1 ( n 1) [ dx] yi f ( )n 1 ( x )dx a a (n 1)! i 0 k 0 xi xk k i
k 0
n
(2)
n
R( f ) I ( f ) I n ( f ) f ( x)dx Ak f ( xk ),
b a k 0
(3)
称(2)为数值求积公式,(3)为求积公式余项(误差). 构造或确定一个求积公式，要讨论解决的问 题有
(i) 确定求积系数Ak和求积节点xk ；
(ii) 求积公式的误差估计和收敛性
b b

a
f ( x)dx ( x)dx
a b
现用第六章介绍的插值多项式Pn(x)来代替被积函数f(x), 即有
b a
f ( x)dx Pn ( x)dx
a
取节点为等距,即
a=x0＜x1＜…＜xn=b
2016/4/12 18
数值计算方法
ba h xk 1 xk , k 0,1,2,, n 1 n xi x0 ih i 0,1,2,, n
k 0
该公式为插值型（即：Ak lk ( x )dx ）
a
b
推论1 求积系数满足:
AHale Waihona Puke j 0nj
ba
2016/4/12
17
数值计算方法
1.1 牛顿―柯特斯公式 (Newton―Cotes)
建立数值积分公式最基本的思想是选取一个既简单又有 足够精度的函数φ(x), 用φ(x)代替被积函数f(x),于是有
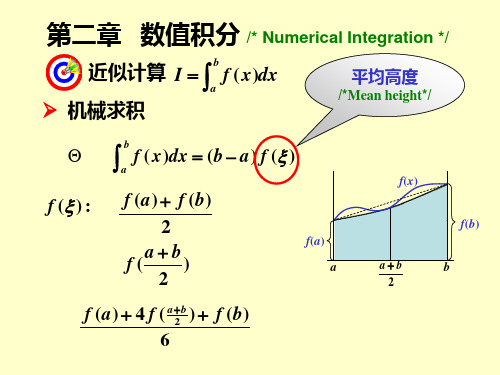
则分别可以看作用 a, b, c=(a+b)/2, 三点 高度的加权平均值 [f(a)+f(b)]/2 和 [f(a)+4f(c)+f(b)]/6 作为平均高度f(ξ)的近似值.
2016/4/12
9
数值计算方法
更一般地,取区间[a,b]内n+1个点 {xi},(i=0,1, 2,…n) 处的高度{f(xi)} (i=0,1,…,n)通过加权平均的方法 近似地得出平均高度f(ξ),这类求积方法称为机械求 积:

b
a
f ( x) F (b) F (a)
(7―1)
来求定积分。
2016/4/12
2
数值计算方法
公式 (7―1) 虽然在理论上或在解决实际问题中 都起了很大的作用,但它并不能完全解决定积分 的计算问题。因为定积分的计算常常会碰到以 下三种情况:
(1)被积函数f(x)的原函数F(x)不易找到。许多
ai yi Rn ( f )
i 0
n
2016/4/12
20
数值计算方法
x xk ai dx a k 0 xi xk
b n k i b 1 ( n 1) Rn ( f ) f ( )n 1 ( x)dx a (n 1)!
（7-8） （7-9）
代入(7―10)式得到求积公式

2016/4/12
b
a
ba f ( x)dx [ f ( x0 ) 3 f ( x1 ) 3 f ( x2 ) f ( x3 )] （7-14） 8
26
数值计算方法 类似地可分别求出 n=4,5,…时的柯特斯系数 ,从而建立相 应的求积公式。具体结果见表7―1。 从表中可以看出,当n≤7时,柯特斯系数为正;从n≥8开始,
n
误 差 R[ f ] a

n
b
f ( x)dx Ak f ( xk ) [ f ( x) Ln ( x)]dx
b k 0 a
b a
f ( n 1) ( x ) n ( x xk ) dx (n 1)! k 0
定理1 形如 Ak f ( xk ) 的求积公式至少有 n 次代数精度
2016/4/12
, ( a, b)
与x有关
23
数值计算方法
称Ci(n)为柯特斯求积系数。很显然,当n=1时,可 算得
C
(1) 0
C1(1)
1 ( s 1)ds 0 2 1 1 sds 0 2
1
此时式(7―10)为

b
a
ba f ( x )dx [ f (a ) f (b)] 2
(7―13)

b
a
ba ab f ( x )dx [ f (a ) 4 f ( ) f (b)] 6 2
这是抛物线(Simpson)公式。
2016/4/12 25
数值计算方法
当n=3时,
C
(3) 0
C1(3)
(3) C2 (3) C3
1 3 1 ( s 1)( s 2)( s 3)ds 18 0 8 1 3 3 s( s 2)( s 3)ds 6 0 8 1 3 3 s( s 1)( s 3)ds 6 0 8 1 3 1 s( s 1)( s 2)ds 18 0 8
表 7―1
(7―2)
5
数值计算方法
同样可得到右矩形公式：

2016/4/12
b
a
f ( x)dx (b a) f (b)
(7―3)
6
数值计算方法
如图7.2,若用梯形的面 积近似地代替曲边梯 形的面积,则得到计算 定积分的梯形公式
图 7.2

2016/4/12
b
a
ba f ( x )dx [ f (a ) f (b)] 2
我们称

b
a
f ( x)dx ai yi
i 0
n
（7-10）
为牛顿―柯特斯(Newton-Cotes)求积公式,Rn(f)为 牛顿―柯特斯求积公式的余项。
2016/4/12
21
数值计算方法
令
b n
x=x0+sh , 0≤s≤n dx=hds=(b-a)/nds
x xk ba n n sk (n) ai dx ds ( b a ) c i a 0 n k 0 xi xk k 0 i k
k i k i
Ci( n )
1 n n sk ds 0 n k 0 i k
k i n n (1) n i ( s k )ds i !(n i )!n 0 k 0 k i
i 0,1, 2,, n
(7―11)
2016/4/12 22
数值计算方法
为了构造形如式(2)的求积公式,需要提供一 种判定求积方法精度高低准则
2016/4/12 12
数值计算方法
求积公式的代数精度
定义1 称求积公式(2)具有m次代数精度,如果它满 足如下两个条件: (i)对所有次数≤ m次的多项式 Pm ( x) ,有 R( Pm ) I ( Pm ) I n ( Pm ) 0 (ii)存在m+1次多项式 Pm1 ( x) ,使得
利用拉格朗日插值多项式 其中
f ( x) pn ( x) Rn ( x)
x xk Pn ( x) li ( x) yi ( ) yi i 0 i 0 k 0 xi xk
n n n k i
(7―6)
f ( n 1) ( ) Rn ( x) n1 ( x) (a, b) (n 1)!
数值计算方法
第7章 数值积分
§1 插值型求积公式 §2 复化求积公式 §3 龙贝格(Romberg)求积方 法
2016/4/12
1
数值计算方法
§1 插值型求积公式
在一元函数的积分学中 ,我们已经熟知,若函 数 f(x) 在区间［ a, b] 上连续且其原函数为 F(x) ,则可用牛顿―莱布尼兹公式
为插值余项
于是有
2016/4/12 14
数值计算方法

b
a
f ( x)dx Ln ( x)dx Rn ( x)dx
a a b b l j ( x)dx f ( x j ) R( x)dx a a j 0 n
b
b
取

b
a
f ( x )dx f ( xk ) l k ( x )dx
(7―4)
7
数值计算方法
如图 7.3, 若用抛物线代 替曲线 f(x), 则可得到抛物 线公式(或辛普生公式)
图7.3

b
a
ba ab f ( x )dx [ f (a ) 4 f ( ) f (b)] b 2
(7―5)
2016/4/12
8
数值计算方法
此外,众所周知的梯形公式: I(f)≈(b-a)[f(a)+f(b)]/2 和 Simpson公式: I(f)≈(b-a)[f(a)+4f((a+b)/2)+f(b)]/6
(7―12)
这是梯形公式。
2016/4/12 24
数值计算方法
当n=2时,可得
C
(2) 0
C1(2)
(2) C2
于是
1 2 1 ( s 1)( s 2)ds 4 0 6 1 2 4 s( s 2)ds 2 0 6 1 2 1 s( s 1)ds 4 0 6

b
a