概率论公式大全

考研概率论与数理统计公式大全一、概率论部分：1.概率公式：-事件的概率：P(A)=n(A)/n(S)，其中n(A)表示事件A发生的可能性，n(S)表示样本空间S中的样本个数。

-互斥事件的概率：P(A∪B)=P(A)+P(B)。

-非互斥事件的概率：P(A∪B)=P(A)+P(B)-P(A∩B)。

2.条件概率公式：-事件A在事件B发生的条件下发生的概率：P(A，B)=P(A∩B)/P(B)。

3.乘法公式：-事件A、B同时发生的概率：P(A∩B)=P(A)*P(B，A)=P(B)*P(A，B)。

4.全概率公式：-事件A可以由一系列互斥且构成样本空间的事件B1、B2、..、Bn发生的概率：P(A)=P(A∩B1)+P(A∩B2)+...+P(A∩Bn)=ΣP(A∩Bi)。

5.贝叶斯公式：-已知事件A发生的条件下事件B发生的概率：P(B，A)=P(A∩B)/P(A)=P(A，B)*P(B)/P(A)。

6.重要的离散概率分布：-二项分布：P(X=k)=C(n,k)*p^k*(1-p)^(n-k)，其中n为试验次数，k为成功次数，p为每次成功的概率。

-泊松分布：P(X=k)=(λ^k*e^(-λ))/k!，其中λ为单位时间（或单位面积）内随机事件发生的平均次数。

7.重要的连续概率分布：-均匀分布：f(x)=1/(b-a)，其中a为最小值，b为最大值。

-正态分布：f(x)=(1/(σ*√(2π)))*e^(-(x-μ)^2/(2σ^2))，其中μ为均值，σ为标准差。

二、数理统计部分：1.基本概念：-总体：研究对象的全体。

-样本：从总体中抽取的一部分个体。

-参数：总体的特征数值。

-统计量：样本的特征数值。

2.基本统计量：- 样本均值：x̄ = (x1 + x2 + ... + xn) / n，其中x1、x2、..、xn为样本数据，n为样本容量。

- 样本方差：s^2 = ((x1-x̄)^2 + (x2-x̄)^2 + ... + (xn-x̄)^2) / (n-1)。

第一章随机事件和概率（1）排列组合公式从m个人中挑出n个人进行排列的可能数。

从m个人中挑出n个人进行组合的可能数。

（2）加法和乘法原理加法原理（两种方法均能完成此事）：m+n某件事由两种方法来完成，第一种方法可由m种方法完成，第二种方法可由n 种方法来完成，则这件事可由m+n 种方法来完成。

乘法原理（两个步骤分别不能完成这件事）：m×n某件事由两个步骤来完成，第一个步骤可由m种方法完成，第二个步骤可由n 种方法来完成，则这件事可由m×n 种方法来完成。

（3）一些常见排列重复排列和非重复排列（有序）对立事件（至少有一个）顺序问题（4）随机试验和随机事件如果一个试验在相同条件下可以重复进行，而每次试验的可能结果不止一个，但在进行一次试验之前却不能断言它出现哪个结果，则称这种试验为随机试验。

试验的可能结果称为随机事件。

（5）基本事件、样本空间和事件在一个试验下，不管事件有多少个，总可以从其中找出这样一组事件，它具有如下性质：①每进行一次试验，必须发生且只能发生这一组中的一个事件；②任何事件，都是由这一组中的部分事件组成的。

这样一组事件中的每一个事件称为基本事件，用来表示。

基本事件的全体，称为试验的样本空间，用表示。

一个事件就是由中的部分点（基本事件）组成的集合。

通常用大写字母A，B，C，…表示事件，它们是的子集。

为必然事件，Ø为不可能事件。

不可能事件（Ø）的概率为零，而概率为零的事件不一定是不可能事件；同理，必然事件（Ω）的概率为1，而概率为1的事件也不一定是必然事件。

（6）事件的关系与运算①关系：如果事件A的组成部分也是事件B的组成部分，（A发生必有事件B发生）：如果同时有，，则称事件A与事件B等价，或称A等于B：A=B。

A、B中至少有一个发生的事件：A B，或者A+B。

属于A而不属于B的部分所构成的事件，称为A与B的差，记为A-B，也可表示为A-AB或者，它表示A发生而B不发生的事件。

概率论的公式大全概率论是一门研究随机现象的数学分支，它使用概率来描述和解释随机事件发生的规律性。

在实际应用中，我们常常需要使用一些基本概率公式来计算和分析各种随机现象。

以下是一些常见的概率论公式：1.概率的定义公式：P(A)=N(A)/N(S)其中P(A)表示事件A的概率，N(A)表示事件A发生的次数，N(S)表示样本空间中发生的总次数。

2.加法公式：P(A∪B)=P(A)+P(B)-P(A∩B)其中P(A∪B)表示事件A和事件B至少发生一个的概率，P(A∩B)表示事件A和事件B同时发生的概率。

3.乘法公式：P(A∩B)=P(A)某P(B，A)其中P(A∩B)表示事件A和事件B同时发生的概率，P(B，A)表示在事件A发生的条件下事件B发生的概率。

4.条件概率公式：P(A，B)=P(A∩B)/P(B)其中P(A，B)表示在事件B发生的条件下事件A发生的概率，P(A∩B)表示事件A和事件B同时发生的概率，P(B)表示事件B的概率。

5.全概率公式：P(A)=ΣP(A，Bi)某P(Bi)其中P(A)表示事件A的概率，P(A，Bi)表示在事件Bi发生的条件下事件A发生的概率，P(Bi)表示事件Bi发生的概率，Σ表示对所有可能的事件Bi求和。

6.贝叶斯公式：P(Bi，A)=P(A，Bi)某P(Bi)/ΣP(A，Bj)某P(Bj)其中P(Bi，A)表示在事件A发生的条件下事件Bi发生的概率，P(A，Bi)表示在事件Bi发生的条件下事件A发生的概率，P(Bi)表示事件Bi发生的概率，P(A，Bj)表示在事件Bj发生的条件下事件A发生的概率，Σ表示对所有可能的事件Bj求和。

7.期望值的公式：E(X)=ΣXi某P(Xi)其中E(X)表示随机变量X的期望值，Xi表示随机变量X的可能取值，P(Xi)表示随机变量X取值为Xi的概率，Σ表示对所有可能的取值Xi求和。

8.方差的公式：Var(X) = E(X^2) - [E(X)]^2其中Var(X)表示随机变量X的方差，E(X^2)表示随机变量X的二阶矩，[E(X)]^2表示随机变量X的期望值的平方。

概率论的公式大全1.基本概率公式：对于一个随机事件A，它发生的概率（记作P(A)）等于A包含的元素数目除以样本空间中元素的总数目。

P(A)=个数(A)/个数(样本空间)2.条件概率公式：对于两个事件A和B，如果B已经发生，则A发生的概率记作P(A，B)。

P(A，B)=P(A交B)/P(B)3.全概率公式：对于一系列互不相容的事件B1，B2，...，Bn，它们的并集等于样本空间，那么对于另一个事件A，可以用条件概率公式表示为：P(A)=Σ(P(A，Bi)*P(Bi))，i=1到n4.贝叶斯定理：对于一系列互不相容的事件B1，B2，...，Bn，它们的并集等于样本空间，那么对于另一个事件A，可以用条件概率公式表示为：P(Bi，A)=(P(A，Bi)*P(Bi))/Σ(P(A，Bj)*P(Bj))，j=1到n5.独立事件公式：对于两个事件A和B，如果它们相互独立（即A的发生与B的发生没有任何关系），则它们的联合概率等于它们的乘积。

P(A交B)=P(A)*P(B)6.乘法公式：对于一系列独立事件A1，A2，...，An，它们的概率等于各个事件发生的概率的乘积。

P(A1交A2交...交An)=P(A1)*P(A2)*...*P(An)7.加法公式：对于两个事件A和B，它们的并集的概率等于各个事件发生的概率之和减去它们的交集的概率。

P(A并B)=P(A)+P(B)-P(A交B)8.期望值公式：对于一个随机变量X和它的概率分布P(X)，它的期望值可以表示为：E(X)=Σ(Xi*P(Xi))9.方差公式：对于一个随机变量X和它的期望值E(X)，它的方差可以表示为：Var(X) = Σ((Xi - E(X))^2 * P(Xi))，i为X的取值范围内的索引10.协方差公式：对于两个随机变量X和Y，它们的协方差可以表示为：Cov(X, Y) = E((X - E(X)) * (Y - E(Y)))11.相关系数公式：对于两个随机变量X和Y，它们的相关系数可以表示为：Corr(X, Y) = Cov(X, Y) / (σ(X) * σ(Y))，其中σ(X)和σ(Y)分别是X和Y的标准差12.大数定律：对于独立同分布的随机变量序列X1，X2，...，Xn，当n趋向于无穷大时，它们的算术平均值逐渐接近它们的期望值。

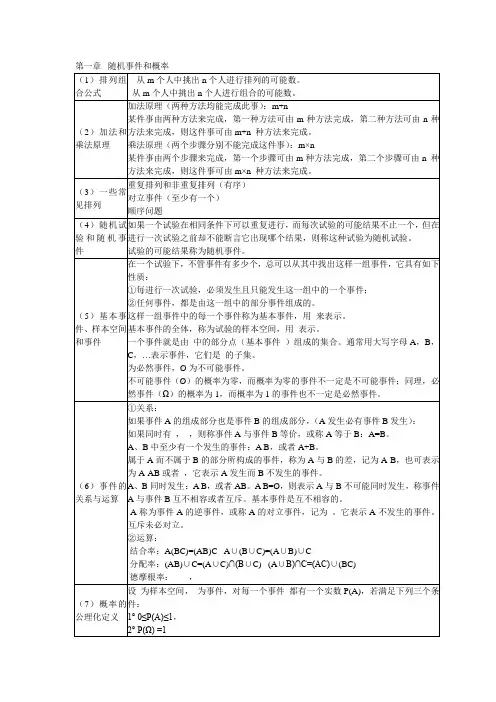
概率论常⽤公式 有些概率公式常常会⼀段时间内要⽤到，但是有经常忘记，这⾥备注⼀下1、乘法法则 p\left ( x,y \right )=p\left ( x|y \right )p\left ( y \right )=p\left ( y|x \right )p\left ( x \right ) 实际上就是条件概率公式的⼀个等价形式2、独⽴性 如果x和y是相互独⽴的，那么有： p\left ( x, y \right ) = p\left ( x\right )p\left ( y\right )3、贝叶斯规则（Bayes' Rule） 贝叶斯规则⼜成为贝叶斯公式，在许多领域都有着⼴泛的应⽤，其公式如下： p\left ( y|x \right )=\frac{p\left ( x|y \right )p\left ( y \right )}{p\left ( x \right )} 分母是标准化常数，⽤于确保左边的后验概率其所有可能的值之和为1。

因此，我们通常可写成： p\left ( y|x \right )=\eta p\left ( x|y \right )p\left ( x \right ) 在给定背景知识e给定的情况下，贝叶斯变成：p\left ( y|x,e \right )=\frac{p\left ( x|y,e \right )p\left ( y|e \right )}{p\left ( x|e \right )}4、边缘化 边缘概率公式如下： p\left ( x \right )= \int_{y}^{ } p\left ( x,y \right )dy 在离散的情况下，积分变成求和： p\left ( x \right )= \sum_{y}^{ } p\left ( x,y \right ) 5、全概率法则 全概率是边缘概率的⼀种变体，能通过乘法法则推导⽽来，即： p\left ( x \right )= \int_{y}^{ } p\left ( x|y \right )p\left ( y \right )dy 且，对于离散情况则为相应概率之和，即： p\left ( x \right )= \sum_{y}^{ } p\left ( x|y \right )p\left ( y \right )dy　对于连续情况，条件概率的全概率公式：p\left ( x|y \right )= \int_{z}^{ } p\left ( x|y,z \right )p\left ( z|y \right )dz 对于离散情况，条件概率的全概率公式：p\left ( x|y \right )= \sum_{z}^{ } p\left ( x|y,z \right )p\left ( z|y \right )dz6、马尔科夫假设 马尔科夫假设是指变量x_{t}，只与它直接的前⼀时刻状态x_{t-1}有关，和x_{t^{‘}-1}⽆关，其中t^{'}<t-1，则有 p\left ( x_{t}|x_{1:t-1} \right )= p\left(x_{t}|x_{t-1} \right)latax公式编辑器：，博客园只需要在选项中勾选⼀下“”即可。

概率论与数理统计公式大全一、概率论公式1.概率的基本性质：-非负性：对于任意事件A，有P(A)>=0；-规范性：对于必然事件S，有P(S)=1；-可列可加性：对于互不相容的事件Ai（i=1,2,...），有P(A1∪A2∪...)=P(A1)+P(A2)+...。

2.条件概率：-事件B发生的条件下，事件A发生的概率：P(A，B)=P(A∩B)/P(B)；-乘法公式：P(A∩B)=P(A，B)*P(B)。

3.全概率公式：-事件A的概率：P(A)=ΣP(A，Bi)*P(Bi)，其中Bi为样本空间的一个划分。

4.贝叶斯公式：-事件Bi发生的条件下，事件A发生的概率：P(Bi，A)=P(A，Bi)*P(Bi)/ΣP(A，Bj)*P(Bj)，其中Bj为样本空间的一个划分。

5.独立性：-事件A与事件B相互独立的充要条件是P(A∩B)=P(A)*P(B)。

二、数理统计公式1.随机变量的概率分布：-离散型随机变量的概率分布函数：P(X=x)；-连续型随机变量的概率密度函数：f(x)。

2.数理统计的基本概念：-样本均值：X̄=ΣXi/n；-样本方差：s^2=Σ(Xi-X̄)^2/(n-1)；-样本标准差：s=√s^2；- 样本协方差：sxy = Σ(Xi-X̄)(Yi-Ȳ) / (n-1)。

3.大数定律：-样本均值的大数定律：当样本容量n趋向于无穷大时，样本均值X̄趋向于总体均值μ。

4.中心极限定理：-样本均值的中心极限定理：当样本容量n足够大时，样本均值X̄服从近似正态分布。

5.参数估计：-点估计：用样本统计量对总体参数进行估计；-置信区间估计：用样本统计量构造一个区间，以估计总体参数的范围。

6.假设检验：-假设检验的基本步骤：提出原假设H0和备择假设H1，选择适当的检验统计量，计算拒绝域，进行假设检验。

以上只是概率论与数理统计中的一些重要公式和定理，还有很多其他的公式和定理没有一一列举。

掌握这些公式和定理，可以帮助我们更好地理解和应用概率论与数理统计的知识。

概率论的公式大全一、基本概率公式：1.定义概率公式：对于任意事件A，概率P(A)的范围是[0,1]。

2.互补事件概率公式：对于任意事件A，概率P(A')=1-P(A)。

3.空集概率公式：对于空集Φ，概率P(Φ)=0。

二、条件概率公式：4.定义条件概率公式：对于事件A和B，当P(B)>0时，条件概率P(A，B)=P(A∩B)/P(B)。

5.乘法公式：对于事件A和B，P(A∩B)=P(A，B)·P(B)。

三、独立事件公式：6.独立事件公式：对于事件A和B，当P(A)>0且P(B)>0，事件A和事件B相互独立的充要条件是P(A∩B)=P(A)·P(B)。

7.乘法公式（多个独立事件）：对于事件A1，A2，...，An，P(A1∩A2∩...∩An)=P(A1)·P(A2)·...·P(An)。

四、加法公式：8.加法公式（两个互不相容事件）：对于事件A和B，当A和B互不相容（即A∩B=Φ）时，P(A∪B)=P(A)+P(B)。

9.加法公式（两个一般事件）：对于事件A和B，P(A∪B)=P(A)+P(B)-P(A∩B)。

五、全概率公式：10.全概率公式：对于任意一系列互不相容的事件B1，B2，...，Bn，且每个事件Bi的概率大于0且小于1，且它们的并集为样本空间S，则对于任意事件A，有P(A)=Σ[P(A，Bi)·P(Bi)]，其中Σ表示求和。

六、贝叶斯公式：11.贝叶斯公式：对于事件A和一系列互不相容的事件B1，B2，...，Bn，且每个事件Bi的概率大于0且小于1，且它们的并集为样本空间S，则对于任意事件A，有P(Bi，A)=P(A，Bi)·P(Bi)/[Σ[P(A，Bj)·P(Bj)]]，其中Σ表示求和。

七、期望与方差公式：12.期望公式：对于随机变量X的概率分布函数P(x)，它的期望E(X)定义为E(X)=Σ[x·P(x)]，其中Σ表示求和。

概率论公式总结 Revised at 2 pm on December 25, 2020.第一章P(A+B)=P(A)+P(B)- P(AB)特别地，当A 、B 互斥时，P(A+B)=P(A)+P(B)条件概率公式概率的乘法公式全概率公式：从原因计算结果Bayes 公式：从结果找原因第二章二项分布（Bernoulli 分布）——X~B(n,p)泊松分布——X~P(λ)概率密度函数怎样计算概率均匀分布X~U(a,b)指数分布X~Exp (θ)分布函数对离散型随机变量 对连续型随机变量分布函数与密度函数的重要关系：二元随机变量及其边缘分布分布规律的描述方法)(b X a P ≤≤∑≤==≤=x k k X P x X P x F )()()(⎰∞-=≤=xdt t f x X P x F )()()(1),(0≤≤y x F联合密度函数 联合分布函数联合密度与边缘密度离散型随机变量的独立性连续型随机变量的独立性第三章数学期望离散型随机变量，数学期望定义连续型随机变量，数学期望定义E(a)=a ，其中a 为常数E(a+bX)=a+bE(X)，其中a 、b 为常数E(X+Y)=E(X)+E(Y)，X 、Y 为任意随机变量随机变量g(X)的数学期望常用公式方差定义式常用计算式常用公式当X 、Y 相互独立时：方差的性质D(a)=0，其中a 为常数D(a+bX)=b2D(X)，其中a 、b 为常数 ),(y x f ),(y x F ∑+∞-∞=⋅=k k k P x X E )([]22)()()(X E X E X D -=当X 、Y 相互独立时，D(X+Y)=D(X)+D(Y)协方差与相关系数协方差的性质独立与相关独立必定不相关相关必定不独立不相关不一定独立第四章 正态分布标准正态分布的概率计算标准正态分布的概率计算公式一般正态分布的概率计算一般正态分布的概率计算公式第五章卡方分布t 分布F 分布 正态总体条件下样本均值的分布：样本方差的分布：两个正态总体的方差之比第六章 ),(~2σμN X )(~)1,0(~212n X N X n i i χ∑=，则若),(~//),(~),(~21212212n n F n V n U n V n U 则若χχ点估计：参数的估计值为一个常数矩估计最大似然估计似然函数 均值的区间估计——大样本结果正态总体方差的区间估计两个正态总体均值差的置信区间大样本或正态小样本且方差已知两个正态总体方差比的置信区间第七章假设检验的步骤① 根据具体问题提出原假设H0和备择假设H1② 根据假设选择检验统计量，并计算检验统计值③ 看检验统计值是否落在拒绝域，若落在拒绝域则拒绝原假设，否则就不拒绝原假设。

概率论公式概率论是一种重要的数学理论，它分析和研究概率事件的可能结果以及它们的概率本质。

概率论的基本思想是：概率事件的发生频率有可能在一定的数量级上出现明显的变化，但是无法判断确切的发生率。

因此，在概率论中，人们通常使用概率公式来说明概率事件的可能结果。

概率论公式是概率论中最重要的数学工具，它们可以帮助人们更好地理解概率事件的发生率以及该事件的可能结果。

下面就来讨论概率论中一些常见的概率公式。

1. 伯努利定理：它是独立事件的基本理论，描述的是同一个概率事件的两种可能结果的概率和关系：P（A）= P（A）× P（B），其中，P（A）和P（B）分别表示概率事件A和B的概率。

2.叶斯定理：它可以明确描述两个概率事件的条件概率，即：P （AB）= P（A）×P（BA）/ P（B），其中，P（A）表示事件A发生的概率，P（BA）表示事件B在事件A发生的条件下发生的概率，P（B）表示事件B发生的概率。

3.律定理：它用于描述一系列的概率事件发生的节律性，即，当概率事件A发生n次后，下一次概率事件A发生的概率为：P（N+1）=P（N）/（1- P（N）），其中，P（N）表示概率事件A发生n次的概率。

4.合概率计算公式：它用于计算两个或多个概率事件发生概率的总和，即：P（A∪B）=P（A）+ P（B）- P（A∩B），其中，P（A∪B）表示概率事件A和B发生的概率之和，P（A）表示概率事件A发生的概率，P（B）表示概率事件B发生的概率，P（A∩B）表示概率事件A和B同时发生的概率。

5.体概率计算公式：它用于计算一组概率事件的概率总和，即：P（T） =∑i =1n（P（Ai）），其中，P（T）表示被考虑的概率事件T 的概率总和，P（Ai）表示概率事件Ai发生的概率。

6.概率公式：它用于计算某一事件发生的概率，即：P（A）=∑i=1n（P（Ai）×P（AAi）），其中，P（A）表示概率事件A发生的概率，P（Ai）表示概率事件Ai发生的概率，P（AAi）表示概率事件A 在Ai发生的条件下发生的概率。

概率论与数理统计基本公式第一部分 概率论基本公式1、)(;A B A B A AB A B A B A -⋃=⋃-==--例：证明：成立。

得证。

成立，也即成立，也即（不发生，从而发生，则不发生，，知由（证明：（B A B A AB A B B A AB A B B B A B A B A AB A B B A --=-⋃-⋃-==-=-⋃--)).) 2、对偶率：.----⋃=⋂⋂=⋃B A B A B A B A ；3、概率性率：(1))()()(212121A P A P A A P A A +=⋃为不相容事件，则、有限可加：(2))()();()()(),()()(B P A P B P A P B A P A B AB P A P B A P ≥-=-⊂-=-时有：特别，（3）)()()()(AB P B P A P B A P -+=⋃对任意两个事件有：)();();();()1(.4.0)(2.0)(5.0)(AB P B A P B A P AB P B P B A P A P ⋃-===--求：，，例：已知：.3.0)(1)(,7.0)()()()(3.0)()()(,5.0)(.,2.0)()()()(,=⋃-=⋃==-+=⋃=-=-∴===+∴=+---B A P B A P AB P AB P B P A P B A P AB P A P B A P A P AB P B P B A P AB P B A B B B A AB 又即是不相容事件，、且解：4、古典概型222n 2!)(n ,22)-n 2)!n 2(22nC n A P C A n n n ==！，则自成一双为：！！（解：分堆法：每堆自成一双鞋的概率只，事件堆，每堆为只，分为双鞋总共例： 5、条件概率称为无条件概率。

的条件概率，条件下，事件称为在事件)(,)()()|(B P B A A P AB P A B P =B)|P(B)P(A P(AB) A)|P(A)P(B P(AB)==乘法公式：)|()()(i i A B P A P B P i∑=全概率公式：)|()()|()()()()|(j j ji i i A B P A P A B P A P B P B A P B A P i ∑==贝叶斯公式：例：有三个罐子，1号装有2红1黑共3个球，2号装有3红1黑4个球，3号装有2红2黑4个球，某人随机从其中一罐，再从该罐中任取一个球，（1）求取得红球的概率；（2）如果取得是红球，那么是从第一个罐中取出的概率为多少？.348.0)()()|()|()2(.639.0)(31)()()(.21)|(;43)|(;32)|()|()()(}{3,2,1i }{)1(111321321i i 321≈=≈∴==========∑A P B P B A P A B P A P B P B P B P B A P B A P B A P A B P A P B P B B B A i B ii 由贝叶斯公式：，，依题意，有：由全概率公式是一个完备事件、、，由题知取得是红球。