动点问题与函数图象

动点的函数图象问题数形结合思想：所谓数形结合，就是根据数与形之间的对应关系，通过数与形的相互转化来解决数学问题的思想，实现数形结合，常与以下内容有关：（1）实数与数轴上的点的对应关系；（2）函数与图象的对应关系；（3所给的等式或代数式的结构含有明显的几何意义。

【典例1】如图，在△ABC中，∠ACB=90°，∠ABC=60°，BD=2，CD⊥AB于点D，点E、F、G分别是边CD、CA、AD的中点，连接EF、FG，动点M从点B出发，以每秒2个单位长度的速度向点A方向运动（点M运动到AB的中点时停止）；过点M作直线MP∥BC与线段AC交于点P，以PM为斜边作Rt△PMN，点N在AB 上，设运动的时间为t(s)，Rt△PMN与矩形DEFG重叠部分的面积为S，则S与t之间的函数关系图象大致为（）A．B．C．D．本题考查几何动点问题的函数图象，正确分段并分析是解题的关键．根据题意先分段，分为0≤t≤0.5，0.5<t≤1，1<t≤2三段，分别列出三段的函数解析式便可解决，本题也可只列出0≤t≤0.5，1<t≤2两段，用排除法解决．解：分析平移过程，①从开始出发至PM与点E重合，由题意可知0≤t≤0.5，如图，则BM=2t，过点M作MT⊥BC于点T，∵∠B=60°，CD⊥AB，∴BC=2BD=4，CD==BT=12BM=t，∵∠ACB=90°，MP∥BC，∴∠ACB=∠MPA=90°，∴四边形CTMP为矩形，∴PM=CT=BC―BT=4―t，∵∠PMN=∠B=60°，PN⊥AB，∴MN=PM2=4―t2，∴DN=MN―MD=MN―BD+BM=3t2，∵E为CD中点，∴DE=CD2=∴S=DE⋅DN=∴S与t的函数关系是正比例函数；②当0.5<t≤1，即从PM与E重合至点M与点D重合，如图，由①可得QN=ED=DM=2―2t，DN=32t，S矩形EDNQ=∵∠PMN=∠B=60°，CD⊥AB，∴SD==，∴ES=ED―SD=∴ER ==2t ―1，∴S =S 矩形EDNQ ―S △ERS =12(2―2t ―1)=―2+此函数图象是开口向下的二次函数；③当1<t ≤2，即从点M 与点D 重合至点M 到达终点，如图，由①可得DN =32t ，MN =4―t 2，∵AD ==6， DG =12AD =3，∴NG =DG ―DN =3―32t ，∴QF =NG =3―32t ，∴PQ==，∴HQ ==1―12t ，∴S =(HQ+MN )×QN 2==―∴S 与t 的函数关系是一次函数，综上，只有选项A 的图象符合，故选：A ．1．（2024·四川广元·二模）如图，在矩形ABCD 中，AB =4cm ,AD =2cm ，动点M 自点A 出发沿AB 方向以每秒1cm 的速度向点 B 运动，同时动点N 自点A 出发沿折线AD －DC －CB 以每秒2cm 的速度运动，到达点B 时运动同时停止．设△AMN的面积为y (cm2)，运动时间为x （秒），则下列图象中能大致反映y 与x 之间的函数关系的是（ ）A．B．C．D．【思路点拨】本题考查动点问题的函数图象问题；根据自变量不同的取值范围得到相应的函数关系式是解决本题的关键．根据题意，分三段（0<x<1，1≤x<3，3≤x<4）分别求解y与x的解析式，从而求解．【解题过程】解：当0<x<1时，M、N分别在线段AB、AD上，此时AM=x cm，AN=2x cm，y=S△AMN=12×AM×AN=x2，为二次函数，图象为开口向上的抛物线；当1≤x<3时，M、N分别在线段、CD上，此时AM=x cm，△AMN底边AM上的高为AD=2cm，y=S△AMN=12×AM×AD=x，为一次函数，图象为直线；当3≤x<4时，M、N分别在线段AB、BC上，此时AM=x cm，△AMN底边AM上的高为BN=(8―2x)cm，y=S△AMN=12×AM×BN=12x(8―2x)=―x2+4x，为二次函数，图象为开口向下的抛物线；结合选项，只有A选项符合题意，故选：A．2．（22-23九年级上·安徽合肥·期中）如图，在△ABC中，∠C=135°，AC=BC=P为BC边上一动点，PQ∥AB交AC于点Q，连接BQ，设PB=x，S△BPQ=y，则能表示y与x之间的函数关系的图象大致是（）A．B．C．D．【思路点拨】过点Q作QE⊥BC交BC延长线于点E，根据S△BPQ=y=12QE⋅BP列出解析式再判断即可．【解题过程】解：如图，过点Q作QE⊥BC交BC延长线于点E，∵AC =BC =∴∠A =∠ABC∵PQ∥AB ，∴∠CQP =∠A,∠CPQ =∠ABC∴∠CQP =∠CPQ∴CQ =CP =―x ．∵∠ACB =135°∴∠ECQ =45°在Rt △CEQ 中，∠ECQ =45°，∴QE ==―x )=2―，∴y =12QE ⋅BP =12x 2x =―2+x =――2+∴当x =y 最大值=故选：C.3．（2024·河北石家庄·二模）如图所示，△ABC 和△DEF 均为边长为4的等边三角形，点A 从点D 运动到点E 的过程中，AB 和DF 相交于点G ，AC 和EF 相交于点H ，(S △BGF +S △FCH )为纵坐标y ，点A 移动的距离为横坐标x ，则y 与x 关系的图象大致为（ ）A ．B ．C ．D ．【思路点拨】如图，过G 作GK ⊥BC 于K ，过H 作HT ⊥BC 于T ，证明四边形ACFD 为平行四边形，可得AD =CF =x ，BF =4―x ，求解CT =FT =12x ，TH ==，同理可得：GK =―x )，再利用面积公式建立函数关系式即可判断．【解题过程】解：如图，过G 作GK ⊥BC 于K ，过H 作HT ⊥BC 于T ，由题意可得：AD∥CF ，DF∥AC ，∴四边形ACFD 为平行四边形，∴AD =CF =x ，∴BF =4―x ，∵△ABC 和△DEF 均为边长为4的等边三角形，AD∥CF ，∴∠D =∠DFB =60°，而∠B =60°，∴△BGF 为等边三角形，同理：△CFH 为等边三角形，∵HT ⊥BC ，∴CT =FT =12x ，TH ==，同理可得：GK =―x )，∴y =12x +12(4―x )⋅―x )=2―+故选B4．（2023·辽宁铁岭·模拟预测）如图，矩形ABCD 中，AB =8cm ，AD =12cm ，AC 与BD 交于点O ，M 是BC 的中点．P 、Q 两点沿着B→C→D 方向分别从点B 、点M 同时出发，并都以1cm/s 的速度运动，当点Q 到达D 点时，两点同时停止运动．在P 、Q 两点运动的过程中，与△OPQ 的面积随时间t 变化的图象最接近的是（ ）A ．B ．C ．D ．【思路点拨】本题考查了动点问题函数图象．根据矩形的性质求出点O 到BC 的距离等于4，到CD 的距离等于6，求出点Q 到达点C 的时间为6s ，点P 到达点C 的时间为12s ，点Q 到达点D 的时间为14s ，然后分①0≤t ≤6时，点P 、Q 都在BC 上，表示出PQ ，然后根据三角形的面积公式列式计算即可；②6<t ≤12时，点P 在BC 上，点Q 在CD 上，表示出CP 、CQ ，然后根据S ΔOPQ =S ΔCOP +S ΔCOQ ―S ΔPCQ 列式整理即可得解；③12<t ≤14时，表示出PQ ，然后根据三角形的面积公式列式计算即可得解．【解题过程】解：∵矩形ABCD 中，AB =8cm ，AD =12cm ，AC 与BD 交于点O ，∴点O 到BC 的距离=12AB =4，到CD 的距离=12AD =6，∵点M 是BC 的中点，∴CM =12BC =6，∴点Q到达点C的时间为6÷1=6s，点P到达点C的时间为12÷1=12s，点Q到达点D的时间为(6+8)÷1=14s，①0≤t≤6时，点P、Q都在BC上，PQ=6，△OPQ的面积=12×6×4=12；②6<t≤12时，点P在BC上，点Q在CD上，CP=12―t，CQ=t―6，SΔOPQ=SΔCOP+SΔCOQ―SΔPCQ，=12×(12―t)×4+12×(t―6)×6―12×(12―t)×(t―6)，=12t2―8t+42，=12(t―8)2+10，③12<t≤14时，PQ=6，△OPQ的面积=12×6×6=18；纵观各选项，只有B选项图形符合．故选：B．5．（2023·江苏南通·模拟预测）如图，在矩形ABCD中，AB=4，BC=6，E为AB中点，动点P从点B开始沿BC方向运动到点C停止，动点Q从点C开始沿CD→DA方向运动，与点P同时出发，同时停止；这两点的运动速度均为每秒1个单位；若设他们的运动时间为x（s），△EPQ的面积为y，则y与x之间的函数关系的图像大致是（）A．B．C．D．【思路点拨】先求出点P在BC上运动是时间为6秒，点Q在CD上运动是时间为4秒，再根据中点的定义可得AE =BE =12AB ，然后分①点Q 在CD 上时，表示出BP 、CP 、CQ ，再根据△EPQ 的面积为y =S 梯形BCQE ―S △BPE ―S △PCQ ，列式整理即可得解；②点Q 在AD 上时，表示出BP 、AQ ，再根据△EPQ 的面积为y =S 梯形ABPQ ―S △BPE ―S △AEQ ，列式整理即可得解，再根据函数解析式确定出函数图象即可．【解题过程】解：∵点P 、Q 的速度均为每秒1个单位，∴点P 在BC 上运动的时间为6÷1=6（秒），点Q 在CD 上运动的时间为4÷1=4（秒），∵E 为AB 中点，∴AE =BE =12AB =12×4=2，①如图1，点Q 在CD 上时，0≤x ≤4，则BP =x,CP =6―x,CQ =x ，∴ △EPQ 的面积为y =S 梯形BCQE ―S △BPE ―S △PCQ ，=12(2+x )×6―12×2x ―12(6―x )⋅x =12x 2―x +6=12(x ―1)2+112②如图2，点Q 在AD 上时，4<x ≤6，则BP =x,AQ =6+4―x =10―x ，∴ △EPQ 的面积为y =S 梯形ABPQ ―S △BPE ―S △AEQ ，=12(x +10―x )×4―12×2x ―12(10―x )⋅2=10，综上所述，y =2―x +6(0≤x ≤4)10(4<x ≤6)，函数图象为对称轴为直线x =1的抛物线的一部分加一条线段，只有A 选项符合．故选：A ．6．（2024·河南开封·一模）如图1，在△ABC 中，∠B =60°，点D 从点B 出发，沿BC 运动，速度为1cm/s ．点P 在折线BAC 上，且PD ⊥BC 于点D ．点D 运动2s 时，点P 与点A 重合．△PBD 的面积S (cm 2)与运动时间t (s)的函数关系图象如图2所示，E 是函数图象的最高点．当S (cm 2)取最大值时，PD 的长为（ ）A ．B ．(1+cm C ．(1+cm D ．(2+cm【思路点拨】本题考查动点函数图象，二次函数图象性质，三角形面积．本题属二次函数与几何综合题目．先根据点D 运动2s 时，点P 与点A 重合．从而求得PD ==，再由函数图象求得BC =(2+×1=(2+cm ，从而求得DC =BC ―BD =2+2=，得出PD =DC ，然后根据由题图2点E 的位置可知，点P 在AC 上时，S △PBD 有最大值．所以当2≤t ≤2+点P 在AC边上，此时BD =t ×1=t (cm)，PD =DC =(2+―t )cm ，根据三角形面积公式求得S △PBD =―12t ―(13)2+2+【解题过程】解：由题意知，点D 运动2s 时，点P ，D 的位置如图1所示．此时，在Rt △PBD 中，BD =2cm ，∠B =60°，PD ⊥BC ，∴PB =2BD =4(cm)，∴PD ==．由函数图象得BC =(2+×1=(2+cm ，∴DC =BC ―BD =2+2=，∴PD =DC ．由题图2点E 的位置可知，点P 在AC 上时，S △PBD 有最大值．当2≤t ≤2+P 在AC 边上，如图2，此时BD =t ×1=t (cm)，PD =DC =(2+―t )cm ，∴S △PBD =12×BD ×PD =12×t ×(2+t )=―12t 2+(1+t ．∵S △PBD =――(1+3)2+2+又∵―12<0，∴当t =1+S △PBD 的值最大，此时PD =CD =2+―(1+=(1+cm ．故选：B ．7．（2024·安徽·一模）如图，在四边形ABCD 中，∠A =60°，CD ⊥AD ，∠BCD =90°, AB =BC =4，动点P ，Q 同时从A 点出发，点Q 以每秒2个单位长度沿折线A ―B ―C 向终点C 运动；点P 以每秒1个单位长度沿线段AD 向终点D 运动，当其中一点运动至终点时，另一点随之停止运动.设运动时间为x 秒，△APQ 的面积为y 个平方单位，则y 随x 变化的函数图象大致为（ ）A ．B ．C ．D ．【思路点拨】分当0≤x <2时，点Q 在AB 上和当2≤x ≤4时，点Q 在BC 上，根据三角形的面积公式即可得到结论．【解题过程】解：过Q 作QN ⊥AD 于N ，当0≤x <2时，点Q 在AB 上，∵∠A =60°，∴∠AQN =90°―60°=30°,∴AN = 12AQ =12×2x =x ，∴QN ==，∴y =12×AP ×NQ =12×x ×=2，当2≤x ≤4时，点Q 在BC 上，过点B 作BM ⊥AD 于点M ，∵BM ⊥AD ，∠A =60°,∴∠ABM =30°,∴AM = 12AB =12×4=2，∴BM ==∵CD ⊥AD ，QN ⊥AD ，∴QN ∥CD ,∴∠BQN =∠BCD =90°,∵BM ⊥AD, CD ⊥AD ，∴四边形BMNQ 是矩形，∴QN =BM = ,y =12AP ⋅QN =12x ×=，综上所述，当0≤x <2时的函数图象是开口向上的抛物线的一部分，当2≤x ≤4时，函数图象是直线的一部分，故选：D ．8．（23-24九年级上·浙江温州·期末）某兴趣小组开展综合实践活动：在Rt △ABC 中，∠C =90°，CD =，D 为AC 上一点，动点P 以每秒1个单位的速度从C 点出发，在三角形边上沿C→B→A 匀速运动，到达点A 时停止，以DP 为边作正方形DPEF ，设点P 的运动时间为t s ，正方形DPEF 的面积为S ，当点P 由点C 运动到点A 时，经探究发现S 是关于t 的二次函数，并绘制成如图2所示的图象，若存在3个时刻t 1，t 2，t 3(t 1<t 2<t 3)对应的正方形DPEF 的面积均相等，当t 3=5t 1时，则正方形DPEF 的面积为（ ）A ．3B ．349C ．4D ．5【思路点拨】由题意可得：CD =CP =t ，当点P 在BC 上运动时S =t 2+2，由图可得，当点P 与点B 重合时，S =6，求出t=2，即BC=2，当P在BA上时，由图可得抛物线过点2，6，顶点为4，2，求出抛物线解析式为S=(t―2)2+2，从两个函数表达式看，两个函数a相同，都为1，则从图象上看t1，t2关于x=2对称，t2，t3关于x=4对称，t1+t2=4①，t2+t3=8②，结合t3=5t1③，求出t的值即可得出答案．【解题过程】解：由题意可得：CD=CP=t，当点P在BC上运动时，S=DP2=CP2+CD2=t2+2，由图可得，当点P与点B重合时，S=6，∴t2+2=6，∴t=2或t=―2（不符合题意，舍去），∴BC=2，当P在BA上时，由图可得抛物线过点2，6，顶点为4，2，则抛物线的表达式为S=a(t―4)2+2，将2，6代入得：a(2―4)2+2=6，∴a=1，∴抛物线的表达式为：S=(t―4)2+2，从两个函数表达式看，两个函数a相同，都为1，若存在3个时刻t1，t2，t3(t1<t2t3)对应的正方形DPEF的面积均相等，则从图象上看t1，t2关于x=2对称，t2，t3关于x=4对称，∴t1+t2=4①，t2+t3=8②，∵t3=5t1③，由①③③解得t1=1，∴S=t2+2=1+2=3，故选：A．9．（22-23九年级上·浙江嘉兴·期中）如图，在Rt△ABC中，∠C=90°，∠ABC=60°，BC=6，点O为AC 中点，点D为线段AB上的动点，连接OD，设BD＝x，OD2＝y，则y与x之间的函数关系图像大致为（ ）A ．B ．C ．D ．【思路点拨】如图:过O 作OE ⊥AB ,垂足为E ，先根据直角三角形的性质求得AB =12,AC =OA =12AC =AE ==92可得DE =152―x ，然后再根据勾股定理求得函数解析式，最后确定函数图像即可．【解题过程】解：如图:过O 作OE ⊥AB ,垂足为E∵∠C =90°，∠ABC =60°∴∠A =30°∵BC =6∴AB =2BC =12∴AC ===∵点O 为AC 中点∴OA =12AC =∵∠A =30°∴OE =12AO =∴AE ===92∴DE =|152―x |∴OD 2=OE 2+DE 2,即y =+―x 2=x +274当x =0时，y =0―+274=63当x =152时，y =―+274=274当x =12时，y =12+274=27则函数图像为．故选C ．10．（2024·广东深圳·三模）如图，在Rt △ABC 中，∠C =90°，AC =12，BC =8，点D 和点E 分别是AB 和AC 的中点，点M 和点N 分别从点A 和点E 出发，沿着A→C→B 方向运动，运动速度都是1个单位/秒，当点N 到达点B 时，两点间时停止运动．设△DMN 的面积为S ，运动时间为t ，则S 与t 之间的函数图象大致为（ ）A ．B ．C ．D ．【思路点拨】本题主要考查动点问题，依托三角形面积考查二次函数的图象和分类讨论思想，取BC 的中点F,连接DF 根据题意得到DF 和DE ，分三种情况讨论三角形的面积：（1）当0<t ≤6时，得MN =AE =6，结合三角形面积公式求解即可；（2）当6<t ≤12时，得AM ，MC ，CN 和BN ，结合S =S ΔABC ―S ΔADM ―S ΔBDN ―S ΔCMN ；（3）当12<t ≤14时，点M 、N 都在BC 上，结合DF 和MN 求面积即可．【解题过程】解：如图，取BC 的中点F ，连接DF ，∴DF ∥AC ，DF =12AC =6∵点D 、E 是中点，∴DE =12BC =4，DF ∥CB ，∵∠C =90°，∴四边形DECF 为矩形，当0<t ≤6时，点M 在AE 上，点N 在EC 上，MN =AE =6，∴S =12MN ⋅DE =12×6×4=12；如图，当6<t ≤12时，点M 在EC 上，点N 在BC 上，∵AM =t ，∴MC =12―t ，CN =t ―6，BN =14―t ，∴S =S ΔABC ―S ΔADM ―S ΔBDN ―S ΔCMN=12×8×12―12×4t ―12×6(14―t)―12(12―t)(t ―6)=12t 2―8t +42；如图，当12<t ≤14时，点M 、N 都在BC 上，∴S =12MN ⋅DF =12×6×6=18，综上判断选项A 的图象符合题意．故选：A ．11．（2024·河南南阳·二模）如图是一种轨道示意图，其中A 、B 、C 、D 分别是菱形的四个顶点，∠A =60°．现有两个机器人(看成点)分别从A ，C 两点同时出发，沿着轨道以相同的速度匀速移动，其路线分别为A→B→C 和C→D→A ．若移动时间为t ，两个机器人之间距离为d ．则 d²与t 之间的函数关系用图象表示大致为（ ）A ．B ．C ．D ．【思路点拨】设菱形的边长为2，根据菱形的性质求出关于两个机器人之间的距离d2的解析式，再利用二次函数的性质即可解答．【解题过程】解：①设AD=2，如图所示，∵移动时间为t，∠A=60°，∴CK=1，FT=KB=∴AE=t，CF=2―t，∴FK=2―t―1=1+t，∴ET=2―t―(1+t)=1+2t，∴在Rt△EFT中，EF2=ET2+FT2=(1+2t)2+2=4t2+4t+4；②设AD=2，如图所示，∵移动时间为t，∠A=60°，∴BM=t―2，CM=2―(t―2)=4―t，CP=1，PD=LQ=∴MQ=CM―CQ=(4―t)―1=―t，∴在Rt△LMQ中，ML2=MQ2+LQ2=(3―t)2+2=t2―6t+12，∴函数图像为两个二次函数图象；③当从A出发的机器人在B点，从C出发的机器人在D点，此时距离是BD；从A出发的机器人在A点，从C出发的机器人在C点，此时距离是AC；∵设AD=2，∠A=60°，∴BD=2，AE=∴AC=2AE=∴BD<AC，∴函数图象的起点和终点高于中间点；综上所述：A项符合题意；故选A．12．（2024·山东聊城·二模）如图，等边△ABC与矩形DEFG在同一直角坐标系中，现将等边△ABC按箭头所指的方向水平移动，平移距离为x，点C到达点F为止，等边△ABC与矩形DEFG重合部分的面积记为S，则S关于x的函数图象大致为（）A．B．C．D．【思路点拨】本题主要考查了动点问题的函数图象，二次函数的图象，等腰三角形的性质等知识，如图，作AQ⊥BC于点Q，可知AQ=0<x≤1或1<x≤2或2<x≤3三种情形，分别求出重叠部分的面积，即可得出图象．【解题过程】解：如图①，设AC与DE交于点H，∵△ABC是等边三角形，∴∠ABC=∠ACB=60°,AB=BC=AC=2,BC=1,过点A作AQ⊥BC于点Q，则BQ=CQ=12∴AQ===∵四边形DEFG 是矩形，∴∠DEF =90°,DE =AQ ==OF ―OE =5―2=3,当0<x ≤1时，在Rt △HCE 中，∠ACE =60°,EC =x,∴∠CHE =30°,∴HC =2x ，∴HE ===∴S =12EC ×HE =12x ×=2，所以，S 关于x 的函数图象是顶点为原点，开口向上且在0<x ≤1内的一段；当1<x ≤2时，如图，设AB 与DE 交于点P ，∵EC =x,BC =2,∴BE =BC ―EC =2―x,同理可得，PE =x ―2)，∴S =S △ABC ―S △PBE =12×2―12(2―x )⋅―x )=―x ―2)2+所以，图象为1<x ≤2时开口向下的一段抛物线索；当2<x ≤3时，如图，S =12×2×=此时的函数图象是在2<x≤3范围内的一条线段，即S=<x≤3)，故选：C13．（2024·河南·模拟预测）如图，在等腰直角三角形ABC中，∠ABC=90°，BD是AC边上的中线，将△BCD 沿射线BA方向匀速平移，平移后的三角形记为△B1C1D1，设△B1C1D1与△ABD重叠部分的面积为y，平移距离为x，当点B1与点A重合时，△B1C1D1停止运动，则下列图象最符合y与x之间函数关系的是（）A．B．C．D．【思路点拨】本题考查了二次函数与几何图形的综合，涉及等腰直角三角形，平移的性质，二次函数的性质等知识，解题的关键是灵活运用这些性质，学会分类讨论．过点D作DM⊥AB于M，由△ABC为等腰直角三角形，∠ABC=90°，可设AB=BC=2，可得AD=CD=BD=DM=AM=BM=1，然后分情况讨论：当0<x≤1时，当1<x≤2时，分别求出关于S、x的函数，再数形结合即可求解．【解题过程】解：过点D作DM⊥AB于M，∵△ABC为等腰直角三角形，∠ABC=90°，∴ AB =BC ，设AB =BC =2，∴ AD =CD =BD =DM =AM =BM =1，当0<x ≤1时，设B 1D 1交AC 于点G ，B 1C 1交BD 于N ，∴ AB 1=AB ―BB 1=2―x ，由平移知B 1G ∥BD ，∠AB 1G =∠ABD ，∴ △AB 1G 是等腰直角三角形，∴ S △AB 1G =12AB 1·12AB 1=14(2―x )2，又∵ S △ABD =12×12×2×2=1，S △BB 1N =12x 2∴ S =S △ABD ―S △AB 1G ―S △BB 1N =1―14(2―x )2―12x 2=―34x 2+x ，当x =―=23时取得最大值，故排除A 、B 选项当1<x ≤2时，B 1D 1交AC 于点G ，B 1C 1交AC 于点H ，∵ B 1H ∥BC ，∴ ∠B 1HG =∠ACB =45°，又∵ ∠D 1B 1C 1=45°，∴ △B 1GH 为等腰三角形，∵ ∠AB 1D 1=∠ABD =45°=∠A ，∴ AB 1G 为等腰三角形，∴ B 1G =1=―x )，∴ S =S △B 1GH =12·―x )―x )=14(2―x )2，即当1<x ≤2时，函数图像为开口向上的抛物线，故排除C 选项故选：D ．14．（23-24九年级上·安徽滁州·期末）如图，菱形ABCD的边长为3cm，∠B=60°，动点P从点B出发以3cm/ s的速度沿着边BC―CD―DA运动，到达点A后停止运动；同时动点Q从点B出发，以1cm/s的速度沿着边BA 向A点运动，到达点A后停止运动．设点P的运动时间为x(s)，△BPQ的面积为y(cm2)，则y关于x的函数图象为（）A．B．C．D．【思路点拨】根据题意可知分情况讨论，分别列出当点P在BC上时，点P在CD上时，点P在AD上时表达式，再画图得到函数解析式，即可得到本题答案．【解题过程】解：设点P的运动时间为x(s)，△BPQ的面积为y(cm2)，①当0≤x≤1时，点P在BC上时，过点P作PE⊥BA，，∵根据题知：∠B =60°，PB =3x,BQ =x ，∴BE =32x ，PE =，∴y =12BQ·PE =12x·=2；②当1<x ≤2时，点P 在CD 上时，过点P 作PH ⊥BA ，，∵根据题知：∠B =60°，BC =3,BQ =x ，∴PH =∴y =12BQ·PH =12x·=；③当2<x ≤3时，点P 在AD 上时，过点P 作PF ⊥BA 交DA 延长线于F ，，∵根据题知：∠B =60°，即∠FAD =60°，∵BC +CD +AD =3+3+3=9cm ，BC +CD +DP =3x ，∴AP =(9―3x)cm ，∴PF =9―3x 2·∴y =12BQ·PF =12x·9―3x 2·=―2；∴结合三种情况，图像如下所示：，故选：D．15．（2023·辽宁盘锦·中考真题）如图，在平面直角坐标系中，菱形ABCD的顶点A在y轴的正半轴上，顶点B、C在x轴的正半轴上，D，P(―1,―1)．点M在菱形的边AD和DC上运动（不与点A，C重合），过点M作MN∥y轴，与菱形的另一边交于点N，连接PM，PN，设点M的横坐标为x，△PMN的面积为y，则下列图象能正确反映y与x之间函数关系的是（）A．B．C．D．【思路点拨】先根据菱形的性质求出各点坐标，分M的横坐标x在0∼1，1∼2，2∼3之间三个阶段，用含x的代数式表示出△PMN的底和高，进而求出分段函数的解析式，根据解析式判断图象即可．【解题过程】解：∵菱形ABCD 的顶点A 在y 轴的正半轴上，顶点B 、C 在x 轴的正半轴上，∴ AB =AD =2，OA=∴ OB===1，∴ OC =OB +BC =1+2=3，∴ A ，B (1,0)，C (3,0)，设直线AB 的解析式为y =kx +b ，将A ，B (1,0)代入，得：k +b = ，解得k =b =∴直线AB 的解析式为y =―+∵ MN∥y 轴，∴N 的横坐标为x ，（1）当M 的横坐标x 在0∼1之间时，点N 在线段AB 上，△PMN 中MN 上的高为1+x ，∴ N (x,―+，∴ MN=(―+=，∴ S △PMN =12MN ⋅(1+x )=⋅(1+x)=2+，∴该段图象为开口向上的抛物线；（2）当M 的横坐标x 在1∼2之间时，点N 在线段BC 上，△PMN 中MN =MN 上的高为1+x ，∴ S △PMN =12MN ⋅(1+x)=(1+x)=∴该段图象为直线；（3）当M 的横坐标x 在2∼3之间时，点N 在线段BC 上，△PMN 中MN 上的高为1+x ，由D ，C (3,0)可得直线CD 的解析式为y =―+∴ M (x,―+，N (x,0)，∴ MN =―+∴ S △PMN =12MN ⋅(1+x )=12(+⋅(1+x )=―2∴该段图象为开口向下的抛物线；观察四个选项可知，只有选项A 满足条件，故选A ．16．（22-23九年级上·安徽蚌埠·期末）如图，在平面直角坐标系中，点A (2,0)，点B，点C (―，点P从点O出发沿O→A→B路线以每秒1个单位的速度运动，点Q从点O出发沿O→C→B的速度运动，当一个点到达终点时另一个点随之停止运动，设y=PQ2，运动时间为t秒，则正确表达y与t 的关系图象是（）A．B．C．D．【思路点拨】先分析各个线段的长，在Rt△OAB中，可知，OA=2，OB AB=4，∠BAO=60°，过点C作CM⊥y轴于点M，易得△OBC是等边三角形，OC=BC=OB P在OA上运动用时2s，在AB上运动用时4s，点Q在OC上运动用时2s，在OC上运动用时2s，则点P和点Q共用时4s，可排除D选项；再算出点P在OA上时，y的函数表达式，结合选项可得结论．【解题过程】解：如图，∵点A（2，0），点B（0，∴OA=2，OB∴AB=4，∠BAO=60°，过点C作CM⊥y轴于点M，则OM =BM CM =3，∴OC =BC ∴△OBC 是等边三角形，∠BOC =60°，∴点P 在OA 上运动用时2s ，在AB 上运动用时4s ，点Q 在OC 上运动用时2s ，在OC 上运动用时2s ，即点P 和点Q 共运动4s 后停止；由此可排除D 选项．当点P 在线段OA 上运动时，点Q 在线段OC 上运动，过点Q 作QN ⊥x 轴于点N ，由点P ，点Q 的运动可知，OP =t ，OQ ，∴QN =12OQ ==32t,∴PN =52t,∴y =PQ 2=(52t)2+2=7t 2.即当0＜t ＜2时，函数图象为抛物线，结合选项可排除A ，C ．故选：B ．17．（2022·辽宁·中考真题）如图，在等边三角形ABC 中，BC ＝4，在Rt △DEF 中，∠EDF ＝90°，∠F ＝30°，DE ＝4，点B ，C ，D ，E 在一条直线上，点C ，D 重合，△ABC 沿射线DE 方向运动，当点B 与点E 重合时停止运动．设△ABC 运动的路程为x ，△ABC 与Rt △DEF 重叠部分的面积为S ，则能反映S 与x 之间函数关系的图象是（ ）A．B．C．D．【思路点拨】分三种情形∶①当0＜x≤2时，△CDG，②当2＜x≤4时，重叠部分为四边形AGDC，③当4＜x≤8时，重叠部分为△BEG，分别计算即可．【解题过程】解：过点A作AM⊥BC，交BC于点M，在等边△ABC中，∠ACB＝60°，在Rt△DEF中，∠F＝30°，∴∠FED＝60°，∴∠ACB＝∠FED，∴AC∥EF，在等边△ABC中，AM⊥BC，BC＝2，AM＝∴BM＝CM＝12BC•AM＝∴S△ABC＝12①当0＜x≤2时，设AC与DF交于点G，此时△ABC与Rt△DEF重叠部分为△CDG，由题意可得CD＝x，DGCD•DG2；∴S＝12②当2＜x≤4时，设AB与DF交于点G，此时△ABC与Rt△DEF重叠部分为四边形AGDC，由题意可得：CD＝x，则BD＝4﹣x，DG4﹣x），×（4﹣x）4﹣x），∴S＝S△ABC﹣S△BDG＝﹣12∴S＝2﹣x﹣4）2③当4＜x≤8时，设AB与EF交于点G，过点G作GM⊥BC，交BC于点M，此时△ABC与Rt△DEF重叠部分为△BEG，由题意可得CD ＝x ，则CE ＝x ﹣4，DB ＝x ﹣4，∴BE ＝x ﹣（x ﹣4）﹣（x ﹣4）＝8﹣x ，∴BM ＝4﹣12x在Rt △BGM 中，GM 4﹣12x ），∴S ＝12BE •GM ＝12（8﹣x ）4﹣12x ），∴S x ﹣8）2，综上，选项A 的图像符合题意，故选：A ．18．（2023·山东聊城·三模）如图（1）所示，E 为矩形ABCD 的边AD 上一点，动点P ，Q 同时从点B 出发，点P 沿折线BE ―ED ―DC 运动到点C 时停止，点Q 沿BC 运动到点C 时停止，它们运动的速度都是1cm/秒，设P ，Q 同时出发t 秒时，△BPQ 的面积为y cm 2．已知y 与t 的函数关系图像如图（2）（曲线OM 为抛物线的一部分），则下列结论不正确的是（ ）A ．AB:AD =4:5B ．当t =2.5秒时，PQ =C ．当t =294时，BQ PQ =53D ．当△BPQ 的面积为4cm 2时，t 或475秒【思路点拨】先由图2中的函数图像得到当t =5时，点Q 到达点C ，即BC =5cm ，然后由5<t <7时，y =10可知△BPQ的面积是定值10cm 2、BE =5cm,ED=2cm ,当t =7时点P 到达点D ，AE ==4cm ，可以判定A ；当0<t ≤5时，根据y =25t 2得到y =2.5cm 2，过点P 作PH ⊥BC 于点H ，根据y =12BQ·PH =12×2.5cm ×PH =2.5cm 2求得PH =2，设QH =x cm ，根勾股定理计算QH =1cm ，可计算PQ =根据AB =CD =4cm ，得到再运动4秒到达C 点即H (11,0),N (7,10)，确定直线HN 或475秒；当t =294>284=7时，故点Q 在DC 上，把t =294代入直线HN 的解析式计算BQ PQ =43．【解题过程】解：设抛物线的解析式为y =at 2，当t =5时，y =10，∴10=25a ，解得a =25，∴y =25t 2，由图2中的函数图像得当t =5时，点Q 到达点C ，即BC =BE =5cm ，∵5＜t ＜7时，y =10，∴△BPQ 的面积是定值10cm 2且BE =5cm,ED=2cm ,当t =7时点P 到达点D ，∴AE =5―2==4cm,AD=BC =5cm ，∴AB:AD =4:5，故A 正确，不符合题意；当0<t ≤5时，∵y =25t 2，t =2.5，∴BP =BQ =2.5cm ，y =2.5cm 2，过点P 作PH ⊥BC 于点H ，∴y =12BQ·PH =12×2.5cm ×PH =2.5cm 2解得PH =2，设QH =x cm ，则BH =BQ ―QH =(2.5―x )cm ，∴2.52=22+(2.5―x )2，解得x =1,x =4（舍去），∴QH =1cm ，∴PQ==故B 正确，不符合题意；根据AB =CD =4cm ，∴再运动4秒到达C 点即H (11,0),N (7,10)，设直线HN 的解析式为y =kt +b ，根据题意，得11k +b =07k +b =10 ，解得k =―52b =552 ，∴直线HN 的解析式为y =―52t +552，∵△BPQ 的面积为4cm 2，故4=25t 2或4=―52t +552解得t==―t =475，故D 正确，不符合题意；∵t =294>284=7时，故点Q 在DC 上，当t =294时，y =―52×294+552=758，12PQ·BC =758解得PQ=154∴BQ PQ =5154=43．故C错误，符合题意．故选：C．19．（2023·辽宁·中考真题）如图，∠MAN=60°，在射线AM，AN上分别截取AC=AB=6，连接BC，∠MAN 的平分线交BC于点D，点E为线段AB上的动点，作EF⊥AM交AM于点F，作EG∥AM交射线AD于点G，过点G作GH⊥AM于点H，点E沿AB方向运动，当点E与点B重合时停止运动．设点E运动的路程为x，四边形EFHG与△ABC重叠部分的面积为S，则能大致反映S与x之间函数关系的图象是（）A．B．C．D．【思路点拨】分三种情况分别求出S与x的函数关系式，根据函数的类型与其图象的对应关系进行判断即可．【解题过程】解：∵∠MAN=60°，AC=AB=6，∴△ABC是边长为6的正三角形，∵AD平分∠MAN，∴∠MAD=∠NAD=30°，AD⊥BC，CD=DB=3，①当矩形EFGH全部在△ABC之中，即由图1到图2，此时0<x≤3，∵EG∥AC，∴∠MAD=∠AGE=30°，∴∠NAD=∠AGE=30°，∴AE=EG=x，在Rt△AEF中，∠EAF=60°，∴EF==，∴S=2；②如图3时，当AE+AF=GE+AF=AF+CF=AC，x=6，解得x=4，则x+12由图2到图3，此时3<x≤4，如图4，记BC，EG的交点为Q，则△EQB是正三角形，∴EQ=EB=BQ=6―x，∴GQ=x―(6―x)=2x―6，而∠PQG=60°，∴PG==2x―6)，∴S=S矩形EFHG―S△PQG=2x 2―12×(2x ―6)×2x ―6)=―2― ③如图6时，x =6，由图3到图6，此时4<x ≤6，如图5，同理△EKB 是正三角形，∴EK =KB =EB =6―x ，FC =AC ―AF =6―12x ，EF =， ∴S =S 梯形EKCF=―x +6―12x 2=―2， 因此三段函数的都是二次函数关系，其中第1段是开口向上，第2段、第3段是开口向下的抛物线， 故选：A ．20．（22-23九年级上·安徽滁州·期末）如图，在平面直角坐标系中，菱形ABCD 的边长为4，且点A 与原点O 重合，边AD 在x 轴上，点B 的横坐标为―2，现将菱形ABCD 沿x 轴以每秒1个单位长度的速度向右平移，设平移时间为t （秒），菱形ABCD 位于y 轴右侧部分的面积为S ，则S 关于t 的函数图像大致为（ ）A ．B ．C ．D ．【思路点拨】过点B 作x 轴的垂线，垂足为点E ，如图所示，由菱形ABCD 沿x 轴以每秒1个单位长度的速度向右平移，分①当0≤t ≤2时；②当2<t <4时；③当4≤t ≤6时；④当t >6时；四种情况，作图求解S 关于t 的函数解析式，作出图像即可得到答案．【解题过程】解：过点B 作x 轴的垂线，垂足为点E ，如图所示：∵菱形ABCD 的边长为4，且点A 与原点O 重合，边AD 在x 轴上，点B 的横坐标为―2，∴OE =2,OB =4，∴∠OBE =30°，∴∠BOE =60°，BE =①当0≤t ≤2时，如图（1）所示：S =12OA ⋅OF =12×t ×=2；②当2<t <4时，如图（2）所示：S =S △ABE +S 矩形OEBG =12AE ⋅BE +BE ⋅OE =12×2×t ―2)=―③当4≤t ≤6时，如图（3）所示：∵∠C =60°，OD =OA ―AD =t ―4，∴∠KDO =60°,OK=t ―4)，∵HO =BE =∴HK =HO ―OK =―t ―4)=―+∵HB =OE =OA ―AE =t ―2，∴CH =BC ―HB =4―(t ―2)=―t +6，S =S 菱形ABCD ―S △CHK =AD ⋅BE ―12CH ⋅HK =4×―12(―t +6)(―+=―2―+=―2―当t >6时，S =S 菱形ABCD =AD ⋅BE=综上所述S =20≤t ≤2―2<t <4t2+―4≤t ≤6t >6 ，∴第一段二次函数部分，开口向上；第二段一次函数部分；第三段二次函数部分，开后向下；第四段平行于x轴的射线，故选：A．。

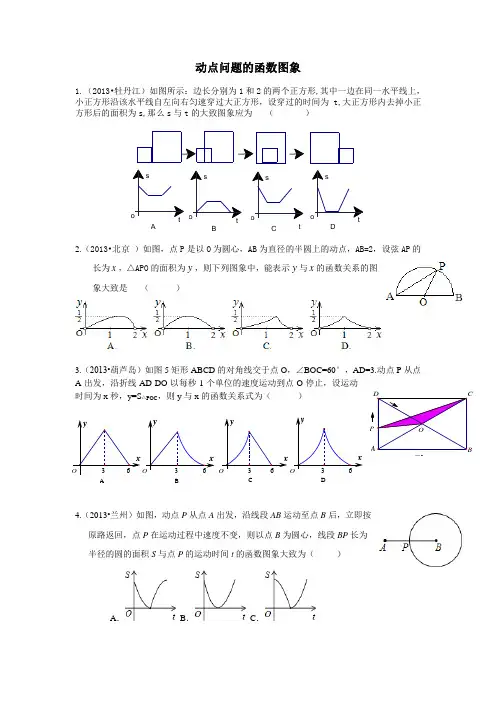
xxxxyy yyDCBA63636363OOOO图5OCD ABP 动点问题的函数图象1.（2013•牡丹江）如图所示：边长分别为1和2的两个正方形,其中一边在同一水平线上，小正方形沿该水平线自左向右匀速穿过大正方形，设穿过的时间为t,大正方形内去掉小正方形后的面积为s,那么s 与t 的大致图象应为 （ ）2.（2013•北京 ）如图，点P 是以O 为圆心，AB 为直径的半圆上的动点，AB=2，设弦AP 的长为x ，△APO 的面积为y ，则下列图象中，能表示y 与x 的函数关系的图象大致是 （ ）3.（2013•葫芦岛）如图5矩形ABCD 的对角线交于点O ，∠BOC=60°，AD=3.动点P 从点A 出发，沿折线AD-DO 以每秒1个单位的速度运动到点O 停止，设运动时间为x 秒，y=S △POC ，则y 与x 的函数关系式为（ ）4.（2013•兰州）如图，动点P 从点A 出发，沿线段AB 运动至点B 后，立即按原路返回，点P在运动过程中速度不变，则以点B 为圆心，线段BP 长为半径的圆的面积S 与点P 的运动时间t 的函数图象大致为（ ）A ．B ． C．D C B A s t o s t o s t o o t sD ．5.（2013•铁岭）如图，点G 、E 、A 、B 在一条直线上，Rt △EFG 从如图所示是位置出发，沿直线AB 向右匀速运动，当点G 与B 重合时停止运动．设△EFG 与矩形ABCD 重合部分的面积为S ，运动时间为t ，则S 与t 的图象大致是（ ） A ．B ．C ．D ．6.（2012•铁岭）如图， ABCD 的边长为8，面积为32，四个全等的小平行四边形对称中心分别在ABCD 的顶点上，它们的各边与 ABCD 的各边分别平行，且与 ABCD 相似.若小平行四边形的一边长为 ，且0＜ ≤8，阴影部分的面积的和为 ，则与 之间的函数关系的大致图象是 （ ）A. B. C. D.7.（2011•安徽）如图，点P 是菱形ABCD 的对角线AC 上的一个动点，过点P 垂直于AC 的直线交菱形ABCD 的边于M 、N 两点．设AC ＝2，BD ＝1，AP ＝x ，△AMN 的面积为y ，则y 关于x 的函数图象大致形状是 （ ）8.（2011•葫芦岛）如图，在矩形中截取两个相同的圆作为圆柱的上下底面，剩余的矩形作为圆柱的侧面，刚好能组合成圆柱．设矩形的长与宽分别为y 和x ，则y 与x 函数的图象大致是( )．OOOOx x x x y y y y 1 2 1 2 1 2 1 2 A ．B ．C ．D ． x x y y x ABCDMN P9.（2012•营口）如图，菱形ABCD 的边长为2，∠B=30°．动点P 从点B 出发，沿B ﹣C ﹣D 的路线向点D 运动．设△ABP 的面积为y （B 、P 两点重合时，△ABP 的面积可以看做0），点P 运动的路程为x ，则y 与x 之间函数关系的图象大致为（ ）10.（2011•辽阳）如图，等边△ABC 的边长为4，M 为BC 上一动点(M 不与B 、C 重合)，若EB ＝1，∠EMF ＝60°，点E 在AB 边上，点F 在AC 边上．设BM ＝x ，CF ＝y ，则当点M 从点B 运动到点C 时，y 关于x 的函数图象是( )．11.（2011•营口）如图，半径为1的圆和边长为3的正方形在同一水平线上，圆沿水平线从左向右匀速穿过正方形，设穿过时间为t ，正方形除去圆部分的面积为S (阴影部分)，则S 与t 的大致图象为( )．12.（2013•营口）如图1，在矩形ABCD 中，动点E 从点B 出发，沿B A DA ．B ．C ．D ．A DEyC 方向运动至点C 处停止，设点E 运动的路程为x ，△BCE 的面积为y ，如果y 关于x 的函数图象如图2所示，则当7 x 时，点E 应运动到（ ）A ．点C 处B ．点D 处C ．点B 处D ．点A 处13.（2012•鞍山）如图，在直角梯形ABCD 中，AD ∥BC ，∠A=90°，AB=BC=4，DE ⊥BC 于点E ，且E 是BC 中点；动点P 从点E 出发沿路径ED→DA→AB 以每秒1个单位长度的速度向终点B 运动；设点P 的运动时间为t 秒，△PBC 的面积为S ，则下列能反映S 与t 的函数关系的图象是（ ） 14.15.（2013•自贡）如图，已知A 、B 是反比例函数上的两点，BC ∥x轴，交y 轴于C ，动点P 从坐标原点O 出发，沿O→A→B→C 匀速运动，终点为C ，过运动路线上任意一点P 作PM ⊥x 轴于M ，PN ⊥y 轴于N ，设四边形OMPN 的面积为S ，P 点运动的时间为t ，则S 关于t 的函数图象大致是（ ）A ．B ．C ．D ．A ．B ．C ．D ．16.（2012•烟台）如图，矩形ABCD 中，P 为CD 中点，点Q 为AB 上的动点（不与A ，B 重合）．过Q 作QM ⊥PA 于M ，QN ⊥PB 于N ．设AQ 的长度为x ，QM 与QN 的长度和为y ．则能表示y 与x 之间的函数关系的图象大致是（ ） A ． B ． C ． D ．17.（2012•岳阳）如图，两个边长相等的正方形ABCD 和EFGH ，正方形EFGH 的顶点E 固定在正方形ABCD 的对称中心位置，正方形EFGH 绕点E 顺时针方向旋转，设它们重叠部分的面积为S ，旋转的角度为θ，S 与θ的函数关系的大致图象是（ ） 18.（2012•攀枝花）如图，直角梯形AOCD 的边OC 在x 轴上，O为坐标原点，CD 垂直于x 轴，D （5，4），AD=2．若动点E 、F 同时从点O 出发，E 点沿折线OA→AD→DC 运动，到达C 点时停止；F 点沿OC 运动，到达C 点是停止，它们运动的速度都是每秒1个单位长度．设E 运动秒x 时，△EOF 的面积为y （平方单位），则y 关于x 的函数图象大致为（ ）A ．B ．C ．D ．19.（2012•桂林）如图，在边长为4的正方形ABCD 中，动点P 从A 点出发，以每秒1个单位A ．B ．C ．D ．长度的速度沿AB 向B 点运动，同时动点Q 从B 点出发，以每秒2个单位长度的速度沿BC →CD 方向运动，当P 运动到B 点时，P 、Q 两点同时停止运动．设P 点运动的时间为t ，△APQ 的面积为S ，则S 与t 的函数关系的图象是（ ）20.（2010•烟台）如图，AB 为半圆的直径，点P 为AB 上一动点，动点P 从点A 出发，沿AB 匀速运动到点B ，运动时间为t ，分别以AP 于PB 为直径做半圆，则图中阴影部分的面积S 与时间t 之间的函数图像大致为A B CD。

函数图像与动点问题一．选择题（共10小题）1．如图，在平行四边形ABCD中，∠A=60°，AB=6厘米，BC=12厘米，点P、Q 同时从顶点A出发，点P沿A→B→C→D方向以2厘米/秒的速度前进，点Q沿A→D方向以1厘米/秒的速度前进，当Q到达点D时，两个点随之停止运动．设运动时间为x秒，P、Q经过的路径与线段PQ围成的图形的面积为y（cm2），则y与x的函数图象大致是（）A．B．C．D．2．如图，某电信公司提供了A，B两种方案的移动通讯费用y（元）与通话时间x（元）之间的关系，则下列结论中正确的有（）（1）若通话时间少于120分，则A方案比B方案便宜20元；（2）若通话时间超过200分，则B方案比A方案便宜12元；（3）若通讯费用为60元，则B方案比A方案的通话时间多；（4）若两种方案通讯费用相差10元，则通话时间是145分或185分．A．1个 B．2个 C．3个 D．4个3．如图，已知点F的坐标为（3，0），点A、B分别是某函数图象与x轴、y轴的交点，点P是此图象上的一动点，设点P的横坐标为x，PF的长为d，且d与x之间满足关系：d=5﹣x（0≤x≤5），则结论：①AF=2；②BF=5；③OA=5；④OB=3，正确结论的序号是（）A．①②③B．①③C．①②④D．③④4．如图是小明在物理实验课上用量筒和水测量铁块A的体积实验，小明在匀速向上将铁块提起，直至铁块完全露出水面一定高度的过程中，则下图能反映液面高度h与铁块被提起的时间t之间的函数关系的大致图象是（）A．B．C．D．5．如图①，在平面直角坐标系中，平行四边形ABCD在第一象限，直线y=﹣x 从原点出发沿x轴正方向平移，被平行四边形ABCD截得的线段EF的长度l与平移的距离m的函数图象如图②所示，那么平行四边形的面积为（）A．B．4 C．6 D．86．函数y=的图象为（）A．B．C．D．7．如图，已知正△ABC的边长为2，E、F、G分别是AB、BC、CA上的点，且AE=BF=CG，设△EFG的面积为y，AE的长为x，则y关于x的函数图象大致是（）A．B．C．D．8．如图所示，一列快车从甲地驶往乙地，一列慢车从乙地驶往甲地，两车同时出发，设慢车行驶的时间为x（h），两车之间的距离为y（km），图中的折线表示y与x之间的函数关系．下列说法中正确的是（）A．B点表示此时快车到达乙地B．B﹣C﹣D段表示慢车先加速后减速最后到达甲地C．快车的速度为km/hD．慢车的速度为125km/h9．如图，矩形ABCD中，AB=3，BC=4，动点P从A点出发，按A→B→C的方向在AB和BC上移动，记PA=x，点D到直线PA的距离为y，则y关于x的函数图象大致是（）A． B． C． D．10．如图1，直径AC、BD将圆O四等分，动点P从圆心O出发，沿O→C→D→O 路线作匀速运动，若圆O的半径为1，设运动x时间为x（s），∠APB=y°，y与x之间的函数关系如图2所示，则点M的横坐标应为（）A．2 B．C． +1 D．﹣1二．填空题（共8小题）11．函数y=中，自变量x的取值范围是．12．在关系式y=3x﹣1中，当x由1变化到5时，y由变化到．13．甲、乙两人骑自行车匀速同向行驶，乙在甲前面100米处，同时出发去距离甲1300米的目的地，其中甲的速度比乙的速度快．设甲、乙之间的距离为y米，乙行驶的时间为x秒，y与x之间的关系如图所示．若丙也从甲出发的地方沿相同的方向骑自行车行驶，且与甲的速度相同，当甲追上乙后45秒时，丙也追上乙，则丙比甲晚出发秒．14．小明画了一个边长为2cm的正方形，如果将正方形的边长增加xcm，那么面积的增加值y（cm2）与边长的增加值x（cm）之间的关系式为．15．地表以下岩层的温度y（℃）随着所处深度x（km）的变化而变化，在某个地点y与x之间的关系可以近似地用关系式y=35x+20来表示．当x的值是5时，y=．16．已知函数y=﹣4x﹣3，当x=时，函数值为0．17．如图表示甲、乙两名选手在一次自行车越野赛中，路程y（千米）随时间x （分）变化的图象．下面几个结论：①比赛开始24分钟时，两人第一次相遇．②这次比赛全程是10千米．③比赛开始38分钟时，两人第二次相遇．正确的结论为．18．如图的程序是一种数值转换程序，当输入的x值为1.5时，输出的y值为．三．解答题（共5小题）19．司机小王开车从A地出发去B地送信，其行驶路s与行驶时间t之间的关系如图所示，当汽车行驶若干小时到达C地时，汽车发生了故障，需停车检修，修理了几小时后，为了按时赶到B地，汽车加快了速度，结果正好按时赶到，根据题意结合图回答下列问题：（1）上述问题中反映的是哪两个变量之间的关系？指出自变量和因变量．（2）汽车从A地到C地用了几小时？平均每小时行驶多少千米？（3）汽车停车检修了多长时间？车修好后每小时走多少千米？20．已知：如图，在Rt△ABC中，∠C=90°，AC=6，BC=8，点P在BC上运动，点P不与点B，C重合，设PC=x，若用y表示△APB的面积，求y与x的函数关系式，并求自变量x的取值范围．21．等腰三角形周长为10cm，底边BC长为ycm，腰AB长为xcm，（1）写出y关于x的函数关系式；（2）求x的取值范围．22．如图1，在△ABC中，∠C=90°，点D在AC上，且CD＞DA，DA=2，点P，Q 同时从点D出发，以相同的速度分别沿射线DC、射线DA运动，过点Q作AC的垂线段QR，使QR=PQ，连接PR，当点Q到达点A时，点P，Q同时停止运动．设PQ=x，△PQR与△ABC重叠部分的面积为S，S关于x的函数图象如图2所示（其中0＜x≤，＜x≤m时，函数的解析式不同）．（1）填空：n的值为；（2）求S关于x的函数关系式，并写出x的取值范围．23．阅读下面材料，再回答问题．一般地，如果函数y=f（x）对于自变量取值范围内的任意x，都有f（﹣x）=f（x）．那么y=f（x）就叫偶函数．如果函数y=f（x）对于自变量取值范围内的任意x，都有f（﹣x）=﹣f（x）．那么y=f（x）就叫奇函数．例如：f（x）=x4当x取任意实数时，f（﹣x）=（﹣x）4=x4∴f（﹣x）=f（x）∴f（x）=x4是偶函数．又如：f（x）=2x3﹣x．当x取任意实数时，∵f（﹣x）=2（﹣x）3﹣（﹣x）=﹣2x3+x=﹣（2x3﹣x）∴f （﹣x）=﹣f（x）∴f（x）=2x3﹣x是奇函数．问题1：下列函数中：①y=x2+1②③④⑤y=x﹣2﹣2|x|是奇函数的有；是偶函数的有（填序号）问题2：仿照例证明：函数④或⑤是奇函数还是偶函数（选择其中之一）参考答案一．选择题（共10小题）1．A；2．C；3．A；4．B；5．D；6．D；7．D；8．C；9．B；10．C；二．填空题（共8小题）11．x≥2；12．2；14；13．15；14．y=x2+4x；15．195；16．；17．①③；18．3.5；三．解答题（共5小题）19-21略；22．；23．②④；①⑤；。

中考数学复习----《动点问题的函数图像》压轴真题练习（含答案解析）1．（2021•益阳）如图，已知▱ABCD的面积为4，点P在AB边上从左向右运动（不含端点），设△APD的面积为x，△BPC的面积为y，则y关于x的函数图象大致是（）A．B．C．D．【答案】B【解答】解：∵▱ABCD的面积为4，x+y是平行四边形面积的一半，∴x+y＝2，∴y＝2﹣x，∴y是x的一次函数，且当x＝0时，y＝2；x＝2时，y＝0；故只有选项B符合题意．2．（2021•河南）如图1，矩形ABCD中，点E为BC的中点，点P沿BC从点B运动到点C，设B，P两点间的距离为x，PA﹣PE＝y，图2是点P运动时y随x变化的关系图象，则BC的长为（）A．4B．5C．6D．7【答案】C【解答】解：由函数图象知：当x＝0，即P在B点时，BA﹣BE＝1．利用三角形两边之差小于第三边，得到PA﹣PE≤AE．∴y的最大值为AE，∴AE＝5．在Rt△ABE中，由勾股定理得：BA2+BE2＝AE2＝25，设BE的长度为t，则BA＝t+1，∴（t+1）2+t2＝25，即：t2+t﹣12＝0，∴（t+4）（t﹣3）＝0，由于t＞0，∴t+4＞0，∴t﹣3＝0，∴BC＝2BE＝2t＝2×3＝6．故选：C．3．（2022•鞍山）如图，在Rt△ABC中，∠ACB＝90°，∠A＝30°，AB＝4cm，CD⊥AB，垂足为点D，动点M从点A出发沿AB方向以cm/s的速度匀速运动到点B，同时动点N从点C出发沿射线DC方向以1cm/s的速度匀速运动．当点M停止运动时，点N也随之停止，连接MN．设运动时间为ts，△MND的面积为Scm2，则下列图象能大致反映S与t之间函数关系的是（）A．B．C．D．【答案】B【解答】解：∵∠ACB＝90°，∠A＝30°，AB＝4，∴∠B＝60°，BC＝AB＝2，AC＝BC＝6，∵CD⊥AB，∴CD＝AC＝3，AD＝CD＝3，BD＝BC＝，∴当M在AD上时，0≤t≤3，MD＝AD﹣AM＝3﹣t，DN＝DC+CN＝3+t，∴S＝MD•DN＝（3﹣t）（3+t）＝﹣t2+，当M在BD上时，3＜t≤4，MD＝AM﹣AD＝t﹣3，∴S＝MD•DN＝（t﹣3）（3+t）＝t2﹣，故选：B．4．（2022•菏泽）如图，等腰Rt△ABC与矩形DEFG在同一水平线上，AB＝DE ＝2，DG＝3，现将等腰Rt△ABC沿箭头所指方向水平平移，平移距离x是自点C到达DE之时开始计算，至AB离开GF为止．等腰Rt△ABC与矩形DEFG的重合部分面积记为y，则能大致反映y与x的函数关系的图象为（）A．B．C．D．【答案】B【解答】解：如图，作CH⊥AB于点H，∵AB＝2，△ABC是等腰直角三角形，∴CH＝1，当0≤x≤1时，y＝×2x•x＝x2，当1＜x≤3时，y＝＝1，当3＜x≤4时，y＝1﹣＝﹣（x﹣3）2+1，故选：B．5．（2022•鄂尔多斯）如图①，在正方形ABCD中，点M是AB的中点，点N 是对角线BD上一动点，设DN＝x，AN+MN＝y，已知y与x之间的函数图象如图②所示，点E（a，2）是图象的最低点，那么a的值为（）A．B．2C．D．【答案】 A【解答】解：如图，连接AC交BD于点O，连接NC，连接MC交BD于点N′．∵四边形ABCD是正方形，∴O是BD的中点，∵点M是AB的中点，∴N′是△ABC的重心，∴N′O＝BO，∴N′D＝BD，∵A、C关于BD对称，∴NA＝NC，∴AN+MN＝NC+MN，∵当M、N、C共线时，y的值最小，∴y的值最小就是MC的长，∴MC＝2，设正方形的边长为m，则BM＝m，在Rt△BCM中，由勾股定理得：MC2＝BC2+MB2，∴20＝m2+（m）2，∴m＝4，∴BD＝4，∴a＝N′D＝BD＝×4＝，故选：A．6．（2021•鞍山）如图，△ABC是等边三角形，AB＝6cm，点M从点C出发沿CB方向以1cm/s的速度匀速运动到点B，同时点N从点C出发沿射线CA 方向以2cm/s的速度匀速运动，当点M停止运动时，点N也随之停止．过点M作MP∥CA交AB于点P，连接MN，NP，作△MNP关于直线MP对称的△MN′P，设运动时间为ts，△MN′P与△BMP重叠部分的面积为Scm2，则能表示S与t之间函数关系的大致图象为（）A．B．C．D．【答案】A【解答】解：如图1中，当点N′落在AB上时，取CN的中点T，连接MT．∵CM＝t（cm），CN＝2t（cm），CT＝TN，∴CT＝TN＝t（cm），∵△ABC是等边三角形，∴∠C＝∠A＝60°，∴△MCT是等边三角形，∴TM＝TC＝TN，∴∠CMN＝90°，∵MP∥AC，∴∠BPM＝∠A＝∠MPN＝60°，∠BMP＝∠C＝60°，∠C+∠CMP＝180°，∴∠CMP＝120°，△BMP是等边三角形，∴BM＝MP，∵∠CMP+∠MPN＝180°，∴CM∥PN，∵MP∥CN，∴四边形CMPN是平行四边形，∴PM＝CN＝BM＝2t，∴3t＝6，∴t＝2，如图2中，当0＜t≤2时，过点M作MK⊥AC于K，则MK＝CM•sin60°＝t，∴S＝•（6﹣t）•t＝﹣t2+t．如图3中，当2＜t≤6时，S＝•MQ•PQ＝×（6﹣t）×（6﹣t）＝×（6﹣t）2，观察图象可知，选项A符合题意，故选：A．7．（2021•威海）如图，在菱形ABCD中，AB＝2cm，∠D＝60°，点P，Q同时从点A出发，点P以1cm/s的速度沿A﹣C﹣D的方向运动，点Q以2cm/s 的速度沿A﹣B﹣C﹣D的方向运动，当其中一点到达D点时，两点停止运动．设运动时间为x（s），△APQ的面积为y（cm2），则下列图象中能大致反映y与x之间函数关系的是（）A．B．C．D．【答案】A【解答】解：∵四边形ABCD为菱形，∴AB＝BC＝CD＝DA＝2cm，∠B＝∠D＝60°．∴△ABC、△ACD都是等边三角形，∴∠CAB＝∠ACB＝∠ACD＝60°．如图1所示，当0≤x≤1时，AQ＝2xcm，AP＝xcm，作PE⊥AB于E，∴PE＝sin∠PAE×AP＝（cm），∴y＝AQ•PE＝×2x×＝，故D选项不正确；如图2，当1＜x≤2时，AP＝xcm，CQ＝（4﹣2x）cm，作QF⊥AC于点F，∴QF＝sin∠ACB•CQ＝（cm），∴y＝＝＝，故B选项不正确；如图3，当2＜x≤3时，CQ＝（2x﹣4）cm，CP＝（x﹣2）cm，∴PQ＝CQ﹣CP＝2x﹣4﹣x+2＝（x﹣2）cm，作AG⊥DC于点G，∴AG＝sin∠ACD•AC＝×2＝（cm），∴y＝＝＝．故C选项不正确，故选：A．8．（2021•日照）如图，平面图形ABD由直角边长为1的等腰直角△AOD和扇形BOD组成，点P在线段AB上，PQ⊥AB，且PQ交AD或交于点Q．设AP＝x（0＜x＜2），图中阴影部分表示的平面图形APQ（或APQD）的面积为y，则函数y关于x的大致图象是（）A．B．C．D．【答案】D【解答】解：当Q在AD上时，即点P在AO上时，有0＜x≤1，此时阴影部分为等腰直角三角形，∴y＝，该函数是二次函数，且开口向上，排除B，C选项；当点Q在弧BD上时，补全图形如图所示，阴影部分的面积等于等腰直角△AOD的面积加上扇形BOD的面积，再减去平面图形PBQ的面积即减去弓形QBF的面积，设∠QOB＝θ，则∠QOF＝2θ，∴，S弓形QBF＝﹣S△QOF，当θ＝45°时，AP＝x＝1+≈1.7，S弓形QBF＝﹣＝﹣，y＝+﹣（﹣）＝≈1.14，当θ＝30°时，AP＝x≈1.87，S弓形QBF＝﹣＝﹣，y＝+﹣（﹣）＝≈1.24，当θ＝60°时，AP＝x≈1.5，y≈0.98，在A，D选项中分别找到这两个特殊值，对比发现，选项D符合题意．故选：D．法二、当1＜x＜2时，即P在OB之间时，设∠QOD＝θ，则θ∈（0，），则PQ＝cosθ，OP＝sinθ，则弧QD的长为θπ，此时S阴影＝+θπ+sinθcosθ＝+θ+sin2θ，∴y随x的增大而增大，而且增加的速度越来越慢，分析四个选项中的图象，只有选项D符合．故选：D．9．（2021•辽宁）如图，在矩形ABCD中，AB＝6，AD＝4，E是CD的中点，射线AE与BC的延长线相交于点F，点M从A出发，沿A→B→F的路线匀速运动到点F停止．过点M作MN⊥AF于点N．设AN的长为x，△AMN 的面积为S，则能大致反映S与x之间函数关系的图象是（）A．B．C．D．【答案】B【解答】解：如图，∵E是CD的中点，∴CE＝DE，∵四边形ABCD是矩形，∴∠D＝∠DCF＝90°，AD＝BC＝4，在△ADE与△FCE中，，∴△ADE≌△FCE（SAS），∴CF＝AD＝4，∴BF＝CF+BC＝8，∴AF＝，当点M在AB上时，在Rt△AMN和Rt△AFB中，tan∠NAM＝，∴NM＝x＝x，∴△AMN的面积S＝×x×x＝x2，∴当点M在AB上时，函数图象是开口向上、经过原点的抛物线的一部分；当点M在BF上时，如图，AN＝x，NF＝10﹣x，在Rt△FMN和Rt△FBA中，tan∠F＝，∴＝﹣，∴△AMN的面积S＝＝﹣，∴当点M在BF上时，函数图象是开口向下的抛物线的一部分；故选：B．10．（2021•苏州）如图，线段AB＝10，点C、D在AB上，AC＝BD＝1．已知点P从点C出发，以每秒1个单位长度的速度沿着AB向点D移动，到达点D后停止移动．在点P移动过程中作如下操作：先以点P为圆心，PA、PB的长为半径分别作两个圆心角均为60°的扇形，再将两个扇形分别围成两个圆锥的侧面，设点P的移动时间为t（秒），两个圆锥的底面面积之和为S，则S关于t的函数图象大致是（）A．B．C．D．【答案】D【解答】解：∵AB＝10，AC＝BD＝1，∴CD＝10﹣1﹣1＝8，∵PC＝t，∴AP＝t+1，PB＝8﹣t+1＝9﹣t，设围成的两个圆锥底面圆半径分别为r和R则：2πr＝；．解得：r＝，R＝，∴两个圆锥的底面面积之和为S＝＝＝，根据函数关系式可以发现该函数图象是一个开口向上的二次函数．故选：D．11．（2021•甘肃）如图1，在△ABC中，AB＝BC，BD⊥AC于点D（AD＞BD）．动点M从A点出发，沿折线AB→BC方向运动，运动到点C停止．设点M的运动路程为x，△AMD的面积为y，y与x的函数图象如图2，则AC的长为（）A．3B．6C．8D．9【答案】B【解答】解：由图2知，AB+BC＝2，∵AB＝BC，∴AB＝，∵AB＝BC，BD⊥AC，∴AC＝2AD，∠ADB＝90°，在Rt△ABD中，AD²+BD²＝AB²＝13①，设点M到AC的距离为h，∴S△ADM＝AD•h，∵动点M从A点出发，沿折线AB→BC方向运动，∴当点M运动到点B时，△ADM的面积最大，即h＝BD，由图2知，△ADM的面积最大为3，∴AD•BD＝3，∴AD•BD＝6②，①+2×②得，AD²+BD²+2AD•BD＝13+2×6＝25，∴（AD+BD）²＝25，∴AD+BD＝5（负值舍去），∴BD＝5﹣AD③，将③代入②得，AD（5﹣AD）＝6，∴AD＝3或AD＝2，∵AD＞BD，∴AD＝3，∴AC＝2AD＝6，故选：B．12．（2021•百色）如图，矩形ABCD各边中点分别是E、F、G、H，AB＝2，BC＝2，M为AB上一动点，过点M作直线l⊥AB，若点M从点A开始沿着AB方向移动到点B即停（直线l随点M移动），直线l扫过矩形内部和四边形EFGH外部的面积之和记为S．设AM＝x，则S关于x的函数图象大致是（）A．B．C．D．【答案】D【解答】解：①当M点运动在AE段，此时S＝S△HAE+S△GHD﹣S△EOM﹣S△GPS，∵四边形ABCD是矩形，直线l⊥AB，H、E、F、G为AD、AB、BC、CD的中点，∴AH＝AD＝＝1，AE＝AB＝，S△HAE＝S△GHD，S△EOM＝S△GPS，∴S＝2S△HAE﹣2S△EOM，∴S△HAE＝AE•AH＝；∵直线l⊥AB，∴∠OME＝∠A＝90°，∠HEA＝∠OEM，∴△HAE∽△OME，∴，∴OM＝，又∵ME＝AE﹣AM＝﹣x，∴OM＝ME＝，∴S△EOM＝，∴S＝2S△HAE﹣2S△EOM＝，此时，对应抛物线开口向下；②当M点运动到在BE段，此时，S＝S△HAE+S△GHD+S△EO1M1+S△GP1S1，即S＝2S△HAE+2S△EO1M1，与①同理，O1M1＝，又∵M1E＝AM1﹣AE＝x﹣，∴O1M1＝M1E＝，∴S△EO1M1＝，∴S＝2S△HAE+2S△EO1M1＝，此时，对应抛物线开口向上，故选：D．13．（2021•鄂尔多斯）如图①，在矩形ABCD中，H为CD边上的一点，点M 从点A出发沿折线AH﹣HC﹣CB运动到点B停止，点N从点A出发沿AB 运动到点B停止，它们的运动速度都是1cm/s，若点M、N同时开始运动，设运动时间为t（s），△AMN的面积为S（cm2），已知S与t之间函数图象如图②所示，则下列结论正确的是（）①当0＜t≤6时，△AMN是等边三角形．②在运动过程中，使得△ADM为等腰三角形的点M一共有3个．③当0＜t≤6时，S＝．④当t＝9+时，△ADH∽△ABM．⑤当9＜t＜9+3时，S＝﹣3t+9+3．A．①③④B．①③⑤C．①②④D．③④⑤【答案】A【解答】解：由图②可知：点M、N两点经过6秒时，S最大，此时点M在点H处，点N在点B处并停止不动，如图，①∵点M、N两点的运动速度为1cm/s，∴AH＝AB＝6cm，∵四边形ABCD是矩形，∴CD＝AB＝6 cm．∵当t＝6s时，S＝9cm2，∴×AB×BC＝9．∴BC＝3cm．∵当6≤t≤9时，S＝且保持不变，∴点N在B处不动，点M在线段HC上运动，运动时间为（9﹣6）秒，∴HC＝3 cm，即点H为CD的中点．∴BH＝cm．∴AB＝AH＝BH＝6cm，∴△ABM为等边三角形．∴∠HAB＝60°．∵点M、N同时开始运动，速度均为1cm/s，∴AM＝AN，∴当0＜t≤6时，△AMN为等边三角形．故①正确；②如图，当点M在AD的垂直平分线上时，△ADM为等腰三角形：此时有两个符合条件的点；当AD＝AM时，△ADM为等腰三角形，如图：当DA＝DM时，△ADM为等腰三角形，如图：综上所述，在运动过程中，使得△ADM为等腰三角形的点M一共有4个．∴②不正确；③过点M作ME⊥AB于点E，如图，由题意：AM＝AN＝t，由①知：∠HAB＝60°．在Rt△AME中，∵sin∠MAE＝，∴ME＝AM•sin60°＝tcm，∴S＝AN×ME＝cm2．∴③正确；④当t＝9+时，CM＝cm，如图，由①知：BC＝3cm，∴MB＝BC﹣CM＝2cm．∵AB＝6cm，∴tan∠MAB＝，∴∠MAB＝30°．∵∠HAB＝60°，∴∠DAH＝90°﹣60°＝30°．∴∠DAH＝∠BAM．∵∠D＝∠B＝90°，∴△ADH∽△ABM．∴④正确；⑤当9＜t＜9+3时，此时点M在边BC上，如图，此时MB＝9+3﹣t，∴S＝×AB×MB＝×6×（9+3﹣t）＝27+9﹣3t．∴⑤不正确；综上，结论正确的有：①③④．故选：A．14．（2021•通辽）如图，在矩形ABCD中，AB＝4，BC＝3，动点P，Q同时从点A出发，点P沿A→B→C的路径运动，点Q沿A→D→C的路径运动，点P，Q的运动速度相同，当点P到达点C时，点Q也随之停止运动，连接PQ．设点P的运动路程为x，PQ2为y，则y关于x的函数图象大致是（）A．B．C．D．【答案】C【解答】解：当0≤x≤3时，在Rt△APQ中，∠QAP＝90°，AP＝AQ＝x，∴PQ2＝2x2．∴y＝PQ2＝2x2；当3≤x≤4时，DQ＝x﹣3，AP＝x，∴y＝PQ2＝32+32＝18；当4≤x≤7时，CP＝7﹣x，CQ＝7﹣x，∴y＝PQ2＝CP2+CQ2＝2x2﹣28x+98．故选：C．15．（2021•湖北）如图，AC为矩形ABCD的对角线，已知AD＝3，CD＝4，点P沿折线C﹣A﹣D以每秒1个单位长度的速度运动（运动到D点停止），过点P作PE⊥BC于点E，则△CPE的面积y与点P运动的路程x间的函数图象大致是（）A．B．C．D．【答案】D【解答】解：∵BC∥AD，∴∠ACB＝∠DAC，∵∠PEC＝∠D＝90°，∴△PCE∽△CAD，∴＝＝，∵AD＝3，CD＝4，∴AC＝＝5，∴当P在CA上时，即当0＜x≤5时，PE＝＝x，CE＝＝x，∴y＝PE•CE＝＝x2，当P在AD上运动时，即当5＜x≤8时，PE＝CD＝4，CE＝8﹣x，∴y＝PE•CE＝×4×（8﹣x）＝16﹣2x，综上，当0＜x≤5时，函数图象为二次函数图象，且y随x增大而增大，当5＜x≤8时，函数图象为一次函数图象，且y随x增大而减小，故选：D．16．（2021•衡阳）如图1，菱形ABCD的对角线AC与BD相交于点O，P、Q 两点同时从O点出发，以1厘米/秒的速度在菱形的对角线及边上运动．点P 的运动路线为O﹣A﹣D﹣O，点Q的运动路线为O﹣C﹣B﹣O．设运动的时间为x秒，P、Q间的距离为y厘米，y与x的函数关系的图象大致如图2所示，当点P在A﹣D段上运动且P、Q两点间的距离最短时，P、Q两点的运动路程之和为厘米．【答案】（2+3）【解答】解：由图分析易知：当点P从O→A运动时，点Q从O→C运动时，y不断增大，当点P运动到A点，点Q运动到C点时，由图象知此时y＝PQ＝2cm，∴AC＝2cm，∵四边形ABCD为菱形，∴AC⊥BD，OA＝OC＝＝cm，当点P运动到D点，Q运动到B点，结合图象，易知此时，y＝BD＝2cm，∴OD＝OB＝BD＝1cm，在Rt△ADO中，AD＝＝＝2（cm），∴AD＝AB＝BC＝DC＝2cm，如图，当点P在A﹣D段上运动，点P运动到点E处，点Q在C﹣B段上运动，点Q运动到点F处时，P、Q两点的距离最短，此时，OE＝OF＝＝，AE＝CF＝＝＝，∴当点P在A﹣D段上运动且P、Q两点间的距离最短时，P、Q两点的运动路程之和为：（cm），故答案为：（2+3）．17．（2021•武汉）如图（1），在△ABC中，AB＝AC，∠BAC＝90°，边AB上的点D从顶点A出发，向顶点B运动，同时，边BC上的点E从顶点B出发，向顶点C运动，D，E两点运动速度的大小相等，设x＝AD，y＝AE+CD，y 关于x的函数图象如图（2），图象过点（0，2），则图象最低点的横坐标是．【答案】﹣1【解答】解：∵图象过点（0，2），即当x＝AD＝BE＝0时，点D与A重合，点E与B重合，此时y＝AE+CD＝AB+AC＝2，∵△ABC为等腰直角三角形，∴AB＝AC＝1，过点A作AF⊥BC于点F，过点B作NB⊥BC，并使得BN＝AC，如图所示：∵AD＝BE，∠NBE＝∠CAD，∴△NBE≌△CAD（SAS），∴NE＝CD，又∵y＝AE+CD，∴y＝AE+CD＝AE+NE，当A、E、N三点共线时，y取得最小值，如图所示，此时：AD＝BE＝x，AC＝BN＝1，∴AF＝AC•sin45°＝，\又∵∠BEN＝∠FEA，∠＝∠AFE∴△NBE∽△AFE∴，即，解得：x＝，∴图象最低点的横坐标为：﹣1．故答案为：．18．（2022•营口）如图1，在四边形ABCD中，BC∥AD，∠D＝90°，∠A＝45°，动点P，Q同时从点A出发，点P以cm/s的速度沿AB向点B运动（运动到B点即停止），点Q以2cm/s的速度沿折线AD→DC向终点C运动，设点Q的运动时间为x（s），△APQ的面积为y（cm2），若y与x之间的函数关系的图象如图2所示，当x＝（s）时，则y＝cm2．【答案】【解答】解：过点D作DE⊥AB，垂足为E，在Rt△ADE中，∵∠AED＝90°，∠EAD＝45°，∴，∵点P的速度为cm/s，点Q的速度为2cm/s，∴AP＝x，AQ＝2x，∴，在△APQ和△AED中，＝，∠A＝45°，∴△AED∽△APQ，∴点Q在AD上运动时，△APQ为等腰直角三角形，∴AP＝PQ＝x，∴当点Q在AD上运动时，y＝AP•AQ＝×x×x＝x2，由图像可知，当y＝9此时面积最大，x＝3或﹣3（负值舍去），∴AD＝2x＝6cm，当3＜x≤4时，过点P作PF⊥AD于点F，如图：此时S△APQ＝S△APF+S四边形PQDF﹣S△ADQ，在Rt△APF中，AP＝x，∠PAF＝45°，∴AF＝PF＝x，FD＝6﹣x，QD＝2x﹣6，∴S△APQ＝x2+（x+2x﹣6）•（6﹣x）﹣×6×（2x﹣6），即y＝﹣x2+6x，当x＝时，y＝﹣（）2+6×＝，故答案为：．。

xxxxyy yyDCBA63636363OOOO图5OCD ABP 动点问题的函数图象1.（2013•牡丹江）如图所示：边长分别为1和2的两个正方形,其中一边在同一水平线上，小正方形沿该水平线自左向右匀速穿过大正方形，设穿过的时间为t,大正方形内去掉小正方形后的面积为s,那么s 与t 的大致图象应为 （ ）2.（2013•北京 ）如图，点P 是以O 为圆心，AB 为直径的半圆上的动点，AB=2，设弦AP 的长为x ，△APO 的面积为y ，则下列图象中，能表示y 与x 的函数关系的图象大致是 （ ）3.（2013•葫芦岛）如图5矩形ABCD 的对角线交于点O ，∠BOC=60°，AD=3.动点P 从点A 出发，沿折线AD-DO 以每秒1个单位的速度运动到点O 停止，设运动时间为x 秒，y=S △POC ，则y 与x 的函数关系式为（ ）4.（2013•兰州）如图，动点P 从点A 出发，沿线段AB 运动至点B 后，立即按原路返回，点P在运动过程中速度不变，则以点B 为圆心，线段BP 长为半径的圆的面积S 与点P 的运动时间t 的函数图象大致为（ ）A ．B ． C．D C B A s t o s t o s t o o t sD ．5.（2013•铁岭）如图，点G 、E 、A 、B 在一条直线上，Rt △EFG 从如图所示是位置出发，沿直线AB 向右匀速运动，当点G 与B 重合时停止运动．设△EFG 与矩形ABCD 重合部分的面积为S ，运动时间为t ，则S 与t 的图象大致是（ ） A ．B ．C ．D ．6.（2012•铁岭）如图， ABCD 的边长为8，面积为32，四个全等的小平行四边形对称中心分别在ABCD 的顶点上，它们的各边与 ABCD 的各边分别平行，且与 ABCD 相似.若小平行四边形的一边长为 ，且0＜ ≤8，阴影部分的面积的和为 ，则与 之间的函数关系的大致图象是 （ ）A. B. C. D.7.（2011•安徽）如图，点P 是菱形ABCD 的对角线AC 上的一个动点，过点P 垂直于AC 的直线交菱形ABCD 的边于M 、N 两点．设AC ＝2，BD ＝1，AP ＝x ，△AMN 的面积为y ，则y 关于x 的函数图象大致形状是 （ ）8.（2011•葫芦岛）如图，在矩形中截取两个相同的圆作为圆柱的上下底面，剩余的矩形作为圆柱的侧面，刚好能组合成圆柱．设矩形的长与宽分别为y 和x ，则y 与x 函数的图象大致是( )．OOOOx x x x y y y y 1 2 1 2 1 2 1 2 A ．B ．C ．D ． x x y y x ABCDMN P9.（2012•营口）如图，菱形ABCD 的边长为2，∠B=30°．动点P 从点B 出发，沿B ﹣C ﹣D 的路线向点D 运动．设△ABP 的面积为y （B 、P 两点重合时，△ABP 的面积可以看做0），点P 运动的路程为x ，则y 与x 之间函数关系的图象大致为（ ）10.（2011•辽阳）如图，等边△ABC 的边长为4，M 为BC 上一动点(M 不与B 、C 重合)，若EB ＝1，∠EMF ＝60°，点E 在AB 边上，点F 在AC 边上．设BM ＝x ，CF ＝y ，则当点M 从点B 运动到点C 时，y 关于x 的函数图象是( )．11.（2011•营口）如图，半径为1的圆和边长为3的正方形在同一水平线上，圆沿水平线从左向右匀速穿过正方形，设穿过时间为t ，正方形除去圆部分的面积为S (阴影部分)，则S 与t 的大致图象为( )．12.（2013•营口）如图1，在矩形ABCD 中，动点E 从点B 出发，沿B A DA ．B ．C ．D ．A DEyC 方向运动至点C 处停止，设点E 运动的路程为x ，△BCE 的面积为y ，如果y 关于x 的函数图象如图2所示，则当7 x 时，点E 应运动到（ ）A ．点C 处B ．点D 处C ．点B 处D ．点A 处13.（2012•鞍山）如图，在直角梯形ABCD 中，AD ∥BC ，∠A=90°，AB=BC=4，DE ⊥BC 于点E ，且E 是BC 中点；动点P 从点E 出发沿路径ED→DA→AB 以每秒1个单位长度的速度向终点B 运动；设点P 的运动时间为t 秒，△PBC 的面积为S ，则下列能反映S 与t 的函数关系的图象是（ ） 14.15.（2013•自贡）如图，已知A 、B 是反比例函数上的两点，BC ∥x轴，交y 轴于C ，动点P 从坐标原点O 出发，沿O→A→B→C 匀速运动，终点为C ，过运动路线上任意一点P 作PM ⊥x 轴于M ，PN ⊥y 轴于N ，设四边形OMPN 的面积为S ，P 点运动的时间为t ，则S 关于t 的函数图象大致是（ ）A ．B ．C ．D ．A ．B ．C ．D ．16.（2012•烟台）如图，矩形ABCD 中，P 为CD 中点，点Q 为AB 上的动点（不与A ，B 重合）．过Q 作QM ⊥PA 于M ，QN ⊥PB 于N ．设AQ 的长度为x ，QM 与QN 的长度和为y ．则能表示y 与x 之间的函数关系的图象大致是（ ） A ． B ． C ． D ．17.（2012•岳阳）如图，两个边长相等的正方形ABCD 和EFGH ，正方形EFGH 的顶点E 固定在正方形ABCD 的对称中心位置，正方形EFGH 绕点E 顺时针方向旋转，设它们重叠部分的面积为S ，旋转的角度为θ，S 与θ的函数关系的大致图象是（ ） 18.（2012•攀枝花）如图，直角梯形AOCD 的边OC 在x 轴上，O为坐标原点，CD 垂直于x 轴，D （5，4），AD=2．若动点E 、F 同时从点O 出发，E 点沿折线OA→AD→DC 运动，到达C 点时停止；F 点沿OC 运动，到达C 点是停止，它们运动的速度都是每秒1个单位长度．设E 运动秒x 时，△EOF 的面积为y （平方单位），则y 关于x 的函数图象大致为（ ）A ．B ．C ．D ．19.（2012•桂林）如图，在边长为4的正方形ABCD 中，动点P 从A 点出发，以每秒1个单位A ．B ．C ．D ．长度的速度沿AB 向B 点运动，同时动点Q 从B 点出发，以每秒2个单位长度的速度沿BC →CD 方向运动，当P 运动到B 点时，P 、Q 两点同时停止运动．设P 点运动的时间为t ，△APQ 的面积为S ，则S 与t 的函数关系的图象是（ ）20.（2010•烟台）如图，AB 为半圆的直径，点P 为AB 上一动点，动点P 从点A 出发，沿AB 匀速运动到点B ，运动时间为t ，分别以AP 于PB 为直径做半圆，则图中阴影部分的面积S 与时间t 之间的函数图像大致为A B CD。

动点问题与函数图象作者：左加亭来源：《第二课堂(初中版)》2016年第05期动点问题是最近几年中考的一个热点题型，所谓“动点问题”是指题设图形中存在一个或多个动点，它们在线段、射线上运动的一类开放性题目.解决函数图象中的动点问题时，首先要抓住动点的瞬间状态，或者相对静止时的状态，再寻找它们的数量关系，以及几何图形的相对位置关系，做到动中求静，灵活运用有关数学知识解决问题.例1 （2015黔南州卷）如图1，在矩形MNPQ中，动点R从点N出发，沿N→P→Q→M 方向运动至点M处停止.设点R运动的路程为x，△MNR的面积为y，如果y关于x的函数图象如图2所示，则当x=9时，点R应运动到（）A.M处B.N处C.P处D.Q处精析根据三角形的面积变化情况，可得R在PQ上时，三角形面积不变，可得答案.解答点R在NP上时，三角形面积增加，点R在PQ上时，三角形面积不变，点R在QM 上时，三角形面积变小，点R在Q处，三角形面积开始变小.故选D.点拨本题考查了动点函数图象，利用三角形面积的变化确定R的位置是解题的关键.例2 （2015荆州卷）如下图，正方形ABCD的边长为3cm，动点P从B点出发以3cm/s 的速度沿着边BC-CD-DA运动，到达A点停止运动；另一动点Q同时从B点出发，以1cm/s 的速度沿着边BA向A点运动，到达A点停止运动.设P点运动时间为x（s），△BPQ的面积为y（cm2），则y关于x的函数图象是（）精析首先根据正方形的边长与动点P、Q的速度可知动点Q始终在AB边上，而动点P可以在BC边、CD边、AD边上，再分三种情况进行讨论：①0≤x≤1；②1解答由题意可得BQ=x.①0≤x≤1时，P点在BC边上，BP=3x，则△BPQ的面积为BP·BQ，则y=·3x·x=x2，则A选项错误；②1点拨本题考查动点问题的函数图象，利用数形结合、分类讨论是解题的关键.例3 （2015本溪卷）如图，在△ABC中，∠C=90°，点P是斜边AB的中点，点M从点C向点A匀速运动，点N从点B向点C匀速运动，已知两点同时出发，同时到达终点，连接PM、PN、MN，在整个运动过程中，△PMN的面积S与运动时间t的函数关系图象大致是（）精析首先连接CP，根据点P是斜边AB的中点，可得S△ACP=S△BCP=S△ABC；然后分别求出出发时，点N到达BC的中点、点M也到达AC的中点时，结束时，△PMN的面积S的大小，即可推得△PMN的面积大小变化情况是：先减小后增大，而且是以抛物线的方式变化，据此判断出△PMN的面积S与运动时间t的函数关系图象大致是哪个即可.解答连接CP，如下图：∵点P是斜边AB的中点，∴ S△ACP=S△BCP=S△ABC，出发时，S△PMN=S△BCP=S△ACP.∵两点同时出发，同时到达终点，∴点N到达BC的中点时，点M也到达AC的中点，∴此时S△PMN=S△ABC.结束时，S△PMN=S△ACP=S△ABC.故△MPQ的面积大小变化情况是：先减小后增大，而且是以抛物线的方式变化，∴△PMN的面积S与运动时间t的函数关系图象大致是：故选A.点拨此题主要考查两个动点问题与函数图象，函数图象是典型的数形结合，图象应用信息广泛，通过看图获取信息，不仅可以解决生活中的实际问题，还可以提高分析问题、解决问题的能力.用图象解决问题时，要理清图象的含义即会识图.（编辑孙世奇）。

函数中的动点问题考点分析1.点在线段上运动：2.根据线段长或图形面积求函数关系.如：如图所示，点P在线段BC,CD,DA上运动，△ABP 的面积变化情况的图象是什么样的？解析：看清横轴和纵轴表示的量.答案：2. 双动点变化：两动点同时运动，分析图形面积变化图象.如图1，在矩形ABCD中，点E是对角线AC 的三等分点（靠近点A），动点F从点C出发沿C→A→B运动，当点F与点B重合时停止运动.设点F运动的路程为x，△BEF的面积为y，那么图2能表示y与x函数关系的大致图象吗？图1 图2解析：动点问题的函数图象，解决本题应首先看清横轴和纵轴表示的量，然后根据动点的行程判断y的变化情况.答案：能.3. 图形运动变化所形成的函数问题：图形整体运动时，形成的函数问题；如图，边长为1和2的两个正方形，其一边在同一水平线上，小正方形自左向右匀速穿过大正方形，设穿过的时间为t，阴影部分面积为S，那么S与t的函数图象大致是什么？解析：图形运动变化所形成的函数问题．关键是理解图形运动过程中的几个分界点.答案：4. 实际问题中的运动变化图象如图，小亮在操场上玩，一段时间内沿M→A→B→M的路径匀速散步，能近似刻画小亮到出发点M的距离y与时间x之间关系的函数图象是（）解析：解决实际问题中的运动变化图象，要根据几何图形和图形上的数据分析得出所对应的函数的类型和所需要的条件，结合实际意义选出正确的图象.答案：总结：研究在不同位置时点的运动变化所产生的线段、面积的变化关系是重点.解题技巧例题 如图，M 是边长为4的正方形AD 边的中点，动点P 自A 点起，由A ⇒B ⇒C ⇒D 匀速运动，直线MP 扫过正方形所形成面积为y ，点P 运动的路程为x ，则表示y 与x 的函数关系的图象为（ ）A .B .C .D .解析：分别求出P 在AB 段、BC 段、CD 段的函数解析式或判断函数的类型，即可判断.答案：解：点P 在AB 段时，函数解析式是：y ＝21AP •AM ＝21×2x ＝x ，是正比例函数y x =；点P 在BC 段时，函数解析式是：1()242y AM BP AB x =+⋅=-，是一次函数24y x =-；则2,1BC AB k k ==，BC AB k k ∴>.在单位时间内点P 在BC 段上的面积增长要大于点P 在AB 上的面积增长，因此函数图象会更靠近y 轴，也就是图象会比较“陡”，故A 、B 选项错误.点P 在CD 段时，面积是△ABC 的面积加上△ACP 的面积，△ABC 的面积不变，而△ACP 中CP 边上的高一定，因而面积是CP 长的一次函数，因而此段的面积是x 的一次函数，应是线段.故C 错误，正确的是D .故选D .点拨：主要考查了函数的性质，注意分段讨论是解决本题的关键.总结提升利用动点形成的函数图象求解析式例题 （翔安模拟）如图1，在矩形ABCD 中，动点P 从点B 出发，沿BC ,CD ,DA 运动至点A 停止.设点P 运动的路程为x cm ，△ABP 的面积为 y cm 2，如果y 关于x 的函数图象如图2所示，则y 关于x 的函数关系式为 .解析：根据图2判断出矩形的AB 、BC 的长度，然后分点P 在BC 、CD 、AD 时，分别求出点P 到AB 的距离，然后根据三角形的面积公式列式即可求出y 关于x 的函数关系式.答案：解：由图2可知，x 从4到9的过程中，三角形的面积不变，所以，矩形的边AB ＝9－4＝5 cm ，边BC ＝4 cm ，则点P 运动的总路程为9＋4＝13 cm ，分情况讨论：①点P 在BC 上时，0≤x ≤4，点P 到AB 的距离为PB 的长度x cm ，y ＝21AB •PB ＝21×5x ＝25x ；②点P 在CD 上时，4<x <9，点P 到AB 的距离为BC 的长度4 cm ，y ＝21AB •BC ＝21×5×4＝10；③点P 在AD 上时，9≤x ≤13时，点P 到AB 的距离为P A 的长度（13－x ） cm ，y ＝21AB •P A ＝21×5（13－x ）＝25（13－x ）；综上，y 关于x 的函数关系式为504210495139132x x y x x x ⎧≤≤⎪⎪=<<⎨⎪⎪≤≤⎩（）（）（－）（）. 故答案为：504210495139132x x y x x x ⎧≤≤⎪⎪=<<⎨⎪⎪≤≤⎩（）（）（－）（）.动点综合型问题例题 （苏州中考）如图①，在平行四边形ABCD 中，AD ＝9 cm ，动点P 从A 点出发，以1 cm/s 的速度沿着A →B →C →A 的方向移动，直到点P 到达点A 后才停止.已知△P AD 的面积y （单位：cm 2）与点P 移动的时间x （单位：s ）之间的函数关系如图②所示，试解答下列问题：（1）求出平行四边形ABCD 的周长；（2）请你利用图①解释一下图②中线段M N 表示的实际意义； （3）求出图②中a 和b 的值.解析：（1）由图②知点P 在AB 上运动的时间为10 s ，根据路程＝速度×时间列式，求出AB ＝10 cm ，又AD ＝9 cm ，根据平行四边形的周长公式即可求解；（2）由线段M N ∥x 轴，可知此时点P 虽然在运动，但是△P AD 的面积y 不变，结合图①，可知此时点P 在BC 边上运动；（3）由AD ＝9可知点P 在边BC 上的运动时间为9 s ，a 为点P 由A →B →C 的时间；分别过B 点、C 点作BE ⊥AD ,CF ⊥AD ，易证△BAE ≌△CDF ，由此得到AE ＝DF ＝6 cm ，AF ＝15 cm ，从而可求得CA ＝17 cm ，则点P 在CA 边上从C 点运动到A 点的时间为17 s ，所以b ＝19＋17＝36.答案：解：（1）由图②可知点P 从A 点运动到B 点的时间为10 s ，又因为P 点运动的速度为1 cm/s ，所以AB ＝10×1＝10（cm ），而AD ＝9 cm ，则平行四边形ABCD 的周长为：2·（AB ＋AD ）＝2×（10＋9）＝38（cm ）；（2）线段M N 表示的实际意义是：点P 在BC 边上从B 点运动到C 点；（3）由AD ＝9可知点P 在边BC 上的运动时间为9 s ，所以a ＝10＋9＝19；分别过B ,C 两点作BE ⊥AD 于E ，CF ⊥AD 于F .由图②知S △ABD ＝36 cm 2，则21×9×BE ＝36 cm 2，解得BE ＝8 cm ，在Rt △ABE 中，由勾股定理，得AE ＝22BE AB -＝6 cm.易证△BAE ≌△CDF ，则BE ＝CF ＝8 cm ，AE ＝DF ＝6 cm ，AF ＝AD ＋DF ＝9＋6＝15 cm.在Rt △ACF 中，由勾股定理，得CA 22AF CF +17 cm ，则点P 在CA 边上从C 点运动到A 点的时间为17 s ，所以b ＝19＋17＝36.巩固训练（答题时间：45分钟）一、选择题1. （静海中考）如图，矩形ABCD中，AB＝1，AD＝2，M是CD的中点，点P在矩形的边上沿A→B→C→M运动，则△APM的面积y与点P经过的路程x之间的函数关系用图象表示大致是（）A. B.C. D.2. （营口中考）如图1，在矩形ABCD中，动点E从点B出发，沿BADC方向运动至点C处停止，设点E运动的路程为x，△BCE的面积为y，如果y关于x的函数图象如图2所示，则当x＝7时，点E应运动到（）A. 点C处B. 点D处C. 点B处D. 点A处3. （绥化中考）如图，在平面直角坐标系中，长、宽分别为2和1的矩形ABCD的边上有一动点P，沿A→B→C→D→A运动一周，则点P的纵坐标y与P所走过的路程S之间的函数关系用图象表示大致是（）A. B.C. D.*4. （荆门中考）如下图所示，已知等腰梯形ABCD，AD∥BC，若动直线l垂直于BC，且向右平移，设扫过的阴影部分的面积为S，BP为x，则S关于x的函数图象大致是（）A. B.C. D.**5.（河池中考）如图，在直角梯形ABCD中，AB＝2，BC＝4，AD＝6，M是CD的中点，点P在直角梯形的边上沿A→B→C→M运动，则△APM的面积y与点P经过的路程x 之间的函数关系用图象表示是（）A. B.C. D.二、填空题：*6. 如图，是一辆汽车的速度随时间变化的图象，请你根据图象提供的信息填空：（1）汽车在整个行驶过程中，最高速度是km/h（2）汽车第二次减速行驶的“时间段”是；（3）汽车出发后，8 min到10 min之间的运动情况如何？.*7. 如图，在正方形ABCD中，边长为2，某一点E从B－C－D－A－B运动，且速度是1，试求：（1）△BEC的面积S和时间t的关系.**8. （随州中考）在四边形ABCD中，AB边的长为4，设动点P沿折线B⇒C⇒D⇒A由点B向点A运动，设点P运动的距离为x，△P AB的面积为y，y与x的函数图象如图所示.给出下列四个结论：①四边形ABCD的周长为14；②四边形ABCD是等腰梯形；③四边形ABCD是矩形；④当△P AB面积为4时，点P移动的距离是 2.你认为其中正确的结论是.（只填所有正确结论的序号例如①）**9. 已知动点P以每秒2 cm的速度沿图甲的边框按从B→C→D→E→F→A的路径移动，相应的△ABP的面积S关于时间t的函数图象如图乙，若AB＝6 cm，试回答下列问题：（1）图甲中BC的长度是.（2）图乙中a所表示的数是.（3）图甲中的图形面积是.（4）图乙中b所表示的数是.图甲图乙三、解答题：10. （潜江）如图，有一边长为5的正方形ABCD与等腰三角形CEF，其中底边CF＝8，腰长EF＝5，若等腰△CEF以每秒1个单位沿CB方向平移，B,C,F在直线L上，请画出0＜t＜6时，两图形重叠部分的不同状态图（重叠部分用阴影标示），并写出对应t的范围.**11. 如图①，在矩形ABCD中，AB＝30 cm，BC＝60 cm.点P从点A出发，沿A→B→C→D 路线向点D匀速运动，到达点D后停止；点Q从点D出发，沿D→C→B→A路线向点A 匀速运动，到达点A后停止.若点P,Q同时出发，在运动过程中，Q点停留了1 s，图②是P,Q两点在折线AB－BC－CD上相距的路程S（cm）与时间t（s）之间的函数关系图象.（1）请解释图中点H的实际意义；（2）求P,Q两点的运动速度；（3）将图②补充完整；（4）当时间t为何值时，△PCQ为等腰三角形？请直接写出t的值.参考答案1. B 解析：①当P 在AB 上运动时，所求三角形底为AP ，高为M 到AB 的距离也就是AD 长度因此S △APM ＝21AD •AP ＝x ，函数关系为：y ＝x （0＜x ≤1）；②当P 在BC 上运动时，S △APM ＝S 梯形ABCM －S △ABP －S △PCM ，S △ABP ＝21AB •BP ，BP ＝x －1，则S △ABP ＝21x －21，S △PCM ＝21PC •CM ，CM ＝12AB ＝21，PC ＝3－x ，S △PCM ＝43x -，S 梯形ABCM ＝21（AB ＋CM ）•BC ＝23，因此S △APM ＝23－21-x －43x -＝－4x ＋45（1＜x ≤3）；③当P 在CM 上运动时，S △APM ＝21CM •AD ，CM ＝27－x ，S △APM ＝21（27－x ）×2＝－x ＋27（3＜x ＜7/2）.故该图象分三段.故选B.2. B 解析：当E 在AB 上运动时，△BCE 的面积不断增大；当E 在AD 上运动时，BC 一定，高为AB 不变，此时面积不变；当E 在DC 上运动时，△BCE 的面积不断减小.∴当x ＝7时，点E 应运动到高不再变化时，即点D 处.故选B .3. D 解析：∵长、宽分别为2和1的矩形ABCD 的边上有一动点P ，沿A →B →C →D →A 运动一周，则点P 的纵坐标y 随点P 走过的路程s 之间的函数关系图象可以分为4部分，∴P 点在AB 上，此时纵坐标越来越小，最小值是1，P 点在BC 上，此时纵坐标为定值1.当P 点在CD 上，此时纵坐标越来越大，最大值是2，P 点在AD 上，此时纵坐标为定值2.故选D.4. A 解析：①当直线l 经过BA 段时，阴影部分的面积越来越大，并且增大的速度越来越快；②直线l 经过AD 段时，阴影部分的面积越来越大，并且增大的速度保持不变；③直线l 经过DC 段时，阴影部分的面积越来越大，并且增大的速度越来越小；结合选项可得，A 选项的图象符合.故选A.5. D 解析：连接AC ，过点C 作CE ⊥AD 于点E ，过点M 作MF ⊥AB 于点F ，易得CE ＝2，MF ＝5，当点P 与点B 重合，即x ＝2时，y ＝21AP ·MF ＝21×2×5＝5；当点P 与点C 重合，即x ＝6时，y ＝1122AD CE ⨯⋅＝21×21×6×2＝3；结合函数图象可判断选项D 正确.故选D.6. 100 km ，22 min －24 min ，8 min 到10 min 之间停止 解析：（1）依题意得：最高速度是100 km/h ；（2）汽车第二次减速行驶的“时间段”是22 min －24v ；（3）汽车出发后，8v 到10 min 之间是停止的.7. 0(02)2(24)2(46)8(68)t t t S t t t ≤≤⎧⎪-<≤⎪=⎨<≤⎪⎪-<≤⎩ 解析：（1）∵在正方形ABCD 中，边长为2，某一点E 从B －C －D －A －B 运动，且速度是1，∴当E 在BC 上时，B ，E ，C 无法构成三角形，此时0≤t ≤2，∴S ＝0，（0≤t ≤2）；当E 在CD 上时，△BEC 的面积为：S ＝21BC ×CE ＝21×2×（t －2）＝t －2，（2＜t ≤4）；当E 在AD 上时，△BEC 的面积为：S ＝21BC ×CD ＝21×2×2＝2，（4＜t ≤6）；当E 在AB 上时，△BEC 的面积为：S ＝21BC ×BE ＝21×2×[2－（t －6）]＝8－t ，（6＜t ≤8）. 8. ①③ 解析：∵AB 边的长为4，设动点P 沿折线B ⇒C ⇒D ⇒A 由点B 向点A 运动，点P 运动的距离为10，∴四边形ABCD 的周长为10＋4＝14，①成立.当点P 在BC 上运动时，面积在不断增加，当移动的距离是3，面积为6时，面积不再变化，说明CD ∥AB ，此时BC ＝3，△ABP 面积＝21×4×高＝6，那么高＝3，说明BC ⊥AB .当点P 运动7时，面积停止变化，此时CD ＝7－3＝4，那么CD ＝AB .根据一组对边平行且相等的四边形是平行四边形得到四边形ABCD 是平行四边形.根据有一个角是直角的平行四边形是矩形得到四边形ABCD 是矩形，③对.由图中可以看出，面积为4的点可在图中找到两处，那么就有相应的两个距离值，④不对.故答案选①③.9. 8 cm ；24；60 cm 2；17 解析：（1）动点P 在BC 上运动时，对应的时间为0到4 s ，易得：BC ＝2 cm/s×4s ＝8 cm.故题图甲中BC 的长度是8 cm ；（2）由（1）可得，BC ＝8 cm ，则：题图乙中a 所表示的数是：21×BC ×AB ＝21×8×6＝24（cm 2）.故题图乙中a 所表示的数是24；（3）由题图可得：CD ＝2×2＝4 cm ，DE ＝2×3＝6 cm ，则AF ＝BC ＋DE ＝14 cm ，又由AB ＝6 cm ，则甲中的梯形面积为AB ×AF －CD ×DE ＝6×14－4×6＝60（cm 2）.故题图甲中的图形面积为60 cm 2；（4）根据题意，动点P 共运动了BC ＋CD ＋DE ＋EF ＋F A ＝（BC ＋DE ）＋（CD ＋EF ）＋F A ＝14＋6＋14＝34（cm ），其速度是2 cm/s ，34÷2＝17（s ）.故题图乙中b 所表示的数是17.故答案为8 cm ；24；60 cm 2；17.10. 解：∵等腰三角形CEF ，其中底边CF ＝8，腰长EF ＝5，∴等腰三角形底边上的高线平分底边，即分为两部分都是4，当0＜t ≤4时，如图1所示；当4＜t ≤5时，如图2所示；当5＜t ＜6时，如图3所示.11. 解答：（1）图中点H 的实际意义：P 、Q 两点相遇；（2）由函数图象得出，当两点在F 点到G 点两点路程随时间变化减慢得出此时Q 点停留1秒，只有P 点运动，此时纵坐标的值由75下降到45，故P 点运动速度为：30cm/s ，再根据E 点到F 点S 的值由120变为75，根据P 点速度，得出Q 点速度为120－75－30＝15（cm/s ），即P 点速度为30cm/s ，Q 点速度为15cm/s ；（3）如图所示：根据4秒后，P 点到达D 点，只有Q 点运动，根据运动速度为15cm/s ，还需要运动120－45＝75（cm ），则运动时间为：75÷15＝5（s ），画出图象即可；（4）如图1所示，当Q P ＝PC ，此时21Q C ＝BP ，即30－30t ＝21（30－15t ），解得：t ＝32，故当时间t ＝32s 时，△PC Q 为等腰三角形，如图2所示，当D 、P 重合，Q D ＝Q C 时，Q 为AB 中点，则运动时间为：（15＋60＋30）÷15＋1＝8（s ），故当时间t ＝8s 时，△PC Q 为等腰三角形.若PC ＝C Q 故90－30t ＝30－15t 解得：t ＝4则4＋1＝5（S ）综上所述：t ＝32或t ＝5或t ＝8秒时，△PC Q 为等腰三角形.。

专题10函动点问题中函数图像压轴突破1．（2022春•上蔡县期末）如图1，矩形ABCD，点E为BC的中点，点P沿BC 从点B运动到点C，设点P运动的路程为x，P A﹣PE＝y，图2是点P运动时y随着x变化的图象，则AB的长为（）A．4B．5C．6D．7【答案】A【解答】解：连接AE，由函数图象知：当x＝0，即P在B点时，BA﹣BE＝1．利用三角形两边之差小于第三边，得到P A﹣PE≤AE．∴y的最大值为AE，∴AE＝5．在Rt△ABE中，由勾股定理得：BA2+BE2＝AE2＝25，设BE的长度为t，则BA＝t+1，∴（t+1）2+t2＝25，即：t2+t﹣12＝0，∴（t+4）（t﹣3）＝0，由于t＞0，∴t+4＞0，∴t﹣3＝0，∴t＝3．∴AB＝3+1＝4．故选：A．2．（2022春•开封期末）小明家与学校之间的距离是1000米，一天，他以每分钟60米的速度去学校，出发5分钟后，小明爸爸发现小明的数学作业忘带了，立即以每分钟360米的速度去追小明，追上小明一分钟后，小明又以每分钟80米的速度去学校，小明爸爸按原速度回家，以下图象中，能反映他们离家的路程y与小明离家的时间x（分钟）的函数关系的是（）A．B．C．D．【答案】A【解答】解：设x分钟爸爸追上小明，60×5+60x＝360x，解得x＝1，可知1分钟后就追上小明，过了1分钟后，小明又以每分钟80米的速度去学校，小明爸爸按原速度回家，所以爸爸又过了一分钟就到家了，小明一共用了5+1+1+＝15分钟到学校，所以A项符合题意，故选：A．3．（2022春•上杭县期末）已知动点H以每秒x厘米的速度沿图1的边框（边框拐角处都互相垂直）按从A﹣B﹣C﹣D﹣E﹣F的路径匀速运动，相应的△HAF 的面积S（cm2）关于时间t（s）的关系图象如图2，已知AF＝8cm，则下列说法正确的有几个（）①动点H的速度是2cm/s；②BC的长度为3cm；③当点H到达D点时△HAF的面积是8cm2；④b的值为14；⑤在运动过程中，当△HAF的面积是30cm2时，点H的运动时间是3.75s和10.25s．A．2个B．3个C．4个D．5个【答案】A【解答】解：当点H在AB上时，如图所示，AH＝xt（cm），S△HAF＝×AF×AH＝4xt（cm2），此时三角形面积随着时间增大而逐渐增大，当点H在BC上时，如图所示，HP是△HAF的高，且HP＝AB，＝×AF×AB，此时三角形面积不变，∴S△HAF当点H在CD上时，如图所示，HP是△HAF的高，C，D，P三点共线，S△HAF＝×AF×HP，点H从点C点D运动，HP逐渐减小，故三角形面积不断减小，当点H在DE上时，如图所示，HP是△HAF的高，且HP＝EF，S△HAF＝×AF×EF，此时三角形面积不变，当点H在EF时，如图所示，S△HAF＝×AF×HF，点H从点E向点F运动，HF逐渐减小，故三角形面积不断减小直至零，对照图2可得0≤t≤5时，点H在AB上，S△HAF＝4xt＝4•5x＝40（cm2），∴x＝2，AB＝2×5＝10（cm），∴动点H的速度是2cm/s，故①正确，5≤t≤8时，点H在BC上，此时三角形面积不变，∴动点H由点B运动到点C共用时8﹣5＝3（s），∴BC＝2×3＝6（cm），故②错误，8≤t≤12时，当点H在CD上，三角形面积逐渐减小，∴动点H由点C运动到点D共用时12﹣8＝4（s），∴CD＝2×4＝8（cm），∴EF＝AB﹣CD＝10﹣8＝2（cm），在D点时，△HAF的高与EF相等，即HP＝EF，＝×AF×EF＝×8×2＝8（cm2），∴S△HAF故③正确，12≤t≤b，点H在DE上，DE＝AF﹣BC＝8﹣6＝2（cm），∴动点H由点D运动到点E共用时2÷2＝1（s），∴b＝12+1＝13，故④错误．当△HAF的面积是30cm2时，点H在AB上或CD上，＝4xt＝8t＝30（cm2），点H在AB上时，S△HAF解得t＝3.75（s），点H在CD上时，S△HAF＝×AF×HP＝×8×HP＝30（cm2），解得HP＝7.5（cm），∴CH＝AB﹣HP＝10﹣7.5＝2.5（cm），∴从点C运动到点H共用时2.5÷2＝1.25（s），由点A到点C共用时8s，∴此时共用时8+1.25＝9.25（s），故⑤错误．故选：A．4．（2022春•镜湖区校级期中）在平面直角坐标系xOy中，对于任意一点P（x，y），规定：f（x，y）＝；比如f（﹣4，）＝4，f（﹣2，﹣3）＝3．当f（x，y）＝2时，所有满足该条件的点P组成的图形为（）A．B．C．D．【答案】D【解答】解：∵f（x，y）＝2，∴|x|＝2，|y|≤2或|y|＝2，|x|＜2．①当|x|＝2，|y|≤2时，点P满足x＝2，﹣2≤y≤2或x＝﹣2，﹣2≤y≤2，在图象上，线段x＝2，﹣2≤y≤2即为D选项中正方形的右边，线段x＝﹣2，﹣2≤y≤2即为D选项中正方形的左边；②当|y|＝2，|x|＜2时，点P满足y＝2，﹣2＜x＜2，或y＝﹣2，﹣2＜x＜2，在图象上，线段y＝2，﹣2＜x＜2即为D选项中正方形的上边，线段y＝﹣2，﹣2＜x＜2即为D选项中正方形的下边．故选：D．5．（2021春•洪山区期末）如图1，将正方形ABCD置于平面直角坐标系中，其中AD边在x轴上，其余各边均与坐标轴平行，直线L：y＝x﹣3沿x轴的负方向以每秒1个单位的速度平移，在平移的过程中，该直线被正方形ABCD 的边所截得的线段长为m，平移的时间为t（秒），m与t的函数图象如图2所示，则图2中a的值为（）A．7B．9C．12D．13【答案】D【解答】解：设直线L与x轴交于点M，令y＝x﹣3＝0，则x＝3，即点M（3，0），由图2，直线AC＝6，则正方形ABCD的边长为6，从图2看，MA＝1，则点A（2，0），故点D的坐标为（﹣4，0），当直线l过点C时，设直线l′交x轴与点N，对应的时间为a，由直线L和x轴坐标轴的夹角为45°，则当直线L在L′的位置时，ND＝CD ＝6，点N（﹣10，0），则a＝10+3＝13，故选：D．6．（2021春•任城区期末）小华和小明是同班同学，也是邻居，某日早晨，小明7：40先出发去学校，走了一段后，在途中停下吃了早餐，后来发现上学时间快到了，就跑步到学校；小华离家后直接乘公共汽车到了学校，如图是他们从家到学校已走的路程S（米）和所用时间t（分钟）的关系图，则下列说法中错误的是（）A．小明家和学校距离1200米B．小华乘公共汽车的速度是240米/分C．小华乘坐公共汽车后7：50与小明相遇D．小明从家到学校的平均速度为80米/分【答案】D【解答】解：由图象可知，小华和小明的家离学校1200米，故A正确；根据图象，小华乘公共汽车，从出发到到达学校共用了13﹣8＝5（分钟），所以公共汽车的速度为1200÷5＝240（米/分），故B正确；小明先出发8分钟然后停下来吃早餐，由图象可知在小明吃早餐的过程中，小华出发并与小明相遇然后超过小明，所以二人相遇所用的时间是8+480÷240＝10（分钟），即7：50相遇，故C正确；小明从家到学校的时间为20分钟，所以小明的平均速度为1200÷20＝60（米/分），故D错误．故选：D．7．（2019秋•垦利区期末）如图，在边长为2的正方形ABCD中剪去一个边长为1的小正方形EFGD，动点P从点A出发，沿A→E→F→G→C→B的路线，绕多边形的边匀速运动到点B时停止，则△ABP的面积S随着时间t变化的函数图象大致是（）A．B．C．D．【答案】B【解答】解：①当点P在AE上运动时，S＝×AB×AP＝2×t＝t；②当点P在EF上运动时，S＝×1×2＝1；③当点P在FG上运动时，S＝×（t﹣1）＝t﹣1；④当点P在GC上运动时，同理S＝2；⑤当点P在BC上运动时，同理可得：函数的表达式为一次函数，图象为线段；故选：B．8．（2021•广州模拟）小元步行从家去火车站，走到6分钟时，以同样的速度回家取物品，然后从家乘出租车赶往火车站，结果比预计步行时间提前了3分钟．小元离家路程S（米）与时间t（分钟）之间的函数图象如图，那么从家到火车站路程是（）A．1300米B．1400米C．1600米D．1500米【答案】C【解答】解：步行的速度为：480÷6＝80米/分钟，∵小元步行从家去火车站，走到6分钟时，以同样的速度回家取物品，∴小元回到家时的时间为6×2＝12（分钟）则返回时函数图象的点坐标是（12，0）设后来乘出租车中S与t的函数解析式为S＝kt+b（k≠0），把（12，0）和（16，1280）代入得，，解得，所以S＝320t﹣3840；设步行到达的时间为t，则实际到达的时间为t﹣3，由题意得，80t＝320（t﹣3）﹣3840，解得t＝20．所以家到火车站的距离为80×20＝1600m．故选：C．9．（2019春•无为县期末）如图1，在矩形ABCD中，动点E从点B出发，沿BADC方向运动至点C处停止，设点E运动的路程为x，△BCE的面积为y，如果y关于x的函数图象如图2所示，则矩形ABCD的周长为（）A．20B．21C．14D．7【答案】C【解答】解：当点E在AB段运动时，y＝BC×BE＝BC•x，为一次函数，由图2知，AB＝3，当点E在AD上运动时，y＝×AB×BC，为常数，由图2知，AD＝4，故矩形的周长为7×2＝14，故选：C．10．（2022秋•莱芜区期末）如图①在长方形ABCD中，动点P从点B出发，沿B﹣C﹣D﹣A方向匀速运动至点A停止，已知点P的运动速度为3cm/s，设点P的运动时间为t（s），△PAB的面积为y（cm2），若y关于t的函数图象如图②所示，则长方形ABCD的面积为（）A．108cm2B．54cm2C．48cm2D．36cm2【答案】A【解答】解：∵动点P从点B出发，沿BC、CD、DA运动至点A停止，当点P在点B，C之间运动时，△ABP的面积随时间t的增大而增大，由图2知，当t＝3时，点P到达点C处，∴BC＝3×3＝9（cm）；当点P运动到点C，D之间时，△ABP的面积不变，由图2可知，点P从点C运动到点D所用时间为7﹣3＝4（s），∴CD＝3×4＝12（cm），∴长方形ABCD面积＝BC×CD＝9×12＝108（cm2），故选：A．11．（2022秋•金东区期末）A，B两地相距640km，甲、乙两辆汽车从A地出发到B地，均匀速行驶，甲出发1小时后，乙出发沿同一路线行驶，设甲、乙两车相距s（km），甲行驶的时间为t（h），s与t的关系如图所示，下列说法：①甲车行驶的速度是60km/h，乙车行驶的速度是80km/h；②甲出发4h后被乙追上；③甲比乙晚到h；④甲车行驶8h或9h，甲，乙两车相距80km；其中错误的（）A．序号①B．序号②C．序号③D．序号④【答案】D【解答】解：①由图可得，甲车行驶的速度是60÷1＝60（km/h），∵甲先出发1h，乙出发3h后追上甲，﹣60）＝60，∴3（v乙∴v＝80（km/h），乙即乙车行驶的速度是80km/h，故①正确；②∵当t＝1时，乙出发，当t＝4时，乙追上甲，∴甲出发4h后追上甲，故②正确；③由图可得，当乙到达B地时，甲乙相距100km，∴甲比乙晚到100÷60＝（h），故③正确；④由图可得，当60t+80＝80（t﹣1）时，解得t＝8；当60t+80＝640时，解得t＝9，∴甲车行驶8h或9h，甲，乙两车相距80km，故④错误；故选：D．12．（2022秋•泗阳县期末）如图，在长方形ABCD中，动点P从点B出发，沿BC、CD、DA运动至点A停止，设点P运动的路程为x，△ABP的面积为y，y关于x的函数图象如图2所示，若b﹣2a＝5，则长方形ABCD的周长为（）A．20B．18C．16D．24【答案】B【解答】解：根据图2的点（a，10），可知BC＝a，AB×BC＝10，∴AB＝，∴BC+CD+DA＝2a+＝b，∴b﹣2a＝，∵b﹣2a＝5，∴＝5，∴a＝4，∴AB＝5，BC＝4，∴长方形ABCD的周长为2×（5+4）＝18．故选：B．13．（2022秋•广饶县校级期末）如图，折线ABCDE描述了一辆汽车在某一直线上的行驶过程中，汽车离出发地的距离s（km）与行驶时间t（h）之间的函数关系，根据图中提供的信息，判断下列结论正确的选项是（）①汽车在行驶途中停留了0.5小时；②汽车在整个行驶过程的平均速度是60km/h；③汽车共行驶了240km；④汽车出发4h离出发地40km．A．①②④B．①②③C．①③④D．①②③④【答案】C【解答】解：①汽车在行驶途中停留了2﹣1.5＝0.5h，故①正确；②平均速度：120×2÷4.5＝千米/小时，故②错误；③汽车共行驶了120×2＝240km，故③正确；④汽车自出发后3h到4.5h速度为：120÷（4.5﹣3）＝120÷1.5＝80千米/小时，∴汽车出发4h离出发地距离为120﹣（4﹣3）×80＝120﹣80＝40千米，故④正确．∴正确的是①③④，故选：C．14．（2022秋•东城区校级期末）如图，在长方形ABCD中，AB＝6，AD＝4，DM＝2，动点P从点A出发，沿路径A→B→C→M运动，则△AMP的面积y 与点P经过的路径长x之间的函数关系用图象表示大致是（）A．B．C．D．【答案】A【解答】解：①当点P在AB上运动时，即0≤x≤6，此时AP＝x，y＝S△AMP＝，∴y＝；②当点P在BC上运动时，即6＜x≤10，此时BP＝x﹣6，CP＝10﹣x，y＝S△AMP＝S长方形ABCD﹣S△ABP﹣S△MCP﹣S△ADM，∴y＝4×6﹣＝﹣x+18；③当点P在CM上运动时，即10＜x≤14，此时MP＝14﹣x，y＝S△AMP＝，∴y＝；根据函数解析式，可知A选项正确．故选：A．15．（2022秋•南京期末）在边长为4的正方形ABCD的边上有一个动点P，从A 出发沿折线ABCD移动一周，回到A点后继续周而复始．设点P移动的路程为x，△PAC的面积为y．请结合右侧函数图象分析当x＝2022时，y的值为（）A．2B．4C．6D．8【答案】B【解答】解：∵点P在正方形ABCD的边上每运动一周，则x的值增加16，∴2022÷16＝126（周）……6（单位长度），∴当x＝2022时，点P位于BC边的中点处，∴y＝×2×4＝4，故选：B．16．（2022秋•孝南区期末）如图1，点P从△ABC的顶点B出发，沿B→C→A 匀速运动到点A，图2是点P运动时，线段BP的长度y随时间x变化的关系图象，其中M为曲线部分的最低点，则△ABC的面积是（）A．6B．9C．12D．15【答案】C【解答】解：根据图象可知点P在BC上运动时，此时BP不断增大，由图象可知：点P从B向C运动时，BP的最大值为5，即BC＝5，由于M是曲线部分的最低点，∴此时BP最小，如图，即BP′⊥AC，BP′＝3，∴由勾股定理可知：PC＝4，由于图象的曲线部分是轴对称图形，∵图象右端点函数值为5，∴AB＝BC＝5，∴P′A＝P′C＝4，∴AC＝8，∴△ABC的面积为：AC•BP′＝×8×3＝12．故选：C．17．（2022秋•江北区校级期末）一辆汽车行驶的速度（km/h）与时间（min）之间的变化关系如图所示，说法正确的是（）A．时间是因变量，速度是自变量B．汽车在1～3min时匀速行驶C．汽车在3～8min时匀速行驶D．汽车最快的速度是10km/h【答案】C【解答】解：速度是因变量，时间是自变量，故选项A不合题意；汽车在1～3分钟时，速度在增加，故选项B不合题意；汽车在3～8分钟，匀速运动，故选项C符合题意；汽车最快速度是30千米/时，故选项D不符合题意；故选：C．18．（2023•西城区校级模拟）如图，将一圆柱形水杯杯底固定在大圆柱形容器底面中央，现用一个注水管沿大容器内壁匀速注水，则水杯内水面的高度h（单位：cm）与注水时间t（单位：s）的函数图象大致为（）A．B．C．D．【答案】B【解答】解：当注入大圆柱形容器的水面高度到达小水杯的高度前，水杯内水面的高度为0，故选项A、C不合题意；当注入大圆柱形容器的水面高度到达小水杯的高后，水杯内水面的高度逐渐增大，当水杯内水面的高度达到水杯高度时，水杯内水面的高度不再增加，故选项B符合题意，选项D不合题意．故选：B．19．（2022春•牡丹区校级期中）如图，在长方形ABCD中，动点P从点B出发，沿BC，CD，DA运动到点A停止，设点P运动路程为x，△ABP的面积为y，如果y关于x的函数图象如图所示，则长方形ABCD的周长是（）A．24B．18C．20D．40【答案】B【解答】解：由y关于x的函数图象可知，BC＝4，CD＝9﹣BC＝9﹣4＝5，∴长方形ABCD的周长是：2×（4+5）＝18；故选：B．20．（2022春•灵宝市校级月考）如图1，点P从菱形ABCD的顶点A出发，沿A →D→B以1cm/s的速度匀速运动到点B，图2是点P运动时，△PBC的面积y（cm2）随时间x（s）变化的函数关系图象，则菱形ABCD的周长为（）A．5B．C．D．【答案】D【解答】解：如图1，过点D作DE⊥BC于点E，∵AD∥BC，∴当点P在边AD上运动时，y的值不变，∴AD＝a，即菱形的边长是a，∴•a•DE＝a，∴DE＝3，当点P在DB上运动时，y逐渐减小，∴DB＝5，∴BE＝＝＝4，在Rt△DCE中，DC＝a，CE＝4﹣a，DE＝3，∴a2＝32+（4﹣a）2，解得a＝，∴菱形ABCD的周长为4a＝．故选：D．21．（2022春•朝阳区校级月考）如图，正方形ABCD的边长为4，P为正方形边上一动点，运动路线是A→D→C→B→A，设P点经过的路程为x，以点A、P、D为顶点的三角形的面积是y，则下列图象能大致反映y与x的函数关系的是（）A．B．C．D．【答案】B【解答】解：当点P由点A向点D运动，即0＜x≤4时，y的值为0；当点P在DC上运动，即4＜x≤8时，y随着x的增大而增大；当点P在CB上运动，即8＜x≤12时，y不变；当点P在BA上运动，即12＜x≤16时，y随x的增大而减小．故选：B．22．（2022•新市区校级三模）如图1，四边形ABCD中，AB∥CD，∠B＝90°，AC＝AD，动点E从点B出发，沿折线B﹣A﹣D﹣C方向以m单位/秒的速度匀速运动，在整个运动过程中，△BCE的面积S与运动时间t（秒）的函数图象如图2所示，则四边形ABCD的面积是（）A．144B．134C．124D．114【答案】A【解答】解：从图2来看，AB＝6m，AD＝16m﹣6m＝10m＝AC，过点A作AH⊥CD交于点H，∵AC＝AD，∴，在Rt△ADH中，AD＝10m，AB＝6m＝CH＝DH，∴，当点P在点D处时，，解得m2＝2，则四边形ABCD的面积＝，故选：A．23．（2022秋•九龙坡区校级月考）匀速地向如图所示的一个空水瓶里注水，最后把空水瓶注满，在这个注水过程中，水面高度h与注水时间t之间函数关系的大致图象是（）A．B．C．D．【答案】C【解答】解：从下往上，空水瓶的横截面积由小变大，再由大到小，结合空瓶子的特点，那么符合题意选项的是C选项．故选：C．24．（2022春•包头期中）如图1，在直角梯形ABCD中，∠B＝90°，动点P从B点出发，沿B→C→D→A匀速运动，设点P运动的路程为x，△ABP的面积为y，图象如图2所示，下列说法错误的是（）A．当x＝4时，y＝16B．AB＝8C．梯形ABCD的面积为26D．当y＝12时，x＝3【答案】D【解答】解：由图可得，当x＝4时，y＝16，故A正确，不符合题意；由图可得，BC＝4，CD＝9﹣4＝5，AD＝14﹣9＝5，当x＝4时，点P和点C重合，＝AB•BP＝16，∴S△ABP∴AB×4＝16，∴AB＝8，故B正确，不符合题意；∵梯形ABCD的面积＝（AB+CD）•BC＝（8+5）×4＝26，故C正确，不符合题意；设当9≤x≤14时，y与x的函数解析式为y＝kx+b（k≠0），把（9，16）和（14，0）代入解析式得：，解得，∴y与x的函数解析式为y＝﹣x+，当y＝12时，﹣x+＝12，解得x＝，故D错误，符合题意．故选：D．25．（2022春•封丘县期末）如图1，在矩形ABCD中，动点P从点B出发，沿B →C→D→A方向匀速运动至点A停止．已知点P的运动速度为1cm/s，设点P 的运动时间为x（s），△PAB的面积为y（cm2），若y关于x的函数图象如图2所示，则矩形对角线AC的长为（）A．5B．6C．8D．10【答案】D【解答】解：∵动点P从点B出发，沿BC、CD、DA运动至点A停止，当点P在点B，C之间运动时，△ABP的面积随时间x的增大而增大，由图2知，当x＝3时，点P到达点C处，∴BC＝3×2＝6（cm）；当点P运动到点C，D之间时，△ABP的面积不变，由图2可知，点P从点C运动到点D所用时间为7﹣3＝4（s），∴CD＝2×4＝8（cm），∴AC＝（cm），故选：D．26．（2022春•金牛区期末）如图1，在长方形ABCD中，动点P从点B出发，沿B→C→D→A的路径匀速运动到点A处停止，设点P运动的路程为x，△PAB的面积为y，表示y与x的关系的图象如图2所示，则a，b的值分别为（）A．a＝4，b＝5B．a＝4，b＝20C．a＝4，b＝10D．a＝5，b＝10【解答】解：∵动点P从点B出发，沿B→C→D→A的路径匀速运动，∴图2为等腰梯形，∴a＝13﹣9＝4，∴BC＝DA＝a＝4，∴在矩形ABCD中，AB＝CD＝9﹣4＝5，∴b＝5×4÷2＝10．故选：C．27．（2022春•惠济区期末）如图1，已知在平行四边形ABCD中，AD＝DC，若点P从顶点A出发，沿A→D→B以1cm/s的速度匀速运动到点B，图2是点P运动时，△PBC的面y（cm2）随时间x（s）变化的关系图象，则a的值为（）A．5B．C．D．【答案】C【解答】解：∵在平行四边形ABCD中，AD＝DC，∴平行四边形ABCD是菱形，过点D作DE⊥BC，∵菱形ABCD中，AD∥BC，∴当点P在边AD上运动时，y的值不变，∴AD＝a，即菱形的边长是a，∴AD•DE＝2a，当点P在DB上运动时，y逐渐减小，∴DB＝5，∴BE＝＝＝3．在Rt△DCE中，DC＝a，CE＝a﹣3，DE＝4，∴a2＝42+（a﹣3）2，解得a＝．故选：C．28．（2022春•镇平县月考）如图1，在平行四边形ABCD中，∠C＝150°，BC ＝6，动点P从C出发，沿C→D→A匀速运动到点A．图2是点P运动时，△PBC的面积y随点P运动路程x变化的关系图象，则a的值是（）A．2B．3C．4D．6【答案】D【解答】解：由题意可知：CD＝4，过D点作DF⊥BC于点F，∵∠BCD＝150°，∴∠DCF＝180°﹣150°＝30°，∴DF＝CD＝2，∵四边形ABCD为平行四边形，BC＝6，＝BC•DF＝6×2＝12，∴S平行四边形ABCD＝S平行四边形ABCD＝6，当P点与D点重合时，S△BCP即当x＝4时，y＝a＝6，故选：D．29．（2022春•天桥区期末）已知动点H以每秒x厘米的速度沿图1的边框（边框拐角处都互相垂直）按从A﹣B﹣C﹣D﹣E﹣F的路径匀速运动，相应的△HAF的面积S（cm2）关于时间t（s）的关系图象如图2，已知AF＝8cm，下列说法错误的是（）A．动点H的速度为2cm/sB．b的值为14C．BC的长度为6cmD．在运动过程中，当△HAF的面积为30cm2时，点H的运动时间是3.75s 或9.25s【答案】B【解答】解：当点H在AB上时，如图所示，AH＝xt（cm），S△HAF＝×AF×AH＝4xt（cm2），此时三角形面积随着时间增大而逐渐增大，当点H在BC上时，如图所示，HP是△HAF的高，且HP＝AB，＝×AF×AB，此时三角形面积不变，∴S△HAF当点H在CD上时，如图所示，HP是△HAF的高，C，D，P三点共线，S△HAF＝×AF×HP，点H从点C点D运动，HP逐渐减小，故三角形面积不断减小，当点H在DE上时，如图所示，HP是△HAF的高，且HP＝EF，S△HAF＝×AF×EF，此时三角形面积不变，当点H在EF时，如图所示，S△HAF＝×AF×HF，点H从点E向点F运动，HF逐渐减小，故三角形面积不断减小直至零，对照图2可得0≤t≤5时，点H在AB上，S△HAF＝4xt＝4•5x＝40（cm2），∴x＝2，AB＝2×5＝10（cm），∴动点H的速度是2cm/s，故A正确，不符合题意，12≤t≤b，点H在DE上，DE＝AF﹣BC＝8﹣6＝2（cm），∴动点H由点D运动到点E共用时2÷2＝1（s），∴b＝12+1＝13，故B错误，符合题意．5≤t≤8时，点H在BC上，此时三角形面积不变，∴动点H由点B运动到点C共用时8﹣5＝3（s），∴BC＝2×3＝6（cm），故C正确，不符合题意，当△HAF的面积是30cm2时，点H在AB上或CD上，＝4xt＝8t＝30（cm2），点H在AB上时，S△HAF解得t＝3.75（s），点H在CD上时，S△HAF＝×AF×HP＝×8×HP＝30（cm2），解得HP＝7.5（cm），∴CH＝AB﹣HP＝10﹣7.5＝2.5（cm），∴从点C运动到点H共用时2.5÷2＝1.25（s），由点A到点C共用时8s，∴此时共用时8+1.25＝9.25（s），故D正确，不符合题意．故选：B．30．（2022•温州）小聪某次从家出发去公园游玩的行程如图所示，他离家的路程为s米，所经过的时间为t分钟．下列选项中的图象，能近似刻画s与t之间关系的是（）。