二次函数根的判别式、韦达定理
- 格式:doc
- 大小:1.24 MB
- 文档页数:7

2023年初高中衔接素养提升专题讲义第三讲 一元二次方程根的判别式与韦达定理(精讲)(解析版)【知识点透析】1、一元二次根的判别式一元二次方程20 (0)ax bx c a ++=≠,用配方法将其变形为:2224()24b b ac x a a -+=,把24b ac -叫做一元二次方程20 (0)ax bx c a ++=≠的根的判别式,表示为:24b ac∆=-(1) 当Δ=240b ac ->时,方程有两个不相等的实数根:x =(2) 当Δ=240b ac -=时,因此,方程有两个相等的实数根:1,22b x a=-(3) 当Δ=240b ac -<时,因此,方程没有实数根.【知识点精讲】【例1】已知关于x 的一元二次方程2320x x k -+=,根据下列条件,分别求出k 的范围:(1) 方程有两个不相等的实数根;(2) 方程有两个相等的实数根(3)方程有实数根;(4) 方程无实数根.【解析】:2(2)43412k k ∆=--⨯⨯=-(1) 141203k k ->⇒<;(2) 141203k k -=⇒=;(3) 141203k k -≥⇒≥;(4) 141203k k -<⇒<.【变式1】((2022秋·重庆开州·八年级统考期中)使得关于x 的不等式组6x ―a ≥―10―1+12x <―18x +32有且只有4个整数解,且关于x 的一元二次方程(a ―5)x 2+4x +1=0有实数根的所有整数a 的值之和为( )A .35B .30C .26D .21【答案】B【分析】先求出不等式组的解集,根据有且只有4个整数解可确定a 的取值范围,再通过根的判别式确定a 的取值范围,最后结合两个取值范围找出满足条件的整数相加即可.【详解】解:整理不等式组得:6x ―a ≥―10①―8+4x <―x +12②由①得:x ≥a ―106,由②得:x<4∵不等式组有且只有4个整数解,∴不等式组的4个整数解是:3,2,1,0,∴―1<a―106≤0,解得:4<a≤10,∵(a―5)x2+4x+1=0有实数根,∴Δ=b2―4ac=16―4×(a―5)×1=36―4a≥0,解得:a≤9,∵方程(a―5)x2+4x+1=0是一元二次方程,∴a≠5∴4<a≤9,且a≠5,满足条件的整数有:6、7、8、9;∴6+7+8+9=30,故选:B.【变式2】.已知关于x的一元二次方程:x2﹣(2k+1)x+4(k―12)=0.(1)求证:这个方程总有两个实数根;(2)若等腰△ABC的一边长a=4b、c恰好是这个方程的两个实数根,求△ABC 的周长.【解答】(1)证明:Δ=(2k+1)2﹣4×1×4(k―12)=4k2﹣12k+9=(2k﹣3)2,∵无论k取什么实数值,(2k﹣3)2≥0,∴△≥0,∴无论k取什么实数值,方程总有实数根;(2)解:∵x=2k+1±(2k―3)2,∴x1=2k﹣1,x2=2,∵b,c恰好是这个方程的两个实数根,设b=2k﹣1,c=2,当a 、b 为腰,则a =b =4,即2k ﹣1=4,解得k =52,此时三角形的周长=4+4+2=10;当b 、c 为腰时,b =c =2,此时b +c =a ,故此种情况不存在.综上所述,△ABC 的周长为10.【例2】已知实数x 、y 满足22210x y xy x y +-+-+=,试求x 、y 的值.【解析】:可以把所给方程看作为关于x 的方程,整理得:22(2)10x y x y y --+-+=由于x 是实数,所以上述方程有实数根,因此:222[(2)]4(1)300y y y y y ∆=----+=-≥⇒=,代入原方程得:22101x x x ++=⇒=-.综上知:1,0x y =-=【变式1】(2022秋·湖北武汉·八年级武汉市第一初级中学校考期末)已知a ,b ,c 满足a 2+6b =7,b 2―2c =―1,c 2―2a =―17,则a ―b +c 的值为( )A .―1B .5C .6D .―7【答案】B【分析】首先把a 2+6b =7,b 2―2c =―1,c 2―2a =―17,两边相加整理成a 2+6b +b 2―2c +c 2―2a +11=0,分解因式,利用非负数的性质得出a 、b 、c 的数值,代入求得答案即可.【详解】解:∵a 2+6b =7,b 2―2c =―1,c 2―2a =―17,∴a 2+6b +b 2―2c +c 2―2a =―,∴a 2+6b +b 2―2c +c 2―2a +11=0∴(a ―1)2+(b +3)2+(c ―1)2=0,∴a =1,b =―3,c =1,∴a ―b +c =1+3+1=5.故选:B .【变式2】((2022秋·江苏扬州·八年级统考期中)新定义,若关于x 的一元二次方程:m (x ―a )2+b =0与n (x ―a )2+b =0,称为“同类方程”.如2(x ―1)2+3=0与6(x ―1)2+3=0是“同类方程”.现有关于x 的一元二次方程:2(x ―1)2+1=0与(a +6)x 2―(b +8)x +6=0是“同类方程”.那么代数式ax 2+bx +2022能取的最大值是_________.【答案】2023【分析】根据“同类方程”的定义,可得出a ,b 的值,从而解得代数式的最大值.【详解】∵2(x ―1)2+1=0与(a +6)x 2―(b +8)x +6=0是“同类方程”,∴(a +6)x 2―(b +8)x +6=(a +6)(x ―1)2+1,∴(a +6)x 2―(b +8)x +6=(a +6)x 2―2(a +6)x +a +7,∴b +8=2(a +6)6=a +7 ,解得:a =―1b =2,∴a x 2+bx +2022=―x 2+2x +2022=―(x ―1)2+2023∴当x =1时,a x 2+bx +2022取得最大值为2023.故答案为:2023.2、一元二次方程的根与系数的关系一元二次方程20 (0)ax bx c a ++=≠的两个根为:x x ==所以:12b x x a+==-,12244ac c x x a a⋅====韦达定理:如果一元二次方程20 (0)ax bx c a ++=≠的两个根为12,x x ,那么:1212,b c x x x x a a+=-=【知识点精讲】【例3】若12,x x 是方程2220070x x +-=的两个根,试求下列各式的值:(1) 2212x x +;(2) 1211x x +;(3) 12(5)(5)x x --;(4) 12||x x -.【解析】:由题意,根据根与系数的关系得:12122,2007x x x x +=-=-(1) 2222121212()2(2)2(2007)4018x x x x x x +=+-=---=(2) 121212112220072007x x x x x x +-+===-(3) 121212(5)(5)5()2520075(2)251972x x x x x x --=-++=---+=-(4) 12||x x -====常见的一些变形结论:利用根与系数的关系求值,要熟练掌握以下等式变形:222121212()2x x x x x x +=+-,12121211x x x x x x ++=,22121212()()4x x x x x x -=+-,12||x x -=2212121212()x x x x x x x x +=+,33312121212()3()x x x x x x x x +=+-+等等.韦达定理体现了整体思想.【例4】.已知关于x 的方程220x mx m -+=.(1)若2m =-,方程两根分别为1x ,2x ,求12x x -和3312x x +的值;(2)若方程有一正数,有一负数根,求实数m 的取值范围.【答案】.(14- (2)m <0【解析】(1)由22121212=()4x x x x x x -+-,33212121212()[()3]x x x x x x x x +=++-,借助韦达定理求解.(2)借助韦达定理表示方程有一正数,有一负数根的等价条件,进而求解.【详解】(1)当2m =-时,2222x x +-=即:210x x +-=1212140,1,1x x x x ∆=+>+=-=-因此:2212121212=()45x x x x x x x x -+-=∴-=3322212121212121212()[]()[()3]4x x x x x x x x x x x x x x +=++-=++-=-(2)220x mx m -+=212128,,22m m m m x x x x ∆=-+==21280002m m m m x x ⎧∆=->⎪∴<⎨=<⎪⎩【变式1】已知两不等实数a ,b 满足222a a =-,222b b =-,求22b a a b +的值.【解析】:b a ,是一元二次方程0222=-+x x 的不等实根则有2,2-=-=+ab b a原式=5)(]3))[(()())(()(22222233-=-++=+-+=+ab ab b a b a ab b ab a b a ab b a 【变式2】(2022秋·浙江杭州·八年级杭州外国语学校校考期末)设m 是不小于﹣1的实数,使得关于x 的方程x 2+2(m ﹣2)x +m 2﹣3m +3=0有两个实数根x 1,x 2.(1)若x 21+x 22=2,求m 的值;(2)令T =mx 11―x 1+mx 21―x 2,求T 的取值范围.【答案】(1)1 (2)0<T ≤4且T ≠2【分析】首先根据方程有两个实数根及m 是不小于-1的实数,确定m 的取值范围,根据根与系数的关系,用含m 的代数式表示出两根的和、两根的积.(1)变形x 12+x 22为(x 1+x 2)2-2x 1x 2,代入用含m 表示的两根的和、两根的积得方程,解方程根据m 的取值范围得到m 的值;(2)化简T ,用含m 的式子表示出T ,根据m 的取值范围,得到T 的取值范围.(1)∵关于x 的方程x 2+2(m -2)x +m 2-3m +3=0有两个实数根,∴Δ=4(m -2)2-4(m 2-3m +3)≥0,解得m ≤1,∵m 是不小于-1的实数,∴-1≤m ≤1,∵方程x 2+2(m -2)x +m 2-3m +3=0x 1,x 2,∴x 1+x 2=-2(m -2)=4-2m ,x 1•x 2=m 2-3m +3.∵x 12+x 22=2,∴(x 1+x 2)2-2x 1x 2=2,∴4(m -2)2-2(m 2-3m +3)=2,整理得m 2-5m +4=0,解得m 1=1,m 2=4(舍去),∴m 的值为1;(2)T =mx 11―x 1+mx 21―x 2,=mx 1(1―x 2)+mx 2(1―x 1)(1―x 1)(1―x 2)=m [(x 1+x 2)―2x 1x 2]1―(x 1+x 2)+x 1x 2=m (4―2m ―2m 2+6m ―6)1―4+2m +m 2―3m +3=―2m(m ―1)2m 2―m=―2m(m ―1)2m (m ―1)=2-2m .∵当x =1时,方程为1+2(m ﹣2)+m 2﹣3m +3=0,解得m =1或m =0.∴当m =1或m =0时,T 没有意义.∴―1≤m <1且m ≠0∴0<2-2m ≤4且T ≠2.即0<T ≤4且T ≠2.【变式3】.已知12x x ,是一元二次方程24410kx kx k -++=的两个实数根.(1)是否存在实数k ,使12123(2)(2)2x x x x --=-成立?若存在,求出k 的值,若不存在,请说明理由;(2)若k 是整数,求使12212x x x x +-的值为整数的所有k 的值.【答案】(1)不存在k ;理由见解析;(2)235k =---,,.【详解】(1)假设存在实数k ,使()()12123222x x x x --=-成立.∵一元二次方程24410kx kx k -++=的两个实数根∴()()24004441160k k k k k k ≠⎧⎪⇒<⎨∆=--⋅+=-≥⎪⎩,又1x ,2x 是一元二次方程24410kx kx k -++=的两个实数根∴1212114x x k x x k +=⎧⎪+⎨=⎪⎩∴()()()()222121212121212222529x x x x x x x x x x x x --=+-=+-939425k k k +=-=-⇒=,但0k < .∴不存在实数k ,使()()12123222x x x x --=-成立.(2)∵()22212121221121244224411x x x x x x k x x x x x x k k +++-=-=-=-=-++∴要使其值是整数,只需1k +能整除4,∴11k +=±,2±,4±,注意到0k <,要使12212x x x x +-的值为整数的实数k 的整数值为-2,-3,-5.所以k 的值为235k =---,,【变式4】(2022秋·四川凉山·八年级校考阶段练习)设一元二次方程x 2―2022x +1=0的两根分别为a ,b ,根据一元二次方程根与系数的关系可知:ab =1,记S 1=11+a +11+b ,S 2=11+a2+11+b2,S3=11+a3+11+b3,⋯,S100=11+a100+11+b100,那么S1+S2+S3+⋯+S100=______.【答案】100【分析】根据ab=1得到b=1a ,b2=1a2,b3=1a3,…b100=1a100,代入计算即可.【详解】∵一元二次方程x2―2022x+1=0的两根分别为a,b,∴ab=1,∴b=1a ,b2=1a2,b3=1a3,…b100=1a100,∴S1=11+a+11+1a=11+a+a1+a=1+a1+a=1,S2=11+a2+11+1a2=11+a2+a21+a2=1+a21+a2=1,S100=11+a100+11+1a100=11+a100+a1001+a100=1+a1001+a100=1,∴S1+S2+S3+⋯+S100=1+1+1+…+1100=100,故答案为:100.。

关于判别式法与韦达定理论述weiqingsong摘要:判别式法与韦达定理除了已知一元二次方程的一个根,求另一根;已知两个数的和与积,求这两个数等简单应用外,还可以求根的对称函数,讨论二次方程根的符号,解对称方程组,以及解一些有关二次曲线的问题等,都有非常广泛的应用。
关键词:判别式法 韦达定理在中学解题中判别式法与韦达定理的应用极其普遍,因此系统的研究一下利用判别式法与韦达定理解题是有必要的。
别式法与韦达定理说明了一元二次方程中根和系数之间的关系。
它们都有着广泛的应用在整个中学阶段。
一、韦达定理的由来法国数学家韦达最早发现代数方程的根与系数之间有这种关系,因此,人们把这个关系称为韦达定理。
历史是有趣的,韦达的16世纪就得出这个定理,证明这个定理要依靠代数基本定理,而代数基本定理却是在1799年才由高斯作出第一个实质性的论性。
判别式法与韦达定理在方程论中有着广泛的应用。
二、对判别式法的介绍及概括一般的关于一元二次方程ax^2+bx+c=0(a 、b 、c 属于R ,a≠0)根的判别,△=b^2-4ac ,不仅用来判定根的性质,而且作为一种解题方法,在代数式变形,解方程(组),解不等式,研究函数乃至几何、三角运算中都有非常广泛的应用。
关于x 的一元二次方程x^2+mx+n=0有两个相等的实数根,求符合条件的一组的实数值。
这是应注意以下问题:如果说方程有实数根,即应当包括方程只有一个实根和有两个不等实根或有两个相等实根三种情况;如果方程不是一般形式,要化为一般形式,再确定a 、b 、c 的值;使用判别式的前提是方程为一元二次方程,即二次项系数a≠0;当二次项系数含字母时,解题时要加以考虑。
判别式的主要应用有:不解方程就可以直接判定方程的根的情况;已知方程根的情况,确定方程中未知系数(或参数)的取值范围;判别或证明一元二次方程的根的性质;判别二次三项式ax^2+bx+c(a≠0)能否在实数范围内分解因式(1) 当△≥0 时,二次三项式在实数范围内能分解因式;(2)当△≤0 时,二次三项式在实数范围内不能分解因式。

二次方程根公式大全,二次函数两个根的公式推导二次方程根公式大全?一元二次方程_31、大多数情况下形式ax²+bx+c=0(a≠0)这当中ax²是二次项,a是二次项系数;bx是一次项;b是一次项系数;c是常数项。
使方程左右两边相等的未知数的值就是这个一元二次方程的解,一元二次方程的解也叫做一元二次方程的根。
2、变形式ax²+bx=0(a、b是实数,a≠0);ax²+c=0(a、c是实数,a≠0);ax²=0(a是实数,a≠0)。
一元二次方程的根与根的判别式当中有请看下方具体内容关系:(1)当△0时,方程有两个不相等的实数根;(2)当△=0时,方程有两个相等的实数根;(3)当△0时,方程无实数根,但有2个共轭复根。
(这当中,△=b²-4ac,a、b、c分别是一元二次方程的二次项系数、一次项系数还有常数项。
)二次函数两个根的公式?二次函数y=ax2+bx+c(a≠0,a、b、c是常数)中含有两个变量x、y,我们只要先确定这当中一个变量,就可利用剖析解读式得出另一个变量,即得到一组解;而一组解就是一个点的坐标,其实二次函数的图象就是由大量个这样的点构成的图形。
设ax^2+bx+c=0的两根为x1,x2。
由韦达定理:(x1+x2)=-b/a,x1x2=c/a==b=-a(x1+x2)c=ax1x2ax^2+bx+c=ax^2-a(x1+x2)+ax1x2=a(x^2-(x1+x2)x+x1x2)。
由十相乘法字法得:ax^2+bx+c=a(x-x1)(x-x2)二次函数两根之积的公式:x1x2=c/a (应是一元二次方程两根之积或是说二次函数与x轴交点)其他公式韦达定理:两根之和公式x1+x2=-b/a 两根之积公式x1x2=c/a二次函数的根计算公式?因为二次函数 y=ax²+bx+c与x轴交点的横坐标,就是当y=0时,即求方程ax²+bx+c=0的根则两个根为:x=(-b±√(b²-4ac))/2a。

韦达定理与根的判别式这个专题是一二次方程是的判别式与韦达定理知识要点和练习韦达定理与根的判别式知识点:1、根的判别式b24ac(1)b24ac 0 ,方程有两个不相等的实数根;(2)b2 4ac 0,方程有两个相等的实数根;(3)b2 4ac 0,方程没有实数根;2、韦达定理已知x1,x2是一元二次方程的两根,则有xb1 x2ax1x2ca例1:已知一元二次方程x22x m 1 0 (1)当m取何值时,方程有两个不相等的实数根?(2)设x21,x2是方程的两个实数根,且满足x1 x1x2 1,求m的值练习:1、方程x23 0的根的情况是()A有两个不等的有理实根B有两个相等的有理实根C有两个不等的无理实根D有两个相等的无理实根2、已知x2 1,x2是方程2x 3x 4 0的两个根,则()A x331 x2 2 ,x1x2 2 B x1 x2 2 ,x1x2 2 C x1 x322,x1x2 2 D x31 x22,x1x2 23、已知方程x2 2 0,则此方程()A 无实数根B两根之和为C两根之积为2D有一根为2 1这个专题是一二次方程是的判别式与韦达定理知识要点和练习4、已知x1,x2是方程2x 3x 1 0的两个根,则3221x11x2的值为()A 3B -3C D5、若将二次三项式x2 px 6因式分解,分解后的一个因式是x-3,则p的值是()A -5 B -1 C 1 D 56、已知x1,x2是方程x 4x 3 0的两个根,那么x1x2的值是() A - 4 B 4 C -3 D 37、在一元二次方程ax2 bx c 0(a 0)中,若a与c异号,则方程()A 有两个不相等的实数根 B 有两个相等的实数根 C 没有实数根 D 根的情况无法确定8、已知一元二次方程的两根分别为x1 3,x2 4,则这个方程为() A (x 3)(x 4) 0 B (x 3)(x 4) 0 C (x 3)(x 4) 0 D (x 3)(x 4) 09、关于x的一元二次方程3x 2x k 1 0有两个不相等的实数根,则k的取值范围是() A k432243且k 1 C k2243D k4310、若关于x的一元二次方程(m 2)x (2m 1)x 1 0有两个不相等的实数根,则m的取值范围为() A m43B m43C m43且m 2 D m43且m 22211、已知一直角三角形的三边为a、b、c,∠B=90 ,那么关于x的方程a(x 1) 2cx b(x 1) 0的根的情况为()A 有两个不相等的实数根B 有两个相等的实数根C 没有实数根D 无法确定12、设x1,x2是方程2x 4x 3 0的两个根,则2221x11x213、已知关于x的方程x 2(m 2)x m 0有两个实数根,且两根的平方和等于16,则m的值为14、已知方程x (12x20的两根为x1,x2,则x1 x2的值为2215、关于x的一元二次方程mx (3m 1)x m 0,其根的判别式的值为1,求m的值及该方程的根。


中考要求知识点基本要求略高要求较高要求一元二次方程了解一元二次方程的概念,会将一元二次方程化为一般形式,并指出各项系数;了解一元二次方程的根的意义能由一元二次方程的概念确定二次项系数中所含字母的取值范围;会由方程的根求方程中待定系数的值一元二次方程的解法理解配方法,会用直接开平方法、配方法、公式法、因式分解法解简单的数字系数的一元二次方程,理解各种解法的依据能选择恰当的方法解一元二次方程;会用方程的根的判别式判别方程根的情况能利用根的判别式说明含有字母系数的一元二次方程根的情况及由方程根的情况确定方程中待定系数的取值范围;会用配方法对代数式做简单的变形;会应用一元二次方程解决简单的实际问题例题精讲板块一根的判别式☞定义:运用配方法解一元二次方程过程中得到2224(24b b acx a a -+=,显然只有当240b ac -≥时,才能直接开平方得:22424b b acx a a -+=也就是说,一元二次方程20(0)ax bx c a ++=≠只有当系数a 、b 、c 满足条件240b ac ∆=-≥时才有实数根.这里24b ac -叫做一元二次方程根的判别式.☞判别式与根的关系在实数范围内,一元二次方程20(0)ax bx c a ++=≠的根由其系数a 、b 、c 确定,它的根的情况(是否有实数根)由24b ac ∆=-确定.设一元二次方程为20(0)ax bx c a ++=≠,其根的判别式为:24b ac ∆=-则①0∆>⇔方程20(0)ax bx c a ++=≠有两个不相等的实数根21,242b b acx a-±-=.根的判别式与韦达定理②0∆=⇔方程20(0)ax bx c a ++=≠有两个相等的实数根122b x x a==-.③0∆<⇔方程20(0)ax bx c a ++=≠没有实数根.☞根的判别式的应用:☞⑴运用判别式,判定方程实数根的个数;【例1】不解方程,判断下列方程的根的情况:⑴22340x x +-=;⑵20ax bx +=(0a ≠)【解析】略【答案】⑴22340x x +-=∵2342(4)410∆=-⨯⨯-=>∴方程有两个不相等的实数根.⑵∵0a ≠∴方程是一元二次方程,此方程是缺少常数项的不完全的一元二次方程,将常数项视为零∵22()40b a b ∆=--⋅⋅=∵无论b 取任何数,2b 均为非负数∴0∆≥,故方程有两个实数根【巩固】不解方程,判别一元二次方程2261x x -=的根的情况是()A .有两个不相等的实数根B .没有实数根C .有两个相等的实数根D .无法确定【解析】由方程可得3680∆=+>,所以方程有两个不相等的实数根.【答案】A【巩固】不解方程判定下列方程根的情况:⑴22340x x +-=;⑵232x +=21x +=;⑷22(21)220m x mx +-+=;⑸2210x ax a ++-=220+=;⑺4(1)30x x +-=;⑻2(1)(2)x x m --=【解析】略【答案】⑴两个不等的实数根;⑵两个相等的实数根;⑶无实数根;⑷无实数根;⑸两个不等的实数根;⑹无实数根;⑺两个不相等的实数根;⑻两个不相等的实数根【例2】已知a ,b ,c 是不全为0的3个实数,那么关于x 的一元二次方程2222()()0x a b c x a b c ++++++=的根的情况().A .有2个负根B .有2个正根C .有2个异号的实根D .无实根【解析】方程2222()()0x a b c x a b c ++++++=的判别式为:2222()4()a b c a b c ∆=++-++222333222a b c ab bc ca=---+++222222222(2)(2)(2)a ab b b bc c c bc a a b c =-+-+-+-+-+----222222[()()()]a b b c c a a b c =--+-+-+++∵a ,b ,c 不全为0,∴0∆<.∴原方程无实数根.故选D .【答案】D☞⑵利用判别式建立等式、不等式,求方程中参数值或取值范围;【例3】m 取什么值时,关于x 的方程222(3)6x mx +-=有两个相等的实数根【解析】略【答案】1m =±【巩固】如果关于x 的一元二次方程2690kx x -+=有两个不相等的实数根,那么k 的取值范围是()A .1k <B .0k ≠C .10k k <≠且D .1k >【解析】由题可得36360k k ∆=->⎧⎨≠⎩所以10k k <≠且【答案】C【巩固】方程2610kx x -+=有两个不相等的实数根,则k 的取值范围是【解析】注意二次项系数不为0【答案】9k <且0k ≠【巩固】若关于x 的二次方程2(1)220m x mx m -++-=有两个不相等的实数根,则m 的取值范围是【解析】注意二次项系数不为0【答案】23m >且1m ≠【巩固】若关于x 的一元二次方程2(1)210k x x ++-=有实数根,则k 的最小整数值为【解析】注意题目要求以及二次项系数不为0的条件【答案】2k =-【巩固】已知方程22(21)10m x m x +++=有实数根,求m 的范围.【解析】注意分两种情况讨论:若0m =,则原方程可化为101x x +=⇒=-满足题意;若0m ≠,则由题意可知221(21)404104m m m m ∆=+-≥⇒+≥⇒≥-.综上可知,14m ≥-【答案】14m ≥-【例4】关于x的一元二次方程2(12)10k x ---=有两个不相等的实数根,求k 的取值范围.【解析】由题意,得4(1)4(12)010120k k k k ++->⎧⎪+≥⎨⎪-≠⎩解得12k -≤<且12k ≠【答案】12k -≤<且12k ≠【巩固】关于x的方程210x ++=有两个不相等的实数根,则k 的取值范围为________.【解析】2400k ⎧∆=->⎪⎨>⎪⎩,解得1k >【答案】1k >【巩固】已知关于x 的方程222(1)50x m x m ++++=有两个不相等的实数根,化简:|1|m -【解析】∵0>△,∴2m >∴|1||1||2|23m m m m --+-=-【答案】23m -【巩固】已知关于x 的一元二次方程20x m -=有两个不相等的实数根,求m 的取值范围.【解析】由题意可知,原方程的判别式21(41303m m m ∆=+=+>⇒>-.又101m m -≥⇒≤,故113m -<≤.【答案】113m -<≤【巩固】k 为何值时,方程2(1)(23)(3)0k x k x k --+++=有实数根.【解析】需要分两种情况来讨论:⑴当10k -=时,原方程是一元一次方程,有一个实数根45x =;⑵当10k -≠时,方程是一元二次方程,故0∆≥,解得214k ≥-且1k ≠,所以当214k ≥-且1k ≠时方程有两个实数根.综上所述,当214k ≥-时,方程有实数根.【答案】214k ≥-【例5】关于x 的方程()26860a x x --+=有实数根,则整数a 的最大值是.【解析】由一元二次方程根的情况可知240b ac -≥,即()()284660a --⨯⨯-≥,解得263a ≤,故max 8a =.【答案】8【巩固】若方程222(1)450x a x a a ++++-=有实数根,求:正整数a .【解析】0∆≥,即()()22414450a a a +-+-≥,解不等式得3a ≤,即123a =,,.【答案】1,2,3【例6】已知关于x 的方程()()2212102x a b x b b -+--+=有两个相等的实数根,且a 、b 为实数,则32a b +=________.【解析】∵()()2212102x a b x b b -+--+=有两个相等的实数根.∴0∆=,即()()222210a b b b ++-+=∴()()22210a b b ++-=,∴0a b +=,10b -=∴1b =,1a =-,因此321a b +=-.【答案】1-【巩固】当a b 、为何值时,方程()2222134420x a x a ab b ++++++=有实根?【解析】要使关于x 的一元二次方程()2222134420x a x a ab b ++++++=有实根,则必有0∆≥,即()()22241434420a a ab b +-+++≥,得()()22210a b a ++-≤.又因为()()22210a b a ++-≥,所以()()22210a b a ++-=,得1a =,12b =-.【答案】1a =,12b =-【例7】已知a ,b ,c 为正数,若二次方程20ax bx c ++=有两个实数根,那么方程22220a x b x c ++=的根的情况是()A .有两个不相等的正实数根B .有两个异号的实数根C .有两个不相等的负实数根D .不一定有实数根【解析】22220a x b x c ++=的422224(2)(2)b a c b ac b ac ∆=-=+-,∵二次方程20ax bx c ++=有两个实数根,∴240b ac ->,∴220b ac ->,∴422224(2)(2)0b ac b ac b ac ∆=-=+->∴方程有两个不相等的实数根,而两根之和为负,两根之积为正.故有两个负根.故选C .【答案】C【巩固】若方程2(2)2(1)0m x m x m +-++=只有一个实数根,那么方程2(1)220m x mx m +-+-=().A .没有实数根B .有2个不同的实数根C .有2个相等的实数根D .实数根的个数不能确定【解析】∵方程2(2)2(1)0m x m x m +-++=只有一个实数根,∴20m +=,得2m =-.∴方程2(1)220m x mx m +-+-=,即为方程2440x x -+-=,∴244(1)(4)0∆=-⨯-⨯-=.∴方程2(1)220m x mx m +-+-=有2个相等的实数根.故选C .特别注意方程2(2)2(1)0m x m x m +-++=只有一个实数根.若20m +≠,则方程要么有2个根(相等或不相等),要么没有实数根.条件指明,该方程只有1个实数根,所以20m +=,且10m +≠.【答案】C☞⑶通过判别式,证明与方程相关的代数问题;【例8】对任意实数m ,求证:关于x 的方程222(1)240m x mx m +-++=无实数根.【解析】略【答案】∵210m +≠,故方程为一元二次方程.()()()2222422414442016m m m m m m ∆=--++=---()424241616444m m m m =---=-++()222m =-+∵220m +≠,∴0∆<,故方程无实根.【巩固】求证:关于x 的一元二次方程2(2)10x m x m -+++=有两个实数根.【解析】略【答案】∵2(2)10x m x m -+++=是关于x 的一元二次方程∴[]22(2)4(1)m m m ∆=-+-+=∵20m ≥∴原方程有两个实数根.【巩固】已知实数a 、b 、c 、r 、p 满足2pr >,20pc b ra -+=,求证:一元二次方程220ax bx c ++=必有实根.【解析】略【答案】2(2)4b ac ∆=-,因2b pc ra =+,则222()4()()2(2)pc m ac pc ra ac pr ∆=+-=++-.又2pr >,所以当0ac ≥时,0∆≥;当0ac <时,40ac ->,2()40pc ra ac ∆=+->.因此,一元二次方程220ax bx c ++=必有实根.【巩固】证明:无论实数m 、n 取何值时,方程2()0mx m n x n +++=都有实数根【解析】注意分类讨论.【答案】⑴若0m =,则方程为nx n =-,当0n ≠时,有实数根1x =-;当0n =时,方程的根为任意实数⑵当0m ≠时,原方程为一元二次方程22()4()0m n mn m n ∆=+-=-≥∴方程必有实数根综合⑴⑵可知,原结论成立【巩固】已知:方程()22250mx m x m -+++=没有实数根,且5m ≠,求证:()()25220m x m x m --++=有两个实数根.【解析】略【答案】当0m =时,()22250mx m x m -+++=可化为450x -+=,此时方程有根,故0m ≠故214(2)4(5)0404m m m m m ∆=+-+<⇒-<⇒>.方程()()25220(5)m x m x m m --++=≠的判别式为:224(2)4(5)4(94)0m m m m ∆=+--=+>故方程()()25220(5)m x m x m m --++=≠有两个实数根.板块二韦达定理☞如果20(0)ax bx c a ++=≠的两根是1x ,2x ,则12b x x a +=-,12c x x a=.(隐含的条件:0∆≥)特别地,当一元二次方程的二次项系数为1时,设1x ,2x 是方程20x px q ++=的两个根,则12x x p +=-,12x x q ⋅=.☞利用韦达定理求代数式的值【例9】不解方程224)0x x +-,求两根之和与两根之积【解析】韦达定理成立的前提条件是0∆≥【答案】令此方程的两个实数根为1x 、2x由韦达定理得124422x x --+=-=,122x x ⋅=-=【巩固】设方程24730x x --=的两个根为1x 、2x ,不解方程求下列各式的值⑴12(3)(3)x x --;⑵211211x xx x +++;⑶12x x -【解析】不解方程,即利用韦达定理将12x x +、12x x 的整体构造出来【答案】由韦达定理得1274x x +=,1234x x ⋅=-⑴12121237(3)(3)3()939344x x x x x x --=-++=--⨯+=;⑵221221112121212121212(1)(1)()2()10111(1)(1)132x x x x x x x x x x x x x x x x x x x x ++++-+++===+++++++⑶2221212127397()()4()4()4416x x x x x x -=+-=-⨯-=,∴12x x -=【巩固】已知方程22430x x +-=的两个根为1x 、2x ⑴12x x +=;⑵12_______x x ⋅=;⑶1211_______x x +=;⑷2212_______x x +=【解析】略【答案】⑴2-;⑵32-;⑶43;⑷7【巩固】已知α、β是方程2520x x ++=+的值.【解析】注意α,β均为负数,很多学生求出的结果均为负值【答案】由韦达定理可得,5αβ+=-,2αβ=∴22222()2522a a ββαβαβαβαβαβ++++=++===+=☞利用韦达定理求参数的值【例10】若3-、2是方程20x px q -+=的两个根,则________p q +=【解析】略【答案】7-【巩固】若方程210x px ++=的一个根为1-,则它的另一根等于,p 等于【解析】部分学生喜欢将1x =-代入原方程,求p 的数值,然后再求方程另外一个根,此方法较慢。

第3讲 一元二次方程根的判别式和韦达定理一、根的判别式21.4022.02043.,22ac b b ac b x x a a ⎧⎪≠-∆⎪⎪∆>⎧⎪⎪⎪∆=⎨⎨⎪⎪∆<⎩⎪⎪-±--±∆⎪==⎪⎩22概念:对于一个一元二次方程ax +bx+c=0(a 0)来说,b 称为根的判别式,记为。
时,方程有个不相等的根根的判别式意义:时,方程有个相等的根时,方程没有实数根公式法:解为即为 【典型例题】1.当m 取什么值时,关于x 的方程0)22()12(222=++++m x m x 。
(1)有两个相等实根;(2)有两个不相等的实根; (3)没有实根。
2.当m 为什么值时,关于x 的方程01)1(2)4(22=+++-x m x m 有实根。
3.已知关于x 的方程01)12(22=+-+x k x k 有两个不相等的实数根1x 、2x ,问是否存在实数k ,使方程的两实数根互为相反数?如果存在,求出k 的值;如果不存在,请说明理由。
【课堂练习】一、填空题:1、下列方程①012=+x ;②02=+x x ;③012=-+x x ;④02=-x x 中,无实根的方程是 。
2、已知关于x 的方程022=+-mx x 有两个相等的实数根,那么m 的值是 。
二、选择题:1、下列方程中,无实数根的是( )A 、011=-+-x xB 、 762=+yy C 、021=++x D 、0232=+-x x2、若关于x 的一元二次方程01)12()2(22=+++-x m x m 有两个不相等的实根,则m 的取值范围是( ) A 、43<m B 、m ≤43 C 、43>m 且m ≠2 D 、m ≥43且m ≠2 3、在方程02=++c bx ax (a ≠0)中,若a 与c 异号,则方程( )A 、有两个不等实根B 、有两个相等实根C 、没有实根D 、无法确定 一、试证:关于x 的方程1)2(2-=+-x m mx 必有实根。


一元二次方的应用及根的判别式、韦达定理一、根的判别式1.一元二次方程根的判别式的定义:运用配方法解一元二次方程过程中得到(x b2b24ac b24ac02a)4a2,显然只有当时,才能直接开平方得: x b b24ac.2a4a2也就是说,一元二次方程 ax2bx c0( a0) 只有当系数 a 、 b 、 c 满足条件b2 4 ac 0时才有实数根.这里 b 24ac 叫做一元二次方程根的判别式.2.判别式与根的关系:ax2在实数范围内,一元二次方程bx c0( a0) 的根由其系数a 、b、 c 确定,它的根的情况(是否有实数根 ) 由b24ac 确定.判别式:设一元二次方程为ax2bx c0(a 0) ,其根的判别式为: b 24ac 则①0方程 ax2bx c0(a0) 有两个不相等的实数根x1,2b b24ac .2a②0方程 ax2bx c0(a0) 有两个相等的实数根1x2b .x2a2③0bx c0(a0) 没有实数根.方程 ax若 a , b , c 为有理数,且为完全平方式,则方程的解为有理根;若为完全平方式,同时b b24ac 是 2a的整数倍,则方程的根为整数根.说明 : (1) 用判别式去判定方程的根时,要先求出判别式的值:上述判定方法也可以反过来使用,当方程有两个不相等的实数根时,0;有两个相等的实数根时,0 ;没有实数根时,0 .(2)在解一元二次方程时,一般情况下,首先要运用根的判别式b24ac 判定方程的根的情况(有两个不相等的实数根,有两个相等的实数根,无实数根) .当b24ac 0时,方程有两个相等的实数根(二重根 ),不能说方程只有一个根.①当 a0 时抛物线开口向上顶点为其最低点;②当 a0 时抛物线开口向下顶点为其最高点.3.一元二次方程的根的判别式的应用:一元二次方程的根的判别式在以下方面有着广泛的应用:(1)运用判别式,判定方程实数根的个数;(2)利用判别式建立等式、不等式,求方程中参数值或取值范围;(3)通过判别式,证明与方程相关的代数问题;(4)借助判别式,运用一元二次方程必定有解的代数模型,解几何存在性问题,最值问题.二、韦达定理如果一元二次方程ax2bx c0 ( a0 )的两根为 x1,x2,那么,就有ax 2bx c a x x1x x2比较等式两边对应项的系数,得x1x2b①,ax1x2c②a①式与②式也可以运用求根公式得到.人们把公式①与②称之为韦达定理,即根与系数的关系.因此,给定一元二次方程ax2bx c0 就一定有①与②式成立.反过来,如果有两数 x1, x2满足①与②,那么这两数 x1,x2必是一个一元二次方程ax2bx c0 的根.利用这一基本知识常可以简捷地处理问题.利用根与系数的关系,我们可以不求方程ax2bx c0 的根,而知其根的正、负性.在b24ac ≥ 0的条件下,我们有如下结论:当c0 时,方程的两根必一正一负.若b≥ 0 ,则此方程的正根不小于负根的绝对值;若b 0 ,aaa则此方程的正根小于负根的绝对值.当c0 时,方程的两根同正或同负.若b 0 ,则此方程的两根均为正根;若b 0 ,则此方程的aaa两根均为负根.⑴ 韦达定理:如果 ax 2bx c 0(a0) 的两根是 x 1 , x 2 ,则 x 1x 2b, x 1x 2c. (隐含的条件:0 )是 ax 2a a⑵ 若 x 1 , x 2 bx c 0( a 0) 的两根 (其中 x 1x 2 ),且 m 为实数,当0 时,一般地:① ( x 1 m)( x 2 m) 0x 1 m , x 2 m② ( x 1 m)( x 2 m) 0 且 ( x 1 m) (x 2 m) 0 x 1 m , x 2 m ③ ( x 1m)( x 2 m)0 且 ( x 1 m) (x 2 m) 0x 1 m , x 2m特殊地:当 m0 时,上述就转化为2bx c 0(a 0) 有两异根、两正根、两负根的条件.ax ⑶ 以两个数 x 1 , x 2 为根的一元二次方程 (二次项系数为 1)是: x 2 (x 1 x 2 ) x x 1x 2 0 .⑷ 其他:① 若有理系数一元二次方程有一根 a b ,则必有一根 ab ( a , b 为有理数 ).② 若 ac 0 ,则方程 ax 2 bx c 0(a 0) 必有实数根.③ 若 ac 0 ,方程 ax 2 bxc 0(a0) 不一定有实数根.④ 若 ab c0 ,则 ax 2bx c 0(a 0) 必有一根 x 1 .⑤ 若 a b c 0 ,则 ax 2bx c 0(a 0) 必有一根 x 1 .⑸ 韦达定理主要应用于以下几个方面:① 已知方程的一个根,求另一个根以及确定方程参数的值;② 已知方程,求关于方程的两根的代数式的值; ③ 已知方程的两根,求作方程;④ 结合根的判别式,讨论根的符号特征;⑤ 逆用构造一元二次方程辅助解题:当已知等式具有相同的结构时,就可以把某两个变元看作某个一元二次方程的两根,以便利用韦达定理;⑤ 利用韦达定理求出一元二次方程中待定系数后,一定要验证方程的 .一些考试中,往往利用这一点设置陷阱.例题一、判断方程根的情况【例 1】 不解方程,判别下列方程的根的情况:( 1) 2x 2 3 x 4 0 ;(2) 16y 2 9 24 y ;( 3) 5 x 2 17x 0 。

【初高中衔接】4-5.三个“二次”的关系【知识要点归纳】 一. 一元二次方程1. 根的判别式:2. 根与系数的关系(韦达定理):如果ax 2+bx +c =0(a ≠0)的两根分别是x 1,x 2,那么 .这一关系也被称为韦达定理.二. 一元二次不等式三.一元二次函数根的分布【经典例题】例1:已知方程2560x kx +-=的一个根是2,求它的另一个根及k 的值.例2:已知x 1,x 2是关于x 的一元二次方程4kx 2-4kx +k +1=0的两个实数根.(1)是否存在实数k ,使(2x 1-x 2)( x 1-2 x 2)=-32成立?若存在,求出k 的值;若不存在,说明理由; (2)求使1221x x x x +-2的值为整数的实数k 的整数值;(3)若k =-2,12xx λ=,试求λ的值.例3:解不等式:(1)x 2+2x -3≤0;(2)x -x 2+6<0;(3)4x 2+4x +1≥0;(4)x 2-6x +9≤0;(5)-4+x -x 2<0.例4:已知不等式20(0)ax bx c a ++<≠的解是2,3x x <>或求不等式20bx ax c ++>的解.例5:解关于x 的一元二次不等式210(x ax a ++>为实数).例6:已知方程2x -2(m+2)x +2m -1=0,根据下列条件求实数m 的取值范围(只列式,无需求出结果) (1) 有两个不相等的正根(2) 有两个不等实根都大于2(3)有两个不等实根,一个根大于0小于1,一个根大于1小于2【课后练习】1.解下列不等式:(1)3x 2-x -4>0;(2)x 2-x -12≤0;答案:(1)x <-1,或x >43; (2)-3≤x ≤4;2.使实系数一元二次方程2(1)0kx k x k --+=有两个实根的k 的取值范围是( ) A .113k -<<且 0k ≠ B .113k -≤≤C .1k ≤-或13k ≥D .113k -≤≤且0k ≠【解析】A. 若方程有两个根,则其必为二次函数,那么0k≠,同时方程的判别式0∆>,即()()()22141310k k k k --=-->,解得113k <<,综合0k ≠,可得A 为正确选项。
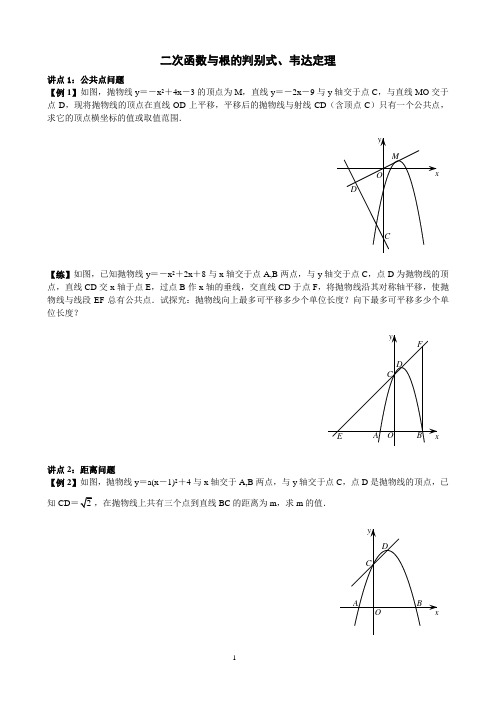
二次函数与根的判别式、韦达定理讲点1:公共点问题【例1】如图,抛物线y =-x 2+4x -3的顶点为M ,直线y =-2x -9与y 轴交于点C ,与直线MO 交于点D ,现将抛物线的顶点在直线OD 上平移,平移后的抛物线与射线CD (含顶点C )只有一个公共点,求它的顶点横坐标的值或取值范围.CO DM yx【练】如图,已知抛物线y =-x 2+2x +8与x 轴交于点A,B 两点,与y 轴交于点C ,点D 为抛物线的顶点,直线CD 交x 轴于点E ,过点B 作x 轴的垂线,交直线CD 于点F ,将抛物线沿其对称轴平移,使抛物线与线段EF 总有公共点.试探究:抛物线向上最多可平移多少个单位长度?向下最多可平移多少个单位长度?FD CE A B O y x讲点2:距离问题【例2】如图,抛物线y =a(x -1)2+4与x 轴交于A,B 两点,与y 轴交于点C ,点D 是抛物线的顶点,已知CD =2,在抛物线上共有三个点到直线BC 的距离为m ,求m 的值.CD BAOyx【练】如图,抛物线y =ax 2-6ax +5a 与x 轴交于A,B 两点(A 左,B 右),若抛物线与直线y =2x 的最近点之间的距离为255,求a 的值. yxO B A讲点3:隐藏判别式【例3】如图,点P 是直线l :y =-2x -2上的点,过点P 的另一条直线m 交抛物线y =x 2与A,B 两点,试证明:对于直线l 上任意给定的一点P ,在抛物线上都能找到点A ,使得PA =AB 成立.PBAO yx【练】如图,已知二次函数y =a(x 2-6x +8)(a >0)的图象与x 轴分别交于点A,B ,与y 轴交于点C ,点D 是抛物线的顶点.当点P 在抛物线对称轴上时,设点P 的纵坐标t 是大于3的常数,试问:是否存在一个正数a ,使得四条线段PA,PB,PC,PD 与一个平行四边形的四条边对应相等(即这四条线段能构成平行四边形)?请说明理由.CPDB AO y x讲点4:交点间的距离【例4】已知二次函数y =x 2-2mx +m 2+m 的图象与函数y =kx +1的图象交于A (x 1,y 1),B (x 2,y 2)(x 1<x 2)两点.(1)如图1,当k =1,m 取不同值时,猜想AB 的长是否不变?并证明你的猜想;A BxOy(2)如图2,当m =0,k 取不同值时,猜想△AOB 的形状,并证明你的猜想.BAyOx【例5】如图,抛物线y =x 2-4x +5与y 轴交于点C ,过点N (1,2)作直线l ,交抛物线于点P ,交y 轴于点E ,连接PC ,若PE =PC ,求直线l 的解析式.lE P CN Oy x【练】如图,抛物线C 1:y =x 2+4x +3交x 轴于A,B 两点,交y 轴于点C ,将抛物线C 1沿y 轴翻折得新抛物线C 2,过点C 作直线l 交抛物线C 1于点M ,交抛物线C 2于点N ,若MN =82,求直线l 的解析式.A B xyO C三、对称问题【例6】如图,已知抛物线y =x 2-2x -3,直线y =kx -1与抛物线交于P,Q 两点,且y 轴平分线段PQ ,求k 的值.QPO y x【练】如图,已知抛物线y =x 2-4x +3,过点D (0,-52)的直线与抛物线交于点M,N ,与x 轴交于点E ,且点M,N 关于点E 对称,求直线MN 的解析式.yxNEMD O四、与面积结合【例7】如图,抛物线y =x 2-4x +5顶点为M ,平移直线y =x 交抛物线于点H,K ,若S △MHK =3,求平移后直线的解析式.【课后反馈】1.如图,已知抛物线y =x 2-2x -3与x 轴交于A,B 两点,与y 轴交于点C ,将抛物线沿对称轴向上平移k 个单位长度后与线段BC 交于D,E 两个不同的点,求k 的取值范围.E C DB A O yx2.如图,抛物线y =ax 2-6ax +5a 与x 轴交于A,B 两点(A 左,B 右),若抛物线不通过直线y =2x 上方的点,求抛物线顶点纵坐标的取值范围.yxO B A3.如图,抛物线y =14x 2+32x +2与x 轴交于A,B 两点(点A 在点B 的左边),与y 轴交于点C ,将抛物线沿直线BC 平移,与射线AC (含点A )仅有一个公共点,求抛物线顶点横坐标的值或取值范围.CBAOyx4.如图,已知抛物线C :y =x 2-2x +4和直线l :y =-2x +8,直线y =kx (k >0)与抛物线C 交于A,B 两点,与直线l 交于点P ,分别过A,B,P 作x 轴的垂线,垂足依次为A 1、B 1、P 1,若11OA +11OB =1u OP ,求u 的值.A 1B 1P 1B AP O yx5.如图1,抛物线C 1:y =x 2+4x +3顶点为M ,抛物线C 2与抛物线C 1开口方向相反,形状相同,顶点为N ,且M,N 关于点P (0,2)对称. (1)求抛物线C 2的解析式;N MPOyx(2)直线y =m 交抛物线C 1于点A,B ,交抛物线C 2于点C,D ,若AB =2CD ,求m 的值;DCB ANMOyx。

一元二次方程之判别式法与韦达定理(一)知识点梳理一元二次方程ax2+bx+c=0(a 、b 、c 属于R ,a≠0)根的判别,△=b2-4ac ,不仅用来判定根的性质,而且作为一种解题方式,在代数式变形,解方程(组),解不等式,研究函数乃至几何、三角运算中都有超级普遍的应用。
韦达定理除已知一元二次方程的一个根,求另一根;已知两个数的和与积,求这两个数等简单应用外,还能够求根的对称函数,计论二次方程根的符号,解对称方程组,和解一些有关二次曲线的问题等,都有超级普遍的应用。
一、一元二次方程根的判别式:ac b 42-=∆ (1)当Δ>0时⇔方程有两个不相等的实数根;(2)当Δ=0时⇔方程有两个相等的实数根;(3)当Δ< 0时⇔方程没有实数根,无解;(4)当Δ≥0时⇔方程有两个实数根(5)根的判别式△=b 2-4ac 的意义,在于不解方程能够判别根的情形,还能够依照根的情形确信未知系数的取值范围。
二、一元二次方程根与系数的关系(韦达定理):(1)若21,x x 是一元二次方程02=++c bx ax 的两个根,那么:a b x x -=+21,a c x x =⋅21 (2)以两个数21,x x 为根的一元二次方程(二次项系数为1)是:0)(21212=++-x x x x x x3、一元二次方程的两根和与两根积和系数的关系在以下几个方面有着普遍的应用:(1)已知方程的一根,求另一个根和待定系数的值。
(2)不解方程,求某些代数式的值。
(3)已知两个数,求作以这两个数为根的一元二次方程。
(4)已知两数和与积,求这两个数。
(5)二次三项式的因式分解。
注意:在应用根与系数的关系时,不要忽略隐含条件。
∆≥≠⎧⎨⎩00a例题讲解例一、当k 为何值时,关于x 的方程()222123x k x k k --=-++:⑴ 两个不相等的实数根; ⑵有两个相等的实数根; ⑶没有实数根。
例二、m x mx mx m 为何值时,关于的方程有两个相等的实数根?并2350-++=求出这时方程的根。

一元二次方程根与系数的关系应用例析及训练对于一元二次方程ax?+bx+c = 0(a式0),当判别式心= b?_4ac兰0时,其求根公式为:%、=―' b——4ac;当2ab c.:_0时,设一元二次方程的两根为X「x2,有:x-i x2,x-i x2;根与系数的这种关系又称为韦达定理;它的a ab c逆定理也是成立的,即当x-i x2,x-i x2时,那么为、x2则是方程ax2bx c = 0(a = 0)的两根。
一元二次方程a a的根与系数的关系,综合性强,应用极为广泛,在中学数学中占有极重要的地位,也是数学学习中的重点。
学习中,除了要求熟记一元二次方程ax2 bx c =0(a =0)根的判别式厶二b2 -4ac存在的三种情况外,还常常要求应用韦达定理解答一些变式题目,以及应用求根公式求出方程ax2 bx 0(^- 0)的两个根为、x2,进而分解因式,即ax2bx • c = a(x-xj(x-x2)。
下面就对韦达定理的应用可能出现的问题举例做些分析,希望能带来小小的帮助。
一、根据判别式,讨论一元二次方程的根。
例1:已知关于x的方程(1) X2 -(1-2a)x • a2 -3 =0有两个不相等的实数根,且关于x的方程⑵x2-2x,2a-1=:0没有实数根,问a取什么整数时,方程(1)有整数解?分析:在同时满足方程(1),(2)条件的a的取值范围中筛选符合条件的a的整数值。
解:a的取值范围,并依靠熟练的解不等式的基本技说明:熟悉一元二次方程实数根存在条件是解答此题的基础,正确确定能和一定的逻辑推理,从而筛选出a,这是解答本题的基本技巧。
二、判别一元二次方程两根的符号。
例2:不解方程,判别方程2x2・3x-7=0两根的符号。
判别根的符号,需要把“根的判别式”和“根与系数的关系”结合起来进行确定,倘若由题中x1 x^:: 0,所以可判定方程的根为一正一负;倘若为x2 0,仍需考虑x1 X2的正负,倘若x1 x2 • 0,则方程有两个正数根;倘若x1 X2:::0,则方程有两个负数根。

第14讲根的判别式与韦达定理模块一一元二次方程根的判别式知识导航式子b2-4ac叫做一元二次方程ax2+bx+c=0(a≠0)根的判别式,通常用希腊字母“△”来表示,即△=b2-4ac.当△>0时,方程ax2+bx+c=0(a≠0)有两个不等的实数根;当△=0时,方程ax2+bx+c=0(a≠0)有两个相等的实数根;当△<0时,方程ax2+bx+c=0(a≠0)无实数根.计算判别式的值,可以判断一元二次方程根的情况;反之,若一元二次方程有两个不等实数根,则△>0;若一元二次方程有两个相等实数根,则△=0;若一元二次方程无实数根,则△<0.注意:①当△=0时,方程有两个相等的实根,不能说方程只有一个根②当△≥0时,方程有两个实根(一元二次方程有实根).例1(1)已知关于x的一元二次方程x2-2x+m=0有解,求m的范围.-1x-m=0有两个不相等实数根,求m的取值范围.(2)己知关于x的一元二次方程x2-m(3)求证:关于x的一元二次方程ax2-(3a+l)x+2(a+l)=0(a≠0)总有实数根(4)已知关于x的方程ax2-(3a+l)x+2(a+l)=0有两个不相等的实数根,求a的取值范围(5) (2016武汉元月调考第9题)关于x的方程(m-2)x2+2x+1=0有实数根,求m的取值范围.拓展己知关于x的方程(n-1)x2+mx+1=0有两个相等的实数根,试说明关于y的方程m2y2—2my-m2—2n2+3=0的根的情况【总结】1、在处理【例1】和【练1】这类问题时,一定要注意先判断方程类型,若方程类型不确定,则需要分类讨论2、关于方程类型,题目在设问方面会有下列说法:(1)“关于x的一元二次方程有解”则方程一定为一元二次方程.(2)“关于x的方程有两实根”则方程一定为一元二次方程.(3)“关于x的方程有解”则方程类型不确定,需要分类讨论例2(1) 己知a、b、c是三角形三边,求证:关于x的方程(a+b)x2+2cx+(a+b)=0无实根.(2) 己知:a、b、c分别是△ABC的三边长,求证:关于x的方程b2x2+(b2+c2一a2)x+c2=0没有实数根.练习己知△ABC三边a,b,c,关于x的方程(a+c)x2 +2bx-a+c=0,x2+2ax+b2=0均有两个相等的实数根,试判断△ABC的形状.模块二 一元二次方程根与系数关系知识导航:由因式分解法可知,方程(x -x 1)(x -x 2)=0(x 1,x 2为已知数)的两根为x 1和x 2,将方程化为x 2+px +q =0的形式,即x 2一(x 1+x 2)x + x 1x 2=0,则二次项系数为1,一次项系数为p =-(x 1+x 2),q = x 1x 2. 于是,上述方程两个根的和、积与系数的关系分别有如下关系:x 1+x 2=-p , x 1x 2=q对于一般地一元二次方程ax 2+bx +c =0,二次项系数a 未必是1.根据求根公式,x 1=a ac b b 24-2-+, x 2=aac b b 24-2-- 由此可知,x 1+x 2=-a b , x 1x 2=ac 这表明任何一个一元二次方程的根与系数的关系为:两根之和等于一次项系数与二次项系数的比的相反数,两根之积等于常数项与二次项系数的比.例3(1)若x 1,x 2是一元二次方程x 2—5x +6=0的两个根,则x 1+x 2的值是____(2)一元二次方程x 2—4x -c =0的一个根是3,则另一个根是____,c =___________(3)若方程x 2-3x 一1=0的两根为x 1、x 2,则11x +21x 的值为____ (4)关于x 的一元二次方程x 2一mx +2m -1=0的两个实数根分别是x 1、x 2,且x 12+x 22=7, 则(x 1-x 2)2的值是_____________练习(1)方程x 2—2x -1=0的两个实数根分别为x 1、x 2,(x 1-l )( x 2-1)=______________cz ,设x 1、x 2是方程2x 2—6x +l =o 的两个实数根,则(x 1-21x )( x 2-11x )的值为__________ 【总结】1、用韦达定理,常见的恒等变形有:11x +21x =2121x x x x +,x 12+x 22=(x 1+x 2)2-2x 1x 2,(x 1-x 2)2=(x 1+x 2)2-4x 1x 2 21x x -=212214)(x x x x -+x 13 +x 23=(x 1 +x 2)(x 12+x 22-x 1x 2)=(x 1+x 2)3-3x 1x 2(x 1+x 2)2、韦达定理只有在两根存在的情况下才成立,故使用韦达定理的前提条件是b 2—4ac ≥0例4已知x 1,x 2是方程x 2—3x +l =0的两个实数根,则x 12+x 22=________________(x 1-2)(x 2-2)=______________;x 12+x 1·x 2+x 22=_____________,12x x +21x x =_________ x 1-x 2=__________, x 12-x 22=________;11x -21x =__________;12x x -21x x =___________练习已知x 1,x 2是方程2x 2—3x -5 =0的两个根,求下列代数式的值:x 12+x 22=__________,12x x +21x x =_________; 21x x -=___________ x 12-x 22=________;12x x -21x x =___________,x 12+3x 22-3x 2=_________________例5已知关于x 的方程x 2—2(k -l )x +k 2=0有两个实数根x 1,x 2.(1)求k 的取值范围.(2) 若x l +x 2 =1-x 1x 2,求k 的值.练习关于x 的方程x 2+2(a -l )x +a 2 -7a -4=0的两根为x 1. x 2,且x 1x 2 -3x l -3x 2 +2=0,求a 的值例6关于一元二次方程x 2 +2x +k +l =0的实数解是x l 和x 2.(1)求k 的取值范围;(2)如果x 1+x 2-x 1x 2<-1且k 为整数,求k 的值.练习己知关于x 的方程x 2 +2(m +2)x +m 2 -5=0有两个实数根,并且这两个根的平方和比这两个根的积大16,求m 的值.例7己知△ABC 的两边AB 、AC 的长是关于x 的一元二次方程x 2 -(2k +3)x +k 2 +3k +2=0的两个实数根,第三边BC 的长是5.(1)k 为何值时,△ABC 是以BC 为斜边的直角三角形;(2)k 为何值时,△ABC 是等腰三角形,并求△ABC 的周长.练习在等腰△ABC 中,∠A 、∠B 、∠C 的对边分别为a 、b 、c ,已知a =3,b 和c 是关于x 的方程x 2+mx +2-21m =0的两个实数根,求△ABC 的周长. 课后作业A 基础巩固1.已知x =l 是方程x 2+bx -2=0的一个根,则方程的另一个根是( )A .1B .2C .-2D .-12. 已知一元二次方程x 2—4x +3=0两根为x 1,x 2,则x 1·x 2=( )A .4B .3C .-4D .-3 3. 己知关于x 的一元二次方程(1-2k )x 2—21+k x -1=0有两个不相等的实数根,则k 的取值范围是____.4. 关于x 的方程kx 2 +(l -k )x -l =0有两个不等实根,则k 的取值范围是____________.5. 关于x 的方程kx 2+(l -k )x -l =0有实根,则k 的取值范围是_______________6. 求证:不论m 为何值时,关于x 的方程x 2一2mx -2m -4=0总有两个不相等的实根.7. 如果一直角三角形的三边长分别为a ,b ,c ,b 为斜边,求证:关于x 的方程a (x 2 -1)一2cx +b (x 2 +1)=0有两个相等的实数根8. 己知x 1,x 2是方程x 2-5x +2=0的两个实数根,则x 12+x 22=________________(x 1-2)(x 2-2)=______________;x 12+x 1·x 2+x 22=_____________,12x x +21x x =_________ x 1-x 2=__________, x 12-x 22=________;11x -21x =__________;12x x -21x x =___________B 综合训练 9. (2015年汉阳区九上期中)己知关于x 的方程x 2—2(k -l )x +k 2=0有两个实数根x 1,x 2.(1)求k 的取值范围;(2) 若x 1+x 2=1- x 1x 2,求k 的值.10.已知关于x 的一元二次方程mx 2—2x +l =0.(1)若方程有两个实数根,求m 的范围;(2)若方程的两个实数根为x 1,x 2,且x 1x 2一x 1一x 2=21,求m 的值 111.己知,关于x 的方程x 2一kx +k -1=0(1)求证:无论k 取何值,方程总有两实数根(2)若等腰△ABC 的一边长为2,另两边为这个方程的两个根,求△ABC 的周长数学故事“石头剪刀布”或能揭示演化策略“石头剪刀布”是游戏中解决争端的常用方式,每人各出剪刀、石头、布中的一种,通过石头砸剪刀、剪刀剪布、布包住石头的规则,可以在两人甚至多人中决出胜负.不过,科学家发现,大自然也用自己的方式玩着类似“石头剪刀布”这样的游戏,数学家和生物学家利用这种方式研究了从人类社会到培养皿中的细菌的各种现象.如今,研究者又发现,当玩家不断改变策略时,三种武器的使用频率会轮流上升与下降,呈现出一种固定的模式.这一发现或许可以帮助我们理解生物在生存之争中是如何维持竞争策略的.一旦应用到生物中来,石头剪刀布就不仅仅是两个小孩子的游戏,而变成多玩家之间的复杂关系了.比方说,某些蜥蜴用来赢得伴侣的策略就有三种:侵略、合作与欺骗,这三种策略就和石头剪刀布一样,有着环状的胜负关系(侵略战胜合作,欺骗战胜侵略,合作战胜欺骗),而对于蜥蜴来说,成功繁衍后代就意味着赢得游戏,在生物的“石头剪刀布”游戏中,通常是大的种群中随机产生一对玩家开始比拼,每个玩家通常都保持一种固定的策略一一即对每一个对手都出同样的姿势(石头、剪刀或者布).每次对决之后,赢家就增加一个(对应着繁衍后代),使用同样的策略,而输家则消失.对这种模型进行仔细的数学研究以后发现,出石头、剪刀和布的玩家会随着时间波动.随着初始情况中每种策略所占比例不同,整个群体的情况会分别演变成不同的长期行为,比如用石头、剪刀、布的个体各占三分之一,或者一种策略大幅减少另两种上升,过一段时间又反过来,呈现剧烈的周期波动.受到计算机模拟的启发,康奈尔大学的两位数学家Steven Strogatz 和Danielle Toupo 决定研究一下如果玩家中途改变策略会发生什么.“我觉得这个想法很吸引人,就想找到一种最简洁的数学模型来描述它,”Strogatz 说.他们试图回到最基础的原理,寻找纯粹的公式,而非复杂的计算机模拟.Strogatz 和Toupo 修正了“石头剪刀布”方程,允许一些“突变子女”存在,它们所采用的策略和亲代不同.此前的研究者也研究了突变,但一直假设突变是对称的,即每种策略变成其他策略的几率相同,但Strogatz 和To upo 考虑到了其他的模式,比如出石头的玩家可能会生下出布的子女,但反过来则不尽然.每种突变最终都会导致一种循环,即出石头、剪刀和布的玩家数都各自不停地上下波动,循环不息.而更令人惊讶的是,他们还证明哪怕突变率极低甚至接近于0,整个游戏还是会进入这种循环模式,论文发表于本月的《物理评论E 》(Physical ReviewE )中,只是增加了一点点突变的因素,游戏结果就不再是三种各占三分之一的稳定态或是剧烈波动态了, “我认为该研究最吸引入的一点是,这种‘游戏’在自然界中真的存在,”加州大学圣克鲁兹分校的生态学家BarrySinervo 说,他没有参与这项工作,“哪怕你不是数学家,也会欣赏这一研究.”Sinervo-直在研究加州一种侧斑鬣蜥,该蜥蜴的种群行为也会进入像“石头剪刀布”一样的振荡状态.Sinervo和同事通过野外的长期观察发现,采取侵略、合作和欺骗三种策略的蜥蜴数目有一个6年的变化周期,每一代新的蜥蜴诞生时,主导策略都会变化.Strogatz和Toupo的新研究为Sinervo的工作提供了数学模型,来解释了这种变化周期,“对我来说,这篇论文的有趣之处就在这里.”Sinervo说,由于数学方面的限制,康奈尔大学的研究者还不能证明他们的发现适用于所有的突变模式,但Strogatz说他们预测会如此.研究更广泛的突变模式也可以更进一步地提供数学基础,帮助我们解释自然界这个大剧场里物种策略的兴衰变迁.。

一元二次方程根与系数的关系应用例析及训练对于一元二次方程)0(02≠=++a c bx ax ,当判别式042≥-=∆ac b 时,其求根公式为:aacb b x 24221-±-=、;当0≥∆时,设一元二次方程的两根为21x x 、,有:a b x x -=+21,acx x =⋅21;根与系数的这种关系又称为韦达定理;它的逆定理也是成立的,即当a b x x -=+21,ac x x =⋅21时,那么21x x 、则是方程)0(02≠=++a c bx ax 的两根。
一元二次方程的根与系数的关系,综合性强,应用极为广泛,在中学数学中占有极重要的地位,也是数学学习中的重点。
学习中,除了要求熟记一元二次方程)0(02≠=++a c bx ax 根的判别式ac b 42-=∆存在的三种情况外,还常常要求应用韦达定理解答一些变式题目,以及应用求根公式求出方程)0(02≠=++a c bx ax 的两个根21x x 、,进而分解因式,即))((212x x x x a c bx ax --=++。
下面就对韦达定理的应用可能出现的问题举例做些分析,希望能带来小小的帮助。
一、根据判别式,讨论一元二次方程的根。
例1:已知关于x 的方程(1)03)21(22=-+--a x a x 有两个不相等的实数根,且关于x 的方程(2)01222=-+-a x x 没有实数根,问a 取什么整数时,方程(1)有整数解?分析:在同时满足方程(1),(2)条件的a 的取值范围中筛选符合条件的a 的整数值。
解: ?说明:熟悉一元二次方程实数根存在条件是解答此题的基础,正确确定a 的取值范围,并依靠熟练的解不等式的基本技能和一定的逻辑推理,从而筛选出a ,这是解答本题的基本技巧。
二、判别一元二次方程两根的符号。
例2:不解方程,判别方程07322=-+x x 两根的符号 。
判别根的符号,需要把“根的判别式”和“根与系数的关系”结合起来进行确定,倘若由题中021<⋅x x ,所以可判定方程的根为一正一负;倘若021>⋅x x ,仍需考虑21x x +的正负,倘若021>+x x ,则方程有两个正数根;倘若021<+x x ,则方程有两个负数根。

一元二次方程(3)【基础知识】(一)一元二次方程的根的判别式)4(2ac b -=∆.000方程没有实数根根;方程有两个相等的实数数根;方程有两个不相等的实⇔<∆⇔=∆⇔>∆(二) 一元二次方程的根与系数的关系(韦达定理) 若21,x x 是方程)0(02≠=++a c bx ax 的两个根,则ac x x a b x x =⋅-=+2121,如果方程02=++q px x 的两个根是21,x x ,那么_______,2121=⋅=+x x x x 。
例题一 1、不解方程,判别下列方程根的情况: (1)x 2-x=5 (2)9x 2-6 2 x+2=0 (3)x 2-x+2=02、如果关于x 的方程20x x k -+=(k 为常数)有两个相等的实数根,那么k = . 3、关于x 的一元二次方程02)12(22=-+++k x k x 有实数根,则k 的取值范围是 。
4、若关于x 的一元二次方程2210kx x --=有两个不相等的实数根,求k 的取值范围。
6、已知关于的一元二次方程有1、不解方程,判断下列一元二次方程的根的情况:1)x 2+3x+3=0; (2)x 2-4x-3=0; (3)4x 2-4x+1=0 2、如果一元二次方程x 2+4x +k 2=0有两个相等的k =3、如果关于x 的方程2x 2-(4k+1)x +2 k 2-1=0有k 的取值范围是4、关于019)13(22=-+--m x m mx x 的方程有m 的取值范围。
1、已知1-=x 是方程0232=++k x x 的一个根,______, k =______. 2、关于的一元二次方程的一个1,则方程的另一根为 . 3、若关于的方程的一个根是0,则另一个根是 .补:十字相乘法解一元二次方程基础公式:()()()ab x b a x b x a x +++=++2,()()()b x a x ab x b a x ++=+++2例1 解方程:(1)x 2+3x+2=0; (2)x 2-7x+6 =0.练习1、解方程(1)652++x x =0 (2)652+-x x =0(3)652-+x x =0 (4)652--x x =0(5)122-+x x =0 (6)18112++x x =0(7)x 2-7x+12=0 (8)a 2+11a+28=0(9)x 2-16x+28=0. (10)x 2-4x-21=0(11)m 2+7m-30=0 (12)a 2-a-56=0(13)m 2-9m+20=0 (14)x 2-9x-36=0(15)8)3(2)3(222-+-+x x x x =0(16)()()2414222++-+x x xx =0例2解方程练习2.解方程 (1)042772=-+x x(4)x x x 86223--=00232)1(2=-+y y 08103)2(2=-+x x 045314)2(2=--x x 024223)3(2=-+-x x。

新方法一元二次方的应用及根的判别式、韦达定理讲义中考要求知识点睛一、根的判别式1.一元二次方程根的判别式的定义:运用配方法解一元二次方程过程中得到 2224()24b b ac x a a -+=,显然只有当240b ac -≥时,才能直接开平方得:2b x a += 也就是说,一元二次方程20(0)ax bx c a ++=≠只有当系数a 、b 、c 满足条件240b ac ∆=-≥时才有实数根.这里24b ac -叫做一元二次方程根的判别式.2.判别式与根的关系:在实数范围内,一元二次方程20(0)ax bx c a ++=≠的根由其系数a 、b 、c 确定,它的根的情况(是否有实数根)由24b ac ∆=-确定.判别式:设一元二次方程为20(0)ax bx c a ++=≠,其根的判别式为:24b ac ∆=-则①0∆>⇔方程20(0)ax bx c a ++=≠有两个不相等的实数根1,2x =.②0∆=⇔方程20(0)ax bx c a ++=≠有两个相等的实数根122bx x a==-.③0∆<⇔方程20(0)ax bx c a ++=≠没有实数根.若a ,b ,c 为有理数,且∆为完全平方式,则方程的解为有理根;若∆为完全平方式,同时b -2a 的整数倍,则方程的根为整数根.说明: (1)用判别式去判定方程的根时,要先求出判别式的值:上述判定方法也可以反过来使用,当方程有两个不相等的实数根时,0∆>;有两个相等的实数根时,0∆=;没有实数根时,0∆<.(2)在解一元二次方程时,一般情况下,首先要运用根的判别式24b ac ∆=-判定方程的根的情况(有两个不相等的实数根,有两个相等的实数根,无实数根).当240b ac ∆=-=时,方程有两个相等的实数根(二重根),不能说方程只有一个根. ① 当0a >时⇔抛物线开口向上⇔顶点为其最低点;② 当0a <时⇔抛物线开口向下⇔顶点为其最高点.3.一元二次方程的根的判别式的应用:2一元二次方程的根的判别式在以下方面有着广泛的应用: (1)运用判别式,判定方程实数根的个数;(2)利用判别式建立等式、不等式,求方程中参数值或取值范围; (3)通过判别式,证明与方程相关的代数问题;(4)借助判别式,运用一元二次方程必定有解的代数模型,解几何存在性问题,最值问题.二、韦达定理如果一元二次方程20ax bx c ++=(0a ≠)的两根为12x x ,,那么,就有()()212ax bx c a x x x x ++=--比较等式两边对应项的系数,得1212b x x a c x x a ⎧+=-⎪⎪⎨⎪⋅=⋅⎪⎩①,② ①式与②式也可以运用求根公式得到.人们把公式①与②称之为韦达定理,即根与系数的关系. 因此,给定一元二次方程20ax bx c ++=就一定有①与②式成立.反过来,如果有两数1x ,2x 满足①与②,那么这两数12x x ,必是一个一元二次方程20ax bx c ++=的根.利用这一基本知识常可以简捷地处理问题.利用根与系数的关系,我们可以不求方程20ax bx c ++=的根,而知其根的正、负性.在24b ac ∆=-≥0的条件下,我们有如下结论:当0c a <时,方程的两根必一正一负.若0b a -≥,则此方程的正根不小于负根的绝对值;若0ba -<,则此方程的正根小于负根的绝对值. 当0c a >时,方程的两根同正或同负.若0b a ->,则此方程的两根均为正根;若0ba -<,则此方程的两根均为负根.⑴ 韦达定理:如果20(0)ax bx c a ++=≠的两根是1x ,2x ,则12b x x a +=-,12cx x a=.(隐含的条件:0∆≥)⑵ 若1x ,2x 是20(0)ax bx c a ++=≠的两根(其中12x x ≥),且m 为实数,当0∆≥时,一般地: ① 121()()0x m x m x m --<⇔>,2x m <② 12()()0x m x m -->且12()()0x m x m -+->1x m ⇔>,2x m > ③ 12()()0x m x m -->且12()()0x m x m -+-<1x m ⇔<,2x m <特殊地:当0m =时,上述就转化为20(0)ax bx c a ++=≠有两异根、两正根、两负根的条件. ⑶ 以两个数12,x x 为根的一元二次方程(二次项系数为1)是:21212()0x x x x x x -++=. ⑷ 其他:① 若有理系数一元二次方程有一根a b +a b a ,b 为有理数). ② 若0ac <,则方程20(0)ax bx c a ++=≠必有实数根. ③ 若0ac >,方程20(0)ax bx c a ++=≠不一定有实数根. ④ 若0a b c ++=,则20(0)ax bx c a ++=≠必有一根1x =. ⑤ 若0a b c -+=,则20(0)ax bx c a ++=≠必有一根1x =-. ⑸ 韦达定理主要应用于以下几个方面:① 已知方程的一个根,求另一个根以及确定方程参数的值; ② 已知方程,求关于方程的两根的代数式的值; ③ 已知方程的两根,求作方程; ④ 结合根的判别式,讨论根的符号特征;⑤ 逆用构造一元二次方程辅助解题:当已知等式具有相同的结构时,就可以把某两个变元看作某个一元二次方程的两根,以便利用韦达定理;⑤ 利用韦达定理求出一元二次方程中待定系数后,一定要验证方程的∆.一些考试中,往往利用这一点设置陷阱.重、难点1. 转化思想的渗透2. 对根的判别式的理解例题精讲一、判断方程根的情况【例1】 不解方程,判别下列方程的根的情况:(1)22340x x +-=;(2)216924y y +=;(3)()25170x x +-=。

一元二次方程根与系数的关系应用例析及训练对于一元二次方程)0(02≠=++a c bx ax ,当判别式042≥-=∆ac b 时,其求根公式为:aacb b x 24221-±-=、;当0≥∆时,设一元二次方程的两根为21x x 、,有:abx x -=+21,a c x x =⋅21;根与系数的这种关系又称为韦达定理;它的逆定理也是成立的,即当ab x x -=+21,ac x x =⋅21时,那么21x x 、则是方程)0(02≠=++a c bx ax 的两根。
一元二次方程的根与系数的关系,综合性强,应用极为广泛,在中学数学中占有极重要的地位,也是数学学习中的重点。
学习中,除了要求熟记一元二次方程)0(02≠=++a c bx ax 根的判别式ac b 42-=∆存在的三种情况外,还常常要求应用韦达定理解答一些变式题目,以及应用求根公式求出方程)0(02≠=++a c bx ax 的两个根21x x 、,进而分解因式,即))((212x x x x a c bx ax --=++。
下面就对韦达定理的应用可能出现的问题举例做些分析,希望能带来小小的帮助。
一、根据判别式,讨论一元二次方程的根。
例1:已知关于x 的方程(1)03)21(22=-+--a x a x 有两个不相等的实数根,且关于x 的方程(2)01222=-+-a x x 没有实数根,问a 取什么整数时,方程(1)有整数解?分析:在同时满足方程(1),(2)条件的a 的取值范围中筛选符合条件的a 的整数值。
解:说明:熟悉一元二次方程实数根存在条件是解答此题的基础,正确确定a 的取值范围,并依靠熟练的解不等式的基本技能和一定的逻辑推理,从而筛选出a ,这是解答本题的基本技巧。
二、判别一元二次方程两根的符号。
例2:不解方程,判别方程07322=-+x x 两根的符号 。
判别根的符号,需要把“根的判别式”和“根与系数的关系”结合起来进行确定,倘若由题中021<⋅x x ,所以可判定方程的根为一正一负;倘若021>⋅x x ,仍需考虑21x x +的正负,倘若021>+x x ,则方程有两个正数根;倘若021<+x x ,则方程有两个负数根。
一元二次方的应用及根的判别式、韦达定理一、根的判别式1.一元二次方程根的判别式的定义:运用配方法解一元二次方程过程中得到 2224()24b b acx a a -+=,显然只有当240b ac -≥时,才能直接开平方得:2b x a += 也就是说,一元二次方程20(0)ax bx c a ++=≠只有当系数a 、b 、c 满足条件240b ac ∆=-≥时才有实数根.这里24b ac -叫做一元二次方程根的判别式.2.判别式与根的关系:在实数范围内,一元二次方程20(0)ax bx c a ++=≠的根由其系数a 、b 、c 确定,它的根的情况(是否有实数根)由24b ac ∆=-确定.判别式:设一元二次方程为20(0)ax bx c a ++=≠,其根的判别式为:24b ac ∆=-则①0∆>⇔方程20(0)ax bx c a ++=≠有两个不相等的实数根1,2x =.②0∆=⇔方程20(0)ax bx c a ++=≠有两个相等的实数根122bx x a==-.③0∆<⇔方程20(0)ax bx c a ++=≠没有实数根.若a ,b ,c 为有理数,且∆为完全平方式,则方程的解为有理根;若∆为完全平方式,同时b -2a 的整数倍,则方程的根为整数根.说明: (1)用判别式去判定方程的根时,要先求出判别式的值:上述判定方法也可以反过来使用,当方程有两个不相等的实数根时,0∆>;有两个相等的实数根时,0∆=;没有实数根时,0∆<.(2)在解一元二次方程时,一般情况下,首先要运用根的判别式24b ac ∆=-判定方程的根的情况(有两个不相等的实数根,有两个相等的实数根,无实数根).当240b ac ∆=-=时,方程有两个相等的实数根(二重根),不能说方程只有一个根. ① 当0a >时⇔抛物线开口向上⇔顶点为其最低点; ② 当0a <时⇔抛物线开口向下⇔顶点为其最高点.3.一元二次方程的根的判别式的应用:一元二次方程的根的判别式在以下方面有着广泛的应用: (1)运用判别式,判定方程实数根的个数;(2)利用判别式建立等式、不等式,求方程中参数值或取值范围; (3)通过判别式,证明与方程相关的代数问题;(4)借助判别式,运用一元二次方程必定有解的代数模型,解几何存在性问题,最值问题.二、韦达定理如果一元二次方程20ax bx c ++=(0a ≠)的两根为12x x ,,那么,就有 ()()212ax bx c a x x x x ++=--比较等式两边对应项的系数,得1212b x x ac x x a ⎧+=-⎪⎪⎨⎪⋅=⋅⎪⎩①,② ①式与②式也可以运用求根公式得到.人们把公式①与②称之为韦达定理,即根与系数的关系.因此,给定一元二次方程20ax bx c ++=就一定有①与②式成立.反过来,如果有两数1x ,2x 满足①与②,那么这两数12x x ,必是一个一元二次方程20ax bx c ++=的根.利用这一基本知识常可以简捷地处理问题.利用根与系数的关系,我们可以不求方程20ax bx c ++=的根,而知其根的正、负性. 在24b ac ∆=-≥0的条件下,我们有如下结论:当0c a <时,方程的两根必一正一负.若0b a -≥,则此方程的正根不小于负根的绝对值;若0ba -<,则此方程的正根小于负根的绝对值. 当0c a >时,方程的两根同正或同负.若0b a ->,则此方程的两根均为正根;若0ba -<,则此方程的两根均为负根.⑴ 韦达定理:如果20(0)ax bx c a ++=≠的两根是1x ,2x ,则12bx x a+=-,12c x x a =.(隐含的条件:0∆≥)⑵ 若1x ,2x 是20(0)ax bx c a ++=≠的两根(其中12x x ≥),且m 为实数,当0∆≥时,一般地: ① 121()()0x m x m x m --<⇔>,2x m <② 12()()0x m x m -->且12()()0x m x m -+->1x m ⇔>,2x m > ③ 12()()0x m x m -->且12()()0x m x m -+-<1x m ⇔<,2x m <特殊地:当0m =时,上述就转化为20(0)ax bx c a ++=≠有两异根、两正根、两负根的条件. ⑶ 以两个数12,x x 为根的一元二次方程(二次项系数为1)是:21212()0x x x x x x -++=. ⑷ 其他:① 若有理系数一元二次方程有一根a +a a ,b 为有理数). ② 若0ac <,则方程20(0)ax bx c a ++=≠必有实数根. ③ 若0ac >,方程20(0)ax bx c a ++=≠不一定有实数根. ④ 若0a b c ++=,则20(0)ax bx c a ++=≠必有一根1x =.⑤ 若0a b c -+=,则20(0)ax bx c a ++=≠必有一根1x =-. ⑸ 韦达定理主要应用于以下几个方面:① 已知方程的一个根,求另一个根以及确定方程参数的值; ② 已知方程,求关于方程的两根的代数式的值; ③ 已知方程的两根,求作方程;④ 结合根的判别式,讨论根的符号特征;⑤ 逆用构造一元二次方程辅助解题:当已知等式具有相同的结构时,就可以把某两个变元看作某个一元二次方程的两根,以便利用韦达定理;⑤ 利用韦达定理求出一元二次方程中待定系数后,一定要验证方程的∆.一些考试中,往往利用这一点设置陷阱.例题一、判断方程根的情况【例1】 不解方程,判别下列方程的根的情况:(1)22340x x +-=;(2)216924y y +=;(3)()25170x x +-=。
【例2】 不解方程,判别方程220x k ++=的根的情况。
【例3】 解关于x 的方程()21230m x mx m -+++=【例4】 已知关于x 的方程2(1)10n x mx -++=①有两个相等的实数根.求证:关于y 的一元二次方程222440m y my m n --+=②必有两个相等的实数根.【巩固】已知0a >,b a c >+,判断关于x 的方程20ax bx c ++=的根的情况,并给出必要的说明.【巩固】(1998年山东省竞赛)设a 、b 、c 为互不相等的非零实数,求证:三个方程220ax bx c ++=, 220bx cx a ++=, 220cx ax b ++=,不可能都有2个相等的实数根.二、应用题【例5】 (2006·湛江市)近年来,我市开展以“四通五改六进村”为载体,以生态文明为主要特色的新农村建设活动取得了明显成效.下面是市委领导和市民的一段对话,请你根据对话内容,替市领导回答市民提出的问题(结果精确到0.1%).领导市民 全市一共有13233个自然村,2005年已建成生态文明村2315个,计划到2007年全市生态文明村数要达到自然村总数的24.4%领导,按这个计划,从2005年到2007年,平均每年生态文明村增长率约是多少?【巩固】(2006·新疆)2004年,自治区党委、人民政府决定在乌鲁木齐、库尔勒等八个城市开办区内初中班,重点招收农牧民子女及其他家庭贫困的学生.某市2004年9月招收区内初中班学生50名,并计划在2006年9月招生结束后,使区内初中班三年招生总人数.......达到450名.若该市区内初中班招生人数平均每年比上年的增长率相同,求这个增长率.【例6】(2006·重庆市)机械加工需要拥有进行润滑以减少摩擦,某企业加工一台大型机械设备润滑用油90千克,用油的重复利用率为60%,按此计算,加工一台大型机械设备的实际耗油量为36千克.为了建设节约型社会,减少油耗,该企业的甲、乙两个车间都组织了人员为减少实际耗油量进行攻关.(1)甲车间通过技术革新后,加工一台大型机械设备润滑用油量下降到70千克,用油的重复利用率仍然为60%.问甲车间技术革新后,加工一台大型机械设备的实际耗油量是多少千克?(2)乙车间通过技术革新后,不仅降低了润滑用油量,同时也提高了用油的重复利用率,并且发现在技术革新的基础上,润滑用油量每减少1千克,用油量的重复利用率将增加1.6%. 这样乙车间加工一台大型机械设备的实际耗油量下降到12千克. 问乙车间技术革新后,加工一台大型机械设备润滑用油量是多少千克?用油的重复利用率是多少?【例7】(2006·南安)某商场将每件进价为80元的某种商品原来按每件100元出售,一天可售出100件.后来经过市场调查,发现这种商品单价每降低1元,其销量可增加10件.(1)求商场经营该商品原来一天可获利润多少元?(2)设后来该商品每件降价x元,,商场一天可获利润y元.①若商场经营该商品一天要获利润2160元,则每件商品应降价多少元?②求出y与x之间的函数关系式,并通过画该函数图像的草图,观察其图像的变化趋势,结合题意写出当x取何值时,商场获利润不少于2160元?【例8】(2006·诸暨市)有一根竹竿, 不知道它有多长. 把竹竿横放在一扇门前, 竹竿长比门宽多4尺; 把竹竿竖放在这扇门前, 竹竿长比门的高度多2尺; 把竹竿斜放, 竹竿长正好和门的对角线等长. 问竹竿长几尺?【例9】(2006·广东省)将一条长为20cm的铁丝剪成两段,并以每一段铁丝的长度为周长做成一个正方形.(1)要使这两个正方形的面积之和等于17cm2,那么这段铁丝剪成两段后的长度分别是多少?三、韦达定理【例10】 (2006·广安市)已知:ABC ∆的两边AB 、AC 的长是关于x 的一元二次方程()2223320x k x k k ++++=-的两个实数根, 第三边BC 的长为5. 试问:k 取何值时,ABC ∆是以BC 为斜边的直角三角形?【例11】 已知关于x 的一元二次方程()2120x m x m --++=.(1)若方程有两个相等的实数根,求m 的值;(2)若方程的两实数根之积等于292m m -+【巩固】 已知关于x 的方程222(1)30x m x m -++-=(1)当m 取何值时,方程有两个不相等的实数根?(2)设1x 、2x 是方程的两根,且21212()()120x x x x +-+-=,求m 的值。
【例12】 (2006·济南市)已知关于x 的方程2210kx x +-=有两个不相等的实数根2x x 1,,且满足212()1x x +=,求k 的值.【例13】 已知1x 、2x 是关于x 的一元二次方程2244(1)0x m x m +-+=的两个非零实数根,问:1x 与2x 能否同号?若能同号请求出相应的m 的取值范围;若不能同号,请说明理由。