支护结构设计计算理论与方法

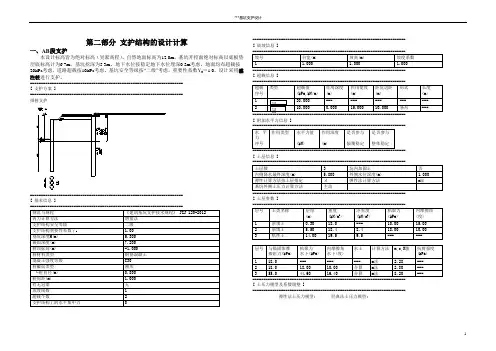
第二部分支护结构的设计计算一、AB段支护本设计标高皆为绝对标高（吴淞高程）。

自然地面标高为12.0m，基坑开挖面绝对标高以底板垫层底标高计为6.7m，基坑挖深为5.3m。

地下水位按稳定地下水位埋深0.5m考虑。

地面均布超载按20kPa考虑，道路超载按10kPa考虑。

基坑安全等级按“二级”考虑，重要性系数Υ0＝1.0。

设计采用灌注桩进行支护。

----------------------------------------------------------------------[ 支护方案 ]----------------------------------------------------------------------排桩支护----------------------------------------------------------------------[ 基本信息 ]----------------------------------------------------------------------规范与规程《建筑基坑支护技术规程》 JGJ 120-2012内力计算方法增量法支护结构安全等级二级支护结构重要性系数γ0 1.00基坑深度H(m) 5.300嵌固深度(m)7.200桩顶标高(m)-1.000桩材料类型钢筋混凝土混凝土强度等级C30桩截面类型圆形└桩直径(m)0.800桩间距(m) 1.000有无冠梁无放坡级数1超载个数2支护结构上的水平集中力0----------------------------------------------------------------------[ 放坡信息 ]----------------------------------------------------------------------坡号台宽(m)坡高(m)坡度系数1 1.000 1.000 1.000----------------------------------------------------------------------[ 超载信息 ]----------------------------------------------------------------------超载类型超载值作用深度作用宽度距坑边距形式长度序号(kPa,kN/m)(m)(m)(m)(m)130.000---------------210.0000.00015.00010.000条形---[ 附加水平力信息 ]水平力作用类型水平力值作用深度是否参与是否参与序号(kN)(m)倾覆稳定整体稳定[ 土层信息 ]土层数3坑内加固土否内侧降水最终深度(m) 5.800外侧水位深度(m) 1.000弹性计算方法按土层指定ㄨ弹性法计算方法m法基坑外侧土压力计算方法主动[ 土层参数 ]层号土类名称层厚重度浮重度粘聚力内摩擦角(m)(kN/m3)(kN/m3)(kPa)(度)1杂填土0.3018.0---10.0015.002杂填土 5.5018.48.418.0010.003粘性土14.0019.59.5------层号与锚固体摩粘聚力内摩擦角水土计算方法m,c,K值抗剪强度擦阻力(kPa)水下(kPa)水下(度)(kPa) 118.0---------m法 2.28---218.018.0010.00合算m法 2.80---355.044.6016.40合算m法8.20---[ 土压力模型及系数调整 ]----------------------------------------------------------------------弹性法土压力模型: 经典法土压力模型:层号土类水土水压力外侧土压力外侧土压力内侧土压力内侧土压力名称调整系数调整系数1调整系数2调整系数最大值(kPa) 1杂填土分算 1.000 1.000 1.000 1.00010000.000 2杂填土合算 1.000 1.000 1.000 1.00010000.000 3粘性土合算 1.000 1.000 1.000 1.00010000.000 [ 工况信息 ]工况工况深度支锚号类型(m)道号1开挖 5.300---[ 设计结果 ]---------------------------------------------------------------------- ---------------------------------------------------------------------- [ 结构计算 ]---------------------------------------------------------------------- 各工况：内力位移包络图：地表沉降图：----------------------------------------------------------------------[ 截面计算 ]----------------------------------------------------------------------钢筋类型对应关系：d-HPB300,D-HRB335,E-HRB400,F-RRB400,G-HRB500,P-HRBF335,Q-HRBF400,R-HRBF500桩是否均匀配筋是混凝土保护层厚度(mm)50桩的纵筋级别HRB400桩的螺旋箍筋级别HPB300桩的螺旋箍筋间距(mm)200弯矩折减系数 1.00剪力折减系数 1.00荷载分项系数 1.25配筋分段数一段各分段长度(m)11.50[ 内力取值 ]段内力类型弹性法经典法内力内力号计算值计算值设计值实用值基坑内侧最大弯矩(kN.m)0.000.000.000.001基坑外侧最大弯矩(kN.m)387.96290.22484.96484.96最大剪力(kN)149.28130.39186.60186.60段选筋类型级别钢筋实配[计算]面积号实配值(mm2或mm2/m)1纵筋HRB40012E224562[4307]箍筋HPB300d8@200503[895]加强箍筋HRB335D16@2000201----------------------------------------------------------------------[ 整体稳定验算 ]----------------------------------------------------------------------计算方法：瑞典条分法应力状态：有效应力法条分法中的土条宽度: 1.00m滑裂面数据整体稳定安全系数 K s = 2.852圆弧半径(m) R = 16.258圆心坐标X(m) X = -0.022圆心坐标Y(m) Y = 9.037----------------------------------------------------------------------[ 抗倾覆稳定性验算 ] ----------------------------------------------------------------------抗倾覆安全系数:M p——被动土压力及支点力对桩底的抗倾覆弯矩, 对于内支撑支点力由内支撑抗压力决定;对于锚杆或锚索，支点力为锚杆或锚索的锚固力和抗拉力的较小值。

深基坑支护结构的设计计算深基坑支护结构设计计算是指在进行深基坑施工时，为了保证基坑的稳定和安全，需要设计合理的支护结构来抵抗土压力和地下水力，并进行相应的计算与分析。

下面将从设计原则、支护结构类型、计算方法和实例分析等方面进行详细介绍。

设计原则：1.充分了解地质环境：通过钻孔、地质勘探等手段对周边地质环境进行充分了解，确定基坑边坡的稳定性和地下水情况等。

2.综合考虑安全和经济性：在满足基坑稳定要求的前提下，尽量优化支护结构的形式和尺寸，使其既能保证施工安全，又能降低成本。

3.遵循现场施工管理规范：根据施工组织方案和现场管理要求，进行支护结构设计，确保施工操作的可行性和安全性。

支护结构类型：常见的深基坑支护结构主要有以下几种类型：1.土方支撑法：包括开挖后土侧临时支护、钢支撑、混凝土支撑、钻孔锚杆支护等。

2.桩承台围护法：采用桩承台、连续墙等结构形式围护基坑。

3.地下连续墙法：采用成排的连续墙围护基坑，形成闭合空间。

4.排浆松土法：通过水平和垂直排浆井人工排除地下水，减小土体侧压力。

5.钢结构支护法：采用钢桩和钢板桩等结构形式围护基坑。

计算方法：1.土体侧压力计算：根据基坑周边土体的物理力学参数和基坑的几何形状，采用经验公式或数值模拟方法计算土体的侧压力。

2.支护结构稳定性计算：根据支护结构的形式和受力状况，进行结构的静力分析和稳定性校核，计算结构内力和变形等。

3.变形计算：根据支护结构的刚度和土体的变形特性，利用有限元分析方法或基于弹性平衡原理的计算方法，对基坑的变形进行计算。

实例分析：以一些深基坑工程为例，具体讲解支护结构设计计算的流程和方法。

1.地质环境调查：通过钻孔和地质勘探，了解地质层位、土壤性质、地下水位等信息。

2.施工组织方案：根据地质环境和工程要求，制定合理的施工组织方案，确定基坑开挖的顺序和方法。

3.土体侧压力计算：根据开挖的深度和基坑周围土体的物理力学参数，计算土体的侧压力，并确定开挖时的土压力分布。

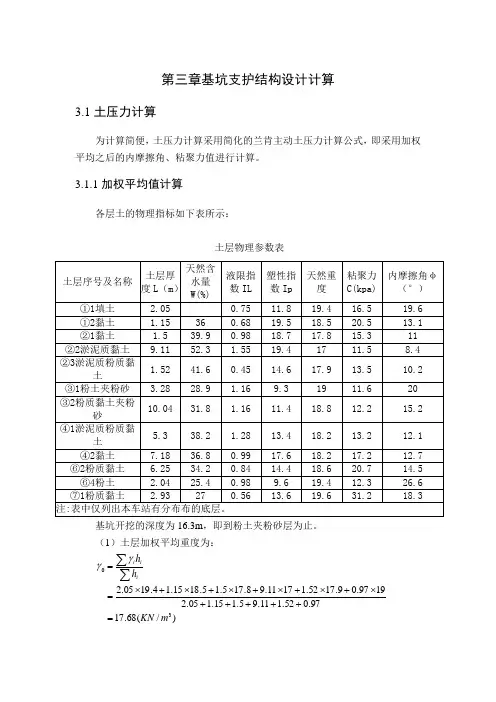
第三章基坑支护结构设计计算3.1土压力计算为计算简便，土压力计算采用简化的兰肯主动土压力计算公式，即采用加权平均之后的内摩擦角、粘聚力值进行计算。

3.1.1加权平均值计算各层土的物理指标如下表所示：基坑开挖的深度为16.3m ，即到粉土夹粉砂层为止。

（1）土层加权平均重度为：)/(68.1797.052.111.95.115.105.21997.09.1752.11711.98.175.15.1815.14.1905.230m KN hh iii =+++++⨯+⨯+⨯+⨯+⨯+⨯==∑∑γγ土层物理参数表土层序号及名称 土层厚度L （m ） 天然含水量W(%)液限指数IL 塑性指数Ip 天然重度粘聚力C(kpa) 内摩擦角φ（°） ①1填土 2.05 0.75 11.8 19.4 16.5 19.6 ①2黏土 1.15 36 0.68 19.5 18.5 20.5 13.1 ②1黏土 1.5 39.9 0.98 18.7 17.8 15.3 11 ②2淤泥质黏土 9.11 52.3 1.55 19.4 17 11.5 8.4 ②3淤泥质粉质黏土1.52 41.6 0.45 14.6 17.913.5 10.2 ③1粉土夹粉砂 3.28 28.9 1.16 9.3 19 11.6 20 ③2粉质黏土夹粉砂10.04 31.8 1.16 11.4 18.812.2 15.2 ④1淤泥质粉质黏土 5.3 38.2 1.28 13.4 18.213.2 12.1 ④2黏土 7.18 36.8 0.99 17.6 18.2 17.2 12.7 ⑥2粉质黏土 6.25 34.2 0.84 14.4 18.6 20.7 14.5 ⑥4粉土 2.04 25.4 0.98 9.6 19.4 12.3 26.6 ⑦1粉质黏土 2.93 27 0.56 13.6 19.6 31.218.3注:表中仅列出本车站有分布布的底层。

深基坑支护结构理论计算方法摘要：本文介绍了常用的深基坑支护结构理论计算方法，将认可度比较高的计算方法进行了归纳，可为相关理论分析提供参考。

关键词：深基坑；基坑支护；理论分析0引言在深基坑支护结构理论计算方法的研究上，目前比较成熟且认可度较高的主要有以下三大类：经典方法、弹性地基梁法、有限元法[1]。

1经典方法经典方法主要有静力平衡法、等值梁法、Terzgahi法、弹性曲线法、等弯矩法及等轴力法[1][2]。

经典方法是基于力的平衡这一基础建立的理论方法。

这种方法主要是选用单位宽度受侧向荷载的梁系作为研究对象，如经典的等值梁法和1/2切割方法等，采用的土压力理论中，既有经典的朗肯土压力理论，也有Terzgahi-Peck表观土压力理论[3]。

该方法将围护结构看作是一条插入土体的竖向梁，假设支撑点固定不动，围护结构即成为一个受土压力的作用的多支承点的梁。

这种方法计算简便，适合手算，可近似的得出围护结构的内力，但计算结果误差较大，且无法同时求出围护结构的位移，无法根据施工情况的变化，求得围护结构确切的内力值。

而在计算机的大范围普及和有限元方法的不断推广情形下，该方法的应用也越来越少。

总之，由于经典方法无法分析不同施工工况下的内力情况，且未考虑土体与围护结构的变形因素，导致该方法逐渐散失了其原有地位。

2弹性地基梁法2.1 弹性地基梁法弹性地基梁法是基于经典法发展起来的一种改进型计算方法，该方法是在经典法的基础上，将土的作用等效成一系列弹簧的弹力作用，同时将支撑与锚杆也用弹簧进行替代，这样可以把整个支护结构看成是一弹性支撑的地基梁。

而计算弹簧刚度的方法有m法、E法、C法等，土压力理论一般采用经典的土压力理论，如库伦土压力理论及朗肯土压力理论。

弹性地基梁的解法主要有结构力学方法、解析法和有限元数值法等。

为方便计算，弹性地基梁法对支撑受力和桩入土段的受力进行了简化：在下一道支撑完成后，假设上一道支撑受力不变；对于入土段的受力情况作了两点假设，一是在土压力达到极限被动土压力时，可通过力的平衡进行求解，二是假定入土段的受力和变形有关[4]。

基坑支护结构的设计原理与计算方法支护结构是指用来稳定和支护地表结构的工程结构。

基坑支护结构是地面施工周围环境和基坑结构构造的工程结构，它具有贯穿基坑深度的结构材料，承受自重、结构荷载和地面施工所产生的力，以确保基坑支护结构的牢固性和稳定性，以保护基坑周围的地表结构。

一、基坑支护结构的设计原理
1、安全稳定性：基坑支护结构的设计首先应考虑安全稳定性，确保基坑结构的牢固性和稳定性，以保护基坑周围的地表结构。

2、结构安全性：基坑支护结构受到重力荷载、地震荷载和其他外力的双重影响，应当考虑结构的稳定性和完整性，确保基坑支护结构的安全性。

3、经济性：基坑支护结构的设计应尽可能考虑成本效益，建议采用适当的结构材料，以尽量减少支护结构的建造成本。

二、基坑支护结构的计算方法
1、支护结构强度计算：应根据基坑支护结构的荷载和结构特性，计算支护结构的强度，确定支护结构的设计原则，以确保支护结构的安全性和可靠性。

2、支护结构位移计算：在设计支护结构时。

基坑支护的结构的计算基坑支护是指在建筑工地或者其他开挖工程中，为了防止土方塌方和保证施工安全而采取的一系列措施。

基坑支护结构的计算是基坑工程设计中重要的一部分，本文将对基坑支护结构的计算进行详细介绍。

一、基坑支护结构的分类基坑支护结构通常可以分为两类：一是按照支护方式的不同分为主动支护和被动支护；二是按照结构形式的不同分为钢支撑结构和混凝土支护结构。

主动支护是指通过设置支撑结构对基坑进行支护，常见的主动支护结构有钢支撑和桩墙支护。

被动支护是指利用土体自身力学性质对基坑进行支撑，常见的被动支护结构有土钉墙和锚杆墙。

钢支撑结构是以钢材为主要材料的支护结构，常见的有钢板桩和钢管桩。

混凝土支护结构则是以混凝土为主要材料的支护结构，常见的有混凝土梁和混凝土墙。

二、基坑支护结构的计算方法基坑支护结构的计算方法主要包括以下几个方面：1.基坑支护结构受力分析：支护结构需要承受土压力、地下水压力和附加荷载等多种作用力，计算时需要对支护结构的受力情况进行全面的分析。

2.支撑杆件的稳定性计算：钢支撑结构中的支撑杆件需要满足一定的稳定性要求，包括弯曲强度、屈曲稳定性和抗扭稳定性等方面的计算。

3.连墙件的选择与计算：在钢支撑结构中，如果需要两个或多个支撑壁之间进行连接，则需要使用连墙件。

连墙件的选择和计算需要考虑其承受的弯曲强度和抗剪强度等。

4.土壁和桩身的稳定性计算：在钢板桩和钢管桩的设计中，需要对土壁和桩身的稳定性进行计算，包括土壁的滑移和失稳以及桩身的稳定性等。

5.锚杆的计算：在锚杆墙的设计中，需要对锚杆的承载力和稳定性进行计算。

三、基坑支护结构计算的基本步骤基坑支护结构的计算一般包括以下几个基本步骤：1.确定基坑的尺寸和形状，确定基坑周围的土质和地下水情况。

2.根据基坑的具体情况，选择适当的支护方案和支撑结构类型。

3.进行基坑支护结构的初步设计，包括确定支护结构的布置形式、支距和锚固长度等参数。

4.对支撑结构进行受力分析，计算支护结构受到的土压力、地下水压力和附加荷载等。

悬臂支点式支护结构计算方法悬臂支点式支护结构是一种常用的土木工程结构，用于在施工过程中保护和支撑土方或挖方的边坡。

本文将介绍悬臂支点式支护结构的计算方法。

一、悬臂支点式支护结构的概述悬臂支点式支护结构是一种常用的土木工程结构，用于在土方开挖或填方过程中保护和支撑边坡。

其基本原理是通过设置支护桩和锚杆来固定边坡，以防止其坍塌或滑动。

二、悬臂支点式支护结构的设计步骤1. 确定边坡的几何形状和土质参数。

这包括边坡的坡度、高度、土质类型、内摩擦角等。

根据这些参数，可以计算出边坡的稳定性分析结果。

2. 选择合适的支护桩。

支护桩的选择应根据边坡的高度、土质的强度和稳定性要求来确定。

常见的支护桩类型包括钢筋混凝土桩、钢管桩等。

3. 设计锚杆。

锚杆用于固定支护桩和边坡，以增加整体的稳定性。

锚杆的数量和布置应根据边坡的高度和土质的强度来确定。

4. 进行结构计算。

根据支护桩和锚杆的尺寸和布置，进行结构计算，包括强度和稳定性的验算。

计算结果应满足相关规范和设计要求。

5. 编制施工图纸。

根据计算结果，编制悬臂支点式支护结构的施工图纸，包括支护桩和锚杆的布置图、尺寸图等。

三、悬臂支点式支护结构的计算方法1. 支护桩的计算。

支护桩的计算主要包括受力分析和强度验算。

受力分析时，需要考虑桩身的自重、土压力、水压力、地震力等。

根据这些受力情况，可以计算出桩身的弯矩、剪力和轴力。

强度验算时，需要根据钢筋混凝土的强度和断面形状，计算出桩身的抗弯强度和抗剪强度。

2. 锚杆的计算。

锚杆的计算主要包括受力分析和抗拉强度验算。

受力分析时，需要考虑锚杆的自重、土压力、水压力等。

根据这些受力情况，可以计算出锚杆的拉力和应力分布。

抗拉强度验算时，需要根据锚杆的材料强度和断面形状，计算出锚杆的抗拉强度。

3. 边坡的稳定性分析。

对于悬臂支点式支护结构，边坡的稳定性分析是非常重要的。

稳定性分析时，需要考虑边坡的自重、土压力、水压力、地震力等。

根据这些受力情况，可以计算出边坡的倾覆稳定性和滑动稳定性。

第二部分基坑支护结构的计算支护结构的设计和施工，影响因素众多，不少高层建筑的支护结构费用已超过工程桩基的费用。

为此，对待支护结构的设计和施工均应采取极慎重的态度，在保证施工安全的前提下，尽量做到经济合理和便于施工。

一、支护结构承受的荷载支护结构承受的荷载一般包括–土压力–水压力–墙后地面荷载引起的附加荷载。

1 土压力⑴主动土压力：若挡墙在墙后土压力作用下向前位移时随位移增大，墙后土压力渐减小。

当位移达某一数值时，土体内出现滑裂面，墙后土达极限平衡状态，此时土压力称为主动土压力，以Ea表示。

⑵静止土压力：若挡墙在土压力作用下墙本身不发生变形和任何位移（移动或滑动），墙后填土处于弹性平衡状态，则此时作用在挡墙上的土压力成为静止土压力。

以E0表示。

(3)被动土压力：若挡墙在外力作用下墙向墙背向移动，随位移增大，墙所受土的反作用力渐增大，当位移达一定数值时，土体内出现滑裂面，墙后土处被动极限平衡状态，此时土压力称为被动土压力，以Ep表示。

主动土压力计算•主动土压力强度•无粘性土粘性土土压力分布对于粘性土按计算公式计算时，主动土压力在土层顶部（H=0处）为负值，即表明出现拉力区，这在实际上是不可能发生的。

只计算临界高度以下的主动土压力。

土压力分布可计算此种情况下的临界高度Zc，进而计算临界高度以下的主动土压力。

被动土压力计算被动土压力强度•无粘性土粘性土计算土压力时应注意•不同深度处土的内聚力C不是一个常数，它与土的上覆荷重有关，一般随深度的加大而增大，对于暴露时间长的基坑，土的内聚力可由于土体含水量的变化和氧化等因素的影响而减小甚至消失。

•、C 值是计算侧向土压力的主要参数，但在工程桩打设前后的、C值是不同的。

在粘性土中打设工程桩时，产生挤土现象，孔隙水压力急剧升高，对、C值产生影响。

另外，降低地下水位也会使、C值产生变化。

水压力作用于支护结构上的水压力一般按静水压力考虑。

有稳态渗流时按三角形分布计算。

第四章现代⽀护结构设计原理与⽅法第四章现代⽀护结构设计原理与⽅法4.1、现代⽀护结构原理与结构类型1、现代⽀护结构原理①现代⽀护结构原理是建⽴在围岩与⽀护共同作⽤的基础上，即把围岩与⽀护看成是由2种材料组成的复合体，且把围岩通过岩体⽀承环作⽤成为结构体系的重要部分。

②充分发挥围岩⾃承能⼒是现代⽀护结构原理的⼀个基本观点，并由此降低围岩压⼒以改善⽀护的受⼒性能。

③现代⽀护结构原理的另⼀个⽀护原则是尽量发挥⽀护材料本⾝的承载⼒。

④根据地下⼯程的特点和当前技术⽔平。

现代⽀护结构原理主张凭借现场监控测试⼿段指导设计和施⼯。

⑤现代⽀护原理结构要求按岩体的不同地质和⼒学特征选⽤不同的⽀护⽅式、⼒学模型、相应的计算⽅法以及不同的施⼯⽅法。

2、理想⽀护结构的基本要求①必须能与周围岩体⼤⾯积地牢固接触，即保证⽀护⼀围岩体系作为⼀个统⼀的整体⼯作。

②要允许⽀护⼀围岩体系产⽣有限制的变形，以允分发挥围岩的承载能⼒，从⽽减少⽀护结构的作⽤，协调地发挥两者的共同作⽤。

③重视早期⽀护的作⽤，并使早期⽀护与后期⽀护相互配合，协调⼀致地⼯作，主动控制围岩的变形。

④必须保证⽀护结构架设及时。

⑤作为⽀护结构要根据围岩的动态(位移、应⼒等)，及时进⾏调整和修改，以适应不断变化的围岩状态。

3、⽀护结构类型按⽀护作⽤机理，⽬前采⽤的⽀护⼤致可以归纳为以下3类：(1)刚性⽀护结构这类⽀护结构通常具有⾜够⼤的刚性和断⾯尺⼨，⼀般⽤来承受强⼤的松动地压。

从构造上看，它有贴壁式结构和离壁式结构2种。

贴壁式结构使⽤泵送混凝⼟，可以和围岩保持紧密接触，但其防⽔和防潮的效果较差；离壁式结构围岩没有直接接触的保护和承载结构，⼀般容易出现事故。

(2)柔性⽀护结构既能及时地进⾏⽀护，限制围岩过⼤变形⾯出现松动，⼜允许围岩出现⼀定的变形，同时还能根据围岩的变化情况及时调整参数。

所以，它是适应现代⽀护原理的⽀护形式。

锚喷⽀护是⼀种主要的柔性⽀护类型。

锚喷⽀护主要有：a、锚杆⽀护;b、喷射混凝⼟⽀护;c、锚杆喷射混凝⼟⽀护;d、钢筋⽹喷射混凝⼟⽀护;e、锚杆钢⽀撑喷射混凝⼟⽀护;f、锚杆钢筋⽹喷射混凝⼟⽀护。

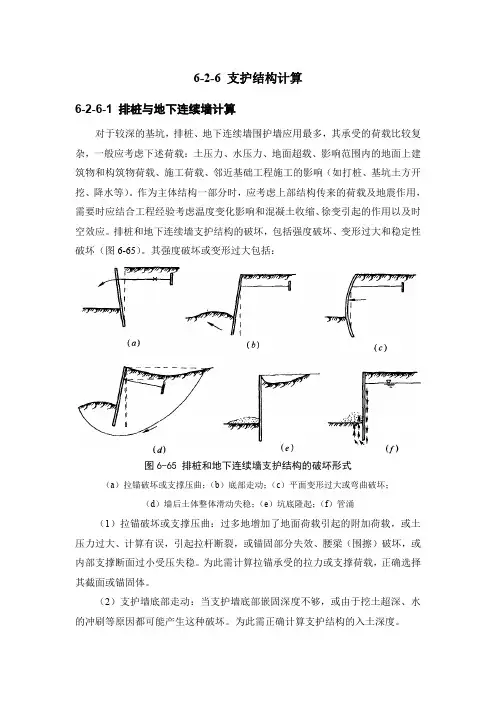
6-2-6 支护结构计算6-2-6-1 排桩与地下连续墙计算对于较深的基坑，排桩、地下连续墙围护墙应用最多，其承受的荷载比较复杂，一般应考虑下述荷载：土压力、水压力、地面超载、影响范围内的地面上建筑物和构筑物荷载、施工荷载、邻近基础工程施工的影响（如打桩、基坑土方开挖、降水等）。

作为主体结构一部分时，应考虑上部结构传来的荷载及地震作用，需要时应结合工程经验考虑温度变化影响和混凝土收缩、徐变引起的作用以及时空效应。

排桩和地下连续墙支护结构的破坏，包括强度破坏、变形过大和稳定性破坏（图6-65）。

其强度破坏或变形过大包括：图6-65 排桩和地下连续墙支护结构的破坏形式（a）拉锚破坏或支撑压曲；（b）底部走动；（c）平面变形过大或弯曲破坏；（d）墙后土体整体滑动失稳；（e）坑底隆起；（f）管涌（1）拉锚破坏或支撑压曲：过多地增加了地面荷载引起的附加荷载，或土压力过大、计算有误，引起拉杆断裂，或锚固部分失效、腰梁（围擦）破坏，或内部支撑断面过小受压失稳。

为此需计算拉锚承受的拉力或支撑荷载，正确选择其截面或锚固体。

（2）支护墙底部走动：当支护墙底部嵌固深度不够，或由于挖土超深、水的冲刷等原因都可能产生这种破坏。

为此需正确计算支护结构的入土深度。

（3）支护墙的平面变形过大或弯曲破坏：支护墙的截面过小、对土压力估算不准确、墙后增加大量地面荷载或挖土超深等都可能引起这种破坏。

平面变形过大会引起墙后地面过大的沉降，亦会给周围附近的建（构）筑物、道路、管线等造成损害。

排桩和地下连续墙支护结构的稳定性破坏包括：（1）墙后土体整体滑动失稳：如拉锚的长度不够，软粘土发生圆弧滑动，会引起支护结构的整体失稳。

（2）坑底隆起：在软粘土地区，如挖土深度大，嵌固深度不够，可能由于挖土处卸载过多，在墙后土重及地面荷载作用下引起坑底隆起。

对挖土深度大的深坑需进行这方面的验算，必要时需对坑底土进行加固处理或增大挡墙的入土深度。

（3）管涌：在砂性土地区，当地下水位较高、坑深很大和挡墙嵌固深度不够时，挖土后在水头差产生的动水压力作用下，地下水会绕过支护墙连同砂土一同涌入基坑。

明沟污水截流工程顶管工作井施工方案工作坑开挖顶管坑支护设计及计算1．顶管坑支护设计顶管坑结构尺寸（长X宽二LXB）：主干线①1500）顶管坑8mX 5m。

施工中顶管坑结构尺寸根居检查井的类型调节开坑尺寸来满足顶进需要, 开挖前，根据顶坑的管内底标高，考虑导轨高度、顶管坑底板厚度等计算出顶管坑实际槽底标高（H）。

顶管坑采用C25钢筋砼厚度30cm.在工作井、接收井分别设置4口大口径降水井进行降水,深度15m,降水时间30天,保证施工时工作面无水。

根顶管坑上部设锁口圈梁，圈梁宽800mm,高500mm，圈梁采用16e20为主筋，①8©200 箍筋，混凝土强度等级C25。

为了顶管工作坑下部钢架能与锁口圈梁连接，锁口圈梁向下预留钢筋接头，方法是在槽底向下打孔，插入800mm长①20钢筋，间距1000mm。

预留钢筋锚入锁口长度不小于400mm。

坑壁采用格栅挂钢筋网片倒挂逆作法，分层开挖，分层锚喷混凝土进行支护，结构厚度为250mm，格栅每750mm设一道，并在坑底设一道格栅。

竖向用①20钢筋连接（采用搭接焊），间距为1m。

钢格栅主筋采用①20、每断面4根，每根钢格栅纵筋与横筋之间采用波浪型连接。

沿钢格栅内侧主筋外缘满铺e6@100钢筋网片，并与主筋焊接成一体。

竖井施工中应沿竖井壁设置“土钉” 长1.5 m的e20锚杆，呈梅花状布置，间隔1.5 m,并在喷射混凝土前与网片及钢格栅焊接牢固，以满足结构整体受力的要求,注意各网片相互搭接坑底要设一道钢格栅,本工程喷射混凝土设计强度等级为C20,中粗砂、豆石（粒径在0.5〜 1.0cm）配比为水泥（PO32.5）:砂子:豆石=1:2:2,速凝剂掺量为水泥重量的5%,水泥、砂子豆石和速凝剂采用人工搅拌，混合料要随拌随用，不掺速凝剂的干料其存放时间不应超过45分钟，喷射作业应分层,分片分段依次进行,喷射顺序应自上向下,沿水平方向螺旋式移动，回旋直径应为300mm左右，一圈压半圈，一次喷射厚度不得大于100mm, 分三层喷满，每次喷1m，不得在一处堆积，要求喷射密实不得露筋，锚喷厚度不得小于250mm厚。

308 基础工程原理与方法第二十六章基坑支护结构的设计原理与计算方法第一节支护结构的破坏形式深基坑支护结构可分为非重力式支护结构（即柔性支护结构）和重力式支护结构（即刚性支护结构）。

非重力式支护结构包括钢板桩、钢筋混凝土板桩和钻孔灌注桩、地下连续墙等;重力式支护结构包括深层搅拌水泥土挡墙和旋喷帷幕墙等。

一、非重力式支护结构的破坏非塑力式支护结构的破坏包括强度破坏和稳定性破坏。

（一）强度破坏强度破坏包括图26所示内容。

（1）支护结构倾覆破坏。

破坏的原因是存在过大的地面荷载，或土压力过大引起拉杆断裂，或锚固部分失效,腰梁破坏等。

（2）支护结构底部向外移动。

当支护结构入土深度不够,或挖土超深、水的冲刷等都可能产生这种破坏。

（3）支护结构受弯破坏。

当选用的支护结构截面不恰当或对土压力估计不足时，容易出现这种破坏。

（二）稳定性破坏支护结构稳定性破坏包括图26-2所示内容。

（1）墙后土体整体滑动失稳。

破坏原因包括:①开挖深度很大，地基土又十分软弱；②地面大就堆载;③锚杆长度不足。

(∙M*≡β 坏第二十六章基坑支护结构的设计原理与计算方法309"r /Z τ√∕γ∕zτ√zr√ZrzzT(C)流砂或管涌图26・2非星力或支护结构的秘定性玻坏(2)坑底隆起。

当地基土软弱、挖土深度过大或地面存在超载时容易出现这种破坏。

(3)管涌或流砂。

当坑底土层为无黏性的细颗粒土，如粉土或粉细砂，且坑内外存在较大水位差时,易出现这种破坏。

二、重力式支护结构的破坏形式觅力式支护结构的破坏也包括强度破坏和稳定性破坏两个方面.强度破坏只有水泥土抗剪强度不足所产生的剪切破坏，为此需验算最大剪应力处的墙身应力。

稳定性破坏包括以下内容。

(1)倾覆破坏。

若水泥土挡墙截面、质量不够大，支护结构在土压力作用下产生整体倾覆失稳。

(2)滑移破坏。

当水泥土挡墙与土之间的抗滑力不足以抵抗墙后的推力时,会产生整体滑动破坏。

其他破坏形式，如土体整体滑动失稳、坑底隆起和管涌或流砂与非直力式支护结构相似。

浅谈支护结构内力与变形计算方法一、支护结构与巖土体的相互作用深基坑开挖及支护不仅涉及岩土力学中典型的变形、强度和稳定性问题，还涉及到支护结构与岩土体的相互作用问题。

支护结构与岩土体的相互作用是影响支护结构内力与变形的重要因素。

因此。

深层坑支护结构计算要考虑坑周边一定范围内岩土体与支护结构的协同作用。

深基坑工程是一门系统工程，支护结构类型多，目前主要有钻孔灌注桩、土钉墙、钢板桩和地下连接墙等。

不同支护结构体系与岩土体的相互作用机制不同。

1.土压力土压力问题是土与结构物相互作用的结果，是岩土工程的基本问题，也是岩土工程设计中首要确定的内容。

传统的支护结构设计理论仅考虑三种极限状态下的土压力，即主动、被动、静止土压力，这些古典土压力理论的完全弹性、平面滑裂面和墙背光滑等架设导致计算结果与实际情况相差甚远。

认识传统土压力理论的缺陷后，很多学者对土压力计算方法进行了改进：用极限分析方法研究古典Coulomb直线破坏机理问题;考虑土拱效应的土压力理论研究;考虑开挖卸荷影响的土压力和考虑墙面摩擦效应的土压力研究;考虑多种影响因素的土压力研究;从地基强度理论方面研究土压力系数;考虑水压力的土压力以及关于水土压力分算与合算问题研究;从概率角度研究岩土体参数对土压力的影响;被动土压力理论研究等等。

支护结构设计的静力平衡法、等值梁法和干系有限元数值模拟方法都是将土压力视为外力形式作用于支护结构。

2.接触力学分析方法支护结构与岩土体的接触面存在着非连续性，而在实际工程中往往简化为连续介质问题，这种简化处理必然带来计算误差。

目前接触行为的分析方法主要有两种：一是经典的接触力学分析方法，二是数值分析方法。

在接触问题研究的初始阶段，仅局限于接触面规则刚体之间的弹性接触，应用范围非常有限。

Hertz 于1881年提出经典的Hertz弹性接触理论。

在该理论的基础上，许多学者系统研究了不同受力条件和不同几何形状的接触问题。

Boussinesq给出了光滑刚体与均匀各向同性弹性半空间表面接触的应力解，还根据势能原理导出压凸回转体的轴线与弹性半空间变形前的边界正交时轴对称问题的解答。

深基坑支护结构的实用计算方法及其应用
一、深基坑支护结构的实用计算方法
1、土体抗压强度计算
为了保证深基坑支护结构的安全，首先必须计算出预设深基坑抗压强度，可以采用U型挖槽模型进行计算，根据给定的挖槽深度，计算出预设抗压强度，一般在挖槽深度大于3m时可采用该方法进行计算。

2、计算孔支护抗压强度
根据深基坑支护结构的构成，一般有多个孔支护围绕着挖槽，为了确保结构的安全，孔支护的抗压强度也必须计算，通常采用支护抗压强度计算函数进行计算，根据函数参数以及结构特性计算出孔支护的抗压强度，以确定具备足够的承载能力。

3、支护体系拱肋柱设计
拱肋柱是深基坑支护结构的支护元素，拱肋柱的设计必须考虑到节点处拱肋柱的结合以及与周围土体的复合效应。

通常采用有限元分析法和Bishop模型分析法，根据分析结果设计计算拱肋柱的形状及承载力。

4、支护体系网管设计
网管是深基坑支护结构的支护要素之一，为了计算出满足工程要求的支护强度，必须计算网管的力学特性，一般采用有限元分析法进行计算。

钢梁支护结构的荷载计算与强度分析概述：钢梁支护结构在现代建筑中扮演着重要角色。

为确保结构的稳定性和安全性，对其进行荷载计算和强度分析是必要的。

本文将介绍钢梁支护结构的荷载计算方法和强度分析原理，以期提供设计和施工过程中的参考。

第一部分：荷载计算1. 静荷载计算静荷载主要包括自重荷载和外部荷载。

自重荷载指钢梁本身的重量，可以通过钢材的密度和尺寸计算得到。

外部荷载包括建筑物的使用荷载、风荷载、雪荷载等，需要根据具体情况进行计算。

常用的计算方法包括等效静力法和有限元法。

2. 动荷载计算动荷载主要包括地震荷载和振动荷载。

地震荷载计算需要结合地震波的特性和建筑物的动力特性进行分析，一般采用谱分析法或时程分析法。

振动荷载是指机械设备、行人、车辆等引起的振动荷载，可以通过测量和模拟得到。

第二部分：强度分析1. 弯曲强度分析在钢梁支护结构中，弯曲是最常见的受力方式之一。

通过计算弯矩和弯矩图，可以得到钢梁的弯曲强度，并与承载能力进行对比。

一般采用弯矩图法、受弯公式法或有限元法进行分析。

2. 剪切强度分析剪切强度是指钢梁在横向受力作用下的抵抗能力。

通过计算剪力和剪力图，可以评估钢梁的剪切强度。

常用的分析方法包括剪力图法、剪切变形法和有限元法。

3. 拉伸和压缩强度分析拉伸和压缩强度分析用于评估钢梁在拉力或压力作用下的抗拉和抗压能力。

通过计算正应力和应力分布图，可以判断钢梁的安全性。

一般采用拉力-位移曲线法、有效宽度法或有限元法进行分析。

第三部分：结论钢梁支护结构的荷载计算和强度分析对于确保建筑物结构的稳定性和安全性至关重要。

通过静荷载计算和动荷载计算，可以得到钢梁所承受的荷载大小并确定结构的受力情况。

弯曲强度、剪切强度和拉伸、压缩强度分析可以评估钢梁的抗力和结构稳定性。

设计和施工过程中，工程师应根据具体情况选择适当的计算方法和分析手段，确保钢梁支护结构的安全可靠。

结尾：本文对钢梁支护结构的荷载计算和强度分析进行了简要介绍，并列举了常用的计算方法和分析手段。