隧道结构计算
- 格式:doc
- 大小:933.00 KB
- 文档页数:28

隧道结构力学计算
隧道结构力学计算是指对隧道结构进行力学分析和计算,以确定其受力状态和安全性。
隧道结构力学计算涉及以下几个方面的内容:
1. 隧道结构受力分析:通过分析隧道结构的受力情况,确定隧道在各个截面上的受力分布,包括截面内的轴力、弯矩、剪力等。
同时还需要考虑隧道的开挖和围岩的变形对结构的影响。
2. 结构稳定性计算:对隧道结构进行稳定性计算,包括抗滑稳定性、抗倾覆稳定性等。
通过确定结构的稳定性,可以评估结构的安全性。
3. 结构设计计算:根据受力分析和稳定性计算的结果,进行结构设计计算。
包括确定结构的截面尺寸、钢筋配筋等。
4. 结构材料力学性能计算:对结构材料的力学性能进行计算,包括混凝土的强度、钢筋的抗拉强度等。
在进行隧道结构力学计算时,需要应用力学原理和数学方法进行分析和计算。
通过合理的力学计算,可以评估隧道结构的安全性,并进行结构设计优化,确保隧道的运行安全。

第6章 隧道结构计算6.1 概 述6.1.1 引 言隧道结构工程特性、设计原则和方法与地面结构完全不同,隧道结构是由周边围岩和支护结构两者组成共同的并相互作用的结构体系。
各种围岩都是具有不同程度自稳能力的介质,即周边围岩在很大程度上是隧道结构承载的主体,其承载能力必须加以充分利用。
隧道衬砌的设计计算必须结合围岩自承能力进行,隧道衬砌除必须保证有足够的净空外,还要求有足够的强度,以保证在使用寿限内结构物有可靠的安全度。
显然,对不同型式的衬砌结构物应该用不同的方法进行强度计算。
隧道建筑虽然是一门古老的建筑结构,但其结构计算理论的形成却较晚。
从现有资料看,最初的计算理论形成于十九世纪。
其后随着建筑材料、施工技术、量测技术的发展,促进了计算理论的逐步前进。
最初的隧道衬砌使用砖石材料,其结构型式通常为拱形。
由于砖石以及砂浆材料的抗拉强度远低于抗压强度,采用的截面厚度常常很大,所以结构变形很小,可以忽略不计。
因为构件的刚度很大,故将其视为刚性体。
计算时按静力学原理确定其承载时压力线位置,检算结构强度。
在十九世纪末,混凝土已经是广泛使用的建筑材料,它具有整体性好,可以在现场根据需要进行模注等特点。
这时,隧道衬砌结构是作为超静定弹性拱计算的,但仅考虑作用在衬砌上的围岩压力,而未将围岩的弹性抗力计算在内,忽视了围岩对衬砌的约束作用。
由于把衬砌视为自由变形的弹性结构,因而,通过计算得到的衬砌结构厚度很大,过于安全。
大量的隧道工程实践表明,衬砌厚度可以减小,所以,后来上述两种计算方法已经不再使用了。
进入本世纪后,通过长期观测,发现围岩不仅对衬砌施加压力,同时还约束着衬砌的变形。
围岩对衬砌变形的约束,对改善衬砌结构的受力状态有利,不容忽视。
衬砌在受力过程中的变形,一部分结构有离开围岩形成“脱离区”的趋势,另一部分压紧围岩形成所谓“抗力区”,如图6-1所示。
在抗力区内,约束着衬砌变形的围岩,相应地产生被动抵抗力,即“弹性抗力”。

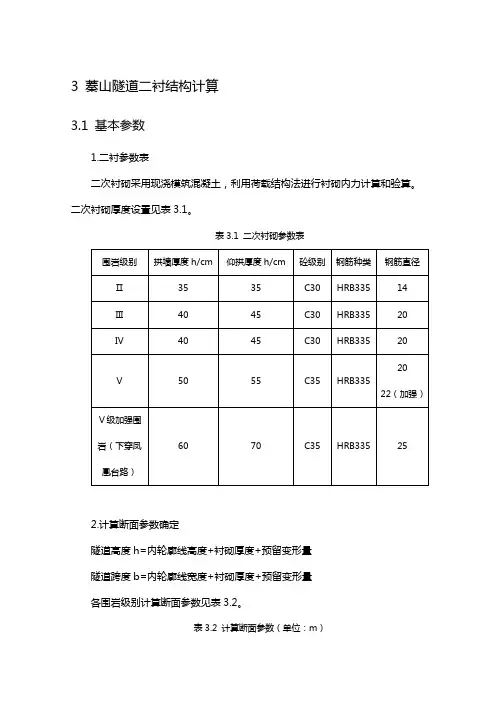
3 蓁山隧道二衬结构计算3.1 基本参数1.二衬参数表二次衬砌采用现浇模筑混凝土,利用荷载结构法进行衬砌内力计算和验算。
二次衬砌厚度设置见表3.1。
表3.1 二次衬砌参数表2.计算断面参数确定隧道高度h=内轮廓线高度+衬砌厚度+预留变形量隧道跨度b=内轮廓线宽度+衬砌厚度+预留变形量各围岩级别计算断面参数见表3.2。
表3.2 计算断面参数(单位:m)3.设计基本资料围岩容重:3/5.20m kN s =γ 二衬材料:C30、C35混凝土 弹性抗力系数:3/250000m kN K = 材料容重:3/25m kN h =γ 弹性模量:kPa E h 7103⨯=二衬厚度:35/40/45/50/55/60/65/70cm 铁路等级:客运专线 行车速度:200km/h隧道建筑限界:双线,按200km/h 及以上的客运专线要求设计 线间距:4.4m曲线半径:1800m ,4000m 牵引种类:电力列车类型:动车组列车运行控制方式:自动控制 运输调度方式:综合调度集中3.2 各级围岩的围岩压力计算按深埋隧道,《规范》公式垂直围岩压力 w q s 1245.0-⨯=γ)]5(1-+=B i w水平围岩压力有垂直围岩压力乘以水平围岩压力系数可得,水平围岩压力系数见表3.3。
各部位垂直围岩压力和水平围岩压力计算结果见表3.4。
表3.3 水平围岩压力系数表3.4 垂直围岩压力及水平围岩压力计算表注:二衬按承担70%的围岩压力进行计算。
3.3 衬砌内力计算衬砌内力计算的原理采用荷载结构法。
该方法用有限元软件MIDAS/GTS实现。
3.3.1 计算简图蓁山隧道衬砌结构为复合式衬砌,二衬结构为带仰拱的三心圆曲墙式衬砌。
典型的计算图式如图3.1所示。
荷载结构模型计算图式如图3.2所示。
围岩用弹簧代替,用弹簧单元模拟,结构用梁单元模拟。
图3.1 三心圆曲墙式衬砌结构图3.2 荷载结构模型计算图式3.3.2 计算过程下面以Ⅱ级围岩为例进行说明。
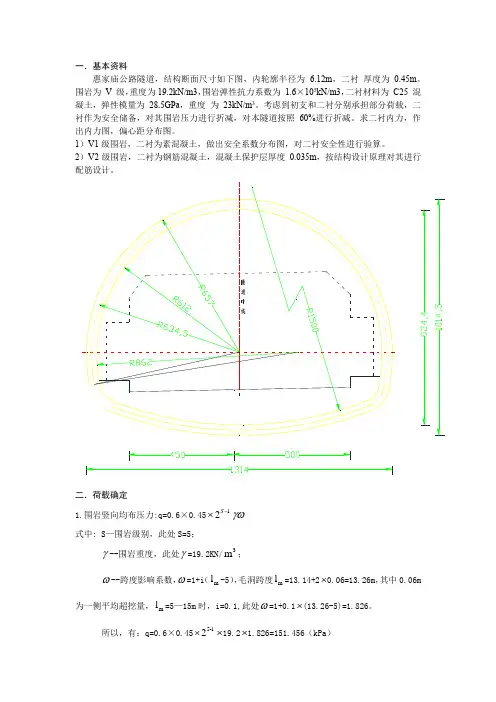
一.基本资料惠家庙公路隧道,结构断面尺寸如下图,内轮廓半径为 6.12m ,二衬 厚度为 0.45m 。
围岩为 V 级,重度为19.2kN/m3,围岩弹性抗力系数为 1.6×105kN/m3,二衬材料为 C25 混凝土,弹性模量为 28.5GPa ,重度 为 23kN/m 3。
考虑到初支和二衬分别承担部分荷载,二衬作为安全储备,对其围岩压力进行折减,对本隧道按照 60%进行折减。
求二衬内力,作出内力图,偏心距分布图。
1)V1级围岩,二衬为素混凝土,做出安全系数分布图,对二衬安全性进行验算。
2)V2级围岩,二衬为钢筋混凝土,混凝土保护层厚度 0.035m ,按结构设计原理对其进行配筋设计。
二.荷载确定1.围岩竖向均布压力:q=0.6×0.45⨯12-S γω式中: S —围岩级别,此处S=5;γ--围岩重度,此处γ=19.2KN/3m ;ω--跨度影响系数,ω=1+i(m l -5),毛洞跨度m l =13.14+2⨯0.06=13.26m ,其中0.06m 为一侧平均超挖量,m l =5—15m 时,i=0.1,此处ω=1+0.1⨯(13.26-5)=1.826。
所以,有:q=0.6×0.451-52⨯⨯19.2⨯1.826=151.456(kPa )此处超挖回填层重忽略不计。
2.围岩水平均布压力:e=0.4q=0.4⨯151.456=60.582(kPa ) 三.衬砌几何要素 5.3.1 衬砌几何尺寸内轮廓线半径126.12m , 8.62m r r ==内径12,r r 所画圆曲线的终点截面与竖直轴的夹角1290,98.996942φφ=︒=︒; 拱顶截面厚度00.45m,d = 墙底截面厚度n 0.45m d =此处墙底截面为自内轮廓半径2r 的圆心向内轮廓墙底做连线并延长至与外轮廓相交,其交点到内轮廓墙底间的连线。
外轮廓线半径:110 6.57m R r d =+= 2209.07m R r d =+=拱轴线半径:'1200.5 6.345m r r d =+= '2200.58.845m r r d =+=拱轴线各段圆弧中心角:1290,8.996942θθ=︒=︒5.3.2 半拱轴线长度S 及分段轴长S ∆分段轴线长度:'11190π 3.14 6.3459.9667027m 180180S r θ︒==⨯⨯=︒︒'2228.996942π 3.148.845 1.3888973m 180180S r θ︒==⨯⨯=︒︒半拱线长度:1211.3556000m S S S =+=将半拱轴线等分为8段,每段轴长为:11.3556 1.4194500m 88S S ∆===5.3.3 各分块接缝(截面)中心几何要素(1)与竖直轴夹角i α11'1180 1.4194518012.8177296π 6.345πS r αθ∆︒︒=∆=⨯=⨯=︒ 21112.817729612.817729625.6354592ααθ=+∆=︒+︒=︒ 32125.635459212.817729638.4531888ααθ=+∆=︒+︒=︒43138.453188812.817729651.2709184ααθ=+∆=︒+︒=︒54151.270918412.817729664.0886480ααθ=+∆=︒+︒=︒ 65164.088648012.817729676.9063776ααθ=+∆=︒+︒=︒ 76176.906377612.817729689.7241072ααθ=+∆=︒+︒=︒2'2180 1.419451809.2748552π8.845πS r θ∆︒︒∆=⨯=⨯=︒ 87289.72410729.194855298.996942ααθ=+∆=︒+︒=︒另一方面,8129012.817729698.996942αθθ=+=︒+︒=︒ 角度闭合差Δ≈0。


西场站〜西村站〜广州火车站〜草暖公园区间盾构隧道结构计算书一、结构尺寸隧道内径:5400:隧道外径:6000:管片厚度:300mm:管片宽度:1500mm。
二、计算原则选择区间隧道地质条件较差、隧道埋深较大、地面有特殊活载(地面建筑物桩基、铁路线等)等不同地段进行结构计算。
三、汁算模型计算模型采用修正惯用设计法。
考虑管片接头影响,进行刚度折减后按均质圆环进行计算;水平地层抗力按三角形抗力考虑;计算结果考虑管片环间错缝拼装效应的影响进行内力调整。
弯曲刚度有效率n二0.8,弯矩增大系数§二0.3。
计算简图如下图所示。
使用AXSYS程序软件进行结构计算。
■ ・■・"・A-l-A一A-ll・・s j. • ・■-••:•••1 I♦' ■i 1 •[ 亡J 'i i•八*•■r-**i F I•f)•I MTMR 力• • •、SM■ ftV4询氯修正惯用设讣法计算模型计算模型节点划分四、计算荷载荷载分为永久荷载、活载、附加荷载和特殊荷载等四种。
1)永久荷载:管片自重、水土压力、上部建筑物基础产生的荷载。
考虑地层特征采取水土合算或水土分算。
2)活载:地面超载一般按20KN/m2计;有列车通过地段按40KN/m2 ITo3)附加荷载:施工荷载一一盾构千斤顶推力,不均匀注浆压力,相邻隧道施工影响等。
4)特殊荷载:地震力一一按抗震基本烈度为7度汁算,人防荷载按六级人防计算,按动载化为静载计算。
五、内力计算1、一般地段:地质条件较差、埋深较大地段(地面超载20KN/m2):里程YCK5+990选取地质钻孔为MEZ2-A073。
隧道埋深约33. 9m,地下水位在地面下5. Om。
地层由上至下分别为<l>-7. 3m: <5-l>-39. 2m; <5-2>-20mo隧道所穿过地层为〈5- 2>o 隧道横断面与地层关系如下图所示:<5-1>隧道横断面与地层关系2、列车通过地段:地面超载40KN/m2,里程YCK6+050选取地质钻孔为MEZ2-A166。


第一章绪论1. 隧道:构筑在离地面一定深度的岩层或土层中用作通到底建筑物2. 隧道分类:按周围介质分:岩石隧道和土层隧道;按用途不同分:交通隧道和市政工程隧道3. 公路隧道:穿越公路路线障碍物的交通隧道4. 公路隧道的主要特点:(1)断面形状复杂:宽而扁,高:宽<=1.; 常有特殊构造:岔洞,紧急停车带回车区,以及双连拱隧道,小间距隧道,双层隧道;(2) 荷载形式单一:主要是围岩压力,方向不会改变;(3)附属设施多:通风,照明,交通信号,消防,监控设施5. 断面几何形状:考虑功能和经济的两方面:马蹄形,圆形(盾构开挖),拱形(山岭隧道),双连拱(浅埋土层,地形受限),矩形(沉管法,城市隧道)6.. 衬砌的结构类型分为四类:整体式砼衬砌;装配式衬砌;锚喷支护衬砌;复合式衬砌7.. 整体式砼衬砌又可分为:半衬砌;厚拱薄墙衬砌;直墙拱形衬砌;曲墙拱形衬砌(1)半衬砌:适用于岩石较坚硬并且整体稳定或基本稳定的围岩; 对于侧压力很大的较软岩层或土层,为避免直墙承受较大压力,采用落地拱(2)厚拱薄衬砌:适用于水平压力很小的情况,拱脚较厚,边墙较薄(3) 直墙拱形衬砌:铁路隧道常用,竖向压力较大,水平侧压力不大(4)曲墙拱形衬砌:地质条件差,岩石破碎松散和易于坍塌地段8. 装配式衬砌:用于盾构法施工,深埋法施工,TBM 法施工9. 锚喷支护衬砌:喷混凝土和加锚杆两方法的统称。
常用方法:喷混凝土,钢筋网喷混凝土,锚杆喷混凝土,钢筋网锚杆混凝土,钢纤维喷混凝土;特点:有很强时效性,新奥法和挪威法10. 复合式衬砌:主要应用于含水量较多的地段,外层为锚喷支护,中间有一层防水层,内层多为整体式衬砌,新奥法多采用11. 初始地应力场由两种力系组成:自重应力分量;构造应力分量影响因素:一类是和地壳的运动,地下水的变化以及人类活动等因素有关12. 构造应力场:区域性明显,测试方法:解析反演法,原位测试法(1)地质的构造过程不公改变了地质的重力应力场,而且还有一总分残余在岩体内(2) 构造应力场在一定深度内普遍存在且多为水平分量(3)构造应力具有明显的区域性和时间性13. 作用在隧道结构上的荷载分为三类:主要荷载(就是长期作用的荷载,包括地层压力,围岩弹性抗力,结构自重力,回填岩土重力,地下静水压力及使用荷载); 附加荷载(指非经常作用的荷载,包括施工荷载,灌浆压力,局部落石以及有温度变化或砼收缩引起的温度应力和收缩用力) ;特殊荷载(一些偶然发生的荷载,如炮弹冲击力和爆炸时产生激波压力,地震力,车祸时冲撞力)14. 形变压力: 由岩体变形所产生的挤压力;15. 松散压力: 岩体坠落、滑移、坍塌所产生的重力16. 围岩压力:形变压力和松散压力统称为围岩压力17. 影响围岩压力的因素:a岩土的重力b岩体的结构c.地下水的分布d.隧道洞室的形状和尺寸e. 初始地应力18•确定围岩压力的方法:a•现场量测b•理论估算c工程类比法19•常用的围岩分类方法:a岩石坚固系数分类法b•太沙基理论c•铁路围岩分类法d•人工岩石洞室围岩分类法e.水工隧道围岩分类法20. 隧道结构计算的任务:就是采用数学力学的方法,计算分析在隧道修筑的整个过程中 (包括竣工,运营)a.隧道围岩及衬砌的强度 b.刚度和稳定性,为隧道的设计及施工提供具体设计参数21. 隧道的计算方法可分为三大部分: a.刚体力学法b.结构力学法(荷载位移法)c.连续介质力学法(地层结构法)22. 附:19 世纪后期,砼材料与钢材料的出现,地下结构的建造于计算进入地下连续拱形框架结构阶段,而计算的理论基础为线弹性结构力学;地下连续拱形框架结构式一种超静定弹性结构系统,荷载为地层压力,优点:以结构力学原理为计算理论基础缺点:没有考虑地层对衬砌结构变形所产生的弹性抵抗力23. 如果人工考虑隧道衬砌和地层的相互作用,地下结构的计算方法仅分为结构力学方法和连续介质力学方法24. 造成隧道结构计算结果不能直接应用的主要原因:(1) 围岩的物理力学参数无法准确确定(2)隧道的荷载量级很大,无法准确给出(3) 围岩自承能力除受围岩自身条件影响外,还受施工方法、时间、支护形式、洞室几何尺寸等的影响( 4)围岩本构关系复杂和屈服性准则不完善性,使围岩自承能力无法发挥第二章隧道结构计算的结构力学法1. 在分析过程中首先要确定地层压力,然后计算衬砌在地层压力和其他荷载作用下的内力分布,最后根据内力分布对衬砌结构断面进行验算2. 荷载结构法和计算地表结构所采用的结构力学方法基本相同,主要差别是衬砌结构在变形过程中要受到周围介质的限制,分为力法与位移法3. 拱形半衬砌隧道的结构计算: ( 1)半衬砌结构可简化为弹性固定平面无铰拱(计算模型) (2)拱顶截面建立位移协调方程,由拱顶截面的位移协调方程得拱脚处的位移和转角( 3) 将拱脚位移和转角方程代入拱顶截面位移协调方程,得关于未知力X1 ,X2 的线性代数方程组,可得拱顶截面未知力( 4)各截面强度校核4. 拱形曲墙隧道的结构计算: (1)假定弹性抗力为镰刀形分布,拱形曲墙式衬砌的计算模型为墙角弹性固定而两侧受周围约束的无铰拱( 2)通过h点的变形协调条件计算弹性抗力bh(3)计算主动荷载作用下衬砌的内力(4) b h=1时衬砌的内力⑸求出最大抗力值b h(6)用叠加的方法求出衬砌内任一点的内力5. 拱形曲墙隧道的结构计算模型:竖向荷载所引起的侧墙部分的变形,将受到侧面围岩的约束,形成一个抗力区,这里假定弹性抗力为镰刀形,其量值用 3 个特征值控制:抗力上零点对一般与对称中线夹角为40°-60°;抗力下零点在拱脚处;最大抗力点h 在衬砌最大跨度处,一般在抗力区2/3 处6. 拱形直墙隧道的局部变形法:在分析拱形直墙式隧道结构时,需将拱圈与直墙分开考虑,拱圈是一个拱脚弹性固定的无铰拱,弹性抗力假定为二次抛物线分布,边墙视为弹性地基梁,全部抗力有文克勒假设确定,墙顶和拱脚弹性固结,墙脚与基岩间有较大的摩擦力,无水平位移发生,他在基岩的作用视为刚性体7•外荷载产生的位移卩hp和直墙拱的结构计算:(1)由弹性地基梁公式,计算系数卩1, 3 1,卩2, 3 2(墙顶位移)(2)由主动荷载及单位弹性抗力所产生的h点位移计算单位弹性抗力所产生的位移h b (3)由口hp和口h b求得弹性抗力b h (4)根据任一截面i处的内力表达式得拱的截面内力( 5)求出直梁的内力( 6)校核8•隧道衬砌结构计算的矩阵力法计算步骤:(1)计算[F0](2)计算[丫SX]并将其转化为[丫SX]'⑶计算[丫SP]并将其转化为[丫SP]' (4)计算[Fxx],[Fxp](5)计算赘余力{x} (6)计算衬砌单元节点{s} ( 7)计算衬砌节点位移{ S }9•隧道衬砌结结构计算的矩阵位移法计算步骤:(1)计算衬砌单元刚度位移矩阵( 2)计算链杆刚度( 3)计算墙底支座的刚度矩阵( 4)集成总体刚度矩阵,并计算各元素值( 5)消去已知位移( 6)计算节点位移( 7)计算单元节点力10•拱形直墙计算模型:拱圈是一个拱脚弹性固定的无铰拱,拱圈弹性抗力假定为二次抛物线分布,边墙视为弹性地基梁,全部抗力由文壳勒假设确定。


顶管隧道结构计算E.1 管道允许顶力计算E.1.1 钢管顶管传力面允许最大顶力可按下式计算: 134ds s pQdF f A r ϕϕϕ=.F ds =0.5φ1φ3φ4γQdf s A p .(E.1.1-1)式中:ds F —— 钢管管道允许顶力设计值(N );1ϕ—— 钢管受压强度折减系数,可取1.00;3ϕ——钢管脆性系数,可取1.00;4ϕ——钢管顶管稳定系数,可取0.36;当顶进长度小于300m 且穿越土层均匀时,可取0.45;s f —— 钢管受压强度设计值(N/mm 2); p A ——管道的最小有效传力面积(mm 2);Qd γγQd ——顶力分项系数,可取1.30。
E.1.2 钢筋混凝土管顶管传力面允许最大顶力可按下式计算: 12350.5dc c pQd F f A r ϕϕϕϕ=⨯F dc =0.5φ1φ2φ3γQd φ5f c A p(E.1.2-1)式中:dc F ——混凝土管道允许顶力设计值(N );1ϕ—— 混凝土材料受压强度折减系数,可取0.90;2ϕ——偏心受压强度提高系数,可取1.05; 3ϕ——材料脆性系数,可取0.85;5ϕ——混凝土强度标准调整系数,可取0.79;c f —— 混凝土受压强度设计值(N/mm 2)。
E.2 套管强度验算E.2.1 钢套管管壁截面的最大组合折算应力应满足下列公式:f θησ≤ (E.2.1-1) x f ησ≤(E.2.1-2)0r f σ≤ (E.2.1-3)σ= (E.2.1-4)200006N Mb t b t θσ=+(E.2.1-5) ,00c Q wd k N F r b φγ=(E.2.1-6)()11,,110030010.732G gm k G SV vm sv k GW wm wk Q c vm ik d p k G F D G Q D r b M E r E t γγκγκγφκφ+++=⎛⎫+ ⎪⎝⎭(E.2.1-7)10.5p x p c Q p E D E T R θσνσφγα=±∆±(E.2.1-8)22111122L f R f ⎛⎫+ ⎪⎝⎭=(E.2.1-9)式中:θσ——钢管管壁横截面最大环向应力(N/mm 2);x σ——钢管管壁横截面最大纵向应力(N/mm 2); σ——钢管管壁的最大组合折算应力(N/mm 2);η——应力折算系数,取0.9;f ——钢材的强度设计值(N/mm 2);0b ——管壁计算宽度(mm ),取1000mm ;ϕ——弯矩折算系数,有水内压时取0.7,无内水压时取1.0;c ϕ——可变作用组合系数,取0.9;0t ——管壁计算厚度(mm ),使用期间试算时设计壁厚应扣除2mm ,施工期间不扣除;0r ——管的计算半径(mm ); M ——在作用组合作用下钢管管壁截面上的最大环向弯矩设计值(N.mm ); N ——在作用组合作用下钢管管壁截面上的最大环向轴力设计值(N );d E ——钢管管侧原状土的变形模量(N/mm 2); p E ——钢管管材的弹性模量(N/mm 2);gm K 、vm K 、wm K ——分别为钢管管道自重、竖向土压力和管内水重作用下管壁截面的最大弯矩系数,分别取0.083、0.138、0.083;1D ——管道外直径(mm ); ik Q ——地面堆载或车载传递至管道顶压力的较大标准值;p ν——钢管管材泊松比,可取0.3;α——钢管管材线膨胀系数; T ∆——钢管的计算温差;1R ——钢管顶进施工变形形成的曲率半径(mm ); 1f ——顶进管道直线顶进允许偏差(mm ),可按表E.2.1-1确定; 1L ——出现偏差的最小间距(mm ),视顶管直径和土质决定,一般可取50m 。
电缆隧道结构计算1、隧道基本尺寸:(m)宽高侧板厚顶板厚底板厚隧道顶板埋深地面荷载底板荷载4.002.300.400.400.503.3010.005.002、计算参数:L 1L 2I 1I 24.402.750.010.013、计算系数:m =L2/L1n =I2/I1K=m*nμ=K*K+4*K+30.63 1.000.63 5.894、荷载(堆料荷载或汽车荷载:堆料荷载由计算确定,汽车荷载根据不同等级选用)从上述数据中选取最大值:294.00覆土荷载覆土深度覆土密度覆土荷载汽车荷载(双轴)覆土深度动力系数汽车荷载3.3020.0066.00200.003.301.0012.7366.00荷载分项系数(恒、活)1.20 1.405、地基土性质(密度、内摩擦角)及埋深20.0030.006.50注:岩石摩擦角90度(1)顶板荷载105.2086.00(2)底板荷载116.70100.58(3)侧板荷载(顶部)31.0625.33侧板荷载(底部)56.6646.666、隧道内力计算(1)顶板底板受力弯矩:设计值标准值顶板支座弯矩:KN.m -102.48-82.89底板支座弯矩:KN.m -117.83-102.36顶板中部弯矩:KN.m 152.11125.23底板中部弯矩:KN.m164.58141.05侧板弯矩:KN.m-110.15-92.62电缆隧道结构计算弯矩(弯矩计算把隧道分成两部分,顶板底板受力+四边都受均布力+侧壁受均布力,然后取代数和)隧道所受荷载:(覆土荷载)第 1 页(6)隧道壁裂缝宽度计算:第 2 页第 3 页第 4 页。
隧道支护结构计算计算模型及方法隧道工程中,隧道支护结构的设计是一个至关重要的环节。
为了保证施工安全和隧道工程的长期稳定运行,需要使用科学的计算模型和方法对隧道支护结构进行设计和分析。
本文就隧道支护结构的计算计算模型及方法进行探讨。
一、计算模型的选择在隧道支护结构设计中,常用的计算模型有数值模型和解析模型两种。
数值模型是利用数值计算方法对隧道支护结构进行力学计算和分析,是一种较为常见和精确的计算方法。
数值模型可以根据隧道的具体条件和支护结构的特点,选取适当的有限元模型或离散元模型进行计算。
该模型考虑了材料的非线性和复杂的力学特性,可以较为真实地模拟隧道的受力情况。
解析模型是利用解析方法对隧道支护结构进行力学计算和分析,是一种简化和推导的计算方法。
解析模型常用的方法有弹性理论、弹塑性理论和弹性刚度法等。
解析模型适用于支护结构形状规则和材料较为简单的情况,计算速度快、结果相对准确。
根据具体情况,可以综合考虑数值模型和解析模型的特点,选择合适的计算模型进行隧道支护结构的设计和分析。
二、计算方法的应用1.强度计算方法隧道支护结构在受到地压和地震力等外载荷作用下,需要具备足够的强度来保证工程的稳定安全。
强度计算方法是根据支护材料的承载能力和结构的变形特点,对支护结构的强度进行计算和分析。
常用的强度计算方法有等效应力法、荷载传递法和有限元法等。
2.变形计算方法隧道支护结构在受到外力作用时会产生一定的变形,为了掌握支护结构的变形特点和变形范围,需要进行相应的变形计算和分析。
变形计算方法可以通过数值模型或解析模型进行,主要考虑隧道支护结构的刚度、材料的变形特性和支护结构与周围土层的相互作用。
3.稳定性计算方法稳定性是指隧道支护结构在受到外力作用时不发生破坏或失稳的能力。
稳定性计算方法是通过对支护结构的受力特点和受力平衡条件进行计算和分析,判断支护结构的稳定性。
常用的稳定性计算方法有平衡条件法、位移平衡法和有限元分析法等。
重庆交通大学教案第6章隧道结构计算6.1 概述6.1.1 引言隧道结构工程特性、设计原则和方法与地面结构完全不同,隧道结构是由周边围岩和支护结构两者组成共同的并相互作用的结构体系。
各种围岩都是具有不同程度自稳能力的介质,即周边围岩在很大程度上是隧道结构承载的主体,其承载能力必须加以充分利用。
隧道衬砌的设计计算必须结合围岩自承能力进行,隧道衬砌除必须保证有足够的净空外,还要求有足够的强度,以保证在使用寿限内结构物有可靠的安全度。
显然,对不同型式的衬砌结构物应该用不同的方法进行强度计算。
隧道建筑虽然是一门古老的建筑结构,但其结构计算理论的形成却较晚。
从现有资料看,最初的计算理论形成于十九世纪。
其后随着建筑材料、施工技术、量测技术的发展,促进了计算理论的逐步前进。
最初的隧道衬砌使用砖石材料,其结构型式通常为拱形。
由于砖石以及砂浆材料的抗拉强度远低于抗压强度,采用的截面厚度常常很大,所以结构变形很小,可以忽略不计。
因为构件的刚度很大,故将其视为刚性体。
计算时按静力学原理确定其承载时压力线位置,检算结构强度。
在十九世纪末,混凝土已经是广泛使用的建筑材料,它具有整体性好,可以在现场根据需要进行模注等特点。
这时,隧道衬砌结构是作为超静定弹性拱计算的,但仅考虑作用在衬砌上的围岩压力,而未将围岩的弹性抗力计算在内,忽视了围岩对衬砌的约束作用。
由于把衬砌视为自由变形的弹性结构,因而,通过计算得到的衬砌结构厚度很大,过于安全。
大量的隧道工程实践表明,衬砌厚度可以减小,所以,后来上述两种计算方法已经不再使用了。
进入本世纪后,通过长期观测,发现围岩不仅对衬砌施加压力,同时还约束着衬砌的变形。
围岩对衬砌变形的约束,对改善衬砌结构的受力状态有利,不容忽视。
衬砌在受力过程中的变形,一部分结构有离开围岩形成“脱离区”的趋势,另一部分压紧围岩形成所谓“抗力区”,如图6-1所示。
在抗力区内,约束着衬砌变形的围岩,相应地产生被动抵抗力,即“弹性94重庆交通大学教案95抗力”。
抗力区的范围和弹性抗力的大小,因围岩性质、围岩压力大小和结构变形的不同而不同。
但是对这个问题有不同的见解,即局部变形理论和共同变形理论。
图6.1.1 图6.1.2局部变形理论是以温克尔(E.Winkler )假定为基础的。
它认为应力(i σ)和变形(i δ)之间呈直线关系,即i i k δσ=,k 为围岩弹性抗力系数,见图6.1.2(a)。
这一假定,相当于认为围岩是一组各自独立的弹簧,每个弹簧表示一个小岩柱。
虽然实际的弹性体变形是互相影响的,施加于一点的荷载会引起整个弹性体表面的变形,即共同变形,见图6.1.2(b)。
但温克尔假定能反映衬砌的应力与变形的主要因素,且计算简便实用,可以满足工程设计的需要。
应当指出,弹性抗力系数k 并非常数,它取决于很多因素,如围岩的性质、衬砌的形状和尺寸、以及荷载类型等。
不过对于深埋隧道,可以视为常数。
共同变形理论把围岩视为弹性半无限体,考虑相邻质点之间变形的相互影响。
它用纵向变形系数E 和横向变形系数μ表示地层特征,并考虑粘结力C 和内摩擦角ϕ的影响。
但这种方法所需围岩物理力学参数较多,而且计算颇为繁杂,计算模型也有严重缺陷,另外还假定施工过程中对围岩不产生扰动等,更是与实际情况不符。
因而,我国很少采用。
本章将讨论局部变形理论中目前仍有实用价值的方法。
6.1.2 隧道结构体系的计算模型国际隧道协会(ITA)在1987年成立了隧道结构设计模型研究组,收集和汇总了各重庆交通大学教案会员国目前采用的地下结构设计方法,如表6.1.1所示。
经过总结,国际隧道协会认为,目前采用的地下结构设计方法可以归纳为以下4种设计模型:表6.1.1 一些国家采用的设计方法概况┌───┬──────────────┬───────────────┬──────────││盾构开挖的│喷锚钢支撑的│中硬石质深埋隧道│││软土质隧道│软土质隧道││├───┼──────────────┼───────────────┼──────────┼│奥地利│弹性地基圆环│弹性地基圆环、有限元法、收敛│经验法││││一约束法││├───┼──────────────┼───────────────┼──────────┤││覆盖层厚<2D,顶部无约束的│覆盖层厚<2D ,顶部无约束的│全支永弹性地基圆环││德国│弹性地基圆环;覆盖层厚>3D,│弹性地基圆环;覆盖层厚>3D,全│、有限元法、连续介质│││全支承弹性地基圆环、有限元法│全支承弹性地基圆环、有限元法│或收敛—约束法│├───┼──────────────┴───────────────┼──────────┤│法国││有限元法、作用-反作用模型、经│连续介质模型、收敛│││弹性地基圆环有限元法│验法│一约束法、经验法│├───┼──────────────┬───────────────┼──────────┤│日本│局部支承弹性地基圆环│局部支承弹性地基圆环、经验加│弹性地基框架、有限││││测试有限元法│元法、特性曲线法│├───┼──────────────┼───────────────┼──────────┤│││初期支护:有限元法、│初期支护:经验法││中国│自由变形或弹性地基圆环│收敛一约束法│永久支护:作用和反││││二期支护;弹性地基圆环│作用模型│││││大型洞室:有限元法│├───┼──────────────┼───────────────┼──────────┤│瑞士││作用一反作用模型│有限元法,有时用│││││收敛-约束法│├───┼──────────────┼───────────────┴──────────┤│英国│弹性地基圆环缪尔伍德法│收敛—约束法、│有限元法、收敛-约束││││经验法│法、经验法│├───┼──────────────┼───────────────┬──────────┤│美国│弹性地基圆环│弹性地基圆环、│弹性地基圆环、││││作用一反作用模型│有限元法、锚杆经验法│└───┴──────────────┴───────────────┴──────────┘(1)以参照过去隧道工程实践经验进行工程类比为主的经验设计法;(2)以现场量测和实验室试验为主的实用设计方法。
例如,以洞周位移量测值为根据的收敛约束法;(3)作用与反作用模型,即荷载—结构模型。
例如,弹性地基圆环计算和弹性地基框架计算等计算法;(4)连续介质模型,包括解析法和数值法。
数值计算法目前主要是有限单元法。
从各国的地下结构设计实践看,目前,在设计隧道的结构体系时,主要采用两类96重庆交通大学教案计算模型,一类是以支护结构作为承载主体,围岩作为荷载同时考虑其对支护结构的变形约束作用的模型。
另一类则相反,视围岩为承载主体,支护结构则为约束围岩变形的模型。
前者又称为传统的结构力学模型。
它将支护结构和围岩分开来考虑,支护结构是承载主体,围岩作为荷载的来源和支护结构的弹性支承, 故又可称为荷载-结构模型。
在这类模型中隧道支护结构与围岩的相互作用是通过弹性支承对支护结构施加约束来体现的,而围岩的承载能力则在确定围岩压力和弹性支承的约束能力时间接地考虑。
围岩的承载能力越高,它给予支护结构的压力越小,弹性支承约束支护结构变形的抗力越大,相对来说,支护结构所起的作用就变小了。
这一类计算模型主要适用于围岩因过分变形而发生松弛和崩塌,支护结构主动承担围岩“松动”压力的情况。
所以说,利用这类模型进行隧道支护结构设计的关键问题,是如何确定作用在支护结构上的主动荷载,其中最主要的是围岩所产生的松动压力,以及弹性支承给支护结构的弹性抗力。
一旦这两个问题解决了,剩下的就只是运用普通结构力学方法求出超静定体系的内力和位移了。
属于这一类模型的计算方法有:弹性连续框架(含拱形)法、假定抗力法和弹性地基梁(含曲梁和圆环)法等都可归属于荷载结构法。
当软弱地层对结构变形的约束能力较差时(或衬砌与地层间的空隙回填,灌浆不密实时),地下结构内力计算常用弹性连续框架法,反之,可用假定抗力法或弹性地基法。
弹性连续框架法即为进行地面结构内力计算时的力法与变形法。
假定抗力法和弹性地基梁法则已形成了一些经典计算方法。
由于这个模型概念清晰,计算简便,易于被工程师们所接受,放至今仍很通用,尤其是对模筑衬砌。
第二类模型又称为岩体力学模型。
它是将支护结构与围岩视为一体,作为共同承载的隧道结构体系,故又称为围岩-结构模型或复合整体模型,见图6.2(b)。
在这个模型中围岩是直接的承载单元,支护结构只是用来约束和限制围岩的变形,这一点正好和上述模型相反。
复合整体模型是目前隧道结构体系设计中力求采用的并正在发展的模型,因为它符合当前的施工技术水平。
在围岩-结构模型中可以考虑各种97重庆交通大学教案几何形状,围岩和支护材料的非线性特性,开挖面空间效应所形成的三维状态,以及地质中不连续面等等。
在这个模型中有些问题是可以用解析法求解,或用收敛-约束法图解,但绝大部分问题,因数学上的困难必须依赖数值方法,尤其是有限单元法。
利用这个模型进行隧道结构体系设计的关键问题,是如何确定围岩的初始应力场,以及表示材料非线性特性的各种参数及其变化情况。
一旦这些问题解决了,原则上任何场合都可用有限单元法围岩和支护结构应力和位移状态。
6.2 隧道衬砌上的荷载类型及其组合围岩压力与结构自重力是隧道结构计算的基本荷载。
明洞及明挖法施工的隧道,填土压力与结构自重力是结构的主要荷载。
《公路隧道设计规范》(JTJ026-90)中在对隧道结构进行计算时,列出了荷载类型,如表6.1.1所示,并按其可能出现的最不利组合考虑。
其他各种荷载除公路车辆荷载之外,在结构计算时考虑的机率很小,有的也很难准确的表达与定量,表中所列荷载不论机率大小,力求其全,是为了体现荷载体系的完整,也是为了在结构计算时荷载组合的安全系数取值,并与《铁路隧道设计规范》(JBJ3-85)的取值保持一致。
同时又本着公路隧道荷载分类向公路荷载分类方法靠的原则,在形式上与《公路桥涵设计通用规范》(JTJ 021—89)保持一致,在取用荷载组合安全系数时又能与铁路隧道荷载分类相对应。
表6-2中的永久荷载加基本可变荷载对应于铁路隧道设计规范中的主要荷载,其它可变荷载对应于铁路隧道的附加荷载,偶然荷载对应于铁路的特殊荷载。
表6.2.1所列的荷载及分类不适用于新奥法(NATM)设计与施工的隧道。
由于隧道设计中贯彻了“早进晚出”的原则,洞口接长明洞的边坡都干很高,加之落石多为滚滑、跳跃落下,直接砸落在明洞上者极少。
而当遇有大量落石和堕落高度较大的石块,可设法避开或者采取清除危石加固坡面等措施,故一般情况下落石冲击力可不考虑。