小学数学《幻方与数阵图》练习题(含答案)
- 格式:doc
- 大小:145.53 KB
- 文档页数:5


小学数学《数阵图》练习题(含答案)数阵图问题千变万化,这一类问题要求数阵中填入了一些数以后,能保证数阵中特定关系线(或关系区域)上的数的和相等,解决这一类问题可以按以下步骤解决问题:第一步:区分数阵图中的普通点(或方格),和交叉点(方格)第二步:在数阵图的少数关键点(一般是交叉点)上设置未知数,计算各个点与该点被重复计算次数之积的和的代数式,即数阵图关系线(关系区域)上和的总和,这个和是关系线(关系区域)的个数的整数倍.第三步:判断少数关键点上可以填入的数的余数性质,并得出相应的数阵图关系线(关系区域)和.第四步:运用已经得到的信息进行尝试:数阵图还有一类题型比较少见,解决这一类问题需要理清数阵中数与数之间的相关关系,找出问题关键.(一)封闭型数阵问题【例1】(★★★)小青蛙不小心爬到一个正方形数阵图中,必须把1,2,3,4,5,6,7,8八个数字填入下图中的○内,使正方形每条边上三个数的和都等于13才能通过这个数阵图,你能帮它吗?【例2】(★★★)小乌龟被困在五个圆里面(如下图),五圆相连,每个位置的数字都是按一定规律填写的,它必须找出规律,并求出x所代表的数才能脱困,你知道该怎么办吗?24273028262218 1720x【例3】(★★★)1~9分别填入小三角形内(每个小三角形内只填一个数),要求靠近大三角形三条边的每五个数相加和相等.想一想,怎样填这些数才能使五个数的和尽可能大一些?【例4】(★★★)能否将数0,1,2,…,9分别填人下图的各个圆圈内,使得各阴影三角形的3个顶点上的数之和相等?【例5】(★★★),小熊和妈妈去外婆家要过一条河,必须要按照下面的要求填数才可以顺利通过,要求如下:20以内共有10个奇数,去掉9和15还剩八个奇数,将这八个奇数填入右图的八个○中(其中3已经填好),使得图中用箭头连接起来的四个数之和都相等.3(二)辐射型数阵【例6】(★★★)将1~7这七个数字,分别填人图中各个○内,使每条线段上的三个○内数的和相等.【例7】 (★★★)把10至20这11个数分别填入下图的各圆圈内,使每条线段上3个圆内所填数的和都相等.如果中心圆内填的数相等,那么就视为同一种填法.请写出所有可能的填法.【例8】 (★★★)左图中有三个正三角形,将1~9填入它们顶点处的九个○中,要求每个正三角形顶点的三数之和都相等,并且通过四个○的每条直线上的四数之和也相等.【例9】 (★★★)在下图的七个圆圈内各填上一个数,要求每条线上的三个数中,当中的数是两边两个数的平均数,现在已填好两个数,求x 是多少?(三)其它类型的数阵图【例10】 (★★★)在下图中的10个○内填入0~9这10个数字,使得按顺时针循环式成立:【例11】 (★★★★)将1~8这八个自然数填入左下图的空格内,使四边形组成的四个等式都成立:【例12】 (★★★★)下图包括6个加法算式,要在圆圈里填上不同的自然数,使6个算式都成立.那么最右边的圆圈中的数最少是多少?+=====----===×÷+=-+=+=1.请分别将1,2,4,6这4个数填在下图的各空白区域内,使得每个圆圈里4个数的和都等于15.2.把1~5这五个数填入下图中的○里,使每条直线上的三个数之和相等.3.把1至6分别填入下图的各方格中,使得横行3个数的和与竖列4个数的和相等.4.将1~7七个数字填入左下图的七个○内,使每个圆周和每条直线上的三个数之和都相等.5.将1~8八个数分别填入右上图的八个○内,使得图中的六个等式都成立.△代表几?37 5=== =+++++(一)封闭型数阵问题【例13】 (★★★)小青蛙不小心爬到一个正方形数阵图中,必须把1,2,3,4,5,6,7,8八个数字填入下图中的○内,使正方形每条边上三个数的和都等于13才能通过这个数阵图,你能帮它吗?75623841或84362571分析:因为每边上的和为13,那么四条边上的数字之和为13×4=52,而1+2+…+7+8=36,所以四个角上的四个数之和等于52-36=16.在1~8中选四个数,四数之和等于16,且其中相邻两个的和与任意三个的和不等于13的只有:16=1+2+6+7=1+2+5+8=1+4+5+6.经试验,只有右上图的两种填法.亮点设计:(1)求数阵问题的关键是找到关键数,也就是重复数,教会学生学会找关键数的方法是最重要的.(2)设计问题:正方形每条边之和是13,13×4=52,但是所有数的和是:1+2+…+7+8=36,为什么会出现结果不同的问题呢?仔细观察这个数阵,四条边上所有数相加的过程中四个角上的数都被重复加了一次,也就是四个角上的数是重复数,52-36=16即为这四个重复数的和. (3)强调分组法与试验法:知道了四个数的和之后,下一步就要先确定这四个数,采用分组法和试验法.分组法是将这个和根据要求拆成四个数,例如本题中要求其中相邻两个的和与任意三个的和不等于13,根据要求将16分成4个数的和:16=1+2+6+7=1+2+5+8=1+4+5+6,但是未必每一组都是合适的,这就需要采用试验法,将它们一一进行试验.(4)小结:对于封闭型的数阵,重复数基本上都是两条线相交的点,这在后面的例题中有大量体现.[前铺]将1~6六个自然数分别填入下图的○内,使三角形每边上的三数之和都等于11.614532分析:因为每边上的和为11,那么三条边上的数字之和为11×3=33,而1+2+…+5+6=21,所以三个角的三个数之和等于33-21=12,在1~6中选3个和为12的数,且其中任意两个的和不等于11,这样的组合有:12=2+4+6=3+4+5,经试验,填法见右上图.[拓展]将1~6填入左下图的六个○中,使三角形每条边上的三个数之和都等于k ,请指出k 的取值范围.654321654321654321654321k=9 k=10 k=11 k=12分析:设三角形三个顶点的数字之和为s.因为每个顶点属于两条边公有,所以把三条边的数字和加起来,等于将1至6加一遍,同时将三个顶点数字多加一遍.于是有(1+2+3+4+5+6)+s=3k,化简后为s+21=3k.由于s是三个数之和,故最小为1+2+3=6,最大为4+5+6=15,由此求出9≤k≤12.s和k有四组取值:通过试验,每组取值都对应一种填数方法(见右上图).【例14】(★★★)小乌龟被困在五个圆里面(如下图),五圆相连,每个位置的数字都是按一定规律填写的,它必须找出规律,并求出x所代表的数才能脱困,你知道该怎么办吗?242730282622181720x分析:经观察,图中所填数的规律为两个圆相交部分的数等于与它相邻两部分里的数的和的一半.比如:(26+18)÷2=22.(30+26)÷2=28.(24+30)÷2=27.所以x+18=17×2,x=16.经检验,16和24相加除以2,也恰好等于20.[拓展]找规律求xx24123082616186452分析:经观察,图中所填数的规律为两个圆相交部分的数等于与它相邻两部分里的数的差的2倍.比如:(26-18)×2=16.(30-26)×2=8.(30-24)×2=12.因为52÷2=26>24,所以x=26+24=50.经检验,(50--18)×2=64.【例15】(★★★)1~9分别填入小三角形内(每个小三角形内只填一个数),要求靠近大三角形三条边的每五个数相加和相等.想一想,怎样填这些数才能使五个数的和尽可能大一些?分析:1+2+3+4+5+6+7+8+9=45,用s表示靠近大三角形三条边的五个数的和.因为有三个小三角形所填的数在求和时只用了一次(用a,b,c来表示这三个数),其余均用了两次.于是,45×2-(a+b+c)=3 s.要使s尽可能大,只要a+b+c尽可能小.所以a+b+c=1+2+3=6,于是90-6=3 s,s=28.剩下的六个数分成三组,并且每组中两数的和是三个连续自然数,那么:4+8=12;6+7=13;5 +9=14.经过调配可得到几十种填法,右上图是填法之一.[拓展一]如图是奥林匹克的五环标志,其中a,b,c,d,e,f,g,h,i处分别填入整数1至9,如果每一个圆环内所填的各数之和都相等,那么这个相等的和最大是多少,最小是多少?ihgfedcba分析:计算五个圈内各数之和的和,其中b,d,f,h被计算了两遍,所以这个和是1+2+3+4+5+6+7+8+9+b+d+f+h,而这个和一定能被5整除,所以b,d,f,h中填入大数时能使这个和取得最大值,最大是6、7、8、9,各圆圈内的和也取得15,由于15=6+9=7+8,所以满足条件的所有数无法配成15,当和为14时可以找出满足条件的填法,所以和最大为14,当b,d,f,h取1、2、3、4时这个和取得最小值,各圆圈内的和也取得最小值11.[拓展二]有10个连续的自然数,9是其中第三大的数.现在把这10个数填到下图的10个方格中,每格内填一个数,要求图中3个2×2的正方形中的4个数之和相等.那么,这个和数的最小值是多少?分析:9是其中第三大的数,所以这10个连续自然数是2、3、4、5……9、10、11,计算三个正方形中的和的和,这个和能被3整除,其中a和b被重复计算了两次,所以2+3+……11+a+b=65+a+b=3s,当a+b=1,4,7……时,65+a+b可以被3整除,因为要取最小值,所以a+b的值越小越好,但是不可能取1与4,所以,a+b=7时,这个和取得最小值,每个正方形中的和也取得最小值(65+7)÷3=24.【例16】(★★★)能否将数0,1,2,…,9分别填人下图的各个圆圈内,使得各阴影三角形5619372481528763049分析:0+…+9=45,45-中心数=3个阴影三角形的3个顶点上的数字之和,所以中心数必须是3的倍数,只能是0,3,6,9.枚举法实验,中心数只能是3,6,答案如右上图.[拓展一]将1~10分别填入图中,使得每个小三角形3个顶点上的数字之和为图中所表示的数值.分析:先确定中间5个重复数,它们的和为(20+16+12+13+10)-(1+2+…+10)=16,所以中间5个重复数只能是1,2,3,4,6的组合.又因为有1个和为20,相应三角形上的三个数只能是4,6,10,逐一试验,答案如右上图.[拓展二]图中有大、中、小3个正方形,组成了8个三角形.现在先把1,2,3,4分别填在大正方形的4个顶点上,再把1,2,3,4分别填在中正方形的4个顶点上,最后把1,2,3,4分别填在小正方形的4个顶点上.(1)能否使8个三角形顶点上数字之和都相等?如果能,请给出填数方法;如果不能,请说明理由. (2)能否使8个三角形顶点上数字之和各不相同?如果能,给出填数方法;如果不能,请说明理由.344341222311分析:(1)不能,如果能,则8个三角形顶点和的总和应该是8的倍数,但是这个总和有三组1、2、3、4组成,其中一组数被重复计算三次,一组数被重复计算两次,一组数仅被计算一次,因此该总和的值为6×(1+2+3+4)=60,不是8的倍数,产生矛盾,因此没有任何填法使8个三角形顶点上数字之和都相等. (2)能,见右上图.【例17】 (★★★),小熊和妈妈去外婆家要过一条河,必须要按照下面的要求填数才可以顺利通过,要求如下:20以内共有个○中(其中3已经填好),使得图中用箭头连接起来的四个数之和都相等.分析:3组数都包括左右两端的数,所以每组数的中间两数之和必然相等.现在还有1、5、7、11、13、17、19七个数供选择,两两之和相等的有1+19=7+13,只有两组,淘汰这一组;还有1+17=5+13+7+11,于是得到右上图的填法.(二)辐射型数阵【例18】 (★★★)将1~7这七个数字,分别填人图中各个○内,使每条线段上的三个○内数的和相等.635412762534175243716(1) (2) (3)分析:设中心○内填a ,由于三条线上的数字和相加应是3的倍数,其中a 一共加了3次,所以1+2+3+4+5+6+7+2a=28+2a 一定是3的倍数.而28÷3—9余1,那么2a ÷3的余数应该是2,因此,a=1,4或7.(1)当a=1时,28+2=30,30÷3=10,10-1=9,除中心外,其他两数的和应是9,只要把2,3,4,5,6,7六个数按“和”是9分成三组填入相应的○内就可以了.填法如图(1) (2)当a=4时,28+8=36,36÷3=12.填法如图(2)(3)当a=7时,28+14=42,42÷3=14.填法如图(3).亮点设计:(1)建议教师首先让学生进行试做,并让学生尝试多种填法。

小学数学六年级(2019全国通用)-数学竞赛部分-幻方(含答案)一、单选题1.在如图方格表中的每个方格中填人一个字母,使得方格表中每行、每列及两条对角线上的四个方格中的字母都是A,B,C,D,那么表中★所在方格应填的字母是()A. AB. BC. CD. D2.将1到8这8个自然数分别填入如图数阵中的8个圆圈,使得数阵中各条直线上的三个数之和都相等,那么A和B两个圆圈中所填的数之和最大是()A. 8B. 10C. 12D. 143.“九宫阵”是一个9×9的方阵,它是由九个3×3的“九宫格”(图中黑实线围住的方阵)组成.请你在下图中将数字1、2、3、4、5、6、7、8、9分别填入空格内,使得每行、每列及9个“九宫格”中数字1~9均恰好出现一次.当填写完后,那么,位于第4行第4列的数字是()A. 2B. 4C. 6D. 84.将1,2,3,4,5,6分别填入6×6的方格网(如图所示)的36个小方格中,使得每一行每一列中的6个数1,2,3,4,5,6各出现一次,并且满足与不等号相邻的两个数中小数是大数的约数,那么,第二行从左到右的第6个数是()(左图是一个3×3的例子)A. 5B. 4C. 3D. 25.我国古代的“河图”是由3×3的方格构成,每个方格内均有数目不同的点图,每一行、每一列以及每一条对角线上的三个点图的点数之和均相等.如图给出了“河图”的部分点图,请你推算出P处所对应的点图.有以下4个点图可供选择其中,正确的是()A. ①B. ②C. ③D. ④二、填空题6.已知如图中每行、每列和对角线上的三个数之和都相等,那么A=________ ,B=________ ,C=________ ,D=________ ,E=________ .7.将1﹣﹣8这八个整数放在正方体的八个顶点上,要求任一面上四个数之和都相等,请在如图正方体八个顶点处写出符合上述要求的一种填法.________ .8.如图的4×4网格里,横、竖、对角线上的四个数之和均等于“2010”,则a+b+c+d=________ .9.把3、5、7、9、11、13、15、17、19填在适当的位置,使每行每列,每条对角线上三个数和为33.10.将2000至2010这11个数不重复地填入图中的圆圈内,每个圆圈恰填入一个数,使得图中十条经过三个格子的线段,每一条线段上的三个圆圈内所填数的总和都相等,请问,左下角所填的数是________ .11.在空格内填入数字1~6,使得每行、每列和每宫内数字不重复.虚线框里的小数表示虚线框里数字的和.那么,最后一行前五个数依次是:________ .12.在3×3的表格中,有3个数分别是3、4、7.又已知表格中的每行、每列和对角线上的三个数的和都相等,那么问号所代表的数是________ .13.将一些数字分别填入下列各表中,要求每个小格中填入一个数字,表中的每横行中从左到右数字由小到大,每一数列中从上到下数字也由小到大排列.(1)将1至4填入表1中,方法有________ 种;(2)将1至6填入表2中,方法有________ 种;(3)将1至9填入表3中,方法有________ 种;表1:表2:表3:14.如图,4×4方格被分成了五块;请你在每格中填入1、2、3、4中的一个,使得每行、每列的四个数各不相同,且每块上所填数的和都相等.则A、B、C、D四处所填数字之和是________ .三、计算题15. 将4至12的九个整数填入下图九个格内,使纵、横及斜三个数字的和均是一样,问A 和B是那两个数字?四、应用题16.在如图的五个小圆圈内分别填上,,,1,1五个数,使每条直线上三个数相加的和都相等.17.将1至8这8个自然数分别填入图中的正方体的八个顶点处的○内,并使每个面上的四个○内的数字之和都相等.18.将1﹣﹣9这九个数填入右边的九宫格(三阶幻方)中.19.利用猴子跳楼法,写出1﹣49的数字并且每一行一列对角线上的数字之和相等.20.只用2,3,5三个数(可重复使用)填在右图中的○内,使得每个三角形三个顶点上的三个数的和都相等.21.如图为6×6的数独游戏,在36方格的大宫格内,每行和每列分别填上1至6的数字.大宫格内有6个分别由6个小方格组成小宫格,以粗线作为分隔.每个小宫格内亦分别填上1至6的数字,请在空白的小格中填上1至6的数字,使得最后每行、每列、每小宫格都不出现重复的数字.22.将1~7 这七个数字,分别填入图中各个圆圈内,使每条线段上的三个圆圈内的三个数字之和相等.答案解析部分一、单选题1.【答案】C【考点】幻方【解析】【解答】解:如图:①≠D、C、A,只能是B;同理,★部分的字母≠A、B、D,只能是C,所以,★部分的方格中填入的字母是C.故选:C.【分析】先确定①的位置:①≠D、C、A,只能是B;同理,根据容斥原理,★部分的字母≠A、B、D,只能是C,据此解答即可.2.【答案】B【考点】幻方【解析】【解答】解:设幻和为a,则5a=2×(1+2+3+…+8)﹣B,5a=72﹣B又因两条斜线和下面一条横线的和也相等,可知3a=(1+2+3+…+8)+A,可得3a=36+A,a=12+A÷3,所以A只能是3或6当A是3时幻和是13,当A是6时幻和是14,再根据5a=72﹣B可确定当A=3时,B=7当A=4时,B=6,所以幻和最大是3+7=10.故选:B.【分析】图中一共有5条线段,每条线段上的数字和相等,可先求出幻和是多少,设幻和为a,则5a=2×(1+2+3+…+8)﹣B,5a=72﹣B,又因两条斜线和下面一条横线的和也相等,可知3a=(1+2+3+…+8)+A,可得3a=36+A,然后再进行分析进行解答即可.3.【答案】A【考点】幻方【解析】【解答】解:由分析可知位于第4行第4列的数字是2;故选:A.【分析】如图,首先找出第4行第4列的数字所在行列的数字为1、3、6、7、8、9,这个数字所在的3×3的“九宫格”内的数字里面有5,那么这个数字只能为2或4;由第4行第5列的数字所在行列的数字为1、2、3、5、6、7、8、9,这个数字所在的3×3的“九宫格”内的数字里面有9,那么第4行第5列的数字是4;由此得出位于第4行第4列的数字只能是2,得出结论.4.【答案】D【考点】幻方【解析】【解答】解:通过排除试填,得到如下答案,如图:故选:D.【分析】首先发现能组成约数的一组为:1、2、4,1、3、6,1、2、6,1和任意一个数;再发现对角线的数只能为6或4,带黑点的空只能为1或2,连续两个小于或大于的只能考虑连续三个数是倍数关系的;而6由两组适合的约数,因此首先确定对角线为6试填,由此逐一分析即可得出答案.5.【答案】C【考点】幻方【解析】【解答】解:每个点表示1,中间数就是5,幻和是5×3=15.左下角的数是:15﹣5﹣2=8,P点的数是:15﹣8﹣1=6.P点有6个点组成,与③相同.故选:C.【分析】把一个点看成1,那么中间数是5,幻和就是5×3=15;再根据这个幻和进行推算.二、填空题6.【答案】40;30;10;15;50【考点】幻方【解析】【解答】解:根据第1行和第1列的各数之和相等,可得第1行的A数为:A=15+50+25﹣35﹣15=40然后根据对角线上的三个数之和和第1列的各数之和相等,可得B数为:B=15+50+25﹣35﹣25=30再根据每行、每列和对角线上的三个数之和都相等,求出:D=15+50+20﹣40﹣30=15C=15+50+25﹣50﹣30=10E=15+50+25﹣15﹣25=50故答案为:40,30,10,15,50.【分析】通过分析:首先根据第1行和第1列的各数之和相等,可得第1行的A数为:A=15+50+25﹣35﹣15=40;然后根据对角线上的三个数之和和第1列的各数之和相等,可得B数为:B=15+50+25﹣35﹣25=30;再根据每行、每列和对角线上的三个数之和都相等,求出D=15+50+20﹣40﹣30=15,C=15+50+25﹣50﹣30=10,E=15+50+25﹣15﹣25=50,据此解答即可.7.【答案】18【考点】幻方【解析】【解答】解:如图所示:【分析】将每个面上的和全都加起来,就相当于每个点上的数都加了3次,总和为:3×(1+2+…+8),而共有6个面,则每个面上的和为即每个面上的和为(1+2+3+4+5+6+7+8)×3÷6=18;于是我们可以将这8个数字放到相应位置,满足每个面的和等于18.8.【答案】2010【考点】幻方【解析】【解答】解:根据分析可得,c=d+1,b=d+4,a=d+5,(d﹣1)+a+b+(d+2)=2010,(d﹣1)+(d+5)+(d+4)+(d+2)=2010,解得:d=500,c=d+1=500+1=501,b=d+4=500+4=504,a=d+5=500+5=505,所以:a+b+c+d=505+504+501+500=2010.故答案为:2010.【分析】根据双偶数阶幻方的制作的对称性可知:d原来在a的位置,c原来在b的位置,(原图如下);因此可得:c=d+1,b=d+4,a=d+5,d原来左面的数是d﹣1,c右面的数是d+2,根据幻和等于2010,可得:(d﹣1)+a+b+(d+2)=(d﹣1)+(d+5)+(d+4)+ (d+2)=2010,得出d=500,进而可得:a=505,b=504,c=501,那么a+b+c+d=505+504+501+500=2010.9.【答案】解:【考点】幻方【解析】【分析】因为每行、每列、每条对角线上各数的和都等于33,所以幻和为33,中心数为33÷3=11,那么每行、每列、每条对角线上其它两数的和是33﹣11=22,所以再根据其它的两个数凑成和为22,即3+19=5+17=7+15=9+13,然后填空即可.10.【答案】2005【考点】幻方【解析】【解答】解:答:左下角所填的数是2005.故答案为:2005.【分析】通过观察可知一共有10条线,1个数字用5次,1个数字用4次,3个数字用3次,6个数字用2次,可把2000到2010看作是0到10,11个数字来进行计算,通过计算平均每条线的和在12.1和18.2之间,然后用5次的数字用5或6去试,再确定4次的数用哪个数,然后再确定其它位置上的数是多少.11.【答案】3、6、2、4、5【考点】幻方【解析】【解答】解:根据分析,可得所以最后一行前五个数依次是:3、6、2、4、5.故答案为:3、6、2、4、5.【分析】首先根据第2列的第3个数和第4个数的和是4,可得第2列的第3个数和第4个数一个是1,另一个是3;再根据第5列的第3个数和第4个数的和是3,可得第5列的第3个数和第4个数一个是2,另一个是1;再根据第4列的第2个数和第3个数的和是4,可得第4列的第2个数和第3个数一个是1,另一个是3.然后根据第1列的第2个数和第3个数的和是10,可得第1列的第2个数和第3个数一个是6,另一个是4;再根据第6列的第2个数和第3个数的和是11,可得第6列的第2个数和第3个数一个是5,另一个是6;再根据第3列的第4个数和第5个数的和是10,可得第3列的第4个数和第5个数一个是6,另一个是4;再根据第4列的第4个数和第5个数的和是11,可得第4列的第4个数和第5个数一个是5,另一个是6.最后根据第3列的第2个数和第3个数的和是8,可得第3列的第2个数和第3个数一个是2,另一个是6,或者一个是3,另一个是5;再根据每行、每列和每宫内数字不重复,判断出各个空格内的数的大小,进而判断出最后一行前五个数依次是多少即可.12.【答案】5【考点】幻方【解析】【解答】解:3+7+★=★+□+4得出□=66×3=18所以?=18﹣7﹣6=5.答:问号所代表的数是5.故答案为:5.【分析】如图,首先由3+7+★=★+□+4,推出中间的数字为6;又因每行、每列以及每条对角线上的三个数的和相等,说明行、列以及对角线上的三个数的和是6的3倍为18,由此解决问题.13.【答案】2;5;42【考点】幻方【解析】【解答】解:(1)如图,1和4是固定的,另外两格随便选,2种.如下:;(2)1和6是固定的,其余的不确定:(3)由(2)的规律已经知道,6格是5种;1、2、3确定后,剩下的6个一定是5种,比如:同理:也对各对应5个;但是例外,对应的不是5个.因为第一排右边的数限制了下面的数.如下:所以:共计5+5+5+4+2=21(种).同理,以上所有情况倒过来后都有一一对应的种类翻了一番,共21×2=42(种).故答案为:2,5,42.【分析】(1)要符合每横行从左到右数字由小到大,每竖列从上到下数字也由小到大排列.图一中,1只能在A的位置,4只能在D的位置,2和3可在B、C这两个格子中排列,所以共有2种方法;(2)图二中,1只能在A的位置,6只能在F的位置,2只能在B和D,5只能在C、E的位置,数字5在C,有2种排列,数字5在E,又有3种排列方法;所以一共有2+3=5(种).(3)由(2)的规律已经知道,6格是5种,1、2、3确定后,剩下的6个一定是5种;由此进行求解.14.【答案】10【考点】幻方【解析】【解答】解:经分析试填,答案如下:【分析】首先16个方格的和为4×(1+2+3+4)=40,所以每一块的和为40÷5=8;4个数的和为8的只有1+2+3+2和1+1+2+4两种,3个数的和为8的有1+3+4、2+2+4、2+3+3三种,其中只有1+3+4三个加数各不相同,所以A只能填1、3、4,所以B只能是2,B所在块中的另外两个数只能是3+3(排除)或2+4,如图:再看C所在的块,这能填1+2+3+2或1+1+2+4,其中C右侧的数只能是重复的数,如图:事实上以上两个中2可以确定位置,以下的数字调整即可得出答案.三、计算题15.【答案】解:这九个数的和是:(4+12)×9÷2=72幻和是:72÷3=24所以,A=24﹣12﹣4=8那么A下面的格子里的数是:24﹣10﹣8=6所以,B=24﹣11﹣6=7答:A和B分别是8和7.【考点】幻方【解析】【分析】这九个数的和是:(4+12)×9÷2=72,那么幻和是:72÷3=24,所以A=24﹣12﹣4=8,那么A下面的格子里的数是:24﹣10﹣8=6,所以,B=24﹣11﹣6=7,据此解答即可.四、应用题16.【答案】解:这个幻方是:【考点】幻方【解析】【分析】﹣=,﹣=,1﹣=,1﹣1=,相邻两个数的差相等,所以这幻方中间的数就是这5个数的中位数[MISSING IMAGE: , ],然后让最大的数和最小的数在一条直线上,剩下的两个数在同一条直线上即可.17.【答案】解:如图所示:【考点】幻方【解析】【分析】将每个面上的和全都加起来,就相当于每个点上的数都加了3次,总和为:3×(1+2+…+8),而共有6个面,则每个面上的和为=18,即每个面上的和为18,于是我们可以将这8个数字放到相应位置,满足每个面的和等于18.18.【答案】解:因为:1+9=2+8=3+7=4+6=10;按上述条件填出并调整可得到一个三阶幻方,其幻和为15.幻方如下(答案不唯一):【考点】幻方【解析】【分析】根据题意,要使三阶幻方的幻和为15,所以中心数必为15÷3=5,那么与5在一条直线上的各个组的其余两个数的和为10,调整和为10的两个数的位置填入幻方即可.19.【答案】解:这个幻方如下:【考点】幻方【解析】【分析】把1﹣49这49个数字放入一个7×7的矩阵中,使每行、每列及对角线上的七个数字之和相等,即构造一个7阶幻方.对所有奇数阶幻方的构造,都可以采取“连续摆数法”(猴子跳楼),其法则如下:把“1”放在中间一列最上边的方格中,从它开始,按对角线方向(比如说按从左下到右上的方向)顺次把由小到大的各数放入各方格中,如果碰到顶,则折向底,如果到达右侧,则转向左侧,如果进行中轮到的方格中已有数或到达右上角,则退至前一格的下方.20.【答案】解:这个幻方可以是(答案不唯一):【考点】幻方【解析】【分析】先把2、3、5写在一个上面三角形的三个顶点上,然后再根据组成其它三角形的各个顶点都是用2、3、5这三个数进行求解即可.21.【答案】解:对各个小宫格编号如下:先看己:已经有了数字1、3、6,缺少2、4、5;观察发现:5不能在第四列,4不能在第五列,而2不能在第五行;所以2只能在第六行第五列,4就在第六行第四列,5在第五行第七列;如下:观察上图发现:第四列已经有数字1、3、4、5,缺少2和6,由于2不能在第一行,所以6在第四列的第一行,那么2在第四列的第四行;如下:再看乙部分:已经有了数字3、4、6,缺少数字1、2、5,观察上图发现:5不能在第六列,所以5在第五列的第二行;1不能在第二行,所以1至你呢个在第一行的第六列,剩下的2在第二行第六列;如下:观察上图可知:第二行缺少4,所以第二行第一列是4;第六列缺少4、6,由于6不能在第四行,所以第六列的第三行是6,那么第四行就是4;第三列已经有了数字1、2、6,缺少3、4、5,4不能在第一行和第六行,所以第三列的第三行是4,3不能在第六行,所以第三列的第六行是5,那么剩下的3在第三列的第一行;如下:再观察甲部分:已经有了数字1、2、3、4、6,缺少5,所以第一行的第二列就是5;第六行的缺少数字6,所以第六行的第一列就是数字6;戊部分:已经有了数字1、2、5、6,缺少数字3、4,4不能在第一列,所以第一列的第五行只能是3,第二列的第五行就是4;第三行已经有了数字4、5、6,缺少1、2、3;第一列有了数字2、3,所以第三行的第一列就是数字1;第五列有了数字2,所以第三行第五列就是3,剩下的2在第三行第二列;丁部分缺少数字1,丙部分缺少数字3、5,3不能在第一列,所以第四行第一列是5,第二列是3;那么这个数独就是:【考点】幻方【解析】【分析】粗线把这个数独分成了6块,为了便于解答,对各部分进行编号:甲、乙、丙、丁、戊、己,先从各部分中数字最多的己出发,找出其各个小方格里面的数,再根据每行、每列、每小宫格都不出现重复的数字进行推算.22.【答案】解:1+2+3+4+5+6+7=28;令中心数为1,三条线段的总和为:28+1+1=30,每条线段上的和是30÷3=10,因为10=1+2+7=1+3+6=1+4+5.所以这个图是:【考点】幻方【解析】【分析】1~7的和为28先确定中心数,如果中心数是1,那么3条线段的上的总和就是28+1+1=30,再使每条线段上的和是10即可.。



拓展、把1~5这五个数分别填在左下图中的方格中,使得横行三数之和与竖列三数之和都等于8和10。
例2、将1—7七个自然数分别填入图中的圆圈里,使每条线上三个数的和相等。
拓展、将1~7这七个自然数填入左下图的七个○内,使得每条边上的三个数之和都等于10。
例3、把1~5这五个数填入下图中的○里(已填入5),使两条直线上的三个数之和相等。
拓展、将 10~20填入下图的○内,其中15已填好,使得每条边上的三个数字之和都相等。
例4、将1—10这十个数填入下图小圆中,使每个大圆上六个数的和是30。
拓展、将1~8个数分别填入图中,使每个圆圈上五个数和分别为20,22。
例5、把1—10这十个数分别填入下图的○内,使每个四边形顶点的○内四个数的和都相等,且和最大。
拓展、将1~11这十一个数分别填入下图的○里,使每条直线上的三个数之和相等,并且尽可能大。
例6、将1—6六个数分别填入下图的○内,使每边上的三个○内数的和相等。
拓展、将1—8八个数分别填入下图的○内,使每条边上三个数的和相等。
例7、将1—8这八个数分别填入下图○内,使外圆四个数的和,内圆四个数的和以及横行、竖行上四个数的和都等于18。
拓展、将1—8八个数填入下图方格里,使上面四格、下面四格、左四格、右四格、中间四格以及对角线四格内四个数的和都是18。
例8、将1—9九个数分别填入下图○内,使外三角形边上○内数之和等于里面三角形边上○内数之和。
拓展、将1—9填入下图的○中,使横、竖行五个数相加的和都等于25。
例9、如下图,将1~9这九个数字填在方格里,使每行、每列、每条对角线上的三个数之和都相等。
拓展、将1—9九个自然数分别填入下图的九个小三角形中,使靠近大三角形每条边上五个数的和相等,并且尽可能大。
这五个数之和最大是多少?例10、将4~12这九个数字填在下图所示的3×3的方格中,使每行、每列及两条对角线上的三个数的和都相等。
拓展、下图的每个空格中,填入不大于12且互不相同的九个自然数,使每行、每列、每条对角线上的三个数之和都等于21。

幻方的概念与基本性质,三阶和四阶幻方的编制,各种在方格表中填入数值或符号要求在每行、每列及对角线上具有某种性质的幻方类型的数阵图问题.其他结构较为独特的数阵图问题。
例题:1.用l至9这9个数编制一个三阶幻方,写出所有可能的结果.所谓幻方是指在正方形的方格表的每个方格内填入不同的数,使得每行、每列和两条对角线上的各数之和相等;而阶数是指每行、每列所包含的方格的个数.[分析与解]为了方便叙述,在幻方内标上字母.显然有a+c+e=h+A+g=f+d+b,而这9个数的和为1+2+3+…+9=45,所以每行,每列,两条对角线的和均为45÷3=15.又有a+A+b=c+A+d=e+A+f=g+A+h,所以有a+b=c+d=e+f=g+h=k,那么有4k+4A=15×4,而4k+A=45,所以A=5,即中间数为5,k=10,试着填入,有如下填充结果满足题意:.2.已知图16-1是一个四阶幻方,那么标有“*”的方格中所填的数是多少?[分析与解]对角线的和为12+9+5+8=34,于是,第三列的和也是34,有34-7-9-16=2知第三列第四行的数为2.有34-8-11-2=13,则第四行第四列为13.有34-12-3-13=6,所以第四列第二行为6,即标有“*”的方格内所填得数为6.3.将自然数l至9分别填在如图16-2所示的3×3方格表内,使得每行、每列及两条对角线上的数满足两端的两个数之和减去中间的数,结果都等于5.[分析与解]设中间的数为A,有a+b=5+A,c+d=5+A,e+f=5+A,g+h=5+A,那么有a+b+c+d+e+f+g+h+A =20+5A=1+2+3+…+9=45.有A=5,a+b=10,c+d=10,e+f=10,g+h=10,即为普通的三阶幻方,答案与题一一样.有如下图给出几种填法:4.把1,2,3,4,6,9,12,18,36这9个数分别填入3×3方格表的各方格内,使每一行、每一列及两条对角线上的3个数的乘积都是216.求位于正中间的方格中所填的数.[分析与解]有1×36=2×18=3×12=4×9,36×6=216,所以有中心填入6.多次调整位置,可得出如下填法:.5.图16-3是一个三阶幻方,那么标有*的方格中所填的数是多少?[分析与解]第一行和第一列都包含“*的方格,且它们的和相等,那么左下角中的方格内数为8+10-1=17.那么这个幻方的和就是(10+17)÷2=13.5.这样,每行每列数的和就应当是10+13.5+17=40.5.标有*的方格内填入的数应是40.5-10-8=22.5.6.在图16-4的每个空格内填入一个数,使得每行、每列及两条对角线上的3个方格中的各数之和都等于19.95.那么,标有*的格内所填的数是多少?[分析与解]中央的数为19.95÷3=6.65,因而第二列第一个数是19.95-6.65-8.80=4.50.从而标有“*”的格内为19.95-4.33-4.50=11.12.7.如图16-5所示,在3×3方格表内已填好了两个数19和95,在其余的空格中填上适当的数,可以使得每行、每列以及两条对角线上的三个数之和都相等.(1)求x;(2)如果中间的空格内填入100,试在上一小题的基础上,完成填图.[分析与解](1) 由于幻方中各行、各列和对角线上三个数之和都相等,可以列出等式:(a+b+c)+(d+e+f)=(a+d+g)+(g+e+c).化简得:b+f=2×g.题目已知f=19,g=95,因此x=2×95-19=171.(2) 因为中间方格填的是100,所以幻方中各行各列三个数的和是100×3=300.这样第二行第一个方格中应填300-100-19=181,并且依次求得其他各个方格中的数.结果如上右图.8.在图16-6所示的方格表的每个方格内填入一个恰当的字母,可以使得每行、每列及两条对角线上4个方格中的字母都是A,B,C,D,那么,表中标有★的方格内应填的字母是什么?[分析与解]从对角线看,★格可能是B、C、D,从第4列看,★格不可能是D.因而★格内只可能为B或C.用上述方法考察左下角,有最小角为B,从而★只能是C.下面给出一种满足题意的填法:.9.请在4×8方格表的每个方格内填入数1,2或3,使得任何排列成如图16-7所示形状的4个方格中所填数的和都是7.[分析与解]我们先考虑3×3的表格情况,按要求填好后,有:a+b+e+f=b+e+f+i=7.所以a=i,同理,c=g.又因为a+b+e+f=c+b+e+d=7,从而:a+f=c+d,同理,g+f=d+i,两式相加,得到a+g+2×f=c+i+2×d.其中a=i,c=g,所以f=d,也就是说中间隔一个方格的两个方格所填入的数相同,我们可以借助上面方法来填写,只用先将一格2×2的小方格填号,使它们的和为7,再将其复制平移知其他的方格内即可.下面给出几种填法:10.如图16-8,有一个11位数,它的每3个相邻数字之和都是20.问标有*的那个数位上的数字应是几?[分析与解]因为每相邻3位数字之和为20,从右边起第一位数字7与第二,三位数字之和是20,第二、三位数字与第四位数字之和也是20,所以第四位数字是7.这样,我们便找到一条规律:每隔2位必出现相同的数字.所以“?”的数字应该是7.11.如图16-9,横、竖各有12个方格,每个方格内都有一个数.已知横行上任意3个相邻数之和为20,竖列上任意3个相邻数之和为21,并且其中4个方格内的数分别是3,5,8和x.那么x所代表的数是多少?[分析与解]竖行上任意三个相邻数之和为21,从而数列上任意三个相邻数都是由同样的三个数组成(只不过顺序不同),这样我们可把“3”向下每隔两格的“移动”,最后得到,由此得出中间的一格应填21-3-8=10.即x的右面一格是10.横行上的任意三个数之和是20.如果把横行最左边的5,每隔两格地“移动”,就知道x的左边一格是5,这样就有x=20-5-10=5,即x代表的数是5.12.把l,2,3,…,13这13个数分别填在如图16-10所示的3个圆圈内,使得同一个圆圈内任意两个数相减,所得的差不在这个圆圈内.现在已经把l,4,7填在第一个圆圈内,3填在第三个圆圈内,请将其余9个数填好.[分析与解]6只能填入第二个圆,这是因为7-1=6,6-3=3.5、8、11都不能填入第一圈,这是因为5-4=1,8-1=7,11-7=4,如果8填入第三个圆,那么5、11都不能填入第三个圆,这是因为8-5=3,11-8=3,从而都只能填入第二个圆,这又导致11-5=6,所以8只能填入第二个圆.因为2不能填入第一个圆,这是因为2-1=1,也不能填入第二个圆,这是因为8-6=2,所以2只能填入第三个圆.于是5只能填入第二个圆,这是因为5-3=2,11只能填入第三个圆,这是因为11-6=5,13只能填入第一个圆,这是因为13-11=2,13-8=5,9只能填入第二个圆,这是因为13-4=9,11-2=9,12只能填入第三个圆,这时因为12-6=6,13-1=12,10只能填入第一个圆,这是因为10-5=5,12-2=10.最终结果如下:13.请在图16-11的每个圆圈内填入不同的自然数,使得图中每个圆圈中所填的数都是上一行与它相邻的两个圆圈中所填数的和.[分析与解]本题填法不唯一,下面给出两种填法:14.在图16-12的7个圆圈内各填一个数,要求对于每一条直线上的3个数,居中的数是旁边两个数的平均数.现在已经填好了两个数,那么x等于多少?[分析与解]如下图所示,将剩下的圆圈内标上字母:于是A=(13+17)÷2=15,即B+15与D+17相等,均为2C,因此B-D=2,于是2D=B+13=D+2+13,故D=15.C=(17+15)÷2=16,x=2C-13=19.15.请在图16-13所示的8个小圆圈内,分别填入1,2,3,4,5,6,7,8这8个数字,使得图中用线段连接的两个小圆圈内所填的数的差(大减小)恰好分别是l,2,3,4,5,6,7.[分析与解]填法有很多,如下给出两种填法:。

四年级数学思维训练:幻方与数阵图扩展(四年级)竞赛测试姓名:_____________ 年级:____________ 学号:______________题型选择题填空题简答题xx题xx题xx题总分得分一、xx题(每空xx 分,共xx分)【题文】把1,2,…,9填入图20﹣1中9个空白圆圈内,使得三个圆周及三条线段上3个数之和都相等.【答案】由以上分析可得:【解析】试题分析:我们从图中可以看出:中间圆圈内所填的数是三条直线上共用的,它是一个“重复用数”.因此,我们在思考时,应该首先把中间圆圈内的数想出来.这样,根据题目中“每条直线上的三个数的和相等”,只需考虑每条直线上两个数的和相等.1~7七个数字的和为28,只有中间圆圈内填上一个数字后,剩下的六个数字的和能被3整除(因为要l当中间圆圈填入4时,剩下的六个数:1+7=2+6=3+5;那么三条直线上的和是1+7+4=12,又1+5+6=12,7+3+2=12;由以上分析可得:点评:解答此题的关键是求出中间圆圈的数是多少,然后再进一步解答即可.【题文】如图,在3×3的方格表的每个方格中填入恰当的数,使得每行、每列、每条对角线上所填数之和都相等.【答案】评卷人得分【解析】试题分析:首先根据第1列的三个数为16、11、12,求出幻和为:16+11+12=39;然后根据幻和为39,分别求出空格里的数即可.解:因为第1列的三个数为16、11、12,所以幻和为:16+11+12=39;因此第2行的第2个数为:39﹣11﹣15=13,第1行的第3个数为:39﹣12﹣13=14,第1行的第2个数为:39﹣16﹣14=9,第2列的第3个数为:39﹣9﹣13=17,第3列的第3个数为:39﹣14﹣15=10..点评:此题主要考查了幻方问题的应用,解答此题的关键是首先求出幻和是多少.【题文】如图,在4×4的方格表的每个方格中填人恰当的数,使得每行、每列、每条对角线上所填数之和都相等.【答案】【解析】试题分析:首先求出每行、每列、每条对角线上所填数之和均为:12+9+5+8=34,然后根据这个共同的和为34,分别求出空格里的数即可.解:每行、每列、每条对角线上所填数之和均为:12+9+5+8=34,所以第3行的第1个数为:34﹣5﹣16﹣3=10,第2列的第1个数为:34﹣4﹣5﹣11=14,第1行的第1个数为:34﹣14﹣7﹣12=1,第2行的第1个数为:34﹣1﹣10﹣8=15,第2行的第4个数为:34﹣15﹣4﹣9=6,第3列的第4个数为:34﹣7﹣9﹣16=2,第4列的第4个数为:34﹣12﹣6﹣3=13..点评:此题主要考查了幻方问题的应用,解答此题的关键是求出每行、每列、每条对角线上所填数之和均为34.【题文】如图所示的3×4方格表的每个方格中填人恰当的数后,可以使各行所填的数之和相等,各列所填的数之和也相等.现在一些数已经填出,标有符号“*”的方格内所填的数是多少?【答案】【解析】试题分析:首先根据第1列的三个数分别为2、3、7,可得各列的各数之和均为:2+3+7=12;然后用12减去6,可得第4列的第1个数和第3个数的和是6,因此第4列的第1个数、第3个数可以分别为5、1;再求出第1行的4个数的和是:2+4+5+5=16,根据各行所填的数之和为16,各列所填的数之和为12,求出其余的空格中的数即可.解:根据第1列的三个数分别为2、3、7,可得各列的各数之和均为:2+3+7=12,所以第4列的第1个数和第3个数的和是:12﹣6=6,因此第4列的第1个数、第3个数可以分别为5、1;因为第1行的4个数的和是:2+4+5+5=16,所以第2行的第2个数和第3个数的和是:16﹣3﹣6=7,第3行的第2个数和第3个数的和是:16﹣7﹣1=8,第2列的第2个数和第3个数的和是:12﹣4=8,第3列的第2个数和第3个数的和是:12﹣5=7,因此第2行的第2个数和第3个数分别是5、2,第3行的第2个数和第3个数分别是3、5.答:标有符号“*”的方格内所填的数是1..点评:此题主要考查了幻方问题的应用,解答此题的关键是灵活应用“各行所填的数之和相等,各列所填的数之和也相等”,注意答案不唯一.【题文】如图,请在空格中填人适当的数,组成一个三阶幻方.【答案】【解析】试题分析:如图,首先根据第1行和对角线上a、15、11三个数的和相等,可得b+12=15+11,解得b=14,所以幻和为14+15+16=45;然后根据幻和为45,分别求出a、c、d、e的值即可.解:如图,根据第1行和对角线上a、15、11三个数的和相等,可得b+12=15+11,解得b=14,所以幻和为:14+15+16=45;因此a=45﹣12﹣14=19,c=45﹣19﹣16=10,d=45﹣10﹣15=20,e=45﹣16﹣11=18.点评:此题主要考查了幻方问题的应用,解答此题的关键是求出幻和是多少.【题文】请将如图所示的5×5方格表补充完整,使得每个方格内都有一个数字,并且具有如下的性质:方格表中每行,每列和每条对角线的5个方格内所填的5个数中,l、2、3、4、5恰好各出现一次.请问:标有符号“△”,“▽”和“○”的方格中所填的数分别是什么?【答案】△=5,▽=5,○=4.【解析】试题分析:根据图示,因为h在第3列中,所以h不能是1、3;又因为h在第3行中,所以h不能是4;因为h在对角线上,所以h不能是5,因此h=2,a、p只能从1、3中各取一个,因为a在第1行中,所以a不能是1,只能是3,则p=1;因为c、l在第4列中,只能从3、5中各取一个,因为c在第1行中,所以c不能是3,只能是5,则l=3;因为e、△在第3列中,只能从4、5中各取一个,因为e在第2行中,所以e不能是5,只能是4,则△=5;因为d、f在第2行中,只能从1、3中各取一个,因为d在第1列中,所以d不能是3,只能是1,则f=3;因为k、m在对角线上,只能从1、4中各取一个,因为m在第1列中,所以m 不能是1,只能是4,则k=1;因为○、b在第1行中,只能从2、4中各取一个,因为b在第4列中,所以b不能是4,只能是2,则○=4;所以j=2,▽=5,g=3,i=1,n=2,o=5,据此解答即可.解:(1)根据图示,因为h在第3列中,所以h不能是1、3;又因为h在第3行中,所以h不能是4;因为h在对角线上,所以h不能是5,因此h=2,a、p只能从1、3中各取一个,因为a在第1行中,所以a不能是1,只能是3,则p=1;(2)因为c、l在第4列中,只能从3、5中各取一个,因为c在第1行中,所以c不能是3,只能是5,则l=3;(3)因为e、△在第3列中,只能从4、5中各取一个,因为e在第2行中,所以e不能是5,只能是4,则△=5;同理,可得d=1,f=3;m=4,k=1;b=2,○=4;j=2,▽=5,g=3,i=1,n=2,o=5.答:△=5,▽=5,○=4..点评:此题主要考查了幻方问题的应用,解答此题的关键是灵活应用“每行,每列和每条对角线的5个方格内所填的5个数中,l、2、3、4、5恰好各出现一次”,逐一确定每个方格中的数字.【题文】请将1至9这9个数填入图中的方框内,使得所有不等号都成立.所有满足要求的填法共有多少种?【答案】2种.【解析】试题分析:首先第一行第二列的数最大,只能是9,第一行的第三列最小只能是1,第一行第一列只能是8,第二行第一列只能是7,第二行第三列只能是2,第三行第三列只能是3,第三行第二列只能是4,中间的数可以是6或5,而第三行第一列可以是6或5,所以满足要求的方法有2种方法.解:答案如下:所以满足要求的填法共有2种.点评:解决此题的关键找出最大最小数的位置,进一步确定固定的数以及可调整的数,得出结论.【题文】请在如图所示的8个小圆圈内,分别填入1至8这8个数字,使得图中用线段连接的两个小圆圈内所填的数的差(大减小)恰好是1、2、3、4、5、6、7.【答案】【解析】试题分析:首先根据两个小圆圈内所填的数的差最大是:8﹣1=7,可得当差为7时,只能是8与1的差;剩下的2、3、4、5、6、7这6个数组成的差最大是:7﹣2=5,所以当差为6时,只能是7与1的差;同理,当差为5时,只能是6与1的差;5与4的差为1,5与3的差为2,5与2的差差为3,5与1的差为4;据此可得中间两个圆圈中的数分别为1、5,然后填上其余圆圈中的数即可.解:因为两个小圆圈内所填的数的差最大是:8﹣1=7,所以当差为7时,只能是8与1的差;因为剩下的2、3、4、5、6、7这6个数组成的差最大是:7﹣2=5,所以当差为6时,只能是7与1的差;同理,当差为5时,只能是6与1的差;5与4的差为1,5与3的差为2,5与2的差差为3,5与1的差为4;因此中间两个圆圈中的数分别为1、5,可得点评:此题主要考查了幻方问题的应用,解答此题的关键是判断出中间两个圆圈中的数只能是1和5.【题文】将1至5这5个数字填入图中的小圆圈内,使得横线、竖线、大圆周上所填数之和都相等.【答案】【解析】试题分析:1+2+3+4+5=15,根据题意,可得计算横线、竖线、大圆周上所填数之和时,圆圈中的每个数均被计算了2次,所以这个共同的和是:15×2÷3=10;然后根据1+4+5=2+3+5=1+2+3+4,可得中心圆圈的数为5,大圆周上所填数为1、2、4、3,据此解答即可.解:1+2+3+4+5=15,根据题意,计算横线、竖线、大圆周上所填数之和时,圆圈中的每个数均被计算了2次,所以这个共同的和是:15×2÷3=10;根据1+4+5=2+3+5=1+2+3+4,可得中心圆圈的数为5,大圆周上所填数为1、2、4、3.点评:此题主要考查了幻方问题的应用,解答此题的关键是求出横线、竖线、大圆周上所填数之和均为10.【题文】请在图中的六块区域内填人1、2、3、4、5、6,使得对每一个小圆圈来说,与它相邻的区域内的数之和都相等.【答案】【解析】试题分析:如图,设图中的六块区域内填入的数分别为:A、B、C、D、E、F,则根据题意,可得A+B+C+D=C+D+E+F=A+B+E+F=B+C+E,整理,可得A+B=C+D=E+F;因为1+6=2+5=3+4,所以A、B可以从1、6中个取一个,C、D可以从2、5中各取一个,E、F可以从3、4中各取一个;最后根据B+C+E=2(A+B)=2×7=14,可得B=6,C=5,E=3,据此解答即可.解:如图,设图中的六块区域内填入的数分别为:A、B、C、D、E、F,则根据题意,可得A+B+C+D=C+D+E+F=A+B+E+F=B+C+E,整理,可得A+B=C+D=E+F;因为1+6=2+5=3+4,所以A、B可以从1、6中个取一个,C、D可以从2、5中各取一个,E、F可以从3、4中各取一个;又因为B+C+E=2(A+B)=2×7=14,所以B=6,C=5,E=3,可得.点评:此题主要考查了幻方问题的应用,解答此题的关键是设图中的六块区域内填入的数分别为:A、B、C 、D、E、F,能判断出A+B=C+D=E+F.【题文】将0至9填入图的10块区域中(阴影区域除外),使得每个圆内的三个数之和都是相等的.请问:这个和最小是多少?最大是多少?【答案】这个和最小是11,最大是16,如图所示:【解析】试题分析:根据图示,可得每个圆圈内的3个数有1个是圆圈独有的,有2个是和其它圆圈共有的;因为每个圆内的三个数之和都是相等的,所以要使这个和最小,则5个圆圈共有的5个数的和最小,是0、1、2、3、4;要使这个和最大,则5个圆圈共有的5个数的和最大,是5、6、7、8、9;据此解答即可.解:0+1+2+3+4+5+6+7+8+9=45,根据图示,可得每个圆圈内的3个数有1个是圆圈独有的,有2个是和其它圆圈共有的;(1)因为每个圆内的三个数之和都是相等的,所以要使这个和最小,则5个圆圈共有的5个数的和最小,是0、1、2、3、4,这个和最小是:(45+0+1+2+3+4)÷5=11;(2)所以要使这个和最大,则5个圆圈共有的5个数的和最大,是5、6、7、8、9,这个和最大是:(45+5+6+7+8+9)÷5=16.答:这个和最小是11,最大是16.点评:此题主要考查了最大与最小问题的应用,解答此题的关键是判断出:要使这个和最小,则5个圆圈共有的5个数的和最小;要使这个和最大,则5个圆圈共有的5个数的和最大.【题文】将1,2,3,…,24,25分别填入图20﹣12的各个方格中,使得每行、每列及两条对角线上的数的和相等.现在已经填入了一些数,标有符号“*”的方格内所填的数是多少?【答案】4.【解析】试题分析:首先根据第1列和对角线19、g、25、13的各数之和相等,可得g+19+25+13=20+9+23+12,解得g=7;然后根据第4列和第5行的各数之和相等,可得b+25+14+3=i+8+15+24,解得b=i+5…①;根据第1列和第1行的各数之和相等,可得i+12+23+9=a+b+*+13,解得b=i﹣a﹣*+31…②;再根据第5行和对角线i、19、7、25、13的各数之和相等,可得j+8+15+24=19+7+25+13,解得j=17;再根据第1行和对角线20、c、7、3、24的各数之和相等,可得a+*+b+13=c+7+3+24,解得c=b+5;再根据第2列和第3行的各数之和相等,可得a+c+19+8=23+7+14+16,解得a+c=33;再根据第5列和第2行的各数之和相等,可得13+16+10+24=9+c+d+25,解得c+d=29;再根据第3列和第4行的各数之和相等,可得*+d+7+15=12+19+3+10,解得*+d=22;解:根据第1列和对角线19、g、25、13的各数之和相等,可得g+19+25+13=20+9+23+12,解得g=7;根据第4列和第5行的各数之和相等,可得b+25+14+3=i+8+15+24,解得b=i+5…①;根据第1列和第1行的各数之和相等,可得i+12+23+9=a+b+*+13,解得b=i﹣a﹣*+31…②;由①②,可得a+*=26;根据第5行和对角线i、19、7、25、13的各数之和相等,可得j+8+15+24=19+7+25+13,解得j=17;根据第1行和对角线20、c、7、3、24的各数之和相等,可得a+*+b+13=c+7+3+24,解得c=b+5;根据第2列和第3行的各数之和相等,可得a+c+19+8=23+7+14+16,解得a+c=33;根据第5列和第2行的各数之和相等,可得13+16+10+24=9+c+d+25,解得c+d=29;根据第3列和第4行的各数之和相等,可得*+d+7+15=12+19+3+10,解得*+d=22;综上,可得a=22,*=4,因此d=22﹣4=18,c=29﹣18=11,b=11﹣5=6,f=b﹣1=5,e=(20+22+4+6)﹣(16+10+24)=52﹣50=2,h=(20+22+4+6+13)﹣(12+19+3+10)=65﹣44=21,i=(20+22+4+6+13)﹣(20+9+23+12)=65﹣64=1,h=(20+22+4+6+13)﹣(1+8+15+24)=65﹣48=17.答:标有符号“*”的方格内所填的数是4..点评:此题主要考查了幻方问题的应用,解答此题的关键是灵活应用“每行、每列及两条对角线上的数的和相等”.【题文】请在图的每个空格内填人一个合适的数,使得每行、每列及两条对角线上的3个方格中的各数之和都相等.【答案】【解析】试题分析:(1)首先根据第2行和第1列的各数之和相等,可得a+95=100+19,解得a=24;然后根据第3列和对角线95、100、c三个数的和相等,可得f+19=95+100,解得f=176;再根据第3行和第2列的三个数的和相等,可得b+100=95+176,解得b=171;再求出另一条对角线上的三个数的和,进而求出c、d、e的值是多少即可.(2)首先根据第2行和第1列的各数之和相等,可得q+6=5+9,解得q=8;然后根据第3列和对角线9、8、n三个数的和相等,可得s+6=9+8,解得s=11;最后根据另一条对角线上的三个数分别是5、8、11,求出三个数的和是多少,进而求出n、m、p、r的值是多少即可.解:(1)根据第2行和第1列的各数之和相等,可得a+95=100+19,解得a=24;根据第3列和对角线95、100、c三个数的和相等,可得f+19=95+100,解得f=176;根据第3行和第2列的三个数的和相等,可得b+100=95+176,解得b=171;另一条对角线上的三个数的和为:24+100+176=300,所以c=300﹣24﹣171=105,d=300﹣100﹣19=181,e=300﹣95﹣176=29.(2)根据第2行和第1列的各数之和相等,可得q+6=5+9,解得q=8;根据第3列和对角线9、8、n三个数的和相等,可得s+6=9+8,解得s=11;根据另一条对角线上的三个数分别是5、8、11,可得三个数的和是:5+8+11=24,所以n=24﹣9﹣8=7,m=24﹣5﹣7=12,p=24﹣8﹣6=10,r=24﹣12﹣8=4..点评:此题主要考查了幻方问题的应用,解答此题的关键是灵活应用“每行、每列及两条对角线上的3个方格中的各数之和都相等”,逐一确定每个空格中的数即可.【题文】在图的每个空格内填入一个数,使得每行、每列及两条对角线上的3个方格中的各数之和都等于19.95.那么,标有“*”的方格内所填的数是多少?【答案】11.12.【解析】试题分析:首先根据题意,可得c+f=19.95﹣4.33=15.62…①,e+f=19.95﹣8.80=11.15…②;然后根据第1行和第2列的三个数的和相等,可得*=8.80+c﹣4.33=4.47+c;再根据两条对角线上的三个数的和相等,可得*=4.33+f ﹣e,所以4.47+c=4.33+f﹣e,整理,可得f﹣c﹣e=0.14…③;由①②③,求出f、c的值,进而求出*是多少即可.解:根据题意,可得c+f=19.95﹣4.33=15.62…①,e+f=19.95﹣8.80=11.15…②;根据第1行和第2列的三个数的和相等,可得*=8.80+c﹣4.33=4.47+c;根据两条对角线上的三个数的和相等,可得*=4.33+f﹣e,所以4.47+c=4.33+f﹣e,整理,可得f﹣c﹣e=0.14…③;由①+②+③,可得3f=26.91,解得f=8.97,所以c=15.62﹣8.97=6.65,所以*=4.47+c=4.47+6.65=11.12.答:标有“*”的方格内所填的数是11.12.点评:此题主要考查了幻方问题的应用,解答此题的关键是灵活应用“每行、每列及两条对角线上的3个方格中的各数之和都等于19.95”,确定出两条对角线上的数分别是多少.【题文】请在图的每个空格内填人一个合适的数,使得每行、每列及两条对角线上的3个方格中的各数之和都相等.【答案】【解析】试题分析:首先根据第1行和第1列的三个数的和相等,可得第1行的第3个数为:29+19﹣17=31;然后根据第2行的三个数和对角线上的三个数的和相等,可得第2行的第3个数为:19+31﹣29=21;再根据第2行和第2列的三个数的和相等,可得第2列的第3个数为:29+21﹣17=33;最后根据第1行和第3列的三个数的和相等,可得第1行的第1个数比第3列的第3个数多:21﹣17=4,再根据两条对角线上的三个数的和相等,可得第1行的第1个数和第3列的第3个数的和为:19+31=50,据此求出第1行的第1个数和第3列的第3个数分别是多少,进而求出中心方格的数是多少即可.解:第1行的第3个数为:29+19﹣17=31;第2行的第3个数为:19+31﹣29=21;第2列的第3个数为:29+21﹣17=33;第1行的第1个数比第3列的第3个数多:21﹣17=4,第1行的第1个数和第3列的第3个数的和为:19+31=50,所以第1行的第1个数为:50÷2+2=27,第3列的第3个数为:50÷2﹣2=23;中心方格的数为:(27+17+31)﹣(29+21)=75﹣50=25.点评:此题主要考查了幻方问题的应用,解答此题的关键是灵活应用“每行、每列及两条对角线上的3个方格中的各数之和都相等”,逐一判断出每个方格中的数是多少.【题文】如图,大正方形的4个角上已填人4个数,4个数之和是264.奇妙的是,把这个图倒过来看,大正方形4个角上的数之和仍然是264.请你在中间的小正方形的4个角的圆圈里,填人另外4个数,使得每条对角线上的4个数正看和倒看时,其和都是264;而且小正方形角上的4个数正看和倒看时,其和也都是264.【答案】【解析】试题分析:首先在0﹣9这10个数字中,找出0、1、6、8、9这5个数字倒过来是0、1、9、8、6;本题中用了1、6、8、9这4个数字,并且对角线上的数的个位相加都是7,所以本题用不上数字0,所以中间的小正方形四个角的圆圈里四个数还是1、6、8、9;然后分析确定出相应的数字即可.解:在0﹣9这10个数字中,有0、1、6、8、9这5个数字倒过l实际上,还有很多种方法,例如:点评:此题主要考查了学生的分析推理能力,分析确定出中间的小正方形四个角的圆圈里四个数还是1、6、8、9是解答本题的关键.【题文】将1、2、3、5、6、7、9、10、11填人图中的小圆圈内,使得每条直线上各数之和都相等.【答案】【解析】试题分析:如图,根据每条直线上各数之和都相等,可得a﹣b=9﹣1=8,除1、3、9之外的8个数中只有10、2两个数相差8,所以a=10,b=2;然后根据a+b=c+d,可得c+d=10+2=12,而且c﹣d=3﹣1=2,解得c=7,d=5;最后求出每条直线上的和是多少,进而求出e、f的值是多少即可.解:根据每条直线上各数之和都相等,可得a﹣b=9﹣1=8,除1、3、9之外的8个数中只有10、2两个数相差8,所以a=10,b=2;因为a+b=c+d,可得c+d=10+2=12,而且c﹣d=3﹣1=2,解得c=7,d=5;因此每条直线上的和为:10+3+5=18,所以e=18﹣5﹣7=6,f=18﹣5﹣2=11.点评:此题主要考查了幻方问题的应用,解答此题的关键是首先根据题意,分别求出四个角上的数分别是多少.【题文】请将1至10填入如图中的10个圆圈中(9已经填好),使得除了第一行外每个圆圈内的数都等于与它相连的上方两个圆圈内的两数之差.【答案】【解析】试题分析:首先根据b、c的差是9,可得b、c只能是10、1各一个;然后根据c是1时,d、f的差是1,所以d、f 是两个相邻的自然数,而且d=f+1;b是10时,a、b的差是e,所以a、e只能是2、8或3、7或4、6;(1)当a=2,e=8时,g=9﹣8=1,与c=1矛盾,因此e=2,则g=9﹣2=7;d、f、h、i从3、4、5、6中各取一个,经验证,可得d=6,f=5,h=4,i=3.(2)当a、e是6、4时,g=9﹣4=5,d、f、h、i从2、3、7、8中各取一个,经验证,可得d=8,f=7,h=2,i=3.(3)经验证,当a、e是3、7时,不符合题意.解:根据b、c的差是9,可得b、c只ld、f、h、i从2、3、7、8中各取一个,经验证,可得d=8,f=7,h=2,i=3.根据对称性,可得满足题意的还有:(3)经验证,当a、e是3、7时,不符合题意.点评:此题主要考查了幻方问题的应用,解答此题的关键是灵活应用“除了第一行外每个圆圈内的数都等于与它相连的上方两个圆圈内的两数之差”,逐一确定出每个圆圈中的数字即可.【题文】如图的7个圆圈内各填一个数,要求对于每一条直线上的3个数,居中的数是旁边两个数的平均数.现在已经填好了两个数,请把剩下的圆圈填好.【答案】【解析】试题分析:如图,根据题意,可得a=(13+17)÷2=15,然后根据13+c=15+d=17+e=2f,可得c=d+2,d=e+2,再根据d+13=2e,可得e+2+13=2e,解得e=15,所以d=15+2=17,c=17+2=19,f=(19+13)÷2=16,据此解答即可.解:如图,根据题意,可得a=(13+17)÷2=15,因为13+c=15+d=17+e=2f,所以c=d+2,d=e+2,又因为d+13=2e,所以e+2+13=2e,解得e=15,所以d=15+2=17,c=17+2=19,f=(19+13)÷2=16.点评:此题主要考查了幻方问题的应用,解答此题的关键是首先求出a的值,并灵活应用“居中的数是旁边两个数的平均数”这一条件.【题文】请将1个1,2个2,3个3,…,8个8,9个9填人图20.20中,使得相同的数所在的方格都连在一起(相连的两个方格必须有公共边);现在已经给出了其中8个方格中的数,并且知道A、B、C、D、E、F、G各不相同;那么,七位数是多少?【答案】6732489.【解析】试题分析:首先根据题意,可得A、B、C、D、E、F、G中不可能有1,也不可能有5,因此A、B、C、D、E 、F、G只能是2、3、4、6、7、8、9各一个;然后根据C的正下方第二个数是3,D的正下方第一个数是2,所以C=3,D=2;根据图示,可得最下面一行中一定没有6,最下面一行中或者左边两个都不是9,或者右边两格都不是9,最下面一行中不可能有2个8,因此最下面一行中必有5,而且只能是A=9,B=8,或者G=9,F=8,经推理,可得G=9,F=8,E=4,A=6,B=7,所以七位数是6732489,据此解答即可.解:因为只有1个1,而且D的正下方第二个数是1,所以A、B、C、D、E、F、G中不可能有1,因为相同的数所在的方格都连在一起(相连的两个方格必须有公共边),所以A、B、C、D、E、F、G中也不可能有5,因此A、B、C、D、E、F、G只能是2、3、4、6、7、8、9各一个;因为C的正下方第二个数是3,D的正下方第一个数是2,所以C=3,D=2;根据图示,可得最下面一行中一定没有6,最下面一行中或者左边两个都不是9,或者右边两格都不是9,最下面一行中不可能有2个8,因此最下面一行中必有5,而且只能是A=9,B=8,或者G=9,F=8,经推理,可得G=9,F=8,E=4,A=6,B=7,所以七位数是6732489.答:七位数是6732489.点评:此题主要考查了幻方问题的应用,考查了分析推理能力的应用,解答此题的关键是灵活应用“相同的数所在的方格都连在一起(相连的两个方格必须有公共边)”,逐一确定出每个字母代表的数是多少即可.【题文】请你将数字1、2、3、4、5、6、7填在图中的圆圈内,使得每个圆圈上的三个数之和与每条直线上的三个数之和相等.应怎样填?【答案】由以上分析可得:.【解析】试题分析:我们从图中可以看出:中间圆圈内所填的数是三条直线上共用的,它是一个“重复用数”.因此,我们在思考时,应该首先把中间圆圈内的数想出来.这样,根据题目中“每条直线上的三个数的和相等”,只需考虑每条直线上两个数的和相等.1~7七个数字的和为28,只有中间圆圈内填上一个数字后,剩下的六个数字的和能被3整除(因为要分成和相等的三组数),才能填写.所以,中间圆圈内所填的数很快可以确定下来:可为1、4、7.这时,其它圆圈内的数也就可以很快填出.解:根据题意可得:当中间圆圈填入1时,剩下的六个数:2+7=3+6=4+5;那么三条直线上的和是2+7+1=10,而两个圆圈上的三个数2+3+5=10,另外三个数7+6+4=17,所以不符合;当中间圆圈填入7时,剩下的六个数:1+6=2+5=3+4,那么三条直线上的和是1+6+7=14,而两个圆圈上的三个数不论怎么填都得不到14,所以不符合;当中间圆圈填入4时,剩下的六个数:1+7=2+6=3+5;那么三条直线上的和是1+7+4=12,又1+5+6=12,7+3+2=12;由以上分析可得:.点评:解答此题的关键是求出中间圆圈的数是多少,然后再进一步解答即可.【题文】将1至9填人图中的9个圆圈内,使4个大圆周上的4个数之和都等于16.【答案】【解析】试题分析:首先求出1﹣9这9个自然数的和为45,4个大圆周上的4个数之和都等于16,中心圆圈的数被计算了4次,另外,4个角上的数字没有重复计算,其余的均被计算了2次,所以中心圆圈数的3倍加上除了4个角上的另外4个数的和等于:16×4﹣45=19,然后根据1+7=2+6=3+5,调整各个数的位置,填入图中即可.解:1+2+3+4+5+6+7+8+9=45,4个大圆周上的4个数之和都等于16,中心圆圈的数被计算了4次,另外,4个角上的数字没有重复计算,其余的均被计算了2次,所以中心圆圈数的3倍加上除了4个角上的另外4个数的和等于:16×4﹣45=19,根据1+7=2+6=3+5,调整各个数的位置,可得.点评:此题主要考查了幻方问题的应用,解答此题的关键是判断出在计算4个大圆周上的4个数之和时,重复计算的情况.【题文】如图中一共有10个方格,现在把2至11这10个自然数填到里面,每个方格各填一个.如果要求图中的3个2×2的正方形中的4个数之和都相等,那么这个和最小可能是多少?请给出一种填法.【答案】和数为24是可能的,如以下两图:【解析】试题分析:图中三个2×2的正方形中四数之和相等,所以2+3+…+11再加上两个重复的数,和被3整除;因为2+3+…+11=65,要使和数最小,两个重复数的和应最小,这两个数可以取2与5,或3与4.这时和数是24.据此解答.解:图中三个2×2的正方形中四数之和相等,所以2+3+…+11再加上两个重复的数,和被3整除.因为2+3+…+11=65,要使和数最小,两个重复数的和应最小,这两个数可以取2与5,或3与4.这时和数是24.和数为24是可能的,如以下两图:点评:此题考查了凑数谜,关键在于明白:2+3+…+11再加上两个重复的数,和被3整除,以及要使和数最小,两个重复数的和应最小,进而得解.【题文】如图,大三角形被分成了9个小三角形.试将1、2、3、4、5、6、7、8、9分别填入这9个小三角形内,每个小三角形内填一个数,要求靠近大三角形三条边的每5个数相加的和相等.这5个数的和最大可能是多少?请给出一种填法.【答案】每条边的5个数之和为28.填法如下:【解析】试题分析:解题的思路是:把靠近大三角形三条边的每5个数加起来就会发现,除每边靠近中间的三个数外,其余的数都重复加了两次,要想使靠近大三角形三条边的每5个数相加的和相等,并且使和尽可能大,那么靠近各边中间的这三个数就应尽量小,因此应填1、2、3,这时每条边的5个数之和为[2×(1+2+3+ (9))﹣1﹣2﹣3]÷3=28.解:填法如下:每条边的5个数之和为[2×(1+2+3+…9)﹣1﹣2﹣3]÷3=84÷3=28.点评:本题应重在找出规律,并利用规律来巧解这道题.【题文】请在图的每个空格内填入一个合适的数,使得每行、每列及两条对角线上的3个方格中的各数之和都相等.【答案】。

小学数学《数阵图》练习题(含答案)数阵图问题千变万化,这一类问题要求数阵中填入了一些数以后,能保证数阵中特定关系线(或关系区域)上的数的和相等,解决这一类问题可以按以下步骤解决问题:第一步:区分数阵图中的普通点(或方格),和交叉点(方格)第二步:在数阵图的少数关键点(一般是交叉点)上设置未知数,计算各个点与该点被重复计算次数之积的和的代数式,即数阵图关系线(关系区域)上和的总和,这个和是关系线(关系区域)的个数的整数倍.第三步:判断少数关键点上可以填入的数的余数性质,并得出相应的数阵图关系线(关系区域)和.第四步:运用已经得到的信息进行尝试:数阵图还有一类题型比较少见,解决这一类问题需要理清数阵中数与数之间的相关关系,找出问题关键.(一)封闭型数阵问题【例1】(★★★)小青蛙不小心爬到一个正方形数阵图中,必须把1,2,3,4,5,6,7,8八个数字填入下图中的○内,使正方形每条边上三个数的和都等于13才能通过这个数阵图,你能帮它吗?【例2】(★★★)小乌龟被困在五个圆里面(如下图),五圆相连,每个位置的数字都是按一定规律填写的,它必须找出规律,并求出x所代表的数才能脱困,你知道该怎么办吗?24273028262218 1720x【例3】(★★★)1~9分别填入小三角形内(每个小三角形内只填一个数),要求靠近大三角形三条边的每五个数相加和相等.想一想,怎样填这些数才能使五个数的和尽可能大一些?【例4】(★★★)能否将数0,1,2,…,9分别填人下图的各个圆圈内,使得各阴影三角形的3个顶点上的数之和相等?【例5】(★★★),小熊和妈妈去外婆家要过一条河,必须要按照下面的要求填数才可以顺利通过,要求如下:20以内共有10个奇数,去掉9和15还剩八个奇数,将这八个奇数填入右图的八个○中(其中3已经填好),使得图中用箭头连接起来的四个数之和都相等.3(二)辐射型数阵【例6】(★★★)将1~7这七个数字,分别填人图中各个○内,使每条线段上的三个○内数的和相等.【例7】 (★★★)把10至20这11个数分别填入下图的各圆圈内,使每条线段上3个圆内所填数的和都相等.如果中心圆内填的数相等,那么就视为同一种填法.请写出所有可能的填法.【例8】 (★★★)左图中有三个正三角形,将1~9填入它们顶点处的九个○中,要求每个正三角形顶点的三数之和都相等,并且通过四个○的每条直线上的四数之和也相等.【例9】 (★★★)在下图的七个圆圈内各填上一个数,要求每条线上的三个数中,当中的数是两边两个数的平均数,现在已填好两个数,求x 是多少?(三)其它类型的数阵图【例10】 (★★★)在下图中的10个○内填入0~9这10个数字,使得按顺时针循环式成立:【例11】 (★★★★)将1~8这八个自然数填入左下图的空格内,使四边形组成的四个等式都成立:【例12】 (★★★★)下图包括6个加法算式,要在圆圈里填上不同的自然数,使6个算式都成立.那么最右边的圆圈中的数最少是多少?+=====----===×÷+=-+=+=1.请分别将1,2,4,6这4个数填在下图的各空白区域内,使得每个圆圈里4个数的和都等于15.2.把1~5这五个数填入下图中的○里,使每条直线上的三个数之和相等.3.把1至6分别填入下图的各方格中,使得横行3个数的和与竖列4个数的和相等.4.将1~7七个数字填入左下图的七个○内,使每个圆周和每条直线上的三个数之和都相等.5.将1~8八个数分别填入右上图的八个○内,使得图中的六个等式都成立.△代表几?37 5=== =+++++(一)封闭型数阵问题【例13】 (★★★)小青蛙不小心爬到一个正方形数阵图中,必须把1,2,3,4,5,6,7,8八个数字填入下图中的○内,使正方形每条边上三个数的和都等于13才能通过这个数阵图,你能帮它吗?75623841或84362571分析:因为每边上的和为13,那么四条边上的数字之和为13×4=52,而1+2+…+7+8=36,所以四个角上的四个数之和等于52-36=16.在1~8中选四个数,四数之和等于16,且其中相邻两个的和与任意三个的和不等于13的只有:16=1+2+6+7=1+2+5+8=1+4+5+6.经试验,只有右上图的两种填法.亮点设计:(1)求数阵问题的关键是找到关键数,也就是重复数,教会学生学会找关键数的方法是最重要的.(2)设计问题:正方形每条边之和是13,13×4=52,但是所有数的和是:1+2+…+7+8=36,为什么会出现结果不同的问题呢?仔细观察这个数阵,四条边上所有数相加的过程中四个角上的数都被重复加了一次,也就是四个角上的数是重复数,52-36=16即为这四个重复数的和. (3)强调分组法与试验法:知道了四个数的和之后,下一步就要先确定这四个数,采用分组法和试验法.分组法是将这个和根据要求拆成四个数,例如本题中要求其中相邻两个的和与任意三个的和不等于13,根据要求将16分成4个数的和:16=1+2+6+7=1+2+5+8=1+4+5+6,但是未必每一组都是合适的,这就需要采用试验法,将它们一一进行试验.(4)小结:对于封闭型的数阵,重复数基本上都是两条线相交的点,这在后面的例题中有大量体现.[前铺]将1~6六个自然数分别填入下图的○内,使三角形每边上的三数之和都等于11.614532分析:因为每边上的和为11,那么三条边上的数字之和为11×3=33,而1+2+…+5+6=21,所以三个角的三个数之和等于33-21=12,在1~6中选3个和为12的数,且其中任意两个的和不等于11,这样的组合有:12=2+4+6=3+4+5,经试验,填法见右上图.[拓展]将1~6填入左下图的六个○中,使三角形每条边上的三个数之和都等于k ,请指出k 的取值范围.654321654321654321654321k=9 k=10 k=11 k=12分析:设三角形三个顶点的数字之和为s.因为每个顶点属于两条边公有,所以把三条边的数字和加起来,等于将1至6加一遍,同时将三个顶点数字多加一遍.于是有(1+2+3+4+5+6)+s=3k,化简后为s+21=3k.由于s是三个数之和,故最小为1+2+3=6,最大为4+5+6=15,由此求出9≤k≤12.s和k有四组取值:通过试验,每组取值都对应一种填数方法(见右上图).【例14】(★★★)小乌龟被困在五个圆里面(如下图),五圆相连,每个位置的数字都是按一定规律填写的,它必须找出规律,并求出x所代表的数才能脱困,你知道该怎么办吗?242730282622181720x分析:经观察,图中所填数的规律为两个圆相交部分的数等于与它相邻两部分里的数的和的一半.比如:(26+18)÷2=22.(30+26)÷2=28.(24+30)÷2=27.所以x+18=17×2,x=16.经检验,16和24相加除以2,也恰好等于20.[拓展]找规律求xx24123082616186452分析:经观察,图中所填数的规律为两个圆相交部分的数等于与它相邻两部分里的数的差的2倍.比如:(26-18)×2=16.(30-26)×2=8.(30-24)×2=12.因为52÷2=26>24,所以x=26+24=50.经检验,(50--18)×2=64.【例15】(★★★)1~9分别填入小三角形内(每个小三角形内只填一个数),要求靠近大三角形三条边的每五个数相加和相等.想一想,怎样填这些数才能使五个数的和尽可能大一些?分析:1+2+3+4+5+6+7+8+9=45,用s表示靠近大三角形三条边的五个数的和.因为有三个小三角形所填的数在求和时只用了一次(用a,b,c来表示这三个数),其余均用了两次.于是,45×2-(a+b+c)=3 s.要使s尽可能大,只要a+b+c尽可能小.所以a+b+c=1+2+3=6,于是90-6=3 s,s=28.剩下的六个数分成三组,并且每组中两数的和是三个连续自然数,那么:4+8=12;6+7=13;5 +9=14.经过调配可得到几十种填法,右上图是填法之一.[拓展一]如图是奥林匹克的五环标志,其中a,b,c,d,e,f,g,h,i处分别填入整数1至9,如果每一个圆环内所填的各数之和都相等,那么这个相等的和最大是多少,最小是多少?ihgfedcba分析:计算五个圈内各数之和的和,其中b,d,f,h被计算了两遍,所以这个和是1+2+3+4+5+6+7+8+9+b+d+f+h,而这个和一定能被5整除,所以b,d,f,h中填入大数时能使这个和取得最大值,最大是6、7、8、9,各圆圈内的和也取得15,由于15=6+9=7+8,所以满足条件的所有数无法配成15,当和为14时可以找出满足条件的填法,所以和最大为14,当b,d,f,h取1、2、3、4时这个和取得最小值,各圆圈内的和也取得最小值11.[拓展二]有10个连续的自然数,9是其中第三大的数.现在把这10个数填到下图的10个方格中,每格内填一个数,要求图中3个2×2的正方形中的4个数之和相等.那么,这个和数的最小值是多少?分析:9是其中第三大的数,所以这10个连续自然数是2、3、4、5……9、10、11,计算三个正方形中的和的和,这个和能被3整除,其中a和b被重复计算了两次,所以2+3+……11+a+b=65+a+b=3s,当a+b=1,4,7……时,65+a+b可以被3整除,因为要取最小值,所以a+b的值越小越好,但是不可能取1与4,所以,a+b=7时,这个和取得最小值,每个正方形中的和也取得最小值(65+7)÷3=24.【例16】(★★★)能否将数0,1,2,…,9分别填人下图的各个圆圈内,使得各阴影三角形5619372481528763049分析:0+…+9=45,45-中心数=3个阴影三角形的3个顶点上的数字之和,所以中心数必须是3的倍数,只能是0,3,6,9.枚举法实验,中心数只能是3,6,答案如右上图.[拓展一]将1~10分别填入图中,使得每个小三角形3个顶点上的数字之和为图中所表示的数值.分析:先确定中间5个重复数,它们的和为(20+16+12+13+10)-(1+2+…+10)=16,所以中间5个重复数只能是1,2,3,4,6的组合.又因为有1个和为20,相应三角形上的三个数只能是4,6,10,逐一试验,答案如右上图.[拓展二]图中有大、中、小3个正方形,组成了8个三角形.现在先把1,2,3,4分别填在大正方形的4个顶点上,再把1,2,3,4分别填在中正方形的4个顶点上,最后把1,2,3,4分别填在小正方形的4个顶点上.(1)能否使8个三角形顶点上数字之和都相等?如果能,请给出填数方法;如果不能,请说明理由. (2)能否使8个三角形顶点上数字之和各不相同?如果能,给出填数方法;如果不能,请说明理由.344341222311分析:(1)不能,如果能,则8个三角形顶点和的总和应该是8的倍数,但是这个总和有三组1、2、3、4组成,其中一组数被重复计算三次,一组数被重复计算两次,一组数仅被计算一次,因此该总和的值为6×(1+2+3+4)=60,不是8的倍数,产生矛盾,因此没有任何填法使8个三角形顶点上数字之和都相等. (2)能,见右上图.【例17】 (★★★),小熊和妈妈去外婆家要过一条河,必须要按照下面的要求填数才可以顺利通过,要求如下:20以内共有个○中(其中3已经填好),使得图中用箭头连接起来的四个数之和都相等.分析:3组数都包括左右两端的数,所以每组数的中间两数之和必然相等.现在还有1、5、7、11、13、17、19七个数供选择,两两之和相等的有1+19=7+13,只有两组,淘汰这一组;还有1+17=5+13+7+11,于是得到右上图的填法.(二)辐射型数阵【例18】 (★★★)将1~7这七个数字,分别填人图中各个○内,使每条线段上的三个○内数的和相等.635412762534175243716(1) (2) (3)分析:设中心○内填a ,由于三条线上的数字和相加应是3的倍数,其中a 一共加了3次,所以1+2+3+4+5+6+7+2a=28+2a 一定是3的倍数.而28÷3—9余1,那么2a ÷3的余数应该是2,因此,a=1,4或7.(1)当a=1时,28+2=30,30÷3=10,10-1=9,除中心外,其他两数的和应是9,只要把2,3,4,5,6,7六个数按“和”是9分成三组填入相应的○内就可以了.填法如图(1) (2)当a=4时,28+8=36,36÷3=12.填法如图(2)(3)当a=7时,28+14=42,42÷3=14.填法如图(3).亮点设计:(1)建议教师首先让学生进行试做,并让学生尝试多种填法。

四年级思维训练18 幻方与数阵图1.在幻方中.每行、每列和每条对角线上的数的和都相同,那么在下图所示的未完成的幻方中该是____。
2.幻方是将n2个数(不重复)排列成纵、横各有n个数的方阵,使其每行、每列和两条对角线上n个数相加的和都相等.请问下图3×3的幻方中丁是多少?3.在下图所示的O内填入不同的数,使得三条边上的三个数的和都是12.若A、B、C的和为18,则三个顶点上的三个数的和是________。
4.下图3×3正方形的每个方格内的字母都代表一个数,已知其每行,每列以及两条对角线上三个数之和都相等,若“a=4,d=19,l=22,那么6=_______ ,h=______。
5.在图1、图2的空格中分别填人适当的数,使得横、竖及对角线上的三个数之和都相等,那么“?”处的数字分别为多少?.6.在下图中每个小方格中填人一个数,使每一行每一列都有1、2、3、4、5,那么,右上角小方格内填人的数字,应该是________。
7.下图是一个3×3幻方,满足每行、每列及两条对角线上三数之和都相等,那么其中“★代表的数是__________。
8.下边的一排方格中,除9、8外,每个方格中的汉字都表示一个数(不同的汉字可表示相同的数),已知其中任意3个连续方格巾的数加起来都为22,则“走”+“进”+“数”+“学”+“花”+“园”=__________9. 所谓“三阶乘法幻方”是指在3×3的方格中填入9个不等于0的整数,使得每行、每列及每条对角线上的三个数之积都相等,请将下图的“乘法幻方”补充完整,则其中的“”所代表的数是___________。
10.将1至8这八个自然数分别填入下图中的正方体的八个顶点处的o内,并使每个面上的四个O内的数字之和都相等,求与填人数字1的O有线段相连的三个O内的数的和的最大值.11.将从8开始的1 1个连续自然数填入下图中的圆圈内,要使每边上的三个数之和都相等,中间数共有__________ 种填法.12.将1--12这十二个自然数分别填人下图的12个圆圈内,使得每条直线上的四个数之和都相等,这个相等的和为___________。
①将1到2n 的自然数排成纵横各有n 个数的正方形,使在同一行、同一列、同一对角线上的n 个数之和都相等。
这样的排列称为n 阶纵横图,或称幻方。
中国汉代已有三阶纵横图,称为九宫。
②把一些数字按照一定的要求,排成各种各样的图形,这类图形叫数阵图,数阵是一种由幻方演变而来的数字图。
➢ 每行、每列和对角线和都相等。
➢ 所有数的和÷ 3 = 幻和。
➢ 幻和 ÷ 3 = 中间数。
➢最大最小数不在对角线。
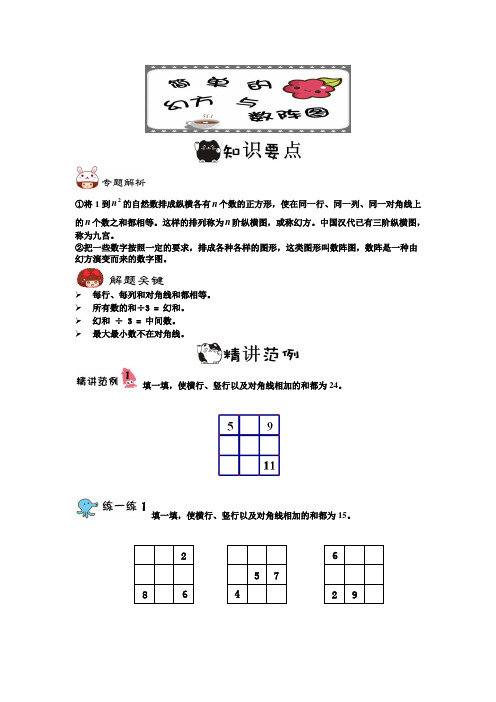
填一填,使横行、竖行以及对角线相加的和都为24。
填一填,使横行、竖行以及对角线相加的和都为15。
628745269把下面的幻方补充完整。
(和为30)4105(和为21)769把下面的幻方填完整。
(和为15)2861615(和为45)19把2~6这五个数分别填入下左图(中间○已填入了数字4),下右图中的○里,使下左图中两条直线上的三个数之和相等,使下右图中两条直线上的三个数之和均为13。
将1、3、5、7、9、11、13、15、17这九个数分别填入下左图(中间○已填入了数字1)、下右图中的○里,使下左图中每条直线上的三个数之和相等,使下右图中每条直线上的三个数之和均为27。
将2、4、6、8、10、12、14这7个数分别填入下图中,使每条线上三个数的和相等。
(写出所有可能的填法)将1~11这11个数分别填入下图中,使每条线上三个数的和相等。
(写出所有可能的填法)把1,2,3,4,5,6,7,8八个数分别填写在下面的方格中,使每边三张卡片上的数的和等于15。
把1,2,3,4,5,6,7,8八个数分别填写在下面的方格中,使每边三张卡片上的数的和等于13。
把下面的幻方填完整。
(和为24)8129在下图的空格中各填入2~10九个数字,使每行、每列及两条对角线上的三个数的和都等于18。
将1~7这七个数填入下图中,使每条直线上的三个数的和为10。
下图是一个九宫格,要将24个●摆到九宫格中,使九宫格的每条边3个格子中都有8个●,现在请你想一想在图中画一画。

小学数学《数阵图》练习题(含答案)课前复习1.在下面的○里填上适当的数,使每条线上的三个数之和都是16.【答案】【答案】2.在空格内填入适当的数,使得每行、每列和两条对角线上的三个数的和都为18.【答案】3. 在空格内填上适当的数,使得图中每行、每列及两对角线上四个数的和都是64.【答案】在神奇的数学王国里,有一类非常有趣的数学问题,它变化多端,引人入胜,奇妙无穷.它就是数阵.到底什么是数阵呢?我们先观察下面2个图:在空格内填上适当的数,使得图中每行、每列及两条对角线上三个数的和都是15.认真观察,你发现每个图中的数字有什么特点?左上图有两条直线,每条直线上都有3个数字,它们的和都分别等于15;而右上图,将l~9九个数字排成三行、三列,每一行、每一列、每一斜行上的3个数字的和都等于15.数阵就是用数(一般指自然数)按一定的要求和规律,组成特定的形状或布成特定的阵势.它一般分为辐射型(左上图)和封闭型(右上图).要把一些数字按一定的规则填入图形中,有没有巧妙的方法来填呢?今天这节课我们就一起来学习.辐射型数阵图【例1】把1,2,3,4,5这5个数分别填入图中的圆圈内,使得横行3个数的和与竖列3个数的和都等于10.【分析】横行的三个数之和加上竖列的三个数之和,只有重叠数a被加了两次,即重叠了一次,其余各数均被加了一次.因为横行的三个数之和与竖列的三个数之和都等于10,所以(1+2+3+4+5)+a=10×2,a=5.剩下4个数中每两个数之和应该等于5,,1+4=2+3。
【例2】把4~8这五个数填入图中(已填入6),使两条直线上的三个数之和相等.【分析】方法一:把6除外,还剩4,5,7,8,这四个数,在这四个数中4+8=5+7,这样可以填出答案。
方法二:与例1不同之处是已知“重叠数”为6,而不知道两条直线上的三个数之和都等于什么数.可以先求出这个“和k”.(4+5+6+7+8)+6=k×2.K=18。

数阵图与幻方知识框架一、数阵图定义及分类:定义:把一些数字按照一定的要求,排成各种各样的图形,这类问题叫数阵图.数阵:是一种由幻方演变而来的数字图.数阵图的种类繁多,这里只向大家介绍三种数阵图:即封闭型数阵图、辐射型数阵图和复合型数阵图.二、解题方法:解决数阵类问题可以采取从局部到整体再到局部的方法入手:第一步:区分数阵图中的普通点(或方格)和关键点(或方格);第二步:在数阵图的少数关键点(一般是交叉点)上设置未知数,计算这些关键点与相关点的数量关系,得到关键点上所填数的范围;第三步:运用已经得到的信息进行尝试.这个步骤并不是对所有数阵题都适用,很多数阵题更需要对数学方法的综合运用.三、幻方起源:幻方也叫纵横图,也就是把数字纵横排列成正方形,因此纵横图又叫幻方.幻方起源于我国,古人还为它编撰了一些神话.传说在大禹治水的年代,陕西的洛水经常大肆泛滥,无论怎样祭祀河神都无济于事,每年人们摆好祭品之后,河中都会爬出一只大乌龟,乌龟壳有九大块,横着数是3行,竖着数是3列,每块乌龟壳上都有几个点点,正好凑成1至9的数字,可是谁也弄不清这些小点点是什么意思.一次,大乌龟又从河里爬上来,一个看热闹的小孩惊叫起来:“瞧多有趣啊,这些点点不论横着加、竖着加还是斜着加,结果都等于十五!”于是人们赶紧把十五份祭品献给河神,说来也怪,河水果然从此不再泛滥了.这个神奇的图案叫做“幻方”,由于它有3行3列,所以叫做“三阶幻方”,这个相等的和叫做“幻和”.“洛书”就是幻和为15的三阶幻方.如下图:987654321我国北周时期的数学家甄鸾在《算数记遗》里有一段注解:“九宫者,二四为肩,六八为足,左三右七,戴九履一,五居中央.”这段文字说明了九个数字的排列情况,可见幻方在我国历史悠久.三阶幻方又叫做九宫图,九宫图的幻方民间歌谣是这样的:“四海三山八仙洞,九龙五子一枝连;二七六郎赏月半,周围十五月团圆.”幻方的种类还很多,这节课我们将学习认识了解它们.四、幻方定义:幻方是指横行、竖列、对角线上数的和都相等的数的方阵,具有这一性质的33的数阵称作三阶幻方,44⨯的数阵称作四阶幻方,55⨯的称作五阶幻方……如图为三阶幻方、四阶幻方的标准式样,98765432113414151612978105113216。
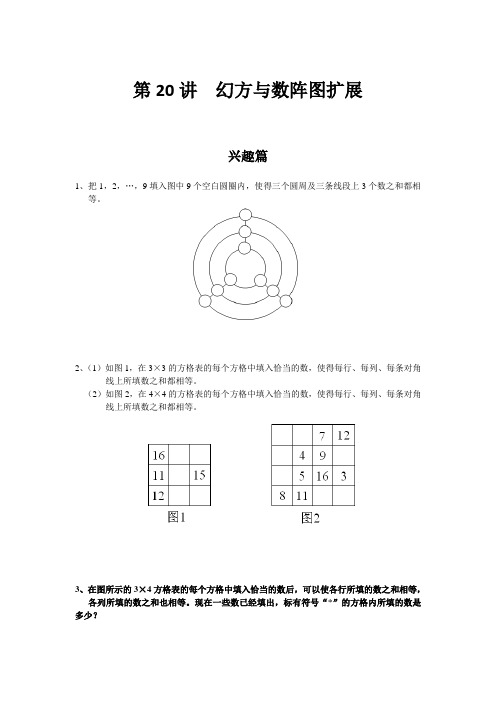
第20讲幻方与数阵图扩展兴趣篇1、把1,2,…,9填入图中9个空白圆圈内,使得三个圆周及三条线段上3个数之和都相等。
2、(1)如图1,在3×3的方格表的每个方格中填入恰当的数,使得每行、每列、每条对角线上所填数之和都相等。
(2)如图2,在4×4的方格表的每个方格中填入恰当的数,使得每行、每列、每条对角线上所填数之和都相等。
3、在图所示的3×4方格表的每个方格中填入恰当的数后,可以使各行所填的数之和相等,各列所填的数之和也相等。
现在一些数已经填出,标有符号“*”的方格内所填的数是多少?4、如图,请在空格中填入适当的数,组成一个三阶幻方。
5、请将图所示的5×5方格表补充完整,使得每个方格内都有一个数字,并且具有如下的性质:方格表中每行,每列和每条对角线的5个方格内所填的5个数中,1、2、3、4、5 恰好各出现一次。
请问:标有符号“△”,“▽”和“◯”的方格中所填的数分别是什么?6、请将1至9这9个数填入图中的方框内,使得所有不等号都成立。
所有满足要求的填法共有多少种?7、请在图所示的8个小圆圈内,分别填入1至8这8个数字,使得图中用线段连接的两个小圆圈内所填的数的差(大减小)恰好是1、2、3、4、5、6、7。
8、将1至5这5个数字填入图中的圆圈内,使得横线、竖线、大圆周上所填数之和都相等。
9、请在图中的六块区域内填入1、2、3、4、5、6,使得对每一个小圆圈来说,与它相邻的区域内的数之和都相等。
10、将0至9填入图的10块区域中(阴影区域除外),使得每个圆内的三个数之和都是相等的。
请问:这个和最小是多少?最大是多少?拓展篇1、将1,2,3,…,24,25分别填入图的各个方格中,使得每行、每列及两条对角线上的数的和相等。
现在已经填入了一些数,标有符号“*”的方格内所填的数是多少?2、请在图的每个空格内填入一个合适的数,使得每行、每列及两条对角线上的3个方格中的各数之和都相等。

小学数学《幻方与数阵图》练习题(含答案)1. 把1~8这8个数,分别填入图中的方格内(每个数必须用一次),使“十一”三笔中每三个方格内数的和都相等.解:2. 把1~11这11个数分别填入如下图11个○内,使每条虚线上三个○内数的和相等,一共有几种不同的和?解:3. 在下图中的几个圈内各填一个数,使每一条直线上的三个数中,当中的数是两边两个数的平均数,现在已经填好两个数,解:4. 在图的每个圆圈内填上适当的质数(不得重复),使每条直线上三个数的和相等,且均为偶数.解:5. 图有五个圆,它们相交相互分成9个区域,现在两个区域里已经填上10与6,请在另外七个区域里分别填进2.3.4.5.6.7.9七个数,使每圆内的和都等于15.解:6. 把1~16这16个数,填入图中的16个○内,使五个正方形的四个顶点上○内数的和相等.解:7. 将1-12这十二个数分别填入图中的十二个小圆圈里,使每条直线上的四个小圆圈中的数字之和26. 解:8. 在图中的空格中填入四个数,使每个横行,每个竖行的三个数的积都相等.解:9. 把1~12这十二个数,填入下图中的12个○内,使每条线段上四个数的和相等,两个同心圆上的数的和也相等.解:10. 将1~9这九个数分别填入图中○内,使每条线段三个数相等.解:作业:1. 10个连续的自然数中第三个的数是9,把这10个数填入图中的10个方格内,每格填一个数,要求图中3个2×2的正方形中4个数之和相等,那么这个和最小值是______.答案: 24.2. 把1~11填入图中,使每条线上三个数的和相等.答案:4 7 1 3 82 9 5 6 11 1 63 9 2 10 5 84 73. 把1~8,填入图中,使每条线及正方形四个顶点上的数的和相等.答案:4. 把1~9,填入下图中,使每条线段三个数和及四个顶点的和也相等.答案:5. 把17,23,25,31,46,53,58,66,72,88,94,100十二个数填入下图,使任意三个相邻的数相加的和除以7的余数相等.答案:。

2014年四年级数学思维训练:幻方与数阵图扩展1.把1,2,…,9填入图20﹣1中9个空白圆圈内,使得三个圆周及三条线段上3个数之和都相等.2.如图,在3×3的方格表的每个方格中填入恰当的数,使得每行、每列、每条对角线上所填数之和都相等.3.如图,在4×4的方格表的每个方格中填人恰当的数,使得每行、每列、每条对角线上所填数之和都相等.4.如图所示的3×4方格表的每个方格中填人恰当的数后,可以使各行所填的数之和相等,各列所填的数之和也相等.现在一些数已经填出,标有符号“*”的方格内所填的数是多少?5.如图,请在空格中填人适当的数,组成一个三阶幻方.6.请将如图所示的5×5方格表补充完整,使得每个方格内都有一个数字,并且具有如下的性质:方格表中每行,每列和每条对角线的5个方格内所填的5个数中,l、2、3、4、5恰好各出现一次.请问:标有符号“△”,“▽”和“○”的方格中所填的数分别是什么?7.请将1至9这9个数填入图中的方框内,使得所有不等号都成立.所有满足要求的填法共有多少种?8.请在如图所示的8个小圆圈内,分别填入1至8这8个数字,使得图中用线段连接的两个小圆圈内所填的数的差(大减小)恰好是1、2、3、4、5、6、7.9.将1至5这5个数字填入图中的小圆圈内,使得横线、竖线、大圆周上所填数之和都相等.10.请在图中的六块区域内填人1、2、3、4、5、6,使得对每一个小圆圈来说,与它相邻的区域内的数之和都相等.11.将0至9填入图的10块区域中(阴影区域除外),使得每个圆内的三个数之和都是相等的.请问:这个和最小是多少?最大是多少?12.将1,2,3,…,24,25分别填入图20﹣12的各个方格中,使得每行、每列及两条对角线上的数的和相等.现在已经填入了一些数,标有符号“*”的方格内所填的数13.请在图的每个空格内填人一个合适的数,使得每行、每列及两条对角线上的3个方格中的各数之和都相等.14.在图的每个空格内填入一个数,使得每行、每列及两条对角线上的3个方格中的各数之和都等于19.95.那么,标有“*”的方格内所填的数是多少?15.请在图的每个空格内填人一个合适的数,使得每行、每列及两条对角线上的3个方格中的各数之和都相等.16.如图,大正方形的4个角上已填人4个数,4个数之和是264.奇妙的是,把这个图倒过来看,大正方形4个角上的数之和仍然是264.请你在中间的小正方形的4个角的圆圈里,填人另外4个数,使得每条对角线上的4个数正看和倒看时,其和都是264;而且小正方形角上的4个数正看和倒看时,其和也都是264.17.将1、2、3、5、6、7、9、10、11填人图中的小圆圈内,使得每条直线上各数之和都相等.18.请将1至10填入如图中的10个圆圈中(9已经填好),使得除了第一行外每个圆19.如图的7个圆圈内各填一个数,要求对于每一条直线上的3个数,居中的数是旁边两个数的平均数.现在已经填好了两个数,请把剩下的圆圈填好.20.请将1个1,2个2,3个3,…,8个8,9个9填人图20.20中,使得相同的数所在的方格都连在一起(相连的两个方格必须有公共边);现在已经给出了其中8个方格中的数,并且知道A、B、C、D、E、F、G各不相同;那么,七位数是多少?21.请你将数字1、2、3、4、5、6、7填在图中的圆圈内,使得每个圆圈上的三个数之和与每条直线上的三个数之和相等.应怎样填?22.将1至9填人图中的9个圆圈内,使4个大圆周上的4个数之和都等于16.23.如图中一共有10个方格,现在把2至11这10个自然数填到里面,每个方格各填一个.如果要求图中的3个2×2的正方形中的4个数之和都相等,那么这个和最小可能是多少?请给出一种填法.24.如图,大三角形被分成了9个小三角形.试将1、2、3、4、5、6、7、8、9分别填相加的和相等.这5个数的和最大可能是多少?请给出一种填法.25.请在图的每个空格内填入一个合适的数,使得每行、每列及两条对角线上的3个方格中的各数之和都相等.26.如图是有名的“六角幻方”:将l到19这19个自然数填人图中的圆圈中,使得每一条直线上圆圈中的各数之和相等,美国数学爱好者阿当斯从l910年开始,到1962年,用了52年的时间才找到了解答.我们给大家填人了6个自然数,请你完成这个“六角幻方”.27.在图中有6个正方形,请你将1至9填人图中,使得每个正方形的4个顶点上的数字之和都相等.28.在图中的七个圆圈中填人一些自然数,要求所填的自然数中最小的一个数是1,并且相邻两个圆圈内的数字之差(大数减小数)恰好等于这两个圆圈之间标出的数字.29.将1至9分别填人图中的9个圆圈内,使图中每条直线(图中有7条直线)上的圆圈内所填数之和都相等,那么这个和是多少?30.将0,1,2,…,9这10个数分别填人图20﹣30中的各个圆圈内,使得各阴影三角形的3个顶点上的数之和相等.这个和最大是多少?最小是多少?请分别给出使得和最大、最小的填法.31.在下面的图中有11个空的圆圈,要求把1~13这些数填入各圈内(其中3,4已经填好),使得上面两个圆圈内数的和,等于与它相连的下面的圆圈内的数(例如,虚线框中上面两个圈中的数相加,它们的和应等于相连的下面一个圈中的数),并且最下面空着的四圆圈中的数之和等于43.32.图中共有10个圆圈,6条直线.请问:(1)能否将l至10填人图中,使得每条直线上各数之和都相等?(2)能否将0至9填入图中,使得每条直线上各数之和都相等?(3)请从1至1l中去掉一个数后,将剩下的数填人图中使得每条直线上各数之和都相等.参考答案1.由以上分析可得:【解析】试题分析:我们从图中可以看出:中间圆圈内所填的数是三条直线上共用的,它是一个“重复用数”.因此,我们在思考时,应该首先把中间圆圈内的数想出来.这样,根据题目中“每条直线上的三个数的和相等”,只需考虑每条直线上两个数的和相等.1~7七个数字的和为28,只有中间圆圈内填上一个数字后,剩下的六个数字的和能被3整除(因为要分成和相等的三组数),才能填写.所以,中间圆圈内所填的数很快可以确定下来:可为1、4、7.这时,其它圆圈内的数也就可以很快填出.解:根据题意可得:当中间圆圈填入1时,剩下的六个数:2+7=3+6=4+5;那么三条直线上的和是2+7+1=10,而两个圆圈上的三个数2+3+5=10,另外三个数7+6+4=17,所以不符合;当中间圆圈填入7时,剩下的六个数:1+6=2+5=3+4,那么三条直线上的和是1+6+7=14,而两个圆圈上的三个数不论怎么填都得不到14,所以不符合;当中间圆圈填入4时,剩下的六个数:1+7=2+6=3+5;那么三条直线上的和是1+7+4=12,又1+5+6=12,7+3+2=12;由以上分析可得:点评:解答此题的关键是求出中间圆圈的数是多少,然后再进一步解答即可.2.【解析】试题分析:首先根据第1列的三个数为16、11、12,求出幻和为:16+11+12=39;然后根据幻和为39,分别求出空格里的数即可.解:因为第1列的三个数为16、11、12,所以幻和为:16+11+12=39;因此第2行的第2个数为:39﹣11﹣15=13,第1行的第3个数为:39﹣12﹣13=14,第1行的第2个数为:39﹣16﹣14=9,第2列的第3个数为:39﹣9﹣13=17,第3列的第3个数为:39﹣14﹣15=10..点评:此题主要考查了幻方问题的应用,解答此题的关键是首先求出幻和是多少.3.【解析】试题分析:首先求出每行、每列、每条对角线上所填数之和均为:12+9+5+8=34,然后根据这个共同的和为34,分别求出空格里的数即可.解:每行、每列、每条对角线上所填数之和均为:12+9+5+8=34,所以第3行的第1个数为:34﹣5﹣16﹣3=10,第2列的第1个数为:34﹣4﹣5﹣11=14,第1行的第1个数为:34﹣14﹣7﹣12=1,第2行的第1个数为:34﹣1﹣10﹣8=15,第2行的第4个数为:34﹣15﹣4﹣9=6,第3列的第4个数为:34﹣7﹣9﹣16=2,第4列的第4个数为:34﹣12﹣6﹣3=13..点评:此题主要考查了幻方问题的应用,解答此题的关键是求出每行、每列、每条对角线上所填数之和均为34.4.【解析】试题分析:首先根据第1列的三个数分别为2、3、7,可得各列的各数之和均为:2+3+7=12;然后用12减去6,可得第4列的第1个数和第3个数的和是6,因此第4列的第1个数、第3个数可以分别为5、1;再求出第1行的4个数的和是:2+4+5+5=16,根据各行所填的数之和为16,各列所填的数之和为12,求出其余的空格中的数即可.解:根据第1列的三个数分别为2、3、7,可得各列的各数之和均为:2+3+7=12,所以第4列的第1个数和第3个数的和是:12﹣6=6,因此第4列的第1个数、第3个数可以分别为5、1;因为第1行的4个数的和是:2+4+5+5=16,所以第2行的第2个数和第3个数的和是:16﹣3﹣6=7,第3行的第2个数和第3个数的和是:16﹣7﹣1=8,第2列的第2个数和第3个数的和是:12﹣4=8,第3列的第2个数和第3个数的和是:12﹣5=7,因此第2行的第2个数和第3个数分别是5、2,第3行的第2个数和第3个数分别是3、5.答:标有符号“*”的方格内所填的数是1..点评:此题主要考查了幻方问题的应用,解答此题的关键是灵活应用“各行所填的数之和相等,各列所填的数之和也相等”,注意答案不唯一.5.【解析】试题分析:如图,首先根据第1行和对角线上a、15、11三个数的和相等,可得b+12=15+11,解得b=14,所以幻和为14+15+16=45;然后根据幻和为45,分别求出a、c、d、e的值即可.解:如图,根据第1行和对角线上a、15、11三个数的和相等,可得b+12=15+11,解得b=14,所以幻和为:14+15+16=45;因此a=45﹣12﹣14=19,c=45﹣19﹣16=10,d=45﹣10﹣15=20,e=45﹣16﹣11=18.点评:此题主要考查了幻方问题的应用,解答此题的关键是求出幻和是多少.6.△=5,▽=5,○=4.【解析】试题分析:根据图示,因为h在第3列中,所以h不能是1、3;又因为h在第3行中,所以h不能是4;因为h在对角线上,所以h不能是5,因此h=2,a、p只能从1、3中各取一个,因为a在第1行中,所以a不能是1,只能是3,则p=1;因为c、l在第4列中,只能从3、5中各取一个,因为c在第1行中,所以c不能是3,只能是5,则l=3;因为e、△在第3列中,只能从4、5中各取一个,因为e在第2行中,所以e不能是5,只能是4,则△=5;因为d、f在第2行中,只能从1、3中各取一个,因为d在第1列中,所以d不能是3,只能是1,则f=3;因为k、m在对角线上,只能从1、4中各取一个,因为m在第1列中,所以m不能是1,只能是4,则k=1;因为○、b在第1行中,只能从2、4中各取一个,因为b在第4列中,所以b不能是4,只能是2,则○=4;所以j=2,▽=5,g=3,i=1,n=2,o=5,据此解答即可.解:(1)根据图示,因为h在第3列中,所以h不能是1、3;又因为h在第3行中,所以h不能是4;因为h在对角线上,所以h不能是5,因此h=2,a、p只能从1、3中各取一个,因为a在第1行中,所以a不能是1,只能是3,则p=1;(2)因为c、l在第4列中,只能从3、5中各取一个,因为c在第1行中,所以c不能是3,只能是5,则l=3;(3)因为e、△在第3列中,只能从4、5中各取一个,因为e在第2行中,所以e不能是5,只能是4,则△=5;同理,可得d=1,f=3;m=4,k=1;b=2,○=4;j=2,▽=5,g=3,i=1,n=2,o=5.答:△=5,▽=5,○=4..点评:此题主要考查了幻方问题的应用,解答此题的关键是灵活应用“每行,每列和每条对角线的5个方格内所填的5个数中,l、2、3、4、5恰好各出现一次”,逐一确定每个方格中的数字.7.2种.【解析】试题分析:首先第一行第二列的数最大,只能是9,第一行的第三列最小只能是1,第一行第一列只能是8,第二行第一列只能是7,第二行第三列只能是2,第三行第三列只能是3,第三行第二列只能是4,中间的数可以是6或5,而第三行第一列可以是6或5,所以满足要求的方法有2种方法.解:答案如下:所以满足要求的填法共有2种.点评:解决此题的关键找出最大最小数的位置,进一步确定固定的数以及可调整的数,得出结论.8.【解析】试题分析:首先根据两个小圆圈内所填的数的差最大是:8﹣1=7,可得当差为7时,只能是8与1的差;剩下的2、3、4、5、6、7这6个数组成的差最大是:7﹣2=5,所以当差为6时,只能是7与1的差;同理,当差为5时,只能是6与1的差;5与4的差为1,5与3的差为2,5与2的差差为3,5与1的差为4;据此可得中间两个圆圈中的数分别为1、5,然后填上其余圆圈中的数即可.解:因为两个小圆圈内所填的数的差最大是:8﹣1=7,所以当差为7时,只能是8与1的差;因为剩下的2、3、4、5、6、7这6个数组成的差最大是:7﹣2=5,所以当差为6时,只能是7与1的差;同理,当差为5时,只能是6与1的差;5与4的差为1,5与3的差为2,5与2的差差为3,5与1的差为4;因此中间两个圆圈中的数分别为1、5,可得点评:此题主要考查了幻方问题的应用,解答此题的关键是判断出中间两个圆圈中的数只能是1和5.9.【解析】试题分析:1+2+3+4+5=15,根据题意,可得计算横线、竖线、大圆周上所填数之和时,圆圈中的每个数均被计算了2次,所以这个共同的和是:15×2÷3=10;然后根据1+4+5=2+3+5=1+2+3+4,可得中心圆圈的数为5,大圆周上所填数为1、2、4、3,据此解答即可.解:1+2+3+4+5=15,根据题意,计算横线、竖线、大圆周上所填数之和时,圆圈中的每个数均被计算了2次,所以这个共同的和是:15×2÷3=10;根据1+4+5=2+3+5=1+2+3+4,可得中心圆圈的数为5,大圆周上所填数为1、2、4、3.点评:此题主要考查了幻方问题的应用,解答此题的关键是求出横线、竖线、大圆周上所填数之和均为10.10.【解析】试题分析:如图,设图中的六块区域内填入的数分别为:A、B、C、D、E、F,则根据题意,可得A+B+C+D=C+D+E+F=A+B+E+F=B+C+E,整理,可得A+B=C+D=E+F;因为1+6=2+5=3+4,所以A、B可以从1、6中个取一个,C、D可以从2、5中各取一个,E、F可以从3、4中各取一个;最后根据B+C+E=2(A+B)=2×7=14,可得B=6,C=5,E=3,据此解答即可.解:如图,设图中的六块区域内填入的数分别为:A、B、C、D、E、F,则根据题意,可得A+B+C+D=C+D+E+F=A+B+E+F=B+C+E,整理,可得A+B=C+D=E+F;因为1+6=2+5=3+4,所以A、B可以从1、6中个取一个,C、D可以从2、5中各取一个,E、F可以从3、4中各取一个;又因为B+C+E=2(A+B)=2×7=14,所以B=6,C=5,E=3,可得.点评:此题主要考查了幻方问题的应用,解答此题的关键是设图中的六块区域内填入的数分别为:A、B、C、D、E、F,能判断出A+B=C+D=E+F.11.这个和最小是11,最大是16,如图所示:【解析】试题分析:根据图示,可得每个圆圈内的3个数有1个是圆圈独有的,有2个是和其它圆圈共有的;因为每个圆内的三个数之和都是相等的,所以要使这个和最小,则5个圆圈共有的5个数的和最小,是0、1、2、3、4;要使这个和最大,则5个圆圈共有的5个数的和最大,是5、6、7、8、9;据此解答即可.解:0+1+2+3+4+5+6+7+8+9=45,根据图示,可得每个圆圈内的3个数有1个是圆圈独有的,有2个是和其它圆圈共有的;(1)因为每个圆内的三个数之和都是相等的,所以要使这个和最小,则5个圆圈共有的5个数的和最小,是0、1、2、3、4,这个和最小是:(45+0+1+2+3+4)÷5=11;(2)所以要使这个和最大,则5个圆圈共有的5个数的和最大,是5、6、7、8、9,这个和最大是:(45+5+6+7+8+9)÷5=16.答:这个和最小是11,最大是16.点评:此题主要考查了最大与最小问题的应用,解答此题的关键是判断出:要使这个和最小,则5个圆圈共有的5个数的和最小;要使这个和最大,则5个圆圈共有的5个数的和最大.12.4.【解析】试题分析:首先根据第1列和对角线19、g、25、13的各数之和相等,可得g+19+25+13=20+9+23+12,解得g=7;然后根据第4列和第5行的各数之和相等,可得b+25+14+3=i+8+15+24,解得b=i+5…①;根据第1列和第1行的各数之和相等,可得i+12+23+9=a+b+*+13,解得b=i﹣a ﹣*+31…②;再根据第5行和对角线i、19、7、25、13的各数之和相等,可得j+8+15+24=19+7+25+13,解得j=17;再根据第1行和对角线20、c、7、3、24的各数之和相等,可得a+*+b+13=c+7+3+24,解得c=b+5;再根据第2列和第3行的各数之和相等,可得a+c+19+8=23+7+14+16,解得a+c=33;再根据第5列和第2行的各数之和相等,可得13+16+10+24=9+c+d+25,解得c+d=29;再根据第3列和第4行的各数之和相等,可得*+d+7+15=12+19+3+10,解得*+d=22;解:根据第1列和对角线19、g、25、13的各数之和相等,可得g+19+25+13=20+9+23+12,解得g=7;根据第4列和第5行的各数之和相等,可得b+25+14+3=i+8+15+24,解得b=i+5…①;根据第1列和第1行的各数之和相等,可得i+12+23+9=a+b+*+13,解得b=i﹣a﹣*+31…②;由①②,可得a+*=26;根据第5行和对角线i、19、7、25、13的各数之和相等,可得j+8+15+24=19+7+25+13,解得j=17;根据第1行和对角线20、c、7、3、24的各数之和相等,可得a+*+b+13=c+7+3+24,解得c=b+5;根据第2列和第3行的各数之和相等,可得a+c+19+8=23+7+14+16,解得a+c=33;根据第5列和第2行的各数之和相等,可得13+16+10+24=9+c+d+25,解得c+d=29;根据第3列和第4行的各数之和相等,可得*+d+7+15=12+19+3+10,解得*+d=22;综上,可得a=22,*=4,因此d=22﹣4=18,c=29﹣18=11,b=11﹣5=6,f=b﹣1=5,e=(20+22+4+6)﹣(16+10+24)=52﹣50=2,h=(20+22+4+6+13)﹣(12+19+3+10)=65﹣44=21,i=(20+22+4+6+13)﹣(20+9+23+12)=65﹣64=1,h=(20+22+4+6+13)﹣(1+8+15+24)=65﹣48=17.答:标有符号“*”的方格内所填的数是4..点评:此题主要考查了幻方问题的应用,解答此题的关键是灵活应用“每行、每列及两条对角线上的数的和相等”.13.【解析】试题分析:(1)首先根据第2行和第1列的各数之和相等,可得a+95=100+19,解得a=24;然后根据第3列和对角线95、100、c三个数的和相等,可得f+19=95+100,解得f=176;再根据第3行和第2列的三个数的和相等,可得b+100=95+176,解得b=171;再求出另一条对角线上的三个数的和,进而求出c、d、e的值是多少即可.(2)首先根据第2行和第1列的各数之和相等,可得q+6=5+9,解得q=8;然后根据第3列和对角线9、8、n三个数的和相等,可得s+6=9+8,解得s=11;最后根据另一条对角线上的三个数分别是5、8、11,求出三个数的和是多少,进而求出n、m、p、r的值是多少即可.解:(1)根据第2行和第1列的各数之和相等,可得a+95=100+19,解得a=24;根据第3列和对角线95、100、c三个数的和相等,可得f+19=95+100,解得f=176;根据第3行和第2列的三个数的和相等,可得b+100=95+176,解得b=171;另一条对角线上的三个数的和为:24+100+176=300,所以c=300﹣24﹣171=105,d=300﹣100﹣19=181,e=300﹣95﹣176=29.(2)根据第2行和第1列的各数之和相等,可得q+6=5+9,解得q=8;根据第3列和对角线9、8、n三个数的和相等,可得s+6=9+8,解得s=11;根据另一条对角线上的三个数分别是5、8、11,可得三个数的和是:5+8+11=24,所以n=24﹣9﹣8=7,m=24﹣5﹣7=12,p=24﹣8﹣6=10,r=24﹣12﹣8=4..点评:此题主要考查了幻方问题的应用,解答此题的关键是灵活应用“每行、每列及两条对角线上的3个方格中的各数之和都相等”,逐一确定每个空格中的数即可.14.11.12.【解析】试题分析:首先根据题意,可得c+f=19.95﹣4.33=15.62…①,e+f=19.95﹣8.80=11.15…②;然后根据第1行和第2列的三个数的和相等,可得*=8.80+c﹣4.33=4.47+c;再根据两条对角线上的三个数的和相等,可得*=4.33+f﹣e,所以 4.47+c=4.33+f﹣e,整理,可得f﹣c﹣e=0.14…③;由①②③,求出f、c的值,进而求出*是多少即可.解:根据题意,可得c+f=19.95﹣4.33=15.62…①,e+f=19.95﹣8.80=11.15…②;根据第1行和第2列的三个数的和相等,可得*=8.80+c﹣4.33=4.47+c;根据两条对角线上的三个数的和相等,可得*=4.33+f﹣e,所以4.47+c=4.33+f﹣e,整理,可得f﹣c﹣e=0.14…③;由①+②+③,可得3f=26.91,解得f=8.97,所以c=15.62﹣8.97=6.65,所以*=4.47+c=4.47+6.65=11.12.答:标有“*”的方格内所填的数是11.12.点评:此题主要考查了幻方问题的应用,解答此题的关键是灵活应用“每行、每列及两条对角线上的3个方格中的各数之和都等于19.95”,确定出两条对角线上的数分别是多少.15.【解析】试题分析:首先根据第1行和第1列的三个数的和相等,可得第1行的第3个数为:29+19﹣17=31;然后根据第2行的三个数和对角线上的三个数的和相等,可得第2行的第3个数为:19+31﹣29=21;再根据第2行和第2列的三个数的和相等,可得第2列的第3个数为:29+21﹣17=33;最后根据第1行和第3列的三个数的和相等,可得第1行的第1个数比第3列的第3个数多:21﹣17=4,再根据两条对角线上的三个数的和相等,可得第1行的第1个数和第3列的第3个数的和为:19+31=50,据此求出第1行的第1个数和第3列的第3个数分别是多少,进而求出中心方格的数是多少即可.解:第1行的第3个数为:29+19﹣17=31;第2行的第3个数为:19+31﹣29=21;第2列的第3个数为:29+21﹣17=33;第1行的第1个数比第3列的第3个数多:21﹣17=4,第1行的第1个数和第3列的第3个数的和为:19+31=50,所以第1行的第1个数为:50÷2+2=27,第3列的第3个数为:50÷2﹣2=23;中心方格的数为:(27+17+31)﹣(29+21)=75﹣50=25.点评:此题主要考查了幻方问题的应用,解答此题的关键是灵活应用“每行、每列及两条对角线上的3个方格中的各数之和都相等”,逐一判断出每个方格中的数是多少.16.【解析】试题分析:首先在0﹣9这10个数字中,找出0、1、6、8、9这5个数字倒过来是0、1、9、8、6;本题中用了1、6、8、9这4个数字,并且对角线上的数的个位相加都是7,所以本题用不上数字0,所以中间的小正方形四个角的圆圈里四个数还是1、6、8、9;然后分析确定出相应的数字即可.解:在0﹣9这10个数字中,有0、1、6、8、9这5个数字倒过来是0、1、9、8、6;本题中用了1、6、8、9这4个数字,并且对角线上的数的个位相加都是7,所以本题用不上数字0,所以中间的小正方形四个角的圆圈里四个数还是1、6、8、9;左下右上的圆圈里已经有了91、86,所以最简单的方法只需要在这条对角线里圈里的两个圆圈里填上19、68即可;左上右下的圆圈里已经有了19、68,所以只需要在这条对角线里圈里的两个圆圈里填上91、86即可.答:左上、左下、右上、右下的圆圈里应分别填上:91、68、19、86.实际上,还有很多种方法,例如:点评:此题主要考查了学生的分析推理能力,分析确定出中间的小正方形四个角的圆圈里四个数还是1、6、8、9是解答本题的关键.17.【解析】试题分析:如图,根据每条直线上各数之和都相等,可得a﹣b=9﹣1=8,除1、3、9之外的8个数中只有10、2两个数相差8,所以a=10,b=2;然后根据a+b=c+d,可得c+d=10+2=12,而且c﹣d=3﹣1=2,解得c=7,d=5;最后求出每条直线上的和是多少,进而求出e、f的值是多少即可.解:根据每条直线上各数之和都相等,可得a﹣b=9﹣1=8,除1、3、9之外的8个数中只有10、2两个数相差8,所以a=10,b=2;因为a+b=c+d,可得c+d=10+2=12,而且c﹣d=3﹣1=2,解得c=7,d=5;因此每条直线上的和为:10+3+5=18,所以e=18﹣5﹣7=6,f=18﹣5﹣2=11.点评:此题主要考查了幻方问题的应用,解答此题的关键是首先根据题意,分别求出四个角上的数分别是多少.18.【解析】试题分析:首先根据b、c的差是9,可得b、c只能是10、1各一个;然后根据c是1时,d、f的差是1,所以d、f是两个相邻的自然数,而且d=f+1;b是10时,a、b的差是e,所以a、e只能是2、8或3、7或4、6;(1)当a=2,e=8时,g=9﹣8=1,与c=1矛盾,因此e=2,则g=9﹣2=7;d、f、h、i从3、4、5、6中各取一个,经验证,可得d=6,f=5,h=4,i=3.(2)当a、e是6、4时,g=9﹣4=5,d、f、h、i从2、3、7、8中各取一个,经验证,可得d=8,f=7,h=2,i=3.(3)经验证,当a、e是3、7时,不符合题意.解:根据b、c的差是9,可得b、c只能是10、1各一个;当c是1时,d、f的差是1,所以d、f是两个相邻的自然数,而且d=f+1;当b是10时,a、b的差是e,所以a、e只能是2、8或3、7或4、6;(1)当a=2,e=8时,g=9﹣8=1,与c=1矛盾,因此e=2,则g=9﹣2=7;d、f、h、i从3、4、5、6中各取一个,经验证,可得d=6,f=5,h=4,i=3.,根据对称性,可得满足题意的还有:(2)当a、e是6、4时,g=9﹣4=5,d、f、h、i从2、3、7、8中各取一个,经验证,可得d=8,f=7,h=2,i=3.根据对称性,可得满足题意的还有:(3)经验证,当a、e是3、7时,不符合题意.点评:此题主要考查了幻方问题的应用,解答此题的关键是灵活应用“除了第一行外每个圆圈内的数都等于与它相连的上方两个圆圈内的两数之差”,逐一确定出每个圆圈中的数字即可.19.【解析】试题分析:如图,根据题意,可得a=(13+17)÷2=15,然后根据13+c=15+d=17+e=2f,可得c=d+2,d=e+2,再根据d+13=2e,可得e+2+13=2e,解得e=15,所以d=15+2=17,c=17+2=19,f=(19+13)÷2=16,据此解答即可.解:如图,根据题意,可得a=(13+17)÷2=15,因为13+c=15+d=17+e=2f,所以c=d+2,d=e+2,又因为d+13=2e,所以e+2+13=2e,解得e=15,所以d=15+2=17,c=17+2=19,f=(19+13)÷2=16.点评:此题主要考查了幻方问题的应用,解答此题的关键是首先求出a的值,并灵活应用“居中的数是旁边两个数的平均数”这一条件.20.6732489.【解析】试题分析:首先根据题意,可得A、B、C、D、E、F、G中不可能有1,也不可能有5,因此A、B、C、D、E、F、G只能是2、3、4、6、7、8、9各一个;然后根据C的正下方第二个数是3,D的正下方第一个数是2,所以C=3,D=2;根据图示,可得最下面一行中一定没有6,最下面一行中或者左边两个都不是9,或者右边两格都不是9,最下面一行中不可能有2个8,因此最下面一行中必有5,而且只能是A=9,B=8,或者G=9,F=8,经推理,可得G=9,F=8,E=4,A=6,B=7,所以七位数是6732489,据此解答即可.解:因为只有1个1,而且D的正下方第二个数是1,所以A、B、C、D、E、F、G中不可能有1,因为相同的数所在的方格都连在一起(相连的两个方格必须有公共边),所以A、B、C、D、E、F、G中也不可能有5,因此A、B、C、D、E、F、G只能是2、3、4、6、7、8、9各一个;因为C的正下方第二个数是3,D的正下方第一个数是2,所以C=3,D=2;根据图示,可得最下面一行中一定没有6,最下面一行中或者左边两个都不是9,或者右边两格都不是9,最下面一行中不可能有2个8,因此最下面一行中必有5,而且只能是A=9,B=8,或者G=9,F=8,经推理,可得G=9,F=8,E=4,A=6,B=7,所以七位数是6732489.答:七位数是6732489.点评:此题主要考查了幻方问题的应用,考查了分析推理能力的应用,解答此题的关键是灵活应用“相同的数所在的方格都连在一起(相连的两个方格必须有公共边)”,逐一确定出每个字母代表的数是多少即可.21.由以上分析可得:.【解析】试题分析:我们从图中可以看出:中间圆圈内所填的数是三条直线上共用的,它是一个“重复用数”.因此,我们在思考时,应该首先把中间圆圈内的数想出来.这样,根据题目中“每条直线上的三个数的和相等”,只需考虑每条直线上两个数的和相等.1~7七个数字的和为28,只有中间圆圈内填上一个数字后,剩下的六个数字的和能被3整除(因为要分成和相等的三组数),才能填写.所以,中间圆圈内所填的数很快可以确定下来:可为1、4、7.这时,其它圆圈内的数也就可以很快填出.解:根据题意可得:当中间圆圈填入1时,剩下的六个数:2+7=3+6=4+5;那么三条直线上的和是2+7+1=10,而两个圆圈上的三个数2+3+5=10,另外三个数7+6+4=17,所以不符合;当中间圆圈填入7时,剩下的六个数:1+6=2+5=3+4,那么三条直线上的和是1+6+7=14,而两个圆圈上的三个数不论怎么填都得不到14,所以不符合;当中间圆圈填入4时,剩下的六个数:1+7=2+6=3+5;那么三条直线上的和是1+7+4=12,又1+5+6=12,7+3+2=12;由以上分析可得:。
小学数学《幻方与数阵图》练习题(含答案)
1. 把1~8这8个数,分别填入图中的方格内(每个数必须用一次),使“十一”三笔中每三个方格内数的和都相等.
解:
2. 把1~11这11个数分别填入如下图11个○内,使每条虚线上三个○内数的和相等,一共有几种不同的和?
解:
3. 在下图中的几个圈内各填一个数,使每一条直线上的三个数中,当中的数是两边两个数的平均数,现在已经填好两个数,
解:
4. 在图的每个圆圈内填上适当的质数(不得重复),使每条直线上三个数的和相等,且均为偶数.
解:
5. 图有五个圆,它们相交相互分成9个区域,现在两个区域里已经填上10与6,请在另外七个区域里分别填进2.3.4.5.
6.
7.9七个数,使每圆内的和都等于15.
解:
6. 把1~16这16个数,填入图中的16个○内,使五个正方形的四个顶点上○内数的和相等.
解:
7. 将1-12这十二个数分别填入图中的十二个小圆圈里,使每条直线上的四个小圆圈中的数字之和26. 解:
8. 在图中的空格中填入四个数,使每个横行,每个竖行的三个数的积都相等.
解:
9. 把1~12这十二个数,填入下图中的12个○内,使每条线段上四个数的和相等,两个同心圆上的数的和也相等.
解:
10. 将1~9这九个数分别填入图中○内,使每条线段三个数相等.
解:
作业:
1. 10个连续的自然数中第三个的数是9,把这10个数填入图中的10个方格内,每格填一个数,要求图中3个2×2的正方形中4个数之和相等,那么这个和最小值是______.
答案: 24.
2. 把1~11填入图中,使每条线上三个数的和相等.
答案:
4 7 1 3 8
2 9 5 6 11 1 6
3 9 2 10 5 8
4 7
3. 把1~8,填入图中,使每条线及正方形四个顶点上的数的和相等.
答案:
4. 把1~9,填入下图中,使每条线段三个数和及四个顶点的和也相等.
答案:
5. 把17,23,25,31,46,53,58,66,72,88,94,100十二个数填入下图,使任意三个相邻的数相加的和除以7的余数相等.
答案:。