广东省江门市2017-2018学年高一上数学10月月考试题(5)含答案(打印版)

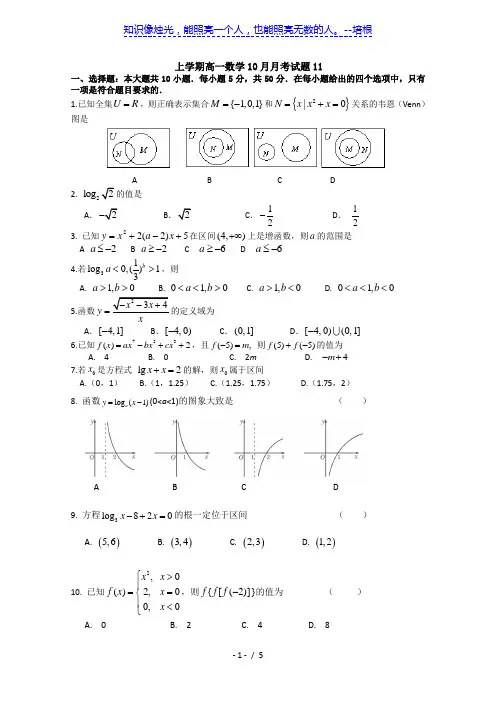
上学期高一数学10月月考试题11一、选择题：本大题共10小题．每小题5分，共50分．在每小题给出的四个选项中，只有一项是符合题目要求的．1.已知全集U R=，则正确表示集合{1,0,1}M=-和{}2|0N x x x=+=关系的韦恩（Venn）图是A B C D2.2log2的值是A．2-B．2C．12-D．123. 已知5)2(22+-+=xaxy在区间(4,)+∞上是增函数，则a的范围是A 2a≤- B 2a≥- C 6-≥a D 6-≤a4.若31log0,()13ba<>，则A. 1,0a b>> B. 01,0a b<<> C. 1,0a b>< D. 01,0a b<<<5.函数234x xy--+=的定义域为A．[4,1]-B．[4,0)-C．(0,1]D．[4,0)(0,1]-6.已知753()2f x ax bx cx=-++，且(5),f m-=则(5)(5)f f+-的值为A. 4B. 0C. 2mD. 4m-+7.若x是方程式lg2x x+=的解，则x属于区间A.（0，1）B.（1，1.25）C.（1.25，1.75）D.（1.75，2）8.函数log(1)ay x=-(0<a<1)的图象大致是（）A B C D9.方程3log820x x-+=的根一定位于区间（）A. ()5,6 B. ()3,4 C. ()2,3 D. ()1,210.已知2,0()2,00,0x xf x xx⎧>⎪==⎨⎪<⎩，则)]}2([{-fff的值为（）A. 0B. 2C. 4D. 8二、填空题：(本大题5个小题，每小题5分，共25分)11．若幂函数()f x 的图象过点2,2⎛ ⎝⎭，则()9f = .12．函数2()ln f x x=的定义域为 .13．若函数f (x )＝(2a －1)x ＋b 在R 上是减函数，则a 的取值范围是________． .14．已知集合{}3log (1)2A x x =-<,1()33x B x ⎧⎫=>⎨⎬⎩⎭则R AC B =_____ .15. 集合M ＝{1，2，3}的子集的个数为________．三、解答题：(本大题5个小题，共75分)各题解答必须答在答题卡上，必须写出必要的文字说明、演算步骤或推理过程.16. （本题满分10分）已知集合A ＝{x |3≤x <7}，B ＝{x |2<x <10}，求∁R (A ∪B )，A ∩B .17.（本题满分12分）已知函数()f x =A ，函数()lg(2)g x x =-的定义域是集合B. （1）求集合A 、B ；（2）若A B B ⋃=，求实数a 的取值范围.18. （本小题满分14分） 计算求值(I ) 1100.753270.064()160.258---++ (II ) 22lg 5lg 5lg 4lg 2+⋅+19. （本小题满分12分）已知),0(56>-=a a x求xx xx aa a a ----33的值。

上学期高一数学10月月考试题08共150分；时间120分钟第Ⅰ卷（选择题共60分）一、选择题：在每小题给出的四个选项中，只有一项是符合题目要求的，请把正确答案的代号填在题后的括号内（每小题5分，共60分）．1.设全集为R ,{}{}|22|1)R M x x N x x M N =-≤≤=<⋂=则(C ( ){}{}|2|21A x x B x x <--<< {}{}|1|21C x x D x x <-≤<2.下列四组函数，表示同一函数的是( )A ．f （x ）=2x ，g （x ）=x B ．f （x ）=x ，g （x ）=2x x C ．2(),()2ln f x lnx g x x == D ．33()log (),()x a f x a a g x x =>0,α≠1=3.设已知函数21,0(),0x x f x x x +≥⎧=⎨<⎩，则f [f (2-)]的值为（ ）． A ．1- B 2 C. 4 D.54.下列函数中，是奇函数是（ ）A .2x y = B. x y lg = C.3y x = D.1+=x y5. 当0＜a ＜1时，在同一坐标系中，函数x y a -=与log a y x =的图象是( )6.下列函数中，在区间)2,0(上递增的是（ ）A xy 1= B x y -= C 1-=x y D 122++=x x y 7．令0.760.76,0.7,log 6a b c ===，则三个数a 、b 、c 的大小顺序是( )A ．b ＜c ＜aB ．b ＜a ＜cC ．c ＜a ＜bD ．c ＜b ＜a8.{}=|1A x x ≤已知集合{}|,B x x a A B R a =≥⋃=且则实数的取值范围是 ( )A 1a <B 1a ≤C 1a >D 1a ≥9.幂函数y=f(x)的图象经过点1(2,)8--，则满足f(x)=27的x 的值为（ ） A 13 B 3 C -3 D 1210. 若2log 31x =，则39x x +的值为( )A ．6B ．3C ．52D ．1211. [)[)22,1,,1,x x a x x x++∈+∞∈+∞已知函数f(x)=若对于,f(x)>0恒成立，则a 的取值范围（ ）A 3a >-B 3a ≥-C 1a >D 1a ≥12.()f x =已知 (23)1,1log , 1x a a x x x --<⎧⎨-≥⎩是R 上的增函数，则实数a 的取值范围为（ ） A 203a << B 1a<13≤ C 213a << D 1233a ≤< 第Ⅱ卷(非选择题共90分)二、填空题(本大题共4小题，每小题5分，共20分)。

上学期高一数学10月月考试题06一、选择题：本大题共10小题，每小题5分，满分50分．在每小题给出的四个选项中，只有一个是符合题目要求的．1. 已知集合{}1,2A =, {}1,0,1B =-, 则A B I 等于 （ ） A .{}1 B. {}1,0,2- C. {}1,0,1,2- D. ∅2. cos120︒的值是 （ ） A . 32-B. 12- C. 12 D. 32 3. 函数sin 2y x =是 （ ）A . 最小正周期为2π的偶函数 B. 最小正周期为2π的奇函数 C. 最小正周期为π的偶函数 D. 最小正周期为π的奇函数 4.已知函数 2()log (1),f x x =+若()1,f α= α=（ ） A 、 0B 、1C 、2D 、35. 若向量a v =(1,1)，b v =(2，5)，c v =(3，x)满足条件(8a v —b v )·c v=30，则x=( ) A ．6 B ．5 C ．4 D ．3 6、设函数()23,(2)()f x x g x f x =++=，则()g x 的表达式是（ ） A 21x + B 21x - C 23x - D 27x + 7. 函数f(x)=23xx +的零点所在的一个区间是( )(A)（-2，-1） (B)（-1,0） (C)（0,1） (D)（1,2） 8.设0abc >，二次函数()2f x ax bx c =++的图象可能是（ ）9、函数)(x f y =的图象如图所示，则)(x f y =的解析式为（ ）A.y=sin2x-2B.13cos 2-=x yC.1)52sin(--=πx yD. )52sin(1π--=x y10. 定义平面向量之间的一种运算“⊙”如下，对任意的a=(m,n)r ，b p,q)=r（，令a r ⊙b r mq np =-，下面说法错误的是（ ）A.若a r 与b r共线，则a r ⊙b r 0= B. a r ⊙b r = b r ⊙a rC.对任意的R λ∈，有()a λr ⊙b r = (a λr ⊙)b rD. (a r ⊙b r )2222()a b a b +⋅=v v v v二、填空题：本大题共4小题，每小题5分，满分20分. 11. 函数()ln 21y x =-的定义域是 .12. 已知向量(2,1),(1,),(1,2)a b m c =-=-=-r r r ,若()a b +r r∥c r ，则m ＝_____________.13、如果a x x x f ++=2)(在[1,1]-上的最大值是2，那么()f x 在[1,1]-上的最小值是_____ 14、在平面内，A 点的坐标为（2，4），B 点的坐标为（-1,0），则AB 两点间的距离为__________ 三.解答题（本题共6小题，共80分） 15、（本题12分）（1）设α为第四象限角，其终边上一个点为()5,-x ，且x 42cos =α，求αsin 。

上学期高一数学10月月考试题10第Ⅰ卷 客观卷（共48分）一、选择题（每小题4分，共48分）1． 设集合{08}U x N x =∈<≤，{1,2,3,4,5}S =，{3,5,7}T =，则()U S C T I = ( )A ．{1,2,4}B ．{1,2,3,4,5,7}C ．{1,2}D ．{1,2,4,5,6,8}2． 三个数20.3，2log 0.3，0.32的大小顺序是( )A. 2log 0.3<0.32<20.3B. 20.3<2log 0.3<0.32C. 2log 0.3<20.3<0.32D. 20.3<0.32<2log 0.3 3． 已知幂函数()f x x α=（α为常数）的图象过1(2,)2，则()f x 的单调递减区间是（ ）A ．(],0-∞B ．(),-∞+∞C ．()(),00,-∞+∞UD ． ()(),0,0,-∞+∞ 4．下列函数中，值域是()0,+∞的是（ ）A. 231y x x =-+B. 21y x =+C. 21y x x =++D. 21y x= 5． 设0x 是方程ln 4x x +=的解，则0x 属于区间（ ）A. ()0,1B. ()1,2C. ()2,3D. ()3,46．若函数()f x 的定义域是[]2,4-，则()()()g x f x f x =+-的定义域是（ ）A ．[]4,4- B. []2,2- C. []4,2-- D. []2,47．已知函数223y x x =-+在区间[]0,m 上的最大值为3，最小值为2，则m 的取值范围是（ ）A ．[)1,+∞B ．[]0,2C ．[]1,2D ．(],2-∞8． 函数()y f x =的图象如下图所示，则函数()0.2log y f x =的图象大致是9．已知定义域为R 的函数()f x 在区间()8,+∞上为减函数，且函数()8y f x =+为偶函数，则（ ）A ．()()67f f >B ．()()69f f >C ．()()79f f >D ． ()()710f f >10．已知()f x 是奇函数，且当0x >时，()2f x x x =-，则0x <时，()f x 的表达式为（ ）A ．()2f x x x =+B ．()2f x x x =-C ．()2f x x x =-+D ．()2f x x x =--11．为了得到函数lg y x =的图象，只需把函数3lg 10x y +=的图象上所有的点（ ） A ．向左平移3个单位长度，再向上平移1个单位长度B ．向右平移3个单位长度，再向上平移1个单位长度C ．向左平移3个单位长度，再向下平移1个单位长度D ．向右平移3个单位长度，再向下平移1个单位长度12． 已知函数()log (4)a a f x x x=+- (0,a >且1)a ≠的值域为R ，则实数a 的取值范围是（ ）A. ()(]0,11,2UB. ()2,+∞C. ()4,+∞D. ()(]0,11,4U 第II 卷 主观卷（共52分）二、填空题（每小题4分，共16分）13．计算23lg12111log 1)lg 4lg 58162-⎛⎫+-++= ⎪⎝⎭ 14．函数213log (65)y x x =-+的单调增区间是15．已知集合{}{}23100,121A x x x B x m x m =--≤=+≤≤+，若A B A =U ，则实数m的取值范围是16．对a b R ∈、，记{}max ,a b =,,a a b b a b≥⎧⎨<⎩，(){}()max 1,2f x x x x R =+-∈的最小值是三、解答题 17．(8分) 已知集合{}2120A x x ax b =++=，集合{}20B x x ax b =-+=，满足 (){}2U C A B =I，(){}4U A C B =I ，U R =，求实数,a b 的值.18．(8分) 作出函数4y x x x =-的图象，根据图象写出函数的单调区间以及在每一单调区间上的函数是增函数还是减函数．19．(8分)()f x 是定义在()0,+∞上的增函数，且()()x f f x f y y ⎛⎫=-⎪⎝⎭ (1) 求(1)f 的值.(2) 若(6)1,f =解不等式1(3)()2f x f x+-<.20．(12分) 已知函数1()1x x a f x a -=+ (1)a >. (1) 判断函数()f x 的奇偶性(2) 求()f x 的值域(3) 用定义证明()f x 在(),-∞+∞上的单调性参考答案。

上学期高一数学10月月考试题01第I 卷（选择题）一、选择题：1．设全集U ＝{1，2，3，4，5}，集合A ＝{1，2}，B ＝{2，3}，则A ∩C U B ＝ A ．{4，5} B ．{2，3} C ．{1} D ．{2} 2．下列表述中错误的是（ ） A ．若A B A B A =⊆ 则, B ．若B A B B A ⊆=，则C ．)(B A A )(B AD ．()()()B C A C B A C U U U =3．符号{}a ⊂≠{,,}P a b c ⊆的集合P 的个数是 ( )A. 2B. 3C. 4D. 54．若集合2{440,}A x kx x x R =++=∈中只有一个元素,则实数k 的值为 ( )A.0B. 1C. 0或1D. 1k <5．若一系列函数的解析式相同，值域相同，但定义域不同，则称这些函数为“孪生函数”，那么函数解析式为y ＝2x 2＋1，值域为{3,9}的“孪生函数”共有( ) A ．10个 B ．9个 C ．8个 D ．7个6．设⎩⎨⎧<+≥-=)10x ()],6x (f [f )10x (,2x )x (f 则)5(f 的值为（ ） A. 10 B. 11C. 12D. 137．已知a 是实数，则下列函数中，定义域和值域都有可能是R 的是( )A ．f(x)＝x 2＋aB ．f(x)＝ax 2＋1C ．f(x)＝ax 2＋x ＋1D ．f(x)＝x 2＋ax ＋1 8．下列两个函数相等的是( )A ．y y ＝xB ．y y ＝|x|C ．y ＝|x|与yD ．y y ＝x x29．定义在R 上的函数()f x 满足(6)()f x f x +=.当31x -≤<-时，2()(2)f x x =-+，当13x -≤<时，()f x x =。

则(1)(2)(3)(2012)f f f f +++⋅⋅⋅=（ ）A ．335B ．338C ．1678D ．201210．下列函数中，既是奇函数又是增函数的为（ ） A ．1y x =+ B ．2y x =- C ．1y x= D ．||y x x =11．函数y ＝x ( )A ．有最小值12，无最大值 B ．有最大值12，无最小值C ．有最小值12，最大值2D ．无最大值，也无最小值 12．（05福建卷）)(x f 是定义在R 上的以3为周期的偶函数，且0)2(=f ， 则方程)(x f =0在区间（0，6）内解的个数的最小值是 （ ） A ．5B ．4C ．3D ．2第II 卷（非选择题）二、填空题（题型注释）13．设集合{211}A x x x =-<<->或,{},B x a x b =≤≤若{2},A B x x ⋃=>-{13}A B x x ⋂=<≤,则a = ,b =14．已知集合}023|{2=+-=x ax x A 至多有一个元素，则a 的取值范围 ；若至少有一个元素，则a 的取值范围 。

上学期高一数学10月月考试题08共150分；时间120分钟第Ⅰ卷（选择题共60分）一、选择题：在每小题给出的四个选项中，只有一项是符合题目要求的，请把正确答案的代号填在题后的括号内（每小题5分，共60分）．1.设全集为R ,{}{}|22|1)R M x x N x x M N =-≤≤=<⋂=则(C ( ){}{}|2|21A x x B x x <--<< {}{}|1|21C x x D x x <-≤< 2.下列四组函数，表示同一函数的是( )A ．f （x ），g （x ）=xB ．f （x ）=x ，g （x ）=2x xC ．2(),()2ln f x lnx g x x ==D ．()log (),()x a f x a a g x =>0,α≠1=3.设已知函数21,0(),0x x f x x x +≥⎧=⎨<⎩，则f [f (2-)]的值为（ ）．A ．1-B 2 C. 4 D.54.下列函数中，是奇函数是（ ）A .2x y = B. x y lg = C.3y x = D.1+=x y5. 当0＜a ＜1时，在同一坐标系中，函数x y a -=与log a y x =的图象是( )6.下列函数中，在区间)2,0(上递增的是（ ）A xy 1= B x y -= C 1-=x y D 122++=x x y7．令0.760.76,0.7,log 6a b c ===，则三个数a 、b 、c 的大小顺序是( ) A ．b ＜c ＜a B ．b ＜a ＜c C ．c ＜a ＜b D ．c ＜b ＜a8.{}=|1A x x ≤已知集合{}|,B x x a A B R a =≥⋃=且则实数的取值范围是 ( )A 1a <B 1a ≤C 1a >D 1a ≥9.幂函数y=f(x)的图象经过点1(2,)8--，则满足f(x)=27的x 的值为（ ）A 13B 3C -3D 1210. 若2log 31x =，则39x x +的值为( )A ．6B ．3C ．52D ．1211. [)[)22,1,,1,x x ax x x++∈+∞∈+∞已知函数f(x)=若对于,f(x)>0恒成立，则a 的取值范围（ ）A 3a >-B 3a ≥-C 1a >D 1a ≥12.()f x =已知 (23)1,1log , 1xa a x x x --<⎧⎨-≥⎩是R 上的增函数，则实数a 的取值范围为（ ） A 203a << B 1a<13≤ C 213a << D 1233a ≤<第Ⅱ卷(非选择题共90分)二、填空题(本大题共4小题，每小题5分，共20分)。

上学期高一数学10月月考试题11一、选择题：本大题共10小题．每小题5分，共50分．在每小题给出的四个选项中，只有一项是符合题目要求的．1.已知全集U R =，则正确表示集合{1,0,1}M =-和{}2|0N x x x =+=关系的韦恩（Venn ）图是A B C D2. 2log 2A ．2B 2C ．12-D ． 123. 已知5)2(22+-+=x a x y 在区间(4,)+∞上是增函数，则a 的范围是 A 2a ≤- B 2a ≥- C 6-≥a D 6-≤a4.若31log 0,()13b a <>，则A. 1,0a b >>B. 01,0a b <<>C. 1,0a b ><D. 01,0a b <<<5.函数234x x y x--+=的定义域为A ．[4,1]-B ．[4,0)-C ．(0,1]D ．[4,0)(0,1]-6.已知753()2f x ax bx cx =-++，且(5),f m -= 则(5)(5)f f +-的值为A. 4B. 0C. 2mD. 4m -+ 7.若0x 是方程式 lg 2x x +=的解，则0x 属于区间A.（0，1）B.（1，1.25）C.（1.25，1.75）D.（1.75，2） 8. 函数log (1)a y x =-(0<a <1)的图象大致是 （ ）A B C D9. 方程3log 820x x -+=的根一定位于区间 （ ）A. ()5,6B. ()3,4C. ()2,3D. ()1,210. 已知2,0()2,00,0x x f x x x ⎧>⎪==⎨⎪<⎩，则)]}2([{-f f f 的值为 （ ）A. 0B. 2C. 4D. 8二、填空题：(本大题5个小题，每小题5分，共25分)11．若幂函数()f x 的图象过点2,2⎛⎫⎪ ⎪⎝⎭，则()9f = .12．函数2()ln f x x=的定义域为 .13．若函数f (x )＝(2a －1)x ＋b 在R 上是减函数，则a 的取值范围是________． .14．已知集合{}3log (1)2A x x =-<,1()33x B x ⎧⎫=>⎨⎬⎩⎭则R AC B =_____ .15. 集合M ＝{1，2，3}的子集的个数为________．三、解答题：(本大题5个小题，共75分)各题解答必须答在答题卡上，必须写出必要的文字说明、演算步骤或推理过程.16. （本题满分10分）已知集合A ＝{x |3≤x <7}，B ＝{x |2<x <10}，求∁R (A ∪B )，A ∩B .17.（本题满分12分）已知函数()1f x x a =-+A ，函数()lg(2)g x x =-的定义域是集合B. （1）求集合A 、B ；（2）若A B B ⋃=，求实数a 的取值范围.18. （本小题满分14分） 计算求值(I ) 1100.753270.064()160.258---++ (II ) 22lg 5lg 5lg 4lg 2+⋅+19. （本小题满分12分）已知),0(56>-=a a x求xx xx aa a a ----33的值。

上学期高一数学10月月考试题05一、选择题：（10小题，每题5分，共50分）1设集合∈<≤=x x x A 且30{N}的真子集．．．的个数是( ) (A) 16 (B) 8； (C) 7 (D) 42设全集U={－2－1，0，1，2}，A={－2－1，0}，B={0，1，2}，则（C U A ）∩B=( )A ．{0}B ． {－2，－1}C ．{1，2}D ．{0，1，2} 3设f (x )＝|x －1|－|x |，则f [f (21)]＝( ) (A) －21 (B)1 (C)21(D) 04.函数)(x f y =的图像在[],a b 内是连续的曲线，若()()0>∙b f a f ，则函数)(x f y =在区间(),a b 内( )A 只有一个零点B 至少有一个零点C 无零点D 无法确定 5．下列各式中成立的是 （ ）A ．1777()m n m n= B ．4312(3)3-=-C ．34()x y =+ D ．=6．下列各组函数中，表示同一个函数的是（ ）A ．211x y x -=-与1y x =+B ．lg y x =与21lg 2y x =C ．1y =与1y x =- D ．y x =与log(01)x ay a a a =≠>且7、函数y ＝log 2x ＋3（x≥1）的值域是( ) A.[)+∞,2 B.（3，＋∞） C.[)+∞,3 D.（－∞，＋∞）8．四位好朋友在一次聚会上，他们按照各自的爱好选择了形状不同、内空高度相等、杯口半径相等的圆口酒杯，如图所示，盛满酒后他们约定：先各自饮杯中酒的一半．设剩余酒的高度从左到右依次为1h ，2h ，3h ，4h ，则它们的大小关系正确的是（ ）Ａ．214h h h >> Ｂ．123h h h >> Ｃ．324h h h >> Ｄ．241h h h >>9、下列函数中，在区间]0,(-∞上是增函数的是 ( ) （A ）842+-=x x y （B ）)(log 21x y -=（C ）12+-=x y （D ）x y -=1 10． 已知函数()f x 的定义域为A ，若其值域也为A ，则称区间A 为()f x 的保值区间．若2()=-2+g x x x m的保值区间是[)0,+∞ ，则m 的值为（ ）A ．0B ．-1C ．1D ．2二、填空题：（4小题，每题5分，共20分） 11. 25lg 50lg 2lg )2(lg2+⋅+的值为 .12、定义在)1,1(-上的奇函数1)(2+++=nx x mx x f ，则常数=m ____,=n _____ 13．指数函数()xg x a =的图象过点(2,4)，()g x 与()f x 互为反函数，则(2)f =__14、函数)(x f 对于任意实数x 满足条件)(1)2(x f x f =+，若5)1(-=f ，则))5((f f = 。

上学期高一数学10月月考试题04一、选择题（每小题3分，共36分） 1、︒420sin 的值是 （ ） A 、－21 B 、 21C 、－23D 、232、下列集合中,不同于另外三个集合的是 （ ）A 、{}1B 、{}2(1)0y R y ∈-=C 、{}1x =D 、{}10x x -=3、函数)652cos(3π-=x y 的最小正周期是 ( ）A 、52πB 、25πC 、π2D 、π54、函数33()2x x f x --=是 （ ） A 、奇函数，在(0,+∞)上是减函数 B 、偶函数，在(0,+∞)上是减函数 C 、奇函数，在(0,+∞)上是增函数 D 、偶函数，在(0,+∞)上是增函数 5、设()83log 3-+=x x x f ,用二分法求方程083log 3=-+x x 在区间()1,3内的近似解中，取区间中点02x =，则下一个区间为 ( )A 、（1,2）或（2,3）B 、[1，2]C 、（1,2）D 、（2,3）6、若函数)sin()(ϕω+=x x f 的图象（部分）如图所示，则ϕω和的取值是（ ) A 、6,21πϕω==B 、6,21πϕω-== C 、3,1πϕω== D 、 3,1πϕω-==7、若⎩⎨⎧≥<+=-)2(,2)2(),2()(x x x f x f x ， 则)1(f 的值为 （ ）A 、8B 、81 C 、2 D 、218、已知sin 2cos 53sin 5cos αααα-=-+,则=αtan （ ）. A 、-2 B 、2 C 、1623 D 、-16239、在△ABC 中，51cos sin =+A A ，则=A tan （ ） A 、34 B 、34- C 、43 D 、43-10、函数x xx x x x y tan tan cos cos sin sin ++=的值域是（ ） A 、{}3,1,0,1- B 、{}3,0,1- C 、{}3,1- D 、{}1,1- 11、若24παπ<<则 （ ）A 、αααtan cos sin >>B 、αααsin tan cos >>C 、αααcos tan sin >>D 、αααcos sin tan >>12、已知1A ，2A ，…n A 为凸多边形的内角，且0sin lg sin lg sin lg 21=+++n A A A ，则这个多边形是（ ）A 、正六边形B 、梯形C 、矩形D 、有一个角是锐角的菱形 二、填空题（每小题3分，共12分）13、半径为πcm ，中心角为120o 的弧长为 14、计算=-++-e ln 25802132π15、)(x f y =是定义在R 上的函数，)()2(x f x f =+，当20≤≤x 时，x x f x 3l o g 2)(+=，则=)3(f .16、已知函数)(x f y =的图象上的每一点的纵坐标扩大到原来的4倍，横坐标扩大到原来的2倍，然后把所得的图象沿x 轴向左平移2π，这样得到的曲线和x y sin 2=的图象相同，则已知函数)(x f y =的解析式为_______________________________.三、解答题：（共52分，解答题应写出文字说明、证明过程或演算步骤）17、（8分）（1）化简：sin(2)sin()cos()sin(3)cos()παπαπαπαπα-+----（2）求证：cos 1sin 1sin cos x xx x+=-18、(8分)已知函数)62sin(2π-=x y .（1）写出它的振幅、周期、频率和初相； （2）求这个函数的单调递减区间；（3）求出使这个函数取得最大值时，自变量x 的取值集合，并写出最大值。

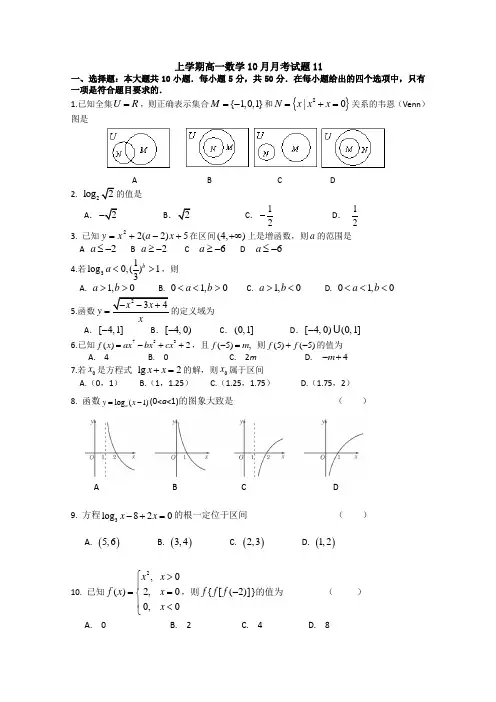
上学期高一数学10月月考试题11一、选择题：本大题共10小题．每小题5分，共50分．在每小题给出的四个选项中，只有一项是符合题目要求的．1.已知全集U R =，则正确表示集合{1,0,1}M =-和{}2|0N x x x =+=关系的韦恩（Venn ）图是A B C D2. 2log 的值是A． BC ．12-D ． 123. 已知5)2(22+-+=x a x y 在区间(4,)+∞上是增函数，则a 的范围是 A 2a ≤- B 2a ≥- C 6-≥a D 6-≤a4.若31log 0,()13b a <>，则A. 1,0a b >>B. 01,0a b <<>C. 1,0a b ><D. 01,0a b <<<5.函数y =的定义域为A ．[4,1]-B ．[4,0)-C ．(0,1]D ．[4,0)(0,1]-6.已知753()2f x ax bx cx =-++，且(5),f m -= 则(5)(5)f f +-的值为A. 4B. 0C. 2mD. 4m -+ 7.若0x 是方程式 lg 2x x +=的解，则0x 属于区间A.（0，1）B.（1，1.25）C.（1.25，1.75）D.（1.75，2） 8. 函数log (1)a y x =-(0<a <1)的图象大致是 （ ）A B C D9. 方程3log 820x x -+=的根一定位于区间 （ ）A. ()5,6B. ()3,4C. ()2,3D. ()1,210. 已知2,0()2,00,0x x f x x x ⎧>⎪==⎨⎪<⎩，则)]}2([{-f f f 的值为 （ ）A. 0B. 2C. 4D. 8二、填空题：(本大题5个小题，每小题5分，共25分)11．若幂函数()f x 的图象过点2,2⎛⎫⎪ ⎪⎝⎭，则()9f = .12．函数2()ln f x x=的定义域为 .13．若函数f (x )＝(2a －1)x ＋b 在R 上是减函数，则a 的取值范围是________． .14．已知集合{}3log (1)2A x x =-<,1()33x B x ⎧⎫=>⎨⎬⎩⎭则R AC B =_____ .15. 集合M ＝{1，2，3}的子集的个数为________．三、解答题：(本大题5个小题，共75分)各题解答必须答在答题卡上，必须写出必要的文字说明、演算步骤或推理过程.16. （本题满分10分）已知集合A ＝{x |3≤x <7}，B ＝{x |2<x <10}，求∁R (A ∪B )，A ∩B .17.（本题满分12分）已知函数()f x A ，函数()lg(2)g x x =-的定义域是集合B. （1）求集合A 、B ；（2）若A B B ⋃=，求实数a 的取值范围.18. （本小题满分14分） 计算求值(I ) 1100.753270.064()160.258---++ (II ) 22lg 5lg 5lg 4lg 2+⋅+19. （本小题满分12分）已知),0(56>-=a a x求xx xx aa a a ----33的值。

上学期高一数学10月月考试题11一、选择题：本大题共10小题．每小题5分，共50分．在每小题给出的四个选项中，只有一项是符合题目要求的．1.已知全集U R =，则正确表示集合{1,0,1}M =-和{}2|0N x x x =+=关系的韦恩（Venn ）图是A B C D2. 2logA． BC ．12-D ． 123. 已知5)2(22+-+=x a x y 在区间(4,)+∞上是增函数，则a 的范围是A 2a ≤-B 2a ≥-C 6-≥aD 6-≤a4.若31log 0,()13ba <>，则A. 1,0a b >>B. 01,0a b <<>C. 1,0a b ><D. 01,0a b <<<5.函数y =的定义域为A ．[4,1]-B ．[4,0)-C ．(0,1]D ．[4,0)(0,1]-6.已知753()2f x ax bx cx =-++，且(5),f m -= 则(5)(5)f f +-的值为A. 4B. 0C. 2mD. 4m -+ 7.若0x 是方程式 lg 2x x +=的解，则0x 属于区间A.（0，1）B.（1，1.25）C.（1.25，1.75）D.（1.75，2） 8. 函数log (1)a y x =-(0<a <1)的图象大致是 （ ）A B C D9. 方程3log 820x x -+=的根一定位于区间 （ ）A. ()5,6B. ()3,4C. ()2,3D. ()1,210. 已知2,0()2,00,0x x f x x x ⎧>⎪==⎨⎪<⎩，则)]}2([{-f f f 的值为 （ ）A. 0B. 2C. 4D. 8二、填空题：(本大题5个小题，每小题5分，共25分)11．若幂函数()f x的图象过点⎛ ⎝⎭，则()9f = .12．函数2()ln f x x=+的定义域为 .13．若函数f (x )＝(2a －1)x ＋b 在R 上是减函数，则a 的取值范围是________． .14．已知集合{}3log (1)2A x x =-<,1()33x B x ⎧⎫=>⎨⎬⎩⎭则R AC B =_____ .15. 集合M ＝{1，2，3}的子集的个数为________．三、解答题：(本大题5个小题，共75分)各题解答必须答在答题卡上，必须写出必要的文字说明、演算步骤或推理过程.16. （本题满分10分）已知集合A ＝{x |3≤x <7}，B ＝{x |2<x <10}，求∁R (A ∪B )，A ∩B .17.（本题满分12分）已知函数()f x A ，函数()lg(2)g x x =-的定义域是集合B. （1）求集合A 、B ；（2）若A B B ⋃=，求实数a 的取值范围.18. （本小题满分14分） 计算求值(I ) 1100.753270.064()160.258---++ (II ) 22lg 5lg5lg4lg 2+⋅+19. （本小题满分12分）已知),0(56>-=a a x求xx xx a a a a ----33的值。

上学期高一数学10月月考试题01第I 卷（选择题）一、选择题：1．设全集U ＝{1，2，3，4，5}，集合A ＝{1，2}，B ＝{2，3}，则A ∩C U B ＝A ．{4，5}B ．{2，3}C ．{1}D ．{2}2．下列表述中错误的是（ ）A ．若AB A B A =⊆ 则,B ．若B A B B A ⊆=，则C ．)(B A A )(B AD ．()()()B C A C B A C U U U =3．符号{}a ⊂≠{,,}P a b c ⊆的集合P 的个数是 ( ) A. 2 B. 3 C. 4 D. 54,则实数k 的值为 ( )A.0B. 1C. 0或1D. 1k <5．若一系列函数的解析式相同，值域相同，但定义域不同，则称这些函数为“孪生函数”，那么函数解析式为y ＝2x 2＋1，值域为{3,9}的“孪生函数”共有( )A ．10个B ．9个C ．8个D ．7个 6．设⎩⎨⎧<+≥-=)10x ()],6x (f [f )10x (,2x )x (f 则)5(f 的值为（ ） A. 10 B. 11 C. 12 D. 137．已知a 是实数，则下列函数中，定义域和值域都有可能是R 的是( )A ．f(x)＝x 2＋aB ．f(x)＝ax 2＋1C ．f(x)＝ax 2＋x ＋1D ．f(x)＝x 2＋ax ＋18．下列两个函数相等的是( )A ．y y ＝xB ．y y ＝|x|C ．y ＝|x|与y ．y y 9．定义在R 上的函数()f x 满足(6)()f x f x +=.当31x -≤<-时，2()(2)f x x =-+，当13x -≤<时，()f x x =。

则(1)(2)(3)(2012)f f f f +++⋅⋅⋅=（ ）A ．335B ．338C ．1678D ．201210）A ．1y x =+B ．2y x =-C ．||y x x =11．函数y ＝x ( )A B C 2 D ．无最大值，也无最小值12．（05福建卷）)(x f 是定义在R 上的以3为周期的偶函数，且0)2(=f ，则方程)(x f =0在区间（0，6）内解的个数的最小值是 （ ） A ．5 B ．4 C ．3 D ．2第II 卷（非选择题）二、填空题（题型注释）1314．已知集合}023|{2=+-=x ax x A 至多有一个元素，则a 的取值范围 ； 若至少有一个元素，则a 的取值范围 。

上学期高一数学10月月考试题09(满分:150分 时间:120分钟)一、选择题(本大题共12个小题，每小题5分，共60分，在每小题给出的四个选项中，只有一项是符号题目要求的。

)1．下列关系中正确的个数为（ ）；①R ∈21②Q ∉2 ③*|3|N ∉- ④Q ∈-|3| A ．1 个 B ．2 个 C ．3 个 D ．4 个 2．若集合}1,1{-=A ，}1|{==mx x B ，且A B A =⋃，则m 的值为（ ）A ．1B ．1-C ．1或1-D ．1或1-或03．已知函数()132f x x +=+，则()f x 的解析式是( )A ．32x +B ．31x +C ．31x -D ．34x +4．已知函数228)(x x x f -+=，那么（ ）A ．)(x f 是减函数B ．)(x f 在]1,(-∞上是减函数C ．)(x f 是增函数D ．)(x f 在]0,(-∞上是增函数 5．若2log 0a ，112b⎛⎫ ⎪⎝⎭，则()A ．1,0abB ．a >1，b <0C ．0<a <1，b >0D ．0<a <1，b <0 6．如果xx mn 对于一切0x 都成立，则正数,m n 的大小关系为( ) A ．m n B ．m n C ．m n = D ．无法确定7. 设217.0=a ，218.0=b ，c 7.0log 3=，则（ ）A ．a b c <<B ．b a c <<C ．c b a <<D ．c a b << 8．已知01a ,1b-,则函数x y a b =+的图像必定不经过（ ）A ．第一象限B ．第二象限C ．第三象限D ．第四象限 9．函数()215log 610y x x =-+在区间[]1,2上的最大值是( )A ．0B ．15log 5 C ．15log 2 D ．110．函数22313xy -⎛⎫= ⎪⎝⎭的单调递增区间是 ( )A.(),0-∞B.()0,+∞C.(),-∞+∞D.11,33⎡⎤-⎢⎥⎣⎦11．已知()2x xe ef x --=，则下列说法正确的是 （ ）A.奇函数，在R 上为增函数B.偶函数,在R 上为增函数C.奇函数,在R 上为减函数D.偶函数,在R 上为减函数12．设()f x 是R 上的任意函数,则下列叙述正确的是（ ）A ．()()f x f x -是奇函数B ．()()f x f x -是奇函数C ．()()f x f x --是偶函数D ．()()f x f x +-是偶函数第Ⅱ卷(非选择题 共90分)二、填空题(本题共4个小题，每小题5分，共20分) 13．若)(x f =⎩⎨⎧≥<+)6(log )6()3(2x xx x f ,则)1(-f 的值为14．函数y x =-在[],a +∞上是减函数，则a 的取值范围是 15．函数()()1301x f x a aa +=-≠且的图象必过定点p ，则p 点坐标为16．已知53()8f x x ax bx =++-且(2)10f -=，那么(2)f =_______三、解答题(本大题共6个小题，其中第17小题10分，其余小题每题12分，共计70分) 17．设集合{}3A x a x a =≤≤+，集合{}15B x x x=-或，分别就下列条件求实数a 的取值范围： (1)A B φ⋂≠，(2)A B A ⋂=.18.求下列函数的定义域和值域：（1）112x y -=；（2）y =19．设函数是定义在R 上的奇函数，若当()0,x ∈+∞时，())1f x x =+，（1）求()27f 与()27f -；（2）求()f x 的解析式.20．已知函数()()10x f x a x -=≥的图象经过点12,,0, 1.2a a ⎛⎫≠ ⎪⎝⎭其中（1）求a 的值； （2）求函数()228,xx f x a a -=-+[]2,1x ∈-的值域.21．对于函数()2()21xf x a a R =-∈+： （1）探索()f x 的单调性;（2）是否存在实数a 使函数()f x 为奇函数？22.（本题12分）函数()f x 对任意的,a b R ∈,都有()()()1f a b f a f b +=+-,并且当0x时，()1f x .（1）求证：()f x 是R 上的增函数；（2）若 ()45f =,解不等式()2323f m m --.答案1---5 BDCDD 6---10 ABACB 11—12AD 13. 3 14 . []0,+∞ 15.()1,2-- 16. 26-17．解：(1)因为A ∩B ≠∅，所以a <－1或a ＋3>5，即a <－1或a >2.(2)因为A ∩B ＝A ，所以A ⊆B ，所以a >5或a ＋3<－1，即a >5或a <－4. 18.解：（1）由10x -≠，得定义域为{},1x x R x ∈≠且。