第二章 GeSi异质结及超晶格的基本特性
- 格式:ppt
- 大小:489.00 KB
- 文档页数:21

异质结超晶格建模异质结超晶格是一种近年来在纳米技术领域引起广泛关注的新型材料。
它的特殊结构使得它具有许多独特的物理和化学性质,因此在光电子学、能源存储和传感器等领域有着广泛的应用前景。
本文将介绍异质结超晶格的建模方法以及其在材料科学中的指导意义。
首先,我们来了解一下什么是异质结超晶格。
异质结超晶格可以被看作是由两种或多种不同材料组成的周期性结构。
其中的材料可以是晶体、非晶体、纳米颗粒或者有机杂化体等。
这些材料的特殊排列使得异质结超晶格具有优异的电子、光学和热学性质。
与普通的材料相比,异质结超晶格的电子结构更加复杂,具有更好的载流子输运性能和较高的量子效率。
因此,通过建模异质结超晶格,我们可以更好地理解其基本性质和物理机制。
针对异质结超晶格的建模方法有很多种,其中最常用的是密度泛函理论(DFT)。
DFT是一种基于量子力学原理的计算方法,可以用来计算材料的基态性质,例如能带结构、密度分布和电子局域性等。
利用DFT方法进行异质结超晶格的建模,可以得到其电子结构的详细信息,并且可以预测其电子输运性能和光学响应等。
此外,还可以利用分子动力学(MD)模拟来研究异质结超晶格的力学性能和热学性质等。
对于纳米尺度的异质结超晶格,建模过程中还需要考虑表面效应。
由于纳米材料的表面与体积相比,具有更高的表面能量和更大的表面积,因此表面效应对于纳米材料的物理和化学性质具有很大影响。
在建模纳米异质结超晶格时,需要对材料的表面进行特殊处理,例如通过引入表面修饰剂或者采用等效表面积的方式来模拟表面效应。
这样一来,建模结果将更加准确地反映纳米异质结超晶格的真实性质。
异质结超晶格的建模工作对于材料科学的发展有着重要的指导意义。
首先,通过建模我们可以预测异质结超晶格的性质,并根据需求进行材料的定向设计。
例如,在太阳能电池领域,通过合理设计异质结超晶格的能带结构和载流子输运性能,可以提高太阳能电池的光电转换效率。
其次,建模可以帮助我们更好地理解材料的物理机制和发展趋势。


超晶格的结构特点(一)
超晶格的结构
特点:
1.高度有序:超晶格由多个晶格单元周期性排列而成,结构有严格的重复性和规则性。
2.多尺度性:超晶格具有多种尺度的调控效果,可以通过调整晶格单元、调节原子间距等方式改变材料的性质。
3.显著的物理和化学性质:超晶格的结构改变了晶体材料的电子结构和能带结构,使其具有独特的光学、磁学等物理性质,同时也影响着化学反应的速率和选择性。
4.可控性强:通过合适的制备方法,可以精确控制超晶格的尺寸、形状和组分,从而实现对材料性能的精细调控。
5.多功能性:超晶格由不同材料的结合形成,可以呈现多种功能,如催化、光电、磁学等,可应用于能源、传感、储存等领域。
文章采用markdown格式:
超晶格的结构
特点:
•高度有序:超晶格由多个晶格单元周期性排列而成,结构有严格的重复性和规则性。
•多尺度性:超晶格具有多种尺度的调控效果,可以通过调整晶格单元、调节原子间距等方式改变材料的性质。
•显著的物理和化学性质:超晶格的结构改变了晶体材料的电子结构和能带结构,使其具有独特的光学、磁学等物理性质,同时也影响着化学反应的速率和选择性。
•可控性强:通过合适的制备方法,可以精确控制超晶格的尺寸、形状和组分,从而实现对材料性能的精细调控。
•多功能性:超晶格由不同材料的结合形成,可以呈现多种功能,如催化、光电、磁学等,可应用于能源、传感、储存等领域。



超晶格结构与特性作者:张海瑞来源:《价值工程》2014年第28期摘要:本文简要论述了半导体超晶格的分类,结构特性,能带结构与应变超晶格,以及它们的发展与应用。
Abstract: This paper briefly discusses the classification, structural characteristics and the band structure of semiconductor superlattice, strained-layer superlattice, and their development and application.关键词:超晶格;结构;类型;特征Key words: superlattice;structure;types;characteristics中图分类号:O431.2 文献标识码:A 文章编号:1006-4311(2014)28-0318-021 超晶格的定义及结构超晶格是指周期性交替生长的两种或多种材料构成的人造晶体。
相邻两层不同材料的厚度合称为超晶格的周期长度,一般来说这个周期长度比各层单层的晶格常数大几倍或更长,因此,这种结构获得了“超晶格”的名称。
下面对半导体超晶格的结构进行简单的介绍。
Ga1-xAlxAs/GaAs半导体超晶格结构是在半绝缘的GaAs衬底上,外延生长GaAs薄层,再在上面交替的生长厚度为几埃甚至上百埃的Ga1-xAlxAs和GaAs薄层而构成的。
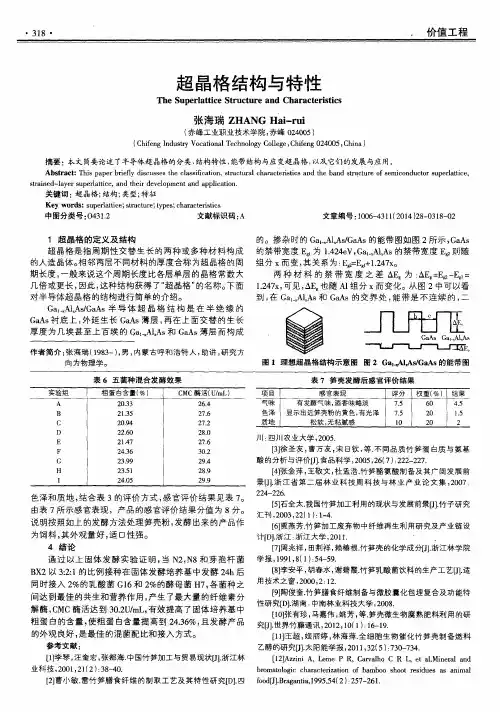
掺杂时的Ga1-xAlxAs/GaAs的能带图如图2所示,GaAs的禁带宽度Eg1为1.424eV,Ga1-xAlxAs的禁带宽度Eg2则随组分x而变,其关系为:Eg2=Eg1+1.247x。
两种材料的禁带宽度之差ΔEg为:ΔEg=Eg2-Eg1=1.247x,可见,ΔEg也随Al组分x而变化。
从图2中可以看到,在Ga1-xAlxAs和GaAs的交界处,能带是不连续的,二者的导带底能量差为ΔEc,价带顶能量差为ΔEν,而且ΔEc+ΔEν=ΔEg。

锗硅异质结双极晶体管概述及解释说明1. 引言1.1 概述锗硅异质结双极晶体管(Germanium-Silicon Heterojunction Bipolar Transistor,简称GeSi HBT)是一种重要的半导体元件,其特点在于将锗和硅这两种不同材料组成异质结,以取得优异的性能和应用效果。
由于GeSi HBT具有高速度、低噪声、低功耗等优势,在通信、微电子学和射频电子学等领域被广泛应用。
1.2 文章结构本文将对锗硅异质结双极晶体管进行详细的介绍和解释说明。
首先,在引言部分概述了该主题的研究背景与意义,并介绍了文章的整体结构。
接着,第二部分将详细介绍GeSi HBT的原理和工作原理,以便读者能够理解其基本工作方式。
第三部分将回顾GeSi HBT发展历程,从初期研究到现阶段的技术突破和应用情况进行梳理,并展望其未来前景。
第四部分将介绍GeSi HBT的制备方法与工艺流程,包括材料选择、加工工艺流程介绍以及结构参数优化和工艺改进等内容。
最后,第五部分将对全文进行总结并提出未来的发展方向和实际应用推广建议。
1.3 目的本文旨在全面介绍锗硅异质结双极晶体管的原理、特点、制备方法以及其在不同领域的应用情况,以帮助读者深入了解该技术,并推动其在科学研究和工程应用中得到更广泛的应用。
通过对GeSi HBT发展历程的回顾,我们可以总结经验教训,并展望未来的研究方向和技术突破点,从而为相关领域研究人员提供有益的指导和参考。
同时,我们也将提出一些建议,以促进锗硅异质结双极晶体管的实际应用推广。
2. 锗硅异质结双极晶体管2.1 原理介绍锗硅异质结双极晶体管是一种利用不同半导体材料构成的异质结的双极晶体管。
它采用了锗和硅这两种特定的半导体材料作为其结构组件,利用锗和硅之间的能带差异以及异质结界面的特性来实现电子器件的功能。
在锗硅异质结双极晶体管中,通常使用p型锗作为基底材料,而n型硅则被用作活性层。
这样的材料选择可以使得电子在两个不同的能带结构中运动,从而产生许多有趣且独特的效应。



超晶格定义引言超晶格是指由两个或多个不同晶格构成的晶体结构,具有比单个晶格更大的周期性结构。
超晶格的形成使得材料具有非常特殊的物理性质,因此引起了广泛的研究兴趣。
本文将全面、详细、完整地探讨超晶格的定义、结构、制备方法以及相关应用。
定义超晶格是由两个或多个不同的晶格周期性地排列在一起形成的结构。
其中,每个晶格由原子、离子或分子构成,它们以一定的规则排列。
当这些晶格互相重叠或错位时,就形成了超晶格。
超晶格的周期性结构可以通过周期性的重复单元来描述,这些单元是由不同晶格的子结构堆叠而成的。
结构超晶格的结构可以通过几何装配的方式来描述。
最简单的超晶格结构是由两个相同的晶格组成的,其中每个晶格都是一个二维结构。
这种结构被称为二维超晶格。
另外,还有一维和三维超晶格,它们分别是由两个相同的一维晶格和三维晶格组成的。
无论是几维超晶格,其结构都可以由一组重复单元来描述,这些单元通过平移或旋转操作重复排列。
在超晶格中,晶格的间距和原子的排列方式会发生改变。
这种改变可以影响到材料的电子结构、力学性能和热传导等物理特性。
因此,超晶格通常表现出与单个晶格不同的性质和行为。
制备方法制备超晶格的方法有多种,下面将介绍几种常用的方法:1.蒸发沉积法:将两种或多种不同材料的薄膜沉积在衬底上。
薄膜的结构由沉积时的温度、沉积速度和组分比例等因素决定。
2.分子束外延法:使用分子束外延装置在晶体表面逐层生长超晶格结构。
该方法可以精确控制材料的组成和厚度。
3.化学合成法:通过溶液中的化学反应合成超晶格结构。
可以根据溶液中不同物质的浓度来控制超晶格的组成和结构。
4.模板合成法:利用模板材料引导晶体的生长,从而形成超晶格结构。
模板可以是纳米颗粒、有序多孔材料或者生物组织等。
这些制备方法各有优缺点,选择适合的方法取决于材料的性质和目标应用。
应用超晶格在多个领域都具有广泛的应用前景,下面列举了几个常见的应用领域:1.光学:超晶格可以用于调控光的传播和散射,从而制备具有特殊光学性质的材料。
二维γ-GeSe基异质结的电子特性研究第一篇范文二维γ-GeSe基异质结的电子特性研究二维材料由于其独特的物理和化学性质,近年来引起了广泛关注。
在众多二维材料中,γ-GeSe基异质结以其优异的电子特性备受瞩目。
本文将对二维γ-GeSe基异质结的电子特性进行详细研究,探讨其潜在应用领域。
一、γ-GeSe基异质结的结构特点γ-GeSe基异质结是由锗(Ge)和硒(Se)组成的二维材料。
在γ-GeSe结构中,Ge和Se原子以特定的比例相互交替排列,形成了一种稳定的二维晶体结构。
这种结构具有较高的热稳定性和化学稳定性,使得γ-GeSe基异质结在实际应用中具有较高的可靠性。
二、γ-GeSe基异质结的电子特性1. 导电性能γ-GeSe基异质结具有优异的导电性能。
研究表明,该材料在室温下的电导率可达到10^3 S/m量级。
这主要得益于γ-GeSe结构中Ge和Se原子的有序排列,形成了较短的载流子传输通道。
同时,该材料具有较低的电子迁移率,使其在实际应用中具有较低的噪声特性。
2. 半导体性能γ-GeSe基异质结具有明显的半导体性能。
其能带结构表明,该材料在室温下具有约0.7 eV的直接带隙。
这使得γ-GeSe基异质结在光电子、光电探测等领域具有广泛的应用前景。
3. 压电性能γ-GeSe基异质结还具有显著的压电性能。
实验结果表明,该材料在受到外力作用时,能产生明显的电荷分离现象。
这为其在压电传感器、能量收集等领域提供了可能的应用方向。
三、γ-GeSe基异质结的应用前景1. 光电子器件由于γ-GeSe基异质结具有优异的电子特性,其在光电子器件领域具有广泛的应用前景。
例如,可以将其应用于太阳能电池、光探测器等设备,提高器件的性能。
2. 光电探测器件γ-GeSe基异质结的光电探测性能优异,可用于制备高性能的光电探测器件。
这些器件在天文观测、生物检测等领域具有重要的应用价值。
3. 传感器和能量收集γ-GeSe基异质结的压电性能使其在传感器和能量收集领域具有潜在应用。
异质结莫尔超晶格中的激子绝缘体引言:激子绝缘体是一种新型的凝聚态物质相,其在异质结莫尔超晶格中具有独特的电子性质。
本文将介绍激子绝缘体的基本概念及其在异质结莫尔超晶格中的特性。
第一节:激子绝缘体的基本概念激子是由电子和空穴通过库伦相互作用结合而形成的一种准粒子,其在固体中具有特殊的电子-空穴耦合行为。
当电子和空穴之间的相互作用强到一定程度时,它们会形成束缚态,从而形成激子。
激子绝缘体是指在低温下,激子之间的相互作用能够导致电子与空穴之间的解禁带变窄,从而形成一个禁闭带,使得固体表现出绝缘体的性质。
第二节:异质结莫尔超晶格中的激子绝缘体异质结莫尔超晶格是一种由具有不同晶格结构的材料通过堆叠形成的晶体结构。
在这种结构中,不同材料的能带结构和电子性质会相互影响,从而导致一些新的电子现象的出现。
激子绝缘体正是在这种异质结构中形成的一种新颖的电子相。
在异质结莫尔超晶格中,由于不同材料的能带结构的差异,电子和空穴在界面处会形成束缚态。
当束缚态之间的距离足够小,且电子-电子和电子-空穴之间的相互作用强度足够大时,激子的形成就会受到这些束缚态的影响。
这种束缚态的形成会导致新的能带结构的出现,使得在界面处形成禁闭带,从而形成激子绝缘体。
激子绝缘体的形成使得异质结莫尔超晶格具有了特殊的电子性质。
一方面,激子的形成使得在禁闭带中的电子和空穴不能自由移动,从而使得异质结莫尔超晶格具有了绝缘体的性质。
另一方面,激子之间的相互作用会导致电子和空穴之间的耦合,从而使得其在外界电场或磁场的作用下表现出奇特的电输运行为。
第三节:异质结莫尔超晶格中的激子绝缘体的应用前景异质结莫尔超晶格中的激子绝缘体具有许多潜在的应用前景。
首先,由于其具有绝缘体的性质,激子绝缘体在电子器件中可以用作高效的隔离层,用于减少电子器件的漏电流和功耗,提高器件的稳定性和可靠性。
激子绝缘体在光电器件中也具有重要的应用价值。
激子的形成使得异质结莫尔超晶格中的材料对光的吸收和发射具有特殊的性质。
超晶格制备
超晶格制备是一种新兴的材料制备技术,它可以制备出具有特殊性质的材料。
超晶格是由多个晶格周期性排列而成的结构,具有比单个晶格更高的对称性和周期性。
超晶格制备技术可以通过控制晶格的排列方式和尺寸,来调控材料的性质,例如光学、电学、磁学等性质。
超晶格制备技术的基本原理是通过纳米加工技术制备出具有特定形状和尺寸的纳米结构,然后将这些纳米结构按照一定的排列方式组装成超晶格结构。
这种制备方法可以通过控制纳米结构的形状和尺寸,来调控超晶格的周期性和对称性,从而实现对材料性质的调控。
超晶格制备技术在材料科学领域有着广泛的应用。
例如,通过制备具有特定形状和尺寸的纳米结构,可以制备出具有高效光吸收和光转换性能的太阳能电池材料。
此外,超晶格结构还可以用于制备具有高效催化性能的催化剂材料,以及具有高强度和高韧性的结构材料等。
超晶格制备技术的发展还面临着一些挑战。
例如,制备具有高质量的超晶格结构需要高精度的纳米加工技术和组装技术,这对制备设备和技术人员的要求较高。
此外,超晶格结构的性质也受到材料的缺陷和表面效应的影响,因此需要对材料的制备和表征技术进行深入研究。
超晶格制备技术是一种具有广泛应用前景的材料制备技术,它可以通过控制纳米结构的形状和尺寸,来调控材料的性质。
随着纳米加工技术和组装技术的不断发展,超晶格制备技术将会在材料科学领域发挥越来越重要的作用。