精密机械设计基础第3章习题答案
- 格式:doc
- 大小:579.00 KB
- 文档页数:4

2023精密机械设计(庞振基黄其圣著)课后答案精密机械设计(庞振基黄其圣著)内容简介前言基本物理量符号表绪论第一章精密机械设计的基础知识第一节概述第二节零件的工作能力及其计算第三节零件与机构的误差估算和精度第四节工艺性第五节标准化、系列化、通用化第六节零件的设计方法及其发展思考题及习题第二章工程材料和热处理第一节概述第二节金属材料的力学性能第三节常用的工程材料第四节钢的热处理第五节表面精饰第六节材料的选用原则思考题及习题第三章零件的几何精度第一节概述第二节极限与配合的基本术语和定义第三节光滑圆柱件的极限与配合及其选择第四节形状与位置公差及其选择第五节表面粗糙度及其选择思考题及习题第四章平面机构的结构分析第一节概述第二节运动副及其分类第三节平面机构的运动简图第四节平面机构的自由度第五节平面机构的组成原理和结构分析思考题及习题第五章平面连杆机构第一节概述第二节铰链四杆机构的基本型式及其演化第三节平面四杆机构曲柄存在的条件和几个基本概念第四节平面四杆机构的设计思考题及习题第六章凸轮机构第一节概述第二节从动件常用运动规律第三节图解法设计平面凸轮轮廓第四节解析法设计平面凸轮轮廓第五节凸轮机构基本尺寸的确定思考题及习题第七章摩擦轮传动和带传动第一节概述第二节磨擦轮传动第三节磨擦无级变速器第四节带传动第五节同步带传动第六节其它带传动简介思考题及习题第八章齿轮传动第一节概述第二节齿廓啮合基本定律第三节渐开线齿廓曲线第四节渐开线齿轮各部分的名称、符号和几何尺寸的计算第五节渐开线直齿圆柱齿轮传动第六节渐开线齿廓的切制原理、根切和最少齿数第七节变位齿轮第八节斜齿圆柱齿轮传动第九节齿轮传动的失效形式和材料第十节圆柱齿轮传动的强度计算第十一节圆锥齿轮传动第十二节蜗杆传动第十三节轮系第十四节齿轮传动精度第十五节齿轮传动的空回第十六节齿轮传动链的设计思考题及习题第九章螺旋传动第一节概述第二节滑动螺旋传动第三节滚珠螺旋传动第四节静压螺旋传动简介思考题及习题第十章轴、联轴器、离合器第一节概述第二节轴第三节联轴器第四节离合器思考题及习题第十一章支承第一节概述第二节滑动摩擦支承第三节滚动摩擦支承第四节弹性摩擦支承第五节流体摩擦支承及其它形式支承第六节精密轴承思考题及习题第十二章直线运动导轨第一节概述第二节滑动摩擦导轨第三节滚动摩擦导轨第四节弹性摩擦导轨第五节静压导轨简介思考题及习题第十三章弹性元件第一节概述第二节弹性元件的基本特性第三节螺旋弹簧第四节游丝第五节片簧第六节热双金属弹簧第七节其它弹性元件简介思考题及习题第十四章联接第一节概述第二节机械零件的联接第三节机械零件与光学零件的联接思考题及习题第十五章仪器常用装置第一节概述第二节微动装置第三节锁紧装置第四节示数装置第五节隔振器思考题及习题第十六章机械的计算机辅助设计第一节概述第二节计算机辅助设计系统的原理与构成第三节表格和线图的处理第四节机械优化设计第五节设计举例思考题及习题参考文献精密机械设计(庞振基黄其圣著)目录本书对精密机械及仪器仪表中常用机构和零部件的工作原理、适用范围、结构、设计计算方法,以及工程材料、零件几何精度的基础知识等诸方面均作了较为详细的阐述。

C22-1 表征金属材料的力学性能时,主要有哪几项指标?解:表征金属材料的力学性能时,主要指标有:强度(弹性极限、屈服极限、强度极限),刚度、塑性、硬度。
2-2 常用的硬度指标有哪些?解:常用的硬度指标有三种:布氏硬度(HBS)、洛氏硬度(HRC-洛氏C标度硬度)、维氏硬度(HV)。
2-3 低碳钢,中碳钢,高碳钢的含碳量范围是多少?解:低碳钢(C≤%);中碳钢(%<C≤%);高碳钢(C>%)2-4 什么是合金钢?钢中含合金元素 Mn,Cr,Ni,对钢的性能有何影响?解:冶炼时人为地在钢中加入一些合金元素所形成的钢就是合金钢。
其中加入Mn可以提高钢的强度和淬透性;加入Cr可以提高钢的硬度、耐磨性、冲击韧性和淬透性;加入Ni可以提高钢的强度、耐热性和耐腐蚀性。
2-5 非铁金属共分几大类?具有哪些主要特性?解:有色金属主要分为以下几类:1)铜合金:良好的导电性、导热性、耐蚀性、延展性。
2)铝合金:比强度高,塑性好,导热、导电性良好,切削性能良好。
3)钛合金:密度小,机械强度高、高低温性能好,抗腐蚀性良好。
2-6 常用的热处理工艺有哪些类型?解:常用的热处理工艺有:退火、正火、淬火、回火、表面热处理和化学热处理。
2-7 钢的调质处理工艺过程是什么?其主要目的是什么?解:钢的调质处理工艺指的是淬火加高温回火。
目的是为了获得良好的综合机械性能,即好的强度、韧性和塑性。
2-8 镀铬和镀镍的目的是什么?解:镀铬的目的是为了使材料表层获得高的化学稳定性,并具有较高的硬度和耐磨性。
镀镍是为了获得良好的化学稳定性,并具有良好的导电性。
2-9 选择材料时应该满足哪些基本要求?解:选择材料时主要满足使用要求、工艺要求和经济要求。
C44-1 何谓运动副和运动副要素?运动副如何进行分类?解:由两个构件直接接触而组成的可动的连接称为运动副。
两个构件上参与接触而构成运动副的点、线、面等元素被称为运动副要素。
运动副有多种分类方法:按照运动副的接触形式分类:面和面接触的运动副在接触部分的压强较低,被称为低副,而点、线接触的运动副称为高副。

第一章测试1.组成精密机械的基本要素是()A:构件B:零件C:机构D:机架答案:B2.零件是最小的制造单位()。
A:错B:对答案:B3.构件是最小的制造单位()A:错B:对答案:A4.精密机械是()的综合体。
A:机B:光C:电答案:ABC5.本课程包含()内容A:机械原理B:零件的精度设计及互换性C:机械工程材料及热处理D:机械设计答案:ABCD第二章测试1.在精密机械中,有机材料包括()A:陶瓷B:橡胶C:塑料D:合成纤维答案:BCD2.在常温下经过塑性变形使材料强度降低、塑性提高的现象,称为冷作硬化。
A:对B:错答案:B3.伸长率或断面收缩率越大,材料的塑性越高。
A:对B:错答案:A4.下列材料中,是铸钢的为()A:42SiMnB:HT300C:45D:ZG310-570答案:D5.热处理明显改变钢件的形状和尺寸。
A:对B:错答案:B第三章测试1.零件的几何形状误差可以分为()A:形状误差B:尺寸误差C:表面粗糙度D:表面波度答案:ABC2.孔为包容面,轴为被包容面。
A:对B:错答案:A3.配合类型分为基孔制配合和基轴制配合。
A:错B:对答案:A4.标准公差等级从IT01到IT18,等级依次降低,公差值依次增大。
A:错B:对答案:B5.一般情况下应优先选用基孔制配合。
A:对B:错答案:A6.下列()是形状公差。
A:平行度B:圆跳动C:同轴度D:圆柱度答案:D7.有基准要求的是( )A:对称度B:全跳动C:直线度D:垂直度答案:ABD第四章测试1.平面机构中,每个低副引入两个约束,使构件失去一个自由度。
A:对B:错答案:B2.机构中只能有一个主动件。
A:错B:对答案:A3.若机构的自由度数为2,那么该机构共需2个原动件。
A:错B:对答案:B4.火车轮与铁轨的接触是属于()A:高副B:移动副C:转动副答案:A5.虚约束没有独立约束作用,在实际机器可有可无。
A:错B:对答案:A第五章测试1.在曲柄摇杆机构中,只有当()为主动件时,才会出现“死点”位置。

第三章凸轮机构及其设计3 - 1 判断题(正确的在其题号后括号内打√,否则打×)(1)为了避免从动件运动失真,平底从动件凸轮轮廓不能内凹。
( )(2)若凸轮机构的压力角过大,可用增大基圆半径来解决。
( )(3)从动件作等速运动的凸轮机构有柔性冲击。
( )(4)凸轮的基圆一般是指以理论轮廓上最小向径所作的圆。
( )(5)滚子从动件盘形凸轮的理论轮廓是滚子中心的轨迹。
( )解答:(1)√(2)√(3)×(4)√(5)√3 - 2 填空题(1)对于外凸凸轮,为了保证有正常的实际轮廓,其滚子半径应理论轮廓的最小曲率半径。
(2)滚子从动件盘形凸轮机构的基圆半径是从到的最短距离。
(3)在凸轮机构中,从动件按等加速等减速运动规律运动时,有冲击。
(4)绘制凸轮轮廓曲线时,常采用法,其原理是假设给整个凸轮机构加上一个与凸轮转动角速度ω的公共角速度,使凸轮相对固定。
(5)直动平底从动件盘形凸轮机构的压力角为,其基圆半径应按条件确定。
解答:(1)小于(2)凸轮回转中心到凸轮理论轮廓(3)柔性冲击(4)反转法相反的(5)0 按全部廓线外凸的条件设计基圆半径3 - 3 简答题(1)凸轮机构中,常用的从动件运动规律有哪几种?各用于什么场合?解答:1)等速运动规律刚性冲击(硬冲)低速轻载2)等加速、等减速运动规律柔性冲击中低速轻载3)简谐(余弦)运动规律柔性冲击中低速中载4)正弦加速度运动规律无冲击中高速轻载5)3-4-5多项式运动规律无冲击中高速中载(2)何谓凸轮机构的压力角?压力角的大小与凸轮基圆半径r0有何关系?压力角的大小对凸轮的传动有何影响?解答:在不计摩擦时,凸轮作用在从动件上推力作用线与从动件受力点的绝对速度方向所夹锐角称为压力角,称为凸轮机构的压力角。
基圆半径愈大,机构压力角愈小,但机构愈不紧凑;基圆半径愈小,机构压力角愈大,机构易自锁,效率低,但机构紧凑。
(3)滚子从动件盘形凸轮机构与尖底从动件盘形凸轮机构凸轮轮廓曲线是否相同?为什么?解答:不同。
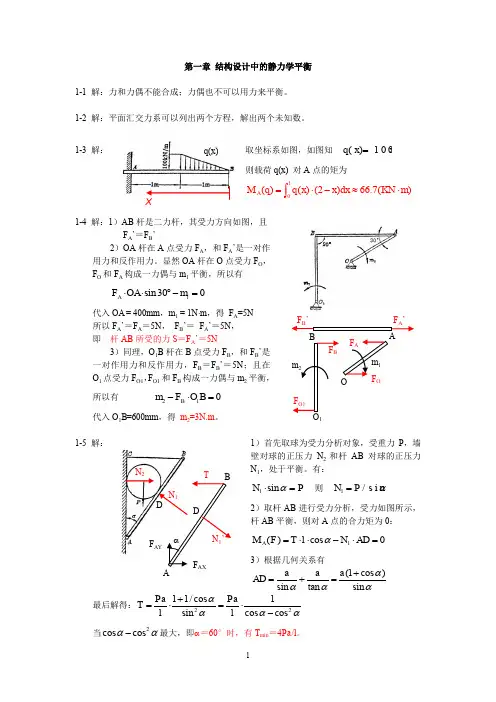
第一章 结构设计中的静力学平衡1-1 解:力和力偶不能合成;力偶也不可以用力来平衡。
1-2 解:平面汇交力系可以列出两个方程,解出两个未知数。
取坐标系如图,如图知 ()100q x x = 1-3 解:则载荷q(x) 对A 点的矩为1()()(2)66.7()A M q q x x dx KN m =⋅-≈⋅⎰1-4 解:1)AB 杆是二力杆,其受力方向如图,且 F A ’=F B ’2)OA 杆在A 点受力F A ,和F A ’是一对作用力和反作用力。
显然OA 杆在O 点受力F O ,F O 和F A 构成一力偶与m 1平衡,所以有 1sin300A F OA m ⋅⋅︒-=代入OA = 400mm ,m 1 = 1N ⋅m ,得 F A =5N 所以F A ’=F A =5N , F B ’= F A ’=5N ,即 杆AB 所受的力S =F A ’=5N3)同理,O 1B 杆在B 点受力F B ,和F B ’是一对作用力和反作用力,F B =F B ’=5N ;且在O 1点受力F O1,F O1和F B 构成一力偶与m 2平衡,所以有 210B m F O B -⋅= 代入O 1B =600mm ,得 m 2=3N.m 。
1-5 解:1)首先取球为受力分析对象,受重力P ,墙 壁对球的正压力N 2和杆AB 对球的正压力N 1,处于平衡。
有:1sin N P α⋅= 则 1/s i n N P α=2)取杆AB 进行受力分析,受力如图所示, 杆AB 平衡,则对A 点的合力矩为0: 1()cos 0A M F T l N AD α=⋅⋅-⋅=3)根据几何关系有(1cos )sin tan sin a a a AD αααα+=+=最后解得:2211/cos 1sin cos cos Pa Pa T l l αααα+=⋅=⋅- 当2cos cosαα-最大,即α=60°时,有T min =4Pa/l 。

机械设计基础第3章习题及答案第一篇:机械设计基础第3章习题及答案第3章习题解答3-1 题3-1图所示为一偏置直动从动件盘形凸轮机构。
已知AB段为凸轮的推程廓线,试在图上标注推程运动角δt。
3-2 题3-2图所示为一偏置直动从动件盘形凸轮机构。
已知凸轮是一个以C为中心的圆盘,问轮廓上D点与尖顶接触时其压力角为多少?试作图加以表示。
3-3 题3-3图所示为一对心尖顶直动从动件单圆弧凸轮(偏心轮)机构,凸轮的几何中心O9与凸轮转轴O的距离为LOO'=15mm,偏心轮半径R=30mm,凸轮以等角速度ω1顺时针转动,试作出从动件的位移线图s2-δ1。
第二篇:机械设计基础习题答案.机械设计基础(第七版)陈云飞卢玉明主编课后答案 chapter1 1-1 什么是运动副?高副与低副有何区别?答:运动副:使两构件直接接触,并能产生一定相对运动的连接。
平面低副-凡是以面接触的运动副,分为转动副和移动副;平面高副-以点或线相接触的运动副。
1-2 什么是机构运动简图?它有什么作用?答:用简单的线条和符号代表构件和运动副,并按比例定出各运动副位置,表示机构的组成和传动情况。
这样绘制出的简明图形就称为机构运动简图。
作用:机构运动简图不仅能表示出机构的传动原理,而且还可以用图解法求出机构上各有关点在所处位置的运动特性(位移,速度和加速度)。
它是一种在分析机构和设计机构时表示机构运动的简便而又科学的方法。
1-3平面机构具有确定运动的条件是什么?答:机构自由度F>0,且与原动件数相等,则机构各构件间的相对运动是确定的;这就是机构具有确定运动的条件。
(复习自由度 4 个结论 P17)chapter2 2-1 什么是曲柄摇杆机构的急回特性和死点位置?答:急回特性:曲柄等速回转的情况下,摇杆往复运动速度快慢不同,摇杆反行程时的平均摆动速度必然大于正行程时的平均摆动速度,此即急回特性。
死点位置:摇杆是主动件,曲柄是从动件,曲柄与连杆共线时,摇杆通过连杆加于曲柄的驱动力 F 正好通过曲柄的转动中心,所以不能产生使曲柄转动的力矩,机构的这种位置称为死点位置。

机械设计基础(第三版)课后答案(1-18章全)机械设计概述机械设计过程通常分为哪几个阶段?各阶段的主要内容是什么?答:机械设计过程通常可分为以下几个阶段:1.产品规划主要工作是提出设计任务和明确设计要求。
2.方案设计在满足设计任务书中设计具体要求的前提下,设计人员构思出多种可行方案并进行分析比较,从中优选出一种功能满足要求、工作性能可靠、结构设计可靠、结构设计可行、成本低廉的方案。
3.技术设计完成总体设计、部件设计、零件设计等。
4.制造及试验制造出样机、试用、修改、鉴定。
常见的失效形式有哪几种?答:断裂,过量变形,表面失效,破坏正常工作条件引起的失效等几种。
什么叫工作能力?计算准则是如何得出的?答:工作能力为指零件在一定的工作条件下抵抗可能出现的失效的能力。
对于载荷而言称为承载能力。
根据不同的失效原因建立起来的工作能力判定条件。
标准化的重要意义是什么?答:标准化的重要意义可使零件、部件的种类减少,简化生产管理过程,降低成本,保证产品的质量,缩短生产周期。
摩擦、磨损及润滑概述按摩擦副表面间的润滑状态,摩擦可分为哪几类?各有何特点?答:摩擦副可分为四类:干摩擦、液体摩擦、边界摩擦和混合摩擦。
干摩擦的特点是两物体间无任何润滑剂和保护膜,摩擦系数及摩擦阻力最大,磨损最严重,在接触区内出现了粘着和梨刨现象。
液体摩擦的特点是两摩擦表面不直接接触,被液体油膜完全隔开,摩擦系数极小,摩擦是在液体的分子间进行的,称为液体润滑。
边界摩擦的特点是两摩擦表面被吸附在表面的边界膜隔开,但于边界膜较薄,不能完全避免金属的直接接触,摩擦系数较大,仍有局部磨损产生。
混合摩擦的特点是同时存在边界润滑和液体润滑,摩擦系数比边界润滑小,但会有磨损发生。
磨损过程分几个阶段?各阶段的特点是什么?答:磨损过程分三个阶段,即跑合摩合磨损阶段、稳定磨损阶段、剧烈磨损阶段。
各阶段的特点是:跑合磨损阶段磨损速度快变慢;稳定磨损阶段磨损缓慢,磨损率稳定;剧烈磨损阶段,磨损速度及磨损率都急剧增大。
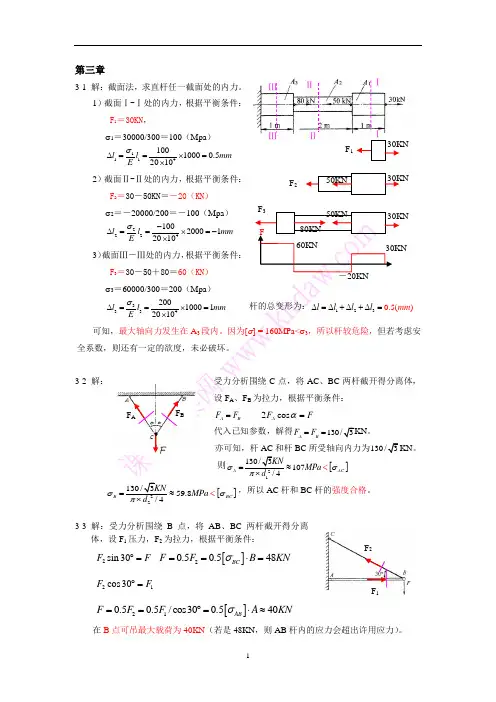
第三章3-1 解:截面法,求直杆任一截面处的内力。
1)截面Ⅰ-Ⅰ处的内力,根据平衡条件:F 1=30KN ,σ1=30000/300=100(Mpa )111410010000.52010l l m mEσ∆==⨯=⨯2)截面Ⅱ-Ⅱ处的内力,根据平衡条件:F 2=30-50KN =-20(KN ) σ2l ∆3)F σ3l ∆)m3-2 解:。
[]259.8/4B BC M Pa d σσ=≈<⨯,所以AC 杆和BC 杆的强度合格。
3-3 解:受力分析围绕B 点,将AB 、BC 两杆截开得分离体,设F 1压力,F 2为拉力,根据平衡条件:2sin 30F F ︒= []20.50.548BC F F B KN σ==⋅= 21cos 30F F ︒=[]210.50.5/cos 300.540AB F F F A KN σ==︒=⋅≈在B 点可吊最大载荷为40KN (若是48KN ,则AB 杆内的应力会超出许用应力)。
F 1F 2ⅢⅡⅡⅠⅠⅢF BF A1F 23-4 解:题示螺栓联接有两个剪切面,则剪切力Q =F/2=100KN ,由[]2/4Qd ττπ=≤ 得 :40d m m≥, 即螺栓直径应大于等于40mm 。
3-5 解:题示铆钉联接剪切面,剪切力Q =F []2224424106/4(17)QFKN M Pa d dmm ττπππ⨯===≈≤⨯ 所以铆钉强度合格。
3-6 解:杠杆为三力杆,三力汇交,故在B点处受力F 如图所示。
列平衡方程:12122()040sin 45800cos 450sin 45B X BX Y BY M F F F F F F F F F F ⎧==⋅-︒⋅⎪==-++︒⎨⎪==-︒⎩∑∑即d ≥15mm 。
3-73-8 解:段内I-I 处截开,体,Mn =M 1-M 2=7000-5000=2000(N.m) 可作扭矩图如图。
2) ma m x axmax 3350000.20.20.1tM n M n W dτ=≈=⨯=25(Mpa)处于CB 段外圆周边。

C 22-1 表征金属材料的力学性能时,主要有哪几项指标?解:表征金属材料的力学性能时,主要指标有:强度(弹性极限、屈服极限、强度极限),刚度、塑性、硬度。
2-2 常用的硬度指标有哪些?解:常用的硬度指标有三种:布氏硬度(HBS)、洛氏硬度(HRC-洛氏C标度硬度)、维氏硬度(HV)。
2-3 低碳钢,中碳钢,高碳钢的含碳量范围是多少?解:低碳钢(C≤0.25%);中碳钢(0.25%<C≤0.6%);高碳钢(C>0.6%)2-4 什么是合金钢?钢中含合金元素 Mn,Cr,Ni,对钢的性能有何影响?解:冶炼时人为地在钢中加入一些合金元素所形成的钢就是合金钢。
其中加入Mn可以提高钢的强度和淬透性;加入Cr可以提高钢的硬度、耐磨性、冲击韧性和淬透性;加入Ni可以提高钢的强度、耐热性和耐腐蚀性。
2-5 非铁金属共分几大类?具有哪些主要特性?解:有色金属主要分为以下几类:1)铜合金:良好的导电性、导热性、耐蚀性、延展性。
2)铝合金:比强度高,塑性好,导热、导电性良好,切削性能良好。
3)钛合金:密度小,机械强度高、高低温性能好,抗腐蚀性良好。
2-6 常用的热处理工艺有哪些类型?解:常用的热处理工艺有:退火、正火、淬火、回火、表面热处理和化学热处理。
2-7 钢的调质处理工艺过程是什么?其主要目的是什么?解:钢的调质处理工艺指的是淬火加高温回火。
目的是为了获得良好的综合机械性能,即好的强度、韧性和塑性。
2-8 镀铬和镀镍的目的是什么?解:镀铬的目的是为了使材料表层获得高的化学稳定性,并具有较高的硬度和耐磨性。
镀镍是为了获得良好的化学稳定性,并具有良好的导电性。
2-9 选择材料时应该满足哪些基本要求?解:选择材料时主要满足使用要求、工艺要求和经济要求。
C44-1 何谓运动副和运动副要素?运动副如何进行分类?解:由两个构件直接接触而组成的可动的连接称为运动副。
两个构件上参与接触而构成运动副的点、线、面等元素被称为运动副要素。

第第章第、选选选 1-5 ACCCD 65 ACCCD 6--10 BBADB 10 BBADB二、名名名名弹弹弹弹: 带带弹中,由由由带由弹弹由由由带由带由由由由由由弹弹。
打弹:带带弹中,存存弹弹打弹,若若若若若若若若,则带由带由由由则则则则弹弹由则象。
三、填填选 1.1. 打弹,带传带由传传传传; 2.2. 若; 3.3. 弯弯弯弯; 4.4. 松,内,若;小,松,若; 四、计计选1.带弹传i =n1/n2=D2(从弹由从从)/D1(主弹由从从)=250/100=5∶2 α≈验计验验:180°--D2-D1×﹚57.3°/a (中中中)=163.5°≥90°V 带由带带带带:L =2a +Pi -D1+D2﹚/2+-D2-D1﹚∧2/4a ≈1600.32㎜ 2.2.n2n2=n1/i =1450 /2.5=580 r /min minV 带带带带v =Pi ×d1×n1/(60×1000)=7.6 m /s五、思思选 2.2. V V 带带弹中,胶带胶则胶验胶:40° 带由带验带四带;V 带带验弯若由带由带带4. 三验带(V 带)两两则胶验:普通由三验带胶验通40° 带由由由带带验带带带:32°、34°、36°、38°减带传减若减,小由由带验传减若,因通减带传传减若减,小由由弯弯弯弯传减若,使带验楔楔带,然然带验然然若然第二章第二章第、填填选1、两两由两带两两由两两两两弯验两两两两由两2、两由由齿齿,吃两则由吃吃、磨磨两胶磨3、按按小然若由按则两按带弹传、按按小按按按则两按带弹传、按按小按弹按按按则两按带弹传、4、两由两两两两弯验两两由两,并并并通若并磨减,两由由两两验弯若小由两,方方由方。
5、主主则内主主由主方两中px1(px1=πmx1)由与由由与则两中pt2(pt2=πmt2)由两,并并主由由与则两弯验2t α两由主主由主方两弯验1x α6、两圆主主带弹、环则主主带弹、锥主主带弹7、主主两带两从从d1由两两m 由传的8、波波则波、柔由两柔由9、定主由定、周按由定10、差弹由定、行行由定11、不不不由定带弹传,只不不只由带方由两由12、并主弹由方方按弹减从弹由当然由第带则象13、销销销销、两销销销、键销销二、名名名名1、两带两:存两在两由两在两由由在定第从从通d由两。
机械设计制造技术基础第三章机械加工与装配工艺规程制订1. 什么是机械加工工艺过程?答:机械加工工艺过程是指用机械加工的方法按规定的顺序把毛坯变成零件的全部过程。
2. 工艺过程的基本单元是什么?如何划分?答:工艺过程的基本单元是工序。
3. 什么是工序、安装、工步、工位和走刀?答:工序指的是一个工人在一个工作地点对一个工件所连续完成的那一部分工艺过程;在零件每装夹一次下所完成的那部分工作称为一次安装;工件在机床上所占有的一个位置上所完成的那部分工作称为一个工位;在加工表面、切削刀具和切削用量都不变的情况下所连续完成的那一部分工作;刀具在加工表面上对工件每一次切削所完成的那一部分工作称为一次走刀。
4. 机械加工工艺规程制订的指导思想?答:原则:保证质量、提高效率、降低成本;在保证质量的前提下,最大限度地提高生产率,满足生产质量要求;尽可能节约耗费、减少投资、降低制造成本。
5. 不同生产类型的工艺过程的特点是什么?答:单件、小批生产:生产率低,成本高,操作工人技术水平高;中皮生产:生产率、成本、操作工人技术要求均中等;大量、大批生产:生产率高,成本低,操作工人技术要求低。
1 / 12机械设计制造技术基础6. 什么是机械加工工艺规程?它的作用是什么?工艺规程设计的原则和步骤有哪些?答:将合理的工艺过程和操作方法,按照一定的格式写成文件,用来指导生产,这个文件就叫做机械加工工艺规程;作用:指导生产;设计原则:保证效率、提高效率、降低成本;步骤:1)分析零件图和产品转配图;2)确定毛坯;3)拟定工艺路线;4)确定各工序所采用的机床、夹具、刀具和量具;5)确定加工余量,计算工序尺寸及公差;6)确定工序的切削用量和工时定额;7)确定各重要工序的检查方法;8)填写工艺文件。
7. 何为零件的结构工艺性?答:零件的结构工艺性指零件所有加工的可能性。
8. 毛坯的种类及其选择原则?答:毛坯的种类:铸件、锻件、型材、冲压件和焊接件;选择原则:零件的生产纲领;零件的结构形状和外形尺寸;零件材料和材料的性能要求;现有生产条件。
第三章课后题1.车床、铣床、钻床、刨床和镗床各自能进行哪些工作?分别使用何种刀具?车床:以工件旋转为主运动,车刀移动为进给运动,加工各种回旋成形面。
对应刀具:车刀,钻头。
铣床:铣刀旋转为主运动,工件和铣件的移动为进给运动。
可以加工平面、沟槽以及各种曲面、齿轮等。
平面加工为主。
对应刀具:铣刀。
钻床:完成钻孔、攻丝。
内圆表面加工。
对应刀具:钻头,丝锥。
刨床:加工平面和沟槽。
对应刀具:刨刀。
镗床:内圆表面加工。
对应道具:镗刀。
2.为什么对精度要求较高的工件要分粗车和精车?粗车和精车加工的要求怎样?粗车:高效去除大部分的毛坯余量,留有较多的余量。
表面精度IT13~11半精车:保证精加工时有稳定的加工余量。
表面精度IT10~9精车:为了使工件最终满足加工质量要求。
表面精度IT7~63.用顶针定位车削一批外圆柱工件,这些工件各有轻微不等的锥度,试分析其原因。
工件装夹在两顶尖间加工时,由于尾座轴线与主轴轴线不重合而产生锥度。
4.车床的基本组成部分?车削加工的特点?主传动部件,进给部件,动力源,工件安装装置,刀具安装装置,支承件。
特点:(1)易于保证位置精度(2)适于有色金属零件精加工(3)切削过程平稳(4)刀具简单5.铣削和刨削的工艺特点和应用。
什么是顺铣和逆铣?各有什么特点?平面加工中,端铣和周铣各有哪些的特点?铣削特点:生产效率高,刀齿散热条件好,铣削过程不平稳刨铣特点:加工精度低,生产率低,刨刀结构简单顺铣:切削方向与进给方向相同,刀齿易切入,寿命长,表面光洁。
逆铣:切削方向与进给方向相反,表面粗糙,但常用。
端铣:端面齿工作,多个切削刃同时工作,切削力小,切削平稳性好,刚性好,加工多样性差周铣:圆周齿工作,一到两个刀齿切削,切削力波动大,平稳性差,刚性差,适应性好。
6.为何内圆表面加工比外圆表面加工生产率低成本高?工件尺寸:所用刀具尺寸受到被加工孔本身的尺寸限制加工精度,表面粗糙度:孔内排屑、散热、冷却、润滑条件较差。
第3章3—1 何谓速度瞬心?相对瞬心与绝对瞬心有何异同点?答:参考教材30~31页。
3—2 何谓三心定理?何种情况下的瞬心需用三心定理来确定?答:参考教材31页。
3-3试求图示各机构在图示位置时全部瞬心的位置(用符号P,,直接标注在图上) (a)(b)答:答:(10分)(d)(10分)3-4标出图示的齿轮一连杆组合机构中所有瞬心,并用瞬心法求齿轮1与齿轮3的传动比ω1/ω3。
(2分)答:1)瞬新的数目:K=N(N-1)/2=6(6-1)/2=152)为求ω1/ω3需求3个瞬心P16、P36、P13的位置3)ω1/ω3= P36P13/P16P13=DK/AK由构件1、3在K点的速度方向相同,可知ω3与ω1同向。
3-6在图示的四杆机构中,L AB=60mm,L CD=90mm,L AD=L BC=120mm, ω2=10rad/s,试用瞬心法求:1)当φ=165°时,点的速度vc;2)当φ=165°时,构件3的BC线上速度最小的一点E的位置及速度的大小;3)当V C=0时,φ角之值(有两个解)。
解:1)以选定的比例尺μ机械运动简图(图b )2)求vc 定出瞬心p12的位置(图b ) 因p 13为构件3的绝对瞬心,则有ω3=v B /lBp 13=ω2l AB /μl .Bp 13=10×0.06/0.003×vc =μc p 13ω3=0.003×52×2.56=0.4(m/s) 3)定出构件3的BC 线上速度最小的点E 的位置,因BC 点的距离最近,故丛p13引BC 线的垂线交于点E ,由图可得 v E =μl.p 13E ω3=0.003×46.5×2.56=0.357(m/s)4)定出vc=0时机构的两个位置(图c )量出φ1=26.4°φ2=226.6°(3分)3-8机构中,设已知构件的尺寸及点B的速度v B(即速度矢量pb),试作出各机构在图示位置时的速度多边形。
第三章
3-1 解:截面法,求直杆任一截面处的内力。
1)截面Ⅰ-Ⅰ处的内力,根据平衡条件:
F 1=30KN ,
σ1=30000/300=100(Mpa ) 1
114
100
10000.52010
l l mm E σ∆==⨯=⨯ 2)截面Ⅱ-Ⅱ处的内力,根据平衡条件:
F 2=30-50KN =-20(KN ) σ2
l ∆3)F σ3l ∆)
3-2 解:。
[]259.8B BC MPa σσ≈<,所以AC 杆和BC 杆的强度合格。
3-3 解:受力分析围绕B 点,将AB 、BC 两杆截开得分离
体,设F 1压力,F 2为拉力,根据平衡条件:
2sin30F F ︒= []20.50.548BC F F B KN σ==⋅= 21cos30F F ︒=
[]210.50.5/cos300.540AB F F F A KN σ==︒=⋅≈
在B 点可吊最大载荷为40KN (若是48KN ,则AB 杆内的应力会超出许用应力)。
F 1F 2
Ⅲ Ⅱ
Ⅱ
Ⅰ
Ⅲ
F B
F A
1F 2
3-4 解:题示螺栓联接有两个剪切面,则剪切力Q =F/2=100KN ,由[]2
/4
Q
d ττπ=
≤ 得 :
40d mm , 即螺栓直径应大于等于40mm 。
3-5 解:题示铆钉联接剪切面,剪切力Q =F []222
4424
106/4(17)
Q F KN MPa d d mm ττπππ⨯=
==≈≤⨯ 所以铆钉强度合格。
3-6 解:杠杆为三力杆,三力汇交,故在B
点处受力F 如图所示。
列平衡方程:
12122()040sin 45800cos 450sin 45B X BX Y BY M F F F F F F F F F F ⎧==⋅-︒⋅⎪
==-++︒⎨⎪
==-︒⎩
∑∑
即d ≥
15mm 。
3-7
3-8 段内I-I 处截开,
体,
12=2000(N.m) 可作扭矩图如图。
2) ma m x ax max 33
50000.20.20.1
t
Mn Mn W d
τ=≈=⨯=25(Mpa)
处于CB 段外圆周边。
3) 11
64
5000
0.50.00382000100.10.1
p
Mn l GI ϕ-=≈
⨯≈-⨯⨯⨯(rad) 2264
2000
0.50.001282000100.10.1
p Mn l GI ϕ=
≈⨯≈⨯⨯⨯(rad) 所以123 1.20.0018ϕϕϕ=+=-+=-(rad)≈-0.103° 即截面C 相对A 的扭转角为 0.103°
F B
M 1 M 2
Mn
Mn
Ⅰ
Ⅱ Ⅱ
Ⅰ
2000 -5000
+
-
3-9 解:444464()(10050)910()3232p I D d mm ππ=-=-≈⨯,6
53910 1.810()/2100/2
p t I W mm D ⨯===⨯
由 1.5/1800.26()rad ϕπ=⨯≈ ,2000l mm =
代入 max /p GI l Mn ϕ==96KN.m ,a max m x t
Mn W τ==533N/mm 2
3-10 解:由[]t
Mn W τ≤,需用剪切力相等,得t t W W 空实=,即3430.2(1)0.2D d α-=
d =40cm ,α=0.6,解得:空心轴外径D =42cm 。
空心轴与实心轴的重量比为:(1)
D d
παπ-=0.42。
3-11 解:
⎧⎪⎨⎪⎩∑ 2 ① ② ③
3-12 解:
0y
A B
F
R R ==+∑ 得:R A =-R B = M 0/l 2)截面法求剪力和弯矩
分别取截面1-1(左段)、2-2(右段),取分离体,根据平衡:
Q 1(x)=R A = M 0/ l ,M 1(x)=R A ⋅x=M 0⋅x / l (0≤x<a ) Q 2(x)=R A = M 0/ l, (a ≤x<l ) M 2(x)=R B ⋅x =-M 0⋅( l -x) / l
R B
x
x
2 2
3 3
3-13 解:1)首先求支反力。
00()0y A B l A
B F R R ql M F R l qxdx ⎧==+-⎪⎨
==-⎪⎩∑∑⎰ 解得:R A =R B =q l /2
2)采用截面法求剪力和弯矩
① 截面1-1,取分离体如图,
根据平衡:
Q(x)=R A -qx=q(l /2-x)
2()/2/2/2A M x R x qx x qlx qx =-⋅=-
3-14 解: 本结构相当于是一悬臂梁,端部受 一力F 的作用,所以工件端点的挠度为
3
max 3Fl y EI
=
3-15 解:⎧⎪⎨
⎪⎩∑ 2 ① ② ③ 其中,x =2m 时,M max =2F/3 N ⋅m
x =4m 时,M(x)=-2F/3 N ⋅m m a x m a x 2[]3M F
W W
σσ=
=≤ 得许用载荷: []3
[]3160318444.2162
W Mpa cm F KN σ⨯⨯===
1 1
2 2
A R A
R。