人教版_选修2-1_第三章_空间向量试卷(含答案)

§3.1.4 空间向量的正交分解及其坐标表示一、选择题1．对于向量a ，b ，c 和实数λ，下列命题中真命题是( )A ．若a ·b ＝0，则a ＝0或b ＝0B ．若λa ＝0，则λ＝0或a ＝0C ．若a 2＝b 2，则a ＝b 或a ＝－bD ．若a ·b ＝a ·c ，则b ＝c2．以下四个命题中正确的是( )A ．空间的任何一个向量都可用其它三个向量表示B ．若{a ，b ，c }为空间向量的一组基底，则a ，b ，c 全不是零向量C ．△ABC 为直角三角形的充要条件是AB →·AC →＝0D ．任何三个不共线的向量都可构成空间向量的一个基底3．长方体ABCD －A 1B 1C 1D 1中，若AB →＝3i ，AD →＝2j ，AA 1→＝5k ，则AC 1→( )A ．i ＋j ＋k B.13i ＋12j ＋15k C ．3i ＋2j ＋5k D ．3i ＋2j －5k4．已知向量{a ，b ，c }是空间的一个基底，p ＝a ＋b ，q ＝a －b ，一定可以与向量p ，q 构成空间的另一个基底的是( )A ．aB ．bC ．cD ．无法确定5．给出下列两个命题：①如果向量a ，b 与任何向量不能构成空间的一个基底，那么a ，b 的关系是不共线；②O ，A ，B ，C 为空间四点，且向量OA →，OB → ，OC →不构成空间的一个基底，那么点O ，A ，B ，C 一定共面． 其中正确的命题是( )A ．仅①B ．仅②C ．①②D ．都不正确6．已知i 、j 、k 是空间直角坐标系O －xyz 的坐标向量，并且AB →＝－i ＋j －k ，则B 点的坐标为( )A ．(－1,1，－1)B ．(－i ，j ，－k )C ．(1，－1，－1)D ．不确定7．设O －ABC 是四面体，G 1是△ABC 的重心，G 是OG 1上的一点，且OG ＝3GG 1，若OG→＝xOA →＋yOB →＋zOC →，则(x ，y ，z )为( )A ．⎝⎛⎭⎫14，14，14B ．⎝⎛⎭⎫34，34，34C ．⎝⎛⎭⎫13，13，13D ．⎝⎛⎭⎫23，23，238．对于空间的四个向量a ，b ，c ，d 最多能构成的基底个数是( )A ．1B ．2C ．3D ．4二、填空题9．已知e 1、e 2、e 3是不共面向量，若a ＝e 1＋e 2＋e 3，b ＝e 1＋e 2－e 3，c ＝e 1－e 2＋e 3， d ＝e 1＋2e 2＋3e 3，又d ＝αa ＋βb ＋γc ，则α、β、γ分别为________．10．向量p 在基底{a ，b ，c }下的坐标为(2,1，－1)，则p 在基底{a ＋b ，a －b ，c }下的坐标为________，在基底{2a ，b ，－c }下的坐标为________．11．在四面体O —ABC 中，OA →＝a ，OB →＝b ，OC →＝c ，D 为BC 的中点，E 为AD 的中点，则OE →＝________.12．棱锥P －ABC 中，∠ABC 为直角，PB ⊥平面ABC ，AB ＝BC ＝PB ＝1，M 为PC 的中点，N 为AC 中点，以{BA →，BC →，BP →}为基底，则MN →的坐标为________．三、解答题13．如图所示，平行六面体OABC －O ′A ′B ′C ′，且OA →＝a ，OC →＝b ，OO ′→＝c .(1)用a ，b ，c 表示向量OB ′→，AC ′→.(2)设G 、H 分别是侧面BB ′C ′C 和O ′A ′B ′C ′的中心，用a ，b ，c 表示GH →.14．如图所示，平行六面体ABCD －A 1B 1C 1D 1中，E 、F 分别在B 1B 和D 1D 上，且BE ＝13BB 1，DF ＝23DD 1. (1)证明：A 、E 、C 1、F 四点共面；(2)若EF →＝xAB →＋yAD →＋zAA 1→，求x ＋y ＋z 的值．参考答案一、选择题1．[答案] B[解析] a ·b ＝0⇒a ⊥b ，|a |2＝|b |2⇒(a ＋b )·(a －b )＝0⇒(a ＋b )⊥(a －b )； a ·b ＝a ·c ⇒a ⊥(b －c )；故A 、C 、D 均错．2．[答案] B[解析] 使用排除法．因为空间中的任何一个向量都可用其它三个不共面．．．的向量来表示，故A 不正确；△ABC 为直角三角形并不一定是AB →·AC →＝0，可能是BC →·BA →＝0，也可能是CA →·CB →＝0，故C 不正确；空间向量基底是由三个不共面的向量组成的，故D 不正确，故选B.3．[答案] C4．[答案] C[解析] ∵a ＝12p ＋12q ，∴a 与p 、q 共面， ∵b ＝12p －12q ，∴b 与p 、q 共面， ∵不存在λ、μ，使c ＝λp ＋μq ，∴c 与p 、q 不共面，故{c ，p ，q }可作为空间的一个基底，故选C.5．[答案] B[解析] ①对空间任意向量c ，都有c 与a 、b 共面，则必有a 与b 共线，∴①错；②∵OA →、OB →、OC →不能构成空间的基底，∴OA →、OB →、OC →必共面，故存在实数λ，μ，使OA →＝λOB →＋μOC →，∴O 、A 、B 、C 四点共面，∴②正确．6．[答案] D[解析] 向量AB →的坐标与B 点的坐标不同．7．[答案] A[解析] 连AG 1交BC 于E ，则E 为BC 中点，AE →＝12(AB →＋AC →)＝12(OB →－2OA →＋OC →)，AG 1→＝23AE →＝13(OB →－2OA →＋OC →)， ∵OG →＝3GG 1→＝3(OG 1→－OG →)，∴OG ＝34OG 1， ∴OG →＝34OG 1→＝34(OA →＋AG 1→) ＝34(OA →＋13OB →－23OA →＋13OC →) ＝14OA →＋14OB →＋14OC →，故选A. 8．[答案] D[解析] 最多的情况是a ，b ，c ，d 中任两个不共线，任三个不共面，从中任选三个都可做一组基底，共4个．二、填空题9．[答案] 52 －1 －12[解析] d ＝αa ＋βb ＋γc ＝α(e 1＋e 2＋e 3)＋β(e 1＋e 2－e 3)＋γ(e 1－e 2＋e 3)＝(α＋β＋γ)e 1＋(α＋β－γ)e 2＋(α－β＋γ)e 3，又因为d ＝e 1＋2e 2＋3e 3，e 1、e 2、e 3不共面，∴⎩⎪⎨⎪⎧ α＋β＋γ＝1α＋β－γ＝2α－β＋γ＝3，解得⎩⎪⎨⎪⎧ α＝52β＝－1γ＝－12.10．[答案] (32，12，－1) (1,1,1) [解析] 由条件p ＝2a ＋b －c .设p 在基底{a ＋b ，a －b ，c }下的坐标为(x ，y ，z )，则p ＝x (a ＋b )＋y (a －b )＋z c ＝(x ＋y )a ＋(x －y )b ＋z c ，∵a 、b 、c 不共面，∴⎩⎪⎨⎪⎧ x ＋y ＝2x －y ＝1z ＝－1，∴⎩⎪⎨⎪⎧ x ＝32y ＝12z ＝－1.即p 在基底{a ＋b ，a －b ，c }下的坐标为(32，12，－1)， 同理可求p 在基底{2a ，b ，－c }下的坐标为(1,1,1)．1１．[答案] 12a ＋14b ＋14c1２．[答案] (12，0，－12) [解析] MN →＝BN →－BM →＝12(BA →＋BC →)－12(BP →＋BC →)＝12BA →－12BP →， 即MN →＝⎝⎛⎭⎫12，0，－12. 三、解答题1３．[解析] (1)OB ′→＝OB →＋BB ′→＝OA →＋OC →＋OO ′→＝a ＋b ＋c .AC ′→＝AC →＋CC ′→＝AB →＋AO →＋AA ′→＝OC →＋OO ′→－OA →＝b ＋c －a .(2)GH →＝GO →＋OH →＝－OG →＋OH →＝－12(OB →＋OC ′→)＋12(OB ′→＋OO ′→) ＝－12(a ＋b ＋c ＋b )＋12(a ＋b ＋c ＋c )＝12(c －b ) 1４．[解析] (1)证明：因为AC 1→＝AB →＋AD →＋AA 1→＝AB →＋AD →＋13AA 1→＋23AA 1→ ＝⎝⎛⎭⎫AB →＋13AA 1→＋⎝⎛⎭⎫AD →＋23AA 1→ ＝(AB →＋BE →)＋(AD →＋DF →)＝AE →＋AF →，所以A 、E 、C 1、F 四点共面．(2)解：因为EF →＝AF →－AE →＝AD →＋DF →－(AB →＋BE →)＝AD →＋23DD 1→－AB →－13BB 1→＝－AB →＋AD →＋13AA 1→， 所以x ＝－1，y ＝1，z ＝13， 所以x ＋y ＋z ＝13.。

3.1.4空间向量的正交分解及其坐标表示双基限时练(十九)1．在空间直角坐标系O －xyz 中，下列说法中正确的是( )A ．向量AB →的坐标与点B 的坐标相同B ．向量AB →的坐标与点A 的坐标相同C ．向量AB →的坐标与向量OB →的坐标相同D ．向量AB →的坐标与OB →－OA →的坐标相同解析 在空间直角坐标系中，从原点出发的向量的坐标等于终点的坐标，不从原点出发的向量AB →的坐标等于终点的坐标减去始点的坐标，所以AB →＝OB →－OA →.答案 D2．以下四个命题中正确的是( )A ．空间的任何一个向量都可用其他三个向量表示B ．若{a ，b ，c }为空间向量的一组基底，则{a ＋b ，b ＋c ，c ＋a }构成空间向量的另一组基底C. △ABC 为直角三角形的充要条件是AB →·AC →＝0D ．任何三个不共线的向量都可构成空间向量的一个基底答案 B3．下列说法不正确的是( )A ．只要空间的三个基本向量的模为1，那么它们就是空间的一个单位正交基底B ．竖坐标为0的向量平行于x 轴与y 轴所确定的平面C ．纵坐标为0的向量都共面D ．横坐标为0的向量都与x 轴上的基向量垂直答案 A4．从空间一点出发的三个不共线的向量a ，b ，c 确定的平面个数是( )A ．1B ．2C ．3D ．1或3解析 当三个向量共面时，可确定一个平面，当三个向量不共面时，可以确定三个平面．答案 D5．正方体ABCD －A ′B ′C ′D ′，O 1，O 2，O 3分别是AC ，AB ′，AD ′，的中点，以{AO 1→，AO 2→，AO 3→}的基底，AC ′→＝xAO 1→＋yAO 2→＋zAO 3→，则x ，y ，z 的值是( )A ．x ＝y ＝z ＝1B ．x ＝y ＝z ＝12C ．x ＝y ＝z ＝22D ．x ＝y ＝z ＝2解析 AC ′→＝AB →＋BC ′→＝AB →＋BB ′→＋B ′C ′→＝AB →＋AA ′→＋AD →＝12(AB →＋AD →)＋12(AB →＋AA ′→)＋12(AA ′→＋AD →)＝12AC →＋12AB ′→＋12AD ′→＝AO 1→＋AO 2→＋AO 3→.对比AC ′→＝xAO 1→＋yAO 2→＋zAO 3→，知x ＝y ＝z ＝1.答案 A6．设{e 1，e 2，e 3}是空间向量的一个单位正交基底，a ＝3e 1＋2e 2－e 3，b ＝－2e 1＋4e 2＋2e 3，则向量a ，b 的坐标分别是________．答案 a ＝(3,2，－1)，b ＝(－2,4,2)7．若{a ，b ，c }构成空间的一个基底，且存在实数x ，y ，z 使得x a ＋y b ＋z c ＝0，则x ，y ，z 满足的条件是__________．解析 ∵{a ，b ，c }构成空间的一个基底，∴a ，b ，c 都是非零向量．由0＝x a ＋y b ＋z c 知，x ＝y ＝z ＝0.答案 x ＝y ＝z ＝08．在四面体O －ABC 中，OA →＝a ，OB →＝b ，OC →＝c ，D 为BC 的中点，E 为AD 的中点，则OE →＝__________(用a ，b ，c 表示)．解析 OE →＝OA →＋AE →＝OA →＋12AD →＝OA →＋12·12(AB →＋AC →)＝OA →＋14(OB →－OA →)＋14(OC →－OA →)＝12OA →＋14OB →＋14OC →＝12a ＋14b ＋14c .答案 12a ＋14b ＋14c9．已知矩形ABCD ，P 为平面ABCD 外一点，且PA ⊥平面ABCD ，M ，N 分别为PC ，PD 上的点，PM ＝2MC ，N 为PD 的中点，求满足MN →＝xAB →＋yAD →＋zAP →的实数x ，y ，z 的值．解 如图所示，取PC 的中点E ，连接NE ，则MN →＝EN →－EM →.由题意易知EN →＝12CD →＝12BA →＝－12AB →，EM →＝PM →－PE →＝23PC →－12PC →＝16PC →，连接AC ，则PC →＝PA →＋AC →＝AB →＋AD →－AP →.∴MN →＝－12AB →－16PC →＝－12AB →－16(AB →＋AD →－AP →)＝－23AB →－16AD →＋16AP →.∴x ＝－23，y ＝－16，z ＝16.10．如图所示，在正四棱柱ABCD －A 1B 1C 1D 1中，O ，O 1分别为底面ABCD 、底面A 1B 1C 1D 1的中心，AB ＝6，AA 1＝4，M 为B 1B 的中点，N 在C 1C 上，且C 1N :NC ＝1:3.(1)若以O 为原点，分别以OA ，OB ，OO 1所在直线为x 轴、y 轴、z 轴建立空间直角坐标系，求图中各点的坐标；(2)若以D 为原点，分别以DA ，DC ，DD 1所在直线为x 轴、y 轴、z 轴建立空间直角坐标系，求图中各点的坐标．解 (1)正方形ABCD 中，AB ＝6，∴AC ＝BD ＝62，从而OA ＝OC ＝OB ＝OD ＝3 2.∴各点坐标分别为A (32，0,0)，B (0,32，0)，C (－32，0,0)，D (0，－32，0)，O (0,0,0)，O 1(0,0,4)，A 1(32，0,4)，B 1(0,32，4)，G 1(－32，0,4)，D 1(0，－32，4)，M (0,32，2)，N (－32，0,3)．(2)同理，A (6,0,0)，B (6,6,0)，C (0,6,0)，D (0,0,0)，A 1(6,0,4)，B 1(6,6,4)，C 1(0,6,4)，D 1(0,0,4)，O (3,3,0)，O 1(3,3,4)，M (6,6,2)，N (0,6,3)．11．如图所示，在正方体ABCD －A 1B 1C 1D 1中，取AB →＝a ，AD →＝b ，AA 1→＝c 作为基底．(1)求BD 1→；(2)若M ，N 分别为边AD ，CC 1的中点，求MN →.解 (1)BD 1→＝AD 1→－AB →＝AD →＋DD 1→－AB →＝AD →＋AA 1→－AB →＝b ＋c －a .(2)MN →＝MA →＋AB →＋BC →＋CN →＝12DA →＋AB →＋AD →＋12CC 1→＝AB →＋12AD→＋12AA1→＝a＋12b＋12c.12．如图所示，在三棱锥O－ABC中，OA，OB，OC两两垂直，OA＝1，OB＝2，OC＝3，E，F分别为AC，BC的中点，建立以OA→，OB→，OC→方向上的单位向量为正交基底的空间坐标系O－xyz.求EF中点P的坐标．解令Ox，Oy，Oz轴方向上的单位向量分别为i，j，k.∵OP→＝OE→＋EP→＝12(OA→＋OC→)＋12EF→＝12(OA→＋OC→)＋12×12AB→＝12 (OA→＋OC→)＋14(OB→－OA→)＝14OA→＋14OB→＋12OC→＝14i＋14×2j＋12×3k＝14i＋12j＋32k∴P点的坐标为⎝⎛⎭⎪⎫14，12，32.。

第3课时 用向量方法求空间中的角课时过关·能力提升基础巩固1若直线l 的方向向量与平面α的法向量的夹角等于120°,则直线l 与平面α所成的角等于( ) A.120° B.60°C.30°D.以上均错l 的方向向量与平面α的法向量的夹角为120°,∴它们所在直线的夹角为60°.则直线l 与平面α所成的角为90°-60°=30°.2设四边形ABCD ,ABEF 都是边长为1的正方形,FA ⊥平面ABCD ,则异面直线AC 与BF 所成的角等于 ( )A.45°B.30°C.90°D.60°,则A (0,0,0),F (0,0,1),B (0,1,0),C (1,1,0), ∴AC⃗⃗⃗⃗⃗ =(1,1,0),BF ⃗⃗⃗⃗⃗ =(0,-1,1). ∴AC ⃗⃗⃗⃗⃗ ·BF⃗⃗⃗⃗⃗ =-1. 设异面直线AC 与BF 所成的角为θ, ∴cos θ=|cos <AC ⃗⃗⃗⃗⃗ ,BF ⃗⃗⃗⃗⃗ >|=12. 又∵θ∈(0°,90°],∴θ=60°.3若a =(λ,1,2)与b =(2,-1,-2)的夹角为钝角,则实数λ的取值范围为( ) A.λ<52B.λ<52,且λ≠-2C.λ≥52,且λ≠4D.λ≥52,得a ·b =2λ+(-1)-4<0,即λ<52.而|a |=√5+λ2,|b |=3,又<a ,b >为钝角,∴3√5+λ≠-1,即λ≠-2.4若斜线段与它在平面α内射影的长之比是2∶1,则AB 与平面α所成角为( ) A.π6 B.π3C.23πD.56πAB 与平面α所成角为θ,由题意知cos θ=12,则AB 与平面α所成角为π3.5若平面α的一个法向量为n =(4,1,1),直线l 的一个方向向量为a =(-2,-3,3),则l 与α所成角的余弦值为 ( )A.-√11B.√11C.-√110D.√913<a ,n >=√4+9+9√16+1+1=3√11=-4√1133, 故l 与α所成角的余弦值为√1-(-4√1133)2=√91333.6在正方体ABCD-A 1B 1C 1D 1中,二面角A-BD 1-B 1的大小为 .,以点C 为原点建立空间直角坐标系.设正方体的边长为a ,则A (a ,a ,0),B (a ,0,0),D 1(0,a ,a ),B 1(a ,0,a ), ∴BA ⃗⃗⃗⃗⃗ =(0,a ,0),BD 1⃗⃗⃗⃗⃗⃗⃗⃗ =(-a ,a ,a ),BB 1⃗⃗⃗⃗⃗⃗⃗ =(0,0,a ). 设平面ABD 1的法向量为n =(x ,y ,z ), 则n ·BA ⃗⃗⃗⃗⃗ =(x ,y ,z )·(0,a ,0)=ay=0, n ·BD 1⃗⃗⃗⃗⃗⃗⃗⃗ =(x ,y ,z )·(-a ,a ,a )=-ax+ay+az=0. ∵a ≠0,∴y=0,x=z.令x=z=1,则n =(1,0,1),同理,求得平面B 1BD 1的法向量m =(1,1,0),∴cos <n ,m >=n ·m |n ||m |=12,∴<n ,m >=60°.而二面角A-BD 1-B 1为钝角,故为120°.°7在正四棱锥P-ABCD 中,高为1,底面边长为2,E 为BC 的中点,则异面直线PE 与DB 所成的角为 .,则B (1,1,0),D (-1,-1,0),E (0,1,0),P (0,0,1),∴DB⃗⃗⃗⃗⃗⃗ =(2,2,0),PE ⃗⃗⃗⃗⃗ =(0,1,-1). ∴cos <DB ⃗⃗⃗⃗⃗⃗ ,PE ⃗⃗⃗⃗⃗ >=DB ⃗⃗⃗⃗⃗⃗ ·PE ⃗⃗⃗⃗⃗⃗|DB ⃗⃗⃗⃗⃗⃗ ||PE ⃗⃗⃗⃗⃗⃗|=√8×√2=12.∴<DB ⃗⃗⃗⃗⃗⃗ ,PE ⃗⃗⃗⃗⃗ >=π.∴PE 与DB 所成的角为π.8在长方体ABCD-A 1B 1C 1D 1中,已知DA=DC=4,DD 1=3,则异面直线A 1B 与B 1C 所成角的余弦值为 .9如图,在长方体ABCD-A 1B 1C 1D 1中,AD=AA 1=1,AB=2,点E 是棱AB 上的动点.若异面直线AD 1与EC 所成角为60°,试确定此时动点E 的位置.DA 所在直线为x 轴,以DC 所在直线为y 轴,以DD 1所在直线为z 轴,建立空间直角坐标系.设E (1,t ,0)(0≤t ≤2),则A (1,0,0),D (0,0,0),D 1(0,0,1),C (0,2,0),D 1A ⃗⃗⃗⃗⃗⃗⃗ =(1,0,-1),CE ⃗⃗⃗⃗⃗ =(1,t-2,0), 根据数量积的定义及已知得:1+0×(t-2)+0=√2×√1+(t -2)2·cos 60°, 所以t=1.所以点E 的位置是AB 的中点. 10如图,在四棱锥P-ABCD 中,已知PA ⊥平面ABCD ,且四边形ABCD 为直角梯形,∠ABC=∠BAD=π,PA=AD=2,AB=BC=1.求平面PAB 与平面PCD 所成二面角的余弦值.{AB ⃗⃗⃗⃗⃗ ,AD ⃗⃗⃗⃗⃗ ,AP ⃗⃗⃗⃗⃗ }为正交基底建立如图所示的空间直角坐标系Axyz ,则各点的坐标为B (1,0,0),C (1,1,0),D (0,2,0),P (0,0,2).因为AD ⊥平面PAB ,所以AD ⃗⃗⃗⃗⃗ 是平面PAB 的一个法向量,AD ⃗⃗⃗⃗⃗ =(0,2,0).因为PC⃗⃗⃗⃗⃗ =(1,1,-2),PD ⃗⃗⃗⃗⃗ =(0,2,-2).设平面PCD 的法向量为m =(x ,y ,z ), 则m ·PC ⃗⃗⃗⃗⃗ =0,m ·PD ⃗⃗⃗⃗⃗ =0. 即{x +y -2z =0,2y -2z =0. 令y=1,解得z=1,x=1.所以m =(1,1,1)是平面PCD 的一个法向量.从而cos <AD ⃗⃗⃗⃗⃗ ,m >=AD ⃗⃗⃗⃗⃗⃗·m |AD ⃗⃗⃗⃗⃗⃗ ||m |=√33,所以平面PAB 与平面PCD 所成二面角的余弦值为√33.能力提升1已知E ,F 分别是棱长为1的正方体ABCD-A 1B 1C 1D 1的棱BC ,CC 1的中点,则截面AEFD 1与底面ABCD 所成二面角的正弦值是( ) A.23B.√23C.√53D.2√33D 为坐标原点,以DA ⃗⃗⃗⃗⃗ ,DC ⃗⃗⃗⃗⃗ ,DD 1⃗⃗⃗⃗⃗⃗⃗⃗ 的方向分别为x 轴、y 轴、z 轴的正方向建立空间直角坐标系,如图,则A (1,0,0),E (12,1,0),F (0,1,12),D 1(0,0,1),∴AD 1⃗⃗⃗⃗⃗⃗⃗ =(-1,0,1),AE ⃗⃗⃗⃗⃗ =(-12,1,0). 设平面AEFD 1的法向量为n =(x ,y ,z ),则 {n ·AD 1⃗⃗⃗⃗⃗⃗⃗ =0,n ·AE ⃗⃗⃗⃗⃗ =0⇒{-x +z =0,-x 2+y =0,∴x=2y=z. 取y=1,则n =(2,1,2),而平面ABCD 的一个法向量为u =(0,0,1),∴cos <n ,u >=2,∴sin <n ,u >=√5.2在棱长为1的正方体ABCD-A 1B 1C 1D 1中,M ,N 分别是A 1B 1,BB 1的中点,那么直线AM 与CN 所成角的余弦值是( )A.√32B.√1010C.35D.25,建立空间直角坐标系,则A (1,0,0),M (1,12,1),C (0,1,0),N (1,1,12),∴AM ⃗⃗⃗⃗⃗⃗ =(0,12,1),CN ⃗⃗⃗⃗⃗ =(1,0,12).∴AM ⃗⃗⃗⃗⃗⃗ ·CN ⃗⃗⃗⃗⃗ =12,|AM ⃗⃗⃗⃗⃗⃗ |=|CN ⃗⃗⃗⃗⃗ |=√52. ∴cos <AM ⃗⃗⃗⃗⃗⃗ ,CN ⃗⃗⃗⃗⃗ >=1252×52=25.3在正方体ABCD-A 1B 1C 1D 1中,EF ⊥AC ,EF ⊥A 1D ,则EF 与BD 1所成的角是( ) A.90°B.60°C.30°D.0°,以D 为原点建立空间直角坐标系,设正方体的棱长为a ,则A 1(a ,0,a ),D (0,0,0),A (a ,0,0),C (0,a ,0),B (a ,a ,0),D 1(0,0,a ), ∴DA 1⃗⃗⃗⃗⃗⃗⃗⃗ =(a ,0,a ),AC ⃗⃗⃗⃗⃗ =(-a ,a ,0),BD 1⃗⃗⃗⃗⃗⃗⃗⃗ =(-a ,-a ,a ). ∵EF ⊥AC ,EF ⊥A 1D ,设EF ⃗⃗⃗⃗⃗ =(x ,y ,z ), ∴EF ⃗⃗⃗⃗⃗ ·DA 1⃗⃗⃗⃗⃗⃗⃗⃗ =(x ,y ,z )·(a ,0,a )=ax+az=0, EF ⃗⃗⃗⃗⃗ ·AC ⃗⃗⃗⃗⃗ =(x ,y ,z )·(-a ,a ,0)=-ax+ay=0.∵a ≠0,∴x=y=-z (x ≠0).∴EF ⃗⃗⃗⃗⃗ =(x ,x ,-x ).∴BD 1⃗⃗⃗⃗⃗⃗⃗⃗ =-aEF ⃗⃗⃗⃗⃗ . ∴BD 1⃗⃗⃗⃗⃗⃗⃗⃗ ∥EF ⃗⃗⃗⃗⃗ ,即BD 1∥EF. 故EF 与BD 1所成的角是0°.4二面角α-l-β内有一点P ,若点P 到平面α,β的距离分别是5,8,且点P 在平面α,β内的射影间的距离为7,则二面角的度数是( ) A.30°B.60°C.120°D.150°,PA ⊥α,PB ⊥β,∠ADB 为二面角α-l-β的平面角.由题意知PA=5,PB=8,AB=7, 由余弦定理,可得cos ∠APB=52+82-72=1,则∠APB=60°,故∠ADB=120°.5在空间中,已知平面α过点(3,0,0)和(0,4,0)及z 轴上一点(0,0,a )(a>0),若平面α与平面xOy 的夹角为45°,则a= .6在长方体ABCD-A 1B 1C 1D 1中,B 1C 和C 1D 与底面所成的角分别为60°和45°,则异面直线B 1C 和C 1D 所成角的余弦值为 .,可知∠CB 1C 1=60°,∠DC 1D 1=45°.设B 1C 1=1,则CC 1=√3=DD 1.∴C 1D 1=√3,则有B 1(√3,0,0),C (√3,1,√3),C 1(√3,1,0),D (0,1,√3).∴B 1C ⃗⃗⃗⃗⃗⃗⃗ =(0,1,√3),C 1D ⃗⃗⃗⃗⃗⃗⃗ =(-√3,0,√3). ∴cos <B 1C ⃗⃗⃗⃗⃗⃗⃗ ,C 1D ⃗⃗⃗⃗⃗⃗⃗ >=B 1C ⃗⃗⃗⃗⃗⃗⃗⃗⃗ ·C 1D⃗⃗⃗⃗⃗⃗⃗⃗⃗ |B 1C ⃗⃗⃗⃗⃗⃗⃗⃗⃗ ||C 1D ⃗⃗⃗⃗⃗⃗⃗⃗⃗ |=2√6=√64.7如图,在三棱锥P-ABC 中,PA=PB=PC=BC ,且∠BAC=π2,则PA 与底面ABC 所成角的大小为 .,∵PA=PB=PC ,∴P 在底面上的射影O 是△ABC 的外心.又∠BAC=π2,∴O 在BC 上且为BC 的中点.∴AO 为PA 在底面上的射影,∠PAO 即为所求的角.在△PAO 中,PO=√32PB=√32PA ,∴sin ∠PAO=PO =√3.∴∠PAO=π3.8在正方体ABCD-A 1B 1C 1D 1中,直线BC 1与平面A 1BD 所成角的余弦值是 .,设棱长为1,则B (1,1,0),C 1(0,1,1),A 1(1,0,1),D (0,0,0). BC 1⃗⃗⃗⃗⃗⃗⃗ =(-1,0,1),A 1D ⃗⃗⃗⃗⃗⃗⃗⃗ =(-1,0,-1),BD ⃗⃗⃗⃗⃗⃗ =(-1,-1,0). 设平面A 1BD 的一个法向量为n =(1,x ,y ),设BC 1与平面A 1BD 所成的角为θ,n ⊥A 1D ⃗⃗⃗⃗⃗⃗⃗⃗ ,n ⊥BD⃗⃗⃗⃗⃗⃗ , 所以n ·A 1D ⃗⃗⃗⃗⃗⃗⃗⃗ =0,n ·BD ⃗⃗⃗⃗⃗⃗ =0, 所以{-1-y =0,-1-x =0,解得{x =-1,y =-1.所以n =(1,-1,-1),则cos <BC 1⃗⃗⃗⃗⃗⃗⃗ ,n >=BC 1⃗⃗⃗⃗⃗⃗⃗⃗⃗ ·n|BC 1⃗⃗⃗⃗⃗⃗⃗⃗⃗|·|n |=-√63,所以sin θ=√63.所以cos θ=√1-(√63)2=√33.9如图,在直三棱柱ABC-A 1B 1C 1中,AA 1=BC=AB=2,AB ⊥BC ,求二面角B 1-A 1C-C 1的大小.,则A (2,0,0),C (0,2,0),A 1(2,0,2),B 1(0,0,2),C 1(0,2,2).设AC 的中点为M ,连接BM.∵BM ⊥AC ,BM ⊥CC 1,∴BM ⊥平面AA 1C 1C ,即BM ⃗⃗⃗⃗⃗⃗ =(1,1,0)是平面AA 1C 1C 的一个法向量.设平面A 1B 1C 的一个法向量是n =(x ,y ,z ).A 1C ⃗⃗⃗⃗⃗⃗⃗ =(-2,2,-2),A 1B 1⃗⃗⃗⃗⃗⃗⃗⃗⃗ =(-2,0,0),∴n ·A 1B 1⃗⃗⃗⃗⃗⃗⃗⃗⃗ =-2x=0,n ·A 1C ⃗⃗⃗⃗⃗⃗⃗ =-2x+2y-2z=0,令z=1,解得x=0,y=1.∴n =(0,1,1).设法向量n 与BM⃗⃗⃗⃗⃗⃗ 的夹角为φ,二面角B 1-A 1C-C 1为θ,显然θ为锐角.∴cos θ=|cos φ|=|n ·BM ⃗⃗⃗⃗⃗⃗⃗ ||n ||BM ⃗⃗⃗⃗⃗⃗⃗ |=12,解得θ=π3.∴二面角B 1-A 1C-C 1的大小为π3.★10四棱柱ABCD-A 1B 1C 1D 1的侧棱AA 1垂直于底面,底面ABCD 为直角梯形,AD ∥BC ,AD ⊥AB ,AD=AB=AA 1=2BC ,E 为DD 1的中点,F 为A 1D 的中点. (1)求证:EF ∥平面A 1BC ;(2)求直线EF 与平面A 1CD 所成角θ的正弦值.E ,F 分别是DD 1,DA 1的中点,∴EF ∥A 1D 1.又A 1D 1∥B 1C 1∥BC ,∴EF ∥BC ,且EF ⊄平面A 1BC ,BC ⊂平面A 1BC , ∴EF ∥平面A 1BC.AB ,AD ,AA 1两两垂直,以AB 所在直线为x 轴,以AD 所在直线为y 轴,以AA 1所在直线为z 轴,建立空间直角坐标系,如图.设BC=1,则A (0,0,0),A 1(0,0,2),C (2,1,0),D (0,2,0),D 1(0,2,2),F (0,1,1),E (0,2,1), 故FE ⃗⃗⃗⃗⃗ =(0,1,0),A 1D ⃗⃗⃗⃗⃗⃗⃗⃗ =(0,2,-2),CD ⃗⃗⃗⃗⃗ =(-2,1,0). 设平面A 1CD 的法向量n =(x ,y ,z ), 则{n ·A 1D⃗⃗⃗⃗⃗⃗⃗⃗ =(x ,y ,z )·(0,2,-2)=2y -2z =0,n ·CD ⃗⃗⃗⃗⃗ =(x ,y ,z )·(-2,1,0)=-2x +y =0.取n =(1,2,2),则sin θ=|cos <n ,FE ⃗⃗⃗⃗⃗ >|=|n ·FE ⃗⃗⃗⃗⃗⃗|n ||FE ⃗⃗⃗⃗⃗⃗ || =|√1+4+4·√0+1+0|=23,故直线EF 与平面A 1CD 所成角θ的正弦值等于23.。

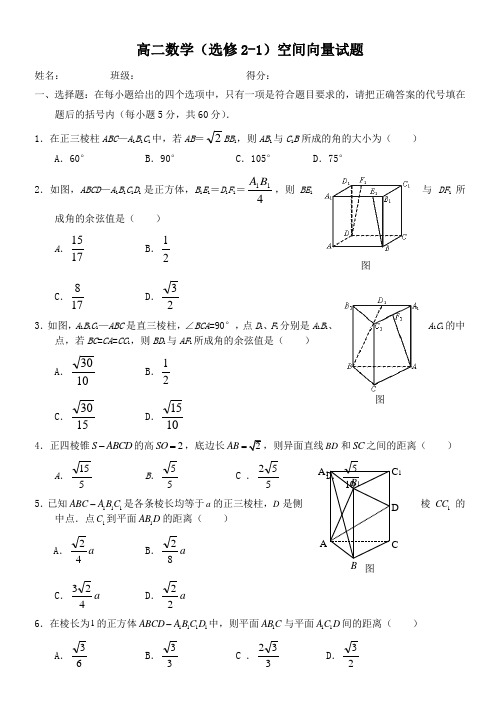
AA 1DCB B 1C 1图高二数学（选修2-1）空间向量试题姓名：_________班级：________ 得分：________一、选择题：在每小题给出的四个选项中，只有一项是符合题目要求的，请把正确答案的代号填在题后的括号内（每小题5分，共60分）． 1．在正三棱柱ABC —A 1B 1C 1中，若AB ＝2BB 1，则AB 1与C 1B 所成的角的大小为（ ）A ．60°B ．90°C ．105°D ．75°2．如图，ABCD —A 1B 1C 1D 1是正方体，B 1E 1＝D 1F 1＝411B A ，则BE 1与DF 1所成角的余弦值是（ ）A ．1715 B ．21 C ．178 D ．23 3．如图，A 1B 1C 1—ABC 是直三棱柱，∠BCA =90°，点D 1、F 1分别是A 1B 1、A 1C 1的中点，若BC =CA =CC 1，则BD 1与AF 1所成角的余弦值是（ ）A ．1030 B ．21 C ．1530 D ．1015 4．正四棱锥S ABCD -的高2SO =，底边长2AB =，则异面直线BD 和SC 之间的距离（ ）A ．515 B ．55 C ．552 D ．105 5．已知111ABC A B C -是各条棱长均等于a 的正三棱柱，D 是侧棱1CC 的中点．点1C 到平面1AB D 的距离（ ）A ．a 42 B ．a 82 C ．a 423 D ．a 22 6．在棱长为1的正方体1111ABCD A B C D -中，则平面1AB C 与平面11A C D 间的距离（ ）A ．63 B ．33 C ．332 D ．23 图图7．在三棱锥P －ABC 中，AB ⊥BC ，AB ＝BC ＝21PA ，点O 、D 分别是AC 、PC 的中点，OP ⊥底面ABC ，则直线OD 与平面PBC 所成角的正弦值（ ）A ．621B ．338 C60210 D ．302108．在直三棱柱111C B A ABC -中，底面是等腰直角三角形，90=∠ACB ，侧棱21=AA ，D ，E分别是1CC 与B A 1的中点，点E 在平面AB D 上的射影是ABD ∆的重心G ．则B A 1与平面AB D 所成角的余弦值（ ）A ．32 B ．37C ．23 D ．73 9．正三棱柱111C B A ABC -的底面边长为3，侧棱3231=AA ，D 是C B 延长线上一点，且BC BD =，则二面角B AD B --1的大小（ ）A ．3π B ．6πC ．65πD ．32π10．正四棱柱1111D C B A ABCD -中，底面边长为22，侧棱长为4，E ，F 分别为棱AB ，CD 的中点，G BD EF =⋂．则三棱锥11EFD B -的体积V （ ）A ．66 B ．3316 C ．316D ．1611．有以下命题：①如果向量b a ,与任何向量不能构成空间向量的一组基底，那么b a ,的关系是不共线； ②,,,O A B C 为空间四点，且向量OC OB OA ,,不构成空间的一个基底，则点,,,O A B C 一定共面；③已知向量c b a ,,是空间的一个基底，则向量c b a b a ,,-+也是空间的一个基底。

这时Q ⎝ ⎛⎭⎪⎫43，43，83.答案：C二、填空题：本大题共4小题，每小题5分，共20分．13．若A (x,5－x,2x －1)，B (1，x ＋2,2－x )，则当|AB →|取最小值时，x 的值等于________．解析：AB →＝(1－x,2x －3，－3x ＋3)，则 |AB →|＝1－x2＋2x －32＋－3x ＋32＝14x 2－32x ＋19＝14⎝⎛⎭⎪⎫x －872＋57，故当x ＝87时，|AB →|取最小值．答案：8714．正方体ABCD －A 1B 1C 1D 1中，直线BC 1与平面A 1BD 夹角的正弦值是________． 解析：如图，以DA 、DC 、DD 1分别为x 轴、y 轴、z 轴建立空间直角坐标系，设正方体的棱长为1，则A (1,0,0)，B (1,1,0)，C 1(0,1,1)， 易证AC 1→是平面A 1BD 的一个法向量．AC 1→＝(－1,1,1)，BC 1→＝(－1,0,1)． cos 〈AC 1→，BC 1→〉＝1＋13×2＝63. 所以BC 1与平面A 1BD 夹角的正弦值为63.答案：63设AC ∩BD ＝N ，连结NE ，则N ⎝ ⎛⎭⎪⎫22，22，0，E (0,0,1)， ∴NE →＝⎝ ⎛⎭⎪⎫－22，－22，1. 又A (2，2，0)，M ⎝ ⎛⎭⎪⎫22，22，1， ∴AM →＝⎝ ⎛⎭⎪⎫－22，－22，1. ∴NE →＝AM →，且NE 与AM 不共线．∴NE ∥AM .又NE ⊂平面BED ，AM ⊄平面BDE ，∴AM ∥平面BDE .(2)设P (t ，t,0)(0≤t ≤2)，则PF →＝(2－t ，2－t,1)，CD →＝(2，0,0)．又∵PF →与CD →所成的角为60°，|2－t ·2|2－t2＋2－t 2＋1·2＝12， 解之得t ＝22，或t ＝322(舍去)． 故点P 为AC 的中点．22．(本小题满分12分)如图，在圆锥PO 中，已知PO ＝2，⊙O 的直径AB ＝2，C 是AB 的中点，D 为AC 的中点．。

学业分层测评(建议用时：45分钟)[学业达标]一、选择题1．设a ，b ，c 是任意的非零平面向量，且它们相互不共线，下列命题：①(a ·b )c －(c ·a )b ＝0；②|a |＝a ·a ；③a 2b ＝b 2a ；④(3a ＋2b )·(3a －2b )＝9|a |2－4|b |2.其中正确的有( )A ．①②B ．②③C ．③④D ．②④【解析】 由于数量积不满足结合律，故①不正确，由数量积的性质知②正确，③中，|a |2·b ＝|b |2·a 不一定成立，④运算正确．【答案】 D2．已知a ＋b ＋c ＝0，|a |＝2，|b |＝3，|c |＝4，则a 与b 的夹角〈a ，b 〉＝( )A ．30°B ．45°C ．60°D ．以上都不对【解析】 ∵a ＋b ＋c ＝0，∴a ＋b ＝－c ，∴(a ＋b )2＝|a |2＋|b |2＋2a ·b ＝|c |2，∴a ·b ＝32，∴cos 〈a ，b 〉＝a ·b |a ||b |＝14.【答案】 D3．已知四边形ABCD 为矩形，P A ⊥平面ABCD ，连接AC ，BD ，PB ，PC ，PD ，则下列各组向量中，数量积不为零的是( )A.PC →与BD →B.DA →与PB →C.PD→与AB → D.P A →与CD→ 【解析】 用排除法，因为P A ⊥平面ABCD ，所以P A ⊥CD ，故P A →·CD→＝0，排除D ；因为AD ⊥AB ，P A ⊥AD ，又P A ∩AB ＝A ，所以AD ⊥平面P AB ，所以AD ⊥PB ，故DA →·PB →＝0，排除B ，同理PD →·AB →＝0，排除C.【答案】 A4.如图3-1-25，已知空间四边形每条边和对角线都等于a ，点E ，F ，G 分别是AB ，AD ，DC 的中点，则下列向量的数量积等于a 2的是( )图3-1-25A ．2BA →·AC →B ．2AD →·DB →C ．2FG→·AC → D ．2EF→·CB → 【解析】 2BA→·AC →＝－a 2，故A 错；2AD →·DB →＝－a 2，故B 错；2EF →·CB →＝－12a 2，故D 错；2FG→·AC →＝AC →2＝a 2，故只有C 正确． 【答案】 C5．在正方体ABCD -A 1B 1C 1D 1中，有下列命题：①(AA 1→＋AD →＋AB →)2＝3AB →2； ②A 1C →·(A 1B 1→－A 1A →)＝0； ③AD 1→与A 1B →的夹角为60°.其中正确命题的个数是( ) 【导学号：18490091】 A ．1个 B ．2个 C ．3个D ．0个【解析】 由题意知①②都正确，③不正确，AD 1→与A 1B →的夹角为120°.【答案】 B 二、填空题6．已知|a |＝2，|b |＝3，〈a ，b 〉＝60°，则|2a －3b |＝________． 【解析】 |2a －3b |2＝(2a －3b )2＝4a 2－12a ·b ＋9b 2 ＝4×|a |2＋9×|b |2－12×|a |·|b |·cos 60°＝61， ∴|2a －3b |＝61. 【答案】617．已知|a |＝2，|b |＝1，〈a ，b 〉＝60°，则使向量a ＋λb 与λa －2b 的夹角为钝角的实数λ的取值范围是________．【解析】 由题意知⎩⎪⎨⎪⎧（a ＋λb ）·（λa －2b ）<0，cos 〈a ＋λb ，λa －2b 〉≠－1.即⎩⎪⎨⎪⎧（a ＋λb ）·（λa －2b ）<0，（a ＋λb ）·（λa －2b ）≠－|a ＋λb ||λa －2b | 得λ2＋2λ－2<0.∴－1－3<λ<－1＋ 3.【答案】 (－1－3，－1＋3)8.如图3-1-26，已知正三棱柱ABC -A 1B 1C 1的各条棱长都相等，M 是侧棱CC 1的中点，则异面直线AB 1和BM 所成的角的大小是________．图3-1-26【解析】 不妨设棱长为2，则AB →1＝BB 1→－BA →，BM →＝BC →＋12BB 1→，cos 〈AB 1→，BM →〉＝（BB 1→－BA →）·⎝ ⎛⎭⎪⎫BC →＋12BB 1→22×5＝0－2＋2－022×5＝0，故填90°.【答案】 90° 三、解答题9．如图3-1-27，在正方体ABCD -A 1B 1C 1D 1中，O 为AC 与BD 的交点，G 为CC 1的中点．求证：A 1O ⊥平面BDG .图3-1-27【证明】 设A 1B 1→＝a ，A 1D 1→＝b ，A 1A →＝c . 则a ·b ＝0，a ·c ＝0，b ·c ＝0.而A 1O →＝A 1A →＋AO → ＝A 1A →＋12(AB →＋AD →) ＝c ＋12(a ＋b )， BD→＝AD →－AB →＝b －a ， OG→＝OC →＋CG → ＝12(AB →＋AD →)＋12CC 1→ ＝12(a ＋b )＋12c .∴A 1O →·BD →＝⎝⎛⎭⎪⎫c ＋12a ＋12b ·(b －a )＝c ·(b －a )＋12(a ＋b )·(b －a ) ＝c ·b －c ·a ＋12(b 2－a 2) ＝12(|b |2－|a |2)＝0. ∴A 1O →⊥BD →. ∴A 1O ⊥BD . 同理可证A 1O →⊥OG →. ∴A 1O ⊥OG .又OG ∩BD ＝O 且A 1O ⊄平面BDG ， ∴A 1O ⊥平面BDG .10．已知长方体ABCD -A 1B 1C 1D 1中，AB ＝AA 1＝2，AD ＝4，E 为侧面AB 1的中心，F 为A 1D 1的中点，试计算：(1)BC →·ED 1→；(2)BF →·AB 1→；(3)EF →·FC 1→. 【解】 如图所示，设AB →＝a ，AD →＝b ，AA 1→＝c ， 则|a |＝|c |＝2，|b |＝4，a·b ＝b·c ＝c·a ＝0.(1)BC →·ED 1→＝AD →·(EA 1→＋A 1D 1→)＝AD →·⎣⎢⎡⎦⎥⎤12（AA 1→－AB→）＋AD → ＝b ·⎣⎢⎡⎦⎥⎤12（c －a ）＋b ＝|b |2＝42＝16.(2)BF →·AB 1→＝(BA 1→＋A 1F →)·(AB →＋BB 1→) ＝⎝ ⎛⎭⎪⎫AA 1→－AB →＋12AD →·(AB →＋AA 1→) ＝⎝⎛⎭⎪⎫c －a ＋12b ·(a ＋c )＝|c |2－|a |2＝22－22＝0.(3)EF →·FC 1→＝(EA 1→＋A 1F →)·(FD 1→＋D 1C 1→) ＝⎣⎢⎡⎦⎥⎤12（AA 1→－AB →）＋12AD →·⎝ ⎛⎭⎪⎫12AD →＋AB → ＝⎣⎢⎡⎦⎥⎤12（c －a ）＋12b ·⎝ ⎛⎭⎪⎫12b ＋a ＝12(－a ＋b ＋c )·⎝ ⎛⎭⎪⎫12b ＋a＝－12|a |2＋14|b |2＝2.[能力提升]1．已知边长为1的正方体ABCD -A 1B 1C 1D 1的上底面A 1B 1C 1D 1的中心为O 1，则AO 1→·AC →的值为( ) A ．－1 B ．0 C ．1D ．2【解析】 AO 1→＝AA 1→＋A 1O 1→＝AA 1→＋12(A 1B 1→＋A 1D 1→)＝AA 1→＋12(AB →＋AD →)，而AC →＝AB →＋AD →，则AO 1→·AC →＝12(AB →2＋AD →2)＝1，故选C.【答案】 C2．已知a ，b 是两异面直线，A ，B ∈a ，C ，D ∈b ，AC ⊥b ，BD ⊥b 且AB ＝2，CD ＝1，则直线a ，b 所成的角为( )A ．30°B ．60°C ．90°D ．45°【解析】 由于AB →＝AC →＋CD →＋DB →，则AB →·CD →＝(AC →＋CD →＋DB →)·CD→＝CD →2＝1. cos 〈AB →，CD →〉＝AB →·CD →|AB →|·|CD →|＝12，得〈AB→，CD →〉＝60°. 【答案】 B3．已知正三棱柱ABC -DEF 的侧棱长为2，底面边长为1，M 是BC 的中点，若直线CF 上有一点N ，使MN ⊥AE ，则CNCF ＝________. 【导学号：18490092】【解析】 设CN CF ＝m ，由于AE →＝AB →＋BE →，MN →＝12BC →＋mAD →，又AE→·MN →＝0， 得12×1×1×⎝ ⎛⎭⎪⎫－12＋4m ＝0，解得m ＝116. 【答案】 1164.如图3-1-28，平行六面体ABCD -A 1B 1C 1D 1中，AB ＝1，AD ＝2，AA 1＝3，∠BAD ＝90°，∠BAA 1＝∠DAA 1＝60°，求AC 1的长．图3-1-28【解】 ∵AC 1→＝AB →＋AD →＋AA 1→， ∴|AC 1→|＝（AB →＋AD →＋AA 1→）2＝ AB →2＋AD →2＋AA 1→2＋2（AB →·AD →＋AB →·AA 1→＋AD →·AA 1→）. ∵AB ＝1，AD ＝2，AA 1＝3，∠BAD ＝90°，∠BAA 1＝∠DAA 1＝60°，∴〈AB →，AD →〉＝90°，〈AB →，AA 1→〉＝〈AD →，AA 1→〉＝60°， ∴|AC 1→| ＝1＋4＋9＋2（1×3×cos 60°＋2×3×cos 60°） ＝23.。

1．已知),,2(),,1,1(t t t t t =--=，则||-的最小值为 （ ）A ．55 B ．555 C ．553 D ．511 2．已知A （1，1，1）、B （2，2，2）、C （3，2，4），则∆ABC 的面积为 （ ） A ．3 B ．32 C ．6 D ．263．空间四边形OABC 中，OB=OC ，∠AOB=∠AOC=600，则= （ ）A ．21 B ．22C ．-21D ．04．设A 、B 、C 、D 是空间不共面的四点，且满足000=∙=∙=∙AD AB ，AD AC ，AC AB ，则∆BCD 是 （ ）A ．钝角三角形B ．锐角三角形C ．直角三角形D ．不确定5．已知空间四边形ABCD 中，，，===，点M 在OA 上，且OM=2MA ，N 为BC 中点，则=（ ）A ．213221+- B ．212132++- C ．c b a 212121-+ D ．c b a 213232-+6．与向量(1,3,2)a =-平行的一个向量的坐标是（ ）A ．（31，1，1） B ．（－1，－3，2） C ．（－21，23，－1） D ．（2，－3，－22）7．已知平行六面体''''ABCD A B C D -中，AB=4，AD=3，'5AA =，090BAD ∠=，''060BAA DAA ∠=∠=，则'AC 等于（ ）A ．85BC ．D ．50 8．在下列条件中，使M 与A 、B 、C 一定共面的是 （ ）A ．OC OB OA OM --=2B ．OC OB OA OM 213151++=C ．=++D ．=+++ 9．正三棱柱111C B A ABC -的底面边长为3，侧棱3231=AA ，D 是CB 延长线上一点，且BC BD =，则二面角B AD B --1的大小 （ ）A ．3π B ．6π C ．65π D ．32π10．在直三棱柱111C B A ABC -中，底面是等腰直角三角形， 90=∠ACB ，侧棱21=AA ，D ，E 分别是1CC 与B A 1的中点，点E 在平面ABD 上的射影是ABD ∆的重心G ．则B A 1与平面ABD 所成角的余弦值（ ）A ．32B ．37C ．23 D ．73 11．在三棱锥P －ABC 中，AB ⊥BC ，AB ＝BC ＝21PA ，点O 、D 分别是AC 、PC 的中点，OP ⊥底面ABC ，则直线OD 与平面PBC 所成角的正弦值 （ ）A ．621 B ．338 C ．60210 D ．3021012．在棱长为1的正方体1111ABCD A B C D -中，则平面1AB C 与平面11A C D 间的距离 （ ）A ．63B ．33 C ．332 D ．23 13．已知111ABC A B C -是各条棱长均等于a 的正三棱柱，D 是侧棱1CC 的中点．点1C 到平面1AB D 的距离（ ） A ．a 42 B ．a 82 C ．a 423 D ．a 2214．正四棱锥S ABCD -的高2SO =，底边长AB BD 和SC 之间的距离（ ） A ．515 B ．55 C ．552 D ．10515．如图，A 1B 1C 1—ABC 是直三棱柱，∠BCA=90°，点D 1、F 1分别是A 1B 1、A 1C 1的中点，若BC=CA=CC 1，则BD 1与AF 1所成角的余弦值是（ ） A ．1030 B ．21 C ．1530 D ．101516．如图，ABCD —A 1B 1C 1D 1是正方体，B 1E 1＝D 1F 1＝411B A ，则BE 1与DF 1所成角的余弦值是（ ）A ．1715B ．21C ．178 D ．2317．在正三棱柱ABC —A 1B 1C 1中，若AB ＝2BB 1，则AB 1与C 1B 所成的角的大小为（ ） A ．60° B ．90° C ．105° D ．75° 18．（本小题12分）如图：四棱锥P —ABCD 中，底面ABCD是矩形，PA ⊥底面ABCD ，PA=AB=1，AD=3，点F 是PB 的中点，点E 在边BC 上移动. （1）证明：无论点E 在BC 边的何处，都有PE ⊥AF;（2）当BE 等于何值时，PA 与平面PDE 所成角的大小为45°. 19．（14分）如图所示，直三棱柱ABC —A 1B 1C 1中，CA=CB=1，∠BCA=90°，棱AA 1=2，M 、AA 1DCB B 1C 1 图N 分别是A 1B 1、A 1A 的中点. （1）求BN 的长；（2）求cos<11,CB BA >的值； （3）求证：A 1B ⊥C 1M.20．（12分）四棱锥P —ABCD 中，底面ABCD 是一个平行四边形，AB ={2，－1，－4}，AD ={4，2，0}，AP ={－1，2，－1}.（1）求证：PA ⊥底面ABCD ； （2）求四棱锥P —ABCD 的体积；（3）对于向量={x 1，y 1，z 1}，={x 2，y 2，z 2}，={x 3，y 3，z 3}，定义一种运算： （×）·=x 1y 2z 3+x 2y 3z 1+x 3y 1z 2－x 1y 3z 2－x 2y 1z 3－x 3y 2z 1，试计算（AB ×AD ）·AP 的绝对值的值；说明其与四棱锥P —ABCD 体积的关系，并由此猜想向量这一运算（AB ×AD ）·AP 的绝对值的几何意义.．21．（12分）若四面体对应棱的中点间的距离都相等，证明这个四面体的对棱两两垂直． 22．（12分）如图在空间直角坐标系中BC=2，原点O 是BC 的中点，点A 的坐标是（21,23，0），点D 在平面yOz 上，且∠BDC=90°，∠DCB=30°. （1）求向量OD 的坐标；（2）设向量AD 和BC 的夹角为θ，求cos θ的值23．（12分）如图，已知正方体''''ABCD A B C D -的棱长为a ，M 为'BD 的中点，点N 在'AC '上，且|'|3|'|A N NC =，试求MN 的长．24．如图，在四棱锥PABCD -中，平面PAD ⊥平面ABCD ，//AB DC ，PAD ∆是等边三角形，已知28,2BD AD AB DC ====（1）设M 是PC 上的一点，证明：平面PAD ⊥平面MBD ； （2）求二面角A PB D --的余弦值.25．如图所示，正方形D D AA11与矩形ABCD 所在平面互相垂直，22==AD AB ，点E 为AB 的中点.（1）求证：1BD ∥平面DE A 1； （2）求证：E D 1⊥D A 1；（3）在线段AB 上是否存在点M ，使二面角D MC D --1的大小为6π？若存在，求出AM 的长；若不存在，请说明理由.26．已知在四棱锥P ABCD -中，底面A B C D 是矩形，PA ⊥平面A B C D ，1PA AD ==，2AB =，,E F 分别是AB PD 、的中点.（1）求证：//AF 平面PEC ；（2）求二面角P EC D --的余弦值.27．已知直角梯形PBCD ，A 是PD 边上的中点（如图甲），=2D C π∠∠=，2BC CD ==，4PD =，将PAB ∆沿AB 折到SAB ∆的位置，使SB BC ⊥,点E 在SD 上，且13SE SD =（如图乙）（Ⅰ）求证：SA ⊥平面ABCD. （Ⅱ）求二面角E −AC −D 的余弦值28．如图，在四棱锥P ABCD -中，PD ⊥底面ABCD ，底面ABCD 为正方形，PD DC =，,E F 分别是,AB PB 的中点．(1)求证：EF CD ⊥；(2)在平面PAD 内求一点G ，使GF ⊥平面PCB ，并证明你的结论； (3)求DB 与平面DEF 所成角的正弦值．29．如图，正三棱柱111ABC A B C -中，点D 是BC 的中点.A EB PCDF（Ⅰ）求证: AD ⊥平面11BCC B ； （Ⅱ）求证: 1AC 平面1AB D .30．已知斜三棱柱111ABC A B C -的底面是直角三角形， 90ACB ∠=，侧棱与底面所成角为θ，点1B 在底面上的射影D 落在BC 上．（1）求证：AC ⊥平面11B B C C ；（2）若1cos 3θ=，且当13AC BC AA ===时，求二面角1C AB C --的大小． 31．如图,在长方体1111ABCD A B C D -,中,11,2AD AA AB ===,点E 在棱AB 上移动.（Ⅰ）证明:11D E A D ⊥;（Ⅱ）当E 为AB 的中点时,求点E 到面1ACD 的距离; （Ⅲ）AE 等于何值时,二面角1D EC D --的大小为4π. 32．在底面边长为2，高为1的正四棱柱1111ABCD A BC D -中，E 、F 分别为BC 、11C D 的中点．ABC DA 1B 1C 1（1）求异面直线1A E 、CF 所成的角； （2）求平面1A EF 与平面11ADD A 所成锐二面角的余弦值．33．如图，四棱锥P —ABCD 中，PAB ∆为边长为2的正三角形，底面ABCD 为菱形，且平面PAB ⊥平面ABCD ，AB PC ⊥，E 为PD 点上一点，满足ED PE 21=(1)证明：平面ACE ⊥平面ABCD ；(2)求直线PD 与平面ACE 所成角正弦值的大小．34．如图（1），等腰直角三角形ABC 的底边4AB =，点D 在线段AC 上，DE AB ⊥于E ，现将ADE ∆沿DE 折起到PDE ∆的位置（如图（2））．（Ⅰ）求证：PB DE ⊥；（Ⅱ）若PE BE ⊥，直线PD 与平面PBC 所成的角为030，求PE 长．35．如图，已知长方形ABCD 中，1,2==AD AB ,M 为DC 的中点. 将ADM ∆沿AM 折起，使得平面⊥ADM 平面ABCM .（I ）求证：BM AD ⊥ ；（II ）若点E 是线段DB 的中点，求二面角D AM E --的余弦值.图 (1)图 (2)ABE C DPE BC D36．（14分）如图：正方体ABCD-A 1B 1C 1D 1，过线段BD 1上一点P （P ∉平面ACB 1）作垂直于D 1B 的平面分别交过D 1的三条棱于E 、F 、G ．(1)求证：平面EFG ∥平面A CB 1，并判断三角形类型；(2)若正方体棱长为a ，求△EFG 的最大面积，并求此时EF 与B 1C 的距离． 37．（14分）已知正方体ABCD －A 1B 1C 1D 1的棱长为2，点E 为棱AB 的中点，求： （Ⅰ）D 1E 与平面BC 1D 所成角的大小； （Ⅱ）二面角D －BC 1－C 的大小；（Ⅲ）异面直线B 1D 1与BC 1之间的距离． 38．（12分）已知棱长为1的正方体AC 1，E 、F 分别是B 1C 1、C 1D 的中点． （1）求证：E 、F 、D 、B 共面；（2）求点A 1到平面的BDEF 的距离； （3）求直线A 1D 与平面BDEF 所成的角．39．（12分）在四棱锥P —ABCD 中，底面ABCD 是一直角梯形，∠BAD=90°，AD ∥BC ，AB=BC=a ，AD=2a ，且PA ⊥底面ABCD ，PD 与底面成30°角． （1）若AE ⊥PD ，E 为垂足，求证：BE ⊥PD ； （2）求异面直线AE 与CD 所成角的余弦值． 40．（12分）已知棱长为1的正方体ABCD －A 1B 1C 1D 1中，E 、F 、M 分别是A 1C 1、A 1D 和B 1A 上任一点，求证：平面A 1EF ∥平面B 1MC ． 41．（12分）已知棱长为1的正方体ABCD －A 1B 1C 1D 1，求平面A 1BC 1与平面ABCD 所成的二面角的大小42．已知O 是△ABC 的外心，AB = 6，AC = 10，若AC y AB x AO +=，且5102=+y x ，则=∠BAC cos ．43．在平面四边形ABCD 中，点,E F 分别是边,AD BC 的中点，且AB =，1EF =，CD =．若15AD BC ⋅=，则AC BD ⋅的值为____ ．44．已知向量)0,3,2(-=a ，)3,0,(k b =，若b a ,成1200的角，则k= ．45．已知点A(1，-2，11)、B(4，2，3)，C(6，-1，4)，则∆ABC 的形状是 ． 46．已知空间四边形OABC ，其对角线为OB 、AC ，M 、N 分别是对边OA 、BC 的中点，点G在线段MN 上，且GN MG 2=，现用基组{},,表示向量OG ，有=x z y ++，则x 、y 、z 的值分别为 ．47．若)1,3,2(-=，)3,1,2(-=，则,为邻边的平行四边形的面积为 ．48．已知棱长为1的正方体ABCD －A 1B 1C 1D 1中，E 、F 分别是B 1C 1和C 1D 1的中点，点A 1到平面DBEF 的距离 ．49． 在棱长为1的正方体1111ABCD A B C D -中，E 、F 分别是11A B 、CD 的中点，求点B 到截面1AEC F 的距离 ．50．在正方体1111ABCD A B C D -中，E 为11A B 的中点，则异面直线1D E 和1BC 间的距离 ．参考答案1．C 【解析】试题分析：由已知(1,21,0)b a t t -=+-，||(1b a t -=+=||-的最小值为553，故选C 。

学业分层测评(建议用时：45分钟)[学业达标]一、选择题1．若异面直线l 1的方向向量与l 2的方向向量的夹角为150°，则l 1与l 2所成的角为( )A ．30°B ．150°C ．30°或150°D ．以上均不对【解析】 l 1与l 2所成的角与其方向向量的夹角相等或互补，且异面直线所成角的范围为⎝⎛⎦⎥⎤0，π2.应选A.【答案】 A2．已知A (0，1，1)，B (2，－1，0)，C (3，5，7)，D (1，2，4)，则直线AB 与直线CD 所成角的余弦值为( )A.52266 B ．－52266 C.52222D ．－52222【解析】 AB→＝(2，－2，－1)，CD →＝(－2，－3，－3)， ∴cos 〈AB →，CD →〉＝AB →·CD →|AB →||CD →|＝53×22＝52266，∴直线AB ，CD 所成角的余弦值为52266. 【答案】 A3．正方形ABCD 所在平面外一点P ，P A ⊥平面ABCD ，若P A ＝AB ，则平面P AB 与平面PCD 的夹角为( )A ．30°B ．45°C ．60°D ．90°【解析】 如图所示，建立空间直角坐标系，设P A ＝AB ＝1.则A (0，0，0)，D (0，1，0)，P (0，0，1)．于是AD→＝(0，1，0)．取PD 中点为E ，则E ⎝ ⎛⎭⎪⎫0，12，12，∴AE →＝⎝ ⎛⎭⎪⎫0，12，12，易知AD →是平面P AB 的法向量，AE →是平面PCD 的法向量，∴cos AD→，AE →＝22，∴平面P AB 与平面PCD 的夹角为45°. 【答案】 B4．如图3-2-28，在空间直角坐标系Dxyz 中，四棱柱ABCD -A 1B 1C 1D 1为长方体，AA 1＝AB ＝2AD ，点E ，F 分别为C 1D 1，A 1B 的中点，则二面角B 1­A 1B ­E 的余弦值为( ) 【导学号：18490121】图3-2-28A ．－33 B ．－32 C. 33D. 32【解析】 设AD ＝1，则A 1(1，0，2)，B (1，2，0)，因为E ，F 分别为C 1D 1，A 1B 的中点，所以E (0，1，2)，F (1，1，1)，所以A 1E →＝(－1，1，0)，A 1B →＝(0，2，－2)，设m ＝(x ，y ，z )是平面A 1BE 的法向量，则⎩⎨⎧A 1E →·m ＝0，A 1B →·m ＝0，所以⎩⎪⎨⎪⎧－x ＋y ＝0，2y －2z ＝0，所以⎩⎪⎨⎪⎧y ＝x ，y ＝z ，取x ＝1，则y ＝z＝1，所以平面A 1BE 的一个法向量为m ＝(1，1，1)，又DA ⊥平面A 1B 1B ，所以DA →＝(1，0，0)是平面A 1B 1B 的一个法向量，所以cos 〈m ，DA →〉＝m ·DA →|m ||DA →|＝13＝33，又二面角B 1­A 1B ­E 为锐二面角，所以二面角B 1­A 1B ­E 的余弦值为33，故选C.【答案】 C5.如图3-2-29，空间正方体ABCD -A 1B 1C 1D 1中，M ，N 分别是CD ，CC 1的中点，则异面直线A 1M 与DN 所成角的大小是( )图3-2-29A.π6B.π4C.π3D.π2【解析】 以D 为原点，DA ，DC ，DD 1所在直线为坐标轴建系，则A 1M →＝⎝⎛⎭⎪⎫－1，12，－1，DN →＝⎝⎛⎭⎪⎫0，1，12，cos 〈A 1M →，DN →〉＝A 1M →·DN →|A 1M →||DN →|＝0.∴〈A 1M →，DN →〉＝π2. 【答案】 D 二、填空题6．在棱长为1的正方体ABCD -A 1B 1C 1D 1中，M ，N 分别为A 1B 1，BB 1的中点，则异面直线AM 与CN 所成角的余弦值是________．【解析】 依题意，建立如图所示的坐标系，则A (1，0，0)，M ⎝ ⎛⎭⎪⎫1，12，1，C (0，1，0)，N ⎝ ⎛⎭⎪⎫1，1，12，∴AM →＝⎝⎛⎭⎪⎫0，12，1，CN →＝⎝⎛⎭⎪⎫1，0，12，∴cos 〈AM→，CN →〉＝1252·52＝25， 故异面直线AM 与CN 所成角的余弦值为25. 【答案】 257．在空间直角坐标系Oxyz 中，已知A (1，－2，0)，B (2，1，6)，则向量AB→与平面xOz 的法向量的夹角的正弦值为________． 【解析】 设平面xOz 的法向量为n ＝(0，t ，0)(t ≠0)，AB →＝(1，3, 6)，所以cos 〈n ，AB →〉＝n ·AB →|n |·|AB →|＝3t 4|t |，因为〈n ，AB→〉∈[0，π]，所以sin 〈n ，AB→〉＝1－⎝ ⎛⎭⎪⎫3t 4|t |2＝74. 【答案】 748．已知点E ，F 分别在正方体ABCD -A 1B 1C 1D 1的棱BB 1，CC 1上，且B 1E ＝2EB ，CF ＝2FC 1，则平面AEF 与平面ABC 所成的二面角的正切值等于________．【解析】 如图，建立空间直角坐标系．设正方体的棱长为1，平面ABC 的法向量为n 1＝(0，0，1)，平面AEF 的法向量为n 2＝(x ，y ，z )．所以A (1，0，0)，E ⎝ ⎛⎭⎪⎫1，1，13，F ⎝ ⎛⎭⎪⎫0，1，23，所以AE →＝⎝⎛⎭⎪⎫0，1，13，EF →＝⎝⎛⎭⎪⎫－1，0，13，则⎩⎨⎧n 2·AE→＝0，n 2·EF →＝0，即⎩⎪⎨⎪⎧y ＋13z ＝0，－x ＋13z ＝0.取x ＝1，则y ＝－1，z ＝3.故n 2＝(1，－1，3)． 所以cos 〈n 1，n 2〉＝n 1·n 2|n 1||n 2|＝31111.所以平面AEF 与平面ABC 所成的二面角的平面角α满足cos α＝31111，sin α＝2211，所以tan α＝23.【答案】 23 三、解答题9.如图3-2-30所示，在四面体ABCD 中，O ，E 分别是BD ，BC 的中点，CA ＝CB ＝CD ＝BD ＝2，AB ＝AD ＝ 2. 【导学号：18490119】图3-2-30(1)求证：AO ⊥平面BCD ；(2)求异面直线AB 与CD 所成角的余弦值． 【解】 (1)证明：连接OC ，由题意知BO ＝DO ，AB ＝AD ， ∴AO ⊥BD .又BO ＝DO ，BC ＝CD ，∴CO ⊥BD .在△AOC 中，由已知可得AO ＝1，CO ＝3， 又AC ＝2，∴AO 2＋CO 2＝AC 2， ∴∠AOC ＝90°，即AO ⊥OC . ∵BD ∩OC ＝O ，∴AO ⊥平面BCD . (2)以O 为坐标原点建立空间直角坐标系，则B (1，0，0)，D (－1，0，0)，C (0, 3，0)，A (0，0，1)，E ⎝ ⎛⎭⎪⎫12，32，0，∴BA→＝(－1，0，1)，CD →＝(－1，－3，0)， ∴cos 〈BA →，CD →〉＝BA →·CD →|BA →|·|CD →|＝24.∴异面直线AB 与CD 所成角的余弦值为24.10．四棱锥P -ABCD 的底面是正方形，PD ⊥底面ABCD ，点E 在棱PB 上．(1)求证：平面AEC ⊥平面PDB ；(2)当PD ＝2AB 且E 为PB 的中点时，求AE 与平面PDB 所成的角的大小．【解】 如图，以D 为原点建立空间直角坐标系Dxyz ，设AB ＝a ，PD ＝h ，则A (a ，0，0)，B (a ，a ，0)，C (0，a ，0)，D (0，0，0)，P (0，0，h )， (1)∵AC→＝(－a ，a ，0)，DP →＝(0，0，h )，DB →＝(a ，a ，0)， ∴AC→·DP →＝0，AC →·DB →＝0， ∴AC ⊥DP ，AC ⊥DB ，又DP ∩DB ＝D ， ∴AC ⊥平面PDB ，又AC ⊂平面AEC ，∴平面AEC ⊥平面PDB .(2)当PD ＝2AB 且E 为PB 的中点时，P (0，0，2a )，E ⎝ ⎛⎭⎪⎫12a ，12a ，22a ，设AC ∩BD ＝O ，O ⎝ ⎛⎭⎪⎫a 2，a 2，0，连接OE ，由(1)知AC ⊥平面PDB于O ，∴∠AEO 为AE 与平面PDB 所成的角，∵EA →＝⎝ ⎛⎭⎪⎫12a ，－12a ，－22a ，EO →＝⎝⎛⎭⎪⎫0，0，－22a ，∴cos ∠AEO ＝EA →·EO →|EA →|·|EO →|＝22，∴∠AEO ＝45°，即AE 与平面PDB 所成的角的大小为45°.[能力提升]1．已知在长方体ABCD -A 1B 1C 1D 1中，AB ＝BC ＝1，AA 1＝2，E 是侧棱BB 1的中点，则直线AE 与平面A 1ED 1所成角的大小为( )A ．60°B ．90°C ．45°D ．以上都不对【解析】 以点D 为原点，分别以DA ，DC ，DD 1所在直线为x 轴、y 轴、z 轴，建立空间直角坐标系，如图．由题意知，A 1(1，0，2)，E (1，1，1)，D 1(0，0，2)，A (1，0，0)，所以A 1E →＝(0，1，－1)，D 1E →＝(1，1，－1)，EA →＝(0，－1，－1)．设平面A 1ED 1的一个法向量为n ＝(x ，y ，z )， 则⎩⎨⎧n ·A 1E →＝0，n ·D 1E →＝0，得⎩⎪⎨⎪⎧y －z ＝0，x ＋y －z ＝0. 令z ＝1，得y ＝1，x ＝0，所以n ＝(0，1，1)，cos 〈n ，EA →〉＝n ·EA →|n ||EA →|＝－22·2＝－1. 所以〈n ，EA→〉＝180°. 所以直线AE 与平面A 1ED 1所成的角为90°. 【答案】 B2.在三棱柱ABC -A 1B 1C 1中，CA ＝CC 1＝2CB ，则直线BC 1与直线AB 1夹角的余弦值为( )图3-2-31A.55 B.53 C.255D.35【解析】 不妨设CA ＝CC 1＝2CB ＝2， 则AB 1→＝(－2，2，1)，C 1B →＝(0，－2，1)， 所以cos 〈AB 1→，C 1B →〉＝AB 1→·C 1B →|AB 1→||C 1B →|＝（－2）×0＋2×（－2）＋1×19×5＝－55.因为直线BC 1与直线AB 1的夹角为锐角，所以所求角的余弦值为55.【答案】 A3．在空间中，已知平面α过(3，0，0)和(0，4，0)及z 轴上一点(0，0，a )(a ＞0)，如果平面α与平面xOy 的夹角为45°，则a ＝________．【解析】 平面xOy 的法向量为n ＝(0，0，1)，设平面α的法向量为u ＝(x ，y ，z )，则⎩⎪⎨⎪⎧－3x ＋4y ＝0，－3x ＋az ＝0，即3x ＝4y ＝az ，取z ＝1，则u ＝⎝ ⎛⎭⎪⎫a 3，a 4，1. 而cos 〈n ，u 〉＝1a 29＋a216＋1＝22， 又∵a ＞0，∴a ＝125.【答案】 1254.如图3-2-32，在直三棱柱A 1B 1C 1­ABC 中，AB ⊥AC ，AB ＝AC ＝2，A 1A ＝4，点D 是BC 的中点．图3-2-32(1)求异面直线A 1B 与C 1D 所成角的余弦值；(2)求平面ADC 1与平面ABA 1所成二面角的正弦值.【导学号：18490120】【解】 (1)以A 为坐标原点，建立如图所示的空间直角坐标系Axyz ，则A (0，0，0)，B (2，0，0)，C (0，2，0)，D (1，1，0)，A 1(0，0，4) ，C 1(0，2，4)，所以A 1B →＝(2，0，－4)，C 1D →＝(1，－1，－4).因为cos 〈A 1B →，C 1D →〉＝A 1B →·C 1D →|A 1B →||C 1D →|＝1820×18＝31010， 所以异面直线A 1B 与C 1D 所成角的余弦值为31010.(2)设平面ADC 1的法向量为n 1＝(x ，y ，z )，因为AD→＝(1，1，0)，AC 1→＝(0，2，4)，所以n 1·AD →＝0，n 1·AC 1→＝0，即x ＋y ＝0且y ＋2z ＝0，取z ＝1，得x ＝2，y ＝－2，所以n 1＝(2，－2，1)是平面ADC 1的一个法向量．取平面AA 1B 的一个法向量为n 2＝(0，1，0)，设平面ADC 1与平面ABA 1所成二面角的大小为θ.由|cos θ|＝⎪⎪⎪⎪⎪⎪n 1·n 2|n 1|·|n 2|＝29×1＝23， 得sin θ＝53.因此，平面ADC 1与平面ABA 1所成二面角的正弦值为53.小课堂：如何培养中学生的自主学习能力？自主学习是与传统的接受学习相对应的一种现代化学习方式。

3.1.4空间向量的正交分解及其坐标表示课时过关·能力提升基础巩固1下列说法正确的是()A.任何三个不共线的向量可构成空间向量的一个基底B.空间的基底有且仅有一个C.两两垂直的三个非零向量可构成空间的一个基底D.基底{a,b,c}中基向量与基底{e,f,g}中基向量对应相等项中应是不共面的三个向量构成空间向量的基底;B项,空间基底有无数个;D项中因为基底不唯一,所以D错.故选C.2已知点A在基底{a,b,c}下的坐标为(8,6,4),其中a=i+j,b=j+k,c=k+i,则点A在基底{i,j,k}下的坐标是()A.(12,14,10)B.(10,12,14)C.(14,12,10)D.(4,3,2)=8a+6b+4c=8(i+j)+6(j+k)+4(k+i)=12i+14j+10k.3在空间直角坐标系Oxyz中,下列说法正确的是()⃗⃗⃗⃗⃗ 与点B的坐标相同A.向量AB⃗⃗⃗⃗⃗ 与点A的坐标相同B.向量ABC.向量AB⃗⃗⃗⃗⃗ 与向量OB ⃗⃗⃗⃗⃗ 的坐标相同 D.向量AB ⃗⃗⃗⃗⃗ 与向量OB ⃗⃗⃗⃗⃗ −OA ⃗⃗⃗⃗⃗ 的坐标相同4点A (-1,2,1)在x 轴上的投影点和在xOy 平面上的投影点的坐标分别为( ) A.(-1,0,1),(-1,2,0)B.(-1,0,0),(-1,2,0)C.(-1,0,0),(-1,0,0)D.(-1,2,0),(-1,2,0)A 在x 轴投影知y=0,z=0,由点A 在xOy 平面投影知z=0.故选B .5设{i ,j ,k }是空间的一个单位正交基底,a =2i -4j+5k ,b=i+2j-3k ,则向量a ,b 的坐标分别为 , .-4,5) (1,2,-3)6已知{a ,b ,c }是空间的一个基底,下列向量可以与p =2a -b ,q =a +b 构成空间的另一个基底的是 (填序号).①2a ②-b ③c ④a +c7如图,在边长为2的正方体ABCD-A 1B 1C 1D 1中,取点D 为原点建立空间直角坐标系,已知O ,M 分别是AC ,DD 1的中点,写出下列向量的坐标.AM ⃗⃗⃗⃗⃗⃗ = ,OB 1⃗⃗⃗⃗⃗⃗⃗⃗ = .-2,0,1) (1,1,2)8如图,在梯形ABCD 中,AB ∥CD ,AB=2CD ,点O 为空间任一点,设OA ⃗⃗⃗⃗⃗ =a ,OB ⃗⃗⃗⃗⃗ =b ,OC ⃗⃗⃗⃗⃗ =c ,则向量OD ⃗⃗⃗⃗⃗⃗ 用a ,b ,c 表示为 .-12b +c9如图所示,已知正方体ABCD-A 1B 1C 1D 1的棱长为1,建立适当的空间直角坐标系,求BD 1⃗⃗⃗⃗⃗⃗⃗⃗ 的坐标.1⃗⃗⃗⃗⃗⃗ =BD ⃗⃗⃗⃗⃗⃗ +DD 1⃗⃗⃗⃗⃗⃗⃗⃗ =BA ⃗⃗⃗⃗⃗ +BC ⃗⃗⃗⃗⃗ +DD 1⃗⃗⃗⃗⃗⃗⃗⃗ =-AB ⃗⃗⃗⃗⃗ +AD ⃗⃗⃗⃗⃗ +DD 1⃗⃗⃗⃗⃗⃗⃗⃗ .以AB ⃗⃗⃗⃗⃗ ,A D ⃗⃗⃗⃗⃗⃗ ,AA 1⃗⃗⃗⃗⃗⃗⃗ 为单位正交基底,建立空间直角坐标系,如图所示,则BD 1⃗⃗⃗⃗⃗⃗⃗⃗ =-AB ⃗⃗⃗⃗⃗ +AD ⃗⃗⃗⃗⃗ +DD 1⃗⃗⃗⃗⃗⃗⃗⃗ =-AB ⃗⃗⃗⃗⃗ +AD ⃗⃗⃗⃗⃗ +AA 1⃗⃗⃗⃗⃗⃗⃗ =(-1,1,1).10已知PA 垂直于正方形ABCD 所在的平面,M ,N 分别是AB ,PC 的中点,并且PA=AD=1,如图所示,设DA ⃗⃗⃗⃗⃗ =e 1,AB ⃗⃗⃗⃗⃗ =e 2,AP ⃗⃗⃗⃗⃗ =e 3,以{e 1,e 2,e 3}为单位正交基底建立空间直角坐标系Axyz ,求向量MN ⃗⃗⃗⃗⃗⃗⃗ ,DC ⃗⃗⃗⃗⃗ 的坐标.DC⃗⃗⃗⃗⃗ =AB ⃗⃗⃗⃗⃗ =e 2. ∵PC ⃗⃗⃗⃗⃗ =AC ⃗⃗⃗⃗⃗ −AP ⃗⃗⃗⃗⃗ =AB ⃗⃗⃗⃗⃗ +AD ⃗⃗⃗⃗⃗ −AP ⃗⃗⃗⃗⃗ =e 2-e 1-e 3, ∴MN ⃗⃗⃗⃗⃗⃗⃗ =MA ⃗⃗⃗⃗⃗⃗ +AP ⃗⃗⃗⃗⃗ +PN⃗⃗⃗⃗⃗⃗ =-12AB ⃗⃗⃗⃗⃗ +AP ⃗⃗⃗⃗⃗ +12PC ⃗⃗⃗⃗⃗=-12e 2+e 3+12(e 2-e 1-e 3)=-12e 1+12e 3.∴MN ⃗⃗⃗⃗⃗⃗⃗ =(-12,0,12),DC ⃗⃗⃗⃗⃗ =(0,1,0). 能力提升1有下列叙述:①在空间直角坐标系中,x 轴上的点的坐标一定是(0,b ,c );②在空间直角坐标系中,在yOz 平面上点的坐标一定可写成(0,b ,c ); ③在空间直角坐标系中,在z 轴上的点的坐标可记作(0,0,c ); ④在空间直角坐标系中,在xOz 平面上点的坐标是(a ,0,c ).其中正确的个数是( ) A.1B.2C.3D.4错,x 轴上的点的坐标应是(a ,0,0).②③④正确.2如图,在长方体ABCD-A 1B 1C 1D 1中,AC 与BD 的交点为M ,设A 1B 1⃗⃗⃗⃗⃗⃗⃗⃗⃗ =a ,A 1D 1⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗ =b ,A 1A ⃗⃗⃗⃗⃗⃗⃗ =c ,则下列向量中与B 1M ⃗⃗⃗⃗⃗⃗⃗⃗ 相等的向量是 ( )A.-12a +12b +cB.12a +12b +cC.12a -12b +cD.-12a -12b +c1M =B 1B ⃗⃗⃗⃗⃗⃗⃗ +BM ⃗⃗⃗⃗⃗⃗=A 1A ⃗⃗⃗⃗⃗⃗⃗ +12BD ⃗⃗⃗⃗⃗⃗ =A 1A ⃗⃗⃗⃗⃗⃗⃗ +12(BA ⃗⃗⃗⃗⃗ +BC ⃗⃗⃗⃗⃗ )=A 1A ⃗⃗⃗⃗⃗⃗⃗ +12(B 1A 1⃗⃗⃗⃗⃗⃗⃗⃗⃗ +A 1D 1⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗ )=c +12(-a +b )=-12a +12b +c .3设p :a ,b ,c 是三个非零向量;q :{a ,b ,c }为空间的一个基底,则p 是q 的( ) A.充分不必要条件 B.必要不充分条件 C.充要条件D.既不充分也不必要条件a ,b ,c 不共面时,{a ,b ,c }可以当基底,否则不能当基底.当{a ,b ,c }为基底时,一定有a ,b ,c 为非零向量.4如图,在空间四边形OABC 中,OA ⃗⃗⃗⃗⃗ =a ,OB ⃗⃗⃗⃗⃗ =b ,OC ⃗⃗⃗⃗⃗ =c ,点M 在OA 上,且OM ⃗⃗⃗⃗⃗⃗ =2MA ⃗⃗⃗⃗⃗⃗ ,N 是BC 的中点,MN ⃗⃗⃗⃗⃗⃗⃗ =x a +y b +z c ,则x ,y ,z 的值为( ) A.12,-23,12B.-23,12,12C.12,12,-23 D.23,23,-125已知向量AB ⃗⃗⃗⃗⃗ =(-4,-3,-1),把AB ⃗⃗⃗⃗⃗ 按向量(2,1,1)平移后所得向量的坐标是 .-4,-3,-1)6设{i ,j ,k }是空间向量的单位正交基底,a =3i+2j-k ,b=-2i+4j+2k ,则向量a ,b 的关系是 .a ·b =-6i 2+8j 2-2k 2=-6+8-2=0,∴a ⊥b .⊥b7已知在空间四边形ABCD 中,AB ⃗⃗⃗⃗⃗ =a-2c ,CD ⃗⃗⃗⃗⃗ =5a+6b-8c ,对角线AC ,BD 的中点分别为E ,F ,则EF⃗⃗⃗⃗⃗ = .EF ⃗⃗⃗⃗⃗ =EA ⃗⃗⃗⃗⃗ +AB ⃗⃗⃗⃗⃗ +BF ⃗⃗⃗⃗⃗ ,且EF ⃗⃗⃗⃗⃗ =EC ⃗⃗⃗⃗⃗ +CD ⃗⃗⃗⃗⃗ +DF ⃗⃗⃗⃗⃗ ,∴两式相加,得2EF ⃗⃗⃗⃗⃗ =(EA ⃗⃗⃗⃗⃗ +EC ⃗⃗⃗⃗⃗ )+AB ⃗⃗⃗⃗⃗ +CD ⃗⃗⃗⃗⃗ +(BF ⃗⃗⃗⃗⃗ +DF ⃗⃗⃗⃗⃗ ).∵E 为AC 的中点,F 为BD 的中点,∴EA ⃗⃗⃗⃗⃗ +EC ⃗⃗⃗⃗⃗ =0,BF ⃗⃗⃗⃗⃗ +DF ⃗⃗⃗⃗⃗ =0.∴2EF ⃗⃗⃗⃗⃗ =AB ⃗⃗⃗⃗⃗ +CD ⃗⃗⃗⃗⃗ =(a-2c )+(5a+6b-8c )=6a+6b-10c .∴EF ⃗⃗⃗⃗⃗ =3a+3b-5c .a+3b-5c8已知向量p 在基底{a ,b ,c }下的坐标是(2,3,-1),求p 在基底{a ,a +b ,a +b +c }下的坐标.p =2a +3b -c .设p =x a +y (a +b )+z (a +b +c )=(x+y+z )a +(y+z )b +z c ,则有{x +y +z =2,y +z =3,z =-1,解得{x =-1,y =4,z =-1,故p 在基底{a ,a +b ,a +b +c }下的坐标为(-1,4,-1).9已知正方体ABCD-A'B'C'D',点E 是上底面A'B'C'D'的中心,求AE ⃗⃗⃗⃗⃗ =x AD ⃗⃗⃗⃗⃗ +y AB ⃗⃗⃗⃗⃗ +z AA '⃗⃗⃗⃗⃗⃗ 中x ,y ,z 的值.⃗⃗⃗ =AA '⃗⃗⃗⃗⃗⃗ +A'E ⃗⃗⃗⃗⃗⃗ =AA '⃗⃗⃗⃗⃗⃗ +12A 'C '⃗⃗⃗⃗⃗⃗⃗ =AA '⃗⃗⃗⃗⃗⃗ +12(A 'B '⃗⃗⃗⃗⃗⃗⃗ +A 'D '⃗⃗⃗⃗⃗⃗⃗ ) =AA '⃗⃗⃗⃗⃗⃗ +12A 'B '⃗⃗⃗⃗⃗⃗⃗ +12A 'D '⃗⃗⃗⃗⃗⃗⃗ =12AD ⃗⃗⃗⃗⃗ +12AB ⃗⃗⃗⃗⃗ +AA '⃗⃗⃗⃗⃗⃗.∵AE ⃗⃗⃗⃗⃗ =x AD ⃗⃗⃗⃗⃗ +y AB ⃗⃗⃗⃗⃗ +z AA'⃗⃗⃗⃗⃗⃗ ,∴x=12,y=12,z=1.★10如图,在正方体ABCD-A 1B 1C 1D 1中,E ,F 分别是BB 1,D 1B 1的中点,求证:EF ⊥平面B 1AC.AB ⃗⃗⃗⃗⃗ =a ,AD ⃗⃗⃗⃗⃗ =c ,AA 1⃗⃗⃗⃗⃗⃗⃗ =b ,把向量EF ⃗⃗⃗⃗⃗ ,AB ⃗⃗⃗⃗⃗ 1和B 1C ⃗⃗⃗⃗⃗⃗⃗ 分别用a ,b ,c 表示出来,证明A F ⃗⃗⃗⃗⃗⃗ ·AB 1⃗⃗⃗⃗⃗⃗⃗ =0,EF ⃗⃗⃗⃗⃗ ·B 1C ⃗⃗⃗⃗⃗⃗⃗ =0即可.AB ⃗⃗⃗⃗⃗ =a ,AD ⃗⃗⃗⃗⃗ =c ,AA 1⃗⃗⃗⃗⃗⃗⃗ =b ,有a ·b =0,a ·c =0,b ·c =0. 则EF ⃗⃗⃗⃗⃗ =EB 1⃗⃗⃗⃗⃗⃗⃗ +B 1F ⃗⃗⃗⃗⃗⃗⃗ =12(BB 1⃗⃗⃗⃗⃗⃗⃗ +B 1D 1⃗⃗⃗⃗⃗⃗⃗⃗⃗ )=12(AA 1⃗⃗⃗⃗⃗⃗⃗ +BD ⃗⃗⃗⃗⃗⃗ )=12(AA 1⃗⃗⃗⃗⃗⃗⃗ +AD ⃗⃗⃗⃗⃗ −AB ⃗⃗⃗⃗⃗ ) =12(-a +b +c ),AB 1⃗⃗⃗⃗⃗⃗⃗ =AB ⃗⃗⃗⃗⃗ +BB 1⃗⃗⃗⃗⃗⃗⃗ =AB ⃗⃗⃗⃗⃗ +AA 1⃗⃗⃗⃗⃗⃗⃗ =a +b . ∴EF ⃗⃗⃗⃗⃗ ·AB 1⃗⃗⃗⃗⃗⃗⃗ =12(-a +b +c )·(a +b ) =12(|b |2-|a |2)=0.∴EF ⃗⃗⃗⃗⃗ ⊥AB 1⃗⃗⃗⃗⃗⃗⃗ ,即EF ⊥AB 1. 同理EF ⊥B 1C.∵AB 1∩B 1C=B 1,∴EF ⊥平面B 1AC.。

高二选修（2—1）第三章3.1空间向量及其运算测试题一、选择题1．已知向量a ＝(3，－2,1)，b =(－2,4,0)，则4a ＋2b 等于 （ ）A ．(16,0,4)B ．(8，－16,4)C ．(8,16,4)D ．(8,0,4)2．在三棱柱ABC -A 1B 1C 1中，若CA →＝a ，CB →＝b ，CC 1→＝c ，则A 1B →＝ （ ）A ．a ＋b －cB ．a －b ＋cC ．－a ＋b ＋cD ．－a ＋b －c3．在棱长都是1的三棱锥A -BCD 中，下列各数量积的值为12的是 （ ） A. ⋅ B. BD AB ⋅ C.DA AB ⋅ D.⋅ 4．在下列条件中，使M 与A 、B 、C 一定共面的是 （ ）A.OM →＝2OA →－OB →－OC →B.OM →＝15OA →＋13OB →＋12OC →C.MA →＋MB →＋MC →＝0D.OM →＋OA →＋OB →＋OC →＝05．若向量{,,}是空间的一个基底，向量-=+=,，那么可以与m 、n 构成空间另一个基底的向量是 ( )A ．aB ．bC ．cD ．2a6．在正方体ABCD -A 1B 1C 1D 1中，给出以下向量表达式：①(A 1D 1→－A 1A →)－AB →；②(BC →＋BB 1→)－D 1C 1→； ③(AD →－AB →)－2DD 1→；④(B 1D 1→＋A 1A →)＋DD 1→.其中能够化简为向量BD 1→的是 （ ）A ．①②B ．②③C ．③④D ．①④7．已知向量a ＝(1，－1,1)，b ＝(－1,2,1)，且k a －b 与a －3b 互相垂直，则k 的值是A ．1B ．15C ．35D ．－2098．若a ＝(2，－3,1)，b ＝(2,0,3)，c ＝(0,2,2)，a ·(b ＋c )的值为 （ ）A ．4B ．15C ．7D ．39．已知四边形ABCD 满足：AB →·BC →>0，BC →·CD →>0，CD →·DA →>0，DA →·AB →>0，则该四边形为 （ ）A ．平行四边形B ．梯形C ．长方形D ．空间四边形10．设OABC 是四面体，G 1是△ABC 的重心，G 是OG 1上一点，且OG ＝3GG 1，若OG →＝xOA →＋yOB →＋zOC →，则(x ，y ，z )为( )A.⎝⎛⎭⎫14，14，14B.⎝⎛⎭⎫34，34，34C.⎝⎛⎭⎫13，13，13D.⎝⎛⎭⎫23，23，23 11. 如图所示，在平行六面体ABCD -A 1B 1C 1D 1中，M 为A 1C 1与B 1D 1的交点．若AB →＝a ， AD →＝b ，AA 1→＝c ，则下列向量中与BM →相等的向量是( )A ．－12a ＋12b ＋cB ．12a ＋12b ＋cC ．－12a －12b ＋cD ．12a －12b ＋c 12.给出命题：①若a 与b 共线，则a 与b 所在的直线平行；②若a 与b 共线，则存在唯一的实数λ，使b ＝λa ；③若A ，B ，C 三点不共线，O 是平面ABC 外一点，OM →＝13OA → ＋13OB →＋13OC ，则点M 一定在平面ABC 上，且在△ABC 的内部．上述命题中的真命 题的个数为（ ）A ．0B ．1C ．2D ．3二、填空题13．A(1,0,1)，B(4,4,6)，C(2,2,3)，D(10,14,17)这四个点________(填“共面”或“不共面”)．14．已知向量a ＝(－1,2,3)，b ＝(1,1,1)，则向量a 在b 方向上的投影为________．15．已知G 是△ABC 的重心，O 是空间与G 不重合的任一点，若OA →＋OB →＋OC →＝λOG →，则λ＝________.16．如果三点A (1,5，－2)，B (2,4,1)，C (a,3，b ＋2)共线，那么a －b ＝________.三、解答题17. 如图所示，已知空间四边形ABCD 的每条边和对角线长都等于1，点E 、F 分别是AB 、AD 的中点，计算： (1)EF →·BA →； (2)EF →·BD →； (3)EF →·DC →.18．如图所示，在空间四边形OABC 中，OA ＝8，AB ＝6，AC ＝4，BC ＝5，∠OAC ＝ 45°，∠OAB ＝60°，求OA 与BC 夹角的余弦值．19．已知空间三点A (0,2,3)，B (－2,1,6)，C (1，－1,5)．(1)求以向量AB →，AC →为一组邻边的平行四边形的面积S ；(2)若向量a 分别与向量AB →，AC →垂直，且|a |＝3，求向量a 的坐标．21. 已知空间三点A (－2,0,2)，B (－1,1,2)，C (－3，0,4)，设a ＝AB →，b ＝AC →.(1)求a 与b 的夹角θ的余弦值；(2)若向量k a ＋b 与k a －2b 互相垂直，求k 的值．22.如图，已知正三棱柱ABC -A 1B 1C 1的底面边长为2，侧棱长为32，点E 在侧棱AA 1上，点F 在侧棱BB 1上，且AE ＝22，BF ＝ 2.(1)求证：CF ⊥C 1E ；(2)求二面角E -CF -C 1的大小．解析：建立如图所示的空间直角坐标系，则由已知可得A (0,0,0)，B (3，1,0)，C (0,2,0)，C 1(0,2，32)，E (0，0，22)，F (3，1，2)．(1) C 1E →＝(0，－2，－2)，CF →＝(3，－1，2)，C 1E →·CF →＝0＋2－2＝0， 所以CF ⊥C 1E .(2)CE →＝(0，－2,22)，设平面CEF 的一个法向量为m ＝(x ，y ，z )，由m ⊥CE →，m ⊥CF →，得⎩⎪⎨⎪⎧ m ·CE →＝0，m ·CF →＝0，即⎩⎨⎧－2y ＋22z ＝0，3x －y ＋2z ＝0.可取m ＝(0，2，1)． 设侧面BC 1的一个法向量为n ，由n ⊥CB →，n ⊥CC 1→，及CB →＝(3，－1,0)，CC 1→＝(0,0,32)， 可取n ＝(1，3，0)．设二面角E -CF -C 1的大小为θ，于是由θ为锐角可得cos θ＝|m·n ||m|·|n |＝63×2＝22，所以θ＝45°， 即所求二面角E -CF -C 1的大小为45°.1.D 提示：4a ＋2b ＝4(3，－2,1)＋2(－2,4,0)＝(12，－8，4)＋(－4,8,0)＝(8,0,4)．2. D 提示： A 1B →＝A 1A →＋AB →＝－c ＋(b －a )＝－a ＋b －c .3\ D 提示：向量的夹角是两个向量始点放在一起时所成的角，经检验只有⋅＝12. 4. C 提示：MA →＋MB →＋MC →＝0，即MA →＝－(MB →＋MC →)，所以M 与A 、B 、C 共面．5\ 解析 C ∵a ＋b ，a －b 分别与a 、b 、2a 共面，∴它们分别与a ＋b ，a －b 均不 能构成一组基底．6. A 提示：①(A 1D 1→－A 1A →)－AB →＝AD 1→－AB →＝BD →1；②(BC →＋BB 1→)－D 1C 1→＝BC 1→－D 1C 1→＝ BD 1→；③(AD →－AB →)－2DD 1→＝BD →－2DD 1→≠BD 1→；④(B 1D 1→＋A 1A →)＋DD 1→＝B 1D →＋DD 1→＝B 1D 1→≠BD 1→，故选A.7. D 提示：∵k a －b ＝(k ＋1，－k －2，k －1)，a －3b ＝(4，－7，－2)，(k a －b )⊥(a －3b )，∴4(k ＋1)－7(－k －2)－2(k －1)＝0，∴k ＝－209. 8\解析 D ∵b ＋c ＝(2,2,5)，∴a ·(b ＋c )＝(2，－3,1)·(2,2,5)＝3.9解析 D 由已知条件得四边形的四个外角均为锐角，但在平面四边形中任一四边 形的外角和是360°，这与已知条件矛盾，所以该四边形是一个空间四边形．10.解析 A OG 1→＝OA →＋AG 1→＝OA →＋23×12(AB →＋AC →)＝OA →＋13[(OB →－OA →)＋(OC →－OA →)] ＝13(OA →＋OB →＋OC →)，由OG ＝3GG 1知，OG →＝34OG 1→＝14(OA →＋OB →＋OC →)， ∴(x ，y ，z )＝⎝⎛⎭⎫14，14，14.11 A 解析 由图形知：BM →＝BB 1→＋B 1M →＝AA 1→＋12(AD →－AB →)＝－12a ＋12b ＋c . 12. B 解析 ①中a 与b 所在的直线也有可能重合，故①是假命题；②中当a ＝0，b ≠0 时，找不到实数λ，使b ＝λa ，故②是假命题；可以证明③中A ，B ，C ，M 四点共面，因为13OA →＋13OB →＋13OC →＝OM →，等式两边同时加上MO →，则13(MO →＋OA →)＋13(MO →＋ OB →)＋13(MO →＋OC →)＝0，即MA →＋MB →＋MC →＝0，MA →＝－MB →－MC →，则MA →与MB →，MC → 共面，又M 是三个有向线段的公共点，故A ，B ，C ，M 四点共面，所以M 是△ABC 的重心，所以点M 在平面ABC 上，且在△ABC 的内部，故③是真命题．13. 解析 AB →＝(3,4,5)，AC →＝(1,2,2)，AD →＝(9,14,16)，设AD →＝xAB →＋yAC →.即(9,14,16)＝(3x ＋y,4x ＋2y,5x ＋2y )，∴⎩⎪⎨⎪⎧x ＝2，y ＝3，从而A 、B 、C 、D 四点共面． 14. 433 解析 向量a 在b 方向上的投影为：|a |·cos a ，b ＝14×－1＋2＋314×3＝433. 15. 3 解析 因为OA →＋AG →＝OG →，OB →＋BG →＝OG →，OC →＋CG →＝OG →，且AG →＋BG →＋CG →＝0，所以OA →＋OB →＋OC →＝3OG →.16. 1 解析:AB →＝(1，－1,3)，BC →＝(a －2，－1，b ＋1)，若使A 、B 、C 三点共线，须满 足BC →＝λAB →，即(a －2，－1，b ＋1)＝λ(1，－1,3)，所以⎩⎪⎨⎪⎧a －2＝λ，－1＝－λ，b ＋1＝3λ，解得a ＝3，b ＝2，所以a －b ＝1.17. 解析 (1)EF →·BA →＝12BD →·BA → ＝12|BD →||BA →|cos 〈BD →，BA →〉＝12cos 60°＝14.(2)EF →·BD →＝12BD →·BD →＝12cos 0°＝12. (3)EF →·DC →＝12BD →·DC →＝12|BD →||DC →|cos 〈BD →，DC →〉＝12cos 120°＝－14. 18. 解析 ∵BC →＝AC →－AB →，∴OA →·BC →＝OA →·AC →－OA →·AB →＝|OA →|·|AC →|·cos 〈OA →，AC →〉－|OA →|·|AB →|·cos 〈OA →，AB →〉＝8×4×cos 135°－8×6×cos 120°＝24－16 2.∴cos 〈OA →，BC →〉＝OA →·BC →|OA →|·|BC →|＝24－1628×5＝3－225. ∴OA 与BC 夹角的余弦值为3－225. 19.解析 (1)∵AB →＝(－2，－1,3)，AC →＝(1，－3,2)，∴cos ∠BAC ＝AB →·AC →|AB →||AC →|＝714×14＝12， ∴∠BAC ＝60°∴S ＝|AB →||AC →|sin 60°＝7 3.(2)设a ＝(x ，y ，z )，则a ⊥AB →⇒－2x －y ＋3z ＝0，a ⊥AC →⇒x －3y ＋2z ＝0，|a |＝3⇒x 2＋y 2＋z 2＝3，解得x ＝y ＝z ＝1或x ＝y ＝z ＝－1，∴a ＝(1,1,1)或a ＝(－1，－1，－1)．21.解析∵A (－2,0,2)，B (－1,1,2)，C (－3,0,4)，a ＝AB →，b ＝AC →，∴a ＝(1,1,0)，b ＝(－1,0,2)．(1) cos θ＝a·b |a||b|＝－1＋0＋02×5＝－1010， ∴a 与b 的夹角θ的余弦值为－1010. (2) ∵k a ＋b ＝k (1,1,0)＋(－1,0,2)＝(k －1，k,2)，k a －2b ＝(k ＋2，k ，－4)，且(k a ＋b )⊥(k a －2b )，∴(k －1，k,2)·(k ＋2，k ，－4)＝(k －1)(k ＋2)＋k 2－8＝2k 2＋k －10＝0，则k ＝－52或k ＝2.。

3.1.3 空间向量的数量积运算一、选择题1．已知向量a 、b 是平面α的两个不相等的非零向量，非零向量c 是直线l 的一个方向向量，则c·a ＝0且c·b ＝0是l ⊥α的( )A ．充分不必要条件B ．必要不充分条件C. 充要条件 D ．既不充分也不必要条件2．已知a ，b 均为单位向量，它们的夹角为60°，那么|a ＋3b |( ) A.7 B.10 C.13 D ．43．已知正方体ABCD －A ′B ′C ′D ′的棱长为 a ，设AB →＝a ，AD →＝b ，AA ′→＝c ，则〈A ′B →，B ′D ′→〉＝( )A ．30°B ．60°C ．90°D ．120°4．已知P A ⊥平面ABC ，垂足为A ，∠ABC ＝120°，P A ＝AB ＝BC ＝6，则PC 等于( )A ．62B ．6C ．12D ．1445．已知a 、b 、c 是两两垂直的单位向量，则|a －2b ＋3c |＝( )A ．14 B.14 C ．4 D ．26．已知|a |＝2，|b |＝3，〈a ，b 〉＝60°，则|2a －3b |等于( )A ．97B ．97C ．61D ．617．空间四边形OABC 中，OB ＝OC ，∠AOB ＝∠AOC ＝π3，则cos 〈OA →，BC →〉等于( ) A ．12 B ．22 C ．－12 D ．08．设A 、B 、C 、D 是空间不共面的四点，且满足AB →·AC →＝0，AC →·AD →＝0，AB →·AD →＝0，则△BCD 是( )A ．钝角三角形B ．锐角三角形C ．直角三角形D ．不确定二、填空题9．已知|a |＝22，|b |＝22，a ·b ＝－2，则〈a ，b 〉＝________.10．已知正方体ABCD －A ′B ′C ′D ′的棱长为1，设AB →＝a ，AD →＝b ，AA ′→＝c ，则(1)AC ′→·DB ′→＝________；〈AC ′→，DB ′→〉＝________；(2)BD ′→·AD →＝________.11．已知正方体ABCD －A 1B 1C 1D 1的棱长为a ，则A 1B →·B 1C →＝________.12．已知在空间四边形OABC 中，OA ⊥BC ，OB ⊥AC ，则AB →·OC →＝________.三、解答题13．已知a ＋3b 与7a －5b 垂直，且a －4b 与7a －2b 垂直，求〈a ，b 〉．14．对于任意空间四边形，试证明它的一组对边中点的连线段与另一组对边可平行于同一平面．15．如图所示，在正方体ABCD －A 1B 1C 1D 1中，求异面直线A 1B 与AC 1所成的角．参考答案一、选择题1．[答案] B[解析] 当a 与b 不共线．．．时，由c ·a ＝0，c ·b ＝0，可推出l ⊥α；当a 与b 为共线向量时，由c·a ＝0，c·b ＝0，不能够推出l ⊥α；l ⊥α一定有c ·a ＝0且c ·b ＝0，故选B. ２．[答案] C[解析] |a ＋3b |2＝(a ＋3b )2＝a 2＋6a·b ＋9b 2＝|a |2＋6|a ||b |cos<a ，b >＋9|b |2，∵|a |＝|b |＝1，〈a ，b 〉＝60°， ∴|a ＋3b |2＝13，∴|a ＋3b |＝13.３．[答案] D[解析] B ′D ′→＝BD →，∵△A ′BD 为正三角形，∴〈A ′B →，BD →〉＝120°.４．[答案] C[解析] ∵PC →＝P A →＋AB →＋BC →，∴PC →2＝P A →2＋AB →2＋BC →2＋2AB →·BC →＝36＋36＋36＋2×36cos60°＝144. ∴|PC →|＝12.５．[答案] B[解析] |a －2b ＋3c |2＝|a |2＋4|b |2＋9|c |2－4a ·b ＋6a ·c －12b ·c ＝14，∴选B. ６．[答案] C[解析] |2a －3b |2＝4a 2＋9b 2－12a·b ＝4×4＋9×9－12×|a ||b |cos60°＝97－12×2×3×12＝61.７．[答案] D[解析] cos 〈OA →，BC →〉＝OA →·BC →|OA →||BC →|＝OA →·(OC →－OB →)|OA →||BC →|＝OA →·OC →－OA →·OB →|OA →||BC →|＝|OA →||OC →|cos ∠AOC －|OA →||OB →|cos ∠AOB |OA →||BC →|. 因为|OB →|＝|OC →|，∠AOC ＝∠AOB ＝π3， 所以cos 〈OA →，BC →〉＝0.８．[答案] B[解析] BD →＝AD →－AB →，BC →＝AC →－AB →，BD →·BC →＝(AD →－AB →)·(AC →－AB →)＝AD →·AC →－AD →·AB →－AB →·AC →＋|AB →|2＝|AB →|2>0，∴cos ∠CBD ＝cos 〈BC →，BD →〉＝BC →·BD →|BC →|·|BD →|>0， ∴∠CBD 为锐角，同理，∠BCD 与∠BDC 均为锐角，∴△BCD 为锐角三角形．二、填空题９．[答案] 3π4[解析] cos 〈a ，b 〉＝a ·b |a |·|b |＝－22， ∴〈a ，b 〉＝3π4. 10．[答案] (1)1，arccos 13(2)1 [解析] (1)AC ′→·DB ′→＝(a ＋b ＋c )·(a －b ＋c )＝a 2＋c 2＋2a ·c －b 2＝1，|AC ′→|2＝(a ＋b ＋c )2＝a 2＋b 2＋c 2＋2a ·b ＋2a ·c ＋2b ·c ＝3，∴|AC ′→|＝3，|DB ′→|2＝(a －b ＋c )2＝a 2＋b 2＋c 2－2a ·b ＋2a ·c －2b ·c ＝3，∴|DB ′→|＝3，∴cos 〈AC ′→，DB ′→〉＝AC ′→·DB ′→|AC ′→|·|DB ′→|＝13， ∴〈AC ′→，DB ′→〉＝arccos 13. (2)BD ′→·AD →＝(b ＋c －a )·b ＝|b |2＋b ·c －b ·a ＝1.11．[答案] a 2[解析] A 1B →·B 1C →＝A 1B →·A 1D →＝|A 1B →|·|A 1D →|·cos 〈A 1B →，A 1D →〉 ＝2a ×2a ×cos60°＝a 2.12．[答案] 0[解析] AB →·OC →＝(OB →－OA →)·(OA →＋AC →)＝OB →·OA →＋OB →·AC →－|OA →|2－OA →·AC →＝OB →·OA →－|OA →|2－OA →·AC →＝OA →·AB →－OA →·AC →＝OA →·CB →＝0.三、解答题13．[解析] (a ＋3b )·(7a －5b )＝7|a |2－15|b |2＋16a ·b ＝0，(a －4b )(7a －2b )＝7|a |2＋8|b |2－30a ·b ＝0，解之得，|b |2＝2a ·b ＝|a |2，∴cos 〈a ，b 〉＝a ·b |a |·|b |＝12，∴〈a ，b 〉＝60°. 14．[证明] 如图所示，空间四边形ABCD ，E 、F 分别为AB 、CD 的中点，利用多边形加法法则可得，EF →＝EA →＋AD →＋DF →，EF →＝EB →＋BC →＋CF →.①又E 、F 分别是AB 、CD 的中点，故有EA →＝－EB →，DF →＝－CF →.②将②代入①后，两式相加得，2EF →＝AD →＋BC →，∴EF →＝12AD →＋12BC →. 即EF →与BC →、AD →共面，∴EF 与AD 、BC 可平行于同一平面．15．[解析] 不妨设正方体的棱长为1, 设AB →＝a ，AD →＝b ，AA 1→＝c ，则|a |＝|b |＝|c |＝1，a·b ＝b·c ＝c·a ＝0，A 1B →＝a －c ，AC 1→＝a ＋b ＋c .∴A 1B →·AC →＝(a －c )·(a ＋b ＋c )＝(a －c )(a ＋c )＋b (a －c )＝0∴<A 1B →，AC 1→>＝90°.因此，异面直线A 1B 与AC 所成的角为90°.[说明] 求异面直线所成的角的关键是求异面直线上两向量的数量积，而要求两向量的数量积，必须把所求向量用空间的一组基向量来表示．。

高二数学选修空间向量试卷及答案Last revised by LE LE in 2021A A 1 DCB B 1C 1 图高二数学（选修2-1）空间向量试题宝鸡铁一中 司婷一、选择题：在每小题给出的四个选项中，只有一项是符合题目要求的，请把正确答案的代号填在题后的括号内（每小题5分，共60分）．1．在正三棱柱ABC —A 1B 1C 1中，若AB ＝2BB 1，则AB 1与C 1B 所成的角的大小为（ ）A ．60°B ．90°C ．105°D ．75°2．如图，ABCD —A 1B 1C 1D 1是正方体，B 1E 1＝D 1F 1＝411B A ，则BE 1与DF 1所成角的余弦值是（ ）A ．1715 B ．21 C ．178 D ．23 3．如图，A 1B 1C 1—ABC 是直三棱柱，∠BCA =90°，点D 1、F 1分别是A 1B 1、A 1C 1的中点，若BC =CA =CC 1，则BD 1与AF 1所成角的余弦值是（ ）A ．1030 B ．21 C ．1530 D ．1015 4．正四棱锥S ABCD -的高2SO =，底边长2AB =，则异面直线BD 和SC 之间的距离（ ）A ．515 B ．55 C ．552 D ．105 5．已知111ABC A B C -是各条棱长均等于a 的正三棱柱，D是侧棱1CC 的中点．点1C 到平面1AB D 的距离（ ） A ．a 42B ．a 82 图图C ．a 423 D ．a 22 6．在棱长为1的正方体1111ABCD A B C D -中，则平面1AB C 与平面11A C D 间的距离（ ）A ．63 B ．33 C ．332 D ．23 7．在三棱锥P －ABC 中，AB ⊥BC ，AB ＝BC ＝21PA ，点O 、D 分别是AC 、PC 的中点，OP ⊥底面ABC ，则直线OD 与平面PBC 所成角的正弦值（ ）A ．621 B ．338 C60210 D ．302108．在直三棱柱111C B A ABC -中，底面是等腰直角三角形，90=∠ACB ，侧棱21=AA ，D ，E 分别是1CC 与B A 1的中点，点E 在平面AB D 上的射影是ABD ∆的重心G ．则B A 1与平面AB D 所成角的余弦值（ ）A ．32B ．37C ．23 D ．73 9．正三棱柱111C B A ABC -的底面边长为3，侧棱3231=AA ，D 是C B 延长线上一点，且BC BD =，则二面角B AD B --1的大小（ ）A ．3π B ．6πC ．65πD ．32π10．正四棱柱1111D C B A ABCD -中，底面边长为22，侧棱长为4，E ，F 分别为棱AB ，CD 的中点，G BD EF =⋂．则三棱锥11EFD B -的体积V （ ）A ．66 B ．3316 C ．316D ．1611．有以下命题：①如果向量b a ,与任何向量不能构成空间向量的一组基底，那么b a ,的关系是不共线；②,,,O A B C 为空间四点，且向量,,不构成空间的一个基底，则点,,,O A B C 一定共面；③已知向量,,是空间的一个基底，则向量,,-+也是空间的一个基底。

空间向量与立体几何1、空间向量的概念：()1在空间，具有大小和方向的量称为空间向量．()2向量可用一条有向线段来表示．有向线段的长度表示向量的大小，箭头所指的方向表示向量的方向．()3向量AB 的大小称为向量的模（或长度），记作AB ． ()4模（或长度）为0的向量称为零向量；模为1的向量称为单位向量． ()5与向量a 长度相等且方向相反的向量称为a 的相反向量，记作a -． ()6方向相同且模相等的向量称为相等向量．2、空间向量的加法和减法：()1求两个向量和的运算称为向量的加法，它遵循平行四边形法则．即：在空间以同一点O 为起点的两个已知向量a 、b 为邻边作平行四边形C OA B ，则以O 起点的对角线C O 就是a 与b 的和，这种求向量和的方法，称为向量加法的平行四边形法则．()2求两个向量差的运算称为向量的减法，它遵循三角形法则．即：在空间任取一点O ，作a OA =，b OB =，则a b BA =-．3、实数λ与空间向量a 的乘积a λ是一个向量，称为向量的数乘运算．当0λ>时，a λ与a 方向相同；当0λ<时，a λ与a 方向相反；当0λ=时，a λ为零向量，记为0．a λ的长度是a 的长度的λ倍．4、设λ，μ为实数，a ，b 是空间任意两个向量，则数乘运算满足分配律及结合律．分配律：()a b a b λλλ+=+；结合律：()()a a λμλμ=．5、如果表示空间的有向线段所在的直线互相平行或重合，则这些向量称为共线向量或平行向量，并规定零向量与任何向量都共线．6、向量共线的充要条件：对于空间任意两个向量a ，()0b b ≠，//a b 的充要条件是存在实数λ，使a b λ=．7、平行于同一个平面的向量称为共面向量． 8、向量共面定理：空间一点P 位于平面C AB 内的充要条件是存在有序实数对x ，y ，使x y C AP =AB +A ；或对空间任一定点O ，有x y C OP =OA +AB +A ；或若四点P ，A ，B ，C 共面，则()1x y z C x y z OP =OA+OB+O ++=． 9、已知两个非零向量a 和b ，在空间任取一点O ，作a OA =，b OB =，则∠AOB 称为向量a ，b 的夹角，记作,a b 〈〉．两个向量夹角的取值范围是：[],0,a b π〈〉∈． 10、对于两个非零向量a 和b ，若,2a b π〈〉=，则向量a ，b 互相垂直，记作a b ⊥．11、已知两个非零向量a 和b ，则cos ,a b a b 〈〉称为a ，b 的数量积，记作a b ⋅．即cos ,a b a b a b ⋅=〈〉．零向量与任何向量的数量积为0．12、a b ⋅等于a 的长度a 与b 在a 的方向上的投影cos ,b a b 〈〉的乘积． 13、若a ，b 为非零向量，e 为单位向量，则有()1cos ,e a a e a a e ⋅=⋅=〈〉；()20a b a b ⊥⇔⋅=；()3()()a b a b a b a b a b ⎧⎪⋅=⎨-⎪⎩与同向与反向，2a a a ⋅=，a a a =⋅； ()4cos ,a b a b a b⋅〈〉=；()5a b a b ⋅≤．14、向量数乘积的运算律：()1a b b a ⋅=⋅；()2()()()a b a b a b λλλ⋅=⋅=⋅；()3()a b c a c b c +⋅=⋅+⋅．15、若i ，j ，k 是空间三个两两垂直的向量，则对空间任一向量p ，存在有序实数组{},,x y z ，使得p xi yj zk =++，称xi ，yj ，zk 为向量p 在i ，j ，k 上的分量．16、空间向量基本定理：若三个向量a ，b ，c 不共面，则对空间任一向量p ，存在实数组{},,x y z ，使得p xa yb zc =++．17、若三个向量a ，b ，c 不共面，则所有空间向量组成的集合是{},,,p p xa yb zc x y z R =++∈．这个集合可看作是由向量a ，b ，c 生成的，{},,a b c 称为空间的一个基底，a ，b ，c 称为基向量．空间任意三个不共面的向量都可以构成空间的一个基底．18、设1e ，2e ，3e 为有公共起点O 的三个两两垂直的单位向量（称它们为单位正交基底），以1e ，2e ，3e 的公共起点O 为原点，分别以1e ，2e ，3e 的方向为x 轴，y 轴，z 轴的正方向建立空间直角坐标系xyz O ．则对于空间任意一个向量p ，一定可以把它平移，使它的起点与原点O 重合，得到向量p OP =．存在有序实数组{},,x y z ，使得123p xe ye ze =++．把x ，y ，z 称作向量p 在单位正交基底1e ，2e ，3e 下的坐标，记作(),,p x y z =．此时，向量p 的坐标是点P 在空间直角坐标系xyz O 中的坐标(),,x y z ．19、设()111,,a x y z =，()222,,b x y z =，则()1()121212,,a b x x y y z z +=+++．()2()121212,,a b x x y y z z -=---． ()3()111,,a x y z λλλλ=． ()4121212a b x x y y z z ⋅=++．()5若a 、b 为非零向量，则12121200a b a b x x y y z z ⊥⇔⋅=⇔++=． ()6若0b ≠，则121212//,,a b a b x x y y z z λλλλ⇔=⇔===． ()721a a a x =⋅=+()821cos ,a b a b a bx ⋅〈〉==+．()9()111,,x y z A ，()222,,x y z B =，则(d x AB =AB =20、在空间中，取一定点O 作为基点，那么空间中任意一点P 的位置可以用向量OP 来表示．向量OP 称为点P 的位置向量．21、空间中任意一条直线l 的位置可以由l 上一个定点A 以及一个定方向确定．点A 是直线l 上一点，向量a 表示直线l 的方向向量，则对于直线l 上的任意一点P ，有ta AP =，这样点A 和向量a 不仅可以确定直线l 的位置，还可以具体表示出直线l 上的任意一点． 22、空间中平面α的位置可以由α内的两条相交直线来确定．设这两条相交直线相交于点O ，它们的方向向量分别为a ，b ．P 为平面α上任意一点，存在有序实数对(),x y ，使得xa yb OP =+，这样点O 与向量a ，b 就确定了平面α的位置． 23、直线l 垂直α，取直线l 的方向向量a ，则向量a 称为平面α的法向量． 24、若空间不重合两条直线a ，b 的方向向量分别为a ，b ，则////a b a b ⇔⇔()a b R λλ=∈，0a b a b a b ⊥⇔⊥⇔⋅=．25、若直线a 的方向向量为a ，平面α的法向量为n ，且a α⊄，则////a a αα⇔ 0a n a n ⇔⊥⇔⋅=，//a a a n a n ααλ⊥⇔⊥⇔⇔=．26、若空间不重合的两个平面α，β的法向量分别为a ，b ，则////a b αβ⇔⇔a b λ=，0a b a b αβ⊥⇔⊥⇔⋅=．27、设异面直线a ，b 的夹角为θ，方向向量为a ，b ，其夹角为ϕ，则有cos cos a b a bθϕ⋅==．28、设直线l 的方向向量为l ，平面α的法向量为n ，l 与α所成的角为θ，l 与n 的夹角为ϕ，则有sin cos l n l nθϕ⋅==．29、设1n ，2n 是二面角l αβ--的两个面α，β的法向量，则向量1n ，2n 的夹角（或其补角）就是二面角的平面角的大小．若二面角l αβ--的平面角为θ，则1212cos n n n n θ⋅=．30、点A 与点B 之间的距离可以转化为两点对应向量AB 的模AB 计算． 31、在直线l 上找一点P ，过定点A 且垂直于直线l 的向量为n ，则定点A 到直线l 的距离为cos ,n d n nPA ⋅=PA 〈PA 〉=．32、点P 是平面α外一点，A 是平面α内的一定点，n 为平面α的一个法向量，则点P 到平面α的距离为cos ,n d n nPA ⋅=PA 〈PA 〉=．空间向量与立体几何练习题1一、选择题（每小题5分，共50分）1.如图，在平行六面体ABCD —A 1B 1C 1D 1中，M 为AC 与BD 的交点.若11B A =a ，11D A =b ，A A 1=c ，则下列向量中与MB 1相等的向量是A.－21a +21b +c B.21a +21b +c C.21a －21b +c D.－21a －21b +c 2.下列等式中，使点M 与点A 、B 、C 一定共面的是A.OC OB OA OM --=23B.OC OB OA OM 513121++=C.0=+++OC OB OA OMD.0=++MC MB MA3.已知空间四边形ABCD 的每条边和对角线的长都等于1，点E 、F 分别是AB 、AD 的中点，则DC EF ⋅等于A.41B.41- C.43 D.43-4.若)2,,1(λ=a ，)1,1,2(-=b ，a 与b 的夹角为060，则λ的值为 A.17或-1 B.-17或1 C.-1 D.15.设)2,1,1(-=OA ，)8,2,3(=OB ，)0,1,0(=OC ，则线段AB 的中点P 到点C 的距离为 A.213 B.253 C.453 D.4536.下列几何体各自的三视图中，有且仅有两个视图相同的是A ．①②B ．①③C ．①④D ．②④7.右图是一个几何体的三视图，根据图中数据，可得该几何体的表面积是 A.9πB.10πC.11πD.12π8.如图，ABCD -A 1B 1C 1D 1为正方体，下面结论错误．．的是 A.BD ∥平面CB 1D 1 B.AC 1⊥BDC.AC 1⊥平面CB 1D 1①正方体 ②圆锥 ③三棱台 ④正四棱锥俯视图 正(主)视图 侧(左)视图2 3 2 2D.异面直线AD 与CB 1所成的角为60°9.如图，在长方体ABCD -A 1B 1C 1D 1中，AB =BC =2,AA 1=1,则BC 1与平面BB 1D 1D 所成角的正弦值为 A.6 B.552 C.15 D.10 10.⊿ABC 的三个顶点分别是)2,1,1(-A ，)2,6,5(-B ，)1,3,1(-C ，则AC 边上的高BD 长为A.5B.41C.4D.52 二、填空题（每小题5分，共20分）11.设)3,4,(x =a ，),2,3(y -=b ，且b a //，则=xy .12.已知向量)1,1,0(-=a ，)0,1,4(=b ，29=+b a λ且0λ>，则λ=________. 13.在直角坐标系xOy 中，设A （-2，3），B （3，-2），沿x 轴把直角坐标平面折成大小为θ的二面角后，这时112=AB ，则θ的大小为． 14.如图，P —ABCD 是正四棱锥，1111ABCD A B C D -是正方体，其中 2,6AB PA ==，则1B 到平面PAD的距离为.三、解答题（共80分）15.（本小题满分12分）如图，在四棱锥P-ABCD 中，底面ABCD 是边长为1的正方形，侧棱PA 的长为2，且PA 与AB 、AD 的夹角都等于600，M 是PC 的中点，设c b a ===AP AD AB ,,． （1）试用c b a ,,表示出向量BM ；（2）求BM 的长．16.（本小题满分14分）如下的三个图中，上面的是一个长方体截去一个角所得多面体的直观图，它的正视图和侧视图在下面画出（单位：cm ）.（1）在正视图下面，按照画三视图的要求画出该多面体的俯视图；（2）按照给出的尺寸，求该多面体的体积；（3）在所给直观图中连结'BC ，证明：'BC ∥面EFG.. 17.（本小题满分12分）如图，在四面体ABCD 中，CB CD AD BD =⊥，，点E F ，分别是AB BD ，的中点．求证：2262GF C'B'D'MP DC BA俯视图正视图121121ED C BA P （1）直线//EF 面ACD ； （2）平面EFC ⊥面BCD ． 18.（本小题满分14分）如图，已知点P 在正方体''''D CB A ABCD -的对角线'BD 上，∠PDA=60°.（1）求DP 与'CC 所成角的大小；（2）求DP 与平面D D AA ''所成角的大小.19.（本小题满分14分）已知一四棱锥P －ABCD 的三视图如下，E 是侧棱PC 上的动点．（1）求四棱锥P －ABCD 的体积； （2）是否不论点E 在何位置，都有BD ⊥AE ？证明你的结论; （3）若点E 为PC 的中点，求二面角D －AE －B 的大小．20.（本小题满分14分）如图，已知四棱锥P ABCD -，底面ABCD 为菱形，PA ⊥平面ABCD ，60ABC ∠=，E F ，分别是BC PC ，的中点．（1）证明：AE PD ⊥；（2）若H 为PD 上的动点，EH 与平面PAD 所成最大角的正切值为62，求二面角E AF C --的余弦值． 参考答案 一、选择题1.)(21111BC BA A A BM B B M B ++=+==c +21(－a +b )=－21a +21b +c ，故选A. 2.1),,(=++∈++=⇔z y x R z y x OC z OB y OA x OM C B A M 且四点共面、、、由于MC MB MA MC MB MA C B A --=⇔=++∴0由于都不正确、、选项.)()()(共面使所以存在MC MB MA MC y MB x MA y x ,,,1,1∴+==-=四点共面，、、、为公共点由于C B A M M ∴故选D. 3.∵的中点分别是AD AB F E ,,,BD EF BD EF BD EF 21,21//=∴=∴且, 41120cos 1121,cos 21210-=⨯⨯⨯>=<⋅=⋅=⋅∴DC BD DC BD DC BD DC EF 故选B.4.B5.B6.D7.D8.D9.D10.由于4,cos =⋅=><⋅=ACAC AB AC AB AB AD ，所以522=-=AD AB BD ,故选A PBECD FAD 'C 'B'A'PD C BA二、填空题 11.912.313.作AC ⊥x 轴于C ，BD ⊥x 轴于D ，则DB CD AC AB ++=∵θθcos 6)180cos(,0,0,2,5,30-=-⋅=⋅=⋅=⋅===DB AC DB AC DB CD CD AC DB CD AC00222222222120,1800 .21cos ),cos 600(2253)112()(2)(=∴≤≤-=∴--+++=∴⋅+⋅+⋅+++=++=∴θθθθ由于AC DB DB CD CD AC DB CD AC DB CD AC AB14.以11B A 为x 轴，11D A 为y 轴，A A 1为z 轴建立空间直角坐标系 设平面PAD 的法向量是(,,)m x y z =，(0,2,0),(1,1,2)AD AP ==，∴02,0=++=z y x y ，取1=z 得(2,0,1)m =-，1(2,0,2)B A =-，∴1B 到平面PAD 的距离1655B A m d m⋅==. 三、解答题15.解：（1）∵M 是PC 的中点，∴)]([21)(21AB AP AD BP BC BM -+=+=c b a a c b 212121)]([21++-=-+= （2）2,1,2,1===∴===c b a PA AD AB 由于160cos 12,0,60,00=⋅⋅=⋅=⋅=⋅∴=∠=∠⊥c b c a b a PAD PAB AD AB 由于),(21c b a ++-=BM 由于 23)]110(2211[41)](2[41)(4122222222=+-+++=⋅+⋅-⋅-+++=++-=∴c b c a b a c b a c b a BM 2626的长为，BM BM ∴=∴. 16.解：（1）如图（2）所求多面体体积V V V =-长方体正三棱锥1144622232⎛⎫=⨯⨯-⨯⨯⨯⨯ ⎪⎝⎭2284(cm )3=．（3）证明：在长方体ABCD A B C D ''''-中，连结AD '，则AD BC ''∥．因为E G ，分别为AA '，A D ''中点， 所以AD EG '∥，从而EG BC '∥．又BC '⊄平面EFG ，ABC DE FGA 'B 'C 'D '所以BC '∥面EFG ． 17.证明：（1）∵E,F 分别是AB BD ，的中点，∴EF 是△ABD 的中位线，∴EF ∥AD ，∵AD ⊂面ACD ，EF ⊄面ACD ，∴直线EF ∥面ACD ；（2）∵AD ⊥BD ，EF ∥AD ，∴EF ⊥BD ，∵CB=CD ，F 是ＢＤ的中点，∴CF ⊥BD 又EF ∩CF=F, ∴BD ⊥面EFC ， ∵BD ⊂面BCD ，∴面EFC ⊥面BCD .18.解：如图，以D 为原点，DA 为单位长建立空间直角坐标系D xyz -．则(100)DA =，，，(001)CC '=，，．连结BD ，B D ''． 在平面BB D D ''中，延长DP 交B D ''于H ．设(1)(0)DH m m m =>，，，由已知60DH DA <>=，， 由cos DA DH DA DH DA DH =<>，，可得2m = 解得m=21DH ⎛⎫= ⎪ ⎪⎝⎭． （1）因为0011cos 2DH CC +⨯'<>==，， 所以45DH CC '<>=，，即DP 与CC '所成的角为45．（2）平面AA D D ''的一个法向量是(010)DC =，，． 因为01101cos 2DH DC ++⨯<>==，， 所以60DH DC <>=，，可得DP 与平面AA D D ''所成的角为30． 19.解：（1）由该四棱锥的三视图可知，该四棱锥P －ABCD 的底面是边长为1的正方形，侧棱PC ⊥底面ABCD ，且PC=2.∴1233P ABCD ABCD V S PC -=⋅=(2)不论点E 在何位置，都有BD ⊥AE证明如下：连结AC ，∵ABCD 是正方形，∴BD ⊥AC∵PC ⊥底面ABCD 且BD ⊂平面ABCD ∴BD ⊥PC又ACPC C =∴BD ⊥平面PAC∵不论点E 在何位置，都有AE ⊂平面PAC ∴不论点E 在何位置，都有BD ⊥AE(3)解法1：在平面DAE 内过点D 作DG ⊥AE 于G ，连结BG∵CD=CB,EC=EC ，∴Rt ECD ∆≌Rt ECB ∆，∴ED=EBzyxEDC BAP∵AD=AB ，∴△EDA ≌△EBA ，∴BG ⊥EA ∴DGB ∠为二面角D －EA －B 的平面角 ∵BC ⊥DE ，AD ∥BC ，∴AD ⊥DE在R ｔ△ADE 中AD DE DG AE ⋅==23=BG在△DGB 中，由余弦定理得212cos 222-=⋅-+=∠BG DG BD BG DG DGB∴DGB ∠=23π，∴二面角D －AE －B 的大小为23π. 解法2：以点C 为坐标原点，CD 所在的直线为ｘ轴建立空间直角坐标系如图示：则(1,0,0),(1,1,0),(0,1,0),(0,0,1)D A B E ,从而(1,0,1),(0,1,0),(1,0,0),(0,1,1)DE DA BA BE =-===-设平面ADE 和平面ABE 的法向量分别为(,,),(',',')m a b c n a b c ==由法向量的性质可得：0,0a c b -+==，'0,''0a b c =-+= 令1,'1c c ==-，则1,'1a b ==-，∴(1,0,1),(0,1,1)m n ==-- 设二面角D －AE －B 的平面角为θ，则1cos 2||||m n m n θ⋅==-⋅∴23πθ=，∴二面角D －AE －B 的大小为23π. 20.（1）证明：由四边形ABCD 为菱形，60ABC ∠=，可得ABC △为正三角形． 因为E 为BC 的中点，所以AE BC ⊥．又BC AD ∥，因此AE AD ⊥．因为PA ⊥平面ABCD ，AE ⊂平面ABCD ，所以PA AE ⊥． 而PA ⊂平面PAD ，AD ⊂平面PAD 且PAAD A =，所以AE ⊥平面PAD ．又PD ⊂平面PAD ， 所以AE PD ⊥．（2）解：设2AB =，H 为PD 上任意一点，连接AH EH ，． 由（1）知AE ⊥平面PAD ，则EHA ∠为EH 与平面PAD 所成的角． 在Rt EAH △中，3AE =， 所以当AH 最短时，EHA ∠最大， 即当AH PD ⊥时，EHA ∠最大．此时tan 2AE EHA AH AH ∠===，因此AH =2AD =，所以45ADH ∠=，所以2PA =．解法一：因为PA ⊥平面ABCD ，PA ⊂平面PAC ， 所以平面PAC ⊥平面ABCD ．过E 作EO AC ⊥于O ，则EO ⊥平面PAC ，过O 作OS AF ⊥于S ，连接ES ，则ESO ∠为二面角E AF C --的平面角， 在Rt AOE △中，3sin 302EO AE ==，3cos302AO AE ==， 又F 是PC 的中点，在Rt ASO △中，32sin 454SO AO ==，又SE ===Rt ESO △中，cos SO ESO SE ∠===， 即所求二面角的余弦值为5． 解法二：由（1）知AE AD AP ，，两两垂直，以A 为坐标原点，建立如图所示的空间直角坐标系，又E F，分别为BC PC ，的中点，所以(000)10)0)(020)A B C D -，，，，，，，，，，1(002)0)12P E F ⎫⎪⎪⎝⎭，，，，，，，， 所以31(300)122AE AF ⎛⎫== ⎪ ⎪⎝⎭，，，，，． 设平面AEF 的一法向量为111()x y z =，，m ，则00AE AF ⎧=⎪⎨=⎪⎩，，m m 因此111101022x y z =++=⎪⎩，． 取11z =-，则(021)=-，，m ， 因为BD AC ⊥，BD PA ⊥，PA AC A =，所以BD ⊥平面AFC ，故BD 为平面AFC 的一法向量．B又(0)BD =-，，所以cos 5BD BD BD<>===，m m m ． 因为二面角E AF C --为锐角，所以所求二面角的余弦值为5． 空间向量与立体几何2一、选择题（每小题5分，共60分） 1．下列各组向量中不平行的是（ ）A ．)4,4,2(),2,2,1(--=-=b aB ．)0,0,3(),0,0,1(-==d cC ．)0,0,0(),0,3,2(==f eD ．)40,24,16(),5,3,2(=-=h g2．已知点(3,1,4)A --，则点A 关于x 轴对称的点的坐标为（ ） A ．)4,1,3(-- B ．)4,1,3(--- C ．)4,1,3( D ．)4,1,3(--3．若向量)2,1,2(),2,,1(-==b a λ，且a 与b 的夹角余弦为98，则λ等于（ ）A ．2B ．2-C ．2-或552D ．2或552-4．若A )1,2,1(-，B )3,2,4(，C )4,1,6(-，则△ABC 的形状是（ ）A ．不等边锐角三角形B ．直角三角形C ．钝角三角形D ．等边三角形5．若A )12,5,(--x x x ，B )2,2,1(x x -+，当B A取最小值时，x 的值等于（ ） A ．19 B ．78-C ．78D ．14196．空间四边形OABC 中，OB OC =，3AOB AOC π∠=∠=，则cos <,OA BC >的值是（）A ．21B ．22C ．－21D ．07．设n m 、表示直线，βα、表示平面，则下列命题中不正确．．．的是（ ）． A ．βα⊥⊥m ,m ，则α//β B ．m//n ,=βαα ，则m//n C ．α⊥m ,β//m , 则βα⊥D ．n //m ,α⊥m , 则 α⊥n 8．在棱长均为2的正四面体BCD A -中，若以三角形ABC 为视角正面的三视图中，其左视图的面积是（ ）．ABDA．3 B．362C．2D．229、如图，将无盖正方体纸盒展开，直线AB,CD在原正方体中的位置关系是（）A．平行 B．相交且垂直C．异面 D．相交成60°10、点P在平面ABC外，若PA=PB=PC，则点P在平面ABC上的射影是△ABC的（）A．外心 B.重心 C.内心 D.垂心11、如果一个水平放置的图形的斜二测直观图是一个底角为45°，腰和上底均为１的等腰梯形，那么原平面图形的面积是（）（A）2（B）12（C）22+（D）112、已知PD⊥矩形ABCD所在的平面，图中相互垂直的平面有（）（A）2对（B）3对（C）4对（D）5对二、填空题（每小题4分，共24分）13．若向量)2,3,6(),4,2,4(-=-=ba，则(23)(2)a b a b-+=__________________。

第三章空间向量与立体几何综合测试题（含详解新人教A版选修2-1）x第三章空间向量与立体几何综合测试题（含详解新人教A版选修2-1）(时间：100分钟；满分：120分)一、选择题(本大题共10小题，在每小题给出的四个选项中，只有一项是符合题目要求的)1．已知a＝(λ＋1,0,2λ)，b＝(6,2μ－1,2)，若a∥b，则λ与μ的值分别为()A.15，12B．5,2C．－15，－12D．－5，－2解析：选A.a∥b，则存在m∈R，使得a＝mb，又a＝(λ＋1,0,2λ)，b＝(6,2μ－1,2)，则有λ＋1＝6m，0＝－，2λ＝2m，可得λ＝15，μ＝12.2．已知A(1，－2,11)，B(4,2,3)，C(6，－1,4)三点，则△ABC是() A．直角三角形B．钝角三角形C．锐角三角形D．等腰三角形解析：选A.AB→＝(3,4，－8)，BC→＝(2，－3,1)，CA→＝(－5，－1,7)，∴BC→•CA→＝－10＋3＋7＝0.∴BC⊥CA.∴△ABC是直角三角形．3．已知在空间四边形OABC中，OA→＝a，OB→＝b，OC→＝c，点M 在OA上，且OM＝2MA，N为BC中点，则MN→等于()A.12a－23b＋12cB．－23a＋12b＋12cC.12a＋12b－12cD.23a＋23b－12c解析：选B.因MN→＝ON→－OM→＝12(OB→＋OC→)－23OA→＝12b ＋12c－23a.4．已知a＝(1,0,1)，b＝(－2，－1,1)，c＝(3,1,0)，则|a－b＋2c|等于() A．310B．210C.10D．5解析：选A.|a－b＋2c|＝－b＋，∵a－b＋2c＝(1,0,1)－(－2，－1,1)＋2(3,1,0)＝(9,3,0)，∴|a－b＋2c|＝92＋32＋0＝310.5．给出下列命题：①已知a⊥b，则a•(b＋c)＋c•(b－a)＝b•c；②A、B、M、N为空间四点，若BA→、BM→、BN→不能构成空间的一个基底，则A、B、M、N四点共面；③已知a⊥b，则a，b与任何向量都不能构成空间的一个基底；④已知{a，b，c}是空间的一个基底，则基向量a，b可以与向量m＝a ＋c构成空间另一个基底．其中正确命题的个数是()A．1B．2C．3D．4解析：选C.当a⊥b时，a•b＝0，a•(b＋c)＋c•(b－a)＝a•b＋a•c＋c•b －c•a＝c•b＝b•c，故①正确；当向量BA→、BM→、BN→不能构成空间的一个基底时，BA→、BM→、BN→共面，从而A、B、M、N四点共面，故②正确；当a⊥b时，a，b不共线，任意一个与a，b不共面的向量都可以与a，b构成空间的一个基底，故③错误；当{a，b，c}是空间的一个基底时，a，b，c不共面，所以a，b，m也不共面，故a，b，m可构成空间的另一个基底，故④正确．6．在下列条件中，使M与A、B、C一定共面的是()A.OM→＝2OA→－OB→－OC→B.OM→＝15OA→＋13OB→＋12OC→C.MA→＋MB→＋MC→＝0D.OM→＋OA→＋OB→＋OC→＝0解析：选C.空间的四点M、A、B、C共面只需满足OM→＝xOA→＋yOB→＋zOC→，且x＋y＋z＝1，或存在实数x，y使得MC→＝xMA→＋yMB→. 7．在空间直角坐标系Oxyz中，i，j，k分别是x轴、y轴、z轴的方向向量，设a为非零向量，且〈a，i〉＝45°，〈a，j〉＝60°，则〈a，k〉＝()A．30°B．45°C．60°D．90°解析：选C.如图所示，设|a|＝m(m＞0)，a＝OP→，PA⊥平面xOy，则在Rt△PBO中，|PB|＝|OP→|•cos〈a，i〉＝22m，在Rt△PCO中，|OC|＝|OP→|•cos〈a，j〉＝m2，∴|AB|＝m2，在Rt△PAB中，|PA|＝|PB|2－|AB|2＝24m2－m24＝m2，∴|OD|＝m2，在Rt△PDO中，cos〈a，k〉＝|OD||OP|＝12，又0°≤〈a，k〉≤180°，∴〈a，k〉＝60°.8．已知点A(－3,4,3)，O为坐标原点，则OA与坐标平面yOz所成角的正切值为()A.34B.35C.53D．1解析：选B.A点在面yOz上的射影为B(0,4,3)且|OB|＝5，所以OA与平面yOz所成角θ满足tanθ＝|AB||OB|＝35.9.如图所示，在正方体ABCD－A1B1C1D1中，以D为原点建立空间直角坐标系，E为BB1的中点，F为A1D1的中点，则下列向量中能作为平面AEF的法向量的是()A．(1，－2,4)B．(－4,1，－2)C．(2，－2,1)D．(1,2，－2)解析：选B.设平面AEF的法向量为n＝(x，y，z)，正方体ABCD－A1B1C1D1的棱长为1，则A(1,0,0)，E(1,1，12)，F(12，0,1)．故AE→＝(0,1，12)，AF→＝(－12，0,1)．由AE→•n＝0，AF→•n＝0，即y＋12z＝0，－12x＋z＝0，所以y＝－12z，x＝2z.当z＝－2时，n＝(－4,1，－2)，故选B.10．正方体ABCD－A1B1C1D1中，二面角A－BD1－B1的大小为() A．90°B．60°C．120°D．45°解析：选C.如图，以C为原点建立空间直角坐标系Cxyz，设正方体的边长为a，则A(a，a,0)，B(a,0,0)，D1(0，a，a)，B1(a,0，a)，于是BA→＝(0，a,0)，BD1→＝(－a，a，a)，BB1→＝(0,0，a)．设平面ABD1的法向量为n＝(x，y，z)，则n•BA→＝(x，y，z)•(0，a,0)＝ay＝0，n•BD1→＝(x，y，z)•(－a，a，a)＝－ax＋ay＋az＝0.∵a≠0，∴y＝0，x＝z.令x＝z＝1，则n＝(1,0,1)，同理，平面B1BD1的法向量m＝(－1，－1,0)．由于cos〈n，m〉＝n•m|n||m|＝－12，而二面角A－BD1－B1为钝角，故为120°.二、填空题(本大题共5小题，把答案填在题中横线上)11．已知a＝(2，－1,0)，b＝(k,0,1)，若〈a，b〉＝120°，则k＝________. 解析：∵cos〈a，b〉＝a•b|a||b|＝2k5•k2＋1＝－12＜0，∴k＜0，且k2＝511.∴k＝－5511.答案：－551112．若a＝(2,3，－1)，b＝(－2,1,3)，则以a，b为邻边的平行四边形的面积为________．解析：cos〈a，b〉＝a•b|a||b|＝－27，得sin〈a，b〉＝357，由公式S＝|a||b|sin〈a，b〉可得结果．答案：6513.如图，空间四边形OABC，点M，N分别为OA，BC的中点，且OA→＝a，OB→＝b，OC→＝c，用a，b，c表示MN→，则MN→＝________. 解析：MN→＝ON→－OM→＝12(OB→＋OC→)－12OA→＝－12a＋12b＋12c.答案：－12a＋12b＋12c14．点P是棱长为1的正方体ABCD－A1B1C1D1内一点，且满足AP→＝34AB→＋12AD→＋23AA1→，则点P到棱AB的距离为__________．解析：如图所示，过P作PQ⊥平面ABCD于Q，过Q作QE⊥AB于E，连接PE.∵AP→＝34AB→＋12AD→＋23AA1→，∴PQ＝23，EQ＝12，∴点P到棱AB的距离为PE＝PQ2＋EQ2＝56.答案：5615．如图所示，在棱长为4的正方体ABCD－A1B1C1D1中，点E是棱CC1的中点，则异面直线D1E与AC所成的角的余弦值是________．解析：如图，建立空间直角坐标系，则A(4,0,0)，C(0,4,0)，D1(0,0,4)，E(0,4,2)，AC→＝(－4,4,0)，D1E→＝(0,4，－2)．cos〈AC→，D1E→〉＝1632×20＝105.∴异面直线D1E与AC所成角的余弦值为105.答案：105三、解答题(本题共5小题，解答写出文字说明、证明过程或演算步骤)16.如图，在平行六面体ABCD－A1B1C1D1中，CM＝2MA，A1N＝2ND，且AB→＝a，AD→＝b，AA1→＝c，试用a，b，c表示向量MN→.解：∵MN→＝MA→＋AA1→＋A1N→＝－13AC→＋AA1→＋23A1D→＝－13(AB→＋AD→)＋AA1→＋23(A1A→＋A1D1→)＝－13AB→－13AD→＋13AA1→＋23AD→＝－13a＋13b＋13c，∴MN→＝－13a＋13b＋13c.17．在正方体ABCD－A1B1C1D1中，P为DD1的中点，M为四边形ABCD 的中心．求证：对A1B1上任一点N，都有MN⊥AP.证明：建立如图所示的空间直角坐标系Dxyz，设正方体的棱长为1，则A(1,0,0)，P0，0，12，M12，12，0，N(1，y,1)．∴AP→＝－1，0，12，MN→＝12，y－12，1.∴AP→•MN→＝(－1)×12＋0×y－12＋12×1＝0，∴AP→⊥MN→，即A1B1上任意一点N都有MN⊥AP.18.如图所示，在四棱锥P－ABCD中，底面ABCD是矩形，PA⊥平面ABCD，PA＝AD＝2，AB＝1，BM⊥PD于点M.(1)求证：AM⊥PD；(2)求直线CD与平面ACM所成角的余弦值．解：(1)证明：∵PA⊥平面ABCD，AB⊂平面ABCD，∴PA⊥AB.∵AB⊥AD，AD∩PA＝A，∴AB⊥平面PAD.∵PD⊂平面PAD，∴AB⊥PD，又∵BM⊥PD，AB∩BM＝B，∴PD⊥平面ABM.∵AM⊂平面ABM，∴AM⊥PD.(2)如图所示，以点A为坐标原点，建立空间直角坐标系Axyz，则A(0,0,0)，P(0,0,2)，B(1,0,0)，C(1,2,0)，D(0，2,0)．∵AM⊥PD，PA＝AD，∴M为PD的中点，∴M的坐标为(0,1,1)．∴AC→＝(1,2,0)，AM→＝(0,1,1)，CD→＝(－1,0,0)．设平面ACM的一个法向量为n＝(x，y，z)，由n⊥AC→，n⊥AM→可得x＋2y＝0y＋z＝0，令z＝1，得x＝2，y＝－1.∴n＝(2，－1,1)．设直线CD与平面ACM所成的角为α，则sinα＝|CD→•n||CD→|•|n|＝63.∴cosα＝33，即直线CD与平面ACM所成角的余弦值为33.19.如图，四棱锥P－ABCD中，底面ABCD为平行四边形，∠DAB＝60°，AB＝2AD，PD⊥底面ABCD.(1)证明：PA⊥BD；(2)若PD＝AD，求二面角A－PB－C的余弦值．解：(1)证明：因为∠DAB＝60°，AB＝2AD，由余弦定理得BD＝3AD，从而BD2＋AD2＝AB2，故BD⊥AD.又因为PD⊥底面ABCD，可得BD⊥PD.又因为AD∩PD＝D，所以BD⊥平面PAD，故PA⊥BD.(2)如图，以D为坐标原点，AD的长为单位长，射线DA为x轴的正半轴建立空间直角坐标系Dxyz，则A(1,0,0)，B(0，3，0)，C(－1，3，0)，P(0,0,1)，AB→＝(－1，3，0)，PB→＝(0，3，－1)，BC→＝(－1,0,0)．设平面PAB的法向量为n＝(x，y，z)，则n•AB→＝0，n•PB→＝0，即－x＋3y＝0，3y－z＝0，因此可取n＝(3，1，3)．设平面PBC的法向量为m，则m•PB→＝0，m•BC→＝0，可取m＝(0，－1，－3)，〈m，n〉等于二面角A－PB－C的平面角，cos 〈m，n〉＝－427＝－277.故二面角A－PB－C的余弦值为－277.20.如图，在四棱锥P－ABCD中，侧面PAD⊥底面ABCD，侧棱PA＝PD＝2，底面ABCD为直角梯形，其中BC∥AD，AB⊥AD，AD＝2AB＝2BC＝2，O为AD中点．(1)求证：PO⊥平面ABCD；(2)求异面直线PB与CD所成角的余弦值；(3)求点A到平面PCD的距离．解：(1)证明：如图所示，以O为坐标原点，OC→、OD→、OP→的方向分别为x轴，y轴，z轴的正方向，建立空间直角坐标系Oxyz.则A(0，－1,0)，B(1，－1,0)，C(1,0，0)，D(0,1,0)，P(0,0,1)．所以OP→＝(0,0,1)，AD→＝(0,2,0)，OP→•AD→＝0，所以，PO⊥AD，又侧面PAD⊥底面ABCD，平面PAD∩平面ABCD＝AD，PO⊂平面PAD，所以PO⊥平面ABCD.(2)CD→＝(－1,1,0)，PB→＝(1，－1，－1)，所以cos〈PB→，CD→〉＝PB→•CD→|PB→||CD→|＝－1－13×2＝－63，所以异面直线PB与CD 所成的角的余弦值为63.(3)设平面PCD的法向量为n＝(x0，y0，z0)，CP→＝(－1,0,1)，CD→＝(－1,1,0)，由n•CP→＝0n•CD→＝0，得－x0＋z0＝0－x0＋y0＝0，即x0＝y0＝z0，取x0＝1，得平面PCD的一个法向量为n＝(1,1,1)．又AC→＝(1,1,0)，从而点A到平面PCD的距离d＝|AC→•n||n|＝23＝233.。

第三章 空间向量及立体几何3.1空间向量及其运算§3.1.1空间向量及其加减运算 §3.1.2空间向量的数乘运算1. 下列命题中不正确的命题个数是( ) ①若A 、B 、C 、D 是空间任意四点，则有AB +BC + CD +DA =0；②对空间任意点O 及不共线的三点A 、B 、C ，若OP =x OA +y OB +z OC （其中x 、y 、z ∈R ），则P 、A 、B 、C 四点共面；③若a 、b 共线，则a 及b 所在直线平行。

A .1 B .2 C .3 D .42.设OABC 是四面体，G 1是△ABC 的重心，G 是OG 1上一点，且OG =3GG 1，若OG =x OA +y OB +z OC ，则（x ，y ，z ）为( )A .（41，41，41） B .（43，43，43） C .（31，31，31） D .（32，32，32） 3．在平行六面体ABCD －EFGH 中，AG xAC y AF z AH =++，________.x y z ++=则4.已知四边形ABCD 中，AB =a －2c ，CD =5a +6b －8c ，对角线AC 、BD 的中点分别为E 、F ，则EF =_____________.5.已知矩形ABCD ，P 为平面ABCD 外一点，且PA ⊥平面ABCD ，M 、N 分别为PC 、PD 上的点，且M 分PC 成定比2，N 分PD 成定比1，求满足MN xAB y AD z AP =++的实数x 、y 、z 的值.§3.1.3空间向量的数量积运算1.已知正四棱柱1111ABCD A B C D -中，1AA =2AB ，E 为1AA 重点，则异面直线BE 及1CD 所形成角的余弦值为( )A .1010 B . 15C .31010 D . 352．如图，设A ，B ，C ，D 是空间不共面的四点，且满足0AB AC ⋅=，0AC AD ⋅=，0AB AD ⋅=，则△BCD 的形状是( )A ．钝角三角形B ．锐角三角形C ．直角三角形D ．不确定的3．已知ABCD －A 1B 1C 1D 1 为正方体，则下列命题中错误的命题为__________．4．如图，已知：平行六面体ABCD －A 1B 1C 1D 1的底面ABCD 是菱形，且∠C 1CB =∠C 1CD =∠BCD =60° （1）证明：C 1C ⊥BD ；_C_D_A_P_ N_B_M（2）当1CDCC 的值为多少时，能使A 1C ⊥平面C 1BD ？请给出证明． §3.1.4空间向量的正交分解及其坐标表示§3.1.5空间向量运算的坐标表示1．已知向量(2，2，3)OA =-，(，1，4)OB x y z =-，且平行四边形OACB 的对角线的中点坐标为M 31(0，，)22-，则(，，)x y z =( ) A ．(2，4，1)--- B ．(2，4，1)-- C ．(2，4，1)-- D ．(2，4，1)--2．已知(2，2，4)a=-，(1，1，2)b =-，(6，6，12)c =--，则向量、、a b c ( )A ．可构成直角三角形B ．可构成锐角三角形C ．可构成钝角三角形D ．不能构成三角形3．若两点的坐标是A （3cosα，3sinα，1），B （2cosθ，2sinθ，1），则|AB |的取值范围是( ) A ．[0，5] B ．[1，5] C ．（1，5） D ．[1，25]4.设点C （2a +1，a +1，2）在点P （2，0，0）、A （1，－3，2）、B （8，－1，4）确定的平面上，则a 的值为 .5.如图，正三棱柱ABC -A 1B 1C 1的底边长为a ，侧棱长为2a .建立适当的坐标系，⑴写出A ，B ，A 1，B 1的坐标；⑵求AC 1及侧面ABB 1A 1所成的角.3.2立体几何中的向量方法1．到一定点（1，0，1）的距离小于或等于2的点的集合为( ) A ．222{(,,)|(1)(1)4}x y z x y z -++-≤ B ．222{(,,)|(1)(1)4}x y z x y z -++-= C ．222{(,,)|(1)(1)2}x y z x y z -++-≤ D ．222{(,,)|(1)(1)2}x y z x y z -++-=2. 正方体ABCD —A 1B 1C 1D 1中，直线BC 1及平面A 1BD 所成角的余弦值为( ) A ．42 B ．32 C ．33 D ．23 3. 已知斜三棱柱111ABC A B C -，90BCA ∠=，2AC BC ==，1A 在底面ABC 上的射影恰为AC 的中点D ，又知11BA AC ⊥.（1）求证：1AC ⊥平面1A BC ；D 1C 1B 1A 1DABCC 1 B 1 A 1B A（2）求1C 到平面1A AB 的距离；（3）求二面角1A A B C --余弦值的大小.B 4. 如图，在直三棱柱111ABC A B C -中， AB =1，1AC AA ==(1)证明：1ABA C ⊥； （2）求二面角A —1A C —B 的大小.5. 如右图，四棱锥S-ABCD 棱S D 上的点. （1）求证：AC ⊥SD ；（2）若SD ⊥平面PAC ，求二面角P-AC-D 的大小 （3）在（2）的条件下，侧棱S C 上是否存在一点E ， 使得BE ∥平面PAC .若存在，求S E ：EC 的值； 若不存在，试说明理由.参考答案第三章 空间向量及立体几何3.1空间向量及其运算§3.1.1空间向量及其加减运算 §3.1.2空间向量的数乘运算1.A2.A3.324.3a +3b －5c5.如图所示，取PC 的中点E ，连结NE ，则MN EN EM =-. 连结AC ，则§3.1.3空间向量的数量积运算1.C2.B3. ③④4.（1）设1,,CB a CD b CC c === ，则||||a b =，BD CD CB b a =-=- ，所以1()||||cos 60||||cos 600CC b a c b c a c b c a c ⋅=-⋅=⋅-⋅=︒-︒=BD ，11BD CC BD CC ∴⊥⊥即 ； （2）1,2,CD x CD CC ==1设则 2CC =x， 设1,,A A a AD b DCc ===，11,A C a b c C D a c =++=-，2211242()()6A C C D a b c a c a a b b c c xx ∴⋅=++⋅-=+⋅-⋅-=+-，令24260xx +-=，则2320x x --=，解得1x =，或23x =-（舍去），_C_D _A_P_ N _B _M _EA 1§3.1.4空间向量的正交分解及其坐标表示§3.1.5空间向量运算的坐标表示 1.A 2.D 3.B 4.165. （1）建系如图，则A （0，0，0） B （0，a ，0）A 1（0，0，2a )，C 1（-23a ，a 2,2a) (2)解法一：在所建的坐标系中，取A 1B 1的中点M ， 于是M （0，a 2,2a），连结AM ，MC 1则有所以，MC 1⊥平面ABB 1A 1.因此，AC 1及AM 所成的角就是AC 1及侧面ABB 1A 1所成的角.∴2194a AC AM ⋅=，而|13||3,||2AC a AM a ==，由cos<1,AC AM >=1132||||AC AM AC AM ⋅=，∴ <1,AC AM >=30°. ∴AC 1及侧面ABB 1A 1所成的角为30°. 3.2立体几何中的向量方法 新 课 标 第 一网1.A2.C3. （1）如右图，取AB 的中点E ，则//DE BC ，因为BC AC ⊥，所以DEAC ⊥，又1A D ⊥平面ABC ，以1,,DE DC DA 为,,x y z 轴建立空间坐标系， 则()0,1,0A -，()0,1,0C ，()2,1,0B ，()2,0,0CB =，由10AC CB ⋅=，知1A C CB ⊥， 又11BA AC ⊥，从而1AC ⊥平面1A BC .（2）由1AC ⋅2130BA t =-+=，得t =.设平面1A AB 的法向量为(),,n x y z =，(1AA =，()2,2,0AB =，所以10220n AA y n AB x y ⎧⋅=+=⎪⎨⋅=+=⎪⎩，设1z =，则()3,n =-，所以点1C 到平面1A AB 的距离1AC n d n⋅==7. （3）再设平面1A BC 的法向量为(),,m x y z =，(10,CA =-，()2,0,0CB =，所以13020m CA y z m CB x ⎧⋅=-+=⎪⎨⋅==⎪⎩，设1z =，则()0,3,1m =，故cos ,m n m n m n⋅<>==⋅77-，根据法向量的方向，可知二面角1A A B C --的余弦值大小为77. 4.（1）三棱柱111ABC A B C -为直三棱柱，由正弦定理030ACB∠=.如右图，建立空间直角坐标系， 则1(0,0,0),(1,0,0)(0,3,0),(0,0,3)A B C A(2) 如图可取(1,0,0)m AB ==为平面1AA C 的法向量，设平面1A BC 的法向量为(,,)n l m n =，则10,0,130BC n AC n BC ⋅=⋅==-又（，，）， 不妨取1,(3,1,1)mn ==则，1A AC BD ∴--15二面角的大小为arccos 5. 5. （1）连结BD ，设AC 交于BD 于O ，由题意知SO ABCD ⊥平面.以O 为坐标原点，OB OC OS ，，分别为x 轴、y 轴、z 轴正方向，建立坐标系O xyz -如右图.设底面边长为a ，则高62SO a =.于是 62(0,0,),(,0,0)22S a D a -，2(0,,0)2C a ，2(0,,0)2OC a =，26(,0,)22SD a a =--，0OC SD ⋅= ，故OC SD ⊥.从而 AC SD ⊥. (2)由题设知，平面PAC 的一个法向量26()2DSa =，平面DAC 的一个法向量600aOS =（，，，设所求二面角为θ，则3cos OS DS OS DSθ⋅==，得所求二面角的大小为30°._C_A_S_F_BO（3）在棱SC 上存在一点E 使//BE PAC 平面.由（2）知DS 是平面PAC 的一个法向量，且),(0,)DS CS ==.设,CEtCS = 则((1)BE BC CE BC tCS t =+=+=-，而 103BE DC t ⋅=⇔=.即当:2:1SE EC =时，BE DS ⊥.而BE 不在平面PAC 内，故//BE PAC 平面. 作 者 于华东 责任编辑 庞保军。

§3.1.2 空间向量的数乘运算(二)一、选择题1．在下列命题中：①若a 、b 共线，则a 、b 所在的直线平行；②若a 、b 所在的直线是异面直线，则a 、b 一定不共面；③若a 、b 、c 三向量两两共面，则a 、b 、c 三向量一定也共面；④已知三向量a 、b 、c ，则空间任意一个向量p 总可以唯一表示为p ＝x a ＋y b ＋z c ．其中正确命题的个数为 （ ）.A ．0 B.1 C. 2 D. 32．如图所示，已知A ，B ，C 三点不共线，P 为一定点，O 为平面ABC 外任一点，则下列能表示向量OP →的为( )A.OA →＋2AB →＋2AC →B.OA →－3AB →－2AC →C.OA →＋3AB →－2AC →D.OA →＋2AB →－3AC →3．i 、 j 不共线，则存在两个非零常数m ，n ，使k ＝m i ＋n j 是i ，j ，k 共面的( )A ．充分非必要条件B ．必要非充分条件C ．充要条件D ．非充分非必要条件4．对空间任一点O 和不共线三点A 、B 、C ，能得到P 、A 、B 、C 四点共面的是( )A.OP →＝OA →＋OB →＋OC →B.OP →＝13OA →＋13OB →＋13OC → C.OP →＝－OA →＋12OB →＋12OC → D ．以上皆错 5．如图所示，空间四边形OABC 中，OA →＝a ，OB →＝b ，OC →＝c, 点M 在OA 上，且OM →＝2MA →，N 为BC 中点，则MN →等于( )A ．12a －23b ＋12c B ．－23 a ＋12b ＋12c C ．12a ＋12 b －23cD ．23a ＋23b －12c6．有下列命题：①当λ∈R ，且a 1＋a 2＋…＋a n ＝0时，λa 1＋λa 2＋…＋λa n ＝0；②当λ1，λ2，…，λn ∈R ，且λ1＋λ2＋…＋λn ＝0时，λ1a ＋λ2a ＋…＋λn a ＝0；③当λ1，λ2，…，λn ∈R ，且λ1＋λ2＋…＋λn ＝0时，a 1，a 2，…，a n 是n 个向量， 且a 1＋a 2＋…，a n ＝0，则λ1a 1＋λ2a 2＋…＋λn a n ＝0.其中真命题有( )A ．0个B ．1个C ．2个D ．3个二、填空题7．如图所示，已知矩形ABCD ，P 为平面ABCD 外一点，且P A ⊥平面ABCD ，M 、N 分别为PC 、PD 上的点，且PM ∶MC ＝2∶1，N 为PD 中点，则满足MN →＝xAB →＋yAD →＋zAP →的实数x ＝________，y ＝________，z ＝________.8．在平行六面体ABCD —A 1B 1C 1D 1中，若AC 1→＝x ·AB →＋2y ·BC →＋3z ·C 1C →，则x ＋y ＋z ＝________.三、解答题9．如图，已知平行六面体ABCD －A ′B ′C ′D ′，点E 在AC ′上，且AE ∶EC ′＝1∶2，点F ，G 分别是B ′D ′和BD ′的中点，求下列各式中的x ，y ，z 的值．(1)AE →＝xAA ′→＋yAB →＋zAD →；(2)BF →＝xBB ′→＋yBA →＋zBC →；(3)GF →＝xBB ′→＋yBA →＋zBC →.10．已知三个向量a ，b ，c 不共面，并且p ＝a ＋b －c ，q ＝2a －3b －5c ，r ＝－7a ＋18b ＋22c ，向量p ，q ，r 是否共面？参考答案一、选择题1. [答案]A2．[答案] C[解析] 根据A ，B ，C ，P 四点共面的条件即可求得AP →＝xAB →＋yAC →.即OP →＝OA →＋xAB →＋yAC →，由图知x ＝3，y ＝－23．[答案] A[解析] 本题考查空间三个向量共面的条件．若i 不平行j ，则k 与i ，j 共面⇔存在惟一的一对实数x ，y 使k ＝x i ＋y j .故选A.4．[答案] B[解析] 解法一：∵13＋13＋13＝1，∴选B. 解法二：∵OP →＝13OA →＋13OB →＋13OC →， ∴3OP →＝OA →＋OB →＋OC →，∴OP →－OA →＝(OB →－OP →)＋(OC →－OP →)，∴AP →＝PB →＋PC →，∴P A →＝－PB →－PC →，∴P 、A 、B 、C 共面．5．[答案] B[解析] MN →＝ON →－OM →＝12(OB →＋OC →)－23OA → ＝12(b ＋c )－23a ＝－23a ＋12b ＋12c .∴应选B. 6．[答案] C[解析] 由于λa 1＋λa 2＋…＋λa n ＝λ(a 1＋a 2＋…＋a n )＝λ0＝0， 故命题①为真命题．由于λ1a ＋λ2a ＋…＋λn a ＝(λ1＋λ2＋…＋λn )a ＝0×a ＝0，故命题②也为真命题．命题③为假命题，例如当n ＝2时，取λ1＝1，λ2＝－1，a 1＝a (a ≠0)，a 2＝－a ， 则λ1a 1＋λ2a 2＝a ＋(－1)(－a )＝2a ≠0，但此时有λ1＋λ2＝0，a 1＋a 2＝0，命题③不成立．二、填空题7．[答案] －23 －16 16[解析] 在PD 上取一点F ，使PF ∶FD ＝2∶1，连结MF ，则MN →＝MF →＋FN →∵FN →＝DN →－DF →＝12DP →－13DP → ＝16DP →＝16(AP →－AD →) MF →＝23CD →＝23BA →＝－23AB → ∴MN →＝－23AB →－16AD →＋16AP → ∴x ＝－23 y ＝－16 z ＝168．[答案] 76[解析] 在进行空间向量的线性表示时，一定要与所求一致，才不至于犯错．如图所示，有AC 1→＝AB →＋BC →＋CC 1→＝AB →＋BC →＋(－1)·C 1C →.又∵AC 1→＝x ·AB →＋2y ·BC →＋3z ·C 1C →，∴x ·AB →＋2y ·BC →＋3z ·C 1C →＝AB →＋BC →＋(－1)·C 1C →，有⎩⎪⎨⎪⎧ x ＝1，2y ＝1，3z ＝－1，解得⎩⎪⎨⎪⎧ x ＝1，y ＝12，z ＝－13，∴x ＋y ＋z ＝1＋12－13＝76. 三、解答题9．[解析] (1)∵AE ∶EC ′＝1∶2，∴AE →＝13AC →＝13(AB →＋BC →＋CC ′→)＝13(AB →＋AD →＋AA ′→) ＝13AA ′→＋13AB →＋13AD →， ∴x ＝13，y ＝13，z ＝13. (2)∵F 为B ′D ′的中点，∴BF →＝12(BB ′→＋BD ′→)＝12(BB ′→＋BA →＋AA ′→＋A ′D ′→) ＝12(2BB ′→＋BA →＋BC →)＝BB ′→＋12BA →＋12BC →， ∴x ＝1，y ＝12，z ＝12. (3)∵G 、F 分别为BD ′、B ′D ′的中点，∴GF →＝12BB ′→，∴x ＝12，y ＝0，z ＝0. 10．[解析] 假设存在实数λ，μ，使p ＝λq ＋μr ，则a ＋b －c ＝(2λ－7μ)a ＋(－3λ＋18μ)b ＋(－5λ＋22μ)c ，∵a ，b ，c 不共面，∴⎩⎪⎨⎪⎧ 2λ－7μ＝1－3λ＋18μ＝1－5λ＋22μ＝－1，∴⎩⎨⎧ λ＝53μ＝13， 即存在实数λ＝53，μ＝13， 使p ＝λq ＋μr ，故p 、q 、r 共面．。