(完整版)机械原理课程设计牛头刨床(完整图纸)
- 格式:doc
- 大小:486.01 KB
- 文档页数:17



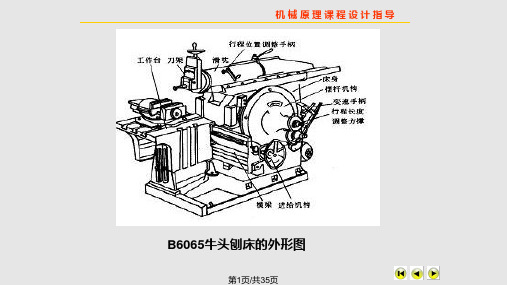
牛头刨床设计一、设计题目(a) (b)图 3-18牛头刨床是一种用于平面切削加工的机床,如图3-18a 。
电动机经皮带和齿轮传动,带动曲柄2和固结在其上的凸轮8。
刨床工作时,刨头6和刨刀7作往复运动。
刨头右行时,刨刀进行切削,称工作行程,此时要求速度较低并且均匀,以减少电动机容量和提高切削质量。
刨头左行时,刨刀切削,称空回行程。
此时要求速度较高,以提高生产率。
刨刀每切削完一次,利用空回行程的时间,凸轮8通过四杆机构1-9-10-11与棘轮带动螺旋机构(图中未画),使工作台连同工件作一次进给运动,以便刨刀继续切削。
刨头在工作行程中,受到很大的切削阻力(在切削的前后各有一段约H 05.0的空刀距离,见图3-18b ),而空回行程中则没有切削阻力。
因此刨头在整个运动循环中,受力变化是很大的,这就影响了主轴的匀速运转.故需安装飞轮来减小主轴的速度波动,以提高切削质量和减少电动机容量。
二、设计数据,见表3-1和表3-2表3-1方案导杆机构的运动分析导杆机构的动态静力分析n 2 l O2O4l O2Al O4Bl BC l O4S4x S6y S6G 4G 6 Py p J S4 r/min mm N mm kg.m 21 60 380 110 5400.25 l O4B0.5l O4B 240502007007000 801.12 64 350 90 580 0.3 l O4B 0.5l O4B 200 50 220 800 9000 80 1.2 3724301108100.36 l O4B0.5l O4B 1804022062080001001.2表3-2方飞轮转动惯量的确定凸轮机构设计齿轮机构的设计案δn O’z1zO’z1’J O2J O1J O"J O’ψmaxl O9D[α]ФФsФ’d O’d O"m12m O"1’αr/minKg.m2o mm o mm o1 0.15 1441240.50.30.20.215 12547517510306 3.5 22 0.15 144131640.50.40.250.215 1353871710306 4 23 0.16 144151950.50.30.20.215 13427516510306 3.5 2三、方案设计及讨论牛头刨床的主传动机构的原动件是曲柄;从动件为刨头(滑块),行程中有急回特性;机构应有较好的动力特性。

设计题目:牛头刨床附图1:导杆机构的运动分析与动态静力分析附图2:齿轮机构的设计目录一.设计题目…………………………….……………………. .4二. 牛头刨床机构简介……………………………….………. .4三.机构简介与设计数据……………………………………. .. .5四. 设计内容…………….………………………….…………. .6五. 体会心得 (14)一、设计题目:牛头刨床1.)为了提高工作效率,在空回程时刨刀快速退回,即要有急回运动,行程速比系数在1.4左右。
2.)为了提高刨刀的使用寿命和工件的表面加工质量,在工作行程时,刨刀要速度平稳,切削阶段刨刀应近似匀速运动。
3.)曲柄转速在64r/min,刨刀的行程H在300mm左右为好,切削阻力约为9000N,其变化规律如图所示。
二、牛头刨床机构简介牛头刨床是一种用于平面切削加工的机床,如图4-1。
电动机经皮带和齿轮传动,带动曲柄2和固结在其上的凸轮8。
刨床工作时,由导杆机构2-3-4-5-6带动刨头6和刨刀7作往复运动。
刨头右行时,刨刀进行切削,称工作行程,此时要求速度较低并且均匀,以减少电动机容量和提高切削质量,刨头左行时,刨刀不切削,称空回行程,此时要求速度较高,以提高生产率。
为此刨床采用有急回作用的导杆机构。
刨刀每切削完一次,利用空回行程的时间,凸轮8通过四杆机构1-9-10-11与棘轮带动螺旋机构(图中未画),使工作台连同工件作一次进给运动,以便刨刀继续切削。
刨头在工作行程中,受到很大的切削阻力(在切削的前后各有一段约5H的空刀距离,见图4-1,b),而空回行程中则没有切削阻力。
因此刨头在整个运动循环中,受力变化是很大的,这就影响了主轴的匀速运转,故需安装飞轮来减小主轴的速度波动,以提高切削质量和减小电动机容量。
三、机构简介与设计数据3.1机构简介牛头刨床是一种用于平面切削加工的机床。
电动机经皮带和齿轮传动,带动曲柄2和固结在其上的凸轮8。

录第一章设计的任务与原始参数............................................................................................ - 3 -1.1设计任务.......................................................................................................................... - 3 -1.2 原始参数......................................................................................................................... - 4 -第二章运动方案设计·............................................................................................................ - 5 -2.1减速装置的选择............................................................................................................. - 5 -2.2刨刀切削运动的实现结构 ............................................................................................ - 5 -第三章电动机的选择................................................................................................................. - 6 -3.1 确定电机功率P d........................................................................................................... - 6 -3.2 根据P d查得电动机部分型号表选择电动机 ............................................................ - 7 -第四章传动比分配..................................................................................................................... - 8 -4.1计算传动比i和选定减速装置..................................................................................... - 8 -第五章减速机构设计................................................................................................................. - 9 -5.1 总体方案图 .................................................................................................................... - 9 -5.2 减速零件参数........................................................................................................... - 10 -第六章主机构设计................................................................................................................ - 12 -1.1机构运动简图及标号.................................................................................................. - 12 -1.2 极位夹角、曲柄1(杆AB)角速度及各杆件长度计算..................................... - 12 -第七章主机构运动分析.......................................................................................................... - 14 -7.1.位置分析....................................................................................................................... - 14 -7.2.速度分析....................................................................................................................... - 15 -7.3.加速度分析 .................................................................................................................. - 15 -7.4矩阵计算及绘图.......................................................................................................... - 15 -7.5输出图像及数据表格.................................................................................................. - 19 -第八章主机构受力分析........................................................................................................ - 21 -8.1 位置1:θ1=0˚........................................................................................................... - 21 -8.2 位置2:θ1=90˚......................................................................................................... - 24 -8.3 位置3:θ1=270˚ ...................................................................................................... - 26 -第九章主机构的速度波动调节........................................................................................... - 29 -9.1 等效驱动力矩及飞轮质量的计算............................................................................ - 29 -9.2 运用excel函数及绘图处理matlab输出的数据................................................ - 30 -第十章小结............................................................................................................................... - 32 -10.1 心得体会................................................................................................................... - 32 -10.2 参考文献................................................................................................................... - 32 -10.3 致谢 ........................................................................................................................... - 32 -第一章设计的任务与原始参数1.1设计任务●题目:牛头刨床●工作原理:牛头刨床是一种常用的平面切削加工机床,电动机经带传动、齿轮传动(图中未画出)最后带动曲柄1(见图1)转动,刨床工作时,是由导杆机构1-2-3-4-5带动刨头和刨刀作往复运动,刨头5右行时,刨刀切削,称工作行程,此时要求速度较低并且均匀;刨头左行时,不进行切削,称空回行程,此时速度较高,以节省时间提高生产率,为此刨床采用有急回作用的导杆机构。
青岛理工大学琴岛学院课程设计说明书课题名称:机械原理课程设计学院:机电工程系专业班级:机械113学号:20110201083学生:张三指导老师:李燕青岛理工大学教务处2013 年 12月 27日《机械原理课程设计》评阅书摘要选取方案三,利用图解法对1点和6电状态时牛头刨床导杆机构进行运动分析、动态静力分析,并汇总本方案所得各位置点的速度、加速度、机构受力数据绘制曲线图。
进行方案比较,确定最佳方案。
将一个班级分为 3 组,每组11人左右,一组选择一个备选方案进行如下分析工作:课程设计内容:牛头刨床导杆机构的运动分析、动态静力分析;(1)绘制机构运动简图(两个位置);(2)速度分析、加速度分析;(3)机构受力分析(求平衡力矩);(4)绘制运动线图。
(上述三项作在一张A1号图纸上)精选文档目录摘要 (I)1设计任务 (1)2导杆机构的基本尺寸确定 (2)3 导杆机构的运动分析 (4)3.1 速度分析 (4)3.2 加速度分析 (5)4导杆机构的动态静力分析 (8)4.1 运动副反作用力分析 (8)4.2 曲柄平衡力矩分析 (10)总结 (11)致谢 (12)参考文献 (13)1设计任务一、课程设计的性质、目的和任务机械原理课程设计是高等工业学校机械类专业学生第一次较全面的机械运动学和动力学分析与设计的训练,是本课程的一个重要教学环节。
其意义和目的在于:以机械系统运动方案设计为结合点,把机械原理课程设计的各章理论和方法融会贯通起来,进一步巩固和加深学生所学的理论知识;培养学生独立解决有关本课程实际问题的能力,使学生对于机械运动学和动力学的分析和设计有一个较完整的概念,具备计算、制图和使用技术资料的能力。
二、课程设计教学的内容和要求将一个班级进行分组,每组10人左右,一组选择一个备选方案进行如下分析工作:课程设计内容:牛头刨床导杆机构的运动分析、动态静力分析;(1)绘制机构运动简图;(2)速度分析、加速度分析;(1张1号图纸)(3)机构动态静力分析;(4)绘制运动线图。
牛头刨床机构简图课程设计1.1设计数据导杆机构的运动分析设计内容符号n2 LO2O4 LO2A Lo4B LBC Lo4s4 xS6 yS6单位r/min mm方60 380 110 540 0.25Lo4B 0.5 Lo4B 240 50案I1.2曲柄位置的确定曲柄位置图的作法为:取1和8’为工作行程起点和终点所对应的曲柄位置,1’和7’为切削起点和终点所对应的曲柄位置,其余2、3…12等,是由位置1起,顺ω2方向将曲柄圆作12等分的位置(如下图)。
图1-2取第I方案的第1位置和第7’位置(如下图1-3)。
图1-3n2=60 r/min;Lo2o4=38mm;LO2A=110mm;LO4B=540 mm;LBC=0.25LO4;LO4S4=0.5LO4B;1.3速度分析以速度比例尺:(0.001m/s)/mm和加速度比例尺:(0.01m/s2)/mm用相对运动的图解法作该两个位置的速度多边形和加速度多边形如下图1-4,1-5机械简图如图(1)由题知ω2=2πn2/60rad/sυA3=υA2=ω2·l O2A=0.69115m/s1:作速度分析,取比例尺0.001/vm smmμ=,由于构件3与4组成移动副,有υA4=υA3+υA4A3大小 ? √ ?方向⊥O4A⊥O2A∥O4B计算结果1-4作速度多边形如图1-4所示,得υA4=0 , ω4=υA4/ l O4A=0 , υB4=0又有υC6=υB5+υC6B5大小 ? √ ?方向∥XX⊥O4B⊥BC得υC6=0,υC6B5=0 υA4=0ω4=0υB4=0υA4A3=02:作加速度分析,取比例尺20.01(/)m smmαμ=,由(2)有a A4=a A4n+a A4t= a A3n +a A4A3k +a A4A3r大小? 0?√0?方向?B→A⊥O4B A→O2⊥O4B(向右)∥O4B(沿导路)取加速度极点为P'. 作加速度多边形图1-5图1-5则由图1─5知a A4t=a A3n=4.34263 m/s2a B5 =a B4 = a A4×l O4B/l O4A= 6.44714m/s2取1构件的研究对象,列加速度矢量方程,得a C6= a B5+ a C6B5n+ a C6B5τ大小 ?√ 0 ?方向∥xx √ C→B ⊥BC作加速度多边形,如图(5)所示,得a C6 = 6.0108 m/s2 方向向右。
机械原理课程设计说明书系部名称: 机电系专业班级: 04机制三班姓名:学号:目录Array概述 (3)设计项目·······························1.设计题目 (4)2.机构简介 (4)3.设计数据 (4)设计内容·······························1.导杆机构的设计 (5)2.凸轮机构的设计 (12)3.齿轮机构的设计 (17)设计体会 (20)参考文献 (21)附图·····························概述一、机构机械原理课程设计的目的:机械原理课程设计是高等工业学校机械类专业学生第一次较全面的机械运动学和动力学分析与设计的训练,是本课程的一个重要实践环节。
其基本目的在于:(1)进一步加深学生所学的理论知识,培养学生独立解决有关本课程实际问题的能力。
(2)使学生对于机械运动学和动力学的分析设计有一较完整的概念。
(3)使学生得到拟定运动方案的训练,并具有初步设计选型与组合以及确定传动方案的能力。
(4)通过课程设计,进一步提高学生运算、绘图、表达、运用计算机和查阅技术资料的能力。
二、机械原理课程设计的任务:机械原理课程设计的任务是对机械的主体机构(连杆机构、凸轮机构、齿轮机构以及其他机构)进行设计和运动分析、动态静力分析,并根据给定机器的工作要求,在此基础上设计凸轮、齿轮;或对各机构进行运动分析。
要求学生根据设计任务,绘制必要的图纸,编写说明书。
三、械原理课程设计的方法:机械原理课程设计的方法大致可分为图解法和解析法两种。
图解法几何概念较清晰、直观;解析法精度较高。
根据教学大纲的要求,本设计主要应用图解法进行设计。
[设计名称]牛头刨床一.机构简介:机构简图如下所示:牛头刨床机构简图牛头刨床是一种用于平面切削加工的机床,如上图所示。
电动机经皮带和齿轮传动,带动曲柄2和固结在其上的凸轮8。
刨床工作时,由导杆机构1-2-3-4-5-6带动刨头6和刨刀7作往复运动。
刨头右行时,刨刀进行切削,称工作行程,此时要求速度较低并且均匀,以减少电动机容量和提高切削质量;刨头左行时,刨刀不切削,称空回行程,此时要求速度较高,以提高生产效率。
因此,刨床采用具有急回特性的导杆机构。
刨刀每切削完成一次,利用空回行程的时间,凸轮8通过四杆机构1-9-10-11与棘轮带动螺旋机构(图中未画),使工作台连同工件作一次进给运动,以便刨刀继续切削。
二.设计数据:第一节 导杆机构的运动分析㈠导杆机构设计要求概述:已知曲柄每分钟的转数2n ,各构件尺寸,且刨头导路x x-位于导杆端头B 所作圆弧的平分线上。
要求作机构的运动简图,并作机构一个位置的速度、加速度多边形以及刨头的运动线图,画在 2号图纸上。
10位置的机构简图:㈡计算过程:由已知数据n2=60r/min得ω2=2π×60/60(rad/s)= 2πrad/s .1、求C点的速度:⑴确定构件3上A点的速度:构件2与构件3用转动副A相联,所以υA3=υA2。
又υA2=ω2l O2A =0.110×2π=0.22πm/s=0.69m/s. ⑵求4AV的速度:选取速度比例尺:μv=0.023(m/s)/mm;υA4 = υA3 + υA4A3 方向:⊥BO4 ⊥AO2 ∥BO4大小:?ω2l O2A?用图解法求解如图1:图1式中υA3、υA4表示构件3和构件4上 A 点的绝对速度,υA4A3表示构件4上A 点相对于构件3上A 点的速度,其方向平行于线段BO 4,大小未知;构件4上A 点的速度方向垂直于线段BO 4,大小未知。
在图上任取一点P ,作υA3 的方向线p a3 ,方向垂直于AO 2,指向与ω2的方向一致,长度等于υA3/μv ,(其中μv 为速度比例尺)。
过点p 作直线垂直于⊥BO 4 代表υA4的方向线,再过a 3作直线平行于线段BO 4 代表υA4A3的方向线这两条直线的交点为a 4,则矢量p a 4和a 3a 4分别代υA4和υA4A3 。
由速度多边形43a pa 得:υA4=μv ´ p a 4=μv ´ 20 = 0.483 m/sυA4A3=μv ´ a 3a 4=μv ´ 19 = 0.437 m/s ⑶ 求BO 4的角速度4ω:曲柄位于起点1时位置图如设计指导书图(1):此时42O AO ∠为: 又由1位置起将曲柄圆周作12等分则当曲柄转到10位置时,如图(1): ∠ο83.1617.7327036042=︒ ︒ ︒=O AO 杆BO 4的角速度4ω:4ω=V A4/l BO 4= 0.4830.277rad/s =1.75 rad/s杆BO 4的速度V 4:V 4=4ω× l BO 4=1.75*1.54m/s =0.9431m/s⑷ 求C 点的速度υc :υc = υB + υCB方向: ∥X-X ⊥BO 4 ⊥BC 大小: ? ω4l O 4B ?图2速度图见图2:式中υc 、υB 表示点的绝对速度。
υCB 表示点C 相对点B 的相对速度其方向垂直于构件CB ,大小未知,点C 的速度方向平行于X-X ,大小未知,图上任取一点p 作代表υB 的矢量pb 其方向垂直于BO 4指向于2ω转向相反,长度等于v B V μ/(v μ为速度比例尺)。
过点p 作直线平行于X-X ,代表υc 的方向线,再点b 作直线垂直于BC 代表υCB 的方向线,这两方向线的交点为C 则矢量pc 和bc 便代表 υc 、υCB 。
则C 点的速度为:υc =μv ×pc =μv × 40 = 0.92 m/s υCB =μv ×cb=μv × 5 = 0.115 m/s 2、求C 点的加速度:⑴ 求a A2:因曲柄匀速转动:故选取加速度比例尺:μa =0.15(m/s 2)/mm ⑵ 求a A4:3434344A A A A K A A n A a a a a a γτ++=+方向: ⊥BO 4 B →O 4 A →O 2 ⊥BO 4 ∥BO 4 大小: ? 424AO l •ω √ 3442A A V •ω ?加速度见下图:∏式中44A n A a a 和τ是4A a 的切向和切法向加速度,34A A a γ是点A 4相对于A 3的相对加速度,由于构件3与构件4构成移动副,所以034=A A n a 则3434A A t A A r a a =其方向平行于相对移动方向,即平行于BO 4,大小未知,34A A K a 为哥氏加速度,它的大小为θωsin 234434A A A A K Va=,其中θ为相对速度34A A V 和牵连角速度4ω矢量之间的夹角,但是对于平面运动,4ω的矢量垂直于运动平面而34A A V 位于运动平面内,故ο90=θ,从而344342A A A A K V a ω=哥氏加速度34A A Ka的方向是将34A A v 沿4ω的转动方向转ο90(即图中'3k a 的方向)。
在上面的矢量方程中只有344A A rA a a 和τ的大小未知,故可用图解法求解。
如右图,从任意极点π连续作矢量'‘4'3aa ππ和代表43A nA a a 和;再过'3a 作''3k a 垂直于线段BO 4 ,大小mm u V w k a a A A 2.10/2'344'3==;然后再过'k 作BO 4的平行线,代表34A A aγ的方向,过'‘4a 作垂直于BO 4,的直线,代表4A na 的方向线,它们相交点'4a 则矢量‘4a ℵ代表4A a 。
4A a =μa ‘4a ℵ=μa * 60.6 = 9.09 2/s m⑶ 求B 点加速度B a : 构件4的角加速度βBO4为:2444/29.3'44s rad l a u l a AO a AO A BO ===ℵ"2244/654.1s m l a BO n B =⊕=⊃ ⑷ 求C 点的加速度:nC B C B B n B n c a a a a a a c+++=+τττ方向: \ ∥x-x B →O 4 ⊥BO 4 ⊥CB C →B大小: \ ? Ú l BO 4βBO4 ? 0.090m/s 2 加速度图见下图:式中,nCB a 表示点C 相对点B 的法向加速度其方向为从C 指B ;τCB a 表示点C 相对点B 的切向加速度,其方向垂直于CB 。
又因速度多边形已作出,所以上式法向加速度可求出(C 点作水平运动,故C 点的法向加速度为0)。
仅有ττCBa a c 和的大小未知,同样可以用图解法求解。
如右图,在图上任取一点π作''b π代表nB a ,方向为平行于BO 4并从B 指向O 4,长度为a BO l μω/424,(其中a μ为加速度比例尺)。
过''b 作'''b b 代表τB a ,方向垂直于BO 4,长度为a BO BO l μβ/44,连接'b π,它表示B a ,再过过'b 作'''c b 代表nCB a ,方向平行CB并从C 指向B ,长度为a cB Bc l V μ/)/(2过''c 作垂直于CB 代表τc B a 的方向线又从π作平行于X-X 的方向线,两线交点为'c ,则矢量'c π便代表ca 。
c a =⊗ca =μa´ 'c P = 1.98 2/s m3、此时C 点位置如下图: 选取长度比例尺为:mm mm l /5=μ则:此时C 点的位移c x 为:第二节 凸轮机构的设计 ㈠ 凸轮机构的设计要求概述:⒈已知摆杆9作等加速等减速运动,要求确定凸轮机构的基本尺寸,选取滚子半径,将凸轮实际轮廓画在2号图纸上。