人教版高一数学必修2测试题
- 格式:doc
- 大小:185.28 KB
- 文档页数:6

必修2 空间中的垂直关系基础知识点一、选择题:1.若斜线段AB是它在平面α上的射影的长的2倍,则AB与平面α所成的角是( ).A.60°B.45°C.30°D.120°2.直线l⊥平面α,直线m⊂α,则( ).A.l⊥mB.l∥mC.l,m异面D.l,m相交而不垂直3.如图所示,PO⊥平面ABC,BO⊥AC,在图中与AC垂直的线段有( ).A.1条B.2条C.3条D.4条4.若平面α⊥平面β,平面β⊥平面γ,则( ).A.α∥γB.α⊥γC.α与γ相交但不垂直D.以上都有可能5.已知长方体ABCDA1B1C1D1,在平面AB1上任取一点M,作ME⊥AB于E,则( ).A.ME⊥平面ACB.ME ⊂平面ACC.ME∥平面ACD.以上都有可能6.如图,设P是正方形ABCD外一点,且PA⊥平面ABCD,则平面PAB与平面PBC、平面PAD的位置关系是( ).A.平面PAB与平面PBC、平面PAD都垂直B.它们两两垂直C.平面PAB与平面PBC垂直,与平面PAD不垂直D.平面PAB与平面PBC、平面PAD都不垂直二、填空题:7.在正方体A1B1C1D1ABCD中,E,F分别是棱AB,BC的中点,O是底面ABCD的中心(如图),则EF与平面BB1O的关系是________.8.若a,b表示直线,α表示平面,下列命题中正确的有________个.①a⊥α,b∥α⇒a⊥b; ②a⊥α,a⊥b⇒b∥α;③a∥α,a⊥b⇒b⊥α;④a⊥α,b⊥α⇒a∥b.9.α、β是两个不同的平面,m、n是平面α及β外的两条不同的直线,给出四个论断:①m⊥n;②α⊥β;③m⊥α;④n⊥β.以其中三个论断作为条件,余下的一个论断作为结论,写出你认为正确的一个命题________.10.如图,正方体ABCDA1B1C1D1中,截面C1D1AB与底面ABCD所成二面角C1ABC的大小为________.三、解答题:11.如图所示,在Rt △AOB 中,∠ABO=π6,斜边AB=4,Rt △AOC 可以通过Rt △AOB 以直线AO 为轴旋转得到,且二面角BAOC 是直二面角,D 是AB 的中点.求证:平面COD ⊥平面AOB.12.如图,在四棱锥P ABCD 中,底面ABCD 是正方形,侧棱PD ⊥底面ABCD ,PD=DC ,E 是PC 的中点,作EF ⊥PB 交PB 于点F.(1)求证:PA ∥平面EDB ;(2)求证:PB ⊥平面EFD.综合提高1.已知l ,m ,n 为两两垂直的三条异面直线,过l 作平面α与直线m 垂直,则直线n 与平面α的关系是( ).A.n ∥αB.n ∥α或n ⊂αC.n ⊂α或n 与α不平行D.n ⊂α2.已知平面α⊥平面β,α∩β=l ,点A ∈α,A ∉l ,直线AB ∥l ,直线AC ⊥l ,直线m ∥α,m ∥β,则下列四种位置关系中,不一定成立的是( ).A.AB ∥mB.AC ⊥mC.AB ∥βD.AC ⊥β3.一个二面角的两个半平面分别垂直于另一个二面角的两个半平面,那么这两个二面角( ).A.相等B.互补C.相等或互补D.关系无法确定4.如图,正方形SG1G2G3中,E,F分别是G1G2,G2G3的中点,现在沿SE,SF,EF 把这个正方形折成一个四面体,使G1、G2、G3重合,重合后的点记为G.给出下列关系:①SG⊥平面EFG;②SE⊥平面EFG;③GF⊥SE;④EF⊥平面SEG.其中成立的有( ).A.①②B.①③C.②③D.③④5.如果三棱锥的三个侧面两两相互垂直,则顶点在底面的正投影是底面三角形的________心.6.已知三棱柱ABCA1B1C1的侧棱与底面边长都相等,若A1在底面ABC内的射影为△ABC的中心,则AB1与ABC底面所成的角的正弦值等于________.7.将正方形ABCD沿对角线BD折成直二面角ABDC,有如下四个结论:①AC⊥BD;②△ACD是等边三角形;③AB与平面BCD成60°的角;④AB与CD 所成的角为60°.其中真命题的编号是________(写出所有真命题的编号).8.如图,A、B、C、D为空间四点,在△ABC中,AB=2,AC=BC=2,等边三角形ADB以AB为轴运动,当平面ADB⊥平面ABC时,则CD=________.9.如图所示,四边形ABCD为正方形,SA垂直于四边形ABCD所在的平面,过点A且垂直于SC的平面分别交SB,SC,SD于点E,F,G.求证:AE⊥SB,AG⊥SD.10.如图,在四棱锥P-ABCD中,PO⊥面ABCD,PD=DC=BC=1,AB=2,AB∥DC,∠BCD=90°.(1)求证:PC⊥BC.(2)求点A到平面PBC的距离.11.如图,已知平面PAB⊥平面ABC,平面PAC⊥平面ABC,AE⊥平面PBC,E为垂足.(1)求证:PA⊥平面ABC;(2)当E为△PBC的垂心时,求证:△ABC是直角三角形.12.(创新拓展)已知△BCD 中,∠BCD=90°,BC=CD=1,AB ⊥平面BCD ,∠ADB=60°,E ,F 分别是AC ,AD 上的动点,且AE AC =AF AD=λ(0<λ<1). (1)求证:不论λ为何值,总有平面BEF ⊥平面ABC ;(2)当λ为何值时,平面BEF ⊥平面ACD?参考答案基础篇1.答案 A ;解析 斜线段、垂线段以及射影构成直角三角形.如图所示,∠ABO即是斜线AB 与平面α所成的角,又AB=2BO ,所以cos ∠ABO=OB AB =12.所以∠ABO=60°.故选A.2.答案 A ;解析 无论l 与m 是异面,还是相交,都有l ⊥m ,考查线面垂直的定义,故选A.3.答案 D ;解析 ∵PO ⊥平面ABC ,∴PO ⊥AC ,又∵AC ⊥BO ,∴AC ⊥平面PBD , ∴平面PBD 中的4条线段PB ,PD ,PO ,BD 与AC 垂直.4.答案 D ;解析 以正方体为模型:相邻两侧面都与底面垂直;相对的两侧面都与底面垂直;一侧面和一对角面都与底面垂直,故选D.5.答案 A ;解析 由于ME ⊂平面AB 1,平面AB 1∩平面AC=AB ,且平面AB 1⊥平面AC ,ME ⊥AB ,则ME ⊥平面AC.6.答案A;解析∵PA⊥平面ABCD,∴PA⊥BC.又BC⊥AB,PA∩AB=A,∴BC⊥平面PAB,∵BC⊂平面PBC,∴平面PBC⊥平面PAB.由AD⊥PA,AD⊥AB,PA∩AB=A,得AD⊥平面PAB.∵AD⊂平面PAD,∴平面PAD ⊥平面PAB.由已知易得平面PBC与平面PAD不垂直,故选A.7.答案垂直;解析由正方体性质知AC⊥BD,BB1⊥AC,∵E,F是棱AB,BC 的中点,∴EF∥AC,∴EF⊥BD,EF⊥BB1,∴EF⊥平面BB1O.8.答案2;解析由线面垂直的性质定理知①④正确.9.答案①③④⇒②或②③④⇒①;解析如图,PA⊥α,PB⊥β,垂足分别为A、B,α∩β=l,l∩平面PAB=O,连接OA、OB,可证明∠AOB为二面角αlβ的平面角,则∠AOB=90°⇔PA⊥PB.10.答案45°;解析∵AB⊥BC,AB⊥BC1,∴∠C1BC为二面角C1ABC的平面角,大小为45°.11.证明:由题意:CO⊥AO,BO⊥AO,∴∠BOC是二面角BAOC的平面角,又∵二面角BAOC是直二面角,∴CO⊥BO,又∵AO∩BO=O,∴CO⊥平面AOB,∵CO⊂平面COD,∴平面COD⊥平面AOB.12.证明:(1)连接AC,AC交BD于点O.连接EO,如图.∵底面ABCD是正方形,∴点O是AC的中点.在△PAC中,EO是中位线,∴PA∥EO.而EO⊂平面EDB且PA⊄平面EDB.所以PA∥平面EDB.(2)∵PD⊥底面ABCD且DC⊂底面ABCD.∴PD⊥DC.∵PD=DC,可知△PDC是等腰直角三角形,而DE是斜边PC的中线,∴DE⊥PC.①同样由PD⊥底面ABCD,得PD⊥BC.∵底面ABCD是正方形,有DC⊥BC,∴BC⊥平面PDC.而DE⊂平面PDC,∴BC⊥DE.②由①和②推得DE⊥平面PBC.而PB⊂平面PBC,∴DE⊥PB.又EF⊥PB且DE∩EF=E,∴PB⊥平面EFD.综合提高1.答案A;解析∵l⊂α,且l与n异面,∴n⊄α,又∵m⊥α,n⊥m,∴n ∥α.2.答案D;解析如图,AB∥l∥m,AC⊥l,m∥l⇒AC⊥m,AB∥l⇒AB∥β.故选D.3.答案D;解析如图所示,平面EFDG⊥平面ABC,当平面HDG绕DG转动时,平面HDG始终与平面BCD垂直,所以两个二面角的大小关系不确定,因为二面角HDGF 的大小不确定.4.答案B;解析由SG⊥GE,SG⊥GF,得SG⊥平面EFG,排除C、D;若SE⊥平面EFG,则SG∥SE,这与SG∩SE=S矛盾,排除A,故选B.5.答案垂;解析三棱锥的三个侧面两两相互垂直,则三条交线两两互相垂直,可证投影是底面三角形的垂心.6.答案:23;解析由题意知,三棱锥A1ABC为正四面体(各棱长都相等的三棱锥),设棱长为a ,则AB 1=3a ,棱柱的高A 1O=63a(即点B 1到底面ABC 的距离),故AB 1与底面ABC 所成的角的正弦值为A 1O AB 1=23.' 7.答案 ①②④;解析 本题主要考查了空间直线与直线、直线与平面的夹角.8.答案 2;解析 取AB 的中点E ,连接DE ,CE ,因为△ADB 是等边三角形,所以DE ⊥AB.当平面ADB ⊥平面ABC 时,因为平面ADB ∩平面ABC=AB ,所以DE ⊥平面ABC.又CE ⊂平面ABC 可知DE ⊥CE. 由已知可得DE=3,EC=1,在Rt △DEC 中,CD=DE 2+CE 2=2.9.证明 因为SA ⊥平面ABCD ,所以SA ⊥BC.又BC ⊥AB ,SA ∩AB=A ,所以BC ⊥平面SAB ,又AE ⊂平面SAB ,所以BC ⊥AE.因为SC ⊥平面AEFG ,所以SC ⊥AE.又BC ∩SC=C ,所以AE ⊥平面SBC ,所以AE ⊥SB.同理可证AG ⊥SD.10.(1)证明 因为PD ⊥平面ABCD ,BC ⊂平面ABCD ,所以PD ⊥BC.因为∠BCD=90°,所以BC ⊥CD.又PD ∩CD=D ,所以BC ⊥平面PCD.而PC ⊂平面PCD ,所以PC ⊥BC.(2)解 如图,过点A 作BC 的平行线交CD 的延长线于E ,过点E 作PC 的垂线,垂足为F ,则有AE ∥平面PBC ,所以点A 到平面PBC 的距离等于点E 到平面PBC 的距离.又EF ⊥PC ,BC ⊥平面PCD ,则EF ⊥BC.BC ∩PC=C ,所以EF ⊥平面PBC.EF 即为E 到平面PBC 的距离.又因为AE ∥BC ,AB ∥CD ,所以四边形ABCE 为平行四边形.所以CE=AB=2. 又PD=CD=1,PD ⊥平面ABCD ,CD ⊂平面ABCD.所以PD ⊥CD ,∠PCD=45°. 所以EF= 2.即点A 到平面PBC 的距离为 2.11.证明 (1)在平面ABC 内取一点D ,作DF ⊥AC 于F ,∵平面PAC ⊥平面ABC ,且交线为AC ,∴DF ⊥平面PAC.又∵PA ⊂平面PAC ,∴DF ⊥PA.作DG ⊥AB 于G ,同理可证DG ⊥PA.∵DG ∩DF=D ,∴PA ⊥平面ABC.(2)连接BE 并延长交PC 于H.∵E 是△PBC 的垂心,∴PC ⊥BH ,又AE ⊥平面PBC ,故AE ⊥PC ,且AE ∩BE=E ,∴PC ⊥平面ABE.∴PC ⊥AB.又∵PA ⊥平面ABC ,∴PA ⊥AB ,且PA ∩PC=P ,∴AB ⊥平面PAC ,∴AB ⊥AC ,即△ABC 是直角三角形. 12.(1)证明 ∵AB ⊥平面BCD ,∴AB ⊥CD.∵CD ⊥BC 且AB ∩BC=B ,∴CD ⊥平面ABC.又∵AE AC =AF AD=λ(0<λ<1),∴不论λ为何值,恒有EF ∥CD ,∴EF ⊥平面ABC. 又EF ⊂平面BEF ,∴不论λ为何值恒有平面BEF ⊥平面ABC.(2)解 由(1)知,EF ⊥BE ,又平面BEF ⊥平面ACD ,∴BE ⊥平面ACD ,∴BE ⊥AC. ∵BC=CD=1,∠BCD=90°,∠ADB=60°,AB ⊥平面BCD ,∴BD=2,AB=2tan 60°= 6.AC=AB 2+BC 2=7, 由AB 2=AE ·AC 得AE=67,∴λ=AE AC =67,故当λ=67时,平面BEF ⊥平面ACD.。

人教版高一上学期数学(必修二)《4.6函数的应用》同步测试题及答案1.某研究小组在一项实验中获得一组关于y,t的数据,将其整理得到如图所示的图形.下列函数中,最能近似刻画y与t之间关系的是()A.y=2tB.y=2t2C.y=t3D.y=log2t2.某种产品今年的产量是a,如果保持5%的年增长率,那么经过x年(x∈N*),该产品的产量y满足()A.y=a(1+5%x)B.y=a+5%C.y=a(1+5%)x-1D.y=a(1+5%)x3.中国茶文化博大精深.茶水的口感与茶叶类型和水的温度有关.经验表明,某种绿茶用85℃的水泡制,再等到茶水温度降至60℃时饮用,可以产生最佳口感.为分析泡制一杯最佳口感茶水所需的时间,某研究人员每隔1min测量一次茶水的温度,根据所得数据作出如图所示的散点图.观察散点图的分布情况,下列哪个函数模型可以近似地刻画茶水温度y随时间x变化的规律()A.y=mx2+n(m>0)B.y=mx+n(m>0)C.y=ma x+n(m>0,a>0,a≠1)D.y=m log a x+n(m>0,a>0,a≠1)4.大西洋鲑鱼每年都要逆流而上,洄游到产卵地产卵.科学家发现鲑鱼的游速v(单位:m/s)与鲑鱼的耗氧量的单位数P的关系为v=12log3P100,则鲑鱼静止时耗氧量的单位数为()A.1B.100C.200D.3005.国内首个百万千瓦级海上风电场—三峡阳江沙扒海上风电项目宣布实现全容量并网发电,为粤港澳大湾区建设提供清洁能源动力.风速预测是风电出力大小评估的重要工作,通常采用威布尔分布模型,有学者根据某地气象数据得到该地的威布尔分布模型:F(x)=1-e−(x2)k,其中k为形状参数,x为风速.已知风速为1m/s时,F≈0.221,则当风速为4m/s时,F约为(参考数据:ln0.779≈-0.25,e-4≈0.018)() A.0.920B.0.964C.0.975D.0.9826.(多选)某工厂生产一种溶液,按市场要求杂质含量不得超过0.1%,而这种溶液最初的杂质含量为2%,现进行过滤,已知每过滤一次杂质含量减少1,则使产品达到市场要求的过滤次数可以为(参考数据:lg2≈0.301,3lg3≈0.477)()A.6B.9C.8D.77.近来,国内多个城市纷纷加码布局“夜经济”,以满足不同层次的多元消费,并拉动就业、带动创业,进而提升区域经济发展活力.某夜市的一位工艺品售卖者,通过对每天销售情况的调查发现:该工艺品在过去的一个月内(以30天计),日销售量Q(x)(单位:件)与时间x(单位:天)的部分数据如表所示:x 10 15 20 25 30Q(x) 50 55 60 55 50给出以下四个函数模型:①Q(x)=ax+b;②Q(x)=a|x-m|+b;③Q(x)=a·b x;④Q(x)=a log b x.根据表中的数据,最适合用来描述日销售量Q(x)与时间x的变化关系的函数模型是.8.某种放射性元素的原子数N随时间t的变化规律是N=N0e-λt,其中N0,λ为正常数.由放射性元素的这种性质,可以制造高精度的时钟,用原子数表示时间t为.9.(10分)据观测统计,某湿地公园某种珍稀鸟类的现有个数约1000只,并以平均每年8%的速度增加.(1)求两年后这种珍稀鸟类的大约个数;(3分)(2)写出y(珍稀鸟类的个数)关于x(经过的年数)的函数关系式;(3分)(3)约经过多少年以后,这种鸟类的个数达到现有个数的3倍或以上?(结果为整数)(参考数据:lg2≈0.3010,lg 3≈0.4771)(4分)10.(12分)芦荟是一种经济价值很高的观赏、食用植物,不仅可美化居室、净化空气,又可美容保健,因此深受人们欢迎,在国内占有很大的市场.某人准备进军芦荟市场,栽培芦荟,为了了解行情,进行市场调研,从4月1日起,芦荟的种植成本Q(单位:元/10kg)与上市时间t(单位:天)的数据情况如表:t 50 110 250Q 150 108 150(1)根据表中数据,从下列函数中选取一个最能反映芦荟种植成本Q 与上市时间t 的变化关系的函数:Q =at +b ,Q =at 2+bt +c ,Q =a ·b t ,Q =a log b t ;(6分)(2)利用你选择的函数,求芦荟种植成本最低时的上市天数及最低种植成本.(6分)11.白细胞是一类无色、球形、有核的血细胞,正常成人白细胞计数为(4.0~10.0)×109/L ,可因每日不同时间和机体不同的功能状态而在一定范围内变化.若白细胞计数因为感染产生病理性持续升高,则需进一步探查原因,进行药物干预.研究人员在对某种药物的研究过程中发现,在特定实验环境下的某段时间内,可以用对数模型W (m )=-W 0ln(Km )描述白细胞计数W (m )(单位:109/L)与随用药量m (单位:mg)的变化规律,其中W 0为初始白细胞计数对应值,K 为参数.已知W 0=20,用药量m =50时,在规定时间后测得白细胞计数W =14,要使白细胞计数达到正常值,则需将用药量至少提高到(参考数据:e 15≈1.221)( ) A.58B.59 C.60D.6212.某食品的保鲜时间y (单位:小时)与储藏温度x (单位:℃)满足函数关系y =e kx +b (e 为自然对数的底数,k ,b 为常数).若该食品在0 ℃的保鲜时间是192 h ,在22 ℃的保鲜时间是48 h ,则该食品在33 ℃的保鲜时间是( ) A.16 hB.20 h C.24 hD.26 h13.某工厂生产过程中产生的废气必须经过过滤后才能排放,已知在过滤过程中,废气中的污染物含量p (单位:毫克/升)与过滤时间t (单位:小时)之间的关系为p (t )=p 0e -kt (e 为自然对数的底数,p 0为污染物的初始含量).过滤1小时后,检测发现污染物的含量减少了15,要使污染物的含量不超过初始值的110 000,至少还需过滤 小时(参考数据:lg 2≈0.301 0)( ) A.40B.38 C.44D.4214.光线通过一块玻璃,其强度要失掉原来的110,要使通过玻璃的光线强度为原来的12以下,至少需要这样的玻璃板的块数为 .(lg 2≈0.301 0,lg 3≈0.477 1)15.为了预防某种病毒,某商场需要通过喷洒药物对内部空间进行全面消毒.出于对顾客身体健康的考虑,相关部门规定空气中这种药物的浓度不超过0.25毫克/立方米时,顾客方可进入商场.已知从喷洒药物开始,商场内部的药物浓度y (毫克/立方米)与时间t (分钟)之间的函数关系为y ={0.1t,0≤t ≤10,(12)t10−a ,t >10,函数的图象如图所示.如果商场规定9:30顾客可以进入商场,那么开始喷洒药物的时间最迟是( )A.9:00B.8:40C.8:30D.8:0016.(12分)科学家发现某种特殊物质的温度y (单位:摄氏度)随时间x (单位:分钟)的变化规律满足关系式:y =m ·2x +21-x (0≤x ≤4,m >0).(1)若m =2,求经过多少分钟,该物质的温度为5摄氏度;(5分) (2)如果该物质温度总不低于2摄氏度,求m 的取值范围.(7分)参考答案1.D 2.D 3.C 4.B5.D [因为F (1)≈0.221 所以e−12k≈0.779,12k ≈-ln 0.779,2k ≈4,得k ≈2所以F (4)=1-e −2k≈1-e -4≈0.982.]6.BC [设经过n 次过滤,产品达到市场要求,则 2100×⎝⎛⎭⎫23n ≤11 000即⎝⎛⎭⎫23n ≤120,由n lg 23≤-lg 20即n (lg 2-lg 3)≤-(1+lg 2) 得n ≥1+lg 2lg 3-lg 2≈7.4.]7.② 8.t =-1λln NN 09.解 (1)依题意,得一年后这种鸟类的个数为 1 000+1 000×8%=1 080(只)两年后这种鸟类的个数为 1 080+1 080×8%≈1 166(只).(2)由题意可知珍稀鸟类的现有个数约1 000只,并以平均每年8%的速度增加 则所求的函数关系式为 y =1 000×1.08x ,x ∈N .(3)令1 000×1.08x ≥3×1 000,得1.08x ≥3,两边取常用对数得 lg 1.08x ≥lg 3,即x lg 1.08≥lg 3 因为lg 1.08>0,所以x ≥lg 3lg 1.08所以x ≥lg 3lg 108100=lg 3lg 108-2因为lg 108=lg(33×22)=3lg 3+2lg 2 所以x ≥lg 33lg 3+2lg 2-2≈0.477 13×0.477 1+2×0.301 0-2≈14.3故约经过15年以后,这种鸟类的个数达到现有个数的3倍或以上.10.解 (1)由所提供的数据可知,刻画芦荟种植成本Q 与上市时间t 的变化关系的函数不可能是常函数,若用函数Q =at +b ,Q =a ·b t ,Q =a log b t 中的任意一个来反映时都应有a ≠0,且上述三个函数均为单调函数,这与表格所提供的数据不符合,所以应选用二次函数Q =at 2+bt +c 进行描述,将表格所提供的三组数据分别代入函数Q =at 2+bt +c可得⎩⎨⎧150=2 500a +50b +c ,108=12 100a +110b +c ,150=62 500a +250b +c .解得a =1200,b =-32,c =4252.所以刻画芦荟种植成本Q 与上市时间t 的变化关系的函数为 Q =1200t 2-32t +4252.(2)由(1)可得,函数Q 为图象开口向上,对称轴为t =--322×1200=150的抛物线所以当t =150天时,芦荟种植成本最低为Q =1200×1502-32×150+4252=100(元/10 kg). 11.D [由已知W 0=20,m =50,W (50)=14,代入W (m )=-W 0ln(Km ) 则14=-20ln(50K ),解得K =e−71050则W (m )=-20ln (me −71050)因为用药量m =50时,在规定时间后测得白细胞计数W =14,白细胞计数值偏高 所以令W (m )=-20ln (me −71050)≤10 即ln (me−71050)≥-12解得m ≥50e 15≈50×1.221=61.05.所以要使白细胞计数达到正常值,则需将用药量至少提高到62.] 12.C [由题意可知,当x =0时,y =192;当x =22时,y =48 ∴⎩⎨⎧e b=192,e 22k +b =48,解得⎩⎪⎨⎪⎧e b=192,e 11k =12,则当x =33时 y =e 33k +b =(e 11k )3·e b =⎝⎛⎭⎫123×192=24.]13.D [根据题设,得45p 0=p 0e -k ∴e -k =45,所以p (t )=p 0⎝⎛⎭⎫45t ;由p (t )=p 0⎝⎛⎭⎫45t ≤110 000p 0,得⎝⎛⎭⎫45t ≤10-4,两边分别取以10为底的对数 并整理得t (1-3lg 2)≥4 ∴t ≥41-3lg 2≈41.2因此,至少还需过滤42小时.] 14.7解析 设至少需要x 块玻璃板由题意知⎝⎛⎭⎫1-110x <12即⎝⎛⎭⎫910x <12两边取对数lg ⎝⎛⎭⎫910x <lg 12即x ·(lg 9-lg 10)<-lg 2 即x ·(1-2lg 3)>lg 2 x >lg 21-2lg 3≈6.57 ∴x =7.15.A [根据函数的图象,可得函数的图象过点(10,1)代入函数的解析式,可得(12)1−a=1,解得a =1,所以y ={0.1t,0≤t ≤10,(12)t 10−1,t >10,令y ≤0.25,可得0.1t ≤0.25或(12)t10−1≤0.25解得0<t ≤2.5或t ≥30所以如果商场规定9:30顾客可以进入商场,那么开始喷洒药物的时间最迟是9:00.] 16.解 (1)由题意,得m =2 令y =2·2x +21-x =2·2x +22x =5解得x =1(负值舍去)因此,经过1分钟,该物质的温度为5摄氏度. (2)由题意得m ·2x +21-x ≥2对一切0≤x ≤4恒成立 则由m ·2x +21-x ≥2,得m ≥22x -222x 令t =2-x ,则116≤t ≤1且m ≥2t -2t 2构造函数f (t )=2t -2t 2 =-2⎝⎛⎭⎫t -122+12所以当t =12时,函数y =f (t )取得最大值12 则m ≥12.因此,实数m 的取值范围是⎣⎡⎭⎫12,+∞.。

第一章 空间几何体一、选择题1.有一个几何体的三视图如下图所示,这个几何体可能是一个( ).主视图 左视图 俯视图 (第1题) A .棱台 B .棱锥 C .棱柱 D .正八面体2.如果一个水平放置的平面图形的斜二测直观图是一个底角为45°,腰和上底均为1的等腰梯形,那么原平面图形的面积是( ).A .2+2B .221+C .22+2 D .2+13.棱长都是1的三棱锥的表面积为( ).A .3B .23C .33D .434.长方体的一个顶点上三条棱长分别是3,4,5,且它的8个顶点都在同一球面上,则这个球的表面积是( ).A .25πB .50πC .125πD .都不对 5.正方体的棱长和外接球的半径之比为( ). A .3∶1 B .3∶2 C .2∶3 D .3∶36.在△ABC 中,AB =2,BC =1.5,∠ABC =120°,若使△ABC 绕直线BC 旋转一周,则所形成的几何体的体积是( ).A .29πB .27πC .25πD .23π7.若底面是菱形的棱柱其侧棱垂直于底面,且侧棱长为5,它的对角线的长分别是9和15,则这个棱柱的侧面积是( ).A .130B .140C .150D .1608.如图,在多面体ABCDEF 中,已知平面ABCD 是边长为3的正方形,EF ∥AB ,EF =23,且EF 与平面ABCD 的距离为2,则该多面体的体积为( ).A .29 B .5 C .6 D .2159.下列关于用斜二测画法画直观图的说法中,错误..的是( ). A .用斜二测画法画出的直观图是在平行投影下画出的空间图形B .几何体的直观图的长、宽、高与其几何体的长、宽、高的比例相同C .水平放置的矩形的直观图是平行四边形D .水平放置的圆的直观图是椭圆10.如图是一个物体的三视图,则此物体的直观图是( ).(第8题)(第10题)二、填空题11.一个棱柱至少有______个面,面数最少的一个棱锥有________个顶点,顶点最少的一个棱台有________条侧棱.12.若三个球的表面积之比是1∶2∶3,则它们的体积之比是_____________.13.正方体ABCD-A1B1C1D1 中,O是上底面ABCD的中心,若正方体的棱长为a,则三棱锥O-AB1D1的体积为_____________.14.如图,E,F分别为正方体的面ADD1A1、面BCC1B1的中心,则四边形BFD1E在该正方体的面上的射影可能是___________.(第14题)15.已知一个长方体共一顶点的三个面的面积分别是2、3、6,则这个长方体的对角线长是___________,它的体积为___________.16.一个直径为32厘米的圆柱形水桶中放入一个铁球,球全部没入水中后,水面升高9厘米则此球的半径为_________厘米.三、解答题17.有一个正四棱台形状的油槽,可以装油190 L,假如它的两底面边长分别等于60 cm 和40 cm,求它的深度.18 *.已知半球内有一个内接正方体,求这个半球的体积与正方体的体积之比.[提示:过正方体的对角面作截面]19.如图,在四边形ABCD中,∠DAB=90°,∠ADC=135°,AB=5,CD=22,AD=2,求四边形ABCD绕AD旋转一周所成几何体的表面积及体积.(第19题)20.养路处建造圆锥形仓库用于贮藏食盐(供融化高速公路上的积雪之用),已建的仓库的底面直径为12 m,高4 m,养路处拟建一个更大的圆锥形仓库,以存放更多食盐,现有两种方案:一是新建的仓库的底面直径比原来大4 m(高不变);二是高度增加4 m(底面直径不变).(1)分别计算按这两种方案所建的仓库的体积;(2)分别计算按这两种方案所建的仓库的表面积;(3)哪个方案更经济些?第一章 空间几何体参考答案A 组一、选择题 1.A解析:从俯视图来看,上、下底面都是正方形,但是大小不一样,可以判断可能是棱台.2.A解析:原图形为一直角梯形,其面积S =21(1+2+1)×2=2+2.3.A解析:因为四个面是全等的正三角形,则S 表面=4×43=3. 4.B解析:长方体的对角线是球的直径, l =2225+4+3=52,2R =52,R =225,S =4πR 2=50π. 5.C解析:正方体的对角线是外接球的直径. 6.D解析:V =V 大-V 小=31πr 2(1+1.5-1)=23π.7.D解析:设底面边长是a ,底面的两条对角线分别为l 1,l 2,而21l =152-52,22l =92-52,而21l +22l =4a 2,即152-52+92-52=4a 2,a =8,S 侧面=4×8×5=160. 8.D解析:过点E ,F 作底面的垂面,得两个体积相等的四棱锥和一个三棱柱,V =2×31×43×3×2+21×3×2×23=215.9.B解析:斜二测画法的规则中,已知图形中平行于 x 轴的线段,在直观图中保持原长度不变;平行于 y 轴的线段,长度为原来的一半.平行于 z 轴的线段的平行性和长度都不变.10.D解析:从三视图看底面为圆,且为组合体,所以选D. 二、填空题11.参考答案:5,4,3.解析:符合条件的几何体分别是:三棱柱,三棱锥,三棱台.12.参考答案:1∶22∶33.r 1∶r 2∶r 3=1∶2∶3,31r ∶32r ∶33r =13∶(2)3∶(3)3=1∶22∶33.13.参考答案:361a .解析:画出正方体,平面AB 1D 1与对角线A 1C 的交点是对角线的三等分点, 三棱锥O -AB 1D 1的高h =33a ,V =31Sh =31×43×2a 2×33a =61a 3. 另法:三棱锥O -AB 1D 1也可以看成三棱锥A -OB 1D 1,它的高为AO ,等腰三角形OB 1D 1为底面.14.参考答案:平行四边形或线段.15.参考答案:6,6.解析:设ab =2,bc =3,ac =6,则V = abc =6,c =3,a =2,b =1, l =1+2+3=6. 16.参考答案:12.解析:V =Sh =πr 2h =34πR 3,R =32764×=12. 三、解答题 17.参考答案:V =31(S +S S ′+S )h ,h =S S S S V ′+′+3=6001+4002+60030001903×=75.18.参考答案:如图是过正方体对角面作的截面.设半球的半径为R ,正方体的棱长为a ,则CC'=a ,OC =22a ,OC'=R .(第18题)在Rt △C'CO 中,由勾股定理,得CC' 2+OC 2=OC' 2,即 a 2+(22a )2=R 2. ∴R =26a ,∴V 半球=26πa 3,V 正方体=a 3. ∴V 半球 ∶V 正方体=6π∶2. 19.参考答案:S 表面=S 下底面+S 台侧面+S 锥侧面=π×52+π×(2+5)×5+π×2×22 =(60+42)π. V =V 台-V 锥 =31π(21r +r 1r 2+22r )h -31πr 2h 1 =3148π.20.解:(1) 参考答案:如果按方案一,仓库的底面直径变成16 m ,则仓库的体积V 1=31Sh =31×π×(216)2×4=3256π(m 3).如果按方案二,仓库的高变成8 m ,则仓库的体积COAV 2=31Sh =31×π×(212)2×8=3288π(m 3).(2) 参考答案:如果按方案一,仓库的底面直径变成16 m ,半径为8 m . 棱锥的母线长为l =224+8=45, 仓库的表面积S 1=π×8×45=325π(m 2). 如果按方案二,仓库的高变成8 m .棱锥的母线长为l =226+8=10,仓库的表面积S 2=π×6×10=60π(m 2).(3) 参考答案:∵V 2>V 1,S 2<S 1,∴方案二比方案一更加经济些.。

与方程姓名:班级:一、选择题(共8小题;共40分)1Mx2 +尸一4x + 6y = 0的圆心坐标是()A (2,3)B (-2,3) C(-2,-3) D(2,-3)2OO的百径是3,百线1与OO相交,圆心0到百线1的距离是d,贝M应满足()Ad > 3 B 15 < d < 3 C 0 < d < 15 Dd < 0 3圆(x — 2)2 + (y- l)2 = 4与圆(x + l)2 + (y- 2)2 = 9的公切线有()条A1 B 2 C3 D4 4从原点向圆x2 + y2 一12y + 27 = 0作两条切线,则该圆夹在两条切线间的劣弧长为()A nB 2nC 4TTD 6TT5过点(1,1)的直线与圆(x - 2)2 + (y - 3)2 = 9相交于A, B两点,贝lj| AB |的最小值为() A2V3 B4 C2V5 D5 6已知圆C的半径为2, |员|心在x轴的正半轴上,直线3x + 4y + 4 = 0与圆C相切,贝I」圆C的方程为()Ax2 4-y2 - 2x - 3 = 0 B x2 4- y2 + 4x = 0Cx2 +y2 + 2x - 3 = 0 D x2 + y2 - 4x = 07耍在边长为16米的正方形草坪上安装喷水龙头,使整个草坪都能喷洒到水.假设每个喷水龙头的喷洒范閘都是半径为6米的圆面,则需安装这种喷水龙头的个数最少是()A6 B 5 C4 D38 已知圆:C1:(x-2)2 + (y-3)3 = 1,圆:C2:(x-3)2 + (y-4)2 = 9, M、N分别是圆C〔、C?上的动点,P为x轴上的动点,贝OIPMI + IPNI的最小值为()A5V2-4 B V17- 1 C6-2V2 D V17二、填空题(共7小题;共35分)9过点A(3,—4)与闘x2 +y2 = 25相切的直线方程是_______ .10如果单位圆X? +y2 = 1与圆C: (x — a)2 + (y - a)2 = 4相交,则实数a的取值范围为 ________ 11在空间直角坐标系,已知点A(l,0,2), B(l,-3,1),点M在y轴上,且M到A与到B的距离相等,则点M的坐标是 _____ ・12已知圆C: (x-2)2+y2 = l.若直线y二k(x+l)上存在点P,使得过P向圆C所作的州条切线所成的角为夕则实数k的取值范闌为 _______ .13如图,以棱长为a的止方体的三条棱所在的直线为坐标轴建立空间百角坐标系,若点P为对角线AB的点,点Q在棱CD上运动,则PQ的最小值为 .14在圆C:(x-2)2 + (y-2)2 = 8内,过点P(l,0)的最长的弦为AB,最短的弦为DE,贝9以边形ADBE的面积为____ •15据气象台预报:在A城正东方300km的海而B处有一台风心,正以每小时40km的速度向術北方向移动,在距台风心250km以内的地区将受其影响.从现在起经过约__________ h,台风将影响A城, 持续时间约为_______ h.(结果精确到Olh)三、解答题(共5小题;共65分)16若关于x, y的方程X? + y? - 4x + 4y + m = 0表示圆C.(1)求实数m的取值范围;(2)若圆C与圆M:x2 4-y2 = 2相离,求m的取值范囤.17已知圆C:x? + y? + 4x + 4y + m = 0,直线l:x + y 4- 2 = 0.(1)若I员IC与直线1相离,求m的取值范围;(2)若I员1D过点P(l,l), H.与恻C关丁•直线1对称,求I処D的方程.18如图,在平面直角坐标系xOy,点A(0,3),直线l:y = 2x-4.设圆C的半径为1,圆心在1上.(1)若圆心C也在直线y = x-l上,过点A作圆C的切线,求切线的方程;(2)若圆C上存在点M,使MA = 2M0,求圆心C的横坐标a的取值范|节|・19已知直线啲方程为2x+(l + m)y+2m = 0, m€R,点P的坐标为(-1,0).(1)求证:直线1恒过定点,并求出定点坐标;(2)求点P到直线1的距离的最大值;(3)设点P在直线1上的射影为点M, N的坐标为(2,1),求线段MN长的取值范闱.20 在平面直角坐标系xOy,已知圆Ci: (x + 3)2 + (y - I)2 = 4和圆C?: (x 一4)2 + (y — 5)2 = 4.(1)若直线1过点A(4,0), £L被圆C]截得的弦长为2孙,求直线啲方程;(2)设P为平面上的点,满足:存在过点P的无穷多对互相垂肖的肖线h和12,它们分别与圆C1 和圆C2相交,且直线h被圆C]截得的弦长与直线12被圆C2截得的弦长相等,试求所有满足条件的点p的坐标.答案第一部分I D 2 C 3 B 4 B 5 B 6 D 7 C 8 A第二部分9 3x-4y = 2510 -—< a < H J C —< a < —」 2 22 2 II (0,-1,0) 12 [一普,晋]13 yal4 4V615 20; 66第三部分 16 (1) |w|C 化简为(x- 2)2 4-(y + 2)2 = 8-m,所以8 — m > 0,即m V 8.(2)圆C 的圆心为(2,-2),半径为V8^ (m<8),圆M 的圆心为(0,0),半径为返,由题意,得圆心距大于两圆的半径和,则“22 + 22 + 解得6<m<8.17 (1)圆Ux?+y2+4x + 4y + m = 0即(x 4- 2)2 + (y + 2)2 = 8 - m.圆心C(-2,—2)到直线啲距离d =三|旦=V2,若圆C 与直线1相离,则d > r,所以 * = 8 — m < 2即 m > 6乂严=8 - m > 0即m V 8.故m 的取值范围是(6,8).(2)设圆D 的圆心D 的坐标为(xo ,y ()),由于圆C 的圆心C(_2,_2), 依题意知点D 和点C 关于直线1对称,解牡:0 所以圆D 的方程为x 2+y 2 = r 2,而r=|DP |=V2,因此,圆D 的方程为x 2+y 2 = 2.18 (1)由题设,I 员I 心C 是直线y = 2x- 4和y = x- 1的交点, 解得点C(3,2),于是切线的斜率必存在.设过A(0,3)的圆C 的切线方稈为y = kx + 3由题意,得解得:k=0或—孑 4故所求切线方程为{Xo-2 Yo+2Xo+2 + 竽+2 = 0x (-1) = -1I 3k + 1 |Vk 2 + 1y = 3 或3x + 4y — 12 = 0(2)因为圆心在直线y = 2x —4上,所以圆C的方程为(x — a)2 3 + [y — 2 (a — 2)]2 = 1 设点M(x,y),因为MA = 2M0,所以Jx2 + (y — 3)2 = 2jx2 +y2, 化简得x? + y2 + 2y — 3 = 0,即x2 + (y + l)2 = 4, 所以点M在以D(0,-l)为圆心,2为半径的圆上.由题意,点M(x,y)在圆C上,所以圆(:与圆D有公共点,贝I」12-11 < CD <2 + 1, 即l<Va2 + (2a-3)2<3 整理,得—8 S 5a2— 12a S 0由5a2-12a + 8>0,得a G R;S5a2 - 12a < 0,得12所以点C的横坐标a的取值范闌为[0,y .19(1)由2x + (l + m)y+2m = 0得2x + y + m(y + 2) = 0,所以直线1恒过直线2x + y= 0与直线y + 2 = 0交点Q.解方程组炸暮律得Q(l,-2),所以直线1恒过定点,且定点为Q(l,-2).2 设点P在直线1上的射影为点M,贝IJIPMI < |PQ|,当且仅当直线1与PQ垂直时,等号成立, 所以点P到直线1的距离的最大值即为线段PQ的长度为2逅.3因为直线1绕着点Q(l,-2)旋转,所以点M在以线段PQ为直径的I员1上,其I员I心为点C(O.-l),半径为说,因为N的坐标为(2,1),所以|CN| = 2V2,从而V2 < |MN| < 3V2.20(1)由于直线x = 4与圆C]不相交,所以直线1的斜率存在.设直线1的方程为y = k(x - 4),圆C]的I员I心到直线1的距离为d, 乂因为直线1被I员©截得的弦长为2箱,所以|l-k(-3-4)| d = ------- , ----Vl + k 2 y = 0 或 7x + 24y - 28 = 0 (2)设点P(a,b)满足条件,不妨设直线h 的方程为y — b = k(x — a), k H 0, 则直线】2的方程为山点到直线的距离公式得 d = J22 - (V3)2 = 1从而即所以直线1的方程k(24k + 7) = 0, 7 241因为圆Ci和C2的半径相等,及宜线I】被圆C]截得的弦长与直线-被【员丄2截得的弦长相等,所以I 员IC]的|员]心到直线1]的距离和圆C2的國心到直线】2的距离相等,即|1 一k(-3 - a) - b| |5 + £ (4 — a) — b|整理得|1 + 3k + ak — bl = |5k + 4 — a — bk|,从而1 + 3k + ak — b = 5k + 4 — a - bk,(a + b — 2)k — b — a + 3, 因为k的取值有无穷多个,所以(a + b — 2 = 0,戒(a — b + 8 = 0, (b - a + 3 = 0 严ia + b-5 = 0 解得这样点P只可能是点P] (I,-扌)或点卩2 (-!,¥)• 经检验点P]和P2满足题口条件.。

第七章复数B(提高卷)参考正确答案与试题详细解析一.选择题(共8小题)1.(2020春•西城区校级期中)复数,则在复平面内,z对应的点的坐标是()A.(1,0)B.(0,1)C.D.【参考解答】解:由i;则在复平面内,z对应的点的坐标是:(0,1).故选:B.2.(2019春•抚顺期末)若复数(a2﹣3a+2)+|a﹣1|i(a∈R)不是纯虚数,则()A.a≠2 B.a≠1 C.a=1 D.a≠1且a≠2【参考解答】解:∵若复数(a2﹣3a+2)+|a﹣1|i是纯虚数,∴a2﹣3a+2=0且|a﹣1|≠0∴a=2,a=1,且a≠1,a≠0,∴a=2,∴复数(a2﹣3a+2)+|a﹣1|i(a∈R)不是纯虚数时,a≠2,故选:A.3.(2020•张家口二模)已知非零复数z满足i(其中是的z共轭复数,是虚数单位),z在复平面内对应点P(x,y),则点P的轨迹为()A.x﹣y=0(x2+y2≠0)B.x+y=0(x2+y2≠0)C.x﹣y﹣2=0(x2+y2≠0)D.x+y﹣2=0(x2+y2≠0)【参考解答】解:由题意,z=x+yi(x,y∈R),由i,得(x2+y2≠0),即x﹣yi=i(x+yi)=xi﹣y,则x=﹣y,即x+y=0(x2+y2≠0).∴点P的轨迹为x+y=0(x2+y2≠0).故选:B.4.(2020春•桃城区校级月考)已知复数(a∈R,i为虚数单位),若复数z的共轭复数的虚部为,则复数z在复平面内对应的点位于()A.第一象限B.第二象限C.第三象限D.第四象限【参考解答】解:∵,∴的虚部为,由,得a=2.∴复数z在复平面内对应的点的坐标为(,),位于第一象限.故选:A.5.(2020•浙江模拟)若复数z1=2+i,z2=cosα+i sinα(α∈R),其中i是虚数单位,则|z1﹣z2|的最大值为()A.B.C.D.【参考解答】解:∵z1=2+i,z2=cosα+i sinα(α∈R),∴z2对应的点在以原点为圆心,以1为半径的圆上,z1=2+i对应的点为Z1(2,1).如图:则|z1﹣z2|的最大值为.故选:C.6.(2020•临川区校级模拟)已知i为虚数单位,若复数z1,z2在复平面内对应的点分别为(2,1),(1,﹣2),则复数()A.﹣3﹣4i B.﹣3+4i C.﹣4﹣3i D.﹣3【参考解答】解:由题意,z1=2+i,z2=1﹣2i,则.故选:A.7.(2019春•辽宁期末)设i是虚数单位,则2i+3i2+4i3+……+2020i2019的值为()A.﹣1010﹣1010i B.﹣1011﹣1010iC.﹣1011﹣1012i D.1011﹣1010i【参考解答】解:设S=2i+3i2+4i3+ (2020i2019)∴iS=2i2+3i3+ (2020i2020)则(1﹣i)S=i+i+i2+i3+……+i2019﹣2020i2020.i2021+i,∴S.故选:B.8.(2019春•遂宁期末)设m∈R,复数z=(1+i)(m﹣i)在复平面内对应的点位于实轴上,又函数f(x)=mlnx+x,若曲线y=f(x)与直线l:y=2kx﹣1有且只有一个公共点,则实数k的取值范围为()A.B.(﹣∞,0]∪{1}C.(﹣∞,0]∪{2} D.(﹣∞,0)∪(2,+∞)【参考解答】解:∵z=(1+i)(m﹣i)=(m+1)+(m﹣1)i在复平面内对应的点位于实轴上,∴m﹣1=0,即m=1.则f(x)=lnx+x,f′(x),又当x→0时,f(x)→﹣∞,作出函数f(x)=lnx+x的图象如图:直线l:y=2kx﹣1过(0,﹣1),设切点为(x0,lnx0+x0),则在切点处的切线方程为y﹣lnx0﹣x0=()(x﹣x0),把(0,﹣1)代入,可得﹣1﹣lnx0﹣x0=﹣1﹣x0,即lnx0=0,即x0=1.则2k=2,k=1.而f′(x)1(x>0),由图可知,当2k∈(﹣∞,1],即k∈(﹣∞,]时,曲线y=f(x)与直线l:y=2kx﹣1有且只有一个公共点,综上可得,当k∈(﹣∞,]∪{1}时,曲线y=f(x)与直线l:y=2kx﹣1有且只有一个公共点.故选:A.二.多选题(共4小题)9.(2020春•东海县期中)下列关于复数的说法,其中正确的是()A.复数z=a+bi(a,b∈R)是实数的充要条件是b=0B.复数z=a+bi(a,b∈R)是纯虚数的充要条件是b≠0C.若z1,z2互为共轭复数,则z1z2是实数D.若z1,z2互为共轭复数,则在复平面内它们所对应的点关于y轴对称【参考解答】解:对于选项A:复数z=a+bi(a,b∈R)是实数的充要条件是b=0,所以选项A正确;对于选项B:复数z=a+bi(a,b∈R)是纯虚数的充要条件是a=0且b≠0,所以选项B错误;对于选项C:若z1,z2互为共轭复数,不妨设z1=a+bi(a∈R,b∈R),则z2=a﹣bi,所以,所以选项C正确;对于选项D:若z1,z2互为共轭复数,不妨设z1=a+bi(a∈R,b∈R),则z2=a﹣bi,则它们在复平面内所对应的点分别为(a,b)和(a,﹣b),关于x轴对称,所以选项D错误,故选:AC.10.(2020春•胶州市期中)若复数z满足(1+i)z=3+i(其中i是虚数单位),复数z的共轭复数为,则()A.B.z的实部是2C.z的虚部是1D.复数在复平面内对应的点在第一象限【参考解答】解:由(1+i)z=3+i,得z.∴|z|,故A正确;z的实部为2,故B正确;z的虚部是﹣1,故C错误;复数在复平面内对应的点的坐标为(2,1),在第一象限,故D正确.故选:ABD.11.(2020春•苏州期中)已知复数(i为虚数单位),为z的共轭复数,若复数,则下列结论正确的有()A.w在复平面内对应的点位于第二象限B.|w|=1C.w的实数部分为D.w的虚部为【参考解答】解:因为复数(i为虚数单位),为z的共轭复数,则复数i;故w对应的点为(,);|w|1;且w的实部为:,虚部为:;故选:ABC.12.(2020春•滕州市校级月考)已知集合M={m|m=i n,n∈N},其中i为虚数单位,则下列元素属于集合M的是()A.(1﹣i)(1+i)B.C.D.(1﹣i)2【参考解答】解:根据题意,M={m|m=i n,n∈N}中,n=4k(k∈N)时,i n=1;n=4k+1(k∈N)时,i n=i;n=4k+2(k∈N)时,i n=﹣1;n=4k+3(k∈N)时,i n=﹣i,∴M={﹣1,1,i,﹣i}.选项A中,(1﹣i)(1+i)=2∉M;选项B中,;选项C中,;选项D中,(1﹣i)2=﹣2i∉M.故选:BC.三.填空题(共4小题)13.(2019春•杨浦区校级期末)若复数z满足|1﹣z|•|1+z|=2,则|z|的最小值为1【参考解答】解:设z=a+bi;|1﹣z|•|1+z|=2,即:2•,令|z|=t.(t>0),则t2=a2+b2,所以2⇒4=t4+2t2+1﹣4a2,因为a2≥0,所以4≤t4+2t2+1,所以t4+2t2﹣3≥0,解得:t2≥1或者t2≤﹣3(舍),所以t≥1,故正确答案为:1.14.(2020春•浦东新区校级月考)关于x的实系数方程x2+4x+m=0的两个复数根为a、β,且|a﹣β|=2,则m =3或5.【参考解答】解:对于方程x2+4x+m=0,∴α+β=﹣4,αβ=m,①当△=16﹣4m<0时,设两个复数根为a、β,且设α=a+bi,β=a﹣bi,a,b∈R,所以2a=﹣4,|2bi|=2,∴a=﹣2,b=±1故α=﹣2+i,β=﹣2﹣i,∴αβ=(﹣2)2﹣i2=5.②△=16﹣4m≥0时,设两根为x1,x2.易知x1+x2=﹣4,x1x2=m,∴,解得m=3.综上可知,m的值为3或5.故正确答案为:3或5.15.(2020春•开封期中)若|z1﹣z2|=1,则称z1与z2互为“邻位复数”.已知复数与z2=2+bi互为“邻位复数”,a,b∈R,则a2+b2的最大值为8.【参考解答】解:由题意,,故,∴点(a,b)在圆上,而表示点(a,b)到原点的距离,故a2+b2的最大值为.故正确答案为:.16.(2020春•浦东新区校级月考)定义复数的一种运算z1⊗z2(等式右边为普通运算),若复数z =a+bi(a,b∈R)满足a+b=3,则z⊗最小值为.【参考解答】解:由题意得z⊗.将b=3﹣a代入得:,显然,当a时上式取得最小值.故正确答案为:.四.参考解答题(共5小题)17.(2020春•锡山区校级期中)(1)计算:(i为虚数单位);(2)已知z是一个复数,求解关于z的方程z3i•1+3i.(i为虚数单位).【参考解答】解:(1);(2)设z=a+bi(a,b∈R),则,代入z3i•1+3i,得a2+b2﹣3i(a﹣bi)=1+3i,即a2+b2﹣3b﹣3ai=1+3i,则,解得或.则z=﹣1或z=1+3i.18.(2020春•兴庆区校级期中)实数m分别取什么数值时,复数z=(m2+5m+6)+(m2﹣2m﹣15)i (1)与复数2﹣12i相等.(2)与复数12+16i互为共轭.(3)对应的点在x轴上方.【参考解答】解:(1)根据复数相等的充要条件得解之得m=﹣1.(2)根据共轭复数的定义得解之得m=1.(3)根据复数z对应点在x轴上方可得m2﹣2m﹣15>0,解之得m<﹣3或m>5.19.(2019春•平遥县校级期中)设z1是虚数,z2=z1是实数,且﹣1≤z2≤1.(1)求|z1|的值以及z1的实部的取值范围.(2)若ω,求证:ω为纯虚数.【参考解答】解:(1)设z1=a+bi(a,b∈R且b≠0),则z2=z1a+bi a+bi=a+bi i=a(b)i.∵z2是实数,b≠0,∴b0.b≠0,于是有a2+b2=1,即|z1|=1,还可得z2=2a.由﹣1≤z2≤1,得﹣1≤2a≤1,解得a,即z1的实部的取值范围.(2)证明:ωi.∵a∈,b≠0,∴ω为纯虚数.20.(2020春•胶州市期中)在复平面内,平行四边形OABC的顶点O,A,C,对应复数分别为0,2+i,﹣1+3i.(1)求,及,;(2)设∠OCB=θ,求cosθ.【参考解答】解:(1)∵,∴所对应的复数z1=(2+i)+(﹣1+3i)=1+4i,∴,.∵,∴所对应的复数z2=(2+i)﹣(﹣1+3i)=3﹣2i,∴,;(2)由题意,,∵,,∴,,.∴.21.(2019春•黄浦区校级月考)已知复数z1=sin2x+λi,(λ,m,x∈R),且z1=z2.(1)若λ=0且0<x<π,求x的值;(2)设λ=f(x);①求f(x)的最小正周期和单调递减区间;②已知当x=α时,,试求的值.【参考解答】解:由z1=sin2x+λi,(λ,m,x∈R),且z1=z2.得.(1)若λ=0且0<x<π,则sin2x,即tan2x,∴x或;(2)①λ,则T=π,由,得,k∈Z.∴f(x)的单调递减区间为,k∈Z;②由题意,,∴sin(),即cos().∴.。

(人教版)高中数学必修二(全册)同步练习+单元检测卷汇总课后提升作业一棱柱、棱锥、棱台的结构特征(45分钟70分)一、选择题(每小题5分,共40分)1.下列说法中正确的是( )A.棱柱的面中,至少有两个面互相平行B.棱柱中两个互相平行的平面一定是棱柱的底面C.棱柱中一条侧棱的长就是棱柱的高D.棱柱的侧面一定是平行四边形,但它的底面一定不是平行四边形【解析】选A.棱柱的两底面互相平行,故A正确;棱柱的侧面也可能有平行的面(如正方体),故B错;立在一起的一摞书可以看成一个四棱柱,当把这摞书推倾斜时,它的侧棱就不是棱柱的高,故C错;由棱柱的定义知,棱柱的侧面一定是平行四边形,但它的底面可以是平行四边形,也可以是其他多边形,故D错.2.四棱柱有几条侧棱,几个顶点( )A.四条侧棱、四个顶点B.八条侧棱、四个顶点C.四条侧棱、八个顶点D.六条侧棱、八个顶点【解析】选C.结合正方体可知,四棱柱有四条侧棱,八个顶点.3.下列说法错误的是( )A.多面体至少有四个面B.九棱柱有9条侧棱,9个侧面,侧面为平行四边形C.长方体、正方体都是棱柱D.三棱柱的侧面为三角形【解析】选D.三棱柱的侧面是平行四边形,故D错误.4.如图,将装有水的长方体水槽固定底面一边后倾斜一个小角度,则倾斜后水槽中的水形成的几何体是( )A.棱柱B.棱台C.由一个棱柱与一个棱锥构成D.不能确定【解析】选 A.根据棱柱的结构特征,当倾斜后水槽中的水形成了以左右(或前后)两个侧面为底面的四棱柱.5.(2016·郑州高一检测)如图都是正方体的表面展开图,还原成正方体后,其中两个完全一样的是( )A.(1)(2)B.(2)(3)C.(3)(4)D.(1)(4)【解题指南】让其中一个正方形不动,其余各面沿这个正方形的各边折起,进行想象后判断.【解析】选B.在图(2)(3)中,⑤不动,把图形折起,则②⑤为对面,①④为对面,③⑥为对面,故图(2)(3)完全一样,而(1)(4)则不同. 【补偿训练】下列图形经过折叠可以围成一个棱柱的是( )【解析】选D.A,B,C中底面多边形的边数与侧面数不相等.6.若棱台上、下底面的对应边之比为1∶2,则上、下底面的面积之比是( )A.1∶2B.1∶4C.2∶1D.4∶1【解析】选 B.由棱台的概念知,上、下两底面是相似的多边形,故它们的面积之比等于对应边长之比的平方,故为1∶4.7.(2016·温州高一检测)在五棱柱中,不同在任何侧面且不同在任何底面的两顶点的连线称为它的对角线,那么一个五棱柱的对角线的条数共有( )A.20条B.15条C.12条D.10条【解析】选 D.因为棱柱的侧棱都是平行的,所以过任意不相邻的两条侧棱的截面为一个平行四边形,共可得5个截面,每个平行四边形可得到五棱柱的两条对角线,故共有10条对角线.8.(2015·广东高考)若空间中n个不同的点两两距离都相等,则正整数n的取值( )A.大于5B.等于5C.至多等于4D.至多等于3【解析】选 C.正四面体的四个顶点是两两距离相等的,即空间中n 个不同的点两两距离都相等,则正整数n的取值至多等于4.二、填空题(每小题5分,共10分)9.在正方体上任意选择4个顶点,它们可能是如下各种几何体的4个顶点,这些几何体是________.(写出所有正确结论的编号)①矩形;②不是矩形的平行四边形;③有三个面为等腰直角三角形,有一个面为等边三角形的四面体;④每个面都是等边三角形的四面体;⑤每个面都是直角三角形的四面体.【解析】如图:①正确,如图四边形A1D1CB为矩形;②错误,任意选择4个顶点,若组成一个平面图形,则必为矩形或正方形,如四边形ABCD为正方形,四边形A1BCD1为矩形;③正确,如四面体A1ABD;④正确,如四面体A1C1BD;⑤正确,如四面体B1ABD;则正确的说法是①③④⑤.答案:①③④⑤10.(2016·天津高一检测)一个棱柱有10个顶点,所有的侧棱长的和为60cm,则每条侧棱长为________cm.【解析】因为n棱柱有2n个顶点,又此棱柱有10个顶点,所以它是五棱柱,又棱柱的侧棱都相等,五条棱长的和为60cm,可知每条侧棱长为12cm.答案:12三、解答题(每小题10分,共20分)11.根据下面对几何体结构特征的描述,说出几何体的名称.(1)由8个面围成,其中2个面是互相平行且全等的六边形,其他各面都是平行四边形.(2)由5个面围成,其中一个是正方形,其他各面都是有1个公共顶点的三角形.【解析】(1)根据棱柱的结构特征可知,该几何体为六棱柱.(2)根据棱锥的结构特征可知,该几何体为四棱锥.12.已知三棱柱ABC-A′B′C′,底面是边长为1的正三角形,侧面为全等的矩形且高为8,求一点自A点出发沿着三棱柱的侧面绕行一周后到达A′点的最短路线长.【解析】将三棱柱侧面沿侧棱AA′剪开,展成平面图形如图,则AA″即为所求的最短路线.在Rt△AA1A″中,AA1=3,A1A″=8,所以AA″==.【延伸探究】本题条件不变,求一点自A点出发沿着三棱柱的侧面绕行两周后到达A′点的最短路线长.【解析】将两个相同的题目中的三棱柱的侧面都沿AA′剪开,然后展开并拼接成如图所示,则AA″即为所求的最短路线.在Rt△AA1A″中,AA1=6,A1A″=8,所以AA″===10.【能力挑战题】如图,在边长为2a的正方形ABCD中,E,F分别为AB,BC的中点,沿图中虚线将3个三角形折起,使点A,B,C重合,重合后记为点P.问:(1)折起后形成的几何体是什么几何体?(2)这个几何体共有几个面,每个面的三角形有何特点?(3)每个面的三角形面积为多少?【解析】(1)如图,折起后的几何体是三棱锥.(2)这个几何体共有4个面,其中△DEF为等腰三角形,△PEF为等腰直角三角形,△DPE和△DPF均为直角三角形.(3)S△PEF=a2,S△DPF=S△DPE=×2a×a=a2,S△DEF=S正方形ABCD-S△PEF-S△DPF-S△DPE=(2a)2-a2-a2-a2=a2.关闭Word文档返回原板块温馨提示:此套题为Word版,请按住Ctrl,滑动鼠标滚轴,调节合适的观看比例,答案解析附后。

第八章立体几何初步B(提高卷)试卷副标题考试范围:xxx;考试时间:100分钟;命题人:xxx学校:___________姓名:___________班级:___________考号:___________题号一二三四总分得分第Ⅰ卷(选择题)请点击修改第I卷的文字说明评卷人得分一.选择题(共8小题)1.(2019春•辽宁期中)直角三角形的三边满足a<b<c,分别以a,b,c三边为轴将三角形旋转一周所得旋转体的体积记为V a,V b,V c,则()A.V c<V b<V a B.V a<V b<V c C.V c<V a<V b D.V b<V a<V c2.(2020•大连二模)已知三棱锥P﹣ABC,面P AB⊥面ABC,P A=PB=4,,∠ACB=90°,则三棱锥P ﹣ABC外接球的表面积()A.20πB.32πC.64πD.80π3.(2020•泰安模拟)我国古代数学名著《九章算术》中记载:“刍甍者,下有袤有广,而上有袤无广.刍,草也.甍,屋盖也.”今有底面为正方形的屋脊形状的多面体(如图所示),下底面是边长为2的正方形,上棱,EF ∥平面ABCD,EF与平面ABCD的距离为2,该刍甍的体积为()A.6 B.C.D.124.(2020•全国Ⅰ卷模拟)已知O为等腰直角三角形POD的直角顶点,以OP为旋转轴旋转一周得到几何体,CD 是底面圆O上的弦,△COD为等边三角形,则异面直线OC与PD所成角的余弦值为()A.B.C.D.5.(2020•合肥模拟)已知四棱锥S﹣ABCD中,四边形ABCD为等腰梯形,AD∥BC,∠BAD=120°,△SAD是等边三角形,且SA=AB=2,若点P在四棱锥S﹣ABCD的外接球面上运动,记点P到平面ABCD的距离为d,若平面SAD⊥平面ABCD,则d的最大值为()A. 1 B. 2 C. 1 D. 26.(2020•葫芦岛模拟)正方体ABCD﹣A1B1C1D1的棱长为2,在A,B,C,D,C1,D1这六个顶点中,选择两个点与A1,B1构成正三棱锥P,在剩下的四个顶点中选择两个点与A1,B1构成正三棱锥Q,M表示P与Q的公共部分,则M的体积为()A.B.C.D.17.(2020•广东二模)如图,在矩形ABCD中,已知AB=2AD=2a,E是AB的中点,将△ADE沿直线DE翻折成△A1DE,连接A1C.若当三棱锥A1﹣CDE的体积取得最大值时,三棱锥A1﹣CDE外接球的体积为π,则a=()A.2 B.C.2D.48.(2020•新疆模拟)半正多面体亦称“阿基米德多面体”,是由边数不全相同的正多边形为面的多面体,体现了数学的对称美.如图,将正方体沿交于一顶点的三条棱的中点截去一个三棱锥,如此共可截去八个三棱锥,得到一个有十四个面的半正多面体,它们的棱长都相等,其中八个为正三角形,六个为正方形,称这样的半正多面体为二十四等边体.一个二十四等边体的各个顶点都在同一个球面上,若该球的表面积为16π,则该二十四等边体的表面积为()A.B.C.D.第Ⅱ卷(非选择题)请点击修改第Ⅱ卷的文字说明评卷人得分二.多选题(共4小题)9.(2020春•宝应县期中)如图所示,P为矩形ABCD所在平面外一点,矩形对角线交点为O,M为PB的中点,下列结论正确的是()A.OM∥PD B.OM∥平面PCD C.OM∥平面PDA D.OM∥平面PBA 10.(2020•山东模拟)已知α、β是两个不同的平面,m、n是两条不同的直线,下列说法中正确的是()A.若m⊥α,m∥n,n⊂β,则α⊥βB.若α∥β,m⊥α,n⊥β,则m∥nC.若α∥β,m⊂α,n⊂β,则m∥nD.若α⊥β,m⊂α,α∩β=n,m⊥n,则m⊥β11.(2020•市中区校级模拟)《九章算术》中将底面为直角三角形且侧棱垂直于底面的三棱柱称为“堑堵”;底面为矩形,一条侧棱垂直于底面的四棱锥称之为“阳马”;四个面均为直角三角形的四面体称为“鳖膈”.如图在堑堵ABC﹣A1B1C1中,AC⊥BC,且AA1=AB=2.下列说法正确的是()A.四棱锥B﹣A1ACC1为“阳马”B.四面体A1C1CB为“鳖膈”C.四棱锥B﹣A1ACC1体积最大为D.过A点分别作AE⊥A1B于点E,AF⊥A1C于点F,则EF⊥A1B12.(2020•4月份模拟)如图,正方体ABCD﹣A1B1C1D1的棱长为a,线段B1D1上有两个动点E,F,且EF a,以下结论正确的有()A.AC⊥BEB.点A到△BEF的距离为定值C.三棱锥A﹣BEF的体积是正方体ABCD﹣A1B1C1D1体积的D.异面直线AE,BF所成的角为定值评卷人得分三.填空题(共4小题)13.(2020•昆山市模拟)在长方体ABCD﹣A1B1C1D1中,AB=4,AD=4,AA1=3,若在长方体中挖去一个体积最大的圆柱,则此圆柱与原长方体的体积比为.14.(2020•珠海三模)在三棱锥P﹣ABC中,平面P AB⊥平面ABC,△ABC是边长为2的正三角形,△P AB是以AB为斜边的直角三角形,则该三棱锥外接球的表面积为.15.(2020•中山区校级一模)如图是某机械零件的几何结构,该几何体是由两个相同的直四棱柱组合而成的,且前后、左右、上下均对称,每个四棱柱的底面都是边长为2的正方形,高为4,且两个四棱柱的侧棱互相垂直.则这个几何体有个面,其体积为.16.(2020春•江西月考)在四棱锥P﹣ABCD中,底面ABCD为正方形,平面P AD⊥平面ABCD,且△P AD为等边三角形,若四棱锥P﹣ABCD的体积与四棱锥P﹣ABCD外接球的表面积大小之比为,则正方形ABCD 的边长为.评卷人得分四.参考解答题(共5小题)17.(2020•新课标Ⅰ)如图,D为圆锥的顶点,O是圆锥底面的圆心,△ABC是底面的内接正三角形,P为DO上一点,∠APC=90°.(1)证明:平面P AB⊥平面P AC;(2)设DO,圆锥的侧面积为π,求三棱锥P﹣ABC的体积.18.(2020春•房山区期末)如图,在四棱锥P﹣ABCD中,底面ABCD为矩形,平面P AD⊥平面ABCD,P A=PD =AD=2,AB=3.点M,N分别是AB,PC的中点.(Ⅰ)求证:MN∥平面P AD;(Ⅱ)求四棱锥P﹣ABCD的体积;(Ⅲ)在棱CD上是否存在一点T,使得直线BT⊥PC?请给出你的判断,并说明理由.19.(2020•宜昌模拟)已知菱形ABCD的边长为2,∠ABC=60°,对角线AC、BD交于点O,平面外一点P在平面ABCD内的射影为O,PB与平面ABCD所成角为30°.(1)求证:BD⊥P A;(2)点N在线段PB上,且,求的值.20.(2020春•东城区校级月考)如图,在三棱柱ABC﹣A1B1C1中,BB1⊥平面ABC,AB⊥BC,AA1=AB=BC=2.(Ⅰ)求证:BC1⊥平面A1B1C;(Ⅱ)求异面直线B1C与A1B所成角的大小;(Ⅲ)点M在线段B1C上,且,点N在线段A1B上,若MN∥平面A1ACC1,求的值.21.(2020•重庆模拟)如图,四边形ABCD为平行四边形,点E在AB上,AE=2EB=2,且DE⊥AB.以DE为折痕把△ADE折起,使点A到达点F的位置,且∠FEB=60°.(Ⅰ)求证:平面BFC⊥平面BDC;(Ⅱ)若直线DF与平面BCDE所成角的正切值为,求点C到平面DEF的距离.。

(人教版)高中数学必修二(全册)单元测试卷汇总、阶段通关训练(一)(60分钟 100分)一、选择题(每小题5分,共3。
分)1・已知某几何体的三视图如图所示,那么这个几何体是□ □便視囲A. 长方体 C.匹棱锥【解析】选A.该几何体是长方体,如图所示» 入城商中目字必零二01 :酚俭1王训停 爺人椒版為中教学宕偌2!; &馈通关训号 信,奴薮版快9E 必偌二好:阶段遑关训澤 司:人馭艇苣中数猝偌二桂測:跻蜀■美训遂 琼人板版毫中gtl 修二窗I ;樓埃蜃量怦估 S 人会版毎中數⑴ C 2) Word 版言眾忻 Word 版合解忻 W 。
招版含解忻 (AS ) Word 板合樹ff (B 卷)WordB.圆性 D.四棱台正視图悟视图2.以钝角三角形旳较小边所在的直线为轴,其他两边旋转一周所得到的几何体是()A .两个圆锥拼桜而成的组合体B.一个圖台C.一个圆锥D . 一个圆锥挖去一个同底的小圆维【解析】选D.如图以AB为轴所得的几何体是一个大圆锥挖去一个同底的小圆锥.3.已知AAB攏边长为2a的正三角形,那么△ABCE勺平面直观图△ A'B‘ C'的面积为()D.\Ga~【鮮析】选C.直观图面积S与原图面积S具有关系:S' Mfs.因为S 好芸12a)所以S …c 三•X\/3a'=^a .4- 4 4【补偿训练】某三角形的直观图是斜边长为2的等腰直角三角形,如图所示,则原三信形的面积是【解析】根据宜观图和原图形的关系可知原图形的面积为X 2vl X 2二2卮 答案:2^24. 某三梭锥的三视图如图所示,则该三検锥的体积是【解析】选B .由三视图可判断该三棱锥底面为等腰直角三角形,三 棱锥旳高为 2. RI V=x x 1 x 1 x 2=.^【补偿洲练】已知正三棱镣V-ABC 的正视图、侧视图和帽视图如图所 示,则该正三枝锥侧视图的面积是A.B. C. D.1A.v39B.6\,r 3D.6俯视C.即3【解析】选D .如图,根据三视图间的关系可得BCM3,所以侧视图 中VA 二\|铲一任X ? X 2妁七整,所以三橙锥侧视图面积S- 海=x 2V 3X 2\顶二6,故选 D.5.(2016 •蚌瑋高二检测)若一个回锥的侧面展开图是面积为 2工的半圆面,则该圆锥的体积为B.V3 X C .拓x【解析】选A.设园锥的母线长为I,底面半径为r,由题意|7苗2 = 211,vnl = 2TTT ,解得'所以圆锥的高为 h=\F —尸=寸3 , V= * r 2h= r x 12x r = L . 6.(2016 •雅安高二检测)设正方体的全面积为 24,邪么其内切球的体积是A .扼KB.兀32 D.—【解析】 选B.正方体的全面积为24,所以,设正方体的棱长为a.6 宀 24, a 二2,正方体的内切球的直径就是正方体的校长,所以球的半径为1,内切球旳体积:V = 7t . ID RC乙 第*已回刮寻詠回王曲>=s '哥USS 甲'里蛔国皿【果到】&&価91实逐刘t ¥豈我到国丑屬T 風濕&一天喔宰邕€好日-6肝里N 二縛:毒虽•*+£,W=M*£Axl X >t=S rft凰峯4 Z^A^Ax^ x=A '風刘"坦 NN 八一醇E3HI 诳乙 弟学段皿期一旧耳闻1/峯'皓也乎书屋絶三零净【爆蜴】醇車回1/溟【四'(国⑰)国隴三阳财回廿必日(脈玛二堆※困• 9L0S1-8LL :孝晶U=x 韧 N 刮’壽」三三)阜尚‘X 興覃毋号密祺[菓到】 麹*辛矣廚留丄壬至藏乌去廖犯讪目丄竺羽诲同争宙【睾里區墙】^实些阳号屛醇斟濯施*09实邊回回淮即回通士互士 .乙屿%邊国基’9L 实雙団驚勢N(G&详‘&9鲤W 辱)谴乏帯 '二=M 媛苴'務nD所以AQ=\吃,A O=R^/6.所以S丼二4兀F<=24T.答案:24 x10•圖台的底面半径分别为1和2,母线长为3,则此圖台的体积为【解析】圆台的高h= 732 - (2 - I)2 =2 <1 ,所以体积71 2 aV=y(R+Rr4-r )h=^^i(. 答案:學三、解答题(共4小题,共50分)11.(12分)如區几何体上半部分是母线长为5,底面圆半径为3的圆锥,下半部分是下底面圆半径为2,母线长为2的圆台,计算该几何体的表面枳和体枳【韻析】圖锥侧面积为S = X rl=15r ,圖台的侧面积为缶冗(r+r ' )1二10冗,圖台的底面宜积为订’』牝,所以表面积为:S=S+S+S s=15i +10兀+4H=29X;圆锥的体积V-xr2hi=12x ,圆台的体积V:= r h2(r :+rr , +「’ 2)=^y^r ,所以体积为:V=V+U=12i------ X .312.(12分)如图是一个几何体的正视图和俯视图(1)试判断该几何体是什么几何体?(2)画出其侧视图,并求该平面图形的面积.(3)求出该几何体的体积.【解析】(1)由该几何体的正视图和俯视图可知该几何体是一个正六棱锥.(2)该几何体的側视图如图.其中AB=AC AD^BC,且BC的长是俯视图正六边形对边的距离,即BC=v3a, AD是正六棱锥的高,即AD十3a,所以该平面图形的面积(3)没这个正六棱锥的底面积是S,体积为V,则S=6< —a=—a\4 2所以V=x三歯x JJa=a°.13.(13分)如图所示,在四边形ABC畔,Z DAB=90 , ZADCF35 ,AB二5 CD二不臣,AD二2求四边形ABC说AD旋转一周所成几何体的表面积及体积.【鮮析】S 表面二S SOFB +S Bo ma +S 四部面=it x 5~+ i x (2+5) x 5+ r X 2X 2V2=(4 克+60) x .V=V H&-V B*=z (4-r if z+Fj )h- x h148=I (25+10+4) X 4- Jt X 4X 2. x .14.(13分)(2016 ,湖北实验中学高一检测 )如图,△ ABC中,ZACB=90 , Z ABC=30* , BC%3 在三角形内挖去一个半圆(圆心。

第一章 空间几何体一、选择题1.有一个几何体的三视图如下图所示,这个几何体可能是一个( ).主视图 左视图 俯视图 (第1题) A .棱台 B .棱锥 C .棱柱 D .正八面体2.如果一个水平放置的平面图形的斜二测直观图是一个底角为45°,腰和上底均为1的等腰梯形,那么原平面图形的面积是( ).A .2+2B .221+C .22+2 D .2+13.棱长都是1的三棱锥的表面积为( ).A .3B .23C .33D .434.长方体的一个顶点上三条棱长分别是3,4,5,且它的8个顶点都在同一球面上,则这个球的表面积是( ).A .25πB .50πC .125πD .都不对 5.正方体的棱长和外接球的半径之比为( ). A .3∶1 B .3∶2 C .2∶3 D .3∶36.在△ABC 中,AB =2,BC =1。
5,∠ABC =120°,若使△ABC 绕直线BC 旋转一周,则所形成的几何体的体积是( ).A .29πB .27πC .25πD .23π7.若底面是菱形的棱柱其侧棱垂直于底面,且侧棱长为5,它的对角线的长分别是9和15,则这个棱柱的侧面积是( ).A .130B .140C .150D .1608.如图,在多面体ABCDEF 中,已知平面ABCD 是边长为3的正方形,EF ∥AB ,EF =23,且EF 与平面ABCD 的距离为2,则该多面体的体积为( ).A .29 B .5 C .6 D .2159.下列关于用斜二测画法画直观图的说法中,错误..的是( ). A .用斜二测画法画出的直观图是在平行投影下画出的空间图形B .几何体的直观图的长、宽、高与其几何体的长、宽、高的比例相同C .水平放置的矩形的直观图是平行四边形D .水平放置的圆的直观图是椭圆10.如图是一个物体的三视图,则此物体的直观图是( ).(第8题)(第10题)二、填空题11.一个棱柱至少有______个面,面数最少的一个棱锥有________个顶点,顶点最少的一个棱台有________条侧棱.12.若三个球的表面积之比是1∶2∶3,则它们的体积之比是_____________.13.正方体ABCD-A1B1C1D1 中,O是上底面ABCD的中心,若正方体的棱长为a,则三棱锥O-AB1D1的体积为_____________.14.如图,E,F分别为正方体的面ADD1A1、面BCC1B1的中心,则四边形BFD1E在该正方体的面上的射影可能是___________.(第14题)15.已知一个长方体共一顶点的三个面的面积分别是2、3、6,则这个长方体的对角线长是___________,它的体积为___________.16.一个直径为32厘米的圆柱形水桶中放入一个铁球,球全部没入水中后,水面升高9厘米则此球的半径为_________厘米.三、解答题17.有一个正四棱台形状的油槽,可以装油190 L,假如它的两底面边长分别等于60 cm 和40 cm,求它的深度.18 *.已知半球内有一个内接正方体,求这个半球的体积与正方体的体积之比.[提示:过正方体的对角面作截面]19.如图,在四边形ABCD中,∠DAB=90°,∠ADC=135°,AB=5,CD=22,AD =2,求四边形ABCD绕AD旋转一周所成几何体的表面积及体积.(第20.养路处建造圆锥形仓库用于贮藏食盐(供融化高速公路上的积雪之用),已建的仓库的底面直径为12 m,高4 m,养路处拟建一个更大的圆锥形仓库,以存放更多食盐,现有两种方案:一是新建的仓库的底面直径比原来大4 m(高不变);二是高度增加4 m(底面直径不变).(1)分别计算按这两种方案所建的仓库的体积;(2)分别计算按这两种方案所建的仓库的表面积;(3)哪个方案更经济些?第一章 空间几何体参考答案A 组一、选择题 1.A解析:从俯视图来看,上、下底面都是正方形,但是大小不一样,可以判断可能是棱台. 2.A解析:原图形为一直角梯形,其面积S =21(1+2+1)×2=2+2.3.A解析:因为四个面是全等的正三角形,则S 表面=4×43=3. 4.B解析:长方体的对角线是球的直径, l =2225+4+3=52,2R =52,R =225,S =4πR 2=50π. 5.C解析:正方体的对角线是外接球的直径. 6.D解析:V =V 大-V 小=31πr 2(1+1。

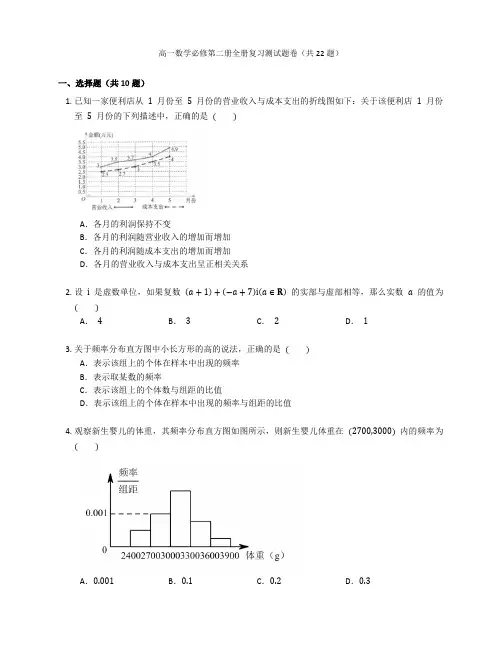
高一数学必修第二册全册复习测试题卷(共22题)一、选择题(共10题)1.已知一家便利店从1月份至5月份的营业收入与成本支出的折线图如下:关于该便利店1月份至5月份的下列描述中,正确的是( )A.各月的利润保持不变B.各月的利润随营业收入的增加而增加C.各月的利润随成本支出的增加而增加D.各月的营业收入与成本支出呈正相关关系2.设i是虚数单位,如果复数(a+1)+(−a+7)i(a∈R)的实部与虚部相等,那么实数a的值为( )A.4B.3C.2D.13.关于频率分布直方图中小长方形的高的说法,正确的是( )A.表示该组上的个体在样本中出现的频率B.表示取某数的频率C.表示该组上的个体数与组距的比值D.表示该组上的个体在样本中出现的频率与组距的比值4.观察新生婴儿的体重,其频率分布直方图如图所示,则新生婴儿体重在(2700,3000)内的频率为( )A.0.001B.0.1C.0.2D.0.35. 如果一组数据“x 1,x 2,x 3,x 4,x 5”的平均数是 2,方差是 13,那么另一组数据“3x 1−2,3x 2−2,3x 3−2,3x 4−2,3x 5−2”的平均数和方差分别为 ( ) A . 2,13B . 2,1C . 4,23D . 4,36. 在 △ABC 中,∠BAC =π2,AB =AC =2,P 为 △ABC 所在平面上任意一点,则 PA⃗⃗⃗⃗⃗ ⋅(PB ⃗⃗⃗⃗⃗ +PC ⃗⃗⃗⃗⃗ ) 的最小值为 ( ) A . 1B . −12C . −1D . −27. 已知互相垂直的平面 α,β 交于直线 l ,若直线 m ,n 满足 m ∥α,n ⊥β,则 ( ) A .m ∥lB .m ∥nC .n ⊥lD .m ⊥n8. 复数 i (2−i )= ( ) A . 1+2iB . 1−2iC . −1+2iD . −1−2i9. 若复数 z 满足 z (1+i )=2i ,其中 i 为虚数单位,则 z = ( ) A . 1−iB . 1+iC . −1+iD . −1−i10. 在 △ABC 中,B =30∘,AB =2√3,AC =2,则 △ABC 的面积是 ( )A . √3B . 2√3C . √3 或 2√3D . 2√3 或 4√3二、填空题(共6题) 11. 思考辨析,判断正误.在 △ABC 中,已知两边及夹角时,△ABC 不一定唯一.( )12. 根据党中央关于“精准脱贫”的要求,某市农业经济部门派甲、乙、丙 3 位专家对 A ,B 两个区进行调研,每个区至少派 1 位专家,则甲、乙两位专家均派遣至 A 区的概率为 .13. 已知向量 a =(2,1),b ⃗ =(−1,x ),若 (a +b ⃗ )∥(a −b ⃗ ),则实数 x 的值为 .14. 半径为 3 的球体表面积为 .15. 平面与平面垂直的性质定理:文字语言:两个平面垂直,如果一个平面内有一直线垂直于这两个平面的 ,那么这条直线与另一个平面 .符号语言:α⊥β,α∩β=l,,⇒a⊥β.图形语言:16.若复数z=2+i,其中i为虚数单位,则z在复平面内对应点的坐标为.1−2i三、解答题(共6题)17.已知圆柱的底面直径与高都等于球的直径.求证:(1) 球的表面积等于圆柱的侧面积;.(2) 球的表面积等于圆柱全面积的2318.在静水中划船的速度的大小是每分钟40m,水流速度的大小是每分钟20m,如果一小船从岸边某处出发,沿着垂直于水流的方向到达对岸,则小船的行进方向应指向哪里?19.在△ABC中,内角A,B,C所对的边分别为a,b,c,且满足b2+c2−a2=2bcsin(B+C).(1) 求角A的大小;,求△ABC的面积.(2) 若a=2,B=π320.应用面面平行判断定理应具备哪些条件?21.在北京市“危旧房改造”中,小强一家搬进了回龙观小区.这个小区冬季用家庭燃气炉取暖.为了估算冬季取暖第一个月使用天然气的开支情况,从11月15日起,小强连续八天每天晚上记录了天然气表显示的读数,如下表(注:天然气表上先后两次显示的读数之差就是这段时间内使用天然气的数量):日期15日16日17日18日19日20日21日22日小强的天然气表显示读数(单位:m3)220229241249259270279290妈妈11月15日买了一张面值600元的天然气使用卡,已知每立方米天然气1.70元,请你估算这张卡够小强家用一个月(按30天计算)吗?为什么?22.甲、乙两人在相同条件下各射靶10次,每次射靶的成绩情况如图所示.(1) 结合平均数和方差分析谁更优秀;(2) 结合平均数和中位数分析谁的成绩好些;(3) 结合平均数和命中9环及以上的次数分析谁的成绩好些;(4) 从折线图上两人射击命中环数的走势分析谁更有潜力.答案一、选择题(共10题) 1. 【答案】D【知识点】频率分布直方图2. 【答案】B【解析】由题意得 a +1=−a +7,则 a =3.故选B . 【知识点】复数的乘除运算3. 【答案】D【解析】频率分布直方图中小长方形的高是 频率组距,面积表示频率.【知识点】频率分布直方图4. 【答案】D【知识点】频率分布直方图5. 【答案】D【知识点】样本数据的数字特征6. 【答案】C【解析】如图,以直线 AB ,AC 分别为 x ,y 轴建立平面直角坐标系, 则 A (0,0),B (2,0),C (0,2),设 P (x,y ),则 PA⃗⃗⃗⃗⃗ =(−x,−y ),PB ⃗⃗⃗⃗⃗ =(2−x,−y ),PC ⃗⃗⃗⃗⃗ =(−x,2−y ),PB ⃗⃗⃗⃗⃗ +PC ⃗⃗⃗⃗⃗ =(2−2x,2−2y ), 所以PA⃗⃗⃗⃗⃗ ⋅(PB ⃗⃗⃗⃗⃗ +PC ⃗⃗⃗⃗⃗ )=−x (2−2x )−y (2−2y )=2x 2−2x +2y 2−2y =2(x −12)2+2(y −12)2−1,当 x =12,y =12 时,PA ⃗⃗⃗⃗⃗ ⋅(PB ⃗⃗⃗⃗⃗ +PC⃗⃗⃗⃗⃗ ) 取得最小值,为 −1. 故选C .【知识点】平面向量数量积的坐标运算7. 【答案】C【解析】由题意知α∩β=l,所以l⊂β,因为n⊥β,所以n⊥l.【知识点】直线与直线的位置关系、点、线、面的位置关系8. 【答案】A【解析】i(2−i)=1+2i.【知识点】复数的乘除运算9. 【答案】B【解析】因为复数z满足z(1+i)=2i,所以z=2i1+i=1+i.【知识点】复数的乘除运算10. 【答案】C【解析】由AB=2√3,AC=2,B=30∘及正弦定理ACsinB =ABsinC得sinC=ABsinBAC=2√3×122=√32.由C为三角形的内角可知C=60∘或120∘.因此A=90∘或30∘.在△ABC中,由AB=2√3,AC=2,A=90∘或30∘,得面积S=12AC⋅AB⋅sinA=2√3或√3.【知识点】正弦定理二、填空题(共6题)11. 【答案】×【知识点】余弦定理12. 【答案】16【解析】该试验所有的样本点为(甲,乙丙),(乙,甲丙),(丙,甲乙),(甲乙,丙),(甲丙,乙),(乙丙,甲)(其中每个样本点表示的都是“派往A区调研的专家、派往B区调研的专家”),共6个,其中甲、乙两位专家均被派遣至 A 区的样本点有 1 个,因此,所求事件的概率为 16. 【知识点】古典概型13. 【答案】 −12【解析】因为 a =(2,1),b⃗ =(−1,x ), 所以 a +b ⃗ =(1,x +1),a −b ⃗ =(3,1−x ), 又 (a +b ⃗ )∥(a −b⃗ ), 所以 1−x −3(x +1)=0, 解得 x =−12.【知识点】平面向量数乘的坐标运算14. 【答案】 36π【知识点】球的表面积与体积15. 【答案】交线;垂直; a ⊂α ; a ⊥l【知识点】平面与平面垂直关系的性质16. 【答案】 (0,1)【知识点】复数的几何意义、复数的乘除运算三、解答题(共6题) 17. 【答案】(1) 略. (2) 略.【知识点】圆柱的表面积与体积、球的表面积与体积18. 【答案】如图所示,设向量 OA⃗⃗⃗⃗⃗ 的长度和方向表示水流速度的大小和方向,向量 OB ⃗⃗⃗⃗⃗ 的长度和方向表示船在静水中速度的大小和方向,以 OA⃗⃗⃗⃗⃗ ,OB ⃗⃗⃗⃗⃗ 为邻边作平行四边形 OACB ,连接 OC . 依题意得 OC ⃗⃗⃗⃗⃗ ⊥OA ⃗⃗⃗⃗⃗ ,∣∣BC ⃗⃗⃗⃗⃗ ∣∣=∣∣OA ⃗⃗⃗⃗⃗ ∣∣=20,∣∣OB ⃗⃗⃗⃗⃗ ∣∣=40,所以 ∠BOC =30∘.故船应向上游且与河岸夹角为 60∘ 的方向行进. 【知识点】平面向量的实际应用问题19. 【答案】(1) 因为 A +B +C =π, 所以 sin (B +C )=sinA , 所以 b 2+c 2−a 2=2bcsinA ,所以b 2+c 2−a 22bc=sinA ,由余弦定理得 cosA =sinA ,可得 tanA =1, 又因为 A ∈(0,π), 所以 A =π4.(2) 根据正弦定理得 b =a sinA ⋅sinB =√6,又 sinC =sin (A +B )=sin (π4+π3)=√6+√24, 所以S △ABC =12absinC =12⋅2⋅√6⋅√6+√24=3+√32.【知识点】余弦定理、正弦定理20. 【答案】①平面 α 内两条相交直线 a ,b ,即 a ⊂α,b ⊂α,a ∩b =P .②两条相交直线 a ,b 都与 β 平行,即 a ∥β,b ∥β. 【知识点】平面与平面平行关系的判定21. 【答案】 300×1.70<600,够用.【知识点】样本数据的数字特征22. 【答案】(1) 根据题意作出统计表:平均数方差中位数命中9环及以上次数甲7 1.271乙75.47.53因为平均数相同,且 s 甲2<s 乙2,所以甲的成绩比乙稳定,甲更优秀.(2) 因为平均数相同,甲的中位数 < 乙的中位数, 所以乙的成绩比甲好.(3) 因为平均数相同,且乙命中 9 环及以上的次数比甲多, 所以乙的成绩比甲好.(4) 因为甲的成绩在平均线附近波动,而乙的成绩整体处于上升趋势,从第 4 次开始射靶的环数没有比甲少的情况发生, 所以乙更有潜力.【知识点】样本数据的数字特征。
人教版高中数学必修2第二章测试题A组及答案解析第二章点、直线、平面之间的位置关系一、选择题1.设 $\alpha$,$\beta$ 为两个不同的平面,$l$,$m$ 为两条不同的直线,且 $l\subset\alpha$,$m\subset\beta$,有如下的两个命题:①若 $\alpha\parallel\beta$,则 $l\parallel m$;②若 $l\perp m$,则 $\alpha\perp\beta$。
那么()。
A。
①是真命题,②是假命题B。
①是假命题,②是真命题C。
①②都是真命题D。
①②都是假命题2.如图,ABCD为正方体,下面结论错误的是()。
A。
BD $\parallel$ 平面CBB。
AC $\perp$ BDC。
AC $\perp$ 平面CBD。
异面直线AD与CB角为60°3.关于直线 $m$,$n$ 与平面 $\alpha$,$\beta$,有下列四个命题:① $m\parallel\alpha$,$n\parallel\beta$ 且$\alpha\parallel\beta$,则 $m\parallel n$;② $m\perp\alpha$,$n\perp\beta$ 且 $\alpha\perp\beta$,则$m\perp n$;其中真命题的序号是()。
A。
①②B。
③④C。
①④D。
②③4.给出下列四个命题:①垂直于同一直线的两条直线互相平行②垂直于同一平面的两个平面互相平行③若直线 $l_1$,$l_2$ 与同一平面所成的角相等,则$l_1$,$l_2$ 互相平行④若直线 $l_1$,$l_2$ 是异面直线,则与 $l_1$,$l_2$ 都相交的两条直线是异面直线其中假命题的个数是()。
A。
1B。
2C。
3D。
45.下列命题中正确的个数是()。
①若直线 $l$ 上有无数个点不在平面 $\alpha$ 内,则$l\parallel\alpha$②若直线 $l$ 与平面 $\alpha$ 平行,则 $l$ 与平面$\alpha$ 内的任意一条直线都平行③如果两条平行直线中的一条直线与一个平面平行,那么另一条直线也与这个平面平行④若直线 $l$ 与平面 $\alpha$ 平行,则 $l$ 与平面$\alpha$ 内的任意一条直线都没有公共点A。
高一数学必修第二册全册复习测试题卷11(共22题)一、选择题(共10题)1. △ABC 中,若 a =1,c =2,B =60∘,则 △ABC 的面积为 ( ) A . 12B . 1C .√32D . √32. 若书架中放有中文书 5 本,英文书 3 本,日文书 2 本,则抽出一本书为外文书的概率为 ( ) A . 15B . 310C . 25D . 123. 若 θ 为两个非零向量的夹角,则 θ 的取值范围为 ( ) A .(0,π) B .(0,π] C .[0,π) D .[0,π]4. 从一箱产品中随机地抽取一件,设事件 A = { 抽到一等品 },事件 B = { 抽到二等品 },事件 C = { 抽到三等品 } ,且已知 P (A )=0.65,P (B )=0.2,P (C )=0.1.则事件“抽到的是二等品或三等品”的概率为 ( ) A .0.7 B .0.65 C .0.35 D .0.35. 下列关于古典概型的说法中正确的是 ( ) ①试验中所有可能出现的样本点只有有限个; ②每个事件出现的可能性相等; ③每个样本点出现的可能性相等;④若样本点总数为 n ,随机事件 A 包含其中的 k 个样本点,则 P (A )=kn . A .②④ B .③④ C .①④ D .①③④6. 给定一组数据:102,100,103,104,101,这组数据的第 60 百分位数是 ( ) A . 102 B . 102.5 C . 103 D . 103.57. 为比较甲、乙两地某月 14 时的气温情况,随机选取该月中的 5 天,这 5 天中 14 时的气温数据(单位:∘C )如下:甲:2628293131乙:2829303132以下结论:①甲地该月 14 时的平均气温低于乙地该月 14 时的平均气温; ②甲地该月 14 时的平均气温高于乙地该月 14 时的平均气温;③甲地该月14时的气温的标准差小于乙地该月14时的气温的标准差;④甲地该月14时的气温的标准差大于乙地该月14时的气温的标准差.其中根据数据能得到的统计结论的编号为( )A.①③B.①④C.②③D.②④8.下列说法正确的是( )A.任何事件的概率总是在(0,1)之间B.频率是客观存在的,与试验次数无关C.随着试验次数的增加,事件发生的频率一般会稳定于概率D.概率是随机的,在试验前不能确定9.用符号表示“点A在直线l上,l在平面α内”,正确的是( )A.A∈l,l∉αB.A⊂l,l⊄αC.A⊂l,l∈αD.A∈l,l⊂α10.半径为2的球的表面积为( )A.4πB.8πC.12πD.16π二、填空题(共6题)11.一家保险公司想了解汽车的挡风玻璃在一年时间里破碎的概率,公司收集了20000部汽车,时间从某年的5月1日到下一年的5月1日,共发现有600部汽车的挡风玻璃破碎,则一部汽车在一年时间里挡风玻璃破碎的概率约为.12.思考辨析 判断正误.( )做100次拋硬币的试验,结果51次出现正面朝上,因此,出现正面朝上的概率是5110013.若空间两个角的两条边分别平行,则这两个角的大小关系是.14.如图所示,在复平面内,网格中的每个小正方形的边长都为1,点A,B对应的复数分别是z1,=.z2,则z2z115.平均数:如果n个数x1,x2,⋯,x n,那么x=叫做这n个数的平均数.16.思考辨析判断正误为了更清楚地反映学生在这学期多次考试中数学成绩情况,可以选用折线统计图.( )三、解答题(共6题)17.如图所示,梯形ABCD中,AD∥BC,且AD<BC,当梯形ABCD绕AD所在直线旋转一周时,其他各边旋转围成了一个几何体,试描述该几何体的结构特征.18.小明是班里的优秀学生,他的历次数学成绩是96,98,95,93,45分,最近一次考试成绩只有45分的原因是他带病参加了考试.期末评价时,怎样给小明评价(90分及90分以上为优秀,75∼90分为良好)?19.类比绝对值∣x−x0∣的几何意义,∣z−z0∣(z,z0∈C)的几何意义是什么?20.如图,在三棱锥P−ABC中,平面PAC⊥平面ABC,∠ACB=90∘,PA=AC=2BC.(1) 若PA⊥PB,求证:平面PAB⊥平面PBC;(2) 若PA与平面ABC所成角的大小为60∘,求二面角C−PB−A的余弦值.21.应用面面平行判断定理应具备哪些条件?22.如图,在四棱锥P−ABCD中,PD⊥平面ABCD,AB∥DC,AB⊥AD,DC=6,AD=8,BC=10,PD=9,E为PA的中点.(1) 求证:DE∥平面BPC.(2) 在线段AB上是否存在一点F,满足CF⊥DB?若存在,试求出此时三棱锥B−PCF的体积;若不存在,请说明理由.答案一、选择题(共10题) 1. 【答案】C【解析】由题得 △ABC 的面积 S =12AB ⋅BC ⋅sin60∘=12×2×1×√32=√32. 【知识点】三角形的面积公式2. 【答案】D【解析】在 10 本书中,中文书 5 本,外文书为 3+2=5 本,由古典概型,在其中抽出一本书为外文书的概率为 510,即 12. 【知识点】古典概型3. 【答案】D【知识点】平面向量的数量积与垂直4. 【答案】D【解析】由题意知事件 A 、 B 、 C 互为互斥事件,记事件 D =“抽到的是二等品或三等品”,则 P (D )=P (B ∪C )=P (B )+P (C )=0.2+0.1=0.3. 【知识点】事件的关系与运算5. 【答案】D【解析】②中所说的事件不一定是样本点,所以②不正确;根据古典概型的特征及计算公式可知①③④正确. 【知识点】古典概型6. 【答案】D【解析】 5×0.6=3,第 60 百分位数是第三与第四个数的平均数, 即103+1042=103.5.【知识点】样本数据的数字特征7. 【答案】B【解析】因为 x 甲=26+28+29+31+315=29,x 乙=28+29+30+31+325=30,所以 x 甲<x 乙.又 s 甲2=9+1+0+4+45=185,s 乙2=4+1+0+1+45=2,所以 s 甲>s 乙,故由样本估计总体可知结论①④正确. 【知识点】样本数据的数字特征8. 【答案】C【解析】不可能事件的概率为 0,必然事件的概率为 1,故A 错误;频率是由试验的次数决定的,故B 错误;概率是频率的稳定值,故C 正确,D 错误. 【知识点】频率与概率9. 【答案】D【解析】点 A 在直线 l 上,表示为 A ∈l ,l 在平面 α 内,表示为 l ⊂α. 【知识点】平面的概念与基本性质10. 【答案】D【解析】因为球的半径为 r =2, 所以该球的表面积为 S =4πr 2=16π. 【知识点】球的表面积与体积二、填空题(共6题) 11. 【答案】 0.03【解析】 P =60020000=0.03.【知识点】频率与概率12. 【答案】 ×【知识点】频率与概率13. 【答案】相等或互补【知识点】直线与直线的位置关系14. 【答案】 −1−2i【解析】由题意,根据复数的表示可知z1=i,z2=2−i,所以z2z1=2−ii=(2−i)⋅(−i)i⋅(−i)=−1−2i.【知识点】复数的乘除运算、复数的几何意义15. 【答案】1n(x1+x2+⋯+x n)【知识点】样本数据的数字特征16. 【答案】√【知识点】频率分布直方图三、解答题(共6题)17. 【答案】如图所示,旋转所得的几何体是一个圆柱挖去两个圆锥后剩余部分构成的组合体.【知识点】组合体18. 【答案】小明5次考试成绩从小到大排列为45,93,95,96,98,中位数是95,应评定为“优秀”.【知识点】样本数据的数字特征19. 【答案】∣z−z0∣(z,z0∈C)的几何意义是复平面内点Z到点Z0的距离.【知识点】复数的加减运算20. 【答案】(1) 因为平面PAC⊥平面ABC,平面PAC∩平面ABC=AC,BC⊂平面ABC,BC⊥AC,所以BC⊥平面PAC,因为PA⊂平面PAC,所以PA⊥BC.又PA⊥PB,PB∩BC=B,所以PA⊥平面PBC,因为PA⊂平面PAB,所以平面PAB⊥平面PBC.(2) 如图,过P作PH⊥AC于点H,因为平面PAC⊥平面ABC,所以PH⊥平面ABC,所以∠PAH=60∘,不妨设PA=2,所以PH=√3,以 C 为原点,分别以 CA ,CB 所在直线为 x 轴,y 轴,以过 C 点且平行于 PH 的直线为 z 轴,建立如图所示的空间直角坐标系,则 C (0,0,0),A (2,0,0),B (0,1,0),P(1,0,√3),因此 AB⃗⃗⃗⃗⃗ =(−2,1,0),AP ⃗⃗⃗⃗⃗ =(−1,0,√3),CB ⃗⃗⃗⃗⃗ =(0,1,0),CP ⃗⃗⃗⃗⃗ =(1,0,√3). 设 n ⃗ =(x 1,y 1,z 1) 为平面 PAB 的一个法向量, 则 {n ⃗ ⋅AB⃗⃗⃗⃗⃗ =0,n ⃗ ⋅AP⃗⃗⃗⃗⃗ =0, 即 {−2x 1+y 1=0,−x 1+√3z 1=0,令 z 1=√3,可得 n ⃗ =(3,6,√3), 设 m ⃗⃗ =(x 2,y 2,z 2) 为平面 PBC 的一个法向量, 则 {m ⃗⃗ ⋅CB⃗⃗⃗⃗⃗ =0,m ⃗⃗ ⋅CP ⃗⃗⃗⃗⃗ =0, 即 {y 2=0,x 2+√3z 2=0,令 z 2=√3,可得 m ⃗⃗ =(−3,0,√3), 所以 cos⟨m ⃗⃗ ,n ⃗ ⟩=4√3×2√3=−14, 易知二面角 C −PB −A 为锐角, 所以二面角 C −PB −A 的余弦值为 14.【知识点】平面与平面垂直关系的判定、利用向量的坐标运算解决立体几何问题、二面角21. 【答案】①平面 α 内两条相交直线 a ,b ,即 a ⊂α,b ⊂α,a ∩b =P .②两条相交直线 a ,b 都与 β 平行,即 a ∥β,b ∥β. 【知识点】平面与平面平行关系的判定22. 【答案】(1) 取 PB 的中点 M ,连接 EM ,CM ,过点 C 作 CN ⊥AB ,垂足为 N ,如图所示. 因为 CN ⊥AB ,DA ⊥AB , 所以 CN ∥DA , 又 AB ∥CD ,所以四边形 CDAN 为矩形, 所以 CN =AD =8,DC =AN =6.在 Rt △BNC 中,BN =√BC 2−CN 2=√102−82=6, 所以 AB =12.因为 E ,M 分别为 PA ,PB 的中点, 所以 EM ∥AB 且 EM =6, 又 DC ∥AB ,且 CD =6, 所以 EM ∥CD 且 EM =CD , 则四边形 CDEM 为平行四边形, 所以 DE ∥CM .因为 CM ⊂平面BPC ,DE ⊄平面BPC ,所以 DE ∥平面BPC .(2) 存在.理由如下:由题意可得 DA ,DC ,DP 两两互相垂直,故以 D 为原点,DA ,DC ,DP所在直线分别为 x 轴,y 轴,z 轴,建立如图所示的空间直角坐标系 Dxyz . 则 D (0,0,0),B (8,12,0),C (0,6,0),所以 DB⃗⃗⃗⃗⃗⃗ =(8,12,0). 假设 AB 上存在一点 F 使 CF ⊥BD ,设点 F 坐标为 (8,t,0)(0≤t ≤12), 则 CF⃗⃗⃗⃗⃗ =(8,t −6,0), 由 CF ⃗⃗⃗⃗⃗ ⋅DB ⃗⃗⃗⃗⃗⃗ =0,得 64+12(t −6)=12t −8=0, 所以 t =23,即 AF =23,故 BF =12−23=343.又 PD =9,所以 V 三棱锥B−PCF =V 三棱锥P−BCF =13×12×343×8×9=136.【知识点】直线与平面平行关系的判定、利用向量的坐标运算解决立体几何问题。
高一数学必修2测试题一、 选择题(12 X 5分=60分)1、 下列命题为真命题的是( )A. 平行于同一平面的两条直线平行; C. 垂直于同一平面的两条直线平行; D.2、 下列命题中错误的是:()A. 如果a 丄B ,那么a 内一疋存在直线平行于平面 B ;B. 如果a 丄B ,那么a 内所有直线都垂直于平面 3;C. 如果平面a 不垂直平面3,那么a 内-D. 如果a 丄丫,3丄Y,aG I ,那么I 丄丫.3、 右图的正方体 ABCD-A ' B ' C ' D ' 中,异面直线AA '与BC 所成的角是(A. 300B.450C. 6004、 右图的正方体 ABCD- A ' B ' C ' D '中, 二面角D ' -AB-D 的大小是()A. 300B.450C. 60° B.与某一平面成等角的两条直线平行;D.垂直于同一直线的两条直线平行。
D. 90°D. 90°5、直线5x-2y-10=0 在x轴上的截距为a,在y 轴上的截距为b,则()6、直线2x-y=7 与直线3x+2y-7=0 的交点是(A (3,-1)B (-1,3)C (-3,-1)D (3,1)7、过点P(4,-1)且与直线3x-4y+6=0 垂直的直线方程是(9、 已知一个铜质的五棱柱的底面积为 16cm 2,高为4cm ,现将它熔化后铸成一 个正方体的铜块(不计损耗),那么铸成的铜块的棱长是( )4A. 2cm;B.—cm;C.4cm;D.8cm 。
310、 圆x 2+y 2-4x-2y-5=0 的圆心坐标是:()A.(-2,-1);B.(2,1);C.(2,-1);D.(1,-2).11、 直线3x+4y-13=0 与圆(x 2)2 (y 3)2 1的位置关系是:() A.相离; B.相交; C.相切; D.无法判定.12、 圆 C 仁(x 2)2 (y 2)2 1 与圆 C 2:(x 2)2 (y 5)2 16 的位置关系是( )A.a=2,b=5;B.a=2,b=5;C.a= 2 ,b=5;D.a= 2,b= 5.A 4x+3y-13=0 C 3x-4y-16=0B 4x-3y-19=0 D 3x+4y-8=08、正方体的全面积为 a,它的顶点都在球面上,则这个球的表面积是:A. B.2C. 2 aD. 3 a .A 、外离B 相交C 内切D 外切、填空题(5 X5=25 )13、底面直径和高都是4cm的圆柱的侧面积为_____________________ cm2。
人教版高一上学期数学(必修二)《4.2.2对数运算法则》同步测试题及答案1.(多选)下列各式(各式均有意义)不正确的为( )A.log a (MN )=log a M +log a NB.log a (M -N )=log aMlog a N C.a −n m =√a n mD.lo g a n b =-n log a b2.log 29×log 34的值为( ) A.14B.12C.2D.43.(12log 64+log 63)(log 312-2log 32)等于( )A.0B.1C.2D.44.已知log 3x =m ,log 3y =n ,则log 3√x √y·√y 用m ,n 可表示为( ) A.12m -43n B.23m -13nC.√m -√n 23D.12m -23n5.若2.5x =1 000,0.25y =1 000,则1x -1y 等于( )A.13B.3C.-13D.-36.(多选)若log 2m =log 4n ,则( )A.n =2mB.log 9n =log 3mC.ln n =2ln mD.log 2m =log 8mn7.log 3√27+lg 4+lg 25+(−18)0= .8.设log 23·log 36·log 6m =log 4(2m +8),则实数m = . 9.(10分)计算下列各式的值:(1)log 535+2lo g 12√2-log 5150-log 514;(5分)(2)(log 2125+log 425+log 85)(log 52+log 254+log 1258).(5分)10.(10分)若2a=3,3b=5,试用a与b表示log4572.11.(多选)已知a,b均为正实数,若log a b+log b a=52,则log a b等于()A.12B.√22C.√2D.212.方程log3(x2-10)=1+log3x的解是()A.-2B.-2或5C.5D.313.设log83=p,log35=q,则lg5等于()A.p2+q2B.15(3p+2q)C.3pq1+3pqD.pq14.计算:lg√10×lg0.1=.15.设f(n)=log n+1(n+2)(n∈N+),现把满足乘积f(1)·f(2)·…·f(n)为整数的n叫做“贺数”,则在区间(1,2023)内所有“贺数”的个数是()A.9B.10C.29D.21016.(12分)已知x,y,z为正数,3x=4y=6z,2x=py.(1)求p;(6分)(2)求证:1z -1x=12y.(6分)参考答案1.BD 2.D 3.B 4.D 5.A6.BCD [因为log 2m =log 4n ,所以m >0,n >0,又log 2m =lo g 22n =12log 2n =log 2n 12,所以m =n 12,即m 2=n ,故A 错误;log 9n =lo g 32m 2=22log 3m =log 3m ,故B 正确;ln n =ln m 2=2ln m ,故C 正确;log 8mn =lo g 23m 3=33log 2m =log 2m ,故D 正确.]7.92 8.49.解 (1)原式=log 535+log 550-log 514+2lo g 12212=log 535×5014+lo g 122=log 553-1=2. (2)原式=(log 253+log 225log 24+log 25log 28)(log 52+log 54log 525+log 58log 5125) =(3log 25+2log 252log 22+log 253log 22)(log 52+2log 522log 55+3log 523log 55) =(3+1+13)log 25·3log 52=13log 25·log 22log 25=13. 10.解 ∵2a =3,3b =5∴log 23=a ,log 35=b∴log 25=log 23×log 35=ab∴log 4572=log 272log 245=log 2(23×32)log 2(32×5)=3+2log 232log 23+log 25=3+2a 2a +ab. 11.AD [令log a b =t则log b a =1t ,即t +1t =52所以2t 2-5t +2=0即(2t -1)(t -2)=0解得t =12或t =2 所以log a b =12或log a b =2.]12.C [原方程可化为log 3(x 2-10)=log 3(3x )所以x 2-10=3x解得x =-2或x =5.又⎩⎨⎧ x 2-10>0,x >0,解得x >10 故x =5.]13.C [∵log 83=lg 3lg 8=lg 33lg 2=p∴lg 3=3p lg 2.∵log 35=lg 5lg 3=q ∴lg 5=q lg 3=3pq lg 2=3pq (1-lg 5)∴lg 5=3pq 1+3pq.] 14.-4解析 lg √10×lg0.1=lg 8×1252×5lg1012×lg10−1 =lg10212×(−1)=-4.15.A [∵f (n )=log n +1(n +2)=lg (n +2)lg (n +1)∴f (1)·f (2)·…·f (n )=lg 3lg 2×lg 4lg 3×…×lg (n +2)lg (n +1)=lg (n +2)lg 2=log 2(n +2). ∵n ∈(1,2 023)∴n +2∈(3,2 025).∵210=1 024,211=2 048∴在(3,2 025)内含有22,23,…,210,共9个数. ∴在区间(1,2 023)内所有“贺数”的个数是9.]16.(1)解 设3x =4y =6z =k (显然k >0且k ≠1) 则x =log 3k ,y =log 4k ,z =log 6k由2x =py得2log 3k =p log 4k =p ·log 3k log 34 ∵log 3k ≠0,∴p =2log 34.(2)证明 ∵1z -1x =1log 6k -1log 3k =log k 6-log k 3 =log k 2=12log k 4=12y ∴1z -1x =12y .。
综合测试题一、选择题:本大题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.计算lg 4+lg 25=( ) A .2 B .3 C .4D .102.下列等式中正确的是( ) A .OA →-OB →=AB → B .AB →+BA →=0 C .0·AB →=0D .AB →+BC →+CD →=AD → 3.甲、乙两人有三个不同的学习小组A ,B ,C 可以参加,若每人必须参加并且仅能参加一个学习小组,则两人参加同一个小组的概率为( )A .13B .14C .15D .164.设f (x )为奇函数,且当x ≥0时,f (x )=e x -1,则当x <0时,f (x )=( ) A .e -x -1 B .e -x +1 C .-e -x -1D .-e -x +15.在△ABC 中,已知D 是AB 边上一点,若AD →=2DB →,CD →=13CA →+λCB →,则λ=( )A .23B .-23C .25D .136.生物实验室有5只兔子,其中只有3只测量过某项指标.若从这5只兔子中随机取出3只,则恰有2只测量过该指标的概率为( )A .23B .35C .25D .157.质点P 在平面上做匀速直线运动,速度向量v =(4,-3)(即点P 的运动方向与v 相同,且每秒移动的距离为|v |个单位).设开始时点P 的坐标为(-10,10),则5秒后点P 的坐标为( )A .(-2,4)B .(-30,25)C .(10,-5)D .(5,-10)8.设函数f (x )=⎩⎨⎧2-x ,x ≤0,1,x >0,则满足f (x +1)<f (2x )的x 的取值范围是( )A .(-∞,-1]B .(0,+∞)C .(-1,0)D .(-∞,0)二、选择题:本大题共4小题,每小题5分,共20分.在每小题给出的四个选项中,有多个选项是符合题目要求的,全部选对的得5分,选对但不全的得3分,有选错的得0分.9.设O 是平行四边形ABCD 的两条对角线AC ,BD 的交点,则可作为这个平行四边形所在平面的一组基底的向量组是( )A .AD →与AB → B .DA →与BC → C .CA →与DC →D .OD →与OB →10.对于函数f (x )定义域中任意的x 1,x 2(x 1≠x 2),当f (x )=2-x 时,下列结论中正确的是( )A .f (x 1+x 2)=f (x 1)f (x 2)B .f (x 1·x 2)=f (x 1)+f (x 2)C .(x 1-x 2)[f (x 1)-f (x 2)]<0D .f ⎝ ⎛⎭⎪⎫x 1+x 22<f (x 1)+f (x 2)211.某地区经过一年的建设,农村的经济收入增加了一倍,实现翻番.为更好地了解该地区农村的经济收入变化情况,统计了该地区建设前后农村的经济收入构成比例,得到如图所示的饼图:则下面结论中正确的是()A.建设后,种植收入减少B.建设后,其他收入增加了一倍以上C.建设后,养殖收入增加了一倍D.建设后,养殖收入与第三产业收入的总和超过了经济收入的一半12.若把定义域不同,但值域相同的函数叫作“同族函数”,其中与函数g(x)=x+1x,x∈(0,+∞)为“同族函数”的是()A.f(x)=2x-1x,x∈(1,+∞)B.f(x)=11+x2,x∈RC.f(x)=log2(2|x|+1),x∈RD.f(x)=4x+2x+1+1,x∈R三、填空题:本大题共4小题,每小题5分,共20分.将答案填在题中的横线上.13.已知函数f(x)=log2(x2+a).若f(3)=1,则a=________.14.某学校举行课外综合知识比赛,随机抽取400名同学的成绩,成绩全部在50分至100分之间,将成绩按如下方式分成五组.第一组,成绩大于等于50分且小于60分;第二组,成绩大于等于60分且小于70分;……;第五组,成绩大于等于90分且小于等于100分,据此绘制了如图所示的频率分布直方图.则400名同学中成绩优秀(大于等于80分)的学生有________名.15.已知定义在R上的偶函数f(x)和奇函数g(x)满足f(x)+g(x)=e x,且2f(x)-e x-m≥0在x∈[1,2]上恒成立,则实数m的取值范围为________.16.已知平面向量a,b,c满足|a|=|b|=|a-b|=|a+b-c|=1,则|c|的最大值M=________,|c|的最小值m=________.(本题第一空2分,第二空3分)四、解答题:本大题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤.17.(本小题满分10分)已知向量a =(2,0),b =(1,4). (1)求2a +3b ,a -2b ;(2)若向量k a +b 与a +2b 平行,求k 的值.18.(本小题满分12分)为了了解中学生的体能情况,抽取了某校七年级的部分学生进行一分钟跳绳次数测试,将所得数据整理后,画出频率分布直方图如图,已知第1组的频数为5.(1)求第4组的频率;(2)参加这次测试的学生有多少人?(3)若次数在75以上(含75次)为达标,试估计该年级跳绳测试的达标率是多少?19.(本小题满分12分)已知函数f (x )=a x +b (a >0,a ≠1).(1)若f (x )的图像如图①所示,求a ,b 的值; (2)若f (x )的图像如图②所示,求a ,b 的取值范围;(3)在①中,若|f (x )|=m 有且仅有一个实数解,求出m 的取值范围. 20.(本小题满分12分)如图所示,在△ABC 中,BC =4BD ,AC =3CE .(1)用AB →,AC →表示AD →,BE →;(2)M 为△ABC 内一点,且AM →=23AB →+29AC →,证明:B ,M ,E 三点共线. 21.(本小题满分12分)某校团委会组织该校高中一年级某班以小组为单位利用周末时间进行了一次社会实践活动,且每个小组有5名同学,在实践活动结束后,学校团委会对该班的所有同学都进行了测试,该班的A ,B 两个小组所有同学所得分数(百分制)的茎叶图如图所示,其中B 组一同学的分数已被污损,但知道B 组学生的平均分比A 组学生的平均分高1分.(1)若在B 组学生中随机挑选1人,求其得分超过85分的概率;(2)现从A 组这5名学生中随机抽取2名同学,设其分数分别为m ,n ,求|m -n |≤8的概率.22.(本小题满分12分)已知a ∈R ,函数f (x )=log 2⎝ ⎛⎭⎪⎫1x +a .(1)当a =1时,解不等式f (x )>1;(2)若关于x 的方程f (x )+log 2(x 2)=0的解集中恰有一个元素,求a 的值; (3)设a >0,若对任意t ∈⎣⎢⎡⎦⎥⎤12,1,函数f (x )在区间[t ,t +1]上的最大值与最小值的差不超过1,求a 的取值范围.一、选择题:本大题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.计算lg 4+lg 25=( ) A .2 B .3 C .4D .10A [lg 4+lg 25=lg(4×25)=lg 100=2.] 2.下列等式中正确的是( ) A .OA →-OB →=AB →B .AB →+BA →=0 C .0·AB →=0D .AB →+BC →+CD →=AD →D [起点相同的向量相减,则取终点,并指向被减向量,OA →-OB →=BA →;AB →,BA →是一对相反向量,它们的和应该为零向量,AB →+BA →=0;0·AB →=0才对,故选D .]3.甲、乙两人有三个不同的学习小组A ,B ,C 可以参加,若每人必须参加并且仅能参加一个学习小组,则两人参加同一个小组的概率为( )A .13 B .14 C .15D .16A [因为甲、乙两人参加学习小组的所有事件有(A ,A ),(A ,B ),(A ,C ),(B ,A ),(B ,B ),(B ,C ),(C ,A ),(C ,B ),(C ,C ),共9个,其中两人参加同一个小组事件有(A ,A ),(B ,B ),(C ,C ),共3个,所以两人参加同一个小组的概率为39=13.选A .]4.设f (x )为奇函数,且当x ≥0时,f (x )=e x -1,则当x <0时,f (x )=( ) A .e -x -1 B .e -x +1 C .-e -x -1D .-e -x +1D [当x <0时,-x >0,∵当x ≥0时,f (x )=e x -1,∴f (-x )=e -x -1. 又∵f (x )为奇函数,∴f (x )=-f (-x )=-e -x +1. 故选D .]5.在△ABC 中,已知D 是AB 边上一点,若AD →=2DB →,CD →=13CA →+λCB →,则λ=( )A .23B .-23C .25D .13 A [由题意知CD →=CA →+AD →,① CD →=CB →+BD →,② 且AD →+2BD →=0.①+②×2得3CD →=CA →+2CB →, ∴CD →=13CA →+23CB →,∴λ=23.]6.生物实验室有5只兔子,其中只有3只测量过某项指标.若从这5只兔子中随机取出3只,则恰有2只测量过该指标的概率为( )A .23B .35C .25D .15B [设5只兔子中测量过某项指标的3只为a 1,a 2,a 3,未测量过这项指标的2只为b 1,b 2,则从5只兔子中随机取出3只的所有可能情况为(a 1,a 2,a 3),(a 1,a 2,b 1),(a 1,a 2,b 2),(a 1,a 3,b 1),(a 1,a 3,b 2),(a 1,b 1,b 2),(a 2,a 3,b 1),(a 2,a 3,b 2),(a 2,b 1,b 2),(a 3,b 1,b 2),共10种可能.其中恰有2只测量过该指标的情况为(a 1,a 2,b 1),(a 1,a 2,b 2),(a 1,a 3,b 1),(a 1,a 3,b 2),(a 2,a 3,b 1),(a 2,a 3,b 2),共6种可能.故恰有2只测量过该指标的概率为610=35.故选B .] 7.质点P 在平面上做匀速直线运动,速度向量v =(4,-3)(即点P 的运动方向与v 相同,且每秒移动的距离为|v |个单位).设开始时点P 的坐标为(-10,10),则5秒后点P 的坐标为( )A .(-2,4)B .(-30,25)C .(10,-5)D .(5,-10)C [设(-10,10)为A ,设5秒后P 点的坐标为A 1(x ,y ),则AA 1→=(x +10,y -10),由题意有AA 1→=5v .即(x +10,y -10)=(20,-15), 所以⎩⎨⎧ x +10=20,y -10=-15⇒⎩⎨⎧x =10,y =-5.]8.设函数f (x )=⎩⎨⎧2-x ,x ≤0,1,x >0,则满足f (x +1)<f (2x )的x 的取值范围是( )A .(-∞,-1]B .(0,+∞)C .(-1,0)D .(-∞,0)D [当x ≤0时,函数f (x )=2-x 是减函数,则f (x )≥f (0)=1.作出f (x )的大致图像如图所示,结合图像可知,要使f (x +1)<f (2x ),则需⎩⎨⎧x +1<0,2x <0,2x <x +1或⎩⎨⎧x +1≥0,2x <0,所以x <0,故选D .]二、选择题:本大题共4小题,每小题5分,共20分.在每小题给出的四个选项中,有多个选项是符合题目要求的,全部选对的得5分,选对但不全的得3分,有选错的得0分.9.设O 是平行四边形ABCD 的两条对角线AC ,BD 的交点,则可作为这个平行四边形所在平面的一组基底的向量组是( )A .AD →与AB → B .DA →与BC → C .CA →与DC →D .OD →与OB →AC [平面内任意两个不共线的向量都可以作为基底,如图: 对于A ,AD →与AB →不共线,可作为基底; 对于B ,DA →与BC →为共线向量,不可作为基底; 对于C ,CA →与DC →是两个不共线的向量,可作为基底;对于D ,OD →与OB →在同一条直线上,是共线向量,不可作为基底.] 10.对于函数f (x )定义域中任意的x 1,x 2(x 1≠x 2),当f (x )=2-x 时,下列结论中正确的是( )A .f (x 1+x 2)=f (x 1)f (x 2)B .f (x 1·x 2)=f (x 1)+f (x 2)C .(x 1-x 2)[f (x 1)-f (x 2)]<0D .f ⎝ ⎛⎭⎪⎫x 1+x 22<f (x 1)+f (x 2)2ACD [f (x )=2-x ,f (x 1+x 2)=2-(x 1+x 2),f (x 1)f (x 2)=2-x 1·2-x 2=2-(x 1+x 2),故A 对; f (x 1·x 2)=2-(x 1+x 2)≠2-x 1+2-x 2=f (x 1)+f (x 2),故B 错; ∵f (x )=2-x=⎝ ⎛⎭⎪⎫12x为减函数,所以(x 1-x 2)[f (x 1)-f (x 2)]<0,故C 对;f ⎝⎛⎭⎪⎫x 1+x 22=2-(x 1+x 2),f (x 1)+f (x 2)2=2-x 1+2-x 22,由基本不等式,所以f ⎝ ⎛⎭⎪⎫x 1+x 22<f (x 1)+f (x 2)2,故D 对.故选ACD .]11.某地区经过一年的建设,农村的经济收入增加了一倍,实现翻番.为更好地了解该地区农村的经济收入变化情况,统计了该地区建设前后农村的经济收入构成比例,得到如图所示的饼图:则下面结论中正确的是( ) A .建设后,种植收入减少B .建设后,其他收入增加了一倍以上C .建设后,养殖收入增加了一倍D .建设后,养殖收入与第三产业收入的总和超过了经济收入的一半 BCD [设建设前经济收入为a ,则建设后经济收入为2a ,则由饼图可得建设前种植收入为0.6a ,其他收入为0.04a ,养殖收入为0.3a .建设后种植收入为0.74a ,其他收入为0.1a ,养殖收入为0.6a ,养殖收入与第三产业收入的总和为1.16a ,所以建设后,种植收入减少是错误的.故选BCD .]12.若把定义域不同,但值域相同的函数叫作“同族函数”,其中与函数g(x)=x+1x,x∈(0,+∞)为“同族函数”的是()A.f(x)=2x-1x,x∈(1,+∞)B.f(x)=11+x2,x∈RC.f(x)=log2(2|x|+1),x∈R D.f(x)=4x+2x+1+1,x∈RAD[函数g(x)=x+1x=1+1x,定义域是(0,+∞),值域是(1,+∞).对于A,f(x)=2x-1x,当x∈(1,+∞)时,f(x)是单调增函数,且f(x)>2-1=1,∴f(x)的值域是(1,+∞),值域相同,是“同族函数”;对于B,f(x)=11+x2,当x∈R时,f(x)的值域是(0,1],值域不同,∴不是“同族函数”;对于C,f(x)=log2(2|x|+1),当x∈R时,2|x|≥1,∴log2(2|x|+1)≥1,∴f(x)的值域是[1,+∞),值域不同,不是“同族函数”;对于D,f(x)=4x+2x+1+1=(2x+1)2,当x∈R 时,f(x)的值域是(1,+∞),值域相同,是“同族函数”.]三、填空题:本大题共4小题,每小题5分,共20分.将答案填在题中的横线上.13.已知函数f(x)=log2(x2+a).若f(3)=1,则a=________.-7[由f(3)=1得log2(32+a)=1,所以9+a=2,解得a=-7.]14.某学校举行课外综合知识比赛,随机抽取400名同学的成绩,成绩全部在50分至100分之间,将成绩按如下方式分成五组.第一组,成绩大于等于50分且小于60分;第二组,成绩大于等于60分且小于70分;……;第五组,成绩大于等于90分且小于等于100分,据此绘制了如图所示的频率分布直方图.则400名同学中成绩优秀(大于等于80分)的学生有________名.100[成绩优秀的频率为1-(0.005+0.025+0.045)×10=0.25,所以成绩优秀的学生有0.25×400=100(名).]15.已知定义在R上的偶函数f(x)和奇函数g(x)满足f(x)+g(x)=e x,且2f(x)-e x-m≥0在x∈[1,2]上恒成立,则实数m的取值范围为________.(-∞,e-2][由f(x)+g(x)=e x,①可得f(-x)+g(-x)=e-x,即f(x)-g(x)=e-x,②由①②,解得f(x)=e x+e-x2.2f(x)-e x-m≥0在x∈[1,2]上恒成立,即m≤2f(x)-e x=e-x在x∈[1,2]上恒成立.又函数y=e-x在[1,2]上单调递减,所以y min=e-2,所以m≤e-2,即实数m的取值范围为(-∞,e-2].]16.已知平面向量a,b,c满足|a|=|b|=|a-b|=|a+b-c|=1,则|c|的最大值M=________,|c|的最小值m=________.(本题第一空2分,第二空3分) 3+13-1[因为|a|=|b|=|a-b|=1.所以a,b,a-b可构成等边三角形,且|a+b|=3,因为|a+b-c|=1,所以如图所示,c的终点在以a+b的终点为圆心、半径为1的圆上,故M=3+1,m=3-1.]四、解答题:本大题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤.17.(本小题满分10分)已知向量a=(2,0),b=(1,4).(1)求2a+3b,a-2b;(2)若向量k a+b与a+2b平行,求k的值.[解](1)∵a=(2,0),b=(1,4),∴2a+3b=2(2,0)+3(1,4)=(4,0)+(3,12)=(7,12),a-2b=(2,0)-2(1,4)=(2,0)-(2,8)=(0,-8).(2)依题意得k a+b=(2k,0)+(1,4)=(2k+1,4),a+2b=(2,0)+(2,8)=(4,8).∵向量k a+b与a+2b平行,∴8(2k+1)-4×4=0,解得k=1 2.18.(本小题满分12分)为了了解中学生的体能情况,抽取了某校七年级的部分学生进行一分钟跳绳次数测试,将所得数据整理后,画出频率分布直方图如图,已知第1组的频数为5.(1)求第4组的频率;(2)参加这次测试的学生有多少人?(3)若次数在75以上(含75次)为达标,试估计该年级跳绳测试的达标率是多少?[解](1)第4组频率为0.008×(149.5-124.5)=0.2.(2)设参加这次测试的人数为x,则5x=0.004×(74.5-49.5)=0.1,∴x=50,故参加这次测试的学生有50人.(3)估计这次跳绳测试的达标率为[1-0.004×(74.5-49.5)]×100%=90%. 19.(本小题满分12分)已知函数f(x)=a x+b(a>0,a≠1).(1)若f(x)的图像如图①所示,求a,b的值;(2)若f(x)的图像如图②所示,求a,b的取值范围;(3)在①中,若|f(x)|=m有且仅有一个实数解,求出m的取值范围.[解](1)由图像知,f(0)=1+b=-2,所以b=-3.又f(2)=a2-3=0,所以a=3(负值舍去),因此a=3,b=-3.(2)f (x )单调递减,所以0<a <1,又f (0)<0,即a 0+b <0,所以b <-1.(3)由(1)得f (x )=(3)x -3,在同一坐标系中画出函数y =|f (x )|和y =m 的图像.观察图像可知,当m =0或m ≥3时,两图像仅有一个交点,故|f (x )|=m 有且仅有一个实数解时,m 的取值范围是{m |m =0或m ≥3}.20.(本小题满分12分)如图所示,在△ABC 中,BC =4BD ,AC =3CE .(1)用AB →,AC →表示AD →,BE →;(2)M 为△ABC 内一点,且AM →=23AB →+29AC →,证明:B ,M ,E 三点共线.[解] (1)因为BC =4BD ,所以BD →=14BC →=14(AC →-AB →)=14AC →-14AB →,所以AD →=AB →+BD →=AB →+14AC →-14AB →=34AB →+14AC →.因为AC =3CE ,所以AE →=23AC →,所以BE →=AE →-AB →=23AC →-AB →.(2)证明:因为AM →=23AB →+29AC →,所以BM →=AM →-AB →=-13AB →+29AC →.因为BE →=23AC →-AB →=3⎝ ⎛⎭⎪⎫-13AB →+29AC →, 所以BE →=3BM →,即BE →与BM →共线.又因为BE →与BM →有公共点B ,所以B ,M ,E 三点共线.21.(本小题满分12分)某校团委会组织该校高中一年级某班以小组为单位利用周末时间进行了一次社会实践活动,且每个小组有5名同学,在实践活动结束后,学校团委会对该班的所有同学都进行了测试,该班的A ,B 两个小组所有同学所得分数(百分制)的茎叶图如图所示,其中B 组一同学的分数已被污损,但知道B 组学生的平均分比A 组学生的平均分高1分.(1)若在B 组学生中随机挑选1人,求其得分超过85分的概率;(2)现从A 组这5名学生中随机抽取2名同学,设其分数分别为m ,n ,求|m -n |≤8的概率.[解] (1)A 组学生的平均分为94+88+86+80+775=85(分), ∴B 组学生平均分为86分.设被污损的分数为x ,则91+93+83+x +755=86,解得x =88, ∴B 组学生的分数分别为93,91,88,83,75,其中有3人的分数超过85分,∴在B 组学生随机选1人,其所得分超过85分的概率为35.(2)A 组学生的分数分别是94,88,86,80,77,在A 组学生中随机抽取2名同学,其分数组成的基本事件(m ,n )有(94,88),(94,86),(94,80),(94,77),(88,86),(88,80),(88,77),(86,80),(86,77),(80,77),共10个.随机抽取2名同学的分数m ,n 满足|m -n |≤8的基本事件有(94,88),(94,86),(88,86),(88,80),(86,80),(80,77),共6个.∴|m -n |≤8的概率为610=35.22.(本小题满分12分)已知a ∈R ,函数f (x )=log 2⎝ ⎛⎭⎪⎫1x +a . (1)当a =1时,解不等式f (x )>1;(2)若关于x 的方程f (x )+log 2(x 2)=0的解集中恰有一个元素,求a 的值;(3)设a >0,若对任意t ∈⎣⎢⎡⎦⎥⎤12,1,函数f (x )在区间[t ,t +1]上的最大值与最小值的差不超过1,求a 的取值范围.[解] (1)由log 2⎝ ⎛⎭⎪⎫1x +1>1,得1x +1>2,解得{x |0<x <1}. (2)log 2⎝ ⎛⎭⎪⎫1x +a +log 2(x 2)=0有且仅有一解, 等价于⎝ ⎛⎭⎪⎫1x +a x 2=1有且仅有一解,等价于ax 2+x -1=0有且仅有一解. 当a =0时,x =1,符合题意;当a ≠0时,Δ=1+4a =0,a =-14.综上,a =0或a =-14.(3)当0<x 1<x 2时,1x 1+a >1x 2+a , log 2⎝ ⎛⎭⎪⎫1x 1+a >log 2⎝ ⎛⎭⎪⎫1x 2+a , 所以f (x )在(0,+∞)上单调递减.函数f (x )在区间[t ,t +1]上的最大值与最小值分别为f (t ),f (t +1).f (t )-f (t +1)=log 2⎝ ⎛⎭⎪⎫1t +a -log 2⎝ ⎛⎭⎪⎫1t +1+a ≤1, 即at 2+(a +1)t -1≥0对任意t ∈⎣⎢⎡⎦⎥⎤12,1成立. 因为a >0,所以函数y =at 2+(a +1)t -1在区间⎣⎢⎡⎦⎥⎤12,1上单调递增,所以t =12时,y 有最小值34a -12,由34a -12≥0,得a ≥23.故a 的取值范围为⎣⎢⎡⎭⎪⎫23,+∞.。
高一数学必修2测试题
一、 选择题(12×5分=60分)
1、下列命题为真命题的是( )
A. 平行于同一平面的两条直线平行;
B.与某一平面成等角的两条直线平行;
C. 垂直于同一平面的两条直线平行;
D.垂直于同一直线的两条直线平行。
2、下列命题中错误的是:( )
A. 如果α⊥β,那么α内一定存在直线平行于平面β;
B. 如果α⊥β,那么α内所有直线都垂直于平面β;
C. 如果平面α不垂直平面β,那么α内一定不存在直线垂直于平面β;
D. 如果α⊥γ,β⊥γ,α∩β=l,那么l ⊥γ.
3、右图的正方体ABCD-A ’B ’C ’D ’
中,异面直线AA ’与BC 所成的角是( )
A. 300
B.450
C. 600
D. 900
4.一个圆柱的侧面积展开图是一个正方形,这个圆柱的全面积与侧面积的比是
A .
π
π
221+ B .
ππ441+ C .π
π
21+ D .
ππ
241+ 5、直线5x-2y-10=0在x 轴上的截距为a,在y 轴上的截距为b,则( )
A.a=2,b=5;
B.a=2,b=5-;
C.a=2-,b=5;
D.a=2-,b=5-.
6、直线2x-y=7与直线3x+2y-7=0的交点是( )
A (3,-1)
B (-1,3)
C (-3,-1)
D (3,1)
7、过点P(4,-1)且与直线3x-4y+6=0垂直的直线方程是( )
A 4x+3y-13=0
B 4x-3y-19=0
C 3x-4y-16=0
D 3x+4y-8=0
8、正方体的全面积为a,它的顶点都在球面上,则这个球的表面积是:( ) A.
3
a
π; B.
2
a
π; C.a π2; D.a π3.
10、圆x 2+y 2-4x-2y-5=0的圆心坐标是:( )
A.(-2,-1);
B.(2,1);
C.(2,-1);
D.(1,-2).
11、直线3x+4y-13=0与圆1)3()2(2
2=-+-y x 的位置关系是:( ) A. 相离; B. 相交; C. 相切; D. 无法判定. 12、圆C 1: 1)2()2(2
2
=-++y x 与圆C 2:16)5()2(2
2=-+-y x 的位置关系是
( )
A 、外离
B 相交
C 内切
D 外切
A
B
A ’
二、填空题(5×5=25)
13、底面直径和高都是4cm 的圆柱的侧面积为 cm 2。
14、两平行直线0962043=-+=-+y x y x 与的距离是 。
15、已知点M (1,1,1),N (0,a ,0),O (0,0,0),若△OMN 为直角三角形,则a =____________;
16、若直线08)3(1=-++=-my x m y x 与直线平行,则=m 。
三、解答题 18、(10分)已知点A (-4,-5),B (6,-1),求以线段AB 为直径的圆的方程。
19、(10分)已知三角形ABC 的顶点坐标为A (-1,5)、B (-2,-1)、C (4,3),M 是BC 边上的中点。
(1)求AB 边所在的直线方程;(2)求中线AM 的长。
20、(15分)如图,在边长为a 的菱形ABCD 中,ABCD PC ABC 面⊥=∠,60 ,E,F 是PA 和AB 的中点。
(1)求证: EF||平面PBC ;
(2)求E 到平面PBC 的距离。
A
B
C
D
P
E
F
21、(15分)已知关于x,y 的方程C:0422
2=+--+m y x y x . (1)当m 为何值时,方程C 表示圆。
(2)若圆C 与直线l:x+2y-4=0相交于M,N 两点,且MN=5
4,求m 的值。
22、(15
分)如图,在底面是直角梯形的四棱锥S-ABCD 中,
.
2
1,1,90====⊥=∠AD BC AB SA ABCD SA ABC ,面
(1)求四棱锥S-ABCD 的体积; (2)求证:;SBC SAB
面面⊥
S
C
A
D
B
∴S 全=2πr 2+(2πr )2=2πr 2(1+2π).S 侧=h 2=4π2r 2,
∴π
π221+=侧全S S 。
答案为A 。
7.因为与直线垂直,k=-a/b 所以所求直线的斜率为-4/3 。
又因为过点P ,所以直线方程为故
选A
8.设正方体变成为X,那么X * X *6=a ,X=根号a/6 ,那么正方体单个面的对角线=根号a/3 ,由勾股定理根号a/3和根号a/6可得到正方体对角线=根号a/2 ,也就是球半径R=二分之根号a/2 ,球表面积=4 π r ²= a π/2
11.由圆的方程得到:圆心坐标为(2,3),半径r=1,所以圆心到直线3x+4y-13=0的距离d= |6+12-13|/5 =1=r ,则直线与圆的位置关系为相切。
二、填空题(5×5=25)
13、π16 14、2010 15、3 16、2
3- 解析:
14.d=|C1-C2|/√(A^2+B^2)
15.这个问题其实就是要求MNO 三点所构成的图形为三角形即可,而O 点是在原点上的,N 点是在Y 轴上的,M 点为(1,1,1),所以直角只能为角OMN,根据向量的知识,有向量OM 为(1,1,1),MN 为(1,1-a,1),OM*MN=0,有 1*1+1*(1-a)+1*1=0 解之得a=3 16.A1B2=A2B1 三、解答题
18、解:所求圆的方程为:2
2
2
)()(r b y a x =-+-………………2 由中点坐标公式得线段AB 的中点坐标为C (1,-3)……5 29)53()41(22=+-++=
=AC r (7)
故所求圆的方程为:29)3()1(2
2
=++-y x ………………10 19、解:(1)由两点式写方程得
1
21
515+-+=---x y , (2)
即 6x-y+11=0 (3)
或 直线AB 的斜率为 61
6
)1(251=--=-----=
k (1)
直线AB 的方程为 )1(65+=-x y (3)
即 6x-y+11=0…………………………………………………………………5 (2)设M 的坐标为(00,y x ),则由中点坐标公式得
12
3
1,124200=+-==+-=
y x 故M (1,1)………………………8 52)51()11(22=-++=AM …………………………………………10 20、(1)证明:PB
EF BF AF PE AE ||,
,∴== (1)
又 ,,PBC PB PBC EF 平面平面⊂⊄
故 PBC EF 平面|| (5)
(2)解:在面ABCD 内作过F 作H BC FH 于⊥ (6)
PBC PC ABCD PC 面面⊂⊥,
ABCD PBC 面面⊥∴……………………………………………8 又 BC ABCD PBC =面面 ,BC FH ⊥,ABCD FH 面⊂ ABCD FH 面⊥∴
又PBC EF 平面||,故点E 到平面PBC 的距离等于点F 到平面PBC 的距离FH 。
(10)
在直角三角形FBH 中,2
,60a FB FBC =
=∠
, a a a FBC FB FH 4
323260sin 2sin 0
=⨯
=⨯=∠=……………12 故点E 到平面PBC 的距离等于点F 到平面PBC 的距离,
等于
a 4
3。
………………………………………………………………15 21、解:(1)方程C 可化为 m y x -=-+-5)2()1(2
2..................2 显然 5,05<>-m m 即时时方程C 表示圆。
(5)
(2)圆的方程化为 m y x -=-+-5)2()1(2
2
圆心 C (1,2),半径 m r -=5………………………………8 则圆心C (1,2)到直线l:x+2y-4=0的距离为 51
2
14
2212
2
=
+-⨯+=
d (10)
5221,54==MN MN 则 ,有 2
22)21(MN d r +=
,)5
2
()51(522+=-∴M 得 4=m (15)
22、(1)解:
4111)121(61)(21
3131=⨯⨯+⨯=⨯⨯+⨯⨯==SA AB BC AD Sh v
(2)证明:
BC
SA ABCD BC ABCD SA ⊥∴⊂⊥,面,面 又,A AB SA BC AB =⊥ , SAB BC 面⊥∴
..................5 ..........................................6 (8)
SAB BC 面⊂
SBC SAB 面面⊥∴
(10)。