北理工通信电路与系统研究型作业
- 格式:docx
- 大小:1.30 MB
- 文档页数:12
![通信电路与系统课程小班研究型教学案例[北交大]](https://uimg.taocdn.com/fc8e391955270722192ef79f.webp)

北京理⼯⼤学电⼦与通信⼯程专硕复试真题本资料由理硕教育整理,理硕教育是全国唯⼀专注于北理⼯考研辅导的学校,相对于其它机构理硕教育有得天独厚的优势。
丰富的理⼯内部资料资源与⼈⼒资源确保每个学员都受益匪浅,确保理硕教育的学员初试通过率89%以上,复试通过率接近100%,理硕教育现开设初试专业课VIP⼀对⼀,假期集训营,复试VIP⼀对⼀辅导,满⾜学员不同的需求。
因为专⼀所以专业,理硕教育助您圆北理之梦。
详情请查阅理硕教育官⽹北京理⼯⼤学信息与通信⼯程复试题⽬⼀、简答题每题10分共40分1、BJT放⼤电路的三种组态及各⾃的特点并画出基本的原理图(共射、共集、共基)2、施密特触发器的传输特性并举例3、负反馈放⼤电路的四种组态及判断⽅法(电压串联、电压并联、电流串联、电流并联)4、好像是差分放⼤电路的知识⼆、计算题共5题,任选三题,多做则选得分较多的三道题计分,每题20分共60分1、⽤74HC138实现下列函数(A’就是A的⾮,卷⼦上打不出来上⾯那⼀横)Y1=A’B+ABC Y2=A’B’+A’BC+ABC Y3=BC+ABC’(就是这个类型的,具体的式⼦可能不准确)2、描述⽐例放⼤电路和积分电路的基本原理(就是画出原理图,然后描述⼯作特性)3、给了⼀个时序电路图,让写出输出⽅程组、激励⽅程组、状态⽅程组然后画出状态图4、好像是电压⽐较器吧,问题忘了5、给了⼀个BJT放⼤电路图,让说出该图的组态(共射or共集or 共基),然后求静态⼯作点参数,IBE、ICE、VCE 其他的参数已知6、还是题5的图,画出⼩信号模型图,并求输⼊输出电阻和电压增益。
笔试是四篇阅读理解(两篇我都在黄⽪书上做过)和20道单选题,就是考语法和单词量,笔试100分钟。
听⼒更简单,就10分钟,⼀个短对话⼀个短⽂,各5题,读两遍。
⾯试,每⼈10分钟左右。
就是桌⼦上有⼀⼤堆纸⽚让你抽,每张字⽚上有5道专业题和⼀道英语⼝语题,专业题都是模电数电的基础知识,记得的有下⾯这些。
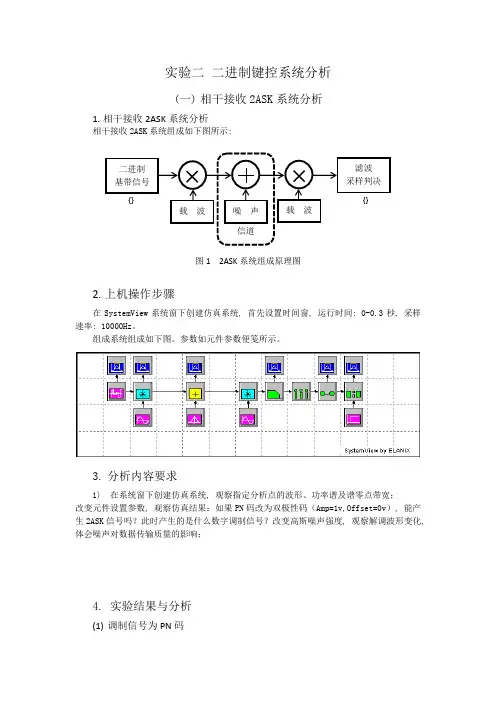
实验二 二进制键控系统分析(一) 相干接收2ASK 系统分析1. 相干接收2ASK 系统分析相干接收2ASK 系统组成如下图所示:图1 2ASK 系统组成原理图2. 上机操作步骤在SystemView 系统窗下创建仿真系统, 首先设置时间窗, 运行时间: 0-0.3秒, 采样速率: 10000Hz 。
组成系统组成如下图。
参数如元件参数便笺所示。
3. 分析内容要求1) 在系统窗下创建仿真系统, 观察指定分析点的波形、功率谱及谱零点带宽;改变元件设置参数, 观察仿真结果:如果PN 码改为双极性码(Amp=1v,Offset=0v ), 能产生2ASK 信号吗?此时产生的是什么数字调制信号?改变高斯噪声强度, 观察解调波形变化, 体会噪声对数据传输质量的影响;4. 实验结果与分析(1) 调制信号为PN 码信道二进制 基带信号噪 声滤波 采样判决载 波 载 波 {}{}a)各分析点波形b)功率谱分析: 由功率谱可以看出, 基带信号能量主要在低频段, 而2ASK调制信号的能量则位于载频的3KHz左右, 符合信号经过乘法器线性搬移的结果。
同时, 谱零点带宽约为200Hz, 也符合码元速率的两倍。
(2)调制信号为双极性码(Amp=1v,Offset=0v)a)各分析点波形b)功率谱分析: 由PN码变为双极性码之后, 调制波形不再是2ASK, 而是BPSK, 两者功率谱密度规律基本一致, 谱零点带宽也均为200Hz左右。
(3)改变高斯噪声强度(Std Dev=1v)分析: 将高斯噪声标准差提高到1V, 发现输出信号与输入信号之间已有明显差别, 发生了较为严重的误码。
可见信道噪声越大, 误码率越高。
(二) 2FSK 系统分析1. 2FSK 系统组成以话带调制解调器中CCITT V.23建议规定的2FSK 标准为例, 该标准为: 码速率1200bit/s ;f0=1300Hz 及f1=2100Hz 。
要求创建符合CCITT V.23建议的2FSK 仿真系统, 调制采用“载波调频法”产生CP-2FSK 信号, 解调采用“锁相鉴频法”。

北京理工大学电子与通信工程(专业学位)专业-882电路、信号与系统考研复习全书-真题-大纲-华文考研报考北京理工大学电子与通信工程(专业学位)专业考研专业课资料的重要性根据考研网的统计,87.3%以上报考北京理工大学电子与通信工程(专业学位)专业考研成功的考生,尤其是那些跨学校的考研人,他们大多都在第一时间获取了北京理工大学电子与通信工程(专业学位)专业考研专业课指定的教材和非指定的北京理工大学电子与通信工程(专业学位)专业内部权威复习资料,精准确定专业课考核范围和考点重点,才确保了自己的专业课高分,进而才才最后考研成功的。
如果咱们仔细的研究下问题的本质,不难发现因为非统考专业课的真题均是由北京理工大学电子与通信工程(专业学位)专业自主命题和阅卷,对于跨校考研同学而言,初试和复试命题的重点、考点、范围、趋势、规律和阅卷的方式等关键信息都是很难获取的。
所以第一时间获取了北京理工大学电子与通信工程(专业学位)专业考研专业课指定的教材和非指定的北京理工大学电子与通信工程(专业学位)专业内部权威复习资料的考生,就占得了专业课复习的先机。
专业课得高分便不难理解。
那么怎么样才能顺利的考入北京理工大学电子与通信工程(专业学位)专业呢?为了有把握的的取得专业课的高分,确保考研专业课真正意义上的成功,考研专业课复习的首要工作便是全面搜集北京理工大学电子与通信工程(专业学位)专业的内部权威专业课资料和考研信息,建议大家做到以下两点:1、快速消除跨学校考研的信息方面的劣势。
这要求大家查询好考研的招生信息,给大家推/shop/2、确定最合适的考研专业课复习资料,明确专业课的复习方法策略,并且制定详细的复习计划,并且将复习计划较好的贯彻执行。
北京理工大学882电路、信号与系统从基础到强化考研复习全书包括两部分。
第一部分:北京理工大学882电路、信号与系统考研复习重点讲义。
由考研网请北京理工大学电子与通信工程(专业学位)专业的多名研究生参与编写(均为考研网的考研高分学员),重点参考了北京理工大学电子与通信工程(专业学位)专业882电路、信号与系统历年真题,并找北京理工大学电子与通信工程(专业学位)专业最权威的导师咨询考点范围。

1.北京理工大学 1999年程序设计试题资料下载2.北京理工大学 2000年信号与系统试题资料下载3.北京理工大学 1999年晶体管原理与制造试题资料下载4.北京理工大学 1999年模拟与数字电路试题资料下载5.北京理工大学 1999年信号与系统试题资料下载6.北京理工大学 1999年微波技术基础试题资料下载7.北京理工大学 2000年程序设计试题资料下载8.北京理工大学 2000年晶体管原理与制造试题资料下载9.北京理工大学 2000年模拟与数字电路试题资料下载10.北京理工大学 2000年微波技术基础试题资料下载11.北京理工大学 2002年半导体物理试题资料下载12.北京理工大学 2001年信号与系统试题资料下载13.北京理工大学 2003年半导体物理试题资料下载14.北京理工大学 2004年会计学试题资料下载15.北京理工大学 2001年半导体物理试题资料下载16.北京理工大学 2002年政治经济学试题资料下载17.北京理工大学 2002年管理信息系统试题资料下载18.北京理工大学 2004年半导体物理试题资料下载19.北京理工大学 2004年经济学试题资料下载20.北京理工大学 2005年半导体物理试题资料下载21.北京理工大学交通运输系统工程学2005试题资料下载22.北京理工大学 2005无机化学(B)试题资料下载23.北京理工大学 2004行政管理试题资料下载24.北京理工大学人文社会科学学院 2003政治经济学试题资料下载25.北京理工大学人文社会科学学院 2004年经济学试题资料下载26.北京理工大学人文社会科学学院 2003年经济学基础试题资料下载27.北京理工大学人文社会科学学院 2002年政治经济学试题资料下载28.北京理工大学人文社会科学学院应用经济学2005试题资料下载29.北京理工大学人文社会科学学院 2005经济学基础试题资料下载30.北京理工大学人文社会科学学院基础英语2002试题资料下载31.北京理工大学人文社会科学学院运筹学2001试题资料下载32.北京理工大学人文社会科学学院日语2002试题资料下载33.北京理工大学人文社会科学学院运筹学2002试题资料下载34.北京理工大学人文社会科学学院运筹学2003试题资料下载35.北京理工大学人文社会科学学院综合考试(英语国家文化概况、汉语)2002试题资料下载36.北京理工大学人文社会科学学院经济学2002试题资料下载37.北京理工大学人文社会科学学院语言学和英美文学2002试题资料下载38.北京理工大学人文社会科学学院运筹学2005试题资料下载39.北京理工大学人文社会科学学院运筹学2004试题资料下载40.北京理工大学企业管理2004试题资料下载41.北京理工大学传感与测试技术2004试题资料下载42.北京理工大学信号处理导论2003试题资料下载43.北京理工大学信号处理导论2004试题资料下载45.北京理工大学传感与测试技术2005试题资料下载46.北京理工大学信号处理导论2005试题资料下载47.北京理工大学分析化学2003试题资料下载48.北京理工大学分析化学2005试题资料下载49.北京理工大学化学2003试题资料下载50.北京理工大学化学2002试题资料下载51.北京理工大学分析化学2004试题资料下载52.北京理工大学化学2005试题资料下载53.北京理工大学化工原理2003试题资料下载54.北京理工大学化工原理2004试题资料下载55.北京理工大学化学2004试题资料下载56.北京理工大学国际贸易2000试题资料下载57.北京理工大学化工原理2005试题资料下载58.北京理工大学国际贸易2002试题资料下载59.北京理工大学国际贸易1999试题资料下载60.北京理工大学国际贸易2001试题资料下载61.北京理工大学安全系统工程2004试题资料下载62.北京理工大学半导体物理学1999试题资料下载63.北京理工大学国际贸易(含经济学)2004试题资料下载64.北京理工大学安全系统工程2003试题资料下载65.北京理工大学安全系统工程2005试题资料下载66.北京理工大学应用光学2002试题资料下载67.北京理工大学工程热力学(不含传热学)2005试题资料下载68.北京理工大学工程热力学(不含传热学)2003试题资料下载69.北京理工大学工程流体力学2005试题资料下载70.北京理工大学工程热力学(不含传热学)2004试题资料下载71.北京理工大学应用光学2005试题资料下载72.北京理工大学应用光学2004试题资料下载73.北京理工大学应用光学2003试题资料下载74.北京理工大学应用电子技术2004试题资料下载75.北京理工大学微机原理及应用2004试题资料下载76.北京理工大学应用经济学2005试题资料下载77.北京理工大学微机控制与应用技术2002试题资料下载78.北京理工大学微机控制与应用技术2005试题资料下载79.北京理工大学微生物学2005试题资料下载80.北京理工大学技术经济学2002试题资料下载81.北京理工大学微机原理及应用2005试题资料下载82.北京理工大学微机控制与应用技术2004试题资料下载83.北京理工大学控制工程基础2003试题资料下载84.北京理工大学微机控制与应用技术2003试题资料下载85.北京理工大学控制工程基础2005试题资料下载86.北京理工大学控制工程基础2004试题资料下载87.北京理工大学数学分析2004试题资料下载89.北京理工大学政治经济学2003试题资料下载90.北京理工大学数学物理方法2000年试题资料下载91.北京理工大学数学分析2005试题资料下载92.北京理工大学数学物理方程2004试题资料下载93.北京理工大学数据结构与程序设计2004试题资料下载94.北京理工大学数学物理方程2002试题资料下载95.北京理工大学数据结构2004试题资料下载96.北京理工大学数学物理方程2003试题资料下载97.北京理工大学数学物理方程2005试题资料下载98.北京理工大学数据结构与程序设计2005试题资料下载99.北京理工大学无机化学(A)2004试题资料下载100.北京理工大学无机化学(B)2004试题资料下载101.北京理工大学无机化学(A)2005试题资料下载102.北京理工大学有机化学2005试题资料下载103.北京理工大学无机化学(A)2003试题资料下载104.北京理工大学无机化学(B)2003试题资料下载105.北京理工大学有机化学2003试题资料下载106.北京理工大学无机化学(B)2005试题资料下载107.北京理工大学机械制造工业基础2005试题资料下载108.北京理工大学机械制造工程基础2003试题资料下载109.北京理工大学有机化学2004试题资料下载110.北京理工大学机械制造工程基础2004试题资料下载111.北京理工大学机械制造工艺学2002试题资料下载112.北京理工大学机械设计原理2001试题资料下载113.北京理工大学机械设计2004试题资料下载114.北京理工大学机械设计2002试题资料下载115.北京理工大学机械设计2005试题资料下载116.北京理工大学机械设计2003试题资料下载117.北京理工大学材料力学2003试题资料下载118.北京理工大学材料力学2005试题资料下载119.北京理工大学材料科学基础2004试题资料下载120.北京理工大学材料力学2004试题资料下载121.北京理工大学材料科学基础2005试题资料下载122.北京理工大学材料科学基础2003试题资料下载123.北京理工大学爆炸与安全技术2005试题资料下载124.北京理工大学波动光学2002试题资料下载125.北京理工大学模拟与数字电路2002试题资料下载126.北京理工大学激光原理2005试题资料下载127.北京理工大学爆轰理论2003试题资料下载128.北京理工大学爆轰理论2004试题资料下载129.北京理工大学爆轰理论2005试题资料下载130.北京理工大学物理光学2003试题资料下载131.北京理工大学物理化学2003试题资料下载132.北京理工大学物理化学2004试题资料下载133.北京理工大学物理光学2004试题资料下载134.北京理工大学理论力学2003试题资料下载135.北京理工大学生物化学2004试题资料下载136.北京理工大学生物化学2003试题资料下载137.北京理工大学理论力学2004试题资料下载138.北京理工大学理论力学2005试题资料下载139.北京理工大学物理化学2005试题资料下载140.北京理工大学生物化学2005年试题资料下载141.北京理工大学电动力学2003试题资料下载142.北京理工大学生物化学(A)2005试题资料下载143.北京理工大学生物化学2005试题资料下载144.北京理工大学电动力学2004试题资料下载145.北京理工大学电化学原理2005试题资料下载146.北京理工大学电化学原理2004试题资料下载147.北京理工大学电化学原理2003试题资料下载148.北京理工大学电子技术(含模拟数字部分)2003试题资料下载149.北京理工大学电子技术(含模拟数字部分)2004试题资料下载150.北京理工大学电子技术2000试题资料下载151.北京理工大学电子技术(含模拟数字部分)2002试题资料下载152.北京理工大学电子技术1999试题资料下载153.北京理工大学电子电路2003试题资料下载154.北京理工大学电子电路2004试题资料下载155.北京理工大学电子技术(含模拟、数字部分)2005试题资料下载156.北京理工大学电磁场理论2003试题资料下载157.北京理工大学电子电路2005试题资料下载158.北京理工大学电磁场理论2000试题资料下载159.北京理工大学电磁场理论1999试题资料下载160.北京理工大学电磁场理论2004试题资料下载161.北京理工大学电磁场理论2002试题资料下载162.北京理工大学电磁场理论2005试题资料下载163.北京理工大学电磁学2005年试题资料下载164.北京理工大学管理学2005试题资料下载165.北京理工大学精密机械设计2004试题资料下载166.北京理工大学管理学基础2003试题资料下载167.北京理工大学管理信息系统2001试题资料下载168.北京理工大学精密机械设计2005试题资料下载169.北京理工大学精密机械基础2003试题资料下载170.北京理工大学细胞生物学2005年试题资料下载171.北京理工大学细胞生物学2004年试题资料下载172.北京理工大学自动控制理论1999试题资料下载173.北京理工大学经济学基础2005试题资料下载174.北京理工大学经济学基础2003试题资料下载175.北京理工大学自动控制理论2000试题资料下载176.北京理工大学自动控制理论2004试题资料下载177.北京理工大学自动控制理论(控制类)2000试题资料下载178.北京理工大学自动控制理论2005试题资料下载179.北京理工大学自动控制理论(非控类)2004试题资料下载180.北京理工大学自动控制理论(控制类)1999试题资料下载181.北京理工大学计算机原理(含操作系统)2000年试题资料下载182.北京理工大学计算机原理(含操作系统)2002试题资料下载183.北京理工大学计算机技术基础2003(含计算机组成原理、操作系统和数据结构)试题资料下载184.北京理工大学计算机技术基础2004(含计算机组成原理、操作系统和数据结构)试题资料下载185.北京理工大学计算机技术基础2005(含计算机组成原理、操作系统和数据结构)试题资料下载186.北京理工大学计算机系统结构基础(含计算机组成原理、计算机网络和数据结构) 2004试题资料下载187.北京理工大学计算机组成原理试题1999年试题资料下载188.北京理工大学计算机组成原理试题2001年试题资料下载189.北京理工大学计算机系统结构基础(含计算机组成原理、计算机网络和数据结构) 2005试题资料下载190.北京理工大学设计创意2005试题资料下载191.北京理工大学软件基础1999试题资料下载192.北京理工大学计算机组成原理试题2000年试题资料下载193.北京理工大学软件基础2000试题资料下载194.北京理工大学软件基础2001试题资料下载195.北京理工大学软件基础2002试题资料下载196.北京理工大学软件理论基础2003试题资料下载197.北京理工大学软件理论基础2004试题资料下载198.北京理工大学过程控制原理2001试题资料下载199.北京理工大学软件理论基础2005试题资料下载200.北京理工大学过程控制原理2000试题资料下载201.北京理工大学过程控制原理2003试题资料下载202.北京理工大学过程控制原理2002试题资料下载203.北京理工大学过程控制原理2004试题资料下载204.北京理工大学运筹学2001试题资料下载205.北京理工大学过程控制原理2005试题资料下载206.北京理工大学运筹学2004试题资料下载207.北京理工大学运筹学2002试题资料下载208.北京理工大学量子力学2005年试题资料下载209.北京理工大学运筹学2005试题资料下载210.北京理工大学运筹学2003试题资料下载211.北京理工大学高分子化学及高分子物理2004试题资料下载212.北京理工大学高分子物理2005试题资料下载213.北京理工大学高分子化学及高分子物理2003试题资料下载214.北京理工大学行政管理2005试题资料下载215.北京理工大学高等代数2004试题资料下载216.北京理工大学高等代数2003试题资料下载217.北京理工大学高等代数2005试题资料下载。

实验一无线通信系统(图像传输)实验一、实验目的1、掌握无线通信(图像传输)收发系统的工作原理;2、了解各电路模块在系统中的作用。
二、实验内容a)测试发射机的工作状态;b)测试接收机的工作状态;c)测试图像传输系统的工作状态;d)通过改变系统内部连接方式造成对图像信号质量的影响来了解各电路模块的作用。
三、无线图像传输系统的基本工作原理发射设备和接收设备是通信设备的重要组成部分。
其作用是将已调波经过某些处理(如放大、变频)之后,送给天馈系统,发向对方或转发中继站;接收系统再将空间传播的信号通过天线接收进来,经过某些处理(如放大、变频)之后,送到后级进行解调、编码等。
还原出基带信息送给用户终端。
为了使发射系统和接收系统同时工作,并且了解各电路模块在系统中的作用,通过实验箱中的天线模块和摄像头及显示器,使得发射和接收系统自闭环,通过图像质量来验证通信系统的工作状态,及各个电路模块的作用和连接变化时对通信或图像质量的影响。
以原理框图为例,简单介绍一下各部分的功能与作用。
摄像头采集的信号送入调制器进频率调制,再经过一次变频后、滤波(滤去变频产生的谐波、杂波等)、放大、通过天线发射出去。
经过空间传播,接收天线将信号接收进来,再经过低噪声放大、滤波(滤去空间同时接收到的其它杂波)、下变频到480MHz,再经中频滤波,滤去谐波和杂波、经视频解调器,解调后输出到显示器还原图像信号。
四、实验仪器信号源、频谱分析仪等。
五.测试方法与实验步骤(一)发射机测试图1原理框图基带信号送入调制器,进行调制(调幅或调频等调制),调制后根据频率要求进行上变频,变换到所需微波频率,并应有一定带宽,然后功率放大,通过天线发射或其它方式传播。
每次变频后,会相应产生谐波和杂波,一般变频后加响应频段的滤波器,以滤除谐波和杂波。
保证发射信号的质量或频率稳定度。
另外调制器或变频器本振信号的稳定度也直接影响发射信号的好坏,因而,对本振信号的质量也有严格的要求。

北京理工大学通信与网络实验室于季弘教授北京理工大学通信与网络实验室(以下简称“实验室”)前身是成立 于1959年的无线电遥控遥测专业,为我国最早的电子工程类专业之一。
在 团队带头人安建平教授(《数据采集与处理》第六届编委会委员)的领导下, 经过多年建设,实验室已成长为国内从事空天通信领域研究的主要科研团 队。
实验室坚持以国家重大需求和国际学术前沿为导向,积极为国家战略 服务,在“智能空天信息网络” “卫星通信” “空间信号处理”等领域开 展了卓有成效的科研工作。
实验室汇聚了以于季弘教授(《数据采集与处理》 第七届编委会委员)为代表的一大批国内空天通信领域专家和中青年拔尖 人才,现有国家百千万人才1名,优青1名,国家高层次人才计划入选者2名, 青年人才托举工程入选者1名;教授10名,副教授8名、博士生导师12名、硕士生导师22名。
为紧密结合国家重大需求,实验室承担国家、部委、国际合作科研项目数十项,包括:国 家高技术研究发展计划、国家重点基础研究发展计划、国家科技重大专项、国家自然基金项目、 基础预研等,年均科研经费超过两千万。
相关科研成果被应用于多个国家重大型号中,并牵头 获得国家技术发明奖一项、国家科技进步奖一项、省部级科研奖励多项;发表学术论文300余篇, 授权国家发明专利150余项。
于季弘,男,北京理工大学准聘教授,博士生导师,《数据采集与处理》编委。
法国巴黎 南大学博士,加拿大西蒙菲莎大学博士后研究员。
研究方向是无源物联网、空天组网与通信, 主持了包括国家自然基金重大研究计划集成项目课题在内的7项项目。
近五年在IEEE/ACM ToN 、IEEE TMC 及INFOCOM 等期刊会议发表论文40余篇,在Spring Nature 出版英文专著2 部,获得IEEE GLOBECOM 2020最佳论文奖,入选第四届中国科协“青年人才托举工程”。
担任工信部电子信息行指委委员,中国电子学会空间电子学分会副秘书长、青年科学家俱乐部 空间信息专业委员会委员、物联网专技组委员,是IEEE IoT Journal 等多个国内外期刊编委,是 IEEE ICNC 2019无线自组网与传感网分会主席和IEEE/CIC ICCC 2020物联网分会主席。
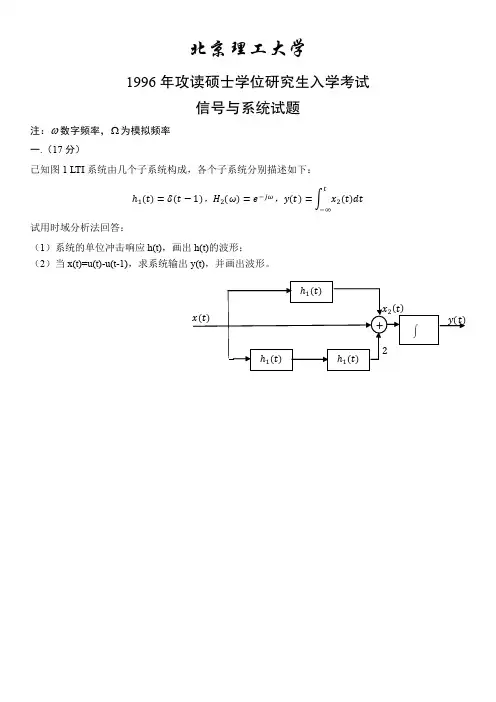
北京理工大学1996年攻读硕士学位研究生入学考试信号与系统试题注:ω数字频率,Ω为模拟频率一.(17分)已知图1 LTI系统由几个子系统构成,各个子系统分别描述如下:tℎ1(t)=δ(t−1),H2(ω)=e−jω,y(t)=∫x2(t)dt−∞试用时域分析法回答:(1)系统的单位冲击响应h(t),画出h(t)的波形;(2)当x(t)=u(t)-u(t-1),求系统输出y(t),并画出波形。
二.(17分)已知离散LTI系统框图如图2所示:(a)写出系统的差分方程;(b)求系统的单位抽样响应h[n];(c)当输入x[n]=u[n-1],用时域分析法求零状态响应y[n],并画出波形。
三.(17分)已知离散时间系统的差分方程为:y [n ]-3y [n -1]+2y [n -2]=x [n -1]-2x [n -2]若21)1(-=-y ,0)0(=y ,且从n=0时对系统施加输入)(n f ,得到系统的全响应)()12(2)(n u n y n -=。
(1)用z 变换法求x [n ];(2)求系统频率响应H (e jΩ),画出系统的频率特性(包括幅频特性和相频特性)。
四,(17分)已知一个连续时间信号x(t)=sinπt[u(t)−u(t−2)]sgn(t),其中sgn(t)={1, t>0−1,t<0(1)画出x(t)的波形以及由x(t)以为T=2周期开拓的周期信号x T(t)的波形;(2)求x(t), x T(t)的频谱X(w),c k,并画出幅度谱图(其中|c k|作图要精确);五.(16分)已知序列x[n]的频谱如图5(a),该序列通过如图5(b)所示系统,其中p[n]=cos nπ2,H(Ω)={1 ,|Ω|<π20 ,其余Ω,在(−π,π)内。
(1)画出p[n]、z[n]、y[n]的频谱图与H(Ω)的图形;(2)求系统输出)(nyX(Ω)六,(16分)已知电路如图所示,在t=0以前开关K1断开,K2闭合,且电路已进入稳态。

北京理工大学882电路、信号与系统一、考试范围“电路、信号与系统”科目考试内容由“信号与系统”(下面1-6项)和“数字电路”(下面7-16项)两部分组成,具体内容要求如下:1.信号与系统的基本概念:信号描述及信号的基本运算,典型信号。
系统模型、互联及主要特性;2.LTI系统的时域分析:卷积积分、卷积和、卷积性质与计算。
用微分/差分方程描述的因果系统的经典解法。
零输入/零状态响应;3. 确定信号的频谱分析:周期信号的傅立叶级数及周期信号的频谱表示。
非周期信号的傅立叶变换及其性质,周期信号的傅立叶级数与非周期信号的傅立叶变换的关系。
抽样定理;4. LTI系统的频域分析:系统频率响应,系统的傅立叶分析法。
无失真传输条件,理想滤波器;5. LTI系统的复频域分析:拉氏变换及其收敛域,Z变换及其收敛域。
变换性质以及典型信号的变换对。
用单边拉氏变换和Z变换求解微分/差分方程。
系统函数。
系统方框图;6. 状态方程: 状态方程的建立,状态转移矩阵的求解;7. 数制与编码:数制,数制转换,符号数的表示方法,利用补码进行加减运算,二-十进制编码,格雷码,ASCII符;8. 逻辑代数基础:逻辑变量与逻辑函数,逻辑代数的基本运算规律,逻辑函数的两种标准形式,逻辑函数的代数化简法,逻辑函数的卡诺图化简法,,非完全描述逻辑函数,逻辑函数的描述;9. 逻辑门电路:晶体管的开关作用,基本逻辑门电路,TTL集成门电路,其他类型的TTL“与非”门电路,MOS门电路,TTL与CMOS电路的级联;10. 组合逻辑电路:常用数字集成组合逻辑电路,组合电路逻辑分析,组合电路逻辑设计,组合逻辑电路中的竞争与冒险现象;11.触发器:基本R-S锁存器,门控R-S锁存器,D锁存器,主从式R-S触发器,TTL主从式JK触发器,TTL维持阻塞式D触发器,CMOS锁存器与触发器,T 触发器和T'触发器,触发器的功能转换,触发器的动态参数;12. 常用时序电路组件:异步计数器,同步二进制计数器,集成计数器,移位寄存器13. 时序逻辑电路:同步时序逻辑电路——状态机的分析,同步时序逻辑电路——状态机的设计,实用时序逻辑电路的分析与设计;14. 脉冲信号的产生和整形:连续矩形脉冲波的产生,单稳态触发器,施密特触发器,555定时器及其应用;15. 数-模、模-数变换器:数模转换器及其参数,模数转换器及其参数;16. 存储器及可编程器件:随机存取存储器RAM,ROM,容量及容量的扩展,可编程逻辑器件(PLA,PAL,GAL,PLD)。

北京理工大学882电路信号系统考研全套资料2000-2011年真题本人为北京理工大学研究生,所以收集了一下难得全面资料,希望对研弟研妹有用!买资料后复试什么的相关问题都可以咨询,作为售后,祝大家考研顺利!北京理工大学09年大纲变动,产生了专业课882,该科目由以往的信号与系统导论826中的信号与系统和811中的数字电子电路组成。
所以,报考北京理工大学光电学院的电子科学与技术专业和信息与电子学院电子科学与技术专业的同学,在选择882专业课的情况下,必须复习信号与系统系统和数字电子电路。
其他资料如下;一1996-2008信号系统真题(2009原版独家882真题,2011年882回忆版很全);2000-2008数字电路考研真题2009年北理工才开始考882含概信号与系统和数字电路两部分。
这里的试题是北理工以前考信号与系统和考数字电路的两份试卷综合而成的。
让大家更好的复习。
二1996-2008年信号与系统真题有详细答案一步一步三信号与系统配套辅导资料1,《信号与系统—概念解题与自测》王晓华闫雪梅王群编此书是07年刚出的一套北理信号与系统配套辅导书,其中的编者曾是北理工信号与系统课本编者沈庭芝教授的学生,现是北理工的老师,(280页)注意;《信号与系统——学习及解题指导》张宝俊李祯祥沈庭芝(课本编者)编那本称之为已绝版的辅导资料,它是北理的信号元老编的,现在就剩沈老一人了。
我原来同学考本校时只做了此书和真题就考了100多,大家要把他的每道题做几遍,包括课后习题,此外我把此书的重点都已标出,部分课后难题我也在旁表明了解题步骤。
以前部分年份的真题在此书中有原型和原题(420页)注意;此书不在全套资料之内有些同学有了王晓华老师编的那本信号系统概念题解与自测的可以与此书进行调换,如果两本书都要的话需要加20元2.,北理信号与系统(官方辅导班)的信号与系统笔记北理信号与系统辅导班的笔记,从04年后北理再没有办过类似的辅导班,重要性不言而喻。
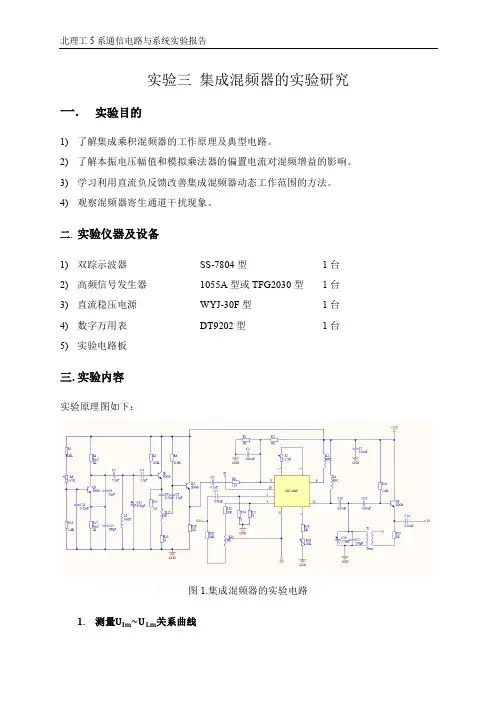
实验三集成混频器的实验研究一.实验目的1)了解集成乘积混频器的工作原理及典型电路。
2)了解本振电压幅值和模拟乘法器的偏置电流对混频增益的影响。
3)学习利用直流负反馈改善集成混频器动态工作范围的方法。
4)观察混频器寄生通道干扰现象。
二.实验仪器及设备1)双踪示波器SS-7804型1台2)高频信号发生器1055A型或TFG2030型1台3)直流稳压电源WYJ-30F型1台4)数字万用表DT9202型1台5)实验电路板三.实验内容实验原理图如下:图1.集成混频器的实验电路1.测量关系曲线1)接通实验板电源,用示波器测量P1点,调整W2使其输出一个不失真的、振荡频率为10MHz、幅值<1V的本振信号电压。
实验结果:本振信号输出为一个频率f=10.026MHz,峰峰值为2.9V的正弦波2)高频信号源输出信号频率,输出电压幅值,将此信号作为混频器输入,记录中频调谐输出电压的频率、幅值及波形。
实验结果:输出为一个频率f=2.0268MHz,峰峰值5.46V的正弦波3)令,调节使I5=1mA,然后调节改变大小,测量关系曲线。
实验结果:的测量结果见表1表1.的测量结果的关系曲线见图2.图2.的关系曲线2.测量关系曲线保持上述信号源频率不变。
令本振信号幅值=500mV,保持,调节,改变I5,测量关系曲线。
实验结果:的测量结果见表2.表2.的测量结果的关系曲线见图3.图3.的关系曲线3.观察串联电流负反馈电阻对输出中频信号幅值的影响。
1)保持本振幅值=500mV,不变,输入一个调幅波,调幅波的载频,调制信号频率为,调制度m=40%,乘法器偏置电流I50.6mA。
2)令,调节高频信号源输出电压幅值的大小,使之逐步加大到中频电压波形开始出现明显失真为止,记下此时的和大小。
实验结果:340mV,=4.49V3)另,重复上述步骤1),记下此时的和大小,并与时的测量结果进行比较。
实验结果:660mV,=4.26V4. 观察混频器中干扰信号的分布情况用高频信号源输入一个等幅波,且 ,本振 ,保持I5=1mA ,在6.5~30MHz 范围内改变高频信号源的输出频率,观察并记录哪些频率点上有明显的中频信号出现,分析出有哪些干扰信号。
通信电路与系统实验班级:学号:姓名:1-1. 简单基带传输系统分析(1)实验目的掌握观察系统时域波形,特别是眼图的操作方法。
(2)实验内容构造一个简单示意性基带传输系统。
以双极性PN码(伪噪声Pseudo-Noise: PN)发生器模拟一个数据信源,码速率为100bit/s,低通型信道噪声为加性高斯噪声(标准差=0.3v)。
要求:(3)系统参数(4)系统框图(5)实验结果nk 10 (dB m 50 o1-2. 利用Costas环解调2PSK信号(1)实验目的通过分析理解Costas环的解调功能。
(2)实验内容构造一个2PSK信号调制解调系统,利用Costas环对2PSK信号进行解调,以双极性PN码发生器模拟一个数据信源,码速率为50bit/s,载波频率为1000Hz。
以PN码作为基准,观测环路同相支路输出和正交支路输出的时域波形。
(3)系统参数及框图(4)实验结果1-3. 二进制差分编码/译码器(1)实验目的通过分析理解差分编码/译码的基本工作原理(2)实验内容创建一对二进制差分编码/译码器,以PN码作为二进制绝对码,码速率R b =100bit/s。
分别观测绝对码序列、差分编码序列、差分译码序列,并观察差分编码是如何克服绝对码全部反相的,以便为分析2DPSK原理做铺垫。
(3)系统参数及框图(4)实验结果1-4. QPSK调制原理分析(1)实验目的通过分析理解QPSK正交调制系统的基本工作原理。
(2)实验内容创建一个QPSK正交调制系统,被调载频为2000Hz,以PN码作为二进制信源,码速率R b=100bit/s。
分别观测I通道和Q通道的2PSK波形、两路合成的QPSK波形、QPSK信号的功率谱。
(3)系统参数(4)系统框图(5)实验结果e-3e-3e-3e-3e-3e-3e-3e-3e-3e-3e-3 e-32-1. 二进制键控系统分析11)相干接收2ASK系统分析(1)实验目的由于本实验是利用SystemView进行仿真分析的第一个上机实验,故安排了较为简单的2ASK和2FSK系统分析内容,上机操作步骤介绍得也很详细。
实验三相位鉴频器的实验研究一.实验目的1)了解乘积型相位鉴频器的工作原理,电路结构和性能特点。
2)学习鉴频特性的测量方法。
3)观察移相网络参数变化对鉴相特性的影响。
二.实验仪器及设备1)高频信号发生器1055A型或TFG2030型1台2)频率特性测试仪BT-3D型1台3)双踪示波器SS-7804型1台4)直流稳压电源WYJ-30F型1台5)实验电路板三.实验内容实验电路板原理图如下:图1.鉴频电路原理图1.用BT-3D型频率特性分析仪观察测试鉴频特性曲线接通实验板电源,将BT-3D的输出扫描信号连接到鉴频器的输入端,再将BT-3D输入电缆连接到实验板鉴频器输出端3点上,这样鉴频器就输入等幅的扫频信号。
使用BT-3测量本实验电路鉴频特性时,调节BT-3的扫频中心频率,使扫频仪屏幕中心位置为8MHz左右,再分别调节其“输出衰减”、“频率偏移”、“Y轴增益”等有关旋钮,可在屏幕上显示出实验电路的鉴频特性曲线。
1)描绘出屏幕上的曲线形状,利用1Mhz频标粗测鉴频器的中心频率和线性鉴频范围。
图2.扫频仪鉴频特性曲线实验粗测中心频率,鉴频范围为(6.152Mhz 8.864Mhz)图1中将接入的R5和R6的鉴频特性曲线都绘制在了一起,其中两个曲线的不同点以及产生的原因都在第2问中进行了分析,此处不做说明。
2.用逐点描记法测绘乘积型相位鉴频器的静态鉴频特性(曲线)1)用高频信号发生器作信号源,输出幅值的载波电压,加到金品器输入端,将鉴频器的输出端P3接到示波器的一个输入端,将实验板开关K1与R5相连接,使之与MC1496P的管脚8连接。
2)调节信号输出频率与扫频仪测量出的中心频率相等,这时示波器的显示在中间零点位置附近,若示波器显示未归零,可调节实验电路中电位器Rw,使示波器归到零点位置,调节信号源频率在附近变化时,可从示波器上看到扫描线在零点附近对称上下摆动,若不对称,重新调整Rw,直至完全对称。
这表明选择的信号源频率已经与移相网络回路中心频率相吻合。
北理工通信电路软件实验报告一The following text is amended on 12 November 2020.实验1数字通信系统仿真分析分析内容构造一个简单示意性基带传输系统。
以双极性PN码发生器来模拟一个数据信源,码速率为100bit/s,低通型信道噪声为加性高斯噪声(标准差=。
要求:1.观测接收输入和滤波输出的时域波形;2.观测接收滤波器输出的眼图。
分析目的掌握观察系统时域波形,重点学习和掌握观察眼图的操作方法。
系统组成及原理简单的基带传输系统原理框图如下所示,该系统并不是无码间干扰设计的,为使基带信号能量更集中,形成滤波器采用高斯滤波器。
②采样频率:Sample Rate:10000Hz。
第二步:调用图符块创建如下图所示的仿真分析系统:其中各元件参数如“图符参数便笺”所示。
Token1为高斯脉冲形成滤波器;Token3为高斯噪声发生器,设标准偏差Std Deviation=,均值Mean=0v;Token4为模拟低通滤波器,它来自操作库中的“LinearSys”图符按钮,在设置参数时,将出现一个设置对话框,在“Design”栏中单击Analog按钮,进一步点击“Filter PassBand”栏中Lowpass按钮,选择Butterworth型滤波器,设置滤波器极点数目: Poles=5,设置滤波器截止频率:LoCuttoff=200Hz。
第三步:单击运行按钮,运算结束后按“分析窗”按钮,进入分析窗后,单击“绘制新图”按钮,则Sink9-Sink12限时活动窗口分别显示出“PN码输出”、“信道输入”、“信道输出”和“判决比较输出”时域波形。
第四步:观察信源PN码和波形形成输出的功率谱。
在分析窗下,单击信宿计算器按钮,在出现的“System Sink Calculator”对话框中单击Spectrum按钮,分别得到Sink9和Sink10的功率谱窗口后,可将这两个功率谱合成在同一个窗口中进行对比,具体操作为:在“System Sink Calculator”对话框中单击Operators按钮和Overlay Plots按钮,在右侧窗口内按住左键选中w4和w5两个信息条,单击OK按钮即可显示出对比功率谱。
080902电路与系统——北京理工大学硕士研究生培养方案(2009版)2009-12-19 18:39:43 北京理工大学考研共济网点击浏览:256次·[考研一站式]北京理工大学硕士招生相关文章索引·[考研一站式]北京理工大学硕士专业课试题、[订购]考研参考书、专业目录电路与系统专080902彰武(一级学科:电子科学与技术)研网络督察电路与系统学科研究电路与系统的理论、分析、测试、设计和物理实现,它是信息与通信工程和电子科学与技术两个学科之间的桥梁,它又是信号与信息处理、通信、控制、计算机乃至电力、电子等诸方面研究和发展的理论与技术基础。
由于电路与系统学科的有力支持,才可能最有效地利用现代的电子科学技术和最新的器件实现复杂的、高性能的各种信息和通信网络与系统。
济近二十年来因为信息与系统产业的高速发展以及微电子器件集成规模的迅速增大,使电子电路与系统走向数字化、集成化、多维化。
电路与系统的经典理论向现代化理论过度,而且与信息和通讯工程、计算机学科与技术、生物电子学等学科交叠,相互渗透,形成一系列的边缘、交叉学科,如新的微处理器设计、各种数字信号处理系统、人工神经网络等。
本学科主要研究方向有:专1.信息处理与传输:信号采集与处理,网络数据融合,现代通信传输理论与技术研究。
济2.应用电子电路与系统:智能与虚拟仪器技术,综合传感器检测技术,多媒体技术、嵌入式技术,电路系统集成技术的应用性研究。
研3.功率电子学:功率控制与驱动技术,电力伺服传动技术,现代电源理论与应用技术研究。
336260 37济一、培养目标112室热爱祖国,有社会主义觉悟和较高道德修养;掌握坚实的数字、模拟、线性和非线性电路与系统的基础理论与技术,信号处理理论与技术,电路与系统的计算机辅助设计,现代信息与通信网络的理论与技术;在本研究方向有系统和深入的专门知识与实验技术;较为熟练地掌握一门外国语,能阅读本专业的外文资料;具有从事科学研究工作和独立担负专门技术工作的能力;能胜任在科研单位、生产部门或高等院校从事有关方面的研究、科技开发、教学和管理工作。
【问题1】已知:二进制信源概率场0121x x X P P ⎛⎫= ⎪-⎝⎭,用Matlab 画出其信源熵H(x)随概率P改变的曲线(0 < P < 1),从曲线中可得到什么结论?解:根据题意可算出信源熵H x =P ∙log 21P + 1−P ∙log 2 11−P通过matlab 绘制其与概率P 的函数关系如下:观察曲线可知,信源熵H(x)关于P=0.5对称分布,且概率P 越接近0.5,信源熵越大。
当概率P 为0或1时,信源熵为0。
可见,概率越接近0.5,说明其不确定性越大,那么他的信息量(信源熵)也越大;反之,概率越远离0.5,其不确定性越小,他的信息量(信源熵)也越小【问题2】按照反馈理论,正反馈环的回归比[]()()()e e A B j j T AB A B T ϕωϕωϕω+===,自激振荡后应严格满足总相角()0ϕω=或2π的整倍数。
这种振荡器在稳幅振荡后的振荡频率取决于什么因素?振荡频率能严格地等于LC 回路的谐振频率吗?为什么?解:(1)取决于放大器的相频特性和反馈网络的相频特性,振荡频率f g 要使放大器的相移φA f 与反馈网络的相移φB f 满足:φA f g =−φB f g ,以满足稳幅振荡的相角条件。
(2)不能严格的等于回路谐振频率。
大多时候,由于晶体管相移φA f 很小,工程上往往将其忽略(φA f ≈0),这时取φB f g =0,而由于在谐振频率f o 下,反馈网络相移φB f o =0,故此时稳幅振荡频率f g 近似等于LC 回路谐振频率f o 。
但是严格来讲,晶体管内有电容存在,其相移φA f ≠0,因此f g 与f o 并不相等。
【问题3】针对基于分立元件构建的LC 正弦波振荡器,请归纳其直流等效电路和交流等效电路(有些教材称为简化交流等效电路)各自的等效原则。
解:直流等效电路:电容开路,电感短路。
交流等效电路:1)所有电源无效(电压源短路,即接地;电流源开路)2)耦合电容(C 较大)短路,回路电容保留3)射频扼流圈(L 较大)开路,回路电感保留4)所有偏置电阻和负载电阻视为开路【问题4】已知:右图电路中单向导电的检波二极管D 导通电阻为D R ,求出该电路的电压传递函数为:11()(1)()()(1)o D L i L D L U s R sR C K s U s R R sR C +==++ 试问:借助拉氏变换求解该电路的传递函数正确吗?指出具体问题所在。
解:不正确。
电路中包含非线性元件二极管,因此此电路是非线性电路,而拉氏变换只能求解线性电路,不能求取该电路的传函。
【问题5】同步检波器组成框如右图,假定:()()210.9cos 0.3cos2=+Ω+Ωf t t t ;10ω=Ωc ,求: (1)用Matlab 计算并用不同颜色绘出A 、B 、C 三处的叠加波形(自定Ω值)。
(2)解释波形的有关物理含义,理解同步检波器原理。
解:(1)取Ω=100rad/s ,波形为:其中,绿色为A 处波形,红色为B 处波形,蓝色为C 处波形。
(2)A 处波形为调制信号f(t)与载波cos w c t 相乘后的调幅波(抑制载波的双边带调幅波);B 处波形为调幅波与提取出来的同步载波相乘后的波;C 处波形是B 波经过一个低通滤波器(滤去高频分量,保留低频分量)后的信号,是最终解调出来的信号。
可以看出同步检波是通过将已调幅波与同步载波相乘,得到一个新的波(B 波),而这个新波的频谱中的低频部分即是原调制信号的频谱,或者说,这个新波包含的低频分量即是原信号(成比例),因此,将这个新信号通过一个低通滤波器,滤去高频成分,保留低频成分,出来的结果就是原信号。
【问题6】(1)普通AM 波的解调是否也可以采用同步检波方式,为什么?(2)假如与接收信号相关的不是同步载波(有频差),即上图B 点信号假定为()cos c t ωω+∆,基于上述【问题5】的条件,自选ω∆取值,用Matlab 绘制上图C 点波形,观察检波效果并给出相应结论。
解:(1)可以采用。
理由:多音普通AM 波可表示为u AM t =U c V +U mΩ(t ) cos w c t ,其中, U mΩ t = U Ωmk n k =1cos Ωk t , Ω1<Ω2<⋯<ΩN−1<ΩN−1,则其同步载为 cos w c t 。
AM 波与同步载波通过乘法器相乘后,输出为:1/2U c V +U mΩ t + 1/2U c V +U mΩ t cos 2w c t 。
通过积分器,滤去高频分量后的输出:1/2U c V +U mΩ t这个结果是原调制信号加上一个直流分量,因此只需要把直流分量去除即可完成检波。
(2)取Δw =3rad /s ,则波形变为(颜色对应同问题五):可以明显看出,解调后的蓝色波形明显失真。
说明解调时提取的载波与调幅波的载波频率必须一致,否则得不到正确的调制信号波形。
【问题7】对于来自超外差接收机末级中放回路输出的调幅电压,如采用右图所示电路中的电容耦合方式,试问:(1)这时可否实现正常的包络检波,为什么?(2)如进行某种电路改进,将RFC跨接在二极管正极到地之间,这时可否实现正常的包络检波?为什么?解:(1) 不能实现。
因为二极管的存在,使得耦合电容只能充电而无法放电,因此耦合电容两端的电压将稳定在AM波的最大值。
此时传输到二极管正极的信号是AM波向下平移一个AM波最大值后的信号,此信号最大值是0,无法导通二极管,因此无法实现包络检波。
(2) 能实现。
加了RFC后,耦合电容能自由充放电,对AM波来说相当于短路,几乎没有影响,因此AM波可以正常通过包络检波器,进行检波。
或者换种解释,RFC能够通直流阻交流,(1)中在耦合电容影响下平移后的信号中的直流成分通过RFC流入地,而交流成分继续传向二极管,相当于向下平移的AM波又被搬回了原位置,因此可以通过检波器进行包络检波。
【问题8】针对线性时不变电路与线性时变电路,请从叠加定理是否满足、各自的放大功能、变频功能等属性或功能角度,归纳总结两种电路的相同与不同之处。
解:相同点:由于都是线性电路,故均满足叠加定理不同点:1)线性时不变电路的输出信号频率与输入信号频率保持一致,不具有变频功能;而线性时变电路,以单一频率输入信号为例,随着时间改变,电路对输入信号的操作(放大,相移等)也在改变,因此输出信号波形会明显不同于输入信号,其频率也自然与输入信号不同,对于多频成分的输入信号,也是如此,因此,线性时变电路具有变频功能。
2)线性时不变电路由于其定常特性,可用于波形成比例放大(放大器);线性时变电路能改变信号频率,可用于频谱搬移,调制解调等。
【问题9】模拟乘法器在什么输入条件下可作为线性时不变电路或线性时变电路使用?解:理想乘法器的特性可表示为z =Kx ∙y此时不妨令输入x 是一个非零常数,即x =C ,那么对于输入y 来说,z =KC ∙y ,KC 是一个不随时间改变的常数,此时这是一个线性非时变电路。
若令输入x 是一个交变信号,那么对于y ,z =(Kx )∙y , Kx 是一个随时间变化的数,这是一个线性时变电路。
【问题10】某非线性电路输入电压为()50.1cos 210i u t π=⨯(V),其中非线性器件的转移伏安特性为2310.70.40.2o i i i i u u u =+++(mA )。
要求:(1)试引用Matlab 中1024点的FFT 函数,绘制非线性器件输出电流o i 的幅度频谱图,说明该非线性电路具有何种特定功能?(2)如果该电路负载为理想BPF (通频带10kHz 、带内阻抗300Ω),再用Matlab 画出BPF 中心频率分别为200kHz 和300kHz 的两个输出电压时域波形,并与i u 波形对照。
解:(1)设置采样时间间隔为1×10−6s ,得到i 0的幅度频谱如下:i 0的频谱集中在低频(几乎是直流)区域,交流份量较小。
此电路能够得到输入信号频率的一倍频,二倍频,三倍频和直流的叠加 输出。
(2)BPF 中心频率分别为200kHz 时,输出频率仅包含4π×105rad /s ,此时u =0.6cos(4π×105t )BPF 中心频率分别为300kHz 时,输出频率仅包含6π×105rad /s ,此时u =0.015cos(6π×105t )这两种输出与u i 比较图如下:【问题11】已知:[][]121212sin sin c m c m u U t u U t ωϕωϕ=+=+为乘积型鉴相器(乘法器+低通滤波器)的两个同频比相电压,彼此相差为12e ϕϕϕ=-,低通滤波器输出电压o U 正比于12u u ⋅乘积的平均分量。
(1)用Matlab 计算画出LPF 输出电压与输入相位差之间的鉴相特性~o e U ϕ曲线。
结合课上学的“正弦型鉴相特性”,指出乘积型鉴相器输出电压为0时两个同频比相信号的绝对相差值。
(2)何为两个同频正交信号的相关运算?该相关值是什么?解:(1)两个输入经过模拟乘法器,在经过低通滤波器后的输出:U o = 12KU 1m U 2m cos φe其中K 为模拟乘法器的比例系数,不妨令系数12KU 1m U 2m =1,则~o e U ϕ曲线如下:当U o =0时,φe =π2+nπ (n ∈Z )。
说明曲线在π2+nπ (n ∈Z )附近可以近似看作是线性的,鉴相器的鉴相范围在π2+nπ (n ∈Z )∓23°.(2)若只考虑实数域,则两信号f (t )与g (t )的相关运算定义为:f ★g = f ∞−∞ τ g τ−t dτ用来反映两个信号的内在相关程度。
同频正交信号的相关值为0.【问题12】幅度归一化的FM 电压0()cos ()tc f u t t k u t dt ωΩ⎛⎫=+ ⎪⎝⎭⎰V ,其中()u t Ω为模拟调制电压,证明可否采用“理想微分器+包络检波器”串联的电路实现鉴频功能? 解:可以采用该电路实现鉴频,证明如下:u (t )经过微分器后,其输出u t =−[w c +k f u Ω t ]sin w c +k f u Ω t dt t 0 , 此输出经过包络检波器,将包络提取出来,输出为−[w c +k f u Ω t ],此时将该信号在通过一个耦合电容,滤去直流成分−w c ,最终输出为k f u Ω t ,实现了鉴频功能。
【问题13】调制制度增益G 定义为:接收端解调器的(输出信噪比)/(输入信噪比);线性网络的噪声系数F 定义为:线性网络的(输入信噪比)/(输出信噪比)。
那么,计算调制制度增益G 是否为解调器的噪声系数F 的倒数?请系统梳理该问题,给出合理解释。