人教版小升初数学知识点归纳
- 格式:doc
- 大小:96.50 KB
- 文档页数:14

人教版数学小升初知识点汇总一、数与代数。
1. 数的认识。
- 整数。
- 整数的意义:像 -3、-2、-1、0、1、2、3……这样的数统称为整数。
整数包括正整数、0和负整数。
- 整数的读法和写法:读数时,从高位到低位,一级一级地读,每一级末尾的0都不读出来,其他数位连续有几个0都只读一个零;写数时,从高位到低位,一级一级地写,哪一个数位上一个单位也没有,就在那个数位上写0。
- 数的大小比较:先看位数,位数多的数大;如果位数相同,从最高位比起,相同数位上的数大的那个数就大。
- 小数。
- 小数的意义:把整数“1”平均分成10份、100份、1000份……这样的一份或几份是十分之几、百分之几、千分之几……可以用小数表示。
- 小数的性质:小数的末尾添上“0”或去掉“0”,小数的大小不变。
- 小数的读法和写法:读小数时,整数部分按照整数的读法来读,小数点读作“点”,小数部分顺次读出每一位上的数字;写小数时,整数部分按照整数的写法来写,小数点写在个位右下角,小数部分顺次写出每一个数位上的数字。
- 小数的大小比较:先比较整数部分,整数部分大的数大;如果整数部分相同,再比较十分位,十分位上数大的数大;如果十分位相同,再比较百分位,依次类推。
- 分数。
- 分数的意义:把单位“1”平均分成若干份,表示这样的一份或几份的数叫做分数。
- 分数单位:把单位“1”平均分成若干份,表示其中一份的数叫做分数单位。
- 分数的分类:分数分为真分数(分子小于分母)和假分数(分子大于或等于分母),假分数可以化成带分数或整数。
- 分数的基本性质:分数的分子和分母同时乘或除以相同的数(0除外),分数的大小不变。
- 分数的大小比较:同分母分数相比较,分子大的分数大;同分子分数相比较,分母小的分数大;异分母分数比较大小,先通分再比较。
- 百分数。
- 百分数的意义:表示一个数是另一个数的百分之几的数叫做百分数,也叫百分率或百分比。
百分数通常不写成分数形式,而采用百分号“%”。


人教版小升初数学知识点汇总这篇文档旨在全面总结人教版小学六年级数学知识点,帮助同学们系统复习,为顺利升入初中打下坚实的基础。
内容涵盖数与代数、图形与几何、统计与概率三大模块,并配以例题讲解和练习题,力求做到深入浅出,通俗易懂。
一、数与代数1. 数的认识:• 整数: 包括自然数(0, 1, 2, 3…)和负整数(-1, -2, -3…)。
理解整数的意义、大小比较、数位和计数单位,掌握整数的读写方法。
熟练运用数轴表示整数。
• 小数: 理解小数的意义、计数单位,掌握小数的读写方法,能进行小数的比较大小、加减乘除运算。
理解小数的意义与分数的关系,能进行小数与分数的互化。
• 分数: 理解分数的意义,掌握分数的基本性质,能进行约分、通分、比较大小、加减乘除运算。
理解分数与小数的关系,能进行分数与小数的互化。
• 百分数: 理解百分数的意义,能进行百分数与分数、小数的互化,并能解决相关的实际问题。
例如,求一个数的百分之几是多少,求百分率等。
• 比和比例: 理解比的意义和性质,会求比值,能解决比例问题。
理解比例的意义,会判断成比例线段,会解比例。
掌握比例尺的计算和应用。
• 数的整除: 理解整除的意义,掌握约数、倍数、质数、合数、质因数的概念,能进行质因数分解。
掌握最大公约数和最小公倍数的求法,并能解决相关的实际问题。
例题1: 一个数由3个亿、5个千万、7个万和2个百组成,这个数写作________,读作________。
例题2: 把分数 35 化成小数是________,把小数 0.75 化成分数是________。
例题3: 求 12 和 18 的最大公约数和最小公倍数。
练习题1:1. 写出下列各数:三千零五万零八百; 二亿零五百万。
2. 将下列分数化成小数:14,38,523. 将下列小数化成分数:0.25,0.6,1.254. 求 24 和 36 的最大公约数和最小公倍数。
5. 一个长方形的长是 15cm ,宽是 10cm ,它的周长是多少?面积是多少?2. 代数初步:•用字母表示数:理解用字母表示数的意义,能用字母表示数量关系和计算公式。

小升初数学复习知识点大全
一、整数运算
1.整数的概念
2.整数的加法、减法
3.整数的乘法、除法
4.整数的大小比较
5.整数的绝对值
二、分数运算
1.分数的概念
2.分数的加法、减法
3.分数的乘法、除法
4.分数的化简
5.分数的大小比较
三、小数运算
1.小数的概念
2.小数的加法、减法
3.小数的乘法、除法
4.小数的大小比较
5.小数与分数的相互转换
四、数字的性质
1.奇数、偶数的概念及判断方法
2.能被2整除的性质
3.能被3整除的性质
4.能被5整除的性质
5.能被9整除的性质
五、算式的变形与意义
1.加减法的结合律、交换律、分配律
2.乘除法的意义与性质
3.乘除法的结合律、交换律
4.简单算式的变形与计算
六、数与代数
1.数的概念及分类
2.自然数、整数、分数、小数等的互相转换
3.代数式的概念及构成
4.代数式的计算
七、常见几何图形
1.点、线、线段、射线的概念
2.直角、钝角、锐角的概念
3.正方形、长方形、三角形、菱形、梯形的定义、性质及判断方法
4.圆的定义、性质及计算
八、面积、体积、容量
1.长方形、正方形、三角形、圆形的面积计算
2.立方体、长方体、圆柱体的体积计算
3.比较两个面积或体积的大小
4.容积的计算
九、时刻、时区
1.时间的概念及表示方法
2.24小时制与12小时制的互换
3.时分数与分数的互换
4.时区的概念与计算
十、逻辑问题
1.推理与判断
2.常见逻辑问题的解答方法。

人教版小升初数学基础知识点整理
本文将介绍人教版小学数学基础知识点,用于小学生小升初考试复备考。
数的认识
自然数
1. 自然数的概念
2. 自然数的认识
3. 自然数的顺序
整数
1. 整数的概念
2. 整数的加减法
分数
1. 分数的概念
2. 分数的加减法(同分母、异分母)
3. 分数的乘除法
小数
1. 小数的概念
2. 小数的加减法
3. 小数的乘除法
计算
算式
1. 算式的组成
2. 算式的性质
整数四则运算
1. 整数加减法
2. 整数乘除法
分数四则运算
1. 分数加减法
2. 分数乘除法
小数四则运算
1. 小数加减法
2. 小数乘除法
除法中的整除和余数
1. 除法中的基本概念
2. 除法中的整除和余数概念
3. 整除和余数的应用
几何
图形的认识
1. 点、线、面的概念
2. 常见图形的认识:三角形、矩形、正方形、圆
长度
1. 长度的概念
2. 常用长度单位
面积
1. 面积的概念
2. 常见图形的面积公式:三角形、矩形、正方形、圆容积和质量
1. 容积的认识和常用容积单位
2. 质量的认识和常用质量单位
数据统计
统计图表
1. 直方图的认识
2. 条形图的认识
3. 折线图的认识
数据的处理
1. 数据的收集和整理
2. 数学中的平均数:平均数的概念和计算方法
以上是人教版小升初数学基础知识点的整理,希望对小学生小升初考试复备考有所帮助。


专题1-相遇问题小升初数学思维拓展行程问题专项训练(知识梳理+典题精讲+专项训练)1、两个运动物体作相向运动或在环形跑道上作背向运动,随着时间的发展,必然面对面地相遇,这类问题叫做相遇问题.它的特点是两个运动物体共同走完整个路程.2、小学数学教材中的行程问题,一般是指相遇问题.相遇问题根据数量关系可分成三种类型:求路程,求相遇时间,求速度.它们的基本关系式如下:总路程=(甲速+乙速)×相遇时间相遇时间=总路程÷(甲速+乙速)另一个速度=甲乙速度和-已知的一个速度.【典例一】如图,有一段山路,从A到B是2千米的上坡路,从B到C是4千米的平路,从C到D是2.4千米的上坡路.欢欢和笑笑分别从A、D同时出发,相向而行,他们下坡的速度都是每小时6千米,平路的速度都是每小时4千米,上坡的速度都是每小时2千米,他们经过_______小时相遇.()A.0.2B.0.3C.1.2D.1.3【分析】此题应先求出欢欢上坡和笑笑下坡分别用的时间,欢欢上坡用的时间是:221÷=(小时),笑笑下坡用的时间是:2.460.4÷=(小时);因为10.4>所以当笑笑走完2.4千米的下坡路时,欢欢还没有走完2千米的上坡路,在欢欢走上坡路的同时,笑笑又走了的平路,(10.4)4 2.4-⨯=(千米);这时欢欢走完了上坡路,两人都走平路,平路还有:-=(千米),又因为平路上速度都是每小时4千米,因此走完平路所用的时间为4 2.4 1.61.6(42)0.2÷⨯=(小时);那么两人相遇时间就10.2+小时.【解答】解:①欢欢上坡用的时间是:221÷=(小时),②笑笑下坡用的时间是:2.460.4÷=(小时);③笑笑先走了平路的路程:(10.4)4 2.4-⨯=(千米);④还剩下的路程(最后欢欢和笑笑共同走的平路):4 2.4 1.6-=(千米);⑤剩下路程需要的时间:1.6(42)0.2÷⨯=(小时);⑥相遇共用时间:10.2 1.2+=(小时);答:两人1.2小时后相遇.故选:C .【点评】此题条件较复杂,注意理清思路,细细分析.本题的关键在于确定相遇的位置.【典例二】已知猫跑5步的路程与狗跑3步的路程相同,猫跑7步的路程与兔跑5步的路程相同.而猫跑3步的时间与狗跑5步的时间相同;猫跑5步的时间和兔跑7步的时间相同,猫、狗、兔沿着周长为400米的圆形跑道,同时同向同地出发,问,当他们出发后,第一次相遇时狗跑了米.【分析】已知猫跑5步的路程与狗跑3步的路程相同,即狗跑1步的路程是猫跑53步的路程,又因为而猫跑3步的时间与狗跑5步的时间相同;所以猫和狗的速度比是53:(5)9:253⨯=;同理可求猫和兔的速度比是75:(7)25:495⨯=;所以,猫、狗、兔的速度比是25491::225:625:441925=,狗追上猫一圈需400(625225)1÷-=(单位时间),兔追上猫一圈需50400(441225)27÷-=(单位时间),所以第一次相遇时间:[1,50]5027=(单位时间),然后乘625就是第一次相遇时狗跑的距离.【解答】解:53:(5)9:253⨯=75:(7)25:495⨯=25491::225:625:441925=400(625225)1÷-=(单位时间)50400(441225)27÷-=(单位时间)[1,50]5027=(单位时间)6255031250⨯=(米)答:第一次相遇时狗跑了31250米.故答案为:31250.【点评】本题考查了比较复杂的环形跑道问题和分数的最小公倍数的综合应用,关键是求出它们的速度比.【典例三】西安和合肥是“:一带一路”战略规划中两个重要的内陆节点城市,客、货两车分别从合肥、西安两地相对开出。

人教部编版小升初数学考试必须掌握的知识点大全一、整数的概念与运算1.整数的概念及表示方法2.整数的加法和减法运算3.同号整数相加减,异号整数相加减4.整数的乘法和除法运算5.正整数的倒数6.整数的乘方运算二、分数与有理数1.分数的概念及表示方法2.分数的比较与大小关系3.分数的加法和减法运算4.分数的乘法和除法运算5.分数的化简与约分6.整数与分数的互化7.有理数的概念三、小数与百分数1.小数的概念及表示方法2.小数与分数的关系3.小数的加减法运算4.小数的乘法和除法运算5.百分数的概念及表示方法6.百分数与分数、小数的关系四、平方根与立方根1.平方根的概念及表示方法2.立方根的概念及表示方法3.整数的平方与立方4.非负数的平方根5.整数的近似平方根6.非负数的近似平方根五、代数式与简便计算1.代数式的概念及表示方法2.代数式的值、项与项数3.简单代数式的加减法4.正数与负数的乘法运算5.开方运算中的代数式六、比例与比例运算1.比例的概念及表示方法2.比例的性质及简化3.比例的延长与缩短4.比例关系与比例的验证5.比例的加减乘除运算七、图形的认识与计算1.点、线、面、角的概念2.直线、直线段、射线、线段的区别3.角的分类及角的比较4.平行线、垂线、相交线及其特点5.三角形、四边形的性质6.平面图形的面积与周长八、图表的分析与应用1.数据的搜集与处理2.直方图及其应用3.折线图及其应用4.圆饼图及其应用九、函数的初步认识1.函数的概念及表示方法2.函数的自变量和因变量3.函数的变化规律4.函数图象的简单认识总结:以上是小升初数学考试必须掌握的知识点大全,涵盖了整数、分数、小数、百分数、代数式、比例、图形、图表和函数等方面的内容。
掌握这些知识点,可以帮助学生全面提高数学能力并顺利应对小升初数学考试。
希望同学们在备考过程中能够重点关注这些知识点,并通过多做练习题来加深理解和掌握。
祝大家考试顺利!。
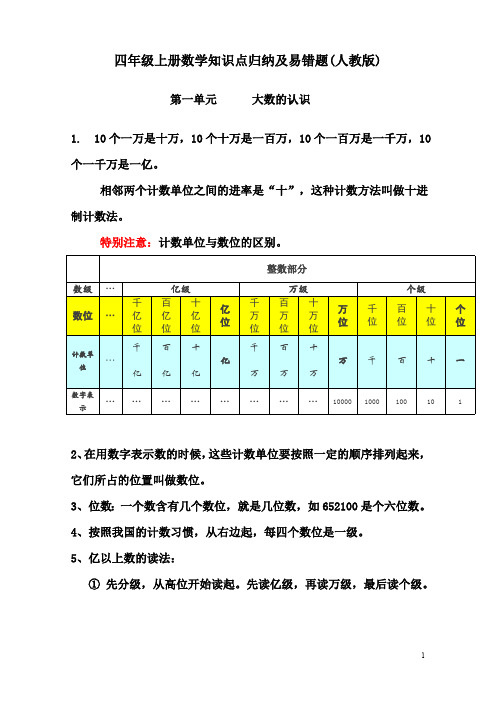
四年级上册数学知识点归纳及易错题(人教版)第一单元大数的认识1. 10个一万是十万,10个十万是一百万,10个一百万是一千万,10个一千万是一亿。
相邻两个计数单位之间的进率是“十”,这种计数方法叫做十进制计数法。
特别注意:计数单位与数位的区别。
2、在用数字表示数的时候,这些计数单位要按照一定的顺序排列起来,它们所占的位置叫做数位。
3、位数:一个数含有几个数位,就是几位数,如652100是个六位数。
4、按照我国的计数习惯,从右边起,每四个数位是一级。
5、亿以上数的读法:①先分级,从高位开始读起。
先读亿级,再读万级,最后读个级。
②亿级的数要按照个级的数的读法来读,再在后面加上一个“亿”字。
万级的数要按照个级的数的读法来读,再在后面加上一个“万”字。
③每级末尾不管有几个0,都不读。
其他数位有一个“0”或连续几个“0”,都只读一个“0”。
6、亿以上数的写法:①从最高位写起,先写亿级,再写万级,最后写个级。
②哪个数位上一个单位也没有,就在那个数位上写0。
7、比较数的大小:①位数不同的两个数,位数多的数比较大。
②位数相同的两个数,从最高位开始比较。
8、求近似数:省略万位后面的尾数,要看千位上的数;省略亿位后面的尾数,要看千万位上的数。
这种求近似数的方法叫“四舍五入法”,是“舍”还是“入”,要看省略的尾数最高位上的数是小于5 还是等于或大于5 。
小于5就舍去尾数,等于或大于5就向前一位进1,再舍去尾数。
9、表示物体个数:1,2 ,3, 4, 5 ,6 ,7 ,8 ,9 ,10, ……. 都是自然数。
一个物体也没有,用0来表示, 0也是自然数。
所有的自然数都是整数。
10、最小的自然数是0,没有最大的自然数,自然数的个数是无限的。
11、每相邻的两个计数单位之间的进率都是十,这种计数方法叫做十进制计数法。
12、ON╱CE:开关及清除屏键,清除显示屏上的内容。
AC:清除键,清除所有内容。
第二单元公顷和平方千米1、边长是100米的正方形面积是1公顷。

专题2-奇偶性问题小升初数学思维拓展数论问题专项训练(知识梳理+典题精讲+专项训练)一、主要用到的知识点。
1.奇数±奇数=偶数;偶数±偶数=偶数;奇数±偶数=奇数;偶数±奇数=奇数。
2.奇数个奇数的和(或差)为奇数,偶数个奇数的和(或差)为偶数,任意多个偶数的和(或差)为偶数。
3.奇数×奇数=奇数;偶数×偶数=偶数;奇数×偶数=偶数。
4.若干个数相乘,其中有一个因数是偶数,则积为偶数;如果所有的因数都是奇数,则积为奇数。
5.偶数的平方能被4整除,奇数的平方被4除余1。
【典例一】桌子上放有20个茶杯,口向上按编号从①到⑳在桌子上排成一行第一次,贝贝将编号是偶数的杯子翻一次第二次,丽丽将编号是3的倍数的杯子翻一次第三次,甜甜将编号是5的倍数的杯子翻一次现在口向上的杯子有()个.(口向上的翻一次口问下,口向下的翻一次口向上)A.12B.0C.10D.11【答案】A【分析】初始所有的杯子都是口朝上的,第一次,贝贝将编号是偶数的杯子翻一次,此时编号是2的倍数的口朝下,奇数口朝上.第二次,丽丽将编号是3的倍数的杯子翻一次,此时编号同时是2和3的倍数的杯子口朝上(比如6,第一次贝贝翻后口朝下,第二次丽丽也会翻它,翻完口朝上),只是2或3倍数的杯子口朝下.第三次,甜甜将编号是5的倍数的杯子翻一次,此时编号同时是2和5的倍数,以及同时是3和5的倍数的杯子口朝上,只是2或3或5倍数的杯子口朝下.总数2-的倍数个数3-的倍数的个数5-的倍数的个数2+和3的公倍数的个数22⨯+和5的公倍数的个数23⨯+和5的公倍数的个数2⨯.【解答】解:20106324221212--+⨯-+⨯+⨯=(个)答:现在杯子口向上的有12个.故选:A 。
【点评】要注意2和3的公倍数、2和5的公倍数、3和5的公倍数都转了两次.【典例二】一名班长在甲车间和乙车间之间往返巡视,最初他在甲车间。

2024年小升初数学总复习资料归纳2024年小升初数学总复习资料归纳一、数与代数1、整数(1)整数及其运算①整数包括自然数、负整数和0 ②加减法:整数加法法则“从右往左,依次相加”,整数减法法则“从右往左,依次相减”③乘除法:整数的乘法法则和除法法则与自然数的相同④分数的初步认识:理解分数的意义,会比较同分母分数的大小,会进行同分母分数的加减法(2)数的整除①整除:如果一个整数能被另一个整数整除,那么第二个整数就是第一个整数的约数,第一个整数是第二个整数的倍数②质数与合数:一个数只有1和它本身两个约数,这样的数叫做质数;一个数除了1和它本身还有别的约数,这样的数叫做合数③分解质因数:把一个合数分解成若干个质数的积④公因数与最大公因数:几个数共有的因数叫做它们的公因数,其中最大的那个公因数叫做它们的最大公因数⑤用最大公因数分解法把一个多项式因式分解2、分数与百分数(1)分数的意义和性质①分数的意义:把单位“1”平均分成若干份,表示这样的一份或几份的数叫做分数②分数的性质:分数的分子和分母同时乘或除以相同的数(0除外),分数的大小不变③分数大小的比较:同分母分数,分子大的分数大;同分子分数,分母小的分数大;不同分母和分子的分数,先通分再比较大小④分数的加减法:同分母分数相加减,分母不变,把分子相加减;异分母分数相加减,先通分,再按同分母分数相加减的方法进行计算(2)百分数:表示一个数是另一个数的百分之几的数叫做百分数,也叫百分比或百分率3、小数(1)小数的意义和性质①小数的意义:把整数“1”平均分成10份、100份、1000份……这样的一份或几份是十分之几、百分之几、千分之几……可以用小数表示,小数点左边写整数部分,右边写小数部分②小数的性质:小数点左边整数部分相同的两个小数,左边的那个比右边的那个大;小数点左边整数部分不同的两个小数,整数部分大的那个比较大;小数点右边部分相同的两个小数,右边的那个比左边的那个大;小数点右边部分不同的两个小数,右边部分大的那个比较大;小数比大小,先比较整数部分,整数部分大的那个数就大;如果整数部分相同,就比较小数部分,小数部分大的那个数就大;若小数部分仍相同,再比较小数部分,小数部分从左往右依次数第几个数字,如果这个数字比别的数字大,那么这个小数就大(2)小数的四则运算①小数的加法:小数加法的计算法则与整数加法的计算法则相同,注意进位;如果几个小数相加的和有整数部分也有小数部分,要先计算小数部分,再与整数部分相加;如果小数部分的末尾有0,根据小数的基本性质,应该去掉小数末尾的0 ②小数的减法:小数减法的计算法则与整数减法的计算法则相同,注意退位;计算小数减法时,如果被减数与减数的整数部分相同,被减数的整数部分要加上小数部分然后再减;如果被减数的整数部分比减数的整数部分大10、100、1000……这时要用被减数的整数部分加1再减,或者把减数化成比它小的整数再减③小数的乘法:根据乘法的意义,小数乘法的计算法则与整数乘法的计算法则相同④小数的除法:小数除法的计算法则与整数除法的计算法则相同,但要从高位起,用一位一位地除下去;除数是整数的小数除法要注意商的小数点要和被除数的小数点对齐;除数是小数的小数除法要把除数和被除数都化成整数再计算;在除得比被除数还多时,可以添0再继续除;一个数除以一个纯小数等于乘这个纯小数的倒数;一个数除以带分数等于这个带分数化成假分数后再乘;在连除或乘除中如果有带分数也要把带分数。

人教版小升初数学总复习知识点归纳一、整数1. 整数的概念和表示法整数包括正整数、负整数和0,用正数、负数和0表示。
2. 整数的比较和序数比较整数的大小和次序,以及正数、负数和0之间的大小关系。
3. 整数的绝对值定义整数的绝对值,掌握求整数绝对值的方法。
4. 整数的运算掌握整数加、减、乘、除、取模的方法,掌握带括号的整数加减法。
5. 整数的混合运算掌握整数的混合运算,包括加减乘除、比较大小等。
二、小数1. 小数的概念和表示法小数是指整数和分数的分数,用小数点及数字表示。
2. 小数的比较和序数比较小数的大小和次序,以及正数、负数和0之间的大小关系。
3. 小数的四则运算掌握小数加、减、乘、除的方法,注意运算规律和精确度。
4. 小数的应用掌握小数的应用,如计算面积、长度、体积等。
三、分数1. 分数的概念和表示法分数是指一个整数除以另一个整数所得的结果,用分数线表示。
2. 分数的比较和序数比较分数的大小和次序,掌握分数的大小关系。
3. 分数的四则运算掌握分数的加减乘除运算,注意分数变形和通分。
4. 分数的应用掌握分数的应用,如计算比例、时间、速度等。
四、代数式1. 代数式的概念和表示法代数式是由数字和字母经过运算符号连接而成的式子。
2. 代数式的运算掌握代数式的加、减、乘、除、化简运算,注意符号变化。
3. 代数式的应用掌握代数式的应用,如解方程、求未知数等。
五、图形与几何1. 二维图形的认识认识平面直角坐标系、点、线、角等基本概念。
2. 二维图形的性质掌握二维图形的长度、面积、角度、对称性等性质。
3. 二维图形的分类认识三角形、四边形、多边形等二维图形,掌握其分类、性质及判定方法。
4. 三维图形的认识认识空间直角坐标系、点、线、面、体等基本概念。
5. 三维图形的性质掌握三维图形的长度、面积、体积、角度、对称性等性质。
6. 三维图形的分类认识立方体、长方体、正方体等三维图形,掌握其分类、性质及判定方法。
六、时间和单位换算1. 时间的基本单位和换算掌握秒、分钟、小时、天之间的换算方法,能够计算时间差。

人教版小升初数学总复习知识点归纳目录•整数•分数•小数•比例和比例的应用•百分数•代数式•平面图形的认识•三角形类比、分类及性质•直角三角形及其三边关系•四边形类比及性质•平面图形的计算•基本统计量整数•整数的概念及表示•整数的比较•加减法及应用•整数的乘法及应用•整数的除法及应用•整数的绝对值•整数的倍数•公约数、最大公约数•公倍数、最小公倍数分数•分数的概念•带分数的概念•真分数、假分数•分数的约分•分数的等分和不等分•分数的比较•分数的加减法及应用•分数的乘法及应用•分数的除法及应用•分数和小数的换算小数•小数的概念和读法•小数的四则运算•小数的比较•小数的整数部分和小数部分•精确到小数的加减法及应用•精确到小数的乘法及应用•精确到小数的除法及应用•小数和分数的换算比例和比例的应用•比例的概念、表示和计算•合、分、比的概念和计算•比例的性质•解决实际问题中的比例关系百分数•百分数的概念和表示•百分数与分数、小数的相互转化•百分数的四则运算•百分数的应用代数式•代数式的概念和表示•代数式的加减和化简•同类项和不同类项•代数式的乘法及应用•代数式的除法及应用•公式的运用平面图形的认识•点、线、面的概念和判断•直线、线段、射线的判断和表示•角的概念与表示•角的比较和分类•角的度量三角形类比、分类及性质•三角形的概念•三角形的种类及构造•三角形的性质直角三角形及其三边关系•直角三角形的性质和分类•勾股定理及解题应用•谁短谁长规律及证明•正弦、余弦、正切比及定义四边形类比及性质•四边形的概念及性质•矩形、平行四边形、菱形和正方形的性质和判定•梯形的性质和判定•多边形名称的认识平面图形的计算•长方体和正方体的认识•圆的概念及计算•周长、面积的概念和计算(矩形、平行四边形、菱形、正方形、三角形、梯形)•直接读数题、间接读数题基本统计量•件数、频数、频率的概念•频数表和频率分布图的绘制•众数和中位数的概念和求法•平均数的概念和求法•统计图的绘制和分析。

【人教版】小升初数学总复习知识点归纳总结常用的数量关系式1、每份数×份数=总数总数÷每份数=份数总数÷份数=每份数2、1倍数×倍数=几倍数几倍数÷1倍数=倍数几倍数÷倍数=1倍数3、速度×时间=路程路程÷速度=时间路程÷时间=速度4、单价×数量=总价总价÷单价=数量总价÷数量=单价5、工作效率×工作时间=工作总量工作总量÷工作效率=工作时间工作总量÷工作时间=工作效率6、加数+加数=和和-一个加数=另一个加数7、被减数-减数=差被减数-差=减数差+减数=被减数8、因数×因数=积积÷一个因数=另一个因数9、被除数÷除数=商被除数÷商=除数商×除数=被除数小学数学图形计算公式1、正方形(C:周长 S:面积 a:边长)周长=边长×4 C=4a面积=边长×边长S=a×a2、正方体(V:体积 a:棱长)表面积=棱长×棱长×6 S表=a×a×6体积=棱长×棱长×棱长V=a×a×a3、长方形( C:周长 S:面积 a:边长)周长=(长+宽)×2 C=2(a+b)面积=长×宽 S=ab4、长方体(V:体积 s:面积 a:长 b: 宽 h:高)(1)表面积(长×宽+长×高+宽×高)×2 S=2(ab+ah+bh)(2)体积=长×宽×高 V=abh5、三角形(s:面积 a:底 h:高)面积=底×高÷2 s=ah÷2三角形高=面积×2÷底三角形底=面积×2÷高6、平行四边形(s:面积 a:底 h:高)面积=底×高 s=ah7、梯形(s:面积 a:上底 b:下底 h:高)面积=(上底+下底)×高÷2 s=(a+b)× h÷28、圆形(S:面积 C:周长л d=直径 r=半径)(1)周长=直径×л=2×л×半径 C=лd=2лr(2)面积=半径×半径×л9、圆柱体(v:体积 h:高 s:底面积 r:底面半径 c:底面周长)(1)侧面积=底面周长×高=ch(2лr或лd) (2)表面积=侧面积+底面积×2(3)体积=底面积×高(4)体积=侧面积÷2×半径10、圆锥体(v:体积 h:高 s:底面积 r:底面半径)体积=底面积×高÷311、总数÷总份数=平均数15、相遇问题相遇路程=速度和×相遇时间相遇时间=相遇路程÷速度和速度和=相遇路程÷相遇时间16、浓度问题溶质的重量+溶剂的重量=溶液的重量溶质的重量÷溶液的重量×100%=浓度溶液的重量×浓度=溶质的重量溶质的重量÷浓度=溶液的重量17、利润与折扣问题利润=售出价-成本利润率=利润÷成本×100%=(售出价÷成本-1)×100%涨跌金额=本金×涨跌百分比利息=本金×利率×时间税后利息=本金×利率×时间×(1-20%)常用单位换算长度单位换算1千米=1000米1米=10分米1分米=10厘米1米=100厘米1厘米=10毫米面积单位换算1平方千米=100公顷1公顷=10000平方米1平方米=100平方分米1平方分米=100平方厘米1平方厘米=100平方毫米体(容)积单位换算1立方米=1000立方分米1立方分米=1000立方厘米1立方分米=1升1立方厘米=1毫升1立方米=1000升重量单位换算1吨=1000 千克1千克=1000克1千克=1公斤人民币单位换算1元=10角1角=10分1元=100分时间单位换算1世纪=100年1年=12月大月(31天)有:1\3\5\7\8\10\12月小月(30天)的有:4\6\9\11月平年2月28天, 闰年2月29天平年全年365天, 闰年全年366天1日=24小时1时=60分1分=60秒1时=3600秒分数的基本性质分数的基本性质:分数的分子和分母都乘以或者除以相同的数(零除外),分数的大小不变。

小升初数学总复习资料归纳常用的数量关系式1、每份数×份数=总数总数÷每份数=份数总数÷份数=每份数2、1倍数×倍数=几倍数几倍数÷1倍数=倍数几倍数÷倍数=1倍数3、速度×时间=路程路程÷速度=时间路程÷时间=速度4、单价×数量=总价总价÷单价=数量总价÷数量=单价5、工作效率×工作时间=工作总量工作总量÷工作效率=工作时间工作总量÷工作时间=工作效率6、加数+加数=和和-一个加数=另一个加数7、被减数-减数=差被减数-差=减数差+减数=被减数8、因数×因数=积积÷一个因数=另一个因数9、被除数÷除数=商被除数÷商=除数商×除数=被除数小学数学图形计算公式1、正方形(C:周长 S:面积 a:边长)周长=边长×4 C=4a面积=边长×边长S=a×a2、正方体(V:体积 a:棱长)表面积=棱长×棱长×6 S表=a×a×6体积=棱长×棱长×棱长V=a×a×a3、长方形( C:周长 S:面积 a:边长)周长=(长+宽)×2 C=2(a+b)面积=长×宽 S=ab4、长方体(V:体积 s:面积 a:长 b: 宽 h:高)(1)表面积(长×宽+长×高+宽×高)×2 S=2(ab+ah+bh)(2)体积=长×宽×高 V=abh5、三角形(s:面积 a:底 h:高)面积=底×高÷2 s=ah÷2三角形高=面积×2÷底三角形底=面积×2÷高6、平行四边形(s:面积 a:底 h:高)面积=底×高 s=ah7、梯形(s:面积 a:上底 b:下底 h:高)面积=(上底+下底)×高÷2 s=(a+b)× h÷28、圆形(S:面积 C:周长л d=直径 r=半径)(1)周长=直径×л=2×л×半径 C=лd=2лr(2)面积=半径×半径×л9、圆柱体(v:体积 h:高 s:底面积 r:底面半径 c:底面周长)(1)侧面积=底面周长×高=ch(2лr或лd) (2)表面积=侧面积+底面积×2(3)体积=底面积×高(4)体积=侧面积÷2×半径10、圆锥体(v:体积 h:高 s:底面积 r:底面半径)体积=底面积×高÷311、总数÷总份数=平均数12、和差问题的公式(和+差)÷2=大数 (和-差)÷2=小数13、和倍问题和÷(倍数-1)=小数小数×倍数=大数 (或者和-小数=大数)14、差倍问题差÷(倍数-1)=小数小数×倍数=大数 (或小数+差=大数)15、相遇问题相遇路程=速度和×相遇时间相遇时间=相遇路程÷速度和速度和=相遇路程÷相遇时间16、浓度问题溶质的重量+溶剂的重量=溶液的重量溶质的重量÷溶液的重量×100%=浓度溶液的重量×浓度=溶质的重量溶质的重量÷浓度=溶液的重量17、利润与折扣问题利润=售出价-成本利润率=利润÷成本×100%=(售出价÷成本-1)×100%涨跌金额=本金×涨跌百分比利息=本金×利率×时间税后利息=本金×利率×时间×(1-20%)常用单位换算长度单位换算1千米=1000米1米=10分米1分米=10厘米1米=100厘米1厘米=10毫米面积单位换算1平方千米=100公顷1公顷=10000平方米1平方米=100平方分米1平方分米=100平方厘米1平方厘米=100平方毫米体(容)积单位换算1立方米=1000立方分米1立方分米=1000立方厘米1立方分米=1升1立方厘米=1毫升1立方米=1000升重量单位换算1吨=1000 千克1千克=1000克1千克=1公斤人民币单位换算1元=10角1角=10分1元=100分时间单位换算1世纪=100年1年=12月大月(31天)有:1\3\5\7\8\10\12月小月(30天)的有:4\6\9\11月平年2月28天, 闰年2月29天平年全年365天, 闰年全年366天1日=24小时1时=60分1分=60秒1时=3600秒基本概念第一章数和数的运算一概念(一)整数1 整数的意义自然数和0都是整数。

2020最新人教版小升初数学知识要点汇总第一部份数与代数(一)数的认识整数【正数、0、负数】一、一个物体也没有,用0表示。
0和1、2、3……都是自然数。
自然数是整数。
二、最小的一位数是1,最小的自然数是0。
三、零上4摄氏度记作+4℃;零下4摄氏度记作-4℃。
“+4”读作正四。
“-4”读作负四。
+4也可以写成4。
四、像 +4、19、+8844这样的数都是正数。
像-4、-11、-7、-155这样的数都是负数。
五、0既不是正数,也不是负数。
正数都大于0,负数都小于0。
六、通常情况下,比海平面高用正数表示,比海平面低用负数表示。
七、通常情况下,盈利用正数表示,亏损用负数表示。
八、通常情况下,上车人数用正数表示,下车人数用负数表示。
九、通常情况下,收入用正数表示,支出用负数表示。
十、通常情况下,上升用正数表示,下降用负数表示。
小数【有限小数、无限小数】一、分母是10、100、1000……的分数都可以用小数表示。
一位小数表示十分之几,两位小数表示百分之几,三位小数表示千分之几……二、整数和小数都是按照十进制计数法写出的数,个、十、百……以及十分之一、百分之一……都是计数单位。
每相邻两个计数单位间的进率都是10。
三、每个计数单位所占的位置,叫做数位。
数位是按照一定的顺序排列的。
四、小数的性质:小数的末尾添上“0”或去掉“0”,小数的大小不变。
五、根据小数的性质,通常可以去掉小数末尾的“0”,把小数化简。
六、比较小数大小的一般方法:先比较整数部分的数,再依次比较小数部分十分位上的数,百分位上的数,千分位上的数,从左往右,如果哪个数位上的数大,这个小数就大。
七、把一个数改写成用“万”或“亿”作单位的数,在万位或亿位右边点上小数点,再在数的后面添写“万”字或“亿”字。
九、整数和小数的数位顺序表:分数【真分数、假分数】三、分数、小数、百分数的互化。
(1)把分数化成小数,用分数的分子除以分母。
(2)把小数化成分数,先改写成分母是10、100、1000……的分数,再约分。

人教版小学数学知识点整理数和数的运算一、数的意义:1、自然数: 我们在数物体的时候,用来表示物体个数的0、1、2、3、4……叫做自然数。
最小的自然数是0,没有最大的自然数。
自然数的单位是(1)。
2、 分数:把单位“1”平均分成若干份,表示这样的一份或几份的数,叫做分数。
在分数里,表示把单位“1”平均分成多少分的数,叫做分数的分母;表示去了多少份的数,叫做分数的分子;其中一份的数,叫做分数单位。
例:①32的分数单位是(31);3个(31)是1。
②32表示把单位“1”平均分成3份,表示这样的2份的数;还可以表示把2平均分成3份,表示这样一份的数。
③看图写分数(区分)(45)(211) ④通分。
8365和 65=4645⨯⨯=242083=3833⨯⨯=249 ⑤约分。
25分=(125)时 想:60分=1小时,⑥分数化成带分数或整数。
④⑤⑥利用的是分数的基本性质:分数的分子和分母同时乘或者除以相同的数(0除外)。
分数的大小不变。
这叫做分数的基本性质。
两个数相除,它们的商可以用分数表示。
即:a ÷b=ba(b ≠0) 3、小数把整数“1”平均分成10份、100份、1000份……这样的一份或几份是十分之几、百分之几、千分之几…..可以用小数表示。
例:0.9表示9个十分之一(0.1);0.28表示28个百分之一(0.01);1.024表示1024个千分之一(0.001)二、计数单位、数位。
(1)整数地计数单位有:个(一)、十、百、千、万、十万、百万、千万、亿……小数的计数单位有:十分之一(0.1)、百分之一(0.01)、千分之一(0.001)…… (2)每相邻的两个计数单位之间的进率都是10,这种计数方法,叫做十进制计数法。
(3)把计数单位按照一定的顺序排列起来,他们各自所占的位置叫做数位。
例如:千位、百位、十位、个位、十分位、百分位…… 都叫数位。
(4)数位顺序表。
整数、小数数位顺序表例:40906这个数中,“4”表示(4个千),“9”表示(9个百),“6”表示(6个一)。

小升初数学所有知识点整理版一、数的认识1.自然数2.整数3.分数4.小数5.负数6.整数的比较与大小二、运算规律1.加法运算2.减法运算3.乘法运算4.除法运算5.运算顺序与优先级6.逆运算三、数的整除与倍数1.整除与倍数的概念2.最大公约数3.最小公倍数4.公约数与公倍数的关系5.求最大公约数和最小公倍数的方法四、四则运算1.加法2.减法3.乘法4.除法5.带括号的四则运算6.含分数的四则运算五、分数的运算1.分数的加法2.分数的减法3.分数的乘法4.分数的除法5.假分数与真分数的互换6.分数的约简与比较六、小数的运算1.小数的加法2.小数的减法3.小数的乘法4.小数的除法5.小数与分数的互换6.百分数的运算及应用七、长度的换算1.厘米、分米、米的互换2.公里、米的换算3.吨、千克、克的换算4.货币单位的换算八、时间的换算1.时、分、秒的换算2.年、月、日的换算3.时、分、秒的加减运算九、长度的比较1.毫米、厘米、分米、米的比较2.公里、米的比较3.千克、克、毫克的比较十、图形与几何1.点、线、面的认识2.直线、曲线的认识3.角的认识4.直角、钝角、锐角的比较5.正方形、长方形、三角形、圆形的认识6.各种图形的计算十一、数的应用1.预算与计算器的使用2.问题解决的方法与步骤3.简单方程式的解法4.平均数5.概率的认识与计算。
数和数的运算一概念(一)整数1 整数的意义自然数和0都是整数。
整数分为正整数和负整数。
整数的个数是无限的,没有最小的整数,也没有最大的整数。
2 自然数我们在数物体的时候,用来表示物体个数的1,2,3……叫做自然数。
一个物体也没有,用0表示。
0也是自然数。
3 正数和负数描述具有相反意义的量,可以用正、负数。
0既不是正数,也不是负数。
4计数单位一(个)、十、百、千、万、十万、百万、千万、亿……都是计数单位。
每相邻两个计数单位之间的进率都是10。
这样的计数法叫做十进制计数法。
5数的整除整数a除以整数b(b ≠0),除得的商是整数而没有余数,我们就说a能被b整除,或者说b能整除a 。
如果数a能被数b(b ≠0)整除,a就叫做b的倍数,b就叫做a的约数(或a的因数)。
倍数和约数是相互依存的。
例如:因为35能被7整除,所以35是7的倍数,7是35的约数。
★一个数的约数的个数是有限的,其中最小的约数是1,最大的约数是它本身。
例如:10的约数有1、2、5、10,其中最小的约数是1,最大的约数是10。
★一个数的倍数的个数是无限的,其中最小的倍数是它本身。
3的倍数有:3、6、9、12……其中最小的倍数是3 ,没有最大的倍数。
★个位上是0、2、4、6、8的数,都能被2整除,例如:202、480、304,都能被2整除。
★个位上是0或5的数,都能被5整除,例如:5、30、405都能被5整除。
★一个数的各位上的数的和能被3整除,这个数就能被3整除,例如:12、108、204都能被3整除。
★一个数的末两位数能被4(或25)整除,这个数就能被4(或25)整除。
例如:16、404、1256都能被4整除,50、325、500、1675都能被25整除。
★一个数的末三位数能被8(或125)整除,这个数就能被8(或125)整除。
例如:1168、4600、12344都能被8整除,1125、13375、5000都能被125整除。
§奇数与偶数能被2整除的数叫做偶数。
不能被2整除的数叫做奇数。
0也是偶数。
自然数按能否被2 整除的特征可分为奇数和偶数。
§质数与合数★一个数,如果只有1和它本身两个约数,这样的数叫做质数(或素数),100以内的质数有:2、3、5、7、11、13、17、19、23、29、31、37、41、43、47、53、59、61、67、71、73、79、83、89、97。
★一个数,如果除了1和它本身还有别的约数,这样的数叫做合数,例如4、6、8、9、12都是合数。
★1不是质数也不是合数,自然数除了1外,不是质数就是合数。
如果把自然数按其约数的个数的不同分类,可分为质数、合数和1。
★每个合数都可以写成几个质数相乘的形式。
其中每个质数都是这个合数的因数,叫做这个合数的质因数,例如15=3×5,3和5 叫做15的质因数。
★把一个合数用质因数相乘的形式表示出来,叫做分解质因数。
★几个数公有的约数,叫做这几个数的公约数。
其中最大的一个,叫做这几个数的最大公约数,例如12的约数有1、2、3、4、6、12;18的约数有1、2、3、6、9、18。
其中,1、2、3、6是12和1 8的公约数,6是它们的最大公约数。
★公约数只有1的两个数,叫做互质数。
其中:1和任何自然数互质。
相邻的两个自然数互质。
两个不同的质数互质。
当合数不是质数的倍数时,这个合数和这个质数互质。
(即质数与合数之间有可能互质,也可能不互质)两个合数的公约数只有1时,这两个合数互质。
(即两个有可能互质,也可能不互质)★几个数公有的倍数,叫做这几个数的公倍数,其中最小的一个,叫做这几个数的最小公倍数,例如:2的倍数有2、4、6 、8、10、12、14、16、18 ……3的倍数有3、6、9、12、15、18 ……其中6、12、18……是2、3的公倍数,6是它们的最小公倍数。
如果较大数是较小数的倍数,那么较大数就是这两个数的最小公倍数。
如果两个数是互质数,那么这两个数的积就是它们的最小公倍数。
★几个数的公约数的个数是有限的,而几个数的公倍数的个数是无限的。
(二)小数1 小数的意义把整数1平均分成10份、100份、1000份……得到的十分之几、百分之几、千分之几……可以用小数表示。
一位小数表示十分之几,两位小数表示百分之几,三位小数表示千分之几……小数的性质:小数的末尾添上“0”或去掉“0”,小数的大小不变。
2.循环小数:一个数的小数部分,有一个数字或者几个数字依次不断重复出现,这个数叫做循环小数。
例如: 3.555 ……0.0333 ……12.109109 ……(三)分数1 分数的意义把单位“1”平均分成若干份,表示这样的一份或者几份的数叫做分数。
把单位“1”平均分成若干份,表示其中的一份的数,叫做分数单位。
2 分数的基本性质分数的分子和分母同时乘上或除以相同的数(0除外),分数的大小不变。
运用分数的基本性质可以进行通分或约分。
(四)百分数1 表示一个数是另一个数的百分之几的数叫做百分数,也叫做百分率或百分比。
百分数通常用"%"来表示。
百分号是表示百分数的符号。
二方法(一)数的读法和写法1. 整数的读法:从高位到低位,一级一级地读。
读亿级、万级时,先按照个级的读法去读,再在后面加一个“亿”或“万”字。
每一级末尾的0都不读出来,其它数位连续有几个0都只读一个零。
2. 整数的写法:从高位到低位,一级一级地写,哪一个数位上一个单位也没有,就在那个数位上写0。
3. 小数的读法:读小数的时候,整数部分按照整数的读法读,小数点读作“点”,小数部分从左向右顺次读出每一位数位上的数字。
4. 小数的写法:写小数的时候,整数部分按照整数的写法来写,小数点写在个位右下角,小数部分顺次写出每一个数位上的数字。
5. 分数的读法:读分数时,先读分母再读“分之”然后读分子,分子和分母按照整数的读法来读。
6. 分数的写法:先写分数线,再写分母,最后写分子,按照整数的写法来写。
7. 百分数的读法:读百分数时,先读百分之,再读百分号前面的数,读数时按照整数的读法来读。
8. 百分数的写法:百分数通常不写成分数形式,而在原来的分子后面加上百分号“%”来表示。
(二)数的改写一个较大的多位数,为了读写方便,常常把它改写成用“万”或“亿”作单位的数。
有时还可以根据需要,省略这个数某一位后面的数,写成近似数。
1. 准确数:在实际生活中,为了计数的简便,可以把一个较大的数改写成以万或亿为单位的数。
改写后的数是原数的准确数。
例如把1254300000 改写成以万做单位的数是125430 万;改写成以亿做单位的数12.543 亿。
2. 近似数:根据实际需要,我们还可以把一个较大的数,省略某一位后面的尾数,用一个近似数来表示。
例如:1302490015 省略亿后面的尾数是13 亿。
3. 四舍五入法:要省略的尾数的最高位上的数是4 或者比4小,就把尾数去掉;如果尾数的最高位上的数是5或者比5大,就把尾数舍去,并向它的前一位进1。
例如:省略345900 万后面的尾数约是35 万。
省略4725097420 亿后面的尾数约是47 亿。
4. 大小比较(1). 比较整数大小:比较整数的大小,位数多的那个数就大,如果位数相同,就看最高位,最高位上的数大,那个数就大;最高位上的数相同,就看下一位,哪一位上的数大那个数就大。
(2). 比较小数的大小:先看它们的整数部分,,整数部分大的那个数就大;整数部分相同的,十分位上的数大的那个数就大;十分位上的数也相同的,百分位上的数大的那个数就大……(3). 比较分数的大小:分母相同的分数,分子大的分数比较大;分子相同的数,分母小的分数大。
分数的分母和分子都不相同的,先通分,再比较两个数的大小。
(三)数的互化1. 小数化成分数:原来有几位小数,就在1的后面写几个零作分母,把原来的小数去掉小数点作分子,能约分的要约分。
2. 分数化成小数:用分母去除分子。
能除尽的就化成有限小数,有的不能除尽,不能化成有限小数的,一般保留三位小数。
3. 一个最简分数,如果分母中除了2和5以外,不含有其他的质因数,这个分数就能化成有限小数;如果分母中含有2和5 以外的质因数,这个分数就不能化成有限小数。
4. 小数化成百分数:只要把小数点向右移动两位,同时在后面添上百分号。
5. 百分数化成小数:把百分数化成小数,只要把百分号去掉,同时把小数点向左移动两位。
6. 分数化成百分数:通常先把分数化成小数(除不尽时,通常保留三位小数),再把小数化成百分数。
7. 百分数化成小数:先把百分数改写成分数,能约分的要约成最简分数。
(四)数的整除1. 把一个合数分解质因数,通常用短除法。
先用能整除这个合数的质数去除,一直除到商是质数为止,再把除数和商写成连乘的形式。
2. 求几个数的最大公约数的方法是:先用这几个数的公约数连续去除,一直除到所得的商只有公约数1为止,然后把所有的除数连乘求积,这个积就是这几个数的的最大公约数。
3. 求几个数的最小公倍数的方法是:先用这几个数(或其中的部分数)的公约数去除,一直除到互质(或两两互质)为止,然后把所有的除数和商连乘求积,这个积就是这几个数的最小公倍数。
4. 成为互质关系的两个数:1和任何自然数互质;相邻的两个自然数互质;当合数不是质数的倍数时,这个合数和这个质数互质;两个合数的公约数只有1时,这两个合数互质。
(五)约分和通分约分的方法:用分子和分母的公约数(1除外)去除分子、分母;通常要除到得出最简分数为止。
通分的方法:先求出原来的几个分数分母的最小公倍数,然后把各分数化成用这个最小公倍数作分母的分数。
\三性质和规律(一)商不变的规律商不变的规律:在除法里,被除数和除数同时扩大或者同时缩小相同的倍,商不变。
(二)小数的性质小数的性质:在小数的末尾添上零或者去掉零小数的大小不变。
(三)小数点位置的移动引起小数大小的变化1. 小数点向右移动一位,原来的数就扩大10倍;小数点向右移动两位,原来的数就扩大100倍;小数点向右移动三位,原来的数就扩大1000倍……2. 小数点向左移动一位,原来的数就缩小10倍;小数点向左移动两位,原来的数就缩小100倍;小数点向左移动三位,原来的数就缩小1000倍……3. 小数点向左移或者向右移位数不够时,要用“0"补足位。
(四)分数的基本性质分数的基本性质:分数的分子和分母都乘以或者除以相同的数(零除外),分数的大小不变。
(五)分数与除法的关系1. 被除数÷除数= 被除数/除数2. 因为零不能作除数,所以分数的分母不能为零。
3. 被除数相当于分子,除数相当于分母。
四运算的意义(一)整数四则运算1整数加法:把两个数合并成一个数的运算叫做加法。
在加法里,相加的数叫做加数,加得的数叫做和。