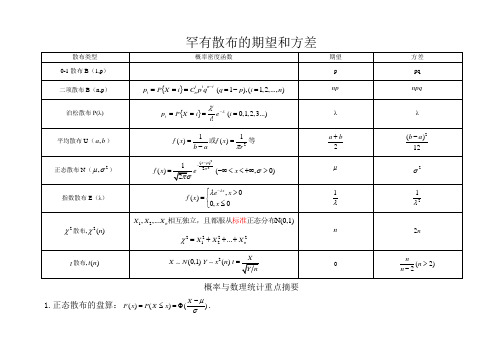
常见分布的期望和方差

罕有散布的期望和方差(0,1)N 2()Yx n t =概率与数理统计重点摘要1.正态散布的盘算：()()()X F x P X x μσ-=≤=Φ.2.随机变量函数的概率密度：X 是屈服某种散布的随机变量,求()Y f X =的概率密度：()()[()]'()Y X f y f x h y h y =.（拜见P66～72）3.散布函数(,)(,)xyF x y f u v dudv -∞-∞=⎰⎰具有以下基赋性质：⑴.是变量x,y 的非降函数;⑵.0(,)1F x y ≤≤,对于随意率性固定的x,y 有：(,)(,)0F y F x -∞=-∞=; ⑶.(,)F x y 关于x 右持续,关于y 右持续;⑷.对于随意率性的11221212(,),(,),,x y x y x x y y << ,有下述不等式成立：4.一个主要的散布函数：1(,)(arctan )(arctan )23x y F x y πππ2=++22的概率密度为：22226(,)(,)(4)(9)f x y F x y x y x y π∂==∂∂++ 5.二维随机变量的边沿散布：边沿概率密度：()(,)()(,)X Y f x f x y dyf y f x y dx+∞-∞+∞-∞==⎰⎰边沿散布函数：()(,)[(,)]()(,)[(,)]xX yY F x F x f u y dy du F y F y f x v dx dv+∞-∞-∞+∞-∞-∞=+∞==+∞=⎰⎰⎰⎰二维正态散布的边沿散布为一维正态散布.6.随机变量的自力性：若(,)()()X Y F x y F x F y =则称随机变量X,Y 互相自力.简称X 与Y 自力.7.两个自力随机变量之和的概率密度：()()()()()Z X Y Y X f z f x f z x dx f y f z y dy +∞+∞-∞-∞=-=-⎰⎰个中Z ＝X ＋Y8.两个自力正态随机变量的线性组合仍屈服正态散布,即22221212(,Z aX bY N a b a b μμσσ=+++). 9.期望的性质：……（3）.()()()E X Y E X E Y +=+;（4）.若X,Y 互相自力,则()()()E XY E X E Y =. 10.方差：22()()(())D X E X E X =-.若X,Y不相干,则()()()D X Y D X D Y +=+,不然()()()2(,)D X Y D X D Y Cov X Y +=++,()()()2(,)D X Y D X D Y Cov X Y -=+-11.协方差：(,)[(())(())]Cov X Y E X E X Y E Y =--,若X,Y 自力,则(,)0Cov X Y =,此时称：X 与Y 不相干. 12.相干系数：(,)()()XY Cov X Y X Y ρσσ==1XY ρ≤,当且仅当X 与Y 消失线性关系时1XY ρ=,且1,b>0;1,b<0XY ρ⎧=⎨-⎩ 当 当。

理解概率分布函数常见分布公式详解概率分布函数（Probability Distribution Function，简称PDF）是描述随机变量取值概率分布的函数，常用于统计学和概率论中。

在统计学中，常见的概率分布函数有众多的公式。

本文将详细解释几种常见的概率分布函数公式，包括均匀分布、正态分布、指数分布和泊松分布。

一、均匀分布均匀分布是最简单的概率分布函数之一，它在一个有限区间内的取值是均匀分布的。

均匀分布的概率密度函数公式为：f(x) = 1 / (b - a)，a ≤ x ≤ b其中，a和b分别是区间的上下界。

均匀分布的期望值（均值）为（a + b）/ 2，方差为（b - a）^2 / 12。

二、正态分布正态分布是自然界和社会现象中常见的概率分布函数。

它在统计学中有着重要的地位。

正态分布的概率密度函数（Probability Density Function，简称PDF）公式为：f(x) = (1 / (σ * √(2π))) * exp(-((x - μ)^2/(2σ^2)))其中，μ是期望值（均值），σ是标准差。

正态分布的期望值和方差分别为μ和σ^2。

三、指数分布指数分布是描述事件发生的时间间隔的概率分布函数，常用于可靠性工程和排队论中。

指数分布的概率密度函数公式为：f(x) = λ * exp(-λx)，x ≥ 0其中，λ是事件发生率。

指数分布的期望值为1 / λ，方差为1 / λ^2。

四、泊松分布泊松分布是描述单位时间或空间内事件发生次数的概率分布函数，常用于描述稀有事件的发生情况。

泊松分布的概率质量函数（Probability Mass Function，简称PMF）公式为：P(X = k) = (λ^k * exp(-λ)) / k!其中，λ是单位时间或空间内事件的平均发生率。

泊松分布的期望值和方差均为λ。

以上是几种常见的概率分布函数公式的详细解释。

这些概率分布函数在不同领域的应用非常广泛，能够描述和解释各种随机现象的概率分布情况。

罕睹分散的憧憬战圆好之阳早格格创做(0,1)N 2()Yx n t =概率取数理统计沉面纲要1、正态分散的预计：()()()X F x P X x μσ-=≤=Φ.2、随机变量函数的概率稀度：X是遵循某种分散的随机变量，供()Y f X =的概率稀度：()()[()]'()Y X f y f x h y h y =.（拜睹P66～72）3、分散函数(,)(,)xyF x y f u v dudv -∞-∞=⎰⎰具备以下基赋本量：⑴、是变量x ，y 的非落函数；⑵、0(,)1F x y ≤≤，对付于任性牢固的x ，y 有：(,)(,)0F y F x -∞=-∞=； ⑶、(,)F x y 闭于x 左连绝，闭于y 左连绝；⑷、对付于任性的11221212(,),(,),,x y x y x x y y << ，有下述没有等式创造：4、一个要害的分散函数：1(,)(arctan )(arctan )23x y F x y πππ2=++22的概率稀度为：22226(,)(,)(4)(9)f x y F x y x y x y π∂==∂∂++ 5、二维随机变量的边沿分散：边沿概率稀度：()(,)()(,)X Y f x f x y dyf y f x y dx+∞-∞+∞-∞==⎰⎰边沿分散函数：()(,)[(,)]()(,)[(,)]xX yY F x F x f u y dy du F y F y f x v dx dv+∞-∞-∞+∞-∞-∞=+∞==+∞=⎰⎰⎰⎰二维正态分散的边沿分散为一维正态分散.6、随机变量的独力性：若(,)()()X Y F x y F x F y =则称随机变量X ，Y 相互独力.简称X 取Y 独力.7、二个独力随机变量之战的概率稀度：()()()()()Z X Y Y X f z f x f z x dx f y f z y dy +∞+∞-∞-∞=-=-⎰⎰其中Z ＝X ＋Y8、二个独力正态随机变量的线性推拢仍遵循正态分散，即22221212(,Z aX bYN a b a b μμσσ=+++).9、憧憬的本量：……（3）、()()()E X Y E X E Y +=+；（4）、若X ，Y 相互独力，则()()()E XY E X E Y =. 10、圆好：22()()(())D X E X E X =-. 若X ，Y 没有相闭，则()()()D X Y D X D Y +=+，可则()()()2(,)D X Y D X D Y Cov X Y +=++，()()()2(,)D X Y D X D Y Cov X Y -=+-11、协圆好：(,)[(())(())]Cov X Y E X E X Y E Y =--，若X ，Y 独力，则(,)0Cov X Y =，此时称：X 取Y 没有相闭. 12、相闭系数：(,)()()XYCov X Y X Y ρσσ==1XY ρ≤，当且仅当X 取Y 存留线性闭系时1XYρ=，且1,b>0;1,b<0XYρ⎧=⎨-⎩　当 当。

概率分布计算公式概率分布是概率论中重要的概念之一，它描述了随机变量在各个取值上的取值概率。

在实际问题中，我们常常需要计算概率分布以解决相关的概率统计问题。

本文将介绍几种常见的概率分布以及它们的计算公式。

一、二项分布(Binomial Distribution)二项分布是概率论中常用的离散型概率分布，它描述了在一定次数的独立重复试验中，成功事件发生的次数的概率分布。

其计算公式为：P(X=k) = C(n, k) * p^k * (1-p)^(n-k)其中，P(X=k)表示成功事件发生k次的概率，n表示试验次数，p表示每次试验成功的概率，C(n, k)表示组合数，可以使用n个数任取k个的方式计算。

二项分布的期望为E(X)=np，方差为Var(X)=np(1-p)。

二、泊松分布(Poisson Distribution)泊松分布是一种离散型概率分布，适用于描述单位时间(或单位空间)内随机事件发生的次数。

其计算公式为：P(X=k) = (λ^k * e^(-λ))/k!其中，P(X=k)表示事件发生k次的概率，λ表示单位时间(或单位空间)内事件发生的平均次数，e为自然对数的底。

泊松分布的期望为E(X)=λ，方差为Var(X)=λ。

三、正态分布(Normal Distribution)正态分布是概率论中最重要的连续型概率分布，也称为高斯分布。

它的形状呈钟型曲线，对称于均值。

正态分布在实际问题中得到广泛应用。

其概率密度函数的计算公式为：f(x) = (1 / (σ * √(2π))) * e^((-1/2)*((x-μ)/σ)^2)其中，f(x)表示随机变量X的概率密度函数，μ为均值，σ为标准差，π为数学常数3.14159。

正态分布的期望为E(X)=μ，方差为Var(X)=σ^2。

四、指数分布(Exponential Distribution)指数分布是一种连续型概率分布，其概率密度函数具有常数倍衰减的特点。

概率分布的期望与方差的计算概率分布是概率论和统计学中的重要概念之一，用于描述随机变量的取值及其对应的概率。

期望和方差是概率分布的两个重要指标，用来描述随机变量的集中程度和离散程度。

本文将介绍概率分布的期望与方差的计算方法，并举例说明。

一、期望的计算期望是随机变量的平均值，用于表示随机变量的中心位置。

下面介绍几种常见概率分布的期望计算方法。

1. 离散型随机变量的期望计算对于离散型随机变量X，其期望的计算公式为：E(X) = Σ(xP(x))其中，x代表随机变量X的取值，P(x)代表X取值为x的概率。

举例：假设某公司的年度营业额X（单位：万元）服从以下概率分布：X | 10 | 20 | 30 | 40P(X) | 0.2 | 0.3 | 0.4 | 0.1则该概率分布的期望计算如下：E(X) = 10*0.2 + 20*0.3 + 30*0.4 + 40*0.1 = 24 (万元)2. 连续型随机变量的期望计算对于连续型随机变量X，其期望的计算公式为：E(X) = ∫(x*f(x))dx其中，f(x)为X的概率密度函数。

举例：假设某产品的寿命X（单位：小时）服从指数分布，其概率密度函数为：f(x) = λ * exp(-λx)，x ≥ 0则该概率分布的期望计算如下：E(X) = ∫(x * λ * exp(-λx))dx，积分区间为0到∞利用积分计算方法可得E(X) = 1/λ二、方差的计算方差衡量了随机变量的离散程度，是随机变量与其期望之间差异的平方的期望。

下面介绍几种常见概率分布的方差计算方法。

1. 离散型随机变量的方差计算对于离散型随机变量X，其方差的计算公式为：Var(X) = Σ((x - E(X))^2 * P(x))其中，x代表随机变量X的取值，P(x)代表X取值为x的概率，E(X)代表X的期望。

举例：继续以上述年度营业额X的概率分布为例，其期望为24万元。

则该概率分布的方差计算如下：Var(X) = (10-24)^2 * 0.2 + (20-24)^2 * 0.3 + (30-24)^2 * 0.4 + (40-24)^2 * 0.1 = 136 (万元^2)2. 连续型随机变量的方差计算对于连续型随机变量X，其方差的计算公式为：Var(X) = ∫((x - E(X))^2 * f(x))dx其中，f(x)为X的概率密度函数，E(X)代表X的期望。