四边形知识点总结(已整理)知识分享

(完整版)平行四边形基本知识点总结平行四边形基本知识点总结
平行四边形是一种特殊的四边形，它具有一些独特的性质和特点。

以下是平行四边形的基本知识点总结：
定义
平行四边形是指具有两组对边分别平行的四边形。

性质
1. 对边平行性质：平行四边形的两组对边分别平行。

2. 对角线性质：平行四边形的对角线互相平分，并且长度相等。

3. 内角和性质：平行四边形的内角的和为180度。

4. 外角性质：平行四边形的外角的和为360度。

5. 对边长度性质：平行四边形的对边长度相等。

6. 同底角性质：与平行四边形的一条边相邻，另一条边平行的两个内角相等。

7. 同旁内角性质：与平行四边形的两条边相邻，另一条边平行的两个内角互补。

判定方法
1. 对边平行判定：如果一个四边形中有两组对边分别平行，则它是一个平行四边形。

2. 对角线平分判定：如果一个四边形的对角线互相平分，并且长度相等，则它是一个平行四边形。

特殊类型
1. 矩形：具有四个内角都为90度的平行四边形。

2. 正方形：具有四个内角都为90度，且四条边长度相等的平
行四边形。

相关公式
1. 平行四边形的面积公式：面积 = 底边长度 ×高度。

2. 平行四边形的周长公式：周长= 2 ×(底边长度+ 侧边长度)。

以上是关于平行四边形的基本知识点总结。

通过了解这些性质
和定理，可以更好地理解和解决相关的数学问题。

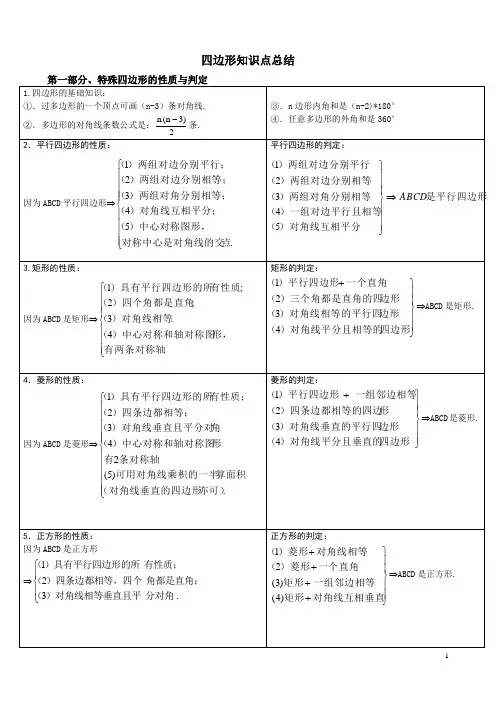
四边形知识点总结6．等腰梯形的性质：因为ABCD 是等腰梯形⇒⎪⎩⎪⎨⎧.321）对角线相等（；）同一底上的底角相等（两底平行，两腰相等；）（ 等腰梯形的判定：⎪⎭⎪⎬⎫+++对角线相等）梯形（底角相等）梯形（两腰相等）梯形（321⇒ABCD 是等腰梯形 7．三角形中位线定理：三角形的中位线平行第三边，并且等于它的一半. 注：被中位线分成的三角形的周长是原三角形的1/2 被中位线分成的三角形的面积是原三角形的1/48．梯形中位线定理：梯形的中位线平行于两底，并且等于两底和的一半. 注：梯形的面积等于中位线乘高.第二部分、常用的辅助线技巧1.平行四边形与特殊的平行四边形常见的辅助线：①.平行四边形:（1）连对角线或平移对角线 （2）过顶点作对边的垂线构造直角三角形 ②.菱形：（1）作菱形的高；（2）连结菱形的对角线.注意：当菱形有一个内角为60°或有一条高垂直平分底边时连接对角线即可得到等边三角形。

③．矩形：计算题型（翻折问题），一般通过作辅助线（垂线等）构造直角三角形借助勾股定理解题 证明题型（探究问题），一般连接对角线借助对角线相等来解决问题注意：当矩形的对角线与一边（或另一条对角线）的夹角为60°时，其对角线与边长围成的三角形是等边三角形。

④．正方形：连接对角线 2．梯形中常见的辅助线：①．延长两腰交于一点（使梯形问题转化为三角形问题。

若是等腰梯形则得到等腰三角形。

）②．平移一腰（使梯形问题转化为平行四边形及三角形问题。

）③．作高（使梯形问题转化为直角三角形及矩形问题。

）④.平移一条对角线(得到平行四边形ACED ，使CE=AD ，BE 等于上、下底的和，S 梯形ABCD =S DBE ）⑤.当有一腰中点时，连结一个顶点与一腰中点并延长交一个底的延长线。

（可得△ADE ≌△FCE ，所以使S 梯形ABCD =S △ABF .）。

四边形一 基本概念：四边形，四边形的内角，四边形的外角，多边形，平行线间的距离，平行四边形，矩形，菱形，正方形，中心对称，中心对称图形，梯形，等腰梯形，直角梯形，三角形中位线，梯形中位线. 二 定理：中心对称的有关定理※1．关于中心对称的两个图形是全等形. ※2．关于中心对称的两个图形，对称点连线都经过对称中心，并且被对称中心平分. ※3．如果两个图形的对应点连线都经过某一点，并且被这一点平分，那么这两个图形关于这一点对称. 三 公式：1．S 菱形 =21ab=ch.（a 、b 为菱形的对角线 ,c 为菱形的边长 ，h 为c 边上的高）2．S 平行四边形 =ah. a 为平行四边形的边，h 为a 上的高） 3．S 梯形 =21（a+b ）h=Lh.（a 、b 为梯形的底，h 为梯形的高,L 为梯形的中位线）四 常识：※1．若n 是多边形的边数，则对角线条数公式是：2)3n (n -.2．规则图形折叠一般“出一对全等，一对相似”.3．如图：平行四边形、矩形、菱形、正方形的从属关系.4．常见图形中，仅是轴对称图形的有：角、等腰三角形、等边三角形、正奇边形、等腰梯形 …… ；仅是中心对称图形的有：平行四边形 …… ；是双对称图形的有：线段、矩形、菱形、正方形、正偶边形、圆 …… .注意：线段有两条对称轴.平行四边形矩形菱形正方形四边形知识点归纳平行四边形平行四边形定义：两组对边分别平行的四边形叫做平行四边形。

平行四边形是中心对称图形，对称中心是两条对角线的交点。

平行四边形性质1：平行四边形的两组对边分别相等。

平行四边形性质2：平行四边形的两组对角分别相等。

平行四边形性质3：平行四边形的两条对角线互相平分。

平行四边形判定1：两组对边分别平行的四边形是平行四边形。

平行四边形判定2：两组对边分别相等的四边形是平行四边形。

平行四边形判定3：两组对角分别相等的四边形是平行四边形。

平行四边形判定4：两条对角线互相平分的四边形是平行四边形。

四边形的知识点总结四边形是指具有四条边的图形。

在数学中，我们经常会遇到各种不同类型的四边形，包括矩形、正方形、平行四边形、梯形、菱形等。

本篇文章将为大家总结四边形的各种知识点，让大家对这些图形有更深入的了解。

一、矩形矩形是指四边都相等且所有内角都是直角的四边形。

下面是矩形的主要特点：1. 矩形的对角线相等。

2. 矩形的面积可以用长和宽相乘得到，即S=lw。

3. 矩形的周长可以用四条边长之和得到，即P=2(l+w)。

4. 矩形的内角都是90度。

5. 根据勾股定理，矩形的长、宽和对角线之间有如下关系：l^2+w^2=d^2，其中d为对角线的长度。

二、正方形正方形是指四边都相等且所有内角都是90度的矩形。

下面是正方形的主要特点：1. 正方形的四条边等长。

2. 正方形的对角线相等且垂直。

3. 正方形的面积可以用任意一条边长的平方得到，即S=a^2。

4. 正方形的周长可以用四条边长之和得到，即P=4a。

5. 角平分线和中线在正方形中重合且同时是对角线的中垂线。

三、平行四边形平行四边形是指具有相对边平行的四边形。

下面是平行四边形的主要特点：1. 平行四边形的对边平行且相等。

2. 平行四边形的邻边互相平行。

3. 平行四边形的内角和为360度。

4. 平行四边形的面积可以用底边长和高得到，即S=bh。

5. 平行四边形的周长可以用两倍的底边长加两倍的高得到，即P=2(b+h)。

四、梯形梯形是指有一对相对边平行的四边形。

下面是梯形的主要特点：1. 梯形的两组对边各自相等。

2. 梯形的内角和为360度。

3. 梯形的面积可以用底边长和高得到，即S=(a+b)h/2。

4. 梯形的周长可以用四条边长之和得到，即P=a+b+c+d。

5. 梯形的高线可以将梯形分成两个三角形，面积为这两个三角形面积之和，即h=h1+h2。

五、菱形菱形是指四边相等且对角线相等的四边形。

下面是菱形的主要特点：1. 菱形的两组对边各自平行且相等。

2. 菱形的对角线相等且垂直。

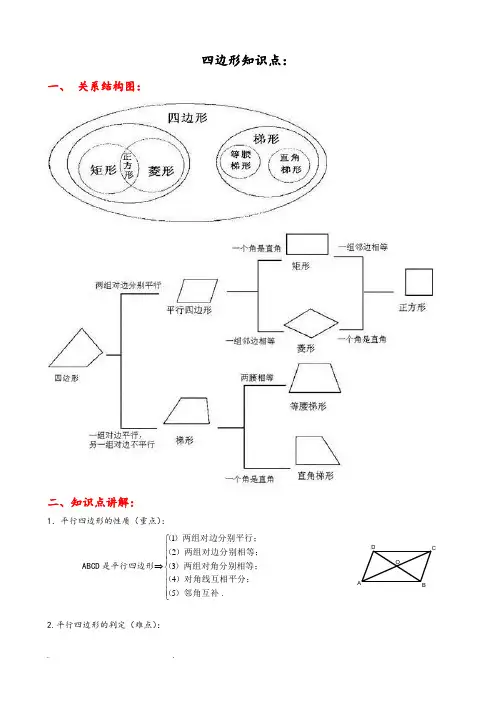
四边形知识点：一、 关系结构图：二、知识点讲解：1．平行四边形的性质（重点）：ABCD 是平行四边形⇒⎪⎪⎪⎩⎪⎪⎪⎨⎧.54321）邻角互补（）对角线互相平分；（）两组对角分别相等；（）两组对边分别相等；（）两组对边分别平行；（2.平行四边形的判定（难点）：ABDOCC D AB A BCD O.3. 矩形的性质：因为ABCD 是矩形⇒⎪⎩⎪⎨⎧.3;2;1）对角线相等（）四个角都是直角（有通性）具有平行四边形的所（ (4)是轴对称图形.它有两条对称轴．4矩形的判定：矩形的判定方法：(1)有一个角是直角的平行四边形；(2)有三个角是直角的四边形； (3)对角线相等的平行四边形；(4)对角线相等且互相平分的四边形． ⇒四边形ABCD 是矩形. 5. 菱形的性质： 因为ABCD 是菱形⇒⎪⎩⎪⎨⎧.321角）对角线垂直且平分对（）四个边都相等；（有通性；）具有平行四边形的所（6. 菱形的判定：⎪⎭⎪⎬⎫+边形）对角线垂直的平行四（）四个边都相等（一组邻边等）平行四边形（321⇒四边形四边形ABCD 是菱形.7.正方形的性质：ABCD 是正方形⇒⎪⎩⎪⎨⎧.321分对角）对角线相等垂直且平（角都是直角；）四个边都相等，四个（有通性；）具有平行四边形的所（8. 正方形的判定：⎪⎭⎪⎬⎫++++一组邻边等矩形）（一个直角）菱形（一个直角一组邻边等）平行四边形（321⇒四边形ABCD 是正方形.ABDOCAD BCAD BC OCDBAOCDBAO②①②1．已知：如图.E、F是平行四边形ABCD的对角线AC上的两点.AE=CF。

求证：（1）△ADF≌△CBE；（2）EB∥DF。

证明：（1）∵ AE=CF ∴ AE+EF=CF+FE 即 AF=CE又ABCD是平行四边形. ∴ AD=CB.AD∥BC ∴∠DAF=∠BCE在△ADF与△CBE中∴△ADF≌△CBE（SAS）（2）∵△ADF≌△CBE ∴∠DFA=∠BEC ∴ DF∥EB例1图例2图2．如图.平行四边形ABCD的对角线AC、BD相交于点O.E、F是直线AC上的两点.并且AE=CF.求证：四边形BFDE是平行四边形。

数学四边形知识点归纳总结一、四边形的分类1. 矩形：具有四条边，四个角均为直角的四边形。

2. 正方形：具有四条边，四个角相等且均为直角的四边形。

3. 平行四边形：具有两组对边平行的四边形。

4. 梯形：具有两对对边平行的四边形。

5. 不规则四边形：具有四条边，四个角不一定相等或一定不是直角的四边形。

二、四边形的性质1. 对角线长度关系：四边形的对角线长度满足一定的关系，例如矩形和正方形的对角线相等，平行四边形的对角线互相等长。

2. 对角关系：四边形的内角之和为360度，即A+B+C+D=360°。

3. 对边关系：平行四边形的对边相等，矩形和正方形的对边相等且相邻边互相垂直。

4. 相关角关系：平行四边形的对角相等，矩形和正方形的内角均为直角。

5. 对角平分：梯形的对角线互相平分对角。

三、四边形的相关定理1. 矩形的定理（1）对角线相等定理：矩形的对角线相等。

（2）角关系定理：矩形的内角均为直角。

（3）对边关系定理：矩形的对边相等且相邻边互相垂直。

2. 正方形的定理（1）对角线垂直平分定理：正方形的对角线互相垂直且平分对角。

（2）对角线相等定理：正方形的对角线相等。

（3）角关系定理：正方形的内角均为直角。

3. 平行四边形的定理（1）对角线长度关系定理：平行四边形的对角线长度关系为AC=BD。

（2）对角关系定理：平行四边形的对角相等。

（3）对边关系定理：平行四边形的对边相等。

4. 梯形的定理（1）梯形中短底角关系定理：梯形的短底边和长底边的非公共边上的内角相等。

四、四边形的面积计算1. 矩形的面积：矩形的面积为长乘以宽。

2. 正方形的面积：正方形的面积为边长的平方。

3. 平行四边形的面积：平行四边形的面积为底边乘以高。

4. 梯形的面积：梯形的面积为上底加下底乘以高再除以2。

五、四边形的应用1. 人工建筑：在建筑领域，四边形的应用非常广泛，例如门窗的设计、房屋的布局等都需要对四边形进行计算和应用。

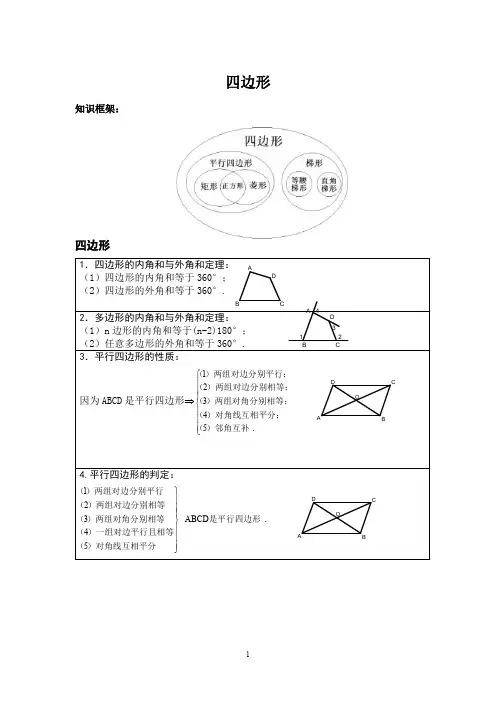
四边形知识点总结大全1.四边形的内角和与外角和定理：四边形的内角和等于360度；四边形的外角和等于360度。

2.多边形的内角和与外角和定理：n边形的内角和等于(n-2)180度；任意多边形的外角和等于360度。

3.平行四边形的性质：两组对边分别平行；两组对边分别相等；两组对角分别相等；对角线互相平分；邻角互补。

4.平行四边形的判定：若两组对边分别平行、相等、对角分别相等或一组对边平行且相等，则四边形为平行四边形。

5.矩形的性质：具有平行四边形的所有通性；四个角都是直角；对角线相等。

6.矩形的判定：若四边形为平行四边形且至少有一个直角，则为矩形；若对角线相等且为平行四边形，则为矩形。

7.菱形的性质：具有平行四边形的所有通性；四个边都相等；对角线垂直且平分对角。

8.菱形的判定：若四边形为平行四边形且一组邻边相等，则为菱形；若四边形四边相等且对角线垂直，则为菱形。

9.正方形的性质：具有平行四边形的所有通性；四个边都相等，四个角都是直角；对角线相等垂直且平分对角。

10.正方形的判定：若四边形为平行四边形且至少有一组邻边相等且有一个直角，则为正方形；若为菱形且有一个直角，则为正方形；若为矩形且一组邻边相等，则为正方形。

11.等腰梯形的性质：两底平行，两腰相等；同一底上的底角相等；对角线相等。

12.等腰梯形的判定：若四边形两底平行且两腰相等，则为等腰梯形；若同一底上的底角相等且对角线相等，则为等腰梯形。

1.等腰梯形的定义：一个四边形，其中两边是平行的且相等，另外两边也相等，但不平行。

根据这个定义，可以得出等腰梯形的性质：底角相等，对角线相等。

2.三角形中位线定理：三角形的中位线是连接一个角的顶点和对边中点的线段。

根据中位线定理，三角形的中位线平行于第三边，并且等于它的一半。

3.梯形中位线定理：梯形的中位线是连接两个非平行边中点的线段。

根据梯形中位线定理，梯形的中位线平行于两底，并且等于两底和的一半。

公式部分：1.菱形的面积公式：S=ab=ch，其中a、b为菱形的对角线，c为菱形的边长，h为c边上的高。

数学四边形知识点大全总结一、四边形的定义四边形是指一个平面图形，其中有四条边和四个顶点。

四边形是平面图形中最简单的多边形之一，同时也是很多其他几何图形的基础和组成部分。

二、四边形的分类根据四边形的性质和特点，可以将其分为以下几种主要类型：1. 矩形：拥有四个直角的四边形，对角线相等，且对角线互相垂直；2. 正方形：拥有四条相等边和四个直角的四边形；3. 平行四边形：拥有对边平行且长度相等的四边形；4. 菱形：拥有四条相等边但非直角的四边形；5. 梯形：至少有一对对边平行的四边形；6. 不规则四边形：没有特定性质和特点的四边形。

在这些基本类型的基础上，还可以根据四边形的角度、边长、对角线等特点对其进行更详细的分类和讨论。

三、四边形的性质1. 任意四边形的内角和等于360度；2. 对角线互相垂直的矩形和正方形；3. 平行四边形的对边相等且平行；4. 菱形的对角线互相垂直，且互相垂直；5. 梯形的一对对边平行；6. 不规则四边形没有特定的性质和特点。

四、四边形的相关定理1. 四边形内角和定理：任意四边形的内角和等于360度；2. 平行四边形定理：如果一对对边平行且长度相等，则该四边形是平行四边形；3. 矩形的性质定理：对角线平分，互相垂直；4. 正方形的性质定理：拥有四条相等边和四个直角；5. 平行四边形的性质定理：对边相等且平行；6. 菱形的性质定理：对角线互相垂直；7. 梯形的性质定理：一对对边平行。

五、四边形的应用和延伸1. 利用四边形的性质和定理进行几何证明和计算；2. 将四边形的性质应用到实际问题中，如建筑设计、工程测量等；3. 通过四边形的性质和特点，进行图形的合理分类和摆放，以满足设计和美学的要求；4. 采用四边形的相关知识进行几何推理和问题解决，培养逻辑思维和问题解决能力。

总结：四边形作为平面几何中最基本的图形之一，其性质和特点对于理解和运用其他更复杂的几何图形具有重要意义。

通过系统地学习和掌握四边形的定义、分类、性质和定理等知识点，可以提高学生的几何思维和解决问题的能力，在实际生活和工作中有着广泛的应用价值。

四边形知识点整理一、四边形的定义和分类1. 四边形的定义：四边形是由四条线段组成的闭合图形。

2. 四边形的分类：（1）矩形：四个角都是直角的四边形。

（2）正方形：四条边相等且四个角都是直角的矩形。

（3）平行四边形：有两组对边平行的四边形。

（4）梯形：有两条平行边的四边形。

（5）菱形：四个边都相等的梯形。

（6）不规则四边形：所有边和角都不相等的四边形。

二、四边形的性质1. 内角和定理：一个四边形的内角和等于360度。

2. 对角定理：一个四边形的对角相等。

3. 同位角定理：同位角相等。

4. 对边角定理：对边角和共为180度。

5. 垂直对边角定理：若一个四边形的对角线互相垂直，则这个四边形是矩形。

6. 判断四边形类型的方法：通过各边长度和各角大小的关系可判断四边形的类型。

三、四边形的重要性质1. 矩形的性质：（1）四个角都是直角；（2）对角相等；（3）对边相等；（4）对角线相等。

2. 正方形的性质：（1）四个边相等；（2）四个角都是直角；（3）对边平行；（4）对角线相等；（5）对角线互相垂直。

3. 平行四边形的性质：（1）对边平行；（2）对角相等；（3）对边相等；（4）对角线互相等长。

4. 梯形的性质：（1）有两边平行；（2）含角和等于180度；（3）对角线互相等长。

5. 菱形的性质：（1）四个边相等；（2）对边平行；（3）对角相等；（4）对角线互相垂直。

四、四边形的相关定理1. 勾股定理：直角三角形的斜边上的正方形面积等于两直角边上的两个矩形面积之和。

2. 夹角相等定理：平行四边形中，同位角相等，内角和等于180度。

3. 等腰梯形的性质：等腰梯形的对角相等。

4. 平行四边形的周长定理：平行四边形的周长等于两对边之和的两倍。

五、四边形的应用1. 在建筑学中，四边形是建筑物的基本形状之一，如矩形的房间和楼层平面图。

2. 在地理学中，四边形可以用来描述地理形状，如国家和州的边界。

3. 在工程学中，四边形有助于设计和建造物体，如桥梁和道路。