正四面体
- 格式:doc
- 大小:40.50 KB
- 文档页数:1

正四面体公式范文正四面体是一种特殊的多面体,它由四个三角形面组成,每个面都与其他三个面相邻,并且每个面的大小和形状都相等。
正四面体公式是一组用于计算正四面体体积、表面积、高度等参数的公式。
下面将详细介绍正四面体的公式及其推导。
首先,我们定义正四面体的一些重要参数:-边长:正四面体的边长等于四边形面所组成的三角形的边长。
-高度:正四面体的高度是指从一个顶点到相对的底面所在的平面的垂直距离。
-侧面积:正四面体的侧面积是指四个三角形面的总面积。
-底面积:正四面体的底面积是指从一个底面顶点出发,与相对底面为底的三角形的高所组成的梯形面积的一半。
-体积:正四面体的体积是指四个三角形面的共同重心到其中一个顶点的距离。
接下来我们将分别推导这些参数的计算公式。
1.侧面积我们可以将正四面体分成四个三角形ABC、ACD、ADB和BDC,它们共同组成了正四面体的表面。
设正四面体的边长为a,则这四个三角形的面积可以根据海伦公式计算:S_ABC=√(p*(p-a)*(p-a)*(p-a))其中p=(3*a)/2是半周长。
所以正四面体的侧面积S_T=S_ABC+S_ACD+S_ADB+S_BDC=4*S_ABC=2.598*a^22.底面积由于正四面体的底面为等边三角形,我们可以直接使用等边三角形的面积公式计算底面积:S_base = (√3 * a^2) / 43.体积对于正四面体的体积V,我们可以通过找到正四面体的重心来计算。
正四面体的重心是指四个顶点和四个面的重心的交点,即正四面体的对称中心。
设正四面体的高度为h,重心到顶点的距离为d,则有如下关系:d=(1/4)*h根据类似的概念,正四面体的体积V可以表示为底面积与高度h的乘积的1/3,即:V = (1/3) * S_base * h而高度h可以通过勾股定理计算,我们可以将正四面体的边长a、高度d和高度h组成一个直角三角形,其中斜边的长度为a,直角边的长度为d,所以有:h=√(a^2-d^2)=√(a^2-(1/16)*h^2)解方程得:h^2=(16/15)*a^2代入体积公式得到正四面体的体积公式:V=(√2/12)*a^3由上面的推导可以得出正四面体的体积、表面积和高度的计算公式。

正四面体知识
正四面体是一种三维几何体,由四个等边等角三角形组成。
以下是有关正四面体的一些基本知识:
1. 定义:正四面体是一种具有四个等边等角三角形为侧面的多面体。
它的四个顶点和六条棱之间都是等长的,每个内角都是完全相等的。
2. 基本特征:
- 顶点:正四面体有四个顶点,每个顶点都与其他三个顶点相连。
- 棱:正四面体有六条棱,每个顶点都与两条棱相连。
- 面:正四面体有四个面,每个面都是一个等边等角三角形。
- 角:正四面体有四个内角,每个内角都相等。
3. 对称性:正四面体具有多种对称性质:
- 旋转对称性:正四面体可以进行120度的旋转,使其中一个顶点重合于另一个顶点。
- 镜像对称性:正四面体可通过某个面进行镜像反射。
4. 其他性质:
- 高度:正四面体的高度是指从一个顶点到相对的面上的垂直距离。
- 体积:正四面体的体积可以通过公式V = (a³ * √2) / 12来计算,其中a为等边三角形的边长。
- 表面积:正四面体的表面积可以通过公式S = √3 * a²来计算,其中a为等边三角形的边长。
- 对角线:正四面体的对角线是指连接不相邻顶点的线段。
正四面体有四条对角线。
5. 应用:
- 几何学:正四面体是基本的多面体之一,对于研究几何学和立体几何具有重要意义。
- 物理学:正四面体的对称性被广泛应用于物理学中的结构分析和量子力学领域。
希望这些基本知识能够帮助你更好地理解正四面体。

正四面体常用结论
正四面体是一种具有四个等边三角形的三维几何体,其常用结论包括以下几个方面。
1. 正四面体的性质
正四面体的四个面都是等边三角形,四个顶点相互连通,其中每个顶点都是三个面的公共点,每条边都是两个面的公共边。
正四面体的底面中心、顶点以及每个面的重心三点共线,且共线比为1:3。
正四面体的每个内角都是70.53度,每个外角为109.47度。
2. 正四面体的体积公式
正四面体的体积公式为V=√2/12a³,其中a为正四面体的棱长。
这个公式可以通过正四面体的高度和底面积来推导得到,也可以通过计算四个棱锥的体积并相加得到。
3. 正四面体的表面积公式
正四面体的表面积公式为S=√3a²,其中a为正四面体的棱长。
这个公式可以通过将正四面体分解成四个等腰三角形和一个正三角形来推导得到。
4. 正四面体的对称性
正四面体具有旋转对称性和镜像对称性。
它有6个旋转对称轴,分
别为通过两个相邻顶点的轴,以及通过中心垂直于某个面的轴。
它也有6个镜像对称面,分别为通过两个相邻顶点和中心的面,以及通过棱中点和面中心的面。
5. 正四面体的嵌入
正四面体可以嵌入到三维空间中的不同形状中。
其中最著名的是嵌入到八面体中,也就是四面体与另外一个四面体共享一个顶点,中心分别连接形成六个正方形。
正四面体作为一种基本几何体,具有独特的性质和应用。
掌握正四面体的常用结论,可以帮助我们更好地理解三维几何空间中的形状和应用。

几何体的正四面体正四面体是一种特殊的几何体,具有很多独特的性质和特点。
在本文中,我将介绍正四面体的定义、属性以及一些有趣的应用。
一、正四面体的定义正四面体是一种具有四个等边等角面的多面体。
它的四个面都是等边三角形,每两个面之间的夹角都是一样的,也都是等于70.53°。
在正四面体中,任意两条边的长度和相等。
这些特点使得正四面体在几何学中有着重要的地位。
二、正四面体的性质1. 对称性:正四面体具有很高的对称性。
它有24个对称操作,包括旋转和翻转等。
这些对称性使得正四面体在立体几何中有广泛的应用,例如建筑设计和立体模型制作等。
2. 共面性:正四面体的四个顶点共面。
这意味着可以通过这四个顶点构成一个平面。
而且在这个平面上,正四面体可以被视为一个等边三角形。
3. 体积和表面积:正四面体的体积和表面积可以通过简单的公式计算得到。
其中,体积公式为V = (a³√2) / 12,表面积公式为S = a²√3,其中a表示正四面体一个面的边长。
4. 空间分割:正四面体可以将三维空间分割成四个完全相同的四面体。
这种空间分割在某些科学领域中非常有用,例如晶体结构的研究和分子模拟等。
三、正四面体的应用1. 立体几何学研究:正四面体是立体几何学中的一个基本概念,它的研究可以帮助我们理解和解决各种与几何学相关的问题,例如立体投影、体积计算等。
2. 建筑设计:正四面体的对称性和美观性使得它成为建筑设计中的常用元素。
例如,一些摩天大楼的外形可以采用正四面体的结构,使得建筑物更加稳定和美观。
3. 教育和娱乐:正四面体的独特性质和形状可以作为教学和娱乐的工具。
通过搭建正四面体模型或者使用虚拟现实技术,人们可以更直观地了解和体验正四面体的一些特点和性质。
总结:正四面体作为一种特殊的几何体,具有对称性、共面性以及特定的体积和表面积等性质。
它在几何学研究、建筑设计和教育娱乐等领域有着广泛的应用。
通过深入研究和探索正四面体,我们可以进一步拓展对几何学的理解和应用。

正四面体的常用结论公式正四面体是我们生活中常见的一种几何图形,它的结构和性质一直以来都是数学家们研究的重点。
在这篇文章中,我将从理论和实践两个方面来探讨正四面体的常用结论公式。
我们来看一下正四面体的定义和性质。
正四面体是一个由四个边长相等的三角形组成的立体图形,它的每个面都是一个等边三角形。
正四面体的特点是它的六个顶点都在同一个球面上,这个球心被称为正四面体的外接球心。
由于正四面体的对称性,我们只需要知道其中一个面的面积和高,就可以计算出其他面的面积和高。
接下来,我将介绍一些常用的结论公式。
一、正四面体的体积公式1.1 底面积公式正四面体的底面积可以用以下公式表示:S = (a2 * b2) / (4 * GCD(a, b))其中,a和b分别是正四面体的两个相邻边的边长,GCD(a, b)表示a和b的最大公约数。
1.2 体积公式正四面体的体积可以用以下公式表示:V = S * h / 3其中,h是正四面体的高,可以通过勾股定理计算得出。
二、正四面体的表面积公式2.1 三个侧面的面积之和公式正四面体的三个侧面的面积分别为A1、A2和A3,它们可以表示为:A1 = a * b * sin60° = ab * √3 / 2A2 = a * c * sin60° = ac * √3 / 2A3 = b * c * sin60° = bc * √3 / 2所以,三个侧面的面积之和为:A_total = A1 + A2 + A3 = (ab + ac + bc) * √3 / 22.2 六个面的总面积公式正四面体的六个面的总面积为:A_total = 3 * (A1 + A2 + A3) = 3 * (ab + ac + bc) * √3 / 2三、正四面体的外接球半径公式3.1 外接球心到任意顶点的距离公式设正四面体的外接球心为O,任意一个顶点为P,那么OP就是外接球心到顶点P的距离。

高二数学正四面体知识点正四面体是一个非常特殊的几何体,它具有很多独特的性质和特点。
在高二数学学习中,正四面体也是一个重要的知识点。
本文将介绍一些关于正四面体的基本定义、性质和相关定理。
一、基本定义正四面体是一个四面都是正三角形的多面体。
它由四个全等的正三角形面围成,其中每个面都与其他三个面相交,且每个交线都是三面交线的角平分线。
四个面所成的四个顶点形成一个四面体。
二、性质1. 四个全等正三角形的三个顶点和四个顶点的连线相互垂直,且都交于同一点,该点称为正四面体的高心。
2. 正四面体的高心到四个顶点的距离相等,并且等于正四面体边长的 $\frac{1}{2}$ 倍。
3. 正四面体的重心是四个顶点和它们的连线的交点,即四个顶点和高心的连线相交于同一点。
4. 正四面体的重心到四个顶点的距离相等,并且等于正四面体边长的 $\frac{\sqrt{3}}{3}$ 倍。
5. 正四面体的面心是四个面的重心的连线相交于同一点,即四个面心和高心的连线相交于同一点。
6. 正四面体的面心到四个面心的距离相等,并且等于正四面体边长的 $\frac{\sqrt{3}}{6}$ 倍。
7. 正四面体的体积可以通过以下公式计算:$V =\frac{1}{12}\sqrt{2}a^3$,其中 $a$ 表示正四面体的边长。
8. 正四面体的表面积可以通过以下公式计算:$S = \sqrt{3}a^2$,其中 $a$ 表示正四面体的边长。
三、相关定理1. 正四面体的四条高线互相垂直,并且彼此平分。
2. 正四面体的四个面的面积互等,并且每个面的面积为$\frac{\sqrt{3}}{4}a^2$,其中 $a$ 表示正四面体的边长。
3. 正四面体的六条棱所构成的六个五面角的面积互等。
4. 正四面体的四条高线与四个面上的高线的交点所构成的四个四面角的面积互等。
通过以上的知识点,我们可以更好地理解正四面体的性质和特点。
正四面体是一种简单但非常重要的几何体,它在数学及其他科学领域中具有广泛的应用。

正四面体的总曲率正四面体是一种非常重要的多面体,它在几何学、物理学和数学中都有广泛的应用。
正四面体的总曲率是描述其表面弯曲程度的一个数学量,它可以帮助我们更好地理解正四面体的几何特性。
1. 正四面体的定义和特性正四面体是由四个等边三角形构成的多面体,每个三角形都是一个侧面,四个顶点都位于同一球面上。
正四面体的边长等于其高度,且所有角的度数为109.471°23′。
正四面体是一种对称图形,具有高度的旋转对称性和反射对称性。
2. 总曲率的计算正四面体的总曲率可以通过高斯曲率来计算。
高斯曲率是描述二维表面在一点处弯曲程度的量,对于正四面体,我们可以通过对每个侧面进行曲率计算,然后求和得到总曲率。
①侧面的曲率首先,我们来计算正四面体一个侧面的曲率。
我们可以将侧面看作是一个等边三角形的边界,使用黎曼曲率公式来计算:其中,是侧面的边长,是侧面的面积,是侧面的法向量。
对于正四面体,边长,面积可以通过海伦公式计算得到:其中,是边长,是半周长。
②总曲率正四面体有四个侧面,因此总曲率为:3. 总曲率的物理意义正四面体的总曲率具有重要的物理意义。
在物理学中,曲率与引力有关,正四面体的总曲率可以用来描述其表面引力的大小。
在数学中,曲率也是研究几何图形性质的重要工具,正四面体的总曲率可以帮助我们更好地理解其几何特性。
4. 总曲率与几何性质的关系正四面体的总曲率与其几何性质密切相关。
例如,正四面体的总曲率越大,其表面引力越大,这可能导致正四面体在物理场中的行为发生变化。
此外,正四面体的总曲率还可以用来研究其稳定性,曲率越大,稳定性越差。
5. 总结总之,正四面体的总曲率是描述其表面弯曲程度的一个重要数学量。
通过计算正四面体的总曲率,我们可以更好地理解其几何性质和物理性质。
正四面体的总曲率在几何学、物理学和数学中都有广泛的应用,对于研究正四面体的性质和发展相关理论具有重要意义。

正四面体公式
正四面体是一种四面均等的三维多面体,它的每一个面都是一个正三角形,每一个顶点都共分布着三条棱。
正四面体经常出现在数学、物理和化学等学科的研究中,因此掌握正四面体的基本公式和性质非常重要。
下面是正四面体的一些基本公式:
1. 正四面体的体积公式
正四面体的体积可以通过以下公式计算:
V = (a^3) / (6√2)
其中,V表示正四面体的体积,a表示正四面体的棱长。
2. 正四面体的表面积公式
正四面体的表面积可以通过以下公式计算:
S = √3(a^2)
其中,S表示正四面体的表面积,a表示正四面体的棱长。
3. 正四面体的外接球半径公式
正四面体的外接球半径可以通过以下公式计算:
R = a / (√3)
其中,R表示正四面体的外接球半径,a表示正四面体的棱长。
4. 正四面体的内接球半径公式
正四面体的内接球半径可以通过以下公式计算:
r = (a√2) / 12
其中,r表示正四面体的内接球半径,a表示正四面体的棱长。
5. 正四面体的重心公式
正四面体的重心位于四个顶点和四个面的重心的平面交点处,其坐标可以通过以下公式计算:
G = (a / 4)(1, 1, 1)
其中,G表示正四面体的重心坐标,a表示正四面体的棱长。
总结:
正四面体是一种常见的三维多面体,掌握它的基本公式和性质对于数学、物理和化学等学科的研究具有非常重要的作用。
正四面体的基本公式包括:体积公式、表面积公式、外接球半径公式、内接球半径公式和重心公式。

正四面体相关公式正四面体是立体几何中一个很有趣的几何体,咱们今天就来好好聊聊跟它有关的那些公式。
我还记得之前在课堂上给学生们讲正四面体的时候,有个小家伙一脸迷茫地问我:“老师,这正四面体到底有啥特别的呀?”我笑着回答他:“这正四面体啊,就像是一个神秘的小城堡,里面藏着好多数学的宝藏呢!”咱们先来说说正四面体的体积公式。
它的体积 V 可以用一个挺特别的式子来表示:V = √2/12 × a³ ,这里的 a 表示正四面体的棱长。
想象一下,正四面体就像是一个装满神秘液体的魔法盒子,这个公式就是打开盒子获取液体容量的密码。
再看看正四面体的表面积公式。
它的表面积 S 等于√3 × a² 。
这就好比正四面体的外衣,用这个公式就能算出这件外衣的大小。
还有正四面体的外接球半径 R 和内切球半径 r 也有相应的公式。
外接球半径R = √6/4 × a ,内切球半径r = √6/12 × a 。
在解题的时候,这些公式可派上大用场啦。
就说有一次考试,有道题给出了正四面体的棱长,让求体积和表面积。
好多同学一看到题就慌了神,可平时认真记住公式的小李同学,不慌不忙地拿起笔,把公式一套,答案很快就出来了。
咱们再深入一点,来探讨一下怎么推导这些公式。
推导的过程就像是一次探险,充满了挑战和惊喜。
比如说体积公式的推导,需要用到一些巧妙的几何方法和三角函数知识。
其实,正四面体不仅仅是一堆公式的组合,它在我们的生活中也有影子呢。
比如一些建筑的设计,可能就借鉴了正四面体的结构特点,既美观又稳定。
总之,正四面体的这些公式虽然看起来有点复杂,但只要咱们用心去理解、去记忆,就能像掌握神奇的魔法一样,轻松应对各种相关的问题。
相信通过不断的学习和探索,我们能在数学的世界里发现更多像正四面体这样有趣的“宝藏”!。

正四面体正四面体是几何学中的一种多面体,也被称为正四面体体,是四面体中最简单的一种。
它有四个等边等面的三角形面和四个顶点,每个顶点相邻的边的夹角是109.47度。
正四面体在数学、物理学、化学等领域中具有重要的应用和意义。
正四面体的特点是每个面都是等边三角形,它有一些独特的性质。
首先,正四面体的所有面都是等边等角的三角形,这意味着每个面的边长和角度都相等。
其次,正四面体的对角线相交于一个点,这个点被称为正四面体的正中心,连结正中心与顶点的线段被称为正四面体的高,并且高的长度等于正四面体边长的根号3倍。
此外,正四面体的各个面都是相等的,并且任意两个面之间的夹角是立体角的二等分线。
正四面体的体积也可以通过公式来计算,公式为V = (a^3)/(6√2),其中V表示体积,a表示正四面体的边长。
正四面体的表面积可以通过公式S = √3*a^2,其中S表示表面积。
通过这些公式,我们可以方便地计算正四面体的体积和表面积。
正四面体在数学中有很多重要的应用。
它是立体几何学中的一个重要研究对象,可以通过正四面体的性质探索其他多面体的性质。
在计算几何学中,正四面体是一个非常有用的模型,可以用来解决与几何形状相关的问题。
正四面体在物理学中也有广泛的应用。
例如,在分子结构研究中,正四面体经常用来表示一些分子的结构,例如硫酸四面体(SO4)。
此外,正四面体也可以用来表示晶体的结构,例如金刚石晶体的结构就是一个正四面体。
在化学中,正四面体也具有重要的意义。
正四面体分子的结构常常具有一定的稳定性,可以用来构建一些特殊的化学物质。
例如,正四面体结构的分子一般具有较高的对称性,这种对称性可以影响分子的性质和反应活性。
总之,正四面体是几何学中的一个重要概念,它具有独特的性质和特点,并在数学、物理学和化学等领域中具有广泛的应用。
通过研究正四面体的性质和应用,我们可以更好地理解立体几何学和其它相关学科的知识,为实际问题的解决提供更加可靠的理论基础。
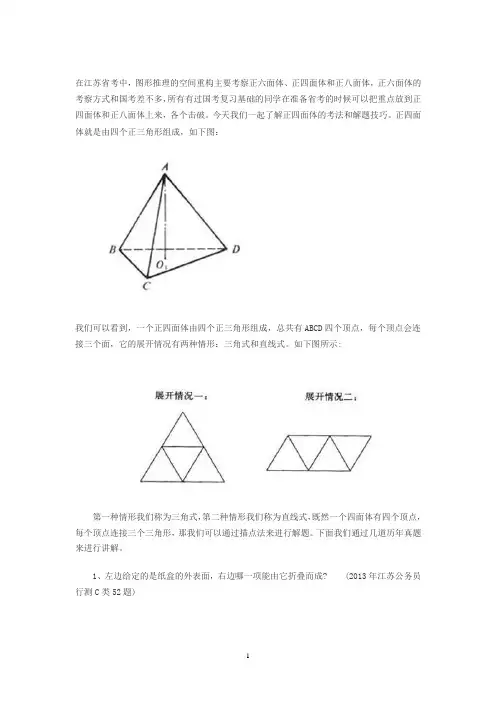
在江苏省考中,图形推理的空间重构主要考察正六面体、正四面体和正八面体,正六面体的考察方式和国考差不多,所有有过国考复习基础的同学在准备省考的时候可以把重点放到正四面体和正八面体上来,各个击破。
今天我们一起了解正四面体的考法和解题技巧。
正四面体就是由四个正三角形组成,如下图:我们可以看到,一个正四面体由四个正三角形组成,总共有ABCD四个顶点,每个顶点会连接三个面,它的展开情况有两种情形:三角式和直线式。
如下图所示:第一种情形我们称为三角式,第二种情形我们称为直线式,既然一个四面体有四个顶点,每个顶点连接三个三角形,那我们可以通过描点法来进行解题。
下面我们通过几道历年真题来进行讲解。
1、左边给定的是纸盒的外表面,右边哪一项能由它折叠而成? (2013年江苏公务员行测C类52题)解析:此题可以采用描点法来解答。
将正四面体的展开图描点之后,如下图所示:将选项A图描点之后,如下图所示:与原图对比发现,若以CAB面为基准面,则ABD面与原图并不相同,错误,则A项错误。
将选项B图描点之后,如下图所示:若以BCD面为基准面,与原图对比发现,原图中并无ACD面,故B项错误。
将选项D图描点之后,如下图所示:若以BCD面为基准面,与原图对比发现,原图的AD边连着黑白相间的图形,而此图中,AD边与黑三角相连,故D项错误。
而只有C项的所有点面均与题干的展开图完全符合,故正确答案为C项。
2、左边给定的是纸盒的外表面,右边哪一项能由它折叠而成?(2013年江苏公务员行测A类57题)解析:此题可以采用描点法来做,将题干的图形描点之后为下图,将选项A图描出如下所示:通过与原图对比发现,BCD面中的D点错误,在原图中应该是C点,故A项错误。
将选项B图中的点描出,如下所示通过与原图对比发现,ABD面错误,应该为CBD,故B项错误。
将选项C图中的点描出如下所示:通过与原图对比发现ABD面错误,应该为ABC面,故C项错误。
将选项D图中的点描出后完全无误,故正确答案为D项。
正四面体与正八面体的性质正四面体是一种特殊的三维几何体,它具有一些独特的性质和特征。
正八面体也是一种特殊的三维几何体,与正四面体有着一些相似和不同的性质。
本文将分别探讨正四面体和正八面体的性质,以便更好地理解它们在几何学中的重要性。
正四面体的性质正四面体是一种四面体,它的底部是一个等边三角形,而其顶部则是一个共平面的点。
这种结构使得正四面体具有一些特殊的性质。
1. 对称性:正四面体具有高度的对称性。
它的任意两个面都能通过某个旋转操作相互转换。
换句话说,正四面体的每个面都是相似的。
这种特性使得正四面体在几何学中非常重要,它可以用于建模和解决各种问题。
2. 边长和角度:正四面体的边长相等,且顶点到中心的距离相等。
其底部三角形的内角为60度,而顶点的内角为70.53度。
这些角度的特殊性质使得正四面体在计算和测量中非常实用。
3. 体积和表面积:正四面体的体积可以通过公式V = (√2/12) × a³来计算,其中a代表边长。
而其表面积则可以通过公式S = √3 × a²来计算。
这些公式对于计算正四面体的空间需求和相关问题非常有用。
正八面体的性质正八面体是一种八面体,它的每个面都是一个正方形。
这使得正八面体具有一些独特的性质和特征。
1. 对称性:正八面体具有高度的对称性,它有24个对称操作。
这些操作包括旋转、反射和转动等,可以使得正八面体的不同面相互转换。
这种对称性使得正八面体在几何学中有着广泛的应用。
2. 边长和角度:正八面体的边长相等,且所有顶点的内角为90度。
这些特性使得正八面体在计算和测量中具有一定的方便性。
3. 体积和表面积:正八面体的体积和表面积可以通过相应的公式进行计算。
其体积公式为V = (√2/3) × a³,而表面积公式为S = 2√2 × a²。
这些公式可以帮助我们计算正八面体的空间需求和相关问题。
正四面体与正八面体的比较尽管正四面体和正八面体都是特殊的三维几何体,但它们在性质和特征上有一些区别。
分子空间构型是化学中一个重要的概念,它描述了分子在空间中排列的方式。
而正四面体构型是一种特殊的构型,其中分子的键角为60度。
本文将深入探讨键角为60度的分子空间构型正四面体。
一、正四面体构型的定义正四面体是一种特殊的几何形状,它由四个相等的三角形构成,这些三角形共享一个顶点。
正四面体构型在化学中指的是分子中的原子之间的排列方式呈现出的几何形状,其中分子的键角为60度。
二、正四面体构型的性质1. 对称性:正四面体具有最高的对称性,具有四个等价的顶点和四个等价的面。
2.键角:正四面体构型中,分子的键角固定为60度。
3.稳定性:正四面体构型的分子通常具有较高的稳定性,这种构型使得分子中的电子云分布均匀,有利于分子的稳定性。
4.应用:正四面体结构广泛存在于化学和生物领域,例如硼烷、甲硼烷等分子中均具有正四面体构型。
三、正四面体构型的实现1. 分子中心原子四面体构型的实例以甲硼烷(BH4)- 分子为例,甲硼烷(BH4)-分子由一个硼原子和四个氢原子组成,硼原子和每个氢原子之间的键角均为120度,而整个甲硼烷分子的结构与正四面体构型非常相似。
硼原子位于正四面体的中心,四个氢原子分别位于四个顶点,形成正四面体构型。
2. 键角为60度构型的原子排列对于分子中的原子排列方式,常见的是分子中含有四个相同的原子,它们均位于分子的四个顶点上,形成正四面体构型。
这样的分子中,每个原子之间的键角均为60度,呈现出对称的几何形状。
四、正四面体构型的意义正四面体构型在化学与生物领域中具有重要的意义:1. 理论意义:正四面体构型的研究有助于深化对分子空间结构的理解,加深对分子之间相互作用的认识。
2. 应用价值:正四面体构型的分子在物理、化学、生物等领域具有广泛的应用价值,例如在材料科学中的应用以及对分子性质的研究等。
3. 化学合成:正四面体构型的分子在化学合成中具有一定的指导意义,有助于设计以及合成具有特定性质的分子,具有重要的应用前景。
正四面体相关结论正四面体是一种具有特殊性质的几何图形,它由四个相等的正三角形组成,每个角都是60度。
在正四面体中,有一些重要的结论和性质,这些结论和性质在解决相关的几何问题时非常有用。
1、中心与顶点之间的关系正四面体的中心到四个顶点的距离相等,也就是说,中心是四个顶点所组成的菱形的中心。
这个结论可以用于计算正四面体的半径和中心到顶点的距离。
2、边长与高之间的关系正四面体的边长和高之间有一个重要的关系,即高是边长的2/3。
这个结论可以用于计算正四面体的高,也可以用于解决与正四面体的边长和高有关的问题。
3、体积与半径之间的关系正四面体的体积与半径之间有一个重要的关系,即体积是半径的立方根。
这个结论可以用于计算正四面体的体积,也可以用于解决与正四面体的体积和半径有关的问题。
4、三个两两垂直的平面相交于一点在正四面体中,三个两两垂直的平面相交于一点,这个结论可以用于解决与正四面体的三个两两垂直的平面相交有关的问题。
5、相对的两条边互相垂直在正四面体中,相对的两条边互相垂直,这个结论可以用于解决与正四面体的相对的两条边互相垂直有关的问题。
正四面体的一些重要结论和性质在解决相关的几何问题时非常有用,这些结论和性质可以帮助我们更好地理解和解决正四面体的问题。
正四面体外接球和内切球的半径的求法在几何学中,正四面体是一种具有特殊性质的几何形态。
它由四个相等的正三角形构成,每个面都是一个等边三角形。
这种几何形态在许多领域都有广泛的应用,包括物理学、化学、工程学等。
在解决实际问题时,我们常常需要找出正四面体的外接球和内切球的半径。
下面将介绍两种求法。
第一种方法是通过几何计算直接求解。
首先,我们需要找到正四面体的中心点。
这个点可以通过连接正四面体的四个顶点并取其中间位置来找到。
一旦找到了中心点,我们就可以通过连接这个点和正四面体的各个顶点,找到外接球的球心。
外接球的半径就是从球心到正四面体顶点的距离。
内切球的半径则是从球心到正四面体四个面的中心的距离。
正四面体是一种柏拉图多面体,正四面体与自身对偶。
正四面体的重心、四条高的交点、外接球、内切球球心共点,此点称为中心。
正四面体有一个在其内部的内切球和七个与四个面都相切的旁切球,其中有三个旁切球球心在无穷远处。
正四面体有四条三重旋转对称轴,六个对称面。
正四面体可与正八面体填满空间,在一顶点周围有八个正四面体和六个正八面体。
化学中CH4,CCl4等分子也呈正四面体状。
相关数据当正四面体的棱长为a时,一些数据如下:高:√6a/3。
中心把高分为1:3两部分。
表面积:√3a^2体积:√2a^3/12对棱中点的连线段的长:√2a/2外接球半径:√6a/4,正四面体体积占外接球体积的2*3^0.5/9*π,约12.2517532%。
内切球半径:√6a/12,内切球体积占正四面体体积的π*3^0.5/18,约30.2299894%。
棱切球半径:√2a/4.两条高夹角:2ArcSin(√6/3)=ArcCos(-1/3)=≈1.91063 32362 49(弧度)或109°28′16″39428 41664 889。
这一数值与三维空间中求最小面有关,也是蜂巢底菱形的钝角的角度.两邻面夹角:2ArcSin(√3/3)=ArcCos(1/3)≈1.23095 94173 4077(弧度)或70°31′43″60571 58335 111,与两条高夹角在数值上互补。
侧棱与底面的夹角:ArcCos(√3/3)正四面体的对棱相等。
具有该性质的四面体符合以下条件:1.四面体为对棱相等的四面体当且仅当四面体每对对棱的中点的连线垂直于这两条棱。
2.四面体为对棱相等的四面体当且仅当四面体每对对棱中点的三条连线相互垂直。
3.四面体为对棱相等的四面体当且仅当四条中线相等。
正四面体在解析几何中的一般建系方法1.设有一正四面体D-ABC棱长为a以AB边为y轴A为顶点ABC所属平面为xOy面建系四个顶点的坐标依次为正四面体侧面展开图。
正四面体的常用结论公式1. 什么是正四面体?好啦,今天我们聊聊正四面体,听起来可能有点生僻,但别担心,咱们一步一步来,让它变得简单易懂。
正四面体就是一种特殊的立体形状,它有四个面,每个面都是等边三角形。
想象一下,你把四个小三角形拼在一起,顶端和底部的角度都那么完美,简直像是天上掉下来的几何精灵。
四个面、六条边和四个顶点,乍一看好像没啥特别,但你可别小瞧它,正四面体可是很多数学问题和物理现象中的明星哦!1.1. 体积的计算说到正四面体,首先得搞清楚它的体积怎么算。
这个公式可真是简单明了,咱们就用个小公式来记住它:( V = frac{a^3{6sqrt{2 )。
这里的 ( a ) 就是你那条边的长度,想象一下,假如你有一个边长为 1 的正四面体,算出来的体积就是约 0.11785。
这点体积听起来不多,但在数学的世界里,什么都能玩出花样来。
1.2. 表面积的计算再说说表面积,正四面体的表面积计算也不麻烦,公式是:( A = sqrt{3 a^2 )。
意思是,你只要知道边长,就能算出它的“外衣”有多大。
比如,边长为 2 的正四面体,表面积就是 ( sqrt{3 times 4 ),大约是 6.928。
这可是个好消息,表面积比体积大,不然它可真成了“体积小得可怜”的小可怜。
2. 正四面体的特性2.1. 对称性接下来说说正四面体的特性。
首先,它的对称性就让人眼前一亮。
想象一下,正四面体从各个方向看上去都一模一样,简直就像是一位被上帝偏爱的“模特”。
不论是从哪个角度看,都是那么的完美,绝对是几何界的“颜值担当”。
2.2. 内切球和外接球而且,正四面体还有个小秘密,那就是它的内切球和外接球。
简单来说,内切球就是正四面体内部最大能容纳的球,而外接球就是把它包裹住的那个球。
内切球的半径( r ) 公式是 ( r = frac{a{2sqrt{6 ),外接球的半径 ( R ) 则是 ( R = frac{asqrt{6{4 )。
高中数学正四面体的结论
正四面体(Regular Tetrahedron),是高中数学中常用的几何体之一,它是一个三维的,拥有四个平行面的晶体。
它是比较容易了解的几何形状,下面就介绍其特性:
一、正四面体的顶角:
正四面体的每个顶角都是一个直角,它们夹在三条互相垂直的边中,其角度为90°,称为正四面体的几何角。
二、正四面体的边:
正四面体的边长都是相等的,它们互相垂直,三个边可以构成相应的三角形,并且相互平行。
三、正四面体的表面:
正四面体有四个平行面,当三条直线连接某三个顶点时,可以形成正四面体的表面,这四个平行面都是矩形,每个平行面跟每条边相等。
四、正四面体的面积:
正四面体的表面积是a²*√3,它可以通过边长a来计算,也可以用边和顶角来计算表面积。
五、正四面体的体积:
正四面体的体积是a³/6√2,它可以通过边长a来计算,也可以用直角三角形的面积、顶角或平面面积来求解。
总之,正四面体是一个边和顶角都是相等的三维几何体,有许多结论可以推导出来,如面积和体积的计算公式等。
正四面体的学习和考察对于理解高中数学的知识和运用至关重要,是高中数学必不可少的一个概念。
正四面体
常用性质:
1、正四面体是由四个全等正三角形围成的空间封闭图形,所有棱长都相等。
它有4个面,6条棱,4个顶点。
正四面体是最简单的正多面体。
2、正四面体属于正三棱锥,但是正三棱锥只需要底面为正三角形,其他三个面是全等的等腰三角形就可以,不需要四个面全等且都是等边三角形。
因此,正四面体是特殊的正三棱锥。
3、基本性质:正四面体是一种柏拉图多面体,正四面体与自身对偶。
正四面体的重心、四条高的交点、外接球、内切球球心共点,此点称为中心。
正四面体的对边相互垂直。
正四面体的对棱相等。
正四面体内任意一点到四个面的距离之和为定值6
3
a。
4、相关数据当正四面体的棱长为a时,一些数据如下:
高:6
3
a。
(中心把高分为1:3两部分} 表面积:2
3a体积:
3
2
12
a
外接球半径:6
4
a
,内切球半径:
6
12
a
,棱切球半径:
2
4
a
对棱中点的连线段的长:2
2
a
,两邻面夹角满足
1
cos
3
α=。
若将正四面体放进一个正方体内,则该正方体棱长为2
2
a
,其实,正四面体的棱切球
即为次正方体的内切球。
5、建系方法1.设有一正四面体D-ABC棱长为a
以AB边为y轴A为顶点ABC所属平面为xOy面建系四个顶点的坐标依次为
其他性质:
正四面体有一个在其内部的内切球和七个与四个面都相切的旁切球,其中有三个旁切球球心在无穷远处。
正四面体有四条三重旋转对称轴,六个对称面。
正四面体可与正八面体填满空间,在一顶点周围有八个正四面体和六个正八面体。
正四面体体积占外接球体积的2*3^0.5/9*π,约12.2517532%。
内切球体积占正四面体体积的π*3^0.5/18,约30.2299894%。
两条高夹角:2ArcSin(√6/3)=ArcCos(-1/3)=≈1.91063 32362 49(弧度)或109°28′16″39428 41664 889。
这一数值与三维空间中求最小面有关,也是蜂巢底菱形的钝角的角度.
侧棱与底面的夹角:ArcCos(√3/3)
正四面体的对棱相等。
具有该性质的四面体符合以下条件:
1.四面体为对棱相等的四面体当且仅当四面体每对对棱的中点的连线垂直于这两条棱。
2.四面体为对棱相等的四面体当且仅当四面体每对对棱中点的三条连线相互垂直。
3.四面体为对棱相等的四面体当且仅当四条中线相等。
化学中CH4,CCl4,SiH4等物质也是正四面体结构。
正四面体键角是109度28分,约为109.47°。