直流激励霍尔传感器实验报告
- 格式:pdf
- 大小:688.89 KB
- 文档页数:5

霍尔传感器的直流激励特性实验报告误差分析
霍尔传感器是用来检测磁场的一种传感器,它可以通过感知磁场的变化来测量物体的位置、速度等。
在实验中,为了使霍尔传感器正常工作,需要给它提供一定的激励电压,这个激励电压的大小和稳定性对实验的准确性有很大的影响。
一般来说,霍尔传感器的直流激励特性实验可以分为两个部分:测量霍尔传感器的输出电压与激励电压的关系,以及测量霍尔传感器的稳定性。
其中,第一个部分是为了确定霍尔传感器的灵敏度,即输出电压与磁场的关系,第二个部分是为了确定霍尔传感器的长期稳定性。
误差分析:
1. 激励电压的稳定性不够:
在实验中,如果激励电压的波动比较大,就会导致输出电压的误差增大。
这种误差可以通过采用稳压电源或者其他控制电压波动的方法来减小。
2. 测量电路的误差:
测量电路也会对实验结果产生误差,如放大器的增益不稳定、滤波器的频率响应不均匀等。
可以通过对测量电路进行校准来减小误差。
3. 环境磁场的影响:
周围的磁场也会对实验结果产生误差,特别是在霍尔传感器接近物体时,物体本身的磁场会对测量产生影响。
可以采取屏蔽措施或者在实验中消除这些影响。
4. 对原始数据处理的误差:
在对实验数据进行处理时,可能会出现计算误差、单位转换误差等。
这些误差可以通过实验操作的规范、数据记录的精准和对数据处理的细心来减小。
综上所述,要减小霍尔传感器的直流激励特性实验的误差,需要在实验设计、实验操作、数据处理等方面都保证科学合理性和准确性,并且提高对实验中各种误差来源的识别和防范能力。

实验二霍尔式传感器1. 霍尔式传感器特性――直流激励实验目的:了解霍尔式传感器的原理与特性。
所需单元及部件:霍尔片、磁路系统、电桥、差动放大器、F/V表、直流稳压电源、测微头、振动平台、主、副电源。
有关旋钮初始位置:差动放大器增益旋钮打大最小,电压表置20V档,直流稳压电源置2V档,主、副电源关闭。
实验步骤:(1)了解霍尔式传感器的结构及试验仪的安装位置,熟悉试验面板上霍尔片的符号。
霍尔片安装在实验仪的振动圆盘上,两个半圆永久磁钢固定在实验仪的顶板上,二者组合成霍尔传感器。
(2)开启主、副电源将差动放大器调零后,增益置最小,关闭主电源,根据图21接线,W1、r为电桥单元的直流电桥平衡网络。
(3)装好测微头,调节测微头与振动台吸合并使霍尔片置于半圆磁钢上下正中位置。
(4)开启主、副电源,调整W1使电压表指示为零。
(5)上下旋动测微头,记下电压表的读数,建议每0.1mm读一个数,将读数填入下表:作出V-X曲线指出线性范围,求出灵敏度,关闭主、副电源。
可见,本实验测出的实际上是磁场情况,磁场分布为梯度磁场与磁场分布有很大差异,位移测量的线性度,灵敏度与磁场分布有很大关系。
(6)试验完毕关闭主、副电源,各旋钮置初始位置。
注意事项:(1)由于磁路系统的气隙较大,应使霍尔片尽量靠近极靴,以提高灵敏度。
(2)一旦调整好后,测量过程中不能移动磁路系统。
(3)激励电压不能过大,以免损坏霍尔片。
2.霍尔传感器的应用--------振幅测量实验目的:了解霍尔传感器在振动测量中的应用所需单元及部件:霍尔片、磁路系统、差动放大器、电桥、移相器、相敏检波器、低频振动器、音频振荡器、振动平台、主、副电源、激振线圈、双线示波器。
有关旋转初始位置:差动放大器增意旋最大、音频振荡器1KHZ。
实验步骤:(1)开启主,副电源,差动放大器输入短接并接地,调零后,关闭主,副电源。
(2)根据电路图24结构,将霍尔式传感器,电桥平衡网络,差动放大器,电压表连接起来,组成一个测量线路(电压表应置于20V档,基本保持实验23电路),并将差放增益置最小。

三、实验效果分析(包过仪器设备等使用效果)三、实验效果分析:由实验数据知在中心位置处霍尔传感器的灵敏度最高,其灵敏度为:S=dy/dx=0.03v/0.2mm=0.15v/mm 线性度为: = 100%=0.01/5.2 *100%=0.192%;由MATLAB图形知线性范围为5.4MM—10.6MM。
教师评语指导教师年月日江西师范大学物理与通信电子学院教学实验报告专业:电子信息工程2010年 4 月28日实验名称霍尔式传感器的直流激励特性指导老师姓名年级08级学号成绩一、预习部分1、实验目的2、实验基本原理3、主要仪器设备(包含必要的元器件、工具)一、实验目的:1.了解霍尔式传感器的原理与特性。
二、实验原理:霍尔式传感器是由两个环形磁钢组成梯度有头磁场和位于梯度磁场中的霍尔元件组成,当霍尔元件通过恒定电流时霍尔元件在梯度磁场中上、下移动时输出的霍尔电势V取决于其在磁场中的位移量X,所以没得霍尔电势的大小便可获知霍尔元件的静位移。
三、主要仪器设备霍尔片、磁路系统、电桥、差动放大器、F/V表、直流稳压电源、测微头、振动平台、主、副电源二、实验操作步骤1.实验数据、表格及数据处理2.实验操作过程(可以用图表示)3.结论1.实验数据、表格及数据处理如下:实验中应该注意的事项:①由于磁路系统的气隙较大,应使霍尔片尽量靠近极靴,以提高灵敏度。
②一旦调整好后,测量过程中不能移动磁路系统。
③激励电压不能过大,以免损坏霍尔片。
x=[3.8:0.2:13.8 ];y=[-38,-38,-38,-38,-36,-35,-34,-33,-31,-28,-26,-23,-20,-17,-14,-10,-6,-4,0,3,7,10,14,18,22,25,30,34,37,41,45,48,51, 54,57,59,61,62,63,64,65,66,66,67,67,67,67,68,68,68,68];a=polyfit(x,y,1);xi=3.6:0.0001:13.8;yi=polyval(a,xi);plot(x,y,'go','MarkerEdgeColor','k','MarkerFaceColor','g','MarkerSize',5)xlabel('位移/mm','fontsize',10);ylabel('电压/mV','fontsize',10);axis([3.6 13.8 -38 68])hold onplot(xi,yi,'linewidth',0.1,'markersize',1)legend('原始数据点','拟合曲线')plot(x,y) 2、实验操作过程如下:(1)了解霍尔式传感器的结构及实验仪上的安装位置,熟悉实验面板上霍尔片的符号。

吉林大学
仪器科学与电气工程学院
本科生实验报告
实验项目:霍尔传感器的直流激励报告示例
学生姓名:
学号:
实验日期:
实验地址:
2010 年月日
一、实验目的
了解霍尔式传感器的原理与特性
二、实验所用仪器设备
霍尔片、磁路系统、电桥、差动放大器、F/V表、直流稳压电源、测微头、振动平台、主副电源
三、实验原理
根据霍尔效应,霍尔电势V H=K H IB,当霍尔元件处在梯度磁场中运动时,它就可以进行位移测量了。
四、实验步骤
(1)开启主副电源,将差动放大器调零,增益最小。
关闭电源,并连接电路图
(2)调节测微头与振动台吸合并使霍尔片至于半圆磁钢上下正中位置
(3)开启主副电源,调整W1使电压表指示为零
(4)上下旋动测微头,记录电压表读数,并填入表中
(5)关闭电源,整理器材
五、实验结果与分析
V—X曲线见下图
从曲线我们可以看出线性度是比较好的,其灵敏度为K=0.02v/0.100mm=0.2v/mm,关系式为V=KX-1.6022(V)
六、实验心得与建议
该实验通过测梯度磁场的情况,从而得到间接得到位移量。
这给我们自己设计传感器提供了一个很好的思路,我们可以通过设置一个容易控制和测量的物理量,使其按一定规律在所测的物理量上分布,从而我们可以通过测量容易测得的物理量来间接得到我们需要测的量,不仅测量方便而且比较准确。
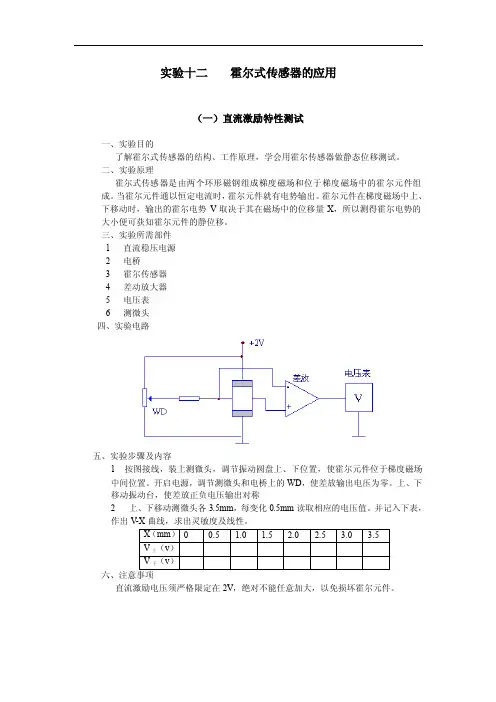
实验十二霍尔式传感器的应用(一)直流激励特性测试一、实验目的了解霍尔式传感器的结构、工作原理,学会用霍尔传感器做静态位移测试。
二、实验原理霍尔式传感器是由两个环形磁钢组成梯度磁场和位于梯度磁场中的霍尔元件组成。
当霍尔元件通以恒定电流时,霍尔元件就有电势输出。
霍尔元件在梯度磁场中上、下移动时,输出的霍尔电势V取决于其在磁场中的位移量X,所以测得霍尔电势的大小便可获知霍尔元件的静位移。
三、实验所需部件1直流稳压电源2电桥3霍尔传感器4差动放大器5电压表6测微头四、实验电路五、实验步骤及内容1 按图接线,装上测微头,调节振动圆盘上、下位置,使霍尔元件位于梯度磁场中间位置。
开启电源,调节测微头和电桥上的WD,使差放输出电压为零。
上、下移动振动台,使差放正负电压输出对称2 上、下移动测微头各3.5mm,每变化0.5mm读取相应的电压值。
并记入下表,作出V-X曲线,求出灵敏度及线性。
六、注意事项直流激励电压须严格限定在2V,绝对不能任意加大,以免损坏霍尔元件。
(二)霍尔传感器的应用——振幅测量和电子秤一、实验目的1 通过本实验了解霍尔传感器在振动测量中的作用。
2 说明线性霍尔传感器的实际应用。
二、实验所需部件1霍尔传感器2电桥3差动放大器4低通滤波器5直流稳压电源6示波器7电压表8砝码9振动圆盘三、实验步骤及内容(一)振幅测量1按上面的实验二十所示的电路连线,调节系统,使其输出为零。
2将低频振荡器接“激振I”,保持适当的振幅,用示波器观察差动放大器输出波形。
3进一步提高低频振荡器的振幅,用示波器观察差放输出波形,当波形出现顶部削顶时,说明霍尔元件已进入均匀磁场,霍尔电压已不再随振动的增加而线性增加。
(二)电子秤1 在上面电路不变的基础上,调节系统使输出电压为零,系统灵敏度尽量大。
2 以振动圆盘作为称重平台,逐步放上砝码,依次记下表头读数,填入下表,并做出V-W曲线。
线中求得其重量。
四、注意事项1 霍尔传感器在做称重时只能工作在梯度磁场中,所以砝码和被称重物都不应太重。

《机械工程测试技术》实验指导书实验一、霍尔传感器的直流激励特性一、实验目的加深对霍尔传感器静态特性的理解。
掌握灵敏度、非线性度的测试方法,绘制霍尔传感器静态特性特性曲线,掌握数据处理方法。
二、实验原理当保持元件的控制电流恒定时,元件的输出正比于磁感应强度。
本实验仪为霍尔位移传感器。
在极性相反、磁场强度相同的两个钢的气隙中放置一块霍尔片,当霍尔元件控制电流I不变时,Vh与B成正比。
若磁场在一定范围内沿X方向的变化梯度dB/dX为一常数,则当霍尔元件沿X方向移动时dV/dX=RhXIXdB/dX=K,K为位移传感器输出灵敏度。
霍尔电动势与位移量X成线性关系,霍尔电动势的极性,反映了霍尔元件位移的方向。
三、实验步骤1.有关旋钮初始位置:差动放大器增益打到最小,电压表置2V档,直流稳压电源置±2V档。
2..RD、r为电桥单元中的直流平衡网络。
3.差动放大器调零,按图6-1接好线,装好测微头。
4.使霍尔片处于梯度磁场中间位置,调整RD使电压表指示为零。
5.上、下旋动测微头,以电压表指示为零的位置向上、向下能够移动5mm,从离开电压表指示为零向上5mm的位置开始向下移动,建议每0.5mm读一数,记下电压表指示并填入下表X(mm)V(v)X(mm)V(v)6.用以上的位移和输出电压数据,绘出霍尔传感器静态特性的位移和输出电压特性V-X曲线, 指出线性范围。
7.将位移和输出电压数据分成两组,用“点系中心法”对数据进行处理,并计算两点联线的斜率,即得到灵敏度值。
实验可见:本实验测出的实际是磁场的分布情况,它的线性越好,位移测量的线性度也越好,它们的变化越陡,位移测量的灵敏度也就越大。
四、思考题1.为什么霍尔元件位于磁钢中间位置时,霍尔电动势为0。
2.在直流激励中当位移量较大时,差动放大器的输出波形如何?实验二、电容传感器的直流特性实验内容:加深对电容传感器静态特性的理解。
掌握灵敏度、非线性度的测试方法,绘制电容传感器静态特性曲线,掌握数据处理方法。

实验二霍尔式传感器1. 霍尔式传感器特性――直流激励实验目的:了解霍尔式传感器的原理与特性。
所需单元及部件:霍尔片、磁路系统、电桥、差动放大器、F/V表、直流稳压电源、测微头、振动平台、主、副电源。
有关旋钮初始位置:差动放大器增益旋钮打大最小,电压表置20V档,直流稳压电源置2V档,主、副电源关闭。
实验步骤:(1)了解霍尔式传感器的结构及试验仪的安装位置,熟悉试验面板上霍尔片的符号。
霍尔片安装在实验仪的振动圆盘上,两个半圆永久磁钢固定在实验仪的顶板上,二者组合成霍尔传感器。
(2)开启主、副电源将差动放大器调零后,增益置最小,关闭主电源,根据图21接线,W1、r为电桥单元的直流电桥平衡网络。
(3)装好测微头,调节测微头与振动台吸合并使霍尔片置于半圆磁钢上下正中位置。
(4)开启主、副电源,调整W1使电压表指示为零。
(5)上下旋动测微头,记下电压表的读数,建议每0.1mm读一个数,将读数填入下表:作出V-X曲线指出线性范围,求出灵敏度,关闭主、副电源。
可见,本实验测出的实际上是磁场情况,磁场分布为梯度磁场与磁场分布有很大差异,位移测量的线性度,灵敏度与磁场分布有很大关系。
(6)试验完毕关闭主、副电源,各旋钮置初始位置。
注意事项:(1)由于磁路系统的气隙较大,应使霍尔片尽量靠近极靴,以提高灵敏度。
(2)一旦调整好后,测量过程中不能移动磁路系统。
(3)激励电压不能过大,以免损坏霍尔片。
2.霍尔传感器的应用--------振幅测量实验目的:了解霍尔传感器在振动测量中的应用所需单元及部件:霍尔片、磁路系统、差动放大器、电桥、移相器、相敏检波器、低频振动器、音频振荡器、振动平台、主、副电源、激振线圈、双线示波器。
有关旋转初始位置:差动放大器增意旋最大、音频振荡器1KHZ。
实验步骤:(1)开启主,副电源,差动放大器输入短接并接地,调零后,关闭主,副电源。
(2)根据电路图24结构,将霍尔式传感器,电桥平衡网络,差动放大器,电压表连接起来,组成一个测量线路(电压表应置于20V档,基本保持实验23电路),并将差放增益置最小。

CYS系列传感器实验组实验23 to 实验33指导老师:冀建利机0301-2:李正祥试0301-1:于佳学号:20031586学号:200314432005年5月30日实验二十三霍尔式传感器的特性—直流激励实验目的:了解霍尔式传感器的原理与特性。
所需单元及部件:霍尔片、磁路系统、电桥、差动放大器、F/V表、直流稳压电源、测微头、振动平台、主、副电源。
有关旋钮初始位置:差动放大器增益旋钮打到最小,电压表置20V档,直流稳压电源置2V档,主、副电源关闭。
实验步骤:(1)了解霍尔式传感器的结构及实验仪上的安装位置,熟悉实验面板上霍尔片的符号。
霍尔片安装在实验仪的振动圆盘上,两个半圆永久磁钢固定在实验仪的顶板上,二者组合成霍尔传感器。
(2)开启主、副电源将差动放大器调零后,增益最小,关闭主电源,根据图21接线,W1、r为电桥单元的直流电桥平衡网络。
图21(3)装好测微头,调节测微头与振动台吸合并使霍尔片置于半圆磁钢上下正中位置。
(4)开启主、副电源,调整W1使电压表指示为零。
(5)上下旋动测微头,记下电压表的读数,建议每0.5mm读一个数,将读数填入下表:作出V-X曲线指出线性范围,(见附)求出灵敏度,关闭主、副电源。
S1=△v/△x=[(-0.050+0.144)+(0+0.086)]/(4*0.5)=0.09S2=△v/△x=[(0.087-0.044)+(0.069-0.077)]/(4*0.5)=0.08S=(s1+s2)/2=0.085可见,本实验测出的实际上是磁场情况,磁场分布为梯度磁场与磁场分布有很大差异,位移测量的线性度,灵敏度与磁场分布有很大关系。
(6)实验完结关闭主、副电源,各旋钮置初始位置。
注意事项:(1)由于磁路系统的气隙较大,应使霍尔片尽量靠近极靴,以提高灵敏度。
(2)一旦调整好后,测量过程中不能移动磁路系统。
(3)激励电压不能过大,以免损坏霍尔片。
实验二十四霍尔式传感器的应用—电子秤之四实验目的:了解霍尔式传感器在静态测量中的应用。

《传感器技术原理与应用》实验报告实验一直流激励下霍尔传感器的位移特性实验一、实验目的:掌握霍尔传感器的特性与应用答:霍尔传感器是根据霍尔元件的电磁特性(控制电流与输出之间的关系,霍尔输出与磁场之间的关系)输出电压与控制电流之间呈线性关系,直线的斜率称为控制电流灵敏度。
固定控制电流,元件的开路霍尔输出随磁场的增加呈线性关系。
二、基本原理在半导体薄片两端通以控制电流I,并在薄片的垂直方向施加磁感应强度为B的匀强磁场,则在垂直于电流和磁场的方向上,将产生电势差为HU的霍尔电势,这种现象为霍尔效应。
根据霍尔效应,人们用半导体材料制成的元件叫霍尔元件。
假设在N型半导体薄片上通以电流I,则半导体中载流子将沿着和电流相反的方向运动,若在垂直于薄片平面的方向加以磁场B,则在洛伦兹力evBf=L(e为电子电量,v为电子速,B为磁场强度)作用下,电子向一边偏转,并使该边电子形成积累,则在另一边积累正电荷,于是产生电场,该电场使电子继续偏转,当电场作用在电子的力leUf H/E=与洛伦兹力L f相等的时候,电子的积累达到动态平衡。
此时,在薄片两横端面间建立的电场为霍尔电场HE,相应的电势为霍尔电势HU,大小为RU HIB/dH=R--霍尔常数;HI--控制电流;B--磁场强度;d--霍尔元件的厚度;令dK成为霍尔元件的灵敏度);则K/HRH=(HU HIBKH=。
三、实验结果记录第一组数据第二组数据第三组数据刻度/mm电压/V刻度/mm电压/V刻度/mm电压/V12.15 0.001 12.45 0.007 12.52 -0.00712.65 -0.525 11.95 0.520 13.02 -0.49813.15 -0.953 11.45 1.083 13.52 -0.98813.65 -1.399 10.95 1.668 14.02 -1.47614.15 -1.754 10.45 2.22 14.52 -1.93214.65 -2.00 9.95 2.70 15.02 -2.3415.15 -2.14 9.45 2.94 15.52 -2.6615.65 -2.23 8.95 3.03 16.02 -2.7716.15 -2.28 8.45 3.03 16.52 -2.7816.65 -2.32 8.95 3.04 16.02 -2.8017.15 -2.35 9.45 2.96 15.52 -2.67 17.65 -2.35 9.95 2.76 15.02 -2.36 17.15 -2.35 10.45 2.33 14.52 -1.92 16.65 -2.32 10.95 1.78 14.02 -1.54 16.15 -2.29 11.45 1.151 13.52 -1.058 15.65 -2.33 11.95 0.592 13.02 -0.544 15.15 -2.14 12.45 0.078 12.52 -0.030 14.65 -2.03 12.95 -0.410 12.02 0.501 14.15 -1.825 13.45 -0.895 11.52 1.081 13.65 -1.062 13.95 -1.396 11.02 1.702 13.15 -0.712 14.45 -1.896 10.52 2.31 12.65 -0.299 14.95 -2.33 10.02 2.79 12.15 0.175 15.45 -2.61 9.52 3.05 11.65 0.672 15.95 -2.71 9.02 3.13 11.15 1.154 16.45 -2.75 8.52 3.11 10.65 1.633 15.95 -2.57 9.02 3.08 10.15 2.03 15.45 -2.43 9.52 3.00 9.65 2.36 14.95 -2.17 10.02 2.71 9.15 2.54 14.45 -1.828 10.52 2.28 8.65 2.63 13.95 -1.431 11.02 1.66 8.15 2.73 13.45 -0.960 11.52 1.07 7.65 2.82 12.95 -0.482 12.02 0.506 7.15 2.83 12.45 -0.016 12.52 0.010 6.65 2.846.15 2.846.65 2.907.15 2.877.65 2.618.15 2.608.65 2.669.15 2.839.65 2.9910.15 2.7110.65 2.1711.15 1.50911.65 0.94212.15 0.384四、实验结果分析1.用matlab做三次测量数据的折线图2.使用一条直线对曲线进行拟合,给出拟合公式如图为传感器位移特性曲线,紫色线为用最小二乘法做出的一次拟合直线,拟合直线公式为:y=kx+b (分别在直线上找到两点带入得到公式)即:y=-1.029x+12.4923.根据图形,计算或者指出传感器的测量范围,灵敏度,线性度,重复性。

北京XXX大学实验报告课程(项目)名称:实验四霍尔式传感器的特性—直流激励学院:专业:班级:学号:姓名:成绩:2013年12月10日一、任务与目的了解霍尔式传感器的原理与特性。
二、实验仪器所需单元及部件:霍尔片、磁路系统、电桥、差动放大器、F/V表、直流稳压电源、测微头、振动平台、主、副电源。
有关旋钮初始位置:差动放大器增益旋钮打到最小,电压表置20V档,直流稳压电源置2V档,主、副电源关闭。
三、原理(条件)霍尔式传感器是由两个环形磁钢组成梯度有头磁场和位于梯度磁场中的霍尔元件组成,当霍尔元件通过恒定电流时霍尔元件在梯度磁场中上、下移动时输出的霍尔电势V取决于其在磁场中的位移量X,所以测得霍尔电势的大小便可获知霍尔元件的静位移。
四、内容与步骤(1)了解霍尔式传感器的结构及实验仪上的安装位置,熟悉实验面板上霍尔片的符号。
霍尔片安装在实验仪的振动圆盘上,两个半圆永久磁钢固定在实验仪的顶板上,二者组合成霍尔传感器。
(2)将差动放大器调零:用连线将差动放大器的正(+)、负(-)、地短接。
将差动放大器的输出端与F/V表的输入插口Vi 相连;开启主、副电源;调节差动放大器的增益到最小位置,然后调整差动放大器的调零旋钮使F/V21接线,W1、r为电桥单元的直流电桥平衡网络。
图21(3)装好测微头,调节测微头与振动台吸合并使霍尔片置于半圆磁钢上下正中位置,记下此时测微头的读数。
(4)开启主、副电源调整W1使电压表指示为零。
(5)上下旋动测微头,记下电压表的读数,建议每0.1mm(副尺转过10个格)读一个数,将读数填入下表:(6)将测微头调制初始位置,然后旋转测微头向相反方向转动,建议每0.1mm读一个电压表的读数,将读书填入表格中(7)作出V-X曲线指出线性范围,求出灵敏度,关闭主、副电源。
五、数据处理(现象分析)(1)上下旋动测微头,记下电压表的读数,每0.1mm(副尺转过10个格)读一个数,读数见(2)将测微头调制初始位置,然后旋转测微头向相反方向转动,每0.1mm读一个电压表的读书,读数见下表:(3)作出V-X曲线指出线性范围,求出灵敏度。

实验二十三霍尔式传感器的直流激励特性一、实验目的了解霍尔式传感器的原理与特性。
二、实验原理霍尔传感器是由两个环形磁钢组成梯度磁场和位于梯度磁场中的霍尔元件组成。
当霍尔元件通过恒定电流时,霍尔元件在梯度磁场中上、下移动时,输出的霍尔电势V取决于其在磁场中的位移量X,所以测得霍尔电势的大小便可获知霍尔元件的静位移。
三、实验单元及部件霍尔片、磁路系统、电桥、差动放大器、F/V表头、直流稳压电源、测微头、振动平台、主副电源。
有关旋钮的初始位置:差动放大器增益旋钮打到最小、电压表置20V档,直流稳压表电源置2V档,主副电源关闭。
三、实验步骤(1)了解霍尔式传感器的结构及在实验仪上的安装位置,熟悉实验面板上霍尔片的符号。
霍尔片安装在实验仪的振动圆盘上,两个半圆永久磁钢固定在实验仪的顶板上,二者组成霍尔传感器。
(2)开启主副电源,将差动放大器调零后增益最小,关闭主副电源,根据图23接线,W1、r为电桥单元的直流电桥平衡网络。
(3)装好测微头,调节测微头与振动台吸合并使霍尔片置于半圆磁钢上下正中位置。
(4)开启主副电源,调整W1使电压表指示为零。
(5)上下旋动测微头米,记下电压表的读数,建议每0.5mm读一个数,将读数填入下表:作出V-X曲线,指出线性范围,求出灵敏度,关闭主副电源。
可见,本实验测出的实际上是磁场情况,磁场分布为梯度磁场与磁场分布有很大差异,位移测量的线性度、灵敏度和磁场分布有很大关系。
(6)实验完结关闭主副电源,各旋钮置初始值。
四、注意事项(1)由于磁路系统的气隙较大,应使霍尔片尽量靠近极化,以提高灵敏度。
(2)一旦调整好后,测量过程中不能移动磁路系统。
(3)激励电压不能过2V,以免损坏霍尔片。
实验二十五霍尔式传感器的直流激励特性一、实验目的了解交流激励霍尔片的特性。
二、实验单元及部件霍尔片、磁路系统、音频振荡器、差动放大器、测微头、电桥、移相器、相敏检波器、低通滤波器、F/V表、示波器、主副电源、振动平台。
实验八 霍尔式传感器直流激励的静态位移性能实验目的:了解霍尔式传感器的工作原理和工作情况。
所需单元和部件:霍尔式传感器、直流稳压电源、差动放大器、电桥、测微器、V/F 表 有关旋钮的初始位置:直流稳压电源输出置于0V 档,V/F 表置于V 表20V 档,差动放 大器增益旋钮置于中间。
注意事项:(1)双平行梁处于(目测)水平位置时,霍耳片应处于环形磁铁(示意图见图24(a )的中间。
(2 )直流激励电压不能过大,以免损坏霍耳片。
(3)本实验测出的实际上是磁场的分布情况,它的线性越好,位移测量的线性度也越好, 它的变化越陡,位移测量的灵敏度也就越大。
实验步骤:(1) 观察霍尔式传感器的结构,根据图 24(b )的电路结构,将霍尔式传感器,直流稳 压电源,电桥,差动放大器,电压表连接起来,组成一个测量线路(这时直流稳 压电源应置于 0V 档,电压表应置于 20V 档)。
(2) 转动测微器,使双平行梁处于(目测)水平位置。
(霍尔片处于磁铁中间)(3) 将直流稳压电源置于 2V 档,调整电桥平衡电位器 W1使电压表指示为零,稳定数 分钟后,将电压表量程置于 2V 档后,再仔细调零。
(4) 左旋测微器,使梁的自由端向上位移 2mm 记下电压表显示的数值。
每次右旋位移 0.5mm 记一个电压数值,将所记数据填入下表,根据所得结果计算灵敏度 S 。
S=A V/ △ X (式 X(mm)V(mv)思考:结合梯度磁场分布,解释为什么霍尔片应处于环形磁铁的中间。
坏形磁铁 -2V电桥平衡囲绻霍傑戎恃感器去渤就大器电压表3)图24运请方简霍尔式传感器交流激励的静态位移性能实验目的:了解霍尔式传感器交流激励下的工作情况。
所需单元和部件:霍尔式传感器、直流稳压电源、差动放大器、电桥、音频振荡器、移相器、相敏检波器、测微器、V/F表、低通滤波器、双踪示波器。
有关旋钮的初始位置:音频振荡器频率为4KH z, LV输出幅度为峰峰值为2V,V/F表置于V表20V档,差动放大器增益旋钮置于中间。
1.直流激励时霍尔传感器的位移特性实验数据
表1 直流激励时霍尔传感器的位移特性实验数据记录
2.交流激励时霍尔传感器的位移特性实验数据
表2 交流激励时霍尔传感器的位移特性实验数据记录
1.直流激励时霍尔传感器的位移特性实验
图1 直流激励时霍尔传感器的位移特性曲线
经观察,我们可以发现曲线可分为3部分,中间、左下和右上,下面对3部分分别进行拟合:
对曲线中间部分进行拟合
图2 直流激励时的位移特性曲线中间部分拟合曲线
对曲线左下部分进行拟合
图3 直流激励时的位移特性曲线左下部分拟合曲线
表5 直流激励时霍尔传感器的位移特性曲线右上部分数据
对曲线右上部分进行拟合
图4 直流激励时的位移特性曲线右上部分拟合曲线
2.交流激励时霍尔传感器的位移特性实验
图5 交流激励时霍尔传感器的位移特性曲线
下面分3段进行拟合,首先对中间段拟合,数据如下
表6 交流激励时霍尔传感器的位移特性曲线中间部分数据
拟合图如下: 图6 交流激励时的位移特性曲线中间部分拟合曲线
对左下段进行拟合,数据如下:
图7 交流激励时的位移特性曲线左下部分拟合曲线对右上段进行拟合,数据如下:
拟合图如下:
图8 交流激励时的位移特性曲线右上部分拟合曲线。
实验四霍尔式传感器激励特性研究及其应用一、实验目的1、了解霍尔式传感器的结构、工作原理;2、实验研究霍尔传感器在交、直流信号激励下的特性;3、掌握霍尔传感器的应用方法。
二、实验原理霍尔式传感器是由两个环形磁钢组成梯度磁场和位于梯度磁场中的霍尔元件组成的。
当霍尔元件通以恒定电流时,霍尔元件就有电势输出。
霍尔元件在梯度磁场中上、下移动时,输出的霍尔电势U取决于其在磁场中的位移量X,所以测得霍尔电势的大小便可获知霍尔元件的位移。
三、实验所需部件直流稳压电源,电桥,霍尔传感器,差动放大器,电压表,测微头,音频振荡器,移相器,相敏检波器,低通滤波器,示波器。
四、实验内容及步骤(一)霍尔式传感器的直流激励特性1、按图10-1接线,装上测微头,调节振动圆盘上、下位置,使霍尔元件位于梯度磁场中间位置。
开启电源,调节测微头和电桥W D,使差放输出为零。
上、下移动振动台,使差放正负电压输出对称。
2、上、下移动测微头各3.5mm,每变化0.5mm读取相应的电压值,并记入表10-1,作出U-X曲线,求出灵敏度及线性度。
(二)霍尔传感器的应用——电子称1、移开测微头,按实验内容(一)直流激励接好系统,使输出为零。
系统灵敏度尽量大。
2、以振动圆盘作为称重平台,逐步放上砝码,依次记下表头读数,填入表10-2中,并作出U-W曲线。
3、移走称重砝码,在平台上另放置一未知重量之物品,根据表头读数从U-W曲线中求得其重量。
4、注意事项①霍尔式传感器在称重时只能工作在梯度磁场中,砝码和被称重物都不应太重。
②砝码应置于平台的中间部分,避免平台倾斜。
实验五开关式霍尔传感器测转速实验一、实验目的:了解开关式霍尔传感器测转速的应用二、基本原理:开关式霍尔传感器是线性霍尔元件的输出信号经放大器放大,再经施密特电路整形成锯型波(开关信号)输出的传感器。
三、需用器件与单元:主机箱中转速调节0—24V直流稳压电源、+5V直流稳压电源、电压表、频率/转速表、霍尔转速传感器、转动源。
《传感器原理及应用》直流激励时霍尔传感器的位移特性
实验验报告
1.实验功能要求
了解霍尔传感器的原理与应用。
2.实验所用传感器原理
根据霍尔效应,霍尔电势U H=K H IB,其中K H为灵敏度系数,由霍尔材料的物理性质决定,当通过霍尔组件的电流I一定,霍尔组件在一个梯度磁场中运动时,就可以用来进行位移测量。
磁场中有一个霍尔半导体片,恒定电流I从A到B通过该片。
在洛仑兹力的作用下,I的电子流在通过霍尔半导体时向一侧偏移,使该片在CD 方向上产生电位差,这就是所谓的霍尔电压。
3.实验电路
4.实验过程
1.将霍尔传感器安装到传感器固定架上,传感器引线接到对应的霍尔
插座上。
按图17-1接线。
2.开启电源,直流数显电压表选择“2V”档,将测微头的起始位置调到“10mm”处,手动调节测微头的位置,先使霍尔片基本在磁钢的中间位置(数显表大致为0),固定测微头,再调节Rw2使数显表显示为零。
3. 分别向左、右不同方向旋动测微头,每隔0.2mm记下一个读数,直到读数近似不变,将读数填入表格。
5.实验结果
作出V-X图:
由图可知霍尔电压与推进距离为线性关系。
霍尔传感器的直流激励特性实验一、实验目的:了解霍尔传感器的直流激励特性。
二、实验内容:给霍尔传感器通以直流电源,经差动放大器放大,当测微头随振动台上、下移动时,就有霍尔电势输出,从而可以测出霍尔传感器在直流激励下的输出特性。
三、实验原理:由两个半圆形永久磁钢组成梯度磁场,位于梯度磁场中的霍尔元件(霍尔片)通过底座连接在振动台上。
当霍尔片通以恒定电流时,将输出霍尔电势。
改变振动台的位置,霍尔片就在梯度磁场中上下移动,霍尔电势V值大小与其在磁场中的位移量X有关。
四、实验要求1、按图1接线,插接线插接要牢靠。
2、直流激励电压为土2V,不能任意加大,否则将损坏霍尔片。
五、实验装置:1 .传感器系统实验仪CSY型1台2 .通用示波器COS5020B 1台3 .系统微机1台4 .消耗材料:霍尔片传用)1个插接线传用)10根图1 霍尔传感器实验接线图六、实验步骤:1 •按图1接线,使霍尔片位于梯度磁场中间位置,差放调零。
2 .上、下移动振动台并调节差放增益与电桥WD电位器,使得电压表双向指示基本对称且趋近最大。
3 •将测微头与振动台吸合,并调节霍尔片使之处于梯度磁场的中间位置。
4 .用测微头驱动霍尔片输入位移量X,每次变化0.5mm ,量程为:-3mm •- +3mm ,读取相应的输出电压值,填入表中。
七、实验数据及处理:1•整理实验数据,作出V-X曲线,求出灵敏度及线性区2 •给出位移测量系统的适宜量程V-X曲线见下图丈验吕环i ii ■'尔心J .- !A^Sh T H 荒激蹄j 忤QD29 U tih 1 4M 2.1072m ”阳 4.010 £⑹ / 21S -1孙5 ・2(M -2 M -J545 OOM 0000 Cl CUD Li« H' l n ■•:Xi G(M» 0000抑t 兮T戳中枢1Ek 起绘(VJ ia 十洪. 1 4 01$ 2 3超D334 OJM7 02.137G J34 0.042 0(X23 2 0 000 0 000 PQOO DGOC0000QOW OCOO 30 000 0 000 OQQO DOW oom 0000 0 000 OoOO 4goDO□ 0000*000ocmowoGOODCOCK)oeoo1. 计算灵敏度: S=0.587V/mm则拟合直线方程为:V=0.857X+0.334由图像得,当 X 在(-1.00 , 3.00 )之间时,图像具有线性。
华南师范大学实验报告实验项目:直流激励时霍尔传感器位移特性实验一、实验目的:了解霍尔式传感器原理与应用。
二、基本原理:金属或半导体薄片置于磁场中,当有电流流过时,在垂直于磁场和电流的方向上将产生电动势,这种物理现象称为霍尔效应。
具有这种效应的元件成为霍尔元件,根据霍尔效应,霍尔电势U H=K H IB,当保持霍尔元件的控制电流恒定,而使霍尔元件在一个均匀梯度的磁场中沿水平方向移动,则输出的霍尔电动势为U H kx,式中k—位移传感器的灵敏度。
这样它就可以用来测量位移。
霍尔电动势的极性表示了元件的方向。
磁场梯度越大,灵敏度越高;磁场梯度越均匀,输出线性度就越好。
三、需用器件与单元:霍尔传感器实验模板、霍尔传感器、±15V 直流电源、测微头、数显单元。
四、实验步骤:1、将霍尔传感器安装在霍尔传感器实验模块上,将传感器引线插头插入实验模板的插座中,实验板的连接线按图9-1 进行。
1、3 为电源±5V,2、4 为输出。
2、开启电源,调节测微头使霍尔片大致在磁铁中间位置,再调节Rw1 使数显表指示为零。
图9-1 直流激励时霍尔传感器位移实验接线图3、测微头往轴向方向推进,每转动0.2mm 记下一个读数,直到读数近似不变,将读数填入表9-1。
表9-1X(mm)V(mv)作出V-X 曲线,计算不同线性范围时的灵敏度和非线性误差。
五、实验注意事项:1、对传感器要轻拿轻放,绝不可掉到地上。
2、不要将霍尔传感器的激励电压错接成±15V,否则将可能烧毁霍尔元件。
六、思考题:本实验中霍尔元件位移的线性度实际上反映的是什么量的变化?答:本人认为应该是实际的输入、输出与拟合的理想的直线的偏离程度的变化,当X 不同的时候,实际的输出值与根据拟合直线得到的数值的偏离值是不相同的。
七、实验报告要求:1、整理实验数据,根据所得得实验数据做出传感器的特性曲线。
实验数据如下:表9-2X(mm)0.2 0.4 0.6 0.8 1.0 1.2 1.4 1.6 1.8 2.0V(mv) 729 523 347 177 85 -80 -235 -354 -465 -575 V-X 曲线如下:V-X 曲线800 600 400 200V V(mv)0 X(mm)-200 -400 -600 -80012 3 4 5 6 7 8 9 10 V(mv) 729 523 347 177 85 -80 -235 -354 -465 -575X(mm) 0.20.40.60.81 1.21.41.61.82X根 据 上 图 和 实 验 数 据 , 在 X[ 0.2,0.8] 区 间 , 霍 尔 传 感 器 的 灵 敏 度 为 :729 177 k920 ; 在 X[1.2,2.0] 区 间 , 霍 尔 传 感 器 的 灵 敏 度 为 :0.8 0.2 235 575 k567 。