第九版机械设计濮良贵课后习习题答案

第九版机械设计濮良贵课后习习题答案欢迎阅读第三章机械零件的强度p45习题答案3-1某材料的对称循环弯曲疲劳极限MPa 1801=-σ，取循环基数60105?=N ，9=m ，试求循环次数 N 分别为7 000、25 000、620 000次时的有限寿命弯曲疲劳极限。

[解] MPa 6.373107105180936910111===--N N σσN 3-2已知材料的⼒学性能为MPa 260=s σ，MPa 1701=-σ，2.0=σΦ，试绘制此材料的简化的等寿命寿命曲线。

[解]得 3-4 ，[解] 3-5 C ，求出该截 [解] （（2）C σ=m⼯作应⼒点在疲劳强度区，根据变应⼒的平均应⼒不变公式，其计算安全系数第五章螺纹连接和螺旋传动p101习题答案解：[ （2）螺栓组受到剪⼒F 和⼒矩（FL T =），设剪⼒F 分在各个螺栓上的⼒为i F ，转矩T 分在各个螺栓上的分⼒为j F ，各螺栓轴线到螺栓组对称中⼼的距离为r ,即mm 27545cos 2150=?=r由图可知，螺栓最⼤受⼒故M 6×40的剪切强度不满⾜要求，不可靠。

5-6 已知⼀个托架的边板⽤6个螺栓与相邻的机架相连接。

托架受⼀与边板螺栓组的垂直对称轴线相平⾏、距离为250mm 、⼤⼩为60kN 的载荷作⽤。

现有如图5-50所⽰的两种螺栓布置形式，设采⽤铰制孔⽤螺栓连接，试问哪⼀种布置形式所⽤的螺栓直径最⼩？为什么？[解] 螺栓组受到剪⼒F 和转矩，设剪⼒F 分在各个螺栓上的⼒为i F ，转矩T 分在各个螺栓上的分⼒为j F（a ）中各螺栓轴线到螺栓组中⼼的距离为r ，即r =125mm由（a ）图可知，最左的螺栓受⼒最⼤kN 302010max =+=+=j i F F F（b ）⽅案中由（b ）图可知，螺栓受⼒最⼤为5-7 图5-52所⽰为⼀拉杆螺纹联接。

已知拉丁所受的载荷F=56KN,载荷稳定，拉丁材料为Q235钢，试设计此联接。

第三章 机械零件的强度p45习题答案3-1某材料的对称循环弯曲疲劳极限MPa 1801=-σ，取循环基数60105⨯=N ，9=m ，试求循环次数N 分别为7 000、25 000、620 000次时的有限寿命弯曲疲劳极限。

[解] MPa 6.373107105180936910111=⨯⨯⨯==--N N σσN MPa 3.324105.2105180946920112=⨯⨯⨯==--N N σσNMPa 0.227102.6105180956930113=⨯⨯⨯==--N N σσN 3-2已知材料的力学性能为MPa 260=s σ，MPa 1701=-σ，2.0=σΦ，试绘制此材料的简化的等寿命寿命曲线。

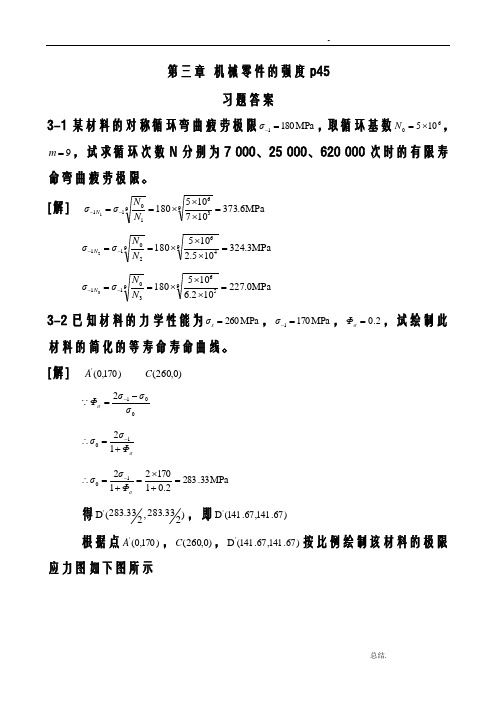
[解])170,0('A)0,260(C012σσσΦσ-=-σΦσσ+=∴-1210MPa 33.2832.0117021210=+⨯=+=∴-σΦσσ得)233.283,233.283(D '，即)67.141,67.141(D '根据点)170,0('A ，)0,260(C ，)67.141,67.141(D '按比例绘制该材料的极限应力图如下图所示3-4 圆轴轴肩处的尺寸为：D =72mm ，d =62mm ，r =3mm 。

如用题3-2中的材料，设其强度极限σB =420MPa ，精车，弯曲，βq =1，试绘制此零件的简化等寿命疲劳曲线。

[解] 因2.14554==dD ，067.0453==d r，查附表3-2，插值得88.1=ασ，查附图3-1得78.0≈σq ，将所查值代入公式，即()()69.1188.178.0111k =-⨯+=-α+=σσσq查附图3-2，得75.0=σε；按精车加工工艺，查附图3-4，得91.0=σβ，已知1=q β，则35.211191.0175.069.1111k =⨯⎪⎭⎫ ⎝⎛-+=⎪⎪⎭⎫ ⎝⎛-+=q σσσσββεK ()()()35.267.141,67.141,0,260,35.2170,0D C A ∴根据()()()29.60,67.141,0,260,34.72,0D C A 按比例绘出该零件的极限应力线图如下图3-5 如题3-4中危险截面上的平均应力MPa 20m =σ，应力幅MPa 20a =σ，试分别按①C r =②C σ=m ，求出该截面的计算安全系数ca S 。

第三章 机械零件的强度p45习题答案3-1某材料的对称循环弯曲疲劳极限MPa 1801=-σ，取循环基数60105⨯=N ，9=m ，试求循环次数N 分别为7 000、25 000、620 000次时的有限寿命弯曲疲劳极限。

[解] MPa 6.373107105180936910111=⨯⨯⨯==--N N σσN MPa 3.324105.2105180946920112=⨯⨯⨯==--N N σσNMPa 0.227102.6105180956930113=⨯⨯⨯==--N N σσN 3-2已知材料的力学性能为MPa 260=s σ，MPa 1701=-σ，2.0=σΦ，试绘制此材料的简化的等寿命寿命曲线。

[解])170,0('A)0,260(C012σσσΦσ-=-σΦσσ+=∴-1210MPa 33.2832.0117021210=+⨯=+=∴-σΦσσ得)233.283,233.283(D '，即)67.141,67.141(D '根据点)170,0('A ，)0,260(C ，)67.141,67.141(D '按比例绘制该材料的极限应力图如下图所示3-4 圆轴轴肩处的尺寸为：D =72mm ，d =62mm ，r =3mm 。

如用题3-2中的材料，设其强度极限σB =420MPa ，精车，弯曲，βq =1，试绘制此零件的简化等寿命疲劳曲线。

[解] 因2.14554==dD ，067.0453==d r，查附表3-2，插值得88.1=ασ，查附图3-1得78.0≈σq ，将所查值代入公式，即()()69.1188.178.0111k =-⨯+=-α+=σσσq查附图3-2，得75.0=σε；按精车加工工艺，查附图3-4，得91.0=σβ，已知1=q β，则35.211191.0175.069.1111k =⨯⎪⎭⎫ ⎝⎛-+=⎪⎪⎭⎫ ⎝⎛-+=q σσσσββεK ()()()35.267.141,67.141,0,260,35.2170,0D C A ∴根据()()()29.60,67.141,0,260,34.72,0D C A 按比例绘出该零件的极限应力线图如下图3-5 如题3-4中危险截面上的平均应力MPa 20m =σ，应力幅MPa 20a =σ，试分别按①C r =②C σ=m ，求出该截面的计算安全系数ca S 。

第三章 机械零件的强度习题答案3-1某材料的对称循环弯曲疲劳极限MPa 1801=-σ，取循环基数60105⨯=N ，9=m ，试求循环次数N 分别为7 000、25 000、620 000次时的有限寿命弯曲疲劳极限。

[解] MPa 6.373107105180936910111=⨯⨯⨯==--N N σσN MPa 3.324105.2105180946920112=⨯⨯⨯==--N N σσN MPa 0.227102.6105180956930113=⨯⨯⨯==--N N σσN 3-2已知材料的力学性能为MPa 260=s σ，MPa 1701=-σ，2.0=σΦ，试绘制此材料的简化的等寿命寿命曲线。

[解] )170,0('A )0,260(C 012σσσΦσ-=- σΦσσ+=∴-1210 MPa 33.2832.0117021210=+⨯=+=∴-σΦσσ 得)233.283,233.283(D '，即)67.141,67.141(D '根据点)170,0('A ，)0,260(C ，)67.141,67.141(D '按比例绘制该材料的极限应力图如下图所示3-4圆轴轴肩处的尺寸为：D=72mm，d=62mm，r=3mm。

如用题3-2中的材料，设其强度极限σB=420MPa，精车，弯曲，βq=1，试绘制此零件的简化等寿命疲劳曲线。

[解] 因2.14554==dD，067.0453==dr，查附表3-2，插值得88.1=ασ，查附图3-1得78.0≈σq，将所查值代入公式，即()()69.1188.178.0111k=-⨯+=-α+=σσσq查附图3-2，得75.0=σε；按精车加工工艺，查附图3-4，得91.0=σβ，已知1=qβ，则35.211191.0175.069.1111k=⨯⎪⎭⎫⎝⎛-+=⎪⎪⎭⎫⎝⎛-+=qσσσσββεK()()()35.267.141,67.141,0,260,35.2170,0DCA∴根据()()()29.60,67.141,0,260,34.72,0DCA按比例绘出该零件的极限应力线图如下图3-5如题3-4中危险截面上的平均应力MPa20m=σ，应力幅MPa20a=σ，试分别按①C r =②C σ=m ，求出该截面的计算安全系数ca S 。

第三章 机械零件的强度p45习题答案3-1某材料的对称循环弯曲疲劳极限MPa 1801=-σ，取循环基数60105⨯=N ，9=m ，试求循环次数N 分别为7 000、25 000、620 000次时的有限寿命弯曲疲劳极限。

[解] MPa 6.373107105180936910111=⨯⨯⨯==--N N σσN MPa 3.324105.2105180946920112=⨯⨯⨯==--N N σσNMPa 0.227102.6105180956930113=⨯⨯⨯==--N N σσN 3-2已知材料的力学性能为MPa 260=s σ，MPa 1701=-σ，2.0=σΦ，试绘制此材料的简化的等寿命寿命曲线。

[解])170,0('A)0,260(C012σσσΦσ-=-ΘσΦσσ+=∴-1210MPa 33.2832.0117021210=+⨯=+=∴-σΦσσ 得)233.283,233.283(D '，即)67.141,67.141(D '根据点)170,0('A ，)0,260(C ，)67.141,67.141(D '按比例绘制该材料的极限应力图如下图所示3-4 圆轴轴肩处的尺寸为：D =72mm ，d =62mm ，r =3mm。

如用题3-2中的材料，设其强度极限σB =420MPa ，精车，弯曲，βq =1，试绘制此零件的简化等寿命疲劳曲线。

[解] 因2.14554==dD ，067.0453==d r，查附表3-2，插值得88.1=ασ，查附图3-1得78.0≈σq ，将所查值代入公式，即()()69.1188.178.0111k =-⨯+=-α+=σσσq查附图3-2，得75.0=σε；按精车加工工艺，查附图3-4，得91.0=σβ，已知1=q β，则35.211191.0175.069.1111k =⨯⎪⎭⎫ ⎝⎛-+=⎪⎪⎭⎫ ⎝⎛-+=q σσσσββεK ()()()35.267.141,67.141,0,260,35.2170,0D C A ∴根据()()()29.60,67.141,0,260,34.72,0D C A 按比例绘出该零件的极限应力线图如下图3-5 如题3-4中危险截面上的平均应力MPa 20m =σ，应力幅MPa 20a =σ，试分别按①C r =②C σ=m ，求出该截面的计算安全系数ca S 。

第十章齿轮传动 习题答案10-1 试分析图10-47所示的齿轮传动各齿轮所受的力（用受力图表示各力的作用位置与方向）。

[解] 受力图如下图：补充题：如图（b ），已知标准锥齿轮mm N 1042,3.0,50,20,5521⋅⨯=====T Φz z m R ，标准斜齿轮24,63==z m n ，若中间轴上两齿轮所受轴向力互相抵消，β应为多少？并计算2、3齿轮各分力大小。

[解]（1）齿轮2的轴向力：()222222222sin tan 5.012sin tan 2sin tan δαz Φm T δαdm T δαF F R t a -=== 齿轮3的轴向力：βz m T ββz m T βd T βF F n n t a sin 2tan cos 2tan 2tan 33333333=⎪⎪⎭⎫ ⎝⎛=== 3232,20,T T αF F a a =︒==()βz m T δαz Φm T n R sin 2sin tan 5.01233222=-∴即()2235.01sin tan sin z Φm δαz m βR n -=由5.22050tan 122===z z δ 928.0sin 2=∴δ371.0cos 2=δ ()()2289.0503.05.015928.020tan 2465.01sin tan sin 223=⨯⨯-⨯⨯︒⨯⨯=-=∴z Φm δαz m βR n即︒=231.13β （2）齿轮2所受各力：()() 3.765kN N 10765.3503.05.01510425.01223522222=⨯=⨯⨯-⨯⨯⨯=-==z Φm T dm T F R t0.508kNN 10508.0371.020tan 10765.3cos tan 33222=⨯=⨯︒⨯⨯==δαF F t r kN 272.1N 10272.1928.020tan 10765.3sin tan 33222=⨯=⨯︒⨯⨯==δαF F t akN 420cos 10765.3cos 322=︒⨯==αF F t n齿轮3所受各力：kN 408.5N 10408.5231.13cos 2461042cos 2cos 22353232333=⨯=︒⨯⨯⨯==⎪⎪⎭⎫ ⎝⎛==βz m T βz m T d T F n n tkN 022.2N 10022.2321.12cos 20tan 10408.5cos tan 3333=⨯=︒︒⨯⨯==βαF F n t rkN 272.1N 10272.1321.12cos 20tan 10408.5tan 10408.5tan 33333=⨯=︒︒⨯⨯⨯⨯==βF F t akN 889.5N 10889.5321.12cos 20cos 10765.3cos cos 3333=⨯=︒︒⨯==βαF F n t n10-6设计铣床中的一对圆柱齿轮传动，已知54,26min,r 1450,kW 5.72111====z z n P ，寿命h 12000=h L ，小齿轮相对其轴的支承为不对称布置，并画出大齿轮的机构图。

机械设计濮良贵课后习题答案机械设计濮良贵课后习题答案机械设计是工程领域中非常重要的一门学科，它涉及到机械结构的设计、分析和优化等方面。

在学习机械设计的过程中，课后习题是非常重要的一环，通过解答习题可以加深对知识点的理解，并提高解决问题的能力。

本文将为大家提供机械设计濮良贵课后习题的答案，希望能对大家的学习有所帮助。

1. 习题一：设计一个滚动轴承支座，要求满足以下条件：- 轴承径向载荷：1000N- 轴承轴向载荷：500N- 轴承转速：1000rpm- 轴承寿命要求：5000小时答案：根据给定条件，我们可以采用滚动轴承来满足要求。

首先，根据轴承径向载荷和转速，可以计算出所需的轴承额定动载荷。

然后，根据轴承轴向载荷和转速，可以计算出所需的轴承额定轴向载荷。

接下来，根据轴承额定寿命和转速，可以计算出所需的轴承额定寿命。

最后，选择合适的滚动轴承型号和尺寸，设计支座结构，满足以上要求。

2. 习题二：设计一个齿轮传动系统，要求满足以下条件：- 输入功率：10kW- 输出转速：1000rpm- 齿轮传动效率要求：90%- 齿轮材料：20CrMnTi答案：根据给定条件，我们可以通过计算来确定齿轮传动系统的参数。

首先，根据输入功率和输出转速，可以计算出所需的输出扭矩。

然后，根据齿轮传动效率要求，可以计算出所需的输入功率。

接下来，选择合适的齿轮模数和齿数，设计齿轮传动系统。

同时，根据齿轮材料的强度和耐磨性要求，选择适当的齿轮材料。

最后，进行齿轮传动系统的校核和优化，确保满足以上要求。

3. 习题三：设计一个平面四杆机构，要求满足以下条件：- 输入角速度：10rad/s- 输出角速度：5rad/s- 输入角度：30°- 输出角度：60°答案：根据给定条件，我们可以通过设计平面四杆机构来满足要求。

首先，根据输入角速度和输出角速度，可以计算出所需的传动比。

然后，根据输入角度和输出角度，可以计算出所需的角度变化。

第三章 机械零件的强度p45习题答案3-1某材料的对称循环弯曲疲劳极限MPa 1801=-σ，取循环基数60105⨯=N ，9=m ，试求循环次数N 分别为7 000、25 000、620 000次时的有限寿命弯曲疲劳极限。

[解] MPa 6.373107105180936910111=⨯⨯⨯==--N N σσN MPa 3.324105.2105180946920112=⨯⨯⨯==--N N σσNMPa 0.227102.6105180956930113=⨯⨯⨯==--N N σσN 3-2已知材料的力学性能为MPa 260=s σ，MPa 1701=-σ，2.0=σΦ，试绘制此材料的简化的等寿命寿命曲线。

[解])170,0('A)0,260(C012σσσΦσ-=-σΦσσ+=∴-1210MPa 33.2832.0117021210=+⨯=+=∴-σΦσσ得)233.283,233.283(D '，即)67.141,67.141(D '根据点)170,0('A ，)0,260(C ，)67.141,67.141(D '按比例绘制该材料的极限应力图如下图所示3-4 圆轴轴肩处的尺寸为：D=72mm，d=62mm，r=3mm。

如用题3-2中的材料，设其强度极限σB=420MPa，精车，弯曲，βq=1，试绘制此零件的简化等寿命疲劳曲线。

[解] 因2.14554==dD，067.0453==dr，查附表3-2，插值得88.1=ασ，查附图3-1得78.0≈σq，将所查值代入公式，即()()69.1188.178.0111k=-⨯+=-α+=σσσq查附图3-2，得75.0=σε；按精车加工工艺，查附图3-4，得91.0=σβ，已知1=qβ，则35.211191.0175.069.1111k=⨯⎪⎭⎫⎝⎛-+=⎪⎪⎭⎫⎝⎛-+=qσσσσββεK()()()35.267.141,67.141,0,260,35.2170,0DCA∴根据()()()29.60,67.141,0,260,34.72,0DCA按比例绘出该零件的极限应力线图如下图3-5 如题3-4中危险截面上的平均应力MPa20m=σ，应力幅MPa20a=σ，试分别按①Cr=②Cσ=m，求出该截面的计算安全系数caS。

第三章 机械零件的强度欧阳家百（2021.03.07）习题答案3-1某材料的对称循环弯曲疲劳极限MPa 1801=-σ，取循环基数60105⨯=N ，9=m ，试求循环次数N 分别为7 000、25 000、620 000次时的有限寿命弯曲疲劳极限。

[解] MPa 6.373107105180936910111=⨯⨯⨯==--N N σσN 3-2已知材料的力学性能为MPa 260=s σ，MPa 1701=-σ，2.0=σΦ，试绘制此材料的简化的等寿命寿命曲线。

[解] )170,0('A )0,260(C得)233.283,233.283(D '，即)67.141,67.141(D '根据点)170,0('A ，)0,260(C ，)67.141,67.141(D '按比例绘制该材料的极限应力图如下图所示3-4 圆轴轴肩处的尺寸为：D =72mm ，d =62mm ，r =3mm 。

如用题3-2中的材料，设其强度极限σB =420MPa ，精车，弯曲，βq =1，试绘制此零件的简化等寿命疲劳曲线。

[解] 因2.14554==d D ，067.0453==d r ，查附表3-2，插值得88.1=ασ，查附图3-1得78.0≈σq ，将所查值代入公式，即查附图3-2，得75.0=σε；按精车加工工艺，查附图3-4，得91.0=σβ，已知1=q β，则根据()()()29.60,67.141,0,260,34.72,0D C A 按比例绘出该零件的极限应力线图如下图3-5 如题3-4中危险截面上的平均应力MPa 20m =σ，应力幅MPa20a =σ，试分别按①C r =②C σ=m ，求出该截面的计算安全系数ca S 。

[解] 由题3-4可知35.2,2.0MPa,260MPa,170s 1-====σσK Φσσ （1）C r =工作应力点在疲劳强度区，根据变应力的循环特性不变公式，其计算安全系数 （2）C σ=m工作应力点在疲劳强度区，根据变应力的平均应力不变公式，其计算安全系数第五章 螺纹连接和螺旋传动习题答案5-5 图5-49是由两块边板和一块承重板焊接的龙门起重机导轨托架。

机械设计课后习题答案濮良贵第三章机械零件的强度p45习题答案3-1某材料的对称循环弯曲疲劳极限MPa 1801=-ζ，取循环基数60105?=N ，9=m ，试求循环次数N 分别为7 000、25 000、620 000次时的有限寿命弯曲疲劳极限。

[解] MPa 6.373107105180936910111===--N N ζζN M P a 3.324105.2105180946920112===--N N ζζNM P a 0.227102.6105180956930113===--N N ζζN 3-2已知材料的力学性能为MPa 260=s ζ，MPa 1701=-ζ，2.0=ζΦ，试绘制此材料的简化的等寿命寿命曲线。

[解])170,0('A)0,260(C012ζζζΦζ-=-ζΦζζ+=∴-1210M P a 33.2832.0117021210=+?=+=∴-ζΦζζ 得)233.283,233.283(D '，即)67.141,67.141(D '根据点)170,0('A ，)0,260(C ，)67.141,67.141(D '按比例绘制该材料的极限应力图如下图所示3-4 圆轴轴肩处的尺寸为：D =72mm ，d =62mm ，r =3mm 。

如用题3-2中的材料，设其强度极限σB =420MPa ，精车，弯曲，βq =1，试绘制此零件的简化等寿命疲劳曲线。

[解] 因2.145 54==dD ，067.0453==d r，查附表3-2，插值得88.1=αζ，查附图3-1得78.0≈ζq ，将所查值代入公式，即()()69.1188.178.0111k =-?+=-α+=ζζζq查附图3-2，得75.0=ζε；按精车加工工艺，查附图3-4，得91.0=ζβ，已知1=q β，则35.211191.0175.069.1111k = ??-+= ??-+=q ζζζζββεK ()()()35.267.141,67.141,0,260,35.2170,0D C A ∴根据()()()29.60,67.141,0,260,34.72,0D C A 按比例绘出该零件的极限应力线图如下图3-5 如题3-4中危险截面上的平均应力MPa 20m =ζ，应力幅MPa 20a =ζ，试分别按①C r =②C ζ=m ，求出该截面的计算安全系数ca S 。

详细答案第三章 机械零件的强度p45习题答案3-1某材料的对称循环弯曲疲劳极限MPa 1801=-σ，取循环基数60105⨯=N ，9=m ，试求循环次数N 分别为7 000、25 000、620 000次时的有限寿命弯曲疲劳极限。

[解] MPa 6.373107105180936910111=⨯⨯⨯==--N N σσN M P a 3.324105.2105180946920112=⨯⨯⨯==--N N σσNM P a 0.227102.6105180956930113=⨯⨯⨯==--N N σσN 3-2已知材料的力学性能为MPa 260=s σ，MPa 1701=-σ，2.0=σΦ，试绘制此材料的简化的等寿命寿命曲线。

[解])170,0('A),260(C012σσσΦσ-=-σΦσσ+=∴-1210M P a 33.2832.0117021210=+⨯=+=∴-σΦσσ 得)233.283,233.283(D '，即)67.141,67.141(D '根据点)170,0('A ，),260(C ，)67.141,67.141(D '按比例绘制该材料的极限应力图如下图所示3-4 圆轴轴肩处的尺寸为：D =72mm ，d =62mm ，r =3mm 。

如用题3-2中的材料，设其强度极限σB =420MPa ，精车，弯曲，βq =1，试绘制此零件的简化等寿命疲劳曲线。

[解] 因2.14554==dD ，067.0453==d r，查附表3-2，插值得88.1=ασ，查附图3-1得78.0≈σq ，将所查值代入公式，即()()69.1188.178.0111k =-⨯+=-α+=σσσq查附图3-2，得75.0=σε；按精车加工工艺，查附图3-4，得91.0=σβ，已知1=q β，则35.211191.0175.069.1111k =⨯⎪⎭⎫ ⎝⎛-+=⎪⎪⎭⎫ ⎝⎛-+=q σσσσββεK ()()()35.267.141,67.141,0,260,35.2170,0D C A ∴根据()()()29.60,67.141,0,260,34.72,0D C A 按比例绘出该零件的极限应力线图如下图3-5 如题3-4中危险截面上的平均应力MPa 20m =σ，应力幅MPa 20a =σ，试分别按①C r =②C σ=m ，求出该截面的计算安全系数ca S 。

第三章 机械零件的强度习题答案3-1某材料的对称循环弯曲疲劳极限MPa 1801=-σ，取循环基数60105⨯=N ，9=m ，试求循环次数N分别为7 000、25 000、620 000次时的有限寿命弯曲疲劳极限。

[解] MPa 6.373107105180936910111=⨯⨯⨯==--N N σσN MPa 3.324105.2105180946920112=⨯⨯⨯==--N N σσN MPa 0.227102.6105180956930113=⨯⨯⨯==--N N σσN 3-2已知材料的力学性能为MPa 260=s σ，MPa 1701=-σ，2.0=σΦ，试绘制此材料的简化的等寿命寿命曲线。

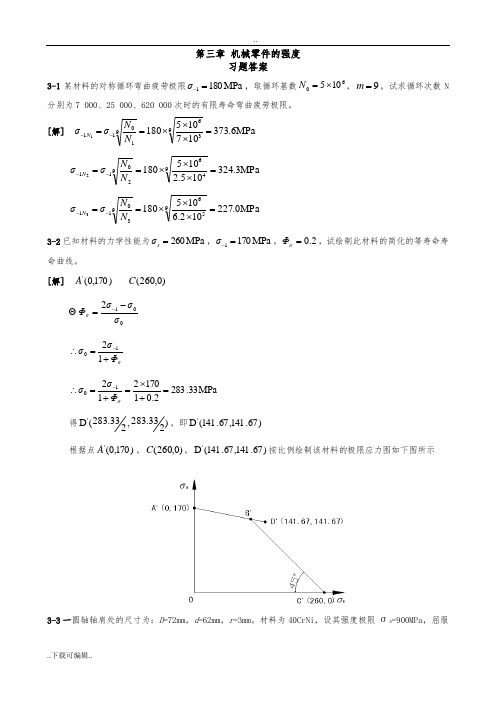
[解] )170,0('A )0,260(C 012σσσΦσ-=-Θ σΦσσ+=∴-121MPa 33.2832.0117021210=+⨯=+=∴-σΦσσ得)233.283,233.283(D '，即)67.141,67.141(D '根据点)170,0('A ，)0,260(C ，)67.141,67.141(D '按比例绘制该材料的极限应力图如下图所示3-3一圆轴轴肩处的尺寸为：D =72mm ，d =62mm ，r =3mm 。

材料为40CrNi ，设其强度极限σB =900MPa ，屈服极限750MPa s σ=试计算周健的弯曲有效应力集中系数k σ。

[解] 因1.16D d =，0.048rd=，查附表3-2，插值得 1.995σα=，查附图3-1得78.0≈σq ，将所查值代入公式，即()()k 1110.78 1.9951 1.896σσσq α=+-=+⨯-=3-4圆轴轴肩处的尺寸为：D =54mm ，d =45mm ，r =3mm 。

如用题3-2中的材料，设其强度极限σB=420MPa ，试绘制此零件的简化等寿命疲劳曲线。

[解] 因2.14554==d D ，067.0453==d r ，查附表3-2，插值得88.1=ασ，查附图3-1得78.0≈σq ，将所查值代入公式，即()()69.1188.178.0111k =-⨯+=-α+=σσσq查附图3-2，得0.7σε=；按精车加工工艺，查附图3-4，得91.0=σβ，已知1=q β，则k 11 1.691111 2.510.70.911σσσσq K εββ⎛⎫⎛⎫=+-=+-⨯= ⎪ ⎪⎝⎭⎝⎭()()()170141.670,,260,0,141.67,2.51 2.51A C D ∴根据()()()0,67.73,260,0,141.67,56.44A C D 按比例绘出该零件的极限应力线图如下图3-5 如题3-4中危险截面上的平均应力MPa 20m =σ，应力幅MPa 20a =σ，试分别按①C r =②C σ=m ，求出该截面的计算安全系数ca S 。

第三章 【2 】机械零件的强度习题答案3-1某材料的对称轮回曲折疲惫极限MPa 1801=-σ,取轮回基数60105⨯=N ,9=m ,试求轮回次数N 分离为7 000.25 000.620 000次时的有限寿命曲折疲惫极限. [解] MPa 6.373107105180936910111=⨯⨯⨯==--N N σσN MPa 3.324105.2105180946920112=⨯⨯⨯==--N N σσN MPa 0.227102.6105180956930113=⨯⨯⨯==--N N σσN 3-2已知材料的力学机能为MPa 260=s σ,MPa 1701=-σ,2.0=σΦ,试绘制此材料的简化的等寿命寿命曲线. [解] )170,0('A )0,260(C12σσσΦσ-=- σΦσσ+=∴-1210 MPa 33.2832.0117021210=+⨯=+=∴-σΦσσ 得)233.283,233.283(D ',即)67.141,67.141(D '依据点)170,0('A ,)0,260(C ,)67.141,67.141(D '按比例绘制该材料的极限应力争如下图所示3-4 圆轴轴肩处的尺寸为：D =72mm,d =62mm,r =3mm.如用题3-2中的材料,设其强度极限σB =420MPa,精车,曲折,βq =1,试绘制此零件的简化等寿命疲惫曲线. [解] 因2.14554==d D ,067.0453==d r ,查附表3-2,插值得88.1=ασ,查附图3-1得78.0≈σq ,将所查值代入公式,即()()69.1188.178.0111k =-⨯+=-α+=σσσq查附图3-2,得75.0=σε;按精车加工工艺,查附图3-4,得91.0=σβ,已知1=q β,则35.211191.0175.069.1111k =⨯⎪⎭⎫ ⎝⎛-+=⎪⎪⎭⎫ ⎝⎛-+=q σσσσββεK ()()()35.267.141,67.141,0,260,35.2170,0D C A ∴依据()()()29.60,67.141,0,260,34.72,0D C A 按比例绘出该零件的极限应力线图如下图3-5 如题3-4中安全截面上的平均应力MPa 20m =σ,应力幅MPa 20a =σ,试分离按①C r =②C σ=m ,求出该截面的盘算安全系数ca S .[解] 由题3-4可知35.2,2.0MPa,260MPa,170s 1-====σσK Φσσ（1）C r =工作应力点在疲惫强度区,依据变应力的轮回特征不变公式,其盘算安全系数28.2202.03035.2170m a 1-=⨯+⨯=+=σΦσK σS σσca（2）C σ=m工作应力点在疲惫强度区,依据变应力的平均应力不变公式,其盘算安全系数()()()()81.1203035.2202.035.2170m a m 1-=+⨯⨯-+=+-+=σσσσca σσK σΦK σS第五章 螺纹衔接和螺旋传动习题答案5-5 图5-49是由两块边板和一块承重板焊接的龙门起重机导轨托架.两块边板各用4个螺栓与立柱相衔接,托架所推却的最大载荷为20kN,载荷有较大的变动.试问：此螺栓衔接采用通俗螺栓衔接照样铰制孔用螺栓衔接为宜？为什么？Q215,若用M 6×40铰孔用螺栓衔接,已知螺栓机械机能等级为8.8,校核螺栓衔接强度.[解] 采用铰制孔用螺栓衔接为宜因为托架所受的载荷有较大变动,铰制孔用螺栓衔接能准确固定被衔接件的相对地位,并能推却横向载荷,加强衔接的靠得住性和慎密性,以防止受载后被衔接件间消失裂缝或产生相对滑移,而通俗螺栓衔接靠联合面产生的摩擦力矩来抵抗转矩,衔接不坚固.（1）肯定M 6×40的许用切应力[τ]由螺栓材料Q215,机能等级8.8,查表5-8,可知MPa 640][s =σ,查表5-10,可知0.5~5.3][=τS()MPa 128~86.1820.5~5.3640][][][s ===τ∴τS σ MPa 67.4265.1640][s ===p p S σσ （2）螺栓组受到剪力F 和力矩（FL T =）,设剪力F 分在各个螺栓上的力为i F ,转矩T 分在各个螺栓上的分力为j F ,各螺栓轴线到螺栓组对称中间的距离为r ,即mm 27545cos 2150=︒=rkN 2510275810300208 kN 5.220818133=⨯⨯⨯⨯===⨯==∴--r FL F F F j i 由图可知,螺栓最大受力kN 015.945cos 255.22)25(5.2cos 22222max =︒⨯⨯⨯++=++=θF F F F F j i j i()][319106410015.9423320max τ>=⨯⨯π⨯=π=τ∴-d F][8.131104.1110610015.9333min 0max p p σL d F σ<=⨯⨯⨯⨯==∴--故M 6×40的剪切强度不知足请求,不靠得住.5-6 已知一个托架的边板用6个螺栓与相邻的机架相衔接.托架受一与边板螺栓组的垂直对称轴线相平行.距离为250mm.大小为60kN 的载荷感化.现有如图5-50所示的两种螺栓布置情势,设采用铰制孔用螺栓衔接,试问哪一种布置情势所用的螺栓直径最小？为什么？[解] 螺栓组受到剪力F 和转矩,设剪力F 分在各个螺栓上的力为i F ,转矩T 分在各个螺栓上的分力为j F（a ）中各螺栓轴线到螺栓组中间的距离为r ,即r =125mmkN 2010125610250606 kN 1060616133=⨯⨯⨯⨯===⨯==∴--r FL F F F ji 由（a ）图可知,最左的螺栓受力最大kN 302010max =+=+=j i F F F （b ）计划中kN 10606161=⨯==F F i kN 39.24101252125421252101252125102506062223223612max612maxmax =⨯⎥⎥⎦⎤⎢⎢⎣⎡⎪⎪⎭⎫ ⎝⎛+⎪⎭⎫ ⎝⎛⨯+⎪⎭⎫ ⎝⎛⨯⨯+⎪⎭⎫ ⎝⎛⨯⨯⨯===---==∑∑i ii ij r FLr r Mr F 由（b ）图可知,螺栓受力最大为kN 63.335239.24102)39.24(10cos 22222max =⨯⨯⨯++=++=θF F F F F j i j i []直径较小）布置形式所用的螺栓可知采用（由a F d τπ≥∴max045-10第六章键.花键.无键衔接和销衔接习题答案6-3在一向径mm80d的轴端,安装一钢制直齿圆柱齿轮（如下图）,轮毂宽度=L=,工作时有稍微冲击.试肯定平键的尺寸,并盘算其许可传递的最大扭矩.1.5d[解] 依据轴径mm 80=d ,查表得所用键的剖面尺寸为mm 22=b ,mm 14=h依据轮毂长度mm 120805.1'=⨯==1.5d L 取键的公称长度 mm 90=L 键的标记 键79-90GB 109622⨯键的工作长度为 68mm 2290=-=-=b L l 键与轮毂键槽接触高度为 mm 7==2h k依据齿轮材料为钢,载荷有稍微冲击,取许用挤压应力 110MPa ][=p σ依据通俗平键衔接的强度前提公式 ][1023p p σkldT σ≤⨯=变形求得键衔接传递的最大转矩为m N 20942000110806872000][⋅=⨯⨯⨯==p max σkld T第八章 带传动 习题答案8-1 V 带传动的m in 14501r n =,带与带轮的当量摩擦系数51.0=v f ,包角︒=α1801,初拉力N 3600=F .试问：（1）该传动所能传递的最大有用拉力为若干？（2）若mm 100d d1=,其传递的最大转矩为若干？（3）若传动效力为0.95,弹性滑动疏忽不计,从动轮输出效力为若干？[解] ()N 4.4781111360211112151.01151.00=+-⨯⨯=+-=ππααee e e F F v vf f ec ()m m N 92.232101004.4782d 2-3d1⋅=⨯⨯==ec F T()kW45.395.0100060100010014.314504.4781000601000d 10003d11=⨯⨯⨯⨯⨯⨯=•⨯⨯π=•=ηn F ηνF P ec ec8-2 V 带传动传递效力7.5kW =P ,带速s m 10=ν,紧边拉力是松边拉力的两倍,即21F F =,试求紧边拉力1F .有用拉力e F 和初拉力0F .[解] 1000νF P e =N 750105.710001000=⨯==∴νP F e21212F F F F F e =-=且 1500N 750221=⨯==∴e F F201eF F F += 1125N 27501500210=-=-=∴e F F F8-4 有一带式输送装配,其异步电念头与齿轮减速器之间用通俗V 带传动,电念头功率P=7kW,转速m in 9601r n =,减速器输入轴的转速m in 3302r n =,许可误差为%5±,运输装配工作时有轻度冲击,两班制工作,试设计此带传动.[解] （1）肯定盘算功率ca P由表8-7查得工作情形系数2.1A =K ,故4kW .872.1A ca =⨯==P K P（2）选择V 带的带型依据ca P .1n ,由图8-11选用B 型.（3）肯定带轮的基准直径d d ,并验算带速ν ①由表8-6和8-8,取自动轮的基准直径mm 1801=d d②验算带速νs m 0432.9100060960180********=⨯⨯⨯π=⨯π=n d νd带速合适∴<<m 30s m 5ν ③盘算从动轮的基准直径()()mm 45.49733005.0196018012112=-⨯⨯=-=n εn d d d d （4）肯定V 带的中间距a 和基准长度d L①由式()()2102127.0d d d d d d a d d +≤≤+,初定中间距mm 5500=a . ②盘算带所需的基准长度()()()()mm221455041805005001802550242222122100≈⨯-++π+⨯=-++π+≈a d d d d a L d d d d d 由表8-2选带的基准长度mm 2240=d L ③现实中间距amm 563222142240550200=-+=-+≈d d L L a a 中间距的变化规模为mm 630~550. （5）验算小带轮上的包角1α()()︒≥︒≈︒--︒=︒--︒=901475633.571805001803.57180121a d d αd d 故包角适合. （6）盘算带的根数z ①盘算单根V 带的额定功率r P由s m 960 m m 18011==n d d 和,查表8-4a 得25kW .30≈P 依据303kW .0B 9.2330960s,m 960 01=∆===P i n 型带，查表得和 查表8-5得914.0k =α,表8-2得1k =L ,于是()kW 25.31914.0)303.025.3(k k 00=⨯⨯+=⋅⋅∆+=L αr P P P②盘算V 带的根数z58.225.34.8ca ===r P P z 取3根.（7）盘算单根V 带的初拉力的最小值()min 0F由表8-3得B 型带的单位长度质量m kg 018=q ,所以()()()N 2830432.918.00432.93914.04.8914.05.2500k k 5.250022min 0=⨯+⨯⨯⨯-⨯=+-=q νz νP F αca α（8）盘算压轴力()N 16282147sin 283322sin21min 0=︒⨯⨯⨯==αF z F p （9）带轮构造设计（略）第九章 链传动 习题答案9-2 某链传动传递的功率kW 1=P ,自动链轮转速m in r 481=n ,从动链轮转速m in r 142=n ,载荷安稳,按期人工润滑,试设计此链传动.[解] （1）选择链轮齿数取小链轮齿数191=z ,大链轮的齿数6519144812112=⨯===z n n iz z （2）肯定盘算功率由表9-6查得0.1=A K ,由图9-13查得52.1=z K ,单排链,则盘算功率为kW 52.1152.10.1=⨯⨯==P K K P z A ca（3）选择链条型号和节距依据m in r 48kW 52.11==n P ca 及,查图9-11,可选16A,查表9-1,链条节距mm 4.25=p（4）盘算链节数和中间距初选中间距m m 1270~7624.25)50~30()50~30(0=⨯==p a .取mm 9000=a ,响应的链长节数为3.1149004.2521965265194.25900222222122100≈⨯⎪⎭⎫ ⎝⎛π-+++⨯=⎪⎭⎫ ⎝⎛π-+++=a pz z z z p a L p 取链长节数节114=p L .查表9-7得中间距盘算系数24457.01=f ,则链传动的最大中间距为()[]()[]mm 895651911424.2524457.02211≈+-⨯⨯⨯=+-=z z L p f a p（5）盘算链速ν,肯定润滑方法s m 386.01000604.25194810006011≈⨯⨯⨯=⨯=p z n ν由s m 386.0=ν和链号16A,查图9-14可知应采用按期人工润滑. （6）盘算压轴力p F有用圆周力为 N 2591386.0110001000≈⨯==νpF e 链轮程度布置时的压轴力系数15.1=pF K ,则压轴力为N 2980259115.1≈⨯=≈e F p F K F p9-3 已知自动链轮转速m in r 8501=n ,齿数211=z ,从动链齿数992=z ,中间距mm 900=a ,滚子链极限拉伸载荷为55.6kN,工作情形系数1A =K ,试求链条所能传递的功率.[解] 由kW 6.55lim =F ,查表9-1得mm 4.25=p ,链型号16A依据m in r 850m m 4.251==n p ，,查图9-11得额定功率kW 35=ca P 由211=z 查图9-13得45.1=z K 且1=A KkW 14.2445.1135=⨯=≤∴z A ca K K P P第十章 齿轮传动习题答案10-1 试剖析图10-47所示的齿轮传动各齿轮所受的力（用受力争表示各力的感化地位及偏向）.[解] 受力争如下图：补充题：如图（b ）,已知标准锥齿轮m m N 1042,3.0,50,20,5521⋅⨯=====T Φz z m R ,标准斜齿轮24,63==z m n ,若中央轴上两齿轮所受轴向力互相抵消,β应为若干？并盘算2.3齿轮各分力大小.[解] （1）齿轮2的轴向力：()222222222sin tan 5.012sin tan 2sin tan δαz Φm T δαdm T δαF F R t a -=== 齿轮3的轴向力：βz m T ββz m T βd T βF F n n t a sin 2tan cos 2tan 2tan 33333333=⎪⎪⎭⎫⎝⎛=== 3232,20,T T αF F a a =︒==()βz m T δαz Φm T n R sin 2sin tan 5.01233222=-∴即()2235.01sin tan sin z Φm δαz m βR n -=由5.22050tan 122===z z δ 928.0sin 2=∴δ371.0cos 2=δ ()()2289.0503.05.015928.020tan 2465.01sin tan sin 223=⨯⨯-⨯⨯︒⨯⨯=-=∴z Φm δαz m βR n即︒=231.13β （2）齿轮2所受各力：()() 3.765kN N 10765.3503.05.01510425.01223522222=⨯=⨯⨯-⨯⨯⨯=-==z Φm T dm T F R t0.508kN N 10508.0371.020tan 10765.3cos tan 33222=⨯=⨯︒⨯⨯==δαF F t r kN 272.1N 10272.1928.020tan 10765.3sin tan 33222=⨯=⨯︒⨯⨯==δαF F t akN 420cos 10765.3cos 322=︒⨯==αF F t n齿轮3所受各力：kN 408.5N 10408.5231.13cos 2461042cos 2cos 22353232333=⨯=︒⨯⨯⨯==⎪⎪⎭⎫ ⎝⎛==βz m T βz m T d T F n n tkN 022.2N 10022.2321.12cos 20tan 10408.5cos tan 3333=⨯=︒︒⨯⨯==βαF F n t rkN 272.1N 10272.1321.12cos 20tan 10408.5tan 10408.5tan 33333=⨯=︒︒⨯⨯⨯⨯==βF F t akN 889.5N 10889.5321.12cos 20cos 10765.3cos cos 3333=⨯=︒︒⨯==βαF F n t n10-6 设计铣床中的一对圆柱齿轮传动,已知54,26m in,r 1450,kW 5.72111====z z n P ,寿命h 12000=h L ,小齿轮相对其轴的支承为不对称布置,并画出大齿轮的机构图. [解] (1) 选择齿轮类型.精度等级.材料 ①选用直齿圆柱齿轮传动.②铣床为一般机械,速度不高,故选用7级精度（GB10095-88）. ③材料选择.由表10-1选择小齿轮材料为40Cr （调质）,硬度为280HBS,大齿轮材料为45刚（调质）,硬度为240HBS,二者材料硬度差为40HBS.（2）按齿面接触强度设计[]3211t 132.2⎪⎪⎭⎫⎝⎛⋅+⋅≥H E d σZ u u ΦKT d 1）肯定公式中的各盘算值①试选载荷系数.51t =K②盘算小齿轮传递的力矩mm N 4939714505.7105.95105.9551151⋅=⨯⨯=⨯=n P T③小齿轮作不对称布置,查表10-7,拔取0.1=d Φ④由表10-6查得材料的弹性影响系数21MPa 8.189=E Z⑤由图10-21d 按齿面硬度查得小齿轮的接触疲惫强度极限MPa 6001lim =H σ;大齿轮的接触疲惫强度极限MPa 5502lim =H σ. ⑥齿数比 08.2265412===z z u ⑦盘算应力轮回次数91110044.112000114506060⨯=⨯⨯⨯==h jL n N991210502.008.210044.1⨯=⨯==u N N⑧由图10-19取接触疲惫寿命系数 0.1,98.021==HN HN K K ⑨盘算接触疲惫许用应力 取掉效概率为1%,安全系数1=S[]MPa 588160098.01lim 11=⨯==S σK σH HN H []MPa 5.566155003.12lim 22=⨯==S σK σH HN H2）盘算①盘算小齿轮分度圆直径1t d ,代入[]H σ中较小值[]mm 577.535.5668.18908.2108.21493975.132.2132.2323211t =⎪⎭⎫ ⎝⎛⨯+⨯⨯=⎪⎪⎭⎫ ⎝⎛⋅+⋅≥H E d σZ u u ΦKT d ②盘算圆周速度νs m 066.41000601450577.5314.310006011t =⨯⨯⨯=⨯π=n d ν③盘算尺宽bm m 577.53577.5311t =⨯==d Φb d④盘算尺宽与齿高之比hbmm 061.226577.5311t ===z d m t m m 636.4061.225.225.2=⨯==t m h56.11636.4577.53==h b ⑤盘算载荷系数依据s m 066.4=ν,7级精度,查图10-8得动载荷系数2.1=v K 直齿轮,1==ααF H K K由表10-2查得应用系数25.1=A K 由表10-4用插值法查得420.1=H βK由56.11=hb ,420.1=H βK ,查图10-13得37.1=F βK 故载荷系数 13.2420.112.125.1=⨯⨯⨯==βαH H v A K K K K K ⑥按现实的载荷系数校订所算的分度圆直径22.605.113.2577.53331t 1=⨯==t K K d d ⑦盘算模数mmm 32.22622.6011===z d m 取5.2=m⑧几何尺寸盘算分度圆直径：m m 65265.211=⨯==mz dm m 135545.222=⨯==mz d中间距： mm 100213565221=+=+=d d a 肯定尺宽：[]mm74.515.5668.1895.208.2108.2654939713.225.212222211=⎪⎭⎫ ⎝⎛⨯⨯+⨯⨯⨯=⎪⎪⎭⎫ ⎝⎛⋅+⋅≥H E σZ u u d KT b 圆整后取m m 57m m ,5212==b b . （3）按齿根曲折疲惫强度校核①由图10-20c 查得小齿轮的曲折疲惫强度极限MPa 5001=FE σ;大齿轮的曲折疲惫强度极限MPa 3802=FE σ.②由图10-18取曲折疲惫寿命93.0,89.021==FN FN K K . ③盘算曲折疲惫许用应力 取曲折疲惫安全系数4.1=S[]MPa 86.3174.150089.0111=⨯==SσK σFE FN F[]MPa 43.2524.150093.0222=⨯==SσK σFE FN F④盘算载荷系数055.237.112.125.1=⨯⨯⨯==βανF F A K K K K K⑤查取齿形系数及应力校订系数 由表10-5查得 6.21=a F Y 304.22=a F Y595.11=a S Y 712.12=a S Y⑥校核曲折强度依据曲折强度前提公式 []F S F F σY Y m bd KT σaa ≤=112进行校核 []111MPa 64.99595.16.25.2655249397055.222111F S F F σY Y m bd KT σa a ≤=⨯⨯⨯⨯⨯⨯==[]211MPa 61.94712.13.25.2655249397055.222222F S F F σY Y m bd KT σa a ≤=⨯⨯⨯⨯⨯⨯==所以知足曲折强度,所选参数适合.10-7 某齿轮减速器的斜齿轮圆柱齿轮传动,已知m in r 7501=n ,两齿轮的齿数为m m m m ,6,'229,108,2421160b m βz z n ==︒===,8级精度,小齿轮材料为38SiMnMo （调质）,大齿轮材料为45钢（调质）,寿命20年（设每年300工作日）,每日两班制,小齿轮相对其轴的支承为对称布置,试盘算该齿轮传动所能传递的功率. [解] （1）齿轮材料硬度查表10-1,依据小齿轮材料为38SiMnMo （调质）,小齿轮硬度217~269HBS,大齿轮材料为45钢（调质）,大齿轮硬度217~255 HBS（2）按齿面接触疲惫硬度盘算[]231112⎪⎪⎭⎫⎝⎛⋅+⋅≤αE H H d Z Z σu u K d εΦT ①盘算小齿轮的分度圆直径m m 95.145'229cos 624cos 11=︒⨯==βm z d n ②盘算齿宽系数096.195.1451601===d b Φd ③由表10-6查得材料的弹性影响系数 21MPa 8.189=E Z ,由图10-30拔取区域系数47.2=H Z④由图10-21d 按齿面硬度查得小齿轮的接触疲惫强度极限MPa 7301lim =H σ;大齿轮的接触疲惫强度极限MPa 5502lim =H σ.⑤齿数比 5.42410812===z z u ⑥盘算应力轮回次数811104.522030017506060⨯=⨯⨯⨯⨯⨯==h jL n N8812102.15.4104.5⨯=⨯==u N N⑦由图10-19取接触疲惫寿命系数 1.1,04.121==HN HN K K ⑧盘算接触疲惫许用应力取掉效概率为1%,安全系数1=S[]MPa 2.759173004.11lim 11=⨯==SσK σH HN H[]MPa 60515501.12lim 22=⨯==SσK σH HN H⑨由图10-26查得63.1,88.0,75.02121=+===αααααεεεεε则 ⑩盘算齿轮的圆周速度s m 729.510006075095.14514.310006011=⨯⨯⨯=⨯π=n d ν盘算尺宽与齿高之比hbmm 626'229cos 95.145cos 11=︒⨯==z βd m ntm m 5.13625.225.2=⨯==nt m h85.115.13160==h b 盘算载荷系数依据s m 729.5=ν,8级精度,查图10-8得动载荷系数22.1=v K 由表10-3,查得4.1==ααF H K K按稍微冲击,由表10-2查得应用系数25.1=A K 由表10-4查得380.1=H βK {按d Φ=1查得} 由85.11=hb ,380.1=H βK ,查图10-13得33.1=F βK故载荷系数 946.2380.14.122.125.1=⨯⨯⨯==βαH H v A K K K K K 由接触强度肯定的最大转矩[][]}{N096.12844648.18947.260515.45.4946.2295.14563.1096.1,min 1223221311=⎪⎭⎫ ⎝⎛⨯⨯+⨯⨯⨯⨯=⎪⎪⎭⎫⎝⎛⋅+⋅≤αE H H H d Z Z σσu u K d εΦT（3）按曲折强度盘算[]SaFa F βn d Y Y σKY m d εΦT ⋅≤α2211 ①盘算载荷系数 840.233.14.122.125.1=⨯⨯⨯==βανF F A K K K K K ②盘算纵向重合度 380.1'229tan 24096.1318.0tan 318.01=︒⨯⨯⨯==βz Φεd β ③由图10-28查得螺旋角影响系数 92.0=βY ④盘算当量齿数()99.24'229cos 24cos 3311=︒==βz z v()3.112'229cos 108cos 3321=︒==βz z v ⑤查取齿形系数Fa Y 及应力校订系数Sa Y 由表10-5查得 62.21=Fa Y 17.22=Fa Y59.11=Sa Y 80.12=Sa Y⑥由图10-20c 查得小齿轮的曲折疲惫强度极限MPa 5201=FE σ;大齿轮的曲折疲惫强度极限MPa 4302=FE σ.⑦由图10-18取曲折疲惫寿命90.0,88.021==FN FN K K . ⑧盘算曲折疲惫许用应力 取曲折疲惫安全系数4.1=S[]MPa 07.3055.152088.0111=⨯==S σK σFE FN F []MPa 2585.143090.0222=⨯==S σK σFE FN F⑨盘算大.小齿轮的[]SaFa F Y Y σ,并加以比较[]23.7359.162.207.305111=⨯=Sa Fa F Y Y σ[]05.6680.117.2258222=⨯=Sa Fa F Y Y σ取[][][]05.66,min 222111=⎩⎨⎧⎭⎬⎫=Sa Fa F Sa Fa F Sa Fa FY Y σY Y σY Y σ ⑩由曲折强度肯定的最大转矩[]mm N 309.288598605.6692.0840.22695.14563.1096.122211⋅=⨯⨯⨯⨯⨯⨯=⋅≤αSa Fa F βn d Y Y σKY m d εΦT（4）齿轮传动的功率取由接触强度和曲折强度肯定的最大转矩中的最小值 即N 096.12844641=TkW 87.1001055.9750096.12844641055.96611=⨯⨯=⨯=∴n T P第十一章 蜗杆传动习题答案11-1 试剖析图11-26所示蜗杆传动中各轴的反转展转偏向.蜗轮轮齿的螺旋偏向及蜗杆.蜗轮所受各力的感化地位及偏向.[解] 各轴的反转展转偏向如下图所示,蜗轮2.4的轮齿螺旋线偏向均为右旋.蜗杆.蜗轮所受各力的感化地位及偏向如下图11-3 设计用于带式输送机的通俗圆柱蜗杆传动,传递效力min r 960,kW 0.511==n P ,传动比23=i ,由电念头驱动,载荷安稳.蜗杆材料为20Cr,渗碳淬火,硬度HRC 58≥.蜗轮材料为ZCuSn10P1,金属模锻造.蜗杆减速器每日工作8h,请求工作寿命为7年（每年按300工作日计）. [解] （1）选择蜗杆传动类型依据GB/T 10085-1988的推举,采用渐开线蜗杆（ZI ）.（2）按齿面接触疲惫强度进行设计[]322⎪⎪⎭⎫⎝⎛≥H P E σZ Z KT a①肯定感化蜗轮上的转矩T 2按21=z ,估取效力8.0=η,则m mN 915208239608.051055.91055.91055.962162262⋅=⨯⨯⨯=⨯=⨯=in ηP n P T②肯定载荷系数K因工作载荷安稳,故取载荷散布不平均系数1=βK ;由表11-5拔取应用系数1=A K ;因为转速不高,无冲击,可取动载系数05.1=V K ,则05.105.111=⨯⨯==V βA K K K K③肯定弹性影响系数E Z 蜗轮为铸锡磷青铜与钢蜗杆相配,故21MPa 160=E Z④肯定接触系数p Z 假设35.01=ad ,从图11-18中可查得9.2=p Z ⑤肯定许用接触应力[]H σ由表11-7中查得蜗轮的根本许用应力[]MPa 268'=H σ 应力轮回系数 ()721021.4830071239606060⨯=⨯⨯⨯⨯⨯==h jL n N寿命系数 8355.01021.410877HN=⨯=K 则 [][]MPa 914.2232688355.0'HN =⨯==H H σK σ ⑥盘算中间距mm 396.160914.2239.216091520805.132=⎪⎭⎫⎝⎛⨯⨯⨯≥a取中间距mm 200=a ,因23=i ,故从表11-2中取模数8mm =m ,蜗杆分度圆直径m m 80=1d .此时4.020080==a d 1,从图11-18中查取接触系数74.2'=p Z ,因为p p Z Z <',是以以上盘算成果可用.（3）蜗杆与蜗轮的重要参数与几何尺寸 ①蜗杆蜗杆头数21=z ,轴向齿距133.258=π=π=m p a ;直径系数10=q ;齿顶圆直径mm 962*11=+=m h d d a a ;齿根圆直径()mm 8.602*11=+-=c m h d d a f ;分度圆导程角"36'1811︒=γ;蜗杆轴向齿厚m m 567.125.0=π=m S a . ②蜗轮蜗轮齿数472=z ;变位系数5.02-=x 验算传动比5.2324712===z z i ,此时传动比误差%17.223235.23=-,是许可的. 蜗轮分度圆直径 m m 37647822=⨯==mz d蜗轮喉圆直径 ()()m 3845.018237622*22=-⨯⨯+=++=x h m d d aa 蜗轮齿根圆直径 ()mm 8.3642.05.0182376222=+-⨯⨯-=-=f f2h d d 蜗轮咽喉母圆直径 mm 12376212002122=⨯-=-=a g d a r（4）校核齿根曲折疲惫强度[]F βF F σY Y m d d KT σa ≤=221253.1 ①当量齿数 85.49"36'1511cos 47cos 3322=︒==γz z v 依据85.49,5.022=-=v z x ,从图11-19中可查得齿形系数75.22=a F Y②螺旋角系数 9192.014031.1111401=︒︒-=︒-=γY β ③许用曲折应力 [][]FN F F K σσ⋅='从表11-8中查得由ZCuSn10P1制作的蜗轮的根本许用曲折应力[]MPa 56'=F σ寿命系数 66.01021.410976=⨯=FNK [][]MPa 958.3666.056'=⨯=⋅=∴FN F F K σσ④校核齿根曲折疲惫强度[]F F σσ<=⨯⨯⨯⨯⨯⨯=445.159192.075.283768091520805.153.1曲折强度是知足的. （5）验算效力η()()v γγηϕ+=tan tan 96.0~95.0已知v v f γarctan ;"36'1811=ϕ︒=;v f 与相对滑动速度a v 相干s m 099.4"36'1811cos 10006096080cos 10006011=︒⨯π⨯=⨯π=γn d v a从表11-18顶用插值法查得0238.0=v f ,"48'21136338.1︒=︒=ϕv ,代入式得η,大于原估量值,是以不用重算..0845.0~854第十三章 滚动轴承习题答案13-1 试解释下列各轴承的内径有多大？哪个轴承公役等级最高？哪个许可的极限转速最高？哪个推却径向载荷才能最高？哪个不能推却径向载荷？ N307/P4 6207 30207 51301[解] N307/P4.6207.30207的内径均为35mm,51301的内径为5mm;N307/P4的公役等级最高;6207推却径向载荷才能最高;N307/P4不能推却径向载荷. 13-5 依据工作前提,决议在轴的两头用︒=25α的两个角接触球轴承,如图13-13b所示正装.轴颈直径mm 35=d ,工作中有中等冲击,转速m in r 1800=n ,已知两轴承的径向载荷分离为N 33901=r F ,N 33902=r F ,外加轴向载荷N 870=ae F ,感化偏向指向轴承1,试肯定其工作寿命. [解] （1）求两轴承的盘算轴向力1a F 和2a F对于︒=25α的角接触球轴承,按表13-7,轴承派生轴向力r d F F 68.0=,68.0=eN 2.2305339068.068.011=⨯==∴r d F F N 2.707104068.068.022=⨯==r d F F两轴盘算轴向力}{}{N 2.23052.707870,2.2305m ax ,m ax 211=+=+=d ae d a F F F F }{}{N 2.14358702.2305,2.707m ax ,m ax 122=-=-=ae d d a F F F F（2）求轴承当量动载荷1P 和21Pe F F r a ===68.033902.230511e F F r a >==38.110402.143522 由表13-5查得径向动载荷系数和轴向动载荷系数为 对轴承1 11=X 01=Y 对轴承2 41.02=X 87.02=Y因轴承运转中有中等冲击载荷,按表13-6,取5.1=p f ,则()()N 50852.23050339015.111111=⨯+⨯⨯=+=a r p F Y F X f P ()()N 536.25122.143587.0104041.05.122222=⨯+⨯⨯=+=a r p F Y F X f P（3）肯定轴承寿命因为标题中没给出在轴承的具体代号,这里假设选用7207AC,查轴承手册得根本额定载荷N 29000=C ,因为21P P >,所以按轴承1的受力大小验算h 5.171750852900018006010601036316=⎪⎭⎫⎝⎛⨯⨯=⎪⎪⎭⎫ ⎝⎛=P C n L h 13-6 若将图13-34a 中的两轴承换为圆锥滚子轴承,代号为30207.其他前提同例题13-2,实验算轴承的寿命.[解] （1）求两轴推却到的径向载荷1r F 和2r F将轴系部件受到的空间力系分化为铅垂面（下图b ）和程度面（下图a ）两个平面力系.个中：图c 中的te F 为经由过程另加转矩而平移到指向轴线;图a 中的ae F 亦应经由过程另加弯矩而平移到感化于轴线上（上诉转化仔图中均未画出）.(c)(b)(a)Fre)由力剖析可知：N 38.22552023144002009003202002200V 1=⨯-⨯=+⨯-⨯=d F F F ae re rN 62.67438.225900V 1V 2=-=-=r re r F F FN 15.8462200520200320200200H 1=⨯=+=te r F FN 85.135315.8462200H 1H 2=-=-=r te r F F FN 65.87515.84638.225222H 12V 11=+=+=r r r F F F N 62.151282.135362.674222H 22V 22=+=+=r r r F F F（2）求两轴承的盘算轴向力1a F 和2a F 查手册的30207的37.0=e ,6.1=Y ,N 54200=CN 64.2736.1265.875211=⨯==∴Y F F r d N 69.4726.1262.1512222=⨯==Y F F r d两轴盘算轴向力}{}{N 69.87269.472400,64.273m ax ,m ax 211=+=+=d ae d a F F F F}{}{N 69.47240064.273,69.472m ax ,m ax 122=-=-=ae d d a F F F F（3）求轴承当量动载荷1P 和2Pe F F r a >==9966.065.87569.87211 e F F r a <==3125.062.151269.47222 由表13-5查得径向动载荷系数和轴向动载荷系数为 对轴承1 4.01=X 6.11=Y 对轴承2 12=X 02=Y因轴承运转中有中等冲击载荷,按表13-6,取5.1=p f ,则()()N 846.261969.8726.165.8754.05.111111=⨯+⨯⨯=+=a r p F Y F X f P ()()N 93.226869.472062.151215.122222=⨯+⨯⨯=+=a r p F Y F X f P（4）肯定轴承寿命因为21P P >,所以按轴承1的受力大小验算'h 342.283802846.2619542005206010601036316h h L P C n L >=⎪⎭⎫ ⎝⎛⨯⨯=⎪⎪⎭⎫ ⎝⎛= 故所选轴承知足寿命请求.13-7 某轴的一端支点上原采用6308轴承,其工作靠得住性为90%,现需将该支点轴承在寿命不下降的前提下将工作靠得住性进步到99%,试肯定可能用来调换的轴承型号.[解] 查手册得6308轴承的根本额定动载荷N 40800=C .查表13-9,得靠得住性为90%时,11=a ,靠得住性为99%时,21.01=a .靠得住性为90%时 363161040800601106010⎪⎭⎫⎝⎛⨯=⎪⎭⎫ ⎝⎛=P n P C n a L靠得住性为99%时 363166021.01060101⎪⎭⎫⎝⎛⨯=⎪⎭⎫ ⎝⎛=P C n P C n a L110L L =36366021.0104080060110⎪⎭⎫⎝⎛⨯=⎪⎭⎫ ⎝⎛⨯∴P C n P n 即 N 547.6864121.0408003==C 查手册,得6408轴承的根本额定动载荷N 65500=C ,根本相符请求,故可用来调换的轴承型号为6408.第十五章 轴 习题答案15-4 图15-28所示为某减速器输出轴的构造图,试指出其设计错误,并画出纠正图. [解] （1）处两轴承应该正装. （2）处应有间隙并加密封圈. （3）处应有轴间定位.（4）处键不能伸入端盖,轴的伸出部分应加长. （5）处齿轮不能保证轴向固定. （6）处应有轴间定位. （7）处应加调剂垫片. 纠正图见轴线下半部分.15-7 南北极睁开式斜齿圆柱齿轮减速器的中央轴（见图15-30a ）,尺寸和构造见图15-30b 所示.已知：中央轴转速m in r 1802=n ,传动功率kW 5.5=P ,有关的齿轮参数见下表：m m n m n αzβ旋向 齿轮2 3 20° 112 '4410︒ 右 齿轮34 20° 23'229︒右（a ） (b) [解] （1）求出轴上转矩mm N 56.2918051805.51055.91055.966⋅=⨯⨯=⨯=n P T （2）求感化在齿轮上的力mm 98.341'4410cos 1123cos 222=︒⨯==βz m d n mm 24.93'229cos 233cos 333=︒⨯==βz m d n N 57.170698.34156.291805222t2=⨯==∴d T F N 24.625924.9356.291805223t3=⨯==d T F N 2.632'4410cos 20tan 57.1706cos tan 2t2r2=︒︒⨯==βαF F n N 96.2308'229cos 20tan 57.1706cos tan 3t3r3=︒︒⨯==βαF F n N 49.323'4410tan 57.1706tan 2t2a2=︒⨯==βF F N 47.1032'229tan 24.6259tan 3t3a3=︒⨯==βF F（3）求轴上载荷作轴的空间受力剖析,如图（a ）. 作垂直受力争.弯矩图,如图（b ）.N 54.46803108057.170621024.6259t2t3=⨯+⨯=⋅+⋅=AD CD F BD F F NHAN 27.328554.468024.625957.1706t3t2=-+=++=NHA NHD F F F F m 468.05N m m N 46805410054.4680⋅=⋅=⨯=⋅=AB F M NHA HB m N 822.262m m N 6.2628218027.3285⋅=⋅=⨯=⋅=CD F M NHD HC作程度受力争.弯矩图,如图（c ）.N28.1067310299.34149.323224.9347.1032802.63221096.2308222a23a3r2r3-=⨯+⨯+⨯+⨯-=⋅+⋅+⋅+⋅-=ADd F d F AC F BD F F NVA N48.609310299.34149.323224.9347.10322302.63210096.2308222a23a3r2r3=⨯+⨯+⨯-⨯=⋅+⋅+⋅-⋅=ADd F d F AC F AB F F NVD m N 728.10610028.1067⋅-=⨯-=⋅=AB F M NVA VBm N 86.154224.9347.103210028.10672'3a3⋅-=⨯-⨯-=⋅-⋅=d F AB F M NVA VB m N 76.488048.609⋅-=⨯-=⋅-=CD F M NHD VCm N 555.68048.609299.34149.3232'2a2⋅=⨯-⨯=⋅-⋅=CD F d F M NHD VC 作合成弯矩图,如图（d ）()m N 068.480728.106468.052222⋅=-+=+=VB HB B M M M()m N 007.49386.154468.05''2222⋅=-+=+=VB HB B M M M()m N 307.26776.48822.2622222⋅=-+=+=VC HC C M M M()m N 804.262555.6822.262''2222⋅=+=+=VC HC C M M M作扭矩图,如图（e ）.mm N 56.291805⋅=T作当量弯矩力,如图（f ）.转矩产生的曲折应力按脉动轮回应力斟酌,取6.0=α.()0m N 068.480caB =⋅==T M M B()()()m N 173.52380556.2916.0007.493''2222caB ⋅=⨯+=+=αT M M Bm N 307.267caC ⋅==C M M()()()m N 868.31580556.2916.0904.262''2222caC ⋅=⨯+=+=αT M M C（4）按弯矩合成应力校核轴的强度,校核截面B.C B 截面333B m m 12500501.01.0=⨯==d WMPa 85.411012500173.523'9B caB =⨯==-W M σcaB C 截面333C mm 5.9112451.01.0=⨯==d WMPa 66.34105.9112868.315'9C caC =⨯==-W M σcaC 轴的材料为45号钢正火,[]MPa 51MPa,560200,HBS 1==≥-σσB[]1-≤≤σσσcaB caC ,故安全.。