机器人运动学PPT演示课件
- 格式:ppt
- 大小:3.16 MB
- 文档页数:147



2章 ロボットの運動学
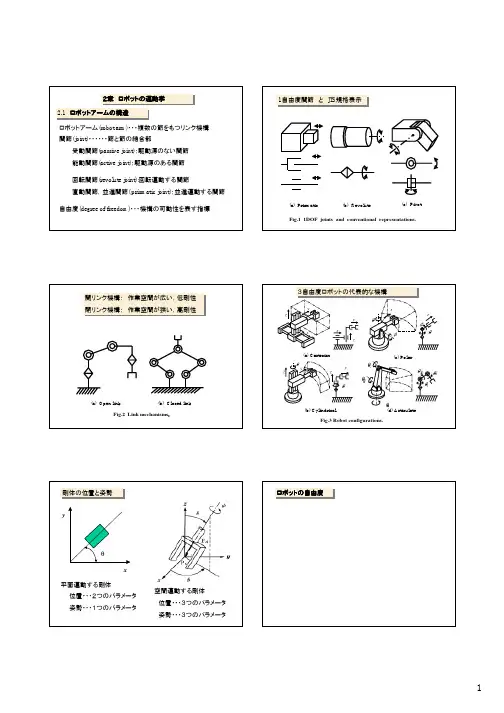
2章 ロボットの運動学2.1 ロボットアームの構造ロボットアームの構造
2.1 ロボットアームの構造ロボットアームの構造ロボットアーム(robot arm)・・・複数の節をもつリンク機構1自由度関節 と JIS 規格表示
1自由度関節 と JIS 規格表示開リンク機構: 作業空間が広い,低剛性閉リンク機構: 作業空間が狭い,高剛性
開リンク機構: 作業空間が広い,低剛性閉リンク機構: 作業空間が狭い,高剛性r
y
3自由度ロボットの代表的な機構
3自由度ロボットの代表的な機構剛体の位置と姿勢剛体の位置と姿勢ロボットの自由度
ロボットの自由度
空間リンク機構(ロボット)の可動度(mobility)
空間リンク機構(ロボット)の可動度(mobility)平面運動機構の自由度と可動度の例
平面運動機構の自由度と可動度の例パラレルリンク機構の自由度と可動度
パラレルリンク機構の自由度と可動度ロボットの座標系(coordinate system)
ロボットの座標系(coordinate system)座標系の平行移動
座標系の平行移動座標系の回転移動
座標系の回転移動
座標系の平行移動と回転移動座標系の平行移動と回転移動
z A
姿勢表現・・・zyzオイラー角
姿勢表現・・・zyzオイラー角
姿勢表現・・・ロール・ピッチ・ヨウ角(zyxオイラー角)姿勢表現・・・ロール・ピッチ・ヨウ角(zyxオイラー角)
z。