当前位置：文档之家 › 人工神经网络算法 基础精讲

人工神经网络算法 基础精讲

  • 格式：ppt
  • 大小：1.33 MB
  • 文档页数：67

下载文档原格式

  / 67

合集下载

人工神经网络算法概述

人工神经网络算法概述
递归网络 前馈网络
人工神经网络的主要学习算法
有师学习 无师学习
强化学习
人工神经网络的典型模型
自适应谐振理论(ART) Kohonen 网络 反向传播(BP发的反向传播训练算法是一种迭代梯度 算法，用于求解前馈网络的实际输出与期望输出间的最小 均方差值。BP网是一种反向传递并能修正误差的多层映 射网络。当参数适当时，此网络能够收敛到较小的均方差， 是目前应用最广的网络之一。BP网的短处是训练时间较 长，且易陷于局部极小。
人工神经网络算法概述
人工神经网络的结构
1,神经元及其特性 神经元及其特性 连接机制结构的基本处理单元与神经生理学类比往往称为神经 元。每个构造起网络的神经元模型模拟一个生物神经元. 神经元单元的偏置（阈值）; 激励函数 ; 权重系数
神经网络的基本类 型
人工神经网络的基本特性 人工神经网络的基本结构
Bp神经网络的几个概念
1，学习率； 2，振荡； 3，归一化； 4，种类字段与数值字段
Bp神经网络的几个问题
1，错误率达不到预期，无限制地训练怎么办？ 2，发生震荡怎么办？ 3，影响Bp神经网络训练时间的因素有哪些？ 4，训练数据对于Bp神经网络的训练结果的影响？ 5，其他一些问题？

人工神经网络基础 PPT

人工神经网络基础 PPT
人工神经网络基础 PPT
人工神经网络概述 前向多层网络 自组织特征映射网络（SOFM）
人工神经网络概述
一 人工神经网络发展 二 生物学基础 三 人工神经网络结构 四 神经网络基本学习算法
一 人工神经网络发展
最早的研究可以追溯到20世纪40年代。1943年， 心理学家McCulloch和数学家Pitts合作提出了形式 神经元的数学模型。这一模型一般被简称M-P神经 网络模型，至今仍在应用，可以说，人工神经网络 的研究时代，就由此开始了。
大家学习辛苦了，还是要坚持
继续保持安静
一 人工神经网络发展
自20世纪80年代中期以来，世界上许多国家掀 起了神经网络的研究热潮，可以说神经网络已 成为国际上的一个研究热点。
一 人工神经网络发展
神经网络研究的两大派：
主要包括:生物学家、物理学家和心理学家
研究目的：给出大脑活动的精细模型和描述。
主要包括:工程技术人员
主要目的：怎样利用神经网络的基本原理，来构 造解决实际问题的算法，使得这些算法具有有趣 的和有效的计算能力。
人工神经网络属于此类
一 人工神经网络发展
人工神经网络概念： 人工神经网络：
就是把一个描述生物神经网络运行机理和工 作过程的抽象和简化了的数学-物理模型，表 达成为一个以其中的人工神经元为节点、以 神经元之间的连接关系为路径权值的有向图， 再用硬件或软件程序实现该有向图的运行， 其稳态运行结果体现生物神经系统的某种特 殊能力。
一 人工神经网络发展
人工神经网络是近年来得到迅速发展的一 个前沿课题。神经网络由于其大规模并行 处理、容错性、自组织和自适应能力和联 想功能强等特点，已成为解决很多问题的 有力工具。
二 生物学基础
生物神经元 突触信息处理 信息传递功能与特点

第6章人工神经网络算法ppt课件

第6章人工神经网络算法ppt课件
1.基本概念 1.3 主要的神经网络模型 目前使用的比较典型的一些神经网络模型主要有以下几类:
4.随机型神经网络 随机型神经网络其基本思想是:不但让网络的误差和能量函数向减小的方
向变化,而且还可按某种方式向增大的方向变化,目的是使网络有可能跳出局部 极小值而向全局最小点收敛。随机型神经网络的典型算法是模拟退火算法。
曲线越陡。
六、人工神经网络算法
1.基本概念 1.2 人工神经元模型 神经元采用了不同的激活函数,使得神经元具有不同的信息处理特性,并且
神经元的信息处理特性是决定神经网络整体性能的主要因素之一。 下面介绍四种常用的激活函数形式：
（4）高斯函数。高斯函数(也称钟型函数)也是极为重要的一类激活函数,常用 于径向基神经网络(RBF网络),其表达式为:
通过调整权值和阈值,使得误差能量达到最小时,网络趋于稳定状态,学习
结束。
（1）输出层与隐含层之间的权值调整。对每一个 wjk 的修正值为:
w jk
E
w jk
E
netk
netk w jk
J
式中: 为学习步长,取值介于(0,1)，对式 netk wjkOj 求偏导得:
j0
netk wjk
Oj
x1
w1i
x2
w2ifΒιβλιοθήκη yixnwni
x0 1
六、人工神经网络算法
1.基本概念 1.2 人工神经元模型 在神经元中,对信号进行处理采用的是数学函数,通常称为激活函数、激励
函数或挤压函数，其输入、输出关系可描述为
u j
f
n
wij xi
j
i1
y f uj
式中xi i 1,2,,n是从其它神经元传来的输入信号; j 是该神经元的阈值;

人工神经网络算法精讲

人工神经网络算法精讲

6.1 概述
6.1.2 人工神经网络的发展
• 第二次高潮期 —— Hopfield网络模型的出现 和人工神经网络的复苏
– 1982年，John Hopfield向美国科学院递交了有关神经网络的 报告，主要内容就是建议收集和重视以前对神经网络的工作， 其中特别强调了每种模型的实用性。 – 根据对神经网络的数学分析和深入理解， Hopfield揭示了以 往的网络是如何工作的，可以做些什么，并提出了他自己的 模型，能从失真的或不完善的数据图像中获得完整的数据图 像，引起了美国军方的兴趣。 – 当时，人工智能对自动制导车的研究失败，而利用神经网络 有可能解决这个问题，从而使人们的注意力重新投向人工神 经网络，导致了人工神经网络的第二次高潮。
6.1 概述
6.1.2 人工神经网络的发展
• 第二次高潮期 —— Hopfield网络模型的出现 和人工神经网络的复苏
6.1 概述
6.1.1 什么是人工神经网络
• 总结和讨论
– 传统计算机采用的是串行处理方式，限制了大量信息的快速 传输和处理，即使用了多个处理器并行工作，还是会把许多 时间浪费在完成串行操作上，而且问题的并行化分解和并行 程序的编写也是一个难题。 – 虽然至今开发出的超型计算机，其速度和容量都大得惊人， 但仍不能很好地完成诸如小孩可以做到的事情，如认识面孔、 学习说话、识别图像等。 – 尽管人工神经网络还是生物大脑的极低水平的模仿，但在图 像识别、语音识别、记忆、预测以及优化等方面表现出了良 好的智能特性和应用前景，可以完成传统计算机不易实现的 智能性工作。
6.1 概述
6.1.1 什么是人工神经网络
• 人工神经网络的两种操作过程
– 训练学习
• 训练时，把要教给神经网络的信息（外部输入）作为网 络的输入和要求的输出，使网络按某种规则（称为训练 算法）调节各处理单元间的连接权值，直至加上给定输 入，网络就能产生给定输出为止。 • 这时，各连接权已调接好，网络的训练就完成了。

人工神经网络讲PPT课件

人工神经网络讲PPT课件

图2-1 神经元的解剖
2、生物神经元
突触，是一个神经元与另一 个神经元之间相联系并进行 信息传送的结构。 突触的存在说明：两个神经 元的细胞质并不直接连通， 两者彼此联系是通过突触这 种结构接口的。有时．也把 突触看作是神经元之间的连 接。
图2-2 突触结构
2生物神经元
目前，根据神经生理学的研究，已经发现神经元及其间的 突触有4种不同的行为。神经元的4种生物行为有：
ykj ——模式k第j个输出单元的期望值； 式中：
y j k ——模式k第j个输出单元的实际值；
M——样本模式对个数；
Q——输出单元个数。
第二种：误差平方和
E
k 2 ( y y ) j kj k 1 j 1
M
Q
MQ
式中：M——样本模式对个数；
Q——输出单元个数。
1 Q Ek ( y j k ykj ) 2 2 j 1 E Ek
r r (Wi , X , di )
权矢量的变化是由学习步骤按时间t，t+1，…，一步一步进行计算的。在 时刻t连接权的变化量为：
Wi (t ) cr[Wi (t ), X i (t ), di (t )] X (t )
其中c是一个正数，称为学习常数，决定学习的速率。
神经元网络的学习规则
——这一能力可以算作是智能的高级形式 ——是人类对世界进行适当改造、推动社会不断发展的能力
4
联想、推理、判断、决策语言的能力
——这是智能高级形式的又一方面 ——主动与被动之分。联想、推理、判断、决策的能力是主动的基础。
1、引言
5 6 7 8
通过学习取得经验与积累知识的能力 发现、发明、创造、创新的能力 实时、迅速、合理地应付复杂环境的能力 预测，洞察事物发展、变化的能力

人工神经网络讲稿ppt课件

人工神经网络讲稿ppt课件

举例：2-3岁小孩能够从人群中认出父母、3-4岁能够顺利地穿过十字路 口，但最先进机器人也难以完成这项任务。
因而模仿人类思维方式能够提升机器人能力
人工神经网络讲稿
5/40
1.2 神经细胞与生物神经网络
1. 神经网络
组织形式 大脑中大约有100亿个神经元，它们相互连接，形成一个复杂庞大网络
系统。所以大脑结构是一个神经（元）网络。 依据预计，每个神经元大约与上千个神经元相互连接。 大脑所形成神经网络是由一些小网络连接而成。依据预计，全部神经元
层次结构：神经元联接按层次排列。 模块结构：主要特点是将整个网络按功效划分为不一样模块，每个模块 内部神经元紧密互联，并完成各自特定功效，模块之间再互联以完成整体功 效； 层次模块结构：将模块结构和层次结构结合起来，使之更靠近人脑神经 系统结构，这也是当前为人们广泛注意一个新型网络互联模式。 依据网络中神经元层数不一样，可将神经网络分为单层网络和多层网络； 依据同层网络神经元之间有没有相互联接以及后层神经元与前层神经元有 没有反馈作用不一样，可将神经网络分为以下各种。
Hopfield网络和BP算法出现，使得人工神经研究出现了复兴。因为人 工神经网络在信息处理方面优点，使得大批学者加入到了这一研究领域， 掀起了神经网络研究新高潮。
人工神经网络讲稿
13/40
4. 全方面发展时期（1987-现在） 1987年在美国召开了第一届国际神经网络学术大会，并宣告成立了
国际神经网络学会，与会代表1600多人。这次大会也宣告了神经网络 学科诞生。神经网络研究进入了一个转折点，其范围不停扩大，领域 几乎包含各个方面。神经网络应用使工业技术发生了很大改变，尤其 是在自动控制领域有了新突破。
互制约，从而能够将层内神经元分为几组，让每组作为一个整体来动作。

人工神经网络课程 PPT课件.ppt

人工神经网络课程 PPT课件.ppt

x0 1, wj0 j , x'0 1, w'k0 'k , x''0 1, w''l0 ''l
则有： n
x' j f ( wji xi ), i0
n1
n2
x''k f ( w'kj x' j ), y l f ( w''lk x''k )
j0
k 0
2021/3/15
马尽文
1. 网络的结构与数学描述
(i). 非线性连续变换单元
对于非线性连续变换单元，其输入、输出变换
函数是非线性、单调上升、连续的即可。但
在BP网络中，我们采用S型函数：
n
ui si
wij x j i
j 1
yi
1 f (ui ) 1 eui
1
n
( wij x j i )
1 e j1
2021/3/15
W(n0 ) W 0
x1
x2
当 E(W 0 ) ，算法以希望误差收敛；
当 E(W 0 ) ，算法不以希望误差收敛，但可按 梯度绝对值小于预定值结束。
2021/3/15
马尽文
19
2.3 非线性连续变换单元组成的网络
4. 算法的改进 (i). 变步长算法（ 是由一维搜索求得） Step 1. 赋予初始权值 W(0) 和允许误差 0 ； Step 2. 在时刻 n0 ，计算误差E(W(n0)) 的负梯度
wsg
E
wsg
N E (W , t , x )
1
wsg
E
s,g
E wsg
wsg

第三讲(2)人工神经网络(BP算法)

第三讲(2)人工神经网络(BP算法)

1974年，Werbos已提出了该方法
2。弱点 ：训练速度非常慢、局部极小点的逃离问题、算法 不一定收敛。 3。优点：广泛的适应性和有效性。
4.1 概述
一、简介
BP算法即反向传播算法，有时也称为BP模型； BP算法是为了解决多层前向神经网络的权系数优化而提出来
的，通常暗示着神经网络的拓扑结构是一种无反馈的多层前向
Xim = Yi
（期望输出）
误差信号e
反向传播修改权系数
2、反向传播 称 为一般化的Delta法则，由公式可知 求取本层 dik时，要用到高一层的 dik+1 ；可见，误差函数的求 取是从输出层开始，到输入层的反向传播过程； 通过多个样本的反复训练，同时向误差渐渐减小的方向对权 系数进行修正，以达最终消除误差。从上面公式也可以知道，
Real Distribution
Overfitted
4.2 BP网的学习算法
二、BP算法原理 （六）几个问题
收敛速度问题 局部极小点问题 网络瘫痪问题 ：训练中当训练步长会变得非常小，将导致训练速度降得非 常低，最终导致网络停止收敛 稳定性问题 步长问题 BP网络的收敛是基于无穷小的权修改量 步长太小，收敛就非常慢 步长太大，可能会导致网络的瘫痪和不稳定 自适应步长，使得权修改量能随着网络的训练而不断变化。
输出Y＝(Y1，Y2，…，Yn)。 3．计算各层的输出。 对于第k层第i个神经元的输出Xik，有：
4.2 BP网的学习算法
二、BP算法原理 （四）BP算法的执行步骤 4．求各层的学习误差dik对于输出层有：
If k=m
else
5．修正权系数Wij和阀值θ
4.2 BP网的学习算法
二、BP算法原理 （四）BP算法的执行步骤

[课件]人工神经网络-算法推导PPT

[课件]人工神经网络-算法推导PPT



ik
E net (i 1 )k
i net N ( i 1 ) k ( O W ) O ih ih k ij w W h 1 ijk ijk
因此： （1）计算 ik
W O ijk ik ij
O E E ( i 1 ) k ik net O net ( i 1 ) k ( i 1 ) k ( i 1 ) k
扩展的deltadelta学习规学习规则bpbp算法算法学习学习方法ep竞争学习输出神经元之间有侧向抑制性连接较强单元获胜并抑制其他单元独处激活状态winnertakesallwtakjkj若神经元获胜若神经元失败学习学习方法离散感知器hebb规则规则widrowhoff规则lms最小二乘法无导师初值为0有导师初值任意有导师初值任意有导师初值任意学习规则比较bp神经网络bp网络神经元分层排列分别组成输入层中间层也叫隐含层可以由若干层组成和输出层
W ( t 1 ) W ( t ) O ij k ij k ik ij W ( t 1 ) W ( t ) O ij k ij k ik ij
因此，BP算法的权值调整公式为
( d y ) y ( 1 y ) i 1 层为输 k k k k E ik O ( 1 O ) ( W i 1 层为 i 1 ) k ( i 1 ) k ( i 1 ) h ( i 1 ) k) h ik (
感知器计算说明
• 例1：苹果和橘子的自动分类问题 • 用一组传感器测量水果的三个特征：外形、质 地和重量。如果水果基本上是圆形的，外形传 感器输出为1，若水果接近于椭圆，外形传感 器输出为0；如果水果表面光滑，质地传感器 输出为1，若水果表面粗糙，质地传感器输出 为0；如果水果重量超过1磅，重量传感器输出 为1，若水果轻于1磅，重量传感器输出为0；

神经计算基础(人工神经网络基础) PPT

神经计算基础(人工神经网络基础) PPT
脑的一些基本特征，同时使得人工神经网络具有良 好的可实现性。
人们期待着，通过大家的不懈努力，在不久的将来，能在 这两种技术的研究上以及其有机结合方面有所突破，也希 望在方法上有一个新的突破，真正打开智能的大门。
IIP’2011-2012(1)
3
3.1 人工神经网络基础
人工神经网络是根据人们对生物神经网络的研究成果设计 出来的，它由一系列的神经元及其相应的联接构成，具有 良好的数学描述，不仅可以用适当的电子线路来实现，更 可以方便的用计算机程序加以模拟。
3 神经计算基础
3.1 人工神经网络基础
School of Information Science & Technology Dalian Maritime University
目录
3 神经计算基础 3.1 人工神经网络基础 3.1.1 人工神经网络的提出 3.1.2 人工神经网络的特点 3.1.3 历史回顾 3.1.4 生物神经网络 3.1.5 人工神经元 3.1.6 人工神经网络的拓扑特性 3.1.7 存储与映射 3.1.8 人工神经网络的训练
✓ 进化主义（或者叫做行动/响应）学派。
IIP’2011-2012(1)
10
物理符号系统
物理符号系统的定义：
✓ 因为信息需要在一定的载体上以某种规定的形式表达出来，
✓ 习惯上，人们用一系列的基本符号以及组合这些符号的一些规则去表 达一些信息和行为，
✓ 这些基本符号以及组合这些符号的规则就是所谓的物理符号系统。
首先简要介绍智能和人工智能，然后简要介绍人工神经网 络的发展过程及其基本特点。
然后将介绍人工神经网络的基本知识，主要包括：
✓ 基本的生物神经网络模型， ✓ 人工神经元模型及其典型的激活函数； ✓ 人工神经网络的基本拓扑特性， ✓ 存储类型（CAM-LTM，AM-STM）及映象， ✓ 有导师（Supervised）训练与无导师（Unsupervised）训练。

人工神经网络的算法

人工神经网络的算法

人工神经网络的算法
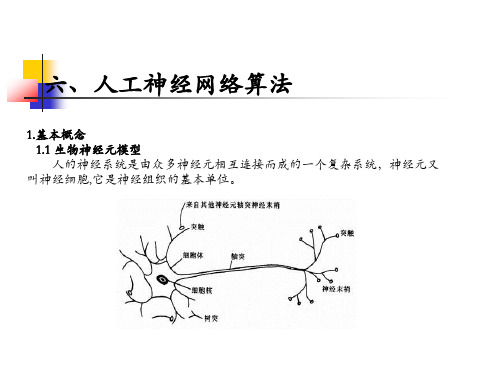
人工神经网络（Artificial Neural Network，ANN）是一种仿照生物神经网络原理构建的计算模型, 是指模仿人脑神经元结构，建立一种模糊推理的模型。

它由大量的神经元及其之间的连接构成，模仿人的大脑、神经系统的思维方式，可以处理模糊、多变、复杂的信息。

人工神经网络的基本结构包括神经元、联络和权重三要素。

神经元的工作原理：每个神经元都有很多杆，它们从其它神经元获取输入信号，并加权聚合，然后将聚合后的信号输出给其它神经元。

联络用于连接不同的神经元，而权重则用于每一个联络信号的加权。

人工神经网络的学习阶段是该网络内部的参数按照一定的机制（如误差反向传播算法）进行调整更新，使其输出的结果是一道题给出的解，使其在一定的范围内尽可能贴近正确答案的过程。

学习主要通过调整连接权重来完成，即为神经元连接权重设置有效值，从而使输出介于正确答案之间，从而达到最佳解的目的。

学习的结果可以决定网络的计算结果，也可以决定网络的性能，这就是学习算法的目的。

通常，学习算法的目标是最小化网络的总体损失，通过更新权重和偏置来增加网络的性能。

此外，人工神经网络还可以实现训练和参数压缩。

最新人工神经网络讲稿ch

最新人工神经网络讲稿ch
• Sejnowski与Rosenberg ，1987年 • ∆wij=α((1-β)δjoi+β∆wij′) • ∆wij′也是上一次的修改量，β在0和1之间取值
2020-11-27
21
4.4 算法的实现
• 主要数据结构 W[H，m]——输出层的权矩阵； V[n，H]——输入（隐藏）层的权矩阵； ∆o[m]——输出层各联接权的修改量组成的向量； ∆h[H]——隐藏层各联接权的修改量组成的向量； O1——隐藏层的输出向量； O2——输出层的输出向量； (X，Y)——一个样本。
2020-11-27
22
算法的主要实现步骤
1 用不同的小伪随机数初始化W，V； 2 初始化精度控制参数ε；学习率α ； 3 循环控制参数E=ε+1；循环最大次数M；循环次数控制参数N=0； 4 while E>ε & N<M do
4.1 N=N+1；E=0； 4.2 对每一个样本(X,Y)，执行如下操作
• 用理想输出与实际输出的方差作为相应的误差测度
1m E2k 1(yk
ok)2
2020-11-27
29
最速下降法，要求E的极小点
取
E
wi j
wi j
E
E
wij
E
w
>0，此时Δwij<0
ij
2020-11-27
wij
E w
ij
<0,
此时Δwij>0
30
最速下降法，要求E的极小点
E E nejt
2020-11-27
25
建议
• 隐藏层的神经元的个数H作为一个输入参数 • 同时将ε、循环最大次数M等，作为算法的输入参数 • 在调试阶段，最外层循环内，加一层控制，以探测网络是否陷入了局部极小点

人工神经网络算法(基础精讲)

人工神经网络算法(基础精讲)
兴奋和抑制状态，当细胞膜电位升高超过阈值时，细胞进入兴奋状态，产生神经冲动；当膜电位低于阈值时，细胞进入抑制状态。
*
1.6激活函数
神经元的描述有多种，其区别在于采用了不同的激活函数，不同的激活函数决定神经元的不同输出特性，常用的激活函数有如下几种类型：
*
1.6激活函数
当f（x）取0或1时，
阈值型激活函数 阈值型激活函数是最简单的，前面提到的M-P模型就属于这一类。其输出状态取二值（1、0或+1、-1），分别代表神经元的兴奋和抑制。
突触结构示意图
1
2
1.3生物神经元的信息处理机理
神经元的兴奋与抑制 当传入神经元冲动，经整和使细胞膜电位升高，超过动作电位的阈值时，为兴奋状态，产生神经冲动，由轴突经神经末稍传出。当传入神经元的冲动，经整和，使细胞膜电位降低，低于阈值时，为抑制状态，不产生神经冲动。
*
1.4生物神经元的特点
*
2.2学习方法
无导师学习也称无监督学习。在学习过程中，需要不断地给网络提供动态输入信息（学习样本），而不提供理想的输出，网络根据特有的学习规则，在输入信息流中发现任何可能存在的模式和规律，同时能根据网络的功能和输入调整权值。
②无导师学习
灌输式学习是指将网络设计成记忆特别的例子，以后当给定有关该例子的输入信息时，例子便被回忆起来。灌输式学习中网络的权值不是通过训练逐渐形成的，而是通过某种设计方法得到的。权值一旦设计好，即一次性“灌输给神经网络不再变动，因此网络对权值的”“学习”是“死记硬背”式的，而不是训练式的。
*
1.6激活函数
概率型激活函数 概率型激活函数的神经元模型输入和输出的关系是不确定的，需要一种随机函数来描述输出状态为1或为0的概率，设神经元输出（状态）为1的概率为：
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
假设oi（n）和oj（n）是神经元i和j在时刻n的状态反应，Wij （n）表示时刻n时，连接神经元i和神经元j的权值，△Wij（n）表 示从时刻n到时刻n+1时连接神经元i和神经元j权值的改变量，则
w （ ij n+1） =w （ ij n） +η go （ i n） go（ j n） =w （ ij n） V w （ ij n）
上述的分类方法是对目前常见的神经网络结构的概括和抽象， 实际应用的神经网络可能同时兼有其中的一种或几种形式。
26
二、人工神经网络的 学习方法
27
2.1学习机理
学习机理
人工神经网络信息处理可以用数学过程来说明，这个过程可以 分为两个阶段：执行阶段和学习阶段。
学习是智能的基本特征之一，人工神经网络最具有吸引力的特 点是它能从环境中学习的能力，并通过改变权值达到预期的目的。 神经网络通过施加于它的权值和阈值调节的交互过程来学习它的环 境，人工神经网络具有近似于与人类的学习能力，是其关键的方面 之一。
突触结构示意图
1.3生物神经元的信息处理机理
电脉冲
输 入
树 突
细胞体 形成 轴突
突
输
触
出
信息处理
传输
图 12.2 生物神经元功能模型
神经元的兴奋与抑制
当传入神经元冲动，经整和使细胞膜电位升高，超过动作电位 的阈值时，为兴奋状态，产生神经冲动，由轴突经神经末稍传出。 当传入神经元的冲动，经整和，使细胞膜电位降低，低于阈值时， 为抑制状态，不产生神经冲动。
4
1.1人工神经网络发展简史
最早的研究可以追溯到20世纪40年代。1943年，心理学家 McCulloch和数学家Pitts合作提出了形式神经元的数学模型。这一 模型一般被简称M-P神经网络模型，至今仍在应用，可以说，人工 神经网络的研究时代，就由此开始了。
1949年，心理学家Hebb提出神经系统的学习规则，为神经网络的 学习算法奠定了基础。现在，这个规则被称为Hebb规则，许多人工 神经网络的学习还遵循这一规则。
9
1.4生物神经元的特点 生物神经元的特点：
阈值特性
单向性传递
延时性传递
生物神经元的特点
1.5人工神经元模型
神经元模型
从神经元的特性和功能可以知道，神经元相当于一个多输入单 输出的信息处理单元，而且，它对信息的处理是非线性的，人工神 经元的模型如图所示：
神经元的n个输入 对应的连接权值
阈值
激活函数
24
1.7人工神经网络模型 分层网络
分层网络将一个神经网络中的所有神经元按功能分为若干层， 一般有输入层、中间层（隐藏层）和输出层。
分层网络按照信息的传递方向可分为前向式网络（如图a）和 反馈网络（如图b、c）。
25
1.7人工神经网络模型 相互连接型网络
相互连接型网络是指网络中任意单元之间都是可以相互双向 连接的。
k=1
其中， Ok=f（netk）为实际输出；yk代表理想输出；W是网络的所有权值组
成权矩阵W=（wij）；K为输出个数。
使用梯度下降法调整权值W，使误差准则函数最小，得到W的修
正Delta规则为：
w ijn + 1 = w ijn jg o i
注：Delta学习规则只适用于线性可分函数，无法用于多层网络
15
1.6激活函数 1.阈值型激活函数
阈值型激活函数是最简单的，前面提到的M-P模型就属于这一类 。其输出状态取二值（1、0或+1、-1），分别代表神经元的兴奋和 抑制。 当f（x）取0或1时，
1，若x0 f (x) 0，若x0
16
1.6激活函数
当f（x）取1或-1时，f（x）为下图所示的sgn（符号）函数
1， 若x 0 sgn（x）= f (x) -1，若x 0
17
1.6激活函数
2.S型激活函数
神经元的状态与输入级之间的关系是在（0,1）内连续取值的单 调可微函数，称为S型函数。
单极性S型函数：
f
(x)
1 1 ex
双极性S型函数：
f(x)12ex 1=11 eexx
18
1.6激活函数 3.分段线性激活函数
神经元和神经网络的关系是元素与整体的关系。 人工神经网络中的神经元常称为节点或处理单元，每个节点均 具有相同的结构，其动作在时间和空间上均同步。
22
1.7人工神经网络模型 人工神经网络的基本属性
23
1.7人工神经网络模型 神经网络模型
神经元的连接方式不同，网络的拓扑结构也不同，人工神经网 络的拓扑结构是决定人工神经网络特征的第二要素，根据神经元之 间连接的拓扑结构不同，可将人工神经网络分成两类，即分层网络 和相互连接型网络。
人工神经网络
二〇一五年十二月
目录
2
一、人工神经网络的 基本概念
3
一、人工神经网络的 基本概念
人工神经网络（Artificial Neural Network，即ANN）可以概 括的定义为：
由大量具有适应性的处理元素（神经元）组成的广泛并行互联 网络，它的组织能够模拟生物神经系统对真实世界物体所作出的交 互反应，是模拟人工智能的一条重要途径。人工神经网络与人脑相 似性主要表现在：
30
2.2学习方法
②无导师学习
无导师学习也称无监督学习。在学习过程中，需要不断地给网 络提供动态输入信息（学习样本），而不提供理想的输出，网络根 据特有的学习规则，在输入信息流中发现任何可能存在的模式和规 律，同时能根据网络的功能和输入调整权值。
③灌输式学习
灌输式学习是指将网络设计成记忆特别的例子，以后当给定有 关该例子的输入信息时，例子便被回忆起来。灌输式学习中网络的 权值不是通过训练逐渐形成的，而是通过某种设计方法得到的。权 值一旦设计好，即一次性“灌输给神经网络不再变动，因此网络对 权值的”“学习”是“死记硬背”式的，而不是训练式的。
在训练周期内，相邻单元的规模是可变的。一般的方法是从定 义较大的相邻单元开始，在训练过程中不断减少相邻的范围。胜利 单元可定义为与输入模式最为接近的单元。Kohonen网络可以模拟 输入的分配
28
2.2学习方法
学习方法
按照广泛采用习
无导师 学习
灌输式 学习
29
2.2学习方法 ①有导师学习
有导师学习又称为有监督学习，在学习时需要给出导师信号 或称为期望输出。神经网络对外部环境是未知的，但可以将导师看 做对外部环境的了解，由输入-输出样本集合来表示。导师信号或 期望响应代表了神经网络执行情况的最佳效果，即对于网络输入调 整权值，使得网络输出逼近导师信号或期望输出。
31
2.3学习规则
学习规则
在神经网络的学习中，各神经元的连接权值需按一定的规则 调整，这种权值调整规则称为学习规则。下面介绍几种常见的学习 规则。
2.3学习规则
1.Hebb学习规则
当神经元i与神经元j同时处于兴奋状态时，在神经网络中表 现为连接权增加 。根据该假设定义权值调整的方法，称为Hebb学 习规则。Hebb学习规则的数学描述：
W jT X =i m 1,2a ,..x .,KW iTX
只有获胜的神经元才有权调整其权向量Wj，调整量为：
W j=XW j
其中，η为学习参数（0＜η≤1）
36
2.3学习规则
5.Kohonen学习规则
该规则只用于无导师指导下训练的网络。在学习过程中，处 理单元竞争学习时，具有高输出的单元为胜利者，它有能力阻止它 的竞争者并激活相邻的单元，只有胜利者才能有输出，也只有胜利 者与其相邻单元可以调节权重。
1957年，F.Rosenblatt提出“感知器”(Perceptron)模型，第一 次把神经网络的研究从纯理论的探讨付诸工程实践，掀起了人工神 经网络研究的第一次高潮。
5
1.1人工神经网络发展简史
20世纪60年代以后，数字计算机的发展达到全盛时期，人们误以 为数字计算机可以解决人工智能、专家系统、模式识别问题，而放 松了对“感知器”的研究。于是，从20世纪60年代末期起，人工神 经网络的研究进入了低潮。
分段线性激活函数的定义为：
1，若x 0 f (x) x，若 1 x 1
1，若x 0
19
1.6激活函数
4.概率型激活函数
概率型激活函数的神经元模型输入和输出的关系是不确定的， 需要一种随机函数来描述输出状态为1或为0的概率，设神经元输出 （状态）为1的概率为：
P（1）=1e1x/T
（其中，T为温度函数）
20
1.6激活函数 激活函数的基本作用表现在:
对输入、输出进行函数转换
控制输入对输出 的激活作用
将可能无限域的输 入变换成指定的有 限范围内的输出
21
1.7人工神经网络模型
人工神经网络模型
神经网络是由许多神经元互相在一起所组成的神经结构。把神 经元之间相互作用关系进行数学模型化就可以得到人工神经网络模 型。
①神经网络获取的知识是从外界环境学习得来的； ②各神经元的连接权，即突触权值，用于储存获取的知识。
神经元是神经网络的基本处理单元，它是神经网络的设计基础 。神经元是以生物的神经系统的神经细胞为基础的生物模型。在人 们对生物神经系统进行研究，以探讨人工智能的机制时，把神经元 数学化，从而产生了神经元数学模型。因此，要了解人工神经模型 就必须先了解生物神经元模型。
其中，η是正常数，它决定了在学习过程中从一个步骤到另一个步骤的学习 速率，称为学习效率
33
2.3学习规则
2.Delta（δ）学习规则
Delta学习规则是最常用的学习规则，其要点是通过改变神经
元之间的连接权来减小系统实际输出与理想输出的误差。假设n时 刻输出误差准则函数如下：
E=1
2
K
2
（yk-o（ k n）)