下载文档原格式
我国农业气象灾害特征及防灾减灾对策摘要：随着我国农业的不断发展，农业气象越来越受到人们的关注。
研究预测频发的气象异常的对策以及防止气象灾害的措施是如今农业气象研究中的重要课题。
需要密切关注作物生长气候的变化，通过改进农业技术，加强田间管理等措施，来抵御气象灾害，防止农作物减产欠收。
基于此，本文主要分析我国农业气象灾害特征及防灾减灾对策。
关键词：农业气象灾害；特征；防灾减灾；对策引言随着全球变暖，气温升高，干旱和洪涝出现了两极分化的问题，过度干旱和过度洪涝限制着我国农业经济的发展。
由于我国国土面积较大，地形结构复杂多样，农业气象自然灾害分布广泛，因此灾害发生时，无法及时应对，制约了粮食产量，阻碍了农业经济的发展。
为此，掌握自然灾害的防御对策至关重要。
1 农业气象灾害特征1.1 具有较强的季节性受到全球气候变化的影响，我国近些年发生农业气象灾害的频率逐渐升高。
通过对全国范围内发生气象灾害的情况进行研究可以发现，农业气象灾害具有较为明显的季节性。
例如在我国沿海地区，每年的夏季容易出现一些台风等强对流天气，而在我国东北地区，旱灾的发生时间主要集中在春季，因此，可以依据这种规律对农业气象灾害进行研究。
1.2 具有较强的局部性在我国很多地区，气象灾害发生往往是多种灾害同时发生，尤其是在一些固定的时间段内，往往会出现多种气象灾害，这些气象灾害影响的地区也比较固定。
例如，每年在我国一些地区发生的冰雹或者霜冻灾害，这些气象灾害发生的规律说明其具有较强的局部性特点[1]。
1.3 具有较强的区域性通过对近几年的气象资料研究可以发现，在一些降水量相对较高的地区，发生洪涝灾害的概率较大。
这些地区往往水网密布，同时地势较低。
台风等气象灾害往往发生在我国的严寒地区，在内陆发生的概率较低。
2 主要农业气象灾害分析2.1 干旱作物发育期内，久旱使土壤中有效水分消耗殆尽，使作物发生凋零枯死的现象，叫作干旱。
作物受干旱危害的程度是多方面因素综合作用的结果，这些因素有降水量、蒸发量、土壤有效水分储存量、作物需水量及耕作措施，此外还与作物品种、水利化程度等有关。
农业气象灾害评估现状和发展趋势摘要：对于农业气象灾害风险进行分析最早起源于国外,分析主要集中领域是重大自然灾害与经济方面,而对于农业气象灾害风险分析却相对较少。
农业气象灾害评估是对灾害规律进行研究对灾害区划、灾害管理以及灾害风险进行预测的重要基础。
本文对农业气象灾害评估现状和发展趋势进行了探讨。
关键词：农业；气象灾害；评估；现状；发展趋势引言:农业气象灾害是对农作物产量与质量产生影响的重要因素。
在我国每1年因为各种气象灾害所导致的农作物受灾面积相等庞大,所造成的经济损失也非常巨大。
特别是近年来,极端气候天气增多,使得农业气象灾害发生的频率与强度都呈现上升趋势,对国家粮食安全产生巨大威胁。
因此,需要加强农业气象灾害评估。
一、农业气象灾害评估的现状分析农业上的气象灾害，是当前中国农业产生严重破坏的一个重要的因素。
农业气象灾害所对农业所产生破坏程度，主要是根据农业灾害性气象的量化体系进行评估的。
而当前我国学者通过多种变量的控制方式，经过多次试验以及对农业气象灾害数据进行整合与分析，渐渐形成一种以农业为主要的对象的灾害性气象的量化指标结构，并且以此作为整个评估的基础，建设起一些与农业气象性灾害评估相关的数学模型，促进了我国气象性灾害问题的评估的发展。
我国的农业气象性灾害的评估已经从定性评估逐渐转化成为量化的评估。
而其中对于主要的农业气象性灾害，比如寒潮、暴雨、台风、干旱以及洪涝等，都被列入到我国农业气象灾害的评估体系之中。
当前国内以及国外主要评估农业气象灾害的程度的指标，主要是人类的社会所造成的各项财产以及物件的损失，折算后的经济损失，以及有关农作物的产量损耗等。
而我国流行的评估方式主要有综合模型式的评估、作物模型式的评估以及灾害风险式的评估。
1、农业气象性灾害的综合模型评估综合模型式的评估，主要所考虑到的因素比较多，包括了受到农业气象性灾害的地区生产力水平状况，以及所种植的相关农作物的抵御气象性灾害的能力、农作物对于农业气象灾害的敏感程度，以及农业气象性灾害的强度、受到气象性灾害的农作物面积等。
影响我国农业生产的气象灾害江西省吉安师范学校彭尾才我国地域辽阔，地形复杂，加之季风气候显著，致使我国的气象灾害种类繁多。
下面主要讨论它们对我国农业生产的影响。
干旱：干旱按季节可分为春旱、夏旱和秋旱。
春旱发生在3—5月份，这个时期气温上升快，空气相对湿度低，土壤水分丧失快。
夏旱多发生在7—8月份，此时我国气温处于最高时期，蒸发快，且作物处于生长旺盛时期，所以危害较大。
秋旱在处暑到秋分这一时期，我国北方干燥少雨，它直接影响了对作物的浇灌和播种。
我国不同地区地区有不同的干旱类型：黄淮流域以春旱为主；长江流域以夏旱为主，有时伴有秋旱。
干旱对作物产量的影响极大，严重时可使作物产量减半。
低温冷害：是指温度在00 C以上，由于低于农作物所能忍耐的临界低温而产生的危害。
主要出现于东北、华北地区，危害水稻、高粱、玉米、大豆等作物。
低温冷害的危害情况因地而异，一般是温度低、生长季短，积温年际变化大、低温年出现频率高的地区受害严重。
同时，冷害还与当地喜温作物和喜凉作物的比例有关。
寒潮：入侵我国的寒潮，它的“故乡”主要在严寒的西伯利亚地区。
寒潮发生时会造成大风、剧烈的降温、雨雪、霜冻等恶劣的寒潮天气。
寒潮过后，气温急剧下降，在24小时之内，，气温急降100C以上，甚至可达200C，继而出现霜冻和结冰。
这在秋季和春季对农作物的危害最大，对正在收割的经济作物和正在生长的农作物可以说是灭顶之灾。
如秋季待收割的大白菜和待采摘的各种水果，若遇到强大的寒潮，很可能造成一无所获；春季时，如果到4月份还出现较强的寒潮，就会使正在生长的冬小麦等夏收受到冻害，使产量大幅度减产。
例如：20世纪50年代，我国北方冬小麦区发生了最严重的冻害，仅小麦作物就减产约30亿千克。
寒潮带来的大风还常常在干燥、土质疏松的地带扬起沙尘，出现天昏地暗的沙尘暴天气。
干热风：每年的4—8月间，我国各地气温迅速回升，若同期降水不足，就会出现高温干燥的风，被称之为“干热风”或“焚风”。
影响我国农业生产的气象灾害分析对我国农业生产影响最大的气象灾害xx年第4期(总第64期) 边疆经济与文化THE BORDER ECONOMY AND CULT URE No 141xxGeneral 1No 164【农民?农村?农业】影响我国农业生产的气象灾害分析孙杭生, 徐芃(南京信息工程大学经济管理学院, 南京210044)摘要:我国是气象灾害的多发区, 气象灾害对我国农业生产影响较大。
气象灾害的类型有:原生气象灾害、次生气象灾害和气象衍生灾害。
影响我国农业生产的干旱、洪涝、低温冷冻、灾害。
关键词:气候变化; 气候变暖; 气象灾害; :P 458 文献标志码:A :2) 203。
它是自然因素和人类活动共同作用的结果。
根据I PCC (, 过去50年发生的气候变化有90%以。
近百年来, 我国年平均气温增加015～018℃, 。
我国地处东亚季风区, 历来就是气象灾害严重多发地区, 气候变暖。
在全国每年自然灾害导致的损失中, 气象灾害占71%, 高居自然灾害首位。
据统计, 我国每年因各种气象灾害造成的农田受灾面积达5000万公顷, 直接经济损失占G DP 总值的3%左右, 占G DP 增加值的10%以上。
一、气象灾害类型分析原生气象灾害通常就叫气象灾害, 是大气因子直接作用于受害体(人类的生命、财产等) 产生的灾害, 例如干旱、洪涝、低温冷冻害、寒潮、冰雹、台风、干热风、雷电、高温热害, 沙尘暴、以及大风、大雾等。
从词语学的意义讲, “次生”就是“再次生成”、“第二次生成”的意思。
次生气象灾害就是再次生成的灾害, 是大气因子作用于非气象因子而间接地对受害体造成的损害, 它与原生气象灾害具有某种共生共存的关系。
例如, 暴雨(气象因子) 作用于山坡(非气象因子) 而引发泥石流所谓“衍生”就是“嬗变生成”、“演变生成”的意思。
气象衍生灾害是由于原生、次生气象灾害的发生而嬗变生成的灾害, 从严格意义上讲, 灾害的属性已经发生异变, 之所以仍然包括在气象灾害中, 是因为气象因子是气象衍生灾害的成因和条件。
《近30年我国主要气象灾害影响特征分析》篇一一、引言随着全球气候变化的加剧，我国近30年来所面临的气象灾害呈现出越来越明显的特点。
气象灾害对国家安全、社会稳定和人民生活产生重要影响，因此对我国主要气象灾害的影响特征进行分析具有重要的现实意义。
本文将从灾害类型、地域分布、时间规律、影响因素及应对策略等方面，对我国近30年的主要气象灾害进行详细分析。
二、气象灾害类型及其特点1. 洪涝灾害近年来，我国洪涝灾害频发，主要集中在长江、黄河、珠江等流域。
洪涝灾害的特点是持续时间长、影响范围广，往往伴随着严重的次生灾害，如山体滑坡、泥石流等。
2. 干旱灾害干旱灾害在我国分布广泛，特别是北方地区。
干旱灾害的特点是持续时间长、影响程度深，容易导致农作物减产、水资源短缺等问题。
3. 台风灾害台风是我国沿海地区的主要气象灾害之一。
台风灾害的特点是破坏力强、影响范围广，往往伴随着强风、暴雨和潮汐等次生灾害。
三、主要气象灾害的影响特征1. 地域分布特征我国主要气象灾害的地域分布特征明显，洪涝灾害主要集中在南方地区，干旱灾害则多发生在北方地区，台风灾害则主要影响沿海地区。
此外，不同地区的气象灾害还具有不同的次生灾害特点。
2. 时间规律特征我国主要气象灾害的时间规律特征表现为季节性和周期性。
例如，洪涝灾害多发生在夏季和秋季，而干旱灾害则多发生在春季和夏季。
此外，一些气象灾害还具有明显的周期性特点，如台风灾害的活跃期和静息期。
四、影响因素及应对策略1. 影响因素我国主要气象灾害的影响因素包括气候变化、地形地貌、人类活动等。
其中，气候变化是导致气象灾害频发的主要原因之一。
此外，地形地貌和人类活动也会对气象灾害的发生和发展产生影响。
2. 应对策略针对我国主要气象灾害的影响特征，应采取以下应对策略：一是加强监测预警系统建设，提高气象灾害的预测和预警能力；二是加强防灾减灾体系建设，提高应对气象灾害的能力；三是加强气候变化应对措施，减缓气候变化对气象灾害的影响；四是加强科普宣传，提高公众的气象灾害防范意识和应对能力。
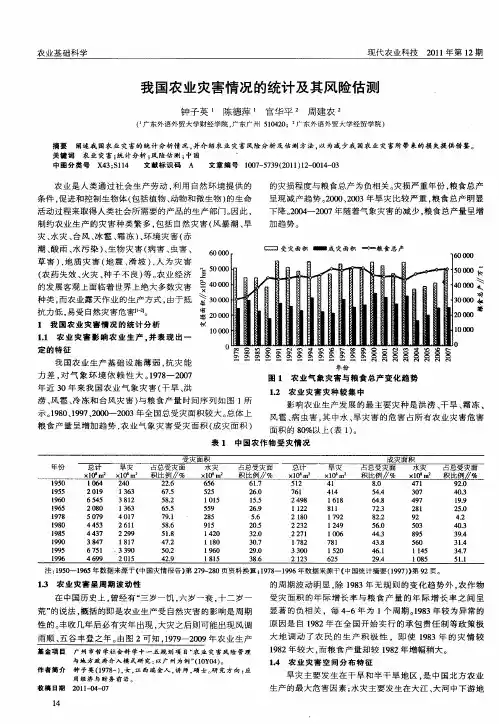
第24卷第1期中国农业气象2003年2月中国近50年旱灾灾情分析Ξ李茂松,李 森,李育慧(中国农业科学院农业气象研究所,北京 100081)摘要:20世纪后50年全国受旱面积和受旱成灾面积呈上升趋势,各年代旱灾成灾率也呈上升趋势;2000年是建国以来旱灾最严重的一年,全国受旱面积和成灾面积分别达4054万hm2和2678万hm2。
黄淮海地区和长江中下游地区受旱面积和成灾面积占全国的60%以上,是中国的干旱重灾区。
总结了有关干旱发展预测的研究,对未来一段时期旱灾的可能发生情况进行了预测,并提出了有关旱灾防御的几点建议。
关键词:中国;旱灾;灾情变化;趋势预测;防御对策 中国是一个干旱灾害频繁发生的国家。
据统计,全国每年旱灾损失占各种自然灾害的15%以上, 1950～2000年所统计的5项气候灾害(干旱、雨涝、台风、冻害、干热风)中,干旱灾害发生频次约占总灾害频次1/3,为各项灾害之首。
由于干旱往往具有发生范围广、持续时间长等特点,对国民经济的影响较大,所以研究中国干旱发生的时空分布特征、变化规律及其对粮食产量、水资源和能源、林牧渔业等经济部门的影响是有意义的[1,2]。
本文结合中国近50年的旱灾统计资料,分析旱灾的分布及变化规律,并对未来旱情的可能发展进行初步分析,以期对干旱的预测、监控、防御和减灾工作提供参考依据。
1 中国旱灾的时空分布规律中国旱灾发生具有明显的时空分布规律。
从全国范围看,春夏季节旱区主要在黄淮海地区和西北地区;夏秋季节旱区转移至长江流域,直至南岭以北地区;秋冬季节则移至华南沿海;冬春季节再由华南扩大到西南地区。
从干旱的地区分布看,华北、西北和东北经常有春旱,有时出现春夏连旱;秦岭、淮河以北春夏连旱较频繁,夏旱次之,个别年份有春、夏、秋连旱,该地区由于降水较少且变率大,干旱发生频率居全国之首,加上该地区人口较多,耕地资源丰富,形成水土资源不平衡,是较突出的受旱区;秦岭、淮河以南,南岭以北多夏旱(伏旱)和秋旱,华南南部干旱主要集中在冬春季和秋季,个别年份有秋、冬、春三季连旱,川西北多春、夏旱,川东多伏旱;北部和西北地区、青藏高原大部地区属常年干旱、半干旱气候,旱灾对这些地区的农业生产也造成严重的影响[3]。
农业气象灾害特征及防灾减灾对策农业气象灾害是指气象因素对农业生产造成的危害，主要包括干旱、水灾、暴雨、冰雹等灾害。
这些灾害对农业生产造成了不同程度的损失，严重影响了农民的生计和国家的粮食安全。
因此，加强农业气象灾害防灾减灾工作，对于维护农业生产稳定和农民利益，具有重要的意义。
一、农业气象灾害特征1.干旱：干旱是农业生产中最为常见的灾害之一，主要表现为缺水、土壤干燥、农作物生长受阻等。
干旱会导致农作物减产、粮食短缺，严重影响农民的生计。
2.暴雨：暴雨是指短时间内降水量大、降水强度大的气象现象。
暴雨容易造成山洪、泥石流等灾害，导致农作物受损、土地受淹等问题。
3.冰雹：冰雹是指直径超过5毫米的结冰降水，会对农作物造成机械伤害，导致农作物减产，影响农民的收益。
4.高温干旱：高温干旱是指高温天气导致土壤水分蒸发加快，使土壤变干燥，严重影响农作物生长发育。
1.加强气象监测预警：建立农业气象监测预警系统，及时掌握气象变化情况，预测和预警可能出现的灾害，做好农民转移、避险等准备工作。
2.提前调整农业生产计划：根据气象预测情况，及时调整农业生产计划，选择适应当地气候特点的农作物品种，采取合理的栽培措施。
3.强化农田水利建设：加强灌溉、排水设施建设，保证农作物的水分供应，防止因干旱或水灾导致农作物减产。
4.推广气象保险：推广农业气象保险，帮助农民规避气象风险，减轻灾害损失，保障农民的生计。
5.积极开展防灾减灾宣传教育：通过开展气象灾害防治知识宣传教育活动，提高农民的气象灾害防范意识和自救互救能力。
6.加强政府和社会组织的支持：政府部门应加大对农业气象灾害防治工作的支持力度，组织专家开展技术指导，提供必要的援助和帮助。
总之，农业气象灾害对农业生产和农民的生计造成了重大影响，需要采取有效的防灾减灾对策。
只有加强气象监测预警、提前调整生产计划、加强农田水利建设、推广气象保险、开展宣传教育等工作，才能有效减轻农业气象灾害带来的损失，确保农业生产的顺利进行。
我国近20年农业气象灾害的受灾年份分析与预测摘要：近年来，农业气象灾害频繁，对阻碍农业发展，本文搜集了我国近20年的旱灾和水灾的受灾面积，通过灰色系统的理论方法，进行灰色关联分析，并剔除重灾和轻灾年份得出相关中灾年份，根据这些中灾年份序列利用灰色系统模型的GM（1,1）模型进行建模，对模型检验合格后进行下一次中灾年份的预测。
关键词：农业气象灾害灰色关联分析 GM（1,1）模型预测引言中国是农业大国，农业是民生之计，那自然对农业气象的关注就显得愈发重要。
农业气象灾害在农业发展中是一个不容忽视的问题，通过对灰色系统的学习与了解，可以发现农业气象灾害系统也是一个信息部分可知，部分未知的灰色系统。
因此通过查找数据，找出近20年来中国气象灾害的受灾面积与农作物播种面积进行分析并建模预测。
正文1、数据来源中国国家统计局网统计年鉴里关于农业的统计数据。
2、灰色关联分析与灰色模型建立通过查找中国统计年鉴得到近20年农业气象灾害受灾情况，对统计数据进行处理，并对数据进行灰色关联分析，建立合适的GM（1,1）灰色系统模型，并对该模型进行检测，是否可以进行模型预测。
2.1、数据处理根据查找到的统计数据，旱灾和水灾在近20年来的受灾面积占总受灾面积的比值为77.62%，可见旱灾和水灾为农业气象灾害里主要的气象灾害，根据旱灾和水灾来进行系统预测是具有一定的科学性的。
而统计中国农业受灾情况时用的指标是受灾面积，但是每年农作物的播种面积是不同的为使得每一年受灾程度具有可比较性，方便对灾害的研究，对数据进行了如下的处理，我们定义，某一种气象灾害当年农作物受灾面积与当年总播种面积的比值为该种气象灾害的受灾率即为：某种气象灾害的受灾率=该种气象灾害当年农作物受灾面积/当年总播种面积由数据可得出表1：表11990年至2010年我国水灾和旱灾受灾情况年份水灾受灾率旱灾受灾率1990 0.0796 0.1225 1991 0.1644 0.1666 1992 0.0632 0.2213 1993 0.1109 0.1428 1994 0.1169 0.2052 1995 0.0850 0.1565 1996 0.1191 0.1322 1997 0.0741 0.2177 1998 0.1432 0.0914 1999 0.0577 0.1928 2000 0.0469 0.2594 2001 0.0388 0.2471 2002 0.0795 0.1431 2003 0.1260 0.1631 2004 0.0476 0.1124 2005 0.0703 0.1031 2006 0.0526 0.1363 2007 0.0682 0.1915 2008 0.0414 0.0777 2009 0.0480 0.1845 20100.10910.08252.2、灰色关联分析——邓氏关联度根据灰色关联分析法，设参考序列的水灾受灾率和旱灾受灾率皆为1，表示受灾面积为农作物播种面积即这是受灾最严重的情况，将表1中各个年份的水灾和旱灾受灾率作为比较数列，进行邓氏关联度的灰色关联分析，在本文中假定旱灾和水灾的受灾致灾程度相同，采取等权处理，利用公式就可计算出各个年份的等权关联度，并按关联度大小进行派讯，关联度越大表明灾情越重，根据关联度就可得出各个年份的受灾情况如表2，邓氏关联度的计算公式和表2如下： 计算公式：0X 表示参考序列，i X 表示比较序列)()()(0k X k X k i i -=∆)()()())(),((0k x a xm a m k x a xm a m k n i nm i m k x k x i kii i iii kii ∆+∆∆+∆=ρξγ∑==nk i i k x k x n X X 100))(),((1),(γγ表21991年至2010年我国气象灾害各年份关联度和排序表年份 水灾关联度 旱灾关联度 平均关联度 排序 1990 0.6715 0.6723 0.6719 16 1991 0.6826 0.6782 0.6804 1 1992 0.6696 0.686 0.6778 6 1993 0.6754 0.675 0.6752 10 1994 0.6762 0.6836 0.6799 2 1995 0.6722 0.6768 0.6745 12 1996 0.6765 0.6735 0.675 11 1997 0.6708 0.6854 0.6781 5 1998 0.6796 0.6684 0.674 14 1999 0.6689 0.6818 0.67535 9 2000 0.6676 0.6917 0.67965 3 2001 0.6667 0.6898 0.67825 4 2002 0.6715 0.6749 0.6732 15 2003 0.6773 0.6776 0.67745 7 2004 0.6677 0.6709 0.6693 20 2005 0.6704 0.6698 0.6701 19 2006 0.6683 0.674 0.67115 17 2007 0.6701 0.6815 0.6758 8 2008 0.667 0.6667 0.66685 21 2009 0.6677 0.6804 0.67405 13 20100.67510.66720.6711518由表2可得出，受灾情况严重程度各个年份依次为1991、1994，,2000,2001,1997,1992,1993,1995,1996,1998,1999,2002,2003,2007,2009, 1990,2006,2010,2005,2004,2008。
假设受灾年份关联度≥0.6778时为重灾年，则可得到1991、1994，,2000,2001,1997,1992为重灾年份，受灾年份关联度≤0.6719时为轻灾年份，则可得到1990,2006,2010,2005,2004,2008为轻灾年份，由于自然灾害存在一定的随机性，所以选取中灾年份对受灾年份进行建模分析预测，则可得到中灾年份为：1993,1995,1996,1998,1999,2002,2003,2007,2009，初步估计，中灾年份的出现大致是,4年为一个周期。
2.3、灰色系统预测——GM （1，1）模型利用GM （1,1）模型对下一次受灾年份的出现进行预测的原理是对原始数据进行累加生成形成新的数据序列，通过新的数据序列的规律性得到的曲线逼近典型曲线，用逼近曲线建模，得到的模型做累减还原，得出预测值。
具体的步骤如下：假定根据灰色关联分析所得出的中灾年份的受灾率的数据序列为灾变序列，灾变序列相应的中灾年份序列为)0(Q，它的1-AGO 序列为)1(Q，则：{}{}{}bk aZ k k q k q k Q k q k q k q Qk q Qmk =+-+====∑=)()(q 1,1GM )1(5.0)(5.0)(Z )()(,)(,)()1()1()1()1()1(1)1()1()1()0(模型为：（设灾变的紧邻均值生成序列其中， 其中，，⎪⎪⎭⎫⎝⎛=Λb a a 为参数序列的最小二乘估计，且 ⎪⎪⎪⎪⎪⎭⎫⎝⎛---=⎪⎪⎪⎪⎪⎭⎫⎝⎛=1)(......1)3(1)2(B )(...)3()2()1()1()1(m Z Z Z m q q q Y ， 因而最小二乘估计参数序列满足Y B B B a TT1)(-Λ= 中灾年份序列)0(Q的GM （1,1,）时间响应式和累减还原式为：⎪⎩⎪⎨⎧-+=++-=+ΛΛΛ-Λ)()1()1())1(()1(q )1()1()1(k q k q k q a be a b q k ak 2.4、检测模型将本次数据代入到公式中：中灾年份日期序列为：)20,18,14,13,10,9,7,6,4())9(),8(),7(),6(),5(),4(),3(),2(),1(()0(==q q q q q q q q q Q其中1-AGO 序列为：)81,63,49,36,26,17,10,4()1(=Q紧邻均值生成序列为：)91,72,56,5.42,31,5.21,5.13,7()1(=Z设b k aZk q =+)()()1(，由⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎭⎫⎝⎛--------=⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎭⎫ ⎝⎛=19117215615.4213115.2115.1317,2018141310976B Y 可以算出⎪⎪⎭⎫ ⎝⎛-==⎪⎪⎭⎫ ⎝⎛=-Λ9903.41706.0)(1Y B B B b a a TT 由中灾年份序列GM(1,1)的序列响应式为：2515.292515.33)1(q 1706.0)1(-=+Λk e k可得到)0(Q的模拟序列为：))9(),8(),7(),6(),5(),4(),3(),2(),1(()0(ΛΛΛΛΛΛΛΛΛΛ=q q q q q q q q q Q=（4.0000,6.1856,7.3365,8.7015,10.3205,12.2407,14.5181,17.2194,20.4232）%8126.3%116..29,8,7,6,5,4,3,2,1;)()()4232.0,7806.0,5181.0,7593.0,3205.0,2985.0,3365.0,1856.0,0()(9,8,7,6,5,4,3,2,1);()()(9k =∆=∆==∆-----==-=Λ—平均相对误差：可得相对误差由得到残差序列k k q k k k k q k q k θθθ最接近0.05，精度等级为二级，发展系数小于0.3，所以该模型可以进行预测。
3、模型预测利用预测模型进行下一步的预测值为：24.2230=-ΛΛ)9()10(q q 4.2230预测结果表明，2014~2015年将是我国农业气象灾害的中灾年份，这是根据近20年的农业气象灾害统计数据所得出的。
4、总结通过本次灰色系统模型对农业气象灾害的预测，首先对灰色预测模型有了更深层次的了解，其次，通过本次分析与预测，了解到农业气象灾害对我国农业发展影响很大，而农业气象灾害的中灾年份又具有一定周期性，因而我们应当利用科学技术积极了解到这种规律的存在，能够对未来作出预测的同时也及时的做好农业的减灾防灾工作，为农业发展作出贡献。
参考文献：[1]中华人民共和国国家统计局.农业统计年报[M].北京：中华人民共和国国家统计局 [2]陈劭锋,杨红.我国各地区农业气象灾害演变趋势分析[J].生态农业研究，2000(6) [3]张星.农业气象灾害灰色评估与预测:农业气象与生态环境年会，2006。
