全国高考数学复习微专题：直线与圆锥曲线的位置关系

高考数学总复习考点知识与题型专题讲解直线与圆锥曲线的位置关系【高考展望】1.直线和圆锥曲线的位置关系判定是基础内容，是高考必考内容；2.直线与圆锥曲线相交有两个交点时的弦长公式是考试的重点内容；3.掌握圆锥曲线有关中点弦问题的求解方法；4.关于直线与圆锥曲线的综合问题历来是考试的重点和难点，需要强化练习，形成必要的技巧和技能。

【知识升华】知识点一：直线与圆锥曲线的位置关系：直线与圆锥曲线的位置关系有相交、相切、相离三种位置关系。

1．直线Ax+By+C ＝0和椭圆+=22221x y a b的位置关系：将直线的方程与椭圆的方程联立成方程组，消元转化为关于x 或y 的一元二次方程，其判别式为Δ.①Δ＞0⇔直线和椭圆相交⇔直线和椭圆有两个交点(或两个公共点）； ②Δ＝0⇔直线和椭圆相切⇔直线和椭圆有一个切点(或一个公共点)； ③Δ＜0⇔直线和椭圆相离⇔直线和椭圆无公共点．2．直线Ax+By+C ＝0和双曲线-=22221x y a b的位置关系：将直线的方程与双曲线的方程联立成方程组，消元转化为关于x 或y 的方程。

（1）若方程为一元一次方程，则直线和双曲线的的渐近线平行，直线和双曲线有一个交点，但不相切不是切点；（2）若为一元二次方程，则①若Δ＞0，则直线和双曲线相交，有两个交点(或两个公共点)； ②若Δ＝0，则直线和双曲线相切，有一个切点； ③若Δ＜0，则直线和双曲线相离，无公共点.3．直线Ax+By+C ＝0和抛物线y 2＝2px(p ＞0)的位置关系：将直线的方程与抛物线的方程联立成方程组，消元转化为关于x 或y 方程。

（1）若方程为一元一次方程，则直线和抛物线的对称轴平行，直线和抛物线有一个交点，但不相切不是切点；（2）若为一元二次方程，则①若Δ＞0，则直线和抛物线相交，有两个交点(或两个公共点)； ②若Δ＝0，则直线和抛物线相切，有一个切点； ③若Δ＜0，则直线和抛物线相离，无公共点. 知识点二：圆锥曲线的弦长1.直线被圆锥曲线截得的线段称为圆锥曲线的弦。

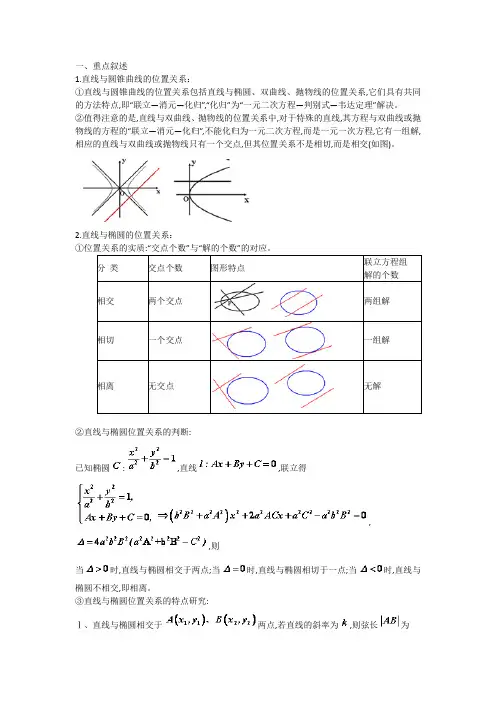
一、重点叙述1.直线与圆锥曲线的位置关系：①直线与圆锥曲线的位置关系包括直线与椭圆、双曲线、抛物线的位置关系,它们具有共同的方法特点,即“联立—消元—化归”,“化归”为“一元二次方程—判别式—韦达定理”解决。

②值得注意的是,直线与双曲线、抛物线的位置关系中,对于特殊的直线,其方程与双曲线或抛物线的方程的“联立—消元—化归”,不能化归为一元二次方程,而是一元一次方程,它有一组解,相应的直线与双曲线或抛物线只有一个交点,但其位置关系不是相切,而是相交(如图)。

2.直线与椭圆的位置关系：①位置关系的实质:“交点个数”与“解的个数”的对应。

两组解一组解无解②直线与椭圆位置关系的判断:已知椭圆:,直线,联立得,,则当时,直线与椭圆相交于两点;当时,直线与椭圆相切于一点;当时,直线与椭圆不相交,即相离。

③直线与椭圆位置关系的特点研究:Ⅰ、直线与椭圆相交于两点,若直线的斜率为,则弦长为。

Ⅱ、直线与椭圆相切于点,若椭圆方程是,则过切点的椭圆切线方程为。

此外,求椭圆切线方程的一般方法是:“联立—消元—”。

Ⅲ、直线与椭圆相离,则可求直线与椭圆距离最近与最远的点,或求直线与椭圆最短与最长的距离。

设椭圆:,直线。

方法1:如图,是椭圆上任意一点,求点到直线的距离的最值,这个最值就是直线与椭圆的最短与最远的距离。

即求的最值。

方法2:如图,平行于直线的动直线:与椭圆相切时,平行线与之间的最短或最远距离就是直线与椭圆最短或最远的距离。

3.直线与双曲线的位置关系①位置关系的实质:“交点个数”与“解的个数”的对应。

图形特点联立方程组解的个数两组解一组解一组解无解②直线与双曲线位置关系的判断:已知双曲线:,直线联立得,1o 若,则方程组有唯一一组解或无解,直线与双曲线相交于一点或不相交; 2o 若,则,那么当时,直线与双曲线相交于两点;当时,直线与双曲线相切于一点;当时,直线与双曲线不相交,即相离。

③直线与双曲线位置关系的特点研究:Ⅰ、直线与双曲线相交于两点,若直线的斜率为k,则弦长为。

考点41直线与圆锥曲线的位置关系（1）了解圆锥曲线的简单应用. （2）理解数形结合的思想.一、直线与圆锥曲线的位置关系 1．曲线的交点在平面直角坐标系xOy 中，给定两条曲线12,C C ，已知它们的方程为12:(,)0,:(,)0C f x y C g x y ==，求曲线12,C C 的交点坐标，即求方程组(,)0(,)0f x y g x y =⎧⎨=⎩的实数解.方程组有几组实数解，这两条曲线就有几个交点.若方程组无实数解，则这两条曲线没有交点.2．直线与圆锥曲线的交点个数的判定设直线:0l Ax By C ++=，圆锥曲线:(,)0C f x y =，把二者方程联立得到方程组，消去()y x 得到一个关于()x y 的方程220(0)ax bx c ay by c ++=++=. （1）当0a ≠时，0∆>⇔方程有两个不同的实数解，即直线与圆锥曲线有两个交点；0∆=⇔方程有两个相同的实数解，即直线与圆锥曲线有一个交点； 0∆<⇔方程无实数解，即直线与圆锥曲线无交点.（2）当a =0时，方程为一次方程，若b ≠0，方程有一个解，此时直线与圆锥曲线有一个交点；若b =0,c ≠0，方程无解，此时直线与圆锥曲线没有交点. 3．直线与圆锥曲线的位置关系直线与圆锥曲线相交时，直线与椭圆有两个公共点，与双曲线、抛物线有一个或两个公共点.（1）直线与椭圆有两个交点⇔相交；直线与椭圆有一个交点⇔相切；直线与椭圆没有交点⇔相离.（2）直线与双曲线有两个交点⇔相交.当直线与双曲线只有一个公共点时，除了直线与双曲线相切外，还有可能是直线与双曲线相交，此时直线与双曲线的渐近线平行. 直线与双曲线没有交点⇔相离. （3）直线与抛物线有两个交点⇔相交.当直线与抛物线只有一个公共点时，除了直线与抛物线相切外，还有可能是直线与抛物线相交，此时直线与抛物线的对称轴平行或重合. 直线与抛物线没有交点⇔相离. 二、圆锥曲线中弦的相关问题 1．弦长的求解（1）当弦的两端点坐标易求时，可直接利用两点间的距离公式求解；（2）当直线的斜率存在时，斜率为k 的直线l 与圆锥曲线C 相交于1122(,),(,)A x y B x y 两个不同的点，则弦长121||A y k x-+-=. （3）当弦过焦点时，可结合焦半径公式求解弦长. 2．中点弦问题（1）AB 为椭圆22221(0)x y a b a b+=>>的弦，1122(,),(,)A x y B x y ，弦中点M (x 0，y 0)，则AB 所在直线的斜率为2020b x k a y =-，弦AB 的斜率与弦中点M 和椭圆中心O 的连线的斜率之积为定值22b a-.（2）AB 为双曲线22221(0,0)x y a b a b-=>>的弦，1122(,),(,)A x y B x y ，弦中点M (x 0，y 0)，则AB 所在直线的斜率为2020b x k a y =，弦AB 的斜率与弦中点M 和双曲线中心O 的连线的斜率之积为定值22b a.（3）在抛物线22(0)y px p =>中，以M (x 0，y 0)为中点的弦所在直线的斜率0p k y =.考向一直线与圆锥曲线位置关系的判断及应用1．判断直线与圆锥曲线的交点个数时，可直接求解相应方程组得到交点坐标，也可利用消元后的一元二次方程根的判别式来确定，需注意利用判别式的前提是二次项系数不为0. 2．依据直线与圆锥曲线的交点个数求参数时,联立方程并消元，得到一元方程,此时注意观察方程的二次项系数是否为0,若为0,则方程为一次方程；若不为0,则将方程解的个数转化为判别式与0的大小关系求解.典例1已知椭圆，直线:y ＝x ＋m ．(1)若与椭圆有一个公共点，求的值；(2)若与椭圆相交于P ,Q 两点，且|PQ |等于椭圆的短轴长，求m 的值．则|PQ12|x x -=解得：.典例2已知抛物线2:2(0)C y px p =>的焦点为(1,0)F ，抛物线2:2(0)E x py p =>的焦点为M ．（1）若过点M 的直线l 与抛物线C 有且只有一个交点，求直线l 的方程； （2）若直线MF 与抛物线C 交于A ，B 两点，求OAB △的面积．【解析】（1）由题意知抛物线2:2(0)C y px p =>的焦点为(1,0)F ，抛物线2:2(0)E x py p =>的焦点为M ，所以2p =，(0,1)M ，则抛物线C 的方程为24y x =，抛物线E 的方程为24x y =.若直线l 的斜率不存在，则易知直线l 的方程为0x =；若直线l 的斜率存在，设为k ，则直线l 的方程为1y k x =+，联立24y x =，可得22(24)10k x k x +-+=，当0k =时，14x =，满足题意，此时直线l 的方程为1y =；当0k ≠时，22(24)40k k ∆=--=，解得1k =，此时直线l 的方程为1y x =+.综上，直线l 的方程为0x =，或1y =，或1y x =+.1．已知直线y=kx-1与双曲线x2-y2=4.(1)若直线与双曲线没有公共点,求实数k的取值范围;(2)若直线与双曲线有两个公共点,求实数k的取值范围;(3)若直线与双曲线只有一个公共点,求实数k的取值范围.考向二直线与圆锥曲线的弦长问题直线与圆锥曲线的弦长问题有三种解法：（1）过圆锥曲线的焦点的弦长问题，利用圆锥曲线的定义可优化解题．（2）将直线的方程与圆锥曲线的方程联立，求出两交点的坐标，再运用两点间距离公式求弦长．（3）它体现了解析几何中的设而不求的思想，其实质是利用两点之间的距离公式以及一元二次方程根与系数的关系.典例3已知抛物线：（），焦点为，直线交抛物线于，两点，为的中点，且．（1）求抛物线的方程； （2）若，求x AB的最小值．（2）设直线的方程为，代入抛物线方程，得，∵，即22111214y y y y +=-， ∴，即，∴，∴，，，()2222121101212121244x x y y x y y y y m ++⎡⎤===+-=+⎣⎦，∴20x AB =令，，则04x AB ==≥，当且仅当1t =时等号成立． 故0x AB.典例4已知椭圆的离心率为12,过右焦点且垂直于轴的直线与椭圆相交于两点,且.(1)求椭圆的方程;(2)设直线经过点且斜率为与椭圆相交于两点,与以椭圆的右顶点为圆心的圆相交于两点(自下至上排列),为坐标原点，95OA OB ⋅=- ,且,求直线和圆的方程.【解析】(1)设,则由题意得,223b a⋅=,解得,∴椭圆的方程为22143x y +=.∴2122934k y y k =-+.∴==2212534k k+-+∵,∴221259345k k +-=-+,解得.由题意可得,等价于.设圆的半径为,21221212,34k AB x PQ k +=-==+将代入，解得2331100r =. 故所求直线的方程为,即与;圆的方程为()223312100x y -+=.2．已知椭圆22221(0)x y a b a b+=>>与双曲线x 2-y 2=1有相同的焦点,椭圆的离心率为e 1,双曲线的离心率为e 2,且满足e 1e 2=1.(1)求椭圆的标准方程;(2)若直线l 恒过点(0,1),且直线l 与椭圆交于A 、B 两点,求|AB|的最大值,并求此时直线l 的方程.考向三圆锥曲线中的定点、定值问题定点、定值问题多以直线与圆锥曲线为背景，常与函数与方程、向量等知识交汇，形成了过定点、定值等问题的证明.解决此类问题的关键是引进参变量表示所求问题，根据等式的恒成立、数式变换等寻找不受参数影响的量.可以先研究一下特殊情况，找出定点或定值，再视具体情况进行研究.同时，也要掌握巧妙利用特殊值解决相关的定点、定值问题，如将过焦点的弦特殊化，变成垂直于对称轴的弦来研究等.典例5在直角坐标系xOy 中，已知一动圆经过点(2,0)且在y 轴上截得的弦长为4，设动圆圆心的轨迹为曲线C ． （1）求曲线C 的方程；（2）过点(1,0)作互相垂直的两条直线1l ，2l ，1l 与曲线C 交于A ，B 两点，2l 与曲线C 交于E ，F 两点，线段AB ，EF 的中点分别为M ，N ，求证：直线MN 过定点P ，并求出定点P 的坐标．【解析】（1）设圆心(,)C x y ，依题意有2224(2)x x y +=-+，即得24y x =， ∴曲线C 的方程为24y x =．2242(24)416160k k k ∆=+-=+>，同理得2(12,2)N k k +-．当1k =或1k =-时，直线MN 的方程为3x =； 当1k ≠且1k ≠-时，直线∴直线MN 的方程为，即2(1)(3)0k y x k -+-=， ∴直线MN 过定点综上所述，直线MN 过定点P ，其坐标为(3,0)．典例6已知椭圆E : 22221(0)x y a b a b+=>>与y 轴的正半轴相交于点M ,点F 1,F 2为椭圆的焦点,且12△MF F 是边长为2的等边三角形,若直线l :y =kx+2与椭圆E 交于不同的两点A ,B .(1)直线MA ,MB 的斜率之积是否为定值?若是,请求出该定值,若不是,请说明理由; (2)求△ABM 的面积的最大值.【解析】(1)因为12△MF F 是边长为2的等边三角形,所以2c =2,b =c ,a =2,所以a =2,b =,所以椭圆E :+=1,点M (0,).将直线l :y =kx+2代入椭圆E 的方程,整理得(3+4k 2)x 2+16kx+36=0. (*)设A (x 1,y 1),B (x 2,y 2),则由(*)式可得Δ=(16k )2-4(3+4k 2)³36=48(4k 2-9)>0,所以k ∈(-∞,-)∪(,+∞),x 1+x 2=x 1x 2=23634k +.所以直线MA ,MB 的斜率之积是定值14. (2)记直线l :y =kx+2与y 轴的交点为N (0,2)，则S △ABM =|S △ANM -S △BNM |=|MN|²|x 2-x 1|=2612342k==≤+,当且仅当4k2-9=12,即k∈(-∞,-)∪(,+∞)时等号成立,所以△ABM3．已知双曲线C的中心在坐标原点，焦点在x 轴上，离心率，虚轴长为2.（1）求双曲线C的标准方程；（2）若直线:l y kx m=+与双曲线C相交于,A B两点（,A B均异于左、右顶点），且以AB 为直径的圆过双曲线C的左顶点D，求证：直线l过定点，并求出定点的坐标.4．已知椭圆C:22221(0)x ya ba b+=>>的左顶点A和上顶点B(0,1)的连线的斜率为,左、右焦点分别为F1、F2,过点A的直线l与椭圆C交于点M,与y轴交于点N,点P在椭圆上,且=λ,=μ(O为坐标原点).(1)求椭圆C的标准方程;(2)若,求12△MF F的面积;(3)证明:λμ是定值,并求出该定值.1．若直线mx+ny =4和☉O :x 2+y 2=4没有交点,则过点(m ,n )的直线与椭圆+=1的交点有 A ．至多1个 B ．2个 C ．1个D ．0个2．已知直线y =kx -k (k 为实数)及抛物线y 2=2px (p >0),则 A ．直线与抛物线有一个公共点 B ．直线与抛物线有两个公共点 C ．直线与抛物线有一个或两个公共点D ．直线与抛物线没有公共点3．若直线30kx y -+=与椭圆221164x y +=有两个公共点,则实数k 的取值范围是A ．kB ．k k =C ．k k <D ．k k ≠4．过双曲线22221(0,0)x y a b a b -=>>的右顶点A 作倾斜角为135°的直线,该直线与双曲线的两条渐近线的交点分别为B ,C ,若2AB BC =,则双曲线的渐近线方程为A ．(+1)x+y =0B ．(+1)y-x =0C ．(+1)x ±y =0D ．(+1)y ±x =05．已知O 是坐标原点，F 是椭圆+=1的一个焦点，过F 且与x 轴垂直的直线与椭圆交于M ,N 两点，则cos ∠MON 的值为A ．513B ．513-C D ． 6．如图,过抛物线22(0)y px p =>的焦点F 的直线l 交抛物线于点A 、B ,交其准线于点C ,若|BC |=2|BF |,且|AF |=3,则此抛物线的方程为A ．29y x =B ．26y x =C ．23y x =D ．y 2=x7．已知椭圆C :+=1,过点M (1,0)的直线l 与椭圆C 交于点A ,B ,若=2,则直线l 的斜率为A ．114±B ．114C ．D 8．若直线y =kx -1与抛物线y 2=4x 有且只有一个公共点,则k 的值为_________.9．过点M (1,1)作斜率为-的直线与椭圆C :22221(0)x y a b a b+=>>相交于A ,B 两点,若M 是线段AB 的中点,则椭圆C 的离心率等于_________.10．过抛物线C :y 2=x 上一点A (1,1)作两条互相垂直的直线分别交抛物线于P ,Q (异于点A )两点,则直线PQ 恒过定点_________.11．已知椭圆C :22221(0)x y a b a b+=>>的离心率为,过右焦点F 且斜率为的直线与椭圆C 相交于A,B 两点,若,则_________.12（0a >，0b >）上，且双曲线的一条渐近线（1）求双曲线C 的方程；（2）若过点(0,1)且斜率为k 的直线l 与双曲线C 有两个不同的交点，求实数k 的取值范围； （3）设（2）中直线l 与双曲线C 交于A B 、两个不同的点，若以线段AB 为直径的圆经过坐标原点，求实数k 的值．13．如图,F 1,F 2分别为椭圆C :22221(0)x y a b a b+=>>的左、右焦点,A ,B 为两个顶点.已知顶点B (0,)到F 1,F 2两点的距离之和为4.(1)求椭圆C 的方程;(2)证明:椭圆C 上任意一点M (x 0,y 0)到右焦点F 2的距离的最小值为1;(3)作AB 的平行线交椭圆C 于P ,Q 两点,求弦长|PQ|的最大值,并求|PQ|取最大值时1△F PQ 的面积.14．已知抛物线21:2(0)C y px p =>的焦点F 焦点及左、右顶点均在圆22:1O x y +=上． （1）求抛物线1C 和椭圆2C 的标准方程；（2）过点F 的直线交抛物线1C 于,A B 不同的两点，交y 轴于点N ，已知1NA AF λ=，2NB BF λ=，求证：12λλ+为定值．15直线:0l x y -=与以原点为圆心，椭圆C 的短半轴长为半径的圆相切．（1）求椭圆C 的方程；（2）设M 是椭圆的上顶点，过点M 分别作直线MA 、MB 交椭圆于A 、B 两点，设两直线的斜率分别为k 1、k 2，且124k k +=，证明：直线AB 过定点1(,1)2--．1．（2017北京理科）已知抛物线C ：22y px =过点P (1，1)．过点(0，12)作直线l 与抛物线C 交于不同的两点M ，N ，过点M 作x 轴的垂线分别与直线OP ，ON 交于点A ，B ，其中O 为原点．（1）求抛物线C 的方程，并求其焦点坐标和准线方程； （2）求证：A 为线段BM 的中点．2．（2017新课标全国III 理科）已知抛物线C ：y 2=2x ，过点（2，0）的直线l 交C 于A ，B两点，圆M 是以线段AB 为直径的圆． （1）证明：坐标原点O 在圆M 上；（2）设圆M 过点(4,2)P -，求直线l 与圆M 的方程．3．（2017天津理科）设椭圆22221(0)x y a b a b+=>>的左焦点为F ，右顶点为A ，离心率为12．已知A 是抛物线22(0)y px p =>的焦点，F 到抛物线的准线l 的距离为12． （1）求椭圆的方程和抛物线的方程；（2）设l 上两点P ，Q 关于x 轴对称，直线AP 与椭圆相交于点B （B 异于点A ），直线BQ 与x 轴相交于点D ．若APD △的面积为2AP 的方程．4．（2017新课标全国I 理科）已知椭圆C ：22221()0x y a ba b +=>>，四点P 1（1,1），P 2（0,1），P 3（–1），P 4（1C 上． （1）求C 的方程；（2）设直线l 不经过P 2点且与C 相交于A ，B 两点．若直线P 2A 与直线P 2B 的斜率的和为–1，证明：l 过定点．5．（2017山东理科）在平面直角坐标系xOy 中，椭圆E ：22221x y a b+=()0a b >>，焦距为2.（1）求椭圆E 的方程；（2）如图，动直线l ：1y k x =交椭圆E 于,A B 两点，C 是椭圆E 上一点，直线OC 的斜率为2k ，且12k k =M 是线段OC 延长线上一点，且:2:3MC AB =，M 的半径为MC ，,OS OT 是M 的两条切线，切点分别为,S T .求SOT ∠的最大值，并求取得最大值时直线l 的斜率.6．（2016上海理科）双曲线2221(0)y x b b-=>的左、右焦点分别为F 1、F 2，直线l 过2F 且与双曲线交于A B 、两点． （1）若l 的倾斜角为2π，1F AB △是等边三角形，求双曲线的渐近线方程；（2）设b =l 的斜率存在，且11()0F A F B AB +⋅=，求l 的斜率．1．【解析】(1)由2214y kx x y =-⎧⎨-=⎩,得(1-k 2)x 2+2kx-5=0 (*). 若直线与双曲线没有公共点,则(*)式无解.所以()2221042010k k k ∆⎧-≠⎪⎨=+-<⎪⎩,解得k <-或k >, 于是实数k 的取值范围为(-∞,2-)∪(2,+∞).(3)若直线与双曲线只有一个公共点,则(*)式只有一解或有两个相等的实数根. 当1-k 2=0,即k =±1时,(*)式只有一解;当1-k 2≠0时,应满足Δ=4k 2+20(1-k 2)=0,解得k=±2. 于是实数k2．【解析】(1)双曲线x 2-y 2=1的焦点为(-,0),(,0),离心率e 2=,故椭圆22221(0)x y a b a b+=>>中c 2=a 2-b 2=2,e 1=,解得a 2=4,b 2=2,故椭圆的标准方程为22142x y +=.(2)当直线l 的斜率不存在时,直线l 的方程为x =0,这时|AB|=2.当直线l 的斜率存在时,设直线l 的方程为y =kx+1,A (x 1,y 1),B (x 2,y 2),由221142y kx x y =+⎧⎪⎨+=⎪⎩得(1+2k 2)x 2+4kx-2=0,故Δ=16k 2+8(1+2k 2)>0 (*),x 1+x 2=-,x 1x 2=,当k =0时,|AB|=2.当k ≠0时,|AB|=3,当且仅当4k 2=21k ,即k 4=14,k=±2时等号成立.即|AB|max =3,这时l :y=±2x+1. 【名师点睛】解决本题的关键有以下几点:(1)熟练掌握双曲线和椭圆中的基础知识;(2)注意讨论特殊情况,本题中讨论了直线斜率不存在的情况,以及斜率为0的情况;(3)正确利用题目给定的条件得到|AB|的函数关系式;(4)灵活运用基本不等式的知识求所得函数的最值.3．【解析】（1）设双曲线的标准方程为22221(0,0)x y a b a b -=>>，由已知得22,2c b a ==又222a b c +=，解得2,1a b ==，所以双曲线的标准方程为2214x y -=. （2）设1122(,),(,)A x y B x y ，由2214y kx m x y =+⎧⎪⎨-=⎪⎩得222(14)84(1)0k x mkx m ---+=，则222212221226416(14)(1)08144(1)14m k k m mk x x k m x x k ∆⎧⎪=+-+>⎪⎪+=⎨-⎪⎪-+=⎪-⎩，2212121212()()()y y kx m kx m k x x mk x x m =++=+++=222414m k k --，以AB 为直径的圆过双曲线C 的左顶点(2,0)D -，1AD BD k k ∴⋅=-，即222121212122221244(1)161,2()40,4022141414y y m k m mky y x x x x x x k k k --+⋅=-∴++++=∴+++=++---，22316200m mk k ∴-+=，解得2m k =或103km =. 当2m k =时，l 的方程为(2)y k x =+，直线过定点(2,0)-，与已知矛盾； 当103k m =时，l 的方程为10()3y k x =+，直线过定点10(,0)3-，经检验符合已知条件，所以直线l 过定点，定点坐标为10(,0)3-.(3)由题意可知,直线l 的斜率一定存在,设为k ,则直线l 的方程为y =k (x+2),则N (0,2k ).设M (x 1,y 1),由()22142x y y k x ⎧+=⎪⎨⎪=+⎩可得(4k 2+1)x 2+16k 2x+16k 2-4=0,则21221216241164241k x k k x k ⎧-+=-⎪⎪+⎨-⎪-=⎪+⎩,故x 1=,代入直线l 的方程得y 1=k (x 1+2)=,则||=又||=2,所以||²||=.由题意可得直线OP 的斜率也是k ,则直线OP 的方程为y =kx ,由2214x y y kx⎧+=⎪⎨⎪=⎩可得(4k 2+1)x 2-4=0,解得22414P x k =+,222414Pk y k =+,则||2=()224141k k ++.又²=||²||=λμ,所以λμ=2·||AM ANOP =2,是定值.1．【答案】B【解析】由直线mx+ny =4和☉O :x 2+y 2=4没有交点,2>,即m 2+n 2<4,故点(m ,n )在椭圆+=1的内部,所以过点(m ,n )的直线与椭圆+=1的交点有2个.2．【答案】C【解析】因为直线y =kx -k 恒过点(1,0),点(1,0)在抛物线y 2=2px 的内部,所以当k =0时,直线与抛物线有一个公共点,当k ≠0时,直线与抛物线有两个公共点.3．【答案】C【解析】由题意知直线过点A (a ,0),且斜率k =tan 135°=-1,则直线的方程为x+y-a =0.将该直线方程分别与两渐近线方程联立,解得B (,),C (,-),则有=(,2222a b a b--),=(aba b-+,).因为,则222ab b a b a b-=+-,化简得+1,则双曲线的渐近线方程为(+1)x ±y =0.故选C.5．【答案】B【解析】由题意,a 2=4,b 2=3,故c ===1.不妨设M (1,y 0),N (1,-y 0),所以+=1,解得y 0=±32,所以|MN |=3,|OM |=|ON.由余弦定理知cos ∠MON =2223+-=513-,故选B. 6．【答案】C程为y =k (x -2p ).联立方程222y pxp y k x ⎧=⎪⎨⎛⎫=- ⎪⎪⎝⎭⎩,消去y 得k 2x 2-p (k 2+2)x +=0,则x 1+x 2=,x 1²x 2=.又由抛物线的定义知|AF |=x 1+2p ,|BF |=x 2+2p,则可得+=,于是有+=,解得2p =3,所以此抛物线的方程是23y x =,选C.【解析】由题意可得,直线l 的斜率存在且不为0,不妨设直线l :y =k (x-1),则由2228y kx kx y =-⎧⎨+=⎩消去y 化简 得,(1+2k 2)x 2-4k 2x +2k 2-8=0.设A (x 1,y 1),B (x 2,y 2),则由根与系数的关系可得x 1+x 2=22412k k +,x 1x 2=222812k k-+.因为=2,所以x 1+2x 2=3,所以x 2=223212k k++,x 1=,所以x 1x 2=²,化简得k 2=,解得k =±,故选C.8．【答案】-1或0【解析】当k =0时,数形结合知,直线与抛物线有一个公共点;当k ≠0时,将直线方程与抛物线方程联立得214y kx y x=-⎧⎨=⎩,得y 2-y -=0,因而Δ=+=0,即k =-1. 从而k =-1或0.9．【答案】2=2,所以e =2. 10．【答案】(2,-1)【解析】由题意可得,这两条直线的斜率均存在,且不为0,设AP :y-1=k (x-1),与抛物线C :y 2=x 联立,消去x ,得ky 2-y+1-k =0,由根与系数的关系可得,1P ky k-= ,即P (()2,),同理可得Q ((k+1)2, -k-1),所以直线PQ 的斜率k PQ =212k k k--,所以直线PQ :(1-k 2-2k )y =kx+k 2-1.通过对比可知,x =2,y =-1满足条件,即直线PQ 恒过定点(2,-1).11．【答案】1【解析】设设直线的方程为将其代入①式,可得212222,22t y y s s --=++，所以()22222232,2t y s y ⎧--=⎪⎪+⎨⎪-=⎪⎩故答案为1.12．【解析】（1）由题意知，22121a b b a ⎧-=⎪⎪⎨⎪=⎪⎩，解得22131a b ⎧=⎪⎨⎪=⎩．因此，所求双曲线C 的方程是，即2231x y -=．（3）设直线l 与双曲线C 的交点为1122(,)(,)A x y B x y 、，由（2）可得1221222323k x x k x x k ⎧+=⎪⎪-⎨-⎪=⎪-⎩，又以线段AB 为直径的圆经过坐标原点，因此，(OA OB O ⊥为坐标原点），于是，0O A O B ⋅=，即12120x x y y +=，即21212(1)()10k x x k xx ++++=，即22222(1)21033k k k k -+++=--，解得1k =±．又1k =±满足230k -≠，且0∆>，所以，所求实数k 的值为1±．13．【解析】(1)由已知得a =2,b =,故椭圆C 的方程为+=1.(2)M (x 0,y 0),F 2(1,0)且x 0∈[-2,2],则|MF 2|==|x 0-2|∈[1,3],当且仅当M (x 0,y 0)为右顶点时,|MF 2|min =1.(3)设P (x 1,y 1),Q (x 2,y 2),由k AB可设直线PQ :y,代入+=1,得3x 2+2mx+2m 2-6=0,由根与系数的关系知,x 1+x 2=3-,x 1x 2=2263m -.则|PQ|====.当且仅当m =0时,|PQ|max =,此时点F 1(-1,0)到直线PQ :x-2y =0的距离h=,故|PQ|²h=222:1O x y +=上，可解得1b c ==，则a =，故椭圆2C 的标准方程为2212y x +=. （2）设直线AB 的方程为(1)(0)y k x k =-≠，11(,)A x y ，22(,)B x y ，则(0,)N k -．由24(1)y x y k x ⎧=⎨=-⎩消去y ，得2222(24)0k x k x k -++=， 则216160k ∆=+>，21212224,1k x x x x k ++==. 由1NA AF λ= ，2NB BF λ=，得111(1)x x λ-=，222(1)x x λ-=，整理得121212,11x x x x λλ==--，故12121212121212()21111()x x x x x x x x x x x x λλ+-+=+==----++. 故12λλ+为定值1-.15．【解析】（1ce a==，又直线:0l x y -=与以原点为圆心，椭圆C的短半轴长为半径的圆相切，则b =，即1b =，由2221c a a b c b ⎧=⎪⎪⎪=+⎨⎪=⎪⎪⎩，解得221a b c ⎧=⎨==⎩.故椭圆C 的方程为2212x y +=．②若直线AB 的斜率存在，设直线AB 的方程为y kx m =+，易知1m ≠±．设1122(,),(,)A x y B x y ，由2222y kx m x y =+⎧⎨+=⎩得222(12)4220k x kmx m +++-=， 则122412kmx x k +=-+，21222212m x x k-=+.（1） ∵124k k +=，∴1212114y y x x --+=，即1212114kx m kx m x x +-+-+=，即12122(1)4x xk m x x ++-=.把（1）代入得21km k m -=+，则2(1)k m =+，故12km =-. 则直线AB 的方程为12k y kx =+-，即1()12y k x =+-， 故直线AB 过定点1(,1)2--．由212y kx y x⎧=+⎪⎨⎪=⎩，得224(44)10k x k x +-+=．则1221k x x k -+=，12214x x k =． 因为点P 的坐标为（1，1），所以直线OP 的方程为y x =，点A 的坐标为11(,)x y ． 直线ON 的方程为22y y x x =，点B 的坐标为2112(,)y x x x ．因为122112211221*********()()22222kx x kx x x x y x y x y x x x y x x x x +++-+-+-== 122121(22)()2k x x x x x -++=22211(22)420k k k k x --⨯+==， 所以211122y x y x x +=，故A 为线段BM 的中点． 【名师点睛】本题考查了直线与抛物线的位置关系，考查了转化与化归能力，当看到题目中出现直线与圆锥曲线时，不需要特殊技巧，只要联立直线与圆锥曲线的方程，借助根与系数的关系，找准题设条件中突显的或隐含的等量关系，把这种关系“翻译”出来即可，有时不一定要把结果及时求出来，可能需要整体代换到后面的计算中去，从而减少计算量．2．【解析】（1）设1122(,),(,)A x y B x y ，:2l x my =+．由222x my y x=+⎧⎨=⎩可得2240y my --=，则124y y =-． 又221212,22y y x x ==，故21212()44y y x x ==．因此OA 的斜率与OB 的斜率之积为1212414y y x x -⋅==-，所以OA OB ⊥． 故坐标原点O 在圆M 上．由（1）可得12124,4y y x x =-=． 所以2210m m --=，解得1m =或12m =-． 当1m =时，直线l 的方程为20x y --=，圆心M 的坐标为(3,1)，圆M圆M 的方程为22(3)(1)10x y -+-=． 当12m =-时，直线l 的方程为240x y +-=，圆心M 的坐标为91(,)42-，圆M 的半径为4，圆M 的方程为229185()()4216x y -++=．【名师点睛】直线与抛物线的位置关系和直线与椭圆、双曲线的位置关系类似，一般要用到根与系数的关系；在解决直线与抛物线的位置关系时，要特别注意直线与抛物线的对称轴平行的特殊情况.中点弦问题，可以利用“点差法”，但不要忘记验证0∆>或说明中点在曲线内部.3．【解析】（1）设F 的坐标为(,0)c -．依题意，12ca =，2p a =，12a c -=，解得1a =，12c =，2p =，于是22234b ac =-=．所以椭圆的方程为22413y x +=，抛物线的方程为24y x =．（2）设直线AP 的方程为1(0)x my m =+≠， 与直线l 的方程1x =-联立，可得点2(1,)P m --，故2(1,)Q m-． 将1x my =+与22413y x +=联立，消去x 整理得22(34)60m y my ++=，解得0y =或2634my m -=+． 由点B 异于点A ，可得点222346(,)3434m mB m m -+-++． 由2(1,)Q m-，可得直线BQ的方程为22262342()(1)(1)()03434m m x y m m m m--+-+-+-=++， 令0y =，解得222332m x m -=+，故2223(,0)32m D m -+，所以2222236||13232m mAD m m -=-=++．又APD △22162232||m m m ⨯⨯=+，整理得23|20m m -+=，解得||m =，所以m =．所以，直线AP 的方程为330x -=或330x -=．【名师点睛】圆锥曲线问题在历年高考中都是较有难度的压轴题，本题中第一步利用椭圆的离心率及椭圆与抛物线的位置关系的特点，列方程组，求出椭圆和抛物线的方程，第二步联立方程组求出点的坐标，写出直线的方程，利用面积求直线方程，利用代数的方法解决几何问题，即坐标化、方程化、代数化，这是解题的关键．（2）设直线P 2A 与直线P 2B 的斜率分别为k 1，k 2，如果l 与x 轴垂直，设l ：x =t ，由题设知0t ≠，且||2t <，可得A ，B 的坐标分别为（t，2），（t，2-）．则121k k +==-，得2t =，不符合题设，从而可设l ：y kx m =+（1m ≠）．将y kx m =+代入2214x y +=得222(41)8440k x kmx m +++-=，由题设可知2216(41)0k m ∆=-+>．设A （x 1，y 1），B （x 2，y 2），则x 1+x 2=2841km k -+，x 1x 2=224441m k -+． 而12121211y y k k x x --+=+121211kx m kx m x x +-+-=+1212122(1)()kx x m x x x x +-+=． 由题设121k k +=-，故1212(21)(1)()0k x x m x x ++-+=，即222448(21)(1)04141m kmk m k k --+⋅+-⋅=++，解得12m k +=-， 当且仅当1m >-时0∆>，于是l ：12m y x m +=-+，即11(2)2m y x ++=--， 所以l 过定点（2，1-）．【名师点睛】椭圆的对称性是椭圆的一个重要性质，判断点是否在椭圆上，可以通过这一方法进行判断；证明直线过定点的关键是设出直线方程，通过一定关系转化，找出两个参数之间的关系式，从而可以判断过定点情况．另外，在设直线方程之前，若题设中未告知，则一定要讨论直线斜率不存在和存在两种情况，其通法是联立方程，求判别式，利用根与系数的关系，再根据题设关系进行化简．由题意知0∆>，且()12122111221x x x x k +==-+，所以121AB x =-=.由题意可知圆M 的半径r为1r =.由题设知12k k =21k =， 因此直线OC的方程为1y =.联立方程2211,2,x y y ⎧+=⎪⎪⎨⎪=⎪⎩得2221221181,1414k x y k k ==++，因此OC 由题意可知1sin21SOT rOC r OCr∠==++，而1OC r==令2112t k =+，则()11,0,1t t>∈，因此1OC r==≥，当且仅当112t =，即2t =时等号成立，此时1k =，所以1sin 22SOT ∠≤，因此π26SOT ∠≤， 所以SOT ∠最大值为π3. 综上所述：SOT ∠的最大值为π3，取得最大值时直线l的斜率为1k =.【名师点睛】本题对考生的计算能力要求较高，是一道难题.解答此类题目，利用,,,a b c e 的关系，确定椭圆（圆锥曲线）的方程是基础，通过联立直线方程与椭圆（圆锥曲线）方程得到的方程组，应用一元二次方程根与系数的关系，得到“目标函数”的解析式，应用确定函数最值的方法---如二次函数的性质、基本不等式、导数等求解.本题易错点是复杂式子的变形能力不足，导致错漏百出.本题能较好地考查考生的逻辑思维能力、运算求解能力、分析问题及解决问题的能力等.（2）由已知，1(2,0)F -，2(2,0)F ．设11(,)A x y ，22(,)B x y ，直线:l (2)y k x =-，显然0k ≠．将(2)y k x =-代入2213y x -=，得2222(3)4430k x k x k --++=．因为l 与双曲线交于两点，所以230k -≠，且236(1)0k ∆=+>． 设AB 的中点为(,)M M M x y ，由11()0F A F B AB +⋅=，即10FM AB ⋅= ，知1F M AB ⊥，故11F M k k ⋅=-．而2122223M x x k x k +==-，26(2)3M M k y k x k =-=-， 12323F M k k k =-，所以23123k k k ⋅=--，得235k =，故l 的斜率为5±． 【名师点睛】本题对考生的计算能力要求较高，是一道难题.解答此类题目时，利用,,,a b c e 的关系，确定双曲线（圆锥曲线）方程是基础，通过联立直线方程与双曲线（圆锥曲线）方程得到方程组，应用一元二次方程根与系数的关系进行求解.本题能较好地考查考生的逻辑思维能力、运算求解能力、分析问题与解决问题的能力等.。

直线与圆锥曲线的综合运用一、知识梳理1．直线与圆锥曲线的位置关系的判断将直线方程与圆锥曲线方程联立，消去一个变量得到关于x(或y)的一元方程：ax2＋bx＋c＝0(或ay2＋by＋c＝0)．(1)若a≠0，可考虑一元二次方程的判别式Δ，有①Δ>0①直线与圆锥曲线相交；①Δ＝0①直线与圆锥曲线相切；①Δ<0①直线与圆锥曲线相离．(2)若a＝0，b≠0，即得到一个一元一次方程，则直线l与圆锥曲线E相交，且只有一个交点．①若E为双曲线，则直线l与双曲线的渐近线的位置关系是平行；①若E为抛物线，则直线l与抛物线的对称轴的位置关系是平行或重合．2．圆锥曲线的弦长设斜率为k(k≠0)的直线l与圆锥曲线C相交于A(x1，y1)，B(x2，y2)两点，则AB＝1＋k2|x2－x1|＝1＋1k2|y2－y1|.3.过一点的直线与圆锥曲线的位置关系(1)过椭圆外一点总有两条直线与椭圆相切；过椭圆上一点有且只有一条直线与椭圆相切；过椭圆内一点的直线与椭圆相交．(2)过抛物线外一点总有三条直线和抛物线有且只有一个公共点：两条切线和一条与对称轴平行或重合的直线；过抛物线上一点总有两条直线与抛物线有且只有一个公共点：一条切线和一条与对称轴平行或重合的直线；过抛物线内一点只有一条直线与抛物线有且只有一个公共点：一条与对称轴平行或重合的直线.(3)过双曲线外不在渐近线上的一点总有四条直线与双曲线有且只有一个交点：两条切线和两条与渐近线平行的直线；过双曲线上条直线与双曲线有且只有一个交点：一条切线和两条与渐近线平行的直线； 过双曲线内一点总有两条直线与双曲线有且只有一个交点：两条与渐近线平行的直线．二、课前预习1.若直线y ＝kx ＋1与椭圆x 25＋y 2m ＝1总有公共点，则m 的取值范围是____．2.斜率为1的直线l 与椭圆x 24＋y 2＝1相交于A ，B 两点，则|AB |的最大值为____．3.直线mx ＋ny ＝4与①O ：x 2＋y 2＝4没有交点，则过点P (m ，n )的直线与椭圆x 29＋y 24＝1的交点个数是____个．4.已知A 1，A 2分别为椭圆C ：x 2a 2＋y 2b 2＝1(a >b >0)的左，右顶点，P 是椭圆C 上异于A 1，A 2的任意一点，若直线P A 1，P A 2的斜率的乘积为－49，则椭圆C 的离心率为____．5.在平面直角坐标系xOy 中，已知椭圆C ：x 2a 2＋y 2b 2＝1(a >b >0)过点)23,1(P ，离心率为12.(1) 求椭圆C 的方程． (2) 若斜率为32的直线l 与椭圆C 交于A ，B 两点，试探究OA 2＋OB 2是否为定值？若为定值，求出此定值；若不是定值，请说明理由．三、典型例题题型一. 直线与圆锥曲线的位置关系例1已知直线l ：y ＝2x ＋m ，椭圆C ：x 24＋y 22＝1.试问当m 取何值时，直线l 与椭圆C ：(1)有两个不重合的公共点； (2)有且只有一个公共点； (3)没有公共点．变式 在平面直角坐标系xOy 中，已知椭圆C 1：x 2a 2＋y 2b 2＝1(a ＞b ＞0)的左焦点为F 1(－1,0)，且点P (0,1)在C 1上． (1)求椭圆C 1的方程；(2)设直线l 同时与椭圆C 1和抛物线C 2：y 2＝4x 相切，求直线l 的方程．例2 如图，在平面直角坐标系xOy 中，已知焦点在x 轴上，离心率为12的椭圆E 的左顶点为A ，点A 到右准线的距离为6． （1）求椭圆E 的标准方程； （2）过点A 且斜率为32的直线与椭圆E 交于点B ，过点B 与右焦点F 的直线交椭圆E 于M 点，求M 点的坐标．题型二 弦长问题例3 如图，在平面直角坐标系xOy中，已知椭圆x 2a 2＋y 2b 2＝1(a ＞b ＞0) 的离心率e ＝22，右焦点F 到左准线l 的距离为3．(1)求椭圆的标准方程；(2)过F 的直线交椭圆于A ，B 两点，线段AB 的垂直平分线分别交直线l 和AB 于点P ，C ，若PC =2AB ，求直线AB 的方程．变式 如图，在平面直角坐标系xOy 中，椭圆x 2a 2＋y 2b 2＝1(a ＞b ＞0)的离心率为12，过椭圆右焦点F 作两条互相垂直的弦AB 与CD .当直线AB 斜率为0时，AB ＝4. (1)求椭圆的方程；(2)若|AB |＋|CD |＝487，求直线AB 的方程．BAOxy lP C题型三 定点问题例4 如图，在平面直角坐标系xOy中，离心率为2的椭圆:C 22221(0)x y a b a b+=>>的左顶点为A ，过原点O 的直线（与坐标轴不重合）与椭圆C 交于,P Q 两点，直线,PA QA 分别与y 轴交于,M N 两点．若直线PQ斜率为2时，PQ = （1）求椭圆C 的标准方程；（2）试问以MN 为直径的圆是否经过定点（与直线PQ 的斜率无关）？请证明你的结论．例5 已知椭圆C ：x 2a 2＋y 2＝1(a ＞1)的上顶点为A ，右焦点为F ，直线AF 与圆M ：x 2＋y 2－6x －2y ＋7＝0相切．(1)求椭圆C 的方程；(2)若不过点A 的动直线l 与椭圆C 相交于P 、Q 两点，且AP →·AQ →＝0，求证：直线l 过定点，并求出该定点N 的坐标．变式1 已知椭圆C ：x 2a 2＋y 2b 2＝1(a >b >0)，四点1P (1,1)，2P (0,1)，)23,1(3 P ，)23,1(4P 中恰有三点在椭圆C 上． (1)求C 的方程；(2)设直线l 不经过P 2点且与C 相交于A ，B 两点．若直线P 2A 与直线P 2B 的斜率的和为－1，证明：l 过定点．变式2 如图，在平面直角坐标系xOy 中，椭圆C ：x 2a 2＋y 2b 2＝1(a >b >0)的离心率为22，椭圆上动点P 到一个焦点的距离的最小值为3(2－1)．(1) 求椭圆C 的标准方程；(2) 已知过点M (0，－1)的动直线l 与椭圆C 交于A ，B 两点，试判断以线段AB 为直径的圆是否恒过定点，并说明理由．题型四 定值问题例6 已知椭圆)(:012222>>=+b a by a x C 的离心率为23，且过点),(12-P ．（1）求椭圆C 的方程；（2）设点Q 在椭圆C 上，且PQ 与x 轴平行，过P 点作两条直线分别交椭圆C 于),(11y x A),(22y x B 两点，若直线PQ 平分APB ∠，求证：直线AB 的斜率是定值，并求出这个定值．变式 在平面直角坐标系xOy 中，已知椭圆22221(0)x y a b a b+=>>的焦距为2，离心率为22，椭圆的右顶点为A . （1）求该椭圆的方程；（2）过点(2,2)D -作直线PQ 交椭圆于两个不同点,P Q ，求证：直线,AP AQ 的斜 率之和为定值.例7 如图，在平面直角坐标系xOy 中，已知椭圆22221x y a b+=(0)a b >>，焦点到相应准线的距离为1． （1）求椭圆的标准方程；（2）若P 为椭圆上的一点，过点O 作OP 的垂线交直线y =于点Q ，求2211OP OQ +的值．变式在平面直角坐标系xOy 中，已知圆222:O x y b +=经过椭圆222:14x y E b +=(02)b <<的焦点.（1）求椭圆E 的标准方程；（2）设直线:l y kx m =+交椭圆E 于,P Q 两点，T 为弦PQ 的中点，(1,0),(1,0)M N -，记直线,TM TN 的斜率分别为12,k k ，当22221m k -=时，求12k k ⋅的值.题型五 最值、范围问题例8 已知椭圆C ：22221(0)x y a b a b+=>>的左焦点为F (－1，0)，左准线方程为x ＝－2.(1) 求椭圆C 的标准方程；(2) 若椭圆C 上有A ，B 两点，满足OA ①OB (O 为坐标原点)，求①AOB 面积的取值范围．例9 如图，在平面直角坐标系xOy 中，椭圆C ：22221(0)x y a b a b+=>>的左顶点为A ，点B 是椭圆C 上异于左、右顶点的任一点，P 是AB 的中点，过点B 且与AB 垂直的直线与直线OP 交于点Q ，已知椭圆C 的离心率为12，点A 到右准线的距离为6。

2008高考数学复习 直线与圆锥曲线的位置关系一、基本知识体系：1、 直线与圆锥曲线的位置关系：① 要解决直线与圆锥曲线的位置关系问题，通常把直线方程与圆锥曲线方程联立，消去y（或消去x ）得到关于x （或关于y ）的一元二次方程，再考查其△，从而确定直线与圆锥曲线的的交点个数：（1）若△<0，则直线与圆锥曲线没有公共点；②若△=0，则直线与圆锥曲线有唯一的公共点；③若△>0，则直线与圆锥曲线有两个不同的公共点； ② 从几何角度来看：直线与圆锥曲线的位置关系对应着相交（有两个交点）、相切（有一个公共点）、相离（没有公共点）三种情况；这里特别要注意的是：当直线与双曲线的渐近线平行时、当直线与抛物线的对称轴平行时，属于相交的情况，但只有一个公共点。

2、 直线被圆锥曲线截得的弦长问题：①直线与圆锥曲线有两个交点A （x 1,y 1)、B(x 2,y 2) ，一般将直线方程L ：y=kx+m 代入曲线方程整理后得到关于x 的一元二次方程⇒则应用弦长公式：|AB|=或将直线方程L:x= 1k y +t 代入曲线方程整理后得到关于y 的一元二次方程⇒则应用弦长公式：②过焦点的弦长的求解一般不用弦长公式去处理,而用焦半径公式会更简捷;③ 垂直于圆锥曲线的对称轴的焦点弦长称为圆锥曲线的通径,其中椭圆、双曲线的通径长都为2b2a,而抛物线的通径长为2p ；④ 对于抛物线y 2=2px （p>0)而言，还有如下的焦点弦长公式，有时用起来很方便：|AB|=x 1+x 2+p ；|AB|=2psin 2α (其中α为过焦点的直线AB 的倾斜角）3、 直线与圆锥曲线相交的中点弦的的问题,常用的求解方法有两种：①设直线方程为y=kx+m ，代入到圆锥曲线方程之中，消元后得到一元二次方程，再利用根与系数的关系去处理（由于直线方程与圆锥曲线方程均未定，因而通常计算量较大）；②利用点差法：例如在椭圆22221x y a b+=内有一定点P （x 0,y 0),求以P 为中点的弦的直线方程时，可设弦的两端点为A （x 1,y 1)、B(x 2,y 2) ，则A 、B 满足椭圆方程，即有22112222222211x y a b x y a b ⎧+=⎪⎪⎨⎪+=⎪⎩两式相减再整理可得：(x 1+x 2) (x 1-x 2)a 2 = - (y 1+y 2) (y 1-y 2)b 2；从而可化出k= y 1-y 2x 1-x 2 = (x 1+x 2) (y 1+y 2)·-b2a 2 = x 0y 0·-b2a2； 对于双曲线也可求得：k= y 1-y 2x 1-x 2 = (x 1+x 2) (y 1+y 2)·b 2a 2= x 0y 0·b2a 2;抛物线也可用此法去求解，值得注意的是，求出直线方程之后，要根据图形加以检验。