南昌大学上半年材料热力学重点题

第一章材料热学性能内容概要：本章讲述材料的热容、热膨胀、热传导、热稳定性等方面的内容，并简述其物理本质。

主要内容和学时安排如下：第一节材料的热容重点掌握经典热容理论和量子热容理论的内容；理解温度、相变等对热容的影响；了解热容的几种测量方法，对热分析法的原理和应用要重点理解。

第二节材料的热膨胀重点掌握线膨胀系数、体膨胀系数、热膨胀的物理本质；了解热膨胀的测量方法；理解热膨胀分析方法在材料中的应用。

第三节材料的热传导掌握热传导定律；热传导的物理本质；理解热传导的影响因素。

（共6个学时）第一节 材料的热容一、热容的定义：不同的物体升高相同的热量时其温度会不同，温度升高1K 所需要的能量定义为热容： ∆T ∆=Q C 定容热容：如果在加热过程中，体积不变，则所提供的热量全部用于粒子动能（温度）的增加，用Cv 表示 ()V V Q C ∆=∆T定压热容：如果在加热过程中保持压力不变，则物体的体积自由膨胀，这时所提供的热量一部分用于升高体系的温度，一部分用于体系对外做功，用Cp 表示()()V V V Q U P V U C T ∆∆+∆∆===∆T ∆∆T ()()()()()P P P P P P Q U P V U V H C P T T T∆∆+∆∆∆∆===+=∆T ∆∆T ∆∆ T c m H =c 为0-TK 时平均比热容，即质量为1Kg 的物质在没有化学反应条件下，温度升高1K 时所需的热量，单位为J/（Kg.K ）定压热容>定容热容，一般实验测得的是恒压热容CpTQ m C P ∆∆=1 即在T T T -+∆温度范围内的平均热容： 当0T ∆→时，P C 即可认为是TK 时的热容dTdQ m C P 1= 摩尔恒压热容：1mol 物质在没有化学反应和相改变条件下，升高1K 所需的能量，用C pm 表示 摩尔恒容热容：KT V v C C m Vm Pm 2∂=- M C C P Pm =（M 为摩尔质量）二、热容理论实验发现：在不发生相变条件下，多数物质的热容Cv 在高温下，逐于一恒定值；低温区3V C T ∝；0T →时，0V C =。

《热力学与统计物理》考试大纲第一章 热力学的基本定律基本概念：平衡态、热力学参量、热平衡定律温度，三个实验系数（α，β，T κ）转换关系，物态方程、功及其计算，热力学第一定律（数学表述式）热容量（C ，C V ，C p 的概念及定义），理想气体的能，焦耳定律，绝热过程及特性，热力学第二定律（文字表述、数学表述），可逆过程克劳修斯不等式，热力学基本微分方程表述式，理想气体的熵、熵增加原理及应用。

综合计算：利用实验系数的任意二个求物态方程，熵增（ΔS ）的计算。

第二章 均匀物质的热力学性质基本概念：焓（H ），自由能F ，吉布斯函数G 的定义，全微公式，麦克斯韦关系（四个）及应用、能态公式、焓态公式，节流过程的物理性质，焦汤系数定义及热容量（Cp ）的关系，绝热膨胀过程及性质，特性函数F 、G ，空窖辐射场的物态方程，能、熵，吉布函数的性质。

综合运用：重要热力学关系式的证明，由特性函数F 、G 求其它热力学函数（如S 、U 、物态方程）第三章、第四章 单元及多元系的相变理论该两章主要是掌握物理基本概念：热动平衡判据（S 、F 、G 判据），单元复相系的平衡条件，多元复相系的平衡条件，多元系的热力学函数及热力学方程，一级相变的特点，吉布斯相律，单相化学反应的化学平衡条件，热力学第三定律标准表述，绝对熵的概念。

统计物理部分第六章 近独立粒子的最概然分布基本概念：能级的简并度，μ空间，运动状态，代表点，三维自由粒子的μ空间，德布罗意关系（k P=，＝ωε），相格，量子态数。

等概率原理，对应于某种分布的玻尔兹曼系统、玻色系统、费米系统的微观态数的计算公式，最概然分布，玻尔兹曼分布律（l l l e a βεαω--=）配分函数（∑∑-==-s l l sl e e Z βεβεω1），用配分函数表示的玻尔兹曼分布（l l l e Z N a βεω-=1），f s ，P l ，P s 的概念，经典配分函数（⎰⎰-=du e h Z l r βε 011）麦态斯韦速度分布律。

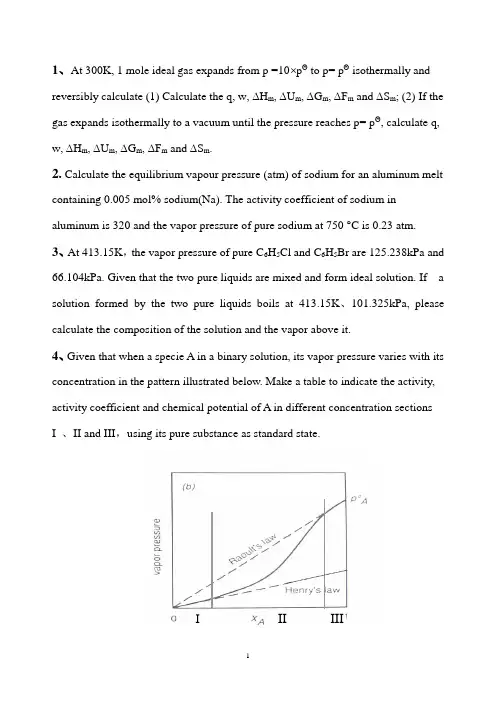
1、At 300K, 1 mole ideal gas expands from p =10⨯pΘ to p= pΘ isothermally and reversibly calculate (1) Calculate the q, w, ∆H m, ∆U m, ∆G m, ∆F m and ∆S m; (2) If the gas expands isothermally to a vacuum until the pressure reaches p= pΘ, calculate q, w, ∆H m, ∆U m, ∆G m, ∆F m and ∆S m.2. Calculate the equilibrium vapour pressure (atm) of sodium for an aluminum melt containing 0.005 mol% sodium(Na). The activity coefficient of sodium in aluminum is 320 and the vapor pressure of pure sodium at 750 °C is 0.23 atm.3、At 413.15K，the vapor pressure of pure C6H5Cl and C6H5Br are 125.238kPa and 66.104kPa. Given that the two pure liquids are mixed and form ideal solution. If a solution formed by the two pure liquids boils at 413.15K、101.325kPa, please calculate the composition of the solution and the vapor above it.4、Given that when a specie A in a binary solution, its vapor pressure varies with its concentration in the pattern illustrated below. Make a table to indicate the activity, activity coefficient and chemical potential of A in different concentration sections I 、II and III，using its pure substance as standard state.III III5、At 300K, the vapor pressure of liquid A and liquid B are 37.33kPa and 22.66kPa.When 2 moles of A and 2 moles of B are mixed to form a solution, the vapor pressure above the solution is 50.66kPa, and the molar fraction of A in the vapor is 0.60. Given that vapors can be taken as ideal gases. ①Calculate a A( R )and a B( R) in the solution, ②γA and γB , ③∆mix G , ④ If the solution is an ideal solution, what is the value of ∆mix G id ? ⑤ What is the value of ∆mix G ex of this solution?6、The variation, with composition, of G E for Fe-Mn alloys at 1863K is listedbelow:X Mn 0.1 0.20.30.40.50.60.7 0.80.9G m E , Joules395703 925 1054 1100 1054 925 703 395a 、Is the process to form Fe-Mn alloy at 1863K an exothermic one or an endothermic one ?b. Does the system exhibit regular solution behavior?c. Calculate E Fe μ and E Mn μ at X Mn = 0.6;d. Calculate m mix G ∆ at X Mn = 0.4;e. Calculate the partial pressures of Mn and Fe exerted by the alloy of X Mn = 0.27、Melts in the system Pb-Sn exhibit regular solution behavior. At 473︒C, a Pb =0.055 in a liquid solution of X Pb = 0.1. Calculate the value of PbSn ωfor the system and calculate the activity of Sn in the liquid solution of X Sn = 0.5 at 500︒C.93.23ln 27.145390)(ln *+--=T Tatm p Fe68.37ln 02.333440)(ln *+--=T Tatm p Mn8、With respect to the Ellingham diagram, answer the following questions:a) Explain the slope changes for the reaction 2Mg + O 2 = 2MgO; b) You want to heat up and a piece of silicon metal to 1600︒C, decide on a suitable crucible material;c) What is the value of ∆H Θ of formation of TiO 2 ? d) Find ∆G Θfor the reaction Fe + 0.5O 2 =FeO at 1200 ︒C;e) Find ∆G Θ for the reaction 3Mg + AlO 3 = 3MgO + 2A1 at 1500 ︒C; f) What is the equilibrium oxygen pressure when metallic titanium is in equilibrium with TiO 2 at 1000 ︒C?g) If you want to reduce pure TiO 2 to pure metallic titanium at 1000︒C using a CO/CO 2 gas mixture, what is the minimum CO/CO 2 ratio that can achieve such a reduction.9、Answer the following questions according to Ellingham diagram:① At what temperature(s) C can reduce SnO 2(s)、Cr 2O 3(s) and SiO 2(s) ？ ② At what temperature, the decomposition pressure of CuO reaches 1.01325⨯105 Pa ?③ The temperature(s) at which Fe 3O 4 can be reduced to FeO by H 2 ? ④ ∆G Θ when Mg reduces Al 2O 3 at 1000︒C, ⑤ Atwhattemperature,forthereaction)(322)(3234S S O Cr O Cr =+,Pa 1019'2－（平）is p O ? ⑥ Calculate the ∆G when Fe reacts with O 2 at 10－5Pa and 10－10Pa respectivelyat1000︒C, and '(2平）O p as well.⑦ Calculate the equilibrium constant of reaction 2)()(CO Mn CO MnO s s +=+ at 1100︒C (CO CO p p K /2=)⑧ At what temperature, for reaction )(2)(2)(g s s O H Mn H MnO +=+, the （平）)/(22O H H is 104/1 ? 10、The standard Gibbs free energy change for reaction I:Ni （s ） + 1/2 O2 == NiO （s ）is -244560 + 98.53TlnT J/ mol , question: a) How much is the standard Gibbs free energy change for reaction II : 2Ni （s ） + O2 == 2 NiO （s ）b) Calculate the equilibrium constants for reaction I and reaction II respectively at 1000︒ C.c) At 1000︒ C, when oxygen pressure is maintained at 10-4 atm, how much is theGibbs free energy change for reaction I ? Can reaction I proceed forward ? Is Ni stable under this condition ? Is NiO stable under this condition ? d) At 1000︒ C, how much should be the oxygen pressure if we want the Gibbs free energy change for reaction I to be 0, and how much should be the oxygen pressure if we want a Ni-NiO-O 2 system to be at equilibrium ?e) At 1000 C, what is the condition to prevent Ni from being oxidized ? and whatis the condition to reduce NiO ?11、Liquid FeO is reduced to metallic iron at 1600 °C with CO(gas) accordingto the following reaction:FeO(liquid) + CO(g) = Fe(liquid) + CO 2 a) Calculate ∆G Θ at 1600 °C for this reactionb) Detennine the minimum CO/C02 ratio required to reduce pure liquid FeO to pure metallic iron at 1600 °C.c) Determine the minimum CO/CO2 ratio required to reduce FeO dissolved in a liquid slag to metallic iron at 1600 °C. The metallic iron formed has a purity of 96 mole % iron. The activity of FeO in the liquid slag is 0.3.CO(g) at 1600 °C: ∆GΘ= -274.9 kJ/molCO2(g) at 1600 °C: ∆GΘ = -396.3 kJ/molFeO at 1600 °C: ∆GΘ = -144.6 kJ/molR= 8.314 J/ mol.K= 1.987 ca1/mol.K12、In an experiment, it was found that the Ar was not pure enough. So a setup was devised in an attempt to purify the Ar, as illustrated below. Ar which was at 2 atm was let to flow through a glass tube and the Cu powder pile in it. Given that the temperature in the glass tube is 600︒C and gas pressure is constant at 2 atm.. Calculate the purity of the outgoing Ar in percentage.Ellingham Diagram补充习题参考答案（魏）1.ΔS m =19.1J/mol.K, ΔG m = -5740 J/mol, ΔF m = -5740 J/molIsothermally expands to a vacuum: w = 0, ΔH m =0 , ΔU m = 0,ΔS m =19.1J/mol.K, ΔG m = -5740 J/mol, ΔF m = -5740 J/mol2. 3.68 × 10-3 atm3、Pa x x Br H C Cl H C 406.0;594.05556==Pa p Pa p Br H C Cl H C 26838;744445556==4.5、 JG J G J G a a ex mix id mix mix B A R B R A 5302)5(;6912)4(;1610)3(;788.1;62.1)2(;894.0;81.0)1()()(=∆-=∆-=∆====γγ 6. a endothermic one; b. Yes; c J J EMn E Fe 704;1584==μμd ;/9363mol J G m m ix -=∆e Pa p Pa p Fe Mn 4;1198==7. J S n P b 4578-=ω; 418.0=Sn a Pure Substance as Standard Statepq（b ）I 、II 、IIIIII:AA AA x RT T p RT T T ln )(ln)()(**+=+=μμμk A8. a) Mg boils and which makes o S ∆more negative, so the slope changes for larger; b) Firstly, we should avoid using metallic material for this purpose since the melting points of metals are mostly too low. Ceramic materials, usually composed of oxides and having high melting points can be chosen The material should not be reduced by pure silicon at 1600ºC. By examing Ellingham diagram, crucibles (坩埚) made of Al 2O 3 .c ) -890kJ /molO2;d ) -170kJ /molFeO; e) -30kJ; f) Pa 2110－; g)721063.0/⨯=pco p CO 9、⑨ 650ºC ，1220 ºC and 1520 ºC ; ⑩ 1480 ºC ;⑪ When the temperature is equal to or higher that 710 ºC ; ⑫ 2/100molO kJ G o -=∆ ⑬ 900 ºC; ⑭0,102/112,1010'25'2=∆=-=∆=--G Pa P molO kJ G Pa P O O , Pa p e O 10')(210-= ⑮ 510-=K ;⑯ 1220ºC10、a) -489120+197.06TlnT J/mol; b) 2.89×10-54 ; c)J G 749429=∆; Ni is stable under this condition,and NiO is not stable; d) Pa p e o 58')(21046.3⨯= e) from the calculation, we found that at 1000ºC, Pa p e o 58')(21046.3⨯=. So at 1000ºC, when theoxygen pressure is less than 3.46×1058Pa, Ni is stable and can not be oxidized, and NiO will be reduced to Ni under this condition. 11. a)mol kJ G o /2.23=∆;b)43.42=⎪⎭⎫ ⎝⎛e CO CO p p . This is the minimumCO/CO2 ratio required to reduce pure FeO to Fe at 1600ºC. c)2.142=⎪⎭⎫ ⎝⎛eCO CO p p . This is the minimum CO/CO2 ratio required to reduce FeO in a slag( 炉渣) to Fe in a metallic iron melt under the given conditions at 1600ºC.12.%100)1015.3%10⨯⨯-＝（Ar。

热力学复习题及答案1. 热力学的定义是什么？答：热力学是研究能量转化和能量传递规律的一个物理学分支。

2. 什么是热力学系统？答：热力学系统是指被选定的一部分物质或空间，用于研究热力学性质和过程的对象或范围。

3. 请简要解释热力学过程中的熵变。

答：热力学过程中的熵变指系统熵的变化，代表了系统无序度的改变。

熵增加表示系统的无序度增加，熵减少表示系统的无序度减少。

4. 热力学第一定律是什么？答：热力学第一定律，也称能量守恒定律，表示能量不会被创造或破坏，只能从一种形式转化为另一种形式，能量的总量保持不变。

5. 温度和热量有什么区别？答：温度是物体分子运动的程度，用来衡量热力学系统的热平衡状态。

热量是能量的传递形式，表示因温度差而引起的能量传递。

6. 请解释等温过程和绝热过程。

答：等温过程是指系统与外界保持恒定温度的热力学过程。

绝热过程是指系统与外界无能量交换的热力学过程。

7. 热力学循环是什么？答：热力学循环是指能量转化过程中系统从一个状态经过一系列过程最终回到原来状态的过程。

8. 请解释热力学可能性原理。

答：热力学可能性原理，也称热力学第二定律，表示任何孤立系统都不可能完全转化热能为有效的功。

9. 热力学第三定律是什么？答：热力学第三定律，也称绝对温标定律，指出在绝对零度（0K）下，所有物质的熵可以达到最低值，即熵的极限为零。

10. 请解释吉布斯自由能。

答：吉布斯自由能，简称G，是热力学系统在等温等压条件下的可用能量。

它在化学平衡时取最小值，可用于预测化学反应的方向。

The problems of the first law1.1 a lead bullet is fired at a frigid surface. At what speed must it travel to melt on impact, if its initial temperature is 25℃ and heating of the rigid surface of the rigid surface is neglected? The melting point of lead is 327℃. The molar heat of fusion of the lead is 4.8kJ/mol. The molar heat capacity C P of lead may be taken as 29.3J/(mol K)Solution: )/(363102.20721]108.4)25327(3.29[2121)(23322s m V v n n WQ nMv mv W H T C n Q Q Q absorb melting p melt increase absorb =⨯=⨯+-⨯===∆+∆=+=-1.2 what is the average power production in watts of a person who burns 2500 kcal of food in a day? Estimate the average additional powder production of 75Kg man who is climbing a mountain at the rate of 20 m/minSolution )/(24560208.975)/(12160602410467000//)(104670001868.4102500sin 3S J t h mg P S J t Q t W PJ Q gincrea Burning Burning =⨯⨯=∆==⨯⨯====⨯⨯=1.3 One cubic decimeter (1 dm 3) of water is broken into droplets having a diameter of one micrometer (1 um) at 20℃.(a) what is the total area of the droplets?(b) Calculate the minimum work required to produce the droplets. Assume that the droplets are rest (have zerovelocity)Water have a surface tension of 72.75 dyn/cm at 20℃ (NOTES: the term surface energy (ene/cm 2) is also used for surface tension dyn/cm)Solution)(6.436)106103(1075.72)(106)105.0(4)105.0(34)101(232523263631J S W m nS S Single total =⨯-⨯⨯⨯=∆=⨯=⨯⨯⨯⨯⨯⨯⨯⨯==-+----σππ1.4 Gaseous helium is to be used to quench a hot piece of metal. The helium is in storage in an insulated tank with a volume of 50 L and a temperature of 25℃, the pressure is 10 atm. Assume that helium is an ideal gas.(a) when the valve is opened and the gas escapes into the quench chamber (pressure=1 atm), what will be thetemperature of the first gas to hit the specimen?(b) As the helium flows, the pressure in the tank drops. What will be the temperature of the helium entering thequench chamber when the pressure in the tank has fallen to 1 atm?Solution: )(180118298)(1185.229810101325501010101325)5500(1)()(118)101(298)()(0334.0/00K T T T K RR nC W T b K T P P T T Adiabatica p CR P=-=∆-==⨯⨯⨯⨯⨯⨯⨯-⨯==∆=⨯==--1.5 An evacuated (P=0), insulted tank is surrounded by a very large volume (assume infinite volume) of an ideal gas at a temperature T 0. The valve on the tank is oðened and the surrounding gas is allowed to flow suickly into t(e tank until the pressure insi`e the tank is equals the pressure outside. Assume that no heat flow takes place. What is the0final tempeture kf t èe gaS in the tank? The heat cap!city mf the gas, C p and C v each íay be(assumed to be c/nsuant over thå temperature rang!spanNed by the døperiment. You answer may be meft in terms of C p and S v hint: one way to approach the xroblem is to define the system as the gas ends up in the tank.solution 0/000/00)0()(T P P T T P PT T Adiabatic PPC R C R ≈-==1.6 Calculate the heat of reaction of methane with oxygen at 298K, assuming that the products of reaction are CO 2 and CH 4 (gas)[This heat of reaction is also called the low calorific power of methane] convert the answer into unites of Btu/1000 SCF of methane. SCF means standard cubic feet, taken at 298 and 1atm NOTE: this value is a good approximation for the low calorific powder of natural gasDATA: )()()(224g O H g CO g CH FOR80.5705.9489.17]/[0298---•∆mol g Kcal Hsolution)1000/(9.2610252103048.01101076.191)/(76.191)89.1780.57205.94()2(22333332982982224422SCF Btu mol g Kcal H H H H H OH CO O CH CH O H CO =⨯⨯⨯⨯⨯=•=∆+⨯---=∆-∆+∆-=∆+=+- 1.7Methane is delivered at 298 K to a glass factory, which operates a melting furnace at 1600 K. The fuel is mixed with a quantity of air, also at 298 K, which is 10% in excess of the amount theoretically needed for complete combustion (air is approximately 21% O 2 and 79% N 2)(a) Assuming complete combustion, what is the composition of the flue gas (the gas following combustion)? (b) What is the temperature of the gas, assuming no heat loss?(c) The furnace processes 2000kg of glass hourly, and its heat losses to the surroundings average 400000 kJ/h.calculate the fuel consumption at STP (in m 3/h) assuming that for gas H 1600-H 298=1200KJ/KG(d) A heat exchanger is installed to transfer some of the sensible heat of the flue gas to the combustion air.Calculate the decrease in fuel consumption if the combustion air is heated to 800K DATA STP means T=298K, P=1atm22224O N O H CO CH for2.82.89.117.1316)/(C mol cal C P •Solution)(210448.1125.9100076.191298)/(25.9)]87.012.72(2.843.179.1171.87.13[01.0)(%87.0%%12.72%%43.17%2%%71.8)11.1(221791.1231%22)(0,,222222224K T T T C mol cal X C C b O N CO O H CO O H CO O CH a i i p p p =⨯⨯+=∆+=•=+⨯+⨯+⨯=======-⨯+⨯⨯+=+=+∑)/(1644)0224.011868.448.11)8001600(48.1125.9189570(102800000)/(189570)298800)](48.1187.8)48.1125.9[(100076.191)()/(87.848.11/]211002.22.816[)()/(3214)0224.011868.448.11)2981600(48.1125.9100076.191(102800000)/(280000040000020001200)(33min ,,,,298,,33min h m V mol g cal dTn C n C H H C mol cal X C C d h m V h KJ P C gConsu i i r p i i p p i i p r p g Consu =⨯⨯-⨯-⨯=•=-⨯-⨯-⨯=--∆=∆•=⨯⨯+===⨯⨯-⨯-⨯⨯==+⨯=⎰∑∑∑1.8 In an investigation of the thermodynamic properties of a-manganese, the following heat contents were determined:H 700-H 298=12113 J/(g atom) H 1000-H 298=22803 J/(g atom)Find a suitable equation for H T -H 298 and also for C P as a function of temperature in the form (a+bT) Assume that no structure transformation takes place in the given tempeture rang.Solution )298(0055.0)298(62.35011.062.35011.062.3522803)2981000(2)2981000(12113)298700(2)298700(]2[2229822222982---=∆-=-===-+-=-+-+=+==∆⎰⎰T T H TC b a ba ba T baT bTdT a dT C H T P T P1.9 A fuel gas containing 40% CO, 10% CO 2, and the rest N 2 (by volume) is burnt completely with air in a furnace. The incoming and ongoing temperatures of the gases in the furnace are 773K and 1250K,respectively. Calculate (a) the maximum flame temperature and (b) heat supplied to the furnace per cu. ft of exhaust gasmolJ Hmol J H CO f CO f /393296/1104580,298,0,298,2-=∆-=∆)/(10184.403.29)/(1067.11010.492.19)/(1037.81020.935.44)/(1042.01097.345.283,253,253,253,222molK J T C molK J T T C molK J T T C molK J T T C N P O P CO P CO P -------⨯+=⨯-⨯+=⨯-⨯+=⨯-⨯+= Solution?0)499.0321.018.1()1067.01019.277.28(28.282831067.01038.477.289.0)1019.01058.528.33(2.0282838)()/(1019.01058.528.33722.0278.0)/(1067.01038.477.281.065.005.02.0)()/(282838110458393296%2.72%8.27%10%65%5%20)4/(1122298127332981523733253253298,,,,298,253,,,,,253,,,,,,,0,298,0,298,298,22222222222222==+--⨯+⨯++⨯=⨯-⨯++⨯⨯-⨯+-⨯=--∆=∆⨯-⨯+=+==⨯-⨯+=+++===-=∆-∆=∆========+-----------⎰⎰⎰∑∑⎰∑∑∑∑T T T T T T T dTT T dTT T dTn C n C n H H molK J T T C C n C C molK J T T C C C C n C C a mol J n Hn H H N CO production O N CO CO reation then O N air mole need fuel mole when CO O CO T TT i i r p i i p p i i N P CO P i i p p r p O P N P CO P CO P i i p p r p i pf i rf idTT T Q dT T T Q b T T T T T T T dTT T dTT T dT n C n C n H H T TT i i r p i i p p i i 9.0)1019.01058.528.33(2.02828389.0)1019.01058.528.33(2.0282838)(0)499.0321.018.1()1067.01019.277.28(28.282831067.01038.477.289.0)1019.01058.528.33(2.0282838)(253125029812502982531250298125029829812125029815231250253253298,,,,298,⨯⨯-⨯++⨯-=⨯⨯-⨯++⨯-===+--⨯+⨯++⨯=⨯-⨯++⨯⨯-⨯+-⨯=--∆=∆-----------⎰⎰⎰⎰⎰∑∑⎰1.10 (a) for the reaction2221CO O CO →+,what is the enthalpy of reaction (0H ∆) at 298 K ?(b) a fuel gas, with composition 50% CO, 50% N 2 is burned using the stoichiometric amount of air. What is the composition of the flue gas?(c) If the fuel gas and the air enter there burner at 298 K, what is the highest temperature the flame may attain(adiabatic flame temperature)? DATA :standard heats of formationfH ∆ at 298 K)/(393000)/(1100002mol J CO mol J CO -=-=Heat capacities [J/(mol K)] to be used for this problem N 2=33, O 2=33, CO=34, CO 2=57Solution )(21100)298)(39889.0(222.02830000)/(3975.03325.057)/(33111.034222.033666.033)(%,75%%,251.111002.22%%1.11%%,6.66%%,2.222.0/25.015.0%)()/(283000393000110000)(,0,,,,,,22220,298,0,298,0K T T dT C n H H K mol J X C C K mol J X C C C N CO product O N CO fuel b mol J n H n H H a P p p i P r i P r i P p i P p i P f i r f ==-⨯-⨯=-∆=∆•=⨯+⨯==•=⨯+⨯+⨯====-====+==+-=∆-∆=∆⎰∑∑∑∑1.11 a particular blast furnace gas has the following composition by (volume): N 2=60%, H 2=4, CO=12%, CO 2=24%(a) if the gas at 298K is burned with the stochiometric amount of dry air at 298 K, what is the composition of the flue gas? What is the adiabatic flame temperature?(b) repeat the calculation for 30% excess combustion air at 298K(C)what is the adiabatic flame temperature when the blast furnace gas is preheated to 700K (the dry air is at 298K) (d) suppose the combustion air is not dry ( has partial pressure of water 15 mm Hg and a total pressure of 760 mm Hg) how will thE dlaMe temperature be affected?DaTA(k J?mol)2CO CO FOR513.393523.110)/(--∆mol kJ H f2222,)(O N g O H CO CO FOR ?? 34505733]/[K mol J C P •SolutionOH O H CO O CO a 222222121)(→+→+ 416.0)(104.0)(:22==N n O n Air6.0)(04.0)(24.0)(12.0)(:222====N n H n CO n CO n Fuel 32.0)(08.0)(:22==N n O n Air 92.0)(04.0)(36.0)(:222===N n O H n CO n Flue)(98.1108)(8108.53106308.43)/(8.533492.05004.05736.092.004.036.06308.43)08.241(04.0)523.11051.393(12.03,,222222K T K T K J C C C n CKJH H H N O H CO ii r P O H H CO CO ==⨯=∆=⨯+⨯+⨯=++==-⨯+-⨯=∆+∆=∆∑--(b)repeat the calculation for 30% excess0combustion air at 298K6.0)(04.0)(24.0)(12.0)(:222====N n H n CO n CO n Fuel024.0)(016.1)(04.0)(36.0)(:2222====O n N n O H n CO n Flue December 13, 2020(C)what is the adiabatic flame temperature when the blasp furnace gas is preheated to 700K (the dry air is at 298K)6.0)(04.0)(24.0)(12.0)(:222====N n H n CO n CO n Fuel 32.0)(08.0)(:22==N n O n Air 92.0)(04.0)(36.0)(:222===N n O H n CO n Flue)(6.1401)(6.11038.5310373.59)/(8.533492.05004.05736.096.004.036.0373.59)346.02804.05724.03312.0()298700()08.241(04.0)523.11051.393(12.03,,298700222222K T K T K J C C C n CKJH H H H N O H CO ii r P fuel O H H CO CO ==⨯=∆=⨯+⨯+⨯=++==⨯+⨯+⨯+⨯⨯-+-⨯+-⨯=∆+∆+∆=∆∑---(d) suppose the combustion air is not dry ( has partial pressure of water 15 mm Hg and a total pressure of 760 mm Hg) how will the flame temperature be affected?)(8.1051)(8.75388.57106308.43)/(88.5734024.034016.15004.05736.0024.0016.104.036.06308.43)08.241(04.0)523.11051.393(12.03,,2222222K T K T K J C C C C n CKJH H H O N O H CO ii r P O H H CO CO ==⨯=∆=⨯+⨯+⨯+⨯=+++==-⨯+-⨯=∆+∆=∆∑--6.0)(04.0)(24.0)(12.0)(:222====N n H n CO n CO n Fuel 008.04.01576015)(32.0)(08.0)(:222=-===O H n N n O n Air 92.0)(048.0)(36.0)(:222===N n O H n CO n Flue)(1103)(8052.54106308.43)/(2.543492.050048.05736.092.0048.036.06308.43)08.241(04.0)523.11051.393(12.03,,222222K T K T K J C C C n CKJH H H N O H CO ii r P OH H CO CO ==⨯=∆=⨯+⨯+⨯=++==-⨯+-⨯=∆+∆=∆∑--1.12 A bath of molten copper is super cooled to 5℃ below its true melting point. Nucleation of solid copper then takes place, and the solidification proceeds under adiabatic conditions. What percentage of the bath solidifies? DATA: Heat of fusion for copper is 3100 cal/mol at 1803℃(the melting point of copper) C P,L =7.5(cal/mol ℃), C P,S =5.41+(1.5*10-3T )(cal/mol ℃) Solution)/(310355.75.0)17981803(105.1541.5310002231798,1798,17981803,18031798,1803,mol cal HH dT C dT C H LS SL L P S P L S =⨯-⨯-⨯+⨯+==+++-⎰⎰1.13 Cuprous oxide (Cu 2O) is being reduced by hydrogen in a furnace at 1000K, (a)write the chemical reaction for the reduced one mole of Cu 2O(b)how much heat is release or absorbed per mole reacted? Given the quantity of heat and state whether heat is evolved (exothermic reaction) or absorbed (endothermic reaction)DATA: heat of formation of 1000K in cal/mol Cu 2O=-41900 H 2O=-59210 solution)/(173104190059210222mol cal H OH Cu H O Cu =-=∆+=+,exothermic reaction1.14(a) what is the enthalpy of pure, liquid aluminum at 1000K?(b) an electric resistance furnace is used to melt pure aluminum at the rate of 100kg/h. the furnace is fed with solid aluminum at 298K. The liquid aluminum leaves the furnace at 1000K. what is the minimum electric powder rating (kW) of furnace.DATA : For aluminum : atomic weight=27g/mol, C p,s =26(J/molK), C p,L =29(J/molK), Melting point=932K, Heat of fusion=10700J/mol Solution)(28.0)(7.2793600110002727184)/(2718410700)9321000(29)298932(261000932,932298,1000,kW W P mol J H dT C dT C H SLL P S P l ==⨯⨯==+-⨯+-⨯=++=⎰⎰1.15 A waste material (dross from the melting of aluminum) is found to contain 1 wt% metallic aluminum. The rest may be assumed to aluminum oxide. The aluminum is finely divided and dispersed in the aluminum oxide; that is the two material are thermally connected.If the waster material is stored at 298K. what is the maximum temperature to which it may rise if all the metallic aluminum is oxidized by air/ the entire mass may be assumed to rise to the same temperature. Data : atomic weight Al=27g/mol, O=16g/mol, C p,s,Al =26(J/molK), C p,s, Al2O3=104J/mol, heat formation of Al 2O 3=-1676000J/molSolution;)(600)(3021041029927275.116122711676000K T K T T ==∆∆⨯⨯++⨯⨯=⨯⨯1.16 Metals exhibit some interesting properties when they are rapidly solidified from the liquid state. An apparatus for the rapid solidification of copper is cooled by water. In the apparatus, liquid copper at its melting point (1356K) is sprayed on a cooling surface, where it solidified and cools to 400K. The copper is supplied to the apparatus at the rate of one kilogram per minute. Cooling water is available at 20℃, and is not allowed to raise above 80℃. What is the minimum flow rate of water in the apparatus, in cubic meters per minute? DATA; for water: C p =4.184J/g k, Density=1g/cm 3; for copper: molecular weight=63.54g/mol C p =7cal/mol k, heat of fusion=3120 cal/molSolution:min)/(10573.2)2080(1min /min54.631000)]4001356(73120[min /33m V VQQ WaterCopper -⨯=-=⨯⨯-⨯+=1.17 water flowing through an insulated pipe at the rate of 5L/min is to be heated from 20℃ to 60℃ b an electrical resistance heater. Calculate the minimum power rating of the resistance heater in watts. Specify the system and basis for you calculation. DA TA; For water C p =4.184J/g k, Density=1g/cm 3 Solution:)(139476010005)2060(184.4W W =⨯⨯-⨯=1.18 The heat of evaporation of water at 100℃ and 1 atm is 2261J/mol (a) what percentage of that energy is used as work done by the vapor?(b)if the density of water vapor at 100℃ and 1 atm is 0.597kg/m 3 what is the internal energy change for the evaporation of water?Solution:)/(375971822613101%6.71822613101%)/(31010224.0273373101325mol J Q W U mol J V P =⨯+-=+=∆=⨯==⨯⨯=∆1.19 water is the minimum amount of steam (at 100℃ and 1 atm pressure) required to melt a kilogram of ice (at 0℃)? Use data for problem 1.20 Solution)(125,3341000)10018.42261(g m m =⨯=⨯+1.20 in certain parts of the world pressurized water from beneath the surface of the earth is available as a source of thermal energy. To make steam, the geothermal water at 180℃ is passed through a flash evaporator that operates at 1atm pressure. Two streams come out of the evaporator, liquid water and water vapor. How much water vapor is formed per kilogram of geothermal water? Is the process reversible? Assume that water is incompressible. The vapor pressure of water at 180℃ is 1.0021 Mpa( about 10 atm) Data: C P,L =4.18J/(g k), C P ,v =2.00J/(g k), △H V =2261J/g, △H m =334 J/g Solution:leirreversib g x x x )(138),1000(8018.4)8018.48022261(=-⨯⨯=⨯-⨯+The problems of the second law2.1 The solar energy flux is about 4J cm 2/min. in no focusing collector the surface temperature can reach a value of about 900℃. If we operate a heat engine using the collector as the heat source and a low temperature reservoir at 25℃, calculate the area of collector needed if the heat engine is to produce 1 horse power. Assume the engine operates at maximum efficiency.Solution)(25.6)(7466010427390)2590(24m S W tWP StQ T T T W H H L H ===⨯⨯+-=-=2.2 A refrigerator is operated by 0.25 hp motor. If the interior of the box is to be maintained at -20℃ ganister a maximum exterior temperature of 35℃, what the maximum heat leak (in watts) into the box that can be tolerated if the motor runs continuously? Assume the coefficient of performance is 75% of the value for a reversible engine.Solution:)(64374625.02035202734375.0W P P T T T P Q T T T W L LL LH HHLH =⨯⨯+-⨯=-=-=2.3 suppose an electrical motor supplies the work to operate a Carnot refrigerator. The interior of the refrigerator is at 0℃. Liquid water is taken in at 0℃ and converted to ice at 0℃. To convert 1 g of ice to 1 g liquid. △H=334J/g is required. If the temperature outside the box is 20℃, what mass of ice can be produced in one minute by a 0.25 hp motor running continuously? Assume that the refrigerator is perfectly insulated and that the efficiencies involved have their largest possible value.Solution:)(4576033474625.020273g m M m P P T T T P L LLLH ===⨯⨯=-=2.4 under 1 atm pressure, helium boils at 4.126K. The heat of vaporization is 84 J/mol what size motor (in hp) is needed to run a refrigerator that must condense 2 mol of gaseous helium at 4.126k to liquid at the same temperature in one minute? Assume that the ambient temperature is 300K and that the coefficient of performance of the refrigerator is 50% of the maximum possible.Solution:)(52.0)(393'60284216.4216.4300'5.0%50hp W P P T T T P P Q T T T W L L L H LLLH ==⨯⨯-=-==-=2.5 if a fossil fuel power plant operating between 540 and 50℃ provides the electrical power to run a heat pump that works between 25 and 5℃, what is the amount of heat pumped into the house per unit amount of heat extracted from the power plant boiler.(a) assume that the efficiencies are equal to the theoretical maximum values(b) assume the power plant efficiency is 70% of maximum and that coefficient of performance of the heat pumpis 10% of maximum(c) if a furnace can use 80% of the energy in fossil foe to heat the house would it be more economical in terms ofoverall fissile fuel consumption to use a heat pump or a furnace ? do the calculations for cases a and b solution:1,2,2,1,212,2,2,2,21,1,1,1,198.82527352527354050540)(H H H H H H L H H H L H P P P P P P P T T T P P T T T P a =+-=+-=-=-= .,)(6286.0)(1,2,not is b ok is a c PP b H H =2.6 calculate △U and △S when 0.5 mole of liquid water at 273 K is mixed with 0.5 mol of liquid water at 373 K and the system is allowed to reach equilibrium in an adiabatic enclosure. Assume that C p is 77J /(mol K) from 273K to 373K Solution:)/(933.0)273323ln(5.0)373323ln(5.0)ln()ln()(02211K J C C T T C n T T C n S J U P P E P E P =+=+=∆=∆2.7 A modern coal burning power plant operates with a steam out let from the boiler at 540℃ and a condensate temperature of 30℃.(a) what is the maximum electrical work that can be produced by the plant per joule of heat provided to theboiler?(b) How many metric tons (1000kg) of coal per hour is required if the plant out put is to be 500MW (megawatts).Assume the maximum efficiency for the plant. The heat of combustion of coal is 29.0 MJ/k g(c) Electricity is used to heat a home at 25℃ when the out door temperature is 10℃ by passing a currentthrough resistors. What is the maximum amount of heat that can be added to the home per kilowatt-hour of electrical energy supplied?Solution:)(3.69)(6937136005000.29)()(89.013054030540)(ton kg m T T T mb J Q T T T W a LH LH H L H ==⨯=-=+-=-= )(9.191102525273)(J Q Q T T T W c H HHLH =-+=-=2.8 an electrical resistor is immersed in water at the boiling temperature of water (100℃) the electrical energy input into the resistor is at the rate of one kilowatt(a) calculate the rate of evaporation of the water in grams per second if the water container is insulated that is noheat is allowed to flow to or from the water except for that provided by the resistor(b) at what rate could water could be evaporated if electrical energy were supplied at the rate of 1 kw to a heatpump operating between 25 and 100℃data for water enthalpy of evaporation is 40000 J/mol at 100℃; molecular weight is 18g/mol; density is 1g/cm 3solution:)(23.2,2510027310010004000018)()(45.0,10004000018)(g m m b g m ma =-+===2.9 some aluminum parts are being quenched (cooled rapidly ) from 480℃ to -20℃ by immersing them in abrine , which is maintained at -20℃ by a refrigerator. The aluminum is being fed into the brine at a rate of one kilogram per minute. The refrigerator operates in an environment at 30℃; that is the refrigerator may reject heat at 30℃. what is them minus power rating in kilowatts, of motor required to operate the refrigerator?Data for aluminum heat capacity is 28J/mol K; Molecular weight 27g/mol Solution:)(5.102)(102474202732030)20480(28271000kW W P P T T T P P L L L L H W L ==---=-=--⨯=2.10 an electric power generating plant has a rated output of 100MW. The boiler of the plant operates at 300℃. The condenser operates at 40℃(a) at what rate (joules per hour) must heat be supplied to the boiler?(b) The condenser is cooled by water, which may under go a temperature rise of no more than 10℃. Whatvolume of cooling water in cubic meters per hour, is require to operate the plant?(c) The boiler tempeture is to be raised to 540℃,but the condensed temperature and electric output will remainthe same. Will the cooling water requirement be increased, decreased, or remain the same?Data heat capacity 4.184, density 1g/cm 3 Solution: )(109.7)(102.21040300273300)(1188J t P Q W P T T T P a H H L H H H ⨯==⨯=-+=-= )(1003.1184.41010)(103.4)(34611m V Q V J Q b LL ⨯==⨯⨯⨯⨯= noW P T T T P c L H H H )(10626.11040540273540)(88⨯=-+=-= 2.11 (a) Heat engines convert heat that is available at different temperature to work. They have been several proposals to generate electricity y using a heat engine that operate on the temperature differences available at different depths in the oceans. Assume that surface water is at 20℃, that water at a great depth is at 4℃, and that both may be considered to be infinite in extent. How many joules of electrical energy may be generated for each joule of energy absorbed from surface water? (b) the hydroelectric generation of electricity use the drop height of water as the energy source. in a particular region the level of river drops from 100m above sea level to 70m above the sea level . what fraction of the potential energy change between those two levels may be converted into electrical energy? how much electrical energy ,in kilowatt-hours, may be generated per cubic meter of water that undergoes such a drop? Solution: )/(1006.136001000)()(055.0127320420)(6h kW h mg P b J Q T T T W a H H L H ⨯=⨯∆==+-=-=2.12 a sports facility has both an ice rink and a swimming pool. to keep the ice frozen during the summer requires the removal form the rink of 105 KJ of thermal energy per hour. It has been suggested that this task be performed by a thermodynamic machine, which would be use the swimming pool as the high temperature reservoir. The ice in the rink is to be maintain at a temperature of –15℃, and the swimming pool operates at 20℃, (a) what is the theoretical minimum power, in kilowatts, required to run the machine? (b) how much heat , in joule per hour , would be supplied t the pool by this machine?Solution: )(1014.1101527320273)()(77.33600/10152731520)(555kJ Q b kW P T T T P a H L L L H ⨯=-+==-+=-=2.13solution:)/(81.6810ln 314.877.45277.6282.4)/(152940)()/(67.4977.45277.6282.4)()/(152940)(22)(2molK cal S mol cal H d molK cal S c mol cal H b AlNN Al a -=+-⨯-⨯=∆=∆-=-⨯-⨯=∆=∆=+ 2.14 solution:)/(2257412000)27340273ln 184.4273336263273ln1.2()(400,010,K J dT T C T H dT T C m S WATER P m m ICE P =+++=+∆+=∆⎰⎰-2.15)(70428)(2896100077773002J W J Q T T T W L L L H ==-=-= 2.16)(4.3719))2.4300(314.85.13.83(3002.4300)(7.58663.832.42.4300J Q T T T W J Q T T T W H H L H L L L H =-⨯+-=-==-=-=2.17 yes d Q c K J P P nR S b J pdV n W Q OU T a )(0)()/(1.1910ln 314.81ln)()(570410ln 298314.810)(0==⨯⨯==∆=⨯⨯=-=-==∆=∆⎰ 2.18)(1222335273020********g m m m T T T L L H =-=-=⨯ Property Relations 1. At -5︒C, the vapor pressure of ice is 3.012mmHg and that of supercooled liquid water is 3.163mmHg. The latent heat of fusion of ice is 5.85kJ/mol at -5︒C. Calculate ∆G and ∆S per mole for the transition of from water to ice at -5︒C. (3.2, 94) Solution: mol J P P RT G waterO H iceO H /9.1089523.0ln 268314.8163.3012.3ln )5273(314.8ln ,,22-=⨯⨯=-⨯==∆mol J H /1085.53⨯=∆)/(23.22268)9.108(5850K mol J T G H S S T H G ⋅=--=∆-∆=∆∴∆-∆=∆ 2. (1) A container of liquid lead is to be used as a calorimeter to determine the heat of mixing of two metals, A andB. It has been determined by experiment that the “heat capacity ” of the bath is 100cal/︒C at 300︒C. With the bath originally at 300︒C, the following experiments are performed;(2) A mechanical mixture of 1g of A and 1g of B is dropped into the calorimeter. A and B were originally at 25︒C. When the two have dissolved, the temperature of the bath is found to have increased 0.20︒C. 2. Two grams of a 50:50(wt.%) A-B alloy at 25︒C is dropped similarly into the calorimeter. The temperature decreases 0.40︒C. (a) What is the heat of mixing of the 50:50 A-B alloy (per gram of alloy)? (b) To what temperature does it apply ? (3.5, 94)Solution: mol J K cal C bath P /418/100,==(a) g cal T C Q bath P /102/2.01002/,=⨯=∆=This is the heat of mixing.(b) The heat capacity of C P, alloy : )/(072.06.27424.0100)254.0300(2,,K g cal TC C bath P alloy P ⋅=⨯⨯=--⨯∆⨯=Assuming that the calorimeter can be applied to the maximum of T ︒C, the for mixing to form 1 gram of alloy:10)'300(,1+-=T C Q bath P , )'(,2T T C Q alloy P -⋅=, 21Q Q =)'(10)'300(,,T T C T C alloy P bath P -=+-3. The equilibrium freezing point of water is 0︒C. At that temperature the latent heat of fusion of ice (the heat required to melt the ice) is 6063J/mol. (a) What is the entropy of fusion of ice at 0︒C ? (b) What is the change of Gibbs free energy for ice →water at 0︒C?(c) What is the heat of fusion of ice at -5︒C ? C P(ice) = 0.5 cal/(g. ︒C); C P(water) = 1.0 cal/(g. ︒C). (d) Repeat parts a and b at -5︒C. (3.6, p94)Solution: (a) At 0︒C, ∆G =0, ∴ T m ∆S = ∆H)./(09.222736030K mol J T H S m ==∆=∆(b) At 0︒C, ∆G =0© )./(62.37)./(1818.45.0)./(5.0,K mol J K mol J K g cal C ice P =⨯⨯==)./(24.75)./(1818.40.1)./(0.1,K mol J K mol J K g cal C water P =⨯⨯==a reversible process can be designed as follows to do the calculation:。

热力学复习题答案1. 热力学第一定律表述了能量守恒的原理，其数学表达式为：\[ \Delta U = Q - W \]其中，\( \Delta U \) 表示内能的变化，\( Q \) 表示系统吸收的热量，\( W \) 表示系统对外做的功。

2. 热力学第二定律指出，热量不能自发地从低温物体传到高温物体，其数学表达式为：\[ \Delta S \geq \frac{Q}{T} \]这里，\( \Delta S \) 表示熵变，\( Q \) 表示热量，\( T \) 表示温度。

3. 理想气体的状态方程为：\[ PV = nRT \]其中，\( P \) 表示压强，\( V \) 表示体积，\( n \) 表示摩尔数，\( R \) 表示理想气体常数，\( T \) 表示温度。

4. 卡诺循环的效率公式为：\[ \eta = 1 - \frac{T_c}{T_h} \]这里，\( \eta \) 表示效率，\( T_c \) 表示冷源温度，\( T_h \)表示热源温度。

5. 热力学第三定律表述了绝对零度不可达到的原理，即：\[ \lim_{T \to 0} S = 0 \]其中，\( S \) 表示熵，\( T \) 表示温度。

6. 熵变可以通过以下公式计算：\[ \Delta S = \int \frac{\delta Q}{T} \]这里，\( \Delta S \) 表示熵变，\( \delta Q \) 表示微小的热量变化，\( T \) 表示温度。

7. 吉布斯自由能的变化可以用来判断反应的自发性，其表达式为：\[ \Delta G = \Delta H - T\Delta S \]其中，\( \Delta G \) 表示吉布斯自由能的变化，\( \Delta H \) 表示焓变，\( T \) 表示温度，\( \Delta S \) 表示熵变。

8. 热力学中的麦克斯韦关系可以通过以下公式表示：\[ \left( \frac{\partial S}{\partial V} \right)_T =\left( \frac{\partial P}{\partial T} \right)_V \]这里，\( S \) 表示熵，\( V \) 表示体积，\( P \) 表示压强，\( T \) 表示温度。

The problems of the first law1.1 a lead bullet is fired at a frigid surface. At what speed must it travel to melt on impact, if its initial temperature is 25℃ and heating of the rigid surface of the rigid surface is neglected? The melting point of lead is 327℃. The molar heat of fusion of the lead is 4.8kJ/mol. The molar heat capacity C P of lead may be taken as 29.3J/(mol K)Solution: )/(363102.20721]108.4)25327(3.29[2121)(23322s m V v n n WQ nMv mv W H T C n Q Q Q absorb melting p melt increase absorb =⨯=⨯+-⨯===∆+∆=+=-1.2 what is the average power production in watts of a person who burns 2500 kcal of food in a day? Estimate the average additional powder production of 75Kg man who is climbing a mountain at the rate of 20 m/minSolution )/(24560208.975)/(12160602410467000//)(104670001868.4102500sin 3S J t h mg P S J t Q t W PJ Q gincrea Burning Burning =⨯⨯=∆==⨯⨯====⨯⨯=1.3 One cubic decimeter (1 dm 3) of water is broken into droplets having a diameter of one micrometer (1 um) at 20℃.(a) what is the total area of the droplets?(b) Calculate the minimum work required to produce the droplets. Assume that the droplets are rest (have zerovelocity)Water have a surface tension of 72.75 dyn/cm at 20℃ (NOTES: the term surface energy (ene/cm 2) is also used for surface tension dyn/cm)Solution)(6.436)106103(1075.72)(106)105.0(4)105.0(34)101(232523263631J S W m nS S Single total =⨯-⨯⨯⨯=∆=⨯=⨯⨯⨯⨯⨯⨯⨯⨯==-+----σππ1.4 Gaseous helium is to be used to quench a hot piece of metal. The helium is in storage in an insulated tank with a volume of 50 L and a temperature of 25℃, the pressure is 10 atm. Assume that helium is an ideal gas.(a) when the valve is opened and the gas escapes into the quench chamber (pressure=1 atm), what will be thetemperature of the first gas to hit the specimen?(b) As the helium flows, the pressure in the tank drops. What will be the temperature of the helium entering thequench chamber when the pressure in the tank has fallen to 1 atm?Solution: )(180118298)(1185.229810101325501010101325)5500(1)()(118)101(298)()(0334.0/00K T T T K RR nC W T b K T P P T T Adiabatica p CR P=-=∆-==⨯⨯⨯⨯⨯⨯⨯-⨯==∆=⨯==--1.5 An evacuated (P=0), insulted tank is surrounded by a very large volume (assume infinite volume) of an ideal gas at a temperature T 0. The valve on the tank is oðened and the surrounding gas is allowed to flow suickly into t(e tank until the pressure insi`e the tank is equals the pressure outside. Assume that no heat flow takes place. What is the0final tempeture kf t èe gaS in the tank? The heat cap!city mf the gas, C p and C v each íay be(assumed to be c/nsuant over thå temperature rang!spanNed by the døperiment. You answer may be meft in terms of C p and S vM hint: one way to approach the xroblem is to define the system as the gas ends up in the tank. hint: one way to approach the xroblem is to define the system as the gas ends up in the tank.solution 0/000/00)()(T P P T T P PT T Adiabatic PPC R C R ≈-==1.6 Calculate the heat of reaction of methane with oxygen at 298K, assuming that the products of reaction are CO 2 and CH 4 (gas)[This heat of reaction is also called the low calorific power of methane] convert the answer into unites of Btu/1000 SCF of methane. SCF means standard cubic feet, taken at 298 and 1atm NOTE: this value is a good approximation for the low calorific powder of natural gasDATA: )()()(224g O H g CO g CH FOR80.5705.9489.17]/[0298---∙∆mol g Kcal Hsolution)1000/(9.2610252103048.01101076.191)/(76.191)89.1780.57205.94()2(22333332982982224422SCF Btu mol g Kcal H H H H H OH CO O CH CH O H CO =⨯⨯⨯⨯⨯=∙=∆+⨯---=∆-∆+∆-=∆+=+- 1.7Methane is delivered at 298 K to a glass factory, which operates a melting furnace at 1600 K. The fuel is mixed with a quantity of air, also at 298 K, which is 10% in excess of the amount theoretically needed for complete combustion (air is approximately 21% O 2 and 79% N 2)(a) Assuming complete combustion, what is the composition of the flue gas (the gas following combustion)? (b) What is the temperature of the gas, assuming no heat loss?(c) The furnace processes 2000kg of glass hourly, and its heat losses to the surroundings average 400000 kJ/h.calculate the fuel consumption at STP (in m 3/h) assuming that for gas H 1600-H 298=1200KJ/KG(d) A heat exchanger is installed to transfer some of the sensible heat of the flue gas to the combustion air.Calculate the decrease in fuel consumption if the combustion air is heated to 800K DATA STP means T=298K, P=1atm22224O N O H CO CH for2.82.89.117.1316)/(C mol cal C P ∙Solution)(210448.1125.9100076.191298)/(25.9)]87.012.72(2.843.179.1171.87.13[01.0)(%87.0%%12.72%%43.17%2%%71.8)11.1(221791.1231%22)(0,,222222224K T T T C mol cal X C C b O N CO O H CO O H CO O CH a i i p p p =⨯⨯+=∆+=∙=+⨯+⨯+⨯=======-⨯+⨯⨯+=+=+∑)/(1644)0224.011868.448.11)8001600(48.1125.9189570(102800000)/(189570)298800)](48.1187.8)48.1125.9[(100076.191)()/(87.848.11/]211002.22.816[)()/(3214)0224.011868.448.11)2981600(48.1125.9100076.191(102800000)/(280000040000020001200)(33min ,,,,298,,33min h m V mol g cal dTn C n C H H C mol cal X C C d h m V h KJ P C gConsu i i r p i i p p i i p r p g Consu =⨯⨯-⨯-⨯=∙=-⨯-⨯-⨯=--∆=∆∙=⨯⨯+===⨯⨯-⨯-⨯⨯==+⨯=⎰∑∑∑1.8 In an investigation of the thermodynamic properties of a-manganese, the following heat contents were determined:H 700-H 298=12113 J/(g atom) H 1000-H 298=22803 J/(g atom)Find a suitable equation for H T -H 298 and also for C P as a function of temperature in the form (a+bT) Assume that no structure transformation takes place in the given tempeture rang.Solution )298(0055.0)298(62.35011.062.35011.062.3522803)2981000(2)2981000(12113)298700(2)298700(]2[2229822222982---=∆-=-===-+-=-+-+=+==∆⎰⎰T T H TC b a ba ba T baT bTdT a dT C H T P T P1.9 A fuel gas containing 40% CO, 10% CO 2, and the rest N 2 (by volume) is burnt completely with air in a furnace. The incoming and ongoing temperatures of the gases in the furnace are 773K and 1250K,respectively. Calculate (a) the maximum flame temperature and (b) heat supplied to the furnace per cu. ft of exhaust gasmolJ Hmol J H CO f CO f /393296/1104580,298,0,298,2-=∆-=∆)/(10184.403.29)/(1067.11010.492.19)/(1037.81020.935.44)/(1042.01097.345.283,253,253,253,222molK J T C molK J T T C molK J T T C molK J T T C N P O P CO P CO P -------⨯+=⨯-⨯+=⨯-⨯+=⨯-⨯+= Solution?0)499.0321.018.1()1067.01019.277.28(28.282831067.01038.477.289.0)1019.01058.528.33(2.0282838)()/(1019.01058.528.33722.0278.0)/(1067.01038.477.281.065.005.02.0)()/(282838110458393296%2.72%8.27%10%65%5%20)4/(1122298127332981523733253253298,,,,298,253,,,,,253,,,,,,,0,298,0,298,298,22222222222222==+--⨯+⨯++⨯=⨯-⨯++⨯⨯-⨯+-⨯=--∆=∆⨯-⨯+=+==⨯-⨯+=+++===-=∆-∆=∆========+-----------⎰⎰⎰∑∑⎰∑∑∑∑T T T T T T T dTT T dTT T dTn C n C n H H molK J T T C C n C C molK J T T C C C C n C C a mol J n Hn H H N CO production O N CO CO reation then O N air mole need fuel mole when CO O CO T TT i i r p i i p p i i N P CO P i i p p r p O P N P CO P CO P i i p p r p i pf i rf idTT T Q dT T T Q b T T T T T T T dTT T dTT T dT n C n C n H H T TT i i r p i i p p i i 9.0)1019.01058.528.33(2.02828389.0)1019.01058.528.33(2.0282838)(0)499.0321.018.1()1067.01019.277.28(28.282831067.01038.477.289.0)1019.01058.528.33(2.0282838)(253125029812502982531250298125029829812125029815231250253253298,,,,298,⨯⨯-⨯++⨯-=⨯⨯-⨯++⨯-===+--⨯+⨯++⨯=⨯-⨯++⨯⨯-⨯+-⨯=--∆=∆-----------⎰⎰⎰⎰⎰∑∑⎰1.10 (a) for the reaction2221CO O CO →+,what is the enthalpy of reaction (0H ∆) at 298 K ?(b) a fuel gas, with composition 50% CO, 50% N 2 is burned using the stoichiometric amount of air. What is the composition of the flue gas?(c) If the fuel gas and the air enter there burner at 298 K, what is the highest temperature the flame may attain(adiabatic flame temperature)? DATA :standard heats of formationfH ∆ at 298 K)/(393000)/(1100002mol J CO mol J CO -=-=Heat capacities [J/(mol K)] to be used for this problem N 2=33, O 2=33, CO=34, CO 2=57Solution )(21100)298)(39889.0(222.02830000)/(3975.03325.057)/(33111.034222.033666.033)(%,75%%,251.111002.22%%1.11%%,6.66%%,2.222.0/25.015.0%)()/(283000393000110000)(,0,,,,,,22220,298,0,298,0K T T dT C n H H K mol J X C C K mol J X C C C N CO product O N CO fuel b mol J n H n H H a P p p i P r i P r i P p i P p i P f i r f ==-⨯-⨯=-∆=∆∙=⨯+⨯==∙=⨯+⨯+⨯====-====+==+-=∆-∆=∆⎰∑∑∑∑1.11 a particular blast furnace gas has the following composition by (volume): N 2=60%, H 2=4, CO=12%, CO 2=24%(a) if the gas at 298K is burned with the stochiometric amount of dry air at 298 K, what is the composition of the flue gas? What is the adiabatic flame temperature?(b) repeat the calculation for 30% excess combustion air at 298K(C)what is the adiabatic flame temperature when the blast furnace gas is preheated to 700K (the dry air is at 298K) (d) suppose the combustion air is not dry ( has partial pressure of water 15 mm Hg and a total pressure of 760 mm Hg) how will thE dlaMe temperature be affected?DaTA(k J?mol)2CO CO FOR513.393523.110)/(--∆m o l kJ H f2222,)(O N g O H CO CO FOR?? 34505733]/[K mol J C P ∙SolutionOH O H CO O CO a 222222121)(→+→+ 416.0)(104.0)(:22==N n O n Air6.0)(04.0)(24.0)(12.0)(:222====N n H n CO n CO n Fuel 32.0)(08.0)(:22==N n O n Air 92.0)(04.0)(36.0)(:222===N n O H n CO n Flue)(98.1108)(8108.53106308.43)/(8.533492.05004.05736.092.004.036.06308.43)08.241(04.0)523.11051.393(12.03,,222222K T K T K J C C C n CKJH H H N O H CO ii r P O H H CO CO ==⨯=∆=⨯+⨯+⨯=++==-⨯+-⨯=∆+∆=∆∑--(b)repeat the calculation for 30% excess0combustion air at 298K6.0)(04.0)(24.0)(12.0)(:222====N n H n CO n CO n Fuel416.0)(104.0)(:22==N n O n Air 024.0)(016.1)(04.0)(36.0)(:2222====O n N n O H n CO n Flue July 16, 2019(C)what is the adiabatic flame temperature when the blasp furnace gas is preheated to 700K (the dry air is at 298K)6.0)(04.0)(24.0)(12.0)(:222====N n H n CO n CO n Fuel 32.0)(08.0)(:22==N n O n Air 92.0)(04.0)(36.0)(:222===N n O H n CO n Flue)(6.1401)(6.11038.5310373.59)/(8.533492.05004.05736.096.004.036.0373.59)346.02804.05724.03312.0()298700()08.241(04.0)523.11051.393(12.03,,298700222222K T K T K J C C C n CKJH H H H N O H CO ii r P fuel O H H CO CO ==⨯=∆=⨯+⨯+⨯=++==⨯+⨯+⨯+⨯⨯-+-⨯+-⨯=∆+∆+∆=∆∑---(d) suppose the combustion air is not dry ( has partial pressure of water 15 mm Hg and a total pressure of 760 mm Hg) how will the flame temperature be affected?)(8.1051)(8.75388.57106308.43)/(88.5734024.034016.15004.05736.0024.0016.104.036.06308.43)08.241(04.0)523.11051.393(12.03,,2222222K T K T K J C C C C n CKJH H H O N O H CO ii r P O H H CO CO ==⨯=∆=⨯+⨯+⨯+⨯=+++==-⨯+-⨯=∆+∆=∆∑--6.0)(04.0)(24.0)(12.0)(:222====N n H n CO n CO n Fuel 008.04.01576015)(32.0)(08.0)(:222=-===O H n N n O n Air 92.0)(048.0)(36.0)(:222===N n O H n CO n Flue)(1103)(8052.54106308.43)/(2.543492.050048.05736.092.0048.036.06308.43)08.241(04.0)523.11051.393(12.03,,222222K T K T K J C C C n CKJH H H N O H CO ii r P OH H CO CO ==⨯=∆=⨯+⨯+⨯=++==-⨯+-⨯=∆+∆=∆∑--1.12 A bath of molten copper is super cooled to 5℃ below its true melting point. Nucleation of solid copper then takes place, and the solidification proceeds under adiabatic conditions. What percentage of the bath solidifies? DATA: Heat of fusion for copper is 3100 cal/mol at 1803℃(the melting point of copper) C P,L =7.5(cal/mol ℃), C P,S =5.41+(1.5*10-3T )(cal/mol ℃) Solution)/(310355.75.0)17981803(105.1541.5310002231798,1798,17981803,18031798,1803,mol cal HH dT C dT C H LS SL L P S P L S =⨯-⨯-⨯+⨯+==+++-⎰⎰1.13 Cuprous oxide (Cu 2O) is being reduced by hydrogen in a furnace at 1000K, (a)write the chemical reaction for the reduced one mole of Cu 2O(b)how much heat is release or absorbed per mole reacted? Given the quantity of heat and state whether heat is evolved (exothermic reaction) or absorbed (endothermic reaction)DATA: heat of formation of 1000K in cal/mol Cu 2O=-41900 H 2O=-59210 solution)/(173104190059210222mol cal H OH Cu H O Cu =-=∆+=+,exothermic reaction1.14(a) what is the enthalpy of pure, liquid aluminum at 1000K?(b) an electric resistance furnace is used to melt pure aluminum at the rate of 100kg/h. the furnace is fed with solid aluminum at 298K. The liquid aluminum leaves the furnace at 1000K. what is the minimum electric powder rating (kW) of furnace.DATA : For aluminum : atomic weight=27g/mol, C p,s =26(J/molK), C p,L =29(J/molK), Melting point=932K, Heat of fusion=10700J/mol Solution)(28.0)(7.2793600110002727184)/(2718410700)9321000(29)298932(261000932,932298,1000,kW W P mol J H dT C dT C H SLL P S P l ==⨯⨯==+-⨯+-⨯=++=⎰⎰1.15 A waste material (dross from the melting of aluminum) is found to contain 1 wt% metallic aluminum. The rest may be assumed to aluminum oxide. The aluminum is finely divided and dispersed in the aluminum oxide; that is the two material are thermally connected.If the waster material is stored at 298K. what is the maximum temperature to which it may rise if all the metallic aluminum is oxidized by air/ the entire mass may be assumed to rise to the same temperature. Data : atomic weight Al=27g/mol, O=16g/mol, C p,s,Al =26(J/molK), C p,s, Al2O3=104J/mol, heat formation of Al 2O 3=-1676000J/molSolution;)(600)(3021041029927275.116122711676000K T K T T ==∆∆⨯⨯++⨯⨯=⨯⨯1.16 Metals exhibit some interesting properties when they are rapidly solidified from the liquid state. An apparatus for the rapid solidification of copper is cooled by water. In the apparatus, liquid copper at its melting point (1356K) is sprayed on a cooling surface, where it solidified and cools to 400K. The copper is supplied to the apparatus at the rate of one kilogram per minute. Cooling water is available at 20℃, and is not allowed to raise above 80℃. What is the minimum flow rate of water in the apparatus, in cubic meters per minute? DATA; for water: C p =4.184J/g k, Density=1g/cm 3; for copper: molecular weight=63.54g/mol C p =7cal/mol k, heat of fusion=3120 cal/molSolution:min)/(10573.2)2080(1min /min54.631000)]4001356(73120[min /33m V VQQ WaterCopper -⨯=-=⨯⨯-⨯+=1.17 water flowing through an insulated pipe at the rate of 5L/min is to be heated from 20℃ to 60℃ b an electrical resistance heater. Calculate the minimum power rating of the resistance heater in watts. Specify the system and basis for you calculation. DA TA; For water C p =4.184J/g k, Density=1g/cm 3 Solution:)(139476010005)2060(184.4W W =⨯⨯-⨯=1.18 The heat of evaporation of water at 100℃ and 1 atm is 2261J/mol (a) what percentage of that energy is used as work done by the vapor?(b)if the density of water vapor at 100℃ and 1 atm is 0.597kg/m 3 what is the internal energy change for the evaporation of water?Solution:)/(375971822613101%6.71822613101%)/(31010224.0273373101325mol J Q W U mol J V P =⨯+-=+=∆=⨯==⨯⨯=∆1.19 water is the minimum amount of steam (at 100℃ and 1 atm pressure) required to melt a kilogram of ice (at 0℃)? Use data for problem 1.20 Solution)(125,3341000)10018.42261(g m m =⨯=⨯+1.20 in certain parts of the world pressurized water from beneath the surface of the earth is available as a source of thermal energy. To make steam, the geothermal water at 180℃ is passed through a flash evaporator that operates at 1atm pressure. Two streams come out of the evaporator, liquid water and water vapor. How much water vapor is formed per kilogram of geothermal water? Is the process reversible? Assume that water is incompressible. The vapor pressure of water at 180℃ is 1.0021 Mpa( about 10 atm) Data: C P,L =4.18J/(g k), C P ,v =2.00J/(g k), △H V =2261J/g, △H m =334 J/g Solution:leirreversib g x x x )(138),1000(8018.4)8018.48022261(=-⨯⨯=⨯-⨯+The problems of the second law2.1 The solar energy flux is about 4J cm 2/min. in no focusing collector the surface temperature can reach a value of about 900℃. If we operate a heat engine using the collector as the heat source and a low temperature reservoir at 25℃, calculate the area of collector needed if the heat engine is to produce 1 horse power. Assume the engine operates at maximum efficiency.Solution)(25.6)(7466010427390)2590(24m S W tWP StQ T T T W H H L H ===⨯⨯+-=-=2.2 A refrigerator is operated by 0.25 hp motor. If the interior of the box is to be maintained at -20℃ ganister a maximum exterior temperature of 35℃, what the maximum heat leak (in watts) into the box that can be tolerated if the motor runs continuously? Assume the coefficient of performance is 75% of the value for a reversible engine.Solution:)(64374625.02035202734375.0W P P T T T P Q T T T W L LL LH HHLH =⨯⨯+-⨯=-=-=2.3 suppose an electrical motor supplies the work to operate a Carnot refrigerator. The interior of the refrigerator is at 0℃. Liquid water is taken in at 0℃ and converted to ice at 0℃. To convert 1 g of ice to 1 g liquid. △H=334J/g is required. If the temperature outside the box is 20℃, what mass of ice can be produced in one minute by a 0.25 hp motor running continuously? Assume that the refrigerator is perfectly insulated and that the efficiencies involved have their largest possible value.Solution:)(4576033474625.020273g m M m P P T T T P L LLLH ===⨯⨯=-=2.4 under 1 atm pressure, helium boils at 4.126K. The heat of vaporization is 84 J/mol what size motor (in hp) is needed to run a refrigerator that must condense 2 mol of gaseous helium at 4.126k to liquid at the same temperature in one minute? Assume that the ambient temperature is 300K and that the coefficient of performance of the refrigerator is 50% of the maximum possible.Solution:)(52.0)(393'60284216.4216.4300'5.0%50hp W P P T T T P P Q T T T W L L L H LLLH ==⨯⨯-=-==-=2.5 if a fossil fuel power plant operating between 540 and 50℃ provides the electrical power to run a heat pump that works between 25 and 5℃, what is the amount of heat pumped into the house per unit amount of heat extracted from the power plant boiler.(a) assume that the efficiencies are equal to the theoretical maximum values(b) assume the power plant efficiency is 70% of maximum and that coefficient of performance of the heat pumpis 10% of maximum(c) if a furnace can use 80% of the energy in fossil foe to heat the house would it be more economical in terms ofoverall fissile fuel consumption to use a heat pump or a furnace ? do the calculations for cases a and b solution:1,2,2,1,212,2,2,2,21,1,1,1,198.82527352527354050540)(H H H H H H L H H H L H P P P P P P P T T T P P T T T P a =+-=+-=-=-= .,)(6286.0)(1,2,not is b ok is a c PP b H H =2.6 calculate △U and △S when 0.5 mole of liquid water at 273 K is mixed with 0.5 mol of liquid water at 373 K and the system is allowed to reach equilibrium in an adiabatic enclosure. Assume that C p is 77J /(mol K) from 273K to 373K Solution:)/(933.0)273323ln(5.0)373323ln(5.0)ln()ln()(02211K J C C T T C n T T C n S J U P P E P E P =+=+=∆=∆2.7 A modern coal burning power plant operates with a steam out let from the boiler at 540℃ and a condensate temperature of 30℃.(a) what is the maximum electrical work that can be produced by the plant per joule of heat provided to theboiler?(b) How many metric tons (1000kg) of coal per hour is required if the plant out put is to be 500MW (megawatts).Assume the maximum efficiency for the plant. The heat of combustion of coal is 29.0 MJ/k g(c) Electricity is used to heat a home at 25℃ when the out door temperature is 10℃ by passing a currentthrough resistors. What is the maximum amount of heat that can be added to the home per kilowatt-hour of electrical energy supplied?Solution:)(3.69)(6937136005000.29)()(89.013054030540)(ton kg m T T T mb J Q T T T W a LH LH H L H ==⨯=-=+-=-=)(9.191102525273)(J Q Q T T T W c H HHLH =-+=-=2.8 an electrical resistor is immersed in water at the boiling temperature of water (100℃) the electrical energy input into the resistor is at the rate of one kilowatt(a) calculate the rate of evaporation of the water in grams per second if the water container is insulated that is noheat is allowed to flow to or from the water except for that provided by the resistor(b) at what rate could water could be evaporated if electrical energy were supplied at the rate of 1 kw to a heatpump operating between 25 and 100℃data for water enthalpy of evaporation is 40000 J/mol at 100℃; molecular weight is 18g/mol; density is 1g/cm 3solution:)(23.2,2510027310010004000018)()(45.0,10004000018)(g m m b g m ma =-+===2.9 some aluminum parts are being quenched (cooled rapidly ) from 480℃ to -20℃ by immersing them in abrine , which is maintained at -20℃ by a refrigerator. The aluminum is being fed into the brine at a rate of one kilogram per minute. The refrigerator operates in an environment at 30℃; that is the refrigerator may reject heat at 30℃. what is them minus power rating in kilowatts, of motor required to operate the refrigerator?Data for aluminum heat capacity is 28J/mol K; Molecular weight 27g/mol Solution:)(5.102)(102474202732030)20480(28271000kW W P P T T T P P L L L L H W L ==---=-=--⨯=2.10 an electric power generating plant has a rated output of 100MW. The boiler of the plant operates at 300℃. The condenser operates at 40℃(a) at what rate (joules per hour) must heat be supplied to the boiler?(b) The condenser is cooled by water, which may under go a temperature rise of no more than 10℃. Whatvolume of cooling water in cubic meters per hour, is require to operate the plant?(c) The boiler tempeture is to be raised to 540℃,but the condensed temperature and electric output will remainthe same. Will the cooling water requirement be increased, decreased, or remain the same?Data heat capacity 4.184, density 1g/cm 3 Solution: )(109.7)(102.21040300273300)(1188J t P Q W P T T T P a H H L H H H ⨯==⨯=-+=-= )(1003.1184.41010)(103.4)(34611m V Q V J Q b LL ⨯==⨯⨯⨯⨯= noW P T T T P c L H H H )(10626.11040540273540)(88⨯=-+=-= 2.11 (a) Heat engines convert heat that is available at different temperature to work. They have been several proposals to generate electricity y using a heat engine that operate on the temperature differences available at different depths in the oceans. Assume that surface water is at 20℃, that water at a great depth is at 4℃, and that both may be considered to be infinite in extent. How many joules of electrical energy may be generated for each joule of energy absorbed from surface water? (b) the hydroelectric generation of electricity use the drop height of water as the energy source. in a particular region the level of river drops from 100m above sea level to 70m above the sea level . what fraction of the potential energy change between those two levels may be converted into electrical energy? how much electrical energy ,in kilowatt-hours, may be generated per cubic meter of water that undergoes such a drop? Solution: )/(1006.136001000)()(055.0127320420)(6h kW h mg P b J Q T T T W a H H L H ⨯=⨯∆==+-=-=2.12 a sports facility has both an ice rink and a swimming pool. to keep the ice frozen during the summer requires the removal form the rink of 105 KJ of thermal energy per hour. It has been suggested that this task be performed by a thermodynamic machine, which would be use the swimming pool as the high temperature reservoir. The ice in the rink is to be maintain at a temperature of –15℃, and the swimming pool operates at 20℃, (a) what is the theoretical minimum power, in kilowatts, required to run the machine? (b) how much heat , in joule per hour , would be supplied t the pool by this machine?Solution: )(1014.1101527320273)()(77.33600/10152731520)(555kJ Q b kW P T T T P a H L L L H ⨯=-+==-+=-=2.13solution:)/(81.6810ln 314.877.45277.6282.4)/(152940)()/(67.4977.45277.6282.4)()/(152940)(22)(2molK cal S mol cal H d molK cal S c mol cal H b AlNN Al a -=+-⨯-⨯=∆=∆-=-⨯-⨯=∆=∆=+ 2.14 solution:)/(2257412000)27340273ln 184.4273336263273ln1.2()(400,010,K J dT T C T H dT T C m S WATER P m m ICE P =+++=+∆+=∆⎰⎰-2.15)(70428)(2896100077773002J W J Q T T T W L L L H ==-=-= 2.16)(4.3719))2.4300(314.85.13.83(3002.4300)(7.58663.832.42.4300J Q T T T W J Q T T T W H H L H L L L H =-⨯+-=-==-=-=2.17 yes d Q c K J P P nR S b J pdV n W Q OU T a )(0)()/(1.1910ln 314.81ln)()(570410ln 298314.810)(0==⨯⨯==∆=⨯⨯=-=-==∆=∆⎰ 2.18)(1222335273020********g m m m T T T L L H =-=-=⨯ Property Relations 1. At -5︒C, the vapor pressure of ice is 3.012mmHg and that of supercooled liquid water is 3.163mmHg. The latent heat of fusion of ice is 5.85kJ/mol at -5︒C. Calculate ∆G and ∆S per mole for the transition of from water to ice at -5︒C. (3.2, 94) Solution: mol J P P RT G waterO H iceO H /9.1089523.0ln 268314.8163.3012.3ln )5273(314.8ln ,,22-=⨯⨯=-⨯==∆mol J H /1085.53⨯=∆)/(23.22268)9.108(5850K mol J T G H S S T H G ⋅=--=∆-∆=∆∴∆-∆=∆ 2. (1) A container of liquid lead is to be used as a calorimeter to determine the heat of mixing of two metals, A andB. It has been determined by experiment that the “heat capacity ” of the bath is 100cal/︒C at 300︒C. With the bath originally at 300︒C, the following experiments are performed;(2) A mechanical mixture of 1g of A and 1g of B is dropped into the calorimeter. A and B were originally at 25︒C. When the two have dissolved, the temperature of the bath is found to have increased 0.20︒C. 2. Two grams of a 50:50(wt.%) A-B alloy at 25︒C is dropped similarly into the calorimeter. The temperature decreases 0.40︒C. (a) What is the heat of mixing of the 50:50 A-B alloy (per gram of alloy)? (b) To what temperature does it apply ? (3.5, 94)Solution: mol J K cal C bath P /418/100,==(a) g cal T C Q bath P /102/2.01002/,=⨯=∆=This is the heat of mixing.(b) The heat capacity of C P, alloy : )/(072.06.27424.0100)254.0300(2,,K g cal TC C bath P alloy P ⋅=⨯⨯=--⨯∆⨯=Assuming that the calorimeter can be applied to the maximum of T ︒C, the for mixing to form 1 gram of alloy:10)'300(,1+-=T C Q bath P , )'(,2T T C Q alloy P -⋅=, 21Q Q =)'(10)'300(,,T T C T C alloy P bath P -=+-3. The equilibrium freezing point of water is 0︒C. At that temperature the latent heat of fusion of ice (the heat required to melt the ice) is 6063J/mol. (a) What is the entropy of fusion of ice at 0︒C ? (b) What is the change of Gibbs free energy for ice →water at 0︒C?(c) What is the heat of fusion of ice at -5︒C ? C P(ice) = 0.5 cal/(g. ︒C); C P(water) = 1.0 cal/(g. ︒C). (d) Repeat parts a and b at -5︒C. (3.6, p94)Solution: (a) At 0︒C, ∆G =0, ∴ T m ∆S = ∆H)./(09.222736030K mol J T H S m ==∆=∆(b) At 0︒C, ∆G =0© )./(62.37)./(1818.45.0)./(5.0,K mol J K mol J K g cal C ice P =⨯⨯==)./(24.75)./(1818.40.1)./(0.1,K mol J K mol J K g cal C water P =⨯⨯==a reversible process can be designed as follows to do the calculation:。

大学热学题库及答案详解一、选择题1. 热力学第一定律的数学表达式是：A. ΔU = Q - WB. ΔH = Q + WC. ΔS = Q/TD. ΔG = Q - W答案：A2. 在等压过程中，系统与外界交换的热能等于：A. ΔUB. ΔHC. ΔSD. ΔG答案：B3. 理想气体的内能只与温度有关，这是因为：A. 理想气体分子间无相互作用力B. 理想气体分子间有相互作用力C. 理想气体分子的动能与温度无关D. 理想气体分子的势能与温度无关答案：A二、填空题4. 根据热力学第二定律，不可能制造一个循环动作，其唯一结果就是______。

答案：从单一热源吸热全部转化为功而不产生其他效果5. 熵是热力学系统无序程度的度量，其变化量总是______。

答案：不小于零三、简答题6. 简述热力学第二定律的克劳修斯表述和开尔文-普朗克表述。

答案：热力学第二定律的克劳修斯表述是：不可能实现一个循环过程，其唯一结果就是从一个单一热源吸热并将这热量完全转化为功。

开尔文-普朗克表述是：不可能从单一热源吸热使之完全转化为功而不产生其他影响。

7. 解释什么是卡诺循环，并说明其效率。

答案：卡诺循环是一种理想化的热机循环，包括两个等温过程和两个绝热过程。

其效率由下式给出：η = 1 - (Tc/Th)，其中Tc是冷热源的绝对温度，Th是热热源的绝对温度。

四、计算题8. 已知理想气体的摩尔质量为M，气体的温度从T1升高到T2，求气体的内能变化量ΔU。

答案：对于理想气体，内能变化量仅与温度变化有关，与压力和体积无关。

内能变化量可以通过以下公式计算：ΔU = n * Cv * (T2 -T1)，其中n是气体的摩尔数，Cv是摩尔定容热容。

9. 一个绝热容器内装有一定量的气体，气体经历一个绝热过程，其体积从V1减小到V2，求气体的温度变化。

答案：对于绝热过程，根据热力学第一定律，Q = ΔU，且W = -P *ΔV。

由于绝热过程Q = 0，所以ΔU = -W = P * (V1 - V2)。

材料工程基础复习一）导热1，热传导：又称导热，指两个相互接触的物体或同一物体的各部分，由于温差而引起的热量传递现象。

（导热是依靠物体微观粒子的热运动而传递热量，其特点是物体各部位不发生宏观相对位移。

） 傅里叶公式：dxdt kq -= k:导热系数（热导率）：单位温度梯度作用下物体内单位时间，单位面积的传热量；一般情况下，固体的k 值较大，液体次之，气体最小。

q:热流密度:单位时间内通过单位面积的热流量。

Q:热流量：单位时间通过面积A 的热量。

单位：sJW 或2，导热热阻：)(kA R k R δδ==或 对流换热热阻：hR 1= 3，导热微分方程：t t2∇=∂∂ατ①导热系数为常数，无内热源：)(222222zt y t x t t ∂∂∂∂∂∂=∂∂ατ :α导温系数（热扩散率）：ckρα=：反映了导热过程中材料的导热能力（k ）与沿途物质储热能力（c ρ）之间的关系。

热扩散系数说明物体被加热或冷却时，物体内各部分温度趋向于均匀一致的能力。

②导热系数为常数，无内热源，稳态导热：0222222=∂∂∂∂∂∂zty t x t （拉普拉斯方程） 4，热传导分析计算①通过单层平壁的导热：kt t q δ21-= 由于通过每层的热流密度q 一定，所以可以根据 k t t k x t t δ211-=-公式算出在x处的温度，112.t x t t t +-=δ②通过多层平壁的导热：33221141k k k t t q δδδ++-=，同样根据通过各层的热流密度q 一定算出各个地方的温度值。

③复合壁的导热：注意：)(i i i i A k R δ= 一定要加入面积来算热流量Q ，不算热流密度q 。

④通过单层圆筒壁的导热（认为圆筒壁长度远大于直径，简化为沿半径方向的一维导热）：1221ln .21r r kl t t Q π-=1221ln 21r r k t t l Q q l π-== 112211ln ln r r r r t t t t --= 12ln 21r rk R tl π=也可以根据q 一定来计算某点的温度值。

热力学复习题答案
1. 热力学第一定律是什么？请简述其物理意义。

2. 描述热力学第二定律，并给出一个实际应用的例子。

3. 什么是熵？熵增原理如何体现热力学第二定律？
4. 简述卡诺循环的四个步骤，并解释其效率与温度的关系。

5. 什么是理想气体的状态方程？请用数学公式表示。

6. 描述绝热过程，并给出其数学表达式。

7. 什么是热机效率？如何计算一个热机的效率？
8. 什么是热力学温标？它与摄氏温标有何不同？
9. 简述热力学第三定律，并解释其对低温物理研究的意义。

10. 什么是相变？请举例说明不同类型的相变。

11. 描述吉布斯自由能和亥姆霍兹自由能，并解释它们在化学反应中的应用。

12. 什么是化学势？它如何影响物质的相平衡？
13. 简述热力学基本方程，并解释其在热力学分析中的作用。

14. 什么是热力学稳定性？如何判断一个系统是否处于热力学稳定状态？
15. 描述麦克斯韦关系，并说明其在热力学性质计算中的重要性。

16. 什么是热力学势？请举例说明其在多组分系统中的应用。

17. 简述热力学中的可逆过程与不可逆过程，并讨论它们对系统熵的影响。

18. 什么是热力学的零度？它在热力学分析中有何意义？
19. 描述热力学中的混合熵，并解释为什么混合过程总是熵增的。

20. 什么是热力学的临界点？它在相变理论中的作用是什么？。

热力学考试题库及答案一、选择题（每题2分，共20分）1. 热力学第一定律表明能量守恒，下列哪项描述是错误的？A. 能量不能被创造或消灭B. 能量可以从一种形式转换为另一种形式C. 能量可以在系统和周围环境之间转移D. 能量可以在系统中无限增加或减少答案：D2. 根据热力学第二定律，下列哪项描述是正确的？A. 热能自发地从低温物体传递到高温物体B. 热能自发地从高温物体传递到低温物体C. 热能自发地从低温物体传递到高温物体，但需要外部工作D. 热能不能自发地从低温物体传递到高温物体答案：B3. 熵是一个状态函数，它表示系统的哪种属性？A. 能量B. 温度C. 混乱程度D. 压力答案：C4. 在理想气体的等温过程中，下列哪项是正确的？A. 体积和压力成正比B. 体积和压力成反比C. 体积和温度成正比D. 体积和温度成反比答案：B5. 热力学第三定律指出，当温度趋近于绝对零度时，下列哪项属性趋近于零？A. 熵B. 内能C. 压力D. 体积答案：A6. 卡诺循环的效率与哪些因素有关？A. 热源和冷源的温度B. 热源的温度C. 冷源的温度D. 工作介质的种类答案：A7. 热力学中，一个系统经历可逆过程时，下列哪项是正确的？A. 系统和周围环境之间没有能量交换B. 系统和周围环境之间有能量交换，但系统状态可以完全恢复C. 系统和周围环境之间有能量交换，且系统状态不能恢复D. 系统和周围环境之间没有能量交换，且系统状态不能恢复答案：B8. 绝热过程是指系统与外界没有热量交换的过程，下列哪项描述是正确的？A. 系统和周围环境之间有热量交换B. 系统和周围环境之间没有热量交换C. 系统和周围环境之间有做功D. 系统和周围环境之间没有做功答案：B9. 理想气体状态方程为PV=nRT，其中R是？A. 气体常数B. 普朗克常数C. 玻尔兹曼常数D. 阿伏伽德罗常数答案：A10. 根据热力学第一定律，下列哪项描述是错误的？A. 系统内能的增加等于系统吸收的热量和对外做的功之和B. 系统内能的减少等于系统放出的热量和对外做的功之差C. 系统内能的增加等于系统吸收的热量和对外做的功之差D. 系统内能的减少等于系统放出的热量和对外做的功之和答案：C二、填空题（每题2分，共20分）1. 热力学第一定律也称为______定律。

大学物理热学知识点和试题(总15页)-CAL-FENGHAI.-(YICAI)-Company One1-CAL-本页仅作为文档封面，使用请直接删除热学知识点总结1.温度的概念与有关定义1)温度是表征系统热平衡时的宏观状态的物理量。

2)温标是温度的数值表示法。

常用的一种温标是摄氏温标，用t表示，其单位为摄氏度（℃）。

另一种是热力学温标，也叫开尔文温标，用T表示。

它的国际单位制中的名称为开尔文，简称K。

热力学温标与摄氏温标之间的换算关系为：T/K=273.15℃ + t温度没有上限，却有下限。

温度的下限是热力学温标的绝对零度。

温度可以无限接近于0 K，但永远不能到达0 K。

2.理想气体的微观模型与大量气体的统计模型。

速度分布的特征。

1)为了从气体动理论的观点出发，探讨理想气体的宏观现象，需要建立理想气体的微观结构模型。

可假设：a气体分子的大小与气体分子之间的平均距离相比要小得多，因此可以忽略不计。

可将理想气体分子看成质点。

b分子之间的相互作用力可以忽略。

c分子键的相互碰撞以及与器壁的碰撞可以看作完全弹性碰撞。

综上所述：理想气体分子可以被看作是自由的，无规则运动着的弹性质点群。

2）每个分子的运动遵从力学规律，而大量分子的热运动则遵从统计规律。

统计规律告诉我们，可以听过对围观物理量求平均值的方法得到宏观物理量。

气体的宏观参量（温度、压强等）是气体分子热运动的为管理的统计平均值。

3.理想气体状态方程与应用当质量一定的气体处于平衡态时，其三个状态参数P、V、T并不相互独立，二十存在一定的关系，其表达式称为气体的状态方程f（P，V，T）= 0最终得：T V p T pV '''=。

此式称为理想气体的状态方程。

标准状态：RT Mm pV =。

R=8.31J ·mol -1·K -1，称为摩尔气体常量。

设一定理想气体的分子质量为m 0，分子数为N ，并以N A 表示阿伏伽德罗常数，可得：T N R V N V RT m N Nm V RT M m p AA ===00 得：nkT p =，为分子数密度，可谓玻耳玆曼常量，值为1.38×10-23J ·K -1.这也是理想气体的状态方程，多用于计算气体的分子数密度，以及与它相关的其它物理量。

热力学复习题答案热力学是物理学中研究能量转换和物质状态变化规律的科学。

在复习热力学时，理解一些基本概念和原理是至关重要的。

以下是一些热力学复习题的答案，供参考。

1. 热力学第一定律：热力学第一定律是能量守恒定律在热力学过程中的表述。

它表明，系统吸收的热量与对外做的功和系统内能的增加量相等。

即：\[ \Delta Q = \Delta U + W \]其中，\(\Delta Q\) 表示系统吸收或放出的热量，\(\Delta U\)表示系统内能的变化，\(W\) 表示系统对外做的功。

2. 热力学第二定律：热力学第二定律指出，不可能从单一热源吸热使之完全变为功而不产生其他影响。

它揭示了自然过程的不可逆性。

3. 熵：熵是表示系统无序程度的物理量。

熵增加意味着系统无序程度增加。

熵的变化可以通过以下公式计算：\[ \Delta S = \frac{Q_{\text{可逆}}}{T} \]其中，\(\Delta S\) 表示熵的变化，\(Q_{\text{可逆}}\) 表示在可逆过程中系统吸收或放出的热量，\(T\) 是绝对温度。

4. 理想气体状态方程：理想气体状态方程是描述理想气体状态的方程，其形式为：\[ PV = nRT \]其中，\(P\) 表示压强，\(V\) 表示体积，\(n\) 表示物质的量，\(R\) 是理想气体常数，\(T\) 是绝对温度。

5. 卡诺循环：卡诺循环是一种理想化的热机循环，它由两个等温过程和两个绝热过程组成。

卡诺循环的效率是所有循环中最高的，其效率由以下公式给出：\[ \eta = 1 - \frac{T_C}{T_H} \]其中，\(\eta\) 是卡诺循环的效率，\(T_C\) 是冷源的绝对温度，\(T_H\) 是热源的绝对温度。

6. 热力学第三定律：热力学第三定律指出，当系统的温度趋近于绝对零度时，系统的熵趋近于一个常数。

这意味着在绝对零度下，所有完美晶体的熵为零。

7. 吉布斯自由能：吉布斯自由能是描述在恒定温度和压力下，系统能够对外做的最大非体积功的能力。

材料热力学与动力学复习题答案一、常压时纯Al 的密度为ρ=2.7g/cm 3，熔点T m =660.28℃，熔化时体积增加5%。

用理查得规则和克-克方程估计一下，当压力增加1Gpa 时其熔点大约是多少？ 解：由理查德规则RTm Hm R Tm Hm Sm ≈∆⇒≈∆=∆ …①由克-克方程VT H dT dP ∆∆=…② 温度变化对ΔH m 影响较小，可以忽略，①代入②得 V T H dT dP ∆∆=dT T1V Tm R dp V T Tm R ∆≈⇒∆≈…③ 对③积分 dT T1V T Tm R p d T Tm Tm pp p ⎰⎰∆+∆+∆= 整理 ⎪⎭⎫ ⎝⎛∆+∆=∆Tm T 1ln V Tm R p V T R V Tm R Tm T ∆∆=∆⨯∆≈ Al 的摩尔体积 V m =m/ρ=10cm 3=1×10-5m 3Al 体积增加 ΔV=5%V m =0.05×10-5m 3K 14.60314.810510R V p T 79=⨯⨯=∆∆=∆- Tm’=Tm+T ∆=660.28+273.15+60.14=993.57K二、热力学平衡包含哪些内容，如何判断热力学平衡。

内容：（1）热平衡，体系的各部分温度相等；（2）质平衡：体系与环境所含有的质量不变；（3）力平衡：体系各部分所受的力平衡，即在不考虑重力的前提下，体系内部各处所受的压力相等；（4）化学平衡：体系的组成不随时间而改变。

热力学平衡的判据：（1）熵判据：由熵的定义知dS Q T δ≥不可逆可逆对于孤立体系，有0Q =δ，因此有dS 可逆不可逆0≥，由于可逆过程由无限多个平衡态组成，因此对于孤立体系有dS 可逆不可逆0≥，对于封闭体系，可将体系和环境一并作为整个孤立体系来考虑熵的变化，即平衡自发环境体系总0S S S ≥∆+∆=∆ （2）自由能判据 若当体系不作非体积功时，在等温等容下，有()0d ,≤V T F 平衡状态自发过程上式表明，体系在等温等容不作非体积功时，任其自然，自发变化总是向自由能减小的方向进行，直至自由能减小到最低值，体系达到平衡为止。

solution:)/(81.6810ln 314.877.45277.6282.4)/(152940)()/(67.4977.45277.6282.4)()/(152940)(22)(2m olK cal S m ol cal H d m olK cal S c m ol cal H b AlNN Al a -=+-⨯-⨯=∆=∆-=-⨯-⨯=∆=∆=+Solution ：)/(173104190059210222mol cal H OH Cu H O Cu =-=∆+=+,exothermic reactionFor the reaction :)()(212g H g H → 035.33121314.823212,)(,-=⨯-⨯=-=∆H P g H P p C C CJC H dT C H H P oP oo 2128241702035.3217990)2982000(29820002982982000=⨯-=-⨯∆+∆=∆+∆=∆⎰JC H dT C H H P oP oo 2128241702035.3217990)2982000(29820002982982000=⨯-=-⨯∆+∆=∆+∆=∆⎰J C S dT C S S P oP oo 57.432982000ln035.335.492982000ln29820002982982000=⨯-=⨯∆+∆=∆+∆=∆⎰J S T H G 12568457.432000212824020000200002000=⨯-=∆-∆=∆56.72000314.8125684ln125684lnln lnln )(2/1)(2/1)(2/12/1)(20002222=⨯=→==-=-=∆g H H g H H g H H H g H o P P P P RT P P RT P P RT K RT GatmP P P P P H g H H g H g H 0005.0562.71ln1,1)(2)(2)(2=→=≈=+Solution: (a) When the equilibrium is reached,0P ln 21ln 2=∆=+∆=∆O o o RT G J RT G G －RT T P O 21)06.1539850(18.4ln 2+-⨯=T = 500︒C = 773KatmP P O O 26221014.169.36773314.821)77306.1539850(18.4ln -⨯=-=⨯⨯⨯+-⨯=(a) at T=300︒C=573K,Although the equilibrium P O2 is very low, kinetically the reaction isnot favoured and reaction speed is very slow. So 300︒C is not suitable atAt T=800︒C=1073K, lnP O2 =-22.2, P O2 =2.28⨯10-10 atm. At 800︒C, if the equilibrium is reached, nitrogen can be of high purity level. However, at this high temperature , particles of Cu will weld together to reduce effective work surface. So it is not suitable to use this high temperature in purification either.(c ) The equilibrium oxygen pressure remains the same when the total pressure increases, which means a higher purity level of N 2 .Solution: N 2 =2N, H 2 = 2H[]21221,N N a P K N = ， [],21221,H H a P K H =For N2 dissolving :For H2 dissolving ：2/1'2'2/12)(][][H HP H P H =（a ）For dissolving N2, P N2 = 1 atm, [N]=35cm 3/100g melt,melt g cm P N P N N N 100/75.24)5.0(35][)(][32/12/122/1'2=⨯==‘similarly: [H]’ =24.75cm 3/100g melttotal gas : [H]'＋[N]' = 49.5 cm 3/100g melt (b) [H]' =24.75 cm 3/100g melt (c ) [H]'＋[N]' =2/1'2'2/12)(][][N N P N P N = [N](0.33)1/2 /1+[H](0.33)1/2/1=20.10+20.10 = 40.2cm 3/100g meltSolution ： （1）0.2H∆ （2）G∆=max W （3）56KJ.696}{0.21P P P P RTlnG KTlnk G G 23O OH CH CO 20H 2322=+∆=+∆=∆）（）（）（）（θθSolution:(a)molJF Z -6252EG =-=∆θθ(b)0.370a ln RT G Cd==∆ (c))(3.42P PPCdmmHg ==θSolution:(b)PaP P g Cl g Cl 21)()(10*86.8-RT ln G 125.4T -605000G 22-==∆=∆θθ(c)-2.485VZF-GE =∆=答案更正为：Temperat ure Phase CompositionFraction1300 Liquid 60 61.5α8 38.5β99 0 1000+ Liquid 70 50.8α9 49.2β98 0 1000- Liquid _ 0α7 63.7β98 36.3Solution: )/(363102.20721]108.4)25327(3.29[2121)(23322s m V v n n WQ nMv m v W H T C n Q Q Q absorb melting p melt increase absorb =⨯=⨯+-⨯===∆+∆=+=-Solution )/(24560208.975)/(12160602410467000//)(104670001868.4102500sin 3S J t h m g P S J t Q t W P J Q g increa Burning Burning =⨯⨯=∆==⨯⨯====⨯⨯=Solution ：)(6.436)106103(1075.72)(106)105.0(4)105.0(34)101(232523263631J S W m nS S Single total =⨯-⨯⨯⨯=∆=⨯=⨯⨯⨯⨯⨯⨯⨯⨯==-+----σππSolution)(25.6)(7466010427390)2590(24m S W tWP StQ T T T W H H L H ===⨯⨯+-=-=Solution:)(64374625.02035202734375.0W P P T T T P Q T T T W L LLLH HHLH =⨯⨯+-⨯=-=-=solution:1,2,2,1,212,2,2,2,21,1,1,1,198.82527352527354050540)(H H H H H H L H H H L H P P P P P P P T T T P P T T T P a =+-=+-=-=-=.,)(6286.0)(1,2,not is b ok is a c P P b H H =Solution:molJ P P RT G waterO H ice O H /9.1089523.0ln 268314.8163.3012.3ln)5273(314.8ln,,22-=⨯⨯=-⨯==∆mol J H /1085.53⨯=∆)/(23.22268)9.108(5850K mol J T G H S ST H G ⋅=--=∆-∆=∆∴∆-∆=∆Solution: (a) At 0︒C, ∆G =0, ∴ T m ∆S = ∆H)./(09.222736030K mol J T H S m ==∆=∆ (b) At 0︒C, ∆G =0 ©)./(62.37)./(1818.45.0)./(5.0,K mol J K mol J K g cal C ice P =⨯⨯==./(1818.40.1)./(0.1,Kmol J K g cal C water P ⨯⨯==a reversible process can be designed as follows to do the calculation:molJ HdT C C dTC H dT C H H H Hwater P ice p water p ice p fu/9.584160305)24.7562.37()(273268,,268273,273268,)3()2()1(=+⨯-=∆+-=+∆+=∆+∆+∆=∆⎰⎰⎰（d ）)./(39.2109.22268273ln )24.7562.37()(3273268,,268273,273268,)3()2()1()4(K m ol J SdT TC C dTTC S dT TC S S S water P ice p waterp icep =+⨯-=∆+-=+∆+=∆+∆+∆=∆⎰⎰⎰38.10939.212689.5841)4()4()4(=⨯-=∆-∆=∆S T H GIce, 0︒Cwater, 0︒Cwater, -5︒Cice, -5︒C（1）（2）（3）（4）Solution: (a)diam ondgr aphite C C =mol kJ H H H ographite f o diam ond f /1897,,=∆-∆=∆)./(36.338.274.5,,K molJ S S S o graphite f o diam ond f -=+-=∆-∆=∆molJ S T H G /28.2898)36.3(2981897=-⨯-=∆-∆=∆(b) No, diamond is not thermodynamically stable relative to graphite at 298K. (c )molJ P V G diamand /29.34101309951.310126=⨯⨯⨯=∆=∆-(c ) Assuming N atm , ∆G = 0, reversible processes as following can be designed to realize this,（4）graphite, 298K, N atmdiamond, 298K, N atm)(14939028.2898194.028.28981013051.3101225.2101228.289810130)1)(V V ()(V 28.2898V 66)3()2()1()4(atm N N N N P P G G G G diamond graphite diamond graphite ==+-=+⨯⎪⎪⎭⎫ ⎝⎛⨯-⨯-=+⨯--=∆-++∆∆∆∆∆--＝＋＋＝,0,0''=∆=∆=∆⎰⎰dT TC dT C C T Tp T T p pmol J H H /1897298900=∆=∆K mol J S S ./36.3298900-=∆=∆molJ S T H G /492136.39001897=⨯+=∆-∆=∆Solution: (a) Ag 2O = 1/2O 2 + 2Ag30514/7300,==∆-=∆mol cal H H o AgO f o K m ol J S S S S O Ag O Ag o ./044.661.2949212.102212298,2298,2298,=-⨯+⨯=∆-∆+∆=∆TS T S T H G o o o o 044.663051430514-=∆-=∆-∆=∆when Ag2O begins to decompose,ln 044.66305140ln 2=+-=+∆=∆O o P RT T ie J RT G G(a) i n pure oxygen at 1 atm, RTlnP O2 = 030514-66.044T = 0 T = 462K(b) i n air at P total = =1 atm , P O2 =0.21ie. 30514- 66.044T + RTln0.21 = 0 T = 386KSolution: (a))1(ln Td R H K d o a ∆-= Plot T K a /1~ln0.880.900.920.940.960.981.001.02 1.04 1.06 1.087.27.47.67.88.08.28.48.6lnK a =2.01+6003(1/T)l n K a1/T, 10-3KduishuLinear Fit of Data1_Kduishu.J R H RH dT K d o oa 4990960036003ln -=⨯-=∆→=∆-=At T=1000K, lnK a =8.01, K a = 3010kJ J K RT G a o 6.666660001.81000314.8ln 1000==⨯⨯-=-=∆(b)aaa o K J K J RT J RT K RT J RT G G <===+-=+∆=∆3%5%15lnln ln lnSo the atmosphere will oxidize Ni.Solution:(-3)10^*3.680.32*0.00005*320PNa==BrH C B Cl H C X AA 5656A *::A P P =325.101)1(P P 325.101P P B *A *B *A *=-=++A A B A X X X Xk P aP k P a P X X B A B A 71.2659.74404.00.5956====Solution:(1)894.0814.0396.3033.37*30.396kPa 50.66*0.6P )()()(=====R B R A R A A a a a同理得(2)788.162.12222)(='=''=+⨯'=B AAA R A r r r r a 同理得(3)JmixG G mix mixG a RT a RT G mix R B R A 16102ln ln )()(-=∆∆=∆+=∆(4)m olJm ixG G m ix m ixGX RT X RT G m ix id ididBA id 69152ln ln -=∆∆=∆+=∆(5)J mixG mixG mixG id ex 5305=∆-∆=∆c.molJWXmolJWXX W X WX FeMn E MnFeE Mn BA M E 87.71846.16176.094.4492a 22=======μμ时， d.m olJX X X X RT X X RT M EMn Mn Fe Fe MEi i M 9370G )ln ln (G )ln (mixG -=∆++=∆+=∆∑ e.Solution:The standard Gibbs free energy change for reaction I: a.[]298.53TlnT244560-G ⨯+=∆θ b.5422711031074.1ln G --⨯=⨯==∆K K KRT 同理可得θ c.JJ RT G 5107ln G ⨯=+∆=∆θ ; Ni is stable under this condition,and NiO is not stable;d.Paatm P J RT G O 5853103.3103.3ln G 2⨯=⨯=+∆=∆θe 。

一、填空题：(每空1分，共16分)得分评阅人1、Pr = ，表明。

Fr = ，表明。

2、表示燃料的组成有：a 元素分析法：通常包括，其中为燃料的能源主要来源；b 工业分析法：通常包括，其中决定着燃料的着火温度。

3、已知煤的工业分析值：Cad = 40 %，Mar= 8 %，Mad= 4 %，则Car= 。

4、物料的干燥过程可以分成预热阶段，___ ___和___ __________。

5、固体的热辐射是_ ________；而气体是容积内辐射。

6、对不饱和空气，t、twb 、td三者之间的关系为：。

7、一种湿物料，其干基水分为25%，那么换算成湿基水分应为_ __%。

8、一般认为气体对于辐射几乎没有反射能力，则其a、ρ、τ三者的关系是：。

9、通过光谱分析仪测得太阳光的λm= 0.5 μm，则可根据维恩偏移定律计算出太阳的表面温度为。

二、名词解释题：(每题4分，共16分)得分 评阅人1、燃料的热值：2、相似准数：3、理论燃烧温度：4、灰体：三、分析简答题：(每题7分，共21分)得分 评阅人1、何谓兰贝特余弦定律，并根据兰贝特余弦定律判断如图所示的真空辐射炉，球心处有一黑体加热元件，指出①，②，③三处中何处定向辐射强度最大?何处辐射热流最大?假设①，②，③处对球心所张立体角相同。

2、已知流场的运动方程为：u x =y 2+z 2，u y =z 2+x 2，u z =x 2+y 2，请分析说明该流场是否满足③①② 黑体不可压缩流体的连续性条件？3、已知空气温度为30度，相对湿度为60%，请在h-d图上示意画出该空气的露点td、含湿量d0和焓值h。

四、计算题：(共47分)得分评阅人1、某厂蒸汽管道为Φ175×5mm的钢管，外面包了一层95mm厚的石棉保温层，管壁和石棉的导热系数分别为50、0.1W/(m·K)，管道内表面温度为300℃，保温层外表面温度为50℃。

试求每米管长散热损失。

大学热学试题及答案解析一、选择题1. 热力学第一定律表明，能量守恒定律在热现象中同样适用，其数学表达式为：A. △U = Q + WB. △U = Q - WC. △U = Q + PD. △U = Q - P答案：B解析：热力学第一定律，也称为能量守恒定律，表示系统内能的变化等于系统吸收的热量减去系统对外做的功。

因此，正确的表达式是△U = Q - W。

2. 理想气体状态方程为：A. PV = nRTB. PV = mRTC. PV = nMRTD. PV = mMRT答案：A解析：理想气体状态方程描述了理想气体在一定温度和压力下体积和物质的量之间的关系。

其中，P表示压力，V表示体积，n表示物质的摩尔数，R表示理想气体常数，T表示温度。

二、填空题1. 热传导的三种基本方式是：______、______和______。

答案：导热、对流、辐射解析：热传导的三种基本方式分别是导热、对流和辐射。

导热是指热量通过物质内部分子振动传递；对流是指热量通过流体的宏观运动传递；辐射是指热量通过电磁波传递。

2. 根据热力学第二定律，不可能从单一热源取热使之完全变为有用功而不产生其他影响，这被称为______。

答案：开尔文-普朗克表述解析：热力学第二定律有多种表述方式，其中开尔文-普朗克表述指出，不可能从单一热源取热使之完全变为有用功而不产生其他影响。

三、简答题1. 简述热力学第三定律。

答案：热力学第三定律指出，当系统的温度趋近于绝对零度时，系统的熵趋近于一个常数。

解析：热力学第三定律是关于低温物理和熵的一个定律。

它表明，绝对零度是无法达到的，因为当系统温度趋近于绝对零度时，系统的熵趋近于一个常数，而不是零。

2. 解释为什么说热机的效率不可能达到100%。

答案：热机的效率不可能达到100%，因为根据热力学第二定律，不可能从单一热源取热使之完全变为有用功而不产生其他影响。

解析：热机是将热能转化为机械能的设备。

由于热力学第二定律的限制，热机在工作过程中不可避免地会有能量损失，如热量散失、摩擦等，因此其效率不可能达到100%。

热力学基础一、基本要求1. 理解功、热量及准静态过程的概念。

2. 掌握热力学第一定律，能分析计算理想气体等容、等压、等温过程和绝热过程中的功、热量、内能改变量；理解循环过程概念及卡诺循环的特征，并能计算效率和致冷系数。

3. 了解可逆过程、不可逆过程及卡诺定理。

4. 了解热力学第二定律及其统计意义。

二、主要内容1. 准静态过程：过程进行的每一时刻，系统的状态都无限接近平衡态。

准静态过程可以用状态图上的曲线表示。

2. 热力学第一定律（1） 热力学第一定律的数学表达式Q=E 2 - E 1 +Ｗ对微分过程为dQ=dE +d Ｗ热力学第一定律的实质是能量守恒与转换定律在热现象中的应用，其内容表示系统吸收的热量一部分转换为系统的内能，一部分对外做功。

（2） 准静态过程系统对外做功：d Ｗ=pd Ｖ ，Ｗ=⎰12V V pd Ｖ（3） 热量：系统和外界之间或两个物体之间由于温度不同而交换的热运动量，热量也是过程量。

一定摩尔的某种物质，在某一过程中吸收的热量，)(C m12m c,T T M Q -=（4） 摩尔热容：1mo1物质温度变化1K 所吸收或放出的热量，定义式为 dTＱd m,=m c C 其中m 为1mo1 物质吸热。

摩尔定容热容：ＣV , m =摩尔定压热容：Ｃp, m =理想气体的摩尔热容：ＣV, m =，Ｃp, m =Ｃp, m =ＣV, m + 摩尔热容比：=3. 热力学第一定律对理想气体等值过程和绝热过程的应用，详见表1 表1 d =0 =恒量=恒量p =恒量mmmM m Ｔ1nMm Ｔ1nＣV, m =Ｃp, m =4. 循环过程（1）循环过程的特征是E =0热循环：系统从高温热源吸热，对外做功，向低温热源放热，致效率为== 1—致冷循环：系统从低温热源吸热，接受外界做功，向高温热源放热，致冷系数为==（2）卡诺循环：系统只和两个恒温热源进行热交换的准静态循环过程。

卡诺热机的效率为= 1—卡诺致冷机的致冷系数为三、习题与解答1、 如图所示，一定量的空气，开始在状态A ，其压强为2.0×105Pa ，体积为2.0 ×10－3m 3 ，沿直线AB 变化到状态B 后，压强变为1.0 ×105Pa ，体积变为3.0 ×10－3m 3 ，求此过程中气体所作的功.解 S ABCD ＝1/2(BC ＋AD)×CD 故 W ＝150 J2、 汽缸内储有2.0mol 的空气，温度为27 ℃，若维持压强不变，而使空气的体积膨胀到原体积的3倍，求空气膨胀时所作的功. 解 根据物态方程11RT pV v =, 则作功为()J 1097.92231112⨯===-=RT pv V V p W v3、64g 氧气（可看成刚性双原子分子理想气体）的温度由0℃升至50℃，〔1〕保持体积不变；(2)保持压强不变。

第一章 热力学第一定律一、选择题1-A; 2-C; 3-A; 4-D; 5-B; 6-D; 7-A; 8-D; 9-A; 10-D; 11-B; 12-B; 13- A; 14-C; 15-C; 16-B; 17-C;1．下述说法中，哪一种正确（a ）(A)热容C 不是状态函数； (B)热容C 与途径无关；(C)恒压热容C p 不是状态函数；(D)恒容热容C V 不是状态函数。

2．对于内能是体系状态的单值函数概念，错误理解是（c ）(A) 体系处于一定的状态，具有一定的内能；(B) 对应于某一状态，内能只能有一数值不能有两个以上的数值；(C) 状态发生变化，内能也一定跟着变化；(D) 对应于一个内能值，可以有多个状态。

3．某高压容器中盛有可能的气体是O 2 ,Ar, CO 2, NH 3中的一种，在298K 时由5dm3绝热可逆膨胀到6dm3，温度降低21K ，则容器中的气体（ a ）(A) O 2 (B) Ar (C) CO 2 (D) NH 34．戊烷的标准摩尔燃烧焓为-3520kJ·mol -1，CO 2(g)和H 2O(l)标准摩尔生成焓分别为-395 kJ·mol -1和-286 kJ·mol -1，则戊烷的标准摩尔生成焓为（ d ）(A) 2839 kJ·mol -1 (B) -2839 kJ·mol -1 (C) 171 kJ·mol -1 (D) -171 kJ·mol -15．已知反应)()(21)(222g O H g O g H =+的标准摩尔反应焓为)(T H m r θ∆，下列说法中不正确的是（ b ）。

(A).)(T H m r θ∆是H 2O(g)的标准摩尔生成焓 (B). )(T H m r θ∆是H 2O(g)的标准摩尔燃烧焓 (C). )(T H m r θ∆是负值 (D). )(T H m r θ∆与反应的θm r U ∆数值相等 6．在指定的条件下与物质数量无关的一组物理量是（ d ）(A) T , P, n (B) U m , C p, C V(C) ΔH, ΔU, Δξ (D) V m , ΔH f,m (B), ΔH c,m (B)7．实际气体的节流膨胀过程中，下列那一组的描述是正确的（ a ）(A) Q=0 ΔH=0 ΔP< 0 ΔT≠0 (B) Q=0 ΔH<0 ΔP> 0 ΔT>0(C) Q>0 ΔH=0 ΔP< 0 ΔT<0 (D) Q<0 ΔH=0 ΔP< 0 ΔT≠08．已知反应 H 2(g) + 1/2O 2(g) →H 2O(l)的热效应为ΔH ，下面说法中不正确的是（ d ）(A) ΔH 是H 2O(l)的生成热 (B) ΔH 是H 2(g)的燃烧热(C) ΔH 与反应 的ΔU 的数量不等 (D) ΔH 与ΔH θ数值相等9．为判断某气体能否液化，需考察在该条件下的（ a ）(A) μJ-T> 0 (B) μJ-T< 0 (C) μJ-T = 0 (D) 不必考虑μJ-T的数值10．某气体的状态方程为PV=RT+bP(b>0)，1mol该气体经等温等压压缩后其内能变化为（d ）(A) ΔU>0 (B) ΔU <0 (C) ΔU =0 (D) 该过程本身不能实现11．均相纯物质在相同温度下C V > C P的情况是（ b ）(A) (∂P/∂T)V<0 (B) (∂V/∂T)P<0(C) (∂P/∂V)T<0 (D) 不可能出现C V>C P12．理想气体从相同始态分别经绝热可逆膨胀和绝热不可逆膨胀到达相同的压力，则其终态的温度，体积和体系的焓变必定是（ b ）(A) T可逆> T不可逆, V可逆> V不可逆, ΔH可逆>ΔH不可逆(B) T可逆< T不可逆, V可逆< V不可逆, ΔH可逆<ΔH不可逆(C) T可逆< T不可逆, V可逆> V不可逆, ΔH可逆<ΔH不可逆(D) T可逆< T不可逆, V可逆< V不可逆, ΔH可逆>ΔH不可逆13．1mol、373K、1atm下的水经下列两个不同过程达到373K、1atm下的水汽：(1)等温可逆蒸发，(2)真空蒸发。

1) 墙壁两侧表面的热流密度； 2) 壁内单位体积的内热源生成热。

解：(1) 由傅里叶定律：dtqdx所以墙壁两侧表面的热流密度：qx0( 4000 x) 4000 xdt dx x0立身以立学为先，立学以读书为本1. 相距很近且彼此平行的两个黑体表面，若( 1)两表面温度分别为 1800K 和 1500K ；(2)两表面 温度分别为 400K 和 100K 。

试求两种情况下辐射换热量的比值。

由此可以得出什么结论？解：(1)两表面温度分别为 1800K 和 1500K 时：q 1(T 14 T 24) 5.67 10 8 (18004 15004) 308170W / m 2(2)两表面温度分别为 400K 和 100K 时：q 2(T 14 T 24) 5.67 10 8 (4004 1004) 1446W / m 2二者比值：q 1 /q 2 308170/1446 213 由此可以看出，尽管冷热表面温度都是相差 300K ，但前者的换热量是后者的 213 倍。

因此，辐射 在高温时更重要。

2. 如图所示的墙壁，其导热系数为 50W /(m K ) ，厚度为 50mm ，在稳态情况下的墙壁内一维温 度分布为：2t 200 2000 x 2式中 t 的单位为℃， x 的单位为 m 。

试求：2q x 4000 x x 4000 50 0.05 10kW / m 2（2）由导热微分方程：d 2t 20 dx 2得：d 2td t2 4000 4000 4000 50 2 105W / m 3dx3. 如图所示的长为 30cm ，直径为 12.5 mm 的铜杆，导热系数为 386W / m K ，两端分别紧固地 连接在温度为 200℃的墙壁上。

温度为 38℃的空气横向掠过铜杆，表面传热系数为17W / m 2 K 求杆散失给空气的热量是多少？解：这是长为 15 cm 的等截面直肋的一维导热问题。

由于物理问题对称，可取杆长的一半作研究对 象。