Ica盲源分离Matlab程序

目录摘要 0abstract (1)1 ICA 的基本原理及特点 (2)1.1盲分离数学模型 (2)1.2 ICA 算法描述 (3)1.3 FICA算法 (4)2 FICA设计思想 (4)3 实验仿真结果记录 (6)3.1 仿真时域波形及频谱 (6)3.1.1 原始信号 (6)3.1.2 混合信号 (9)3.1.3 分离信号 (12)3.2 仿真所用的源程序 (15)4 实验结果分析 (24)5 小结与体会 (25)6 参考文献 (26)摘要混合信号中恢复出未知源信号。

语音信号盲分离技术被成功地用在了通信、医学、图像和语音信号处理等领域。

我们所要研究的混合语音信号盲分离问题就是用麦克风阵列或多个麦克风阵列来模仿人的耳朵,采集得到相互干扰的混叠语音信号,然后通过分离算法将混叠的语音信号相互分离开来,提取我们所感兴趣的信号。

举个例子就是在多人同时说话的嘈杂环境下,我们能够辨识感兴趣人的说话声的能力。

然后把它分辨出来。

abstractThe speech signal blind source is in the source signal and the source signal how to mix all unknown, from observations of mixed signal in recovering the unknown sourcecommunication, medical, image and voice signal processing, etc. We have to study mix of speech signal is blind source separation with a microphone array or more microphone array to imitate human ears, acquisition get each other interference aliasing speech signal, and then through the separation algorithm will aliasing voice signal mutual separated, extraction we are interested in signal. For example is more than in noisy environment of speak at the same time, we can identify interested in the ability of the human voice. And then take it apart.1 ICA 的基本原理及特点1.1 盲分离数学模型盲信号分离是指在没有任何先验知识的条件下，仅根据源信号之间的统计独立特性和由传感器输出的观测信号，把源信号分离出来。

盲源分离matlab【最新版】目录1.盲源分离的概念2.MATLAB 在盲源分离中的应用3.盲源分离的步骤和方法4.盲源分离的实例与结果分析5.盲源分离的优缺点及发展前景正文1.盲源分离的概念盲源分离（Blind Source Separation，简称 BSS）是一种信号处理技术，其目的是从观测到的混合信号中分离出相互独立的原始信号。

这些原始信号通常是未知的，且可能具有不同的统计特性。

盲源分离在许多领域都有应用，如通信、语音处理、生物医学信号处理等。

2.MATLAB 在盲源分离中的应用MATLAB 是一种广泛使用的数学软件，它提供了丰富的函数库和强大的计算能力，使得盲源分离算法的实现变得简便。

在盲源分离领域，MATLAB 可以用于信号模拟、算法设计和结果分析等。

通过 MATLAB，研究者可以轻松地尝试不同的分离算法，并对比其性能，从而为实际应用提供有力支持。

3.盲源分离的步骤和方法盲源分离的过程主要包括以下几个步骤：（1）信号模型建立：根据问题的实际情况，建立混合信号的数学模型，如线性混合模型、非线性混合模型等。

（2）统计特性分析：分析原始信号的统计特性，如均值、方差、相关性等，为后续算法设计提供依据。

（3）分离算法选择：根据信号模型和统计特性，选择合适的盲源分离算法，如独立成分分析（ICA）、广义逆滤波（GIV）、非负矩阵分解（NMF）等。

（4）算法实现与性能评估：利用 MATLAB 实现选定的分离算法，并通过仿真实验评估其性能。

4.盲源分离的实例与结果分析以下是一个简单的盲源分离实例：假设有两个原始信号 x1(t) 和 x2(t)，它们通过线性混合器后得到观测信号 y(t)：y(t) = x1(t) + x2(t)通过盲源分离，我们可以从 y(t) 中恢复出 x1(t) 和 x2(t)。

利用 MATLAB，我们可以实现以下步骤：（1）生成两个原始信号 x1(t) 和 x2(t)，它们具有不同的统计特性。

复数信号盲源分离matlab摘要：1.引言2.复数信号盲源分离原理3.MATLAB实现方法4.仿真结果及分析5.结论正文：【引言】随着科技的发展，信号处理技术在各个领域得到了广泛的应用。

在实际应用中，常常遇到复数信号的盲源分离问题。

复数信号盲源分离是指在未知信号源的幅度、相位和频率等信息的情况下，仅通过观测到的复数信号来实现信号的分离。

MATLAB作为一种强大的数学软件，可以方便地实现复数信号的盲源分离。

本文将介绍复数信号盲源分离的MATLAB实现方法及仿真结果。

【复数信号盲源分离原理】复数信号盲源分离的核心是利用信号之间的相互关系和某种优化算法来达到分离目的。

常见的盲源分离算法有：独立成分分析（ICA）、非线性独立成分分析（NICA）、联合diagonalization（JADE）等。

这些算法在实数信号盲源分离领域取得了较好的效果，对于复数信号盲源分离，可以通过对实部与虚部进行独立成分分析来实现。

【MATLAB实现方法】在MATLAB中，可以使用现成的盲源分离工具箱（如BSSbox）来实现复数信号的盲源分离。

以下是一个简单的MATLAB实现步骤：1.导入所需库：如bssbox、plot等。

2.读取或生成复数信号数据。

3.对复数信号进行预处理，如白化、窗函数处理等。

4.选择合适的盲源分离算法，如ICA、NICA、JADE等。

5.使用盲源分离算法对预处理后的信号进行分离。

6.绘制分离后的信号，分析分离效果。

【仿真结果及分析】通过MATLAB仿真，可以得到复数信号盲源分离的结果。

分离效果可以通过比较分离后的信号与原始信号的相似度来评价。

在实际应用中，可以根据需求选择合适的分离算法和参数，以达到较好的分离效果。

【结论】本文介绍了复数信号盲源分离的MATLAB实现方法。

通过使用盲源分离工具箱和选择合适的算法，可以有效地实现复数信号的盲源分离。

仿真结果表明，所选算法在复数信号盲源分离问题上具有一定的可行性。

Matlab 盲源分离 JADE 算法一、引言盲源分离是信号处理中的一个关键问题，用于从混合信号中分离出各个独立的源信号。

在实际生活中，混合信号往往是通过各种传感器或者设备采集得到的，源信号可能是声音、图像等各种形式的信息。

而盲源分离的任务就是从这些混合信号中还原出源信号，为后续的分析和处理提供基础。

JADE（Joint Approximate Diagonalization of Eigenmatrices）算法是一种经典的盲源分离算法，本文将介绍如何使用Matlab实现JADE算法，并探讨其在实际应用中的效果。

二、JADE算法的原理JADE算法是一种高阶统计方法，主要用于盲源分离和独立成分分析。

其基本思想是通过对数据的高阶统计特性进行分析，从而实现对独立源信号的估计和分离。

具体来说，JADE算法利用了信号的高阶统计独立性来实现盲源分离，通过对数据进行协方差矩阵的估计和特征值分解，进而得到信号的独立成分。

三、Matlab实现JADE算法的步骤使用Matlab实现JADE算法通常包括以下几个步骤：1. 数据准备：首先需要准备混合信号的数据，可以是从传感器采集得到的音频数据、图像数据等各种形式的信号数据。

2. 数据预处理：对采集到的数据进行预处理，包括降噪、滤波、归一化等操作，以保证数据的质量和稳定性。

3. JADE算法实现：利用Matlab提供的相关函数或者自行编写代码，实现JADE算法的核心步骤，包括协方差矩阵的估计、特征值分解等。

4. 结果分析：对JADE算法得到的分离后的独立成分进行分析和评估，包括信噪比的计算、频谱分析等。

四、JADE算法在实际应用中的效果JADE算法作为一种经典的盲源分离方法，在实际应用中取得了广泛的应用。

以语音信号分离为例，利用JADE算法可以将混合的多个说话人的语音信号分离成独立的单一说话人的语音信号，为语音识别、语音合成等应用提供了重要的基础。

另外，在无线通信、生物医学信号处理等领域，JADE算法也发挥了重要作用。

Matlab中的盲源信号分离方法与示例分析引言：随着科学技术的发展，信号处理在各个领域中扮演着重要的角色。

其中，盲源信号分离（Blind Source Separation，BSS）作为一种重要的信号处理方法，用于从混合信号中恢复出原始信号的成分，已经在音频处理、图像处理、生物医学工程等多个领域得到了广泛的应用。

在本文中，将介绍Matlab中的盲源信号分离方法以及相关示例分析。

一、盲源信号分离方法介绍1.1 独立成分分析（Independent Component Analysis，ICA）独立成分分析是一种基于统计原理的盲源信号分离方法。

其核心思想是假设混合信号是通过独立的源信号进行线性叠加得到的。

通过对混合信号的统计特性进行分析，可以估计出源信号的独立成分，从而实现信号的分离。

1.2 因子分析（Factor Analysis）因子分析是一种基于概率模型的盲源信号分离方法。

它假设混合信号是通过一组共享的隐变量与线性映射关系得到的。

通过对混合信号的协方差矩阵进行分解和对隐变量的估计，可以恢复出源信号的成分。

1.3 主成分分析（Principal Component Analysis，PCA）主成分分析是一种常见的线性降维方法，也可以用于盲源信号分离。

其基本思想是通过找到数据中最大方差的方向，将原始数据映射到一个低维的子空间中，从而实现信号分离。

二、示例分析2.1 音频信号的分离在音频处理中，盲源信号分离方法可以用于提取出不同的音频源，例如乐器音轨、人声等。

下面以一个示例进行分析。

首先，我们随机选择两段音频，分别为X1和X2，并将它们混合产生一个混合音频Y。

然后，利用盲源信号分离方法对Y进行处理，尝试将其恢复出X1和X2。

在Matlab中，可以使用FastICA工具箱实现独立成分分析。

具体步骤如下：（1）读取音频文件，并将音频信号转化为时间序列的形式。

（2）利用FastICA函数对混合音频Y进行处理，得到分离后的音频信号S。

单通道信号盲源分离代码这是一个使用Python和sklearn库进行单通道信号盲源分离的简单示例。

假设我们有一些混合的信号，我们希望恢复原始的源信号。

在这个示例中，我们将使用FastICA算法进行盲源分离。

首先，你需要安装必要的库，如果还没有安装的话，可以使用以下命令进行安装：pythonpip install numpy scipy sklearn然后，你可以使用以下代码进行盲源分离：pythonimport numpy as npfrom sklearn.decomposition import FastICAimport matplotlib.pyplot as plt# 生成一些混合的信号np.random.seed(0)n_samples = 2000time = np.linspace(0, 8, n_samples)s1 = np.sin(2 * time) # Signal 1 : sinusoidal signals2 = np.sign(np.sin(3 * time)) # Signal 2 : square signals3 = signal.sawtooth(2* np.pi * time) # Signal 3: sawtooth signal S = np.c_[s1, s2, s3]S += 0.2 * np.random.normal(size=S.shape) # Add noiseS /= S.std(axis=0) # Standardize data# Mix dataA = np.array([[1, 1, 1], [0.5, 2, 1.0], [1.5, 1.0, 2.0]]) # MixingmatrixX = np.dot(S, A.T) # Generate observations# Compute ICAica = FastICA(n_components=3)S_ = ica.fit_transform(X) # Reconstruct signals# We can `prove` that the ICA model applies by reverting the unmixing.assert np.allclose(S, np.dot(S_, ica.mixing_.T) + ica.mean_) # For comparison, compute PCA (e.g. for denoising)from sklearn.decomposition import PCApca = PCA(n_components=3)H = pca.fit_transform(X) # Reconstruct signals based on orthogonalcomponents# Plot resultsplt.figure()colors = ['navy', 'turquoise', 'darkorange']for ii, (s, (ica_s, pca_s)) in enumerate(zip(S_.T, H.T)):plt.plot(time, s, color=colors[ii], label='True signal')plt.plot(time, ica_s, color=colors[ii], label='ICA recovered signal')plt.plot(time, pca_s, color=colors[ii], label='PCA recovered signal')plt.legend()plt.show()这段代码首先生成了三个不同的信号（正弦波、方波和锯齿波），然后将它们混合在一起。

说明文档
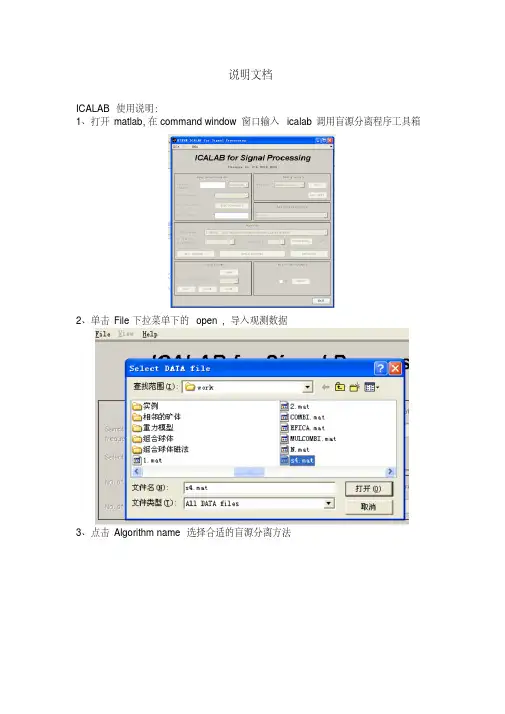
ICALAB使用说明：
1、打开matlab，在command window 窗口输入icalab 调用盲源分离程序工具箱
2、单击File下拉菜单下的open ，导入观测数据
3、点击Algorithm name 选择合适的盲源分离方法
4、点击按钮，开始计算
5、点击View按钮选择要显示的信号
选择图中所示的信号，点击ok 然后点击PLOT按钮
6、点击PLOT后显示窗口如下依次为观测信号、分离信号、混合矩阵
7、打开Estimated matrix A中的Edit菜单，选择参数设置，双击图片，然后点击
Inspector按钮弹出参数设置对话框。

8、点击弹出Cdata参数，并记录下其
系数
9、点击SAVE按钮，弹出下面的对话框，保存数据
10、点击EXIT按钮，退出工具箱
11、在matlab中导入刚才保存的数据S为观测信号，Y为分离结果
12、用Y乘以步骤9中记录下来的数据，分别得到各条测线上的各个异常
s1(1,:)=Y(1,:)*CData（1,1）; s1(2,:)=Y(2,:)*CData（1,2）;
s2(1,:)=Y(1,:)*CData（2,1）; s2(2,:)=Y(2,:)*CData（2,2）;
其中，s1是第一条测线上两个异常分离结果，s2是第二条测线上两个异常分离结果。

Matlab中的声源定位与分离方法声源定位与分离是一项重要的音频处理技术，它可以在多麦克风阵列下实现对声源的准确定位和分离。

在实际应用中，声源定位与分离技术在语音增强、声音识别、智能语音交互等领域具有广泛的应用。

本文将介绍Matlab中的声源定位与分离方法，为读者提供深入了解和应用该技术的指南。

一、声源定位方法1. 波束形成波束形成是一种常用的声源定位方法，它利用多麦克风阵列中的麦克风接收到的声音信号的时延差异来确定声源的方向。

在Matlab中，可以使用波束形成算法实现声源定位。

该算法通常包括以下步骤：麦克风阵列中的麦克风位置确定、计算声音信号的时延差异、选择主波束方向以及实时更新波束方向等。

2. 声音源距离估计声音源距离估计是一种基于声音信号传播速度的声源定位方法。

在Matlab中，可以通过估计声音信号传播时间来确定声音源的距离。

该方法通常需要一个已知位置的参考点，并利用声音信号在参考点和麦克风之间的延迟来计算声源的距离。

3. 声纹识别声纹识别是一种基于声音信号的个体辨识方法，通过对声音信号的频谱和声纹特征进行分析来实现声源定位。

在Matlab中，可以使用声纹识别算法来识别声纹特征并确定声源的位置。

该方法具有高准确率和较好的实时性，适用于复杂环境下的声源定位。

二、声源分离方法声源分离是指将多个混合在一起的声音信号中的目标声源提取出来的过程。

在Matlab中，可以使用不同的声源分离方法来实现这一目标。

1. 盲源分离盲源分离是一种无需任何先验信息的声源分离方法，它通过对混合信号进行统计特性分析和基于统计模型的信号分解来实现声源的分离。

在Matlab中，可以使用独立成分分析（ICA）等算法来实现盲源分离。

该方法适用于混合信号中声源之间相对独立的情况。

2. 基于经典音频特征的分离方法除了盲源分离方法，还可以使用基于经典音频特征的分离方法来实现声源的分离。

例如，通过对声音信号的时域特性、频域特性和谱图特性进行分析，并利用特征提取和分类算法来实现声源分离。

ICA算法是一种用于分离混合信号的计算机算法。

它是一种盲源分离方法，可以在不知道混合信号的确切成分的情况下，将混合信号解耦为原始信号。

ICA算法在信号处理、机器学习、神经科学和医学图像处理等领域有着广泛的应用。

在介绍ICA算法的代码实现之前，让我们先来理解一下ICA算法是如何工作的。

ICA算法的核心思想是找到一个转换矩阵，使得混合信号经过这个转换后能够被分离成相互独立的原始信号。

ICA算法的目标是找到一个矩阵，使得原始信号经过这个矩阵的线性变换后，各个维度上的信号能够相互独立。

这个转换矩阵可以通过最大化信号的非高斯性来进行估计，从而实现信号的盲分离。

现在让我们来看一下ICA算法的代码实现。

以下是一个简单的Python代码示例，用于演示如何使用sklearn库中的FastICA模块来实现ICA算法的信号分离。

# 导入所需的库import numpy as npfrom sklearn.decomposition import FastICAimport soundfile as sf# 读取混合信号数据data, sr = sf.read('mixed_signal.wav')# 初始化FastICA模型ica = FastICA(n_components=3)# 对混合信号进行ICA分离S_ = ica.fit_transform(data)# 计算混合矩阵A_ = ica.mixing_# 保存分离后的信号for i in range(3):sf.write('separated_signal_{}.wav'.format(i), S_[:, i], sr)在这段代码中，首先我们使用soundfile库来读取混合信号的数据。

我们初始化FastICA模型，并通过fit_transform方法对混合信号进行分离，得到分离后的信号数据。

我们将分离后的信号保存为.wav文件。

盲源分离程序流程Blind source separation is a process that involves separating a set of mixed signals into their individual source components. This is a challenging problem in signal processing, and there are several methods and algorithms used to address it. 盲源分离是一个涉及将一组混合信号分离成其各自源组件的过程。

这在信号处理中是一个具有挑战性的问题，有几种方法和算法用于解决它。

One common approach to blind source separation is independent component analysis (ICA). ICA is based on the assumption that the observed signals are linear mixtures of independent source signals, and it aims to recover the original sources by estimating the mixing matrix. 盲源分离的一种常见方法是独立成分分析（ICA）。

ICA基于这样的假设：观测到的信号是独立源信号的线性混合，并且旨在通过估计混合矩阵来恢复原始信号源。

Another method for blind source separation is non-negative matrix factorization (NMF). NMF is based on the idea that a matrix can be factorized into two non-negative matrices, which can be used to represent the original data. This method has been widely applied inspeech and audio signal processing. 盲源分离的另一种方法是非负矩阵分解（NMF）。

复信号fastica算法
FastICA算法是一种用于盲源信号分离的算法，它可以从混合信号中分离出独立的源信号。

以下是FastICA控制台指令的使用方法：
1. 打开控制台：在命令行中输入“control”并按回车键，即可打开控制台。

2. 选择FastICA算法：在控制台中选择“信号处理”选项卡，然后在“盲源信号分离”中选择“FastICA”算法。

3. 导入数据：使用“import”命令导入需要分离的混合信号数据。

4. 参数设置：根据具体情况设置FastICA算法的参数，例如迭代次数、收敛阈值等。

5. 运行算法：使用“run”命令运行FastICA算法，开始分离源信号。

6. 查看结果：在控制台中查看分离出的源信号结果，可以使用绘图命令将结果可视化。

7. 保存结果：使用“save”命令将分离出的源信号结果保存到文件中，以便后续处理和分析。

需要注意的是，以上控制台指令的具体命令可能因不同版本或不同平台而有所不同，用户需根据具体的软件环境或编程环境进行调整和修改。

盲源分离程序流程盲源分离（Blind Source Separation, BSS）是一种无监督的学习方法，其目的是从混合的信号中恢复出原始的独立源信号，而不需要知道混合模型的具体参数。

以下是盲源分离的主要程序流程：1. 信号采集目的：收集需要进行盲源分离的混合信号。

操作：使用适当的传感器或仪器从实际环境中获取混合信号。

注意：确保采集的信号质量，减少噪声和干扰。

2. 预处理目的：去除或减少信号中的噪声、失真和其他不需要的成分。

操作：+ 滤波：使用滤波器（如低通、高通或带通滤波器）去除噪声。

+ 标准化：调整信号的幅值，使其满足特定范围。

+ 去均值：确保信号的均值为0。

3. 特征提取目的：从预处理后的信号中提取出对于盲源分离有用的特征。

操作：+ 时域分析：计算信号的时域统计特性。

+ 频域分析：通过傅里叶变换等方法分析信号的频域特性。

+ 时频分析：使用短时傅里叶变换、小波变换等方法分析信号的时频特性。

4. 分离算法目的：根据提取的特征，使用适当的算法将混合信号分离成独立的源信号。

操作：+ 独立成分分析（ICA）：通过最大化非高斯性来分离独立源。

+ 主成分分析（PCA）：通过去除信号中的冗余成分进行分离。

+ 二次规划等优化算法：用于更复杂的盲源分离问题。

5. 结果评估目的：评估盲源分离的效果，判断分离出的信号是否接近真实的源信号。

操作：+ 主观评估：通过人工听测或其他方式，直接评价分离效果。

+ 客观评估：使用如信噪比（SNR）、互信息（MI）等量化指标来评估。

6. 结果输出目的：将分离得到的源信号以适当的方式呈现出来。

操作：+ 信号重构：将分离得到的源信号重构为原始的时间序列。

+ 可视化：使用图表、波形图等方式展示分离结果。

+ 数据存储：将分离得到的源信号保存为文件或数据库，以便后续分析或使用。

总结：盲源分离程序流程包括信号采集、预处理、特征提取、分离算法、结果评估和结果输出等步骤。

每个步骤都有其特定的目的和操作，通过这一流程可以有效地从混合信号中恢复出原始的独立源信号。

复数信号盲源分离matlab摘要：一、复数信号盲源分离概述1.盲源分离的定义2.复数信号的特点3.复数信号盲源分离的应用二、MATLAB 在复数信号盲源分离中的应用1.MATLAB 简介2.使用MATLAB 进行复数信号盲源分离的方法3.MATLAB 在盲源分离中的优势三、复数信号盲源分离的步骤1.数据准备2.信号模型建立3.信号分离4.结果分析四、复数信号盲源分离的实例1.实例介绍2.使用MATLAB 进行实例分析3.结果展示正文：一、复数信号盲源分离概述盲源分离是一种从多个信号中提取独立信号的方法，这些信号通常被混合在一起并且无法单独识别。

复数信号盲源分离是盲源分离的一种特殊形式，它主要处理复数信号。

复数信号具有实部和虚部，可以更好地反映信号的频率特性。

复数信号盲源分离在通信、语音处理、生物医学等领域有着广泛的应用。

二、MATLAB 在复数信号盲源分离中的应用MATLAB 是一种非常强大的数学软件，可以用于各种数学计算和数据处理。

在复数信号盲源分离中，MATLAB 可以提供各种工具和函数，方便用户进行信号处理和分析。

使用MATLAB 进行复数信号盲源分离的方法主要包括独立成分分析（ICA）和小波变换等。

MATLAB 的优势在于它可以高效地处理大量数据，同时提供丰富的图形和可视化工具，方便用户观察和分析信号分离的结果。

三、复数信号盲源分离的步骤复数信号盲源分离主要包括以下几个步骤：1.数据准备：首先，需要收集和整理待处理的复数信号数据。

这些数据可以是来自实验室的测量数据，也可以是来自实际应用场景的信号，如通信信号、语音信号等。

2.信号模型建立：在收集到数据之后，需要建立一个合适的信号模型。

这个模型需要能够准确地描述复数信号的特性，如信号的幅度、相位、频率等。

3.信号分离：使用建立的信号模型，可以采用各种方法（如ICA、小波变换等）从复数信号中分离出独立的信号。

4.结果分析：最后，需要对分离结果进行分析，检查分离出的信号是否符合预期，是否满足应用需求。

文章标题：深度探讨复数信号盲源分离在Matlab中的应用一、引言复数信号盲源分离是一种在信号处理领域中广泛应用的技术，它可以从混合信号中分离出原始的复数信号成分。

在Matlab中，我们可以通过各种算法和工具来实现复数信号盲源分离，这为我们的信号处理工作提供了便利。

本文将对复数信号盲源分离在Matlab中的应用进行全面评估，并深入探讨其原理、算法和实际应用。

二、原理和算法复数信号盲源分离的原理是基于独立成分分析（ICA）的方法，它通过对混合信号进行适当的处理，使得在处理后的信号中各个成分之间具有尽可能独立的性质。

在Matlab中，我们可以使用FastICA等函数和工具来实现这一算法，从而达到复数信号盲源分离的效果。

值得注意的是，不同的算法对于不同类型的复数信号可能有不同的适用性，因此在实际应用中需要根据具体情况选择合适的算法来实现盲源分离。

三、实际应用复数信号盲源分离在实际应用中具有广泛的用途，例如在语音信号处理、生物医学信号处理、雷达信号处理等领域都有着重要的应用。

在Matlab中，我们可以通过编写相应的脚本和程序来实现对不同类型复数信号的盲源分离，从而为实际应用提供了便利。

Matlab提供了丰富的可视化工具，可以帮助我们直观地观察盲源分离的效果，从而对处理结果进行评估和调整。

四、个人观点和理解在我看来，复数信号盲源分离在Matlab中的应用是一项非常有挑战性和有趣的工作。

通过深入学习和实践，我发现这一技术可以帮助我们从复杂的混合信号中提取出有用的信息，为信号处理和分析工作提供了新的思路和方法。

我也意识到在实际应用中，需要结合具体问题的特点和算法的适用性来选择合适的盲源分离方法，这需要我们不断学习和探索。

五、总结和回顾通过本文的深度探讨，我们对复数信号盲源分离在Matlab中的应用有了全面的了解。

从原理和算法到实际应用，我们对这一技术有了更深入的认识，并对其在信号处理领域的重要性有了更加清晰的认识。

结合matlab代码案例解释ICA独立成分分析原理更多技术干货第一时间送达Hello，大家好！Rose小哥今天介绍一篇来自于arnauddelorme网站上的结合matlab代码案例来解释ICA原理(案例代码在后文中有提供)。

关于ICA，可以查看Rose小哥之前分享的《ICA独立成分分析去除EEG伪影》以及Scott等大神关于ICA的原理与应用的文献汇总《Scott等大神的33篇ICA独立成分分析论文汇总》。

介绍独立分量分析是一种将多个传感器中的独立源线性混合分离的信号处理方法。

例如，当在头皮上记录脑电图（EEG）时，ICA可以分离出嵌入在数据中的伪像（因为它们通常彼此独立）。

什么是ICA？ICA是一种分离线性混合源的技术。

例如，我们可以尝试混合然后分开两个源。

下面，我们定义两个独立源A(顶部)和B(底部)的时间过程（matlab代码在后文中有提供）然后，我们将这两个源线性混合。

顶部曲线等于A减去B的两倍，而底部线性组合为1.73 * A + 3.41 * B。

然后，将这两个信号输入ICA算法(在本例中为fastICA)，该算法能够发现A和B的原始激活。

请注意，该算法无法恢复源活动的确切振幅(稍后可以看到原因)。

建议尝试使用不同程度的噪音进行测试，看看它是相当稳健。

值得注意的是，从理论上讲，ICA只能提取线性组合的源。

对数据进行白化不过在使用ICA算法之前，需要说明一下大多数ICA算法在实际应用ICA之前需要执行的预处理。

许多ICA算法的第一步是白化数据。

这意味着我们删除了数据中的所有相关性，即不同的通道(矩阵Q)必须保证不相关。

为什么这样做呢?一个几何解释是，它恢复数据的初始“形状”，然后ICA必须只旋转结果矩阵(见下文)。

下面，再次将两个随机的源A和B混合。

在下图中，A的值是数据点的横坐标，B的值是它们的纵坐标。

(见代码 ica_test2.m)取A和B的两个线性混合物，并绘制这两个新变量然后，如果我们把这两种线性混合物白化，就得到下面的图两个轴上的方差现在是相等的，数据在两个轴上的投影的相关性是0(意味着协方差矩阵是对角的，所有对角线上的元素都是相等的)。

Matlab盲源分离方法与实例在信号处理领域中，盲源分离是一项重要的任务。

盲源分离即通过对混合信号进行分析和处理，将原始信号从混合信号中分离出来。

这项技术在语音识别、音频处理、图像处理等领域中有着广泛的应用。

在本文中，我们将通过介绍Matlab中的盲源分离方法和实例，帮助读者更好地理解和应用这一技术。

一、盲源分离的基本原理盲源分离的基本原理是利用混合信号中的统计特性来估计信号源的分布。

通过对混合信号的统计特性进行分析，可以得到源信号的估计结果。

这样，就可以实现对混合信号中的源信号的分离和重构。

1.1 盲源分离的前提假设盲源分离的方法一般基于以下两个假设：1) 混合信号是线性叠加的。

2) 源信号之间是相互独立的。

在实际应用中，尽管这两个假设并不总是成立，但是通常可以通过一定的预处理方法来满足这些假设。

例如，可以通过滤波、噪声抑制等方式来满足混合信号是线性叠加的假设。

1.2 盲源分离的方法盲源分离的方法可以分为线性方法和非线性方法两类。

线性方法主要包括独立成分分析（ICA）、主成分分析（PCA）等，而非线性方法包括二次熵最小化（QCM）、最小均方误差（MMSE）等。

在本文中，我们将重点介绍其中的独立成分分析（ICA）方法。

二、Matlab中的盲源分离方法Matlab是一种常用的科学计算软件，提供了丰富的工具箱和函数来支持信号处理任务。

在盲源分离领域，Matlab提供了ICA工具箱，可以方便地实现独立成分分析方法。

下面将介绍Matlab中ICA工具箱的使用方法，并通过一个实例来展示其应用效果。

2.1 Matlab中的ICA工具箱Matlab中的ICA工具箱是一个方便易用的工具，提供了多种ICA算法的实现。

使用该工具箱，可以通过简单的函数调用实现对混合信号的盲源分离。

以下是在Matlab中使用ICA工具箱实现盲源分离的基本步骤：1) 加载混合信号数据：首先，需要将混合信号数据加载到Matlab中。

可以使用Matlab提供的文件读取函数将数据读入到变量中。

盲源分离matlab盲源分离是一种信号处理技术，用于从组合信号中分离出各个源信号。

在盲源分离中，不需要事先了解源信号的特点或统计信息，只利用组合信号的统计特性来进行分离。

在Matlab中，可以使用独立分量分析（ICA）方法来实现盲源分离。

ICA是一种基于统计独立性原理的盲源分离方法，假设混合信号可以通过线性变换从独立源信号生成。

ICA方法的步骤如下：1. 准备混合信号数据矩阵X，其中每一列代表一个混合信号观测值。

2. 对混合信号进行预处理，如中心化和白化，使其均值为0且协方差矩阵为单位阵。

3. 选定一个ICA算法，如FastICA算法，调用Matlab中的ica函数进行盲源分离。

以下是一个实现盲源分离的示例代码：matlab% 生成混合信号s1 = randn(1, 1000); % 源信号1s2 = randn(1, 1000); % 源信号2A = [2, 1; 1, 2]; % 混合矩阵X = A * [s1; s2]; % 混合信号% 盲源分离[icasig, A_est, T_est] = fastica(X);% 绘制源信号和分离结果figure;subplot(3, 1, 1);plot(s1);title('源信号1');subplot(3, 1, 2);plot(s2);title('源信号2');subplot(3, 1, 3);plot(icasig(1, :));hold on;plot(icasig(2, :));title('分离结果');legend('分离信号1', '分离信号2');在上述代码中，首先生成两个源信号s1和s2，然后通过混合矩阵A将它们线性混合得到混合信号X。

然后调用fastica函数进行盲源分离，得到分离信号icasig。

最后，绘制源信号和分离结果的波形图。

需要注意的是，ICA方法的盲源分离结果具有多个不确定性，即结果的顺序、符号和比例都是不确定的。