几何图形计算公式大全

多面体的体积和表面积图形尺寸符号立方体长方体∧棱柱∨三棱柱棱锥棱台圆柱和空心圆柱∧管∨斜线直圆柱直圆锥圆台球球扇形∧球楔∨球缺圆环体∧胎∨球带体桶形椭a,b,c-半轴球体交叉圆柱体梯形体常用图形求面积公式图形尺寸符号面积（F）表面积（S）正方形长方形三角形平行四边形任意四边形正多边形菱形梯形圆形椭a·b-主轴F= (π/4) a·b 圆形扇形弓形圆环部分圆环新月形L d/10 2d/10 3d/10 4d/10 5d/10 6d/10 7d/10 P 0.40 0.79 1.18 1.56 1.91 2.25 2.55抛物线形等多边形土方开挖体积：V=（长+2垫层超出基础长度+2工作面宽+放坡系数×高度）×（宽+2垫层超出基础长度+2工作面宽+放坡系数×高度）×高度+1/3×放坡系数²×高度³几何图形及计算公式大全平面图形名称符号周长C和面积S正方形a—边长C＝4a S＝a2长方形a和b－边长C＝2(a+b) S＝ab三角形a,b,c－三边长h－a边上的高s－周长的一半A,B,C－角其中s＝(a+b+c)/2S＝ah/2＝ab/2·sinC＝[s(s-a)(s-b)(s-c)]1/2＝a2sinBsinC/(2sinA)四边形d,D－对角线长α－对角线夹角S＝dD/2·sinα平行四边形a,b－边长h－a边的高S＝ah＝absinαα－两边夹角菱形a－边长α－夹角D－长对角线长d－短对角线长S＝Dd/2＝a2sinα梯形a和b－上、下底长h－高m－中位线长S＝(a+b)h/2＝mh圆r－半径d－直径C＝πd＝2πrS＝πr2＝πd2/4扇形r—扇形半径a—圆心角度数C＝2r＋2πr×(a/360)S＝πr2×(a/360)弓形l－弧长b－弦长h－矢高r－半径α－圆心角的度数S＝r2/2·(πα/180-sinα)＝r2arccos[(r-h)/r] - (r-h)(2rh-h2)1/2＝παr2/360 - b/2·[r2-(b/2)2]1/2＝r(l-b)/2 + bh/2≈2bh/3圆环R－外圆半径r－圆半径D－外圆直径d－圆直径S＝π(R2-r2)＝π(D2-d2)/4椭圆d－短轴S＝πDd/4立方图形名称符号面积S和体积V正方体a－边长S＝6a2 V＝a3长方体a－长b－宽c－高S＝2(ab+ac+bc)V＝abc棱柱S－底面积h－高V＝Sh棱锥S－底面积h－高V＝Sh/3棱台S1和S2－上、下底面积h－高V＝h[S1+S2+(S1S1)1/2]/3拟柱体S1－上底面积S2－下底面积S0－中截面积h－高V＝h(S1+S2+4S0)/6圆柱r－底半径h－高C—底面周长S底—底面积S侧—侧面积C＝2πrS底＝πr2S侧＝ChS表＝Ch+2S底V＝S底h＝πr2h积空心圆柱R－外圆半径r－圆半径h－高V＝πh(R2-r2)直圆锥r－底半径h－高V＝πr2h/3圆台r－上底半径R－下底半径h－高V＝πh(R2＋Rr＋r2)/3球r－半径d－直径V＝4/3πr3＝πd2/6球缺h－球缺高r－球半径a－球缺底半径V＝πh(3a2+h2)/6＝πh2(3r-h)/3a2＝h(2r-h)球台r1和r2－球台上、下底半径h－高V＝πh[3(r12＋r22)+h2]/6圆环体R－环体半径D－环体直径r－环体截面半径d－环体截面直径V＝2π2Rr2＝π2Dd2/4桶状体D－桶腹直径V＝πh(2D2＋d2)/12(母线是圆弧形,圆心是桶的中心)d－桶底直径h－桶高V＝πh(2D2＋Dd＋3d2/4)/15 (母线是抛物线形)。

高中数学几何公式大全在高中数学中，几何学是一门重要的数学分支。

几何学研究的是空间中的图形和形状的性质、变换以及其关系。

几何学的公式是解决几何问题的基础，本文将为您介绍一些高中数学几何公式。

1.平面几何公式1.1.面积公式-矩形面积公式：面积=长×宽-正方形面积公式：面积=边长×边长-三角形面积公式：面积=（底边长×高）/2-任意多边形面积公式：如果已知多边形所有顶点的坐标，可以使用行列式的方法计算面积。

1.2.周长公式-矩形周长公式：周长=2×(长+宽)-正方形周长公式：周长=4×边长-三角形周长公式：周长=边1+边2+边3-任意多边形周长公式：周长=边1+边2+...+边n1.3.直角三角形公式-勾股定理：a²+b²=c²，其中a、b为直角边，c为斜边。

- 正弦定理：a/sinA=b/sinB=c/sinC，其中a、b、c为三角形边长，A、B、C为对应的角度。

- 余弦定理：c²=a²+b²-2ab*cosC，其中a、b、c为三角形边长，C为对边的角度。

2.立体几何公式2.1.体积公式-立方体体积公式：体积=边长³-球体体积公式：体积=(4/3)πr³，其中r为球的半径-圆柱体体积公式：体积=πr²h，其中r为底面半径，h为高度-锥体体积公式：体积=(1/3)πr²h，其中r为底面半径，h为高度2.2.表面积公式-立方体表面积公式：表面积=6边长²-球体表面积公式：表面积=4πr²- 圆柱体表面积公式：表面积=2πrh+2πr²，其中r为底面半径，h为高度- 锥体表面积公式：表面积=πrl+πr²，其中r为底面半径，l为斜高以上只是高中数学几何公式的一部分，还有许多其他公式未在此列出。

掌握这些公式可以帮助高中生更好地解决几何问题，提高几何学习的效果。

几何图形计算公式大全在几何学中，几何图形的计算公式是非常重要的，它们可以帮助我们计算图形的各种属性，比如面积、周长、体积等。

本文将为大家整理几何图形的计算公式大全，希望能对大家的学习和工作有所帮助。

一、基本图形的计算公式。

1. 正方形，正方形的面积计算公式为，A = a²，其中a为正方形的边长；周长计算公式为，P = 4a。

2. 长方形，长方形的面积计算公式为，A = l w，其中l为长，w为宽；周长计算公式为，P = 2(l + w)。

3. 圆形，圆的面积计算公式为，A = πr²，其中π为圆周率，r为圆的半径；周长计算公式为，C = 2πr。

4. 三角形，三角形的面积计算公式为，A = 1/2 b h，其中b为底边长，h为高；周长计算公式为，P = a + b + c。

5. 正方体，正方体的体积计算公式为，V = a³，其中a为边长；表面积计算公式为，S = 6a²。

二、特殊图形的计算公式。

1. 梯形，梯形的面积计算公式为，A = 1/2 (a + b) h，其中a和b为上下底长，h为高；周长计算公式为，P = a + b + c + d。

2. 圆柱，圆柱的体积计算公式为，V = πr²h，其中r为底面半径，h为高；表面积计算公式为，S = 2πr² + 2πrh。

3. 锥形，锥形的体积计算公式为，V = 1/3 πr²h，其中r为底面半径，h为高；表面积计算公式为，S = πr² + πrl，其中l为斜高。

4. 球体，球体的体积计算公式为，V = 4/3 πr³，其中r为半径；表面积计算公式为，S = 4πr²。

三、复合图形的计算公式。

1. 复合图形的面积计算公式，首先将复合图形分解为基本图形，然后分别计算各个基本图形的面积，最后将各个基本图形的面积相加即可得到复合图形的总面积。

2. 复合图形的周长计算公式，同样的方法，将复合图形分解为基本图形，然后分别计算各个基本图形的周长，最后将各个基本图形的周长相加即可得到复合图形的总周长。

几何图形及计算公式查询
鲁班算量2006在计算独立基础时，发现所有的正四棱台计算正确，而计算有长边与短边的四棱台时，就不对了，量都偏大的原因：
独立基础体积正确的计算公式为：
四棱台计算公式为(s1+s2+sqr(s1*s2))*h/3,sqr(x)对x求根
或
A*B*H+h/6*(AB+ab+(A+a)(B+b))其中A、B、H分别为独立基础下部长方体的长、宽、高；
a、b、h分别为四棱台的长、宽、高，当然，A与a、B与b相对应。

用A*B*H+h/6*(AB+ab+(A+a)(B+b))是偏小
实际工作中，这两种公式都有人用，结果有时是不一样.
而使用鲁班算量计算结果偏大，计算不等边长的四梭台与计算公式算出结果不一样是因为我们预算中的四梭台计算公式是近似的计算方法，而鲁班用的是微积分算法，结果相差很小另外鲁班的带马牙槎的构造柱计算结果也与实际算法有差别，其实我们算构造柱时是按如果有两边有马牙槎的为边长上加6cm计算，鲁班算量考虑了层高的不同与马牙槎的高度位也考虑了（马牙槎在板底时正好为退时鲁班的计算结果就会小，但其实鲁班算的是实际的量）。

一、小学数学几何图形计算公式。

1★长方形的周长=（长+宽）×2 ★ C长方形=(a+b)×2 2★正方形的周长=边长×4 ★ C正方形=4a3★长方形的面积=长×宽★S长方形=ab4★正方形的面积=边长×边长★S正方形=a·a=a²5★三角形的面积=底×高÷2 ★S三角形=ah÷26★平行四边形的面积=底×高★S平行四边形=ah7★梯形的面积=（上底+下底）×高÷2★S梯形=（a＋b）h÷28★直径=半径×2 ★d=2r9★半径=直径÷2 ★r= d÷210★圆的周长=圆周率×直径=圆周率×半径×2★ C圆=πd =2πr 11★圆的面积=圆周率×半径×半径★S圆=πr²12★长方体的体积＝长×宽×高★V长方体=abh13★长方体（或正方体）的体积＝底面积×高★V长方体=abh=s底h14★正方体的体积＝棱长×棱长×棱长★V正方体=a·a·a=a³15★圆柱的侧面积=底面的周长×高★S圆柱侧= C圆h=πdh＝2πrh 16★圆柱的表面积=底面周长×高+两头的圆的面积★S圆柱表= C圆h+2S圆=2πrh+2πr²=2πr（h+r）17★圆柱的体积=底面积×高圆柱=S圆h=πr²h18底面积×高★V圆锥S圆πr²h二、数量关系。

1★每份数×份数＝总数★总数÷每份数＝份数★总数÷份数＝每份数2★倍数×倍数＝几倍数★几倍数÷倍数＝倍数★几倍数÷倍数＝1倍数3★速度×时间＝路程★路程÷速度＝时间★路程÷时间＝速度4★单价×数量＝总价★总价÷单价＝数量★总价÷数量＝单价6★加数①＋加数②＝和★和－加数①＝加数②★和－加数②＝加数①7★被减数－减数＝差★被减数－差＝减数★差＋减数＝被减数8★因数①×因数②＝积★积÷因数①＝因数②★积÷因数②＝因数①9★被除数÷除数＝商★被除数÷商＝除数★商×除数＝被除数三、单位换算。

图形公式大全表所有图形的公式一、平面图形公式：1、正方形 s=a²或对角线×对角线÷2 c=4a2、平行四边形 s=ah3、三角形s=ah÷24、梯形s=(a b)×h÷25、圆形s=πr2 c=πd6、椭圆s=πr7、扇形 s=lr/2二、立体图形公式：1、长方体的表面积=2×（长×宽长×高宽×高) 用符号表示是：s=2（ab bc ca）2、长方体的体积 =长×宽×高用符号表示是：v=abh 或底面积×高用符号表示是：v=sh3、正方体的表面积=棱长×棱长×6 用符号表示是：s=a²×64、正方体的体积=棱长×棱长×棱长用符号表示是：v=a³5、圆柱的侧面积=底面周长×高用符号表示是：s侧=πd×h6、圆柱的表面积=2×底面积侧面积用符号表示是：s=πr²×2 dπh7、圆柱的体积=底面积×高用符号表示是：v=πr²×h8、圆锥的体积=底面积×高÷3 用符号表示是：v=πr²×h÷39、圆锥侧面积=1/2*母线长*底面周长10、圆台体积=[s s′ √(ss′)]h÷311、球体体积=(1/3*s*h)*(4*pi*r²)/s=4/3*pi*r²三、立体几何图形：1、柱体：包括圆柱和棱柱。

棱柱又可分为直棱柱和斜棱柱，按底面边数的多少又可分为三棱柱、四棱柱、n棱柱；棱柱体积都等于底面面积乘以高，即v=sh;2、锥体：包括圆锥体和棱锥体，棱锥分为三棱锥、四棱锥及n棱锥；棱锥体积为v=sh/3 ;3、旋转体：包括圆柱、圆台、圆锥、球、球冠、弓环、圆环、堤环、扇环、枣核形等。

六年级数学几何公式大全
小学六年级的数学几何公式主要包括各类平面图形的面积和周长计算公式，以及部分立体图形的表面积和体积计算公式。

平面图形计算公式如下：
三角形：面积=底×高÷2，公式S=a×h÷2；周长=三边之和。

正方形：面积=边长×边长，公式S=a×a；周长=4×边长，公式C=4a。

长方形：面积=长×宽，公式S=a×b；周长=2×(长+宽)，公式C=2(a+b)。

平行四边形：面积=底×高，公式S=a×h。

梯形：面积=(上底+下底)×高÷2，公式S=(a+b)h÷2；周长=上底+下底+两个腰长。

立体图形计算公式如下：
圆柱：侧面积=底面的周长×高，公式S=ch=πdh=2πrh；表面积=侧面积+2×底面积，公式S=ch+2s=ch+2πr2；体积=底面积×高，公式V=Sh。

圆锥：体积=1/3×底面积×高，公式V=1/3Sh。

圆：圆的周长=直径×π，公式C=πd=2πr；圆的面积=半径×半径×π，公式S=πr2。

以上公式中的字母含义如下：a、b代表长方形、平行四边形、梯形的相邻两边；h代表高；c代表底面的周长；r代表半径；d代表直径；s代表底面积；V 代表体积。

这些公式是小学六年级数学几何部分的重要内容，需要同学们熟练掌握并灵活运用。

同时，也需要同学们理解这些公式的含义和推导过程，以便更好地掌握数学知识。

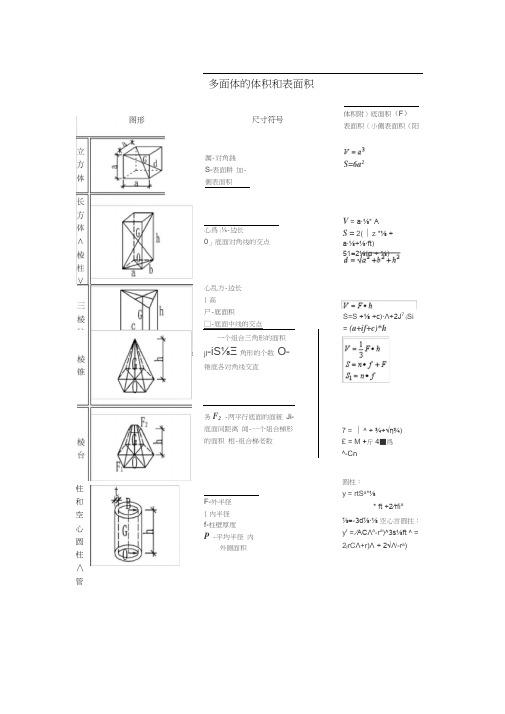
多面体的体积和表面积心乱方-边长 1高 尸-底面积 □-底面中线的交点一个组合三角形的面积jl -iS⅛Ξ角形的个数 O-锥底各对角线交直务F 2 -两平行底面的面粧 Ji-底面间距离 闻-一个爼合梯形的面积 相-组合梯老数7 = ∣^ + ¾÷√η¾) £ = M +斤4■爲 ^-Cn厲-对角銭S-表面耕 加-侧表面积尺寸符号心爲1⅛-边长0」底面对角线的交点体积附）底面积（F ） 表面积（小侧表面积（阳S=6a 2V = a∙⅛* AS = 2(∣z *⅛ +a∙⅛+⅛∙ft)51=2⅛(α + ⅛)柱和 空 心 圆 柱 ∧ 管F-外半径1内半径f-柱壁厚度P -平均半径 内外侧面积圆柱：y = rtS a *⅛* ft +2∕τfi a⅞=-3d⅞∙⅛ 空心言圆拄： y r = ∕ACΛa -r a )^3s⅛ft ^ = 2f rC Λ+r)Λ + 2√Λi -r a )S=S +⅛ +c)∙Λ+2J 7 (Si = (a+if+c)*hVy = ψ∙(j⅞2 3 + √+⅛) 5*1 = KHR+r)I= y ∣(R-r)2+h 2 £ =址十疔(0+/)y = -jιr⅛ =2W44r⅛3 y=^(4ft+rf) = 157f(⅛?+^£斜 线 直 圆 柱 ⅛-≡小高度¾-盘大高度T -底面半径^-^c⅛+⅛>rtf 1∙α+J —) cc≤ αS l - πr(⅛ +¾)r-廐面半径卜母线长+⅛2 =鈕球半径 d ・弓定底11直径A-弓形高一半径d-直径4 3皿'— L.PV = Lf I f =——=0.5236 护36 S=A f tr 2 ==V⅛-球駛的高J--球銭半径d-平切圆直径=曲面面积S-球缺表而稅R -圆球擁平均半径D-圆环体平均半径d-圆怀体截面直径T-匾!环∙⅛⅛⅛面半径尺-球半径①孩-底面半径沟-腰高⅞-⅛∣i<≡Φ底圆⅛3L的距离^ = n fi∖r-¾3¾ -⅛A-rr(^ + A3)护土畋彷-附3⅛ -√D⅛ -3P 478⅛Pr = ^(3⅛+3⅛ + ⅛i) ⅛¾ = 2∕⅛⅛。

几何图形计算公式大全在几何学中，我们经常会遇到各种各样的几何图形，如三角形、矩形、圆形等等。

对于这些几何图形，我们需要掌握它们的计算公式，以便能够准确地计算它们的各种属性。

本文将为大家总结几何图形的计算公式大全，希望能对大家有所帮助。

一、三角形。

1. 面积公式。

三角形的面积可以用以下公式计算：\[ S = \frac{1}{2} \times 底 \times 高 \]其中，S代表三角形的面积，底代表三角形的底边长，高代表三角形的高。

2. 周长公式。

三角形的周长可以用以下公式计算：\[ 周长 = 边1 + 边2 + 边3 \]其中，边1、边2、边3分别代表三角形的三条边长。

3. 三角形内角和公式。

三角形的内角和为180度，即：\[ 内角和 = 角1 + 角2 + 角3 = 180度 \]其中，角1、角2、角3分别代表三角形的三个内角。

二、矩形。

1. 面积公式。

矩形的面积可以用以下公式计算：\[ S = 长 \times 宽 \]其中，S代表矩形的面积，长代表矩形的长，宽代表矩形的宽。

2. 周长公式。

矩形的周长可以用以下公式计算：\[ 周长 = 2 \times (长 + 宽) \]其中，长代表矩形的长，宽代表矩形的宽。

三、圆形。

1. 面积公式。

圆形的面积可以用以下公式计算：\[ S = \pi \times 半径^2 \]其中，S代表圆形的面积，π代表圆周率，半径代表圆形的半径。

2. 周长公式。

圆形的周长可以用以下公式计算：\[ 周长 = 2 \times \pi \times 半径 \]其中，π代表圆周率，半径代表圆形的半径。

四、正方形。

1. 面积公式。

正方形的面积可以用以下公式计算：\[ S = 边长^2 \]其中，S代表正方形的面积，边长代表正方形的边长。

2. 周长公式。

正方形的周长可以用以下公式计算：\[ 周长 = 4 \times 边长 \]其中，边长代表正方形的边长。

以上就是几何图形的计算公式大全，希望对大家有所帮助。

几何图形计算公式大全正方形面积公式：F = 边长²周长公式：P = 4 ×边长名称：长方形面积公式：F = 长 ×宽周长公式：P = 2 × (长 + 宽)名称：三角形面积公式：F = 1/2 ×底边长 ×高周长公式：P = 边长1 + 边长2 + 边长3名称：平行四边形面积公式：F = 底边长 ×高周长公式：P = 2 × (边长1 + 边长2)名称：任意四边形面积公式：F = 1/2 ×对角线1 ×对角线2 × sin(对角线夹角)周长公式：无固定公式，需根据具体情况计算名称：正多边形（n边形）面积公式：F = (n ×边长²)/(4 × tan(π/n))周长公式：P = n ×边长立体图形名称：立方体体积公式：V = 边长³表面积公式：S = 6 ×边长²名称：长方体体积公式：V = 长 ×宽 ×高表面积公式：S = 2 × (长 ×宽 + 长 ×高 + 宽 ×高)名称：棱柱体积公式：V = 底面积 ×高表面积公式：S = 底面积 + 侧面积名称：棱锥体积公式：V = 1/3 ×底面积 ×高表面积公式：S = 底面积 + 侧面积名称：圆柱体体积公式：V = π × 半径² ×高表面积公式：S = 2 × π × 半径² + 2 × π × 半径 ×高名称：圆锥体体积公式：V = 1/3 × π × 半径² ×高表面积公式：S = π × 半径² + π × 半径 ×斜高名称：球体体积公式：V = 4/3 × π × 半径³表面积公式：S = 4 × π × 半径²以上是常见几何图形的计算公式，可根据具体情况灵活运用。

小学数学公式大全第一部分：几何图形计算公式1 、正方形周长＝边长×4 面积=边长×边长2 、正方体表面积=棱长×棱长×6 体积=棱长×棱长×棱长3 、长方形周长=(长+宽)×2 面积=长×宽4 、长方体表面积(长×宽+长×高+宽×高)×2 体积=长×宽×高5、三角形面积=底×高÷2 三角形高=面积×2÷底三角形底=面积×2÷高6 平行四边形面积=底×高7 梯形面积=(上底+下底)×高÷28 圆形(1)周长=直径×∏=2×∏×半径(2)面积=半径×半径×∏9 圆柱体(1)侧面积=底面周长×高(2)表面积=侧面积+底面积×2(3)体积=底面积×高（4）体积＝侧面积÷2×半径10 圆锥体体积=底面积×高÷3三角形内角和＝180度。

平行线：同一平面内不相交的两条直线叫做平行线垂直：两条直线相交成直角，像这样的两条直线，我们就说这两条直线互相垂直，其中一条直线叫做另一条直线的垂线，这两条直线的交点叫做垂足。

总数÷总份数＝平均数第二部分：定义、概念1、加法交换律：两数相加交换加数的位置，和不变。

2、加法结合律：三个数相加，先把前两个数相加，或先把后两个数相加，再同第三个数相加，和不变。

3、乘法交换律：两数相乘，交换因数的位置，积不变。

4、乘法结合律：三个数相乘，先把前两个数相乘，或先把后两个数相乘，再和第三个数相乘，它们的积不变。

5、乘法分配律：两个数的和同一个数相乘，可以把两个加数分别同这个数相乘，再把两个积相加，结果不变。

如：（2+4）×5＝2×5+4×56、除法的性质：在除法里，被除数和除数同时扩大（或缩小）相同的倍数，商不变。

几何体计算公式大全长方形的面积=长×宽长方形的周长=（长+宽）×2正方形的周长=边长×4正方形的面积=边长×边长三角形的面积=底×高÷2平行四边形的面积=底×高梯形的面积=（上底+下底）×高÷2直径=半径×2 半径=直径÷2圆的周长=圆周率×直径= 圆周率×半径×2圆的面积=圆周率×半径×半径长方体的表面积= （长×宽+长×高＋宽×高）×2 长方体的体积=长×宽×高正方体的表面积=棱长×棱长×6正方体的体积=棱长×棱长×棱长圆柱的侧面积=底面圆的周长×高圆柱的表面积=上下底面面积+侧面积圆柱的体积=底面积×高圆锥的体积=底面积×高÷3长方体（正方体、圆柱体）的体积=底面积×高平面图形名称符号周长C和面积S正方形a—边长C＝4aS＝a2长方形a和b－边长C＝2(a+b)S＝ab三角形a,b,c－三边长h－a边上的高s－周长的一半A,B,C－内角其中s＝(a+b+c)/2S＝ah/2＝ab/2·sinC＝[s(s-a)(s-b)(s-c)]1/2＝a2sinBsinC/(2sinA)四边形d,D－对角线长α－对角线夹角S＝dD/2·sinα平行四边形a,b－边长h－a边的高α－两边夹角S＝ah＝absinα菱形a－边长α－夹角D－长对角线长d－短对角线长S＝Dd/2＝a2sinα梯形a和b－上、下底长h－高m－中位线长S＝(a+b)h/2＝mh圆r－半径d－直径C＝πd＝2πr S＝πr2＝πd2/4扇形r—扇形半径a—圆心角度数C＝2r＋2πr×(a/360)S＝πr2×(a/360)弓形l－弧长b－弦长h－矢高r－半径α－圆心角的度数S＝r2/2·(πα/180-sinα) ＝r2arccos[(r-h)/r] - (r-h)(2rh-h2)1/2＝παr2/360 - b/2·[r2-(b/2)2]1/2＝r(l-b)/2 + bh/2 ≈2bh/3圆环R－外圆半径r－内圆半径D－外圆直径d－内圆直径S＝π(R2-r2) ＝π(D2-d2)/4椭圆D－长轴d－短轴S＝πDd/4立方图形名称符号面积S和体积V正方体a－边长S＝6a2V＝a3长方体a－长b－宽c－高S＝2(ab+ac+bc)V＝abc棱柱S－底面积h－高V＝Sh棱锥S－底面积h－高V＝Sh/3棱台S1和S2－上、下底面积h－高V＝h[S1+S2+(S1S1)1/2]/3拟柱体S1－上底面积S2－下底面积S0－中截面积h－高V＝h(S1+S2+4S0)/6圆柱r－底半径h－高C—底面周长S底—底面积S侧—侧面积S表—表面积C＝2πrS底＝πr2S侧＝ChS表＝Ch+2S底V＝S底h＝πr2h空心圆柱R－外圆半径r－内圆半径h－高V＝πh(R2-r2)直圆锥r－底半径h－高V＝πr2h/3圆台r－上底半径R－下底半径h－高V＝πh(R2＋Rr＋r2)/3球r－半径d－直径V＝4/3πr3＝πd2/6球缺h－球缺高r－球半径a－球缺底半径V＝πh(3a2+h2)/6 ＝πh2(3r-h)/3a2＝h(2r-h)球台r1和r2－球台上、下底半径h－高V＝πh[3(r12＋r22)+h2]/6 圆环体R－环体半径D－环体直径r－环体截面半径d－环体截面直径V＝2π2Rr2＝π2Dd2/4桶状体D－桶腹直径d－桶底直径h－桶高V＝πh(2D2＋d2)/12 (母线是圆弧形,圆心是桶的中心) V＝πh(2D2＋Dd＋3d2/4)/15(母线是抛物线形)。

几何计算公式大全一、平面几何公式：1.周长和面积公式：-矩形：周长=2*(长+宽)，面积=长*宽-正方形：周长=4*边长，面积=边长^2-圆：周长=2*π*半径，面积=π*半径^2-三角形：周长=边1+边2+边3，面积=(底边*高)/2-梯形：周长=边1+边2+边3+边4，面积=(上底+下底)*高/22.角度和三角函数公式：-弧度和角度的转换关系：度=弧度*(180/π)，弧度=度*(π/180)- 正弦定理：a/sin(A) = b/sin(B) = c/sin(C)，其中a、b、c是三角形的三条边，A、B、C是对应的角度。

- 余弦定理：c^2 = a^2 + b^2 - 2ab*cos(C)，其中c是三角形的斜边，a、b是两个相邻角的边长，C是这两个边对应的夹角。

3.直线和平面的方程公式：-点斜式方程：y-y1=斜率(x-x1)，其中(x1,y1)是直线上的一点，斜率可以用两点之间的高度差除以水平距离表示。

-两点式方程：(y-y1)/(y2-y1)=(x-x1)/(x2-x1)，其中(x1,y1)和(x2,y2)是直线上的两个点。

-一般式方程：Ax+By+C=0，其中A、B、C是常数，表示直线上的所有点。

二、立体几何公式：1.体积和表面积公式：-立方体：体积=边长^3，表面积=6*边长^2-正方体：体积=边长^3，表面积=6*边长^2-圆柱体：体积=π*半径^2*高，曲面积=2*π*半径*高，总表面积=2*π*半径*(半径+高)-圆锥体：体积=(π*半径^2*高)/3，曲面积=π*半径*侧面长度，总表面积=π*半径*(侧面长度+半径)-球体：体积=(4/3)*π*半径^3，表面积=4*π*半径^22.直角三角形的性质：-毕达哥拉斯定理：直角三角形的两条直角边的平方和等于斜边的平方，即a^2+b^2=c^2- 直角三角形的角度关系：直角的两个锐角的正弦、余弦和正切函数值满足sin(A) = cos(B) = a/c，sin(B) = cos(A) = b/c，tan(A) =a/b，tan(B) = b/a。

小学五年级数学几何图形周长、面积、体积计算公式大全长方形、正方形的周长和面积公式：长方形的周长=（长+宽）×2 C=(a+b)×2正方形的周长=边长×4 C=4a长方形的面积=长×宽S=ab正方形的面积=边长×边长S=a·a= a2三角形、平行四边形、梯形的面积公式：三角形的面积=底×高÷2 S=ah÷2平行四边形的面积=底×高S=ah梯形的面积=（上底+下底）×高÷2S=（a＋b）h÷2圆的周长和面积公式：圆的周长＝直径×π公式：L＝πd＝2πr圆的面积＝半径×半径×π公式：S＝πr2圆柱的侧面积和表面积公式：圆柱的侧面积：圆柱的侧面积等于底面的周长乘高。

公式：S=ch=πdh＝2πrh圆柱的表面积：圆柱的表面积等于底面的周长乘高再加上两头的圆的面积。

公式：S=ch+2s=ch+2πr2圆柱圆锥的体积公式：圆柱的体积：圆柱的体积等于底面积乘高。

公式：V=Sh圆锥的体积＝1/3底面×积高。

公式：V=1/3Sh分数的加、减法则：同分母的分数相加减，只把分子相加减，分母不变。

异分母的分数相加减，先通分，然后再加减。

分数的乘法则：用分子的积做分子，用分母的积做分母。

分数的除法则：除以一个数等于乘以这个数的倒数。

一、周长公式1. 长方形的周长=（长宽）×22. 正方形的周长=边长×43. （重点）圆的周长=圆周率×直径= 2×圆周率×半径二、面积公式1. 长方形的面积=长×宽2. 正方形的面积=边长×边长3. 三角形的面积=底×高÷24. 平行四边形的面积=底×高5. 梯形的面积=（上底下底）×高÷26. （重点）圆的面积=圆周率×半径27. （重点）圆柱的侧面积：圆柱的侧面积等于底面的周长乘高。

几何图形计算公式1、长方形的周长=（长+宽）×2 C=(a+b)×22、正方形的周长=边长×4 C=4a3、长方形的面积=长×宽S=ab4、正方形的面积=边长×边长S=a.a= a5、三角形的面积=底×高÷2 S=ah÷26、平行四边形的面积=底×高S=ah7、梯形的面积=（上底+下底）×高÷2 S=（a＋b）h÷28、直径=半径×2 d=2r 半径=直径÷2 r= d÷29、圆的周长=圆周率×直径=圆周率×半径×2 c=πd =2πr10、圆的面积=圆周率×半径×半径S=π2r11、长方体的表面积=（长×宽+长×高＋宽×高）×212、长方体的体积=长×宽×高V =abh13、正方体的表面积=棱长×棱长×6 S =6a14、正方体的体积=棱长×棱长×棱长s=3a15、圆柱的侧面积=底面圆的周长×高S=ch16、圆柱的表面积=上下底面面积+侧面积S=2πr +2πrh=2π(d÷2) +2π(d÷2)h=2π(C÷2÷π) +Ch17、圆柱的体积=底面积×高V=Sh18、圆锥的体积=底面积×高÷319、半圆的周长=圆的周长的一半+一条直径 C=∏R+2R≈5.14R20、半圆的面积=圆的面积的一半21、圆环的面积=外圆的面积-内圆的面积 S=∏(2R-2r)22、钢管的体积=外圆柱的体积-内圆柱的体积=环形的面积×高。