圆心角弧弦弦心距之间的关系

九年级上册数学圆的定理
九年级上册数学中有关圆的定理有很多，以下是其中一部分：
1.垂径定理：垂直于弦的直径平分这条弦，并且平分弦所对的两
条弧。

推论：（1）平分弦（不是直径）的直径垂直于弦，并且
平分弦所对的两条弧；（2）弦的垂直平分线经过圆心，并且平
分弦所对的两条弧。

2.圆心角、弧、弦、弦心距之间的关系：在同圆或等圆中，相等
的圆心角所对的弧相等，所对的弦的弦心距相等。

推论：在同
圆或等圆中，如果两个圆心角、两条弧、两条弦或两条弦的'
弦心距中有一组量相等，那么它们所对应的其余各组量都分别
相等。

3.过三点的圆：不在同一条直线上的三点确定一个圆。

三角形的
外接圆圆心（外心）是三边垂直平分线的交点。

以上信息仅供参考，建议查阅九年级上册数学教材或相关辅导资料，获取更全面和准确的信息。

垂径定理1.弦心距：（1）圆心到弦的距离叫做弦心距。

（2）圆心角、弧、弦、弦心距之间的相等关系：在同圆或等圆中，相等的圆心角所对的弧相等，所对的弦相等，所对的圆心角也相等，所对弦的弦心距也相等。

四者有一个相等，则其他三个都相等。

圆心到弦的垂线段的长度称为这条弦的弦心距。

2.垂径定理及推论：（1）垂直于弦的直径平分这条弦，并且平分弦所对的两条弧。

（2）平分弦（此弦不能是直径）的直径垂直于弦，并且平分弦所对的两条弧。

（3）弦的垂直平分线过圆心，且平分弦对的两条弧。

（4）平分一条弦所对的两条弧的直线过圆心，且垂直平分此弦（5）平行弦夹的弧相等。

1.把球放在长方体纸盒内，球的一部分露出盒外，其截面如图所示，已知EF=CD=4cm，求球的半径。

2.如图，AB是半圆的直径，O是圆心，C是半圆上一点，D是弧AC中点，OD交弦AC于E，连接BE，若AC=8，DE=2，求（1）求半圆的半径长；（2）BE的长度。

3.如图，小明将一块三角板放在⊙O上，三角板的一直角边经过圆心O，测得AC=5cm，AB=3cm，求⊙O的半径1、（2011年北京四中中考模拟18）已知：如图1，AB是⊙O的弦，半径OC图1⊥AB 于点D ，且AB=8m ，OC=5m ，则DC 的长为（ ）A 3cmB 2.5cmC 2cmD 1cm2、（2011年北京四中中考模拟20）如图，C 是以AB 为直径的⊙O 上一点，已知AB=5，BC=3，则圆心O 到弦BC 的距离是( )A 、1.5B 、2C 、2.5D 、33、（2011年浙江杭州五模）如图，圆O 过点Ｂ、Ｃ，圆心Ｏ在等腰直角ABC∆的内部，090,1,6BAC OA BC ∠===，则圆O 的半径为（ ） Ａ、13 Ｂ、１３ Ｃ、６ Ｄ、213AOB C第3题图 4、（2011年浙江杭州六模）如图，把⊙O 1向右平移8个单位长度得⊙O 2，两圆相交于A.B ，且O 1A ⊥O 2A ，则图中阴影部分的面积是（ ）A.4π-8 B . 8π-16 C.16π-16 D. 16π-325.（2011年重庆江津区七校联考）如图，一条公路的转弯处是一段圆弧（图中的AB 弧），点O 是这段弧的圆心，AB =120m ，C 是AB 弧上一点，OC ⊥AB 于D ，CD =20m ，则该弯路的半径为________米6. （2011浙江慈吉 模拟）如图，△ABC 内接于⊙O , ∠B=42°, 则∠OCA=__________.7．（2011年杭州市西湖区）工程上常用钢珠来测量零件上小孔的宽口，假设钢珠的直径是10mm ，测得钢珠顶端离零件表面的距离为8mm ，如图所示，则这个小孔的宽口AB 是 mm ．8.（2011年北京中考）一个圆形花圃的面积为300лm 2，你估计它的半径为 （误差小于0.1m ）9.（2011年北京四中中考模拟19）在平面直角坐标系中，圆心O 的坐标为（-3，4），以半径r 在坐标平面内作圆，（1）当r 时，圆O 与坐标轴有1个交点；C A B OC A BO 第4题O C B A 第6题图 B A 8mm 第7题D C B A O 第5题图（2）当r 时，圆O与坐标轴有2个交点；（3）当r 时，圆O与坐标轴有3个交点；（4）当r 时，圆O与坐标轴有4个交点；10.（2011年黄冈市浠水县中考调研试题）在半径为5的⊙O中，有两平行弦AB．CD，且AB＝6，CD＝8，则弦AC的长为__________．AB与CD间距离为。

圆心 弧 弦 弦心距之间的关系1. 圆不但是轴对称图形，而且也是中心对称图形，实际上圆绕圆心旋转任意一个角度，都能够与原来的图形重合。

2. 圆心角：顶点在圆心的角叫做圆心角。

从圆心到弦的距离叫做弦心距。

3. 定理：在同圆或等圆中，相等的圆心角所对的弧相等，所对的弦相等，所对的弦的弦心距相等。

4. 推论：在同圆或等圆中，如果两个圆心角、两条弧、两条弦或两弦的弦心距中有一组量相等，那么它们所对应的其余各组量都分别相等。

注意：要正确理解和使用圆心角定理及推论。

一般地，n °的圆心角对着n °的弧，n °的弧对着n °的圆心角，也就是说，圆心角的度数和它所对的弧的度数相等。

注意：这里说的相等是指角的度数与弧的度数相等。

而不是角与弧相等，在书写时要防止出现“∠=⋂AOB AB ”之类的错误。

因为角与弧是两个不能比较变量的概念。

相等的弧一定是相同度数的弧，但相同度数的弧却不一定是相等的弧。

6. 圆中弧、圆心角、弦、弦心距的不等关系（1）在同圆或等圆中，如果弦不等，那么弦心距也就不等，大弦的弦心距较小，小弦的弦心距反而大，反之弦心距较小时，则弦较大。

当弦为圆中的最大弦（直径）时，弦心距缩小为零；当弦逐步缩小时，趋近于零时，弦心距逐步增大，趋近于半径。

（2）在同圆或等圆中，如果弧不等，那么弧所对的弦、圆心角也不等，且大弧所对的圆心角较大，反之也成立。

注意：不能认为大弧所对的弦也较大，只有当弧是劣弧时，这一命题才能成立，半圆对的弦最大，当弧为优弧时，弧越大，对的弦越短。

7. 辅助线方法小结：（1）有弦的中点时，常连弦心距，进而可利用垂径定理或圆心角、弦、弧、弦心距关系定理；另外，证明两弦相等也常作弦心距。

（2）在计算弧的度数时，或有等弧的条件时，或证等弧时，常作弧所对的圆心角。

（3）有弧的中点或证弧的中点时，常有以下几种引辅助线的方法：∴AB＝CD弦AB、DC若PO平分∠APC弦AB、CD交于P点（PO平分∠APC=⎩OP OP ∴≅∆∆P O M P O N AAS ()∴=PM PN AM AB CN CD AB CD ===1212，， ∴=AM CN（）把作出来，变成一段弧，然后比较与的大小。

圆心角、弧、弦、弦心距之间的关系（二）1. 弧在前文中我们已经介绍了圆心角和弧之间的关系。

在这篇文章中，我们将进一步探讨弦和弦心距与圆心角、弧之间的关系。

首先，我们先来了解一下什么是弧。

在一个圆上，两个点之间的曲线部分叫做弧。

弧的长度可以通过圆心角来计算，即弧长等于圆心角的大小乘以半径。

假设圆的半径为r，圆心角为θ，那么弧长L可以表示为：L = r * θ2. 弦接下来，我们来介绍一下弦。

弦是连接圆上的两个点的线段。

弦的长度可以通过圆心角来计算，通过以下公式计算：S = 2 * r * sin(θ/2)其中S表示弦的长度。

3. 弦心距弦心距是指从圆的中心点到弦的距离。

弦心距可以通过以下公式计算：D = 2 * r * cos(θ/2)其中D表示弦心距。

4. 圆心角与弦、弦心距的关系圆心角与弦和弦心距之间有一定的关系。

当圆心角的大小固定时，弦和弦心距的大小也是固定的。

具体可以通过以下公式进行计算：•弦长S与圆心角θ之间的关系：S = 2 * r * sin(θ/2)•弦心距D与圆心角θ之间的关系：D = 2 * r * cos(θ/2)可以看出，当圆心角θ固定时，弦长和弦心距都与半径r成正比。

也就是说，如果增加半径r的大小，弦长和弦心距也会增加；减小半径r的大小，弦长和弦心距也会减小。

另外，当圆心角θ固定时，弦长和弦心距之间也有一定的关系。

根据三角函数的性质，可以得到以下关系：S^2 + D^2 = (2r)^2该关系也被称为勾股定理。

5. 总结综上所述，圆心角、弧、弦和弦心距之间存在一定的关系。

圆心角决定了弧的长度，可以通过半径和圆心角的关系进行计算；弦的长度和弦心距都与圆心角成正比，可以通过圆心角和半径的关系进行计算。

另外，弦和弦心距之间也满足勾股定理。

通过理解和掌握这些关系，我们可以在解决相关问题时更加灵活和准确。

实际应用中，这些关系经常用于计算圆中的各个要素，对于解决与圆相关的问题非常有帮助。

结论1在同圆或等圆中，如果：①两个圆心角②两条弧③两条弦④两条弦的弦心距中，有任意一组量相等，那么其它各组量都相等。

结论2:称一段弧所对圆心角的度数为弧的度数。

即：圆心角度数=该圆心角所对弧的度数例1如图，已知AB、CD为O O的两条弦，AD二BC，求证AB= CD.A例2如图7-23，点0是/ EPF的平分线上的一点，以0为圆心的圆和角的两边分别交于点A、B和C、D.求证：AB=CD.变式1：变式2:例3如图，已知AB 和CD 是O O 的两条直径，弦CE //AB , EC 的度数为40°求/ BOC 的度数. L 1BMA P NDDE变式：已知：如图，AB和CD是两条直径，弦CE// AB,求证:1例4如图，在。

O中，弦AB所对劣弧为。

O的-，圆的半径为2cm,3例5如图，MN是半径为1的O O的直径，点A在O O上，/ AMN =30° B为AN弧的中点, P是直径MN上一动点，则PA+ PB的最小值为（）（A）2 2 (B) 2 (C)1(D)2OE例6如图，CD与EF为O O的弦，AB与之交于M、N,若AM=BN,/ 仁/2,求证：CD=EF作业：1. 如图，在半径为2cm的O O内有长为_的弦AB,求此弦所对的圆心角二此二的度数及AB上弦心距的长度。

2. 在O O中，弦AB的长恰好等于半径，求弦AB所对的圆心角度数。

3. O O的一条弦长与半径之比是，这条弦将圆周分成的两部分中，求其劣弧的度数：优弧的度数的比值。

4•如图，在O O中，D、E分别为半径OA、OB中点，C为AB中点,C5.如图，AB 是O O直径，AC 二CD,求证：OC// BD. AC 二CD。

圆心角、弧、弦心距
一、圆心角
圆心角是位于圆心的正多边形的角度单位，它是由端点组成的角的量化表示。

圆心角的数量与正多边形的边数有关，比如正六边形的圆心角为60°，正十二边形的圆心角为30°，正二十四边形的圆心角为15°等。

圆心角的单位是度，也可以用弧度（radian）表示。

二、弧
弧是一条曲线，作为圆柱面的切面而成，它是由圆心和曲线前端两个端点构成的圆心角所确定。

弧又称为圆弧；一般当圆半径r恒定时，圆心角$\theta$时，弧长可表示为$L=r\theta$。

三、弦心距
弦心距是指圆弦的两个端点之间的距离，表示为$d$。

由圆心角 $\theta$ 所确定，由圆上两点到圆心的距离之差而定，其公式为：$d=2r \sin \frac{\theta}{2}$。

在正多边形里，圆心角、弧以及弦心距之间存在着对应关系。

圆心角和正多边形的边数有关，圆心角确定弧的长度，又由圆心角以及圆半径来确定弦心距。

圆心角就是控制圆弦长度和弦心距的重要因素，它们三者的关系在图形学中具有重要意义。

27.2圆心角、弧、弦、弦心距之间的关系圆上任意两点之间的部分叫做圆弧，简称弧；联结圆上任意两点的线段叫做弦，过圆心的弦就是直径，以圆心为顶点的角叫做圆心角。

圆的任意一条直径的两个端点将圆分成两条弧，每一条弧都叫做半圆。

大于半圆的⌒，读弧叫做优弧，小于半圆的弧叫做劣弧。

如图27-8，以A、C为端点的劣弧记作AC⌒作“弧AC”；以A、C为端点的优弧记作ABC ，读作“弧ABC”。

如图27-9，⊙O的一个圆心角的两边与⊙O分别相交于点A、B，这个圆心角记作∠AOB，这时，相应得到弧AB和弦AB。

反过来看，对于弧AB或弦AB，相应可作∠AOB。

⌒⌒通常的说AB （或弦AB）是∠AOB所对的弧（或弦），∠AOB是AB （或弦AB）所对的圆心角。

圆心到弦的距离叫做弦心距。

在图27-9中，过圆心O作弦AB的垂线，垂足为C，则垂线段OC的长时弦AB的弦心距。

在平面上，一个圆绕着它的圆心旋转任何一个角度（大于0°且小于360°），都能与原来图形重合。

所以，圆是以圆心为旋转对称中心的旋转对称图形，旋转角可为大于0°且小于360°的任何一个角。

问题1⌒和A`B`⌒如图27-10，在⊙O中，当圆心角∠AOB=∠A'OB'时，它们分别所对的AB是否能重合？把扇形OAB绕圆心O旋转，使OA与OA'重合。

因为∠AOB=∠A'OB'，所以OB ⌒和OB'重合；而⊙O的半径长都相等，因此点A与点A'重合，点B与点B'重合，这样AB⌒就一定重合。

与A`B`⌒与能够重合的两条弧称为等弧，或者说这两条弧相等，上述AB⌒是等弧，记作AB⌒ =A`B`⌒。

A`B`半径长相等的两个圆一定能够重合，我们把半径相等的两个圆称为等圆。

⌒⌒在上述问题中，AB 与A`B` 所对的弦分别是AB和A'B'，通过旋转可知，AB与A'B'重合，两弦的垂线段OC、OC'也重合（为什么），得AB=A'B'，OC=OC'.于是，可以得到圆心角、弦、弦心距之间关系的定理。

圆心角、弧、弦、弦心距之间关系【重点、难点】重点：圆心角、弧、弦、弦心距之间的关系定理及推论，在同圆或等圆中，相等的圆心角所对的弧相等，所对的弦相等，所对的弦的弦心距相等；在同圆或等圆中，如果两个圆角、两条弧、两条弦或两条弦的弦心距有一组量相等，那么它们所对应的各组量都分别相等（即“知一得三”） 难点：正确区分定理的题设和结论及对︒1弧的理解.考点：圆心角、弧、弦、弦心距之间的关系，本节内容是中考的必考内容，大多以填空、选择的形式命题.【知识要点】（1）圆的中心对称性：圆是以圆心为对称中心的中心对称图形． （2）概念：圆心角、弦心距（3）定理：在同圆或等圆中，相等的圆心角所对的孤相等，所对的弦相等，所对的弦的弦心距相等 推论：在同圆式等圆中，如果两个圆心角，两条弧，两条弦或两条弦的弦心距中有一组量相等，那么它们所对应的其余各组量都分别相等．【经典例题】例1、如图，在△ABC 中，︒=∠︒=∠25,90B BCA ，以C 为圆心， CA 为半径的圆交AB 于D ，则的度数是 ．例2、如图所示，点O 是∠EPF 的平分线上一点，以O 为圆心的圆和角的两边分别交于A 、B 和C 、D ，求证：AB=CD ．例3、已知：如图，EF 为⊙O 的直径，过EF 上一点P 作弦AB 、CD ，且∠APF=∠CPF 。

求证：PA=PC 。

例4、如图所示，在⊙O 中，AB 是直径，CO ⊥AB ，D 是CO 的中点，DE ∥AB ．求证 ACBD ABEFO PC12D例5、如图所示，已知AB 为⊙O 的弦，从圆上任一点引弦CD ⊥AB ，作∠OCD 的平分线交⊙O 于P 点，边结PA 、PB ．求证:PA=PB.例6、已知：如图，∠AOB=90°，C 、D 是弧AB 的三等分点，AB 分别交OC 、OD 于点E 、F 。

求证：AE=BF=CD 。

【课堂小测】（1--8每题8分，9--14每题6分）1．圆不仅是轴对称图形，而且还是 图形，圆独有的性质是 ． 2．过已知⊙O 中一已知点P 的弦中，最短的弦是 ；最长的弦是 ．3．在⊙O 中，AB 所对的弦AB 与B 点的半径夹角为︒55，那么弦AB 所对的优弧AMB 的度数为 。

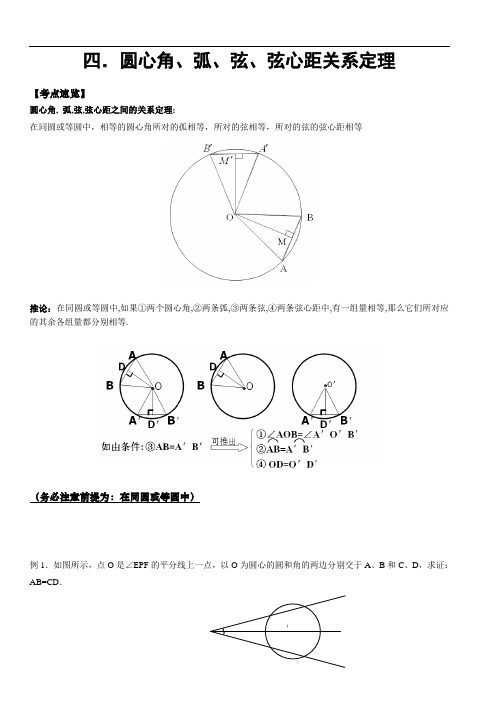
四．圆心角、弧、弦、弦心距关系定理【考点速览】圆心角, 弧,弦,弦心距之间的关系定理:在同圆或等圆中，相等的圆心角所对的孤相等，所对的弦相等，所对的弦的弦心距相等推论：在同圆或等圆中,如果①两个圆心角,②两条弧,③两条弦,④两条弦心距中,有一组量相等,那么它们所对应的其余各组量都分别相等.（务必注意前提为：在同圆或等圆中）例1．如图所示，点O是∠EPF的平分线上一点，以O为圆心的圆和角的两边分别交于A、B和C、D，求证：AB=CD．ABE OOPO 1O 2O例2、已知：如图，EF 为⊙O 的直径，过EF 上一点P 作弦AB 、CD ，且∠APF=∠CPF 。

求证：PA=PC 。

例3．如图所示，在ABC ∆中，∠A=︒72，⊙O 截ABC ∆的三条边长所得的三条弦等长，求∠BOC.例4．如图，⊙O 的弦CB 、ED 的延长线交于点A ，且BC=DE ．求证：AC=AE ．·OAB CO ·CAEBD例5．如图所示，已知在⊙O 中，弦AB=CB ，∠ABC=︒120，OD ⊥AB 于D ，OE ⊥BC 于E ． 求证：ODE ∆是等边三角形．综合练习一、选择题1．下列说法中正确的是（ ）A 、相等的圆心角所对的弧相等B 、相等的弧所对的圆心角相等C 、相等的弦所对的弦心距相等D 、弦心距相等，则弦相等2．如图，在⊙O 中，AB 的度数是︒50，∠OBC=︒40，那么∠OAC 等于（ ） A 、︒15 B 、︒20 C 、︒25 D 、︒303．P 为⊙O 内一点，已知OP=1cm ，⊙O 的半径r=2cm ，则过P 点弦中，最短的弦长为（ ） A 、1cm B 、3cm C 、32cm D 、4cm4．在⊙O 中，AB 与CD 为两平行弦，AB >CD ，AB 、CD 所对圆心角分别为︒︒60,120，若⊙O 的半径为6，则AB 、CD 两弦相距（ ）A 、3B 、6C 、13+D 、333± 5.如图所示，已知△ABC 是等边三角形，以BC 为直径的⊙O 分别交AB 、AC 于点D 、E 。

2圆心角、弧、弦、弦心距之间的关系.(总21页)-本页仅作为预览文档封面，使用时请删除本页-2圆心角、弧、弦、弦心距之间的关系教学目标1．使学生理解圆的旋转不变性，理解圆心角、弦心距的概念；2．使学生掌握圆心角、弧、弦、弦心距之间的相等关系定理及推论，并初步学会运用这些关系解决有关问题；3．培养学生观察、分析、归纳的能力，向学生渗透旋转变换的思想及由特殊到一般的认识规律．教学重点和难点重点;圆心角、弧、弦、弦心距之间的相等关系；难点;从圆的旋转不变性出发，推出圆心角、弧、弦、弦心距之间的相等关系．2圆心角、弧、弦、弦心距之间的关系一、创设情景，引入新课圆是轴对称图形．圆的这一性质，帮助我们解决了圆的许多问题．今天我们再来一起研究一下圆还有哪些特性．1．动态演示，发现规律图7－47，并动态显示：平行四边形绕对角线交点O旋转180°后．(1)结果怎样？(2)这样的图形叫做什么图形？图7－48，并动态显示：⊙O绕圆心O旋转180°．，归纳出：圆是以圆心为对称中心的中心对称图形．让学生观察发现什么结论？得出：不论绕圆心旋转多少度，都能够和原来的图形重合．进一步演示，让圆绕着圆心旋转任意角度α，知识点一、圆的旋转不变性于是归纳总结，得出圆所特有的性质：圆的旋转不变性．即圆绕圆心旋转任意一个角度α，都能够与原来的图形重合．知识点二、弧、弦、圆心角的关系1.圆心角定义如图所示，∠AOB的顶点在圆心，像这样顶点在圆心的角叫做圆心角(central angle),从圆心到弦的距离叫做弦心距2.定理：在同圆或等圆中，相等的圆心角所对的弧相等，所对的弦也相等．已知；在⊙O中求证；3.推论：在同圆或等圆中，如果两条弧相等，那么它们所对的圆心角相等，所对的弦也相等．在同圆或等圆中，如果两条弦相等，那么它们所对的圆心角相等，所对的弧也相等．要点诠释：(1)一个角要是圆心角，必须具备顶点在圆心这一特征.(2)注意定理中不能忽视“同圆或等圆”这一前提.4推论：在同圆或等圆中，如果两个圆心角、两条弧、两条弦或两条弦的弦心距中有一组量相等，那么它们所对应的其余各组量都分别相等．注意：要正确理解和使用圆心角定理及推论。