2017—2018学年度第一学期期中质量检测 高一数学试卷

第Ⅰ卷（选择题共60分）一、选择题（本大题共12小题，每小题5分，满分60分，每题四个选项中只有一项是符合题目要求的）1、设集合{|4},{1,2},{2,3}U x N x A B ，则()()U U C A C B =( )(A){0,4}(B){4}(C) {1,2,3}(D)2、下列函数中，既是偶函数，又在)0,(上为减函数的是( )(A)x y 2(B)x y (C)2x y (D)||lg x y 3、已知函数122x y ，当自变量]1,0[x 时，因变量y 的取值范围为( )(A)]2,1[(B)]1,0[(C)]3,2[(D)]2,0[4、已知函数x x x f 3)(，则函数)1(x f 的定义域为( )(A)1,4x x x (B)1,2x x x (C)0,2x x x (D)1,4x x x 5、函数1()1x a f x a x (0a 且1a )的图象恒经过定点( )(A)(1,1)(B)(1,2)(C)(1,3)(D)(0,2)6、用二分法求方程x x 2)1ln(的近似解时，可以取的一个区间是( )(A)(1,2)(B)(2,)e (C)(3,4)(D)(0,1)7、函数223()log ()f x x x 的单调减区间为( )(A) 1(,)2(B) 1(,1)2(C) 1(,)2(D) 1(0,)28、设集合(,),0A x y x R y ，B R ，点(,)x y 在映射:f A B 的作用下的象是2x y ，则对于B 中的数5，与之对应的A 中的元素不．可能．．是( )(A)(1,3)(B)2(log 3,2)(C)(0,5)(D)(2,1)9、在平面直角坐标下，函数21()22x xf x x x 的图象( )(A) 关于x 轴对称(B) 关于y 轴对称(C) 关于原点对称(D) 关于直线y x 轴对称。

2017—2018学年人教版高一数学上学期期中考试卷（一）（考试时间120分钟满分150分）一、单项选择题（本大题包括12小题，每小题5分，共60分，每小题只有一个选项符合题意）1．已知集合M=（﹣1，1），N={x|﹣1＜x＜2，x∈Z}，则M∩N=（）A．{0}B．{0，1}C．（﹣1，1）D．（1，2）2．满足{1，3}∪A={1，3，5}的所有集合A的个数（）A．1个 B．2个 C．3个 D．4个3．函数f（x）=a2x﹣1（a＞0且a≠1）过定点（）A．（1，1） B．（，0）C．（1，0） D．（，1）4．已知f（x）=3x+3﹣x，若f（a）=3，则f（2a）等于（）A．3 B．5 C．7 D．95．已知函数f（x）是R上的奇函数，且当x＞0时，f（x）=x3﹣2x2，则x＜0时，函数f（x）的表达式为f（x）=（）A．x3+2x2B．x3﹣2x2C．﹣x3+2x2 D．﹣x3﹣2x26．如果偶函数f（x）在[3，7]上是增函数且最小值是2，那么f（x）在[﹣7，﹣3]上是（）A．减函数且最小值是2 B．减函数且最大值是2C．增函数且最小值是2 D．增函数且最大值是27．如果函数f（x）=x2+2（a﹣1）x+2在（﹣∞，4]上是减函数，那么实数a取值范围是（）A．a≤﹣3 B．a≥﹣3 C．a≤5 D．a≥58．三个数20.3，0.32，log0.32的大小顺序是（）A．0.32＜log0.32＜20.3B．0.32＜20.3＜log0.32C．log0.32＜20.3＜0.32D．log0.32＜0.32＜20.39．下列函数中，既是偶函数又在（0，+∞）上单调递增的函数是（）A．y=2x3B．y=|x|+1 C．y=﹣x2+4 D．y=2﹣|x|10．函数f（x）=（x∈R）的值域是（）A．（0，2） B．（0，2]C．[0，2） D．[0，2]11．设函数y=x3与y=（）x的图象的交点为（x0，y0），则x0所在的区间是（）A．（0，1） B．（1，2） C．（2，3） D．（3，4）12．若直角坐标平面内A、B两点满足条件：①点A、B都在f（x）的图象上；②点A、B关于原点对称，则对称点对（A，B）是函数的一个“姊妹点对”（点对（A，B）与（B，A）可看作同一个“姊妹点对”）．已知函数f（x）=，则f（x）的“姊妹点对”有（）个．A．1 B．2 C．3 D．4二、非选择题（本题包括4个小题，每小题5分，共20分）13．已知函数y=f（x+1）定义域是[﹣2，3]，则y=f（2x﹣1）的定义域是．14．已知函数y=f（x+3）是偶函数，则函数y=f（x）图象的对称轴为．15．求满足＞16的x的取值集合是．16．设函数f（x）=x|x|+bx+c，给出下列四个命题：①当c=0时，y=f（x）是奇函数；②当b=0，c＞0时，函数y=f（x）只有一个零点；③函数y=f（x）的图象关于点（0，c）对称；④函数y=f（x）至多有两个零点．其中正确命题的序号为．三、解答题（本大题共6小题，共70分，解答应写出文字说明，证明过程或演算步骤）17．求值：（1）（2）log25．18．设全集是实数集R，A={x|≤x≤3}，B={x|x2+a＜0}．（1）当a=﹣4时，求A∩B和A∪B；（2）若（∁R A）∩B=B，求实数a的取值范围．19．已知二次函数f（x）的图象过点（0，4），对任意x满足f（3﹣x）=f（x），且有最小值．（Ⅰ）求函数f（x）的解析式；（Ⅱ）求函数h（x）=f（x）﹣（2t﹣3）x在[0，1]上的最小值g（t）．20．某厂生产某种产品x（百台），总成本为C（x）（万元），其中固定成本为2万元，每生产1百台，成本增加1万元，销售收入（万元），假定该产品产销平衡．（1）若要该厂不亏本，产量x应控制在什么范围内？（2）该厂年产多少台时，可使利润最大？（3）求该厂利润最大时产品的售价．21．已知函数f（x）=（a＞0，b＞0）为奇函数．（1）求a与b的值；（2）判断并用定义证明函数f（x）的单调性，再求不等式f（x）＞﹣的解集．22．已知函数f（x）=|x﹣a|，g（x）=ax，（a∈R）．（1）若a=1，求方程f（x）=g（x）的解；（2）若方程f（x）=g（x）有两解，求出实数a的取值范围；（3）若a＞0，记F（x）=g（x）f（x），试求函数y=F（x）在区间[1，2]上的最大值．参考答案一、单项选择题1．A．2．D．3．D．4．C．5．A．6．A．7．A 8．D．9．B．10．B．11．A．12．B．二、非选择题13．答案为：．14．答案为x=3．15．答案为：（﹣∞，﹣1）．16．答案为：①②③．三、解答题17．解：（1）==；（2）=；所以（1）原式=，（2）原式=．18．解：（1）∵，当a=﹣4时，B={x|﹣2＜x＜2}，则，A∪B={x|﹣2＜x≤3}（2）若（C R A）∩B=B，则B⊆C R A={x|x＞3或，1°、当a≥0时，B=∅，满足B⊆C R A．2°当a＜0时，，又B⊆C R A，则．综上，．19．解：（Ⅰ）∵函数f（x）对任意x满足f（3﹣x）=f（x），且有最小值．∴函数图象的顶点坐标为（，），设f（x）=a（x﹣）2+，∵函数f（x）的图象过点（0，4），∴a（﹣）2+=4，∴a=1，∴f（x）=（x﹣）2+=x2﹣3x+4，（Ⅱ）函数h（x）=f（x）﹣（2t﹣3）x=x2﹣2tx+4的图象是开口朝上，且以直线x=t为对称轴的抛物线，当t＜0时，函数h（x）在[0，1]上为增函数，当x=0时，函数h（x）的最小值g（t）=4；当0≤t≤1时，函数h（x）在[0，t]上为减函数，在[t，1]上为增函数，当x=t 时，函数h（x）的最小值g（t）=﹣t2+4；当t＞1时，函数h（x）在[0，1]上为减函数，当x=1时，函数h（x）的最小值g（t）=5﹣3t；综上所述，值g（t）=20．解：由题意得，成本函数为C（x）=2+x，从而利润函数．（1）要使不亏本，只要L（x）≥0，当0≤x ≤4时，L （x ）≥0⇒3x ﹣0.5x 2﹣2.5≥0⇒1≤x ≤4， 当x ＞4时，L （x ）≥0⇒5.5﹣x ≥0⇒4＜x ≤5.5． 综上，1≤x ≤5.5．答：若要该厂不亏本，产量x 应控制在100台到550台之间． （2）当0≤x ≤4时，L （x ）=﹣0.5（x ﹣3）2+2， 故当x=3时，L （x ）max =2（万元）， 当x ＞4时，L （x ）＜1.5＜2．综上，当年产300台时，可使利润最大．（3）由（2）知x=3，时，利润最大，此时的售价为（万元/百台）=233元/台．21．解：（1）根据题意，由函数f （x ）是奇函数，得f （﹣x ）=﹣f （x ）， 即﹣=，对定义域内任意实数x 都成立，整理得（2a ﹣b ）﹣22x +（2ab ﹣4）•2x +（2a ﹣b ）=0对定义域内任意实数都成立，即有，解可得或，经检验符合题意．（2）由（1）可知，f （x ）==（﹣1+），易判断f （x ）为R 上的减函数．证明如下：设任意的实数x 1、x 2且满足x 1＜x 2，f （x 1）﹣f （x 2）=（﹣）=，又由y=2x 在R 上递增且函数值大于0， 则有f （x 1）﹣f （x 2）＞0， 则函数f （x ）在R 是的减函数；对于f（x）==（﹣1+），有f（1）=﹣，f（x）＞﹣，即f（x）＞f（1），又由函数为减函数，则必有x＜1，即不等式f（x）＞﹣的解集为{x|x＜1}．22．解：（1）当a=1时，|x﹣1|=x，即x﹣1=x或x﹣1=﹣x，解得x=；（2）当a＞0时，|x﹣a|﹣ax=0有两解，等价于方程（x﹣a）2﹣a2x2=0在（0，+∞）上有两解，即（a2﹣1）x2+2ax﹣a2=0在（0，+∞）上有两解，令h（x）=（a2﹣1）x2+2ax﹣a2，因为h（0）=﹣a2＜0，所以，故0＜a＜1；同理，当a＜0时，得到﹣1＜a＜0；当a=0时，f（x）=|x|=0=g（x），显然不合题意，舍去．综上可知实数a的取值范围是（﹣1，0）∪（0，1）．（3）令F（x）=f（x）•g（x）①当0＜a≤1时，则F（x）=a（x2﹣ax），对称轴x=，函数在[1，2]上是增函数，所以此时函数y=F（x）的最大值为4a﹣2a2．②当1＜a≤2时，F（x）=，对称轴x=，所以函数y=F（x）在（1，a]上是减函数，在[a，2]上是增函数，F（1）=a2﹣a，F（2）=4a﹣2a2，1）若F（1）＜F（2），即1＜a＜，此时函数y=F（x）的最大值为4a﹣2a2；2）若F（1）≥F（2），即，此时函数y=F（x）的最大值为a2﹣a．③当2＜a≤4时，F（x）=﹣a（x2﹣ax）对称轴x=，此时F（x）max=F（）=，④当a＞4时，对称轴x=，此时F（x）max=F（2）=2a2﹣4a．综上可知，函数y=F（x）在区间[1，2]上的最大值．2017—2018学年人教版高一数学上学期期中考试卷（二）（考试时间100分钟满分120分）一、单项选择题（每小题4分，满分60分）1．设A={a}，则下列各式中正确的是（）A．0∈A B．a∈A C．a⊆A D．a=A2．设全集U={﹣2，﹣1，0，1，2}，A={﹣2，﹣1，0}，B={0，1，2}，则（∁U A）∩B=（）A．{0}B．{﹣2，﹣1}C．{1，2}D．{0，1，2}3．若集合M={（x，y）|x+y=0}，P={（x，y）|x﹣y=2}，则M∩P=（）A．（1，﹣1）B．{x=1}∪{y=﹣1} C．{1，﹣1}D．{（1，﹣1）}4．函数的定义域是（）A．（﹣∞，0]B．[0，+∞）C．[1，+∞）D．（﹣∞，1]5．已知奇函数f（x）在（0，+∞）上是增函数，且f（2）=0，则f（x）＞0的解集为（）A．（0，2）B．（﹣2，0）C．（﹣2，0）∪（2，+∞）D．（﹣2，2）6．如图：若0＜a＜1，函数y=a x与y=x+a的图象可能是（）A．B．C．D．7．函数y=ax2+bx+3在（﹣∞，﹣1]上是增函数，在[﹣1，+∞）上是减函数，则（）A．b＞0且a＜0 B．b=2a＜0 C．b=2a＞0 D．b=﹣2a＜08．如果函数f（x）=（a2﹣1）x在R上是减函数，那么实数a的取值范围是（）A．|a|＞1 B．|a|＜2 C．|a|＞3 D．1＜|a|＜9．如果函数f（x）=x2+bx+c对任意实数t都有f（2+t）=f（2﹣t），那么（）A．f（2）＜f（1）＜f（4） B．f（1）＜f（2）＜f（4） C．f（2）＜f（4）＜f （1）D．f（4）＜f（2）＜f（1）10．已知二次函数y=ax2+bx+c=0（a≠0）的图象如图所示，记p=|a﹣b+c|+|2a+b|，q=|a+b+c|+|2a﹣b|，则（）A．p＞q B．p=qC．p＜q D．p，q大小关系不能确定11．下列四组函数中，表示相等函数的一组是（）A．f（x）=|x|，B．，C．，g（x）=x+1 D．，12．若函数f（x）的定义域为[1，2]，则函数y=f（x2）的定义域为（）A．[1，4]B．[1，]C．[﹣，]D．[﹣，﹣1]∪[1，]13．函数y=1﹣的图象是（）A．B．C．D．14．若二次函数y=﹣x2+bx+c的图象的对称轴是x=2，则有（）A．f（1）≤f（2）≤f（4） B．f（2）＞f（1）＞f（4） C．f（2）＜f（4）＜f （1）D．f（4）＞f（2）＞f（1）15．如果奇函数f（x）在区间[3，7]上是增函数且最小值为5，那么f（x）在区间[﹣7，﹣3]上是（）A．增函数且最小值为﹣5 B．增函数且最大值为﹣5C．减函数且最小值为﹣5 D．减函数且最大值为﹣5二、填空题（每小题4分，满分32分）16．若函数y=x2+（a+2）x+3，x∈[a，b]的图象关于直线x=1对称，则b=．17．设f（x）=2x﹣1，g（x）=x+1，则f[g（x）]=．18．f（2x+1）=x2﹣2x，则f（）=．19．已知一次函数y=f（x）中，f（8）=16，f（2）+f（3）=f（5），则f（1）+f （2）+f（3）+…+f（100）=．20．若函数f（x）=为奇函数，则a=，b=．21．若函数f（x）=x2+px+3在（﹣∞，1]上单调递减，则p的取值范围是．22．若函数f（x）是定义在R上的偶函数，且图象经过点（﹣1，2），则f（﹣1）+f（1）=．23．已知函数f（x）=x2+ax+1，若对于任意x∈R，都有f（1+x）=f（1﹣x），求a的值．三、解答题（共28分）24、已知函数f（x）=log a（x+1）﹣log a（1﹣x），a＞0且a≠1．（1）求f（x）的定义域；（2）判断f（x）的奇偶性并予以证明．25．（7分）已知函数f（x）=ax2+bx+c的图象在y轴上的截距为1，且满足f（x+1）=f（x）+x+1，试求：（1）f（x）的解析式；（2）当f（x）≤7时，对应的x的取值范围．26．（7分）若关于x的二次函数f（x）=﹣x2+bx+c对一切实数x都有：f（2+x）=f（2﹣x）恒成立．（1）求实数b的值；（2）当a∈R时，判断f（）与f（﹣a2﹣a+1）的大小，并说明理由．27．（7分）判断函数f（x）=x2在R上的增减性．参考答案一、单项选择题．1．B．2．C3．D．4．A．5．C．6．B．7．B8．D．9．A．10．C．11．A．12．D．13．B．14．B．15．B．二、填空题．16．答案为617．答案为：2x+1．18．答案为：19．答案为：10100．20．答案为：0，021．答案为：（﹣∞，﹣2]．22．答案为：4．23．答案为：﹣2．三、解答题．24、解：（1）由题得，使解析式有意义的x范围是使不等式组成立的x范围，解得﹣1＜x＜1，所以函数f（x）的定义域为{x|﹣1＜x＜1}．（2）函数f（x）为奇函数，证明：由（1）知函数f（x）的定义域关于原点对称，且f（﹣x）=log a（﹣x+1）﹣log a（1+x）=﹣log a（1+x）+log a（1﹣x）=﹣[log a（1+x）﹣log a（1﹣x）]=﹣f（x）所以函数f（x）为奇函数．25．解：（1）函数f（x）=ax2+bx+c的图象在y轴上的截距为1，可得c=1；f（x+1）=f（x）+x+1，可得：a（x+1）2+bx+b+1=ax2+bx+x+2；可得：解得a=，b=．可得函数的解析式为：f（x）=x2+x+1．（2）f（x）≤7，可得：x2+x+1≤7，可得x2+x﹣12≤0，解得﹣4≤x≤3．26．解：（1）关于x的二次函数f（x）=﹣x2+bx+c对一切实数x都有：f（2+x）=f（2﹣x）恒成立，故二次函数的对称轴方程为x=2=，∴b=4，（2）由（1）知f（x）=﹣x2+4x+c，显然函数在（﹣∞，2）上是减函数．由于﹣a2﹣a+1═﹣，∴f（）＜f（﹣a2﹣a+1）．27．解：因为f（x）=x2为偶函数，当x∈（0，+∞）时，设x1＜x2∈（0，+∞），∴f（x1）﹣f（x2）=x12﹣x22=（x1﹣x2）（x1+x2），∵x1＜x2∈（0，+∞），∴x1﹣x2＜0，x1+x2＞0，∴f（x1）﹣f（x2）＜0，∴f（x1）＜f（x2），∴f（x）在（0，+∞）上为增函数，∴f（x）在（﹣∞，0]上为减函数．2017—2018学年人教版高一数学上学期期中考试卷（三）（考试时间120分钟满分150分）一．单项选择题（每小题5分，共80分）1．已知集合M={0，1，2，3，4}，N={1，3，5}且P=M∪N，则P的元素有（）个．A．2 B．4 C．6 D．82．设集合A={x|x2﹣4x+3＜0}，B={x|2x﹣3＞0}，则A∩B=（）A．（﹣3，﹣）B．（﹣3，）C．（1，）D．（，3）3．函数的定义域是（）A．B．{x|x＜1}C．D．4．下列各组中的两个函数是同一函数的有（）个（1）y=和y=x﹣5（2）y=和y=（3）y=x和y=（4）y=x和y=（5）y=t2+2t﹣5和y=x2+2x﹣5．A．1 B．2 C．3 D．45．下列函数中，在区间（0，+∞）上单调递增且为偶函数的是（）A．y=x3 B．y=2xC．y=[x]（不超过x的最大整数）D．y=|x|6．已知函数f（x）=a x+b的图象如图所示，则g（x）=log a（x+b）的图象是（）A．B． C．D．7．已知函数f（x）=，若f（f（1））=4a，则实数a等于（）A．B．C．2 D．48．若函数f（x）=﹣x2+2ax与函数在区间[1，2]上都是减函数，则实数a的取值范围为（）A．（0，1）∪（0，1）B．（0，1）∪（0，1]C．（0，1） D．（0，1]9．已知2a=5b=m且=2，则m的值是（）A．100 B．10 C． D．10．若函数f（x）=a﹣是奇函数，则实数a的值为（）A．B．C．D．11．已知函数在区间[3，5]上恒成立，则实数a的最大值是（）A．3 B．C．D．12．函数f（x）是定义在实数集R上的偶函数，且在[0，+∞）上是减函数，若f（a）≥f（3），则实数a的取值范围是（）A．（0，3]B．（﹣∞，﹣3]∪[3，+∞）C．R D．[﹣3，3]13．已知，，c=，则（）A．a＞b＞c B．b＞a＞c C．a＞c＞b D．c＞a＞b14．已知函数．若f（x）在R上是单调递增函数，则实数a的取值范围是（）A．（2，3]B．（2，3） C．（2，+∞）D．（1，2）15．设函数，若f（a）＞f（﹣a），则a的范围为（）A．（﹣1，0）∪（0，1）B．（﹣1，0）∪（1，+∞） C．（﹣∞，﹣1）∪（1，+∞）D．（﹣∞，﹣1）∪（0，1）16．设奇函数f（x）在（0，+∞）上为单调递减函数，且f（2）=0，则不等式x•f（x）≤0的解集为（）A．（﹣∞，﹣2]∪（0，2]B．[﹣2，0]∪[2，+∞）C．（﹣∞，﹣2]∪[2，+∞）D．[﹣2，0）∪（0，2]二．填空题（每小题5分，共35分）17．集合A={x|ax﹣1=0}，B={x|x2﹣3x+2=0}，且A∪B=B，则a的值是．18．已知函数f（x）=，则f（f（﹣2））=．19．设全集U=R，，则如图中阴影部分表示的集合为．20．已知函数y=f（x）是定义在R上的奇函数，当x≥0时，f（x）=x（1+x），则x＜0时，f（x）的表达式是．21．设定义在[﹣2，2]上的奇函数f（x）在区间[0，2]上单调递减，若f（m）+f（m﹣1）＞0，则实数m的范围是．22．若﹣2≤x≤2，则函数的值域为．23．设f（x）=max，其中max{a，b，c}表示三个数a，b，c中的最大值，则f（x）的最小值是．三．解答题（第24题10分，第25题12分，第26题13分，共35分）24．设全集为R，集合A={x|2x2﹣x﹣6≥0}，B={x|log2x≤2}．（1）分别求A∩B和（∁R B）∪A；（2）已知C={x|a＜x＜a+1}且C⊆B，求实数a的取值范围构成的集合．25．计算：（1）0.027﹣（﹣）﹣2+256﹣3﹣1+（﹣1）0（2）（3）．26．设a为实数，函数f（x）=2x2+（x﹣a）|x﹣a|．（1）若a=3，求f（2）的值；（2）求f（x）的最小值．参考答案一．单项选择题1．C．2．D3．A．4．B．5．D．6．D．7．C．8．D．9．C．10．B．11．D．12．D．13．C．14．A．15．B．16．C．二．填空题17．答案为：0或1或18．答案为：3．19．答案为：[1，2）．20．答案为：f（x）=x（1﹣x）21．答案为：．22．答案为：．23．答案为：2三．解答题24．解：（1）全集为R，集合A={x|2x2﹣x﹣6≥0}={x|x≤﹣或x≥2}，B={x|log2x≤2}={x|0＜x≤4}；则A∩B={x|2≤x≤4}，∴∁R B={x|x≤0或x＞4}，∴（∁R B）∪A={x|x≤0或x≥2}；（2）C={x|a＜x＜a+1}，且C⊆B，∴，解得0≤a≤3；∴实数a的取值集合是{a|0≤a≤3}．25．解：（1）原式=﹣7﹣1×（﹣2）+﹣+1=﹣49+64﹣+1=19；（2）原式=2﹣2+﹣2×3=；（3）原式=2（lg5+lg2）+lg5（lg2+1）+（lg2）2=2+lg2（lg5+lg2）+lg5=2+lg2+lg5=3．26．解：（1）当a=3时，f（x）=2x2+（x﹣3）|x﹣3|，∴f（2）=2×4+（2﹣3）×|2﹣3|=8﹣1=7，（2）当x≥a时，f（x）=3x2﹣2ax+a2，∴f（x）min==，如图所示：当x≤a时，f（x）=x2+2ax﹣a2，∴f（x）min==．综上所述：f（x）min=2017—2018学年人教版高一数学上学期期中考试卷（四）（考试时间120分钟满分150分）一、单项选择题．本题共12个小题，每小题5分，共60分．在每题列出的四个选项中，只有一项是最符合题目要求的．1．下列表示错误的是（）A．{a}∈{a，b}B．{a，b}⊆{b，a} C．{﹣1，1}⊆{﹣1，0，1} D．∅⊆{﹣1，1}2．设集合M={x|﹣3＜x＜2}，N={x|1≤x≤3}，则M∩N=（）A．[2，3]B．[1，2]C．（2，3]D．[1，2）3．函数y=+lg（2﹣x）的定义域是（）A．（1，2） B．[1，4]C．[1，2） D．（1，2]4．函数f（x）=2x﹣1+x﹣5的零点所在的区间为（）A．（0，1） B．（1，2） C．（2，3） D．（3，4）5．三个数a=0.3﹣2，b=log20.3，c=20.3之间的大小关系是（）A．a＜b＜c B．b＜c＜a C．b＜a＜c D．a＜c＜b6．若f（x）=﹣x2+2（a﹣1）x+2在（﹣∞，4]上单调递增，则实数a的取值范围是（）A．a≥﹣3 B．a≤﹣3 C．a≤5 D．a≥57．要得到y=3×（）x的图象，只需将函数y=（）x的图象（）A．向左平移3个单位B．向右平移3个单位C．向左平移1个单位D．向右平移1个单位8．函数f（x）=a x﹣1+2（a＞0且a≠1）的图象恒过定点（）A．（1，3） B．（0，1） C．（1，1） D．（0，3）9．在下列图象中，二次函数y=ax2+bx及指数函数y=（）x的图象只可能是（）A．B．C．D．10．若实数a、b、c满足3a=4b=6c，则下列等式成立的是（）A．=B．=C．=D．=11．已知定义在R上函数f（x）=对任意x1≠x2都有（x1﹣x2）[f（x1）﹣f（x2）]＜0，那么a的取值范围是（）A．（0，1） B．（0，）C．[，）D．[，1）12．设f（x）满足f（﹣x）=﹣f（x），且在[﹣1，1]上是增函数，且f（﹣1）=﹣1，若函数f（x）≤t2﹣2at+1对所有的x∈[﹣1，1]，当a∈[﹣1，1]时都成立，则t的取值范围是（）A．﹣≤t≤B．﹣2≤t≤2C．t≥或t≤﹣或t=0 D．t≥2或t≤﹣2或t=0二、填空题（本大题共4小题，每小题5分，共20分）13．幂函数f（x）的图象过点（4，2），那么f（16）的值为．14．化简（log43+log49）（log32+log38）=．15．设g（x）=，则g（g（））=．16．知0＜a＜1，则方程a|x|=|log a x|的实根个数是．三、解答题（本大题共6小题，共70分.解答题应写出文字说明、证明过程或演算步骤）17．计算下列各式的值：（1）0.064﹣（﹣）0+160.75+0.01；（2）．18．已知集合A={x|a﹣1＜x＜2a+1}，B={x|0＜x＜1}，若A∩B=∅，实数a的取值范围是．19．若二次函数满足f（x+1）﹣f（x）=2x且f（0）=1．（1）求f（x）的解析式；（2）若在区间[﹣1，1]上不等式f（x）＞2x+m恒成立，求实数m的取值范围．20．解关于x的不等式：．21．正在建设中的郑州地铁一号线，将有效缓解市内东西方向交通的压力．根据测算，如果一列车每次拖4节车厢，每天能来回16次；如果每次拖7节车厢，则每天能来回10次；每天来回次数是每次拖挂车厢节数的一次函数，每节车厢单向一次最多能载客110人，试问每次应拖挂多少节车厢才能使该列车每天营运人数最多？并求出每天最多的营运人数．（注：营运人数指列车运送的人数）．22．设函数f（x）=log2（a x﹣b x），且f（1）=1，f（2）=log212．（1）求a，b的值；（2）当x∈[1，2]时，求f（x）最大值．参考答案一、单项选择题1．A．2．D3．C．4．C．5．B．6．D．7．D．8．A 9．A 10．B．11．C12．D．二、填空题13．答案为：4．14．答案为：6．15．答案为：．16．答案为：2．三、解答题17．解：（1）原式===；﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣（2）原式===log39﹣9=2﹣9=﹣7．﹣﹣﹣﹣18．解：∵A={x|a﹣1＜x＜2a+1}，B={x|0＜x＜1}，而A∩B=∅，∴①a﹣1≥2a+1时，A=∅，a≤﹣2②解得：﹣2＜a③解得：a≥2综上，a的范围为：a≤或a≥2故答案为：a≤或a≥219．解：（1）设f（x）=ax2+bx+c（a≠0），由f（0）=1，∴c=1，∴f（x）=ax2+bx+1∵f（x+1）﹣f（x）=2x，∴2ax+a+b=2x，∴∴f（x）=x2﹣x+1（2）由题意：x2﹣x+1＞2x+m在[﹣1，1]上恒成立，即x2﹣3x+1﹣m＞0在[﹣1，1]上恒成立其对称轴为，∴g（x）在区间[﹣1，1]上是减函数，∴g（x）min=g（1）=1﹣3+1﹣m＞0，∴m＜﹣1．20．解：由，得当0＜a＜1时，原不等式可化为x2﹣8≤2x，解得﹣2≤x≤4．当a＞1时，原不等式可化为x2﹣8≥2x，解得x≤﹣2或x≥4．∴当0＜a＜1时，原不等式的解集为{x|﹣2≤x≤4}；当a＞1时，原不等式的解集为{x|x≤﹣2或x≥4}．21．解：设该列车每天来回次数为t，每次拖挂车厢数为n，每天营运人数为y．由已知可设t=kn+b，则根据条件得，解得，∴t=﹣2n+24．所以y=tn×110×2=440（﹣n2+12n）；∴当n=6时，y最大=15840．即每次应拖挂6节车厢，才能使该列车每天的营运人数最多，最多为15840人．22．解：∵函数f（x）=log2（a x﹣b x），且f（1）=1，f（2）=log212∴∴∴（2）由（1）得令g（x）=4x﹣2x=（2x）2﹣2x令t=2x，则y=t2﹣t∵x∈[1，2]，∴t∈[2，4]，显然函数y=（t﹣）2﹣在[2，4]上是单调递增函数，所以当t=4时，取得最大值12，∴x=2时，f（x）最大值为log212=2+log232017—2018学年人教版高一数学上学期期中考试卷（五）（考试时间120分钟满分150分）一、单项选择题（本大题共12个小题，每小题5分，共60分.在每小题给出的四个选项中，只有一项是符合题目要求的.）1．设集合M={﹣1，0，1}，N={﹣2，0，1}，则M∩N=（）A．{﹣1，0，1}B．{0，1}C．{1}D．{0}2．给定映射f：（x，y）→（x+2y，2x﹣y），在映射f下，（3，1）的原像为（）A．（1，3） B．（5，5） C．（3，1） D．（1，1）3．函数y=x2﹣2x﹣1在闭区间[0，3]上的最大值与最小值的和是（）A．﹣1 B．0 C．1 D．24．函数f（x）=+lg（3x+1）的定义域是（）A．（﹣，+∞）B．（﹣，1）C．（﹣，）D．（﹣∞，﹣）5．设f（x）=，则f（1）+f（4）=（）A．5 B．6 C．7 D．86．函数f（x）=a x﹣1+4（a＞0，且a≠1）的图象过一个定点，则这个定点坐标是（）A．（5，1） B．（1，5） C．（1，4） D．（4，1）7．定义在R的奇函数f（x），当x＜0时，f（x）=﹣x2+x，则f（2）=（）A．6 B．﹣6 C．2 D．﹣28．三个数60.7，（0.7）6，log0.76的大小顺序是（）A．（0.7）6＜log0.76＜60.7B．（0.7）6＜60.7＜log0.76C．log0.76＜60.7＜（0.7）6D．log0.76＜（0.7）6＜60.79．已知f（x）=ax5+bx3+cx﹣8，且f（﹣2）=4，那么f（2）=（）A．﹣20 B．10 C．﹣4 D．1810．已知a＞0，b＞0且ab=1，则函数f（x）=a x与g（x）=﹣log b x的图象可能是（）A．B．C．D．11．已知函数f（x）=若关于x的方程f（x）=k有两个不等的实根，则实数k的取值范围是（）A．（0，+∞）B．（﹣∞，1）C．（0，1]D．（1，+∞）12．定义在R上的奇函数f（x）在（0，+∞）上是增函数，又f（﹣3）=0，则不等式xf（x）＜0的解集为（）A．（﹣3，0）∪（0，3）B．（﹣∞，﹣3）∪（3，+∞）C．（﹣3，0）∪（3，+∞）D．（﹣3，3）二、填空题（本大题共4小题，每题5分，满分20分．）13．已知f（x+1）=x2﹣2x，则f（2）=．14．若幂函数y=（m2﹣2m﹣2）x﹣4m﹣2在x∈（0，+∞）上为减函数，则实数m 的值是．15．函数f（x）=（x﹣x2）的单调递增区间是．16．关于x的不等式ax2+bx+2＞0的解集是{x|﹣＜x＜}，则a+b=．三、解答题（本大题共6小题，共70分.解答应写出文字说明、证明过程或演算步骤.）17．求下列各式的值：（1）2×﹣；（2）lg200+lg25+5（lg2+lg5）3﹣（）．18．已知集合A={x|2≤2x≤16}，B={x|log3x＞1}．（1）分别求A∩B，（∁R B）∪A；（2）已知集合C={x|1＜x＜a}，若C⊆A，求实数a的取值范围．19．已知：f（x）=ln（1+x）﹣ln（1﹣x）．（1）求f（0）；（2）判断此函数的奇偶性；（3）若f（a）=ln2，求a的值．20．（1）设函数，求证：函数f（x）在（﹣∞，+∞）上是增函数；（2）若f（x）=（log4x﹣3）•log44x＞m在区间[1，2]上恒成立，求实数m的取值范围．21．若f（x）是定义在（0，+∞）上的增函数，且对于任意x＞0满足f （）=f（x）﹣f （y）．（1）求f（1）的值；（2）若f（6）=1，试求解不等式f（x+5）﹣f （）＜2．22．已知函数g（x）=ax2﹣2ax+b+1（a＞0）在区间[2，3]上有最大值4和最小值1．设f（x）=．（1）求a、b的值；（2）若不等式f（2x）﹣k•2x≥0在x∈[﹣1，1]上有解，求实数k的取值范围．参考答案一、单项选择题1．B2．D．3．B4．B．5．A．6．B．7．A．8．D．9．A．10．B．11．C．12．A．二、填空题13．解：令x+1=t，∴x=t﹣1，∴f（t）=（t﹣1）2﹣2（t﹣1）=t2﹣4t+3，∴f（x）=x2﹣4x+3，∴f（2）=﹣1故答案为：﹣114．解：因为函数y=（m2﹣2m﹣2）x﹣4m﹣2既是幂函数又是（0，+∞）的减函数，所以，⇒，解得：m=3．故答案为：m=3．15．解：令t=x﹣x2＞0，求得0＜x＜1，故有函数的定义域为（0，1），且f（x）=h（t）=t，故本题即求二次函数t在（0，1）上的减区间．利用二次函数的性质可得t=x﹣x2 =﹣﹣在（0，1）上的减区间为[，1），故答案为：[，1）．16．解：∵不等式ax2+bx+2＞0的解集为{x|﹣}，∴﹣和为方程ax2+bx+2=0的两个实根，且a＜0，由韦达定理可得，解得a=﹣12，b=﹣2，∴a+b=﹣14．故答案为：﹣14．三、解答题17．解：（1）原式=2×﹣2=2×﹣2=，（2）原式=2+lg2+lg5+5﹣=2+1+5﹣=．18．解：（1）∵集合A={x|2≤2x≤16}=[1，4]，B={x|log3x＞1}=（3，+∞）．∴A∩B=（3，4]，C R B=（﹣∞，3]，（C R B）∪A=（﹣∞，4]；（2）∵集合C={x|1＜x＜a}，C⊆A，当a≤1时，C=∅，满足条件；当a＞1时，C≠∅，则a≤4，即1＜a≤4，综上所述，a∈（﹣∞，4]．19．解：（1）因为f（x）=ln（1+x）﹣ln（1﹣x），所以f（0）=ln（1+0）﹣ln（1﹣0）=0﹣0=0．（2）由1+x＞0，且1﹣x＞0，知﹣1＜x＜1，所以此函数的定义域为：（﹣1，1）．又f（﹣x）=ln（1﹣x）﹣ln（1+x）=﹣（ln（1+x）﹣ln（1﹣x））=﹣f（x），由上可知此函数为奇函数．（3）由f（a）=ln2 知ln（1+a）﹣ln（1﹣a）=，可得﹣1＜a＜1且，解得，所以a的值为．20．解：（1）证明：∵，∴f′（x）=＞0，∴函数f（x）在（﹣∞，+∞）上是增函数；（2）∵1≤x≤2，∴0≤log4x≤，又f（x）=（log4x﹣3）•log44x=（log4x﹣3）•（1+log4x）=﹣2log4x﹣3=（log4x ﹣1）2﹣4，∴当x=2，log4x=时，f（x）取得最小值，为f（2）=﹣，∴f（x）＞m在区间[1，2]上恒成立⇔m＜[f（x）]min=﹣，即实数m的取值范围为（﹣∞，﹣）．21．解：（1）∵对于任意x＞0满足f （）=f（x）﹣f （y），令x=y=1，得：f（1）=0；（2）若f（6）=1，则f（）=f（36）﹣f（6），即f（36）=2f（6）=2，∴f（x+5）﹣f （）＜2⇔f[x（x+5）]＜f（36），∵f（x）是定义在（0，+∞）上的增函数，∴，解得：0＜x＜4．∴不等式f（x+5）﹣f （）＜2的解集为{x|0＜x＜4}．22．解：（1）函数g（x）=ax2﹣2ax+b+1=a（x﹣1）2+1+b﹣a，因为a＞0，所以g（x）在区间[2，3]上是增函数，故，解得．…．（2）由已知可得f（x）=x+﹣2，所以，不等式f（2x）﹣k•2x≥0可化为2x+﹣2≥k•2x，可化为1+﹣2•≥k，令t=，则k≤t2﹣2t+1．因x∈[﹣1，1]，故t∈[，2]．故k≤t2﹣2t+1在t∈[，2]上能成立．记h（t）=t2﹣2t+1，因为t∈[，2]，故h（t）max =h（2）=1，所以k的取值范围是（﹣∞，1]．…2017—2018学年人教版高一数学上学期期中考试卷（六）（考试时间120分钟满分150分）一、单项选择题：（共12小题，每小题5分，共60分）1．已知集合M={﹣1，0，1}，则下列关系式正确的是（）A．{0}∈M B．{0}∉M C．0∈M D．0⊆M2．已知函数f（x）=1+log2x，则的值为（）A．B． C．0 D．﹣13．函数y=（2k﹣1）x+b在（﹣∞，+∞）上是减函数，则（）A．B．C．D．4．与函数y=x相等的函数是（）A．y=（）2B．y=C．y=D．y=5．函数y=x2+2x﹣4，x∈[﹣2，2]的值域为（）A．[﹣5，4] B．[﹣4，4] C．[﹣4，+∞）D．（﹣∞，4]6．若函数y=a x﹣1﹣2（a＞0，且a≠1）的图象恒过点P，则点P为（）A．（0，﹣1）B．（0，﹣2）C．（1，﹣2）D．（1，﹣1）7．下列式子中，成立的是（）A．log0.44＞log0.46 B．1.013.4＞1.013.5C．3.50.3＜3.40.3D．log78＜1og878．函数f（x）=﹣x3的图象关于（）A．y轴对称B．直线y=﹣x对称C．坐标原点对称 D．直线y=x对称x2=0的一个根所在的区间为（）．（﹣，）．（，）．（，）D．（2，3）10．函数y=a x﹣（a＞0，a≠1）的图象可能是（）A． B． C．D．11．若一系列函数的解析式和值域相同，但是定义域不同，则称这些函数为“同族函数”，例如函数y=x2，x∈[1，2]，与函数y=x2，x∈[﹣2，﹣1]即为“同族函数”．下面的函数解析式也能够被用来构造“同族函数”的是（）A．y=x B．y=|x﹣3| C．y=2x D．y=log12．若函数f（x）是偶函数，其定义域为（﹣∞，+∞），且在[0，+∞）上是减函数，则不等式f（lgx）＞f（﹣1）成立的x的取值范围为（）A．B．C．（0，10） D．（10，+∞）二、填空题：（本大题共4小题，每小题5分，共20分）13．已知A={﹣1，3，m}，集合B={3，5}，若B∩A=B，则实数m=．14．已知幂函数y=f（x）的图象过点，则f（x）=．15．函数f（x）=的定义域为．16．下列四个结论中：（1）如果两个函数都是增函数，那么这两个函数的积运算所得函数为增函数；（2）奇函数f（x）在[0，+∞）上是增函数，则f（x）在R上为增函数；（3）既是奇函数又是偶函数的函数只有一个；（4）若函数f（x）的最小值是a，最大值是b，则f（x）值域为[a，b]．其中正确结论的序号为．三、解答题：（本题共6小题，共70分，解答过程应写出文字说明，证明过程或演算步骤）17．已知集合A={x|3≤x≤7}，B={x|3＜2x﹣1＜19}，求：（1）求A∪B；（2）求（∁R A）∩B．18．（1）计算：（2）+（lg5）0+（）；（2）解方程：log3（6x﹣9）=3．19．已知函数f（x）=x2+bx+c，（1）若函数f（x）是偶函数，求实数b的值（2）若函数f（x）在区间[﹣1，3]上单调递增，求实数b的取值范围．20．已知函数f（x）=．（1）判断函数f（x）在区间[1，+∞）上的单调性，并用定义证明你的结论；（2）求函数f（x）在区间[2，4]上的最大值与最小值．21．销售甲、乙两种商品所得利润分别是P（万元）和Q（万元），它们与投入资金t（万元）的关系有经验公式P=3，Q=t．今将3万元资金投入经营甲、乙两种商品，其中对甲种商品投资x（万元）．求：（1）经营甲、乙两种商品的总利润y（万元）关于x的函数表达式；（2）怎样将资金分配给甲、乙两种商品，能使得总利润y达到最大值，最大值是多少？22．已知f（x）是定义在R上的奇函数，当x≥0时，f（x）=a x﹣1（a＞0，且a≠1）．（1）求f（2）+f（﹣2）的值；（2）求f（x）的解析式；（3）解关于x的不等式f（x）＜4，结果用集合或区间表示．参考答案一、单项选择题：1．C．2．C．3．B．4．B．5．A．6．D．7．A．8．C 9．C．10．D．11．B；12．A．二、填空题：13．答案为：5．14．答案为：15．答案为：{x|x≥﹣4，且x≠0}．16．答案为：（2）．三、解答题：17．解：（1）∵集合A={x|3≤x≤7}，B={x|3＜2x﹣1＜19}={x|2＜x＜10}，∴A∩B=[3，7]（2）C R A={x|x＜3或x＞7}，∴（C R A）∩B={x|2＜x＜3或7＜x＜10}．18．解：（1）=（）+（lg5）0+[（）3]=+1+=4．（2）由方程log3（6x﹣9）=3得6x﹣9=33=27，∴6x=36=62，∴x=2．经检验，x=2是原方程的解．∴原方程的解为x=2．19．解：（1）因为f（x）为偶函数，所以f（﹣x）=f（x），∴（﹣x2）+b（﹣x）+c=x2+bx+c，∴b=0，（2）函数f（x）的对称轴为，开口向上所以f（x）的递增区间为，∴，∴，∴b≥2，故实数b的取值范围为[2，+∞）．20．解：（1）函数f（x）在[1，+∞）上是增函数；证明：任取x1，x2∈[1，+∞），且x1＜x2，…∵x1﹣x2＜0，（x1+1）（x2+1）＞0，所以，f（x1）﹣f（x2）＜0，即f（x1）＜f（x2），所以函数f（x）在[1，+∞）上是增函数…（2）由（1）知，f（x）在[2，4]上是增函数．…所以最大值为，最小值为…21．解：（1）根据题意，得，x∈[0，3]．…（2）．∵∈[0，3]，∴当=时，即x=，3﹣x=时，．即给甲、乙两种商品分别投资万元、万元可使总利润达到最大值万元．…22．解：（1）∵f（x）是R上的奇函数，∴f（﹣2）=﹣f（2），即f（2）+f（﹣2）=0．（2）设x＜0，则﹣x＞0，∴f（﹣x）=a﹣x﹣1．由f（x）是奇函数，有f（﹣x）=﹣f（x），∵f（﹣x）=a﹣x﹣1，∴f（x）=﹣a﹣x+1（x＜0），∴所求的解析式为．（3）不等式等价于，即，即．当a＞1时，有，∵log a5＞0，所以不等式的解集为（﹣∞，log a5）；当0＜a＜1时，有，∵log a5＜0，所以不等式的解集为（﹣∞，0）．综上所述，当a＞1时，不等式的解集为（﹣∞，log a5）；当0＜a＜1时，不等式的解集为（﹣∞，0）．2017—2018学年人教版高一数学上学期期中考试卷（七）（考试时间120分钟满分150分）一、单项选择题：（本大题共12小题，每小题5分，共60分）1．设f：x→|x|是集合A到集合B的映射，若A={﹣1，0，1}，则A∩B只可能是（）A．{0}B．{1}C．{0，1}D．{﹣1，0，1}2．设集合A={x|1≤x≤2}，B={x|x≤a}，若A⊆B，则a的取值范围是（）A．{a|a≥2}B．{a|a＞2}C．{a|a≥1}D．{a|a≤2}3．函数f（x）=2x﹣x2（0≤x≤3）的值域是（）A．R B．（﹣∞，1]C．[﹣3，1]D．[﹣3，0]4．设f（x）=，则f（1）+f（4）=（）A．5 B．6 C．7 D．85．函数f（x）=2x﹣的零点所在的区间是（）A． B． C． D．6．设a=logπ3，b=20.3，c=log2，则（）A．a＞b＞c B．a＞c＞b C．c＞a＞b D．b＞a＞c7．已知，则f（x+1）的解析式为（）A．x+4（x≥0）B．x2+3（x≥0）C．x2﹣2x+4（x≥1）D．x2+3（x≥1）8．定义在R的奇函数f（x），当x＜0时，f（x）=﹣x2+x，则x＞0时，f（x）等于（）A．x2+x B．﹣x2+x C．﹣x2﹣x D．x2﹣x9．函数f（x）=在区间（﹣2，+∞）上单调递增，则实数a的取值范围是（）A．（0，）B．（，+∞）C．（﹣2，+∞）D．（﹣∞，﹣1）∪（1，+∞）10．若奇函数f（x）=ka x﹣a﹣x（a＞0且a≠1）在R上是增函数，那么的g（x）=log a（x+k）大致图象是（）A．B．C．D．11．函数f（x）=（m2﹣m﹣1）x4m+3是幂函数，对任意x1，x2∈（0，+∞），且x1≠x2，满足，若a，b∈R，且a+b＞0，ab＜0．则f（a）+f （b）的值（）A．恒大于0 B．恒小于0 C．等于0 D．无法判断12．偶函数y=f（x）满足下列条件①x≥0时，f（x）=x；对任意x∈[t，t+1]，不等式f（x+t）≥2f（x）恒成立，则实数t的取值范围是（）A．B．C．D．二、填空题：（本大题共4小题，每小题5分，共20分）13．若函数f（2x+1）=x2﹣2x，则f（3）=．14．已知y=f（2x）的定义域为[﹣1，1]，则y=f（log2x）的定义域是．15．已知f（x）=log a（8﹣3ax）在[﹣1，2]上单调减函数，则实数a的取值范围为．16．已知函数f（x）=，则不等式f（f（x））≤3的解集为．三、解答题：（本大题共6小题，共70分）17．计算下列各式：（1）（2）．18．已知函数f（x）=的定义域为集合A，B={x∈Z|2＜x＜10}，C={x∈R|x＜a或x＞a+1}（1）求A，（∁R A）∩B；（2）若A∪C=R，求实数a的取值范围．19．已知定义域为R的函数是奇函数．（1）求a，b的值；（2）试判断函数f（x）的单调性，并用函数单调性的定义说明理由．20．已知二次函数f（x）与x轴的两个交点分别是（﹣3，0），（5，0），且f（2）=15．（1）求函数f（x）的解析式；（2）令g（x）=（2﹣2m）x﹣f（x），求函数g（x）在x∈[0，2]的最小值．21．已知函数f（x）=a x﹣a+1，（a＞0且a≠1）恒过定点（3，2），（1）求实数a；（2）在（1）的条件下，将函数f（x）的图象向下平移1个单位，再向左平移a 个单位后得到函数g（x），设函数g（x）的反函数为h（x），求h（x）的解析式；（3）对于定义在[1，9]的函数y=h（x），若在其定义域内，不等式[h（x）+2]2≤h（x2）+m+2 恒成立，求m的取值范围．22．定义在D上的函数f（x），如果满足：对任意x∈D，存在常数M≥0，都有|f（x）|≤M成立，则称f（x）是D上的有界函数，其中M称为函数f（x）的一个上界，已知函数f（x）=1+a（）x+（）x，g（x）=log．（1）求函数g（x）在区间[，3]上的所有上界构成的集合；（2）若函数f（x）在[0，+∞）上是以3为上界的有界函数，求实数a的取值范围．参考答案一、单项选择题：1．C2．A．3．C．4．A．5．B．6．D．7．B．8．A9．B．10．C11．A．12．B．二、填空题：13．答案为：﹣114．答案为：[，4]．15．答案为1＜a＜．16．答案为：（﹣∞，]三、解答题：17．解：（1）原式=﹣1++×=10﹣1+8+8×32=89．（2）原式=+lg已知函数f（x）=的定义域为集合A，B={x∈Z|2＜x＜10}，C={x∈R|x＜a或x＞a+1}（1）求A，（∁R A）∩B；（2）若A∪C=R，求实数a的取值范围．18、解：（1）由题意，解得7＞x≥3，故A={x∈R|3≤x＜7}，B={x∈Z|2＜x＜10}═{x∈Z|3，4，5，6，7，8，9}，∴（C R A）∩B{7，8，9}（2）∵A∪C=R，C={x∈R|x＜a或x＞a+1}∴解得3≤a＜6实数a的取值范围是3≤a＜619．解：（1）∵f（x）是定义域为R的奇函数，∴f（0）=0，即f（0）==0，则b=1，此时f（x）=，且f（﹣x）=﹣f（x），则=﹣，即==，则2+a•2x=2•2x+a，则a=2；（2）当a=2，b=1时，f（x）==（）=•=﹣f（x）在R上是单调减函数，用定义证明如下；任取x1、x2，且x1＜x2，则f（x1）﹣f（x2）=﹣+=﹣==；∵x1＜x2，∴﹣＞0，1+＞0，1+＞0；∴f（x1）﹣f（x2）＞0，即f（x1）＞f（x2），∴f（x）是R上的单调减函数．20．解：（1）设f（x）=a（x+3）（x﹣5），∵f（2）=15，∴a（2+3）（2﹣5）=15，解得：a=﹣1，∴函数f（x）的表达式为f（x）=﹣x2+2x+15；（2）∵g（x）=（2﹣2m）x﹣f（x）=x2﹣2mx﹣15，函数图象是开口朝上，且以x=m为对称轴的抛物线，当m≤0时，g（x）在[0，2]上为增函数，当x=0时，函数g（x）取最小值﹣15；当0＜m＜2时，g（x）在[0，m]上为减函数，在[m，2]上为增函数，当x=m时，函数g（x）取最小值﹣m2﹣15；当m≥2时，g（x）在[0，2]上为减函数，当x=2时，函数g（x）取最小值﹣4m ﹣11；∴函数g（x）在x∈[0，2]的最小值为．21．解：（1）由f（x）=a x﹣a+1，知令x=a，则f（a）=2，所以f（x）恒过定点（a，2），由题设得a=3；（2）由（1）知f（x）=3x﹣3+1，将f（x）的图象向下平移1个单位，得到m（x）=3x﹣3，再向左平移3个单位，得到g（x）=3x，所以函数g（x）的反函数h（x）=log3x．（3）[h（x）+2]2≤h（x2）+m+2，即[log3x+2]2≤+m+2，所以+2log3x+2﹣m≤0，令t=log3x，则由x2∈[1，9]得t∈[0，1]，则不等式化为t2+2t+2﹣m≤0，不等式[h（x）+2]2≤h（x2）+m+2 恒成立，等价于t2+2t+2﹣m≤0恒成立，因为t2+2t+2﹣m=（t+1）2+1﹣m在[0，1]上单调递增，所以t2+2t+2﹣m≤12+2×1+2﹣m=5﹣m，所以5﹣m≤0，解得m≥5．故实数m的取值范围为：m≥5．22．解：（1）t===1+，在≤x≤3上为减函数，∴2≤t≤4，则log4≤g（x）≤log2，即﹣2≤g（x）≤﹣1，则|g（x）|≤2，即M≥2，即函数g（x）在区间[，3]上的所有上界构成的集合为[2，+∞）．（2）由题意知，|f（x）|≤3在[0，+∞）上恒成立设，t∈（0，1]，由﹣3≤f（x）≤3，得﹣3≤1+at+t2≤3∴在（0，1]上恒成立…设，，h（t）在（0，1]上递增；p（t）在（0，1]上递减，h（t）在（0，1]上的最大值为h（1）=﹣5；p（t）在（0，1]上的最小值为p（1）=1，…所以实数a的取值范围为[﹣5，1]．…2017—2018学年人教版高一数学上学期期中考试卷（八）（考试时间120分钟满分150分）一、填空题（本大题共12小题，满分36分）1．若全集U={1，2，3，4，5}，且∁U A={2，3}，则集合A=．2．已知集合A={﹣1，0，1}，，则A∩B=．3．函数f（x）=，g（x）=x+3，则f（x）•g（x）=．4．函数f（x）=的定义域为．5．设函数f（x）=，若f（a）=2，则实数a=．6．若0＜a＜1，则不等式（a﹣x）（x﹣）＞0的解集为．7．已知p：x2+x﹣2＞0，q：x＞a，若q是p的充分不必要条件，则q的取值范围是．8．若关于x的不等式|ax﹣2|＜3的解集为{x|﹣＜x＜}，则a=．9．若关于x的不等式（a﹣1）x2+2（a﹣1）x﹣4≥0的解集为∅，则实数a的取值范围是．10．已知集合A={﹣1，2}，B={x|mx+1＞0}，若A∪B=B，则实数m的取值范围是．11．设函数f（x）=x﹣2，若不等式|f（x+3）|＞|f（x）|+m对任意实数x恒成立，则m的取值范围是．12．满足不等式|x﹣A|＜B（B＞0，A∈R）的实数x的集合叫做A的B邻域，若a+b﹣2的a+b邻域是一个关于原点对称的区间，则的取值范围是．二、单项选择题（本大题共有4小题，满分12分）13．若集合中三个元素为边可构成一个三角形，则该三角形一定不可能是（）A．锐角三角形B．直角三角形C．钝角三角形D．等腰三角形14．设x取实数，则f（x）与g（x）表示同一个函数的是（）A．f（x）=x，g（x）=B．f（x）=，g（x）=C．f（x）=1，g（x）=（x﹣1）0D．f（x）=，g（x）=x﹣315．若a和b均为非零实数，则下列不等式中恒成立的是（）A．B．C．D．16．若一系列函数的解析式相同，值域相同，但定义域不同，则称这些函数为“孪生函数”，那么函数解析式为y=2x2+1，值域为{5，19}的“孪生函数”共有（）A．4个 B．6个 C．8个 D．9个三、解答题（本大题共5题，满分52分）17．解不等式组．18．已知集合A={x|x2﹣px﹣2=0}，B={x|x2+qx+r=0}，若A∪B={﹣2，1，5}，A ∩B={﹣2}，求p+q+r的值．19．已知集合P={a|不等式x2+ax+≤0有解}，集合Q={a|不等式ax2+4ax﹣4＜0对任意实数x恒成立}，求P∩Q．20．我校为进行“阳光运动一小时”活动，计划在一块直角三角形ABC的空地上修建一个占地面积为S（平方米）的矩形AMPN健身场地．如图，点M在AC上，点N在AB上，且P点在斜边BC上．已知∠ACB=60°，|AC|=30米，|AM|=x米，x∈[10，20]．设矩形AMPN健身场地每平方米的造价为元，再把矩形AMPN以外（阴影部分）铺上草坪，每平方米的造价为元（k为正常数）．（1）试用x表示S，并求S的取值范围；（2）求总造价T关于面积S的函数T=f（S）；（3）如何选取|AM|，使总造价T最低（不要求求出最低造价）．21．设函数，函数，其中a为常数且a＞0，令函数f（x）=g（x）•h（x）．（1）求函数f（x）的表达式，并求其定义域；（2）当时，求函数f（x）的值域；（3）是否存在自然数a，使得函数f（x）的值域恰为？若存在，试写出所有满足条件的自然数a所构成的集合；若不存在，试说明理由．参考答案一、填空题1．答案为：{1，4，5}．2．答案为：{0}．3．答案为x﹣3，（x∈（﹣∞，﹣3）∪（﹣3，+∞））4．答案为：[1，2）∪（2，+∞）5．答案为：﹣2或．6．答案为：{x|a}．7．答案为：[1，+∞）8．答案为：﹣3．9．答案为：{a|﹣3＜a≤1}．10．答案为（﹣，1）．11．答案为（﹣∞，﹣3）12．答案为．二、单项选择题13．D14．B．15．A．16．D．三、解答题17．解：∵由原不等式组⇒⇒⇒x＞2∴原不等式组的解集为（2，+∞）18．解：由题意得，﹣2∈A，代入A中方程得p=﹣1，故A={﹣2，1}，由A∪B={﹣2，1，5}和A∩B={﹣2}得：B={﹣2，5}，代入B中方程得：q=﹣3，r=﹣10所以p+q+r=﹣14．19．解：，故，解得或，集合Q={a|不等式ax2+4ax﹣4＜0对任意实数x恒成立}，对a分类：当a=0时恒成立；当a＜0时，，解得﹣1＜a＜0综合得：﹣1＜a≤0故．20．解：（1）在Rt△PMC中，显然|MC|=30﹣x，∠PCM=60°，∴，矩形AMPN的面积，x∈[10，20]，由x（30﹣x）≤（）2=225，当x=15时，可得最大值为225，当x=10或20时，取得最小值200，于是为所求．（2）矩形AMPN健身场地造价T1=，又△ABC的面积为，即草坪造价T2=，由总造价T=T1+T2，∴，．（3）∵，当且仅当即时等号成立，此时，解得x=12或x=18，答：选取|AM|的长为12米或18米时总造价T最低．21．解：（1），其定义域为[0，a]；（2）令，则且x=（t﹣1）2∴∴∵在[1，2]上递减，在[2，+∞）上递增，∴在上递增，即此时f（x）的值域为（3）令，则且x=（t﹣1）2∴∵在[1，2]上递减，在[2，+∞）上递增，∴y=在[1，2]上递增，上递减，t=2时的最大值为，∴a≥1，又1＜t≤2时∴由f（x）的值域恰为，由，解得：t=1或t=4即f（x）的值域恰为时，所求a的集合为{1，2，3，4，5，6，7，8，9}．2017—2018学年人教版高一数学上学期期中考试卷（九）（考试时间100分钟满分120分）一、单项选择题（共12题，每题5分，共60分）1．已知全集U={0，1，2，3，4}，集合A={1，2，3}，B={2，4}，则（∁U A）∪B为（）A．{1，2，4}B．{2，3，4}C．{0，2，3，4} D．{0，2，4}2．已知函数f（x）=，则f（﹣1）的值等于（）A．π2﹣1 B．π2+1 C．πD．03．指数函数f（x）=a x（a＞0且a≠1）在R上是增函数，则a的取值范围是（）A．a＞1 B．a＞2 C．0＜a＜1 D．1＜a＜24．下列四组函数中，表示同一函数的是（）A．f（x）=2﹣x，g（x）=x﹣2B．C．D．5．下列函数中，在定义域内是单调递增函数的是（）A．y=|x|B． C．y=x2D．y=2x6．若，则f（3）=（）A．2 B．4 C． D．107．函数f（x）=+的定义域为（）A．（﹣3，0] B．（﹣3，1] C．（﹣∞，﹣3）∪（﹣3，0]D．（﹣∞，﹣3）∪（﹣3，1]8．已知a=，b=20.3，c=0.30.2，则a，b，c三者的大小关系是（）A．b＞c＞a B．b＞a＞c C．a＞b＞c D．c＞b＞a9．函数y=x2﹣2x+3，﹣1≤x≤2的值域是（）A．R B．[3，6]C．[2，6]D．[2，+∞）10．设f（x）是定义在R上的奇函数，当x≤0时，f（x）=2x2﹣x，则f（1）=（）A．﹣3 B．﹣1 C．1 D．3。

2017-2018学年度第一学期期中考试高一数学试题一、选择题：（本大题共12小题，每小题3分，共36分．在每小题给出的四个选项中，只有一项是符合题目要求的）1．设集合{}1,2,3A =，{}2,3,4B =，则A B =（ ）．A ．{}1,2,3,4B ．{}1,2,3C ．{}2,3,4D ．{}1,3,4【答案】A【解析】本题主要考查集合之间的关系． 根据集合之间的关系，{}1,2,3,4A B =．故选A ．2．有一组数据，如表所示：）．A ．指数函数B ．反比例函数C ．一次函数D ．二次函数【答案】C【解析】随着自变量每增加1函数值大约增加2， 函数值的增量几乎是均匀的，故一次函数最接近地表示这组数据满足的规律． 故选C ．3．已知全集U =R ，142A x x ⎧⎫=-<<⎨⎬⎩⎭，{}|4B x x =-≤，12C x x ⎧⎫=⎨⎬⎩⎭≥，则集合C =（ ）．A ．A BB ．()U A B ðC ．()U A B ðD ．A B【解析】解:∵全集U =R ，142A x x ⎧⎫=-<<⎨⎬⎩⎭，{}|4B x x =-≤，∴12AB x x ⎧⎫=<⎨⎬⎩⎭，∴1()2U AB x xC ⎧⎫==⎨⎬⎩⎭ð≥．故选B ．4．已知4m <-，点1(1,)m y -，2(,)m y ，3(1,)m y +都在二次函数61y x x 2=+-的图像上，则（ ）．A ．123y y y <<B ． 213y y y <<C ．132y y y <<D ．321y y y <<【答案】D【解析】解：∵2m <-， ∴111m m m -<<+<-，即三点都在二次函数对称轴的左侧，又二次函数22y x x =-在对称轴的左侧是单调减函数， ∴321y y y <<． 故选D ．5．已知12()3f x x =，若01a b <<<，则下列各式中正确的是（ ）．A ．11()()f a f b f f a b ⎛⎫⎛⎫<<<⎪ ⎪⎝⎭⎝⎭B ．11()()f f f b f a a b ⎛⎫⎛⎫<<< ⎪ ⎪⎝⎭⎝⎭C ．11()()f a f b f f b a ⎛⎫⎛⎫<<<⎪ ⎪⎝⎭⎝⎭D ．11()()f f a f f b a b ⎛⎫⎛⎫<<< ⎪ ⎪⎝⎭⎝⎭【答案】C【解析】解：因为函数12()f x x =在(0,)+∞上是增函数， 又110a b b a<<<<．6．若函数()y f x =是函数x y a =（0a >且1a ≠）的反函数，且(2)1f =，则()f x =（ ）．A ．2log xB ．22x -C ．12log xD ．1x -【答案】A【解析】本题主要考查反函数． 由()y f x =是x y a =的反函数，可知()log a f x x =，再由(2)1f =，可知log 21a =， 所以2a =，2()log f x x =． 故选A ．7．函数2()ln(28)f x x x =--的单调递增区间是（ ）．A ．(,2)-∞-B ．(,1)-∞C ．(1,)+∞D ．(4,)+∞【答案】D【解析】本题主要考查函数的概念与性质．首先考虑函数的定义域，2280x x -->，解得2x <-或4x >， 且函数2()28g x x x =--在(,2)-∞-上单调递减， 在(4,)+∞上单调递增，而ln y x =是单调递增函数，根据复合函数性质，函数2()ln(28)f x x x =--的单调递增区间为(4,)+∞． 故选D ．8．设3log 2a =，5log 2a =，2log πc =，则（ ）．A ．a c b >>B ．b c a >>C ．c b a >>D ．c a b >>【答案】C【解析】因为321log 2log 3a ==，521log 2log 5b ==，而22log 3log 21c =>=，2log 51>， 所以01a <<，01b <<， 又22log 5log 31>>， 所以2211log 5log 3<， 即01b a <<<， 所以有c a b >>． 故选C ．【考点】比较对数大小．9．设()338x f x x =+-，用二分法求方程3380x x +-=在(1,2)x ∈内近似解的过程中得(1)0f <，(1.5)0f >，(1.25)0f <，则方程的根落在的区间是（ ）．A ．(1,1.25)B ．(1.25,1.5)C ．(1.5,2)D ．不能确定【答案】B【解析】方程3380x x +-=的解等价于()338x f x x =+-的零点． 由于()f x 在R 上连续且单调递增，(1.25)(1.5)0f f ⋅<． 所以()f x 在(1.25,1.5)内有零点且唯一， 所以方程3380x x +-=的根落在区间(1.25,1.5)． 故选B ．10．函数1()ln(1)f x x =++ ）．A ．[)(]2,00,2-B ．(](1,0)0,2-C ．[2,2]-D ．(]1,2-【答案】B【解析】解：要使函数有意义，必须：2401011x x x ⎧-⎪+>⎨⎪+≠⎩≥，所以(](1,0)0,2x ∈-．所以函数的定义域为：(](1,0)0,2-．故选B ．11．已知函数()log x a f x a x =+（0a >且1a ≠）在[1,2]上的最大值与最小值之和为6log 2a +，则a 的值为（ ）．A ．12B ．14C ．2D ．4【答案】C【解析】解：因为函数()log x a f x a x =+（0a >且1a ≠）， 所以函数()f x 在1a >时递增，最大值为22(2)log f a a =+； 最小值为11(1)log f a a =+， 函数()f x 在01a <<时递减，最大值为11(1)log f a a =+，最小值为22(2)log f a a =+；故最大值和最小值的和为：22112(1)(2)log log log 6f f a a a a a +=+++=+． ∴2602a a a +-=⇒=，3a =-（舍）． 故选C ．12．函数2x y =与2y x =图像的交点个数是（ ）．A ．0B ．1C ．2D ．3【答案】D【解析】解：函数2x y =与2y x =的图象的交点个数即函数2()2x f x x =-的零点的个数． 显然，2x =和4x =是函数()f x 的两个零点． 再由11(1)1022f -=-=-<，(0)101f =-=， 可得(1)(0)0f f -<，故函数在区间(1,0)-上有一个零点．故函数2x y =与2y x =的图象的交点个数为3．故选D ．二、填空题：（本大题5小题，每小题4分，共20分） 13．若1005a =，102b =，则2a b +=__________． 【答案】1【解析】解：∵1005a =，102b =， ∴2lg51lg5lg102a ==，lg2b =， ∴2lg2lg51a b +=+=， 因此，本题正确答案是1．14．设集合{}1,2,4A =，{}2|40B x x x m =-+=．若{}1AB =，则B =__________．【答案】{}1,3【解析】本题主要考查集合的运算． 因为{}1AB =，所以1x =为方程240x x m -+=的解， 则140m -+=，解得3m =，所以2430x x -+=，(1)(3)0x x --=，集合{}1,3B =．15．若函数()|22|x f x b =--有两个零点，则实数b 的取值范围是__________． 【答案】(0,2)【解析】本题主要考查指数与指数函数． 因为可知当02b <<时，函数|22|x y =-与函数y b =的图象有两个交点， 即实数b 的取值范围是(0,2)． 故本题正确答案为(0,2)．16．设函数lg ,0,()10,0,x x x f x x >⎧=⎨⎩≤则((2))f f -=__________．【答案】2-【解析】本题主要考查分段函数和复合函数． 由题意可得2(2)10f --=，所以22((2))(10)lg102f f f ---===-．17．已知函数()f x 的定义域是1,82⎛⎤⎥⎝⎦，则(2)x f 的定义域是__________．【答案】(]1,3-【解析】解：己知()f x 的定义域是1,82⎛⎤⎥⎝⎦，由12128232x =-<=≤，得13x -<≤， 所以(2)f x 的定义域为(]1,3-． 故答案为：(]1,3-．三、解答题：（本大题4小题共44分．要求写出必要的推理过程） 18．（本小题满分10分）已知二次函数的图像经过点(1,6)A -，(1,2)B ，(2,3)C ，求该二次函数的解析式． 【答案】见解析．【解析】解：设二次函数解析式为2y ax bx c =++，0a ≠， ∵二次函数的图象经过点(1,6)A --、(1,2)B -、(2,3)C ， ∴ 62423a b c a b c a b c -+=-++=-++=， 解得：1a =，2b =，5c =-，∴该二次函数的解析式是：225y x x =+-． 故答案为：225y x x =+-．19．（本小题满分10分）已知0a >且1a ≠，0b >且1b ≠，0N >，求证：log log log a b a NN b=． 【答案】见解析．【解析】lg()lg log ()log ()lg()lg m n na m ab n b nb b a m a m===．20．（本小题满分12分）已知函数()y f x =的定义域为R ，且()()f x f x -=-，当(0,1)x ∈时，2()41x x f x =+．（1）求()f x 在(1,0)-上的解析式． （2）求证：()f x 在(0,1)上是减函数． 【答案】见解析．【解析】解：（1）∵()()f x f x -=-，(0,1)x ∈时，2()41xx f x =+， ∴当(1,0)x ∈-时，2()()41x x f x f x =--=-+．（2）证明：设1201x x <<<， 则12121222()()4141x x x x f x f x -=-++， 1221122(41)2(41)(41)(41)x x x x x x +-+=++，122112122(22)(22)(41)(41)x x x x x x x x +-+-=++，121212(22)(12)(41)(41)x x x x x x +--=++，∵1201x x <<<，∴12220x x -<，12120x x +-<，1410x +>，2410x +>， ∴12()()0f x f x ->，即12()()f x f x >， ∴()f x 在(0,1)是减函数．21．（本小题满分12分）设函数2(41)84, 1.()log , 1.a x a x a x f x x x ⎧-+-+<⎪=⎨⎪⎩≥（1）当12a =时，求函数()f x 的值域． （2）若函数()f x 是(,)-∞+∞上的减函数，求实数a 的取值范围． 【答案】见解析．【解析】解：（1）12a =时，2123,1()log ,1x x x f x x x ⎧-<⎪=⎨⎪⎩≥，当1x <时，2()3f x x x =-是减函数，所以()(1)2f x f >=-，即1x <时，()f x 的值域是(2,)-+∞． 当1x ≥时，12()log f x x=是减函数，所以()(1)0f x f =≤，即1x ≥时，()f x 的值域是(],0-∞．于是函数()f x 的值域是(],0(2,)-∞-+∞=R ．（2）若函数()f x 是(,)-∞+∞上的减函数，则下列①②③三个条件同时成立： ①当1x <， 2()(41)84f x x a x a =-+-+是减函数， 于是4112a +≥，则14a ≥． ②1x ≥时，12()log f x x=是减函数，则01a <<．③21(41)1840a a -+⋅-+≥，则13a ≤．于是实数a 的取值范围是11,43⎡⎤⎢⎥⎣⎦．。

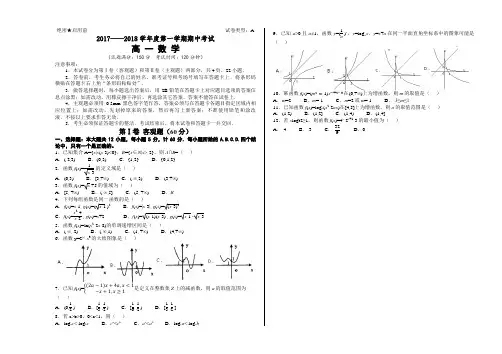
绝密★启用前 试卷类型：A2017——2018学年度第一学期期中考试高 一 数 学（试题满分：150分 考试时间：120分钟）注意事项：1．本试卷分为第Ⅰ卷（客观题）和第Ⅱ卷（主观题）两部分，共4页，22小题． 2．答卷前，考生务必将自己的姓名、准考证号和考场号填写在答题卡上．将条形码横贴在答题卡右上角“条形码粘贴处”．3．做答选择题时，每小题选出答案后，用2B 铅笔在答题卡上对应题目选项的答案信息点涂黑；如需改动，用橡皮擦干净后，再选涂其它答案。

答案不能答在试卷上．4．主观题必须用0.5mm 黑色签字笔作答，答案必须写在答题卡各题目指定区域内相应位置上；如需改动，先划掉原来的答案，然后再写上新答案；不准使用铅笔和涂改液．不按以上要求作答无效．5．考生必须保证答题卡的整洁．考试结束后，将本试卷和答题卡一并交回．第Ⅰ卷 客观题（60分）一、选择题：本大题共12小题，每小题5分，计60分．每小题所给的A.B.C.D.四个结论中，只有一个是正确的。

1．已知集合A={x |x (x -3)<0}，B ={x ∈N |x >-2}，则A ∩B =（ ） A ．(-2,3) B ．(0,3) C ．{1,2} D ．{0,1,2}2．函数f (x )=1x -3的定义域是（ ）A ．(0,3)B ．[3,+∞)C ．(-∞,3)D ．(3,+∞) 3．函数f (x )=x +5的值域为（ ）A ．[5, +∞)B ．(-∞,5]C ．(5, +∞)D ．R 4．下列每组函数是同一函数的是（ ）A ．f (x )=x -1, g (x )=(x -1 )2B ．f (x )=|x -3|, g (x )=(x -3)2C ．f (x )=x 2-4x -2, g (x )=x +2 D ．f (x )=(x -1)(x -3) , g (x )=x -1 ·x -35．函数f (x )=ln(x 2-2x -8)的单调递增区间是（ ）A ．(-∞,-2)B ．(-∞,1)C ．(1, +∞)D ．(4,+∞) 6．函数y=2|x |-x 3的大致图象是（ ）7．已知f (x )=是定义在整数集Z 上的减函数，则a 的取值范围为（ ）A ．(0,12 )B ．[13 ,12 )C ．[16 ,12 )D ．[13 ,12 ]8．若a>b>0，0<c<1，则（ ）A ．log a c < log b cB ．c a <c bC ．a c <a bD ．log c a < log c b9．已知a >0且a ≠1，函数y =(1a)x ，y =log a x ，y =x +a 在同一平面直角坐标系中的图象可能是（ ）10．幂函数f (x )=(m 2-m -1)x m ²+2m -3在(0,+∞)上为增函数，则m 的取值是（ ） A ．m =2 B ．m =-1 C ．m =2或m =-1 D ．-3≤m ≤111．已知函数f (x )=log a (x 2-2ax )在[4,5]上为增函数，则a 的取值范围是（ ） A ．(1,2) B ．(1,2] C ．(1,4) D ．(1,4]12．若x log 32≥1，则函数f (x )=4x -2x +1-3的最小值为（ ）A ．-4B ．-3C ．-329D ．0第Ⅱ卷 主观题（90分）二、填空题：本大题共4小题，每小题5分，计20分．只要求写出最后结果．13．已知集合A ={x |x <a }，B ={y |y =(13)x ²-1}，且B ⊆A ，则实数a 的取值范围是_____．14．函数f (x )=，若存在x 1<x 2，使得f (x 1)= f (x 2)，则x 1· f (x 1)的最大值为_____．15．函数f (x )= 2x +x 3-2的零点个数为_____． 16．给出下列四个命题：①函数y =1-x 2|x +2|-2为奇函数；②奇函数的图象一定通过直角坐标系的原点；③函数y = 的值域是(0,+∞)；④若函数f (2x )的定义域为[1,2]，则函数f (2x )的定义域为[1,2]．其中正确命题的序号是_____．（填上所有正确命题的序号）三、解答题：本大题共6小题，计70分．解答应写出必要的文字说明、证明过程或演算步骤．17．（本小题满分10分）已知集合A ={x |14 ≤2x -1≤128}，B ={y |y =log 2x ,x ∈[18,32]}，（1）求集合A ，B ；（2）若C ={x |m +1≤x ≤2m -1}，C ⊆(A ∩B )，求实数m 的取值范围．18．（本小题满分12分）（1）计算：9log 32+(log 35)×(log 1003)+log 52log 510；（2）已知 =2+ 3 ，求a +a -1a 13+a -13 的值．19．（本小题满分12分）已知f (x )是定义域为R 的偶函数，且当x ≥0时，f (x )=x 3-4x ． （1）求f (-3)+f (-2)-f (3)的值；（2）求f (x )的解析式，并写出f (x )的单调递增区间．20．（本小题满分12分）提高过江大桥的车辆通行能力可改善整个城市的交通状况，在一般情况下，大桥上的车流速度v （单位：千米/小时）是车流密度x （单位：辆/千米）的函数．当桥上的车流密度达200辆/千米时，造成堵塞，此时车流速度为0；当车流密度不超过20辆/千米时，车流速度为60千米/小时．研究表明：当20≤x ≤200时，车流速度v 是车流密度x 的一次函数． （1）当0≤x ≤200时，求函数v (x )的表达式；（2）当车流密度x 为多大时，车流量（单位时间内通过桥上某观测点的车辆数，单位：辆/小时）f (x )=x ·v (x )可以达到最大，并求出最大值．（精确到1辆/小时）21．（本小题满分12分） 已知函数f (x )=(log 4x -3)·log 44x ．（1）当x ∈[14,16]时，求该函数的值域；（2）令g (x )= f (x )+ log 4x 2-2a log 4x ，求g (x )在x ∈[42,44]上的最值．22．（本小题满分12分）已知二次函数f (x )=ax 2+x +1 (a >0)．（1）求函数f (x )在区间[-4,-2]的最大值M (a )；（2）若关于x 的方程f (x )=0有两个实数根x 1、 x 2，且x 1x 2 ∈[110,10]，求实数a 的最大值．2017——2018学年度第一学期期中考试13．(3,+∞) 14．252415．1 16．①④17．（本小题满分10分） （1）A =[-1,8]，B =[-3,5]． （2）A ∩B ={x |-1≤x ≤5}，①若C=∅，则m +1>2m -1，∴ m <2．②若C ≠∅，则∴2≤m ≤3 综上，m ≤3．18．（本小题满分12分）（1）9log 32+(log 35)×(log 1003)+log 52log 510 =4+lg5lg3 ×lg3lg100 +lg 2 =4+12 (lg5+lg2)=92．（2）设 =t ，则t 2=2+ 3 ，且a +a -1a 13+a -13 =t 3+1t 3t +1t= t 2+1t 2 -1=2+ 3 +12+3 -1=3． 19．（本小题满分12分）（1）f (-3)+ f (-2)- f (3)= f (2)=-4．（2）设x <0，则-x >0，∴f (x )= f (-x )=x 2-4(-x )=x 2+4x ，∴f (x )=，根据分段函数性质及二次函数的单调性可得单调递增区间为(-2,0)，(2,+∞) ．20．（本小题满分12分） （1）当0≤x ≤20时，v (x )=60；当20≤x ≤200时，设v (x )=ax +b ，∵ ，∴．∴v (x )=． （2）f (x )=， ①当0≤x ≤20时，f (x )为增函数，故当x =20时，其最大值为60×20=1200．②当20≤x ≤200时，f (x )=-13 x 2+2003 x =-13 (x -100)2+100003当x =100时，f (x )在[20,200]上有最大值100003．综上，当x =100时，f (x )在[0,200]上有最大值100003≈3333．即当车流密度为100辆/千米时，车流量可以达到最大，最大值约为3333辆/小时． 21．（本小题满分12分）（1）f (x )=(log 4x )2-2log 4x -3，令t =log 4x ，则x ∈[14,16]时，t ∈[-1,2]，此时有y =t 2-2t -3，∴y ∈[-4,0]．（2）g (x )= (log 4x )2-2a log 4x -3，令t = log 4x ，则x ∈[42,44]时，t ∈[2,4]，此时有y = t 2-2at -3， ①当a ≤2时，y min =y |t=2=1-4a ；y max = y |t=4=13-8a ； ②当2<a ≤3时，y min = y |t=a =-a 2-3；y max = y |t=4=13-8a ； ③当3<a <4时，y min = y |t=a =-a 2-3；y max = y |t=2=1-4a ； ④当a ≥4时，y min = y |t=4=13-8a ；y max = y |t=2=1-4a ．综上：当a ≤2时，y min =1-4a ；y max =13-8a ；当2<a ≤3时，y min =-a 2-3；y max =13-8a ；当3<a <4时，y min =-a 2-3；y max =1-4a ；当a ≥4时，y min =13-8a ；y max =1-4a ． 22．（本小题满分12分）（1）对称轴x =-12a，x ∈[-4,-2]，a >0二次函数开口向上，①当-12a ≤-3，即0<a ≤16 时：M (a )=f (-2)=4a -1，②当-12a >-3，即a >16时：M (a )=f (-4)=16a -3．综上，M (a )=．（2）方程ax 2+x +1=0的两个根分别为x 1、 x 2．∵x 1· x 2=1a ，x 1+ x 2=-1a ，x 1x 2 =t ∈[110 ,10]．∴x 1=-t (1+t )a ，x 2=-1(1+t )a带入x 1· x 2=1a得t (1+t )2a 2 =1a ，即a =t (1+t )2 =1t +1t+2 ，其中t ∈[110,10] 当t =1时，有(t +1t +2)min =4，有a max =14．。

2017-2018学年第一学期高一年级期中测试题数学试卷考试时间：上午7：30-9：30一．选择题（本大题共12 个小题，每小题3 分，满分36 分，在每出的小题给出的四个选项中，只有一项是符合题目要求的，请将字母代码填入相应位置）1.已知集合A { 1, 0,1} ，集合B {0,1, 2}，则A I BA 0,1 B. 0,1 C. 1, 0,1, 2 D. 1, 2.考点：集合的运算解析：∵A={-1,0,1}B {0,1, 2}, A I B 0,1答案：A12.函数f x lg xx 1的定义域是A 0, B. 0,1 1, C. 0,1 D. 1,.考点：函数的定义域ìx-1¹0解析：∵í， x 0,1 1,x>0î答案：B3 .函数x1f x)( 在区间 1,1 上的最小值是2A.121B.C. 2D. 22考点：指数函数的性质.1解析：0 1， f(x) 在区间 1,1 上单调递减，在x 1处取到最小值.2答案：B4 .下列函数中，在区间 0， 上单调递减的函数是A.y l o g2xB.y xC.y xD.y 1x考点：函数单调性判断.解析：A、B、C选项在 0， 上都是增函数，只有D选项在 0， 上是减函数. 答案：D.5.已知函数l o g x,x 0 f(2，则f( 3) x)f(x 2),x 0A. 1B.0C.1D.2考点：分段函数求值.解析：因为-3 0 ，则f( 3) f( 1) f(1) ；因为1 0 ，则f(1) log21 0 ，所以选B.6.已知幂函数f(x) (m2 m 1)x m在（0， ）上增函数，则实数mA B. 1C. 1或 2 . 2 1 2D.考点：幂函数定义式及性质.解析：f(x) (m2 m 1)x m是幂函数，则m2 m 1 1，解得m 1或m 2 ；又因为在（0， ）上是增函数，所以m 2 . 答案：A7. 已知lg a lg b 0 ，则函数y a x与函数y log x的图象可能是bA B C D考点：对数函数性质及其图象应用解析：lg a lg b 0 ，所以ab 1，所以函数y a x与函数y log x的单调性一致，所以选Db答案：D8. 下列结论正确的是1A B.0.93 30.9 2.log5 2 3log 2 C.log 3 log 32 0.3 D.log.3 122考点：指、对数函数比较大小解析：A. 由函数y log3 x与函数y log5 x的图象可知x 0,1 时，y x 的上方，x 1， 时，log 的图象恒在函数y xlog5 3y log3 的图象恒在y log5 x的图象的上方，所以A项错误；B. 0.93 1 30.9 ，所以B项错误；C. log0.3 2 0 0.32 ，所以C项错误；xD. 1111 1log log3互为倒数，log3 log3 log31 ，所以 1 log3 0 ，则它的相反数log13 1，所以D项正确。

2017——2018学年度第一学期期中考试高一数学 2017.11考试说明：1.本试题分第I 卷和第II 卷两部分。

第I 卷和第II 卷答案填涂在答题卡的相应位置，考试结束只上交答题卡。

2.满分150分，考试时间120分钟。

注意事项：1．答卷前，考生务必用0.5毫米黑色签字笔将自己的姓名、座号、准考证号、县区和科类填写在答题卡和试卷规定的位置上．2．第Ⅰ卷每小题选出答案后，用2B 铅笔把答题卡上对应题目的答案标号涂黑，如需改动，用橡皮擦干净后，再选涂其它答案，不能答在试题卷上．3．第Ⅱ卷必须用0.5毫米黑色签字笔在答题纸（或答题卡）上各题的答题区域内作答，不能写在试卷上；如需改动，先划掉原来的答案，然后再写上新的答案；不能使用涂改液、胶带纸、修正带．不按以上要求作答的答案无效．4．填空题请直接填写答案，解答题应写出文字说明、证明过程或演算步骤．第Ⅰ卷（共50分）一．选择题：（本大题共10小题，每小题5分，共50分．在每小题给出的四个选项中，只有一项是符合题目要求的）． 1 下列集合中，是空集的是（ ）A {}0B {}210x R x ∈+= C {}84x x x ><或 D {}∅2 若集合A={1，2，3},B={2,4}，定义集合A,B 间的运算：A*B={}x x A x B ∈∉且，则集合A*B 等于（ ）A ．{1，2，3} B.{2，4} C.{1，3} D.{2} 3.下列函数中,在区间()0,1上是增函数的是（ ） A ．x y =B ．x y -=3C ．xy 1= D ．42+-=x y4. 已知()f x 是偶函数，当x ＜0时，()(1)f x x x =+，则当x ＞0时，()f x =（ ） A ．(1)x x - B ．(1)x x -- C (1)x x + D ．(1)x x -+ 5 ．函数||2x y =的大致图象是（ ）6．设()()f x x R ∈为偶函数，且()f x 在[)0,+∞上是增函数，则(2)f -、()f π-、(3)f 的大小顺序是（ ）A ．()(3)(2)f f f π->>-B ．()(2)(3)f f f π->->C ．()(2)f f f π-<(3)<-D ．()(2)(3)f f f π-<-< 7．设 0.90.480.512314,8,()2y y y -===，则（ ）A. 312y y y >>B. 213y y y >>C. 123y y y >>D. 132y y y >>8.已知3()4f x ax bx =+-其中,a b 为常数，若(2)2f -=，则(2)f 的值等于( )A ．2-B ．4-C ．6-D ．10-9．设函数221,1()2,1x x f x x x x ⎧-≤⎪=⎨+->⎪⎩，则1()(2)f f 的值为（ ） A.1516 B. 2716- C. 89D.18 10.设偶函数()f x 在(0,)+∞上为增函数，且(2)f =0，则(2)0f x ->的解集（ ） A. {}2x x <-或x>4 B. {}0x x <或x>4 C. {}0x x <或x>6 D. {}2x x <-或x>2第II 卷（非选择题100分）二、填空题：本大题共5小题，每小题5分，共25分。

2017-2018学年高一（上）期中数学试卷一、选择题：本大题共12小题，每小题5分，共60分.在每小题给出的四个选项中，只有一项符合要求.1．集合A={1，2}的非空子集个数为（）A．4 B．2 C．1 D．32．设集合A={x|x＜3}，B={x|2x＞4}，则A∩B=（）A．∅B．{x|0＜x＜3} C．{x|1＜x＜3} D．{x|2＜x＜3}3．已知角α的终边经过点P（﹣3，4），则sinα的值等于（）A．﹣B．C．D．﹣4．周长为9，圆心角为1rad的扇形面积为（）A．B．C．πD．25．与函数f（x）=|x|表示同一函数的是（）A．f（x）=B．f（x）=C．f（x）=（）2D．f（x）=6．下列函数既是奇函数，又在区间（0，+∞）上是增函数的是（）A．y=x﹣1B．y=x2C．y=lgx D．y=x37．已知函数f（x）=的图象如图所示，则a+b+c=（）A．B．C．3 D．8．已知函数y=f（x）与函数y=e x的图象关于直线y=x对称，函数y=g（x）的图象与y=f（x）的图象关于x轴对称，若g（a）=1，则实数a的值为（）A．﹣e B．C．D．ex+x 的零点依次为a，b，c，则下9．已知三个函数f（x）=2x+x，g（x）=x﹣3，h（x）=log2列结论正确的是（）A．a＜b＜c B．a＜c＜b C．b＜a＜c D．c＜a＜b10．设函数f（x）定义在实数集R上，满足f（1+x）=f（1﹣x），当x≥1时，f（x）=2x，则下列结论正确的是（）A．f（）＜f（2）＜f（）B．f（）＜f（2）＜f（）C．f（）＜f（）＜f（2）D．f（2）＜f（）＜f（）11．已知函数f（x）定义在实数集R上的偶函数，且在区间[0，+∞）上单调递减，若实数aa）+f（log a）≤2f（﹣1），则a的取值范围是（）满足f（log2A．[2，+∞]∪（﹣∞，] B．（0，]∪[2，+∞）C．[，2] D．（0，]12．已知函数，则函数y=f[f（x）]﹣1的图象与x轴的交点个数为（）A．3个B．2个C．0个D．4个二、填空题：本大题共4小题，每小题5分，共20分.把正确答案填在答题纸的横线上，填在试卷上的答案无效.13．f（x）=的定义域为．14．函数f（x）=a x﹣1﹣2恒过定点．15．函数f（x）=lg（﹣x2+2x）的单调递减区间是．16．已知tanα=，，则sinα﹣cosα= ．三、解答题：共70分，解答应写出必要的文字说明、证明过程或演算步骤.17．（10分）已知全集U=R，集合A={x|1≤x＜5}，B={x|2≤x≤8}，C={x|﹣a＜x≤a+3}．A）∩B；（1）求A∪B，（∁R（2）若A∩C=C，求a的取值范围．18．（12分）已知f（α）=+cos（2π﹣α）．（1）化简f（α）；（2）若f（α）=，求+的值．19．（12分）已知函数f（x）=log2（1）判断f（x）的奇偶性并证明；（2）若f（3m+1）＜f（m），求m的取值范围．20．（12分）已知函数g（x）=x2﹣（m﹣1）x+m﹣7．（1）若函数g（x）在[2，4]上具有单调性，求实数m的取值范围；（2）若在区间[﹣1，1]上，函数y=g（x）的图象恒在y=2x﹣9图象上方，求实数m的取值范围．21．（12分）某化工厂生产的一种溶液，按市场要求，杂质含量不能超过0.1%．若初时含杂质2%，每过滤一次可使杂质含量减少，问至少应过滤几次才能使产品达到市场要求？（已知：lg2=0.3010，lg3=0.4771）22．（12分）已知f（x）=ln（e x+1）+ax是偶函数，g（x）=e x﹣be﹣x是奇函数．（1）求a，b的值；（2）判断g（x）的单调性（不要求证明）；（3）若不等式g（f（x））＞g（m﹣x）在[1，+∞）上恒成立，求实数m的取值范围．2017-2018学年高一（上）期中试卷（理科数学）参考答案与试题解析一、选择题：本大题共12小题，每小题5分，共60分.在每小题给出的四个选项中，只有一项符合要求.1．集合A={1，2}的非空子集个数为（）A．4 B．2 C．1 D．3【考点】子集与真子集．【分析】若集合A中有n个元素，则集合A中有2n﹣1个真子集．【解答】解：集合{1，2}的子集的个数为22=4个，去掉空集，得到集合{1，2}的非空子集的个数为22﹣1=3个．故选：D．【点评】本题考查子集的概念和应用，解题时要熟记若集合A中有n个元素，则集合A中有2n个子集，有2n﹣1个真子集．2．设集合A={x|x＜3}，B={x|2x＞4}，则A∩B=（）A．∅B．{x|0＜x＜3} C．{x|1＜x＜3} D．{x|2＜x＜3}【考点】交集及其运算．【分析】求解指数不等式化简集合B，然后直接利用交集运算求解【解答】解：∵B={x|2x＞4}={x|x＞2}，又A={x|x＜3}，∴A∩B={x|2＜x＜3}，故选：D【点评】本题考查了交集及其运算，考查了一元二次不等式及指数不等式的解法，是基础的计算题．3．已知角α的终边经过点P（﹣3，4），则sinα的值等于（）A．﹣B．C．D．﹣【考点】任意角的三角函数的定义．【分析】由任意角的三角函数的定义可得x=﹣3，y=4，r=5，由此求得sinα=的值．【解答】解：∵已知角α的终边经过点P（﹣3，4），由任意角的三角函数的定义可得x=﹣3，y=4，r=5，∴sinα==，故选C．【点评】本题主要考查任意角的三角函数的定义，4．周长为9，圆心角为1rad的扇形面积为（）A．B．C．πD．2【考点】扇形面积公式．【分析】根据扇形的面积公式进行求解，即可得出结论．【解答】解：设扇形的半径为r，弧长为l，则l+2r=9，∵圆心角为1rad的弧长l=r，∴3r=9，则r=3，l=3，则对应的扇形的面积S=lr=×3=，故选A．【点评】本题主要考查扇形的面积计算，根据扇形的面积公式和弧长公式是解决本题的关键．5．与函数f（x）=|x|表示同一函数的是（）A．f（x）=B．f（x）=C．f（x）=（）2D．f（x）=【考点】判断两个函数是否为同一函数．【分析】根据两个函数的定义域相同，对应关系也相同，即可判断它们是同一函数．【解答】解：对于A，函数f（x）==|x|（x≠0），与函数f（x）=|x|（x∈R）的定义域不同，所以不是同一函数；对于B，函数f（x）==|x|（x∈R），与函数f（x）=|x|（x∈R）的定义域相同，对应关系也相同，所以是同一函数；对于C，函数f（x）==x（x≥0），与函数f（x）=|x|（x∈R）的定义域不同，对应关系也不同，所以不是同一函数；对于D，函数f（x）==x（x∈R），与函数f（x）=|x|（x∈R）的对应关系不同，所以不是同一函数．故选：B．【点评】本题考查了判断两个函数是否为同一函数的应用问题，是基础题目．6．下列函数既是奇函数，又在区间（0，+∞）上是增函数的是（）A．y=x﹣1B．y=x2C．y=lgx D．y=x3【考点】函数奇偶性的判断；函数单调性的判断与证明．【分析】根据函数奇偶性和单调性的性质分别进行判断即可．【解答】解：A．y=x﹣1为奇函数，在（0，+∞）上是减函数，不满足条件．B．y=x2是偶函数，当x＞0时，函数为增函数，不满足条件．C．y=lgx定义域为（0，+∞），函数为非奇非偶函数，不满足条件．D．y=x3是奇函数，在（﹣∞，+∞）上是增函数，满足条件．故选：D【点评】本题主要考查函数奇偶性和单调性的判断，要求熟练掌握常见函数奇偶性和单调性的性质．7．已知函数f（x）=的图象如图所示，则a+b+c=（）A．B．C．3 D．【考点】函数的图象．【分析】先由图象可求得直线的方程，又函数的图象过点（0，2），将其坐标代入可得c值，从而即可求得a+b+c的值．【解答】解：由图象可求得直线的方程为y=2x+2，（x+）的图象过点（0，2），又函数y=logc将其坐标代入可得c=，所以a+b+c=2+2+=．故选：B【点评】本题考查了函数图象的识别和应用，属于基础题．8．已知函数y=f（x）与函数y=e x的图象关于直线y=x对称，函数y=g（x）的图象与y=f（x）的图象关于x轴对称，若g（a）=1，则实数a的值为（）A．﹣e B．C．D．e【考点】指数函数的图象与性质．【分析】根据y=f（x）与y=e x的图象关于直线y=x对称，求出f（x），再根据y=g（x）的图象与y=f（x）的图象关于x轴对称，求出y=g（x），再列方程求a的值即可．【解答】解：函数y=f（x）与函数y=e x的图象关于直线y=x对称，∴f（x）=lnx，函数y=g（x）的图象与y=f（x）的图象关于x轴对称，∴y=﹣lnx，∴g（a）=﹣lna=1，a=．故选：C．【点评】本题考查了函数图象对称的应用问题，是基础题目．x+x 的零点依次为a，b，c，则下9．已知三个函数f（x）=2x+x，g（x）=x﹣3，h（x）=log2列结论正确的是（）A．a＜b＜c B．a＜c＜b C．b＜a＜c D．c＜a＜b【考点】函数零点的判定定理．【分析】根据零点存在定理，分别求三个函数的零点，判断零点的范围，再判断函数的单调性，确定函数的零点的唯一性，从而得到结果．【解答】解：函数f（x）=2x+x，f（﹣1）=﹣1=﹣＜0，f（0）=1＞0，可知函数的零点a ＜0；令g（x）=x﹣3=0得，b=3；函数h（x）=logx+x=0，h（）=﹣1+=﹣＜0，h（1）=1＞0，2∴函数的零点满足＜c＜1，∵f（x）=2x+x，g（x）=x﹣3，h（x）=logx+x在定义域上是增函数，2∴函数的零点是唯一的，则a＜c＜b，故选：B．【点评】本题考查的重点是函数的零点及个数的判断，基本初等函数的单调性的应用，解题的关键是利用零点存在定理，确定零点的值或范围．10．设函数f（x）定义在实数集R上，满足f（1+x）=f（1﹣x），当x≥1时，f（x）=2x，则下列结论正确的是（）A．f（）＜f（2）＜f（）B．f（）＜f（2）＜f（）C．f（）＜f（）＜f（2）D．f（2）＜f（）＜f（）【考点】抽象函数及其应用．【分析】由已知得函数f（x）的图象关于直线x=1对称，⇒函数f（x）在（1，+∞）上递增，在（﹣∞，1）上递减，⇒f（）＜f（）＜f（0），及f（）＜f（）＜f（2）．【解答】解：函数f（x）定义在实数集R上，且满足f（1+x）=f（1﹣x），∴函数f（x）的图象关于直线x=1对称，∴f（2）=f（0）．又∵当x≥1时，f（x）=2x，∴函数f（x）在（1，+∞）上递增，在（﹣∞，1）上递减，∴f （）＜f （）＜f （0），及f （）＜f （）＜f （2）．故选：C ．【点评】本题考查了函数的对称性及单调性，属于中档题．11．已知函数f （x ）定义在实数集R 上的偶函数，且在区间[0，+∞）上单调递减，若实数a满足f （log 2a ）+f （log a ）≤2f （﹣1），则a 的取值范围是（ ）A ．[2，+∞]∪（﹣∞，]B ．（0，]∪[2，+∞）C ．[，2]D ．（0，]【考点】奇偶性与单调性的综合．【分析】由偶函数的性质将f （log 2a ）+f （log a ）≤2f （﹣1），化为：f （log 2a ）≤f （1），再由f （x ）的单调性列出不等式，根据对数函数的性质求出a 的取值范围．【解答】解：因为函数f （x ）是定义在R 上的偶函数，所以f （log a ）=f （﹣log 2a ）=f （log 2a ），则f （log 2a ）+f （loga ）≤2f （﹣1），为：f （log 2a ）≤f （1）， 因为函数f （x ）在区间[0，+∞）上单调递减，所以|log 2a|≥1，解得0＜a ≤或a ≥2，则a 的取值范围是（0，]∪[2，+∞）故选：B ．【点评】本题考查函数的奇偶性、单调性的应用，以及对数函数的性质，属于中档题．12．已知函数，则函数y=f[f （x ）]﹣1的图象与x 轴的交点个数为（ ） A ．3个 B ．2个 C ．0个 D ．4个【考点】函数的图象．【分析】函数y=f[f （x ）]﹣1的图象与x 轴的交点个数即为f[f （x ）]﹣1=0的解得个数，根据函数解析式的特点解得即可，【解答】解：y=f[f （x ）]﹣1=0，即f[f （x ）]=1，当f（x）+1=1时，即f（x）=0时，此时log2x=0，解得x=1，或x+1=0，解得x=﹣1，当log2f（x）=1时，即f（x）=2时，此时x+1=2，解得x=1（舍去），或log2x=2，解得x=4，综上所述函数y=f[f（x）]﹣1的图象与x轴的交点个数为3个，故选：A．【点评】此题考查的是函数于函数图象交点个数的问题．在解答的过程当中充分体现了函数与方程的思想、问题转化的思想．值得同学们体会反思．二、填空题：本大题共4小题，每小题5分，共20分.把正确答案填在答题纸的横线上，填在试卷上的答案无效.13．f（x）=的定义域为[﹣1，1）∪（1，+∞）．【考点】函数的定义域及其求法．【分析】根据函数f（x）的解析式，列出不等式组，求出解集即可．【解答】解：要使函数f（x）=有意义，应满足，即，解得x≥﹣1且x≠1；所以函数f（x）的定义域为[﹣1，1）∪（1，+∞）．故答案为：[﹣1，1）∪（1，+∞）．【点评】本题考查了根据函数解析式求定义域的应用问题，是基础题目．14．函数f（x）=a x﹣1﹣2恒过定点（1，﹣1）．【考点】指数函数的单调性与特殊点．【分析】根据指数函数的性质进行求解．【解答】解：令x﹣1=0得x=1，此时f（1）=1﹣2=﹣1．故函数f（x）=a x﹣1﹣2恒过定点（1，﹣1）．故答案为：（1，﹣1）．【点评】本题主要考查指数函数的图象和性质，利用指数函数过定点，是解决本题的关键．15．函数f（x）=lg（﹣x2+2x）的单调递减区间是[1，2）．【考点】复合函数的单调性．【分析】令t=﹣x2+2x＞0，求得函数的定义域，根据f（x）=g（t）=lgt，故本题即求函数t 的减区间．再利用二次函数的性质，得出结论．【解答】解：令t=﹣x2+2x＞0，求得0＜x＜2，故函数的定义域为（0，2），则f（x）=g（t）=lgt，故本题即求函数t的减区间．利用二次函数的性值可得令t=﹣x2+2x在定义域内的减区间为[1，2），故答案为：[1，2）．【点评】本题主要考查复合函数的单调性，二次函数、对数函数的性质，属于中档题．16．已知tanα=，，则sinα﹣cosα= ．【考点】同角三角函数基本关系的运用．【分析】根据同角三角函数的基本关系，以及三角函数在各个象限中的符号，求得sinα、cosα的值，可得sinα﹣cosα的值．【解答】解：∵tanα==，，sin2α+cos2α=1，∴sinα=﹣，cosα=﹣，∴sinα﹣cosα=，故答案为：．【点评】本题主要考查同角三角函数的基本关系，以及三角函数在各个象限中的符号，属于基础题．三、解答题：共70分，解答应写出必要的文字说明、证明过程或演算步骤.17．（10分）（2016秋•扶余县校级期中）已知全集U=R，集合A={x|1≤x＜5}，B={x|2≤x ≤8}，C={x|﹣a＜x≤a+3}．（1）求A∪B，（∁A）∩B；R（2）若A∩C=C，求a的取值范围．【考点】集合的包含关系判断及应用；交、并、补集的混合运算．【分析】（1）直接利用并集、补集和交集的概念求解；（2）由C∩A=C，∴C⊆A，然后分C为空集和不是空集分类求解a的范围，最后取并集．【解答】解：（1）A∪B={x|1≤x≤8}，∁R A═{x|x≥5或x＜1}，（∁RA）∩B═{x|5≤x≤8}，（2）∵A∩C=C，∴C⊆A当C=∅时 a+3＜﹣a解得a≤﹣当C≠∅时解得：﹣综上所述：a≤﹣1【点评】本题考查了交、并、补集的混合运算，考查了集合间的关系，解答的关键是端点值的取舍，是基础题．18．（12分）（2016秋•扶余县校级期中）已知f（α）=+cos（2π﹣α）．（1）化简f（α）；（2）若f（α）=，求+的值．【考点】同角三角函数基本关系的运用．【分析】（1）利用诱导公式即可化简求值得解．（2）将已知等式两边平方，利用同角三角函数基本关系式可求sinαcosα的值，即可化简所求计算得解．【解答】解：（1）f（α）=+cosα=sinα+cosα．﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣（6分）（2）∵f（α）=sinα+cosα=，∴1+2sinαcosα=，∴sinαcosα=﹣，﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣（10分）∴+==﹣．﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣（12分）【点评】本题主要考查了诱导公式，同角三角函数基本关系式在三角函数化简求值中的应用，考查了转化思想，属于基础题．19．（12分）（2016秋•扶余县校级期中）已知函数f（x）=log2（1）判断f（x）的奇偶性并证明；（2）若f（3m+1）＜f（m），求m的取值范围．【考点】复合函数的单调性；函数奇偶性的判断；对数函数的图象与性质．【分析】（1）f（x）为奇函数，结合对数的运算性质和奇偶性的定义，可得答案．（2）根据复合函数的单调性“同增异减”的原则，可得f（x）在定义域（﹣1，1）上是减函数，则f（3m+1）＜f（m）可化为：﹣1＜m＜3m+1＜1，解得答案．【解答】解：（1）f（x）为奇函数，﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣（1分）证明如下：因为，定义域为（﹣1，1）关于原点对称﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣f（﹣x）=，∴f（x）+f（﹣x）=0，即f（﹣x）=﹣f（x），故f（x）为奇函数﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣（6分）（2）令u==﹣1为（﹣1，1）上的减函数，﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣（8分）由复合函数的单调性可知f（x）在定义域（﹣1，1）上是减函数，﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣（9分）所以f（3m+1）＜f（m）可化为：﹣1＜m＜3m+1＜1，解得：＜m＜0﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣（12分）【点评】本题考查的知识点是复合函数的单调性，函数的奇偶性，对数函数的图象和性质，难度中档．20．（12分）（2016秋•扶余县校级期中）已知函数g（x）=x2﹣（m﹣1）x+m﹣7．（1）若函数g（x）在[2，4]上具有单调性，求实数m的取值范围；（2）若在区间[﹣1，1]上，函数y=g（x）的图象恒在y=2x﹣9图象上方，求实数m的取值范围．【考点】二次函数的性质；函数单调性的判断与证明．【分析】（1）求出函数的对称轴，根据二次函数的单调性求出m的范围即可；（2）问题转化为x2﹣（m+1）x+m+2＞0对任意x∈[﹣1，1]恒成立，设h（x）=x2﹣（m+1）x+m+2，求出函数的对称轴，通过讨论对称轴的范围，求出m的范围即可．【解答】解：（1）对称轴x=，且图象开口向上．若函数g（x）在[2，4]上具有单调性，则满足≤2或≥4，解得：m≤5或m≥9；（2）若在区间[﹣1，1]上，函数y=g（x）的图象恒在y=2x﹣9图象上方，则只需：x2﹣（m﹣1）x+m﹣7＞2x﹣9在区间[﹣1，1]恒成立，即x2﹣（m+1）x+m+2＞0对任意x∈[﹣1，1]恒成立，设h（x）=x2﹣（m+1）x+m+2其图象的对称轴为直线x=，且图象开口向上①当≥1即m≥1时，h（x）在[﹣1，1]上是减函数，=h（1）=2＞0，所以h（x）min所以：m≥1；②当﹣1＜＜1，即﹣3＜m＜1，函数h（x）在顶点处取得最小值，=h（）=m+2﹣＞0，解得：1﹣2＜m＜1；即h（x）min③当≤﹣1即m≤﹣3时，h（x）在[﹣1，1]上是增函数，所以，h（x）min=h（﹣1）=2m+4＞0，解得：m＞﹣2，此时，m∈∅；综上所述：m＞1﹣2．【点评】本题考查了二次函数的性质，考查函数的单调性以及分类讨论思想，是一道中档题．21．（12分）（2014秋•增城市期末）某化工厂生产的一种溶液，按市场要求，杂质含量不能超过0.1%．若初时含杂质2%，每过滤一次可使杂质含量减少，问至少应过滤几次才能使产品达到市场要求？（已知：lg2=0.3010，lg3=0.4771）【考点】指数函数的实际应用．【分析】设出过滤次数，由题意列出基本不等式，然后通过求解指数不等式得n的取值．【解答】解：设过滤n次，则，即，∴n≥．又∵n∈N，∴n≥8．即至少要过滤8次才能达到市场要求．【点评】本题考查了等比数列，考查了等比数列的通项公式，训练了指数不等式的解法，是基础题．22．（12分）（2016秋•扶余县校级期中）已知f（x）=ln（e x+1）+ax是偶函数，g（x）=e x ﹣be﹣x是奇函数．（1）求a，b的值；（2）判断g（x）的单调性（不要求证明）；（3）若不等式g（f（x））＞g（m﹣x）在[1，+∞）上恒成立，求实数m的取值范围．【考点】函数恒成立问题；函数单调性的判断与证明；函数奇偶性的判断．【分析】（1）根据函数奇偶性的性质即可求a，b的值；（2）根据指数函数的单调性即可判断g（x）的单调性；（3）根据函数的单调性将不等式g（f（x））＞g（m﹣x）在[1，+∞）上恒成立，进行转化，即可求实数m的取值范围．【解答】解：（1）∵f（x）=ln（e x+1）﹣ax是偶函数，∴f（﹣x）=f（x），即f（﹣x）﹣f（x）=0，则ln（e﹣x+1）+ax﹣ln（e x+1）+ax=0，ln（e x+1）﹣x+2ax﹣ln（e x+1）=0，则（2a﹣1）x=0，即2a﹣1=0，解得a=．若g（x）=e x﹣be﹣x是奇函数．则g（0）=0，即1﹣b=0，解得b=1；（2）∵b=1，∴g（x）=e x﹣e﹣x，则g（x）单调递增；（3）由（II）知g（x）单调递增；则不等式g（f（x））＞g（m﹣x）在[1，+∞）上恒成立，等价为f（x）＞m﹣x在[1，+∞）上恒成立，即ln（e x+1）﹣x＞m﹣x在[1，+∞）上恒成立，则m＜ln（e x+1）+x，设m（x）=ln（e x+1）+x，则m（x）在[1，+∞）上单调递增。

2017—2018学年度第一学期期中质量检测高一数学试卷一、选择题(本大题共12个小题，每小题4分，共48分)1 集合A ={0,2, a}，B ={1，a2}，若AU B 二{0,1,2,4,16}，则a 的值为( ).A. 0B. 1C. 2D. 4【答案】D【解析】集合A ={0,2, a} , B ={1,a2}，若AU B 二{0,1,2,4,16},可得a =4 .故选D .2 .设集合A与集合B嗾使自然数集N，映射f:A—；B把集合A中的元素n映射到集合B中为元素n2 n，则在映射f下，像20的原像是( ).A . 2B . 3 C. 4 D . 4 或-5【答案】C【解析】由2n - n=20求n，用代入验证法可知n =4.故选C .3. 若函数y = f (x)的定义域是[0,2]，则函数g(x)二f(2x)的定义域是( ).x —1A . [0,1]B . [0,1)C . [0,1)U(1,4] D. (0,1) 【答案】B【解析】T函数f (x)的定义域是[0,2],•••函数f (2x)的定义域是[0,1].•••函数g(x)=空凶，•,x -1综上0 < x <1 .故选B .A . 2B . 3C . 4D .与a值有关4. 已知f (x) =(m _1)x2・3mx・3为偶函数，则f (x)在区间(_4,2)上为A •增函数B •减函数C.先递增再递减【答案】C【解析】因为f (x^(m -1)x2 3mx 3为偶函数，所以f(-x)二f(x), 所以(m -1)x -3mx 亠3 =(m -1)x2亠2mx 亠3，即3m =0 ,所以m =0 ,即f (x) = -x23，由二次函数的性质可知，f(x) - -x2・3在区间(40)上单调递增，在(0,2)递减.故选C .5. 三个数a =0.32, b =log20.3 , c=2°.3之间的大小关系是( ).A. a ：：c ：： b B . a ：：b ：：c C. b ::: a ：： c【答案】C【解析】由对数函数的性质可知： b =log20.3 ：：：0 ,由指数函数的性质可知：0 ：：：a ：：：1, c 1 ,二b ■■■.a ::c .故选C .36 •函数f (x)二x x的图像关于( ).A . y轴对称B .直线y = -x对称C .坐标原点对称【答案】C【解析】A . 2B . 3C . 4D .与a值有关7.已知0cac1，则方程｛冷log；|的实根个数是( ).)•D .先递减再递增D . b ：： c ：： aD.直线y = x对称A . 2B . 3C . 4D .与a值有关【解析】作出y=a% y屮og a x|的函数图象如图所示:由图象可知两函数图象有两个交点，故方程a lx|=|log a X|的有两个根. 故选A .8在下列四个图中，二次函数y=ax2・bx与指数函数y r*X的图像只可能为（).A.【答案】C 【解析】9 •设2a=5 =m，且1 12，贝U m等于（).a bA.10B. 10C. 20 【答案】A【解析】1 1--=log ma b2 logm5= IOgm10 =2,D . 100又••• m 0 ,二m = 10 .•••若分成 10 , 10 , 11 , 11,（a 「3）x 亠5,x w 110.已知函数f （x ） = 2a是R 上的减函数，则实数 a 的取值范围是（）•,x"xA . （0,3）B . （0,3] 【答案】D【解析】因为f （x ）为R 上的减函数， 所以x w 1时，f （x ）递减，即a-3：：：0，①x 1时，f （x ）递减，即a 0，② 且（a -3） 1 5 >2a，③1联立①②③解得，0 ：：： a w 2 . 故选D .11 •方程log 3x • x -3 =0的解所在的区间是（）.【答案】C 【解析】12.某购物网站在2016年11月开展 全部6折”促销活动，在11 日当天购物还可以再享受 每张订单金 额（6折后）满300元时可减免100元”.某人在11日当天欲购入原价 48元（单价）的商品共 42件，为 使花钱总数最少，它最多需要下的订单张数为（）.A . 1B . 2C . 3D . 4【答案】C【解析】•••原价是： 48 42 =2016 （元），2016 0.6 =1209.6 （元）.•• •每张订单金额（6折后）满300元时可减免100,A . (0,1)B . (1,2)C . (2,3)D . (3,4)C . (0,2)D . (0,2]由于48 10=480, 480 0.6=288,达不到满300元时可减免100,•••应分成9 , 11 , 11, 11 ••••只能减免3次.二、填空题(本大题共4个小题，每小题5分，共20分)13•函数f(2x)=x2—2x，贝y f(1)= _____________ •【答案】0【解析】14. y =log a(2x -3) _______________________________________ 恒过定点P , P在幕函数f (x)图像上，f (9) = •【答案】-3【解析】15. ______________________________________________________________________ 若一次函数f(x)=ax b有一个零点2，那么g(x)=bx2-ax的零点是 _______________________________________________ .1【答案】0或-丄2【解析】由题意可得b - -2a得a = 0，由g(x)二_2 ,2 1ax -ax =0,得x =0或x ~•f (x)的值16•已知f(x)是定义在［-2,0)U(0,2］上的奇函数，当x 0时，f(x)的图象如图所示，那么域是 ___________ •当 0 ：：t ：：5 时，v =t + 10 ,【答案】【解析】由图象可得：当X. (0,2]时，f (x) (2,3] •又••• f (x)是定义在[-2,0) U (0,2]上奇函数, 故当 x [ -2,0)时，f (x) [£,-2). 故 f (x)的值域是[-3, -2) J (2,3].三、解答题(本大题共 6个小题，共52分)17. (本题8分)某质点在30s 内运动速度v 是时间t 的函数，它的图象如图，解析法表示出这个函数, 并求出9s 时质点的速度.【答案】【解析】(1 )根据折线为直线，可设 v=kt + b ，图中点的坐标:(0,10) , (5,15) , (20,30) , (25,0),代入解析式得：当 5 < t <10 时，v =3t , 当 10 < t ：：：20 时，v =30 , 当 20< t < 25 时，v 二(t+150.20 50505 O 00221 1所以：t + 10,0 ::: t ：：：5,3t,5 w t<10 v(t)：30,10 w tc20 ' -6t+150,20 w t w 259s时速度为27cm/s .18. (本题8分)已知函数f(x rj log j x—“的定义域为集合A ,函数g(x)=3心心-1的值域为集合B , 且A[J B=B，求实数m 的取值范围.【答案】x -1 >0【解析】log 1 (x -1) > 0，得1 x < 2 ,.2即A =(1,2],2 2又g(x)=32Q —1=3g)+1+m_1 ,即B =(0,31+m -1].•/ AUB =B，二B ,••• 31+m _1 > 2 解得m > 0 ,••• m的取值范围为[0, + ：：).19. (本题8分)是否存在实数a，使函数y二a2x 2a x-1 ( a 0且a =1 )在[-1,1]上的最大值是14 ?【答案】【解析】设t =a x，贝y y =f(t) =t2 +2t —1 =(t+1)2 -2 ,当a ・1 时，0：：：a，< t < a，此时y max = a? + 2a -1 ,由题设a2 +2a -1 =14 得a =3或a = -5,由a・1,知a =3 ；1 1由题设a ? + 2a丄_1 =14得a 或a =-5，3 51由0 ::: a ::: 1，知a =—,当0：：：a”：1 时，t・[a,a°]，此时y max =(a-1)2 + 2a，-1 .31故所求的a的值为3或—.32 220. (本题8分)设U = R，集合 A ={x x +3x +2 =0} , B ={x x +(m +1)x + m =0}.若(e u A)“ B =0 , 试求实数m的值.【答案】【解析】•••(e,A)riB =_ ,••• B - A .2根据题意A={xx +3x + 2=0}，则A 的子集有0, {1} , {2} , {1,2},若B = _，即x2 + (m + 1)x+ m =0 无解，而(m + 1)2 -4m = (m -1)2> 0 ,即x2 + (m + 1)x + m =0必有解，则B V 不成立.若B ={1} , x2+(m + 1)x+m =0有两个相等的实根1，则有m + 1 =2 , m=1，解可得m=1.若B ={2} , x2 + (m + 1)x + m =0有两个相等的实根2，则有m + 1=4 , m = 2无解.若B ={1,2} , x2 +(m + 1)x+m =0有两个实根1 或2，则有m + 1 =3 , m=2，解可得m=2 .综合可得：m =1或m =2 ..2x亠b21 .(本题10分)已知定义域为R的函数f(x) 是奇函数.2 +a(1 )求a, b的值.2 2(2 )若对任意的r R，不等式f(t -2t) f(2t -k) ：：：0恒成立，求k的取值范围.【答案】【解析】(1 )因为f (x)为R上的奇函数，所以f (0) =0 ,即土b=0，解得b =1, 2 + a由f(_i)=「f⑴，得耳上！斗，解得a = 2 ,2+a 2 +a所以a =2 , b =1.(2 )因为f (x)为奇函数，所以f (t2—2t) + f (2t2—k) ：：：0 可化为f(t2—2t) ：：： f (2t2—k) = f (k —2t2).又由(1 )知f(x)为减函数，所以t2 -2t k -2t2，即3t2-2t .k 恒成立,r i W i 1而3t2 -2t =3 t —— > —,I 3 丿3 31所以k ：：：--.3ax —122.(本题10分)设函数f(x) ，其中a・R .x +1(1 )若a =1 , f(x)的定义域为区间［0,3］，求f (x)的最大值和最小值.(2 )若f(x)的定义域为区间(0,；)，求a的取值范围，使f(x)在定义域内是单调减函数. 【答案】【解析】f (x)二ax 1x +1a(x+1) -a -1x+1a + 1=ax + 1设X1 , X2 • R ,a + 1 a+1 则f (xj —f(X2)=x2 +1 为+ 1 _(a + 1)(X1 - X2)一(X1+1)(X2+1).2 (1 )当 a =1 时，f (x) = 1 ，设 0 < x 1 ： x 2 < 3,x + 1又 X| _x 2 c0 , X 1 + ^>0 ,冷 +1 >0 ,f (X 1)—f (X 2)：：：0 f(X 1)：：： f (X 2).••• f (x)在［0,3］上是增函数，2 1• f(X )max "⑶=1-2 专,f(X )min "(0).(2 )设 X 1 X 2 0 ,则为一 X 2 0 , X 1 +1 . 0 , X 2 +1 0 . 若使f (x)在(0,+ ：：)上是减函数，只要 f(xj - f (X 2)：：：0，而 •••当 a + 1 ：：：0，即 a ：：：-1 时，有f (为)- f(X 2)：：：0 ,f (X 1)::： f(X 2).••当 a ：： -1时，f (x)在定义域(0, + ：：)内是单调减函数. 则 f (X 1) -f(X 2)口 2(x i —X 2)(X i +1)(X 2 +1)f (X 1)_f (X 2)= (a+1)(X1 -X 2)(X 1 +1)(X 2 +1)。

2017-2018年高一第一学期数学期中试卷适用班级：17级综高班 （满分150分） 2017年11月一．选择题(共10题，每题5分，共计50分）1.下列符号正确的是（ ） A.N ∈2 B.)}1,1{(}1,1{-=- C.},{}{b a a ∈ D.}0{⊆φ2．含n 个元素的集合，下列说法正确的是（ ）A.有个子集B.有个子集C.有个子集D.有个子集3．满足{}{}5,3,13,1=A 的所有集合A 的个数（ ） A ．1个 B.2个 C.3个 D.4个4．下列几个图形中,可以表示函数关系)(x f y =的那一个图是（ ）A B C D5. 下列说法真确的是 （ ）A. 空集没有子集B.任一集合必有子集C.任一集合必有真子集D.任一集合必有至少两个子集6.“不等式在R 上恒成立”的一个必要不充分条件是（ ） A.B . C. D. 7.设是定义在R 上的奇函数，且是减函数，若a+b<0，则 （ ） A. B. C. D.8.函数 （ ）A ．是奇函数 B.是偶函数 C.非奇函数 D.非奇非偶函数9.．已知集合{},1A x =，{},1,2,4B y =，且A 是B 的真子集．若实数x 与y 都在集合{}0,1,2,3,4中，则不同的集合{},x y 共有（ ）A.4个B.5个C.6个D.7个21-n 12-n 2nn 202>+-m x x 41>m 10<<m 0>m 1>m )(x f )()(b f a f >)()(b f a f <0)()(>+b f a f 0)()(<+b f a f x y 3=10. 的单调减区间是（ ） A.（0，1） B.（1，2） C.(-1,1) D.(0,-1)二、填空题（共5题，每题5分，共25分）11.集合元素的三个特征是：____________，______________，______________.12.函数()32++=x x x f 的递增区间是____________. 13. 已知1(0)()(0)0(0)x x f x x x π+>⎧⎪==⎨⎪<⎩，则)]}2([{-f f f ＝____________. 14.函数的定义域是_____________.15.函数（）的值域是___________.三、解答题（共5题，每题15分，共75分） 16.已知定义在R 上的偶函数和奇函数满足，求与.17. 解不等式123--=x x x y )1(0)(-=x x f x x f 1)(=0<x )(x f )(x g 1)()(22323+-=-x x x g x f )(x f )(x g 312+<-x x18.讨论函数的单调性19.判断函数的奇偶性1-=x x y 11)(22-+-=x x x f20. 通过研究学生的学习行为，专家发现，学生的注意力随着老师讲课时间的变化而变化，讲课开始时，学生的兴趣激增；中间有一段时间，学生的兴趣保持较理想的状态；随后学生的注意力开始分散，设)(t f 表示学生注意力随时间t(分钟）的变化规律（)(t f 越大，表明学生注意力越集中），经过实验分析得知（1）讲课开始后多少分钟学生的注意力最集中？能坚持多少分钟？（2）讲课开始后5分钟与讲课开始后25分钟比较，何时学生的注意力更集中？（3）一道数学难题需要讲解24分钟，并且要求学生的注意力至少达到180，那么经过适当安排，老师能否在学生达到所需的状态下讲授完这道题目？（通过计算解释）⎪⎩⎪⎨⎧≤<+-≤<≤<++-=4020,38072010,240100,10024)(2t t t t t t f t。

2017-2018学年度高一上学期期中考试 数 学(总分150) 时间:120分钟一、选择题（本大题共12小题，每小题5分，共60分。

在每小题给出的四个选项中，只有一项是符合题目要求的）1. 设集合}1,0,1{-=M ，{}1,0,2-=N ，则N M ⋂＝( )A ．{－1,0,1}B ．{0,1}C ．{1}D ．{0} 2. 函数)13lg(13)(2++-=x xx x f 的定义域是( )A ．),31(+∞-B ．)1,31(- C. )31,31(- D.)31,(--∞3. 设221(1),()log (1).x x f x x x ⎧+≤=⎨>⎩ 则(1)(4)f f += ( )A. 5B. 6C. 7D. 8 4.判断下列各组中的两个函数是同一函数的为（ ）A ．3)5)(3(1+-+=x x x y ，52-=x y ；B ．x x f =)(，2)(x x g =；C．()f x =()F x = D ．1()|25|f x x =-, 2()25f x x =- 5．()2333)2(ππ-+-的值为（ ）A.5B. 52-πC. 1-D.π25-6.如果集合A={x |a x 2＋2x ＋1=0}中只有一个元素，则a 的值是（ ） A ．0 B ．0 或1 C ．1 D ．不能确定7、已知幂函数()y f x =的图象过⎛ ⎝⎭，则它的一个单调递减区间是（ ） A.),2(+∞ B ．(),0-∞ C ．(),-∞+∞ D ．[)0,+∞8. 方程330x x --=的实数解落在的区间是（ ）A ．[1,0]-B ．[0,1]C ．[1,2] D.[2,3] 9．若2()2(1)2f x x a x =+-+在(,4]-∞上是减函数，则a 的取值范围是 （ ） A ．(,3]-∞- B ．[3,)-+∞ C ．(,5]-∞D ．[3,)+∞10. 函数121()3xf x x ⎛⎫=- ⎪⎝⎭的零点个数为A ．3B ．2C ．1D ．011.函数 与 （） 在同一坐标系中的图像只可能是( ）12.若函数()y f x =定义域为R ，且满足f (－x )＝－f (x )，当a ∈(－∞，0], b ∈(－∞，0]时,总有()()0f a f b a b->-(a ≠b )，若f (m ＋1)＞f (2)，则实数m 的取值范围是( )A ．－3≤m ≤1B ．m ＞1C ．－3＜m ＜1D ．m ＜－3或m ＞1二、填空题：请把答案填在题中横线上（本大题共4个小题，每小题5分，共20分）13.已知f (x )是定义在R 上的奇函数,当x >0时,f (x)=1+,则f (-2)=14.函数32+=-x a y （a >0且a ≠1）的图象必经过点 15.函数)2(log 22+=x y 的值域为 .16．关于函数f(x)＝lg 21x x＋(x>0，x ∈R)，下列命题正确的是____ ____．(填序号)①函数y ＝f(x)的图象关于y 轴对称； ②在区间(－∞，0)上，函数y ＝f(x)是减函数； ③函数y ＝f(x)的最小值为lg2；④在区间(1，＋∞)上，函数y ＝f(x)是增函数．x a y =x y alog -=1,0≠>a a 且三、解答题（本大题共6小题，满分70分，解答题写出必要的文字说明、推演步骤）。

2017-2018学年第一学期高一年级期中考试数学试卷命题人： 审题人：（考试时间：120分钟 试卷分值：150分）第Ⅰ卷一．选择题：本大题共12小题，每小题5分1．计算sin 600°=（ ）A ．B ．12-CD ．122．设0.335log 2,log 2,a b c π===，则（ ）A ．a c b >>B ．b c a >>C ．c b a >>D ．c a b >>3．已知a 是第二象限角，(P x 为其终边上一点，且cos α=x 等于（ ） AB ．C ．D ．4．函数()2312x f x x -⎛⎫=- ⎪⎝⎭的零点所在的区间为（ ） A ．()0,1 B ．()12， C ．()23， D ．()34-，5．对于定义在R 上的函数()f x ，则（ ）A ．若()()22f f -=，则()f x 是偶函数B ．若()()22f f -≠，则()f x 可能是偶函数C ． 若()()22f f -=，则()f x 是奇函数D ．若()()22f f -≠，则()f x 是非奇非偶函数6．已知2tan sin 3,02πααα⋅=-<<，则sin α等于（ ）A B ． C ．12 D ．12- 7．已知函数()2f x x x x =-+，则下列结论正确的是（ ）A ．()f x 是偶函数，递增区间是()0∞，B ．()f x 是偶函数，递减区间是()1-∞-，Ｃ．()f x 是奇函数，递增区间是()∞-，-1D ．()f x 是奇函数，递增区间是()-1，18．汽车的“燃油效率”是指汽车每消耗1升汽油行驶的里程．右图描述了甲、乙、丙三辆汽车在不同速度下的燃油效率情况．下列叙述中正确的是（ ）A ．消耗1升汽油，乙车最多可行驶5千米B ．以相同速度行驶相同路程，三辆车中，甲车消耗汽油最多C ．甲车以80千米/小时的速度行驶1小时，消耗10升汽油D ．某城市机动车最高限速80千米/小时，相同条件下，在该市用丙车比用乙车更省油9．函数()412x x f x x ⎛⎫-=- ⎪⎝⎭的图像（ ）对称 A ．关于原点 B ．关于直线y x = C ．关于x 轴 D ．关于y 轴10．函数()()f x x R ∈是奇函数，且对于任意x 都有()()4f x f x +=，已知()f x 在[]02，上的解析式()()1,01sin ,12x x x f x x x π⎧-≤≤⎪=⎨<≤⎪⎩，则154146f f ⎛⎫⎛⎫+= ⎪ ⎪⎝⎭⎝⎭（ ） A ．716 B ． 516 C ．1116 D ．131611．若函数()y f x =的图像上不同两点M N ，关于原点对称，则称点对[],M N 是函数()y f x =的对“优美点对”（点对[],M N 与[],N M 看作同一对“优美点对”），已知函数()ln 2,02,0x e x f x x x x ⎧>⎪=⎨+<⎪⎩，而此函数的“优美点对”有（ ）A ．3对B ．2对C ．1对D ．0对12．已知函数()10,0lg ,0x x f x x x -⎧≤=⎨<⎩，函数()()()()24g x f x f x m m R =-+∈，若函数()g x 有四个零点，则实数m 的取值范围是（ ）A ．[)lg5,4B ．[)34，C ．[){}34lg5，D ．(]4-∞，二．填空题：本题共4小题，每小题5分．13．函数ln y x 的定义域为14．幂函数()f x k x α=⋅的图像过点12⎛ ⎝⎭，则k α+= 15．已知函数()221x f x -=-在区间[]0m ，上的值域为[]0，3，则实数m 的范围是16．如图，已知正方形ABCD 的边长为6，边BC 平行于x 轴，顶点,,A B C 分别在函数13log a y x =，()232log log 1a a y x y x a ==>，的图像上，则是实数a 的值为三．解答题：解答应写出文字说明、证明过程或演算步骤．17．（本小题满分10分）已知集合{}{}12,1A x x B x m x m =-≤≤=≤≤+（1）当2m =-时，求()R C A B（2）若B A ⊆，求实数m 的取值范围18．化简求值（1）()13022720.259π⎛⎫-+ ⎪⎝⎭ （2）()222lg5lg8lg5lg 20lg 23++⋅+ 19．已知角θ的顶点在坐标原点，始边与x 轴正半轴重合，终边在直线20x y -=上，（1）求tan θ（2）求()()3sin cos 2sin sin 2πθπθπθπθ⎛⎫++- ⎪⎝⎭⎛⎫--- ⎪⎝⎭的值 20．某家用电器公司生产一款新型热水器，首先每年需要固定投入200万元，其次每生产1百台，需再投入0．9万元．假设该公司生产的该款热水器全年能全部售出，但生销售1百台需要付运费0．1万元．根据以往的经验，年销售总额()g x （万元）关于年产量x （百台）的函数为()214,040200800400.x x x g x x ⎧-≤≤⎪=⎨⎪>⎩ （1）将年利润()f x 表示为年产量x 的函数；（2）求该公司生产的该款热水器的最大年利润及相应的年产量．21．（本题满分12分）已知函数()122x x p f x q+-=+的定义域为R ，且()y xf x =是偶函数． （1）求实数,p q 的值；（2）证明：函数()f x 在R 上是减函数；（3）当132x ≤≤时，()()21320f mx x f x -++->恒成立，求实数m 的取值范围．22．已知函数()2f x x x a =-，期中a R ∈．（1）设0a >，函数()f x 在(),m n 上既有最大值又有最小值，请写出m 的取值范围（不必说明理由）．（2）当01x ≤≤时，求()f x 的最大值．。

2017-2018学年度高一(上)期中测试 数学试题考试范围：必修一+部分必修四一、选择题（每小题只有一个选项正确，每小题5分，共60分） 1. 设集合A={}14<<-x x ，B={}23<<-x x ，则B A ⋂等于（ ） A ．{}13<<-x x B ．{}21<<x x C ．{x | x>－3｝ D ．｛x | x<1｝ 2．下列各组函数中，表示同一函数的是（ ） A. 22lg ,lg y x y x == B. ()()()01,1f x x g x =-=C. ()()21,11x f x g x x x -==+- D. ()()f x g t t ==3．已知cos θ·tan θ<0，那么角θ是( ) A ．第一或第二象限角 B ．第二或第三象限角 C ．第三或第四象限角D ．第一或第四象限角4．已知函数f(x)＝⎩⎨⎧log 3x ，x ＞0，2x ，x ≤0，则⎥⎦⎤⎢⎣⎡⎪⎭⎫ ⎝⎛91f f ＝( ) A ．4 B.14 C ．－4 D ．－145．已知函数()26log f x x x=-，在下列区间中，包含()f x 零点的区间是（ ） A.()0,1 B.()1,2 C.()2,4 D.()4,8+6．设0.3777,0.3,log 0.3a b c ===，则c b a ,,的大小关系是 （ ）A ．c b a <<B ．a b c <<C ．b a c <<D ．a c b <<7.2510a b ==则11a b+=（ ）A ．-1B ．1C ．2D ．58．函数f(x)=x 2-2ax+2在区间(-∞，1］上递减，则a 的取值范围是（ ） A ．［1,+∞)B ．(-∞,-1］C ．(-∞,1］D ．［-1,+∞)9．幂函数()()215m f x m m x +=--在()0,+∞上单调递减，则m 等于（ ）A.3B.-2C.-2或3D.-3 10．已知2tan =θ，则θθθθ22cos 2cos sin 2sin +⋅+的值为（ ）A ．-1B ．1C ．2D ．511．已知偶函数f(x)在区间[0，＋∞)上单调递减，则满足不等式f(2x －1)>f(53)成立的x 的取值范围是( )A ．[－13，43)B ．[13，43)C ．(13，43)D ．(－13，43) 12．已知函数()()()()3512log 1a a x x f x a xx -+≤⎧⎪=⎨->⎪⎩对于任意21x x ≠都有()()02121<--x x x f x f 成立，则实数a 的取值范围是（ ） A. (]1,3 B. ()1,3 C. (]1,2 D. ()1,2二、填空题：（每小题5分，4个小题共20分）13. __________1470sin 0=14．已知扇形的面积为2，扇形圆心角的弧度数是4，则扇形的周长为________15．函数y ＝log 12(x 2－6x ＋17)的值域是________． 16．给出下列几种说法：①若,1log log 3=⋅b a a 则3b =；②若13a a -+=，则1a a --=③()(lg f x x =+为奇函数；④()1f x x=为定义域内的减函数； ⑤若函数()y f x =是函数x y a =（0a >且1a ≠）的反函数，且()21f =，则()12log f x x =，其中说法正确的序号为 .{}{}AC B A B A x x y x B x A R x ,,10)4(log ,162123⋃⋂-+-==<<=-求：已知集合三、解答题：（6个小题，共70分）17．计算下列各式的值：（10分）（1（2）()()2log 14839log 3log 3log 2log 22+++18. ．19.已知5sin 13α=,求cos ,tan αα的值.()1)a 0(),2(log 2log )(≠>--+=且已知函数a x x x f a a20.已知角α的终边任一点为P (k ，－3k ))0(≠k 求10sin α＋3cos α的值．21.已知函数f （x ）=110110+-x x（1）判断f （x ）的奇偶性； （2）讨论函数f （x ）的单调性.22.（1）求定义域；（2）判断的奇偶性，并说明理由；（3）求使的的解集．{(](](][)+∞⋃∞-==⋃=⋂=≤<>≥,73,3,10B A (4,7);B A 4,10B 10x 404-x 0x -10A C R 即得由参考答案选择题答案栏第II 卷（非选择题 ， 共 90 分）198(2)()()2log 14839log 3log 3log 2log 22+++()()2323223log 3log 3log 2log 21=+++ 233111log3log 3log 2log 21232⎛⎫⎛⎫=+++ ⎪⎪⎝⎭⎝⎭23535log 3log 211624⎛⎫⎛⎫=+=+= ⎪⎪⎝⎭⎝⎭9418.解：集合A={x|1<2x ﹣3＜16}={x|0≤x ﹣3＜4}={x|3<x ＜7}=(3，7），19解∵sin 0,sin 1αα>≠,∴α是第一或第二象限角,由22sin cos 1αα+=得2222512cos 1sin 11313αα⎛⎫⎛⎫=-=-= ⎪ ⎪⎝⎭⎝⎭（1）如果α是第一象限角,那么cos 0α>,于是12cos 13α=,从而sin 5135tan cos 131212ααα==⨯= （2）如果α是第二象限角,那么cos 0α<,于是12cos 13α=-,从而sin 5135tan cos 131212ααα⎛⎫==⨯-=- ⎪⎝⎭ 20解：设α终边上任一点为P (k ，－ 3k )，则r ＝k 2＋(－3k )2＝10|k |.当k >0时，r ＝10k ，∴sin α＝－3k 10k ＝－310，1cos α＝10 kk ＝10，∴10sin α＋3cos α＝－310＋310＝0；当k <0时，r ＝－10k ，∴sin α＝－3k －10k ＝310，1cos α＝－10k k ＝－10， ∴10sin α＋3cos α＝310－310＝0.综上，10sin α＋3cos α＝0.21.解：（1）∵m x ＞0，m x +1≠0恒成立，∴函数的定义域为R .∵函数的定义域为R ，关于原点对称，又∵f （－x ）=110110+---x x =110101+---xx=－f （x ），∴函数f （x ）是奇函数. （2）任取x 1＜x 2，则f （x 1）－f （x 2）=11011011+-x x －11011022+-x x =.()()110)110(101021221++-x x x x∵101x +1＞0，102x +1＞0，101x －102x ＜0，f （x 1）－f （x 2）＜0，即f （x 1）＜f （x 2） ∴函数f （x ）在R 上为增函数；.22. 解：（1）由题意得 ，即﹣2＜x ＜2．∴f （x ）的定义域为（﹣2，2）；（2）∵对任意的x ∈（﹣2，2），﹣x ∈（﹣2，2）f （﹣x ）=log a （2﹣x ）﹣log a （2+x ）=﹣f （x ），∴f （x ）=log a （2+x ）﹣log a （2﹣x ）是奇函数；（3）f （x ）=log a （2+x ）﹣log a （2﹣x ）＞0，即log 2（2+x ）＞log a （2﹣x ），∴当a ∈（0，1）时，可得2+x ＜2﹣x ，即﹣2＜x ＜0．当a ∈（1，+∞）时，可得2+x ＞2﹣x ，即x ∈（0，2）.。

2017—2018学年度第一学期期中考试题（卷）高一 数 学一、选择题（每小题5分，共60分） 1、①{}00∈，②{}0∅⊂，③{}{}0,1(0,1)⊆，④{}{}(,)(,)a b b a =.上面关系中正确的个数为（ ）A ．1B ．2C ．3D ．4 2、下列一定是指数函数的是（ ）A ．x y a =B ．(01)ay x a a =>≠且 C ．1()2x y = D ．(2)xy a a =-3、设集合{}02A x x =≤≤，{}12B y y =≤≤，在下图中能表示从集合A 到集合B 的映射的是（ ）4、下列运算结果中，正确的是（ ）A ．235a a a =B ．2332()()a a -=-C ．0(1)1a -= D ．236()a a -=5、函数121()log 1f x x =+的定义域为（ ）A ．(2,)+∞B ．(0,2)C ．(,2)-∞D ．1(0,)2 6、函数121log (1)y x =+-的图像一定经过点（ ）A ．（1，1）B ．（1，0）C ．（2，1）D ．（2，0）7、下列四组函数中表示同一函数的是（ ）A ．2(),()()f x x g x x == B ．22(),()(1)f x x g x x ==+C ． ()0,()11f x g x x x ==-+-D ． 2(),()f x x g x x ==8、已知3log 2a =，则33log 82log 6-=（ ）A ．2a -B ．52a -C ．23(1)a a -+D ．231a a --9、函数11y x =+的零点是（ ）A ．(1,0)-B ．1x =-C ．1x =D ．0x = 10、设集合{}2,0,1,3A =-，集合{},1B x x A x A =-∈-∉，则集合B 中元素的个数为（ ）A ．1B ．2C ．3D ．4 11、下列四个函数中在(0,)+∞上为增函数的是（ ）A ．()3f x x =-B ．2()(1)f x x =-C ．1()f x x =D ．2()2f x x x =+12、函数()lg 3f x x x =+-的零点所在的区间为（ ）A ．(0,1)B ．(1,2)C ．(2,3)D ．(3,)+∞ 二、填空题（共20分）13、集合A 含有两个元素3a -和21a -，则实数a 的取值范围是 . 14、设集合{}260A x x x =+-=，{}10B x mx =+=，则满足B A ⊆的实数m 的取值集合为 . 15、对数式(23)log (1)x x --中实数x 的取值范围是 .16、已知函数()y f x =是一次函数，且[]22()3()4104f x f x x x -=-+，则()f x = ..高一数学答题卡一、选择题（每小题5分，共60分） 1 2 3 4 5 6 7 8 9 10 11 12二、填空题（共20分）13、 14、 15、 16、 三、计算题 17、设全集为R ，{}37A x x =≤<，{}210B x x =<<，求：（1）A B I ； （2）cR A ； （3）cR )A B U18、比较下列各组数的大小： （1）1.9π-与31.9-；（2）230.7-与0.30.7；（3）0.40.6与0.60.4.19、求值：（1）222lg5lg8lg5lg20(lg2)3+++g；（2）lg182755 log9log32(31)log35log7--+-g20、设定义在[]2,2-上的奇函数()f x在区间[]0,2上单调递减，若(1)()f m f m-<，求实数m的取值范围.21、已知函数1 ()2f xx=-，（1）判断()f x在[]3,5上的单调性，并证明；（2）求()f x在[]3,5上的最大值和最小值.22、有甲乙两家健身中心，两家设备和服务都相当，但收费方式不同。

高一数学期中考试题一、选择题（本大题共12小题，每小题5分，共60分） 1、设集合{23}M x x =-<<，{1}N x x =≤-，则()R M N =I ð.（ ）A 、(3,)+∞B 、(2,1]--C 、(1,3)-D 、[1,3)-2、19sin()6π-的值为.（ ）A 、12B 、12-C 、32D 、32-3、若sin()0, tan()0πθπθ-<+>，则θ的终边在.（ ） A 、第一象限 B 、第二象限 C 、第三象限D 、第四象限4、设2212log , log , a b c πππ-===，则.（ ）A 、a b c >>B 、b a c >>C 、a c b >>D 、c b a >>5、下列函数中，满足“()()()f x y f x f y +=”的单调递增函数是.（ ）A 、3()f x x =B 、()3xf x =C 、12()f x x =D 、1()()2xf x = 6、函数238log y x x=-+的零点一定位于的区间是（ ）A 、（0，1）B 、（1，2）C 、（2，3）D 、（3，4）7、若lg lg 0a b +=（其中1,1a b ≠≠），则函数()x f x a =与函数()x g x b =的图象.（ ）A 、关于直线y x =对称B 、关于x 轴对称C 、关于原点对称D 、关于y 轴对称8、函数()sin()2f x x x π=⋅+是.（ ）A 、奇函数B 、偶函数C 、既是奇函数又是偶函数D 、非奇非偶函数9、函数5()sin(2)2f x x π=+的图象的一条对称轴方程是.（ ） A 、4xπ=-B 、2x π=-C 、8x π=D 、54x π= 10、若5sin()613πα+=-，且(,)2παπ∈，则2sin()3απ+=（ ）A 、513B 、513-C 、1213D 、1213-11、已知函数, 0()(2)2, 0x a x f x a x a x ⎧<=⎨-+≥⎩，若对任意12x x ≠，都有1212()()0f x f x x x -<-成立，则实数a 的取值范围是.（ ）A 、1(0,]2 B 、1(,1)2C 、(1,2)D 、(1,2)-12、函数()(1cos )sin f x x x =-在[,]ππ-上的图象大致为（ ）二、填空题（本大题共4小题，每小题5分，共20分。

贵池区2017～2018学年度第一学期期中教学质量检测高一数学试卷一.选择题（本大题共12个小题，每小题5分，共60分。

下列每小题所给选项只有一项符合题意，请将正确答案的序号填涂在答题卡上）1.1.已知全集（）A. B. C. D.【答案】B【解析】由于，所以，结合可得，故选B.2.2.已知集合，，则（）A. B. C. D.【答案】C【解析】∵，∴，即，结合得，故选C.点睛：研究一个集合，我们首先要看清楚它的研究对象，是实数还是点的坐标还是其它的一些元素，这是很关键的一步.第二步常常是解一元二次不等式，我们首先用十字相乘法分解因式，求得不等式的解集.在解分式不等式的过程中，要注意分母不能为零.解指数或对数不等式要注意底数对单调性的影响. 在求交集时注意区间端点的取舍. 熟练画数轴来解交集、并集和补集的题目.3.3.函数 , [0,3]的值域为（）A. [0,3]B. [1,3]C. [-1,0]D. [-1,3]【答案】D【解析】∵，∴函数开口向上，对称轴为，∴函数在上单调递减，单调递增，∴当时，函数值最小，最小值为；当时，函数值最大，最大值为3，即函数的值域为，故选D.4.4.三个数，，之间的大小关系是（）A. B. C. D.【答案】C【解析】∵，，∴故选C点睛：本题考查了指数函数的性质和对数函数的性质及其应用，属于基础题，解答本题的关键熟记指数函数与对数函数的图象与性质，利用指数函数与对数函数的性质，判定的范围，不明确用中间量“1”，“0”进行传递比较，从而得到的大小关系．5.5.若lg2＝a，lg3＝b，则＝（）A. B. C. D.【答案】D【解析】∵，，∴，故选D.6.6.已知函数在区间上是增函数，则实数的取值范围是( )A. B. C. D.【答案】B【解析】二次函数的对称轴为；∵该函数在上是增函数；∴，∴，∴实数的取值范围是，故选B.7.7.若，则的表达式为（）A. B. C. D.【答案】D【解析】试题分析：令，于是有，分别用、替换中的、得：最后仍用作自变量，得故选D.考点：1、指数、对数式的互化；2、换元法求函数的解析式.8.8.当时,在同一坐标系中,函数的图象是( )A. B. ..................C. D.【答案】A【解析】∵函数与可化为函数，底数，其为增函数，又，当时是减函数，两个函数是一增一减，前增后减，故选A.9.9.已知函数，那么的值为 ( )A. B. C. D.【答案】B【解析】，那么，故选B.10.10.在直角坐标系中，函数的零点大致在下列哪个区间上（）A. B. （1，2） C. D.【答案】C【解析】∵函数在内为连续函数且单调递增，，，，故由零点存在定理可得函数的零点大致在上，故选C.11.11.若不等式对于一切恒成立，则的最小值是（）A. 0B. －2C.D. －3【答案】C【解析】试题解析：∵对称轴为（1）当时，函数在为增函数，在成立（2）当时，，解得成立（3）当时，，解得∴的最小值是考点：本题考查不等式恒成立问题点评：解决本题的关键是恒成立问题转化成对轴定区间问题12.12.已知是定义在R上不恒为零的偶函数，且对任意，都有，则的值是（）A. 0B.C. 1D.【答案】A【解析】试题分析：因为函数f(x)是定义在R上不恒为零的偶函数，那么可知f(x)=f(-x),同时又xf(x+1)=(x+1)f(x),那么可知函数令x=-,则可知-f（）=f(-),解得f（）=0,将x=,代入得到f(0,同理依次得到f()=0，故选A.考点：本题主要考查了函数的奇偶性的运用，以及函数值的求解。