基于matlab的平面四连杆机构设计以及该机构的运动分析
- 格式:docx
- 大小:155.36 KB
- 文档页数:8

基于matlab的四杆机构运动分析一、四杆机构基本概念四杆机构是一种通过变换连杆长度,改变机构运动形态的机械系统。
四杆机构通常由固定连杆、推动连杆、连接杆和工作连杆四个连杆组成,其中固定连杆和推动连杆固定不动,连接杆和工作连杆则沿固定轴线的方向做平动或旋转运动。
四杆机构的基本构造如下图所示:四杆机构的四个连杆的长度和构造参数,以及驱动机构的运动决定了机构的运动特性。
在进行四杆机构运动分析时,需要通过求解运动学关系式和动力学方程,得到连杆的运动规律和力学特性。
二、四杆机构运动学分析1.运动学基本方程四杆机构的运动学分析基本方程是连杆长度变化的定理,即:l₁²+l₂²-2l₁l₂cosθ₂=l₃²+l₄²-2l₃l₄cosθ₄其中,l₁,l₂分别为固定连杆和推动连杆长度;l₃,l₄分别为连接杆和工作连杆长度;θ₂,θ₄分别为推动连杆和工作连杆的夹角。
2.运动学求解方法根据四杆机构运动学基本方程,可以求解机构中任意连杆的角度和位置,从而分析机构运动规律。
在matlab程序中,运动分析可以采用分析法或图解法。
分析法通常采用向量法或坐标法,即将四杆机构中各连杆和运动副的运动量表示为向量或坐标,然后根据连杆长度变化的定理,求解四个未知角度θ₁、θ₂、θ₃、θ₄。
图解法则先通过画图确定机构的运动规律,在图上求解连杆的角度。
比如可以采用伯格(Bourgeois)图法或恰普利恩(Chaplygin)图法等。
四杆机构动力学分析基本方程包括平衡方程和力平衡方程。
平衡方程:当四杆机构处于平衡状态时,连杆的受力关系可以表示为:ΣF=0其中ΣF为各连杆受力的合力。
ΣF=m×a其中,m为每个连杆的质量,a为连杆的加速度。
四杆机构动力学求解方法以matlab为工具,可借助matlab的求解器完成求解。
具体可以利用matlab的优化工具箱、控制工具箱和系统动态学工具箱等,来实现机构模型的动态模拟、仿真和优化设计。

基于MATLAB的四杆机构运动分析石河子大学毕业设计(论文)题目:基于MATLAB的四杆机构运动分析与动画模拟系统院(系):机械电气工程学院专业:机械设计制造及其自动化学号: 2002071189姓名:娄元建指导教师:葛建兵完成日期:二零零六年五月基于MATLAB的四杆机构运动分析与动画模拟系统[摘要] 本文介绍MATLAB开发机构运动分析和动画模拟系统的方法,并且利用MATLAB软件实现平面四杆机构的运动仿真。
以MATLAB程序设计语言为平台,将参数化设计与交互式相结合,设计出四杆机构仿真系统,能够实现四杆机构的参数化设计,并且能够进行机构的速度和加速度分析。
系统具有方便用户的良好界面,并给出界面设计程序,从而使机构分析更加方便、快捷、直观和形象,设计者只需输几参数就可得到仿真结果,为平面四杆机构的设计与分析提供一条便捷的途径。
[关键词] 机构;运动分析;动画模拟;仿真;参数化;MATLABAbstract: The kinematical analysis and animation method of the mechanism using MATLAB was discussed in the paper , and the kinematic simulation of planar four—bar mechanism with software MATLAB . And emulational system was developed , the system adopted Matlab as a design , It combined parametic design with interactive design and had good interface for user , that can realize parametic design of four-bar mechanism , also to make real speed and acceleration of mechanism . The emulational resut was obtained as soon as input parameters was imported and the devisers can make decision –making of modification by the comparing emulational result with design demand , which give another efficacious way for the design and analysis of planar four—bar mechanism.Key words:Mechanism;Kenimatical analysis;Animation;Emulation ;parametic ;MATLAB目录第一章绪论 (1)1.1 本论文的研究意义 (1)1.2 本文的研究任务 (2)第二章四杆机构运动学 (3)2.1 四杆机构简介 (3)2.2 四杆机构的综合概述 (4)第三章软件介绍 (6)3.1 MATLAB的简介 (6)3.2 Matlab/Simulink (6)3.3 SimMechanics机构系统应用 (7)第四章机构运动分析的实现过程 (9)4.1 机构简图的参数化绘制方法 (9)4.2 平面图形运动的动画模拟方法 (9)4.3 机构运动的数学模型 (10)4.4 用户界面设计 (11)4.5 程序运行 (12)第五章连杆机构的运动仿真 (16)5.1 平面连杆机构的运动分析 (16)5.2 几种仿真软件的探索 (17)的图象处理功能 (17)基于PRO/M的四杆机构的仿真 (19)5.3 用SimMechanics来实现的仿真 (19)第六章运算程序 (22)6.1四杆机构位置问题的Matlab求解 (22)6.2四杆机构的位移、速度、加速度的求解程序 (23)6.3定义求解方程的程序 (25)6.4四杆机构的绘制及其动画程序 (25)6.5绘制三条曲线的命令 (27)6.6参数调整的程序 (27)第七章结论 (28)参考文献: (29)第一章绪论1.1 本论文的研究意义随着计算机、智能材料等科学技术的飞速发展,人类正在经理一场新的产业革命。

基于matlab的连杆机构设计————————————————————————————————作者: ————————————————————————————————日期:目录1平面连杆机构的运动分析 (1)1.2 机构的工作原理 (1)1.3机构的数学模型的建立 (1)1.3.1建立机构的闭环矢量位置方程...................................................11.3.2求解方法.....................................................................22基于MATLAB程序设计 (4)2.1 程序流程图 (4)2.2 M文件编写 (6)2.3程序运行结果输出 (7)3 基于MATLAB图形界面设计 (11)3.1界面设计……………………………………………………………………………………………113.2代码设计……………………………………………………………………………………………124 小结 (17)参考文献 (18)1平面连杆机构的运动分析1.1 机构运动分析的任务、目的和方法曲柄摇杆机构是平面连杆机构中最基本的由转动副组成的四杆机构,它可以用来实现转动和摆动之间运动形式的转换或传递动力。
对四杆机构进行运动分析的意义是:在机构尺寸参数已知的情况下,假定主动件(曲柄)做匀速转动,撇开力的作用,仅从运动几何关系上分析从动件(连杆、摇杆)的角位移、角速度、角加速度等运动参数的变化情况。
还可以根据机构闭环矢量方程计算从动件的位移偏差。
上述这些内容,无论是设计新的机械,还是为了了解现有机械的运动性能,都是十分必要的,而且它还是研究机械运动性能和动力性能提供必要的依据。
机构运动分析的方法很多,主要有图解法和解析法。
当需要简捷直观地了解机构的某个或某几个位置的运动特性时,采用图解法比较方便,而且精度也能满足实际问题的要求。

基于MATLAB的平面连杆机构运动分析及动画摘要建立了平面机构运动分析的数学模型,利用MATLAB进行了编程并设计了计算交互界面进而求解,为解析法的复杂计算提供了便利的方法,此方法也同样适用于复杂平面机构的运动分析,并为以后机构运动分析的通用软件的设计提供了基础。
建立了平面四杆机构运动分析的数学模型,以MATLAB 程序设计语言为平台,将参数化设计与交互式相结合,设计了平面四杆机构仿真软件,该软件具有方便用户的良好界面,并给出界面设计程序,从而使机构分析更加方便、快捷、直观和形象。
设计者只需输入参数就可得到仿真结果,再将运行结果与设计要求相比较,对怎样修改设计做出决策,它为四杆机构设计提供了一种实用的软件与方法。
以一种平面六连杆为例建立了平面多连杆机构的运动分析数学模型,应用MATLAB 软件进行了优化设计和仿真分析,为机构优化设计提供了一种高效、直观的仿真手段,提高了对平面多连杆机构的分析设计能力。
同时,也为其他机构的仿真设计提供了借鉴。
关键词:解析法,平面连杆机构,MATLAB,运动分析,运动仿真Based on the MATLAB Planar Linkage Mechanism MotionAnalysis and AnimationABSTRACTThis article established the kinematical mathematic model of the planar mechanism ,which is programmed and solved with designing the mutual interface of the calculation by MATLAB.This convenient method is provided for the complicated calculation of the analysis and also applicable to the kinematical analysis of the complex planar mechanism.A mathematical model of motion analysis was established in planar four- linkage ,and emulational software was developed. The software adopted MATLAB as a design language. It combined parametric design with interactive design and had good interfacefor user. Thus,it was faster and more convenient to analyse linkage. The emulational result was obtained as soon as input parameters was imported and the devisers can make decision-making of modification by the comparing emulational result with design demand. It provides an applied software and method for linkage.This paper took a planar six-linkage mechanism as a example to set up the mathematics model of planar multi-linkage mechanisms, and made the optimization design and simulation by the MATLAB software. It gave a efficiently and directly method to optimization design of mechanisms, and improved the ability of analyzing and designing the planar multi-linkage mechanisms. At the same time, it also provides a use for reference to the design and simulation for other mechanisms.KEY WORDS: analysis, planar linkage mechanisms, MATLAB, kinematical analysis, kinematical simulation目录1.1 平面连杆机构的研究意义 (1)1.2 平面连杆机构的研究现状 (1)1.3 MATLAB软件介绍 (2)1.3.1 MATLAB简介 (2)1.3.2 MATLAB软件的特点 (4)1.3.3 用MATLAB处理工程问题优缺点 (5)第2章平面机构运动分析的复数矢量解 (6)第3章平面四杆机构运动分析 (8)3.1 铰链四杆机构曲柄存在条件 (8)3.2 平面四杆机构的位移分析 (9)3.3 平面四杆机构的速度分析 (14)3.4 平面四杆机构的加速度分析 (15)第4章基于MATLAB的平面四杆机构运动分析 (17)4.1 基于MATLAB的平面四杆机构运动参数输入界面 (17)4.2 基于MATLAB的平面四杆机构运动参数计算 (21)4.3 基于MATLAB的平面四杆机构运动分析界面 (24)4.4 基于MATLAB的平面四杆机构运动仿真 (26)4.5 基于MATLAB的平面四杆机构运动参数清空及退出 (30)第5章平面六杆机构运动分析 (32)5.1 构建平面六杆机构数学模型 (32)5.2 平面六杆机构的运动分析 (33)5.2.1 曲柄导杆机构的运动分析 (33)5.2.2 摆动滑块机构的运动分析 (36)第6章基于MATLAB的平面六杆机构运动分析 (39)6.1 基于MATLAB的平面六杆机构运动参数输入界面 (39)6.2 基于MATLAB的平面六杆机构运动参数计算 (45)6.3 基于MATLAB的平面六杆机构运动分析界面 (49)6.4 基于MATLAB的平面六杆机构运动仿真 (52)6.5 基于MATLAB的平面六杆机构运动参数清空及退出 (56)结论 (57)参考文献 (59)第1章前言1.1 平面连杆机构的研究意义机构运动分析是不考虑引起机构运动的外力的影响,而仅从几何角度出发,根据已知的原动件的运动规律(通常假设为匀速运动),确定机构其它构件上各点的位移、速度、加速度,或构件的角位移、角速度、角加速度等运动参数。
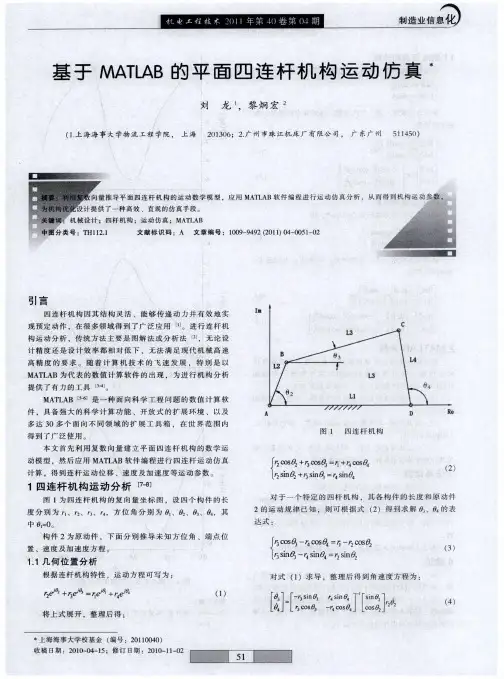


基于MATLAB的四连杆机构运动分析软件设计开题报告云南农业大学本科生毕业设计开题报告工程技术学院车辆工程专业( 工科) 2008级设计题目:基于MATLAB的四连杆机构运动分析软件设计人机交互界面的设计云南农业大学教务处制2011年10月8日云南农业大学毕业设计开题报告1(本课题所涉及的问题在国内(外)的研究现状综述目前,MATLAB软件是功能强大的科学计算软件,被国内外高校和科研单位所使用。
尤其是基于矩阵运算的数据处理,还可用符号运算计算解析解;还可以实现数值分析、图像处理等若干个领域的计算和图形显示功能。
在工程技术界,MATLAB 也被用来解决一些实际课题和数学模型问题。
典型的应用包括数值计算、算法预设计与验证,以及一些特殊的矩阵计算应用,如自动控制理论、统计、数字信号处理(时间序列分拆)等。
平面连杆机构是一种应用十分广泛的机构。
对它的分析及设计一直是机构学研究的一个重要课题。
但传统方法对于常见的连杆机构的运动学、动力学分析仍然是非常繁琐,以至于很难对它进行深入的研究,如果建立一个连杆机构的仿真系统,使设计人员在进行设计时,从复杂的机构分析和烦琐的计算中摆脱出来,集中精力从事于创新工作,那将是很有意义的。
基于这样一种考虑,本课题尝试建立一个平面连杆机构的运动学仿真系统。
应用Matlab/Simulink对机构领域中应用广泛的基本机构——双曲柄机构、曲柄摇杆机构、曲柄滑块机构等的连杆点轨迹作仿真,该方法编程工作量小、轨迹图形显示便捷,所建模型只需作少量更改即可适应四杆机构的不同特征值,并可推广至多杆机构情况。
建立四杆机构的优化设计模型,用 MATLAB 优化工具箱实现四杆机构的优化设计及仿真,得到的优化结果有足够的精度,能满足设计需求,同时表明MATLAB 优化工具箱在四杆机构优化设计及其相关问题中具有较好的应用前景。
2(本人对课题提出的任务要求及实现预期目标的可行性分析由于连杆机构的性能受机构上繁多的几何参数的影响,呈复杂的非线性关系,无论从性能分析上还是性能综合上都是一个比较困难的工作。

……………………. ………………. …………………毕业论文基于MATLAB的平面四杆机构运动分析院部机械与电子工程学院装订线……………….……. …………. …………. ………摘要 (I)Abstract (II)1 绪论 (1)2 平面四杆机构运动分析 (2)2.1 平面四杆机构简介 (2)2.2 平面四杆机构类型分析 (3)2.3 建立平面四杆机构的数学模型 (4)2.3.1 建立平面四杆机构的封闭矢量位置方程式 (4)2.3.2 运用矢量法和矩阵法求解封闭矢量方程式 (5)2.3.3 求解过程涉及的数学、物理计算方法 (6)3 基于MATLAB 的运动分析程序设计 (7)3.1 MATLAB简介 (7)3.2 程序设计流程 (8)3.3 编写程序的M文件 (10)3.3.1编写fun函数 (10)3.3.2编写主程序 (10)3.4 程序运行输出结果 (12)4 基于MATLAB的GUI分析系统设计 (15)4.1 GUI简介 (15)4.2 GUI界面设计 (15)4.3 GUI代码编写 (16)4.3.1 Edit Text代码编写 (16)4.3.2 Pop-up Menu代码编写 (16)4.4 GUI分析系统运行效果 (17)5 结论 (18)参考文献 (20)致谢 (20)附录 (20)附录一主函数程序代码 (20)附录二popupmenu4_Callback函数下程序代码 (23)Abstract (II)1 Introduction (1)2 The analysis of motion for planar four-bar mechanism (2)2.1 Intoduction to the planar four-bar mechanism (2)2.2 Analysis for the types of planar four-bar mechanism (3)2.3 Build the mathematical model of planar four-bar mechanism (4)2.3.1 Build the closed position vector equation for planar four-bar mechanism (4)2.3.2 Apply the vector & matrix method to solve the closed vector equation (4)2.3.3 Mathematical & physical calculation method involved in the solving process (5)3 The program design for the motion analysis based on MATLAB (7)3.1 Introduction to MATLAB (7)3.2 The program design process (7)3.3 Write the M-file for program (9)3.3.1 Write the fun function (9)3.3.2 Write the main function (9)3.4 The output of running the program (11)4 The design of GUI analysis system based on MATLAB (14)4.1 Introducton to GUI (14)4.2 The interface design of GUI (14)4.3 Write the GUI code (15)4.3.1 Write the Edit Text code (15)4.3.2 Write the Pop-up Menu code (15)4.4 The running effect of the GUI analysis system (16)5 Conclusion (19)References (20)Acknowledgement (21)Appendix (22)Appendix I The main function code (22)Appendix II The popupmenu4_Callback function code (25)基于MATLAB的平面四杆机构运动分析摘要:建立以平面四杆机构为研究对象的数学模型,以MATLAB软件为载体,利用MATLAB矩阵数据分析处理功能,设计了平面四杆机构运动分析程序。

第14卷第2期2019年6月Vol.14No.2Jun.2019陕西工业职业技术学院学报Journal of Shaanxi Polytechnic Institute基于MATLAB给定连杆预定位置的四杆机构设计韩二豹(陕西工业职业技术学院土木工程学院,陕西咸阳712000)摘要:连杆机构是一种典型的机械机构,运动设计是一个比较复杂和困难的问题,给定连杆预定位置的四杆机构的设计常用的设计方法主要为解析法。
本文以MATLAB语言为基础,利用计算机对给定连杆预定位置的四杆机构进行设计。
结果表明,此方法设计过程简洁,结果合理,准确,效率高。
关键词:四杆机构;MATLAB;预定位置中图分类号:TB121文献标识码:A文章编号=9459-2019(2)-0006-03A MATLAB-based Design of Four-bar Linkage with PresetPosition of Connecting RodHan Erbao(School of Civil Engineering,Shaanxi Polytechnic Institute,Xianyang Shaanxi712000,China)Abstract:Connecting rod is a typical mechanical linkage and its motion design is complex and ually, analytical method is the main method used in the design of four一bar linkage with preset position of connecting rod. In the study,a MATLAB一based design of four bar mechanism was made to link the preset position given by com・puter.The results show that the design process is simple Key words:Four bar linkage;MATLAB;Preset positiono引言MATLAB是一种高级技术语言和发展环境,特提供了一个人机交互的系统环境,并以矩阵作为基础的数据结构,节省编程时间,语法简单、容易掌握、调试方便,可以设置调试断点、快速查找程序错误等优点,可以将使用者从繁重重复的计算中解脱出来,已经被大家认可和广泛使用,充分展现其高效、直观、简单的特点⑷。

MATLAB 解题1.设有如图所示四杆机构,其中→R 4为机架(常矢),→R1为主动杆,→R3为从动杆,→R 2为连杆。
设在某一工作位置时各杆的角速度和角加速度分别取如下值:ω1=20 rad/s, ε1= 0;ω2=8.5 rad/s, ε2=-10 rad /s 2;ω3=13 rad/s, ε3=-160rad /s 2.试根据上述要求确定该机构尺寸比。
根据图(2),回路闭合方程可写为:→R 1 +→R 2 +→R 3=-→R 4 回路闭合方程对时间求导一次,利用(6)式,可得: 图2 ω1→R 1 +ω2→R 2 +ω3→R 3 = 0回路闭合方程对时间求导两次,利用(7)式,可得c 1→R 1 + c 2 →R 2 + c 3→R 3 = 0其中 c 1=ε1+j ω12 , c 2=ε2+j ω22, c 3=ε3+j ω32解关于→R 1 ,→R 2 和→R 3的线性方程组:⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡-=⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎣⎡⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡→→→001111321321321R R R c c c ωωω→R 4 (13) 可得 →R 1=DDx →R 4, →R 2=DDy →R 4 , →R 3=DDz →R 4注意到上述解中含有相同的分母D,它是一个复数,不妨记为D =k<j α|,被它除的效果是把各杆的长度都缩小k 倍,同时方向都顺时针旋转α角,相当于机构不动,坐标轴逆时针旋转α角。
设计机构时,重要的是机构的形状与尺寸比例。
基于这种考虑,可设→R 4 / D =1,则有→R 1=D x =32320111c c ωω-=1230-j497.3 ; →R 2= D y =311030111c c ωω-=-3200-j1820 ; →R 3= D z =001112121c c ωω-=200+j1955 . 于是:→R 4 = -(→R 1 +→R 2+→R 3) = 1770+j362.3在坐标系上作出上述各杆矢量图,根据各杆矢量图作出机构的闭合矢量图,再根据实际需要选定某一杆长度,其它各杆长度按图比例相似放大。

在MATLAB环境下开发平面连杆机构运动分析系统摘要建立了铰链四杆机构运动分析的数学模型 ,以MATLAB程序设计语言为平台 ,将参数化设计与交互式相结合 ,设计了铰链四杆机构分析软件 ,该软件具有方便用户的良好界面 ,并给出界面设计程序 ,从而使机构分析更加方便、快捷、直观和形象.设计者只需输入参数就可得到分析结果 ,再将运行结果与设计要求相比较 ,对怎样修改设计做出决策.它为四杆机构设计提供了一种实用的软件与方法.关键词:平面四杆机构,MATLAB软件,运动分析,分析THE DEVELOPMENT OF SYSTEM FOR ANALYSIS OF MOTION IN PLANE FOUR BAR MECHANISM BASED ONMATLAB SOFTWAREAbstractA mathematical model of motion analysis was established in planefour - linkage , and analytical software was developed. The software adopted Matlab as a design language. It combined parametric design with interactive design and as input parameters was imported and the devisers can make decision - making of modification by the comparing analytical result with design demand. It provides an applied software and method for linkage.Key words:Plane Four Bar Mechanism, MATLAB, Analysis of Motion, Analyze目录1 绪论 (1)2 平面连杆机构的设计分析 (4)2.1平面四连杆机构的运动分析 (4)2.2 机构的数学模型的建立 (4)2.2.1 建立机构的闭环矢量位臵方程 (5)2.2.2 求解方法 (7)3 基于MATLAB程序设计 (8)3.1 程序流程 (8)3.2M文件编写 (8)3.3程序运行结果输出 (12)4 基于MATLAB图形界面设计 (23)4.1界面设计 (23)4.2代码设计 (24)5 结论.......................................................................................... 错误!未定义书签。
基于MATLAB/Simulink的平面四连杆机构仿真一、题目及自由度分析如图1所示,该平面四杆机构中有三根运动的均质钢杆,其中有两根钢杆的一端与接地点连接,第三根杆就与这两根杆剩下的端点连接起来,两个接地点就可认为是第四杆,机构中相关尺寸如图2所示。
计算结构自由度,三个运动杆被限制到平面内运动,因此每个杆都有两个移动和一个转动,即在考虑约束之前,自由度为:3×(2+1)=9但是由于每个杆都受到约束,所以并不是每个自由度都是独立的。
在二维状态下,刚体间的连接或者刚体与接地点的连接就会增加两个约束。
这样就会使得刚体其中一端不能够作为独立的自由运动点,而是要受到邻近刚体的约束。
该题中有四个刚体--刚体或刚体—接地点的连接,这就隐含8个约束。
那么最后的自由度为9-8=1.虽然有四个转动自由度,但是,其中三个都是非独立的,只要确定其中一个,就可确定其余三个。
二、模型建立及参数设置1应用MATLAB/Simulink建立初始模型2在初始模型的基础上添加Joint Sensor模块3依题意设置相关参数⑴配置Ground模块由图2可得系统的基本尺寸为:①固定构件长86.7厘米②Ground_1表示接地点,在World CS坐标轴原点右边43.3cm处③Ground_2表示接地点,在World CS坐标轴原点左边43.4cm处④最下端的铰处于X-Z平面内原点以上4cm图5Ground_1模块参数设置图6Ground_2模块参数设置4配置Joint模块三个没有接地的联杆都是在X-Y平面内的,所以Revolute轴必须是Z轴。
⑴依次打开Revolute参数对话框,保持默认值,即Axis of rotation[x y z]默认设置为[001],Reference csys都是WORLD。
图7Revolute坐标设置⑵根据连接情况依次设置Revolute参数对话框中的Connection parameters参数图8Revolute模块参数对话框Connection parameters参数图9Revolute模块参数对话框Connection parameters参数图10Revolute模块参数对话框Connection parameters参数图11Revolute模块参数对话框Connection parameters参数5配置Body模块本题中Body模块(即Bar)定位方式不是直接相对于WORLD坐标系统,而是采用相对坐标形式,Bar1的CS1相对于Ground_1,Bar2的CS1相对于Bar1,以此类推。
一、课程设计容及要求:1.对连杆机构运动工作原理及运动参数有一定理解2.掌握MATLAB基本命令3.了解MATLAB编程的基本知识,并能编写简单M文件4.了解MATLAB图形界面设计的基本知识5.课程设计说明书:应阐述整个课程设计容,要突出重点和特色,图文并茂,文字通畅。
应有目录、摘要及关键词、正文、参考文献等容,字数一般不少于6000字。
二、主要参考资料有关复杂刀具参数计算及结构设计、机械制造工艺与设备的手册与图册。
三、课程设计进度安排指导教师(签名):时间:教研室主任(签名):时间:院长(签名):时间:目录1平面连杆机构的运动分析 (1)1.1 机构运动分析的任务、目的和方法 (1)1.2 机构的工作原理 (1)1.3 机构的数学模型的建立 (1)1.3.1建立机构的闭环矢量位置方程 (1)1.3.2求解方法 (2)2 基于MATLAB程序设计 (4)2.1 程序流程图 (4)2.2 M文件编写 (6)2.3 程序运行结果输出 (7)3 基于MATLAB图形界面设计 (11)3.1界面设计 (11)3.2代码设计 (12)4 小结 (17)参考文献 (18)1平面连杆机构的运动分析1.1 机构运动分析的任务、目的和方法曲柄摇杆机构是平面连杆机构中最基本的由转动副组成的四杆机构,它可以用来实现转动和摆动之间运动形式的转换或传递动力。
对四杆机构进行运动分析的意义是:在机构尺寸参数已知的情况下,假定主动件(曲柄)做匀速转动,撇开力的作用,仅从运动几何关系上分析从动件(连杆、摇杆)的角位移、角速度、角加速度等运动参数的变化情况。
还可以根据机构闭环矢量方程计算从动件的位移偏差。
上述这些容,无论是设计新的机械,还是为了了解现有机械的运动性能,都是十分必要的,而且它还是研究机械运动性能和动力性能提供必要的依据。
机构运动分析的方法很多,主要有图解法和解析法。
当需要简捷直观地了解机构的某个或某几个位置的运动特性时,采用图解法比较方便,而且精度也能满足实际问题的要求。
基于matlab GUI的平面四杆机构的运动分析一、目的通过matlab对平面四杆机构进行运动仿真,并以GUI界面方式实现输入输出的参数化,对平面四杆机构进行位置分析、速度分析、加速度分析和静力学分析。
此外,通过动画演示,更加形象直观地观察机构的运动过程。
最后,将程序编译成.exe独立可执行文件,可以在其它没有安装matlab的机器上运行。
二、设计思路通过matlab的GUI功能模块,创建一个图形用户界面,在自动生成的代码框架中对初始化函数和回调函数等进行编辑,建立与控件相关联的程序:控件属性、位置分析、速度分析、加速度分析、静力学分析、动画演示等。
图1是平面四杆机构的示意图,输入角q的运动规律为q=pi/50*t^2+q0,r1、r2是从动角。
对t时刻沿着杆长距离原点A的任意一点进行分析。
注意:输入输出角的单位为度,时间t的取值范围为0:0.05:10,任意点lx的取值范围为0~a1+a2+a3,估算的从动角r1、r2的迭代初始值不能偏离平衡位置太大。
图1、平面四杆机构示意图三、设计流程1、通过GUI模块创建图形用户界面命令方式:在Matlab命令窗口键入>>guide;菜单方式:在Matlab的主窗口中,选择File>New>GUI命令,就会显示GUI的设计模板。
如图1所示。
图2、创建图形界面2、设计图形界面在创建之后的图形界面中插入坐标轴axes,静态文本框static text,编辑文本框edit text,按钮push button等等。
如图所示。
图3、图形界面设计3、编辑回调函数1)位置分析:输入角的函数为:q=pi/50*t^2+q0。
在时间t=0~10s内,每一个时间点估算两个初始从动角,根据牛顿-拉普森迭代得到准确的机构位置。
10s刚好主动角经历了360度,记录每一时刻的位置,便可以动画演示。
2)速度分析:输入角速度为:dq=pi/25*t。
选择杆件上的任意一点(坐标表示为质点沿着杆件到原点A的距离)做分析,正确表达出角速度系数和速度系数,便可以求出质点的速度。
基于matlab的4连杆机构设计第一篇:基于matlab的4连杆机构设计目录1平面连杆机构的运动分析 (1)1.2 机构的工作原理................................................................................................1 1.3 机构的数学模型的建立.......................................................................................1 1.3.1建立机构的闭环矢量位置方程...................................................1 1.3.2求解方法.....................................................................2 2 基于MATLAB程序设计..........................................................................................4 2.1 程序流程图 (4)2.2 M文件编写 (6)2.3 程序运行结果输出.............................................................................................7 3 基于MATLAB图形界面设计....................................................................................11 3.1界面设计 (11)3.2代码设计 (12)4 小结 (17)参考文献………………………………………………………………………………………………18平面连杆机构的运动分析1.1 机构运动分析的任务、目的和方法曲柄摇杆机构是平面连杆机构中最基本的由转动副组成的四杆机构,它可以用来实现转动和摆动之间运动形式的转换或传递动力。
MATLAB软件由美国MathWorks公司于1982年推出,经过十几年的发展和竞争,现已成为国际公认的最优秀的科技应用软件之一。
MATLAB提供了强大的矩阵处理和绘图功能。
它主要包括两部分内容:核心函数和工具箱。
Matlab编程代码接近数学推导公式,简洁直观,与科技人员的思维方式和书写习惯相适应,操作简易,人机交互性能好,且可以方便迅速地用三维图形、图像、声音、动画等表达计算结果,拓展思路。
编制相应的M函数文件。
Pos.m用于求解位置、角度和角加速度。
th1为初始角度,w1为杆1角速度,其余为杆长。
将课本P35(i)、(ii)、(iii)式用MATLAB语言表述,即可编制为四杆机构求解函数文件pos.m。
function f=pos(th1,w1,l1,l2,l3,l4)syms x21 x31 x22 x32x1=th1*pi/180;x11=cos(x1);x12=sin(x1);eq1=l1*x11+l2*x21-l3*x31-l4;eq2=l1*x12+l2*x22-l3*x32;eq3=x21^2+x22^2-1;eq4=x31^2+x32^2-1;s=solve(eq1,eq2,eq3,eq4,x21,x22,x31,x32);s1=double(s.x21); s2=double(s.x22);s3=double(s.x31); s4=double(s.x32);x2=(acos(s1(1,1)))/pi*180;x3=(acos(s3(1,1)))/pi*180;A=[l2*s2(1,1),-l3*s4(1,1);l2*s1(1,1),-l3*s3(1,1)];B=[-l1*x12;-l1*x11];w=A\(w1*B);w2=w(1,1);w3=w(2,1);C=[-l2*w(1,1)*s1(1,1),l3*w(2,1)*s3(1,1);l2*w(1,1)*s2(1,1),-l3*w(2,1)*s4(1,1)];D=[w(1,1);w(2,1)];E=[-l1*w1*x11;l1*w1*x12];F=[l2*s2(1,1),-l3*s4(1,1);l2*s1(1,1),-l3*s3(1,1)];t=F\(C*D+w1*E);a2=t(1,1);a3=t(2,1);l1=cat(1,th1,w1,0);l2=cat(1,x2,w2,a2);l3=cat(1,x3,w3,a3);f=(cat(2,l1,l2,l3))';subplot(2,2,1);plot(th1,w2,'r-');hold on;title('连杆2角速度分析');subplot(2,2,2);plot(th1,a2,'b-');hold on;title('连杆2角加速度分析');subplot(2,2,3);plot(th1,w3,'r-');hold on;title('连杆3角速度分析');subplot(2,2,4);plot(th1,a3,'b-');hold on;title('连杆3角加速度分析');return在MA TLAB命令窗口输入命令:>> th1=60;w1=pi/3;l1=20;l2=30;l3=40;l4=45;>> function f=pos(th1,w1,l1,l2,l3,l4)60°,ω=pi/3时的值即可得到theta=采用实时动画的方法编写draw.m文件:function dw = draw(l1,l2,l3,l4,x1,x2,x3)figure(2);th1=x1*pi/180;th2=x2*pi/180;th3=x3*pi/180;x=0:0.001:l4;plot(x,0,'r-');axis([-25,70,-25,60]);hold onfor i=0:0.1:l1;s=i*cos(th1); c=i*sin(th1);plot(s,c,'b-');hold on;end;for x=0:0.1:l3;s2=x*cos(th3)+l4;c2=x*sin(th3);plot(s2,c2);hold on;endfor x=0:0.1:l2;s3=l1*cos(th1)+x*cos(th2); c3=l1*sin(th1)+x*sin(th2);plot(s3,c3);hold on;endreturn代入pos.m中所得的结果,输入命令:>>draw(l1,l2,l3,l4,y(1,1),y(2,1),y(3,1))即可得到当前位置下的四杆图形。
基于MATLAB/Simulink的平面四连杆机构仿真一、题目及自由度分析如图1所示,该平面四杆机构中有三根运动的均质钢杆,其中有两根钢杆的一端与接地点连接,第三根杆就与这两根杆剩下的端点连接起来,两个接地点就可认为是第四杆,机构中相关尺寸如图2所示。
计算结构自由度,三个运动杆被限制到平面内运动,因此每个杆都有两个移动和一个转动,即在考虑约束之前,自由度为:3×(2+1)=9但是由于每个杆都受到约束,所以并不是每个自由度都是独立的。
在二维状态下,刚体间的连接或者刚体与接地点的连接就会增加两个约束。
这样就会使得刚体其中一端不能够作为独立的自由运动点,而是要受到邻近刚体的约束。
该题中有四个刚体--刚体或刚体—接地点的连接,这就隐含8个约束。
那么最后的自由度为9-8=1.虽然有四个转动自由度,但是,其中三个都是非独立的,只要确定其中一个,就可确定其余三个。
二、模型建立及参数设置1应用MATLAB/Simulink建立初始模型2在初始模型的基础上添加Joint Sensor模块3依题意设置相关参数⑴配置Ground模块由图2可得系统的基本尺寸为:①固定构件长86.7厘米②Ground_1表示接地点,在World CS坐标轴原点右边43.3cm处③Ground_2表示接地点,在World CS坐标轴原点左边43.4cm处④最下端的铰处于X-Z平面内原点以上4cm图5Ground_1模块参数设置图6Ground_2模块参数设置4配置Joint模块三个没有接地的联杆都是在X-Y平面内的,所以Revolute轴必须是Z轴。
⑴依次打开Revolute参数对话框,保持默认值,即Axis of rotation[x y z]默认设置为[001],Reference csys都是WORLD。
图7Revolute坐标设置⑵根据连接情况依次设置Revolute参数对话框中的Connection parameters参数图8Revolute模块参数对话框Connection parameters参数图9Revolute模块参数对话框Connection parameters参数图10Revolute模块参数对话框Connection parameters参数图11Revolute模块参数对话框Connection parameters参数5配置Body模块本题中Body模块(即Bar)定位方式不是直接相对于WORLD坐标系统,而是采用相对坐标形式,Bar1的CS1相对于Ground_1,Bar2的CS1相对于Bar1,以此类推。
基于matlab 的平面四连杆机构设计以及该机构的运动仿真分析
摘要
四连杆机构因其结构方便灵活,能够传递动力并实现多种运动形式而被广泛应用于各个领域,因此对其进行运动分析具有重要的意
义。
传统的分析方法主要应用几何综合法和解析综合法,几何综合法简单直观,但是精确度较低;解析法精确度较高,但是计算工作量大。
随着计算机辅助数值解法的发展,特别是MATLAB 软件的引入,解析法已经得到了广泛的应用。
对于四连杆的运动分析,若应用MATLAB 则需要大量的编程,因此我们引入proe 软件,我们不仅可以在此软件中建立实物图,而且还可以对其进行运动仿真并对其运动分析。
在设计四连杆时,我们利用解析综合法建立数学模型,再根据数学模型在MATLAB 中编程可以求得其他杆件的长度。
针对范例中所求得的各连杆的长度,我们在proe 软件中画出其三维图(如图4)并在proe软件中进行仿真分析得出B,C的角加速度的变化,从而得到B,C两接触处所受到的力是成周期性变化的,可以看出B,C两点处极易疲劳断裂,针对B,C两点处的疲劳断裂,我们提出了在设计四连杆中的一些建议。
关键字:解析法MATLAB软件proe软件运动仿真
建立用解析法设计平面四杆机构模型
对于问题中所给出的连架杆AB的三个位置与连架杆CD的三个位置相对应,即三组对应位置为: f 1」2卜2,「3卜3,其中他们对应的值分别为:135 ,112 ,90 ,82 ,45 ,52,为了便于写代数式,可作出AB与CD对应的关系,其图如下:
图一2 AB与CD三个位置对应的关系
通过上图我们可以通过建立平面直角坐标系并利用解析法来求解,其直角坐标系图如下:
图一3平面机构直角坐标系
通过建立直角坐标系OXY,如上图所示,其中:0与°为AB杆与
CD杆的初始角,各杆件的长度分别用矢量a,b,c,d,表示,将各矢量分
别在X轴与丫轴上投影的方程为
'a* cos©) +b* cos®) = d + c* cos仲)
a* si n(a pH b* si n(日)=c* si n仲)
在上述的方程中我们可以消除二,从而可以得到:与•之间的关系
如下:
2 2 2 2
(a c d -b ) 2cd cos( ) = 2accos© ■■') 2abcos(v) (1)
为便于化简以及matlab编程我们可以令:
2丄2丄』2 ,2
a +c +d -b
H 1 :
2ac
d
a
d
H3
c
通过将(2)式代入(1)式中则可以化简得到如下等式:
H 1 H 2 cos( ) =cos(= ?) - H3cos(:) (3)
我们可以通过(3)式将两连架杆对应的位置带入(3)式中, 我们
可以得到如下方程:
H 1H 2 cos(- •!)= cos( \ -,!\)H3 cos( \)
H 4 H 2 COS(- 2)= COS(;:22)H 3
cos(2)(4)
联立(4)方程组我们可以求得H I,H2,H3,再根据(2)中的条件
H1 H2 cosC 3)=cos( 3 —3) H3COS( 3)
以及所给定的机架d的长度,我们可以求出其它杆件的长度为:
j 2 2 2 b 二 a c d - 2acH 1 四连杆设计范例:
在日常生活中,我们经常看到消防门总能自动关上, 其实它是利
用四连杆机构与弹簧组成的。
已知门与另一连架杆三组对应的位置值 分别为:135 ,112 ,90 ,82 ,45 ,52。
1试设计一四连杆机构用于消防门上, 2并对你所设计的四连杆机构提出一些建议。
范例的求解:
在matlab 中,我们首先构建用于求 比出2出3,的矩阵,并调用求
可逆函数inv 来求解线性方程组,即可得到H1,H2,H3,的值,然后可以
根据机架的长度d ,可以求出a,b,c 的长度(程序见附录一),求解的 结果为:
«
c (5)
范例的分析:
根据四连杆的判别方法可知:对上述设计所得到四连杆长度可 知,a 是
最短的并且最短杆与最长杆要小于其他两杆之和即;
a b :: c d ,故上述所设计得到的四连杆机构中存在曲柄,由于杆 d 为
机架且与曲柄a 相连,故可以进一步判定该四连杆机构为曲柄摇杆机
构。
范例中四连杆机构的运动仿真分析:
针对问题二我们利用proe 软件对已经设计好的四连杆进行 仿真
运动分析,则其在proe 中的实物图如下:
求解的系数为: 各杆的长度为: 比= 0.7384 «
H 2 =1.2162
H 3 =1.8097
a =27.6293
b =57.2363
c = 41.1104
d =50.0000
图一4四连杆实物图
根据问题一中我们已经设计好的四连杆可知杆 a 曲柄,杆b 为连 杆,
为了便于仿真分析,我们假设曲柄 a 的角速度为20./s ,则可以 对图一3中的B ,C 点进行角加速度分析,则可以利用proe 软件的运动 仿真分析可知: 图一5 B 点处角加速度的变化
通过对图 5,6 出角加速度的变化可知, B ,c 两点的角加速度变 化
10.00
\ i) J
I6.(j J
5.00 J
o.o
o
较大且呈现周期性变化,故所受到的力也是呈现周期性变化,因此在B,C 两点处极易疲劳断裂。
对于问题二,由于在B,C 两点处极易疲劳断裂,故我们可以从连杆本身以及工作环境入手,因此我们可以提出以下几条建议:
一在连杆结构设计方面应尽量避免尖角,缺口和截面突变,以避免应力集中及由此引起的疲劳断裂。
二降低零件表面的粗糙度,尤其是B,C 两点接触处的粗糙度,提高B,C 表面的质量,以及尽量减少能成为疲劳源的表面缺陷与表面伤损。
三可以采用各种表面强化处理,尤其是B,C 两点接触处的表面硬度,对于B,C 两处应采用表面淬火以增强其表面硬度同时也可以保持其内部韧性,还可获得有益的表层残余应力,以抵消或降低产生疲劳裂纹的拉应力。
四对于四连杆所受到的力是呈周期性变化,故不宜用于高速,重载的场合。
参考文献
[1] 杨柯桢•程光蕴•李仲生机械设计基础第5版[M].北京:高等教育出版社.2009
[2] 郭仁生.机械工程设计分析和matlab应用第3版[M].北京:机械
工业出版社.2012
[3] 王运炎•朱莉.机械工程材料第3版[M].北京:机械工业出版
社.2010
[4] 李南南.吴清.曹辉林MATLAB 简明教程[M]. 北京:清华大学出版社.2006
[5] 祝凌云.李斌.pro/ENGINEER运动仿真和有限元素分析[M].北京:人民邮电出版社.2004
附录一:
[f]=[45 90 135]*pi/180;
[p]=[52 82 112]*pi/180;
a1=[1 -cos(f(1)) cos(p(1))];
a2=[1 -cos(f(2)) cos(p(2))];
a3=[1 -cos(f(3)) cos(p(3))];
a=[a1;a2;a3];
b1=[cos(f(1)-p(1))];
b2=[cos(f(2)-p(2))];
b3=[cos(f(3)-p(3))];
b=[b1 b2 b3]';
r=inv(a)*b
d=50;
a=d/r(3)
c=d/r(2)
b=sqrt(a A2+c A2+d A2-2*a*c*r(1))。