中考数学专题复习(三) 网格作图题

《网格作图题》复习专题教学设计一、教材分析网格作图题是对图形变换的综合考查，在网格中可以同时考察平移、旋转、轴对称、中心对称等几种图形变换。

这类题目属于图形的操作问题，在网格中进行图形变换的操作时，图形的每一个顶点都是关键点，可以将图形的变换操作转化为点的变换操作。

本节课，知识点较多，但应该抓住关键点，分清变换类型，用变换的性质来解决实际问题，以训练为主。

2．考标要求：（1）应用平移、旋转、轴对称、中心对称等几种图形变换的性质解决数学问题。

（2）培养学生几何空间思维能力。

二、教学目标：(1).知识与技能：回忆所学的平移、旋转、轴对称、中心对称等几种图形变换的基础知识，理解掌握运用基础知识解决相关问题，提高解决问题的能力。

(2).数学思考：建立几何空间思维能力。

(3).过程与方法：学生自查遗忘的知识点，通过讨论、交流，教师答疑、解惑、指导，经历例题、习题的解答，提高技能，(4).情感态度：经历对所学的平移、旋转、轴对称、中心对称等几种图形变换的基础知识的复习，用所学知识解决相关问题，提高解决问题的能力。

三、教学重、难点：教学重点：对面积的计算。

教学难点：教学准备：多媒体课件、导学案、四、教学过程教学内容与教师活动学生活动设计意图一、知识梳理加强理解（1）中考题型（2）考点1.对称图形的计算和运用;2.平移图形的计算和运用;3.旋转图形的计算和运用;4.在网格中求面积;（3）准备知识1.对称作图的方法：轴对称（或中心对称）图形的作法：先找出原图形的各顶点，作出它们关于对称轴的对称点，然后根据原图连接各对称点。

2.平移作图的方法：（1）确定平移的方向和平移的距离；（2）找出原图形的关键点；（3）按平移方向和平移距离，平移各个关键点，得到关键点的对应点；（4）按原图形依次连接各关键点的对应点，即的平移后的图形。

3.旋转作图的方法：（1）确定旋转中心及旋转方向、旋转角；（2）找出原图的关键点；（3）连接关键点与旋转中心，按旋转方向与旋转角旋转，得到个关键点的对应点；（4）按按原图形依次连接各关键点的对应点，即的旋转后的图形。

2023中考真题抢先练：数学网格作图1.（2023达州18题）如图，网格中每个小正方形的边长均为1，△ABC 的顶点均在小正方形的格点上.（1）将△ABC 向下平移3个单位长度得到△A 1B 1C 1，画出△A 1B 1C 1；（2）将△ABC 绕点C 顺时针旋转90度得到△A 2B 2C 2，画出△A 2B 2C 2；（3）在（2）的运动过程中请计算出△ABC 扫过的面积.第1题图【推荐区域：安徽陕西】【参考答案】解：（1）如解图，△A 1B 1C 1即为所求；（2）如解图，△A 2B 2C 2即为所求；第1题解图（3）由图可得，△ABC 为等腰直角三角形，∴51222=+==BC AB ，AC =101322=+，∴25552121=´´=×=D BC AB S ABC ，∴△A 1B 1C 1在旋转过程中扫过的面积为2ABCACA S S D +扇形290360p ´=+52=52π+52.反比例与一次函数性质综合题2.（2023自贡24题）如图，点A (2，4)在反比例函数xm y =1图象上，一次函数b kx y +=2的图象经过点A ，分别交x 轴，y 轴于点B ，C ，且△OAC 与△OBC 的面积比为2：1.（1）求反比例函数和一次函数的解析式；（2）请直接写出y 1≥y 2时，x 的取值范围.第2题图【推荐区域：安徽江西甘肃】【参考答案】解：（1）将A （2，4）代入x m y =1中得24m =，解得m =8，∴xy 81=，∵C （0，b ），∴12OAC S OC D =·2=b ，∵△OAC 与△OBC 的面积比为2：1，∴b OB OC S OBC 2121=´=D ，解得OB =1，∴B （-1，0）或（1，0），①将A （2，4），B （-1，0）代入b kx y +=2中，得îíì+-=+=，，b k b k 024解得ïîïíì==，，3434b k ∴34342+=x y ；②将A （2，4），B （1，0）代入b kx y +=2中，得îíì+=+=，，b k b k 024解得îíì-==，，44b k ∴442-=x y ；综上可知，一次函数的解析式为34342+=x y 或442-=x y ；（2）当34342+=x y 时，x ≤-3或0＜x ≤2；当442-=x y 时，x ≤-1或0＜x ≤2.解直角三角形的实际应用3.（2023达州19题）莲花湖湿地公园是当地人民喜爱的休闲景区之一，里面的秋千深受孩子们喜爱，如图所示，秋千链子的长度为3m ，当摆角∠BOC 恰为26°时，座板离地面的高度BM 为0.9m ，当摆动至最高位置时，摆角∠AOC 为50°，求座板距地面的最大高度为多少m?(结果精确到0.1m ；参考数据：sin 26°=0.44，cos 26°≈0.9，tan 26°≈0.49，sin 50°≈0.77，cos 50°≈0.64，tan 50°≈1.2)第3题图【推荐区域：安徽江西河南甘肃】【参考答案】解：如解图，过点B 作BD ⊥ON 于点D ，过点A 作AE ⊥ON 于点E ，作AF ⊥MN于点F，第3题解图∴四边形BDNM，AENF均为矩形，∴BM=DN=0.9，AF=EN，在Rt△OBD中，OD=OB·cos26°=3cos26°，∴ON=OD+DN=3cos26°+0.9，在Rt△OAE中，OE=OA·cos50°=3cos50°，∴EN=ON-OE=3cos26°+0.9-3cos50°，∴AF=3cos26°+0.9-3cos50°≈3×0.9+0.9-3×0.64=1.68≈1.7（m），答：座板距地面的最大高度为1.7m.4.（2023重庆A卷24题）为了满足市民的需求，我市在一条小河AB两侧开辟了两条长跑锻炼线路，如图：①A—D—C—B；②A—E—B.经勘测，点B在点A的正东方，点C在点B的正北方10千米处，点D在点C的正西方14千米处，点D在点A的北偏东45°方向，点E在点A的正南方，点E在点B的南偏西60°方向.( 1.41≈1.73)（1）求AD的长度；(结果精确到1千米)（2）由于时间原因，小明决定选择一条较短线路进行锻炼，请计算说明他应该选择线路①还是线路②?第4题图【推荐区域：安徽江西河南甘肃】【参考答案】解：（1）如解图，过点D作DF⊥AB于点F.第4题解图由题意可知，AB∥CD，BC⊥AB，∴四边形BCDF是矩形，且BC=10，CD=14.∴DF=BC=10，在Rt△ADF中，∠DAF=45°，∴AD≈14（千米），答：AD的长度约为14千米；（2）由题意可知，EA⊥AB，∠ABE=90°-60°=30°，∵AF=DF=10，BF=CD=14，∴AB=AF+BF=10+14=24，∴在Rt△ABE中，AE AB BE=2AE线路①：AD+CD+BC≈38.1（千米），线路②：AE+BE41.52（千米），∵38.1＜41.52，∴小明应选择线路①.二次函数的实际应用5.（2023南充23题）某工厂计划从A ，B 两种产品中选择一种生产并销售，每日产销x 件，已知A 产品成本价m 元/件(m 为常数，且4≤m ≤6)，售价8元/件，每日最多产销500件，同时每日共支付专利费30元；B 产品成本价12元/件，售价20元/件，每日最多产销300件，同时每日支付专利费y 元，y (元)与每日产销x （件）满足关系式201.080x y +=.（1）若产销A ，B 两种产品的日利润分别为1w 元，2w 元，请分别写出1w ，2w 与x 的函数关系式，并写出x 的取值范围；（2）分别求出产销A ，B 两种产品的最大日利润；(A 产品的最大日利润用含m 的代数式表示)（3）为获得最大日利润，该工厂应该选择产销哪种产品?并说明理由.[利润=(售价一成本)×产销数量一专利费]【推荐区域：安徽河北云南江西】【参考答案】解：（1）根据题意，得30)8(1--=x m w ，0≤x ≤500.)01.080()1220(22x x w +--=80801.02-+-=x x ，0≤x ≤300；（2）∵8-m >0，∴1w 随x 的增大而增大，又0≤x ≤500，∴当x =500时，1w 的值最大，39705001+-=m w 最大.1520)400(01.080801.0222+--=-+-=x x x w .∵-0.01<0，对称轴为直线x =400，当0≤x ≤300时，2w 随x 的增大而增大，∴当x =300时，2w 最大=-0.01×(300-400)2+1 520=1 420（元）.（3）①若最大1w =最大2w ，即-500m +3970=1420，解得m =5.1；②若最大1w >最大2w ，即-500m +3970>1 420，解得m <5.1；③若最大1w <最大2w ，即-500m +3 970<1420，解得m >5.1.又∵4≤m ≤6，∴综上可得，为获得最大日利润：当m =5.1时，选择A ，B 产品产销均可；当4≤m <5.1时，选择A 种产晶产销；当5.1<m ≤6时，选择B 种产品产销.二次函数性质综合题6.（2023遂宁25题）在平面直角坐标系中，O 为坐标原点，抛物线c bx x y ++=241经过点O (0，0)，对称轴过点B (2，0)，直线l 过点C (2，-2)且垂直于y 轴.过点B 的直线1l 交抛物线于点M ，N ，交直线l 于点Q ，其中点M ，Q 在抛物线对称轴的左侧.（1）求抛物线的解析式；（2）如图1，当BM ：MQ =3：5时，求点N 的坐标；（3）如图2，当点Q 恰好在y 轴上时，P 为直线1l 下方的抛物线上一动点，连接PQ ，PO ，其中PO 交1l 于点E ，设△OQE 的面积为1S ，△PQE 的面积为2S ，求12S S 的最大值.第6题图【推荐区域：安徽陕西】【参考答案】解：（1）由题意得0b 2124c =ìïïí-=ï´ïî，，解得01c b =ìí=-î，，∴抛物线的解析式为y =214x -x ；（2）如解图，过点M ，Q 作MD ⊥x 轴，QH ⊥x 轴分别于点D ，H ，第6题解图∴DM ∥HQ ，∴△BDM ∽△BHQ ，∴BM BQ =DM HQ ，∴38=2DM ，∴DM =34，∴点M 的纵坐标为-34，代入y =34x 2-x 中，解得x M =1或x M =3，∵点M 在抛物线对称轴的左侧，∴x M =1，∴点M （1，-34），设直线BM 的解析式为y =kx +b 1，将点M （1，-34）和点B （2，0）代入，得113=402k b k b ì-+ïíï=+î，，解得13=432k b ìïïíï=-ïî，，∴直线BM 的解析式为y =2343-x ，联立2143342y x x y x ì=-ïïíï=-ïî，，解得134x y =ìïí=-ïî，或63x y =ìí=î，，∵点N 在对称轴的右侧，∴点N （6，3）；（3）由题意可知，点Q 的坐标为（0，-2），设点P （m ，14m 2-m ），由题意得直线y OP =（14m -1）x ，直线l 1的解析式为y BQ =x -2，联立1(1)42y m x y x ì=-ïíï=-î，，∴点E 的横坐标为x E =88m -，∴S 1=21OQ ·x E =21×2×m -88=m-88，S 2=21OQ ·(P E x x -）=21×2（m -m-88）=m m m ---8882，∴22188888S m m m S m ---=-=1812-+-m m =1)4812+--m （，∵81-＜0，∴当m =4时，12S S 有最大值，最大值为1，∴12S S 的最大值为1.。

授课设计教师学生科目数学上课时间课次 1授课内容中考中的格点图形问题授课重难点解题方法授课设计：近来几年来，有关格点问题已成为中考的亮点，这类问题题型多样，形式爽朗，主要观察同学们的直觉推理能力和问题研究能力．格点问题操作性强、兴趣性浓，表现了新课标的“在‘玩’中学，在学中思，在思中得”的崭新理念．下面就中考中的几类格点问题归纳以下，望能对学习有所帮助．一、格点中的对称问题例 1 （绍兴市）如图 1，在网格中有两个全等的图形 (阴影部分 )，用这两个图形拼成轴对称图形，试分别在图(1) 、(2) 中画出两种不同样的拼法．图1图2二、格点中的画图问题例 2 （黑龙江鸡西市）如图3，在网格中有一个四边形图案．（1）请你画出此图案绕点 O 顺时针方向旋转 900， 1800，2700的图案，你会获取一个美丽的图案，千万不要将阴影地址涂错；图 3图4（2）若网格中每个小正方形的边长为l ，旋转后点 A 的对应点依次为 A1、 A2、A3，求四边形 AA1A2A3的面积；(3)这个美丽图案可以说明一个出名结论的正确性，请写出这个结论．三、格点中的坐标问题例3 （苏州市）如图 5．围棋盘的左下角表现的是一局围棋比赛中的几手棋．为记录棋谱方便，横线用数字表示．纵线用英文字母表示，这样，黑棋①的地址可记为(C，4)，白棋②的地址可记为( E， 3) 则白棋⑨的地址应记为＿＿＿．图 5四、格点中的相似问题例 4 （福州市罗源平潭）如图成的相似三角形有（）A ． 4 对B ． 3 对C． 2 对6，在 7×12 的正方形网格中有一只可爱的小狐狸，算算看画面中由实线组DD ．1 对A C F析解：本题是一道以网格为背景的结论研究性问题， B E J H在正方形网格中画了一只可爱的小狐狸，增强了题目G I R L的兴趣性．由网格的特色结合勾股定理，可以获取三角图6形三边的长，从而利用“三边对应成比率，两三角形相似”的判断来求解．．五、格点中的位似问题例5 （广东省）如图 7，图中的小方格都是边长为 1 的正方形，△ ABC 与△ A′B′C′是关于点 O 为位似中心的位似图形，它们的极点都在小正方形的极点上．（1）画出位似中心点 O；（2）求出△ ABC 与△ A/B/C/的位似比；（ 3）以点 O 为位似中心，再画一个△A1B1C1，使它与△ ABC的位似比等于．C/ C/C1B/ C B/ CA/BA/B1 BA A1 A O 图 7 图 8六、格点中的面积问题例 6 （浙江湖州市）一青蛙在如图8×8 的正方形（每个小正方形的边长为 1）网格的格点（小正方形的极点）上跳跃，青蛙每次所跳的最远距离为 5 ，青蛙从点A开始连续跳六次正好跳回到点 A，则所组成的封闭图形的面积的最大值是_______．图 9析解：本题以青蛙这一幽默且有益的动物为背景设计题目，增加了题目的兴趣性．解题时涉及无理数、勾股定理的应用、图形面积的计算等知识．只要正确画出图形，再运用割补法即可求得面积为 12．七、格点中等腰三角形问题例 7 （重庆市）以下列图，A、 B 是 4×5 网络中的格点，网格中的每个小正方形的边长为晰标出使以Ａ、B、C 为极点的三角形是等腰三角形的所有格点 C 的地址．1，请在图中清A AB B图10 图11析解：依照网格的特色及等腰三角形的有关知识易得，AB 只能为一腰，且AB= 13 ，由勾股定理即可知点C1、 C2、 C3吻合要求（如图11）．八、格点中的拼图问题例 8 （北京市）请阅读以下资料：问题：现有 5 个边长为画出切割线并在正方形网格图1 的正方形，排列形式如图①，请把它们切割后拼接成一个新的正方形．(图中每个小正方形的边长均为1)中用实线画出拼接成的新正方形．要求：小东同学的做法是：设新正方形的边长为x(x＞ 0)．依题意，割补前后图形的面积相等，有x2=5 ，解得x= 5 ．由此可知新正方形得边长等于两个小正方形组成得矩形对角线得长．于是，画出如图②所示的分割线，拼出如图③ 所示的新正方形．图①图②图③图④图⑤图12请你参照小东同学的做法，解决以下问题：现有 10 个边长为 1 的正方形，排列形式如图④，请把它们切割后拼接成一个新的正方形．要求：在图④中画出切割线，并在图⑤的正方形网格图 (图中每个小正方形的边长均为 1)中用实线画出拼接成的新正方形．说明：直接画出图形，不要求写解析过程．析解：本题是一道综合型网格作图试题，涉及到无理数、勾股定理等知识，主要观察同学们的计算能力、着手操作能力．类比小东的作法，可设新正方形的边长为x(x>0)，便有 x2=10 ，解得 x=10 ．由此可知，新正方形得边长等于两个小正方形组成得矩形对角线得长．于是，画出如图②所示的切割线，拼出如图③所示的新正方形．图 13图14温州历年中考中的格点问题19．（ 2009?温州） ( 本题 8 分 ) 在所给的 9×9方格中，每个小正方形的边长都是1．按要求画平行四边形，使它的四个极点以及对角线交点都在方格的极点上．(1) 在图甲中画一个平行四边形，使它的周长是整数； (2) 在图乙中画一个平行四边形，使它的周长不是整数． ( 注：图甲、图乙在答题纸上 )19、（ 2011?温州）（本题8 分）七巧板是我们祖先的一项优异创立，用它可以拼出多种图形，请你用七巧板中标号为○1 ○2 ○3的三块板（如图1）经过平移、旋转拼成图形。

中考题型训练——网格作图1.(07．云南）(6分）如图，在所给网格图(每小格均为边长是１的正方形)中完成下列各题：（１)作出格点△AＢC关于直线ＤE对称的△A1B1Ｃ1； (２)作出△A1B1C１绕点Ｂ1顺时针方向旋转90°后的△A２B１C2;（3)求△A2B1Ｃ2的周长；（第１题) (第2题)2.（06.云南)(７分)在如图的方格纸中,每个小正方形的边长都是１，△ABC与△Ａ１B1C1构成的图形是中心对称图形. （1)画出此中心对称图形的对称中心O; （２)画出将△Ａ１Ｂ1C1沿直线DE方向向上平移5格得到的△Ａ2B２C2;(3)要使△A２B ２Ｃ２与△CC1C２重合,则△A２B2C2绕点C2顺时针方向旋转,至少要旋转多少度?（不要求证明）3.（0５.云南)（７分)如图,梯形AＢMN是直角梯形．（1)请在图中拼上一个直角梯形,使它与梯形ABＭN构成一个等腰梯形;(3)将补上的直角梯形以点M为旋转中心,逆时针方向旋转180°,再向上平移一格,画出这个直角梯形(不要求写作法)(第3题) (第4题) 4．（０7.安徽）△ABC和点S在平面直角坐标系中的位置如图所示:(１）将△AＢC向右平移4个单位得到△A1B1C1，则点A1 、B1的坐标分别为和 .(2)将△AＢC绕点S按顺时针方向旋转９0°，画出旋转后的图形．5.（０7．江苏)如图,网格中每一个小正方形的边长为１个单位长度.(1)请在所给的网格内画出以线段AB,ＢC为边的菱形ABＣD；(2)填空:菱形ABCD的面积等于．(第5题）(第6题）6．（07.福州)如图的方格纸中,每个小正方形的边长都为1个单位的正方形，在建立平面直角坐标系后, △ABＣ的顶点均在格点上,点Ｃ的坐标为(４,-1）.(1)把△ABC向上平移5个单位后得到对应的△A１B1C1,画出△A1B1Ｃ1,并写出点C１的坐标;（２）以原点O为对称中心,再画出与△A１B1Ｃ１关于原点Ｏ对称的△Ａ2B2C2，并写出点Ｃ2的坐标.7.（０7.哈尔滨)△ABC在平面直角坐标系中的位置如图所示．（1)作出与△ABＣ关于y轴对称的△A１Ｂ1C;(２）将△ABＣ向下平移３个单位长度,画出平移后的△Ａ2Ｂ2C2.(第７题) (第8题)８.（０７.辽宁）如图, 在平面直角坐标系中,图错误!与图错误!关于点P成中心对称.(1)画出对称中心P，并写出点Ｐ的坐标;(2)将图形＼o＼ac（○,2)向下平移4个单位,画出平移后的图形错误!,并判断图形错误!与图形错误!的位置关系.（直接写出结果)９.（０７.安徽)如图，在直角坐标系中△ＡBC的A、B、Ｃ三点坐标为Ａ(7，1）、B(8，2）、C(９,0)．(1)请在图中画出△ABC的一个以点P(12,0)为位似中心,相似比为3的位似图形(要求与△ＡＢＣ同在P点一侧);（2)求线段BC的对应线段Ｂ′Ｃ′所在直线的表达式.(第９题） (第10题）10．(０７.长沙)如图是某设计师在方格纸中设计图案的一部分,请你帮他完成余下的工作: (1）作出关于直线AB的轴对称图形；（2）将你画出的部分连同原图形绕点O逆时针旋转90°;(3)发挥你的想象,给得到的图案适当涂上阴影,让图案变得更加美丽．1１.(０7．海南)在如图的方格纸中,△ABC的顶点坐标分别为A（－２，5)、Ｂ(-４，１)和C（-1,3）.（1)作出△ＡＢC关于x轴对称的△A1B1C1，并写出点Ａ、B、Ｃ的对称点A1、B1、C1的坐标；（２)作出△ABＣ关于原点Ｏ对称的△A2Ｂ2C２,并写出点A、B、Ｃ的对称点A2、B2、C2的坐标;（３）试判断:△Ａ1Ｂ1Ｃ１与△Ａ2B2Ｃ2是否关于y轴对称（只需写出判断结果）(第11题) （第12题）１2．(07.青海)如图所示,图错误!和图错误!中的每个小正方形的边长都为1个单位长度．(1）将图错误!中的格点△AＢC（顶点都在网格线交点的三角形叫格点三角形）向在平移2个单位长度得到△A1B1C1,请你在图中画出△A1Ｂ1C1;(2)在图错误!中画一个与格点△AＢC相似的格点△A２B2C2，且△A2B2Ｃ２与△ABC的相似比为2：１．１3.（07．广西)如图，在正方形网格中,△ＡＢC的三个顶点Ａ、B、C均在格点上，将△ABC向右平移5格,得到△Ａ1Ｂ１Ｃ1,再将△A1B１Ｃ1绕点B1按顺时针方向旋转90°，得到△A２Ｂ２C2.（1)请在网格中画出△A1Ｂ1Ｃ1和△A2Ｂ２C2（不要求写画法）(2)画出△Ａ１B1C1和△A2B2Ｃ２后,填空：∠C1B1Ｃ2= 度，∠A2＝度.（第1３题）１４.(0６.成都)如图,在平面直角坐标系中,点B的坐标为（-１，-１).(1）把△ABC向左平移8格后得到△Ａ1B1C１,画出△A１B1Ｃ1并写出点Ｂ１的坐标; (２）把△ABＣ绕点C按顺时针方向旋转９0°后得到△Ａ２B２C，画出△A2Ｂ2Ｃ并写出点B2的坐标；(3）把△AＢC以点Ａ为位似中心放大，使放大前后对应边长的比为1:2,画出△AB3C3.(第1４题）１5.(0６.广东)如图，图中的小正方形是边长为1的正方形,△AＢC与是关于O为位似中心的位似图形,它们的顶点都在小正方形的顶点上．(1)画出位似中心点O;(2)求出△ABC与的位似比；（３）以点Ｏ为位似中心,再画一个△A1B1C1，使它与△ABＣ的位似比为1.5；。

专题复习(三)网格作图题1．拟)如图，在边长为1个单位长度的小正方形组成的网格中，给出了格点四边形ABCD(顶点是网格线的交点)，按要求画出四边形AB1C1D1和四边形AB2C2D2.(1)以A为旋转中心，将四边形ABCD顺时针旋转90°，得到四边形AB1C1D1；(2)以A为位似中心，将四边形ABCD作位似变换，且放大到原来的两倍，得到四边形AB2C2D2.解：(1)如图，四边形AB1C1D1为所作．(2)如图，四边形AB2C2D2为所作．2．二模)如图，方格纸中的每个小方格都是边长为1个单位的正方形，在建立平面直角坐标系后，△ABC的顶点均在格点上，点B的坐标为(1，0)．(1)画出△ABC关于x轴对称的△A1B1C1，写出B1点的坐标；(2)画出将△ABC绕原点O按逆时针旋转90°所得的△A2B2C2，写出B2点的坐标．解：(1)如图所示，△A1B1C1即为△ABC关于x轴对称的图形，B1点的坐标是(1，0)．(2)如图所示，△A2B2C2即为△ABC绕原点O按逆时针旋转90°的三角形，B2点的坐标是(0，1)．3．模)如图，已知A(2，3)，B(1，1)，C(4，1)是平面直角坐标系中的三点．(1)请画出△ABC关于y轴对称的△A1B1C1；(2)画出△A1B1C1向下平移3个单位得到的△A2B2C2；(3)若△ABC中有一点P坐标为(x，y)，请直接写出经过以上变换后△A2B2C2中点P的对应点P2的坐标．解：(1)如图所示，△A1B1C1即为所求．(2)如图所示，△A2B2C2即为所求．(3)根据题意，可得P的对应点P2的坐标为(－x，y－3)．4．拟)如图，在9×7的小正方形网格中，△ABC的顶点A，B，C在网格的格点上．将△ABC向左平移3个单位，再向上平移3个单位得到△A′B′C′.再将△ABC按一定规律依次旋转：第1次，将△ABC绕点B顺时针旋转90°得到△A1BC1；第2次，将△A1BC1绕点A1顺时针旋转90°得到△A1B1C2；第3次，将△A1B1C2绕点C2顺时针旋转90°得到△A2B2C2；第4次，将△A2B2C2绕点B2顺时针旋转90°得到△A3B2C3，依次旋转下去．(1)在网格中画出△A′B′C′和△A2B2C2；(2)请直接写出至少在第几次旋转后所得的三角形刚好为△A′B′C′.解：(1)△A′B′C′和△A2B2C2的图象如图所示.(2)通过画图可知，△ABC至少在第8次旋转后得到△A′B′C′.5.如图，△ABC的三个顶点和点O都在正方形网格的格点上，每个小正方形的边长都为1.(1)将△ABC先向右平移4个单位，再向上平移2个单位得到△A1B1C1，请画出△A1B1C1；(2)请画出△A2B2C2，使△A2B2C2和△ABC关于点O成中心对称；(3)在(1)、(2)中所得到的△A1B1C1与△A2B2C2成轴对称吗？若成轴对称，请画出对称轴；若不成轴对称，请说明理由．解：(1)如图所示，△A1B1C1，即为所求．(2)如图所示，△A2B2C2，即为所求．(3)如图所示，△A1B1C1与△A2B2C2成轴对称，直线a，b即为所求．6．级二模)如图所示，在边长为1个单位长度的小正方形组成的网格中，△ABC 的顶点A ，B ，C 在小正方形的顶点上．将△ABC 向下平移2个单位得到△A 1B 1C 1，然后将△A 1B 1C 1绕点C 1顺时针旋转90°得到△A 2B 2C 1.(1)在网格中画出△A 1B 1C 1和△A 2B 2C 1；(2)计算线段AC 在变换到A 2C 1的过程中扫过区域的面积．(重叠部分不重复计算)解：(1)如图，△A 1B 1C 1和△A 2B 2C 1为所作．(2)线段AC 在变换到A 2C 1的过程中扫过区域的面积S ＝2×2＋90·π·（22）2360＝4＋2π.7．如图，△ABC 三个顶点的坐标分别为A(1，1)，B(4，2)，C(3，4)．(1)请画出将△ABC 向左平移4个单位长度后得到的图形△A 1B 1C 1；(2)请画出△ABC 关于原点O 成中心对称的图形△A 2B 2C 2；(3)在x 轴上找一点P ，使PA ＋PB 的值最小，请直接写出点P 的坐标．解：(1)如图所示．(2)如图所示．(3)找出A 关于x 轴的对称点A′(1，－1)，连接BA′，与x 轴交点即为P.如图所示，点P 坐标为(2，0)．8．模拟)如图，已知△ABC 的三个顶点的坐标分别为A(3，3)，B(－1，0)，C(4，0)．(1)经过平移，可使△ABC 的顶点A 与坐标原点O 重合，请直接写出此时点C 的对应点C 1坐标；(不必画出平移后的三角形)(2)将△ABC 绕点B 逆时针旋转90°，得到△A′BC′，画出△A′BC′并写出A′点的坐标；(3)以点A 为位似中心放大△ABC ，得到△AB 2C 2，使放大前后的面积之比为1∶4，请你在网格内画出△AB 2C 2.解：(1)∵经过平移，可使△ABC的顶点A与坐标原点O重合，∴A点向下平移3个单位再向左平移3个单位，故C1坐标为(1，－3)．(2)如图所示，△A′BC′即为所求，A′点的坐标为(－4，4)．(3)如图所示，△AB2C2即为所示．。

中考数学专题复习格点作图题学校:___________姓名：___________班级：___________考生__________评卷人得分一、解答题1．图①，图①，图①都是4×4的正方形网格，每个小正方形的顶点称为格点，每个小正方形的边长均为1．在图①，图①中已画出线段AB，在图①中已画出点A．按下列要求画图：（1）在图①中，以格点为顶点，AB为一边画一个等腰三角形；（2）在图①中，以格点为顶点，AB为一边画一个正方形；（3）在图①中，以点A为一个顶点，另外三个顶点也在格点上，画一个面积最大的正方形．2．图①、图①、图①都是由边长为1的小等边三角形构成的网格，每个小等边三角形的顶点称为格点．线段AB的端点在格点上．（1）在图①、图2中，以AB为边各画一个等腰三角形，且第三个顶点在格点上；（所画图形不全等）（2）在图①中，以AB为边画一个平行四边形，且另外两个顶点在格点上．3．图①、图①均是8×8的正方形网格，每个小正方形的顶点称为格点，线段OM、ON 的端点均在格点上．在图①、图①给定的网格中以OM、ON为邻边各画一个四边形，使第四个顶点在格点上．要求：（1）所画的两个四边形均是轴对称图形．（2）所画的两个四边形不全等．4．如图是由边长为1的小正方形组成的8×4网格，每个小正方形的顶点叫做格点，点A，B，C，D均在格点上，在网格中将点D按下列步骤移动：第一步：点D绕点A顺时针旋转180°得到点D1；第二步：点D1绕点B顺时针旋转90°得到点D2；第三步：点D2绕点C顺时针旋转90°回到点D．（1）请用圆规画出点D→D1→D2→D经过的路径；（2）所画图形是什么对称图形；（3）求所画图形的周长（结果保留π）．5．图①、图②、图③均是6×6的正方形网格，每个小正方形的顶点称为格点，小正方形的边长为1，点A B C D E F、、、、、均在格点上．在图①、图②、图③中，只用无刻度的直尺，在给定的网格中按要求画图，所画图形的顶点均在格点上，不要求写出画法．（1）在图①中以线段AB为边画一个ABM∆，使其面积为6．（2）在图②中以线段CD为边画一个CDN∆，使其面积为6．（3）在图③中以线段EF为边画一个四边形EFGH，使其面积为9，且090EFG∠=．6．图①，图①均为44⨯的正方形网格，每个小正方形的顶点称为格点．在图①中已画出线段AB ，在图①中已画出线段CD ，其中A B C D 、、、均为格点，按下列要求画图：①在图①中，以AB 为对角线画一个菱形AEBF ，且,E F 为格点；①在图①中，以CD 为对角线画一个对边不相等的四边形CGDH ，且,G H 为格点，090CGD CHD ∠=∠=.7．如图①、图①、图①都是33⨯的正方形网格，每个小正方形的顶点称为格点．A ，B ，C 均为格点．在给定的网格中，按下列要求画图：（1）在图①中，画一条不与AB 重合的线段MN ，使MN 与AB 关于某条直线对称，且M ，N 为格点．（2）在图①中，画一条不与AC 重合的线段PQ ，使PQ 与AC 关于某条直线对称，且P ，Q 为格点．（3）在图①中，画一个DEF ∆，使DEF ∆与ABC ∆关于某条直线对称，且D ，E ，F 为格点．8．图①、图①、图①均是33⨯的正方形网格，每个小正方形的边长为1，每个小正方形的顶点称为格点，线段AB的端点均在格点上，只用无刻度的直尺，在给定的网格中，按下列要求以AB为边画ABC．要求：（1）在图①中画一个钝角三角形，在图①中画一个直角三角形，在图①中画一个锐角三角形；（2）三个图中所画的三角形的面积均不相等；（3）点C在格点上．9．图①、图①、图①均是44⨯的正方形网格，每个小正方形的边长均为1．每个小正方形的顶点称为格点，点A、B、C均为格点，只用无刻度的直尺，分别在给定的网格中找一格点M，按下列要求作图：（1）在图①中，连结MA、MB，使MA MB=．（2）在图①中，连结MA、MB、MC，使MA MB MC==．（3）在图①中，连结MA、MC，使2AMC ABC∠=∠．10．图①、图2均是44的正方形网格，每个小正方形的顶点称为格点，小正方形的边长为1，点A，点B均在格点上，在给定的网格中按要求画图，所画图形的顶点均在格点上．（1）在图①中，以点A，B，C为顶点画一个等腰三角形；（2）在图①中，以点A，B，D，E为顶点画一个面积为3的平行四边形．参考答案：1．（1）作图见解析；（2）作图见解析；（3）作图见解析.【解析】【详解】试题分析：（1）根据勾股定理，结合网格结构，作出两边分别为5的等腰三角形即可；（2）根据勾股定理逆定理，结合网格结构，作出边长为5的正方形；（3）根据勾股定理逆定理，结合网格结构，作出最长的线段作为正方形的边长即可．试题解析：（1）如图①，符合条件的C点有5个：；（2）如图①，正方形ABCD即为满足条件的图形：；（3）如图①，边长为10的正方形ABCD的面积最大．．考点：作图—应用与设计作图．2．（1）见解析；（2）见解析．【解析】【分析】（1）根据等腰三角形的定义作图可得；（2）根据平行四边形的判定作图可得．【详解】（1）如图①、①所示，①ABC和①ABD即为所求；（2）如图①所示，①ABCD即为所求．【点睛】本题考查了等腰三角形的判定、等边三角形的性质、平行四边形的判定，正确分析网格特点是解题的关键．3．作图见解析.【解析】【详解】【分析】结合网格特点以及轴对称图形的定义进行作图，然后用全等四边形的定义判断即可得符合题意的图形．【详解】如图所示：【点睛】本题考查了作图﹣轴对称变换，以及全等形的判定，熟练掌握各自的性质是解本题的关键．4．（1）点D→D1→D2→D经过的路径如图所示见解析；（2）轴对称；（3）周长为8π．【解析】【分析】(1)利用旋转变换的性质画出图象即可；(2)根据轴对称图形的定义即可判断；(3)利用弧长公式计算即可.【详解】解：(1)点D→D1→D2→D经过的路径如图所示：(2)观察图象可知图象是轴对称图形，(3)周长=4×904180π⨯⨯=8π．故答案为(1)点D→D1→D2→D经过的路径如图所示见解析；(2)轴对称；(3)8π．【点睛】本题考查作图——旋转变换、轴对称图形等知识，解题的关键是理解题意，正确画出图形. 5．（1）详见解析；（2）详见解析；（3）详见解析.【解析】【分析】（1）直接利用三角形的面积的计算方法得出符合题意的图形；（2）直接利用三角形面积求法得出答案；（3）根据矩形函数三角形的面积的求法进而得出答案．【详解】解：（1）如图①所示，ABM∆即为所求；（2）如图①所示，CDN∆即为所求；（3）如图①所示，四边形EFGH即为所求；【点睛】考核知识点：作三角形和四边形.利用三角形面积公式求解是关键.6．（1）见解析；（2）见解析.【解析】【分析】（1）根据菱形的定义画出图形即可（答案不唯一）．（2）利用数形结合的思想解决问题即可．【详解】解：（1）如图，菱形AEBF即为所求．（2）如图，四边形CGDH即为所求．【点睛】本题考查作图-应用与设计，菱形的判定和性质，直角三角形的判定和性质等知识，解题的关键是灵活运用所学知识解决问题，属于中考常考题型．7．（1）图见解析；（2）图见解析；（3）图见解析．【解析】【分析】⨯的正方形网格的对称轴，根据对称性即可在图①中，描出点AB的对（1）先画出一条33称点MN，它们一定在格点上，再连接MN即可．（2）同（1）方法可解；（3）同（1）方法可解；【详解】⨯的正方形网格的对称轴l，描出点AB关于直线l的对称点MN，连解：（1）如图①，33接MN即为所求；（2）如图①，同理（1）可得，PQ即为所求；（3）如图①，同理（1）可得，DEF∆即为所求．【点睛】本题考查了作图-轴对称变换，解决本题的关键是找到图形对称轴的位置．8．见详解（答案不唯一）【解析】【分析】因为点C在格点上，故可将直尺的一角与线段AB点A重合，直尺边长所在直线经过33⨯正方形网格左上角第一个格点，继而以点A为旋转中心，逆时针旋转直尺，当直尺边长所在直线与正方形格点相交时，确定点C的可能位置，顺次连接A、B、C三点，按照题目要求排除不符合条件的C点，作图完毕后可根据三角形面积公式判断其面积是否相等．【详解】经计算可得下图中：图①面积为12；图①面积为1；图①面积为32，面积不等符合题目要求（2），且符合题目要求（1）以及要求（3）．故本题答案如下：【点睛】本题考查三角形的分类及其作图，难度较低，按照题目要求作图即可．9．（1）见解析；（2）见解析；（3）见解析【解析】【分析】（1）由勾股定理可求得AM=BM=5，即可得点M的位置；（2）由勾股定理可求得AB=BC=10，AC=25，即可得22220AB BC AC+==，再由勾股定理的逆定理可判定①ABC为等腰直角三角形，点M即为斜边AC的中点，由此可得点M的位置；（3）作出AB、AC的垂直平分线，交点即为M，M即为①ABC外接圆的圆心，连接AM，CM，根据圆周角定理可得2AMC ABC∠=∠，由此即可确定点M的位置．【详解】（1）如图①所示，点M即为所求．（2）如图①所示，点M即为所求．（3）如图①所示，点M即为所求．【点睛】本题考查了基本作图，解决第（3）题时，确定①ABC外接圆的圆心是解决问题的关键．10．（1）见解析；（2）见解析【解析】【分析】（1）根据等腰三角形的定义画出图形即可：如以B为顶点，AC为底边，即可做出等腰三角形；（2）作底为1，高为3的平行四边形即可．【详解】解：（1）如图①中，此时以B为顶点，AC为底边，该ABC即为所求（答案不唯一）．（2）如图①中，此时底1AE=，高3h=，因此四边形ABDE即为所求．【点睛】本题考查了等腰三角形的性质和平行四边形的性质，解题的关键掌握等腰三角形和平行四边形的基本性质．。

全国181套中考数学试题分类汇编33⽹格问题33⽹格问题⼀、选择题1.（浙江⾈⼭、嘉兴3分）如图，点A、B、C、D、O都在⽅格纸的格点上，若△COD是由△AOB 绕点O按逆时针⽅向旋转⽽得，则旋转的⾓度为（A）30°（B）45°（C）90°（D）135°【答案】C。

【考点】旋转的性质，勾股定理的逆定理。

【分析】△COD是由△AOB绕点O按逆时针⽅向旋转⽽得，由图可知，∠AOC为旋转⾓，可利⽤△AOC的三边关系解答：设⼩⽅格的边长为1，从图知，=AC=4。

从⽽OA，OC，AC满⾜OC2+OA2=AC2，∴△A OC是直⾓三⾓形，∴∠AOC=90°。

故选C。

2.（浙江⾦华、丽⽔3分）如图，在平⾯直⾓坐标系中，过格点A，B，C作⼀圆弧，点B与下列格点的连线中，能够与该圆弧相切的是A、点（0，3）B、点（2，3）C、点（5，1）D、点（6，1）【答案】 C。

【考点】切线的性质；坐标与图形性质；勾股定理；垂径定理。

【分析】如图，根据垂径定理的性质得出圆⼼所在位置O（2，0），再根据切线的性质得出∠OBD+∠EBF=90°时，BF与圆相切，∴当△BOD≌△FBE时，∴EF=BD=2，F点的坐标为：（5，1）。

故选C。

3.（⼴西贺州3分）如图，在⽅格纸中的△ABC经过变换得到△DEF，正确的变换是A．把△ABC向右平移6格，B．把△ABC向右平移4格，再向上平移1格C．把△ABC绕着点A顺时针⽅向90o旋转，再右平移6格D．把△ABC绕着点A逆时针⽅向90o旋转，再右平移6格【答案】D。

【考点】平移和旋转变换。

【分析】根据平移和旋转变换的特点，直接得出结果。

故选D。

4.（⼴西南宁3分）在边长为1的⼩正⽅形组成的⽹格中，有如图所⽰的A 、B 两点，在格点中任意放置点C ，恰好能使△A BC 的⾯积为1的概率为A ．3 25 B ．4 25 C ． 1 5 D ． 625【答案】D 。

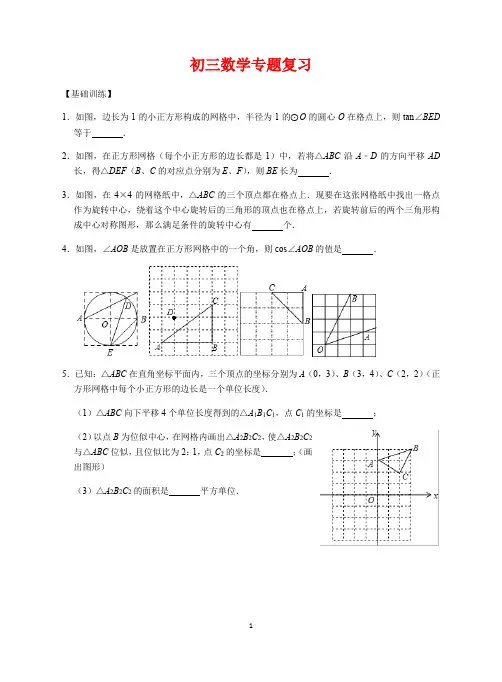
初三数学专题复习【基础训练】1．如图，边长为1的小正方形构成的网格中，半径为1的⊙O的圆心O在格点上，则tan∠BED 等于．2．如图，在正方形网格（每个小正方形的边长都是1）中，若将△ABC沿A﹣D的方向平移AD 长，得△DEF（B、C的对应点分别为E、F），则BE长为．3．如图，在4×4的网格纸中，△ABC的三个顶点都在格点上．现要在这张网格纸中找出一格点作为旋转中心，绕着这个中心旋转后的三角形的顶点也在格点上，若旋转前后的两个三角形构成中心对称图形，那么满足条件的旋转中心有个．4．如图，∠AOB是放置在正方形网格中的一个角，则cos∠AOB的值是．5．已知：△ABC在直角坐标平面内，三个顶点的坐标分别为A（0，3）、B（3，4）、C（2，2）（正方形网格中每个小正方形的边长是一个单位长度）．（1）△ABC向下平移4个单位长度得到的△A1B1C1，点C1的坐标是；（2）以点B为位似中心，在网格内画出△A2B2C2，使△A2B2C2与△ABC位似，且位似比为2：1，点C2的坐标是；（画出图形）（3）△A2B2C2的面积是平方单位．【典型例题】例1．（1）如图所示的网格是正方形网格，则∠BAC﹣∠DAE＝°（点A，B，C，D，E是网格线交点）．（2）10个全等的小正方形拼成如图所示的图形，点P、X、Y是小正方形的顶点，Q是边XY一点．若线段PQ恰好将这个图形分成面积相等的两个部分，则的值为．例2．如图是4×4的正方形网格，每个小正方形的边长均为1且顶点称为格点，点A，B均在格点上．在网格中建立平面直角坐标系，且A（﹣1，1），B（1，2）．如果点C也在此4×4的正方形网格的格点上，且△ABC是等腰三角形，那么当△ABC的面积最大时，点C的坐标为．例3．如图，每个小正方形的边长都是1的方格纸中，有线段AB和线段CD，点A、B、C、D的端点都在小正方形的顶点上．（1）在方格纸中画出一个以线段AB为一边的菱形ABEF，所画的菱形的各顶点必须在小正方形的顶点上，并且其面积为20．（2）在方格纸中以CD为腰画出等腰三角形CDK，点K在小正方形的顶点上，且∠KCD＝45°．（3）在（1）、（2）的条件下，连接EK，请直接写出线段EK的长．例4．定义：如果一个直角三角形的两条直角边的比为1：2，那么这个三角形叫做“半正切三角形”．（1）如图①，正方形网格中，已知格点A，B，在格点C，D，E，F中，与A，B能构成“半正切三角形”的是点；（2）如图②，△ABC（BC＜AC）为“半正切三角形”，点M在斜边AB上，点D在边AC上，将射线MD绕点M逆时针旋转90°，所得射线交边BC于点E，连接DE．小彤发现：若M为斜边AB的中点，则△DEM一定为“半正切三角形”．请判断“小彤发现”是否正确？并说明理由；【巩固练习】1．如图，在5×4的正方形网格中，每个小正方形的边长都是1，△ABC的顶点都在这些小正方形的顶点上，则sin∠BAC的值为．2．如图，A、B、C三点在正方形网格线的交点处，若将△ACB绕着点A逆时针旋转得到△AC′B′，使点B′落在射线AC上，则cos∠B′CB的值为．3．如图所示的网格是正方形网格，点A，B，C，D均落在格点上，则∠BAC+∠ACD＝°．4．如图在8×8的正方形网格中，△ABC的顶点在边长为1的小正方形的顶点上．（1） 填空：∠ABC＝，BC＝．（2）若点A在网格所在的坐标平面里的坐标为（1，﹣2），请你在图中找出一点D，并作出以A、B、C、D四个点为顶点的平行四边形，求出满足条件的D点的坐标．5．已知△ABC中，AB＝，AC＝，BC＝6（1）如图1，点M为AB的中点，在线段AC上取点N，使△AMN与△ABC相似，求线段MN 的长；（2）如图2，是由100个边长为1的小正方形组成的10×10的正方形网格，设顶点在这些小正方形顶点的三角形为格点三角形．①请你在所给的网格中画出格点△A1B1C1与△ABC全等（画出一个即可，不需证明）②试直接写出所给的网格中与△ABC相似且面积最大的格点三角形的个数，并画出其中一个（不需证明）．6．在如图9×9的网格中，横纵坐标均为整数的点叫做格点，例如：A（1，1）、B（8，3）都是格点，E、F为小正方形边的中点，C为AE、BF的延长线的交点．（1）AE的长等于；（2）若点P在线段AC上，点Q在线段BC上，且满足AP＝PQ＝QB，无需画图，直接写出P、Q两点的坐标．7．如图是由边长相等的小正方形组成的网格，点A、B均在格点上．（1）在网格中，用无刻度的直尺画等腰直角三角形ACB．使∠ACB＝90；（2）在（1）的条件下，点D在AC上（点D可以不在格点上）．在网格中，用无刻度的直尺画出∠CBD，使tan∠CBD＝．8．按要求作图，不要求写作法，但要保留作图痕迹．（1）如图1，A为⊙O上一点，请用直尺（不带刻度）和圆规作出⊙O的内接正方形；（2）我们知道，三角形具有性质：三边的垂直平分线相交于同一点，三条角平分线相交于一点，三条中线相交于一点，事实上，三角形还具有性质：三条高所在直线相交于一点．请运用上述性质，只用直尺（不带刻度）作图．①如图2，在▱ABCD中，E为CD的中点，作BC的中点F．②如图3，在由小正方形组成的4×3的网格中，△ABC的顶点都在小正方形的顶点上，作△ABC的高AH．9．如图，半圆O的直径AB＝5cm，点M在AB上且AM＝1cm，点P是半圆O上的动点，过点B 作BQ⊥PM交PM（或PM的延长线）于点Q．设PM＝xcm，BQ＝ycm．（当点P与点A或点B 重合时，y的值为0）小石根据学习函数的经验，对函数y随自变量x的变化而变化的规律进行了探究．下面是小石的探究过程，请补充完整：（1）通过取点、画图、测量，得到了x与y的几组值，如下表：x/cm1 1.52 2.53 3.54y/cm0 3.7 3.8 3.3 2.5（2）建立平面直角坐标系，描出以补全后的表中各对对应值为坐标的点，画出该函数的图象；（3）结合画出的函数图象，解决问题：当BQ与直径AB所夹的锐角为60°时，PM的长度约为cm．10.如图，网格中每个小正方形边长为1，△ABC的顶点都在格点上．将△ABC向左平移2格，再向上平移3格，得到△A′B′C′．（1）请在图中画出平移后的△A′B′C′；（2）画出平移后的△A′B′C′的中线B′D′（3）若连接BB′，CC′，则这两条线段的关系是________（4）△ABC在整个平移过程中线段AB 扫过的面积为________（5）若△ABC与△ABE面积相等，则图中满足条件且异于点C的格点E共有______个。

中考数学之尺规作图真题汇编一、网格纸作图【2019·武汉】如图是由边长为1的小正方形构成的网格，每个小正方形的顶点叫做格点．四边形ABCD的顶点在格点上，点E是边DC与网格线的交点．请选择适当的格点，用无刻度的直尺在网格中完成下列画图，保留连线的痕迹，不要求说明理由．（1）如图1，过点A画线段AF，使AF∥DC，且AF＝DC．（2）如图1，在边AB上画一点G，使∠AGD＝∠BGC．（3）如图2，过点E画线段EM，使EM∥AB，且EM＝AB．【解答】解：（1）如图所示，线段AF即为所求；（2）如图所示，点G即为所求；（3）如图所示，线段EM即为所求．【2019·无锡】按要求作图，不要求写作法，但要保留作图痕迹．（1）如图1，A为⊙O上一点，请用直尺（不带刻度）和圆规作出⊙O的内接正方形；（2）我们知道，三角形具有性质：三边的垂直平分线相交于同一点，三条角平分线相交于一点，三条中线相交于一点，事实上，三角形还具有性质：三条高所在直线相交于一点．请运用上述性质，只用直尺（不带刻度）作图．①如图2，在▱ABCD中，E为CD的中点，作BC的中点F．②如图3，在由小正方形组成的4×3的网格中，△ABC的顶点都在小正方形的顶点上，作△ABC的高AH．【解答】解：（1）如图1，连结AO并延长交圆O于点C，作AC的中垂线交圆于点B，D，四边形ABCD即为所求．（2）①如图2，连结AC，BD交于点O，连结EB交AC于点G，连结DG并延长交CB 于点F，F即为所求②如图3所示，AH即为所求．【2020·安徽】如图1，在由边长为1个单位长度的小正方形组成的网格中，给出了以格点(网M N在网格线上，格线的交点)为端点的线段AB，线段,()1画出线段AB关于线段MN所在直线对称的线段11A B(点A B分别为,A B的对应点)；11()2将线段11B A ，绕点1B ，顺时针旋转90︒得到线段12B A ，画出线段12B A ．【答案】（1）见解析；（2）见解析．【解析】【分析】（1）先找出A ，B 两点关于MN 对称的点A 1，B 1，然后连接A 1B 1即可； （2）根据旋转的定义作图可得线段B 1A 2．【详解】（1）如图所示，11A B 即为所作；（2）如图所示，12B A 即为所作．【点睛】本题主要考查作图-旋转与轴对称，解题的关键是掌握旋转变换和轴对称的定义与性质．【2021·荆州】如图，在5×5的正方形网格图形中，小正方形的边长都为1，线段ED 与AD 的端点都在网格小正方形的顶点（称为格点）上．请在网格图形中画图：（1）以线段AD 为边画正方形ABCD ，再以线段DE 为斜边画等腰直角三角形DEF ，其中顶点F在正方形ABCD外；（2）在（1）中所画图形基础上，以点B为其中一个顶点画一个新正方形，使新正方形的面积为正方形ABCD和△DEF面积之和，其它顶点也在格点上．【分析】（1）根据正方形，等腰直角三角形的定义画出图形即可．（2）画出边长为的正方形即可．【解答】解：（1）如图，正方形ABCD，△DEF即为所求．（2）如图，正方形BKFG即为所求．二、角平分线【2021·铜仁】．如图，在Rt△ABC中，∠C＝90°，AB＝10，BC＝8，按下列步骤作图：步骤1：以点A为圆心，小于AC的长为半径作弧分别交AC、AB于点D、E．步骤2：分别以点D、E为圆心，大于DE的长为半径作弧，两弧交于点M．步骤3：作射线AM交BC于点F．则AF的长为（）A．6B．3C．4D．6【分析】利用基本作图得到AF平分∠BAC，过F点作FH⊥AB于H，如图，根据角平分线的性质得到FH＝FC，再根据勾股定理计算出AC＝6，设CF＝x，则FH＝x，然后利用面积法得到×10•x+×6•x＝×6×8，解得x＝3，最后利用勾股定理计算AF的长．【解答】解：由作法得AF平分∠BAC，过F点作FH⊥AB于H，如图，∵AF平分∠BAC，FH⊥AB，FC⊥AC，∴FH＝FC，在△ABC中，∵∠C＝90°，AB＝10，BC＝8，∴AC＝＝6，设CF＝x，则FH＝x，∵S△ABF+S△ACF＝S△ABC，∴×10•x+×6•x＝×6×8，解得x＝3，在Rt△ACF中，AF＝＝＝3．故选：B．三、垂直平分线【2019·泰州】如图，△ABC中，∠C＝90°，AC＝4，BC＝8．（1）用直尺和圆规作AB的垂直平分线；（保留作图痕迹，不要求写作法）（2）若（1）中所作的垂直平分线交BC于点D，求BD的长．【解答】解：（1）如图直线MN即为所求．（2）∵MN垂直平分线段AB，∴DA＝DB，设DA＝DB＝x，在Rt△ACD中，∵AD2＝AC2+CD2，∴x2＝42+（8﹣x）2，解得x＝5，∴BD＝5．【2021·北部湾】如图，四边形ABCD中，AB//CD，∠B=∠D，连接AC．(1)求证：△ABC≌△CDA；(2)尺规作图：过点C作AB的垂线，垂足为E(不要求写作法，保留作图痕迹)；(3)在(2)的条件下，已知四边形ABCD的面积为20，AB=5，求CE的长．【答案】(1)证明：∵AB//CD，∴∠ACD=∠CAB，在△ABC和△CDA中，{∠B=∠D∠CAB=∠ACD AC=CA，∴△ABC≌△CDA(AAS)；(2)解：过点C作AB的垂线，垂足为E，如图：(3)解：由(1)知：△ABC≌△CDA，∵四边形ABCD的面积为20，∴S△ABC=S△CDA=10，∴12AB⋅CE=10，∵AB=5，∴CE=4．【2019·盐城】如图，AD是△ABC的角平分线．（1）作线段AD的垂直平分线EF，分别交AB、AC于点E、F；（用直尺和圆规作图，标明字母，保留作图痕迹，不写作法．）（2）连接DE、DF，四边形AEDF是形．（直接写出答案）【解答】解：（1）如图，直线EF即为所求．（2）∵AD平分∠ABC，∴∠BAD＝∠CAD，∴∠BAD＝∠CAD，∵∠AOE＝∠AOF＝90°，AO＝AO，∴△AOE≌△AOF（ASA），∴AE＝AF，∵EF垂直平分线段AD，∴EA＝ED，F A＝FD，∴EA＝ED＝DF＝AF，∴四边形AEDF是菱形．故答案为菱形．四、全等或相似【2019·福建】如图，已知△ABC为和点A'.(1)以点A'为顶点求作△A'B'C',使△A'B'C'∽△ABC，S△A'B'C'=4S△ABC;(尺规作图，保留作图痕迹，不写作法)(2)设D、E、F分别是△ABC三边AB、BC、AC的中点，D'、E'、F'分别是你所作的△A'B'C'三边A'B'、B'C'、A'C'的中点，求证：△DEF∽△D'E'F'.(2)证明(略)【答案】见解析【解析】【2021·贵港】尺规作图（只保留作图痕迹，不要求写出作法）．如图，已知△ABC，且AB ＞AC．（1）在AB边上求作点D，使DB＝DC；（2）在AC边上求作点E，使△ADE∽△ACB．CBACBA【分析】（1）作线段BC的垂直平分线交AB于点D，连接CD即可．（2）作∠ADT＝∠ACB，射线DT交AC于点E，点E即为所求．【解答】解：（1）如图，点D即为所求．（2）如图，点E即为所求．五、三角形四心（内心、外心、重心、垂心）【2019·陇南】已知：在△ABC中，AB=AC．（1）求作：△ABC的外接圆．（要求：尺规作图，保留作图痕迹，不写作法）（2）若△ABC的外接圆的圆心O到BC边的距离为4，BC=6，则S⊙O=______．【答案】25π【解析】解：（1）如图⊙O即为所求．（2）设线段BC的垂直平分线交BC于点E．由题意OE=4，BE=EC=3，在Rt△OBE中，OB=√32+42=5，∴S圆O=π•52=25π．故答案为25π．（1）作线段AB，BC的垂直平分线，两线交于点O，以O为圆心，OB为半径作⊙O，⊙O即为所求．（2）在Rt△OBE中，利用勾股定理求出OB即可解决问题．本题考查作图-复杂作图，等腰三角形的性质，三角形的外接圆与外心等知识，解题的关键是熟练掌握基本知识，属于中考常考题型．五、其他类型【2021·山西】已知正方形ABCD的边长为4个单位长度，点E是CD的中点，请仅用无刻度直尺按下列要求作图（保留作图痕迹）．（1）在图1中，将直线AC绕着正方形ABCD的中心顺时针旋转45°；（2）在图2中，将直线AC向上平移1个单位长度．【分析】（1）根据正方形的性质和旋转的性质即可作出图形；（2）根据平移的性质即可作出图形．【解答】解：（1）如图1，直线l即为所求；（2）如图2中，直线a即为所求．。

关于网格图形问题我们知道，能够完全重合的两个图形，叫做全等形。

请你把下面4×4的正方形方格图形沿着虚线分割成两个全等的图形。

〖解〗：分割方法如下：〖反思〗：1、还有其它分割方法吗？2、从上面的分割方法中，你能发现分割的规律吗？题目：在△ABC中，AB=AC，CG⊥BA交BA的延长线与点G，一等腰三角尺按如图1所示的位置摆放，该三角尺的直角顶点为F，一直角边与AC边在一条直线上，另一条直角边恰好经过点B，（1）、在图1中，请你通过观察、测量BF与CG的长度，猜想并写出BF与CG满足的数量关系，然后证明你的猜想。

（图1）（2）、当三角尺沿AC方向平移到图2所示的位置时，一直角边仍与AC边在同一条直线上，另一条直角边交BC边于点D，过点D作DE⊥BA交BA于点E，此时，请你通过观察、测量DE、DF与CG 的长度，猜想并写出DE+DF与CG满足的数量关系，然后证明你的猜想。

（图2）（3）、当三角尺在（2）、的基础上沿AC方向继续平移到图3所示的位置（点F在线段AC上，且点F与点C不重合）时，（2）中的猜想是否仍然成立？（不用说明理由）（图3）〖点评〗：本题以图形的平移为素材，要求学生发现并证明自己所得的结论，将合情推理与逻辑推理融为一体，突出对数学思考的考察。

本题选自《2008年安徽省初中毕业学业考试纲要》数学试题样卷，仅题目文字就超过300字，又出现动点和平移问题，实在可以称之为一个“庞然大物”，如果你是一位初中生，千万不要被它吓到。

仔细审题，你会发现实际考察平时学习的两个小问题：1、等腰三角形两腰上的高相等（应用三角形的全等或三角形的面积公式证明）；2、等腰三角形底边上任意一点到两腰的距离和等于腰上的高（综合应用等腰三角形的性质、三角形的全等、矩形的判定和性质或三角形的面积公式证明）。

所以，在第一轮数学复习时，要注意概念复习和基础题的复习，不要脱离课本，注重数学思想和数学方法的复习。

对一些比较典型的题目，进行一题多思，一题多变，培养我们分析问题和解决问题的能力，以适应中考的需要。

2022年中考数学三轮复习：尺规作图一．选择题（共10小题）1．（2021•通山县模拟）如图，在直径为AB的半圆O中，C为半圆上一点，连接AC，BC，利用尺规在AB，AC上分别截取AD，AE，使AE＝AD；分别以D，E为圆心、以大于DE 的长为半径作弧，两弧在∠BAC内交于点F；作射线AF交BC于点G．若AC＝，AG ＝3，P为AB上一动点，则GP的最小值为（）A．2B．C．4D．无法确定2．（2021•兰州模拟）如图，在Rt△ABC中，∠C＝90°，以顶点A为圆心，小于AC的长为半径画弧，分别交AC，AB于点E，D．再分别以点E，D为圆心，大于DE的长为半径画弧，两弧在△ABC的内部交于点F，延长AF交BC于点G，若BG＝5，tan B＝，则AC＝（）A．B．C．8D．6 3．（2021•方城县三模）如图，点C在x轴上，OA＝OC，分别以点A，C为圆心、大于AC 的长为半径作弧，两弧交于点E，作射线OE，交AC于点B，在射线OE上任取一点D，连接DC．若BO＝AC＝8，CD＝5，则点D的坐标为（）A．（，4）B．（，4）C．（，4）D．（）4．（2021•思明区校级二模）如图，已知∠AOB，按以下步骤作图：①在射线OA上取一点，以点O为圆心，OC长为半径作，交射线OB于点D；②连接CD，分别以点C、D为圆心，CD长为半径作弧，交于点M、N；③连接OM，MN．根据以上作图过程及所作图形，下列结论中错误的是（）A．∠COM＝∠CODB．点M与点D关于直线OA对称C．若∠AOB＝20°，则D．MN∥CD5．（2021•天宁区校级二模）如图，在△ABC中，∠ABC＝90°，分别以点A和C为圆心，以大于AC的长为半径作弧，两弧相交于点M和N，作直线MN交AC于点E，交BC 于点F，若＝，则tan∠ACB的值为（）A．B．C．D．6．（2021•岳麓区校级三模）如图，在△ABC中，AD平分∠BAC，按如下步骤作图：第一步，分别以点A、D为圆心，大于AD的长为半径在AD两侧作弧，交于两点M、N；第二步，连接MN，分别交AB、AC于点E、F；第三步，连接DE，DF．若BD＝6，AF＝4，CD＝3，则BE的长是（）A．2B．4C．6D．8 7．（2021•荆州模拟）如图，在等腰△ABC中，AB＝AC＝．BC＝8，按下列步骤作图：①以点A为圆心，适当的长为半径作弧，分别交AB．AC于点E，F，再分别以点E，F为圆心，大于EF的长为半径作弧相交于点H，作射线AH；②分别以点A，B为圆心，大于AB的长为半径作弧相交于点M．N作直线MN．交射线AH于点O；③以点O为圆心，线段OA的长为半径作圆．则⊙O的半径为（）A．2B．10C．4D．5 8．（2021•河南模拟）如图，在▱ABCD中，以A为圆心，以AB长为半径作弧，交AD于点F，连接BF，再分别以B，F为圆心，以大于BF的长为半径作弧，两弧交于点G，连接AG并延长，交BC于点E，交BF于点M，则∠AMB的度数为（）A．80°B．90°C．100°D．120°9．（2021•定海区模拟）如图，在△ABC中，∠B＝2∠C，以点A为圆心，AB长为半径作弧，交BC于点D，交AC于点G；再分别以点B和点D为圆心，大于BD的长为半径作弧，两弧相交于点E，作射线AE交BC于点F，若以点G为圆心，GC长为半径作两段弧，一段弧过点C，而另一段弧恰好经过点D，则此时∠C度数为（）A．20°B．30°C．36°D．40°10．（2021•三门峡一模）如图，在平面直角坐标系中，△ABC为等腰直角三角形，A（﹣2，0），B（0，2），按以下步骤作图：①以点A为圆心，任意长为半径作弧，分别交AB，AC于点M，N；②再分别以点M，N为圆心，大于MN的长为半径作弧，两弧相交于点G，作射线AG，交BC于点E．则点E的坐标为（）A．（1，1）B．（1，4）C．（2，4）D．（2，2）二．填空题（共5小题）11．（2021•靖西市模拟）如图，菱形ABCD的边长为2，∠A＝45°，分别以点A和点B为圆心，大于AB的长为半径作弧，两弧相交于M，N两点，直线MN交AD于点E，连接CE，则CE的长为．12．（2021•荆州模拟）如图，已知直线AB及其外一点P，求作经过点P且与直线AB平行的直线．作法：（1）连接BP并延长至C，使PC＝PB，连接AC；（2）作线段AC的中垂线EF，与AC交于点D，则直线PD为所求．该作法用到的主要数学依据有．13．（2021•兴庆区校级二模）如图，在Rt△ABC中，∠C＝90°，按以下步骤作图：①以点A为圆心，以小于AC的长为半径作弧，分别交AC，AB于点M，N；②分别以点M，N 为圆心，以大于的长为半径作弧，两弧相交于点P；③连接AP，交BC于点D．若CD＝3，BD＝5，则AC的长为．14．（2021•梁园区二模）如图，在▱ABCD中，以A为圆心，以AB长为半径作弧，交AD 于点F，连接BF，再分别以B、F为圆心，以大于BF的长为半径作弧，两弧交于点G，连接AG并延长，交BC于点E，交BF于点M，则∠AMB的度数为．15．（2021•昆明模拟）如图，已知△ABC，AB＝BC＝1，∠B＝36°，以点A为圆心，任意长为半径作弧，分别交AB、AC于点M、N，分别以M、N为圆心，以大于MN长为半径作弧，两弧在∠BAC内交于点P，连接AP交BC于点E，则BE的长是．三．解答题（共5小题）16．（2021•南关区四模）如图是7×5的正方形网格，每个小正方形的边长为1，每个小正方形的顶点称为格点，△ABC的顶点均在格点上，回答下列问题．（要求：作图只用无刻度的直尺）（1）边AC的长度为；（2）作△ABC的角平分线AD；（3）已知点P在线段AB上，点Q在（2）作出的线段AD上，当PQ+BQ的长度最小时，在网格中作出△PBQ．17．（2021•思明区校级二模）如图，已知△ABC．（1）请用不带刻度的直尺和圆规在AC边上作一点D，使△ABD的周长等于AB+AC；（保留作图痕迹，不写作法）（2）在（1）的条件下，若AB＝BC＝3，CD＝．求证：AB⊥BD．18．（2021•思明区校级二模）如图，Rt△ACB中，∠C＝90°，点O为边AB中点，且AB ＝10，AC＜BC．（1）请用尺规作图在BC上作一点D，使得BD＝AC+CD；（不写作法，保留痕迹）（2）在（1）的条件下，连接OD，若OD＝，求Rt△ABC的面积．19．（2021•福建模拟）如图，菱形ABCD中，∠B＝60°，AC为对角线，P是边BC延长线上一点，连接AP．（1）在线段AP上求作点M，使得∠AMC＝120°（要求：尺规作图，保留痕迹，不写作法）；（2）在（1）的作图条件下，直线AB交直线CM与点Q，求证：P，D，Q三点共线．20．（2021•武汉模拟）如图是由边长为1的小正方形构成的网格，每个小正方形的顶点叫格点，△ABC的顶点都在格点上，请仅用无刻度的直尺在所给的网格中完成下列画（画图过程用虚线，画图结果用实线）：（1）△ABC的周长为；（2）如图1，点D，P分别是AB与竖格和横格线的交点、画出点P关于过点D竖格线的对称点Q；（3）在图1中画△ABC的角平分线BE；（4）将边AB绕点B逆时针旋转∠ABC的度数得到线段BF，在图2中画出点F．2022年中考数学三轮复习：尺规作图参考答案与试题解析一．选择题（共10小题）1．（2021•通山县模拟）如图，在直径为AB的半圆O中，C为半圆上一点，连接AC，BC，利用尺规在AB，AC上分别截取AD，AE，使AE＝AD；分别以D，E为圆心、以大于DE 的长为半径作弧，两弧在∠BAC内交于点F；作射线AF交BC于点G．若AC＝，AG ＝3，P为AB上一动点，则GP的最小值为（）A．2B．C．4D．无法确定【考点】作图—复杂作图；勾股定理．【专题】作图题；几何直观；推理能力．【分析】利用基本作图得到AG平分∠BAC，再根据圆周角定理得到∠C＝90°，则利用勾股定理可计算出CG＝2，接着利用角平分线的性质得到GH＝GC＝2，然后根据垂线段最短求解．【解答】解：由作法得AG平分∠BAC，∵AB为直径，∴∠C＝90°，在Rt△ACG中，CG＝＝＝2，∵AG平分∠BAC，GC⊥AC，GH⊥AB，∴GH＝GC＝2，∵P为AB上一动点，∴GP的最小值为2．故选：A．【点评】本题考查了作图﹣复杂作图：解决此类题目的关键是熟悉基本几何图形的性质，结合几何图形的基本性质把复杂作图拆解成基本作图，逐步操作．也考查了角平分线的性质、圆周角定理和垂线段最短．2．（2021•兰州模拟）如图，在Rt△ABC中，∠C＝90°，以顶点A为圆心，小于AC的长为半径画弧，分别交AC，AB于点E，D．再分别以点E，D为圆心，大于DE的长为半径画弧，两弧在△ABC的内部交于点F，延长AF交BC于点G，若BG＝5，tan B＝，则AC＝（）A．B．C．8D．6【考点】角平分线的性质；作图—基本作图；解直角三角形．【专题】作图题；几何直观；推理能力．【分析】过G点作GH⊥AB于H，如图，由作法得AG平分∠BAC，根据角平分线的性质得到GH＝GC，利用正切的定义得到tan B＝＝，则可设GH＝3t，BH＝4t，所以BG＝5t＝5，解得t＝1，从而得到CG＝GH＝3，然后在Rt△ABC中利用正切的定义可求出AC的长．【解答】解：过G点作GH⊥AB于H，如图，由作法得AG平分∠BAC，而GH⊥AB，GC⊥AC，∴GH＝GC，在Rt△BGH中，∵tan B＝＝，∴设GH＝3t，BH＝4t，∴BG＝5t，即5t＝5，解得t＝1，∴CG＝GH＝3，∴BC＝BG+CG＝5+3＝8，在Rt△ABC中，∵tan B＝＝，∴AC＝BC＝×8＝6．故选：D．【点评】本题考查了作图﹣基本作图：熟练掌握5种基本作图是解决此类问题的关键．也考查了角平分线的性质和解直角三角形．3．（2021•方城县三模）如图，点C在x轴上，OA＝OC，分别以点A，C为圆心、大于AC 的长为半径作弧，两弧交于点E，作射线OE，交AC于点B，在射线OE上任取一点D，连接DC．若BO＝AC＝8，CD＝5，则点D的坐标为（）A．（，4）B．（，4）C．（，4）D．（）【考点】作图—复杂作图．【专题】作图题；几何直观；推理能力．【分析】利用基本作图可判断OD平分∠AOC，则根据等腰三角形的性质得到OD⊥AC，AB＝CB＝4，再利用勾股定理计算出BD＝3，OC＝4，作DH⊥x轴于H，如图，证明△OBC∽△OHD，然后利用相似比计算出OH、DH，从而得到D点坐标．【解答】解：由作法得OD平分∠AOC，∵OA＝OC，∴OD⊥AC，AB＝CB＝AC＝×8＝4，在Rt△CBD中，BD＝＝＝3，在Rt△OBC中，OC＝＝＝4，作DH⊥x轴于H，如图，∵∠COB＝∠DOH，∠OBC＝∠OHD，∴△OBC∽△OHD，∴＝＝，即＝＝，∴OH＝，DH＝，∴D点坐标为（，）．故选：D．【点评】本题考查了作图﹣复杂作图：解决此类题目的关键是熟悉基本几何图形的性质，结合几何图形的基本性质把复杂作图拆解成基本作图，逐步操作．也考查了等腰三角形的性质和相似三角形的判定与性质．4．（2021•思明区校级二模）如图，已知∠AOB，按以下步骤作图：①在射线OA上取一点，以点O为圆心，OC长为半径作，交射线OB于点D；②连接CD，分别以点C、D为圆心，CD长为半径作弧，交于点M、N；③连接OM，MN．根据以上作图过程及所作图形，下列结论中错误的是（）A．∠COM＝∠CODB．点M与点D关于直线OA对称C．若∠AOB＝20°，则D．MN∥CD【考点】平行线的判定；作图—复杂作图；轴对称的性质．【专题】作图题；几何直观．【分析】根据等弧所对圆周角相等可以判断A；根据平行线的判定可以判断D；根据CM ＝CD，OM＝OD，可得OA垂直平分MD，可以判断B；根据∠AOB＝∠AOM＝∠BON ＝20°，得∠MON＝60°，由OM＝ON，可得△OMN为等边三角形，进而可以判断C．【解答】解：由作法得CM＝CD，∴＝，∴∠COM＝∠COD，所以A选项的结论正确；连接MD，∵＝，∴∠DMN＝∠MDC，∴CD∥MN，所以D选项的结论正确；∵CM＝CD，OM＝OD，∴OA垂直平分MD，∴点M与点D关于OA对称，所以B选项的结论正确；∵∠AOB＝∠AOM＝∠BON＝20°，∴∠MON＝60°，∵OM＝ON，∴△OMN为等边三角形，∴OM＝MN，所以C选项的结论错误．故选：C．【点评】本题考查了作图﹣复杂作图：复杂作图是在五种基本作图的基础上进行作图，一般是结合了几何图形的性质和基本作图方法．解决此类题目的关键是熟悉基本几何图形的性质，结合几何图形的基本性质把复杂作图拆解成基本作图，逐步操作．也考查了圆心角、弧、弦的关系和垂径定理．5．（2021•天宁区校级二模）如图，在△ABC中，∠ABC＝90°，分别以点A和C为圆心，以大于AC的长为半径作弧，两弧相交于点M和N，作直线MN交AC于点E，交BC 于点F，若＝，则tan∠ACB的值为（）A．B．C．D．【考点】线段垂直平分线的性质；作图—基本作图；解直角三角形．【专题】作图题；几何直观；推理能力．【分析】连接AF，设AF＝CF＝5k，BF＝3k，利用勾股定理求出AB，可得结论．【解答】解：连接AF．由作图可知，MN垂直平分线段AC，∴F A＝FC，∵BF：FC＝3：5，∴可以假设BF＝3k，CF＝AF＝5k，∵∠B＝90°，∴AB＝＝＝4k，∴BC＝BF+CF＝8k，∴tan∠ACB＝＝＝，故选：D．【点评】本题考查作图﹣基本作图，线段的垂直平分线，解直角三角形等知识，解题的关键是学会利用参数解决问题，属于中考常考题型．6．（2021•岳麓区校级三模）如图，在△ABC中，AD平分∠BAC，按如下步骤作图：第一步，分别以点A、D为圆心，大于AD的长为半径在AD两侧作弧，交于两点M、N；第二步，连接MN，分别交AB、AC于点E、F；第三步，连接DE，DF．若BD＝6，AF＝4，CD＝3，则BE的长是（）A．2B．4C．6D．8【考点】线段垂直平分线的性质；作图—复杂作图．【专题】作图题；推理能力；应用意识．【分析】根据已知得出MN是线段AD的垂直平分线，推出AE＝DE，AF＝DF，求出DE ∥AC，DF∥AE，得出四边形AEDF是菱形，根据菱形的性质得出AE＝DE＝DF＝AF，根据平行线分线段成比例定理得出＝，代入求出即可．【解答】解：∵根据作法可知：MN是线段AD的垂直平分线，∴AE＝DE，AF＝DF∴∠EAD＝∠EDA，∵AD平分∠BAC，∴∠BAD＝∠CAD，∴∠EDA＝∠CAD，∴DE∥AC，同理DF∥AE，∴四边形AEDF是菱形，∴AE＝DE＝DF＝AF，∵AF＝4，∴AE＝DE＝DF＝AF＝4，∵DE∥AC，∴＝，∵BD＝6，AE＝4，CD＝3，∴＝，∴BE＝8，故选：D．【点评】本题考查了平行线分线段成比例定理，菱形的性质和判定，线段垂直平分线性质，等腰三角形的性质的应用，能根据定理四边形AEDF是菱形是解此题的关键，注意：一组平行线截两条直线，所截得的对应线段成比例．7．（2021•荆州模拟）如图，在等腰△ABC中，AB＝AC＝．BC＝8，按下列步骤作图：①以点A为圆心，适当的长为半径作弧，分别交AB．AC于点E，F，再分别以点E，F为圆心，大于EF的长为半径作弧相交于点H，作射线AH；②分别以点A，B为圆心，大于AB的长为半径作弧相交于点M．N作直线MN．交射线AH于点O；③以点O为圆心，线段OA的长为半径作圆．则⊙O的半径为（）A．2B．10C．4D．5【考点】作图—复杂作图；等腰三角形的性质．【专题】作图题；几何直观；运算能力；推理能力．【分析】设OA交BC于T．解直角三角形求出AT，再在Rt△OCT中，利用勾股定理构建方程即可解决问题．【解答】解：如图，设OA交BC于T．半径为r，∵AB＝AC＝2，AO平分∠BAC，∴AO⊥BC，BT＝TC＝BC＝4，∴AT＝＝＝2，设圆的半径为r，在Rt△OCT中，则有r2＝（r﹣2）2+42，解得r＝5，故选：D．【点评】本题考查作图﹣复杂作图，等腰三角形的性质，垂径定理等知识，解题的关键是理解题意，灵活运用所学知识解决问题．8．（2021•河南模拟）如图，在▱ABCD中，以A为圆心，以AB长为半径作弧，交AD于点F，连接BF，再分别以B，F为圆心，以大于BF的长为半径作弧，两弧交于点G，连接AG并延长，交BC于点E，交BF于点M，则∠AMB的度数为（）A．80°B．90°C．100°D．120°【考点】平行四边形的性质；作图—复杂作图．【专题】作图题；几何直观．【分析】利用等腰三角形的三线合一的性质解决问题即可．【解答】解：由作图可知，AF＝AB，AM平分∠BAD，∴AM⊥BF，∴∠AMB＝90°，故选：B．【点评】本题考查作图﹣复杂作图，平行四边形的性质，等腰三角形的三线合一的性质等知识，解题的关键是理解题意，灵活运用所学知识解决问题．9．（2021•定海区模拟）如图，在△ABC中，∠B＝2∠C，以点A为圆心，AB长为半径作弧，交BC于点D，交AC于点G；再分别以点B和点D为圆心，大于BD的长为半径作弧，两弧相交于点E，作射线AE交BC于点F，若以点G为圆心，GC长为半径作两段弧，一段弧过点C，而另一段弧恰好经过点D，则此时∠C度数为（）A．20°B．30°C．36°D．40°【考点】作图—复杂作图．【专题】作图题；几何直观．【分析】连接AD，根据作图过程可得，AE是BD的垂直平分线，DG＝CG，AB＝AD＝AG，设∠C＝x，则∠CDG＝x，∠AGD＝2x，根据∠ADB+∠ADG+∠GDC＝2x+2x+x＝180°，求出x的值即可．【解答】解：如图，连接AD，根据作图过程可知：AE是BD的垂直平分线，DG＝CG，AB＝AD＝AG，设∠C＝x，则∠CDG＝x，∠AGD＝2x，∴∠ADG＝∠AGD＝2x，∵∠B＝2∠C，∴∠B＝2x，∵AD＝AB，∴∠ADB＝∠B＝2x，∴∠ADB+∠ADG+∠GDC＝2x+2x+x＝180°，∴x＝36°，∴∠C＝36°，故选：C．【点评】本题考查了作图﹣复杂作图，解决本题的关键是理解作图过程，利用线段垂直平分线的性质、等腰三角形的性质、三角形外角的性质．10．（2021•三门峡一模）如图，在平面直角坐标系中，△ABC为等腰直角三角形，A（﹣2，0），B（0，2），按以下步骤作图：①以点A为圆心，任意长为半径作弧，分别交AB，AC于点M，N；②再分别以点M，N为圆心，大于MN的长为半径作弧，两弧相交于点G，作射线AG，交BC于点E．则点E的坐标为（）A．（1，1）B．（1，4）C．（2，4）D．（2，2）【考点】坐标与图形性质；等腰直角三角形；作图—复杂作图．【专题】作图题；等腰三角形与直角三角形；运算能力；推理能力．【分析】过点E作EH⊥AC于点H，由题目作图知，AD是∠CAB的平分线，则EH＝EB，AB＝AH，证明△CEH是等腰直角三角形，进而求解．【解答】解：过点E作EH⊥AC于点H，由题目作图知，AE是∠CAB的平分线，则EH＝EB，∴AB＝AH，∵△ABC为等腰直角三角形，故∠ACB＝45°，则△EHC为等腰直角三角形，故EH＝HC，∵A（﹣2，0），B（0，2），∴OA＝OB＝OC＝2，∴AB＝2，∴AH＝2，∴OH＝OC﹣CH＝2﹣CH，∴AH＝OA+OH＝4﹣CH，∴4﹣CH＝2，∴CH＝4﹣2，∴OH＝2﹣CH＝2﹣（4﹣2）＝2﹣2．∴点E的坐标为（2，4）．故选：C．【点评】本题考查的是作图﹣复杂作图，坐标与图形性质，角平分线的性质，等腰直角三角形的性质等，有一定的综合性，难度适中．解决本题的关键是掌握角平分线的作法．二．填空题（共5小题）11．（2021•靖西市模拟）如图，菱形ABCD的边长为2，∠A＝45°，分别以点A和点B为圆心，大于AB的长为半径作弧，两弧相交于M，N两点，直线MN交AD于点E，连接CE，则CE的长为．【考点】作图—基本作图；线段垂直平分线的性质；菱形的性质．【专题】作图题；几何直观；推理能力．【分析】连接BE，如图，利用基本作图可判断MN垂直平分AB，则EA＝EB，所以∠EBA＝∠A＝45°，再根据菱形的性质得到AB＝BC＝2，AD∥BC，所以AE＝BE＝，然后利用平行线的性质得到∠EBC＝∠AEB＝90°，最后利用勾股定理可计算出CE的长．【解答】解：连接BE，如图，由作法得MN垂直平分AB，∴EA＝EB，∴∠EBA＝∠A＝45°，∴∠AEB＝90°，∵菱形ABCD的边长为2，∴AB＝BC＝2，AD∥BC，∴AE＝BE＝AB＝，∵AE∥BC，∴∠EBC＝∠AEB＝90°，∴CE＝＝＝．故答案为：．【点评】本题考查了作图﹣基本作图：熟练掌握5种基本作图是解决此类问题的关键．也考查了线段垂直平分线的性质和菱形的性质．12．（2021•荆州模拟）如图，已知直线AB及其外一点P，求作经过点P且与直线AB平行的直线．作法：（1）连接BP并延长至C，使PC＝PB，连接AC；（2）作线段AC的中垂线EF，与AC交于点D，则直线PD为所求．该作法用到的主要数学依据有三角形中位线平行于第三边．【考点】平行线的性质；线段垂直平分线的性质；三角形中位线定理；作图—复杂作图．【专题】作图题；几何直观．【分析】利用三角形中位线定理解决问题即可．【解答】解：由作图可知：BP＝PC，AD＝CD，∴PD∥AB（三角形的中位线平行于第三边），故答案为：三角形的中位线平行于第三边．【点评】本题考查作图﹣复杂作图，三角形中位线定理，线段的垂直平分线等知识，解题的关键是灵活运用所学知识解决问题．13．（2021•兴庆区校级二模）如图，在Rt△ABC中，∠C＝90°，按以下步骤作图：①以点A为圆心，以小于AC的长为半径作弧，分别交AC，AB于点M，N；②分别以点M，N 为圆心，以大于的长为半径作弧，两弧相交于点P；③连接AP，交BC于点D．若CD＝3，BD＝5，则AC的长为6．【考点】作图—复杂作图；角平分线的性质．【专题】作图题；几何直观．【分析】作DE⊥AB，由作图知AP平分∠BAC，依据∠C＝∠AED＝90°知CD＝DE＝3，结合BD＝5知BE＝4，再证Rt△ACD≌Rt△AED得AC＝AE，设AC＝AE＝x，由AC2+BC2＝AB2得x2+82＝（x+4）2，解之可得答案．【解答】解：如图所示，过点D作DE⊥AB于点E，由作图知AP平分∠BAC，∵∠C＝∠AED＝90°，∴CD＝DE＝3，∵BD＝5，∴BE＝4，∵AD＝AD，CD＝DE，∴Rt△ACD≌Rt△AED（HL），∴AC＝AE，设AC＝AE＝x，由AC2+BC2＝AB2得x2+82＝（x+4）2，解得：x＝6，即AC＝6，故答案为：6．【点评】本题主要考查作图﹣复杂作图，解题的关键是掌握角平分线的尺规作图及角平分线的性质、勾股定理等知识点．14．（2021•梁园区二模）如图，在▱ABCD中，以A为圆心，以AB长为半径作弧，交AD 于点F，连接BF，再分别以B、F为圆心，以大于BF的长为半径作弧，两弧交于点G，连接AG并延长，交BC于点E，交BF于点M，则∠AMB的度数为90°．【考点】平行四边形的性质；作图—复杂作图．【专题】作图题；推理填空题；多边形与平行四边形；几何直观；推理能力．【分析】连接FE，首先证明四边形ABEF是菱形，根据菱形的性质即可得结论．【解答】解：如图，结论EF，由作图可知：AB＝AF，AE平分∠BAD，∵四边形ABCD是平行四边形，∴AD∥BC，∴∠F AE＝∠AEB＝∠BAE，∴AB＝BE，∴AF＝BE，∵AF∥BE，∴四边形ABEF是平行四边形，∵AB＝AF，∴四边形ABEF是菱形，∴AE⊥BF，∴∠AMB＝90°．故答案为：90°．【点评】本题考查平行四边形的性质和角平分线的性质等知识，解题的关键是灵活运用所学知识解决问题，属于中考常考题型．15．（2021•昆明模拟）如图，已知△ABC，AB＝BC＝1，∠B＝36°，以点A为圆心，任意长为半径作弧，分别交AB、AC于点M、N，分别以M、N为圆心，以大于MN长为半径作弧，两弧在∠BAC内交于点P，连接AP交BC于点E，则BE的长是．【考点】解一元二次方程﹣公式法；角平分线的性质；等腰三角形的性质；作图—基本作图；相似三角形的判定与性质．【专题】作图题；等腰三角形与直角三角形；几何直观；运算能力；推理能力．【分析】根据作图过程可得AE平分∠BAC，根据AB＝BC＝1，∠B＝36°，可得BE＝AE＝AC，证明△BAC∽△AEC，对应边成比例解方程即可求出BE的长．【解答】解：∵AB＝BC＝1，∠B＝36°，∴∠BAC＝∠C＝72°，根据作图过程可知：AE平分∠BAC，∴∠BAE＝∠CAE＝BAC＝36°，∴∠B＝∠BAE＝∠CAE，∴BE＝AE，∵∠AEC＝∠B+∠BAE＝72°，∴∠AEC＝∠C，∴AE＝AC，∴BE＝AE＝AC，∴△BAC∽△AEC，∴＝，∴＝，解得BE＝（舍去），故答案为：．【点评】本题考查的是作图﹣基本作图，角平分线的性质，等腰三角形的性质，相似三角形的判定与性质，解一元二次方程熟练掌握角平分线的性质是解题的关键．三．解答题（共5小题）16．（2021•南关区四模）如图是7×5的正方形网格，每个小正方形的边长为1，每个小正方形的顶点称为格点，△ABC的顶点均在格点上，回答下列问题．（要求：作图只用无刻度的直尺）（1）边AC的长度为5；（2）作△ABC的角平分线AD；（3）已知点P在线段AB上，点Q在（2）作出的线段AD上，当PQ+BQ的长度最小时，在网格中作出△PBQ．【考点】勾股定理；作图—应用与设计作图；轴对称﹣最短路线问题．【专题】作图题；网格型；平移、旋转与对称；几何直观．【分析】（1）利用网格根据勾股定理即可求出边AC的长度；（2）根据网格即可作△ABC的角平分线AD；（3）已知点P在线段AB上，点Q在（2）作出的线段AD上，当PQ+BQ的长度最小时，在网格中作出△PBQ．【解答】解：（1）根据勾股定理，得AC＝＝5．故答案为：5；（2）如图，AD即为所求；（2）如图，△PBQ即为所求．【点评】本题考查了作图﹣应用与设计作图，勾股定理，轴对称﹣最短路线问题，解决本题的关键是掌握轴对称的性质．17．（2021•思明区校级二模）如图，已知△ABC．（1）请用不带刻度的直尺和圆规在AC边上作一点D，使△ABD的周长等于AB+AC；（保留作图痕迹，不写作法）（2）在（1）的条件下，若AB＝BC＝3，CD＝．求证：AB⊥BD．【考点】作图—复杂作图；勾股定理的逆定理．【专题】作图题；推理能力；应用意识．【分析】（1）作线段BC的垂直平分线交AC于点D，连接BD即可；（2）证明△DBC∽△BAC，推出，可得，，再利用勾股定理的逆定理证明即可．【解答】（1）解：如图，点D为所作；（2）证明：∵AB＝AC，∴∠A＝∠C，由（1）点D在BC的垂直平分线上，∴∠DBC＝∠C，∴∠DBC＝∠A，∵∠C＝∠C，∴△DBC∽△BAC，∴，∴BC2＝AC⋅DC，∴，∴，∵，AB＝3，∴AB2+BD2＝AD2，∴△ABD是直角三角形，∠ABD＝90°，∴AB⊥BD．【点评】本题考查作图﹣复杂作图，相似三角形的判定和性质，勾股定理的逆定理等知识，解题的关键是正确寻找相似三角形解决问题，属于中考常考题型．18．（2021•思明区校级二模）如图，Rt△ACB中，∠C＝90°，点O为边AB中点，且AB ＝10，AC＜BC．（1）请用尺规作图在BC上作一点D，使得BD＝AC+CD；（不写作法，保留痕迹）（2）在（1）的条件下，连接OD，若OD＝，求Rt△ABC的面积．【考点】作图—复杂作图；三角形的面积；直角三角形斜边上的中线．【专题】作图题；几何直观；推理能力．【分析】（1）在BC延长线上截取CE＝AC，然后作BE的垂直平分线交BC于点D，即可解决问题；（2）连接AE，OD，证明OD是△AEB的中位线，可得AE＝2OD＝6，根据等腰直角三角形可得AC＝6，利用勾股定理可得BC＝8，进而可以解决问题．【解答】解：（1）如图，点D即为所求；（2）如上图，连接AE，OD，∵OA＝OB，DB＝DE，OD＝，∴OD是△AEB的中位线，∴AE＝2OD＝6，∵∠ACE＝90°，AC＝CE，∴AC＝AE＝6，∵AB＝10，∴BC＝＝8，∴S△ABC＝6×8＝24．∴Rt△ABC的面积为24．【点评】本题考查了作图﹣复杂作图，三角形的面积，直角三角形斜边上的中线，线段垂直平分线的性质，等腰直角三角形的性质，解决本题的关键是掌握线段垂直平分线的作法．19．（2021•福建模拟）如图，菱形ABCD中，∠B＝60°，AC为对角线，P是边BC延长线上一点，连接AP．（1）在线段AP上求作点M，使得∠AMC＝120°（要求：尺规作图，保留痕迹，不写作法）；（2）在（1）的作图条件下，直线AB交直线CM与点Q，求证：P，D，Q三点共线．【考点】作图—复杂作图；等边三角形的判定与性质；菱形的性质．【专题】作图题；证明题；矩形菱形正方形；几何直观；推理能力．【分析】（1）记AP与CD交于点N，在AD上截取AR＝DN，连接CR交AP于点M，即可在线段AP上求作点M，使得∠AMC＝120°；（2）根据菱形的性质证明△CAQ∽△PCA，可得，由AC＝AD＝CD，所以，再由∠QAD＝∠DCP＝60°，证明△QAD∽△DCP，可得∠AQD＝∠CDP，进而可得∠QDP＝180°，即得Q，D，P三点共线．【解答】解：（1）如图，点M即为所求；（可以尺规作出△ABC的外接圆与AP的交点M；还可以记AP与CD交于点N，在AD 上截取AR＝DN，连接CR交AP于点M）．（2）证明：如图，∵四边形ABCD是菱形，∠B＝60°∴∠ACB＝60°，AC＝AD＝CD，∵∠AMC＝120°，∴∠3＝60°，∴∠1+∠2＝60°，又∠ACB＝60°，∴∠1+∠CP A＝60°，∴∠2＝∠CP A，∵AC为对角线，∴∠CAQ＝∠PCA＝120°，∴△CAQ∽△PCA，∴，∵AC＝AD＝CD，∴，∵∠QAD＝∠DCP＝60°，∴△QAD∽△DCP，∴∠AQD＝∠CDP，在△QAD中，∠AQD+∠QDA＝120°，∴∠CDP+∠QDA＝120°，∴∠CDP+∠QDA+∠ADC＝180°，∴∠QDP＝180°，∴Q，D，P三点共线．【点评】本题考查了作图﹣复杂作图，菱形的性质，相似三角形的判定与性质，解决本题的关键是得到△QAD∽△DCP．20．（2021•武汉模拟）如图是由边长为1的小正方形构成的网格，每个小正方形的顶点叫格点，△ABC的顶点都在格点上，请仅用无刻度的直尺在所给的网格中完成下列画（画图过程用虚线，画图结果用实线）：（1）△ABC的周长为9+；（2）如图1，点D，P分别是AB与竖格和横格线的交点、画出点P关于过点D竖格线的对称点Q；（3）在图1中画△ABC的角平分线BE；（4）将边AB绕点B逆时针旋转∠ABC的度数得到线段BF，在图2中画出点F．【考点】勾股定理；勾股定理的逆定理；作图—应用与设计作图；旋转的性质．【专题】作图题；几何直观．【分析】（1）利用勾股定理求出AB，AC，可得结论．（2）连接CD交网格线于Q，点Q即为所求作．（3）取格点E，作射线BE即可．（4）取格点P，作射线CP，取格点M，N连接MN交CP于C′，作射线BC′，取格点Q，K，作直线QK交射线BC′于点F，点F即为所求作．【解答】解：（1）∵AB＝＝5，AC＝＝，BC＝4，∴△ABC的周长＝9+，故答案为：9+．（2）如图1中，点Q即为所求作．（3）如图2中，射线BE即为所求作．（4）如图2中，点F即为所求作．【点评】本题考查作图﹣应用与设计作图，平行四边形的判定和性质，菱形的判定和性质等知识，解题的关键是熟练掌握基本知识，属于中考常考题型．。

中考网格作图题的命题立意及解答策略本文对2019年全国各地中考网格作图问题进行梳理, 提炼其命题意图, 并归纳网格作图问题的解题策略, 以期与同行交流探讨。

一、技能立意, 计算作答在格点画图中, 以画图技能立意的试题通常都比较基础, 考查的知识点比较单一, 以格点画图为主要考查目标.例1 (2019年哈尔滨中考题)图1.2是两张形状和大小完全相同的方格纸, 方格纸中每个小正方形的边长均为1, 线段的两个端点均在小正方形的顶点上.(1)在图1中画出以为底边的等腰, 点在小正方形顶点上;(2)在图2中画出以为腰的等腰, 点在小正方形的顶点上, 且的面积为8.分析第(1)问, 要确定格点的位置, 从“形”的角度出发, 点是的垂直平分线和以为直径的圆的交点.从“数”的角度出发, 先由勾股定理, 可以算出, 以为底的等腰直角三角形的腰长, 从而可以确定点的位置(如图3).第(2)问, “画出为腰的等腰”, 既要考虑的情况, 又要考虑的情况, 再根据条件“的面积为8”确定点的位置(如图4).例2 (2019年长春中考题)图5.图6.图7均是的正方形网格, 每个小正方形的顶点称为格点, 小正方形的边长为1, 点均在格点上。

在图5.图6.图7中, 只用无刻度的直尺, 在给定的网格中按要求画图, 所画图形的顶点均在格点上, 不要求写出画法.(1)在图5中以线段为边画一个, 使其面积为6;(2)在图6中以线段为边画一个, 使其面积为6;(3)在图7中以线段为边画一个四边形, 使其面积为9, 且.格点, 如图8(答案不唯一).当底为4时, 面积就为6, 如图9(答案不唯一).第(3)问, 我们知道边长为3的正方形的面积为9, 但不是网格上的边, 我们可用割补法来得到我们想要的图形, 如图10所示, , 则.解题策略在网格中作图, 最基本、最常规的问题就是利用正方形网格的边长为1, 运用勾股定理计算格点线段的长度, 或是利用网格线平行或垂直的基本特征画平行线和垂线.本类型常见的问题跟图形的周长、面积联系比较多, 遇到这类问题的时候, 要先算出周长、面积, 然后利用割补, 平移、旋转等手段来解决.二、思维立意, 分析推理很多格点作图问题, 考查的结果是画图, 实际上是以格点为依托, 把考查逻辑推理能力和分析问题、解决问题的能力融合在一起二例3 (2019年嘉兴中考题)在的方格纸中, 点都在格点上, 按要求画.(1)在图11中找一个格点, 使以点为顶点的四边形是平行四边形;(2)在图12中仅用无刻度的直尺, 把线段三等分(保留画图痕迹, 不写画法).分析第(1)问, 当考虑以为对角线构造平行四边形时, 根据“两组对边分别平行的四边形是平行四边形”, 找到的平行线, 的平行线, 交点即为点.或者根据“两组对边分别相等的四边形是平行四边形”, 找到格点.(如图13, 答案不唯一)第(2)问, 显然在上不能直接找到三等分点.但我们可以另外找到一条三个单位长度的格点线段, 点为的三等分格点.根据“平行线分线段成比例”, 只要过点分别作出的平行线, 就能把线段三等分了。

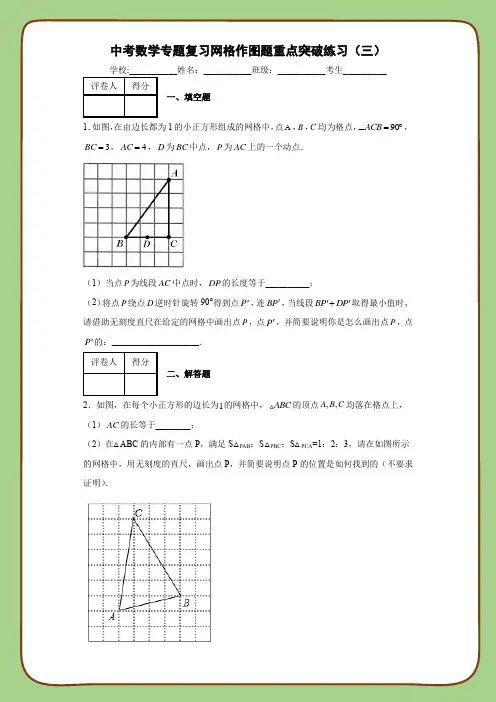
2021年天津市数学中考专题训练网格作图题31.如图，在每个小正方形的边长为1的网格中，A，B，C均在格点上．（Ⅰ）△ABC的面积为______；（Ⅱ）若有一个边长为6的正方形，且满足点A为该正方形的一个顶点，且点B，点C 分别在该正方形的两条边上，请在如图所示的网格中，用无刻度的直尺，画出这个正方形，并简要说明其它顶点的位置是如何找到的（不要求证明）______．2.如图，在每个小正方形的边长为1的网格中，A，B，C均为格点．（Ⅰ）△ABC的面积等于______；（Ⅱ）请用无刻度的直尺，在如图所示的网格中画出△ABC的角平分线BD，并在AB 边上画出点P，使得PB=PD，并简要说明△ABC的角平分线BD及点P的位置是如何找到的（不要求证明）．3.在每个小正方形的边长为1的网格中，点A，B，C均在格点上，点P，Q分别为线段AB，AC上的动点．（Ⅰ）如图（1），当点P，Q分别为AB，AC中点时，PC+PQ的值为______；（Ⅱ）当PC+PQ取得最小值时，在如图（2）所示的网格中，用无刻度的直尺，画出线段PC，PQ，简要说明点P和点Q的位置是如何找到的______．4.如图，在每个小正方形的边长为1的网格中，A，B，C为格点，D为小正方形边的中点．（I）AC的长等于______；（II）点P，Q分别为线段BC，AC上的动点，当PD+PQ取得最小值时，请在如图所示的网格中，用无刻度的直尺，画出线段PD，PQ，并简要说明点P和点Q的位置是如何找到的（不要求证明）______．5.如图，在每个小正方形的边长为1的网格中，△ABC的顶点A，B，C均落在格点上．；（Ⅰ）AC的长等于______；（Ⅱ）点P落在格点上，M是边BC上任意一点，点B关于直线AM的对称点为B'，当PB'最短时，请在如图所示的网格中，用无刻度的直尺，画出点B'，并简要说明点B'的位置是如何找到的．（不要求证明）6.如图，在每个小正方形的边长为1的网格中，点A、B、C均在格点上．（Ⅰ）△ABC的面积为______．（Ⅱ）点P是△ABC内切圆与AB的切点，请在如图所示的网格中，用无刻度的直尺画出点P，并简要说明点P的位置是如何找到的（不要求证明）______．7.如图，在每个小正方形的边长为1的网格中，A，B，D，E为格点，C为AD，BE的延长线的交点．（Ⅰ）sin∠CAB的结果为______；（Ⅱ）若点R在线段AB上，点S在线段BC上，点T在线段AC上，且满足四边形ARST 为菱形，请在如图所示的网格中，用无刻度的直尺，画出菱形ARST，并简要说明点R，S，T的位置是如何找到的（不要求证明）______．8.如图所示，在每个边长都为1的小正方形组成的网格中，点A、P分别为小正方形的中点，B为格点．（I）线段AB的长度等于______；（Ⅱ）在线段AB上存在一个点Q，使得点Q满足∠PQA=45°，请你借助给定的网格，并利用不带刻度的直尺作出∠PQA，并简要说明你是怎么找到点Q的：______．9.如图，将△ABC放在每个小正方形的边长为1的网格中，点A、B、C均落在格点上．（Ⅰ）△ABC的面积等于______；（Ⅱ）若四边形DEFG是△ABC中所能包含的面积最大的正方形，请你在如图所示的网格中，用直尺和三角尺画出该正方形，并简要说明画图方法（不要求证明）______．10.如图，将△ABC放在每个小正方形的边长为1的网格中，点A，点B，点C均落在格点上．（Ⅰ）△ABC的面积等于______；（Ⅱ）点P为边BC上的动点，当√5AP+BP取得最小值时，请在如图所示的网格中，用无刻度的直尺，画出线段AP，并简要说明点P的位置是如何找到的（不要求证明）______．11.如图，在由边长都为1的小正方形组成的网格中，点A，B，C均为格点，点P，Q为线段AB上的动点，且满足PQ=1．（Ⅰ）当点Q为线段AB中点时CQ的长度等于______．（Ⅱ）当线段CQ+CP取得最小值时，请借助无刻度直尺在给定的网格中画出点Q，并简要说明你是怎么画出点Q的：______．12.如图，将△ABC放在每个小正方形的边长为1的网格中，点A，点B，点C均落在格点上（Ⅰ）BC的长等于______．（Ⅱ）请在如图所示的网格中，用无刻度的直尺，画出△ABC关于直线BC对称的图形，并简要说明画图方法（不要求证明）．13.如图，在由边长都为1的小正方形组成的网格中，点A，B，C，D均为格点（1）线段BC的长度等于______S ABCD，请你借助无刻度直尺在给定的网（2）若K为线段CD上一点，且满足S△BCK=13格中画出满足条件的线段BK，并简要说明你是怎么画出点K的．14.如图，在每个边长都为1的小正方形组成的网格中，A为格点，B，P为小正方形的中点．（I）线段AB的长为______．（Ⅱ）在线段AB上存在一个点Q，使得点Q满足∠PQB=45°，请你借助给定的网格，用无刻度的直尺作出∠PQB，并简要说明你是怎么找到点Q的______．15.在每个小正方形的边长为1的网格中，有△ABC，点A，B，C都在格点上（Ⅰ）△ABC的面积等于______．（Ⅱ）求作其内接正方形，使其一边在BC上，另两个顶点各在AB，AC上．在如图所示的网格中，请你用无刻度的直尺，画出该正方形，并简要说明画图的方法（不要求证明）______．16.如图，在每个小正方形的边长为1的网格中，A，B均为格点．（1）AB的长等于______．（2）请用无刻度的直尺，在如图所示的网格中求作一点P，使得以AB为底边的等腰三角形，并简要说明点P的位置是如何找到的（不要求证明）．PAB的面积等于32。

中考网格作图题专项训练一．填空题（共1小题）1．（2006•烟台）正方形网格中，小格的顶点叫做格点．小华按下列要求作图：①在正方形网格的三条不同的实线上各取一个格点，使其中任意两点不在同一条实线上；②连接三个格点，使之构成直角三角形．小华在左边的正方形网格中作出了Rt△ABC．请你按照同样的要求，在右边的两个正方形网格中各画出一个直角三角形，并使三个网格中的直角三角形互不全等_________ ．二．解答题（共17小题）2．作图题，在网格中作图：①过C点作线段CD，使CD∥AB．②过C点作线段CE，使CE⊥AB．3．作图题，在如图所示的网格图中，画出一个与图中三角形相似的三角形．4．作图题：如图，是一个边长为1的正方形网格，请在网格中画出一个边长为2，和3的三角形．（要求三角形的顶点在小格的顶点处）．5．在如图的网格中作图：（1）过点C作直线AB的垂线；（2）过点C作直线AB的平行线．6．基本作图（保留作图痕迹不写作法．）在网格中求作一个三角形A′B′C′，使它与已知△ABC相似，且相似比为1：2；并分别求出两个三角形的周长．7．在如图所示的正方形网格中，已知线段AB，A、B均为格点．（1）请在网格中画出一个以AB为底边的等腰三角形ABC，且点C也为格点；（2）作出△ABC的外接圆（尺规作图，保留作图痕迹，不写作法与证明）．8．正方形网格中，小格的顶点叫做格点，小华按下列要求作图：①在正方形网格的三条不同实线上各取一个格点，使其中任意两点不在同一条实线上；②连接三个格点，使之构成直角三角形．小华在左边的正方形网格中作出了Rt△ABC，请你按照同样的要求，在右边的两个正方形网格中各画出一个直角三角形，并求出这个直角三角形的面积．（要求：三个网格中的直角三角形互不全等）9．（2010•丰台区二模）在正方形网格中，小格的顶点叫做格点．小华按下列要求作图：①在正方形网格的三条不同实线上各取一个格点，使其中任意两点不在同一条实线上；②连接三个格点，使之构成直角三角形，小华在左边的正方形网格中作出了Rt△ABC．请你按照同样的要求，在右边的两个正方形网格中各画出一个直角三角形，使三个网格中的直角三角形互不全等，并分别求出这三个直角三角形的斜边长．10．△ABC在网格中如图，请根据下列要求作图：（1）过点C作AB的平行线．（2）将△ABC平移，使顶点B平移到点A，画出平移后的三角形．11．作图题：正方形网格中有△OAB，请你以O为位似中心放大，使新图形与原图形的对应线段比是2：1（不写作法）12．如图所示，在8×8的网格中，我们把△ABC在图1中作轴对称变换，在图2中作旋转变换，已知网格中的线段ED、线段MN分别是边AB经两种不同变换后所得的像，请在两图中分别画出△ABC经各自变换后的像，并标出对称轴和旋转中心（要求：不写作法，作图工具不限，但要保留作图痕迹）．13．按下列要求作图：（1）在正方形网格中三条不同实线上各取一个格点，使其中任意两点，不在同一实线上；（2）连接三个格点，使之构成直角三角形（如图1），请在右边网格在作出三个直角三角形，使四个直角三角形互不全等．14．作图：（1）在图1中画出△ABC关于点O的中心对称图形．（2）正方形网格中，每个小正方形的顶点称为格点，以格点为顶点的三角形叫做格点三角形，在图2正方形网格（每个小正方形边长为1）中画出格点△DEF，使DE=DF=5，EF=．15．如图：在正方形网格中有一个△ABC，按要求进行下列作图（只能借助于网格）：（1）画出△ABC中BC边上的高（需写出结论）；（2）画出先将△ABC向右平移6格，再向上平移3格后的△DEF；（3）画一个锐角△MNP（要求各顶点在格点上），使其面积等于△ABC的面积．16．如图，在边长为1个单位长度的小正方形组成的网格中，给出了格点△ABC（顶点是网格线的交点）和点A1．利用网格完成下面的作图：（1）画出点B关于直线AC的对称点D；（2）画出一个格点△A1B1C1，并使它的三边长分别是3、、．17．作图题：（不要求写作法）如图，在边长为单位1的正方形网格中，有一个格点△ABC（各个顶点都是正方形网格的格点）（1）画出△ABC关于直线1对称的格点△A1B1C1；（2）画出以O点为位似中心，把△ABC放大到2倍的△A2B2C2．18．如图，图（1）、图（2）是边长为1的正方形网格，按下列要求作图并回答问题．（1）画出△ABC，点C在格点上且△ABC是等腰三角形，其腰长是_________ ；（2）画出正方形ABCD，且C、D在格点上，其周长是_________ ．2014年5月294464107的初中数学组卷参考答案与试题解析一．填空题（共1小题）1．（2006•烟台）正方形网格中，小格的顶点叫做格点．小华按下列要求作图：①在正方形网格的三条不同的实线上各取一个格点，使其中任意两点不在同一条实线上；②连接三个格点，使之构成直角三角形．小华在左边的正方形网格中作出了Rt△ABC．请你按照同样的要求，在右边的两个正方形网格中各画出一个直角三角形，并使三个网格中的直角三角形互不全等如图．考点：作图—复杂作图．专题：压轴题；网格型．分析：本题中得出直角三角形的方法如图：如果设AE=x，BE=4﹣x，如果∠FEG=90°，△AFE∽△GBE。