韦达定理在圆锥曲线综合题中的应用

韦达定理在圆锥曲线中的应用
1、韦达定理
韦达定理是17世纪法国数学家威塔·韦达在有关圆锥曲线几何方面发现的一条定理，定理指出：在位于同一直线上且圆交于同一直径的任意两个圆，两个圆可以推出之间的比例关系，即将外圆的半径写成内圆的半径 n 倍，这条关系称为韦达定理。

2、圆锥曲线中韦达定理的应用
在圆锥曲线中，韦达定理可以用来解决三维空间中的圆相关问题，例如圆锥曲线上两个圆相交的情况，韦达定理可以利用外圆半径除以内圆半径的比例来定义椭圆圆环上两个圆的关系。

在抛物线中，韦达定理也可以应用，将一条抛物线分成两段，这样通过比例关系，可以将抛物线分成两个相类似的曲线，从而得到所需的抛物线函数，这种方法也可以应用于圆锥曲线的参数方程求解中。

此外，在计算形态学上，可以利用韦达定理在xy平面上椭圆圆环上找到曲线加权最小值以及凹曲面研究。

3、实例分析
下面我们给出一个简单的例子，假设有一个圆锥曲线，外圆半径为R，内圆半径为r，则韦达定理指出，外圆与内圆之间的比例是:
R:r = n
即外圆为内圆n倍半径，我们可以根据这一比例关系，计算出内圆的
半径。

例如，假设椭圆圆环的外圆半径为 5m，那么按照韦达定理，椭
圆圆环的内圆的半径就可以推算出来，半径为: R:r = 5:1，即内圆的半
径为1m。

4、结论
针对圆锥曲线，韦达定理对诸多几何形状求解有着十分重要的作用，圆锥曲线的外圆与内圆之间的比例关系是韦达定理指出的，从而可以
计算出内圆的半径值。

另外，韦达定理也能够用于椭圆圆环、抛物线
等函数中，从而求解所需的曲线参数。

韦达定理在解析几何中的应用韦达定理步骤 1、 设直线0Ax By C ++=与曲线交于两点1122(,),(,)A x y B x y ,既设而不求。

2、 直线与曲线方程联立方程组。

3、 消去x, 得到关于或y 的一元二次方程.4、结合具体问题与韦达定理建立联系， 如求弦长等。

韦达定理注意与向量的联系一，求弦长.直线与圆锥曲线相交的弦长计算:(1)连结圆锥曲线上两点的线段称为圆锥曲线的弦;(2)易求出弦端点坐标时用距离公式求弦长;(3)一般情况下,解由直线方程和圆锥曲线方程组成的方程组,得到关于x(或y)的一元二次方程,利用方程组的解与端点坐标的关系,结合韦达定理得到弦长公式∣AB ∣=∣x 1-x 2∣21k +⋅=)1](4)[(221221k x x x x +-+ 或∣AB ∣=∣y 1-y 2∣211k +⋅ =)11](4)[(221221ky y y y +-+ ， 1．设直线21y x =-交曲线C 于1122(,),(,)A x y B x y 两点。

（1）若12||x x -=||AB = （2）12||y y -=||AB =2．斜率为1的直线经过抛物线24y x =的焦点，与抛物线相交于,A B 两点，则||AB =3、抛物线 y 2=4x 的焦点作直线交抛物线A(x 1,y 1),B(x 2,y 2)两点,如果x 1+x 2=6, 那么|AB|=( ) (A)10 (B)8 (C)6 (D)44、y=kx-2交椭圆x 2+4y 2=80交于不同的两点P 、Q ，若PQ 中点的横坐标为2，则∣PQ ∣等于___________.例1,已知直线 L 的斜率为2，且过抛物线y 2=2px 的焦点，求直线 L 被抛物线截得的弦长。

已知向量()()()()m x n m x n y 1122201101====，，，，，，，（其中x ，y 是实数），又设向量1221m m n m ==u r u u r u r r u u r r，，且m n ∥，点()P x y ，的轨迹为曲线C 。

圆锥曲线常见问题及基本方法（二）【一】利用韦达定理，结合设而不求的方法，使原问题转化为参数（k 参）的函数问题，例如题目中出现过定点的直线，或出现向量数量积，或者面积等能够利用韦达定理将原问题都转化为参数的问题 例1：已知点M(-2，0)，N(2,0)，动点P满足条件||||PM PN -=记动点P 的轨迹为W.（Ⅰ）求W 的方程；（Ⅱ）若A ，B 是W 上的不同两点，O 是坐标原点，求OA OB ⋅的最小值.解：（Ⅰ）依题意，点P 的轨迹是以M ，N 为焦点的双曲线的右支，所求方程为：22x y 122－＝ （x >0）（Ⅱ）当直线AB 的斜率不存在时，设直线AB 的方程为x ＝x 0，此时A （x 0），B （x 0，），OA OB ⋅＝2当直线AB 的斜率存在时，设直线AB 的方程为y ＝kx ＋b ，代入双曲线方程22x y 122－＝中，得：(1－k 2)x 2－2kbx －b 2－2＝0 依题意可知方程1︒有两个不相等的正数根，设A(x 1,y 1),B(x 2,y 2)，则2222122212244(1)(2)0201201k b k b kb x x k b x x k ⎧⎪∆=--∙--≥⎪⎪+=>⎨-⎪⎪+=>⎪-⎩解得|k|>1， 又OA OB ⋅＝x 1x 2＋y 1y 2＝x 1x 2＋（kx 1＋b ）（kx 2＋b ）＝（1＋k 2）x 1x 2＋kb （x 1＋x 2）＋b2＝2222k 242k 1k 1＋＝＋－－>2，综上可知OA OB ⋅的最小值为2 【二】利用韦达定理将两点坐标统一为单点坐标（适用点参）例1：给定抛物线C ：24,y x =F 是C 的焦点，过点F 的直线l 与C 相交于A 、B 两点. （Ⅰ）设l 的斜率为1，求OA OB 与夹角的余弦（Ⅱ）设,[4,9]FB AF λλ=∈若，求l 在y 轴上截距的变化范围.解：（Ⅰ）C 的焦点为F （1，0），直线l 的斜率为1，所以l 的方程为.1-=x y将1-=x y 代入方程x y 42=，并整理得 .0162=+-x x设),,(),,(2211y x B y x A 则有 .1,62121==+x x x x.31)(2),(),(212121212211-=++-=+=⋅=⋅x x x x y y x x y x y x OB OA.41]16)(4[||||21212122222121=+++=+⋅+=x x x x x x y x y x.41143||||),cos(-=⋅=OB OA OB OA（Ⅱ）由题设λ= 得 ),,1(),1(1122y x y x --=-λ即⎩⎨⎧-=-=-.1212),1(1y y x x λλ由②得21222y y λ=， ∵ ,4,4222121x y x y == ∴.122x x λ=③联立①、③解得λ=2x ，依题意有.0>λ ∴),2,(),2,(λλλλ-B B 或又F （1，0），得直线l 方程为 ),1(2)1()1(2)1(--=--=-x y x y λλλλ或当]9,4[∈λ时，l 在方程y 轴上的截距为,1212---λλλλ或由 ,121212-++=-λλλλλ 可知12-λλ在[4，9]上是递减的， ∴ ,431234,341243-≤--≤-≤-≤λλλλ直线l 在y 轴上截距的变化范围为].34,43[]43,34[⋃--【三】最值：与圆锥曲线有关的最值和范围问题的讨论常用以下方法解决：【1】结合定义利用图形中几何量之间的大小关系；例1：（2009四川卷理）已知直线1:4360l x y -+=和直线2:1l x =-，抛物线24y x =上一动点P 到直线1l 和直线2l 的距离之和的最小值是（ A ） A.2 B.3 C.115 D.3716解析2：如下图，由题意可知2d ==【2】不等式（组）求解法：利用题意结合图形（如点在曲线内等）列出所讨论的参数适合的不等式（组），通过解不等式组得出参数的变化范围；例1：（2009重庆卷文）已知椭圆22221(0)x y a b a b+=>>的左、右焦点分别为12(,0),(,0)F c F c -，若椭圆上存在一点P 使1221sin sin a cPF F PF F =，则该椭圆的离心率的取值范围为)1,1 ．解法1：因为在12PF F ∆中，由正弦定理得211221sin sin PF PF PF F PF F =则由已知，得1211a cPF PF =，即12aPF cPF = 设点00(,)x y 由焦点半径公式，得1020,PF a ex PF a ex =+=-则00()()a a ex c a ex +=- 记得0()(1)()(1)a c a a e x e c a e e --==-+由椭圆的几何性质知0(1)(1)a e x a a e e ->->-+则，整理得 ① ②2210,e e +->解得11(0,1)e e e <∈或，又，故椭圆的离心率1,1)e ∈解法2 由解析1知12cPF PF a=由椭圆的定义知 212222222c a PF PF a PF PF a PF a c a+=+==+则即，由椭圆的几何性质知22222,,20,a PF a c a c c c a c a<+<++->+则既所以2210,e e +->以下同解析1.【3】函数值域求解法：把所讨论的参数作为一个函数、一个适当的参数作为自变量来表示这个函数，通过讨论函数的值域来求参数的变化范围。

圆锥曲线综合大题（易错必刷32题15种题型专项训练）➢韦达定理基础型➢直线横截式应用➢直线双变量型应用➢面积最值型➢面积比值范围型➢动直线过定点➢圆过定点➢圆锥切线➢定直线➢向量型定比分点➢斜率型：和定➢斜率型：积定➢斜率型：商定➢求轨迹➢新定义型第19题一．韦达定理基础型（共2题）1．（23-24高二下·四川成都·期中）已知椭圆C：22221x ya b+=（0a b>>），131,2Pæö-ç÷èø，231,2Pæöç÷èø，(30,P，()41,1P四点中恰有三点在椭圆C上．(1)求椭圆C的标准方程；(2)过右焦点F且斜率为1的直线l交椭圆C于M，N两点，点P为直线4x=上任意一点，求证：直线PM，PF，PN的斜率成等差数列．2．（23-24高二下·上海·期中）如图，由部分椭圆22221(0,0)x y a b y a b +=>>£和部分双曲线22221(0)x y y a b -=³，组成的曲线C 称为“盆开线”．曲线C 与x 轴有(2,0),(2,0)A B -两个交点，．(1)设过点(1,0)的直线l 与C 相切于点(4,3)M ，求部分椭圆方程、部分双曲线方程及直线l 的方程；(2)过A 的直线m 与C 相交于点,,P A Q 三点，求证：PBA QBA Ð=Ð．二． 直线横截式应用（共2题）3．（23-24高二上·广西南宁·期中）已知椭圆2222:1(0)x y C a b a b +=>>.(1)求椭圆C 的方程：(2)过点()1,0M 的直线l 与椭圆C 交于点A 、B ，设点1(,0)2N ，若ABN V 的面积为310，求直线l 的斜率k .4．（23-24高二下·云南玉溪·期中）在直角坐标平面内，已知点()()122,0,2,0A A -，动点P (x,y ).设1PA ､2PA 的斜率分别为12k k ､，且1234k k ×=-.设动点P (x,y )的轨迹为曲线C .(1)求曲线C 的方程；(2)过点F 1(―1,0)的直线l 交曲线C 于M N ､两点，是否存在常数l ，使11MN F M F N l =×uuuu r uuuu r恒成立？三． 直线双变量型（共2题）5．（23-24高二下·天津·期中）已知椭圆2222:1(0)x y C a b a b +=>>经过点()2,0A -，离心率为12．(1)求椭圆C 的方程；(2)点P Q 、为椭圆C 上不同的两点，直线AP 与y 轴交于点M ，直线AQ 与y 轴交于点),N E，设()0,(0)M m m >，且满足,EM EN PQ OE ^×=-uuu r uuu r，求点M 的坐标．6．（21-22高三上·湖北·期中）已知圆O ：222x y +=，椭圆C ：(22221x y a b a b+=>>，P是C 上的一点，A 是圆O 上的一点，PA 的最大值为(1)求椭圆C 的方程；(2)点M 是C 上异于P 的一点，PM 与圆O 相切于点N ，证明：2PO PM PN =×.四．面积最值型（共2题）7．（23-24高二下·福建泉州·期中）已知抛物线2:2(03)C y px p =<<，其焦点为F ，点(,Q m 在抛物线C 上，且4QF =．(1)求抛物线C 的方程；(2)O 为坐标原点，,A B 为抛物线上不同的两点，且OA OB ^，（i ）求证直线AB 过定点；（ii ）求AFO V 与ABO V 面积之和的最小值．8．（23-24高二下·内蒙古呼和浩特·期中）已知在平面直角坐标系xOy 中，动点P 到()和)的距离和为4，设点11,2A æöç÷èø.(1)求动点P 的轨迹方程；(2)M 为线段PA 的中点，求点M 的轨迹方程；(3)过原点O 的直线交P 的轨迹于B ，C 两点，求ABC V 面积的最大值.五．面积比值范围（共2题）9．（23-24高二·山东·期中）已知抛物线()2:20C y px p =>.过抛物线焦点F 作直线1l 分别在第一、四象限交C 于K P 、两点，过原点O 2与抛物线的准线交于E 点，设两直线交点为S .若当点P 的纵坐标为2-时，OP =(1)求抛物线的方程.(2)若EP 平行于x 轴，证明：S 在抛物线C 上.(3)在（2）的条件下，记SEP V 的重心为R ，延长ER 交SP 于Q ，直线EQ 交抛物线于N T 、（T 在右侧），设NT 中点为G ，求PEG △与ESQ V 面积之比n 的取值范围.10．（23-24高三上·青海西宁·期中）已知椭圆()2222:10x y E a b a b +=>>点P 在椭圆E 上运动，且12PF F V (1)求椭圆E 的方程；(2)设A ，B 分别是椭圆E 的右顶点和上顶点，不过原点的直线l 与直线AB 平行，且与x 轴，y 轴分别交于点M ，N ，与椭圆E 相交于点C ，D ，O 为坐标原点.（ⅰ）求OCM V 与ODN △的面积之比；（ⅱ）证明：22CM MD +为定值.六．动直线过定点 （共2题）11．（23-24高二下·安徽阜阳·期中）已知抛物线()2:20C y px p =>的焦点为F ，P 是C 上一点，线段PF的中点为5,22Q æöç÷èø．(1)求C 的方程；(2)若7p <，O 为原点，点M ，N 在C 上，且直线OM ，ON 的斜率之积为2024，求证：直线MN 过定点．12．（22-23高二上·四川雅安·期中）已知()0,1P 为椭圆2222:1(0)x y C a b a b +=>>上一点，点P 与椭圆C 的两(1)求椭圆C 的标准方程；(2)不经过点P 的直线l 与椭圆C 相交于,A B 两点，若直线PA 与PB 的斜率之和为1-，证明：直线l 必过定点，并求出这个定点坐标．七． 圆过定点（共2题）13．（23-24高二下·上海·期中）已知椭圆22:12x C y +=(1)若双曲线22221x y a b -=(0,0)a b >>的一条渐近线方程为y x =，且与椭圆C 有公共焦点，求此双曲线的方程；(2)过点10,3S æö-ç÷èø的动直线l 交椭圆C 于,A B 两点，试问在坐标平面上是否存在一个定点T ，使得以AB 为直径的圆恒过定点T ？若存在，求出T 的坐标，若不存在，说明理由．14．（23-24高二上·江苏常州·期中）已知双曲线()2222:10,0x y C a b a b-=>>F 到渐近线的距离为1．(1)求双曲线C 的方程；(2)若直线l 过定点()4,0M 且与双曲线C 交于不同的两点A 、B ，点N 是双曲线C 的右顶点，直线AN 、BN 分别与y 轴交于P 、Q 两点，以线段PQ 为直径的圆是否过x 轴上的定点？若是，求出定点坐标；若不是，说明理由．八．圆锥切线 （共2题）15．（23-24高二下·上海·期中）已知圆()22:21F x y -+=，动圆P 与圆F 内切，且与定直线3x =-相切，设圆心P 的轨迹为G (1)求G 的方程(2)若直线l 过点F ，且与G 交于,A B 两点①若直线l 与y 轴交于M 点，满足(),0,0MA AF MF FB l μl μ==>>uuu r uuu r uuur uuu r，试探究l 与μ的关系；②过点,A B 分别作曲线G 的切线相交于点P ，求PAB V 面积的最小值.16．（23-24高二下·上海·期中）已知抛物线2Γ:2x y =的焦点为F ，过Γ在第一象限上的任意一点P 作Γ的切线l ，直线l 交y 轴于点Q ．过F 作l 的垂线m ，交Γ于,A B 两点．(1)若点Q 在Γ的准线上，求直线l 的方程；(2)求PF 的中点M 的轨迹方程；(3)若三角形PAB ，求点Q 的坐标．九．定直线（共2题）17．（2024高二·全国·期中）已知椭圆()2222:10x y C a b a b +=>>，A ，B 分别为C 的上、下顶点，O 为坐标原点，直线4y kx =+与C 交于不同的两点M ，N ．(1)设点P 为线段MN 的中点，证明：直线OP 与直线MN 的斜率之积为定值；(2)若AB 4=，证明：直线BM 与直线AN 的交点G 在定直线上．18．（2024·河北·期中）已知椭圆C 的中心在原点O 、对称轴为坐标轴，A æççè、12B ö÷÷ø是椭圆上两点．(1)求椭圆C 的标准方程；(2)椭圆C 的左、右顶点分别为1A 和2A ，M ，N 为椭圆上异于1A 、2A 的两点，直线MN 不过原点且不与坐标轴垂直．点M 关于原点的对称点为S ，若直线1A S 与直线2A N 相交于点T ．（i ）设直线1MA 的斜率为1k ，直线2MA 的斜率为2k ，求12k k -的最小值；（ii ）证明：直线OT 与直线MN 的交点在定直线上．十．向量型定比分点 （共2题）19．（23-24高二下·江苏南京·期中）已知椭圆C ：()222210+=>>x y a b a b (P ．(1)求椭圆C 的方程；(2)过右焦点F 的直线l 与椭圆C 交于A ，B 两点，若3AF FB =uuu r uuu r，求PAB V 的面积．20．（2023·河南·期中）已知椭圆()2222:10x y C a b a b +=>>的右焦点()10F ,，点12M ö÷÷ø在椭圆C 上．(1)求椭圆C 的标准方程；(2)过点()2,1P 的直线l 与椭圆C 交于A ，B 两点．若PA PB l =uu u r uuu r ，()0AQ QB l l =>uuu ruuu r ，求OQ uuu r 的最小值（O是坐标原点）．十一．斜率型：和定 （共2题）21．（2024·河南郑州·期中）设抛物线2:2(0)C y px p =>的焦点为F ，()00,P x y 是C 上一点且2200||||PF PF x x -=+，直线l 经过点(8,0)Q -．(1)求抛物线C 的方程；(2)①若l 与C 相切，且切点在第一象限，求切点的坐标；②若l 与C 在第一象限内的两个不同交点为,A B ，且Q 关于原点O 的对称点为R ，证明：直线,AR BR 的倾斜角之和为π．22．（23-24高二上·云南昆明·期中）在平面直角坐标系xOy 中，动点(,)M x y 1x =+.记点M 的轨迹为C .(1)求C 的方程；(2)设点T 在y 轴上（异于原点），过点T 的两条直线分别交C 于A ，B 两点和P ，Q 两点，并且||||||||TA TB TP TQ =，求直线AB 的斜率与直线PQ 的斜率之和.十二．斜率型：积定（共2题）23．（23-24高二·辽宁鞍山·期中）已知椭圆2222:1(0)x y C a b a b+=>>，右焦点为()2,0F 且离心率为23，直线:6l x =，椭圆C 的左右顶点分别为12,A A P ､为l 上任意一点，且不在x 轴上，1PA 与椭圆C 的另一个交点为2,M P A 与椭圆C 的另一个交点为N .(1)直线1MA 和直线2MA 的斜率分别记为12M A M A k k ､，求证：12MA MA k k ×为定值；(2)求证：直线MN 过定点.24．（23-24高二·云南昆明·期中）已知点P 在椭圆C:x2a 2+y 2b 2=1(a >b >0)上，过点P 作直线l 与椭圆C 交于点Q ，过点P 作关于坐标原点O 的对称点P ¢，PP ¢的最小值为l 的斜率为0时，存在第一象限内的一点P 使得4,PP PQ =¢=(1)求椭圆C 的方程；(2)设直线l 的斜率为k （k ≠0），直线QP ¢的斜率为k ¢，求k k ¢×的值．十三．斜率型：商定（共2题）25．（2024·广东广州·期中）已知在平面直角坐标系xOy 中，双曲线C ：()22221,0x y a b a b -=>过和(两点.(1)求双曲线C 的标准方程；(2)若S ，T 为双曲线C 上不关于坐标轴对称的两点，M 为ST 中点，且ST 为圆G 的一条非直径的弦，记GM 斜率为1k ，OM 斜率为2k ，证明：12k k 为定值.26．（23-24高二·广东汕头·期中）已知椭圆C:x 2a 2+y 2b 2=1(a >b >0)的左、右顶点分别为A ，B ，点31,2æöç÷èø在该椭圆上，且该椭圆的右焦点F 的坐标为(1,0)．(1)求椭圆C 的标准方程；(2)如图，过点F 且斜率为k 的直线l 与椭圆交于M ，N 两点，记直线AM 的斜率为1k ，直线BN 的斜率为2k ，求证：1213k k =．十四．求轨迹 （共2题）27．（23-24高二下·上海·期中）已知A 、B 、C 是我方三个炮兵阵地，A 地在B 地的正东方向，相距6km ；C 地在B 地的北偏西30°，相距4km ．P 为敌方炮兵阵地．某时刻A 地发现P 地产生的某种信号，12s 后B地也发现该信号（该信号传播速度为13km/s ）．以BA 方向为x 轴正方向，AB 中点为坐标原点，与AB 垂直的方向为y 轴建立平面直角坐标系．(1)判断敌方炮兵阵地P 可能分布在什么样的轨迹上，并求该轨迹的方程；(2)若C 地与B 地同时发现该信号，求从A 地应以什么方向炮击P 地？28．（23-24高二上·安徽宿州·期中）已知直线BC 经过定点()0,2,N O 是坐标原点，点M 在直线BC 上，且OM BC ^．(1)当直线BC 绕着点N 转动时，求点M 的轨迹E 的方程；(2)已知点()3,0T -，过点T 的直线交轨迹E 于点P Q 、，且65OP OQ ×=uuu r uuu r ，求PQ ．十五．新定义型第19题（共4题）29．（2024·福建·期中）贝塞尔曲线是由法国数学家Pierre Bézier 发明的，它为计算机矢量图形学奠定了基础．贝塞尔曲线的有趣之处在于它的“皮筋效应”，即随着控制点有规律地移动，曲线会像皮筋一样伸缩，产生视觉上的冲击．(1)在平面直角坐标系中，已知点1T 在线段AB 上．若A (x 1,y 1)，B (x 2,y 2)，1AT a AB =，求动点1T 坐标；(2)在平面直角坐标系中，已知(2,4)A -，(2,0)B -，(2,4)C ，点,M N 在线段,AB BC 上，若动点2T 在线段MN 上，且满足2AM BN MT a ABBCMN===，求动点2T 的轨迹方程；(3)如图，已知((A B C D ，若点3,,,,,M N P X Y T 分别在线段,,,,,AB BC CD MN NP XY 上，且3AM BN CP MX NY XT a ABBCCDMNNPXY======，求动点3T 的轨迹方程．30．（23-24高三上·湖北荆州·期中）已知双曲线E 的中心为坐标原点，渐近线方程为y =，点(2,1)-在双曲线E 上.互相垂直的两条直线12,l l 均过点()(,0n n P p p >)*N n Î，直线1l 交E 于,A B 两点，直线2l 交E 于,C D 两点，,M N 分别为弦AB 和CD 的中点.(2)若直线MN 交x 轴于点()()*,0N n Q t n Î，设2n n p =.①求n t ；②记n a PQ =，()*21N n b n n =-Î，求211(1)nkk k k k b b a +=éù--ëûå.31．（2024·四川·期中）已知抛物线C ：()220y px p =>的焦点为F ，过点F 的直线与C 相交于点A ，B ，AOB V 面积的最小值为12（O 为坐标原点）.按照如下方式依次构造点()*N n F n Î：1F 的坐标为(),0p ，直线n AF ，n BF 与C 的另一个交点分别为n A ，n B ，直线n n A B 与x 轴的交点为1n F +，设点n F 的横坐标为n x .(2)求数列{}n x 的通项公式；(3)数列{}n x 中，是否存在连续三项（按原顺序）构成等差数列？若存在，指出所有这样的连续三项；若不存在，请说明理由.32．（2024·江西新余·期中）通过研究，已知对任意平面向量(),AB x y =uuu r，把AB uuu r绕其起点A 沿逆时针方向旋转q 角得到向量()cos sin ,sin cos AP x y x y q q q q =-+uuu r，叫做把点B 绕点A 逆时针方向旋转q 角得到点P ，(1)已知平面内点(A ，点B-，把点B 绕点A 逆时针旋转π3得到点P ，求点P 的坐标：(2)已知二次方程221+-=x y xy 的图像是由平面直角坐标系下某标准椭圆()222210+=>>x y a b a b绕原点O 逆时针旋转π4所得的斜椭圆C ，（i ）求斜椭圆C 的离心率；（ⅱ）过点Q 作与两坐标轴都不平行的直线1l 交斜椭圆C 于点M 、N ，过原点O 作直线2l 与直线1l垂直，直线2l 交斜椭圆C 于点G 、H 理由.。

专题3 圆锥曲线大题处理策略：非对称韦达定理在圆锥曲线解答题中我们通常利用直线与二次曲线联立得到一元二次方程的韦达定理来处理类似12212122212111,y x y x x x x x x x +++-，，等结构，这些形式通过合理的变形均可以用2121x x x x ⋅+，整体带入的方法达到避开解交点坐标的目的。

（这是圆锥曲线大题中普遍使用韦达定理的初衷）。

但我们在做题中也经常会遇到类似于11212122121232,2x x x x x x x x x x x x λμ+-+-+，这种系数不对称的结构，称之为“非对称韦达定理”。

显然按照先前的方法就很难顺利的处理掉，本专题就此类问题给出几个常见的处理策略。

（1）求椭圆C 方程（2）B A ,分别为椭圆C 的上下顶点，过()40，P 点斜率为k 的直线与椭圆C 交于N M ,两点，求证：直线ANBM ,的交点在定直线上 韦达化处理由引例1可知，核心条件坐标化后，并不全是直接韦达化的形式．对于坐标化后的表达式不是韦达形式的，还需进行韦达化处理．韦达化处理主要有以下几种处理方法：代换（直线代换或曲线代换）、和积消元法、配凑、解方程组．韦达化处理一：代换——即消去x 或y 中的一个由于我们联立后的方程式关于x 或y 的二次方程，韦达定理中的两根之和与两根之积只式单独的x 或y 的形式，而此时坐标表达式并非是直接的韦达形式，因此需进行代换：方向一：直线代换：1122x ty m x ty m =+⎧⎨=+⎩）又1122x ty mx ty m =+⎧⎨=+⎩，即()()()2212121212x x ty m ty m t y y tm y y m =+⋅+=+++ 方向二：曲线代换：若两个点均在直线12y kx =-和曲线2219x y +=上，那么形如()()122111x y x y +-的式子，如果用直线替换显然麻烦，注意到()()2222211111111999119x y x y x y y +=⇒=-⇒=-+，替换掉原式中含有的()11y -，可以得到()()1212911y y x x ++。

韦达定理与非对称结构 设线联立、韦达定理一．基本原理1.斜率和（积）构造与韦达定理目前我们市面上的斜率型题目中一大类就是斜率和（积）构造，这其中主要特征就是一定点两动点，而定点的特征又可进一步分成在坐标轴上和一般点. 倘若定点),0(t P ，在椭圆上的动点),(),,(2211y x B y x A ，那么： ①.21221212211)(x x t y y t y y x t y x t y k k PBPA ++-=-⋅-=⋅，此时已经凑出韦达定理的形式，就无需再解点，可直接代入韦达定理求解. ②.212112212211)(x x x x t y x y x x t y x t y k k PB PA +-+=-+-=+,这里对交叉项1221y x y x +的处理可进一步代入直线方程：m kx y AB +=:，化简可得：212121211221))((2)(x x x x t m k x x x x t y x y x k k PB PA +-+=+-+=+（*），再代入韦达定理.注意，这一步代入很重要，（*）式是一个非常简洁的结构，易于操作.当然，对于交叉项1221y x y x +的处理亦可通过其他方法来完成，我会在后续设点法中介绍. ③.))(()()()(11212112212211t y t y y y t y x y x t y x t y x k k PB PA --+-+=-+-=+. 二．典例分析例1．已知椭圆C ：()222210x y a b a b +=>>，3a b =，点⎛ ⎝⎭在椭圆C 上． （1）求椭圆C 的方程；（2）若过点()1,0Q 且不与y 轴垂直的直线l 与椭圆C 交于M ，N 两点，()3,0T ，证明TM ，TN 斜率之积为定值．解析：（1）由题意得3a b =，故椭圆C 为222219x y b b +=，又点⎛ ⎝⎭在C 上，所以2218199b b+=，得21b =，29a =，故椭圆C 的方程即为2219x y +=；（2）由已知直线l 过()1,0Q ，设l 的方程为1x my =+，联立两个方程得22191x y x my ⎧+=⎪⎨⎪=+⎩，消去x 得：()229280m y my ++-=，()2243290m m ∆=++>得R m ∈，设()11,M x y ，()22,N x y ，则12229my y m +=-+，12289y y m =-+（*），因为()3,0T ，故121212123322TM TNy y y y k k x x my my ⋅=⋅=⋅----()122121224y y m y y m y y =-++，将（*）代入上式，可得：22228829823692499m m m m m m -+==---⎛⎫⋅--+ ⎪++⎝⎭，∴直线TM 与TN 斜率之积为定值29-． 例2．（2020山东卷）已知椭圆C ：22221(0)x y a b a b +=>>()2,1A ．（1）求C 的方程：（2）点M ，N 在C 上，且AM AN ⊥，AD MN ⊥，D 为垂足．证明：存在定点Q ，使得DQ 为定值．解析：（1）由题意可得：22222411c aa b a b c ⎧=⎪⎪⎪+=⎨⎪=+⎪⎪⎩，解得：2226,3a b c ===，故椭圆方程为：22163x y +=.（2）设点()()1122,,,M x y N x y ，若直线MN 斜率存在时，设直线MN 的方程为：y kx m =+， 代入椭圆方程：消去y 并整理得：()222124260kxkmx m +++-=，可得122412km x x k +=-+，21222612m x x k -=+，因为AM AN ⊥，所以·0AM AN =，即()()()()121222110x x y y --+--=，根据1122,kx m y kx m y =+=+,代入整理可得：()()()()22121212140x x km k x x km ++--++-+=，所以()()()22222264121401212m kmk km k m k k-⎛⎫++---+-+= ⎪++⎝⎭，整理化简得()()231210k m k m +++-=，因为(2,1)A 不在直线MN 上，所以210k m +-≠，故23101k m k ++=≠，，于是MN 的方程为2133y k x ⎛⎫=-- ⎪⎝⎭()1k ≠，所以直线过定点直线过定点21,33P ⎛⎫- ⎪⎝⎭.当直线MN 的斜率不存在时，可得()11,N x y -，由·0AM AN =得：()()()()111122110x x y y --+---=，得()1221210x y -+-=，结合2211163x y +=可得：2113840x x -+=， 解得：123x =或22x =（舍）.此时直线MN 过点21,33P ⎛⎫- ⎪⎝⎭.令Q 为AP 的中点，即41,33Q ⎛⎫⎪⎝⎭，若D 与P 不重合，则由题设知AP 是Rt ADP △的斜边，故12DQ AP ==D 与P 重合，则12DQ AP =，故存在点41,33Q ⎛⎫ ⎪⎝⎭，使得DQ 为定值.注：此题我在上一节用了设线解点法计算过一次，这次采用第二种方法计算.例3.（2022新高考1卷）已知点(2,1)A 在双曲线2222:1(1)1x y C a a a -=>-上，直线l 交C 于P ，Q 两点，直线AP ，AQ 的斜率之和为0．（1）求l 的斜率；（2）若tan PAQ ∠=PAQ ∆的面积． 解析：（1）将点A 代入双曲线方程得224111a a -=-，化简得42440a a -+=，22a ∴=，故双曲线方程为2212x y -=，由题显然直线l 的斜率存在，设:l y kx m =+，设1(P x ，12)(y Q x ，2)y ，则联立双曲线得：222(21)4220k x kmx m -+++=，故122421kmx x k +=--，21222221m x x k +=-， 12121212111102222AP AQ y y kx m kx m k k x x x x --+-+-+=+=+=----， 化简得：12122(12)()4(1)0kx x m k x x m +--+--=，故2222(22)4(12)()4(1)02121k m kmm k m k k ++-----=--，即(1)(21)0k m k ++-=，当012=-+k m 时，直线1)2(:+-=x k y l 过点A ，不合题意，舍去.,故1k =-.。

直线与圆锥曲线问题中韦达定理的应用策略直线与圆锥曲线问题中韦达定理的应用策略韦达定理是解决直线与圆锥曲线问题的重要工具之一。

它是由法国数学家韦达在18世纪提出的，用于求解直线与圆锥曲线的交点坐标。

在解决这类问题时，我们可以采用以下的应用策略：1. 确定直线和圆锥曲线的方程首先，我们需要确定直线和圆锥曲线的方程。

对于直线而言，我们可以使用点斜式或两点式来表示；对于圆锥曲线而言，我们需要根据其类型来确定其方程。

例如，对于椭圆而言，其方程为(x/a)^2+(y/b)^2=1；对于双曲线而言，其方程为(x/a)^2-(y/b)^2=1等等。

2. 将直线方程代入圆锥曲线方程接下来，我们将直线方程代入圆锥曲线方程中，得到一个关于未知数的一元二次方程。

通过求解这个方程，我们可以得到直线与圆锥曲线的交点坐标。

3. 判断交点个数在求解交点坐标之前，我们需要先判断交点的个数。

如果一元二次方程的判别式为正，那么直线与圆锥曲线将会有两个交点；如果判别式为零，那么直线与圆锥曲线将会有一个交点；如果判别式为负，那么直线与圆锥曲线将不会有交点。

4. 求解交点坐标在确定了交点个数之后，我们可以通过求解一元二次方程来得到交点坐标。

如果直线与圆锥曲线有两个交点，那么我们需要分别求解两个交点的坐标；如果直线与圆锥曲线只有一个交点，那么我们只需要求解这个交点的坐标即可。

总之，韦达定理是解决直线与圆锥曲线问题的重要工具之一。

在应用韦达定理时，我们需要先确定直线和圆锥曲线的方程，然后将直线方程代入圆锥曲线方程中，求解一元二次方程，最后判断交点个数并求解交点坐标。

通过这些步骤，我们可以有效地解决直线与圆锥曲线问题。

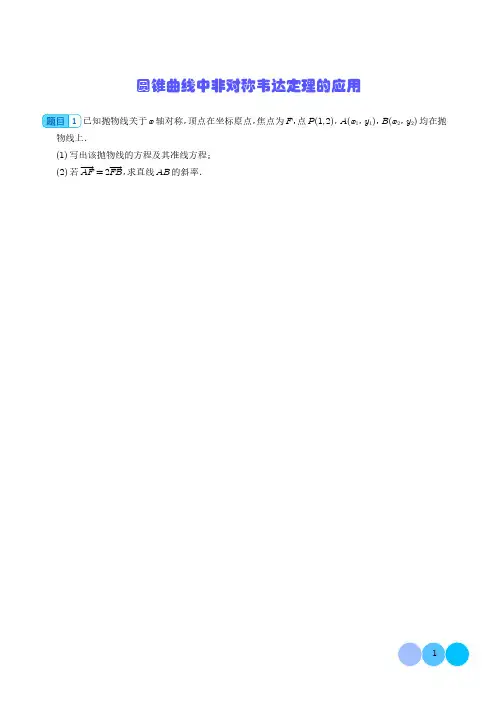
圆锥曲线中非对称韦达定理的应用1已知抛物线关于x 轴对称，顶点在坐标原点，焦点为F ，点P (1,2)，A (x 1，y 1)，B (x 2，y 2)均在抛物线上．(1)写出该抛物线的方程及其准线方程；(2)若AF =2FB ，求直线AB 的斜率．2已知椭圆E的左、右焦点分别为F1(-c,0)，F2(c,0)(c>0)．点M在E上，MF2⊥F1F2，△MF1F2的周长为6+42，面积为13 c.(1)求E的方程；(2)设E的左、右顶点分别为A，B，过点32，0的直线l与E交于C，D两点，记直线AC的斜率为k1，直线BD的斜率为k2，则．(从以下①②③三个问题中任选一个填到横线上并给出解答)①求直线AC和BD交点的轨迹方程；②是否存在实常数λ，使得k1=λk2恒成立；③过点C作关于x轴的对称点C′，连接C′D得到直线l1，试探究：直线l1是否恒过定点．3(2023·新高考全国Ⅱ)已知双曲线C的中心为坐标原点，左焦点为(-25，0)，离心率为5.(1)求C的方程；(2)记C的左、右顶点分别为A1，A2，过点(-4,0)的直线与C的左支交于M，N两点，M在第二象限，直线MA1与NA2交于点P.证明：点P在定直线上．4已知椭圆C ：x 2a 2+y 2b2=1(a >b >0)的左、右焦点分别为F 1(-c ,0)，F 2(c ,0)，M ，N 分别为左、右顶点，直线l ：x =ty +1与椭圆C 交于A ，B 两点，当t =-33时，A 是椭圆的上顶点，且△AF 1F 2的周长为6.(1)求椭圆C 的方程；(2)设直线AM ，BN 交于点Q ，证明：点Q 在定直线上．(3)设直线AM ，BN 的斜率分别为k 1，k 2，证明：k 1k 2为定值．5(2023·深圳模拟)在平面直角坐标系Oxy 中，已知双曲线C ：y 2a 2-x 2b2=1(a >0，b >0)的一条渐近线为y =33x ，且点P 3，2 在C 上．(1)求C 的方程；(2)设C 的上焦点为F ，过F 的直线l 交C 于A ，B 两点，且AF =7BF ，求l 的斜率．6已知点A (0，-2)，椭圆E ：x 2a 2+y 2b2=1(a >b >0)的离心率为32，F 是椭圆E 的右焦点，直线AF 的斜率为233，O 为坐标原点．(1)求E 的方程；(2)设过点A 的直线l 与E 相交于P ，Q 两点，且AP =12AQ ，求△OPQ 的面积及直线l 的方程．圆锥曲线中非对称韦达定理的应用1已知抛物线关于x 轴对称，顶点在坐标原点，焦点为F ，点P (1,2)，A (x 1，y 1)，B (x 2，y 2)均在抛物线上．(1)写出该抛物线的方程及其准线方程；(2)若AF =2FB ，求直线AB 的斜率．【答案】解：(1)由已知条件，可设抛物线的方程为y 2=2px (p >0)，∵点P (1,2)在抛物线上，∴22=2p ×1，解得p =2.故抛物线的方程是y 2=4x ，其准线方程是x =-1.(2)方法一　由(1)可知F (1,0)，A (x 1，y 1)，B (x 2，y 2)，则直线AB 的方程可设为x =ty +1，联立y 2=4x ，x =ty +1，整理得y 2-4ty -4=0，所以y 1+y 2=4t ，y 1y 2=-4.又AF =2FB ，即(1-x 1，-y 1)=2(x 2-1，y 2)，可得-y 1=2y 2，即y1y 2=-2，则y 1y 2+y 2y 1=(y 1+y 2)2y 1y 2-2=-52，即(4t )2-4-2=-52，解得t =±122，故k AB =-1t =±22.方法二　A (x 1，y 1)，B (x 2，y 2)，F (1,0)，AF =(1-x 1，-y 1)，2FB =(2x 2-2,2y 2)，AF =2FB ⇒1-x1=2x 2-2，-y 1=2y 2⇒x 1=3-2x 2，①y 1=-2y 2，②∵A ，B 在抛物线上，∴y21=4x1，③y22=4x2，④由①②③④联立可得x2=1 2，则y2=±2，由③-④得(y1+y2)(y1-y2) =4(x1-x2)，即k AB=y1-y2x1-x2=4y1+y2=4-2y2+y2=-4y2=±22.2已知椭圆E的左、右焦点分别为F1(-c,0)，F2(c,0)(c>0)．点M在E上，MF2⊥F1F2，△MF1F2的周长为6+42，面积为13 c.(1)求E的方程；(2)设E的左、右顶点分别为A，B，过点32，0的直线l与E交于C，D两点，记直线AC的斜率为k1，直线BD的斜率为k2，则．(从以下①②③三个问题中任选一个填到横线上并给出解答)①求直线AC和BD交点的轨迹方程；②是否存在实常数λ，使得k1=λk2恒成立；③过点C作关于x轴的对称点C′，连接C′D得到直线l1，试探究：直线l1是否恒过定点．【答案】解：(1)依题意，得2a+2c=6+42，12·2c·b2a=b2a·c=13c，a2=b2+c2，即a+c=3+22，b2a=13，a2=b2+c2，解得a2=9，b2=1，c2=8，所以E的方程为x29+y2=1.(2)选择①.设直线l的方程为x=ty+32，联立方程x29+y2=1，x=ty+32，化简整理，得4(t2+9)y2+12ty-27=0，假设C(x1，y1)，D(x2，y2)，由韦达定理，得y1+y2=-3tt2+9，y1y2=-274(t2+9)，得ty1y2=94(y1+y2)，直线AC的方程为y=y1x1+3(x+3)，直线BD的方程为y=y2x2-3(x-3)，联立方程，得y=y1x1+3(x+3)，y=y2x2-3(x-3)，两式相除，得x+3x-3=y2x2-3·x1+3y1=(x1+3)y2(x2-3)y1=ty1+92y2ty2-32y1=2ty1y2+9y22ty1y2-3y1=2·94(y1+y2)+9y22·94(y1+y2)-3y1=3(y1+y2)+6y23(y1+y2)-2y1=3(y1+3y2)y1+3y2=3，即x+3x-3=3，解得x=6，所以直线AC和BD交点的轨迹方程是直线x=6.选择②.联立方程x29+y2=1，x=ty+32，化简整理，得4(t2+9)y2+12ty-27=0，假设C(x1，y1)，D(x2，y2)，由韦达定理，得y1+y2=-3tt2+9，y1y2=-274(t2+9)，得ty1y2=94(y1+y2)，于是k1k2=y1x1+3·x2-3y2=(x2-3)y1(x1+3)y2=ty2-32y1ty1+92y2=2ty1y2-3y12ty1y2+9y2=2·94(y1+y2)-3y12·94(y1+y2)+9y2=32y1+92y292y1+272y2=32(y1+3y2)92(y1+3y2)=13，故存在实数λ=13，使得k1=λk2恒成立．选择③.设C(x1，y1)，D(x2，y2)，C′(x1，-y1)，联立方程x29+y2=1，x=ty+32，化简整理，得4(t 2+9)y 2+12ty -27=0，由韦达定理，得y 1+y 2=-3t t 2+9，y 1y 2=-274(t 2+9)， 设直线C ′D 与x 轴交于点M (m ,0)，由对称性可知k CM +k DM =0，即y 1x 1-m +y 2x 2-m=0，则y 1(x 2-m )+y 2(x 1-m )=0，所以y 1(x 2-m )+y 2(x 1-m )=x 1y 2+x 2y 1-m (y 1+y 2)=ty 1+32 y 2+ty 2+32 y 1-m (y 1+y 2)=2ty 1y 2+32-m (y 1+y 2)=2t ·-274(t 2+9)+32-m ·-3t t 2+9=0，即-9t +(3-2m )·(-t )=0，解得m =6，所以直线C ′D 恒过定点M (6,0)．3(2023·新高考全国Ⅱ)已知双曲线C 的中心为坐标原点，左焦点为(-25，0)，离心率为5.(1)求C 的方程；(2)记C 的左、右顶点分别为A 1，A 2，过点(-4,0)的直线与C 的左支交于M ，N 两点，M 在第二象限，直线MA 1与NA 2交于点P .证明：点P 在定直线上．【答案】(1)解：设双曲线C 的方程为x 2a 2-y 2b2=1(a >0，b >0)，由焦点坐标可知c =25，则由e =c a=5，可得a =2，b =c 2-a 2=4，所以双曲线C 的方程为x 24-y 216=1.(2)证明　由(1)可得A 1(-2,0)，A 2(2,0)，设M (x 1，y 1)，N (x 2，y 2)，显然直线MN 的斜率不为0，设直线MN 的方程为x =my -4，且-12<m <12，与x 24-y 216=1联立可得(4m 2-1)y 2-32my +48=0，且Δ=64(4m 2+3)>0，则y 1+y 2=32m 4m 2-1，y 1y 2=484m 2-1，直线MA 1的方程为y =y 1x 1+2(x +2)，直线NA 2的方程为y =y 2x 2-2(x -2)，联立直线MA 1与直线NA 2的方程可得x +2x -2=y 2(x 1+2)y 1(x 2-2)=y 2(my 1-2)y 1(my 2-6)=my 1y 2-2y 2my 1y 2-6y 1，方法一　(和积转化)因为my 1y 2=32(y 1+y 2)，所以my 1y 2-2y 2my 1y 2-6y 1=32(y 1+y 2)-2y 232(y 1+y 2)-6y 1=32y 1-12y 2-92y 1+32y 2=-13.方法二　(配凑)因为my 1y 2=32(y 1+y 2)，所以my 1y 2-2y 2my 1y 2-6y 1=my 1y 2-2y 1-2y 2+2y 1my 1y 2-6y 1=my 1y 2-2(y 1+y 2)+2y 1my 1y 2-6y 1=32y 1-12y 2-92y 1+32y 2=-13.由x +2x -2=-13可得x =-1，即x P =-1，据此可得点P 在定直线x =-1上运动．4已知椭圆C ：x 2a 2+y 2b2=1(a >b >0)的左、右焦点分别为F 1(-c ,0)，F 2(c ,0)，M ，N 分别为左、右顶点，直线l ：x =ty +1与椭圆C 交于A ，B 两点，当t =-33时，A 是椭圆的上顶点，且△AF 1F 2的周长为6.(1)求椭圆C 的方程；(2)设直线AM ，BN 交于点Q ，证明：点Q 在定直线上．(3)设直线AM ，BN 的斜率分别为k 1，k 2，证明：k 1k 2为定值．【答案】(1)解：当t =-33时，直线l ：x =-33y +1，令x =0，得y =3，即椭圆的上顶点为0，3 ，则b =3，又△AF 1F 2的周长为6，即2a +2c =6，即a +c =3，又a 2-c 2=b 2=3，解得a =2，c =1，所以椭圆C 的方程为x 24+y 23=1.(2)证明　由(1)知，M (-2,0)，N (2,0)，设A (x 1，y 1)，B (x 2，y 2)，依题意，点A ，B 不在x 轴上，由x =ty +1，x 24+y 23=1，消去x 并整理得(3t 2+4)y 2+6ty -9=0，Δ>0，则y 1+y 2=-6t3t 2+4，y 1y 2=-93t 2+4，得ty 1y 2=32(y 1+y 2)，直线AM 的方程为y =y 1x 1+2(x +2)，直线BN 的方程为y =y 2x 2-2(x -2)，联立直线AM ，BN 的方程得x +2x -2=y 2(x 1+2)y 1(x 2-2)=y 2(ty 1+3)y 1(ty 2-1)=ty 1y 2+3y 2ty 1y 2-y 1=32(y 1+y 2)+3y 232(y 1+y 2)-y 1=32y 1+92y 212y 1+32y 2=3，于是得x =4，所以直线AM ，BN 的交点Q 在定直线x =4上．(3)证明　由(2)知，k 1k 2=y 1(x 2-2)y 2(x 1+2)=y 1(ty 2-1)y 2(ty 1+3)=ty 1y 2-y 1ty 1y 2+3y 2=12y 1+32y 232y 1+92y 2=13，为定值．5(2023·深圳模拟)在平面直角坐标系Oxy 中，已知双曲线C ：y 2a 2-x 2b2=1(a >0，b >0)的一条渐近线为y =33x ，且点P 3，2 在C 上．(1)求C 的方程；(2)设C 的上焦点为F ，过F 的直线l 交C 于A ，B 两点，且AF =7BF ，求l 的斜率．【答案】解：(1)由双曲线标准方程可知，其渐近线方程为y =±a b x ，所以33=a b ，可得b 2=3a 2，将点P 3，2 代入双曲线C 的方程可得2a 2-3b 2=1，解得a 2=1，b 2=3，所以双曲线C 的方程为y 2-x 23=1.(2)由(1)可知，上焦点F (0,2)，设直线l 的斜率为k ，A (x 1，y 1)，B (x 2，y 2)，则直线l 的方程为y =kx +2，联立y 2-x 23=1，y =kx +2，整理得(3k 2-1)x 2+12kx +9=0，所以x 1+x 2=-12k3k 2-1，x 1x 2=93k 2-1，又AF =7BF ，即(-x 1,2-y 1)=7(-x 2,2-y 2)，可得x 1=7x 2，方法一　因为x 1x 2=7，所以x 1x 2+x 2x 1=(x 1+x 2)2x 1x 2-2=507，即-12k 3k 2-1 293k 2-1-2=507，解得k =±255，所以直线l 的斜率为±255.方法二　x 1+x 2=8x 2=-12k 3k 2-1，x 1x 2=7x 22=93k 2-1， 即-3k 2(3k 2-1) 2=97(3k 2-1)，解得k =±255，所以直线l 的斜率为±255.方法三　利用焦点弦定理(此方法只能在小题中使用)：|e cos α|=λ-1λ+1.由题意得AF =-7FB ，则λ=-7，e =2，α为直线l 的倾斜角，则有|2cos α|=43，解得|cos α|=23，则k =tan α=±255.6已知点A (0，-2)，椭圆E ：x 2a 2+y 2b2=1(a >b >0)的离心率为32，F 是椭圆E 的右焦点，直线AF 的斜率为233，O 为坐标原点．(1)求E 的方程；(2)设过点A 的直线l 与E 相交于P ，Q 两点，且AP =12AQ ，求△OPQ 的面积及直线l 的方程．【答案】解：(1)设F (c ,0)，因为直线AF 的斜率为233，A (0，-2)，所以2c =233，解得c =3.又c a =32，b 2=a 2-c 2， 解得a =2，b =1， 所以椭圆E 的方程为x 24+y 2=1.(2)设P (x 1，y 1)，Q (x 2，y 2)，由题意可设直线l 的方程为y =kx -2，联立x 24+y 2=1，y =kx -2， 消去y 得(1+4k 2)x 2-16kx +12=0，当Δ=16(4k 2-3)>0，即k 2>34，即k <-32或k >32时，x 1+x 2=16k 1+4k 2，x 1x 2=121+4k 2，由AP =12AQ，得x 2=2x 1，即x 2x 1=2，所以x 1x 2+x 2x 1=(x 1+x 2)2x 1x 2-2=52，解得k 2=2720>34.又|PQ |=1+k 2(x 1+x 2)2-4x 1x 2=1+k 216k1+4k 2 2-481+4k 2=41+k 24k 2-31+4k 2，点O 到直线l 的距离d =2k 2+1，所以S △OPQ =12·d ·|PQ |=44k 2-31+4k 2=154，此时直线l 的方程为y =31510x -2或y =-31510x -2.。

圆锥曲线非对称性韦达定理怎么处理
在解决直线与圆锥曲线的位置关系的问题中，我们通常要联立直线与圆锥曲线的方程，消去x或y,得到一个一元二次方程。

很多都是利用韦达定理得到两根之间的关系来处理有关x1,x2（或y1,y2）的对称量，诸如：
x1+x2,x1x2,|x1−x2|,x12+x22,x1
x2+x2
x1
,y1
x1−2
·y2
x2−2
等，它们都是关于x1,x2（或y1,y2）的轮换对称
式，即将x1与x2互换之后，结果不变，被称之为“对称性”。

这类问题，我们称之为“对称型韦达定理”题型，只需要将韦达定理代入化简即可得到结果。

但还有少部分题不是关于x1,x2（或y1,y2）的轮换对称式，比如我们会遇到两根不对称的结构，比如：
x1 x2,λx1+μx2(λ≠μ),kx1x2+3x1−2x2
kx1x2−3x2+2x1
,m y1y2−3y1
m y
1
y
2
+2y
2
这类问题我们称之为“非对称型韦达定理”题型，一般
都是定值定点的证明题，这类问题我们不能简单的代入韦达定理来得到结果，那么这类问题我们该怎么处理呢？
最常见的处理办法是——和积代换（非对称结构中不含常数项时可尝试使用此法）
即寻求x1x2与x1+x2或y1y2与y1+y2之间的关系，将积式替换成和式，从而求定点定值最值问题。

同类题：解答：。