高中立体几何公式

109．证明直线与直线的平行的思考途径（1）转化为判定共面二直线无交点；（2）转化为二直线同与第三条直线平行；（3）转化为线面平行；（4）转化为线面垂直；（5）转化为面面平行.110．证明直线与平面的平行的思考途径（1）转化为直线与平面无公共点；（2）转化为线线平行；（3）转化为面面平行.111．证明平面与平面平行的思考途径（1）转化为判定二平面无公共点；（2）转化为线面平行；（3）转化为线面垂直.112．证明直线与直线的垂直的思考途径（1）转化为相交垂直；（2）转化为线面垂直；（3）转化为线与另一线的射影垂直；（4）转化为线与形成射影的斜线垂直.113．证明直线与平面垂直的思考途径（1）转化为该直线与平面内任一直线垂直；（2）转化为该直线与平面内相交二直线垂直；（3）转化为该直线与平面的一条垂线平行；（4）转化为该直线垂直于另一个平行平面；（5）转化为该直线与两个垂直平面的交线垂直.114．证明平面与平面的垂直的思考途径（1）转化为判断二面角是直二面角；（2）转化为线面垂直.115.空间向量的加法与数乘向量运算的运算律(1)加法交换律：a ＋b =b ＋a ．(2)加法结合律：(a ＋b )＋c =a ＋(b ＋c )．(3)数乘分配律：λ(a ＋b )=λa ＋λb ．116.平面向量加法的平行四边形法则向空间的推广始点相同且不在同一个平面内的三个向量之和，等于以这三个向量为棱的平行六面体的以公共始点为始点的对角线所表示的向量.117.共线向量定理对空间任意两个向量a 、b (b ≠0 )，a ∥b ⇔存在实数λ使a =λb ．P A B 、、三点共线⇔||AP AB ⇔AP t AB =⇔(1)OP t OA tOB =-+.||AB CD ⇔AB 、CD 共线且AB CD 、不共线⇔AB tCD =且AB CD 、不共线. 118.共面向量定理向量p 与两个不共线的向量a 、b 共面的⇔存在实数对,x y ,使p ax by =+．推论 空间一点P 位于平面MAB 内的⇔存在有序实数对,x y ,使MP xMA yMB =+， 或对空间任一定点O ，有序实数对,x y ，使OP OM xMA yMB =++.119.对空间任一点O 和不共线的三点A 、B 、C ，满足OP xOA yOB zOC =++（x y z k ++=），则当1k =时，对于空间任一点O ，总有P 、A 、B 、C 四点共面；当1k ≠时，若O ∈平面ABC ，则P 、A 、B 、C 四点共面；若O ∉平面ABC ，则P 、A 、B 、C 四点不共面．C A B 、、、D 四点共面⇔AD 与AB 、AC 共面⇔AD x AB y AC =+⇔(1)OD x y OA xOB yOC =--++（O ∉平面ABC ）.120.空间向量基本定理如果三个向量a 、b 、c 不共面，那么对空间任一向量p ，存在一个唯一的有序实数组x ，y ，z ，使p ＝x a ＋y b ＋z c ．推论 设O 、A 、B 、C 是不共面的四点，则对空间任一点P ，都存在唯一的三个有序实数x ，y ，z ，使OP xOA yOB zOC =++.121.射影公式已知向量AB =a 和轴l ，e 是l 上与l 同方向的单位向量.作A 点在l 上的射影'A ，作B 点在l 上的射影'B ，则''||cos A B AB =〈a ，e 〉=a ·e122.向量的直角坐标运算设a ＝123(,,)a a a ，b ＝123(,,)b b b 则(1)a ＋b ＝112233(,,)a b a b a b +++；(2)a －b ＝112233(,,)a b a b a b ---；(3)λa ＝123(,,)a a a λλλ (λ∈R)；(4)a ·b ＝112233a b a b a b ++；123.设A 111(,,)x y z ，B 222(,,)x y z ，则AB OB OA =-= 212121(,,)x x y y z z ---.124．空间的线线平行或垂直设111(,,)a x y z =，222(,,)b x y z =，则a b ⇔(0)a b b λ=≠⇔121212x x y y z z λλλ=⎧⎪=⎨⎪=⎩；a b ⊥⇔0a b ⋅=⇔1212120x x y y z z ++=.125.夹角公式设a ＝123(,,)a a a ，b ＝123(,,)b b b ，则cos 〈a ，b 〉.推论 2222222112233123123()()()a b a b a b a a a b b b ++≤++++，此即三维柯西不等式. 126. 四面体的对棱所成的角四面体ABCD 中, AC 与BD 所成的角为θ,则2222|()()|cos 2AB CD BC DA AC BDθ+-+=⋅. 127．异面直线所成角cos |cos ,|a b θ= =21||||||a b a b x ⋅=⋅+（其中θ（090θ<≤）为异面直线a b ,所成角，,a b 分别表示异面直线a b ,的方向向量）128.直线AB 与平面所成角sin ||||AB m arc AB m β⋅=(m 为平面α的法向量). 129.若ABC ∆所在平面若β与过若AB 的平面α成的角θ,另两边AC ,BC 与平面α成的角分别是1θ、2θ,A B 、为ABC ∆的两个内角，则 2222212sin sin (sin sin )sin A B θθθ+=+.特别地,当90ACB ∠=时,有22212sin sin sin θθθ+=.130.若ABC ∆所在平面若β与过若AB 的平面α成的角θ,另两边AC ,BC 与平面α成的角分别是1θ、2θ,''A B 、为ABO ∆的两个内角，则 222'2'212tan tan (sin sin )tan A B θθθ+=+.特别地,当90AOB ∠=时,有22212sin sin sin θθθ+=.131.二面角l αβ--的平面角 cos ||||m n arc m n θ⋅=或cos ||||m n arc m n π⋅-（m ，n 为平面α，β的法向量）. 132.三余弦定理设AC 是α内的任一条直线，且BC ⊥AC ，垂足为C ，又设AO 与AB 所成的角为1θ，AB 与AC 所成的角为2θ，AO 与AC 所成的角为θ．则12cos cos cos θθθ=.133. 三射线定理若夹在平面角为ϕ的二面角间的线段与二面角的两个半平面所成的角是1θ,2θ,与二面角的棱所成的角是θ，则有22221212sin sin sin sin 2sin sin cos ϕθθθθθϕ=+- ;1212||180()θθϕθθ-≤≤-+(当且仅当90θ=时等号成立).134.空间两点间的距离公式若A 111(,,)x y z ，B 222(,,)x y z ，则,A B d =||AB AB AB =⋅=135.点Q 到直线l 距离h =(点P 在直线l 上，直线l 的方向向量a =PA ，向量b =PQ ).136.异面直线间的距离||||CD n d n ⋅=(12,l l 是两异面直线，其公垂向量为n ，C D 、分别是12,l l 上任一点，d 为12,l l 间的距离).137.点B 到平面α的距离||||AB n d n ⋅=（n 为平面α的法向量，AB 是经过面α的一条斜线，A α∈）. 138.异面直线上两点距离公式d θ=.',d EA AF =.d =（'E AA F ϕ=--）.(两条异面直线a 、b 所成的角为θ，其公垂线段'AA 的长度为h.在直线a 、b 上分别取两点E 、F ，'A E m =,AF n =,EF d =).139.三个向量和的平方公式2222()222a b c a b c a b b c c a ++=+++⋅+⋅+⋅ 2222||||cos ,2||||cos ,2||||cos ,a b c a b a b b c b c c a c a =+++⋅+⋅+⋅140. 长度为l 的线段在三条两两互相垂直的直线上的射影长分别为123l l l 、、，夹角分别为123θθθ、、,则有2222123l l l l =++222123cos cos cos 1θθθ⇔++=222123sin sin sin 2θθθ⇔++=. （立体几何中长方体对角线长的公式是其特例）.141. 面积射影定理'cos S S θ=. (平面多边形及其射影的面积分别是S 、'S ，它们所在平面所成锐二面角的为θ). 142. 斜棱柱的直截面已知斜棱柱的侧棱长是l ,侧面积和体积分别是S 斜棱柱侧和V 斜棱柱,它的直截面的周长和面积分别是1c 和1S ,则①1S c l =斜棱柱侧.②1V S l =斜棱柱.143．作截面的依据三个平面两两相交，有三条交线，则这三条交线交于一点或互相平行.144．棱锥的平行截面的性质如果棱锥被平行于底面的平面所截，那么所得的截面与底面相似，截面面积与底面面积的比等于顶点到截面距离与棱锥高的平方比（对应角相等，对应边对应成比例的多边形是相似多边形，相似多边形面积的比等于对应边的比的平方）；相应小棱锥与小棱锥的侧面积的比等于顶点到截面距离与棱锥高的平方比．145.欧拉定理(欧拉公式)2V F E +-=(简单多面体的顶点数V 、棱数E 和面数F).（1）E =各面多边形边数和的一半.特别地,若每个面的边数为n 的多边形，则面数F 与棱数E 的关系：12E nF =； （2）若每个顶点引出的棱数为m ，则顶点数V 与棱数E 的关系：12E mV =. 146.球的半径是R ，则其体积343V R π=, 其表面积24S R π=． 147.球的组合体(1)球与长方体的组合体:长方体的外接球的直径是长方体的体对角线长.(2)球与正方体的组合体:正方体的内切球的直径是正方体的棱长, 正方体的棱切球的直径是正方体的面对角线长, 正方体的外接球的直径是正方体的体对角线长.(3) 球与正四面体的组合体:棱长为a 的正四面体的内切球的半径为12a ,外接球的半径为4a . 148．柱体、锥体的体积 13V Sh =柱体（S 是柱体的底面积、h 是柱体的高）. 13V Sh =锥体（S 是锥体的底面积、h 是锥体的高）.。

高中立体几何内接圆外接圆公式在高中数学的学习中，立体几何中的内接圆和外接圆公式可是让不少同学感到头疼的知识点呢。

但别怕，让咱们一起来把它们捋捋清楚！先来说说外接圆吧。

外接圆是指一个多面体的顶点都在同一个圆上，这个圆就叫做该多面体的外接圆。

对于常见的几何体，比如正三棱柱、正三棱锥、正方体等等，都有相应的外接圆公式。

就拿正三棱柱来说吧，假设底面正三角形的边长为a，侧棱长为h。

那外接球的半径 R 就可以通过公式R = √[(a²/3) + (h²/4)] 来计算。

这个公式咋来的呢？这就得从正三棱柱的结构特点说起。

我记得有一次给学生们讲这个知识点的时候，有个特别调皮的学生就问我：“老师，这公式到底有啥用啊？”我笑着回答他：“你想想啊，要是你以后要盖一个正三棱柱形状的房子，得知道外接圆的半径才能算出需要多少材料来做房顶的支撑结构呀！”全班同学都被我这个例子逗笑了，也对这个公式有了更深刻的印象。

再说说内接圆。

内接圆呢，是指一个多面体的面都与同一个圆相切，这个圆就是内接圆啦。

比如正三棱锥，如果底面正三角形的边长为 a，那它的内切球半径 r 可以通过公式 r = √3a / 6 来计算。

在学习这些公式的时候，同学们可不能死记硬背，得理解它们背后的原理。

比如说外接圆的半径，它跟多面体的棱长、面的形状都有关系。

咱们得通过分析多面体的结构，找到关键的线段和角度，才能推导出公式。

还记得我上高中那会，立体几何也是让我头疼了好一阵子。

特别是这些外接圆内接圆的公式，总是搞混。

有一次考试，就因为把外接圆和内接圆的公式弄反了，白白丢了好多分。

那叫一个懊悔呀！从那以后，我就下定决心，一定要把这些公式搞明白。

我找了好多练习题，一道道地做，一点点地琢磨，终于把它们都拿下了。

所以同学们，遇到难题别害怕，多思考，多练习，相信你们一定能掌握这些公式的！总之，高中立体几何中的内接圆外接圆公式虽然有点复杂，但只要咱们用心去学，多做练习，多总结规律，就一定能攻克这个难关。

高中数学立体几何体积计算公式的推导与应用在高中数学中，立体几何是一个重要的内容，其中体积计算是其中的一个重点。

掌握了立体几何体积计算公式的推导与应用，不仅可以帮助我们更好地理解几何概念，还可以提高解题的效率。

本文将以常见的几何体为例，详细介绍体积计算公式的推导与应用。

一、立方体的体积计算公式我们首先来推导立方体的体积计算公式。

立方体是一种所有边长相等的六面体，假设边长为a，则立方体的体积V等于边长的立方，即V = a³。

例如，如果一个立方体的边长为2cm，则它的体积为8cm³。

在解题时，我们可以利用立方体的体积计算公式来计算未知量。

例如，已知一个立方体的体积为64cm³，我们需要求解它的边长。

根据立方体的体积计算公式，我们可以得到a³ = 64，进而得到a = 4。

因此，该立方体的边长为4cm。

二、长方体的体积计算公式接下来，我们来推导长方体的体积计算公式。

长方体是一种所有相邻面都是矩形的六面体，假设长、宽、高分别为l、w、h，则长方体的体积V等于长乘以宽乘以高，即V = lwh。

例如，如果一个长方体的长为3cm，宽为4cm，高为5cm，则它的体积为60cm³。

在解题时，我们可以利用长方体的体积计算公式来计算未知量。

例如，已知一个长方体的体积为120cm³，长为4cm，宽为3cm，我们需要求解它的高。

根据长方体的体积计算公式，我们可以得到4 * 3 * h = 120，进而得到h = 10。

因此，该长方体的高为10cm。

三、圆柱体的体积计算公式接下来，我们来推导圆柱体的体积计算公式。

圆柱体是一种由两个平行圆面和一个连接两个圆面的侧面组成的几何体，假设底面半径为r，高为h，则圆柱体的体积V等于底面积乘以高，即V = πr²h。

例如，如果一个圆柱体的底面半径为2cm，高为5cm，则它的体积为20πcm³。

在解题时，我们可以利用圆柱体的体积计算公式来计算未知量。

长方形的周长=（长+宽）×2长方体的表面积=正方形的周长=边长×4（长×宽+长×高＋宽×高）×2长方形的面积=长×宽长方体的体积 =长×宽×高正方形的面积=边长×边长正方体的表面积=棱长×棱长×6三角形的面积=底×高÷2正方体的体积=棱长×棱长×棱长平行四边形的面积=底×高圆柱的侧面积=底面圆的周长×高梯形的面积=（上底+下底）×高÷2圆柱的表面积=上下底面面积+侧面积直径=半径×2 半径=直径÷2圆柱的体积=底面积×高圆的周长=圆周率×直径=圆锥的体积=底面积×高÷3圆周率×半径×2长方体（正方体、圆柱体）圆的面积=圆周率×半径×半径的体积=底面积×高平面图形正方形 a—边长 C＝4a S＝a2梯形 a和b－上、下底长 h－高m－中位线长 S＝(a+b)h/2 ＝mh长方形 a和b－边长 C＝2(a+b) S＝ab圆 r－半径 d－直径三角形 a,b,c－三边长 h－a边上的高C＝πd＝2πrs－周长的一半 A,B,C－内角其中S＝πr2＝πd2/4s＝(a+b+c)/2S＝ah/2＝ab/2·sinC扇形 r—扇形半径 a—圆心角度数＝[s(s-a)(s-b)(s-c)]1/2C＝2r＋2πr×(a/360)＝a2sinBsinC/(2sinA)S＝πr2×(a/360)四边形 d,D－对角线长 α－对角线夹角弓形 l－弧长 b－弦长 h－矢高S＝dD/2·sinαr－半径 α－圆心角的度数S＝r2/2·(πα/180-sinα)平行四边形 a,b－边长 h－a边的高＝r2arccos[(r-h)/r] - (r-h)(2rh-h2)1/2α－两边夹角 ＝παr2/360 - b/2·[r2-(b/2)2]1/2S＝ah ＝absinα＝r(l-b)/2 + bh/2≈2bh/3菱形 a－边长 α－夹角 D－长对角线长d－短对角线长圆环 R－外圆半径 r－内圆半径S＝Dd/2 ＝a2sinα立方图形正方体 a－边长空心圆柱 R－外圆半径S＝6a2 V＝a3r－内圆半径 h－高V＝πh(R2-r2)长方体 a－长 b－宽 c－高S＝2(ab+ac+bc)直圆锥 r－底半径 h－高V＝abc V＝πr2h/3棱柱 S－底面积 h－高圆台 r－上底半径 R－下底半径V＝Sh h－高V＝πh(R2＋Rr＋r2)/3棱锥 S－底面积 h－高V＝Sh/3球 r－半径 d－直径V＝4/3πr3＝πd2/6棱台 S1和S2－上、下底面积h－高球缺 h－球缺高 r－球半径V＝h[S1+S2+(S1S1)1/2]/3a－球缺底半径V＝πh(3a2+h2)/6拟柱体 S1－上底面积 S2－下底面积＝πh2(3r-h)/3S0－中截面积 h－高a2＝h(2r-h)圆柱 r－底半径 h－高球台 r1和r2－球台上、下底半径C—底面周长 S底—底面积h－高S侧—侧面积 S表—表面积V＝πh[3(r12＋r22)+h2]/6C＝2πr S底＝πr2 S侧＝ChS表＝Ch+2S底V＝S底h ＝πr2h。

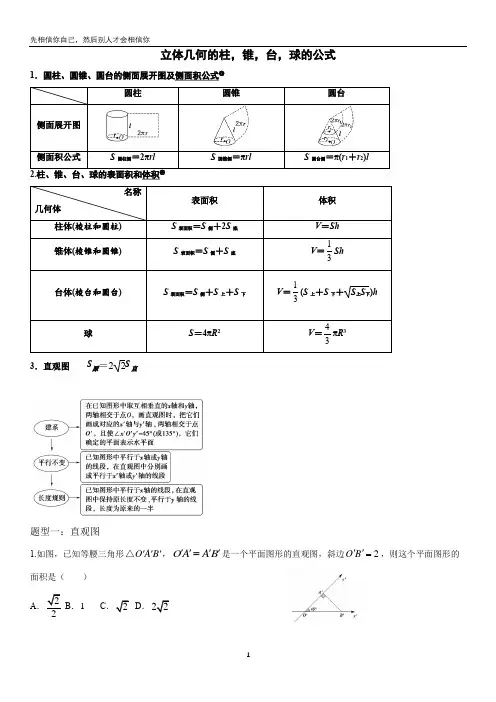
立体几何的柱，锥，台，球的公式1．圆柱、圆锥、圆台的侧面展开图及侧面积公式❶圆柱圆锥圆台侧面展开图侧面积公式S 圆柱侧＝2πrlS 圆锥侧＝πrlS 圆台侧＝π(r 1＋r 2)l2.柱、锥、台、球的表面积和体积❷名称几何体表面积 体积 柱体(棱柱和圆柱) S 表面积＝S 侧＋2S 底 V ＝Sh 锥体(棱锥和圆锥)S 表面积＝S 侧＋S 底V ＝13Sh 台体(棱台和圆台) S 表面积＝S 侧＋S 上＋S 下 V ＝13(S 上＋S 下＋S 上S 下)h 球S ＝4πR 2V ＝43πR 3 3．直观图 S 原＝22S 直题型一：直观图1.如图，已知等腰三角形O A B '''△，OA AB ''''=是一个平面图形的直观图，斜边2O B ''=，则这个平面图形的面积是（ ） A ．22B ．1C ．2D ．222.一个梯形的直观图是一个如图所示的等腰梯形，且1A B ''=，3O C ''=，2O A ''=，则原梯形的面积为( )A ．22B ．42C ．8D ．43．如图所示为水平放置的正方形ABCO ，在平面直角坐标系xOy 中点B 的坐标为(2,2)，用斜二测画法画出它的直观图A ′B ′C ′O ′，则四边形A ′B ′C ′O ′的面积为___________.4．如图所示，是三角形ABC 的直观图，则三角形ABC 的面积S △ABC =_______；（请用数字填写）5．如图，正方形O ′A ′B ′C ′的边长为1，它是一个水平放置的平面图形的直观图，则原图形的周长为（ ） A ．4 B ．6C ．8D ．222+6.正三角形ABC 的边长为2 cm ，如图，△A’B’C’为其水平放置的直观图，则△A’B’C’的周长为（ ） A .8 cmB .6 cmC .（2 +√6）cmD .（2 + 2√3）cm7.用斜二测画法画出水平放置的△ABC 的直观图如图所示，已知A’C’ = 3，B’C’ = 2，则△ABC 中AB 边上的中线长为_________.8.(多空题)在如图所示的直观图中，四边形O ′A ′B ′C ′为菱形且边长为2 cm ，则在平面直角坐标系中原四边形OABC 为________(填具体形状)，其面积为________ cm 2.9．已知用斜二测画法得到的某水平放置的平面图形的直观图是如图所示的等腰直角△O B C '''，其中1O B ''=，则原平面图形中最大边长为( ) A ．2B ．22C ．3D ．2310.如图，△A ′B ′C ′表示水平放置的△ABC 根据斜二测画法得到的直观图，A B ''在x '轴上，B ′C ′与x '轴垂直，且2B C ''=，则△ABC 的边AB 上的高为（ ）A ．2B ．22C ．4D ．4211.如图所示，△A ′B ′C ′表示水平放置的△ABC 在斜二测画法下的直观图，A ′B ′在x ′轴上，B ′C ′与x ′轴垂直，且B ′C ′＝3，则△ABC 的边AB 上的高为（ ） A ．6√2 B ．3√3 C ．3√2 D ．3题型二棱柱、棱锥、棱台的表面积和体积1.正三棱锥的所有棱长均为a ，则该三棱锥的表面积为（ ） A .33a 2B .23a 2C .3a 2D .4a 22.已知正四棱锥的底面边长是2，侧棱长是5，则该正四棱锥的表面积为（ ） A .3B .12C .8D .433.已知高为3的棱柱ABC -A 1B 1C 1的底面是边长为1的正三角形，如图，则三棱锥B -AB 1C 的体积为（ ） A .41 B .21 C .63 D .43 4.将一个棱长为a 的正方体，切成27个全等的小正方体，则表面积增加了（ ） A .26aB .212aC .218aD.224a5.将一个正方体截去四个角后得到一个正四面体，这个正四面体的体积是正方体体积的（ ）A .21 B .31 C .61 D .41 6.如图所示，在三棱台ABC - A 1B 1C 1中，A 1B 1：AB = 1：2，则三棱锥B - A 1B 1C 1与三棱锥A 1 - ABC 的体积比为（ ） A .1：2 B .1：3 C .1：2D .1：47.在底面半径为1的圆锥中，若该圆锥侧面展开图的面积是2π，则该圆锥的体积为（ ）A ．B ．C ．D ．8.已知球A 与球B 的体积之比为8：27，则球A 与球B 的半径之比为（ ） A ．：B ．4：9C ．2：3D ．3：29.球的一个截面面积为49πcm 2，球心到球截面距离为24cm ，则球的表面积是 ． 10.用一个平面截半径为25cm 的球，截面面积是49πcm 2，则球心到截面的距离是 ． 11.已知一个长方体的三个面的面积分别是2，3，6，则这个长方体的体积为_________。

数学高考常考公式数学是一个重要的学科，它需要掌握各种知识和技能。

高中数学高考常考公式对于学生来说至关重要，因为它们是其基础。

学生如果能够熟练掌握这些公式，就会有很大的优势。

下面是一些常见的高考数学公式，可以帮助学生更好地准备数学考试。

一、初三数学常考公式1. 三角函数公式：sin（a+b）=sinacosb+cosasinb；cos（a+b）=cosacosb-sinasinb；tan（a+b）=tanatnb/1-tanatanb。

2. 平面几何公式：△ABC的面积S=1/2abc=sqrt[p(p-a)(p-b)(p-c)]。

3. 立体几何公式：空间中的一条直线l，它的一般式方程为：Ax+By+Cz+D=0；空间中的一条直线l和平面π，它们的交点为A(x0,y0,z0)，则l的方向向量即为π的法向量；立体角的三视角公式：tanα1+tanα2+tanα3-tanα1tanα2tanα3=0。

二、高一数学常考公式1. 二次函数公式：y=ax²+bx+c（a≠0）; Δ=b²-4ac是二次函数的判别式。

2. 勾股定理：a²+b²=c²。

3. 三角形面积公式：S=1/2absinC。

三、高二数学常考公式1. 导数公式：f’(x)=lim（f(x+Δx)-f(x)）/Δx。

2. 柯西-施瓦茨不等式：| ∑ ai bi | ≤ (∑ai²)^1/2 (∑bi²)^1/2。

3. 弧度公式：角度度数转成弧度制，用弧度表示为π/180×角度。

四、高三数学常考公式1. 微积分基本公式：∫[a,b]f(x)dx=F(b)−F(a)。

2. 泰勒公式：f(x)=f(a)+f’(a)(x-a)+f’’(a)(x-a)²/2!+……+f（n）（a）（x-a）n/n!+……，其中f(n)(a)表示f(x)在x=a处的n阶导数。

3. 不等式公式：平均数不等式：（a1+a2……an)/n≥(n√a1a2……an)；柯西不等式：(∑ai²)×(∑bi²)≥(∑aibi)²；阿贝尔不等式：∑aibi≤c×∑ai+（1/c）∑bi²。

正三棱锥正三棱锥是指底面为正三角形,顶点在底面的射影是正三角形的中心的三棱锥= 在ABC 中,AB BC CA a ===,CM AB ⊥于M ,则2CM a =,23CO OM ==R =(ABC 的外接圆半径) MO =r = (ABC 的内切圆半径),24ABC S = , 在特征三角形VOM ∆和VOC ∆中当VO h =时,侧高=,侧棱VC ==正四面体:正四面体是特殊的正三棱锥,其三侧棱长也等于底面正三角形边长.此时,AB BC CA PA PB PA a ======, 在特征三角形POD ∆和POA ∆中斜高==∴高h =,则2S 侧=,2S 全, 313P ABC ABC V h S -==侧棱互相垂直的正三棱锥:侧棱互相垂直的正三棱锥可看做在正方体过一顶点的三个面的对角线截得立体图形.AB BC CA a ===,则侧棱2PA PB PC a ===,AACA斜高1h'=2a =高6h a =(等于原正方体对角线的13),234S a 侧=,234S +全=,38P ABC V a -=正四棱锥正四棱锥是指底面为正方形,顶点在底面的射影是正方形的中心的四棱锥AB BC CD DA a ====,在特征三角形POE ∆和PBO ∆中OA =,12OE a =,2S a 底=,当PO h =时,侧高=侧棱PC ==正六棱锥正六棱锥是指底面为正六边形,顶点在底面的射影是正方形的中心的六棱锥AB BC CD DE EF FA a ======, 在特征三角形VOH ∆和VOA ∆中OA a =,OH =,22S =底=6, 当VO h =时,侧高=侧棱PC ==球CD如图,球O 的半径OA R =,24S R π=,343V R π=正三棱台正三棱台是指上下底面为正三角形,两正三角形中心的连线垂直于上下底面的三棱台.如图, AB BC CA a ===,A'B'=B'C'=C'A'=b ,OO'=h ,则AD=2,3AO a R ==,6DO r ==,24S a 下=,A'O''R ==,'r =,2S 上, 在特征梯形形''A O OA 和''D O OD 中 侧高侧棱,正四棱台正四棱台是指上下底面为正方形,两正方角形中心的连线垂直于上下底面的四棱台.如图,AB BC CD DA a ====,A'B'=B'C'=C'D'=D'A'=b .OO'=h .则AO =,12OE a =,2S a 下=.A'O'=,1O'E'2b =,2S b 上=,C在特征梯形形''A O OA 和''E O OE 中侧高侧棱正六棱台正六棱台是指上下底面为正六边形, 正六边形中心的连线垂直于上下底面的六棱台.AB BC CD DE EF FA a ======,''''''''''''A B B C C D D E E F F A a ====== 在特征梯形''ODD O 和''OHH O 中 OD a =,OH=,22S =下底=6, ''O D b =,''O H=,22S =上底=6 当'O O h =时,侧高=, 侧棱PC ==圆锥如图.圆锥P O - 中,底面半径OB r =,母线PB l =,则高h =,侧面展开图扇形圆心角B'=BO n ∠,2360n S rl l ππ= 侧=,()22360n S r r l r l ππ⎛⎫+=+ ⎪⎝⎭全= 360r n l =, '2180n BB r l ππ==圆台如图.圆台'O O - 中,下底面半径OA R =.上底面半径''O A r =,母线'AA l =, 则高h =侧面展开图扇形圆心角为n ,()2360n R r S R r l l R rππ++=- 侧= ()222360n R r S l R r R rππ+=++-全 360R r n l -= ,)22V R Rr r =++ B 'P B。

高中数学立体几何总结立体几何是高中数学中一个重要的内容，大致内容包括立体几何基本概念、体积、体积计算公式、侧棱、正三棱柱、正四棱锥、正八棱锷、台面等等。

（一）立体几何基本概念1、三视图：即从三个不同的视角把物体有条不紊的绘出来的文字图形，可以根据它来确定物体的三维形状。

2、几何体：是由把平面图形几何关系组合而成的任何在空间中由一致点构成的物体。

3、棱：即立体几何中各几何体的侧面所围成的线段或面称为棱，如正三棱柱的侧棱。

（二）体积1、体积的定义：体积是立体图形的面积之和，反映物体内部空间的容积大小。

2、体积的计算公式：几何体的体积可用面积的乘积公式计算，比如正三棱柱的体积的表示公式：V=ah；正四棱锥的体积的表示公式：V=1/3bh；正八棱锷的表示公式为：V=1/3πr²h。

（三）正三棱柱1、正三棱柱，是一种方形底面，面积相同的三角柱体，它有三个直角，等边的三个棱，以及一个正方形的底部。

2、侧棱：正三棱柱的侧棱可以分别表示为a，b，c三条线段，表示a=b=c，它们在同一平面且互相垂直。

3、体积计算：正三棱柱的体积可以用面积乘积公式来计算：V=ah；其中，a表示正三棱柱的侧棱，h表示高度。

（四）正四棱锥1、正四棱锥是由正方形底面、顶面和棱构成的三角锥体，它有四个直角棱，棱之间相互垂直，底面和顶面也相互垂直。

2、侧棱：正四棱锥的侧棱只有一条，用a表示，它的四条边都要等于。

（五）正八棱锷1、正八棱锷是一种八个棱组成的几何体，其四条边中有三条边为互相垂直的折线，其余五条边为圆形弧线。

2、侧棱：正八棱锷有八个侧棱，用a1，a2，a3…a8表示，但它们互相之间不相等，作用上也不是等距的。

（六）台面1、台面，又称台体，是由一个小三角形共同构成的平面图形。

当该平面图形在三维空间中展开时，可以形成一个台体，它由三个等高的并列棱构成。

2、台体体积计算：台体的体积可以由其三角面积和三边长共同确定，台体的体积公式为：V=1/3(A1+A2+A3)H；其中，A1，A2，A3表示三个三角面积，H表示高度。

高中数学立体几何公式大全高中数学立体几何公式整理如下：1. 正方体：a-边长，S=6a²，V=a³2. 长方体：a-长，b-宽，c-高，S=2(ab+ac+bc)，V=abc3. 圆柱：r-底半径，h-高，C=2πr，S底=πr²，S侧=Ch，S表=Ch+2S底，V=S底h=πr²h4. 空心圆柱：R-外圆半径，r-内圆半径，h-高，V=πh(R²-r²)5. 直圆锥：r-底半径，h-高，V=πr²h/36. 圆台：r-上底半径，R-下底半径，h-高，V=πh(R²+Rr+r²)/37. 棱柱：S-底面积，h-高，V=Sh8. 棱锥：S-底面积，h-高，V=Sh/39. 棱台：S1和S2-上、下底面积，h-高，V=h[S1+S2+(S1S1)1/2]/310. 拟柱体：S1-上底面积，S2-下底面积，S0-中截面积，h-高，V=h(S1+S2+4S0)/611. 球：r-半径，d-直径，V=4/3πr³=πd²/612. 球缺：h-球缺高，r-球半径，a-球缺底半径，V=πh(3a²+h²)/6=πh²(3r-h)/3a²=h(2r-h)13. 球台：r1和r2-球台上、下底半径，h-高，V=πh[3(r1²+r2²)+h²]/614. 圆环体：R-环体半径，D-环体直径，r-环体截面半径，d-环体截面直径，V=2π²Rr²=π²Dd²/415. 桶状体：D-桶腹直径，d-桶底直径，h-桶高，V=πh(2D²+d²)/12以上公式涵盖了几何体各个方面的内容。

高中数学知识点总结及公式大全关于高中数学知识点总结及公式大全空间几何体表面积体积公式：1、圆柱体:表面积:2πRr+2πRh体积:πR2h(R为圆柱体上下底圆半径，h 为圆柱体高)2、圆锥体:表面积:πR2+πR[(h2+R2)的]体积:πR2h/3(r为圆锥体低圆半径，h为其高，3、a-边长，S=6a2，V=a34、长方体a-长，b-宽，c-高S=2(ab+ac+bc)V=abc5、棱柱S-h-高V=Sh6、棱锥S-h-高V=Sh/37、S1和S2-上、下h-高V=h[S1+S2+(S1S2)^1/2]/38、S1-上底面积，S2-下底面积，S0-中h-高，V=h(S1+S2+4S0)/69、圆柱r-底半径，h-高，C—底面周长S底—底面积，S侧—，S表—表面积C=2πrS底=πr2，S侧=Ch，S表=Ch+2S底，V=S底h=πr2h10、空心圆柱R-外圆半径，r-内圆半径h-高V=πh(R^2-r^2)11、r-底半径h-高V=πr^2h/312、r-上底半径，R-下底半径，h-高V=πh(R2+Rr+r2)/313、球r-半径d-直径V=4/3πr^3=πd^3/614、球缺h-球缺高，r-球半径，a-球缺底半径V=πh(3a2+h2)/6=πh2(3r-h)/315、球台r1和r2-球台上、下底半径h-高V=πh[3(r12+r22)+h2]/616、圆环体R-环体半径D-环体直径r-环体截面半径d-环体截面直径V=2π2Rr2=π2Dd2/417、桶状体D-桶腹直径d-桶底直径h-桶高V=πh(2D2+d2)/12，(母线是圆弧形，圆心是桶的中心)V=πh(2D2+Dd+3d2/4)/15(母线是抛物线形) 二面角和二面角的平面角①二面角的定义：从一条直线出发的两个半平面所组成的图形叫做二面角,这条直线叫做二面角的棱,这两个半平面叫做二面角的面.②二面角的平面角：以二面角的棱上任意一点为顶点,在两个面内分别作垂直于棱的两条射线,这两条射线所成的角叫二面角的平面角.③直二面角：平面角是直角的二面角叫直二面角.两相交平面如果所组成的二面角是直二面角,那么这两个平面垂直;反过来,如果两个平面垂直,那么所成的二面角为直二面角④求二面角的方法定义法：在棱上选择有关点,过这个点分别在两个面内作垂直于棱的射线得到平面角垂面法：已知二面角内一点到两个面的垂线时,过两垂线作平面与两个面的交线所成的角为二面角的平面角高一必修二数学复习知识点总结空间中的垂直问题(1)线线、面面、线面垂直的定义①两条异面直线的垂直：如果两条异面直线所成的角是直角,就说这两条异面直线互相垂直.②线面垂直：如果一条直线和一个平面内的任何一条直线垂直,就说这条直线和这个平面垂直.③平面和平面垂直：如果两个平面相交,所成的二面角(从一条直线出发的两个半平面所组成的图形)是直二面角(平面角是直角),就说这两个平面垂直.(2)垂直关系的判定和性质定理①线面垂直判定定理和性质定理判定定理：如果一条直线和一个平面内的两条相交直线都垂直,那么这条直线垂直这个平面.性质定理：如果两条直线同垂直于一个平面,那么这两条直线平行.②面面垂直的判定定理和性质定理判定定理：如果一个平面经过另一个平面的一条垂线,那么这两个平面互相垂直.性质定理：如果两个平面互相垂直,那么在一个平面内垂直于他们的交线的直线垂直于另一个平面.棱锥棱锥的定义：有一个面是多边形，其余各面都是有一个公共顶点的三角形，这些面围成的几何体叫做棱锥棱锥的性质：(1)侧棱交于一点。

立体几何体积公式一、立方体的体积公式立方体是一种最简单的立体几何体，它的六个面都是正方形，且边长相等。

立方体的体积公式非常简单，即边长的立方。

例如，一个边长为a的立方体的体积可以用公式表示为V = a³。

二、长方体的体积公式长方体是另一种常见的立体几何体，它的六个面都是矩形，且相邻两个面的边长相等。

长方体的体积公式可以通过三个边长相乘得到。

设长方体的长、宽、高分别为a、b、c，那么它的体积可以表示为V = a * b * c。

三、正方体的体积公式正方体是一种特殊的长方体，它的六个面都是正方形，且边长相等。

正方体的体积公式与立方体相同，即边长的立方。

假设正方体的边长为a，那么它的体积可以表示为V = a³。

四、圆柱体的体积公式圆柱体是一种具有底面和侧面的立体几何体，底面为圆形，侧面为矩形。

圆柱体的体积公式可以通过底面积与高相乘得到。

设圆柱体的底面半径为r，高为h，那么它的体积可以表示为V = π * r² * h，其中π为圆周率，约等于3.14。

五、球体的体积公式球体是一种具有曲面的立体几何体，所有点到球心的距离都相等。

球体的体积公式可以通过半径的立方与4/3乘积得到。

设球体的半径为r，那么它的体积可以表示为V = (4/3) * π * r³。

六、锥体的体积公式锥体是一种具有底面和侧面的立体几何体，底面为任意多边形，侧面为三角形。

锥体的体积公式可以通过底面积与高相乘再除以3得到。

设锥体的底面积为S，高为h，那么它的体积可以表示为V = (1/3) * S * h。

七、棱台的体积公式棱台是一种具有上底面、下底面和侧面的立体几何体，上下底面都为任意多边形，侧面为梯形。

棱台的体积公式可以通过上底面积、下底面积和高的和再乘以高的一半得到。

设棱台的上底面积为S₁，下底面积为S₂，高为h，那么它的体积可以表示为V = (1/2) * (S₁ + S₂) * h。

八、四面体的体积公式四面体是一种具有四个面的立体几何体，它的四个面都是三角形。

立体几何公式大全1.证明直线与直线的平行的思考途径(1)转化为判定共面二直线无交点;(2)转化为二直线同与第三条直线平行;(3)转化为线面平行;(4)转化为线面垂直;(5)转化为面面平行.2.证明直线与平面的平行的思考途径(1)转化为直线与平面无公共点;(2)转化为线线平行;(3)转化为面面平行.3.证明平面与平面平行的思考途径(1)转化为判定定二平面无公共点;(2))转化为线面平行;(3))转化为线面垂直.4.证证明直线与直线的垂直的思考考途径(1)转化为相交垂垂直;(2)转化为线面垂垂直;(3)转化为线与另另一线的射影垂直;(4))转化为线与形成射影的斜线线垂直.5.证明直线与平平面垂直的思考途径(1))转化为该直线与平面内任一一直线垂直;(2)转化为为该直线与平面内相交二直线线垂直;(3)转化为该直直线与平面的一条垂线平行;;(4)转化为该直线垂直直于另一个平行平面;(55)转化为该直线与两个垂直直平面的交线垂直.6.证证明平面与平面的垂直的思考考途径(1)转化为判断二二面角是直二面角;(2))转化为线面垂直.7.空空间向量的加法与数乘向量运运算的运算律(1)加法交交换律：a+b=b+a.(2)加法结合律：(a++b)+c=a+(b+c)).(3)数乘分配律：&&lambda;(a+b))=&lambda;a+&&lambda;b.8..平面向量加法的平行四边形形法则向空间的推广始点相相同且不在同一个平面内的三三个向量之和，等于以这三个个向量为棱的平行六面体的以以公共始点为始点的对角线所所表示的向量.学习方法。

《立体几何》主要公式与定理：
主要公式：（*引申公式)
=
S 直棱柱侧面积
=
S 正棱锥侧 =
=S 正棱台侧 = S =扇形面积 = S =圆柱侧 S =圆锥侧 *S =圆台侧 （找出三者联系）
V =立方体 *=L 立方体对角线长
*=R 立方体外接球 *=R 立方体棱切球 *=R 立方体内切球 （找出三者比例关系）
V =长方体 *=L 长方体对角线长 *=R 长方体外接球
*从长方体对角线的一个端点沿表面到另一个端点的最短距离=
V =柱体 V =锥体 V =台体 （找出三者联系） V =圆柱 V =圆锥 V =圆台 （找出三者联系） S =球 =V 球 （二者有何关系？）
*=h 正四面体 *=S 正四面体 *=V 正四面体 *=R 正四面体内切球 *=R 正四面体外接球 （设正四面体的棱长为a ） 主要定理（立体几何藏宝图）：
17、等角定理 18、平行平面截线段成比例定理
19-24、平面的3个基本性质及3个推论（课本35-37页）。

高中数学知识点总结及公式大全立体几何中的平行与垂直问题高中数学知识点总结及公式大全：立体几何中的平行与垂直问题在高中数学中，几何是一个重要的分支，而立体几何更是其中的重要内容之一。

在立体几何中，平行和垂直是我们经常遇到的问题。

本文将对高中数学中的立体几何知识点进行总结，并提供一些常用的公式。

一、平行与垂直的概念在几何中，平行和垂直是两个基本的关系。

平行指的是两条直线永远不会相交的情况，可以想象成两条铁轨永远平行。

垂直则指的是两条直线相互成直角，可以想象成两根彼此垂直的木棍。

二、平行与垂直的判定方法1. 平行关系的判定方法：(1) 同位角相等定理：如果两条直线被一组相交线段所切割，且这些相交线段的对应角相等，则这两条直线是平行的。

(2) 平行线的性质定理：如果一条直线上的两个点分别与另一条直线上的两个点相连，且相连的线段互相平行，则这两条直线是平行的。

(3) 平行线的判定定理：如果两条直线的斜率相等且不相交，则这两条直线是平行的。

2. 垂直关系的判定方法：(1) 两条直线相交且相交角为90度，则这两条直线是垂直的。

(2) 垂直线的性质定理：如果一条直线与另一条直线相互垂直，且这两条直线各自还与第三条直线相交，则第三条直线与这两条直线也是垂直的。

(3) 垂直线的判定定理：如果两条直线的斜率互为负倒数，则这两条直线是垂直的。

三、常用公式在立体几何中，我们经常使用一些公式来求解问题。

下面是一些常用的公式：1. 立方体的表面积公式：立方体的表面积等于6倍的边长平方。

2. 立方体的体积公式：立方体的体积等于边长的立方。

3. 正方体的表面积公式：正方体的表面积等于6倍的边长平方。

4. 正方体的体积公式：正方体的体积等于边长的立方。

5. 圆柱体的表面积公式：圆柱体的表面积等于2πr² + 2πrh，其中r为底面半径，h为高。

6. 圆柱体的体积公式：圆柱体的体积等于πr²h，其中r为底面半径，h为高。

立体几何公式总结立体几何，又称立体几何学，是数学中一门研究空间几何结构和变换的学科。

人们通过探索和研究空间几何从而获得几何知识和几何技能，以及通过几何技能来更好地理解空间关系的能力。

立体几何不仅仅是为了学习几何知识而创造的，它还能够用来解决复杂的实际问题，比如建筑设计、机器人技术、地质勘探等。

在几何理论的发展历史上，立体几何主要是欧几里德于公元前四世纪末提出的，他在《几何原本》中提出了空间距离，变换，以及垂直于两线段的规律，这些都是立体几何的基础。

欧几里德由此创立了空间几何学，开创了数学史上的新纪元。

此后，许多数学家和几何学家都延续和改善了欧几里德的理论，其中著名的代表人物有哥白尼、牛顿、科学家们等。

立体几何通常被归类为初等几何学，有时也被归类为中等几何学，重点探究空间几何问题，其中包括三角学、圆锥体学、球学、投影学、视线学等空间几何问题。

一般情况下，我们可以从以下几种方式总结立体几何的相关理论：一、距离公式。

距离公式用于测量两个点之间的距离，公式如下： d=√((x1-x2)^2+(y1-y2)^2+(z1-z2)^2)其中，x1，y1，z1分别表示第一个点的横纵坐标，x2，y2，z2分别表示第二个点的横纵坐标。

二、体积公式。

这是用于计算物体体积的常见公式，其中有三种形式：1、立方体体积公式：V=a^3 (其中a表示立方体的边长)2、圆柱体体积公式：V=πr^2h (其中r表示圆柱体的底面半径，h表示容器的高度)3、球体体积公式：V=4/3πr^3 (其中r表示球体的半径)三、面积公式。

面积公式是用于计算物体面积的概念，其中有多种形式：1、三角形面积公式：S=1/2ab (其中a、b分别表示三角形的两条边长)2、圆形面积公式：S=πr^2 (其中r表示圆形的半径)3、矩形面积公式：S=ab (其中a、b分别表示矩形的长宽)4、平面圆弧面积公式：S=πr^2α (πr^2表示弧度所在圆形的面积，α表示弧度的大小)四、投影公式。

立体几何公式大全时间：2009-8-3 11:10:43 点击：1859核心提示：长方形的周长=（长+宽）×2 正方形的周长=边长×4 长方形的面积=长×宽正方形的面积=边长×边长三角形的面积=底×高÷2 平行四边形的面积=底×高梯形的面积=（上底+下底）×高÷2 直径=半径×2 半径=直径÷2 圆的周长=圆周率×直径= 圆周率×半径×2 圆的面积=圆周率×半径×半径长方...长方形的周长=（长+宽）×2正方形的周长=边长×4长方形的面积=长×宽正方形的面积=边长×边长三角形的面积=底×高÷2平行四边形的面积=底×高梯形的面积=（上底+下底）×高÷2直径=半径×2 半径=直径÷2圆的周长=圆周率×直径=圆周率×半径×2圆的面积=圆周率×半径×半径长方体的表面积=（长×宽+长×高＋宽×高）×2长方体的体积=长×宽×高正方体的表面积=棱长×棱长×6正方体的体积=棱长×棱长×棱长圆柱的侧面积=底面圆的周长×高圆柱的表面积=上下底面面积+侧面积圆柱的体积=底面积×高圆锥的体积=底面积×高÷3长方体（正方体、圆柱体）的体积=底面积×高平面图形名称符号周长C和面积S正方形a—边长C＝4aS＝a2长方形a和b－边长C＝2(a+b)S＝ab三角形a,b,c－三边长h－a边上的高s－周长的一半A,B,C－内角其中s＝(a+b+c)/2 S＝ah/2＝ab/2·sinC＝[s(s-a)(s-b)(s-c)]1/2＝a2sinBsinC/(2sinA)四边形d,D－对角线长α－对角线夹角S＝dD/2·sinα平行四边形a,b－边长h－a边的高α－两边夹角S＝ah＝absinα菱形a－边长α－夹角D－长对角线长d－短对角线长S＝Dd/2＝a2sinα梯形a和b－上、下底长h－高m－中位线长S＝(a+b)h/2＝mh圆r－半径d－直径C＝πd＝2πrS＝πr2＝πd2/4扇形r—扇形半径a—圆心角度数C＝2r＋2πr×(a/360)S＝πr2×(a/360)弓形l－弧长b－弦长h－矢高r－半径α－圆心角的度数S＝r2/2·(πα/180-sinα) ＝r2arccos[(r-h)/r] - (r-h)(2rh-h2)1/2 ＝παr2/360 - b/2·[r2-(b/2)2]1/2＝r(l-b)/2 + bh/2≈2bh/3圆环R－外圆半径r－内圆半径D－外圆直径d－内圆直径S＝π(R2-r2)＝π(D2-d2)/4椭圆D－长轴d－短轴S＝πDd/4立方图形名称符号面积S和体积V正方体a－边长S＝6a2V＝a3长方体a－长b－宽c－高S＝2(ab+ac+bc)V＝abc棱柱S－底面积h－高V＝Sh棱锥S－底面积h－高V＝Sh/3棱台S1和S2－上、下底面积h－高V＝h[S1+S2+(S1S1)1/2]/3 拟柱体S1－上底面积S2－下底面积S0－中截面积h－高V＝h(S1+S2+4S0)/6圆柱r－底半径h－高C—底面周长S底—底面积S侧—侧面积S表—表面积C＝2πrS底＝πr2S侧＝ChS表＝Ch+2S底V＝S底h＝πr2h空心圆柱R－外圆半径r－内圆半径h－高V＝πh(R2-r2)直圆锥r－底半径h－高V＝πr2h/3圆台r－上底半径R－下底半径h－高V＝πh(R2＋Rr＋r2)/3球r－半径d－直径V＝4/3πr3＝πd2/6球缺h－球缺高r－球半径a－球缺底半径V＝πh(3a2+h2)/6 ＝πh2(3r-h)/3a2＝h(2r-h)球台r1和r2－球台上、下底半径h－高V＝πh[3(r12＋r22)+h2]/6 圆环体R－环体半径D－环体直径r－环体截面半径d－环体截面直径V＝2π2Rr2＝π2Dd2/4桶状体D－桶腹直径d－桶底直径h－桶高V＝πh(2D2＋d2)/12 (母线是圆弧形,圆心是桶的中心)V＝πh(2D2＋Dd＋3d2/4)/15 (母线是抛物线形)。

高二数学立体几何知识点_立体图形公式_立体几何学习方法立体几何方是高中数学的重要知识点，那么你知道立体几何知识点和立体图形公式有哪些吗今天，店铺为大家整理了立体几何知识点和立体图形公式，欢迎阅读。

高二数学立体几何知识点1.位置关系：(1)两条异面直线相互垂直证明方法：①证明两条异面直线所成角为90o;②证明线面垂直，得到线线垂直;③证明两条异面直线的方向量相互垂直。

(2)直线和平面相互平行证明方法：①证明直线和这个平面内的一条直线相互平行;②证明这条直线的方向量和这个平面内的一个向量相互平行;③证明这条直线的方向量和这个平面的法向量相互垂直。

(3)直线和平面垂直证明方法：①证明直线和平面内两条相交直线都垂直，②证明直线的方向量与这个平面内不共线的两个向量都垂直;③证明直线的方向量与这个平面的法向量相互平行,高考。

(4)平面和平面相互垂直证明方法：①证明这两个平面所成二面角的平面角为90o;②证明一个平面内的一条直线垂直于另外一个平面;③证明两个平面的法向量相互垂直。

2.求距离：求距离的重点在点到平面的距离，直线到平面的距离和两个平面的距离可以转化成点到平面的距离，一个点到平面的距离也可以转化成另外一个点到这个平面的距离。

(1)两条异面直线的距离求法：利用公式法。

(2)点到平面的距离求法：①“一找二证三求”，三步都必须要清楚地写出来。

②等体积法。

③向量法。

3.求角(1)两条异面直线所成的角求法：①先通过其中一条直线或者两条直线的平移，找出这两条异面直线所成的角，然后通过解三角形去求得;②通过两条异面直线的方向量所成的角来求得，但是注意到异面直线所成角得范围是，向量所成的角范围是，如果求出的是钝角，要注意转化成相应的锐角。

(2)直线和平面所成的角求法：①“一找二证三求”，三步都必须要清楚地写出来。

②向量法，先求直线的方向量于平面的法向量所成的角α，那么所要求的角为或。

(3)平面与平面所成的角求法：①“一找二证三求”，找出这个二面角的平面角，然后再来证明我们找出来的这个角是我们要求的二面角的平面角，最后就通过解三角形来求。

立体几何公式定理嘿，咱们今天来聊聊立体几何那些公式定理。

立体几何这玩意儿，一开始接触的时候，可能会让咱觉得有点头疼，可一旦搞懂了，那还真挺有意思的。

就说我以前教过的一个学生吧，叫小李。

这孩子刚开始学立体几何的时候，那叫一个懵，看着那些图形和公式，感觉就像看外星文似的。

咱们先从最基础的长方体体积公式说起，V = lwh ，这里的 l 、 w 、h 分别代表长、宽、高。

这公式多简单直白呀，想象一下，咱有一个大大的长方体盒子，要算它能装多少东西，就用这个公式一捣鼓，答案就出来啦。

再说说正方体体积公式 V = a³，其中 a 是正方体的棱长。

这就更简单了，正方体嘛，每条边都一样长。

有次上课，我就拿了个魔方当道具，问同学们这个魔方的体积咋算，大家一下子就反应过来了，用这个公式就行。

然后是圆柱的体积公式V = πr²h ，这里的 r 是底面半径， h 是高。

想象一下，一根大柱子，要知道它能占多大空间，就靠这个公式。

我记得有一回，带学生们去工厂参观，看到那些大圆柱形状的储存罐，我就趁机让他们算算体积，大家都算得可认真了。

还有圆锥的体积公式V = 1/3πr²h 。

这圆锥体积呀，正好是等底等高圆柱体积的三分之一。

记得有次做练习题，有道题是关于圆锥形冰淇淋的，问如果底面半径和高是多少，能装多少冰淇淋，不少同学就因为没记住这个三分之一，结果算错啦。

球的体积公式V = 4/3πr³ ，这个r 是球的半径。

每次讲到这个公式，我都会跟同学们说，想象一下一个圆滚滚的足球或者篮球，要知道它里面的空间有多大，就用这个公式。

立体几何里的表面积公式也很重要。

长方体的表面积 S = 2(lw + lh+ wh) ，就是把六个面的面积都加起来。

正方体的表面积 S = 6a²，六个面都一样大，算起来省事多啦。

圆柱的表面积S = 2πr² + 2πrh ，这得把两个底面和侧面的面积都算上。