二次根式的有关概念及性质

前提知识之阳早格格创做
1、二次根式的定义：
咱们已经知讲：每一个正真数有且惟有二个仄圆根，一个记做，称为的算术仄圆根；另一个是.
咱们把形如的式子喊做二次根式，根号下的数喊做被启圆数.
由于正在真数范畴内，背真数不仄圆根，果此惟有当被启圆数利害背真数时，二次根式才正在真数范畴内蓄意思．
2、二次根式的本量
3、二次根式的积的算数仄圆根的本量
4、末尾的估计截止，具备以下特性：
（1）被启圆数中不含启得尽圆的果数（或者果式）；（2）被启圆数不含分母.
咱们把谦脚上述二个条件的二次根式，喊做最简二次根式.
注意：①化简二次根式时，末尾截止央供被启圆数中不含启得尽圆的果数.
②化简二次根式时，末尾截止央供被启圆数不含分母.
③以后正在化简二次根式时，不妨曲交把根号下的每一个仄圆果子来掉仄圆号以来移到根号中（注意：从根号下曲交移到根号中的数必须利害背数）.
题型一、二次根式的观念战条件
【例1】
【例2】
【例3】
【例4】
【例5】
【例6】
题型二、二次根式的本量
【例7】估计
【例8】
【例??】
【练一练】
??、
??、
??、
7、
题型三积的算数仄圆根的本量【例10】
【例11】
【例12】
【例13】
【例14】
题型四二次根式的化简
【例题粗析】
【例15】
【例16】
【例17】
【例18】
【练一练】
4、
5、6、6、
7、。

第十六章 二次根式16.1 二次根式一、复习1、什么叫平方根？开平方？如果一个数的平方等于a ，那么这个数叫做a 的平方根，求一个数a 平方根的运算叫做开平方2、平方根如何表示？一个非负数a 的平方根可以表示为a ±3、求下列各数的平方根：4、求下列各数的正平方根：（1）4； （2）0.16； （3）925. （1）225; （2）0.0001； （3）1681. 二、二次根式的意义1. 二次根式的意义_根号a,其中a 是被开方数. 做二次根式.。

2．二次根式何时有意义：二次根式有意义的条件是被开方数大于等于零 即：a ≥03. 例题例题1 下列各式是二次根式吗？2、32、2-、 12+a 、)0(<b b例题2 设x 是实数，当x 满足什么条件时，下列各式有意义？（1）12-x ； （2）x -2； （3）x1； （4）21x + 4．练习（一）设x 是实数，当x 满足什么条件时，下列各式有意义？（1 （2 （3三、二次根式的性质性质1a a 2=; 性质2：_________________________;性质3：______________________; 性质4：________________________________.例题3 求下列二次根式的值：（1）2)3(π-； （2）122+-x x ，其中3-=x .（1（2（3)0x ≥；（4（5（60)b > 例题5 设a 、b 、c 分别是三角形三边的长，化简：22)()(a c b c b a --++-练习（二）：1、化简下列二次根式（1（20)x ≥； （30)n ≥； （4（5） （6）2、选择题（1）、实数a 、b 在数轴上对应的位置如图，则=---22)1()1(a b （ ）A 、b-aB 、2-a-bC 、a-bD 、2+a-b（2）、化简2)21(-的结果是（ ） A 、21- B 、12- C 、)12(-± D 、)21(-±（3）、如果2121--=--x x x x ，那么x 的取值范围是（ ） A 、1≤x ≤2 B 、1＜x ≤2 C 、x ≥2 D 、x ＞216．2最简二次根式和同类二次根式1、最简二次根式符合的两个条件：（1）_________________________________________________;（2）_________________________________________________.例题6 判断下列二次根式是不是最简二次根式：（1（2（3（41)a ≥-例题7 将下列二次根式化成最简二次根式：（1)0y >；（2)0a b ≥≥；（3)0m n >>· · · · a b 0 12、练习（三）（1）判断下列二次根式中，哪些是最简二次根式：（2）找出下列二次根式中的非最简二次根式，并把它们化成最简二次根式：))00a y >> （3）将下列各二次根式化成最简二次根式：)))000b x y p q >>>>>3、同类二次根式几个二次根式化成_____________________后，如果_______________相同,那么这几个二次根式叫做同类二次根式. 例题8 下列二次根式中，哪些是同类二次根式？))0,0a a >>例题9 合并下列各式中的同类二次根式：（1）323132122++-； （2）xy b xy a xy +-34、练习（四）（1）判断下列各组中的二次根式是不是同类二次根式：B. )0;x ≥))00a y >>（2）合并下列各式中的同类二次根式：A.-B.。

二次根式总结一、引言二次根式是数学中一个重要的概念，涉及到对平方根的运算和性质。

掌握好二次根式的基本知识对于理解和解决数学问题至关重要。

本文将对二次根式进行总结，从定义、性质到应用方面进行探讨。

二、定义与基本性质二次根式可以表示为√a（其中a≥0），这里√a称为二次根，a称为被开方数。

在二次根式中，一些基本性质需要予以关注。

首先，二次根式满足乘法分配律。

对于任意的非负实数a和b，有√(ab)=√a × √b。

这个性质与平方根的性质一致，可以利用它对二次根式进行简化。

其次，二次根式可以进行合并化简。

如果a和b都是非负实数，则√a + √b可以合并成一个根式。

例如，√2 + √3 = √(2+3) = √5。

这一点在化简二次根式的过程中常常应用到。

另外，二次根式的乘法也有一定的规律。

对于任意非负实数a 和b，有(√a × √b) = √(ab)。

同样地，在乘法的过程中可以利用这一性质对二次根式进行化简。

三、进一步探讨与应用1. 二次根式的化简化简二次根式是使用二次根式的基本性质，将复杂的根式表示简化为更简洁的形式。

例如，√8可以化简为2√2，√5 × √3可以化简为√15。

化简二次根式有助于简化运算和解决数学问题。

在化简二次根式时，可以利用约束性质，并通过提取公因数的方式进行。

例如，对于√8，可以提取公因数2，即√(2 × 4) = 2√2。

2. 二次根式的加减运算二次根式的加减运算可以通过化简和合并根式进行。

对于√a + √b，如果a和b无法合并，则不能再继续进行简化。

例如，对于√2 + √3，不能再进行进一步的运算。

但是可以计算其近似值，如√2 ≈ 1.414，√3 ≈ 1.732，因此√2 + √3 ≈ 1.414 + 1.732 ≈ 3.146。

3. 二次根式的乘除运算二次根式的乘除运算可以利用乘法分配律和二次根式的乘法规律进行。

利用这两个性质，可以轻松地计算复杂的二次根式。

专题01 二次根式的有关概念和性质知识网络重难突破知识点一 二次根式的有关概念 二次根式概念：一般地，我们把形如（a ≥0）的式子叫做二次根式，“”称为二次根号。

【注意】 1.二次根式，被开方数a 可以是一个具体的数，也可以是代数式。

2.二次根式是一个非负数。

3.二次根式与算术平方根有着内在联系，（a ≥0）就表示a 的算术平方根。

二次根式有意义的条件：由二次根式的意义可知，当a ≧0时，有意义，是二次根式，所以要使二次根式有意义，只要使被开方数大于或等于零即可。

【典型例题】1．（2018·黔西县期中）下面式子是二次根式的是（ A ） A 21a +B 333C 1-D ．12a 2．（2019·朝阳市期中）下列各式中不是二次根式的是（B ） A 21x +B 4-C 0D 2()a b -3．（2018·48n n 是（ B ） A ．6B ．3C ．48D ．24．（2018·26的值在（ D ） A ．2和3之间B ．3和4之间C ．4和5之间D ．5和6之间5．（2019·虹桥区期末）在平面直角坐标系中，点M （a ，b ）的坐标满足（a ﹣3）22b -0，则点M 在（ A ）A ．第一象限B ．第二象限C ．第三象限D ．第四象限6．（2019·孝感市期中）已知三角形的三边长为a 、b 、c ，如果2(5)12130a b c -+--=，则△ABC 是（ C ）A ．以a 为斜边的直角三角形 B ．以b 为斜边的直角三角形C ．以c 为斜边的直角三角形D ．不是直角三角形7．（2019·滨州市期中）下列式子：①13；②3-；③﹣21x +；④327；⑤2(2)-，是二次根式的有（B ）A ．①③ B ．①③⑤C ．①②③D ．①②③⑤8．（2019·汕头市期末）若211a aa a--=，则a 的取值范围是（ D ） A ．0a >B ．1a ≥C ．01a ≤≤D ．01a <≤9．（2019·抚顺市期末）若二次根式51x -有意义，则x 的取值范围是( B ) A ．x ＞15B ．x≥15C ．x≤15D ．x≤510．（2018·德州市期末）使代数式34x x --有意义的自变量x 的取值范围是（C ） A ．x≥3B ．x ＞3且x≠4C ．x≥3且x≠4D ．x ＞311．（2017·东胜市期末）方程有两个实数根，则的取值范围（B ）A ．B ．且C ．D ．且12．（2018·泉州市期中）若a ab+有意义，那么直角坐标系中点A(a,b)在（ A ） A ．第一象限B ．第二象限C ．第三象限D ．第四象限知识点二 二次根式的性质 二次根式的性质：1．含有两种相同的运算，两者都需要进行平方和开方。

专题01二次根式的概念和性质（知识点考点串编）【思维导图】例．（2022·浙江·九年级专题练习）当0x =的值等于（ ）A ．4B ．2CD ．0练习1．（2021·全国·八年级专题练习）当a 为实数时，下列各式中是二次根式的是（）个A ．3个B ．4个C ．5个D ．6个练习2．（2021·河北·结果相同的是（ ）．◉知识点一：二次根式的定义知识点技巧：二次根式概念：一般地，我们把形如（a≥0）的式子叫做二次根式，“”称为二次根号。

【注意】1.二次根式，被开方数a 可以是一个具体的数，也可以是代数式。

2.二次根式是一个非负数。

3.二次根式与算术平方根有着内在联系，（a ≥0）就表示a 的算术平方根。

A ．321-+B ．321+-C ．321++D ．321--练习3．（2021·河南林州·八年级期末）已知当12a <<a -的值是（ ）A ．3-B ．12a-C ．32a-D ．23a -例．（2021·n 的最小值是（ ）A ．2B ．4C ．6D ．8练习1．（2020·甘肃·酒泉市第二中学八年级期中）若x 、y 为实数，且0x +=，则2019x y æöç÷èø的值( )A ．-2B ．1C ．2D练习2．（2020·江苏·丰县欢口镇欢口初级中学八年级阶段练习）如果3y ，则2x y -的平方根是（ ）A ．-7B．1C ．7D ．±1练习3．（2021·全国·n 的值是( )A ．B ．1C ．2D ．5例．（2022·全国·九年级专题练习）在函数1y =中，自变量x 的取值范围是（ ）A ．x ＜2B ．x ≥2C．x ＞2D ．x ≠2练习1．（2022·全国·九年级专题练习）函数y =x 的取值范围是（ ）A ．x ≥2B ．x ＞﹣2C ．x ≤2D ．x ＜2练习2．（2022·全国·九年级专题练习）函数y 中自变量x 的取值范围是（）◉知识点二：二次根式有意义的条件知识点技巧：二次根式有意义的条件：由二次根式的意义可知，当a ≧0时，有意义，是二次根式，所以要使二次根式有意义，只要使被开方数大于或等于零即可。

二次根式的定义与性质二次根式基本知识点1.a ≥0）叫做二次根式。

2.最简二次根式：必须同时满足下列条件：⑴被开方数中不含开方开的尽的因数或因式；⑵被开方数中不含分母；⑶分母中不含根式。

3.同类二次根式：二次根式化成最简二次根式后，若被开方数相同，则这几个二次根式就是同类二次根式。

4.二次根式的性质：（1）2,(0)a a =≥ （2）==a a 2（3）积的算术平方根的性质：b a ab ⋅=（a≥0，b≥0），即积的算术平方根等于积中各因式的算术平方根的积. （4）商的算术平方根的性质b a ba =（0≥a ，0>b ） ，即商的算术平方根等于被除式的算术平方根除以除式的算术平方根.注：注一： 二次根式的概念在二次根式中，被开放数可以是数，也可以是单项式、多项式、分式等代数式，但必须注意：因为负数没有平方根，所以0a ≥0a ≥）的非负性0a ≥）表示a 的算术平方根，0a ≥）0≥（0a ≥） 这个性质也就是非负数的算术平方根的性质，和绝对值、偶次方类似。

这个性质在解答题目时应用较多，0=，则a=0,b=0；||0b =，则a=0,b=0；20b =，则a=0,b=0。

0=，则2018()x y +=____________ a （a ＞0） a -（a ＜0） 0 （a =0）；注三：二次根式2的性质：2,(0)a a =≥文字语言叙述为：一个非负数的算术平方根的平方等于这个非负数。

文字语言叙述为：一个数的平方的算术平方根等于这个数的绝对值。

1、 a 是正数还是负数。

若是正数或0，则等于a ||,(0)a a a ==≥若a 是负数，则等于a 的相反数-a,||,(0)a a a ==<；2a 的取值范围可以是任意实数，即不论a3||a ，再根据绝对值的意义来进行化简。

注五：22,(0)a a =≥1、不同点：a 的取值范围不同，化简的结果也可能不同2、相同点：当被开方数都是非负数，即0a ≥时，2=例：1、二次根式有意义(1)、x 的取值范围是 ．(2)x 的取值范围是(3)有意义，那么，直角坐标系中点(,)P m n 的位置在（）A 、第一象限B 、第二象限C 、第三象限D 、第四象限2、二次根式定义的运用(1) 若2021y =，则x y +=⇒2()x y =+，则x －y 的值为（ ）A ．－1B ．1C ．2D ．3(2)、当a 1取值最小，并求出这个最小值。

二次根式的概念和性质是什么一般地，形如√a的代数式叫做二次根式，其中，a 叫做被开方数。

下面是店铺给大家整理的二次根式的概念和性质简介，希望能帮到大家!二次根式的概念和性质定义如果一个数的平方等于a，那么这个数叫做a的平方根。

a可以是具体的数，也可以是含有字母的代数式。

即：若，则叫做a的.平方根，记作x= 。

其中a叫被开方数。

其中正的平方根被称为算术平方根。

关于二次根式概念，应注意：被开方数可以是数，也可以是代数式。

被开方数为正或0的，其平方根为实数;被开方数为负的，其平方根为虚数。

最简二次根式最简二次根式条件：1.被开方数的因数是整数或字母，因式是整式;2.被开方数中不含有可化为平方数或平方式的因数或因式。

二次根式化简一般步骤：1.把带分数或小数化成假分数;2.把开方数分解成质因数或分解因式;3.把根号内能开得尽方的因式或因数移到根号外;4.化去根号内的分母，或化去分母中的根号;5.约分。

算术平方根非负数的平方根统称为算术平方根，用(a≥0)来表示。

负数没有算术平方根，0的算术平方根为0。

二次根式的性质1. 任何一个正数的平方根有两个，它们互为相反数。

如正数a的算术平方根是，则a的另一个平方根为﹣ ;最简形式中被开方数不能有分母存在。

2. 零的平方根是零，即 ;3. 负数的平方根也有两个，它们是共轭的。

如负数a的平方根是。

4. 有理化根式：如果两个含有根式的代数式的积不再含有根式，那么这两个代数式互为有理化根式，也称互为有理化因式。

5. 无理数可用连分数形式表示，如: 。

6. 当a≥0时， ; 与中a取值范围是整个复平面。

7. [任何一个数都可以写成一个数的平方的形式;利用此性质可以进行因式分解。

8. 逆用可将根号外的非负因式移到括号内，如(a>0) ， (a<0)，﹙a≥0﹚， (a<0)。

9.注意：，然后根据绝对值的运算去除绝对值符号。

10.具有双重非负性，即不仅a≥0而且≥0。

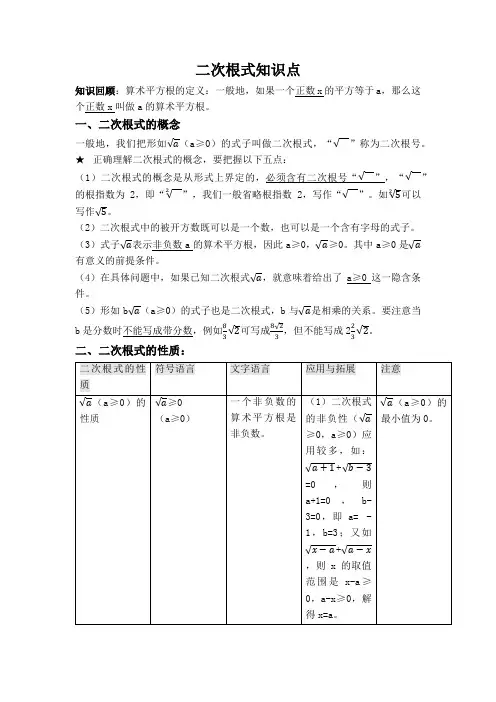
二次根式知识点知识回顾：算术平方根的定义：一般地，如果一个正数x的平方等于a，那么这个正数x叫做a的算术平方根。

一、二次根式的概念一般地，我们把形如√a（a≥0）的式子叫做二次根式，“√”称为二次根号。

★正确理解二次根式的概念，要把握以下五点：（1）二次根式的概念是从形式上界定的，必须含有二次根号“√”，“√”的根指数为2，即“√2”，我们一般省略根指数2，写作“√”。

如√52可以写作√5。

（2）二次根式中的被开方数既可以是一个数，也可以是一个含有字母的式子。

（3）式子√a表示非负数a的算术平方根，因此a≥0，√a≥0。

其中a≥0是√a 有意义的前提条件。

（4）在具体问题中，如果已知二次根式√a，就意味着给出了a≥0这一隐含条件。

（5）形如b√a（a≥0）的式子也是二次根式，b与√a是相乘的关系。

要注意当b是分数时不能写成带分数，例如83√2可写成8√23，但不能写成223√2。

二、二次根式的性质：=｜a｜=a （a≥0）或=｜a｜= - a（a＜0）★(√a)2（a≥0）与√a2的区别与联系：典型例题剖析题型一：二次根式有意义的条件当x取何值时，下列各式在实数范围内有意义？；（3）√x−3+√3+x（1）√x+5-√3−2x；（2）√2x−1√1−x题型二：利用二次根式的非负性化简求值已知a+√b−2=4a-4，求√ab的值。

题型三：二次根式非负性的简单应用已知实数x，y满足｜x-4｜+√y−8=0，则以x，y的值为两边长的等腰三角形的周长是（）题型四：利用√a2=｜a｜并结合数轴化简求值已知实数a，b在数轴上的位置如图所示。

试化简：√a2+√b2+√(a−b)2+√(b−1)2-√(a−1)2题型五：√a2=｜a｜与三角形三边关系的综合应用在△ABC中，a，b，c是三角形的三边长，化简√(a−b+c)2-2｜c-a-b｜题型六：逆用(√a)2= a（a≥0）在实数范围内分解因式在实数范围内分解因式：（1）x-4；（2）x-4√x+4三、二次根式的乘除：1、单项式与单项式相乘，把它们的系数、相同字母的幂分别相乘，对于只在一个单项式里含有的字母，则连同它的指数作为积的一个因式。

二次根式的应用二次根式是数学中重要的一种特殊形式，它在实际生活中有着广泛的应用。

本文将介绍二次根式的概念以及在几个实际场景中的具体应用。

一、二次根式的概念和性质二次根式是指具有形如√a的表达式，其中a为非负实数。

它可以用带有根号的形式表示，也可以用有理数的形式表示，具体取决于根号内的数是否为完全平方数。

二次根式的运算包括加减、乘除、化简等。

二次根式在几何上有着重要的应用，它可以表示一些与平方相关的几何问题。

例如，在解决面积、体积等问题时，常常会遇到二次根式的出现。

二、二次根式在几何中的应用1. 面积问题二次根式在计算面积问题中起到重要的作用。

例如，当我们需要计算一个圆的面积时，就需要用到半径的平方，而半径的平方可以表示为二次根式。

同样地，计算一个三角形的面积时，需要用到底边和高的乘积，其中高可以表示为二次根式。

2. 体积问题二次根式在计算体积问题中也有广泛的应用。

例如，在计算一个圆柱体的体积时，我们需要用到半径的平方和高的乘积，其中半径的平方可以表示为二次根式。

三、二次根式在物理中的应用1. 物理运动问题在物理学中，二次根式常常用于描述物体的运动状态。

例如，在自由落体运动中，物体下落的距离可以用二次根式表示。

同样地，在抛体运动中，物体的轨迹也可以用二次根式表示。

2. 波动问题二次根式在描述波动问题中也有重要的应用。

例如，在波的传播中，波的幅度通常可以用二次根式表示。

另外，在声音的传播中，声音的强度也可以用二次根式表示。

四、二次根式在工程中的应用1. 结构稳定性问题在工程领域中，二次根式可以用于研究结构的稳定性。

例如，在分析桥梁结构的承载能力时，需要用到材料的强度，而材料的强度可以用二次根式表示。

2. 电路问题二次根式在电路分析中也有着重要的应用。

例如，在求解电阻、电容等元件的阻抗时，常常会遇到二次根式的计算。

综上所述，二次根式作为数学中重要的一种特殊形式，在实际生活、几何、物理和工程等领域中都有着广泛的应用。

二次根式的定义及性质1、二次根式的定义形如)0(≥a a 的代数式叫二次根式（1）式子中含有二次根号“”；（2）a 可以表示数也可以表示代数式（3）二次根式)0(≥a a 表示非负数a 的算术平方根，0≥a ，即二次根式的两个非负性 二次根式的两个非负性：)0(≥a a ；0≥a ，具有非负性的还有02≥a ；0≥a ；几个非负数的和等于零，那么这几个非负数均为零。

2、二次根式的主要性质 （1）())0(2≥=a a a （2）⎪⎩⎪⎨⎧<-=>==)0()0(0)0(2a a a aa a a3、分母有理化：把分母中的根号化去，叫做分母有理化.方法:①单项二次根式：利用a =来确定．②两项二次根式：利用平方差公式()()22b a b a ba -=-+来确定．如: aa4、最简二次根式：被开方数中不含分母，并且被开方数中不含开的尽方的因数或因式叫最简二次根式 最简二次根式的条件①号内不含有开的尽方的因数或因式，②根号内不含有分母，③分母不含有根号。

5、 同类二次根式：被开方数相同的最简二次根式叫做同类二次根式6、 乘法公式：)0,0______(≥≥=⋅b a b a ；反之：)0,0_______(≥≥=b a ab7、除法公式：)0,0______(>≥=b a ba ；反之：)0,0______(>≥=b a b a 8、合并同类二次根式：__________________;=-=+a n a m a n a m形如)0(≥a a 的代数式叫二次根式例1、下列式子中二次根式的个数有（ ）（1）31（2）3-（3）12+-x （4）38（5）2)31(-（6）)1(1>-x x A.2个 B.3个 C.4个 D.5个【变式练习】1、下列各式中，一定是二次根式的有______________________________① a ；②z y +；③6a ；④32+x ；⑤962++x x ；⑥12-x2、222++a a 是不是二次根式？___________（填“是”或“否”）二次根式)0(≥a a 表示非负数a 的算术平方根，0≥a ，即二次根式的两个非负性例2、（2012.德阳）使代数式12-x x 有意义的x 的取值范围是（ ） A.0≥x B.21≠x C.210≠≥x x 且 D.一切实数 例3、 函数1213-+-=x x y 的自变量x 的取值范围是_______________【变式练习】1、 使12--x x 在实数范围内有意义的x 的取值范围是______________ 2、（2012.杭州）已知0)3(<-a a ，若a b -=2，则b 的取值范围是___________3、若2)(11y x x x +=---，则______=-y x())0(2≥=a a a例4、计算： (1) (2) (3) (4)(b ≥0) (5)【变式练习】计算： (1)； (2)； (3)； (4). ⎪⎩⎪⎨⎧<-=>==)0()0(0)0(2a a a a a a a例5、化简: (1)； (2)； (3)； (4).例6、2x =，则x 的取值范围是 。

二次根式的计算与性质二次根式是数学中的一个重要概念，在许多数学问题的解答中经常涉及。

它的计算和性质具有一定的规律和特点。

本文将深入探讨二次根式的计算方法和性质，并结合实例进行说明。

一、二次根式的定义与基本性质二次根式是指形如√a的数，其中a为非负实数，是它的被开方数。

二次根式具有以下基本性质：1. 当a≥0时，二次根式有意义。

2. 当a＞0时，√a＞0。

3. 当a＞b≥0时，有√a＞√b。

4. 二次根式的平方等于被开方数本身。

二、二次根式的四则运算1. 二次根式的加减运算：对于二次根式√a与√b，满足以下运算规律：√a ± √b = √(a ± b)。

这意味着可以通过合并二次根式进行简化。

举例：（1）化简√8 + √2。

解：√8 + √2 = √(4 × 2) + √2 = 2√2 + √2 = 3√2。

2. 二次根式的乘法运算：对于二次根式√a与√b，满足以下运算规律：√a × √b = √(a × b)。

这意味着可以通过合并二次根式进行简化。

举例：（1）化简√3 × √5。

解：√3 × √5 = √(3 × 5) = √15。

3. 二次根式的除法运算：对于二次根式√a与√b，满足以下运算规律：√a ÷ √b = √(a ÷ b)。

这意味着可以通过合并二次根式进行简化。

举例：（1）化简√16 ÷ √4。

解：√16 ÷ √4 = √(16 ÷ 4) = √4 = 2。

三、二次根式的化简与有理化1. 化简二次根式：对于二次根式√a，可以通过确定a的因式分解式来进行化简。

举例：（1）化简√72。

解：√72 = √(2 × 2 × 2 × 3 × 3) = √(2^2 × 3^2) = 2√2 × 3 = 6√2。

二次根式的性质与计算二次根式是数学中一个重要的概念，它涉及到了根号以及平方等运算，具有一些特殊的性质和计算规律。

本文将介绍二次根式的一些基本性质和计算方法，帮助读者更好地理解和应用这个概念。

一、二次根式的定义二次根式是指形如√a的数，其中a是一个非负实数。

在二次根式中，根号下的数被称为被开方数。

被开方数的值必须大于等于零，否则二次根式就没有意义。

二、二次根式的性质1. 二次根式的值：对于二次根式√a，它的值是满足b^2 = a的非负实数b。

例如，√9的值是3，因为3^2等于9。

2. 二次根式的性质：(a) 任意非负实数a和b，有以下性质成立：a)√(a*b) = √a * √b；b)√(a/b) = √a / √b。

(b) 对于任意的非负实数a和b，有以下性质成立：a) √(a + b) ≠ √a + √b；b) √(a - b) ≠ √a - √b。

(c) 对于任意非负实数a，有以下性质成立：a) √(a^2) = |a|。

3. 二次根式的化简：当被开方数是特殊形式时，我们可以通过化简来简化二次根式的计算。

常见的化简规则包括：(a) 约分：如果被开方数能够被某个因数整除，那么可以将该因数提出到根号外。

(b) 分解因式：将被开方数分解成多个因数的乘积，然后将相同的因数提出到根号外。

(c) 完全平方数：如果被开方数是一个完全平方数，那么可以直接将其开方并化简。

三、二次根式的基本计算方法1. 二次根式的加减法：当两个二次根式相加或相减时，如果它们的被开方数相同，那么可以直接将系数相加或相减，并保持根号下的数不变。

例如，√3 + √3 =2√3，√5 - √2 = √5 - √2。

2. 二次根式的乘法：当两个二次根式相乘时，可以将它们的被开方数相乘，并保持根号下的数不变。

例如，√3 * √5 = √15，√2 * √2 = 2。

3. 二次根式的除法：当两个二次根式相除时，可以将它们的被开方数相除，并保持根号下的数不变。

二次根式的定义和基本性质二次根式，也称为平方根，是数学中常见的一种运算。

它的定义和基本性质在代数学和几何学中有着广泛的应用。

本文将介绍二次根式的定义，并探讨其基本性质。

在此之前，我们先来了解一下二次根式的定义。

二次根式的定义：二次根式是指一个数的平方根，如√x表示x的平方根，其中x为一个非负实数。

当x小于0时，√x是一个虚数。

在计算平方根时，我们通常提取其中的正根，即非负实数解。

基本性质：1. 非负数的平方根：对于非负实数a，它的平方根√a是一个非负实数。

例如，√9 = 3，因为3的平方等于9。

2. 平方根的乘法：对于非负实数a和b，有以下运算规则：√(a * b) = √a * √b例如，√(4 * 9) = √4 * √9 = 2 * 3 = 63. 平方根的除法：对于非负实数a和b（b不等于0），有以下运算规则：√(a / b) = √a / √b例如，√(25 / 4) = √25 / √4 = 5 / 2 = 2.54. 平方根的加法与减法：对于非负实数a和b，有以下运算规则：√a ± √b 通常不能进行化简，可以合并成一个复合根。

例如，√2 + √3 无法化简，但可以合并为一个复合根√(2 + 3) = √55. 平方根的乘方：对于非负实数a和正整数n，有以下运算规则：(√a)^n = a^(1/n)例如，(√9)^2 = 9^(1/2) = 36. 平方根的传递性：对于非负实数a和b，如果a小于b，则√a小于√b。

例如，√4小于√9，因为4小于9。

通过以上基本性质，我们可以在实际问题中用到二次根式。

例如，在几何学中，可以通过求解平方根来计算物体的边长或面积；在代数学中，平方根可以用来求解方程的解等。

需要注意的是，对于负数的平方根，我们引入了虚数单位i。

虚数单位i定义为√(-1)，它满足i^2 = -1。

负数的平方根被称为虚数，属于复数的一种。

虚数在物理学和电气工程等领域有着重要的应用。