T检验法

t 检验方法t检验方法是一种常用的统计方法，用于比较两组样本均值是否有显著差异。

它是由英国统计学家William Sealy Gosset（1876-1937）开发的，因为他在Guinness酒厂工作，所以也被称为“学生t检验”。

t检验方法的应用广泛，可以用于医学、社会科学、商业等领域的研究。

它的基本思想是通过比较两组样本的均值，判断它们之间是否存在显著差异。

在进行t检验之前，我们需要满足以下几个假设：样本数据应该是独立的、正态分布的，且方差相等。

t检验方法可以分为独立样本t检验和配对样本t检验两种。

独立样本t检验适用于两个独立样本之间的比较。

例如，我们想比较男性和女性的平均身高是否有差异，我们可以采集一组男性和一组女性的身高数据，然后使用独立样本t检验来判断两组数据的均值是否显著不同。

配对样本t检验适用于同一组样本在不同条件下的比较。

例如，我们想研究一种新药物对患者血压的影响，我们可以在给患者使用新药物之前和之后分别测量他们的血压，并使用配对样本t检验来判断新药物是否对血压产生显著影响。

进行t检验时，我们首先计算两组样本的均值和标准差，然后计算t值。

t值可以用来判断两组样本均值是否有显著差异。

在t检验中，我们还需要设置显著性水平，一般为0.05，即我们认为当p值小于0.05时，结果具有统计学意义。

除了独立样本t检验和配对样本t检验，t检验方法还有一些扩展应用，如单样本t检验、多样本t检验等。

单样本t检验适用于只有一个样本的情况，例如我们想知道某个产品的平均销售量是否达到预期值；多样本t检验适用于比较多个样本之间的差异，例如我们想比较不同品牌手机的平均续航时间是否有显著差异。

虽然t检验方法在统计学中被广泛应用，但也有一些限制。

首先，t 检验方法要求样本数据满足一些假设，如独立性、正态分布和方差相等，如果这些假设不满足，t检验的结果可能不可靠。

其次，t检验只能用于比较两组样本的均值差异，无法比较其他统计指标的差异。

t检验法简介t检验法（t-test）是一种常用的统计方法，用于检验两个样本之间的差异是否具有统计学意义。

t检验法最早由威廉·塞德威克于1908年提出，广泛应用于医学研究、社会科学和市场调研等领域。

原理t检验法基于t分布，通过比较两个样本的均值和方差之间的差异，判断差异是否具有统计学意义。

t检验法的原理基于以下假设：1.零假设（H0）：两个样本的均值没有显著差异。

2.备择假设（H1）：两个样本的均值存在显著差异。

在进行t检验时，首先计算样本的均值和标准差，然后根据样本容量和自由度选择合适的t分布来计算t值。

最后，根据指定的显著性水平来比较计算得到的t 值与临界值，以确定是否拒绝零假设。

t检验的应用场景t检验法常用于以下场景：1.了解两个样本均值之间是否存在显著差异。

2.比较一个样本与总体均值之间的差异是否具有统计学意义。

3.比较两个相互独立的样本的均值差异是否具有显著性。

4.比较两个相关样本的均值差异是否具有显著性。

t检验的类型根据不同的应用场景，t检验可以分为以下几种类型：1.单样本t检验：用于比较一个样本与总体均值之间的差异。

2.独立样本t检验：用于比较两个相互独立的样本的均值差异。

3.配对样本t检验：用于比较两个相关样本的均值差异。

t检验的步骤进行t检验时，通常需要按照以下步骤进行：1.建立假设：根据实际问题，明确零假设和备择假设。

2.收集数据：收集样本数据，并计算样本的均值和标准差。

3.计算t值：根据样本容量和自由度，计算t值。

4.确定显著性水平：设定显著性水平（如0.05），选择合适的t分布临界值。

5.比较t值和临界值：根据计算得到的t值和临界值，比较判断差异是否具有统计学意义。

6.得出结论：根据结果，判断是否拒绝零假设。

t检验的限制使用t检验法时需要注意以下几个限制：1.样本容量要求：对于t检验来说，样本容量一般要求大于30，否则可能会影响检验结果的准确性。

2.正态分布假设：t检验要求数据符合正态分布，如果数据不满足正态分布假设，可能会导致错误的结论。

t检验法的详细步骤例题
假设我们想要通过t检验法来判断男生和女生在数学考试成绩上是否存在显著差异。

以下是一个详细步骤的例题：
步骤1: 建立假设(Hypotheses)
- 零假设(H0)：男生和女生在数学考试成绩上没有差异，即两个样本的均值相等。

- 对立假设(H1)：男生和女生在数学考试成绩上存在差异，即两个样本的均值不相等。

步骤2: 收集样本数据
- 随机抽取一定数量的男生和女生学生作为样本，记录他们在数学考试中的成绩。

步骤3: 计算统计量
- 对于两个独立样本的t检验，统计量t的计算公式为： t = (x1-x2) / sqrt(s1^2/n1 + s2^2/n2)
其中，x1和x2是两个样本的平均值，s1和s2是两个样本的标准差，n1和n2是两个样本的样本容量。

步骤4: 设置显著性水平
- 根据实际情况和问题的重要性，选择一个显著性水平（例如α = 0.05或α = 0.01）。

步骤5: 计算临界值
- 在给定的显著性水平下，查表或使用统计软件来计算临界值。

对于双尾检验，需要计算两侧的临界值。

步骤6: 做出决策
- 比较统计量t与临界值。

如果统计量t的绝对值大于临界值，就拒绝零假设，即表明男生和女生在数学考试成绩上存在显著差异；否则就接受零假设，认为差异不显著。

步骤7: 得出结论
- 根据统计推断的结果，结合具体问题，得出是否拒绝零假设的结论，并解释结果的意义。

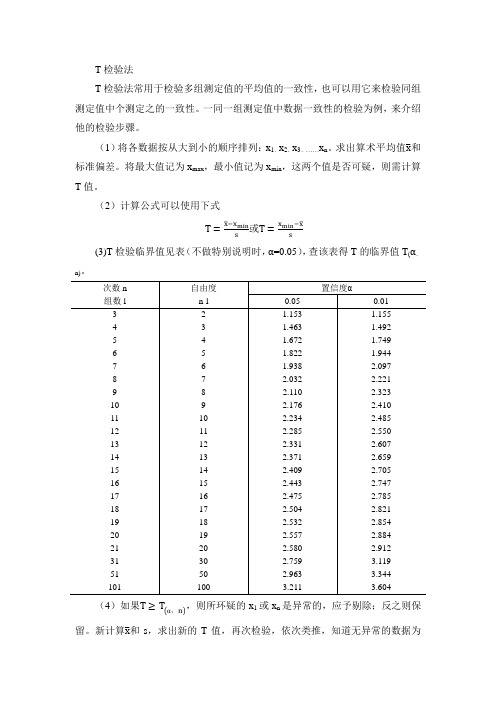
T检验法
T检验法常用于检验多组测定值的平均值的一致性，也可以用它来检验同组测定值中个测定之的一致性。

一同一组测定值中数据一致性的检验为例，来介绍他的检验步骤。

（1）将各数据按从大到小的顺序排列：x1
、x2、x3、……x n。

求出算术平均值x和标准偏差。

将最大值记为x max，最小值记为x min，这两个值是否可疑，则需计算T值。

（2）计算公式可以使用下式
T=x−x min
s 或T=x min−x
s
(3)T检验临界值见表（不做特别说明时，α=0.05），查该表得T的临界值T(α，n)。

（4）如果T≥T
α，n
，则所环疑的x1或x n是异常的，应予剔除；反之则保留。

新计算x和s，求出新的T值，再次检验，依次类推，知道无异常的数据为
止。

（5）在第1个异常数据剔除舍弃后，如果仍有可疑数据需要判别时，则应重对多组测定值的检验，只要把平均值作为1个数据用以上步骤进行计算与检验。

t 检验方法T检验方法是统计学中常用的假设检验方法之一，用于比较两组样本的均值是否有显著差异。

下面将介绍T检验方法的原理、应用场景以及实施步骤。

一、原理：T检验方法是基于样本均值的差异来判断总体均值是否存在显著差异的统计方法。

其基本思想是通过计算样本均值之间的差异，再与标准误差进行比较，从而得出样本之间均值差异是否显著。

二、应用场景：T检验方法适用于以下场景：1. 比较两组样本均值是否有显著差异，例如比较不同性别、年龄、教育程度等对某一变量的影响；2. 比较同一组样本的均值在不同时间点或不同处理条件下的差异，例如比较某一药物在服用前后对疾病指标的影响；3. 比较两个相关样本的均值是否有显著差异，例如比较同一组受试者在不同治疗条件下的指标变化。

三、实施步骤：T检验方法的实施步骤如下：1. 确定研究对象和目标，明确两组样本的差异假设；2. 收集两组样本数据，确保样本具有独立性和随机性；3. 计算两组样本的均值和标准差；4. 计算T值，即通过比较两组样本均值的差异与标准误差的比值得出的统计量；5. 根据显著性水平确定临界值，一般情况下使用0.05作为显著性水平；6. 比较T值与临界值，若T值大于临界值，则拒绝原假设，认为两组样本均值存在显著差异；若T值小于临界值，则接受原假设，认为两组样本均值无显著差异；7. 若拒绝原假设，可以进行进一步的数据分析和解释。

四、注意事项：在使用T检验方法时，需要注意以下几点：1. 样本容量要足够大，一般要求每组样本大于30个，以保证结果的可靠性；2. 样本要具有独立性，避免重复采样或相关性干扰结果；3. 数据要满足正态分布或近似正态分布的假设，否则可能会影响结果的准确性；4. 对于不同的T检验方法，例如独立样本T检验和配对样本T检验，应选择合适的方法进行分析；5. 结果的解释要慎重，应结合实际情况和研究背景进行综合分析。

T检验方法是一种常用的假设检验方法，可以用于比较两组样本的均值是否有显著差异。

事件研究法t检验事件研究法t检验（ERT）是一种用于检测实验研究差异的统计方法，是基于实验研究原理的一种重要统计工具。

ERT研究常用于比较两个独立样本间不同结果发生率的差异。

其中，“t”指的是t分布，而“ERT”代表“事件研究法”，也就是说，ERT是一种基于t分布的统计方法。

ERT研究一般适用于两个独立样本之间存在结果发生率差异的实验研究。

其中，一个样本是实验组，另一个样本是对照组。

ERT的目的是检验实验组相对于对照组的结果发生率的差异是否具有统计学意义。

ERT假设实验组和对照组之间的结果发生率是服从t分布的，也就是说，两个样本之间有可能存在统计学上显著性的差异。

ERT首先推断样本间的发生率差异是否有统计学意义，即是否可以拒绝零假设（实验组和对照组结果发生率相同）。

如果拒绝零假设，就可以说实验组和对照组之间的结果发生率存在显著性差异，而差异的大小可以由t检验的结果来衡量。

通过这种方式，可以有效地检验研究实验的有效性。

ERT有两种假设，即两个样本之间不存在显著性差异（零假设），或者两个样本之间存在显著性差异（备择假设）。

此外，ERT还有四个步骤，即观察和数据输入步骤、假设分析步骤、数据分析和结论步骤。

观察和数据输入步骤：在此步骤中，首先根据实验条件和实验设计，将实验对象分为实验组和对照组，然后观察这两组实验对象的结果发生率。

接着，将实验组和对照组的结果发生率分别输入优化处理的ERT软件，以计算t值，计算相应的t值即为t检验的基础。

假设分析步骤：在此步骤中，根据零假设和备择假设，将t值与给定的alpha水平比较，以检验零假设的健全性，判断实验组和对照组之间的结果发生率是否具有统计学意义。

数据分析和结论步骤：在此步骤中，根据假设分析结果，判断实验组与对照组之间的差异是否具有统计学意义，从而得出结论。

ERT是一种常用的统计方法，可以有效地检验实验研究结果差异的有效性。

它基于t分布，可以有效地检验实验研究之间存在的结果发生率差异是否具有统计学意义，从而为科学研究提供有效的数据支持。

T检验分为三种方法T检验（t-test）是一种统计分析方法，用于比较两个样本或两组数据之间的差异。

T检验根据不同的问题和数据类型有三种不同的方法，分别是独立样本T检验、配对样本T检验和单样本T检验。

1. 独立样本T检验（Independent Samples T-test）：独立样本T检验用于比较两个相互独立的样本或组之间的均值差异。

它的基本假设是两个样本的均值相等，而备择假设是两个样本的均值不相等。

独立样本T检验的过程包括计算两个样本的均值、方差和样本大小，然后根据计算得到的统计量T值和自由度，进行假设检验并计算P值。

如果P值小于设定的显著性水平（通常为0.05），则可以拒绝原假设并认为两个样本的均值存在显著差异。

2. 配对样本T检验（Paired Samples T-test）：配对样本T检验用于比较同一组样本或组在不同条件下的均值差异。

它的基本假设是两个条件下的均值相等，而备择假设是两个条件下的均值不相等。

配对样本T检验的过程包括计算两个条件下的均值差、方差和样本大小，然后根据计算得到的统计量T值和自由度，进行假设检验并计算P值。

如果P值小于设定的显著性水平，则可以拒绝原假设并认为两个条件下的均值存在显著差异。

3. 单样本T检验（One Sample T-test）：单样本T检验用于比较一个样本或组的均值与已知的理论值之间的差异。

它的基本假设是样本均值与理论值相等，而备择假设是样本均值与理论值不相等。

单样本T检验的过程包括计算样本的均值、方差和样本大小，然后根据计算得到的统计量T值和自由度，进行假设检验并计算P值。

如果P值小于设定的显著性水平，则可以拒绝原假设并认为样本的均值与理论值存在显著差异。

T检验是一种常用的统计方法，适用于许多实验设计和数据分析场景。

它可以帮助研究人员确定两个样本或组之间是否存在显著差异，为科学研究和决策提供支持。

然而，使用T检验时需要注意样本的随机性和正态分布的假设，合理选择适当的T检验方法，同时关注P值和置信区间的解释和应用。

T检验法T检验，亦称student t检验（Student's t test），主要用于样本含量较小（例如n<30），总体标准差σ未知的资料。

T检验是用于小样本（小于30）的两个平均值差异程度的检验方法。

它是用T分布理论来推断差异发生的概率，从而判定两个平均数的差异是否显着。

T检验是为了观测酿酒质量而发明的。

戈斯特在位于都柏林的健力士酿酒厂担任统计学家。

戈特特于1908年在Biometrika上公布T检验，但因其老板认为其为而被迫使用笔名（学生）。

T检验的适用条件：正态分布资料单个样本的t检验目的：比较样本均数所代表的未知总体均数μ和已知总体均数μ。

计算公式：t统计量：自由度：v=n - 1适用条件：(1) 已知一个总体均数；(2) 可得到一个样本均数及该样本标准误；(3) 样本来自正态或近似正态总体。

[]单个样本的t检验实例分析例1 难产儿出生体重= （大规模调查获得），问相同否一般婴儿出生体重μ解：1.建立假设、确定检验水准αH 0:μ = μ（难产儿与一般婴儿出生体重的总均数相等；H0无效假设，nullhypothesis）（难产儿与一般婴儿出生体重的总均数不等；H1备择假设，alternative hypothesis，）双侧检验，检验水准:α =2.计算检验统计量3.查相应界值表，确定P值，下结论查附表1:/= ,t = ,t < / ,P > ,按α = 水准，不拒绝H0，两者的差别无统计学意义，尚不能认为难产儿平均出生体重与一般婴儿的出生体重不同[]配对样本t检验配对设计：将受试对象的某些重要特征按相近的原则配成对子，目的是消除混杂因素的影响，一对观察对象之间除了处理因素/研究因素之外，其它因素基本齐同，每对中的两个个体随机给予两种处理。

•两种同质对象分别接受两种不同的处理，如性别、年龄、体重、病情程度相同配成对。

•同一受试对象或同一样本的两个部分，分别接受两种不同的处理•自身对比。

实验室比对 t检验法的详细步骤
宝子，今天来给你唠唠实验室比对t检验法的步骤哈。

t检验法呢，是用来比较两组数据平均值是否有显著差异的方法。

第一步呀，咱得先把两组要比对的数据收集好。

这就好比你要比较两个小朋友的身高，得先知道他俩各自的身高数据一样。

这两组数据可不能是随随便便弄来的，得是按照正确的实验方法得到的哦。

然后呢，计算两组数据的平均值。

这个平均值就像是这组数据的代表啦。

比如说一组数据是1、2、3、4、5，那平均值就是把这些数加起来除以个数，也就是(1 + 2 + 3 + 4 + 5)÷5 = 3。

两组数据都要算出平均值哟。

接着呢，计算两组数据的标准差。

标准差这个东西有点像在描述这组数据有多“散”。

如果数据都挨得很近，标准差就小；要是数据很分散，标准差就大。

计算标准差有专门的公式，这里就不细说了，反正你可以用计算器或者软件来算啦。

再之后呀，就可以计算t值啦。

t值的计算公式有点复杂，不过别怕，就是用两组数据平均值的差，除以一个和两组数据的标准差还有样本数量有关的式子。

这一步就像是把两组数据的差异用一个数值表示出来。

算出t值后呢，咱得看看这个t值有没有意义呀。

这就需要查t分布表啦。

这个表就像是一个大字典，你根据你的自由度（自由度和样本数量有关哦）去找对应的临界值。

如果算出来的t值比临界值大或者小（看你是做单侧检验还是双侧检验啦），那就说明两组数据的平均值有显著差异；要是t值在临界值范围内呢，就说明两组数据平均值差异不显著。

宝子，实验室比对t检验法大概就是这么个流程啦，是不是还挺有趣的呢？ 。

t检验的反证法通俗解释
t检验的反证法是指假设原假设成立并进行t检验，然后通过反证来推翻这个假设。

反证法通常用于证明原假设的对立假设成立，即证明两组数据之间存在显著差异。

具体步骤是首先假设原假设成立，即两组数据之间不存在显著差异。

然后进行t检验，得到样本平均值之间的t值。

接下来利用t分布表或计算机软件计算出对应t值的临界值，确定显著性水平。

如果计算得到的t值超过了临界值，就可以拒绝原假设，即认为两组数据之间存在显著差异。

反证法的思路是通过假设原假设成立，然后通过对统计量的计算来推断概率，最后得出结论。

但需要注意的是，反证法不能证明两组数据没有差异，只能得出数据之间可能存在显著差异的结论。

事件研究法t检验事件研究法t检验是一种常用的统计方法，它是由20世纪初期统计学家Sir Ronald A. Fisher所发展的，用于检验研究要素是否有主要变异的方法。

事件研究法t检验的精髓是计算两个样本之间的差异，从而推断各研究要素之间的关系，决定他们之间的差异是否是仅仅是偶然的结果还是有统计学意义的结果。

在使用事件研究法t检验之前，首先要明确假设，具体而言就是研究者要确定样本群体之间的差异是否有统计学意义，或者说，是否可以解释由变量自身属性而取得，而不能仅仅归因于随机变量。

这一过程中，将样本群体分组，对每一组变量进行检验，以确定差异是否有统计学意义。

一般情况下，可以将样本分为实验组和控制组。

实验组意味着研究人员认为有可能存在变异的组，而控制组则是研究人员认为变异不会发生的组。

接下来，研究者可以使用t检验来测量这两组之间的差异。

事件研究法t检验的运用涉及到许多方面的变量，如社会学，心理学，市场营销，人力资源管理，教育学等研究领域，可以用来评估各类事件，如实验，问卷调查，回放，焦点小组等。

事件研究法t检验可以在涉及多变量分析的研究中发挥重要作用，可以有效地检验变量之间的相关性，检查结果的可信度，提高研究的准确率。

事件研究法t检验所涉及的步骤为：确定假设、定义样本、计算差异平均值、计算标准误差、计算t统计量、检验t统计量、计算p 值、根据p值决定是否拒绝零假设。

首先，研究者需要定义一个研究假设，用于检验两个组间是否存在差异。

然后，根据假设定义样本，并测量不同样本之间的差异。

将每一组的变量值求和，计算他们的差异平均值，即分子的和除以组数；然后，求取标准误差，标准误差是方差的简单平方根。

接下来，计算t统计量，即将每一组的均值除以它们的标准误差得出的统计量。

最后，根据t统计量检验的结果以及定义的假设，计算p值，比较此值是否小于设定的显著性水平，如果是，则说明研究假设有效，也就是说有差异；如果p值大于设定的显著性水平，则说明零假设有效，也就是说变量之间没有差异。

t检验法例题及计算过程高中题嘿，同学们！咱今儿来聊聊 t 检验法，这可是高中题里有点厉害的角色呢！想象一下，就像我们在知识的海洋里探索，t 检验法就是那把能打开神秘大门的钥匙。

比如说有这样一道题，已知两组数据，一组是[具体数据 1]，另一组是[具体数据 2]，然后让我们判断这两组数据有没有显著差异。

这时候，t 检验法就该闪亮登场啦！那计算过程是咋样的呢？首先，我们得算出两组数据的均值。

这就好比是找到每一组数据的“中心”。

然后呢，再算出每组数据的方差，这就像是看看每组数据的“波动情况”。

接下来，把这些值代入到 t 检验的公式里，就像给公式这个“大机器”喂进去原料。

哎呀，可别小看了这个过程，就像盖房子一样，每一步都得稳稳当当的。

如果有一点小差错，那可就全乱套啦！比如说，要是均值算错了，那后面的结果不就像没了方向的小船，飘到哪里算哪里啦？再举个例子，有两组同学的考试成绩，一组成绩比较高，另一组稍微低一些。

那怎么知道这两组的差异是不是真的很明显呢？这就得靠 t 检验法啦！它能帮我们判断出这种差异是不是只是偶然，还是真的有实质性的不同。

在计算的时候，可得仔细再仔细，一个数字都不能错哟！这就跟走钢丝似的，得小心翼翼地保持平衡。

咱再回过头来看看 t 检验法，它真的是很神奇呢！能从一堆看似杂乱无章的数据中找出规律来。

高中的我们，面对这样的题目，就像是勇敢的探险家，一点点去揭开数据背后的秘密。

你们说，t 检验法是不是很有趣呀？它就像是一个隐藏在数学世界里的小宝藏，等着我们去发现和挖掘。

所以呀，同学们，可别害怕这些题目，只要我们认真去对待，就一定能找到答案，解开这些数据的谜团！加油吧，少年们！让我们在 t 检验法的世界里畅游，把难题都一个个攻克掉！。

什么是t检验如何计算t统计量和p值t检验是一种常用的统计方法，用于比较两个样本均值是否存在显著差异。

在进行t检验前，首先需要计算t统计量和p值。

本文将介绍t检验的原理和计算方法。

一、t检验的原理t检验是利用样本数据来推断总体差异的一种统计方法。

它基于假设检验的原理，通过计算t统计量来判断两个样本均值是否具有显著性差异。

常见的t检验有独立样本t检验和配对样本t检验。

独立样本t检验适用于比较两个独立样本的均值差异，例如比较男性和女性的平均身高是否存在显著差异；配对样本t检验适用于比较同一个样本在不同条件下的均值差异，例如比较同一组学生的考试前后得分是否有显著变化。

二、如何计算t统计量计算t统计量需要以下几个步骤：1. 计算样本均值：对于独立样本t检验，分别计算两个样本的均值；对于配对样本t检验，计算差值样本的均值。

2. 计算标准误差：标准误差表示样本均值的不确定性，用于度量样本均值与总体均值的差异。

对于独立样本t检验，计算两个样本的标准误差，公式为：标准误差 = sqrt( (标准差1^2 / 样本大小1) + (标准差2^2 / 样本大小2) )其中，标准差1和标准差2分别代表两个样本的标准差，样本大小1和样本大小2分别代表两个样本的样本大小。

对于配对样本t检验，计算差值样本的标准误差，公式为：标准误差 = 标准差 / sqrt(样本大小)3. 计算t统计量：t统计量衡量了两个样本均值的差异程度，计算公式为：t统计量 = (样本均值1 - 样本均值2) / 标准误差三、如何计算p值计算t统计量后，需要计算p值来判断均值差异是否显著。

p值代表了在零假设成立时，观察到当前t统计量或更极端结果的概率。

对于独立样本t检验，p值需根据自由度和t统计量进行查表或使用统计软件进行计算；对于配对样本t检验，p值的计算方法也类似。

根据p值的大小可以进行如下判断：- 如果p值小于设定的显著性水平（通常为0.05），则可以拒绝零假设，认为两个样本的均值存在显著差异；- 如果p值大于显著性水平，则无法拒绝零假设，认为两个样本的均值差异不显著。

事件研究法t检验事件研究法T检验是一种常用的统计方法，它可以用来检验一个抽样样本中的每个变量与另一变量之间的关联性，以及判断这种关联是否具有统计学意义。

在许多研究领域中，它被广泛用于检验研究结论的正确性和可靠性。

T检验也称为单因素T检验（又称独立样本T检验），是一种基于假设检验的统计技术。

T检验的基本思想是：通过计算抽取的样本的均值和标准差，来检验样本的分布的不同性。

它的基本假设是：抽取的两个样本的均值是不同的，标准差相同。

即一个样本的均值大于另一个样本的均值，而双方的方差相等。

在这种假设的基础上，可以计算T检验统计量，从而对抽样样本在均值上的差异进行检验。

T检验用于检验抽样样本不同样本间（可以是自变量与因变量之间）的均值差异是否具有统计学意义。

这体现了T检验的优势：在所关注的抽样样本中，可以判断一个变量是否与另一变量相关，以及这种关联是否具有统计学意义。

T检验的计算步骤如下：1.定抽样样本中的自变量和因变量，计算每个变量的样本均值和样本方差。

2.据均值和方差，计算T检验统计量T。

3.据T检验统计量T，检验自变量与因变量之间是否存在显著性差异。

4.据检验结果，对原假设做出推断，判断自变量与因变量之间是否存在关联。

T检验的应用非常广泛，它可以用来在许多研究领域中检验研究结论的正确性和可靠性，如经济学、心理学和教育学等。

例如，心理学家可以使用T检验来检验不同心理测评的结果是否存在显著性差异；经济学家可以使用T检验来检验不同政策对经济发展的影响是否具有统计学意义。

尽管T检验被广泛应用于各种研究领域，但也存在一些限制和缺点。

首先，T检验是基于假设检验，因此它受到假设检验的局限性：它假定在不同样本间的变量是独立的；其次，T检验不能用于检验非正态分布的样本。

因此，若要对非正态分布的样本做T检验，需要进行变换后再检验。

最后，T检验仅适用于两个变量之间的关联性检验，不能用于多元变量之间的关联性检验。

综上所述，事件研究法T检验是一种统计方法，它可以用来检验抽样样本不同样本间（可以是自变量与因变量之间）的均值差异是否具有统计学意义。

t检测法的计算方法
t检验法的计算方法主要有单样本t检验和配对样本t检验。

在单样本t检验中，首先需要计算样本均值和标准误差。

标准误差的计算公式为SE=SD/√n，其中SD为样本数据的标准差，n为样本大小。

然后，根据公式t=(X̄-μ)/SE计算t值，其中μ为总体均值。

接着，查找t分布表，根据自由度（n-1）和所选的α水平，找到临界值tα/2。

最后，比较t值和临界值，判断结果：当t>tα/2时，拒绝原假设，认为样本均值与总体均值
不同；当t<=tα/2时，接受原假设，认为样本均值与总体均值无显著差异。

在配对样本t检验中，首先需要计算配对样本的差值d，然后计算差值的均值和标准误差。

标准误差的计算公式为SEd=SDd/√n，其中SDd为差值的标准差，n为配对样本大小。

接着根据公式t=d̄/SEd计算t值。

最后，比较t值和临界值，判断结果：当t>tα/2时，拒绝原假设，认为配对样本的
差值不符合预期；当t<=tα/2时，接受原假设，认为配对样本的差值符合
预期。

以上是关于t检验法的计算方法的相关信息。

如需了解更多信息，建议查阅统计学专业书籍或咨询统计学专家。

线性趋势的t检验法
线性趋势的t检验法是一种统计方法，用于判断一个变量随时间变化的趋势是否呈现线性关系。

具体步骤如下：
1. 假设假设值：首先，我们假设变量的变化趋势是线性的，即随时间变化的斜率是常数。

2. 数据收集：收集相关的时间序列数据，包括变量的取值和对应的时间点。

3. 回归分析：对时间序列数据进行回归分析，建立线性回归模型。

依据回归分析的结果，得到回归方程的斜率和截距。

4. 计算t统计量：根据回归方程以及实际观测值，计算每个观测点的残差。

然后，计算回归斜率的标准误差，并根据样本量和自由度计算t统计量。

5. 判断显著性：根据t统计量得到的p值，判断在显著性水平上线性趋势是否存在。

如果p值小于设定的显著性水平（通常为0.05），则可以拒绝原假设，认为线性趋势是显著存在的；否则，接受原假设，认为线性趋势不存在。

需要注意的是，线性趋势的t检验法通常适用于一些连续性的数据，如时间序列。

同时，该方法还需要满足一些基本假设，如数据的正态分布、同方差性等。

在实际应用中，可以结合其他的检验方法，如残差分析，来综合判断线性趋势的存在与否。

t检验法判断系统误差步骤
嘿，咱今儿就来说说这用 t 检验法判断系统误差的步骤哈！
你看哈，这就好比咱走路，得一步一步来，才能走得稳当不是？第
一步呢，得先提出个假设，就跟咱出门前先想好要往哪儿走一个理儿。

咱得假设这系统误差不存在呀，不然咋往下判断呢。

然后呢，计算统计量t 值。

这可就像是咱走在路上得看清楚路一样，这 t 值就是咱判断的重要依据呢。

可不能马虎，得认真算好咯。

接下来，就是根据自由度和给定的显著性水平，去查 t 分布表，找
到对应的临界值。

这就好像咱走路的时候要看着地图找方向，找到那
个对的点。

再之后呢，比较计算得到的 t 值和临界值的大小。

这就好比咱看看
自己走的路对不对，是不是走偏了呀。

要是计算的 t 值小于等于临界值，那咱就可以高兴地说，嘿，这系
统误差不显著呀，没问题！这就跟咱走在路上一路顺畅一样，多让人
开心。

但要是计算的 t 值大于临界值呢，那可就得小心咯，这就可能意味着系统误差比较显著啦，得好好找找原因，看看是哪儿出了问题。

你想想，这系统误差要是没判断好，那后面的事儿不就都可能出错啦？就好比走路走歪了，那能走到想去的地方吗？所以说呀，这每个
步骤都得认真对待，不能稀里糊涂的。

咱在实际操作中可得把这些步骤都记牢咯，就跟记熟回家的路一样。

可别嫌麻烦，这可是为了保证结果的准确性呢！要是随便糊弄一下，
那最后得出个错的结论，那不就白忙活啦？
总之呢，用 t 检验法判断系统误差，就得一步一步稳稳当当的来，
这样才能得出可靠的结果呀，大家说是不是这个理儿呀！。

t检验法中p值的计算方法1. 嘿，你知道吗？t 检验法中 p 值的计算方法其实就像是搭积木一样！比如说，你想比较两组人的身高差异，那这个过程不就像把两组人的身高数据当成积木来拼凑，然后看看它们之间的差别到底有多大嘛。

2. 哇塞，t 检验法的 p 值计算方法真的超有趣的！就好比你在找宝藏，数据就是那些隐藏的线索，通过一步步计算 p 值来找到宝藏的位置呀！像比较不同品牌手机的电池续航能力，不就是在找那个“最佳宝藏”嘛。

3. 嘿呀，t 检验法的 p 值计算方式其实没那么难理解啦！就像你玩拼图游戏一样，把那些数据碎片拼起来。

比如说研究吃药前后病人症状的变化，这就是在拼一个健康的“大拼图”呀，p 值就是告诉你拼对了多少。

4. 哎呀，t 检验法中 p 值的计算方法可是很关键的哟！这就好像是一场比赛的裁判，决定着谁赢谁输。

比如看两种教学方法哪种更有效，p 值就像是那个判定胜负的哨声咯。

5. 哇哦，搞懂 t 检验法中 p 值的计算方法可太重要啦！好比你走路要有方向一样。

像是比较男生和女生对某种颜色的喜好程度，就得靠计算 p 值来找到答案呢！6. 嘿，告诉你哦，t 检验法里的 p 值计算不复杂啦！就像是解一道有趣的谜题。

假设研究夏天和冬天人们的运动量差异，p 值就是解开这个谜题的关键钥匙呀。

7. 哟呵，t 检验法中 p 值的计算不难的啦！想象一下像搭乐高一样有趣。

比如说分析不同锻炼方式对减肥的效果，p 值就是那个能展示成果的“小模型”哟。

8. 哇，t 检验法中 p 值的计算真的很神奇呀！就如同在黑暗中点亮一盏灯。

比如判断药物对某个疾病是否有效果，p 值就是那盏照亮真相的灯嘛！结论：t 检验法中 p 值的计算方法其实没那么可怕，只要掌握了其中的关键步骤，就能像搭积木、玩游戏一样有趣地进行计算和分析啦！。