当前位置：文档之家 › 第六章 狭义相对论

第六章 狭义相对论

  • 格式：ppt
  • 大小：836.50 KB
  • 文档页数：52

下载文档原格式

  / 52

合集下载

第六章狭义相对论

第六章狭义相对论
原长最长
2
l
l0

l0
u 1 2 c
运动长度 l l0
★ 注意：长度收缩只发生在速度方向
例4（4357）在O参照系中，有一个静止的正方
形，其面积为100cm2。观测者O’以0.8C的
匀速度沿正方形的对角线运动求O’所测得
的该图形的面积。 解：在O参照系中A、B间对角线长度
在O’参照系中A、B间长 度 ★ O’所测得的该图形的面积
u
例5（4370）在K惯性系中，相距 的两个地方发生两事件，时间间隔 而在相对于K系沿正 方向匀速运动的K’系中 观测到这两事件却是同时发生的。试计算:在 K’系中发生这两事件的地点间的距离是多少？ 解1 ：
解2 :
作业：P339~340 6.1 6.3
6.4
6.5 6.6
练习（5616）一列高速火车以速度 驶过车站时， 固定在站台上的两只机械手在车厢上同时划 出两个痕迹，静止在站台上的观察者同时测 出两痕迹之间的距离为1m，则车厢上的观察 者应测出这两个痕迹之间的距离为多少？ 解：车上观察者测的两痕迹之间的距离 =原长 l0 静止在站台上的观察者同时测出两痕迹之间 的距离 =运动长 l
5 4 u2 1 2 c
0
（2）乙测得这两个事件发生的地点的距离
例2（4167） 子是一种基本粒子，在相对于它静 止的坐标系中测得其寿命为 ，如 果 子相对于地球的速度为 （ 为真空中光速），则在地球坐标系中测 出的 子的寿命 解：设：相对于 子静止的参照系为 S’
★ 在地球坐标系中测出的 子的寿命
两个事件的空间间隔 事件二：测量尺子（棒） 右端坐标
长度 右端坐标 — 左端坐标
★
在相对于尺子（棒）运动的参照系中要 条件： 同时记录尺子（棒）两端的坐标。 （如：相对于尺子（棒）运动的参照系是S’ 系 则： t1’ ） t2’ l x’ x ’

第六章狭义相对论

第六章狭义相对论

′ = αλν αµσTνσ 二阶张量： Tλµ
对称张量： Tµν = Tνµ ，有10个独立分量（四维） 例如三维空间中对称张量：电四极矩张量Qij；转动惯量 张量I；材料力学中的应力张量 ；Maxwell应力张量；电 磁场动量流密度张量Tij等等。
Tµν = −Tνµ 只有6个独立分量,因为 Tµ µ＝0 反对称张量：
三阶张量有43=64个分量：Tµνλ
三阶全反对称张量：Tµνλ ，若对每两个脚标都是反对称的 称之为三阶全反对称张量。即有二个及二个以上脚标相同 时矩阵元为零，共40个0元素，24个非零元素。 24个非零元素中只有4个独立元素T234,T314，T412 和 T123. 它们可用一个4维矢量表示。
A′ µ = α µν A ν
同意味着求和。
约定脚标希腊字母从1取到4，英文字母从1取到3，脚标相 这种约定求和的脚标如上式中ν称为“哑标”，对不参加求和 的脚标，如上式中的μ称为“自由脚标”。 等式两边的自由脚标必须对应。 由于哑标只表示对该脚标从1到4求和的一个约定，所以哑 脚标的字母可以更换，如上式中 A′ µ = α µν A ν = α任意一个二阶张量总可以分解为一个二阶对称张量和一个 二阶反对称张量之和”。 证明：设Tµ σ 为任意一个二阶张量，
Tµ σ = Tµ σ + Tσµ 2 + Tµ σ − Tσµ 2 = Sµ σ + Aµ σ
式中 S µ σ = S σµ 是对称张量，
A µ σ = − A σ µ 是反对称张量，证毕。
三维空间中反对称张量是两矢量叉乘出来的，又叫赝矢 r r r r r r r r r r r υ = ω× r，L = r × F ， J = r × p 量。例如 B = ∇ × A ， r r r r B, ω, L, J 构成三维空间的二阶反对称张量，因只有三个独 立分量故可用一矢量表示，叫赝矢量。 在坐标变换时不能当矢量处理，否则会出错。 在四维空间二阶反对称张量有六个独立分量，比空间维数 多2，不能用4-矢量表示。 坐标变换时必须还物理量的本来面目。 顺便指出:在正交变换下,对称张量保持为对称;反对称张量 保持为反对称。

第6章 狭义相对论简介

第6章 狭义相对论简介
一、同时的相对性
v
A B
闪光 同时 到达A 、B镜子； 小兰看到： 闪光 先 到达A镜子， 后 达到B镜子； 小红看到： 由此可见：不同地点的“同时”是相对性（与惯性系有关）
闪 电
闪 电
先 发 生
v
若小红看到：两束闪电(闪光) 同时 击中车头和车尾； 车头 ，后击中_______ 则小兰看到：闪电先击中_______ 车尾 ； 所以：不同地点的“同时”是相对性（与惯性系有关）
◆相对惯性系做匀速直线运动的另一个参考系也是惯性系。
2、推论： ◆推论1： 通过任何力学实验，都不可能 证明惯性系是处于绝对静止还是 在做绝对匀速直线运动状态。
◆推论2：
任何惯性参考系都是平权的。
二、经典时空观、伽利略速度变换
1、经典时空观： （绝对时空观） 长度L 是 时间和空间彼此独立、互不关联， 时间t 是 且不受物质或运动的影响。 质量m 是 同时性是 2、伽利略速度变换： 绝对的 绝对的 绝对的 绝对的
若地面上小红观察到A、B两地有两个事件同时发生，对于 坐在火箭中沿A、B连线飞行的小兰来说，哪个事件先发生？
A事件先发生
A B
v
二、时间的相对性 (动钟变慢）
u t0
u
u
t
思考：小红测得的时间t 和小兰测得的时间t0 相等吗？
(不相等，t ＞ t0）
狭义相对论的时间变换公式 发生在同一地点的参考系内 所测量的时间 t 称为固有时
v人地 v人车 v车地
3、狭义相对论产生的背景：
v人车
v车地
光速问题
三、狭义相对论的两个基本假设：
（爱因斯坦相对性原理） 1、第一条假设： 在任何惯性系参考系中，物理规律（包括力学和电磁学） 都是一样的。

大学物理第6章 狭义相对论基础

大学物理第6章 狭义相对论基础

第6章
狭义相对论基础
1905年6月， A. Einstein发表 了长论文《论动体的电动力学》， 完整地提出了狭义相对性理论，即 狭义相对论。它是区别于牛顿时空 观的一种新的时空理论。
狭义（特殊）——只适用于惯 性参照系。 相对论和量子论是近代物理学的两大基础理论。
第6章 狭义相对论基础
狭义相对论的产生背景
3
x' x
Δt t2 t1
S' 系 (车厢参考系 )
y'
1
( x'1 , y '1 , z '1 , t '1 ) ( x '2 , y '2 , z '2 , t '2 )
u
12
2
12
o'9
3 6
9 6
3
x'
在一个惯性系同 时发生的两个事件， 在另一个惯性系是 否同时?
u Δt Δx c Δt 1
设 S系中x1、x2两处发生两事件,时间 间隔为 Δt t2 t1 .问 S′系中这两事件 发生的时间间隔是多少？
S 系 ( 地面参考系 ) 事件 1
( x1, y1, z1, t1 )
y
y'
1
12
u
12
事件 2
2
12
( x2 , y2 , z2 , t2 )
o o'9
3 6
9 6
3
9 6
例3 设想一光子火箭以 u 0.95c 速率相对地球作直线运动 ，火箭上宇航 员的计时器记录他观测星云用去 10 min , 则地球上的观察者测此事用去多少时间 ？ 解 设火箭为 S 系、地球为 S 系

大学物理曲晓波-第6章 狭义相对论

大学物理曲晓波-第6章 狭义相对论

x
x u t 1 u2 /c2
洛 仑
y
y
兹 z z
逆 变 换
t
t
ux c2
1 u2 /c2
洛伦兹逆变换只是把洛伦兹变换中的u→ - u，x与x’，
y与y’，z与z’交换位置。
说明：
①洛伦兹变换表示同一事件在不同惯性系中时空坐标的变换关系。 规定每个惯性系使用对该系统为静止的时钟和尺进行量度。
在所有惯性系中，物理定律的表达形式都相同。这就是爱因 斯坦相对性原理，即相对性原理。
此原理说明所有惯性系对于描述物理规律都是等价的，不存 在特殊的惯性系。可以看出，爱因斯坦相对性原理是力学相对 性原理的推广。
由此可得出，在任何惯性系中进行物理实验，其结果都是一 样的，运动的描述只有相对意义，而绝对静止的参考系是不存 在的。因此不论设计力学实验，还是电磁学实验，去寻找某惯 性系的绝对速度是没有意义的。
S 系v 中 x d d x t,v y d d y t,v z d d z t
v
x
vx 1
u
uvx c2
速 度 变 换
v
y
vy
1 u2 /c2
1
uvx c2
v
z
vz
1 u2 /c2
1
uvx c2
vx
v
x
1
u
u v x c2
速 度 逆 变 换
v
y
v
y
1 u2 /c2Biblioteka 1u v x c2
vz
v
z
1 u2 /c2
1
u v x c2
讨论：
①当u,v（vx,vy,vz)远小于光速ｃ时，相对论速度变换式退化

第6章狭义相对论基础

第6章狭义相对论基础

设相对S’系静止有一光脉冲仪
Mo
d
发射光信号与接受光信号时间差 o
t' 2d
X’
c
发射与接受在同一地点
t ' 称之为固有时或本征时,常用 o
在S系中观察,光脉冲仪以 u 向右运动
光脉冲走的是一个三角形的两边,每边长为
d 2 ( ut )2 2
Su Y
t 2 2 d 2 ( ut )2
由洛仑兹逆变换
t

t
u c2
x
1
u2 c2
t

1

u2 c2
x 0
t
1
>1
1
u2 c2
t
原时最短
长度缩短
对运动长度的测量问题。 怎么测？ 同时测。
S S
u
l0
原长：棒静止时测得的它的长度 也称静长
棒静止在 S 系中， l0 静长
S
事件1：测棒的左端 事件2：测棒的右端
1
u2 c2
同时性的相对性
x2 x1 t2 t1
5) 时序，因果关系
x2 x1 t2 t1
6) 由洛仑兹变换看时间膨胀 长度缩短
时间膨胀 研究的问题是： 在某系中，同一地点先后发生的两个事件的时间 间隔(同一只钟测量) ，与另一系中，两个地点发 生的两个事件的时间间隔(两只钟分别测量)的关系。
零结果
c
1

u2 c2
1

u2 c2
b 2
否定以太存在 否定伽利略变换
M2
cu
a2 a1 M1
1 b1
C2 u2
b 1

狭义相对论

狭义相对论
不存在特殊方向. b.时空均匀性:同参照系中空间间隔(即二事件发生地间距离)与
坐标位置无关,时间间隔与时空位置无关.
2.间隔不变性:
事件p1和p2：在 ：(x1, y1, z1,t1), (x2 , y2 , z2 ,t2 )
: (x1, y1, z1,t1), (x2, y2 , z2 ,t2)
两朵小乌云: 迈克耳逊——莫雷“以太漂移”实验
黑体辐射实验
狭义相对论 量子力学
近代物理学的两大 支柱，逐步建立了 新的物理理论。
强调:
近代物理不是对经典理论的补充，是全新的理论。
近代物理不是对经典理论的简单否定。
§6.1相对论的实验基础
一.伽利略的相对性原理
1.伽利略变换:
设以v相对于运动,t=0时,两坐标系原点重合
2.光速不变原理:真空中的光速在任意惯性系中沿各
个方向均为c,与光源运动无关.
• 说明： • ⑴它否定了经典速度公式，即否定伽利略变换。 • ⑵光的速度大小与参照系无关，但方向在不同参照系中
可以不同。 • ⑶光速数值不变，则不同参照系中时间、空间、尺度关系
不同。
狭义相对论原理与经典时空的不同:
'
按照二事件间隔将相对论时空划分为三个区域. (1)类时区域(类时间隔):
s2 0,即c2t2 x2
x 2
二事件可用小于光速的信号联系,信号速度 u
c
t
(2)类空区域： s2 0,即c2t2 x2 ,u c，这种讯号不存在
(3)类光区域：s2 0, u c
类空
类时 类空
类时
系中静止。 • 在以太中静止的物体为绝对静止，相对以太运动的物体为
绝对运动。
二.相对论实验基础:

第6章狭义相对论

第6章狭义相对论
1905 年爱因斯坦在《论动体的电动力学》中提 出两条基本原理：
1. 物理规律对所有惯性系都是一样的。
这后来被称为爱因斯坦相对性原理。
2. 任何惯性系中，真空中光的速率都为 c 。
这一规律称为光速不变原理。 光速不变原理与伽利略变换是彼此矛盾的， 若保持光速不变原理，就必须抛弃伽利略变换， 也就是必须抛弃绝对时空观。
力学相对性原理的另一种表述： 在一个惯性系内部 所作的任何力学的实验都不能区分这一惯性系本身 是在静止状态还是在作匀速直线运动状态。
6
2. 经典力学的绝对时空观
(1)同时性是绝对的。
S系：两事件同时发生，S 系：也是同时发生。 (2)时间间隔是绝对的。
t1 t 2 t1 或写为 t t t2
8
—— 常量
根据伽利略变换，光在不同惯性系中速度不同。
那么在哪个参考系中才是标准光速？ 经典理论中认为光在以太中传播，于是以太可以 被视为“绝对静止参考系”。也即通过光学实验， 可以区分惯性系的运动状态。
9
于是必然导致以下结论之一： 一、麦克斯韦方程组不正确。
二、麦克斯韦方程组在伽利略变换下不满足力 ？ 学相对性原理。
ux 22 ) t 2 (t 2 c ux1 2 ) t1 ( t1 c
23
ux 22 ) t 2 (t 2 c ux1 2 ) t1 ( t1 c t t u2 1 2 c
ux t ( t 2 ) c ( x 0 )

u 1 2 c
2

1
2
19

1 u 1 2 c
2

1 1
2
如果u≥c,则 就变为无穷大或有虚数值，这显然 是没有物理意义的。 因而得出推论：任何物体相对于另一物体的速 度不可能等于或大于真空中的光速。即真空中的光 速c是一切物体运动速度的极限。 这一推论与实验符合，也符合因果律的要求。

第六章 狭义相对论

第六章 狭义相对论
16
二、爱因斯坦相对性原理和光速不变原理 （Einsteins principle of relativity and principle of constant speed of light）
1905年爱因斯坦在《论动体的电动力学》一书中提 出如下两条基本原理： 1. 物理规律对所有惯性系都是一样的。 这后来被称为爱因斯坦相对性原理。 2. 任何惯性系中，真空中光的速率都为 c 。
21
22
23
t — 原时（proper time） 原时：同一地点两事件的时间间隔
u t t 1 2 t， c
2
∴ 原时最短 。
一个运动的钟C 和一系列静止的钟C1、C2… 比较，运动的钟C 变慢了。 一个运动时钟的“1秒”比一系列静止时钟的
“1秒”长，这称为运动时钟的“时间延缓”。 时间延缓完全是一种相对效应。
两朵令人不安的乌云，----”
2
这两朵乌云是指什么呢？ 迈克尔逊莫雷实验
热辐射实验
后来的事实证明，正是这两朵乌 云掀起了一场物理界的革命风暴，乌 云落地化为一场春雨，浇灌着两朵鲜 花。
3
量子力学诞生
爱因斯坦的相对论问世
经典 力学
高速领域 微观领域
相对论 量子力学
4
相对论由爱因斯坦（Albert Einstein）创立， 它包括了两大部分： 狭义相对论（Special Relativity）（1905）
当 u << c 时t = t ，这就回到绝对时间了。
26
结论：
1）运动的钟变慢：
t
0
1 u / c
2 2
2）运动参照系中所有物理过程的节奏都变慢了。
27

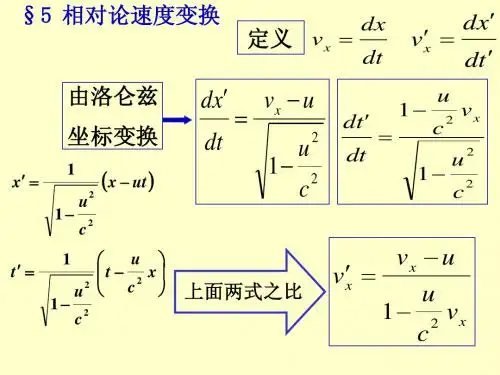
第6章 狭义相对论课件

第6章 狭义相对论课件

2mc M 0c M 0 2m
2 2
五、相对论的能量、动量关系
由 m
m0 v 1 2 c
2
两边 平方
2 2
m (c v ) m c
2 2 2 2 0 2 2 2 0 2
2
m (c v ) c m c c
2 2 2 2 2
2
(mc ) m v c (m0c )
2 16
27
12
1kg这种核燃料所释放的能量为：
E 2.79910 14 3.3510 J/kg 27 m1 m2 8.348610
这相当于同质量的优质煤燃烧所释放热量的1千多万倍！
12
大亚湾核电站夜景
例
两全同粒子以相同的速率相向运动，碰后复合
解：设复合粒子质量为M ,速度为 V v1 v2 m1 m2 V 0 碰撞过程，动量守恒 m1v1 m2v2 MV
四、相对论能量 质能关系
动能 总能量
静止能量
2
EK mc m0c
2
除动能以外的能量
1.静能
当物体静止时，尽管EK=0，仍有能量 2 E0 m0c m0c2，称为物体的静能量E0(分子间势 能、分子热运动能量等)。
虽然静止物体不存在整体运动，动能EK=0，但在其内部 仍有很大的能量m0c2 。例m0=1Kg的任何物体，它的静止 能量E0=1×(3 × 108)2=9 × 1016(J) ，直到目前为止，人 们还无法把这么巨大的静止能量全部释放出来，为人类 服务。
S系
u v
x
§6
狭义相对论动力学基础
高速运动时动力学概念如何？ 基本出发点： 基本规律在洛仑兹变换下形式不变；

第六章狭义相对论

第六章狭义相对论

第六章狭义相对论6.1相对论的基本原理和时空理论认为时空和质量的测量有绝对意义,与观测者所处的参考系⽆关,这种绝对时空和绝对质量观念是经典⼒学的“公理”基础,其集中反映便是伽俐略变换.但从19世纪末年起,⼈们发现这种观念与电磁现象和⾼速运动的实验事实不符.在迈克尔孙等⼈光速测量实验的基础上,爱恩斯坦于1905年创⽴了狭义相对论.这⼀理论的两个基本假设是:相对性原理——物理定律在所有惯性系都有相同的形式；光速不变原理——真空中的光速在所有惯性系沿任何⽅向都是常数c,与光源的运动⽆关.间隔不变性间隔不变性是相对性原理与光速不变原理的数学表述.设惯性系中,任意两事件的空时坐标为和,定义两事件的间隔为(6.1)在另⼀惯性系中,这两事件的空时坐标为,,间隔为(6.2)惯性系概念要求空时坐标变换必须是线性变换,即,,⽽当两个惯性系的相对速度时,这两个惯性系将等同于⼀个惯性系.因⽽对任何两个惯性系,应当有(6.3)洛伦兹变换设惯性系以速度沿惯性系的x轴正向运动,两参考系相应坐标轴平⾏,时两参考系的原点重合(⼀个事件),由(6.3)式,可导出任⼀事件的空时坐标从系到系的变换——洛伦兹变换,,, (6.4)其中 , (6.5)将(6.4)式中的换为,可得逆变换.当, (6.4)过渡到伽俐略变换.因果律与相互作⽤的最⼤传播速度洛伦兹变换表明,时空的测量有相对意义,即测量结果与观测者所处的参考系有关,这是相对论时空观的⼀个⽅⾯.另⼀⽅⾯,是认为事物发展变化的因果关系有绝对意义,即因果关系不因参考系的变换⽽改变,从时间次序来说,就是在⼀个惯性系中,作为结果的事件必定发⽣在作为原因的事件之后,变换到任何其它惯性系,都必须保持这⼀时间次序.从这⼀要求出发,由间隔不变性或洛伦兹变换,可得出推论——真空中的光速c是⾃然界⼀切相互作⽤传播速度的极限.间隔分类在任何⼀个惯性系中,任何两事件的间隔只能属于如下三种分类之⼀：类时间隔；类光间隔；类空间隔.在⼀个惯性系中有因果关系的两事件,两者之间必定存在某种相互作⽤,其传播速度只能⼩于c或等于c,因⽽有因果关系的两事件之间隔必定类时或类光,变换到任何其它惯性系,绝对保持因果关系,相互作⽤的传播速度仍然⼩于c或等于c,即间隔仍然类时或类光.在⼀个惯性系中⽆因果关系的两事件,间隔必定类空,变换到任何其它惯性系,绝对保持⾮因果关系,间隔仍然类空.同时相对性在某个惯性系中,如果两事件于不同地点同时发⽣,即这两事件⽆因果关系,由洛伦兹变换可推知,在其它惯性系看来,这两事件的发⽣不同时.这意味着,在某个惯性系不同地点对准的时钟,在其它惯性系看来没有对准.时钟延缓效应在物体静⽌的参考系中,测得任⼀过程进⾏的时间,称为这过程的“固有时”.由洛伦兹变换,在其它惯性系中,测得这过程进⾏的时间变慢了：(6.6)这效应对于两个惯性系来说是相对的,即在系上看系的时钟变慢,在系上看系的时钟也变慢.但是在有加速运动的情形,时间延缓效应是绝对效应.尺度缩短效应当物体以速度相对于惯性系运动,若在平⾏于运动⽅向上这物体的静⽌长度为,由洛伦兹变换,在系中测得这长度缩短为(6.7)这效应对于两个惯性系来说,也是相对的.但在垂直于运动的⽅向,这⼀效应不会发⽣.时钟延缓与尺度缩短效应,是在不同参考系中观察物质运动在时空关系上的客观反映,是统⼀时空的两个基本属性,与具体过程和物质的具体结构⽆关.速度变换由洛伦兹变换(6.4),可导出物体速度从惯性系到之间的变换, ,(6.8)将换为-,可得逆变换.可以证明,若在⼀个参考系中物体的速度,变换到任何其它参考系仍有.仅当,(6.8)式才过渡到经典速度变换.6.2 洛伦兹变换的四维形式四维协变量相对论认为时空是统⼀的.为此将三维空间与第四维虚数坐标统⼀为四维复空间(6.9)于是当系以速度沿系的轴正向运动时,洛伦兹变换(6.4)可表为, (6.10)重复指标(上式中右⽅的)意味着要对它从1⾄4求和.变换系数构成的矩阵为(6.11)由于洛伦兹变换(6.10)满⾜间隔不变性(6.3),亦即不变量 (6.12)因此,洛伦兹变换是四维时空中的正交变换,即变换矩阵满⾜(6.13)(6.10)的逆变换为(6.14)在洛伦兹变换下,按物理量的变换性质分类为：标量(零阶张量,不变量) (6.15)四维⽮量(⼀阶张量) (6.16)四维⼆阶张量 (6.17)例如,间隔和固有时就是洛伦兹不变量.可以证明,每⼀类四维协变量的平⽅都是洛伦兹变换下的不变量.利⽤这⼀普遍规律,可将物体的速度和光速,能量和动量,电荷密度和电流密度,标势和⽮势,电场和磁场等物理量统⼀为四维协变量,由此可以清楚地显⽰出被统⼀起来的物理量之间的内在联系,并将描写物理定律的⽅程式表⽰成相对性原理所要求的协变形式.6.3 相对论⼒学相对论⼒学⽅程在低速运动情形下,经典⼒学⽅程在伽利略变换下满⾜协变性.为使⾼速运动情况下⼒学⽅程也满⾜协变性,构造四维速度 (6.18)四维动量 (6.19)四维⼒ (6.20) (四维加速度 ),其中是三维速度,是三维⼒,是⼒的功率,是四维⼒的空间分量.由于固有时和静⽌质量是洛伦兹不变量,因此、和都是按(6.16)⽅式变换的四维协变⽮量,于是相对论⼒学⽅程(6.21)在洛伦兹变换下满⾜协变性.由,这⽅程包含的两个⽅程为(6.22)(6.23)相对论质量、动量和能量由⽅程(6.22)和(6.23)可知,⾼速运动情形下物体的质量、动量和能量分别为(6.24)(6.25)(6.26)质速关系(6.24)表明,物体的质量随其运动速度的增⼤⽽增加,即质量测量与时空测量⼀样,存在相对论效应.仅当,才有,此时相对论动量(6.25)过渡到经典动量.质能关系(6.26)中,是运动物体或粒⼦的总能量,是其静⽌能量,是其相对论动能.仅当物体或粒⼦的速度,才有,即⾮相对论动能.质能关系的重要意义在于它表明,⼀定的质量来源于⼀定的相互作⽤能量.由可推知,静⽌质量的粒⼦,必定有静⽌能量,因⽽应当存在某种深层次的内部结构,物体或粒⼦的静⽌质量,来源于其内部存在的相互作⽤能量.由多粒⼦组成的复合物之所以出现质量亏损,便是这复合物内部的粒⼦存在⼀定相互作⽤能(结合能)的反映.(6.19)式表⽰的四维动量,是将相对论动量和能量统⼀起来的协变⽮量：(6.27)在物体或粒⼦静⽌的参考系中,其动量,能量,在任⼀惯性系中,设其动量为,能量为,由的平⽅是洛伦兹变换下的不变量,可得能量、动量和质量的普遍关系式(6.28)由(6.26)和(6.28),可得粒⼦静⽌质量的⼀种表达式(6.29)即通过测量粒⼦的动量和动能,可计算其静⽌质量.光⼦的能量和动量由质能关系(6.26)可推知,以速度运动的粒⼦,例如光⼦,其静⽌质量应当为零,即这类粒⼦应当没有内部结构.由波粒⼆象性,光⼦能量为,其中为⾓频率,,为普朗克常数.因光⼦,由(6.28)式,其动量为,为波⽮量,表⽰光⼦运动⽅向的单位⽮量.6.4 电动⼒学的相对论协变性相对论电动⼒学⽅程定义四维算符(6.30)(6.31)是协变⽮量算符,是标量算符.电流是电荷的运动效应,⽽电荷电流是电磁势和电磁场的激发源.因此,有理由将电荷密度与电流密度,标势与⽮势 ,电场E与磁场B ,统⼀为四维协变量.四维电流密度 (6.32)四维势 (6.33)其中,带电体静⽌时的电荷密度是洛伦兹标量,和均按(6.16)变换.由,构造电磁场张量(6.34)它按(6.17)变换.这是⼀个反对称张量,其矩阵形式为(6.35)构造四维洛伦兹⼒密度(6.36)它按(6.16)变换,其中是三维洛伦兹⼒密度,是电场对电荷作的功率密度.于是,电动⼒学的基本⽅程电荷守恒定律 (6.37)洛伦兹规范 (6.38)达朗贝尔⽅程 (6.39)麦克斯韦⽅程(6.40)能量动量守恒定律 (6.41)都满⾜相对论协变性.(6.41)式中,是将电磁场的能量密度,能流密度S,动量密度g和动量流密度统⼀起来的协变张量：(6.42)矩阵形式为(6.43)势和场的相对论变换在参考系变换下,电荷与电流存在相对性,电磁势和电磁场必然也存在相对性.当惯性系以速度沿系x 1轴的正向运动时,电磁势按变换,即, , , (6.44)电磁场按变换,即，, (6.45)其中下标∥表⽰与运动⽅向平⾏的分量,⊥表⽰垂直分量.将(6.44)式和(6.45)式中的改为-,即得逆变换.在参考系变换下,电磁波的相位是不变量.构造四维波⽮量(6.46)它与四维时空的乘积反映了相位不变性.因此,四维波⽮量必定按变换.当光源沿系x 1轴的正向以速度运动时,便有, , , (6.47)由此可得相对论多普勒效应与光⾏差的表达式, (6.48)其中,为光源静⽌参考系系中的辐射频率,是波⽮即辐射⽅向与x 1轴正向的夹⾓；是在系中观测到的频率,是这参考系中辐射⽅向与光源运动⽅向的夹⾓.6.5电磁场中带电粒⼦的拉格朗⽇量和哈密顿量静⽌质量为,电荷为e的带电粒⼦在电磁场中以速度相对于系运动时,粒⼦的相对论运动⽅程为(6.49)为粒⼦的动量.由, ,可导出粒⼦的拉⽒量(6.50)⽽和作⽤量S都是洛伦兹变换下的不变量:(6.51)(6.52)由⼴义动量的定义 ,可得粒⼦的正则动量和哈密顿量H：(6.53)(6.54)于是拉格朗⽇⽅程(6.55)和正则运动⽅程, (6.56)均与⽅程(6.49)等价.哈密顿量(6.54)第⼀项是粒⼦的相对论能量,故可构造四维正则动量(6.57)由此可得相对论正则运动⽅程, (6.58)。

6狭义相对论基础

6狭义相对论基础

系无关。质量的测量与运动无关。
牛顿力学的回答: 对于任何惯性参照系 , 牛顿力学的规律都具有
相同的形式 . 这就是经典力学的相对性原理 .
或 牛顿力学规律在伽利略变换下形式不变 或 牛顿力学规律是伽利略不变式
三.伽利略变换的困难
对于不同的惯性系，电磁现象基本规律的形式 是一样的吗 ？
真空中的光速
y
s
x1
o 12
9
3
6
12
9
3
6
d
x2
12 x
93
6
t (t' ux')
c2
x' 0
t t2 t1 t'
t t'
1 2
固有时间 ：同一地点发生的两事件的时间间隔 .
t t' t0 固有时间
时间延缓 ：运动的钟走得慢 .
注意 1）时间延缓是一种相对效应 .
2）时间的流逝不是绝对的，运动将改变 时间的进程.（例如新陈代谢、放射性的衰变、 寿命等 . ）
c
d
v
t1 t2
结果:观察者先看到投出后的球，后看到投出前的球.
900 多年前（公元1054年5月）一次著名的超新星 爆发， 这次爆发的残骸形成了著名的金牛星座的蟹状 星云。北宋天文学家记载从公元 1054年 ~ 1056年均能 用肉眼观察, 特别是开始的 23 天, 白天也能看见 .
当一颗恒星在发生超新星爆发时, 它的外围物质向 四面八方飞散, 即有些抛射物向着地球运动, 现研究超 新星爆发过程中光线传播引起的疑问 .
*
(x', y', z'
x'
x
ma'

第06章 狭义相对论

第06章 狭义相对论

t2
M2 2l
G
30 30
M2
M1
s
T
G
T
s
G M1
M2
N
2Δ
v
v

2
v 2l 2 c
4
l 10m, 500 nm, v 3 10 m/s
N 0.4
实验结果
仪器可测量精度
N 0.01
N 0
31
未观察到地球相对于“以太”的运动.
以后又有许多人在不同季节、时刻、 方向上反复重做迈克尔孙-莫雷实验．近年 来,利用激光使这个实验的精度大为提高, 但结论却没有任何变化． 迈克尔孙-莫雷实验测 到以太漂移速度为零,对以 太理论是一个沉重的打击, 被人们称为是笼罩在9世纪 物理学上空的一朵乌云.
大学物理3
10
热力学和经典统计力学—热力学第一、第二 及第三定律及分子运动论
成功地解释了热现象。 经典电磁理论—麦克斯韦电磁理论 成功地解释了波动光学及许多电磁现象
大学物理3
11 11
•
有一个故事很可以说明在人们心目中，古 典物理学的完善程度。 德国著名的物理学家普朗克年轻时曾向他的 老师表示要献身于理论物理学，老师劝他说： “年轻人，物理学是一门已经完成了的科学， 不会再有多大的发展了，将一生献给这门学科， 太可惜了！”
凭直觉，爱因斯坦给出的答案是：
爱因斯坦说： “只有大胆的思辨而不是经验的堆积，才能 使我们进步。”
36
二、爱因斯坦的两个重要假设
⑴ 物理规律对所有惯性系都是一样的,不存在任 何一个特殊的(例如“绝对静止”的)惯性系
——爱因斯坦相对性原理
⑵ 在任何惯性系中,光在真空中的速率都相等

高一物理章节内容课件 第六章狭义相对论

高一物理章节内容课件 第六章狭义相对论

在地球坐标系中测出的 子的寿命
解：
例3（4378）火箭相对于地面以V=0.6C （C
为真空中光速）的匀速度飞离地球。在
火箭发射
秒钟后（火箭上的
钟），该火箭向地面发射一导弹，其速
度相对于地面为V1=0.3C，问火箭发射 后多长时间，导弹到达地球？（地球上
的钟）计算中假设地面不动。
解：火箭飞离地球到发射 导弹经历的时间间隔
中，两个事件同地发生）
4. 长度收缩（条件：在相对棒运动的参照 系中，要同时纪录棒两端的 坐标）
5. 相对论质量 6. 相对论能量 7. 相对论动量 8. 质点系动量守恒
9. 核反应的总能量守恒、释放的能量、质量 亏损
10 .相对论动量与能量的关系
例一（4604）设快速运动的介子的能量约为
E=3000MeV，而这种介子在静止时的
的速率V沿隧道长度方向通过隧道，若 从列车上观测：
（1）隧道的尺寸如何？ （2）设列车的长度为 ，它全部通过隧
道的时间？
1．（4720）解答 （1） 从列车上观察，隧道的长度缩短， 其他尺寸不变。隧道长度为
（2）列车全部通过隧道的时间为
2．（4373）静止的 子的平均寿命约
为
，今在8Km的高空，由于
能量为E0=100MeV。若这种介子的固有
寿命是
，求它运动的
距离。
例二（4733）已知一静止质量为m0的粒子， 其固有寿命为实验室测量到的寿命的
1/n，则此粒子的动能是多少？
例一（4604）解答
例二（4733）解答
例三（4735）已知 子的静止能量为
105.7MeV ，平均寿命为
。
试求动能为150MeV的子的速度是多少？

第6章狭义相对论

第6章狭义相对论
8
绝对时空观念只适用于低速运动； 绝对时空观念只适用于低速运动；而在 低速运动 高速运动中，它的缺陷就明显表现出来了。 高速运动中，它的缺陷就明显表现出来了 四 . 伽利略变换的困难 电磁现象总结出来的麦克斯韦方程组，给出电磁 电磁现象总结出来的麦克斯韦方程组， 波(光) 以恒定速度 在真空中传播 光 以恒定速度c在真空中传播
2. 经典力学的绝对时空观 (1)同时性是绝对的。 同时性是绝对的。 同时性是绝对的 S系：两事件同时发生， 两事件同时发生， S′ 系：两事件也是同时 发生的。 发生的。 (2)时间间隔是绝对的。 时间间隔是绝对的。 时间间隔是绝对的
x′ = x ut
y′ = y z′ = z t′ = t
S′
x′ = γ ( x ut )
逆 y = y′ 变 z = z′ 换 t = γ ( t′ + ux′ ) 2
c
x = γ ( x′ + ut′ )
γ=
1 u 1 2 c
2
18
(1) 当u<<c时,洛仑兹 时 洛仑兹 变换式就变成伽利略变 换式： 换式：
S′
S
x′ = γ ( x ut )
ux t′ = γ ( t 2 ) c
S
′ ′ t2 t1 = t2 t1
或写为
t′ = t
7
(3)空间间隔 距离 是绝对的。 空间间隔(距离 是绝对的。 空间间隔 距离)是绝对的
d′ = ( x′ ) + ( y′ ) + ( z′ )
2 2
y′ = y z′ = z 2 2 2 = ( x ) + ( y ) + ( z ) = d t′ = t
2
x′ = x ut

电动力学-第六章-狭义相对论

电动力学-第六章-狭义相对论

2.相互作用最大传播速度
既然同时是相对的，那因果关系是否会发生颠倒呢？当 然，这种因果关系是不能发生颠倒的！即因果关系是绝对 的。这就对相对论提出了要求。 由洛伦兹变换：
t2 t1
t2 t1 x2 x1 / c 2
1 2 / c2
若两事件有因果关系，即若t2 - t1 0，则必有t2 - t1 0。
x1 x, x2 y, x3 z , x4 ict
另外：
/c
1 1 2
18
物理与电子工程学院 张福恒
电动力学
第六章 狭义相对论
2.物理量按空间变换性质分类
变换规律：
所有物理量称为张量：
1）零阶张量称为标量，经坐标变换后保持不变的量；
2）一阶张量称为矢量； 3）二阶张量称为二阶张量；等等。
24
物理与电子工程学院 张福恒
电动力学
第六章 狭义相对论
3.电磁场张量
25
物理与电子工程学院 张福恒
电动力学
第六章 狭义相对论
4.电磁场的不变量
26
物理与电子工程学院 张福恒
电动力学
第六章 狭义相对论 §6 相对论力学
1.能量－动量四维矢量
27
物理与电子工程学院 张福恒
电动力学
第六章 狭义相对论
4.运动的尺子缩短了
在系中有一位于x轴的尺子，测得其长度为l0（静 止长度）。由洛伦兹变换得：
x2 x1
即：
x2 x1 t2 t1 / c 2 1 2 / c2

l 1 2 / c2
l l0 1 2 / c2
即有：
l l0

6狭义相对论

6狭义相对论

实验装置：
M2
v
l S M
l
M1
T
说明：由光源S发出的光线在半反射镜M上分为两 束，一束通过M，被M1反射回到M，再被M反射而
达到目镜T；另一束被M反射到M2，再反射回M而 直达目镜T。 调整两臂长度使有效光程为MM1=MM2=l. 设地 球相对于以太的绝对运动速度 v 沿MM1方向，则 由于光线MM1M与MM2M的传播时间不同，因而有 光程差，在目镜T中将观察到干涉效应。 当地球相对于以太的速度为v运动时，可看出 光线MM1和M1M间犹为如顺水和逆水行舟，它相对 于仪器的速度应各自为(c-v)和(c+v)，如果MM1的长 度为l时，那么光通过距离MM1+M1M所需的时间为
y ∑
r
y’ ∑’
v
P (x, y, z, t, x’, y’,z’,t’) x, x’
r
0 z z’
0’
设在P点站着一人，按了一个闪光灯，在∑系中 观察者看来，按灯的这个现象发生于t 时刻、（x,y,z） 点；在 系中观察者看来，按灯这个现象发生于t’ 时 刻、（x’,y’,z’）点；这两组数（x,y,z,t）与（x’,y’,z’,t’） 之间的关系是与时空观有关的。 根据经典时空观，得到
电磁现象不服从传统的相对性原理。历史上，把这 个在绝对时间和绝对空间（长度）假设下得出的、 Maxwell’s equations和电磁波传播速度各向同性定律 在其中成立的特殊参考系，称为绝对参考系。 然而，绝对参考系是对哪个参照物建立的呢？ 当时人们认为传播电磁波的媒质是以太，电磁波传 播速度c是对以太这一特殊参考系而言的。也就是 说，以太就是那个绝对参考系。 为了找出或证明这个绝对惯性系的存在，迈克 尔逊（michelson）和莫雷（Morley）于1887年利用 灵敏的干涉仪，企图用光学方法测定地球的绝对运 动。假定以太相对太阳静止，这个运动就是地球绕 太阳的运动。

第六章-狭义相对论基础

第六章-狭义相对论基础

c
1 2
1 2
得
l l 12
（5）
空间间隔（或称物体长度）是相对的,和 物体一起运动的惯性系中测得的长度最长,而 与物体相对运动的惯性系中测得的长度就短 些,即运动物体沿其运动方向的长度变短了。
尺缩效应动画
6.4 洛仑兹变换 相对论时空观的再讨论
6.4.1 洛仑兹变换 两个惯性系
S 和 S′,因二者只 沿 x 方向有相对
（3）长度缩短（尺缩效应）
t2 t1 2lc (3) •
l
入射段：
o
图1
lVt1ct1
t1
l c V
V t1
••
o o
l
图2
反射段：
lV t2ct2
t2
l c V
V(t1t2)
•
•
o
o
l
图3
M
V
M
M
tt1t2c lVc lV12 lc2
由 (2)式 ,得
t t
1 2
（4）
于是有
2l
2l
c
物体的速度不能超过真 空中的光速。
6.4.2 相对论时空观的再讨论
（1）同时的相对性
S S V
a l •
O (x1,t1) O
( x1 , t1 )
M l b
•
•
x (x2,t2 )
x ( x2 , t2 )
在S'系看
t2 t1
x2x1 2l
在S系看，由洛仑兹变换
t1
t1 Vx1 1V 2
c2 c2
由洛仑兹变换
xa
xa Vta
1 2
b(xb ,tb ) x

第六章 狭义相对论

第六章 狭义相对论
2
12

R
例8（
V
）解答
o
B A
（转台+二人）对转轴 角动量守恒
2V
台
1 2 L台 mR 0 2
1 1 LA rA ( m )VA地 mR 20 2 2
1 1 1 2 LB rB ( m )VB 地 m( R ) 0 2 2 2
13
走动前
成的摩擦阻力矩）
4
解：
（1）子弹击中圆盘后，圆盘 所获得的角速度
R
v0
m
子弹和圆盘在碰撞前后角动量守恒
1 mv0 R ( MR 2 mR 2 ) 2
mv0 1 ( 2 M m)R
5
（2）经过多少时间后，圆盘停止转动 解一：据定轴转动定律 根
d M J J dt
27
1887 年 ， 体 现 上 面 思 想 的 迈 克 耳 孙 — 莫 雷 （Michelson-Morlay）实验却得到了“零”结 果！ 地球就是“绝对静止”的参考系？ 用各种企图保持绝对参考系的假说来解 释该实验结果，均遭到失败。典型的有： 发射说：光速要叠加上光源的速度。 双星观测否定了发 c + u1 双 射说，即实际上观测 地球 星 u2 不到双星位置的扭曲， 不能同时 c u2 m2 到达地球 28 而是符合力学规律。 应观察到双星位置的扭曲
7
例7（ ）一匀质细棒长为2L，质量 为m。以与棒长方向相垂直 的速度 V0在光滑水平面内平动时与前方一 固定的光滑支点O发生完全非弹性 A 碰撞。碰撞点位于棒 L 2 o 中心的一方L/2处， L 2 如图所示。 L 求棒在碰撞后的瞬时绕 O点转动时的角速度 B V0
8
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

x1 ut1 1 u2 c2
[(x2 x1) u(t2 t1)]
因为需同时测得杆两端长度，所以t1=t2
L
x2 x1 1 u2 c2
L 1 u2 c2
L 1 u2 c2 L
观测者与被测物体相对静止时，长度的测量值最大，
叫固有长度（L0）,观测者与被测物体有相对运动时，测
得的长度等于其固有长度的 缩效应。
( x2,t2)
解：设地面为S系，火车为S´系
在S´系中观测
t1'
t1
u c2
x1
1 u2 c2
(x1 ,t1)
( x2,t2)
t
' 2
t2
u c2
x2
1 u2 c2
t
' 2
t1'
(t2
t1 )
u c2
( x2
1 u2 c2
x1 )
∵ t1 = t2 x1 < x2 ∴ t1´ > t2´
c2 t2 t1
x2 x1 为子弹飞行的速率，小于c t2 t1
所以
t2' t1' 0
飞船上的观察者也看到子弹先出膛，后击中靶子
由于真空中的光速c是物体运动或信息传递速度 的极限，因此对于有因果关系的两个事件，不会 因参考系的不同而使因果顺序颠倒。
二 时间膨胀(动钟变慢)
u
y
y'
S
S'
质量乘光速的平方 E = mc2 。
本章内容提要
第一节 伽利略变换和经典力学时空观 第二节 狭义相对论的基本假设
洛仑兹变换 第三节 狭义相对论的时空观 第四节 狭义相对论动力学
第一节 伽利略变换和经典力学时空观
一 伽利略相对性原理（Galileo principle of relativity ）
dr
d (mv)
dt
dr
v
0 d (mv) v
d
(mv)
v
dmv
v
mdv
v
v2dm
mvdv
由质速关系可得
m2
m0 2 1 v2 c2
m2 (c2 v2 ) m02c2
m2v2 m2c2 m02c2
对上式两边取微分
2v2mdm 2m2vdv 2c2mdm
v2dm mvdv c2dm
Ek
m c2dm
m0
mc2
m0c 2
此式为相对论动能公式
Ek mc2 m0c2 m0c2 (
1
1)
1 v2 / c2
当 v<<c 时，可将(1 v2 / c作2 )泰12勒展开
(1
v2 c2
1
)2
1
1 2
v2 c2
3 v4 8 c4
取前两项代入上式
Ek
m0c2 (1
1 2
v2 c2
1)
洛仑兹速度变换
vx'
vx u 1 uvx / c2
v
' y
vy 1u2 / c2 1 uvx / c2
或
vz'
vz 1 u2 / c2 1 uvx / c2
vx
vx' u 1 uvx' / c2
vy
v'y 1 u2 / c2 1 uvx' / c2
vz
vz' 1 u2 / c2 1 uvx' / c2
倍。1这 u个2 c效2 应叫长度收
L L0
1u2
c2
L0
物体沿其运动方向缩短了
例三 隧道和列车静止时长度相等。现列车以速度u高 速通过隧道。地面上的观察者观测到当列车完全进入 隧道时，隧道的进、出口处同时发生了雷击，当然并 未击中列车，问列车上的旅客会观测到列车遭到雷击 了吗？
(x1 ,t1)
1971 年 ， 美 国空军用两组 CS （ 铯 ） 原 子 钟绕地球一周， 得到运动钟变 慢 ： 20310ns ， 而理论值为： 184 23ns ， 在误差范围内 二者相符。
例二 有两只事前对准的完全相同的钟A、B。A钟放 在宇宙飞船内，B钟留在地面上。飞船在某日上午8时 出发，以 3的c 速度相对地球飞行。宇航员经过1小时 飞行后，看2到A钟指到9时整。问地面上的观测者看到 B钟此刻指在几点。
m
m0 1 v2 c2
m0 称为静质量
m 称为相对论质量
二 . 相对论动力学基本方程
相对论动量：
P mv
m0v 1 v2 c2
F
ma
m
dv
d (mv)
dp
dt
dt
dt
F
dp
dt
d( dt
m0v ) 1 v2 c2
此式称为相对论动力学基本方程
三 . 相对论动能
Ek
F
x' x ut
由
y' y z' z
t' t
r r
在伽利略变换下时间和空间均与参考系的运 动状态无关，时间和空间之间互不相联系，是绝 对的，这就是经典力学的时空观，也称为绝对时 空观。伽利略变换是其具体体现。
返回
第二节 狭义相对论的基本假设 洛仑兹变换
一 狭义相对论产生的背景和条件
u c c u
L0
0
方法二：设火车为S系，地面为S´系,则S系中 任意时刻车头均在L0处。
S´系：A（0,0）；B（ L0,0） S系：A（0,0）；B（ L,t）
xB xB (utB ) xB L0
tB
tB
(
u c2
xB
)
u c2
L0
u c2
L0
0
第四节 狭义相对论动力学
一. 质速关系
解：设地球为S系，飞船为S´系
0 1h
0
1
2h
1u2 c2
1 ( 3 c)2 / c2 2
所以 B 钟指10点整
三 长度收缩
y
S
u
y' S'
o
z
o' x1´
z'
x2´ x 'x
在S´系中 在 S 系中
L x2' x1' L x2 x1
L x2' x1' x2 ut2 1 u2 c2
当 x1 x2 时
u( x1 x2 )
t t2' t1'
c2 0 1 u2 c2
在一个惯性系中同时同地发生的两个事件，在其 他的惯性系中观测也是同时发生的。
例一 一射击运动员在t1时刻扣动扳机，t2时刻子弹 击中百米以外的靶子。问在以速率u相对于地球运动 的宇宙飞船上观测，是否会出现子弹先击中靶子而 后出膛的现象。
解：设地球为S系，飞船为S`系
t1
t2
x1
x2
t2 t1
t1'
t1 ux1 c 2 1 u2 c2
t
' 2
t2 ux2 c 2 1 u2 c2
tx11
tx22
t2 t1
t2' t1'
(t2
t1)
u c2
( x2
x1 )
1 u2 c2
t2 t1 (1 u x2 x1 )
1u2 c2
1905 年 ， 除 去 博 士 论 文 外，爱因斯坦连续发表了4 篇重要论文，其中任何一篇， 都够得上拿诺贝尔奖。
3月，发表了解释光电效应的论文，提出光子说；
5月，发表关于布朗运动的论文，间接证明了分子 的存在；
6月，发表“论运动媒质的电动力学”的论文，提 出了狭义相对论；
9月发表了有关质能关系式的论文，指出能量等于
v
'
S系
vz'
vz
v u
F ma
a
' x
ax
a'y ay
aa'z'
S`系
az a F
ma
三 经典力学的时空观
（1）同时性是绝对的
y
St
A
y' u
S'
B
o
o'
x
x'
z
t1' t t2' t
z' t1' t2' 或t t '
（2）时间间隔是绝对的
S y t1
A
y' u
S'
t2 B
o
A
o
z
o' x
z'
B
x'
设S´系中x0´处先后发生二事件A、B
A: t1´ B: t2´
t t2' t1'
在S系中这两个事件发生的时刻分别为t1和t2
t t2 t1
t' 2
ux0' c 2
1 u2 c2
t' 1
ux0'
c2
1 u2 c2
t2' t1' t
1u2 c2
1u2 c2
在与事件发生地点相对静止的参考系中测得
x x ut 1u2 / c2
x x ut 1u2 / c2
y y
或
z z
t t ux / c2 1u2 /c2
y y
z z
t t ux / c2 1u2 /c2
t'
t ux c2 1 u2 c2
因为 t 必须是实数，所以速率u必须满足
1
u c
2 2
0
uc
一切物体的运动速度都不能超过真空中的光速c， 或者说真空中的光速c是物体运动的极限速度。