精选叠加原理例题

数学上叠加原理的应用题介绍在数学中，叠加原理是一种常用的方法，通过将问题转化为多个简单的部分，然后将这些部分求和，来解决复杂的问题。

本文将通过几个应用题来介绍数学上叠加原理的具体应用。

应用题1：购物账单小明去超市购物，他买了3件商品，价格分别是20元、30元和40元。

如果小明付款时给了50元，那么找给他多少钱？答案：根据叠加原理，我们可以将这个问题分解为3个部分：第一件商品找零10元，第二件商品找零20元，第三件商品找零10元。

所以，小明应该找零10+20+10=40元。

应用题2：公路里程计算假设小明要从A城市开车到B城市，途中经过C和D两个城市。

A到C的距离是100公里，C到D的距离是200公里，D到B的距离是150公里。

那么小明整个行程的总里程是多少？答案：根据叠加原理，整个行程的总里程就是A到C的距离加上C到D的距离再加上D到B的距离。

所以，总里程是100+200+150=450公里。

应用题3：物体运动中的位移计算一个物体从原点出发，以每秒5米的速度向东移动。

经过10秒钟后，物体的位移是多少？答案：根据叠加原理，物体的位移等于每秒的位移乘以总时间。

每秒的位移是5米，总时间是10秒，所以位移就是5乘以10=50米。

应用题4：温度计算某市在上午9：00的时候，气温是24摄氏度。

在上午11：00时，气温上升了5摄氏度。

那么上午11：00时的气温是多少摄氏度？答案：根据叠加原理，上午11：00时的气温是上午9：00时的气温加上气温的上升量。

上午9：00时的气温是24摄氏度，上升了5摄氏度，所以上午11：00时的气温是24+5=29摄氏度。

应用题5：考试成绩计算小明在一次数学考试中，第一次得了80分，第二次得了90分，第三次得了70分。

如果每次考试的成绩占总成绩的20%，那么小明的总成绩是多少？答案：根据叠加原理，小明的总成绩是每次考试成绩乘以对应的权重再求和。

第一次考试得了80分，权重是20%，所以贡献了0.280=16分。

叠加原理例题叠加原理是物理学中的一个重要概念，它在解决复杂物理问题时起着至关重要的作用。

通过叠加原理，我们可以将一个复杂的物理系统分解成若干简单的部分，分别进行分析，最后再将它们的效果叠加在一起，得到整个系统的行为。

下面，我们通过几个例题来深入理解叠加原理的应用。

例题一，弹簧振子叠加。

假设有两个弹簧振子，它们的振动方程分别为：振子A，$x_1 = A_1 \sin(\omega_1 t + \phi_1)$。

振子B，$x_2 = A_2 \sin(\omega_2 t + \phi_2)$。

其中，$A_1$和$A_2$分别为振幅，$\omega_1$和$\omega_2$分别为角频率，$\phi_1$和$\phi_2$分别为初相位。

现在将这两个振子连接起来，形成一个新的系统。

根据叠加原理，整个系统的振动方程可以表示为：$x = x_1 + x_2 = A_1 \sin(\omega_1 t + \phi_1) + A_2 \sin(\omega_2 t + \phi_2)$。

通过叠加原理，我们可以将复杂的双振子系统简化为两个单振子系统的叠加。

这样，我们就可以更容易地分析整个系统的振动特性。

例题二，电场叠加。

假设有两个点电荷，它们分别产生的电场分别为：电荷A产生的电场，$E_1 = \frac{kQ_1}{r_1^2}$。

电荷B产生的电场，$E_2 = \frac{kQ_2}{r_2^2}$。

现在将这两个点电荷放在同一空间中，根据叠加原理，整个空间中的电场可以表示为：$E = E_1 + E_2 = \frac{kQ_1}{r_1^2} + \frac{kQ_2}{r_2^2}$。

通过叠加原理，我们可以将复杂的电场分布问题简化为两个点电荷产生的电场的叠加。

这样，我们就可以更方便地计算任意位置的电场强度。

例题三，波的叠加。

假设有两个波源，它们分别产生的波动方程分别为：波源A产生的波动方程，$y_1 = A_1 \sin(kx \omega t + \phi_1)$。

叠加原理例题叠加原理是物理学中非常重要的一个原理，它在解决复杂问题时起着至关重要的作用。

通过叠加原理，我们可以将一个复杂的问题分解成若干个简单的部分，然后分别求解，最后再将它们合并在一起，得到整个问题的解。

下面，我们通过一些例题来深入理解叠加原理的应用。

例题一：一根长为L的均匀细杆，质量为m，静止放在光滑水平桌面上。

现在在离杆的一端距离为a处有一个质量为M的小物块，求杆的加速度。

解析：根据叠加原理，我们可以分别考虑杆和小物块的受力情况。

对于杆来说，它受到重力和支持力的作用，而对于小物块来说，它受到重力和杆的支持力的作用。

我们可以分别求解杆和小物块的加速度，然后将它们合并在一起得到整个系统的加速度。

首先，考虑杆的受力情况。

杆受到重力和支持力的作用，根据牛顿第二定律，杆的加速度为a1 = (Mg T)/m，其中T为支持力。

其次，考虑小物块的受力情况。

小物块受到重力和杆的支持力的作用，根据牛顿第二定律，小物块的加速度为a2 = T/M。

最后，将杆和小物块的加速度合并在一起，得到整个系统的加速度为a = a1 +a2 = (Mg T)/m + T/M。

通过这个例题，我们可以看到叠加原理的应用。

通过分别求解每个部分的问题，然后将它们合并在一起，得到整个系统的解。

这种分而治之的思想在物理学中有着广泛的应用。

例题二：一根长为L的均匀细杆，质量为m，静止放在光滑水平桌面上。

现在在离杆的一端距离为a处有一个质量为M的小物块，同时在离杆的另一端距离为b处有一个质量为m的小物块，求杆的加速度。

解析：同样地，根据叠加原理，我们可以分别考虑杆和两个小物块的受力情况。

对于杆来说，它受到重力和支持力的作用，而对于两个小物块来说，它们分别受到重力和杆的支持力的作用。

我们可以分别求解杆和两个小物块的加速度，然后将它们合并在一起得到整个系统的加速度。

首先，考虑杆的受力情况。

杆受到重力和支持力的作用，根据牛顿第二定律，杆的加速度为a1 = (Mg T)/m，其中T为支持力。

叠加原理例题
叠加原理是物理学中一个常用的概念，用于描述多个波在同一空间中叠加的效果。

以下是一个例题，通过运用叠加原理来解决问题：
一艘船在湖面上行驶，船头的声源以800 Hz的频率发出声波，船尾的声源以700 Hz的频率发出声波。

假设声波在水中的传
播速度为340 m/s，求在某个位置上观察到的声波频率是多少？
根据叠加原理，当两个波相遇时，其位移应该叠加在一起。

我们可以将这两个波视为两个正弦函数，然后进行叠加。

设观察点距离船头的距离为x1，距离船尾的距离为x2。

声波
的传播速度为v，频率为f，波长为λ，那么可以得到以下关系：
x1 = v/f1
x2 = v/f2
在观察点上，由于船头和船尾的声源会同时发出声波，那么观察到的声波位移应该是这两个波的位移叠加在一起。

由叠加原理可以得到：
x_total = x1 + x2
根据波长的定义，可以将x_total表示为：
x_total = v/f_total
将上述各式联立求解，得到：
1/f_total = 1/f1 + 1/f2
代入已知数据，有：
1/f_total = 1/800 + 1/700
计算得到：
1/f_total = 0.00125 + 0.0014285714
1/f_total = 0.0026785714
f_total = 1/0.0026785714
f_total ≈ 373.95 Hz
因此，在观察点上，我们将会听到约为373.95 Hz的声音。

这个例题展示了叠加原理在声波叠加问题中的应用。

通过将波视为正弦函数，并运用叠加原理，我们可以求得在观察点上的声波频率。

电场的叠加原理例题1. 两个点电荷叠加的电场设有两个点电荷q1和q2分别位于点A和点B，距离为r。

根据电场的叠加原理，两点的电场可以叠加为：E = E1 + E2其中E1是点电荷q1在点A处产生的电场，E2是点电荷q2在点B处产生的电场。

根据库仑定律，可以求得各个电场分量的数值：E1 = k * q1 / r^2E2 = k * q2 / r^2所以两点的电场叠加为：E = k * q1 / r^2 + k * q2 / r^22. 线电荷产生的电场考虑一个长度为L的直线带电体，电量为Q，位于直线上的任意一点P处。

根据电场叠加原理，可以将线电荷分解为无数个微小电荷dq，并叠加它们所产生的电场。

设dq位于离P 处的距离为r。

由于电荷dq的电场是等距离的，而且线电荷上各点电荷数量密度相同，所以可以计算dq在点P处产生的电场为：dE = k * dq / r^2对于整个线电荷，可以将其分解为无数个微小线段dl，并对每个微小线段应用上述公式。

然后将所有微小线段的电场矢量相加，即可得到整个线电荷带来的总电场。

3. 均匀带电平面产生的电场考虑一个无限大的均匀带电平面，电荷密度为σ，位于平面上的任意一点P处。

根据电场叠加原理，可以将平面分解为无数个微小面元dA，并叠加它们所产生的电场。

根据库仑定律，可以计算微小面元dA在点P处产生的电场为：dE = (k * σ * dA) / r^2对于整个平面，可以将其分解为无数个微小面元dA，并对每个微小面元应用上述公式。

然后将所有微小面元的电场矢量相加，即可得到整个平面带来的总电场。

叠加原理练习题及答案在学习物理的过程中，我们经常会遇到叠加原理这一概念。

叠加原理在物理学中扮演着重要的角色，因为它可以帮助我们分析和解决各种物理问题。

在本文中，我们将介绍一些叠加原理的练习题，并提供答案以供参考。

第一道题目是关于力学的。

假设有两个力，一个向右施加50N的力，另一个向左施加30N的力。

请问物体受到的合力是多少？根据叠加原理，我们可以将这两个力进行矢量相加。

由于力是矢量量，我们需要考虑其大小和方向。

向右施加的力是正方向，向左施加的力是负方向。

因此，合力为50N - 30N，即20N向右。

第二道题目涉及电路。

一个电路中有两个电池，一个电池的电动势为2V，另一个电池的电动势为3V。

两个电池的正负极分别相连，形成一个闭合电路。

请问电路中的总电动势是多少？根据叠加原理，我们可以将两个电动势相加，即2V + 3V，得出总电动势为5V。

第三道题目考察光学。

一束红光和一束绿光同时照射到一个反射镜上。

红光的波长为650nm，绿光的波长为550nm。

请问，反射镜上的光的波长是多少？根据叠加原理，我们可以将这两束光的波长进行叠加。

由于光的波长足够小，我们可以简单地将两个波长相加。

即650nm + 550nm，得出反射镜上的光的波长为1200nm，即1.2μm。

第四道题目涉及声音。

一个人同时发出两个频率为200Hz和400Hz的声音。

请问，听到的声音频率会是多少？根据叠加原理，我们可以将这两个频率进行叠加。

听到的声音频率实际上是两个声音频率的平均值。

即 (200Hz + 400Hz) / 2，得出听到的声音频率为300Hz。

以上是四个关于叠加原理的练习题及其答案。

通过这些题目，我们可以看到在物理学中，叠加原理始终都是一个重要的工具。

它可以帮助我们分析和解决各种问题，无论是力学、电路、光学还是声学。

通过理解和应用叠加原理，我们能够更好地理解物理学的基本原理，并应用于实际场景中。

练习题对于学习叠加原理来说是非常重要的。

选择题在使用叠加定理分析电路时，下列哪个条件必须满足？A. 电路中的元件必须是线性的（正确答案）B. 电路中的元件必须是非线性的C. 电路中的电源必须是直流的D. 电路中的电源必须是交流的叠加定理适用于下列哪种电路的分析？A. 含有受控源的电路B. 线性电路（正确答案）C. 非线性电路D. 只含有电阻和电容的电路当使用叠加定理分析电路时，下列哪个步骤是正确的？A. 分别计算每个独立电源作用下的响应，然后求和（正确答案）B. 同时考虑所有电源的作用，直接计算总响应C. 只考虑最大的电源，忽略其他电源D. 只考虑最近的电源，忽略远距离的电源在叠加定理中，当某个电源单独作用时，其他电源应如何处理？A. 保持不变B. 置为零（正确答案）C. 置为最大值D. 置为最小值使用叠加定理分析电路时，下列哪个物理量是可以叠加的？A. 电阻值B. 电容值C. 电压或电流（正确答案）D. 电感值下列哪种情况下，叠加定理不适用？A. 电路中含有二极管（正确答案）B. 电路中含有电阻C. 电路中含有电容D. 电路中含有电感在叠加定理中，当所有电源同时作用时，电路中的响应等于什么？A. 各个电源单独作用时响应的代数和（正确答案）B. 各个电源单独作用时响应的算术和C. 各个电源单独作用时响应的最大值D. 各个电源单独作用时响应的最小值使用叠加定理分析电路时，下列哪个步骤是不必要的？A. 确定电路中的独立电源B. 分别计算每个独立电源作用下的响应C. 考虑电源之间的相互作用（正确答案）D. 将各个响应叠加得到总响应叠加定理在电路分析中的主要作用是什么？A. 简化复杂电路的计算（正确答案）B. 提高电路的效率C. 改变电路的参数D. 优化电路的设计。

微专题44 磁场的叠加【核心考点提示】磁场的叠加原理： 磁场的叠加体现在磁感应强度的叠加，而磁感应强度为矢量，叠加时遵循平行四边形或三角形定则。

【经典例题选讲】【例题】(2017·全国卷Ⅲ)如图，在磁感应强度大小为B0的匀强磁场中，两长直导线P和Q 垂直于纸面固定放置，两者之间的距离为l。

在两导线中均通有方向垂直于纸面向里的电流I时，纸面内与两导线距离均为l的a点处的磁感应强度为零。

如果让P中的电流反向、其他条件不变，则a点处磁感应强度的大小为 (　C　)A．0 B．B0 C．B0 D．2B0[解析]　导线P和Q中电流I均向里时，设其在a点产生的磁感应强度大小B P＝B Q＝B1，如图所示，则其夹角为60°，它们在a点的合磁场的磁感应强度平行于PQ向右、大小为B1。

又根据题意B a＝0，则B0＝B1，且B0平行于PQ向左。

若P中电流反向，则B P反向、大小不变，B Q和B P大小不变，夹角为120°，合磁场的磁感应强度大小为B1′＝B1(方向垂直PQ 向上、与B0垂直)，a点合磁场的磁感应强度B＝＝B0，则ABD项均错误，C项正确。

【变式】(2018·福建漳州联考)如图所示，等边三角形ACD的三个顶点处分别有垂直于纸面的长直导线，三处的导线都通以大小为I的电流，方向如图所示，O为三角形外接圆的圆心。

已知通电直导线周围空间某点的磁感应强度B＝k，其中r为该点到导线的垂直距离。

当只有A、D处导线中通有电流时，它们在O处产生的磁感应强度为B0；则当A、D、C三处导线都通有电流时，三根导线在O处产生的磁感应强度为 ( D )A．0　B．B0 C．2B0　D．B0[解析]　分别作出A、D处两根导线在O点的磁感应强度方向，大小均设为B1，则合磁感应强度B ′＝2B 1cos30°＝B 1＝B 0，而三根导线共同在O 处产生的磁感应强度应为B ″＝2B 1，所以B ″＝，D 正确，A 、B 、C错误。

高中物理每日一点十题之静电力叠加原理一知识点静电力叠加原理对于两个以上的点电荷，其中每一个点电荷所受的总的静电力，等于其他点电荷分别单独存在时对该点电荷的作用力的矢量和，这个结论叫作静电力叠加原理．静电力的合成与分解遵循平行四边形定则．十道练习题（含答案）一、单选题（共9小题）1. 如图，带电荷量分别为q a、q b、q c的小球，固定在等边三角形的三个顶点上，q a所受库仑力的合力F方向垂直于q a、q b的连线，则( )A. q b、q c异号，且q c＝2q bB. q a、q b异号，且q b＝2q aC. q a、q c同号，且q c＝2q aD. q a、q b同号，且q b＝2q a2. 如图所示，三个固定的带电小球a、b和c，相互间的距离分别为ab＝5 cm，bc＝3 cm，ca＝4 cm.小球c所受库仑力的合力的方向平行于a、b的连线．设小球a、b所带电荷量的比值的绝对值为k，则( )A. a、b带同种电荷，k＝B. a、b带异种电荷，k＝C. a、b带同种电荷，k＝D. a、b带异种电荷，k＝3. 如图所示，直角三角形ABC中∠B＝30°，点电荷A、B所带电荷量分别为Q A、Q B，测得在C处的某正点电荷所受静电力的合力方向平行于AB向左，则下列说法正确的是( )A. A带正电，Q A∶Q B＝1∶8B. A带负电，Q A∶Q B＝1∶8C. A带正电，Q A∶Q B＝1∶4D. A带负电，Q A∶Q B＝1∶44. 如图所示，在等腰直角三角形ABC的三个顶点A、B、C上分别固定三个带电荷量分别为Q1、q、Q2的点电荷，点电荷q受到的库仑力的合力F垂直于AB斜向右下方，关于点电荷Q1、Q2的电性及带电荷量之间的关系，下列说法正确的是( )A. 电性相反，Q1＝2Q2B. 电性相反，Q1＝Q2C. 电性相同，Q1＝2Q2D. 电性相同，Q1＝Q25. 如图所示，有三个点电荷A、B、C位于一个等边三角形的三个顶点上，已知三角形的边长为1 cm，B、C所带电荷量为q B＝q C＝＋1×10－6 C，A所带电荷量为q A＝－2×10－6 C，静电力常量k＝9.0×109 N·m2/C2，A所受B、C两个电荷的静电力的合力F的大小和方向为( )A. 180 N，沿AB方向B. 180N，沿AC方向C. 180 N，沿∠BAC的角平分线D. 180N，沿∠BAC的角平分线6. 中子内有一个电荷量为＋e的上夸克和两个电荷量为－e的下夸克，一个简单的模型是三个夸克都在半径为r的同一圆周上，如图所示．则下列四幅图中，能正确表示出各夸克所受静电作用力的是( )A. B. C. D.7. 如图所示，在边长为1 m的正方形的每个顶点都放置一个点电荷，其中a和b均带正电，电荷量为＋2×10－5 C，c和d均带负电，电荷量为－2×10－5 C．则a电荷受到的其他三个电荷的静电力的合力大小是( )A. 0B. 5.4 NC. 2.7 ND. 10.8 N8. 如图所示，棱长为a的立方体ABCD－A′B′C′D′八个顶点上有八个带电质点，其中顶点A、C′电荷量分别为q、Q，其他顶点电荷量未知，顶点A上的质点仅在静电力作用下处于平衡状态，现将顶点C′上质点电荷量变成－Q，则顶点A上质点所受静电力的合力为(不计重力)( )A. B. C. D. 09. 如图甲所示，直线上固定两个正点电荷A与B，其中B带＋Q的电荷量，C、D两点将AB连线三等分．现有一个带负电的粒子从C点开始以某一初速度向右运动，不计粒子所受的重力，并且已知该粒子在C、D间运动的速度v与时间t的关系图像如图乙所示，则A点电荷所带电荷量可能是( )A. ＋5QB. ＋3QC. ＋2QD. ＋Q二、多选题（共1小题）10. 如图所示，可视为点电荷的三个带电小球a、b和c分别固定在三角形的顶点上，已知ab＝4 cm，bc ＝3 cm，ca＝5 cm，a球所受静电力的合力方向恰好平行于b、c的连线，则下列说法正确的是( )A. b、c一定带异种电荷B. b、c一定带同种电荷C. b、c所带电荷量绝对值的比为64∶125D. c球所受静电力的合力方向可能垂直于a、b的连线1. 【答案】A【解析】根据题意可知，小球a、c之间存在排斥力，q a、q c同号，小球a、b之间存在吸引力，q a、q b异号，所以q b和q c异号，根据平行四边形定则，排斥力是吸引力的两倍，根据库仑定律F＝k，在F ac＝k，F ab＝k，根据题意得F ac＝2F ab，所以有q c＝2q b，故B、C、D错误，A正确．2. 【答案】D【解析】如果a、b带同种电荷，则a、b两小球对c的作用力均为斥力或均为引力，此时c在垂直于a、b连线的方向上的合力一定不为零，因此a、b不可能带同种电荷，A、C错误；若a、b带异种电荷，假设a对c的作用力为斥力，则b对c的作用力一定为引力，受力分析如图所示，由题意知c所受库仑力的合力方向平行于a、b的连线，则F a、F b在垂直于a、b连线的方向上的合力为零，由相似三角形可知＝＝，结合库仑定律可得＝＝，同理易知若a对c的作用力为引力，b对c的作用力为斥力，结果相同，B错误，D正确．3. 【答案】B【解析】要使C处的正点电荷所受静电力的合力方向平行于AB向左，该正点电荷所受静电力的情况应如图所示，所以A带负电，B带正电．设AC间的距离为L，则BC间的距离为2L.F B sin 30°＝F A，即k·sin 30°＝，解得＝，故选项B正确．4. 【答案】B【解析】根据题意可判断出，Q1与q相互排斥，Q2与q相互吸引，Q1、Q2的电性相反，设AC＝BC ＝l，则AB＝l根据库仑定律得F1＝、F2＝，由题意画出示意图，可知sin 45°＝代入解得Q1＝Q2故选B.5. 【答案】D【解析】点电荷B、C对点电荷A的静电力大小相等，为F BA＝F CA＝＝N＝180 N．如图所示，A受大小相等的两个静电力，两静电力夹角为60°，故由矢量的平行四边形定则和几何知识得A受到的静电力的合力大小为F＝2F BA cos 30°＝2×180×N＝180N．方向沿∠BAC的角平分线，故选项D正确．6. 【答案】B【解析】电荷量为＋e的上夸克，受到电荷量为－e的两个夸克等大的静电力作用，由对称性得，上夸克所受静电力竖直向下．对电荷量为－e的下夸克，另一个下夸克对它的静电力F＝k，上夸克对它的静电力F′＝k ，方向沿着连线方向，由几何关系知F′sin 30°＝F，因此F与F′的合力方向竖直向上，且FF′cos 30°(如图所示)，同理可知，另一个下夸克所受静电力的合力也竖直向上．B正确．合＝7. 【答案】B【解析】根据库仑定律，则对角线上a和c点的电荷给它的库仑引力为F c＝＝，相邻两点的电荷给它的库仑力大小均为F b＝F d＝k，a和b点为斥力，a和d点为引力，则a电荷受到两个电荷的合力F′＝2k cos 45°＝，则根据力的合成法则，则a电荷受到三个电荷的静电力的合力F ＝＝5.4 N，故选B.8. 【答案】B【解析】A上的质点仅在静电力作用下处于平衡状态，说明除C′上质点以外的其他质点对A上质点的作用力与C′上质点对A上质点的作用力等大反向；根据库仑定律可得F C′A＝，现将C′上质点电荷量变成－Q，其他质点对A上质点作用力不变，C′上质点对A上质点作用力大小不变、方向相反，则顶点A上质点所受静电力的合力为.9. 【答案】A【解析】由v－t图像可知该粒子在两正电荷A、B的作用下做加速度逐渐减小的减速运动，故点电荷A对其的库仑引力大于点电荷B对其的库仑引力，根据库仑定律，在D点时有k＞k，即Q A＞4Q，故选A.10. 【答案】AC【解析】因为a球所受静电力的合力方向恰好平行于b、c的连线，若b、c带同种电荷，根据力的合成可知，a受的合力方向不可能平行b、c连线，故b、c一定带异种电荷，故A正确，B错误；由题可知∠bac＝37°，根据受力可知F ca cos 37°＝F ba，即k，cos 37°＝k，解得b、c所带电荷量绝对值的比为64∶125，故C正确；垂直于a、b的连线是b、c间库仑力的方向，而c球所受静电力的合力是b对c和a对c的合力，故c球所受静电力的合力方向不可能垂直于a、b的连线，故D错误．。

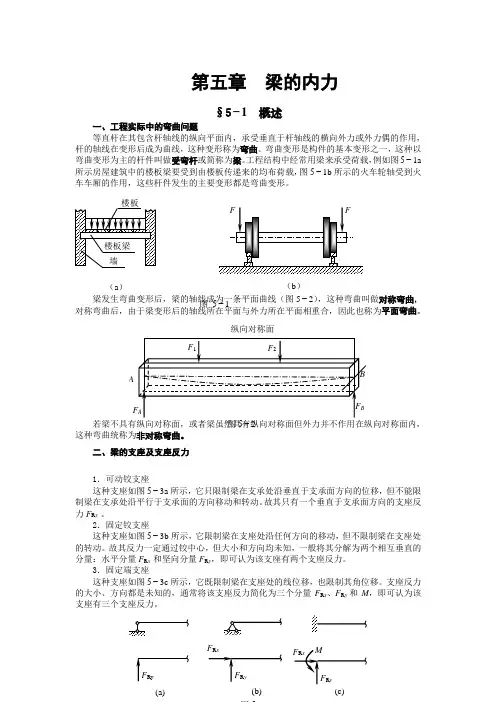
第五章梁的内力§5−1概述一、工程实际中的弯曲问题等直杆在其包含杆轴线的纵向平面内，承受垂直于杆轴线的横向外力或外力偶的作用，杆的轴线在变形后成为曲线，这种变形称为弯曲。

弯曲变形是构件的基本变形之一，这种以弯曲变形为主的杆件叫做受弯杆或简称为梁。

工程结构中经常用梁来承受荷载，例如图5−1a 所示房屋建筑中的楼板梁要受到由楼板传递来的均布荷载，图5−1b所示的火车轮轴受到火车车厢的作用，这些杆件发生的主要变形都是弯曲变形。

梁发生弯曲变形后，梁的轴线成为一条平面曲线（图5−2），这种弯曲叫做对称弯曲，对称弯曲后，由于梁变形后的轴线所在平面与外力所在平面相重合，因此也称为平面弯曲。

这种弯曲统称为非对称弯曲。

二、梁的支座及支座反力1．可动铰支座这种支座如图5−3a所示，它只限制梁在支承处沿垂直于支承面方向的位移，但不能限制梁在支承处沿平行于支承面的方向移动和转动。

故其只有一个垂直于支承面方向的支座反力F R y 。

2．固定铰支座这种支座如图5−3b所示，它限制梁在支座处沿任何方向的移动，但不限制梁在支座处的转动。

故其反力一定通过铰中心，但大小和方向均未知，一般将其分解为两个相互垂直的分量：水平分量F R x 和坚向分量F R y，即可认为该支座有两个支座反力。

3．固定端支座这种支座如图5−3c所示，它既限制梁在支座处的线位移，也限制其角位移。

支座反力的大小、方向都是未知的，通常将该支座反力简化为三个分量F R x、F R y和M，即可认为该支座有三个支座反力。

(a)纵向对称面A图5−2图5−1（b）（a）三、静定梁的基本形式常见的简单静定梁有下列三种：1．简支梁。

这种梁的一端是固定铰支座，另一端是可动铰支座（图5−4a ）。

2．悬臂梁。

这种梁的一端是固定端支座，另一端是自由端（图5−4b ）。

3．外伸梁。

这种梁相当于简支梁的一端或两端伸出支座以外（图5−4c ）。

四、梁的荷载 1．集中力。

2．集中力偶。

叠加原理例题叠加原理是指当有多个力作用于物体时，物体所受的合力等于各个力的矢量和。

下面是一个例题：一个物体在水平地面上受到两个力的作用，一个力F1以角度α施加在物体上方，另一个力F2以角度β施加在物体下方。

力F1的大小为5N，角度α为30°，力F2的大小为8N，角度β为60°。

求物体所受合力的大小和方向。

解答：首先根据叠加原理，求出物体在x轴和y轴上受到的力的分量。

设物体所受合力的大小为F，夹角与x轴的夹角为θ。

物体在x轴上受到的力的分量为Fx = F1 * cos(α) + F2 * cos(β)= 5N * cos(30°) + 8N * cos(60°)= 5N * √3/2 + 8N * 1/2= 5√3/2 N + 4N物体在y轴上受到的力的分量为Fy = F1 * sin(α) - F2 * sin(β)= 5N * sin(30°) - 8N * sin(60°)= 5N * 1/2 - 8N * √3/2= 5/2 N - 4√3 N/2= (5 - 4√3)/2 N然后根据勾股定理，可以求得物体所受合力的大小：F = √(Fx^2 + Fy^2)= √((5√3/2 N + 4N)^2 + (5 - 4√3)/2 N)^2)= √(75/4 + 20√3 + 16 + 25/4 - 10√3 + 12/4)= √(53/4 + 10√3)最后，根据三角函数的性质，可以求得物体所受合力的方向：tan(θ) = Fy / Fx= ((5 - 4√3)/2 N) / (5√3/2 N + 4N)= (5 - 4√3) / (5√3 + 8)至此，我们求得物体所受合力的大小为√(53/4 + 10√3) N，方向为θ = arctan((5 - 4√3) / (5√3 + 8))。

高中物理每日一点十题之电场强度的叠加一知识点1.电场强度叠加原理在几个点电荷共同形成的电场中，电场中任意一点的总电场强度等于各个点电荷在该点各自产生的电场强度的矢量和.这就是场强叠加原理.2.注意(1)独立性——各个场源电荷产生的电场互不干扰.(2)叠加原理——只有同时作用在同一区域内的电场才可以进行叠加.电场强度叠加遵循平行四边形定则.3.一个半径为R的均匀带电球体(或球壳)在外部产生的电场，与一个位于球心的、电荷量相等的点电荷产生的电场相同.十道练习题（含答案）一、单选题（共10小题）1. 如图，xOy平面直角坐标系所在空间有沿x轴负方向的匀强电场(图中未画出)，电场强度大小为E.坐标系上的A、B、C三点构成边长为L的等边三角形．若将两电荷量相等的正点电荷分别固定在A、B两点时，C点处的电场强度恰好为零．则A处的点电荷在C点产生的电场强度大小为( )A. EB. EC. ED. E2. 如图，真空中a、b、c、d四点共线且等距．先在a点固定一点电荷＋Q，测得b点场强大小为E.若再将另一等量异种点电荷－Q放在d点，则( )A. b点场强大小为EB. c点场强大小为EC. b点场强方向向左D. c点场强方向向左3. 如图所示，M、N和P是以MN为直径的半圆弧上的三点，O点为半圆弧的圆心，∠MOP＝60°.电荷量相等、电性相反的两个点电荷分别置于M、N两点，这时O点电场强度的大小为E1；若将N 点处的点电荷移至P点，此时O点的场强大小为E2，则E1与E2之比为( )A. 1∶2B. 2∶1C. 2∶D. 4∶4. 如图所示，A、B、C三点的连线构成一个等腰直角三角形，∠A是直角．在B点放置一个电荷量为＋Q的点电荷，测得A点的电场强度大小为E.若保留B点的电荷，再在C点放置一个电荷量为－Q 的点电荷，则A点的电场强度大小等于( )A. 0B. EC. ED. 2E5. 如图所示，以O为圆心的圆周上有六个等分点a、b、c、d、e、f.等量正、负点电荷分别放置在a、d两处时，在圆心O处产生的电场强度大小为E.现改变a处点电荷的位置，关于O点的电场强度变化，下列叙述正确的是( )B. 移至b处，O处的电场强度大小减半，方向沿OdC. 移至e处，O处的电场强度大小减半，方向沿OcD. 移至f处，O处的电场强度大小不变，方向沿Oe6. 如图所示，a、b、c、d四个点在一条直线上，a和b、b和c、c和d间的距离均为R，在a点处固定一电荷量为Q的正点电荷，在d点处固定另一个电荷量未知的点电荷，除此之处无其他电荷，已知b点处的场强为零，则c点处场强的大小为(k为静止力常量)( )A. 0B. kC. kD. k7. 如图所示，A、B、C是直角三角形的三个顶点，∠A＝90°，∠B＝30°.在A、B两点分别放置两个点电荷q A、q B，测得C点的电场强度E c方向与AB平行．下列说法正确的是( )A. 点电荷q A、q B的电性可能都为正B. 点电荷q A、q B的电荷量大小之比是1∶2C. 点电荷q A、q B的电荷量大小之比是1∶4D. 点电荷q A、q B的电荷量大小之比是1∶88. 如图所示，直角三角形ABC的∠A＝37°，∠B＝90°，在A、B两点各放一个点电荷，则C点的电场强度大小为E，方向与AC垂直指向右下，sin 37°＝0.6，cos 37°＝0.8，则( )A. A、B两点处点电荷都带正电B. A点处点电荷带负电，B点处点电荷带正电C. A、B两点处点电荷的带电量之比为5∶3D. A、B两点处点电荷的带电量之比为4∶39. 如图所示，a、b、c、d分别是一个菱形(竖直放置)的四个顶点，∠abc＝120°，O点为菱形对角线的交点，现将三个电荷量均为＋Q的点电荷分别固定在a、b、c三个顶点上，下列说法正确的是( )A. d点电场强度的方向由O指向dB. O点电场强度的方向由d指向OC. d点的电场强度大于O点的电场强度D. d点的电场强度等于O点的电场强度10. 如图，真空中有三个电荷量相等的点电荷A、B、C，它们固定在等边三角形的三个顶点上，A、B 带正电，C带负电，三角形的中心O处的电场强度大小为E.当把点电荷C移至AB连线的中点D时，中心O处的电场强度大小为( )A. B. C. D.1. 【答案】B【解析】C点三个电场方向如图所示，根据题意可知E1cos 30°＋E2cos 30°＝E，又知道E1＝E2，故解得E2＝E，B正确．2. 【答案】B【解析】设ab＝bc＝cd＝L，＋Q在b点产生的场强大小为E，方向水平向右，由点电荷的场强公式得：E＝k，－Q在b点产生的场强大小为E1＝k＝E，方向水平向右，所以b点的场强大小为E b＝E＋E＝E，方向水平向右，故A、C错误；根据对称性可知，c点与b点的场强大小相等，为E，方向水平向右，故B正确，D错误．3. 【答案】B【解析】依题意，两点电荷在O点产生的场强大小均为，当N点处的点电荷移至P点时，O点场强如图所示，则合场强大小E2＝，故＝，选项B正确．4. 【答案】C【解析】正电荷Q在A点产生的电场强度为E，沿BA方向，负电荷Q在A点产生的电场强度也为E，方向沿AC方向，根据电场强度的叠加原理可知E合＝＝E，故C正确，A、B、D错误．5. 【答案】C【解析】由题意可得，正、负点电荷在O处产生的电场强度的大小都为，方向沿Od；当a处点电荷移至c处时，两点电荷在O处的电场强度方向的夹角为120°，合电场强度大小为，方向沿Oe，选项A错；同理，当a处点电荷移至b处时，O处的合电场强度大小为，方向沿Oe与Od的角平分线斜向上，选项B错；同理，当a处点电荷移至e处时，O处的合电场强度大小为，方向沿Oc，选项C对；同理，当a处点电荷移至f处时，O处的合场强大小为，方向沿Oc与Od的角平分线斜向下，选项D错．6. 【答案】B【解析】据题可知，点处的场强为零，说明点处和点处的两个点电荷在点处产生的场强大小相等、方向相反，则有：k＝k，得Q′＝4Q，电性与Q相同．则Q在c点处产生的场强大小E1＝k＝k，方向向右，Q′在c点处产生的场强大小E2＝k＝k，方向向左，故c点处场强的大小为E＝E2－E1＝k，B正确．7. 【答案】D【解析】放在A点和B点的点电荷在C处产生的电场强度方向分别在AC和BC的连线上，因C点电场强度方向与BA方向平行，放在A点的点电荷和放在B点的点电荷产生的电场强度方向只能如图所示，q A带负电，q B带正电，且E B＝2E A，即＝2，又由几何关系知：＝2，所以q A∶q B＝1∶8，故D正确，A、B、C错误．8. 【答案】C【解析】由于A点点电荷在C点产生的场强与AC平行，因此B点点电荷在C点的场强沿AC方向的分量与A点点电荷在C点的场强等大反向，因此场强E是B点点电荷在C点场强的分量，由此可以判断B点点电荷带负电，A点点电荷带正电，A、B项错误；设AC间的距离为r，则BC间的距离为0.6r，由k＝k sin 37°，解得q A∶q B＝5∶3，C项正确，D项错误．9. 【答案】A【解析】a、c两点的点电荷在d点叠加的电场强度的方向由O指向d，b点的点电荷在d点的电场强度的方向也由O指向d，所以d点电场强度的方向由O指向d，选项A正确；同理，O点电场强度的方向由O指向d，选项B错误；设菱形的边长为L，a点的点电荷在d点产生的电场场强在竖直方向的分量为E0y＝，由对称性及电场叠加原理知，d点的电场强度E d＝2×＋＝，同理得O 点的场强为E O＝＝，所以E d＜E O，选项C、D错误．10. 【答案】D【解析】设等边三角形的边长为L，由题意可知E＝2k＝2k＝，当把点电荷C移至AB连线的中点D时，中心O处的电场强度E′＝k－k＝－＝＝E，故选D.。

电路叠加原理例题例题1：已知电路中有一个电源为2V的电池，串联了一个10Ω的电阻和一个5Ω的电阻。

求电源两端的电压和通过每个电阻的电流。

解析：首先，我们可以通过电路叠加原理将电路分解成两个部分：一个是电源和10Ω电阻的电路，另一个是电源和5Ω电阻的电路。

对于第一个电路，电源和10Ω电阻的串联，根据欧姆定律，电流I1可以表示为I1 = U1 / R1。

其中U1为电源两端的电压，R1为10Ω电阻的电阻值。

由于电源电压为2V，电阻为10Ω，将其代入公式可得I1 = 2V / 10Ω = 0.2A。

对于第二个电路，电源和5Ω电阻的串联，同理可以得到电流I2 = U2 / R2。

其中U2为电源两端的电压，R2为5Ω电阻的电阻值。

将电源电压2V和电阻5Ω代入公式，可得I2 = 2V / 5Ω = 0.4A。

综上所述，电源两端的总电压为2V，通过10Ω电阻的电流为0.2A，通过5Ω电阻的电流为0.4A。

例题2：一台电视机接在220V的电源上，电视机内部并联着一个100Ω的电阻和一个40Ω的电阻。

求电视机两端的电压和通过每个电阻的电流。

解析：根据电路叠加原理，我们可以将电视机内部的电路看成两个并联的电阻：一个是100Ω的电阻，另一个是40Ω的电阻。

对于100Ω的电阻，根据欧姆定律，电流I1可以表示为I1 = U / R1。

其中U为电视机两端的电压，R1为100Ω电阻的电阻值。

由于电视机接在220V的电源上，将其代入公式可得I1 =220V / 100Ω = 2.2A。

对于40Ω的电阻，同理可以得到电流I2 = U / R2。

其中R2为40Ω电阻的电阻值。

将电视机两端的电压U代入公式，可得I2 = 220V / 40Ω = 5.5A。

综上所述，电视机两端的电压为220V，通过100Ω电阻的电流为2.2A，通过40Ω电阻的电流为5.5A。

叠加原理题
好的，我明白了。

以下是一道关于叠加原理的题目：
有一根长为1米的直杆，上面有两个小球A和B，小球A位
于离杆左端0.2米的位置，小球B位于离杆右端0.3米的位置。

小球A和小球B的质量分别为0.1千克和0.2千克。

小球A相
对于杆绕杆顺时针方向旋转，角速度为5弧度/秒；小球B相
对于杆绕杆逆时针方向旋转，角速度为2弧度/秒。

求在任意
时刻，杆的角加速度。

解析：
根据叠加原理，杆的角加速度等于小球A产生的角加速度和
小球B产生的角加速度的代数和。

小球A产生的角加速度为αA = I·α/rA，其中，I为小球A围绕杆旋转的转动惯量，rA为小球A距离杆顶的距离。

小球B产生的角加速度为αB = I·α/rB，其中，I为小球B围绕
杆旋转的转动惯量，rB为小球B距离杆顶的距离。

根据叠加原理，得到杆的角加速度为：α = αA + αB
小球A的转动惯量 I = m·rA^2，其中，m为小球A的质量，
rA为小球A距离杆顶的距离。

小球B的转动惯量 I = m·rB^2，其中，m为小球B的质量，rB 为小球B距离杆顶的距离。

代入数据计算即可得到杆的角加速度。