数学分析PPT课件第四版华东师大研制 第3章 函数极限
- 格式:ppt
- 大小:3.84 MB
- 文档页数:122

第三章函数极限§1函数极限的概念引言在《数学分析》中,所讨论的极限基本上分两部分,第一部分是“数列的极限”,第二部分是“函数的极限”.二者的关系到是“特殊”与“一般”的关系;数列极限是函数极限的特例.通过数列极限的学习.应有一种基本的观念:“极限是研究变量的变化趋势的”或说:“极限是研究变量的变化过程,并通过变化的过程来把握变化的结果”.例如,数列这种变量即是研究当时,的变化趋势.我们知道,从函数角度看,数列可视为一种特殊的函数,其定义域为,值域是,即; 或或.研究数列的极限,即是研究当自变量时,函数变化趋势.此处函数的自变量n只能取正整数!因此自变量的可能变化趋势只有一种,即.但是,如果代之正整数变量n而考虑一般的变量为,那么情况又如何呢?具体地说,此时自变量x可能的变化趋势是否了仅限于一种呢?为此,考虑下列函数:类似于数列,可考虑自变量时,的变化趋势;除此而外,也可考虑自变量时,的变化趋势;还可考虑自变量时,的变化趋势;还可考虑自变量时,的变化趋势,由此可见,函数的极限较之数列的极限要复杂得多,其根源在于自变量性质的变化.但同时我们将看到,这种复杂仅仅表现在极限定义的叙述有所不同.而在各类极限的性质、运算、证明方法上都类似于数列的极限.下面,我们就依次讨论这些极限.一、时函数的极限1.引言设函数定义在上,类似于数列情形,我们研究当自变量时,对应的函数值能否无限地接近于某个定数A.这种情形能否出现呢?回答是可能出现,但不是对所有的函数都具此性质.例如无限增大时,无限地接近于0;无限增大时,无限地接近于;无限增大时,与任何数都不能无限地接近.正因为如此,所以才有必要考虑时,的变化趋势.我们把象,这样当时,对应函数值无限地接近于某个定数A的函数称为“当时有极限A”.[问题]如何给出它的精确定义呢? 类似于数列,当时函数极限的精确定义如下.2.时函数极限的定义定义1设为定义在上的函数,A为实数.若对任给的,存在正数M,使得当时有, 则称函数当时以A为极限.记作或.3.几点注记(1)定义1中作用与数列极限中作用相同,衡量与A的接近程度,正数M的作用与数列极限定义中N相类似,表明充分大的程度;但这里所考虑的是比M大的所有实数,而不仅仅是正整数n.(2)的邻域描述:当时,(3)的几何意义:对,就有和两条直线,形成以A为中心线,以为宽的带形区域.“当时有”表示:在直线的右方,曲线全部落在这个带形区域内.如果给得小一点,即带形区域更窄一点,那么直线一般往右移;但无论带形区域如何窄,总存在正数M,使得曲线在的右边的全部落在这个更窄的带形区域内.(4)现记为定义在或上的函数,当或时,若函数值能无限地接近于常数A,则称当或时时以A为极限,分别记作,或,或.这两种函数极限的精确定义与定义1相仿,简写如下:当时,,当时,.(5)推论:设为定义在上的函数,则.4.利用=A的定义验证极限等式举例例1证明.例2证明1);2).二、时函数的极限1.引言上节讨论的函数当时的极限,是假定为定义在上的函数,这事实上是,即为定义在上,考虑时是否趋于某个定数A.本节假定为定义在点的某个空心邻域内的函数,.现在讨论当时,对应的函数值能否趋于某个定数A数列.先看下面几个例子:例1.(是定义在上的函数,当时,)例2.(是定义在上的函数,当时,)例3.(是定义在上的函数,当时,)由上述例子可见,对有些函数,当时,对应的函数值能趋于某个定数A;但对有些函数却无此性质.所以有必要来研究当时,的变化趋势.我们称上述的第一类函数为当时以A为极限,记作.和数列极限的描述性说法一样,这是一种描述性的说法.不是严格的数学定义.那么如何给出这类函数极限的精确定义呢?作如下分析:“当自变量越来越接近于时,函数值越来越接近于一个定数A”只要充分接近,函数值和A的相差就会相当小欲使相当小,只要充分接近就可以了.即对,当时,都有.此即.2.时函数极限的定义定义2设函数在点的某个空心邻域内有定义,A为定数,若对任给的,使得当时有,则称函数当趋于时以A为极限(或称A为时的极限),记作或(.3.说明如何用定义来验证这种类型的函数极限4.函数极限的定义的几点说明:(1)是结论,是条件,即由推出.(2)是表示函数与A的接近程度的.为了说明函数在的过程中,能够任意地接近于A,必须是任意的.这即的第一个特性——任意性,即是变量;但一经给定之后,暂时就把看作是不变的了.以便通过寻找,使得当时成立.这即的第二特性——暂时固定性.即在寻找的过程中是常量;另外,若是任意正数,则均为任意正数,均可扮演的角色.也即的第三个特性——多值性;()(3 是表示与的接近程度,它相当于数列极限的定义中的N.它的第一个特性是相应性.即对给定的,都有一个与之对应,所以是依赖于而适当选取的,为此记之为;一般说来,越小,越小.但是,定义中是要求由推出即可,故若满足此要求,则等等比还小的正数均可满足要求,因此不是唯一的.这即的第二个特性——多值性.(4)在定义中,只要求函数在的某空心邻域内有定义,而一般不要求在处的函数值是否存在,或者取什么样的值.这是因为,对于函数极限我们所研究的是当趋于的过程中函数的变化趋势,与函数在该处的函数值无关.所以可以不考虑在点a的函数值是否存在,或取何值,因而限定“”.(5)定义中的不等式;.从而定义2,当时,都有,使得.(6)定义的几何意义.例1.设,证明.例2.证明1);2).例3.证明.例4.证明.练习:1)证明; 2)证明.三、单侧极限1.引言有些函数在其定义域上某些点左侧与右侧的解析式不同,如或函数在某些点仅在其一侧有定义,如.这时,如何讨论这类函数在上述各点处的极限呢?此时,不能再用前面的定义(讨论方法),而要从这些点的某一侧来讨论.如讨论在时的极限.要在的左右两侧分别讨论.即当而趋于0时,应按来考察函数值的变化趋势;当而趋于0时,应按来考察函数值的变化趋势;而对,只能在点的右侧,即而趋于0时来考察.为此,引进“单侧极限”的概念.2.单侧极限的定义定义3设函数在内有定义,A为定数.若对任给的,使得当时有, 则称数A为函数当趋于时的右极限,记作或或.类似可给出左极限定义(,,或或).注:右极限与左极限统称为单侧极限.3.例子例5讨论在的左、右极限.例6讨论函数在处的单侧极限.4.函数极限与的关系.定理3.1.注:1)利用此可验证函数极限的存在,如由定理3.1知:.还可说明某些函数极限不存在,如由例2知不存在.2),,可能毫无关系,如例2.作业:P47. 1(3), (5), 3,7。


lim()x xf x A→= *点击以上标题可直接前往对应内容定理3.2(唯一性)证 不妨设以及 A x f x x =→)(lim 0.)(lim 0B x f x x =→由极限的定义,对于任意的正数 ,1δ存在正数,||010时当δ<-<x x (1),2|)(|ε<-A x f ,||020时当δ<-<x x )(lim 0x f x x →存在, 则此极限唯一.若 的基本性质 A x f xx =→)(lim 0,2δ,ε后退 前进 目录 退出(2) 式均成立,.|)(||)(|||ε<-+-≤-B x f x f A B A 由ε 的任意性,推得 A = B. 这就证明了极限是唯一的.12min{,},δδδ=令(1) 式与.2|)(|ε<-B x f (2)(1),2|)(|ε<-A x f 00||,x x δ<-<当时所以定理3.3(局部有界性)证 ,1=ε取.1|)(|<-A x f .1|||)(|+<A x f 由此得,)(lim 0A x f x x =→若上在)()(0x U x f,)(0x U则存在有界.这就证明了 在某个空心邻域 上有界.),(0δx U)(x f ,0>δ存在00x x δ<-<当时,注(1) 试与数列极限的有界性定理(定理 2.3)作一 (2) 有界函数不一定存在极限; 这上并不是有界的在但.)2,0(1,11lim )3(1xx x =→说明定理中 “局部” 这两个字是关键性的.比较;定理3.4(局部保号性)则对任何正数)(A r A r -<<或使得存在,)(,0x U.)0)((0)(<-<>>r x f r x f 或.|)(|ε<-A x f .)(r A x f >->ε由此证得 有对一切,)(0x U x∈有时,当δ<-<||00x x 证 不妨设 0.A >,)0(0)(lim 0<>=→或A x f x x 若 ,0>δ存在,r A -=ε取 (0,),r A ∈对于任何定理3.5(保不等式性))(lim )(lim 0x g x f x x x x →→与设则内有且在某邻域,)()()(0x g x f x U ≤).(lim )(lim 0x g x f x x x x →→≤证 0lim (),lim (),x x x x f x A g x B →→==设;)(ε->A x f 有时而当,||020δ<-<x x .)(ε+<B x g 分别存在正数 12,,δδ有 都存在,0,ε>则对于任意使当 010||x x δ<-<时, 满足时则当令,||0,},min{021δδδδ<-<=x x ,)()(εε+<≤<-B x g x f A所以证得是任意正数因为从而有,.2εε+<B A .B A ≤定理3.6(迫敛性)lim ()lim (),x x x x f x g x A →→==设0x 且在的某个空心).()()(x g x h x f ≤≤.)(lim 0A x h x x =→那么证 因为 00lim ()lim (),x x x x f x g x A →→==有时当,||00δ<-<x x (),A f x A εε-<<+().A g x A εε-<<+.)()()(εε+<≤≤<-A x g x h x f A 再由定理的条件,又得这就证明了 0)(x x h 在点的极限存在,并且就是 A .0,ε>所以对于任意,0>δ存在0()U x 邻域内有定理3.7(四则运算法则);)(lim )(lim )]()([lim )1(0x g x f x g x f x x x x x x →→→±=±;)(lim )(lim )()(lim )2(000x g x f x g x f x x x x x x →→→⋅=g f g f ⋅±,在点 x 0 的极限也存在, 且都存在, ,0)(lim )3(0≠→x g x x 又若在点 x 0 的极限也存在,g f则.)(lim )(lim )()(lim 00x g x f x g x f x x x x x x →→→=并有,)(lim 0x f x x →若)(lim 0x g xx → 则§2 函数极限概的性质A x f x x =→)(lim 0范例这个定理的证明类似于数列极限中的相应定理, 这就可以知道这些定理是显然的.里将证明留给读者. 在下一节学过归结原则之后, 的基本性质 A x f xx =→)(lim 0的基本性质 §2 函数极限概的性质A x f xx =→)(lim 0范例arctan lim x x x→+∞πlim arctan ,2x x →+∞=因解为例1 .arctan limxxx ∞+→求002=⋅=π范例1lim 0,x x →∞=所以1=lim arctan lim x x x x →+∞→+∞⋅例 2 .1lim 0⎥⎦⎤⎢⎣⎡→x x x 求有时又当,0<x 0>x 当,11lim )1(lim 00==-++→→x x x 由于,111x x x -≤⎥⎦⎤⎢⎣⎡<于是求得.11lim 0=⎥⎦⎤⎢⎣⎡→x x x 解 由取整函数的性质, .1111xx x ≤⎥⎦⎤⎢⎣⎡<-时, 有 ,111≤⎥⎦⎤⎢⎣⎡<-x x x 因此由迫敛性得 ;11lim 0=⎥⎦⎤⎢⎣⎡+→x x x 同理得 .11lim 0=⎥⎦⎤⎢⎣⎡-→x x x例 3 求极限 π4lim(tan 1).x x x →-π4lim tan tan1,4x x π→==解 因为所以π4ππlim(tan 1)11 1.44x x x →-=⋅-=-例4 .)1(1lim 0>=→a a xx 求证特别又有.1111εε+<<<--NNa a ,1N=δ取,|0|0时当δ<-<x ,1111εε+<<<<--NxNa a a .1lim 0得证即=→xx a 证 ,11lim ,1lim ==∞→∞→n n nn aa 因为所以 ,,0N ∃>∀ε有时当,N n ≥,1111εε+<<<--nna a复习思考题1. lim (), lim (),x x x x f x a g x →→=设存在不存在试问02. lim (),lim (),x x u u g x u f u A →→==设这时是否必有lim (())?x x f g x A →=0lim ()()?x x f x g x →极限是否必定不存在。







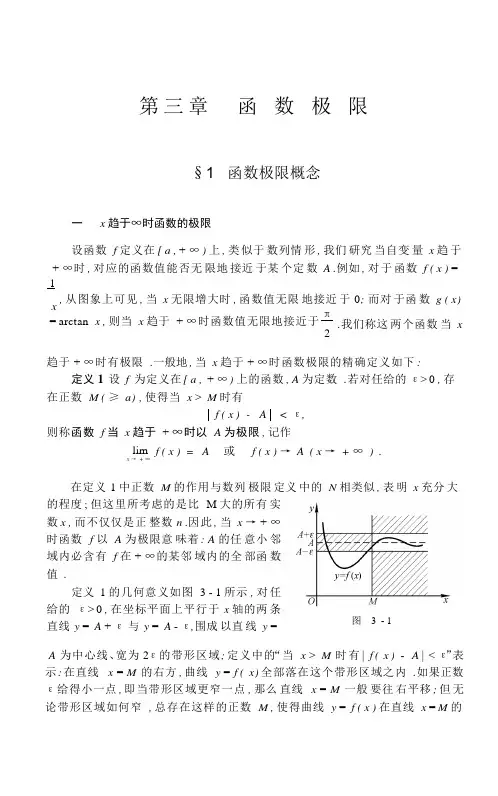
第 三 章 函 数 极 限§1 函数极限概念一 x 趋于∞时函数的极限设函数 f 定义在 [ a , + ∞ ) 上 , 类 似于 数列情 形 , 我们 研究 当自变 量 x 趋 于 + ∞时 , 对应的函数值能否无 限地 接近 于某 个定 数 A .例如 , 对 于 函数 f ( x ) =1x, 从图象上可见 , 当 x 无限增大时 , 函数值无限 地接近 于 0; 而对 于函 数 g ( x) = arctan x , 则当 x 趋于 + ∞时函数值无限地接近于 π2 .我们称这 两个函数 当 x趋于 + ∞时有极限 .一般地 , 当 x 趋于 + ∞时函数极限的精确定义如下 :定义 1 设 f 为定义在 [ a , + ∞ ) 上的函数 , A 为定数 .若对任给的 ε> 0 , 存 在正数 M ( ≥ a) , 使得当 x > M 时有f ( x ) - A < ε,则称函数 f 当 x 趋于 + ∞时以 A 为极限 , 记作lim x → + ∞f ( x ) = A 或 f ( x ) → A ( x → + ∞ ) .在定义 1 中正数 M 的作用与数列 极限 定义 中的 N 相类似 , 表 明 x 充分 大 的程度 ; 但这里所考虑的是比 M 大的所有 实 数 x , 而不仅仅是正 整数 n .因 此 , 当 x → + ∞ 时函数 f 以 A 为极限意 味着 : A 的任 意小 邻 域内必含有 f 在 + ∞的某邻 域内的全 部函 数 值 .定义 1 的几何意义如图 3 - 1 所示 , 对 任 给的 ε> 0 , 在坐标平面上平行于 x 轴的两 条 直线 y = A + ε与 y = A - ε, 围成 以直 线 y =图 3 - 1A 为中心线、宽为 2ε的带形区域 ; 定义中的“当 x > M 时 有 | f ( x ) - A | < ε”表 示 : 在直线 x = M 的右方 , 曲线 y = f ( x) 全部落在这个带形区域之内 .如果正数 ε给得小一点 , 即当带形区域更窄一点 , 那么 直线 x = M 一般 要往 右平移 ; 但 无 论带形区域如何窄 , 总存在这样的正数 M , 使得曲线 y = f ( x ) 在直线 x = M 的§1 函数极限概念 43右边部分全部落在这更窄的带形区域内 .现设 f 为定义在 U( - ∞ ) 或 U ( ∞ ) 上的 函数 , 当 x → - ∞ 或 x →∞ 时 , 若 函数值 f ( x ) 能无限地接近某定数 A , 则称 f 当 x → - ∞或 x → ∞时 以 A 为 极 限 , 分别记作lim x → - ∞ lim x → ∞f ( x ) = A 或 f ( x ) → A ( x → - ∞ ) ;f ( x) = A 或 f ( x) → A ( x → ∞ ) .这两种函数极限的精确定义与 定义 1 相 仿 , 只 须把 定义 1 中 的“ x > M ”分别 改 为“ x < - M ”或“ | x | > M ”即可 .读者不难证明 : 若 f 为定义在 U ( ∞ ) 上的函数 , 则lim x → ∞f ( x) = A ! lim x → + ∞f ( x ) = lim x → - ∞f ( x ) = A .( 1)例 1 证明 lim 1= 0 .x → ∞x证 任给 ε> 0 , 取 M = 1ε, 则当 | x | > M 时有所以 l im 1= 0 .1 1 x - 0 =x<1 M= ε, x → ∞x例 2 证明 : 1) limarctan x = - π; 2) lim arctan x = π. x → - ∞证 任给 ε> 0 , 由于2x → + ∞2arctan x --π 2< ε( 2)等价于 - ε-π < arctan x < ε- π, 而此不等式的左半部分对任 何 x 都 成立 , 所 2 2以只要考察其右半部分 x 的变化范围 .为此 , 先限制 ε< π, 则有2x < tan ε - π 2 = - tan π2 - ε .故对任给的正数 ε <π 2 , 只须 取 M = tan π- ε , 则 当 x < - M 时 便有 ( 2) 2式成立 .这就证明了 1 ) .类似地可证 2 ) .注 由结论 (1 ) 可知 , 当 x →∞时 arctan x 不存在极限 .二 x 趋于 x 0 时函数的极限设 f 为定义在点x0 的某个空心邻域U°( x0 ) 内的函数.现在讨论当x 趋于x0 ( x≠x0 ) 时, 对应的函数值能否趋于某个定数 A .这类函数极限的精确定义如下:2 044第三章 函 数 极 限定义 2 ( 函 数 极 限 的 ε - δ 定 义 ) 设 函 数 f 在 点 x 0 的 某 个 空 心 邻 域 U °( x 0 ;δ′) 内有定义 , A 为定数 .若对任给 的 ε> 0 , 存在正数 δ( < δ′) , 使得当 0 < | x - x 0 | < δ时有f ( x ) - A < ε, 则称函数 f 当 x 趋于 x 0 时以 A 为极限 , 记作lim x → xf ( x) = A 或 f ( x) → A ( x → x 0 ) .下面我们举例说明如何应 用 ε- δ定义 来验 证 这种 类型 的函 数极 限 .请 读 者特别注意以下各例中 δ的值是怎样确定的 .例 3 设 f ( x) = x- 4 , 证明lim f ( x) = 4 .x - 2证 由于当 x ≠ 2 时 ,2x → 2 f ( x) - 4 =x - 4x - 2- 4 = x + 2 - 4 = x - 2 ,故对给定的 ε> 0 , 只要取 δ= ε, 则当 0 < | x - 2 | < δ时 有 | f ( x ) - 4 | < ε .这 就 证明了lim f ( x ) = 4 .x → 2例 4 证明 : 1) lim sin x = sin x 0 ; 2 ) lim cos x = cos x 0 .x → xx → x证 先建立一个不等式 : 当 0 < x < π时有2sin x < x < tan x . ( 3)事实上 , 在如图 3 - 2 的单位圆内 , 当 0 < x < π时 , 显 然2有S △ O A D < S 扇 形 O A D < S △ O AB ,1 2 sin x < 12 x < 1 2 tan x , 由此立得(3 ) 式 . 图 3 - 2又当 x ≥π时有 sin x ≤1 < x , 故对一切 x > 0 都有2sin x < x; 当 x < 0 时 , 由 sin ( - x) < - x 得 - sin x < - x .综上 , 我 们又得到 不 等式sin x ≤ x , x ∈ R ,( 4)其中等号仅当 x = 0 时成立 .现证 1) . 由 ( 4) 式得sin x - sin x 0 = 2 cosx + x 02sinx - x 0≤ x - x .2对任给的 ε> 0 , 只要取 δ= ε, 则当 0 < | x - x 0 | < δ时 , 就有sin x - sin x 0< ε .即0 1 - x 2 -1 - x 0 2或 等 § 1 函数极限概念 45所以 lim sin x = sin x 0 . 2) 的证明留给读者作为练习。
0sin lim 1x x x →=1lim 1e xx x →∞⎛⎫+= ⎪⎝⎭*点击以上标题可直接前往对应内容)1(.cos 1sin 1xx x <<不等式中的三个表达式均是偶函数, 证πsin tan 0,2x x x x ⎛⎫<<<< ⎪⎝⎭因为所以命题1π0||12x <<时,()式仍成立.后退前进目录退出x 故当sin lim 1x xx →=001lim =1=lim =1cos x x x →→=因为,0lim 1,sin x xx →=所以0sin lim 1.x xx →=即πsin lim πx x x →-解π,t x =-令所以例1 求πsin lim .πx xx →-()sin sin πsin ,x t t =+=-则0sin lim 1.t t t→-==-例2.arctan lim 0x xx →求x x x arctan lim 0→arctan ,tan ,t x x t ==令解.cos 1lim 20xxx -→求例3解2202sin 2lim xx x →=.21=20cos 1lim x x x -→2022sin 21lim ⎪⎪⎪⎭⎫ ⎝⎛=→x x x t t t tan lim 0→=t t tt t cos lim sin lim 00→→⋅=1=则命题2e 11lim =⎪⎭⎫ ⎝⎛++∞→xx x .e 11lim =⎪⎭⎫ ⎝⎛+∞-→xx x 和证我们只需证明:();,2,1,1,111 =+<≤⎪⎭⎫ ⎝⎛++=n n x n n x f n 设两个分段函数分别为1lim 1exx x →∞⎛⎫+= ⎪⎝⎭().,2,1,1,111=+<≤⎪⎭⎫ ⎝⎛+=+n n x n n x g n显然有()().),1[,11∞+∈≤⎪⎭⎫⎝⎛+≤x x g x x f x因为(),e 111lim lim =⎪⎭⎫ ⎝⎛++=∞→+∞→nn x n x f (),e 11lim lim 1=⎪⎭⎫ ⎝⎛+=+∞→+∞→n n x n x g 所以由函数极限的迫敛性,得到1x§4 两个重要的极限sin lim 1x x x →=.e 11lim =⎪⎭⎫ ⎝⎛+∞→xx x 这就证明了())3(.e 1lim 1=+→t t t 注,1xt =若令由此可得在实际应用中,公式(2)与(3)具有相同作用..e 111111lim 11lim 1=⎪⎭⎫ ⎝⎛-+⎪⎭⎫ ⎝⎛-+=⎪⎭⎫ ⎝⎛+-+∞→-∞→y y x y y xx .0,→∞→t x 时则1lim 1e xx x →∞⎛⎫+= ⎪⎝⎭.1111111xy y x ⎪⎭⎫ ⎝⎛-+=⎪⎭⎫ ⎝⎛-=⎪⎭⎫ ⎝⎛+所以时,因为当,+∞→-∞→y x解),3(由公式例4xx x 1)21(lim +→求()10lim 12xx x →+()2120=lim 12xx x →⎡⎤+⎢⎥⎣⎦2e .=例51lim(1)xx x →-求解()10lim 1xx x →-()110=lim 1xx x --→⎡⎤-⎢⎥⎣⎦1e .-=,01,e 11lim 2→-⎪⎭⎫ ⎝⎛+∞→n n n nn =而.e 11lim 122=⎪⎭⎫ ⎝⎛-+-∞→n n n n n 所以由归结原则,.111lim 2nn n n ⎪⎭⎫ ⎝⎛-+∞→求例6解因为2111nn n ⎛⎫+- ⎪⎝⎭1122211111---⎪⎭⎫ ⎝⎛-+=⎪⎭⎫ ⎝⎛-+n nn n nn n n n .112122--⎪⎭⎫ ⎝⎛-+≥n n n n 11e,nn ⎛⎫<+→ ⎪⎝⎭.e 111lim 2=⎪⎭⎫ ⎝⎛-+∞→nn n n 再由迫敛性, 求得。